A Review on Stability Analysis of Roadbed Slope and Prevention Technologies

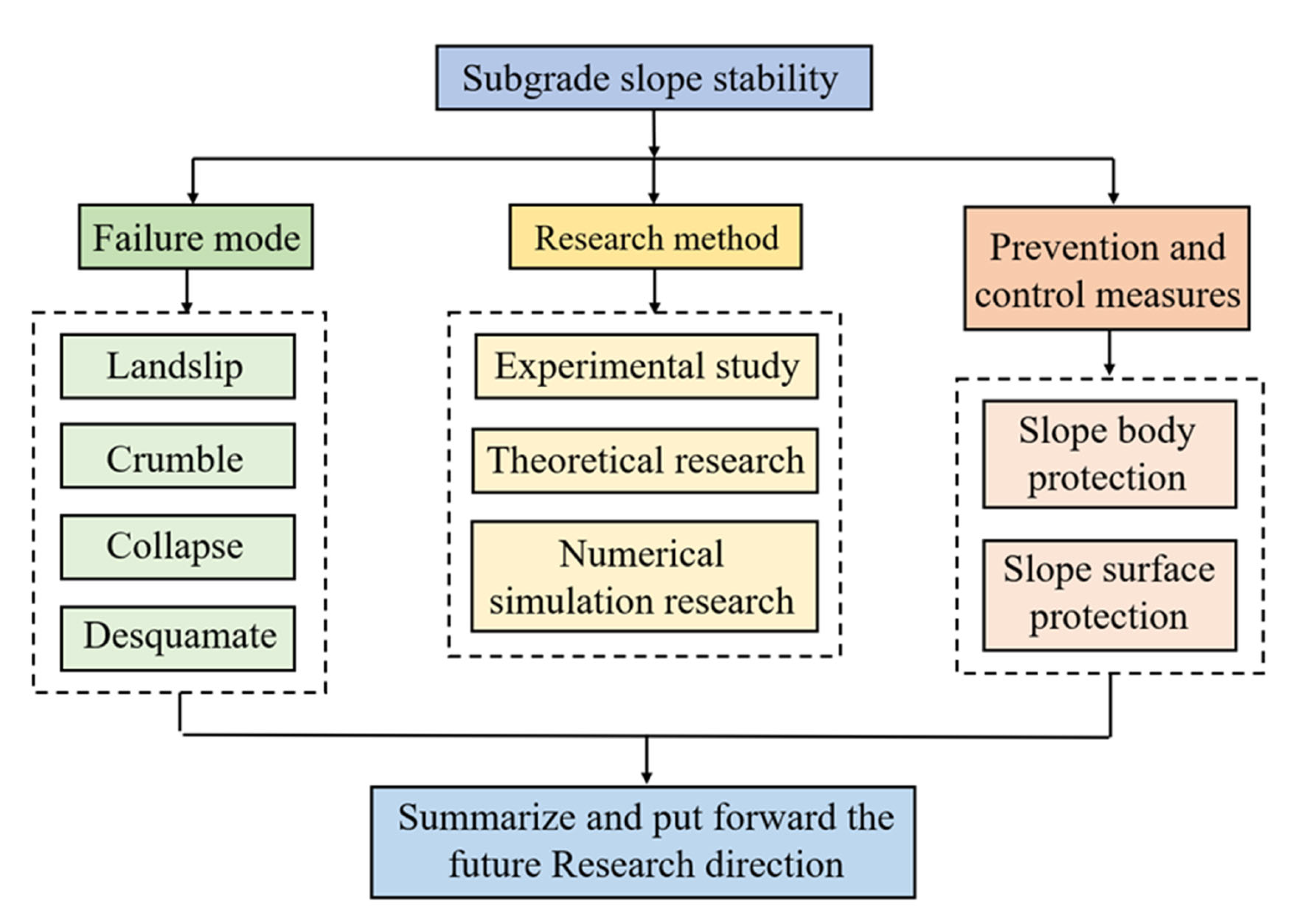
1. Introduction

With the rapid development of China’s highway business, as of the end of 2022, the total mileage of China’s highways is 5,354,800 kilometers, and highway construction will inevitably involve a large number of slope engineering problems. With the expansion and development of the scale of the new round of economic construction, the slope engineering disaster problems in the form of landslides will become more and more prominent [1]. A large number of slope engineering disaster problems often lead to an increase in the cost of construction and the delay of the construction period, and some even during the operation of the project there are potential hazards, bringing serious impacts to the construction projects and even threatening the safety of human life. Therefore, it becomes especially important to study the slope stability. In recent years, many scholars have conducted a series of studies on the stability of roadbed slopes, and KARDANI N et al. [2] indicated that rainwater infiltration, snow melting, glacial melting, groundwater rise, physical and chemical weathering of geotechnical bodies, and ground vibration caused by earthquakes or human activities may cause damage to slopes either individually or jointly. SUMAN S et al. [3] showed that whether a slope is stable or not is basically controlled by the ratio of effective shear strength to the acting shear stress, in addition, several key parameters such as slope geometry (height and slope angle), shear strength parameters (angle of internal friction and cohesion), pore water pressure, and soil properties (unit weight and degree of saturation) play a crucial role in slope stability. Lv Qing [4] concluded that the slope stability analysis methods can be divided into four categories: bar division method, limit analysis method, slip line method, and numerical analysis method. Among them, the most widely used slope stability analysis method in engineering practice is the strip partition method. The strip partition method is characterized by treating the landslide body as a rigid body, adopting the Moore-Coulomb damage criterion on the hypothetical slip surface, considering only the static equilibrium conditions, and solving the problem by analyzing the equilibrium of forces of the landslide body in the limit equilibrium state. Gordan et al. [5] evaluated the stability of slopes under the effect of earthquakes using artificial neural networks and particle swarm optimization. Qi et al. [6] conducted a comparative study of integrated meta-heuristics and machine learning methods, including logistic regression, decision trees, random forests, support vector machines, multilayer perceptron artificial neural networks and gradient propulsion machines Bishop [7] firstly, by proposing the definition of the safety coefficient, and then by assuming that the force between the soil strips is in the horizontal direction to find out the normal force between the soil strips, which makes an important improvement to the traditional Fellenius method has made important improvements and modeled a simplified method. Among them, both the Swedish arc method and Bishop’s method determine the safety factor by moment balance. Fell and Anlalagan R and Singh B et al. [8,9] applied the improved method of risk evaluation to landslide geohazards and discussed issues such as guidelines for acceptable risk, and used the zoning map of landslide geohazards to evaluate the potential risk of landslide hazards, and based on the fuzzy set theory, the potential risk indicator of each shadow was calculated for each factor. factors to calculate the potential risk index. In summary, for the research of roadbed slope stability, rich research results have been achieved at home and abroad. Researchers at home and abroad start from the type of slope damage, and use a variety of research methods to explore the stability of slopes, however, due to the limitations of experimental conditions, there are advantages and disadvantages of all types of research methods. In the stability study of slopes, the most important thing is to determine the advantages and disadvantages of the research method and the scope of application, so that it can be more accurately applied to the slope stability research method. The factors affecting slope stability are divided into internal and external factors, and a comprehensive analysis of the factors affecting slope stability is of great significance to the field of road engineering, and it is also conducive to the proposal of more efficient measures to prevent and control slope damage.

This paper integrates the existing forms of slope damage, summarizes the types and advantages and disadvantages of current research methods from both experimental and theoretical aspects, deeply analyzes the role of internal and external factors of slope stability, and explores the effective measures of slope protection and slope protection. The overall goal of this paper is to sort out the existing research results in the field of roadbed slopes and provide theoretical support for possible future research. The research content of this review is shown in Figure 1.

2. Forms of Slope Failure

Roadbed slope damage forms are mainly controlled by the engineering geological conditions of the rock body, especially the structural surface of the rock body, which will produce various forms of damage under the coupled influence of a variety of internal and external factors, in order to ensure the safety and stability of the road, it is necessary to sort out and summarize the damage forms of roadbed slopes, and to promote the proposal of efficient prevention and control measures for roadbed slopes. Roadbed slope damage often occurs on the basis of deformation, when the deformation reaches an irreversible degree, so that the displacement, cracks and inclination of the geotechnical body increases significantly and reaches the critical threshold, the original function or structural integrity of the slope is destroyed, unable to withstand the original load or external influence, and then the slope collapse, landslide, collapse and other phenomena. Specific forms of slope damage can be divided into the following four forms.

2.1. Landslides

As the most important type of slope engineering problems, landslide problems are also the most studied slope engineering disasters by scholars. People’s concern and research on slope stability first started from the landslide phenomenon. Slope stability analysis and evaluation is also the core of landslide research. Landslide refers to the phenomenon of continuous sliding or flowing of a local or whole geotechnical body along a certain line or surface due to the destabilization of the geotechnical body by internal or external factors [10], as shown in Figure 2.

Landslides are one of the most frequent and hazardous geological disasters, especially in areas with soft soil, humid climate and frequent earthquakes [10]. Landslide susceptibility evaluation refers to qualitatively or quantitatively evaluating the possibility of landslides according to the landslide database, topography, meteorology and hydrology, and other basic geologic environment and disaster-preventing conditions within the regional scale, and obtaining the spatial distribution of potential landslides. Since the 1870s, scholars at home and abroad have conducted a lot of research on landslide susceptibility evaluation. Van Westen et al. [11] evaluated landslide susceptibility using bivariate statistical analysis method of geographic information statistics (GIS) software with an area in Italy as the research object. Herrera et al. [12] used GB-SAR to obtain the deformation time series of the Portlet landslide located in central Spain, and corrected the parameters of the one-dimensional infinite slope model with a series of monitoring data, and derived a model that integrates the clay-plastic properties of the landslide rock and soil bodies, as well as the intensity of the daily rainfall and the amount of dissipation of the superporous water pressure, and used the corrected model for the deformation prediction of landslides. Meanwhile, better prediction results were achieved. Sun et al. [13] inverted the parameters of Sanmendong landslide in the Three Gorges reservoir area based on a finite element model and then used the inverted parameters to predict the deformation of Sanmendong landslide under different boundary conditions; Zhao et al. [14] further considered the creep characteristics of the landslide geotechnical body and predicted the deformation of the Huangniba landslide in the Three Gorges Reservoir Area using the Singh-Mitchell creep model simulation in the finite element software. Tang et al. [15] carried out seepage and stability calculations based on the finite element method for the reservoir bank landslide with different slip surface morphology, permeability coefficients, reservoir water level change rate, and bank slope inundation area, and finally obtained the mechanism law of the destabilizing hydraulic action of the reservoir bank landslide. Paronuzzi et al. [16] used the finite element method and limit equilibrium method to invert the landslide of Vaion Reservoir, Italy, and the results showed that the main triggering factor of the landslide was the rapid increase of the water table at the foot of the landslide due to the reservoir storage, which led to the reduction of the effective stress in the anti-slip section, and the stability of the landslide was reduced by 12% after the storage of the water compared with the pre-storage period.

2.2. Crumble

A landslide is a geological phenomenon in which part or all of the soil body suddenly collapses, tilts, or slides because the slope is affected by external factors, causing the bottom to be crushed, fractured, or generating localized slippage [17], thus losing its original stability. Avalanche is also one of the common forms of slope damage, but it occurs on a smaller scale, with a small degree of damage, and may form mudslides during the accumulation process.

As early as the 1960s, research scholars at home and abroad conducted relevant studies on the vulnerability of collapse disasters [18,19,20,21,22]. However, in the early stage of the research, due to the limitations of technology and other aspects, most of the scholars focused on qualitative evaluation, which mainly included hierarchical analysis method, multi-criteria analysis method, and so on. With the rapid development of computer technology, remote sensing technology, and GIS technology, the research work of collapse disaster analysis has become more convenient and precise. Shi Genhua and Goodman et al. [23,24] proposed a new method to analyze the stability of rocky slopes—block theory, the main purpose of this method is to identify the key blocks, so as to determine the potential collapse area, which provides the basis for collapse monitoring and forecasting. Clough A.K [25] introduced a variable factor of safety based on the traditional limit equilibrium method by defining a special curve to reflect the site-specific boundary conditions; Bishop [26] modified the slope failure bar-splitting method by assuming that the slope sliding surface is a circular arc and satisfying both the moment equilibrium condition as well as the force equilibrium condition in the vertical direction, but still failing to meet the the external force equilibrium condition in the horizontal direction.

2.3. Collapse

Collapse refers to the geological phenomenon of sudden subsidence or collapse of the ground or structures due to partial or total loss of the original stability of the surface or underground structures under the action of external forces or under the action of self-weight, which has the characteristics of landslides and avalanches at the same time. Highway roadbed slope collapse is a common roadbed disease, highway slope collapse disaster is inevitable. After the slope collapse, it is generally necessary to clear the square and reset the protection. After removing the collapsed loose squares, the slope of the normal section is steeper, while the slope of the collapsed section is slower, which often produces the problem of gradual change of slope rate between the slope of the collapsed section and the slope of the normal section [28].

The causes of roadbed slope collapse are more [28], but categorized from the perspective of slope form, it can be roughly divided into two categories. The first category is the fill slope, in which there are three main reasons for the collapse: respectively, the poor geological environment of the fill section makes the foundation soil easy to be damaged, the existence of unreasonable engineering design program, and the damage caused by external factors. The other category is the excavation slope, and there are also three collapse forms of such slopes: rockfall type collapse, sliding type collapse, and flow type collapse [29]. Zhang Baolong [30] combined with the actual situation of slope damage at K368 of Huji Expressway, analyzed and determined that poor slope drainage is the main reason for slope damage, while using the method of finite element modeling and calculation, established a model that considers two kinds of models of slope ground water seepage or not, and the results obtained through the calculations are highly consistent with the actual situation of slope sliding slumps, so as to determine the management plan of slope disease in this case. Qin Shujuan [31] combined with a mountainous highway slope collapse case in China, the method of reinforced geogrid repair and reinforcement, and accordingly formed a relevant reinforcement program to guide the construction, and post-construction monitoring, the results proved that the reinforced slopes can be effective in reinforcing slopes.

2.4. Flake

Spalling is a phenomenon in which the surface of a slope is gradually loosened by weathering or other adverse weather conditions and is dislodged by gravity or rainfall. Spalling is random in nature, and the dislodged stones or soil clods may pose a threat to oncoming people or vehicles, or accumulate on the road surface to affect safe driving on the road. Ye Wanjun et al. [32] carried out macroscopic crack analysis and indoor straight shear test on soil specimens under different water content states to investigate the effect of water content state of loess body on slope spalling disease. The results showed that with the increase of the number of dry and wet cycles and cycle amplitude, the surface cracks of the soil specimens continued to expand and extend, and the degree of internal structural damage increased, and the spalling disease occurred along the dominant surface when a dominant surface inside the soil body was penetrated.

Xu Jian et al. [33] studied the mechanism and stability of freeze-thaw spalling disease on loess slopes through on-site research, indoor freeze-thaw test and calculation analysis. The study showed that the freeze-thaw spalling disease is divided into superficial freeze-thaw spalling, freeze-thaw laminar spalling and micro freeze-thaw collapse. And with the increase of the number of freeze-thaw, the cohesive force showed an exponential decay trend, and the angle of internal friction did not change significantly; with the increase of water content, the cohesive force showed a decreasing trend, and the angle of internal friction showed a linear decay characteristic.

3. Slope Stability Research Methods

China’s geological conditions are rich and complex, influenced by topographic and geomorphic features, slope stability has become one of the classical problems in geotechnical engineering. At present, many scholars have carried out a series of studies on roadbed slope stability, including experimental studies [34], theoretical studies [35] and numerical simulation [36] studies. Among them, the experimental study mainly investigates in detail the change rule of geotechnical parameters of slope geotechnical body under different conditions through experiments; the theoretical analysis mainly establishes the geotechnical body’s constitutive equation or mechanical model involving various influencing factors; Numerical simulation research methods, such as finite element, mainly through the simulation of slope stability under a variety of influencing factors, to further provide data reference for the stability of roadbed slopes in the actual project [37].

3.1. Pilot Study

3.1.1. Indoor Pilot Studies

Indoor test is a universal method to analyze the destructive mechanism of slope stability and investigate the mechanical evolution behavior of slopes, and the indoor test realizes the targeted research on slope stability by artificially simulating the influence of the external environment and controlling the variables of technical parameters. Yao Ting [34] analyzed the effect of water content and freeze-thaw action on the shear strength of soil by conducting freeze-thaw test and direct shear test on pulverized clay. The study showed that the cohesion and internal friction angle of soil decreased with the increase of water content, and according to the test results, the relationship equation of the change of cohesion and internal friction angle with water content was obtained. Chamberlain [38] analyzed the effect of water content and freeze-thaw action on shear strength of soil by conducting indoor infiltration test. soil samples after crystallization-fusion by freeze-thaw machine, and the experiment concluded that both soil porosity and vertical permeability were affected by freeze-thaw cycle. Song F et al. [39] used a large triaxial test to study the effect of density of fill, strength and stiffness of the chamber and the height-to-diameter ratio of the specimen on the stress-strain of geocell-reinforced soil. Konrad et al. [40,41] concluded that the structure and effective porosity of pulverized clay will be changed under the action of freeze-thaw cycles, but will no longer be changed when experiencing the action of three to four freeze-thaw cycles; in addition, the shear strength, pore water pressure, and deformation characteristics of the soil will also be affected after experiencing the action of freeze-thaw cycles. Gao Chunjun [42] conducted a series of tests on slope instability caused by drainage pipes in order to find out the crystallization law of drainage pipes. Wang Yan [43] discussed the mechanical state of geocells under different slope rates, loading conditions, and precipitation conditions through the indoor tests of geocell protection of embankment slopes, and analyzed the role of geocells in the embankment slope protection system.

The study shows that the greater the slope rate, loading weight and precipitation, the more obvious the effect of geocell protection on the slope to reduce the displacement and disperse the soil pressure under the geocell. In general, although many scholars have carried out a lot of research on the stability of roadbed slopes through indoor tests and obtained valuable results, there is still a big gap between indoor conditions and materials and the actual site, which leads to a certain degree of deviation between the test results and the actual situation of slopes.

2.1.2. Model Test Studies

In order to further improve the precision and accuracy of the study, researchers have established slope models at different scales [44], all of which are mainly characterized by large-scale machines to simulate the outdoor conditions for testing. Cheng et al. [45] successfully developed a rainfall simulation equipment and analyzed the destabilization mechanism of slopes affected by rainfall based on centrifugal model tests. Zeng Wanfu [46] used a model test to simulate the change of slope seepage field in the process of water level descent, and found that with the acceleration of the rate of water level descent, the increase of water level difference, and the increase of slope ratio, the slope is more likely to be destabilized and damaged. Cai Jiale [47] obtained the way of macroscopic dominant infiltration as well as the trend of fissure extension evolution by using a model box test setup.

Meanwhile, the visualization model test can intuitively observe the change process of the geotechnical body, which is helpful for the mechanism explanation of various types of geotechnical problems [48]. Jingyun Gu et al. [49] developed a latent erosion visualization test equipment based on planar laser-induced fluorescence (PLIF) technology, and observed the particle movement inside the soil body. However, most of the modeling tests are for homogeneous slopes, which is difficult to adapt to natural slopes with mostly non-uniform media, in addition, it is difficult to control the accuracy of the external environment of the modeling tests in line with the actual situation.

2.1.3. Field Pilot Study

In situ tests are the most accurate and practical research tools in slope stability studies. Li Yaonan studied the rock mass of a slope at a site using in situ straight shear test to obtain the shear strength parameters of the rock mass and then evaluate the stability of the slope [50]. Wang Guangshuai investigated the feasibility and effectiveness of electrochemical method for reinforcing soft slopes in open pit coal mines through on-site reinforcement tests [51]. Liu Dongdong comprehensively used two research methods, field test and numerical simulation, to thoroughly explore the influencing factors of high slope stability during tunnel construction and analyzed the mechanical behavior of anti-slip piles in detail [52]. Shan et al. [53] summarized the manifestations of freeze-thaw landslides on road graben slopes in seasonal permafrost zones through field investigations of engineering geology and hydrogeology.

In view of the complexity and uncertainty of the actual engineering environment, the establishment of an intelligent remote monitoring and warning system has become an indispensable part of the current slope engineering construction. For example, with the help of the monitoring system of real aperture radar, the slope stability is accurately assessed for risk. These studies and practices have not only enriched the monitoring means of slope stability, but also provided strong technical support for engineering construction. However, it is difficult to control the boundary conditions of the field test, the monitoring physical quantities are significantly affected by environmental factors, and the relationship between the engineering properties of the geotechnical body and the slope stability needs to rely on a large amount of data, so how to efficiently and intelligently carry out the field test of the slope is one of the directions of the future research and development.

2.2. Theoretical Studies

Since most of the slopes are exposed in the field environment, which leads to extremely complicated slope destabilization process, how to predict slope destabilization in time and accurately judge the slope destabilization point is the key issue to improve the stability of slopes. With the deepening of theoretical research and long-term accumulation, three types of theoretical research methods are mainly formed: qualitative analysis, quantitative analysis and uncertainty analysis.

Qualitative analysis method is mainly based on professional experience and engineering common sense, analyzing the slope stability state and slope destabilization factors through geological exploration, which provides an important reference for the subsequent quantitative analysis. Gao et al. studied the rocky slope stability with the help of engineering geological analogy method [54]. However, the engineering geological analogy method requires more engineering experience accumulation, and is more specialized and subjective. Liu and Wang [55] analyzed the effect of soil inhomogeneity on permafrost slope characteristics under freeze-thaw cycles using the local average subdivision method.Azarafza et al. analyzed the application of expert system method in slope failure modeling and assessment [56].

The quantitative analysis method is to quantify and analyze the parameters of the slope by establishing an engineering mechanics model and applying the principles of engineering mechanics, so as to derive the specific indexes of slope stability, such as the coefficient of safety. Quantitative analysis method can provide more data support and more technical support for the construction of slope engineering. In the quantitative analysis method, the limit equilibrium method, as an important quantitative analysis method, is applied by the majority of scholars. The limit equilibrium method is mainly based on the principle of mechanical equilibrium to determine the potential sliding surface of the slope, and then get a reasonable slope safety coefficient. The main methods of limit equilibrium method include Fellenius method, Bishop method, Janbu method, Spencer method, Morgenstem-Price method and so on. Kalatehjari et al. [58] gave a calculation method for determining the sliding direction, which is able to eliminate the limitations of various methods for calculating the sliding direction and improve the convergence, and this method can be applied in various 3D limit equilibrium methods. Wan et al. [59] proposed a simplified method based on Spencer’s method to evaluate the stability of three-dimensional asymmetric slopes. The method assumes that the sliding direction is unique and satisfies the force balance in three directions and the moment balance in two directions, and the computational study of two asymmetric examples concludes that the slope stability will be overestimated if the unique sliding direction is ignored. This shows that the limit equilibrium method is universal in the field of slope stability study.

Uncertainty analysis method is based on the survey technology to obtain the data of slope geotechnical body, and use the uncertainty principle and method to calculate the slope stability. Uncertainty analysis includes reliability analysis, fuzzy mathematical analysis, gray system analysis, neural network analysis, genetic algorithm, cluster analysis and machine learning, etc. It is one of the ideal theoretical analysis methods to combine as many slope stability influencing factors as possible. Griffiths et al. [60] analyzed the stability of slopes under different working conditions based on the finite element strength discount method, and compared and analyzed the test results with the limit equilibrium method to further verify the feasibility of the proposed method. Li et al. [61] studied and analyzed the stability of rocky slopes based on the Hoek-Brown criterion using the finite element limit analysis method, and finally obtained dimensionless slope stability coefficients and safety coefficients.

The above three methods are the most commonly used theoretical research methods at present, but the actual situation of the slope is complex and changeable, and the scope of application and advantages and disadvantages of each analysis method should be fully considered in the process of practical application, as shown in Table 1.

The actual situation of slope engineering is complex and variable, and a single analysis and evaluation method is often difficult to comprehensively respond to the actual problem. Therefore, in the study of slope stability, according to the characteristics and complexity of the specific slope, a variety of analytical methods are used to accurately determine the evolution status and trend of the geotechnical body, so as to improve the stability and safety of slope engineering.

2.3. Numerical Simulation Studies

Numerical analysis method is the mainstream analysis method in geotechnics as compared to limit equilibrium method in addition to calculating the stability coefficient of the slope, it can also derive the displacement, strain and stress distribution of the slope. The advantages and disadvantages of different numerical methods are shown in Table 2. The finite element method (FEM) is currently the most common numerical simulation method. FEM can effectively deal with the non-homogeneity and discontinuity problems of slopes, and realize the equivalent system conversion between infinite and finite degree of freedom structures; FEM is not only excellent in linear analysis, but also suitable for nonlinear analysis, which is suitable for almost all computational fields. In addition to this, the method can approximate the critical points where the slope is most susceptible to yielding damage as well as the need for reinforcement, and simulate the interaction mechanism between the geotechnical body and the supporting structure. Kim and Lee et al. [65] analyzed the stress field distribution pattern during the deformation process occurring in the slope and finally derived the safety factor of the slope. Su et al. [66] analyzed the effect of vibration on high slopes subjected to vibration in staged excavation based on FLAC software, and proved that the support works can increase the slope stability under this condition. Wang Rui [67] developed a series of modules based on FLAC3D software Fish language programming from the principle of saturated-unsaturated seepage, including the unsaturated seepage analysis module, unsaturated zone shear strength modification module and rainfall infiltration boundary function module, and used the module to carry out the analysis of seepage and transient stability of saturated and unsaturated slopes in the rainfall process. The analysis method takes into account the influence of seepage in saturated and unsaturated slopes, and provides a reference basis for engineering design and construction.

However, there are still some limitations of the finite element method in practical engineering. One of the main problems is that it is very sensitive to the selection of physical parameters, which may have a large impact on the analysis results. In addition, the finite element method also has some difficulties in dealing with problems such as large deformations and stress concentrations, which need to be further improved and optimized. Compared with the finite element method, the boundary element method (BEM) is able to reduce the dimensionality of the problem to be solved, which can model two-dimensional problems into one-dimensional ones, and three-dimensional problems into two-dimensional ones [68]. Therefore, the boundary element method has a high solving efficiency. The base variables of the boundary element method are the boundary variables, and all other variables can be obtained by solving the base variables.

The discrete element method (DEM) is an emerging method that has attracted much attention in recent years in the study of slope stability, and it is capable of analyzing the damage mechanism of slopes more accurately. By taking into account the discontinuities and interactions of the rock and soil, the discrete element method is able to simulate the deformation and damage process of the rock and soil in a finer way, and thus the stability of the slope can be assessed more accurately. Li X et al. [69] used DEM to numerically simulate a homogeneous cohesive soil constituting a slope using contact-bonded graded aggregates with diameters ranging from 80-160 mm to simulate cohesive soils, and investigated microcrack extensions, particle displacements, particle motions, and porosity variations within the slope fill. The simulation results show that the failure mechanism is a rotational mechanism at the beginning stage and gradually changes to a sliding/flow mode as the failure occurs; In addition to this, the sediment porosity increases significantly due to swelling and block voiding. However, it should be noted that there are some challenges in the use of the discrete element method, one of which is the high requirement for the accuracy of the initial parameters and boundary conditions of the geotechnical soil.

3. Slope Damage Prevention and Control Measures

The stability of roadbed slopes plays a key role in the safe and smooth flow of highways. However, slope problems occur from time to time, giving the passage of the highway buried a huge safety hazard, so in-depth study of the prevention and control measures of roadbed slopes is of great significance. The prevention and control measures of roadbed slope damage can be divided into two kinds of protection: slope protection and slope protection. Slope protection is to take vegetation planting or engineering measures to prevent the natural factors caused by slope scouring and deformation damage caused by the slope itself. Slope protection is mainly to enhance the integrity and stability of the soil body of the roadbed slope as an engineering measure.

3.1. Slope Protection

3.1.1. Vegetation Cover

Vegetation protection is to utilize the growth characteristics and ecological functions of plants to enhance the stability and erosion resistance of slopes by covering the slopes, fixing the soil and improving the soil structure. The plant fixes the soil through its root system to reduce rainwater scouring, while the plant growth will also play an improvement role in soil structure, soil water and fertilizer retention capacity.

In order to improve the stability, service life and aesthetics of existing slopes, researchers and scholars have carried out a lot of studies.In the 1950s, the spraying technology of thick growing base was researched in Japan. Yang et al. [72] simulated the mechanical effect of grass roots by using the unconfined compression test and three-dimensional finite element method study, and confirmed that the horizontal fine roots and transverse fine roots played a greater role in reinforced soil than vertical fine roots, and that the reinforcing effect of grass roots was better on the upper and middle slopes of slopes than on the lower slopes. Fan et al. [73] found that on steep slopes (greater than 45°), plant roots alone do not provide sufficient shear resistance, so additional stabilization methods are needed to prevent sliding. Okura Y et al. [74] showed that the use of slope protection measures that destroy the natural environment (slurry masonry schist, sprayed cement mortar shoring, etc.) has been abolished in many countries and replaced by the active promotion of slope greening and various flexible slope protection methods, i.e., methods that combine plant measures and engineering measures. Weaver et al. [75] pioneered the study of root ecology and took the root system of field crops and the root development of vegetable crops as the main research object.

3.1.2. Engineering Protection

Slope engineering protection is an important measure to ensure the safety and stability of slopes. It involves the application of a variety of technologies and materials, which should be determined according to the geological, hydrological and climatic conditions of the slope as well as the construction conditions. The engineering protection of the slope surface is mainly to protect some weathered soft rocks, and the steep slope surface which is not suitable for the growth of grass and trees can be protected by engineering protection methods, such as smoothing, whacking, grouting, hooking (grouting), and slope retaining wall. These methods can form a solid protective layer on the surface of the slope, effectively preventing the loosening and collapse of the slope. The applicable conditions for slope engineering protection are shown in Table 2.

3.1.3. Flexible Protection

Flexible protection refers to the reinforcement and protection of slopes using flexible materials such as geogrids and geotextiles. The use of geocells in slope protection allows the water flow rate to be alleviated to a large extent, and also avoids the formation of runoff on the slope surface. In addition, the integrity and flexibility of geocells overcomes the problems of schist skeleton protection in terms of loosening and caving. Sawangsuriya et al. [76] used different types of materials to rehabilitate highway roadbed slopes and obtained geocell protected slopes with better erosion prevention characteristics. Mehdipour et al. [77] investigated the effect of slope geometry, shear strength characteristics and soil compaction on geocell reinforced slope protection by numerical simulation, and the results of the study showed that, when the geocell layer fabric was set up in the middle of the slope and in the middle of the critical damage surface of the unreinforced slope, the highest safety coefficient was obtained when the ratio of the length of the geocells to the thickness of the geocells was 2, and the gradient of the geocells was 60°. Wang De-yong et al. [78] conducted an erosion resistance study of berms using geocells of degradable materials, and the results showed that the geocells of this material were able to reduce the maximum water erosion by more than 10%, and furthermore, the maximum water erosion could be reduced by about 20% compared to the un-reinforced bare slopes in case of strong precipitation. Suraj Vedpathak et al. [79] carried out the design of geocell vegetated slope protection for slopes with severe soil erosion and proposed a new calculation method and construction process.

3.2. Slope Protection

3.2.1. Retaining Wall

Retaining wall as a support for roadbed fill or hillside soil, to prevent fill, soil deformation and instability, landslide or collapse of the engineering structures, by the earthquake effect is significantly affected. Classified from the structural form, retaining wall can be mainly divided into gravity retaining wall, thin-walled retaining wall, reinforced soil retaining wall, anchor-rod retaining wall, anchored plate retaining wall, vertical prestressed anchor retaining wall, soil nail retaining wall, and pile-and-slab retaining wall and other types. In general, there are various types of retaining walls, and the choice of which type of retaining wall to choose needs to be based on specific engineering conditions, geological conditions, environmental factors and economic factors for comprehensive consideration.

Nadim and Whitman [81] analyzed the motion of a retaining wall considering the amplification effect of vibration in the fill behind a gravity retaining wall wall using the finite element method. The acceleration at the top of the fill (3.125H from the wall), the total dynamic earth pressure on the retaining wall, the shear force at the base of the wall, and the time course of the dynamic displacements (including permanent displacements) were computed for different frequencies in sinusoidal form, as well as for three actual seismic records as inputs. Suklje et al. [82] investigated the effect of creep action on lateral pressures in cohesive soils and showed that in certain clays the retaining wall moves slowly outward for a long period of time, and if this deformation is prevented, the lateral pressures will gradually increase until they approach the static earth pressure. Nakai et al. [82] performed elasto-plastic finite element analysis of active and passive earth pressure problems on rigid retaining walls and proved that the distribution of earth pressure acting on rigid retaining walls is related to the dislocation mode of the retaining wall, and that the value of the total earth pressure and the point of action of the combined earth pressure force acting on the retaining wall are related to the friction characteristics of the wall surface, the mode of wall dislocation, and the displacement of the wall, and that there is a nonlinear relationship between the magnitude of the earth pressure and the displacement of the wall. Fathipour et al. [83] used the limit analysis lower limit finite element method to analyze the soil pressure of retaining wall under unsaturated steady state seepage condition, and explored the effect of different parameters on soil pressure under unsaturated condition. Fan et al. [84] modeled a rigid retaining wall by the finite element software PLAXIS and analyzed the effects of aspect ratio and friction angle of the fill behind the wall on the active earth pressure coefficient and the location of the active earth pressure ensemble. tom Wörden et al. [44] borrowed ABAQUS to study the three-dimensional active earth pressure in sandy fill, and compared the results obtained from numerical simulation with those from model tests to verify the accuracy of the numerical model.

In addition, for the reinforced retaining wall, after analyzing by numerical simulation, Wang Yimin et al. found that the lateral displacement of geogrids and panels of the reinforced retaining wall increased due to the increase of the seismic duration, and the effect of seismic time duration on the resistance and deformation of the reinforced retaining wall was stronger [63]. Lou Huafeng et al. established a numerical model of reinforced retaining wall based on FLAC3D and analyzed the effect of wall inclination on lateral deformation, earth pressure and reinforcement tension of modular reinforced retaining wall, and found that 75° is the inflection point of the deformation of modular reinforced retaining wall affected by the strength of the inclination of the wall, and when the inclination of the wall is less than 75°, the continual decrease of the inclination of the wall will not bring about the significant decrease of the deformation of the retaining wall [64].

3.2.2. Slope Stabilization

(1) Anchor (cable) protection

If the slope is a hard rock, which has a broken structure or a stratum with discontinuous laminar structure, it is advisable to adopt the anchor rod (cable) technique to prevent rock fracture. C. A. Stamatopoulosa [88] conducted centrifuge model tests on slopes supported by anchors, and suggested the application of the anchor support method in seismic engineering of slopes by analyzing the response law and deformation characteristics of slopes under dynamic loading. N. Ma et al. [89] used a large shaking table test to comparatively study the dynamic response of slopes supported by pile-anchor structure and pile-beam structure under seismic action, and through the analysis of acceleration spectra and displacement spectra of the slopes, they obtained the conclusion that pile-anchor structure has better dynamic slope fixing effect. Chen WF et al. [90] introduced compliant geotechnical materials into Hoek-Brown’s nonlinear damage criterion based on the limit analysis upper limit theory, so as to calculate the optimal solution algorithm for critical yield acceleration of anchored slopes.

(2) Soil nail support

Some soil slopes will be supported by soil nails, the principle of which is basically the same as that of anchor (cable) protection, by driving soil nails into the soil body, so as to enhance the anti-slip capacity of the soil body and ensure the good stability of the soil body. C. Thomas et al. [91] conducted numerical simulation based on soil nail wall support structure, and obtained that the change of cohesion and elastic modulus of soil body has a significant effect on the deformation of the foundation pit. Emanuele [92] developed a non-metallic glass fiber reinforced polymer soil nail and applied it to a long river embankment in the Netherlands. Carlos et al. [93] investigated the puncture resistance, tensile properties and water permeability of geotextiles under loading and further evaluated the mechanical damage of the geotextiles by performing repeated loading tests on flexible face geotextiles. Ahmadi et al. [94] concluded that the maximum soil nail resistance generally occurs at a certain distance behind the wall by means of soil nail wall model scaling tests.

(3) Skid pile

Slope anti-slip pile is a kind of support structure installed on the surface or inside of the slope, and its function is to increase the stability of the slope. Yang et al. [95] established a new model of h-type anti-slip pile based on Winkler foundation model, and found that compared with ordinary anti-slip pile, the top displacement of h-type anti-slip pile is 41.4% smaller than that of ordinary anti-slip pile with the same cross-sectional area, and further parametric analysis shows that increasing the width of the pile can significantly reduce the top displacement of h-type anti-slip pile. Sawwaf et al. [96] analyzed the force and deformation characteristics of sandy soil slope loaded at the top of the slope based on a small-size model, and found that the anti-slip piles can effectively improve the bearing capacity of the slope, in addition, it was also found that the pile spacing and the depth of burial of the piles have a greater effect on the stability of the slope than the diameter of the piles. S. Yang et al. [97] found that with the increase of anti-slip pile pile length, the influence parameter also changes, which further improves the bearing capacity of the soil body.

In summary, roadbed slope damage is jointly influenced by a variety of factors, which interact and influence each other, constituting a complex system of slope stability. In future research and practice, these factors need to be considered comprehensively and comprehensive measures need to be taken to effectively prevent and control the occurrence of roadbed slope damage.

4. Conclusions and Outlook

The study of slope stability is a long-term research topic in order to prevent disasters caused by slope damage. Obviously, the research discussed in this paper is only the beginning stage of a long road to provide final, complete and valuable slope stability research, for which we still need to make great efforts. By reviewing the existing studies and synthesizing and analyzing the roadbed slope stability studies, the following main conclusions are drawn:

(1) Slope damage is the further development of slope deformation, the form of damage has been basically clear, mainly divided into landslide, avalanche, collapse, spalling four forms.

(2) Field test is the most accurate and potential research method, which solves the problem that indoor test and model test are difficult to be consistent with the actual situation of the slope, and the future research can be carried out for the intelligence of field test of the slope; the complexity of roadbed slope engineering determines that it is difficult to solve the practical problems with the study of a single theory, and the study of coupling multiple theoretical methods will become the mainstream of the future study of slope stability.

(3) Slope stability is affected by both internal and external factors, how to analyze the coupling mechanism of internal and external factors and realize the decoupling of the coupling effect is the key point of slope stability research.

(4) The prevention and control of slope damage is carried out from two aspects: the slope surface and the slope body. Considering that the slope damage is caused by the coupling of many factors, the future research on the prevention and control measures of slope damage should consider the comprehensive prevention and control measures.