Submitted:
02 July 2025
Posted:
03 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Models
2.3. Metrics
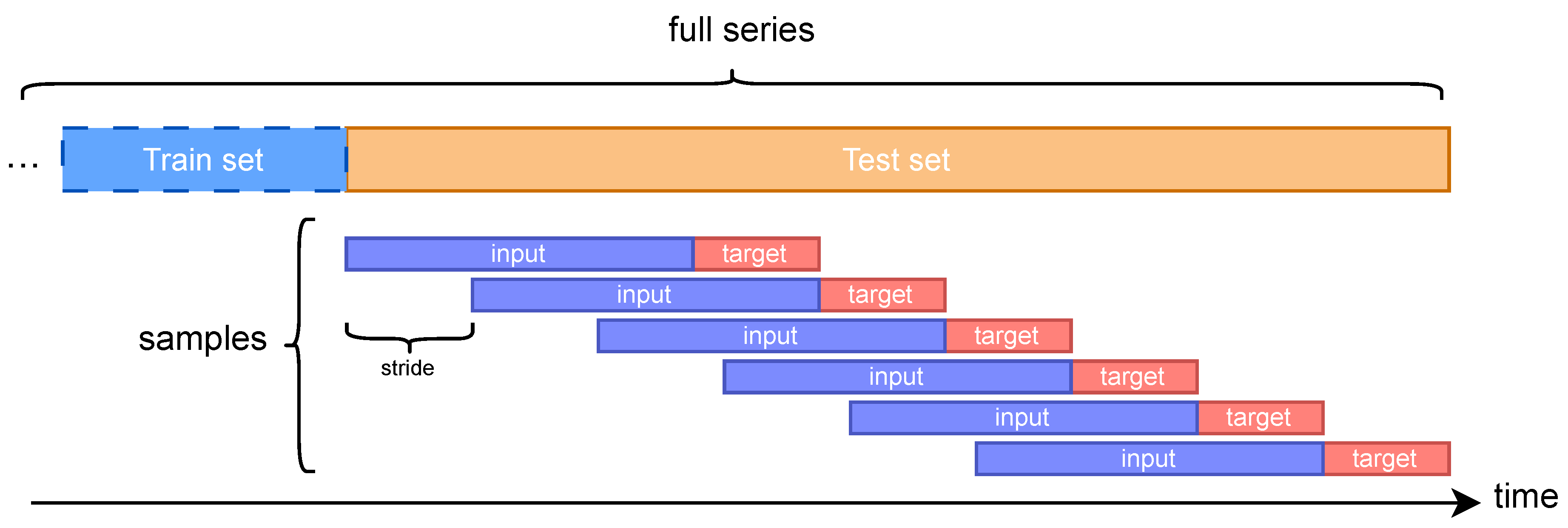
2.4. Scenarios
2.5. Evaluation Framework and Infrastructure
3. Results
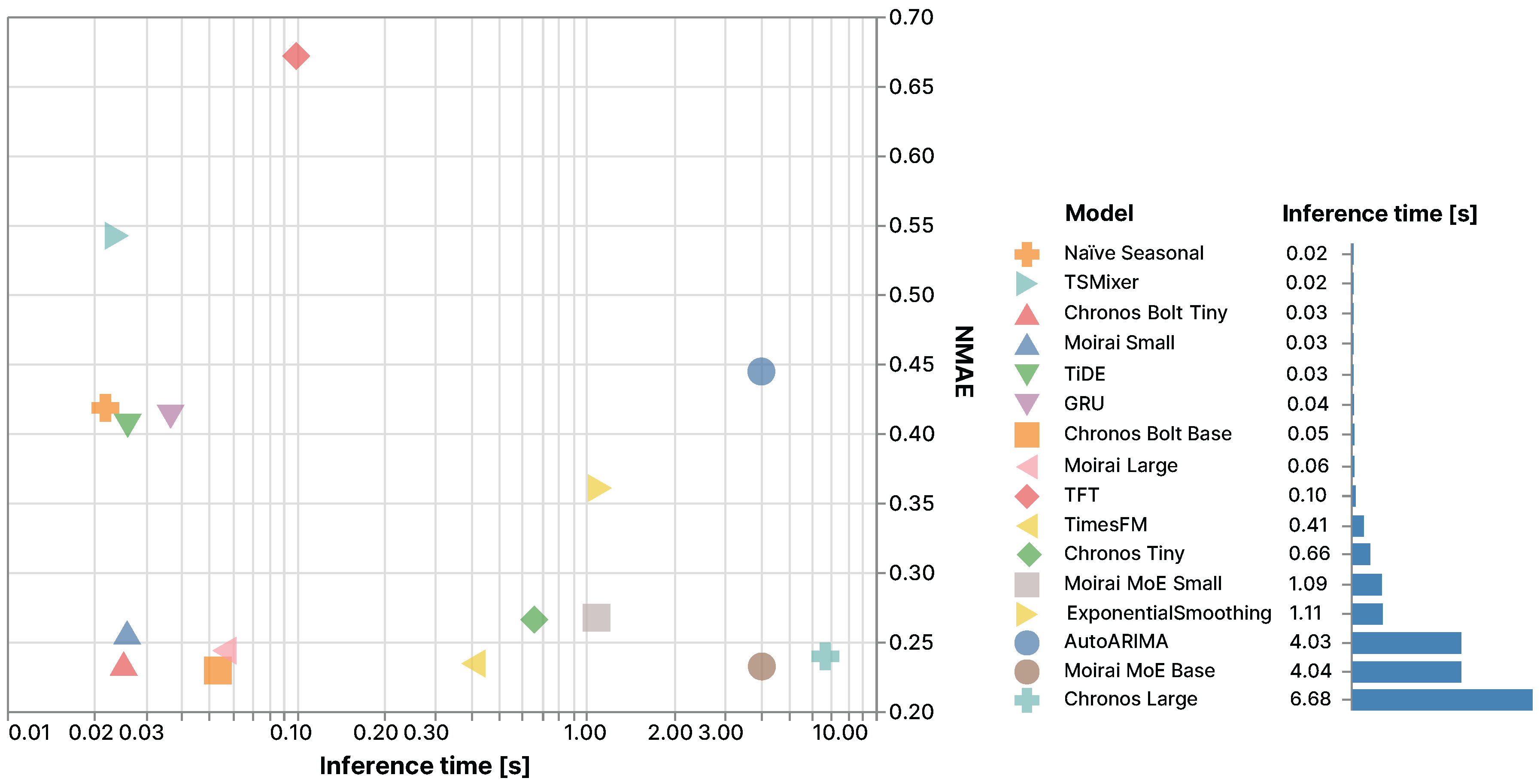
3.1. Predictions Across Models
3.2. Predictions Horizons
3.3. Few-Shot Learning with Various Data Proportions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ansari, A.F.; Stella, L.; Turkmen, C.; Zhang, X.; Mercado, P.; Shen, H.; Shchur, O.; Rangapuram, S.S.; Pineda Arango, S.; Kapoor, S.; et al. Chronos: Learning the Language of Time Series. arXiv preprint arXiv:2403.07815 2024.
- Liu, X.; Liu, J.; Woo, G.; Aksu, T.; Liang, Y.; Zimmermann, R.; Liu, C.; Savarese, S.; Xiong, C.; Sahoo, D. Moirai-MoE: Empowering Time Series Foundation Models with Sparse Mixture of Experts, 2024, [arXiv:cs.LG/2410.10469].
- Das, A.; Kong, W.; Sen, R.; Zhou, Y. A decoder-only foundation model for time-series forecasting, 2024, [arXiv:cs.CL/2310.10688].
- Aksu, T.; Woo, G.; Liu, J.; Liu, X.; Liu, C.; Savarese, S.; Xiong, C.; Sahoo, D. GIFT-Eval: A Benchmark For General Time Series Forecasting Model Evaluation, 2024, [arXiv:cs.LG/2410.10393].
- Zhang, J.; Wen, X.; Zhang, Z.; Zheng, S.; Li, J.; Bian, J. ProbTS: Benchmarking Point and Distributional Forecasting across Diverse Prediction Horizons, 2024, [arXiv:cs.LG/2310.07446].
- Herzen, J.; Lässig, F.; Piazzetta, S.G.; Neuer, T.; Tafti, L.; Raille, G.; Pottelbergh, T.V.; Pasieka, M.; Skrodzki, A.; Huguenin, N.; et al. Darts: User-Friendly Modern Machine Learning for Time Series. Journal of Machine Learning Research 2022, 23, 1–6.
- Energy Consumption, Generation, Prices and Weather, 2019. Accessed: 2024-11-17.
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the The Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Virtual Conference. AAAI Press, 2021, Vol. 35, pp. 11106–11115.
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks. In Proceedings of the The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, New York, NY, USA, 2018; SIGIR ’18, p. 95–104. [CrossRef]
- Max Planck Institute for Biogeochemistry. Weather Data from the Max Planck Institute for Biogeochemistry, Jena, Germany. https://www.bgc-jena.mpg.de/wetter/, 2025. Accessed: 2025-05-16.
- Umwelt- und Gesundheitsschutz Zürich. Stündlich aktualisierte Meteodaten, seit 1992. https://data.stadt-zuerich.ch/dataset/ugz_meteodaten_stundenmittelwerte, 2025. Accessed: 2025-05-16.
- Elektrizitätswerk der Stadt Zürich. Viertelstundenwerte des Stromverbrauchs in den Netzebenen 5 und 7 in der Stadt Zürich, seit 2015. https://data.stadt-zuerich.ch/dataset/ewz_stromabgabe_netzebenen_stadt_zuerich, 2025. Accessed: 2025-05-16.
- MeteoSwiss. Federal Office of Meteorology and Climatology, 2024. Accessed: 2024-11-18.
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. Journal of Statistical Software 2008, 27, 1–22. [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation, 2014, [arXiv:cs.CL/1406.1078].
- Das, A.; Kong, W.; Leach, A.; Mathur, S.; Sen, R.; Yu, R. Long-term Forecasting with TiDE: Time-series Dense Encoder, 2024, [arXiv:stat.ML/2304.08424].
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. International Journal of Forecasting 2021, 37, 1748–1764. [CrossRef]
- Chen, S.A.; Li, C.L.; Yoder, N.; Arik, S.O.; Pfister, T. TSMixer: An All-MLP Architecture for Time Series Forecasting, 2023, [arXiv:cs.LG/2303.06053].
- Woo, G.; Liu, C.; Kumar, A.; Xiong, C.; Savarese, S.; Sahoo, D. Unified Training of Universal Time Series Forecasting Transformers, 2024, [arXiv:cs.LG/2402.02592].
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 2019; KDD ’19, p. 2623–2631. [CrossRef]
- ontime.re. onTime: Your Library to Work with Time Series. GitHub repository, 2024. https://github.com/ontime-re/ontime (accessed on 18.11.2024).
| Dataset | Type | # Features | Resolution | # Target Features | Size |
|---|---|---|---|---|---|
| Energy [7] | Academic | 20 | 1 hour | 1 (Total load) | 35,064 |
| ETTh1 [8] | Academic | 7 | 1 hour | 1 (Oil temp.) | 17,420 |
| ETTm1 [8] | Academic | 7 | 15 minutes | 1 (Oil temp.) | 69,680 |
| ExchangeRate [9] | Academic | 8 | 1 day | 8 (All) | 7,588 |
| Weather [10] | Academic | 21 | 10 minutes | 21 (All) | 52,704 |
| ZurichElectricity [11,12] | Academic | 10 | 15 minutes | 2 (Consumption) | 93,409 |
| HEIA1h | Industrial | 8 | 1 hour | 8 (All) | 11,664 |
| MeteoSwiss [13] | Industrial | 8 | 10 minutes | 24 (All) | 105,264 |
| Model | Type | Prediction type | # Parameters |
|---|---|---|---|
| NaïveSeasonal | Statistical | Univariate | Not applicable |
| AutoARIMA [14] | Statistical | Univariate | < 100 |
| ExpotentialSmoothing | Statistical | Univariate | Not applicable |
| GRU [15] | Deep learning | Multivariate | 3-160K |
| TiDE [16] | Deep learning | Multivariate | 285K-8.5M |
| TFT [17] | Deep learning | Multivariate | 3-36K |
| TSMixer [18] | Deep learning | Multivariate | 19-931K |
| Chronos Tiny† [1] | Foundation | Univariate | 8M |
| Chronos Large† [1] | Foundation | Univariate | 710M |
| Chronos Bolt Small [1] | Foundation | Univariate | 48M |
| Chronos Bolt Base [1] | Foundation | Univariate | 205M |
| Moirai small† [19] | Foundation | Multivariate | 14M |
| Moirai large† [19] | Foundation | Multivariate | 311M |
| Moirai MoE Small [2] | Foundation | Multivariate | 117M |
| Moirai MoE Base [2] | Foundation | Multivariate | 935M |
| TimesFM [3] | Foundation | Univariate | 500M |
| Deep learning | Statistical | |||||||
|---|---|---|---|---|---|---|---|---|
| Metrics | GRU | TFT | TiDE | TSMixer | Naive Seasonal | AutoARIMA | ES† | |
| Energy | sMAPE | 13.49 | 15.25 | 8.102 | 9.724 | 20.56 | 13.34 | 22.67 |
| NMAE | .1332 | .1507 | .0825 | .0952 | .1946 | .1318 | .2215 | |
| ETTh1 | sMAPE | 35.00 | 47.15 | 40.11 | 38.13 | 34.49 | 33.60 | 35.80 |
| NMAE | .4003 | .6310 | .4097 | .5261 | .3627 | .3526 | .3781 | |
| ETTm1 | sMAPE | 32.11 | 41.53 | 55.02 | 26.05 | 22.27 | 23.59 | 24.55 |
| NMAE | .3190 | .6568 | 1.040 | .2950 | .2325 | .2369 | .2462 | |
| ExchangeRate | sMAPE | 15.55 | 18.06 | 11.45 | 15.34 | 2.336 | 2.514 | 2.537 |
| NMAE | .1428 | .1631 | .1049 | .1416 | .0234 | .0249 | .0252 | |
| Weather | sMAPE | 79.09 | 81.48 | 62.53 | 65.67 | 54.58 | 61.77 | 66.82 |
| NMAE | 250.0 | 223.5 | 50.21 | 39.41 | 1.073 | 10.85 | 38.16 | |
| ZurichElectricity | sMAPE | 14.20 | 21.87 | 5.395 | 8.260 | 18.53 | 18.49 | 23.39 |
| NMAE | .1401 | .2160 | .0548 | .0835 | .1871 | .1858 | .2416 | |
| HEIA | sMAPE | 42.26 | 52.47 | 29.56 | 39.48 | 39.99 | 41.65 | 31.28 |
| NMAE | .5380 | .6706 | .3240 | .5422 | .4182 | .4445 | .3606 | |
| MeteoSwiss | sMAPE | 75.64 | 89.08 | 64.64 | 80.11 | 68.98 | 71.96 | 72.76 |
| NMAE | 1.641 | 2.170 | 1.085 | 1.810 | 2.152 | 1.768 | 2.664 | |
| Moirai | Moirai-MoE | Chronos | Chronos Bolt | TFM† | BB‡ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Metrics | Small | Large | Small | Base | Tiny | Large | Tiny | Base | |||
| Energy | sMAPE | 7.360 | 7.134 | 7.088 | 7.062 | 7.508 | 4.854 | 6.183 | 5.095 | 7.035 | 8.102 |
| NMAE | .0744 | .0718 | .0719 | .0718 | .0751 | .0491 | .0622 | .0511 | .0708 | .0825 | |
| ETTh1 | sMAPE | 32.64 | 34.61 | 33.25 | 34.04 | 31.15 | 30.68 | 31.95 | 30.56 | 31.40 | 33.60 |
| NMAE | .3382 | .3344 | .3333 | .3370 | .3242 | .3217 | .3408 | .3334 | .3231 | .3526 | |
| ETTm1 | sMAPE | 23.66 | 24.64 | 24.78 | 23.64 | 22.95 | 21.61 | 21.58 | 22.40 | 22.45 | 22.27 |
| NMAE | .2461 | .2658 | .2569 | .2488 | .2347 | .2303 | .2346 | .2329 | .2521 | .2325 | |
| ExchangeRate | sMAPE | 2.505 | 2.687 | 2.470 | 2.535 | 2.714 | 2.583 | 2.412 | 2.552 | 2.565 | 2.336 |
| NMAE | .0251 | .0273 | .0248 | .0255 | .0270 | .0260 | .0242 | .0255 | .0256 | .0234 | |
| Weather | sMAPE | 64.20 | 64.43 | 62.01 | 59.47 | 63.47 | 61.83 | 62.40 | 61.81 | 45.05 | 54.58 |
| NMAE | 2.663 | 9.052 | 11.05 | 5.192 | 13.03 | .4987 | 6.455 | 4.629 | 1.243 | 1.073 | |
| ZurichElectricity | sMAPE | 17.92 | 18.06 | 17.30 | 15.63 | 8.368 | 6.119 | 5.635 | 4.177 | 7.292 | 5.395 |
| NMAE | .1769 | .1804 | .1727 | .1540 | .0872 | .0639 | .0592 | .0440 | .0768 | .0548 | |
| HEIA | sMAPE | 22.74 | 20.89 | 23.31 | 20.20 | 23.33 | 20.73 | 20.37 | 19.71 | 20.67 | 29.56 |
| NMAE | .2570 | .2423 | .2670 | .2321 | .2687 | .2411 | .2343 | .2294 | .2343 | .3240 | |
| MeteoSwiss | sMAPE | 67.72 | 66.98 | 66.14 | 66.49 | 67.99 | 62.95 | 67.58 | 65.18 | 62.74 | 64.64 |
| NMAE | .8146 | 1.488 | 2.442 | 1.173 | 1.657 | 1.662 | .9932 | 1.377 | .9777 | 1.085 | |
| Moirai | Moirai-MoE | Chronos | Chronos Bolt | TFM† | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Horizons | Small | Large | Small | Base | Tiny | Large | Tiny | Base | ||
| Energy | 24 | .0643 | .0592 | .0591 | .0528 | .0563 | .0338 | .0503 | .0385 | .0589 |
| 48 | .0719 | .0678 | .0678 | .0628 | .0678 | .0414 | .0587 | .0442 | .0676 | |
| 96 | .0744 | .0718 | .0719 | .0718 | .0751 | .0491 | .0622 | .0511 | .0708 | |
| 192 | .0773 | .0755 | .0746 | .0802 | .0754 | .0529 | .0646 | .0556 | .0734 | |
| ETTh1 | 24 | .2048 | .2104 | .1970 | .2021 | .2011 | .2074 | .1999 | .1944 | .2077 |
| 48 | .2619 | .2713 | .2503 | .2547 | .2447 | .2490 | .2495 | .2517 | .2536 | |
| 96 | .3382 | .3344 | .3333 | .3370 | .3242 | .3217 | .3408 | .3334 | .3231 | |
| 192 | .2883 | .2969 | .3063 | .2905 | .2849 | .2838 | .3070 | .2870 | .2784 | |
| ETTm1 | 24 | .1616 | .1967 | .1752 | .1755 | .1796 | .1446 | .1479 | .1443 | .1643 |
| 48 | .2515 | .2742 | .2574 | .2571 | .2382 | .2166 | .2397 | .2307 | .2594 | |
| 96 | .2461 | .2658 | .2569 | .2488 | .2347 | .2303 | .2346 | .2329 | .2521 | |
| 192 | .2917 | .3094 | .3055 | .3007 | .2950 | .2870 | .3008 | .3017 | .2977 | |
| ExchangeRate | 24 | .0138 | .0133 | .0128 | .0130 | .0140 | .0136 | .0131 | .0136 | .0132 |
| 48 | .0177 | .0179 | .0171 | .0174 | .0186 | .0184 | .0170 | .0182 | .0180 | |
| 96 | .0251 | .0273 | .0248 | .0255 | .0270 | .0260 | .0242 | .0255 | .0256 | |
| 192 | .0350 | .0472 | .0394 | .0397 | .0406 | .0375 | .0340 | .0343 | .0346 | |
| Weather | 24 | .8605 | .4102 | .5990 | .8083 | 2.260 | .3976 | 2.760 | .6189 | .6271 |
| 48 | 2.915 | 1.317 | 6.538 | 7.237 | 1.779 | .9095 | 6.655 | 1.919 | 1.834 | |
| 96 | 2.663 | 9.052 | 11.05 | 5.192 | 13.03 | .4987 | 6.455 | 4.629 | 1.243 | |
| 192 | .5276 | .6359 | .8007 | .7821 | .7816 | .5519 | .6735 | .5559 | .6298 | |
| Horizons | Small | Large | Small | Base | Tiny | Large | Tiny | Base | ||
| ZurichElectricity | 24 | .0883 | .0758 | .0721 | .0596 | .0339 | .0244 | .0292 | .0233 | .0316 |
| 48 | .1576 | .1413 | .1403 | .1076 | .0501 | .0297 | .0348 | .0289 | .0441 | |
| 96 | .1769 | .1804 | .1727 | .1540 | .0872 | .0639 | .0592 | .0440 | .0768 | |
| 192 | .1757 | .1838 | .1752 | .1621 | .1056 | .0825 | .0667 | .0501 | .0926 | |
| HEIA | 24 | .2220 | .1959 | .2131 | .1924 | .2123 | .1837 | .1998 | .1937 | .2013 |
| 48 | .2459 | .2177 | .2479 | .2111 | .2322 | .2086 | .2173 | .2098 | .2206 | |
| 96 | .2570 | .2423 | .2670 | .2321 | .2687 | .2411 | .2343 | .2294 | .2343 | |
| 192 | .2687 | .2659 | .2807 | .2467 | .2762 | .2540 | .2437 | .2408 | .2507 | |
| MeteoSwiss | 24 | .6949 | .8155 | .8457 | .6222 | .7558 | .7167 | .6576 | .8176 | .6057 |
| 48 | 1.153 | 1.441 | 1.771 | 1.016 | 1.457 | 1.297 | 1.045 | 1.346 | .9871 | |
| 96 | .8146 | 1.488 | 2.442 | 1.173 | 1.657 | 1.662 | .9932 | 1.377 | .9777 | |
| 192 | 1.226 | 1.530 | 1.850 | 1.898 | 1.584 | 1.374 | 1.295 | 1.231 | 1.336 | |
| Moirai | Chronos | ||||
|---|---|---|---|---|---|
| Proportions | Small | Large | Tiny | Large | |
| Energy | 0% | .0744 | .0718 | .0751 | .0491 |
| 33% | .0727 | .0704 | .0649 | .0549 | |
| 67% | .0667 | .0658 | .0594 | .0495 | |
| 100% | .0687 | .0661 | .0599 | .0445 | |
| ETTh1 | 0% | .3382 | .3344 | .3242 | .3217 |
| 33% | .3146 | .3307 | .3315 | .3161 | |
| 67% | .3173 | .3167 | .3157 | .3272 | |
| 100% | .3127 | .3346 | .3099 | .3460 | |
| ETTm1 | 0% | .2461 | .2658 | .2347 | .2303 |
| 33% | .2404 | .3616 | .2459 | .2540 | |
| 67% | .2686 | .3693 | .2484 | .2754 | |
| 100% | .2437 | .2558 | .2198 | .2308 | |
| ExchangeRate | 0% | .0251 | .0273 | .0270 | .0260 |
| 33% | .0282 | .0694 | .0319 | .0319 | |
| 67% | .0250 | .0360 | .0285 | .0299 | |
| 100% | .0285 | .0779 | .0251 | .0302 | |
| Weather | 0% | 2.663 | 9.052 | 13.03 | .4987 |
| 33% | 3.793 | 6.041 | 2.053 | .9532 | |
| 67% | 6.670 | 2.425 | 1.670 | 3.274 | |
| 100% | 2.459 | 3.703 | 8.644 | 5.433 | |
| ZurichElectricity | 0% | .1769 | .1804 | .0872 | .0639 |
| 33% | .0482 | .0475 | .0326 | .0295 | |
| 67% | .0419 | .0526 | .0323 | .0277 | |
| 100% | .0499 | .0535 | .0333 | .0265 | |
| HEIA | 0% | .2570 | .2423 | .2687 | .2411 |
| 33% | .2631 | .2736 | .3271 | .2574 | |
| 67% | .2991 | .2920 | .2981 | .2488 | |
| 100% | .2653 | .2728 | .2494 | .2420 | |
| MeteoSwiss | 0% | .8146 | 1.488 | 1.657 | 1.662 |
| 33% | .5650 | .6690 | .6111 | .9706 | |
| 67% | .4954 | .4532 | 1.446 | .7739 | |
| 100% | .5396 | .5316 | .7382 | .6285 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





