Unsupervised Temporal Encoding for Stock Price Prediction through Dual-Phase Learning

I. Introduction

Stock price prediction, as a critical task in financial engineering and quantitative investment, faces persistent challenges such as high volatility, high dimensionality, and temporal dependence. In real financial markets, price movements are driven not only by historical trading data but also by macroeconomic conditions, industry trends, and market sentiment. Effectively modeling the interactions among these complex factors is essential for enhancing forecasting accuracy[1]. This task holds both theoretical and practical value. With the advancement of artificial intelligence, particularly deep learning, data-driven prediction methods have gained attention in the financial domain. However, many approaches still rely heavily on large-scale labeled data or overlook the structural and temporal nature of the input, limiting their ability to capture underlying informative patterns[2].

In financial data modeling, labeled data is often scarce and costly. This is especially true in regression-based forecasting tasks. While price labels may appear readily available, the non-stationary and nonlinear characteristics of financial markets make it difficult to use raw price values as strong supervisory signals. Therefore, achieving high-quality representation learning under weak supervision is crucial for improving forecasting performance. Recently, self-supervised learning has emerged as a promising solution to the lack of labeled data, as demonstrated in several recent studies[3,4,5,6]. It enables robust feature extraction from large volumes of unlabeled data by solving pre-defined tasks [7,8,9]. This approach is well suited for financial markets, which are characterized by high-frequency fluctuations and complex structures[10].

However, traditional self-supervised learning methods often struggle to capture the fine-grained temporal dynamics of financial time series. They tend to underutilize sequence structure and rely on single-objective designs[11]. As a result, the learned representations may fail to reflect the detailed movements in stock prices. To address this limitation, a two-stage self-supervised pretraining framework has recently shown promise, as evidenced by its successful adoption in various natural language processing models [12,13,14,15,16].The first stage focuses on modeling global temporal relationships to extract long-term trend features. The second stage enhances local dynamic patterns and price fluctuations. This enables multi-scale fusion and cross-granularity perception. The staged design improves the model's ability to represent multi-level financial patterns and provides a more expressive foundation for downstream forecasting tasks[17].

Moreover, the diversity and heterogeneity of stock markets impose greater demands on model generalization. Stocks vary significantly in terms of volatility, trading frequency, and industry characteristics. Modeling from a single scale or perspective is often insufficient. The two-stage self-supervised approach provides a flexible mechanism to jointly model global and local structures. It improves consistency across time scales and strengthens adaptability across different sectors and market conditions. This method also demonstrates strong transferability and scalability, laying a solid foundation for building more generalizable stock forecasting models.

Therefore, from both the perspective of practical demands and modeling challenges, a two-stage self-supervised pretraining strategy offers a promising path. It aligns with the broader trend of integrating self-supervised learning with time series prediction. It also addresses the complexity and diversity of real-world financial markets. This direction opens new opportunities for exploring the link between model structure, representation learning, and forecasting accuracy. Furthermore, it provides essential support for the development of low-supervision, high-performance financial intelligence systems.

II. Related Work

Deep learning has become a cornerstone in modeling complex temporal dependencies within financial time series, with sequence-based architectures like LSTM demonstrating robust performance in extracting and representing dynamic stock trends [18]. Extensions of this paradigm, such as hybrid models that combine sequential neural networks with probabilistic components, have proven effective for capturing both distributional and sequential patterns in asset price movements, which informs the multi-layer temporal sequence modeling in the present work [19]. To further address the challenge of representing multi-scale temporal information, advanced hybrid frameworks incorporating LSTM, convolutional, and attention-based modules have been explored. These architectures leverage the strengths of different neural components for comprehensive temporal feature extraction, and directly motivate the multi-granularity encoder design adopted in this study [20]. The use of adaptive and structure-aware representation mechanisms, such as capsule networks, has also shown promise in enhancing feature expressiveness and structure perception, aligning closely with the representation learning objectives of the proposed model [21].

Self-supervised and unsupervised learning methods have emerged as powerful solutions for representation learning under limited supervision. Structure-aware diffusion mechanisms for unsupervised sequence modeling, for instance, demonstrate that robust feature extraction from unlabeled data is achievable and essential for downstream prediction tasks—a principle central to the self-supervised pretraining strategy utilized here [22]. Generative frameworks designed for temporal data, particularly those incorporating time-aware diffusion processes, further illustrate the potential of generative self-supervised tasks for modeling financial volatility and non-stationary behaviors. This perspective is integrated into the two-phase pretraining procedure of the proposed approach [23]. Representation learning strategies that emphasize causal and multi-objective formulations have also been shown to provide more interpretable and transferable features for financial forecasting. This underpins the motivation for dual self-supervised objectives and staged pretraining in this framework [24].

Beyond direct temporal modeling, leveraging relational structure and network-based learning has proven valuable for financial representation. Heterogeneous network learning approaches demonstrate how implicit relationships within complex datasets can be captured to improve robustness and adaptability—insights that guide the structure-aware modeling and multi-granularity integration in the encoder [25]. Methods that employ reinforcement learning for sampling and ensemble strategies have highlighted techniques for improving robustness and generalization of learned representations. The perturbation robustness and ensemble aspects of this paper’s experimental design draw from such methodologies [26].

Further contributions to the field underscore the importance of integrating deep learning models into traditional financial forecasting pipelines, revealing that the combination of multiple information sources and modeling strategies enhances generalization and forecasting accuracy [27]. Advances in federated and collaborative learning provide techniques for handling data heterogeneity and distributed modeling, which can be mapped to the multi-source integration problem addressed by the present framework [28]. Automated feature extraction for sequential data through deep convolutional models has also been demonstrated as a practical and effective strategy for enhancing predictive performance, complementing the sequence encoding methods in this work [29].

Collectively, these advancements support the technical direction of the current study. By synthesizing innovations from deep sequential modeling, hybrid neural architectures, self-supervised and structure-aware learning, and robust multi-source representation, this work aims to advance the state of stock price prediction under real-world conditions of label scarcity, structural complexity, and temporal non-stationarity.

III. Proposed Methodology

A. Overall Framework

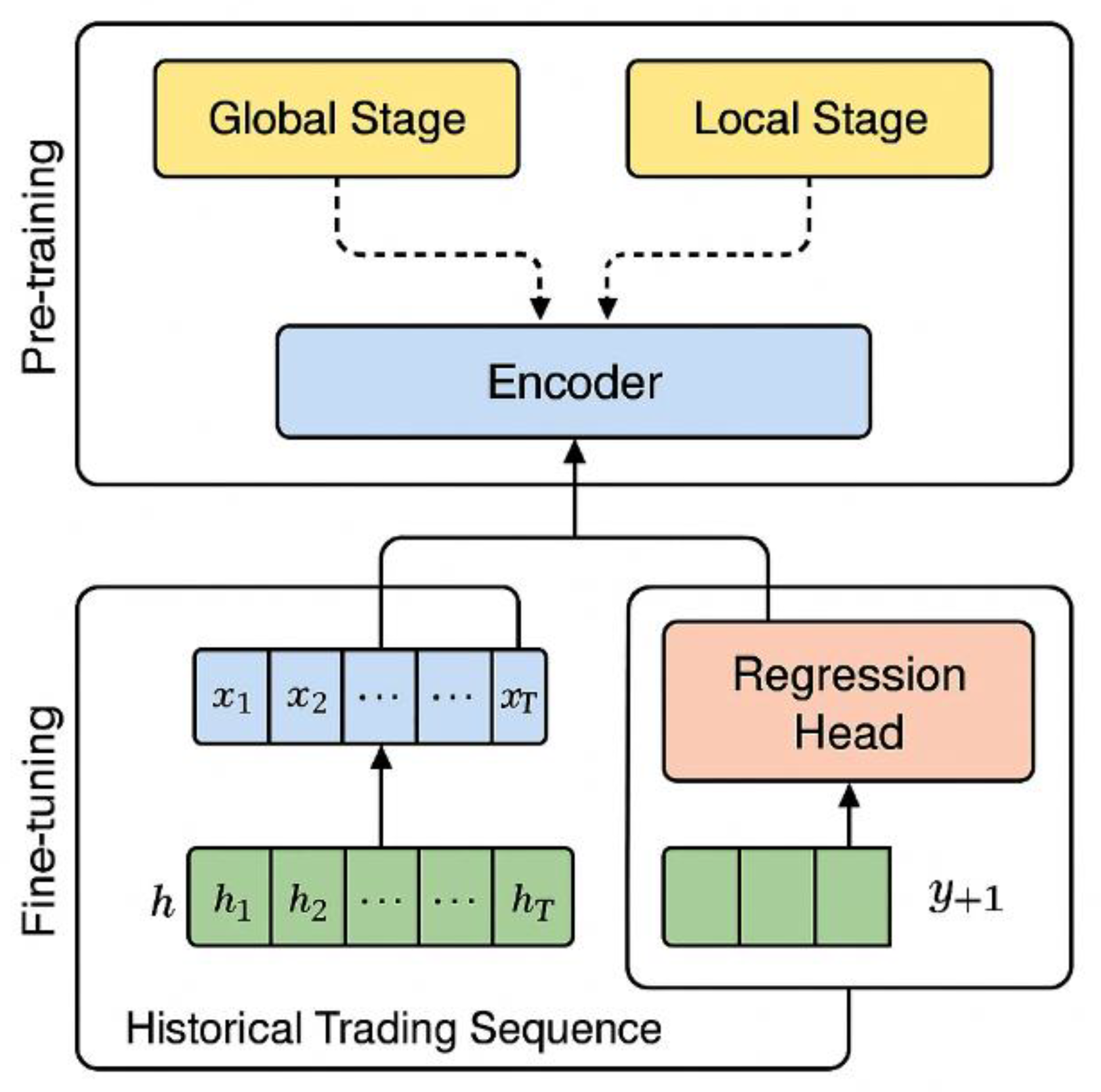
This method is based on a two-stage self-supervised pre-training framework, which aims to improve the modeling ability of stock price trend changes through a hierarchical representation learning mechanism. The overall structure consists of a pre-training stage and a fine-tuning prediction stage. The pre-training stage uses an unsupervised method to encode the features of the original time series data and guides the model to capture multi-granular time-dependent structures and dynamic patterns through staged tasks [30]. The model architecture is shown in Figure 1.

In this stage, the input data is the historical trading sequence $X=\{x_1,x_2,\dots ,x_T\}$ of the stock, which is mapped into the potential representation sequence $H=\{h_1,h_2,\dots ,h_T\}$ by the encoder $f_{\theta }(\cdot )$, that is:

$$H=f_{\theta }(X)$$

Subsequently, the fine-tuning phase inputs the pre-trained time representation into the regression prediction head to generate the predicted value of the future price. This phase focuses on maintaining the trend evolution and volatility structure and maps the high-level representation to a continuous value output. The prediction function is denoted as $g_{\phi }(\cdot )$, and the output is the predicted price ${\stackrel{⌢}{y}}_{t+1}$ for the next time step. The relationship is defined as:

$${\stackrel{⌢}{y}}_{t+1}=g_{\phi }(h_t)$$

This two-stage framework facilitates a seamless transition from unsupervised representation learning to supervised price prediction, thereby effectively improving the model’s capacity for both representation and generalization when addressing the complex characteristics of financial time series.

B. Optimization Objective

In the overall optimization process of the model, the input is a historical stock trading sequence, denoted as $X=\{x_1,x_2,\dots ,x_T\}$, where each time step $x_t$ contains multiple feature dimensions such as opening price, closing price, highest price, lowest price, and trading volume. The sequence is first fed into the encoder module, which consists of a set of stacked time modeling units to extract deep temporal features in the sequence. After being processed by the encoder, the sequence is mapped to the latent representation space to generate an intermediate feature representation $H=\{h_1,h_2,\dots ,h_T\}$, where each $h_t\in R^d$ is a context vector in the latent space.

Then, in the pre-training phase, the model constructs two task paths: the global phase and the local phase [31,32]. The global phase extracts the long-term trend information of the sequence by modeling the complete time series, which is formally expressed as:

$$z^{local}=f^{local}(h_t,h_{t+1},\dots ,h_{t+k})$$

These two stages are performed in parallel, and the output representations are merged and used as the basic feature input for the fine-tuning stage.

After entering the fine-tuning phase, the fused representation is input into the regression prediction head to generate the target value prediction result for the future time step [33]. Assuming the current time is T and the goal is to predict the price ${\stackrel{⌢}{y}}_{T+1}$ at the next moment, the final prediction expression is:

$${\stackrel{⌢}{y}}_{T+1}=g(z^{global},z^{local})$$

This structure ensures a closed loop of multi-granular information paths from raw input to final prediction results while retaining the ability to model temporal dynamic features at each stage.

The entire data flow achieves efficient information extraction and task separation through modular design. The model can flexibly adjust the representation dimension and modeling depth of different stages to adapt to the diverse financial time series structure. Ultimately, all forecast results will be organized into an output sequence $Y=\{{\stackrel{⌢}{y}}_{T+1}.{\stackrel{⌢}{y}}_{T+2},\dots ,{\stackrel{⌢}{y}}_{T+M}\}$ in chronological order for further analysis or decision support.

IV. Dataset

The dataset used in this study consists of historical stock trading data for Tesla Inc. in the public securities market. The period covers the period from 2010 to 2024, reflecting the company's full market cycle from early development to industry maturity. This dataset is obtained from a public financial data platform. It has high credibility and continuity and accurately captures the impact of market dynamics on stock prices across different periods.

The dataset includes several typical financial attributes, such as opening price, highest price, lowest price, closing price, adjusted closing price, and trading volume. Each data entry corresponds to a single trading day. By preprocessing and standardizing these structured fields, the dataset can be used to construct multivariate input features for time series forecasting. This effectively supports the model in learning price trends and volatility patterns.

Because the dataset spans multiple major market events and economic cycles, the price movements show rich nonlinear variation patterns. This makes it suitable for evaluating the model's ability to adapt under complex financial conditions. Additionally, the long period of the dataset allows for the construction of extended training and testing sequences. It provides sufficient data support for both the pretraining and fine-tuning stages of the model.

V. Experimental Results

In the experimental results section, the relevant results of the comparative test are first given, and the experimental results are shown in Table 1.

The proposed method demonstrates consistent superiority over mainstream baseline models across various evaluation metrics, highlighting its enhanced capability in stock price prediction. Compared to traditional multilayer perceptron (MLP) architectures, the two-stage self-supervised modeling framework achieves notably lower mean squared error (MSE) and mean absolute error (MAE), suggesting a more precise and effective capture of temporal structures and fluctuation patterns within financial time series. The underperformance of the MLP further underscores the necessity of modeling temporal dependencies, as static architectures fail to accommodate evolving price dynamics.

Beyond MLP, the proposed approach also outperforms standalone LSTM and Transformer models. While these baselines can model long-term dependencies to some extent, our method not only retains this strength but also improves the extraction of local dynamic features, thereby enhancing both representational richness and predictive stability. Notably, the R² value increases by nearly 0.09 compared to the LSTM, indicating superior modeling of the nonlinear relationships between historical and future prices. This improvement can be attributed to the synergy of the two-stage pretraining mechanism, which facilitates multi-scale temporal modeling.

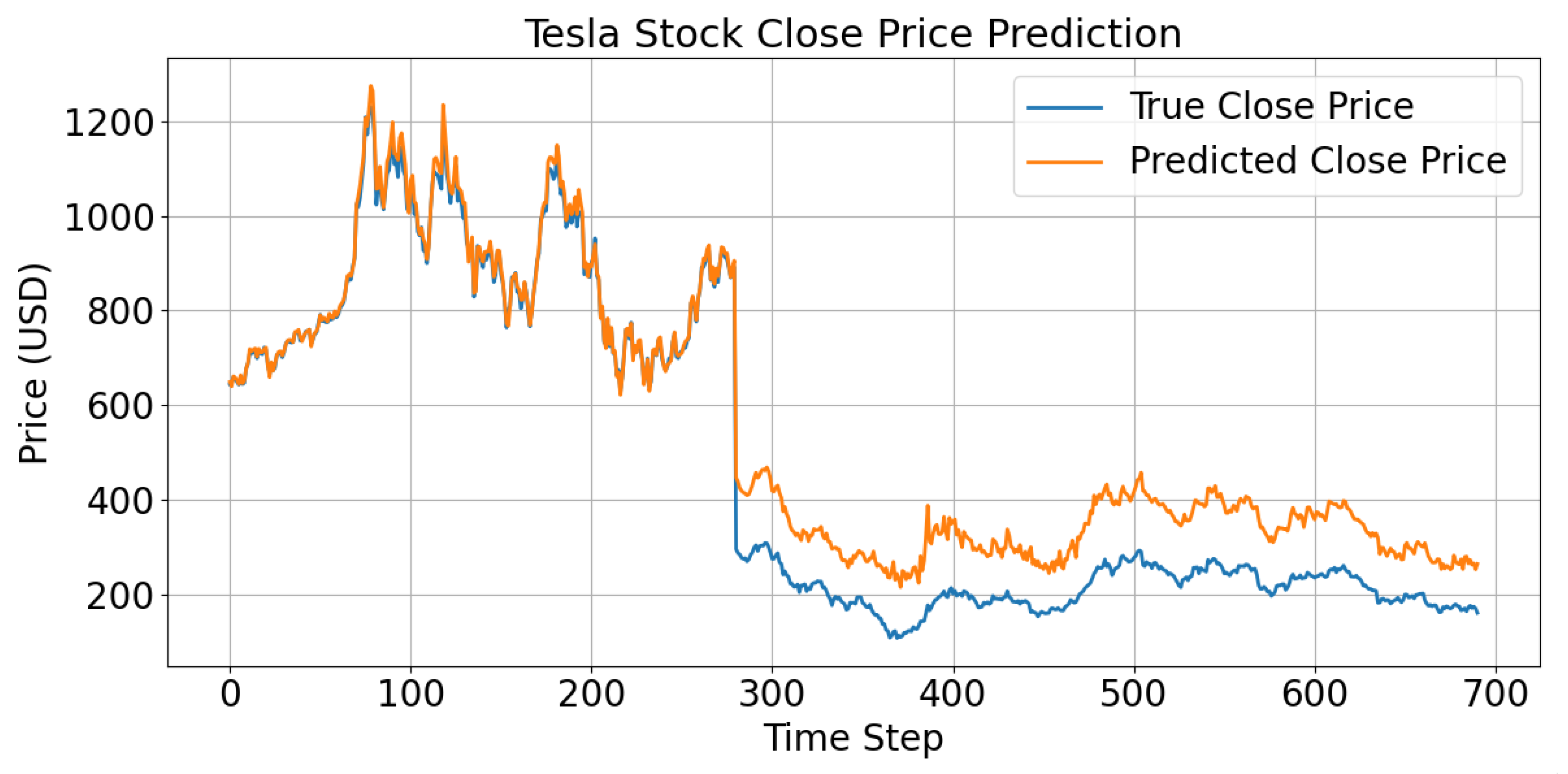
Moreover, when benchmarked against hybrid models such as Transformer-LSTM combinations, the proposed method continues to maintain a leading position across all relevant metrics. This sustained advantage suggests that the model design effectively balances deep information fusion with improved adaptability in unsupervised representation learning. By integrating structured pretraining and supervised fine-tuning, the method ensures better coordination between parameter initialization and feature extraction, leading to robust generalization in volatile financial environments. These experimental results collectively demonstrate the method’s strengths in accuracy, stability, and adaptability, and confirm the effectiveness of the two-stage self-supervised learning strategy for stock price forecasting. The comparative analysis between true and predicted values, as shown in Figure 2, further illustrates the model’s predictive effectiveness.

As shown in the figure, the predicted closing price curve generated by the proposed model remains highly consistent with the actual trend during most periods. This indicates that the model has a strong capability to capture overall price movement. In particular, during the relatively stable price intervals, the predicted results closely match the real values. This reflects that the model effectively learns stationary patterns and structural features from historical sequences and performs well under low-volatility market conditions.

In high-volatility segments, such as between time steps 100 and 200, the model does not perfectly reproduce the extreme values. However, it still tracks the overall direction and turning points of the actual trend. This suggests that the model maintains effective modeling and responsiveness to local dynamics even under sharp market changes. It also confirms the model's ability to perceive nonlinear fluctuation structures.

In some periods, such as between time steps 300 and 400, systematic deviations are observed. The predicted values tend to overestimate the overall price level. This may result from a lack of similar patterns in the training data or imbalanced price distributions. It indicates that the model still faces generalization challenges under extreme market conditions. However, it is worth noting that the predicted curve remains directionally consistent and avoids major trend errors, which shows the model's stability in structural learning.

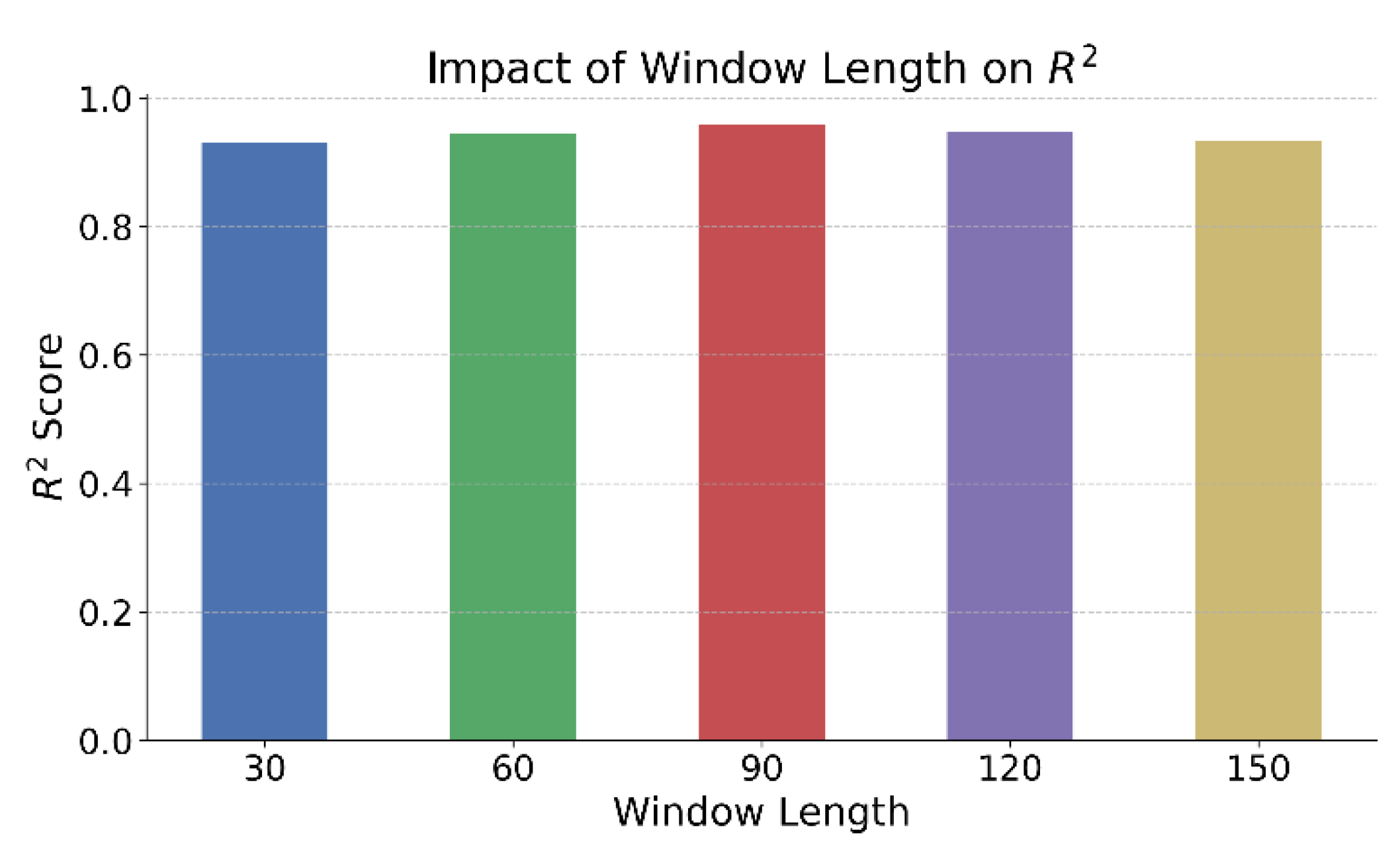
This paper further gives the impact of different time window lengths on the model effect, and the experimental results are shown in Figure 3.

As shown in the figure, the length of the time window has a clear impact on the prediction performance of the model. When the window is set to 90, the model achieves the highest R² score. This indicates that this window length strikes a balance between preserving sufficient historical information and reducing redundant noise. It enhances the model's ability to capture price trends. The result suggests that selecting an appropriate historical observation length is crucial for structure-aware prediction in financial time series.

When the time window is relatively short, such as 30 or 60, the model shows limited capacity to capture long-term dependencies. This weakens its response to trend changes. Although shorter windows improve training efficiency, they lack global context and are more easily misled by local fluctuations. This eventually affects the quality of representation and prediction stability. The result shows that in complex financial scenarios, the trade-off between information coverage and structural extraction must be carefully managed.

When the window length increases further to 120 or 150, the model's R² score begins to decline. This indicates that excessively long input sequences may introduce redundant or even conflicting information. Such redundancy weakens the model's ability to focus on key features. Accumulated irrelevant inputs may distract the model during representation learning and reduce the precision of the final regression output.

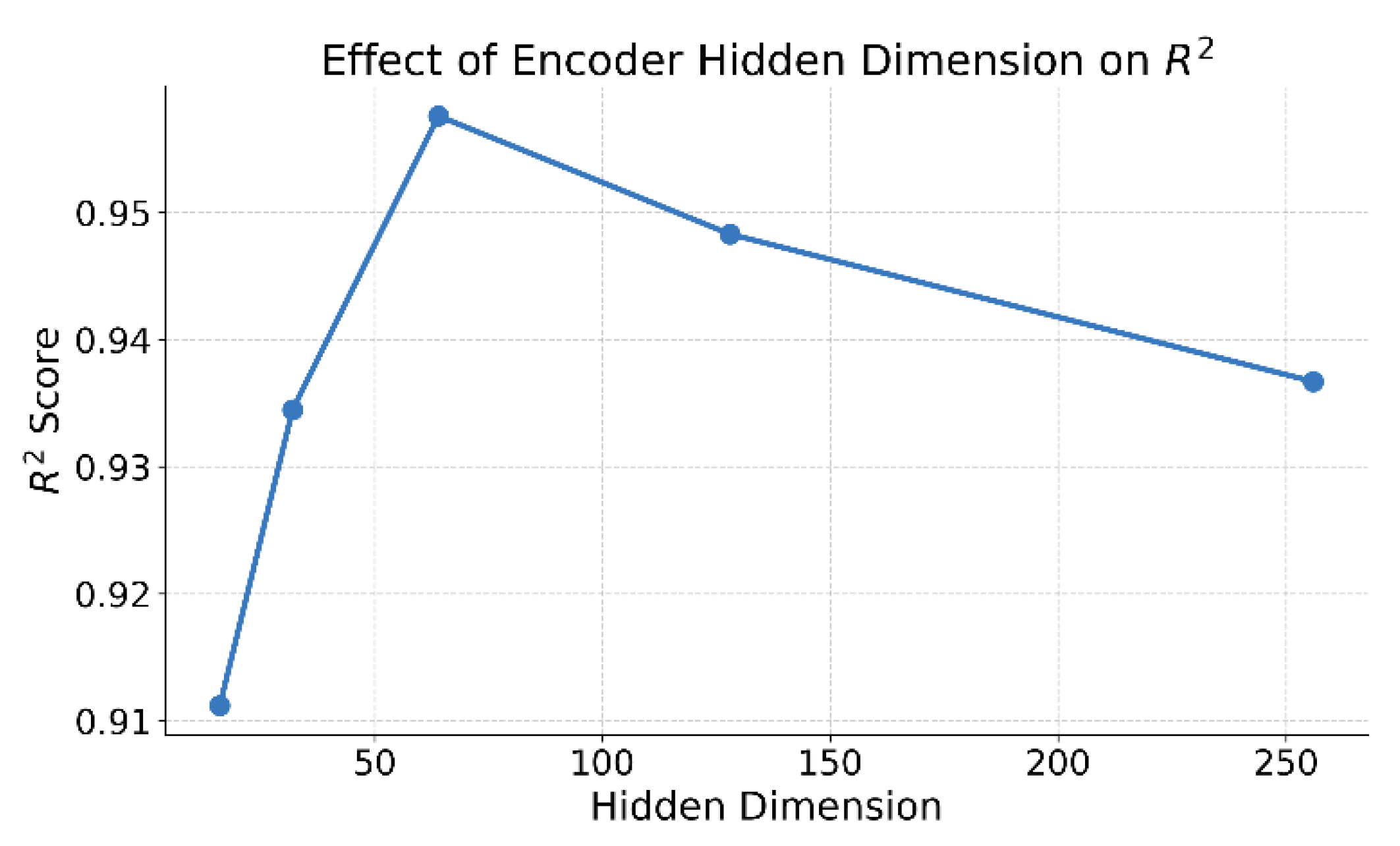
This paper also gives a sensitivity analysis of the encoder's hidden dimension on the prediction performance, and the experimental results are shown in Figure 4.

As shown in the figure, the encoder's hidden dimension has a significant impact on the model's prediction performance. In particular, there is a clear upward trend in performance from low to medium dimensions. When the hidden dimension increases from 16 to 64, the model's R² score improves rapidly. This indicates that a larger hidden space provides stronger representation capacity, allowing the model to better capture nonlinear structures and temporal dependencies in stock price sequences.

However, when the hidden dimension further increases to 128 and 256, the prediction performance begins to decline. This suggests that an overly large representation space may introduce redundant features. As a result, the model's attention becomes scattered, weakening its ability to model core temporal structures. Higher-dimensional representations also increase the risk of overfitting, especially when the available financial data is relatively limited.

The best performance is achieved when the hidden dimension is set to 64. This setting strikes a desirable balance between representational capacity and model complexity. It ensures the model can capture multi-granularity structures while also maintaining efficiency in computation and generalization. This demonstrates the sensitivity and robustness of the proposed method in structural configuration.

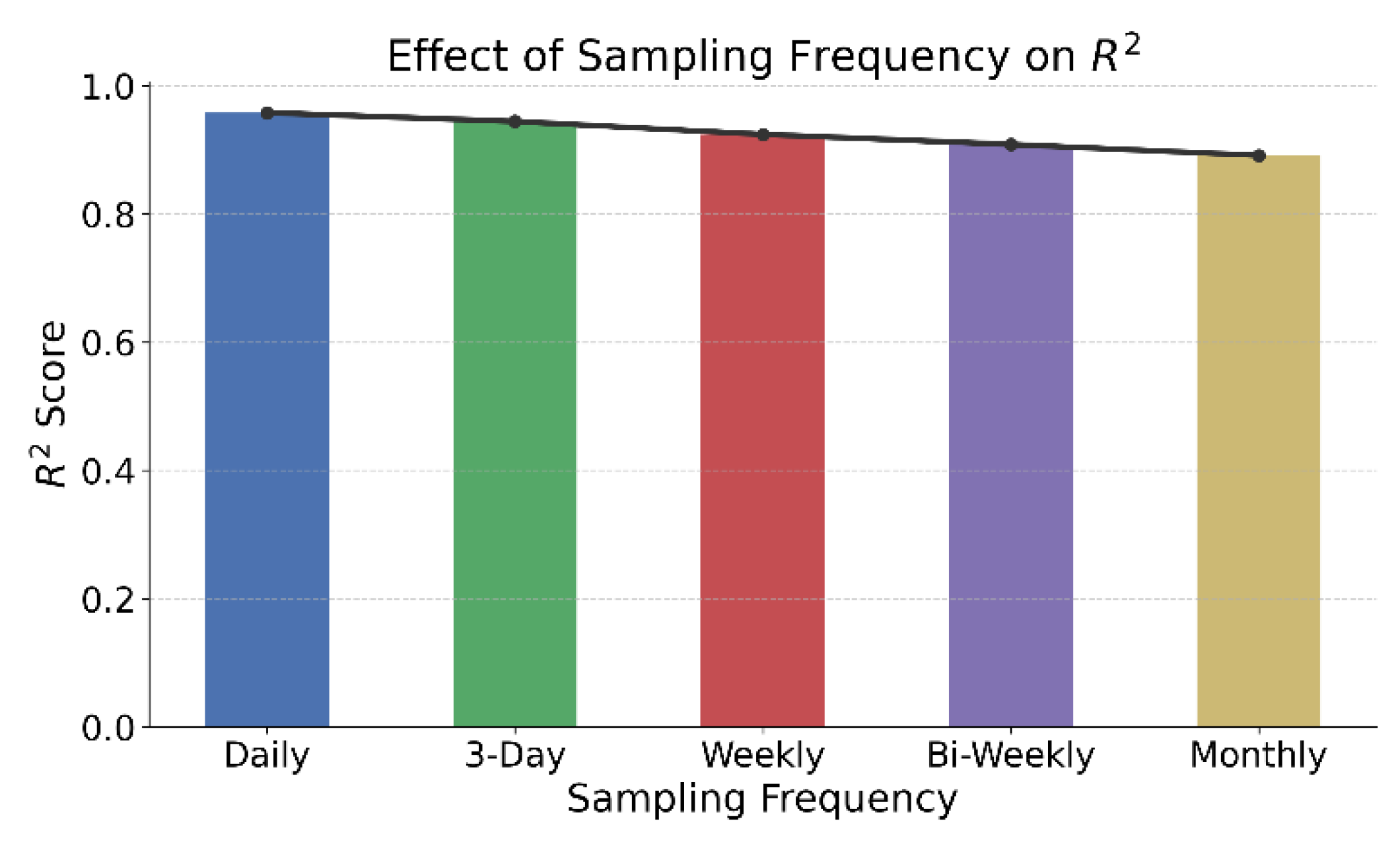
This paper further gives the impact of data sampling frequency on time modeling capability, and the experimental results are shown in Figure 5.

As shown in the figure, the model's R² performance shows a gradual decline as the sampling frequency decreases. This indicates that high-frequency data contains greater information density and structural expressiveness for temporal modeling tasks. Inputs based on daily data provide continuous and detailed price movement information. This helps the model learn more complete trend structures and short-term fluctuation patterns, thereby improving prediction accuracy.

When the sampling frequency is reduced to weekly or monthly levels, the model performance drops significantly. This is because low-frequency data introduces gaps in temporal resolution, which limits the model's ability to capture continuity and contextual dependencies. Critical price turning points, local peaks, and rapid fluctuations may be compressed or lost in low-frequency sampling. This weakens the model's ability to perceive structure and reduces the effectiveness of temporal modeling.

From the trend, the 3-day sampling still maintains a relatively high performance, slightly below daily data. This shows that when data sparsity is limited, the model can still adapt to temporal structures effectively. However, from biweekly to monthly data, the model's ability to extract underlying structures continues to weaken. This confirms that temporal granularity has a direct impact on self-supervised feature learning.

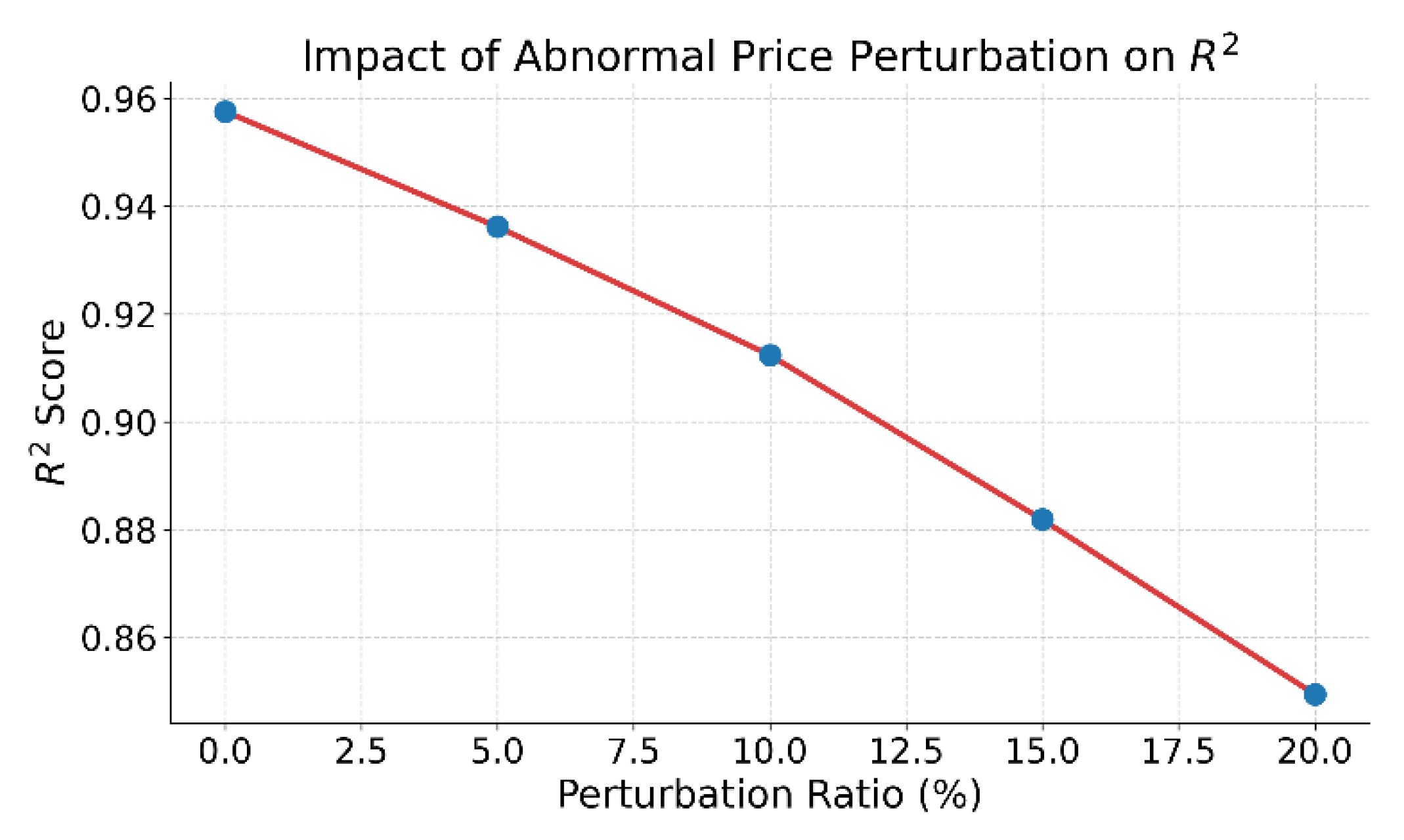
This paper further gives the impact of abnormal price disturbance injection on prediction accuracy, and the experimental results are shown in Figure 6.

The figure shows the impact of abnormal price disturbance ratios on the model's prediction performance. As the disturbance ratio increases from 0% to 20%, the R² score drops significantly. This indicates that the model's ability in temporal modeling and feature robustness is weakened under structural perturbation. The stability of predictions declines as local patterns in the original sequence are disrupted, making it harder for the model to align historical patterns with future trends.

At lower disturbance levels, such as below 5%, the model still maintains relatively strong prediction performance. This suggests that the model has some structural adaptability and fault tolerance. This is attributed to the structural awareness learned during the self-supervised phase, which enables the extraction of stable features under noisy conditions. However, as the disturbance level increases, structural damage intensifies. The model's responsiveness to temporal changes begins to decline.

When the disturbance ratio reaches 15% or higher, the model experiences a sharp drop in predictive accuracy. This implies that a high proportion of abnormal price points exceeds the model's reconstruction tolerance. As a result, the structural balance is broken. The encoding stability in the hidden representation space is reduced, making it difficult for supervised fine-tuning to produce accurate regressions. This severely affects the final prediction results.

This experiment highlights the impact boundary of abnormal disturbances in financial time series modeling. It also confirms the importance of robust self-supervised representations in resisting noise. To handle abnormal fluctuations in real-world trading data, the model needs to incorporate anomaly detection or denoising mechanisms. By enhancing the structural pathway from input to representation, the model can improve its resilience and stability in practical financial applications.

VI. Conclusion

This paper addresses the challenges of limited supervision signals, complex structural modeling, and multi-scale temporal heterogeneity in stock price prediction tasks. A two-stage self-supervised pretraining modeling method is proposed. In the pretraining phase, the model captures global trends and local dynamics in separate stages. This guides the model to learn high-quality temporal representations under unsupervised conditions. In the fine-tuning phase, supervised signals are integrated to perform refined regression prediction. This enhances the model's ability to perceive and fit the trajectory of price changes. The entire architecture forms a structural loop from feature extraction to prediction, offering good stability, generalization, and structural adaptability.

Through multiple model comparisons and sensitivity experiments, the proposed method demonstrates strong robustness and flexibility under varying conditions. These include different time window lengths, encoding dimensions, data sampling frequencies, and input disturbance levels. The results confirm the applicability and effectiveness of the two-stage self-supervised mechanism in complex financial time series settings. The model also maintains a lightweight structure while effectively integrating multi-granularity features. This avoids the redundancy often found in deep architectures and provides a practical optimization path for real-world financial system deployment.

This study enriches the application paradigm of self-supervised learning in the financial domain. It also lays a methodological foundation for multi-task and multi-structure financial time series modeling. The design is highly generalizable and can be extended to other financial sub-markets, such as foreign exchange, futures, and digital currencies. It shows good compatibility and transferability, offering theoretical and practical support for building efficient and intelligent financial decision-making systems.

VII. Future Work

Future work can explore several directions. First, incorporating dynamic graph-based cross-asset modeling can enhance the model's ability to capture market linkages. Second, integrating modules such as anomaly detection and causal inference can strengthen the model's response to unexpected events. Third, in multi-source heterogeneous data scenarios, exploring the complementary effect of multimodal self-supervised signals may improve predictive accuracy. These extensions will support the advancement of financial AI systems toward higher levels of cognitive intelligence, improving their practicality and interpretability in real-world environments.

VIII. Use of AI

Utilizing artificial intelligence to assist with grammar and wording, I personally conceived and developed the significant ideas, conducted thorough analysis, and crafted the original writing.