Towards Building a Unified Adsorption Model for Goethite Based on Variable Crystal Face Contributions: III. Carbonate Adsorption

1. Introduction

Goethite (α-FeOOH), a thermodynamically stable Fe(III) oxyhydroxide, is an abundant mineral in the earth’s critical zone. It is found in very small particle sizes, which makes it a highly influential player in the adsorption of nutrient and contaminant ions, and thus in their fate and transport in geochemical environments [1].

Carbon dioxide and its carbonate dissolution products are ubiquitous components of aqueous environments, affecting the reactivity of ionic species through complexing and competitive reactions. Among these, their binding to mineral surfaces affects the adsorption behavior of other anions, but also that of cations, and therefore it is of wide interest to determine the carbonate adsorption behavior and surface affinity parameters in relevant minerals, especially on goethite [2,3,4].

In this work we report the surface complexation modeling results of a previously generated extensive data set for carbonate adsorption unto goethite [2] under closed and open CO₂ systems, spanning a wide range of conditions in total carbonate concentrations, pH and ionic strength. We used the extended Charge-Distribution MultiSite Ion Complexation Model (CD-MUSIC) [5], to unify adsorption parameters for goethite, following two previous articles published in this series [6,7].

Synthetic goethite particles expose two different crystal faces: {101} and {210} (Pnma space group), and show a lath morphology [8,9]. As their specific surface areas (SSAs) decrease below ca 82 m²/g, they show progressively higher adsorption capacities per surface area due to increasing reactive surface site densities, which in turn is related to a progressive increase in the total proportion of crystal face {210} over {101}, because {210} has more than twice the surface density of singly-coordinated (SC) sites than {101} (7.5 sites/nm² vs. 3.03 sites/nm²). We have carefully characterized the surfaces of four different goethites in the range 42-94 m²/g through high resolution electron microscopy techniques, to determine with accuracy the total crystal face contributions of each goethite [8,9].

With the above information, in turn we calculated for the same four goethites in the first part of this series [6], the total reactive surface site densities, i.e., of SC and triply-coordinated (TC) >O(H) sites bound to central Fe(III) atoms in the structural octahedral arrangements of the exposed goethite faces. With this information, we have been able to better constrain parameter optimization in the CD-MUSIC model, by fixing the above site densities for each goethite. This allowed us to determine the acidity constants of the two proton-reactive surface groups of goethite, as log K formation of 8.82 for $\equiv FeO{H}_2^{+0.5}$ sites, and of 9.65 for $F{e}_{3}O{H}^{+0.5}$sites [6].

The SC reactive surface sites show different arrangements on each crystal face. However, we have approximated equal behavior, independently of the crystal face where they’re found, and have computed their total site density (cf. sum of SC site densities for the two crystal faces in Table 1) to simplify an already highly complex model [6]. The surface proton charge modeling show excellent results and point that along the whole pH range, SC sites, considered the most reactive towards ions, show a wide range of significant surface density both of positively-charged proton sites and of negatively-charged proton sites, although the net proton charge for these sites is negative from pH values of ca. 4, depending on the ionic strength. Further model results have provided successful unified parameters that additionally describe the affinity for Pb(II), Zn(II), As(V) and phosphate on the same four goethites previously characterized [6,7].

There is controversy in the literature regarding whether carbonate adsorbs unto goethite as a monodentate or as a bidentate complex. Previous work using the Triple Layer Model has shown successful simulations of the same adsorption dataset we will use in the present work, by defining a monodentate non-protonated complex [3], but a small contribution of a protonated complex was required. In a later work using the Basic Stern CD-MUSIC model, a bidentate non-protonated complex yielded the best simulations [4]. Several arguments were employed to arrive at the latter conclusion, but the most important lies in the close coincidence of the optimized charge distribution parameters with the expected theoretical values based on Pauling and valence bond strengths considerations, which point to the carbonate moiety directing two of its oxygen atoms to the surface. Therefore, a bidentate (bridging) complex on two SC sites was found to describe the data quite well [4].

In the present work we revisit this surface complexation modeling procedure of carbonate adsorption unto goethite, considering the extended CD-MUSIC model and in light of our recent developments regarding unification of the goethite parameters. These have been particularly successful so far for describing the adsorption of oxyanions arsenate and phosphate. We explored different possible surface carbonate complex configurations, including two simultaneous ones, taking into account the size of the carbonate moiety and the interatomic sites distances, to describe the experimental data and report the optimal configuration, affinity constant and charge distribution (CD) parameters.

2. Materials and Methods

2.1. Carbonate Adsorption Data

An extensive adsorption dataset generated previously with a carefully designed apparatus was used [2,3,10]. The vast majority of data were collected on a goethite reported to have 70 m²/g, as determined by nitrogen adsorption BET, and in ionic strengths of 0.01 M and 0.1 M imposed by NaCl. The conditions for the latter were: Closed systems with total volumes of 800 mL divided between gaseous (V_g) and aqueous (V_l) phases in ranges of V_g/V_l from 0.67 to 1.30, and total CO₂ concentrations investigated of ca. 63, 90 and 133 µM; open systems of 237, 400, and 5520 µatm CO₂, one system at 327 µatm CO₂ in NaNO₃ electrolyte, and finally one system at 400 µatm CO₂ in 0.1 NaNO₃ electrolyte on a 94 m²/g goethite [10]. The pH ranges investigated were from 3 to 7.3-7.9 for closed systems and from 3.2 or 4 to 7.8 or 8.8 for open systems, except for the 94 m²/g goethite from pH 4 to 8.5 [10].

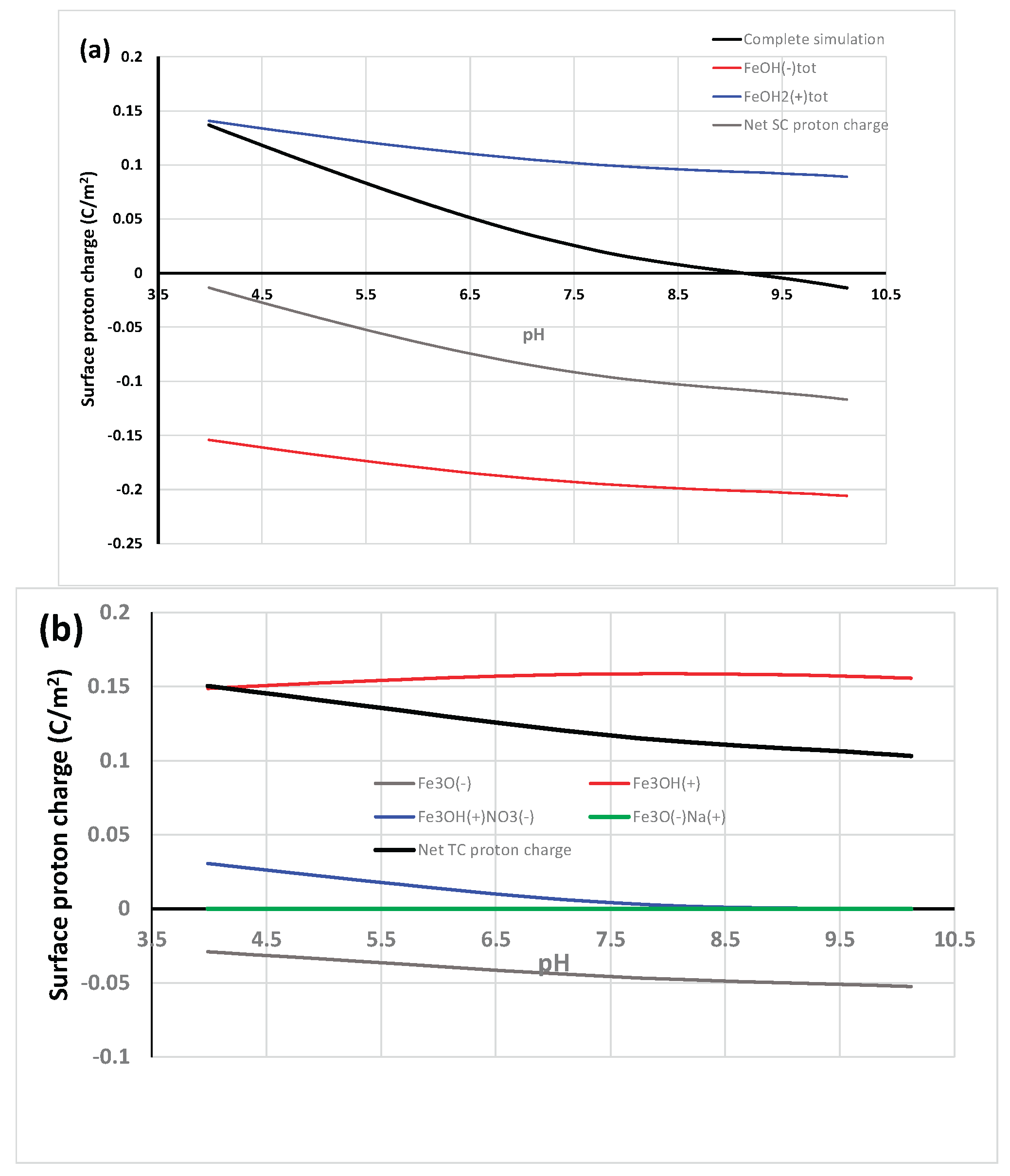
2.2. Goethite Surface Protonation Behavior and CD-MUSIC Modeling in NaCl

The protonation parameters are required before modeling any other ion adsorption behavior, but all previous unified work [6,7] had been performed with NaNO₃ as the background electrolyte, and with goethites of 42, 53, 76 and >82 m²/g (cf. CD-MUSIC model parameters in Table 2).

In the carbonate adsorption experimental work [2], the acid-base titrations were performed at three different ionic strengths (0.01 M, 0.05 M and 0.1 M) both in NaCl and in NaNO₃, on a 70 m²/g goethite. Therefore, initially we had two unknown variables: the corresponding site density and capacitance parameters for this latter goethite, and the affinity constants for Cl^- towards goethite SC and TC positively charged sites. However, we realized that the acid-base titration (proton adsorption) data in NaNO₃ for this goethite [2] were relatively close to those of our well-characterized 76 m²/g also in NaNO₃ [6]. We then corrected the 70 m²/g adsorption data from [2] to 76 m²/g and obtained identical results to our data [6] for the 76 m²/g goethite (cf. Figure 1a).

With this, and our previous modeling of the 76 m²/g [6] we obtained excellent description of the proton charging behavior of the goethite previously labelled as 70 m²/g in NaNO₃. This gave us confidence to optimize the proton charging data with NaCl using the model parameters optimized previously (cf. Table 2), given that most carbonate adsorption data were obtained using this latter electrolyte. The only parameters that needed optimization were thus the Cl^- binding constants, while all remaining parameters were maintained constant, including the site densities and capacitance 1 values for the 76 m²/g goethite (cf. Table 1 and Table 2).

Figure 1. Surface proton charging curves as a function of pH and three ionic strengths (in the legends) (a) in NaNO₃ goethite 76 m²/g [6] and a preparation previously reported as 70 m²/g [2] but corrected to 76 m²/g,; and (b) in NaCl, for goethite previously reported [2] as 70 m²/g but corrected to 76 m²/g. Symbols are experimental data and lines are optimized simulations using CD-MUSIC model parameters reported in Table 2.

Figure 1. Surface proton charging curves as a function of pH and three ionic strengths (in the legends) (a) in NaNO₃ goethite 76 m²/g [6] and a preparation previously reported as 70 m²/g [2] but corrected to 76 m²/g,; and (b) in NaCl, for goethite previously reported [2] as 70 m²/g but corrected to 76 m²/g. Symbols are experimental data and lines are optimized simulations using CD-MUSIC model parameters reported in Table 2.

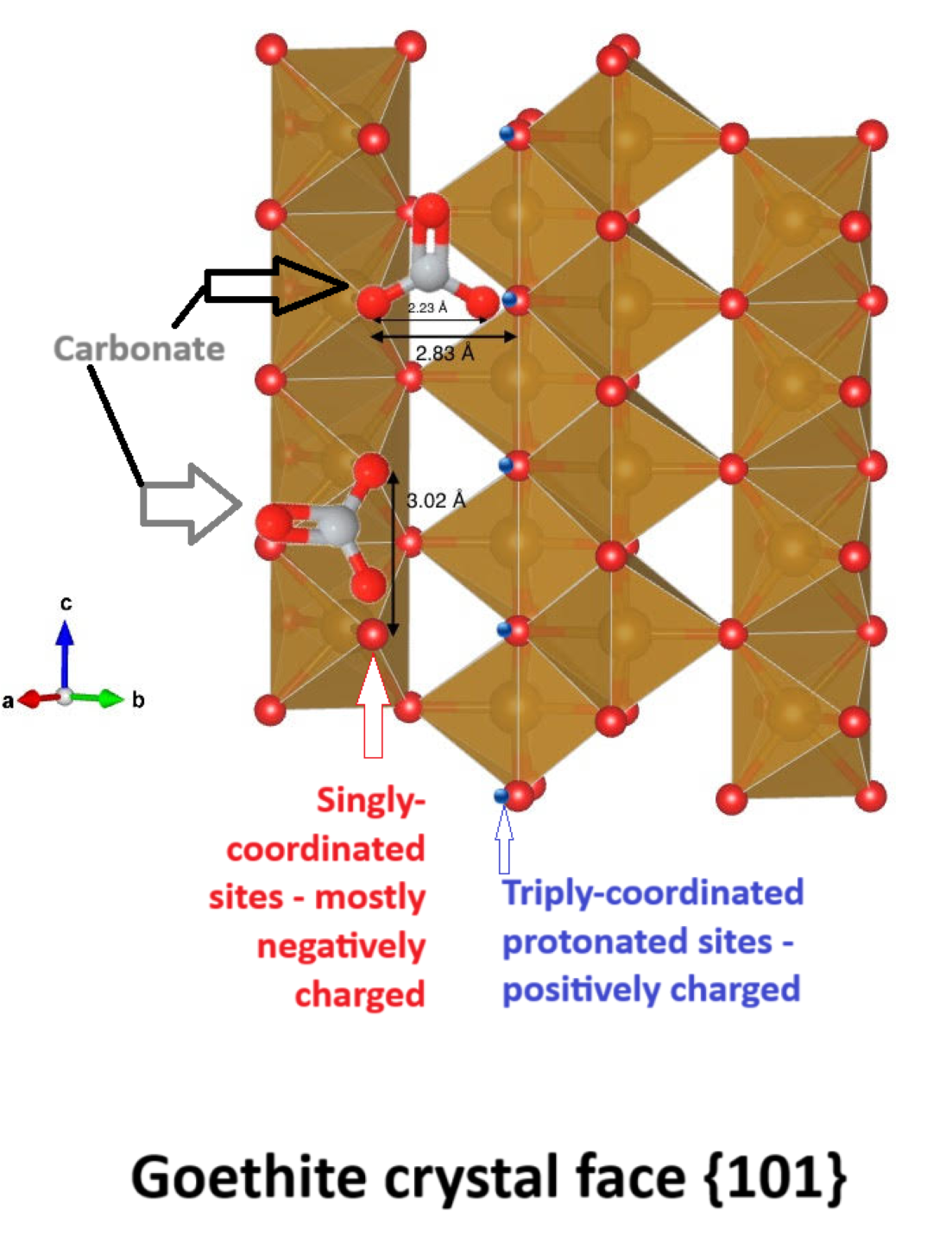
2.3. Carbonate Adsorption Description Using the CD-MUSIC Model

The three-plane formalism of the CD-MUSIC surface complexation model [5] with an extended Stern model was used to simulate the carbonate adsorption data and obtain the optimal binding parameters. The ECOSAT and FIT program codes were used, and the system was fed with the fixed site densities listed in Table 1 and other parameters listed in Table 2 for goethites of 76 and 94 m²/g.

2.3.1. Configuration of the Adsorbed Carbonate Complex

Both monodentate and bidentate non-protonated surface carbonate complexes were tested initially, all on SC sites of both crystal faces. The protonated versions performed poorly in simulating the experimental data, as did the combinations of one protonated and the other non-protonated complex, and viceversa. As was found earlier [4], both monodentate and bidentate complexes alone yielded acceptable simulations with low global errors; however, the monodentate complex was always accompanied by a large proportion of the negative carbonate charge distributed on the 0-plane in comparison with the 1-plane. This is physically unrealistic given that in a monodentate complex only one of the carbonate oxygens is bound to the surface, and thus the remaining two are set to occupy the 1-plane, contributing ideally 2/3 of the -2 charge of carbonate to this latter plane. Similar results have been reported before for the same carbonate adsorption dataset [4], and a very detailed quantitative explanation has been provided using Pauling bond strength and valence concepts. It shows conclusive evidence of how the charge distribution parameter with two oxygens at the 0-plane defines the adequate modeling of carbonate adsorption to goethite [4]; in fact, whatever the configuration of the complex used (protons included), the optimization procedure always pointed to a higher negative charge brought in by the carbonate anion to the 0-plane. Therefore, the optimal complex configuration would seem to be a bidentate complex on adjacent (bridging) SC sites, and only one complex is necessary to describe the whole set of experimental data available.

Nevertheless, there are a couple of complicating factors when proposing this bidentate binuclear complex. Carbonate is a relatively small oxyanion that shows a planar trigonal structure between the C atom and the three oxygens, with O-O interatomic distances of 2.22-2.23 Å, which are highly constant in crystalline solids and aqueous ions [11,12]. On the other hand, the O-O interatomic distances from adjacent SC surface sites on goethite faces {101} and {210} are 3.02 Å (cf. Figure 2a) and 2.90, 2.96 Å, respectively [13], if no bond relaxation occurred. In order to fit a bidentate bridged (binuclear) carbonate complex between two adjacent SC >O sites, a very large stretch of the involved oxygens would have to occur, i.e. of 0.7-0.8 Å. These values are too large to justify possible relaxation of bonds. In fact, given the C-O bond average distances of 1.28 Å, if the angle of the trigonal anion stretched to yield a maximum of 180^o (i.e., making an O-C-O straight line), the interatomic distance would become only 2.56 Å (=2 x 1.28 Å); therefore, it is physically impossible for carbonate to form a bidentate carbonate on adjacent SC sites of either crystal faces.

Instead, we propose a surface complex that binds to a SC >O site and to an adjacent TC >OH site, positively charged across the whole pH range [6,7] (cf. Figure 3b), which lies at a distance of 2.83 Å from the former (Figure 2b). This is only possible on crystal face {101} because face {210} does not have TC sites, and we have considered DC sites (present in both faces) as unreactive. An adjacent SC site will probably not be positively charged (Figure 3a) and lies further away (3.02 Å – Figure 2a) from the one that binds the carbonate anion in a covalent fashion. In the newly proposed complex, the other carbonate oxygen would be strongly electrostatically attracted to this TC positive charge, forming a semi-ionic bond between C-O^- and Fe₃OH^0.5+. The energy of this OH^0.5+--^-O bond would be somewhere between that of a hydrogen bond and that of a covalent bond, and as such the carbonate oxygen physically lies a certain short distance away from the TC site, i.e., the 0.6 Å that are missing to complete the O-O distance from the carbonate anion (or less if some atomic relaxation occurred at the surface sites). We do not consider this part of the complex as an outer sphere interaction since the separation is small, relative to that of the diameter of a water molecule in a hydration shell (ca. 2.75 Å), and thus the charge on both sides is semineutralized (c.a. half of the -1 charge of the carbonate oxygen would remain). When we tried to add a second monodentate complex only on face {210}, optimizations did not yield an adequate combination of both complexes, with the monodentate complex yielding highly unrealistic CD values.

Figure 2. Goethite crystal face {101} (only the top-most structural octahedral layer is shown) rotated in different directions to show more clearly (a) the O-O interatomic distances for adjacent SC sites (3.02 Å) and from SC sites adjacent to reactive TC sites (2.83 Å); and (b) the configuration of the carbonate complex proposed bound to a SC site and an adjacent positively charged TC OH site. The O-O interatomic distances for carbonate are 2.22 Å in average. The blue circles denote protons that confer a net positive charge to the vast majority of these sites, across the pH range studied (Figure 3b). The structures were cut from a multiplied goethite unit cell [13] using the VESTA software [14].

Figure 2. Goethite crystal face {101} (only the top-most structural octahedral layer is shown) rotated in different directions to show more clearly (a) the O-O interatomic distances for adjacent SC sites (3.02 Å) and from SC sites adjacent to reactive TC sites (2.83 Å); and (b) the configuration of the carbonate complex proposed bound to a SC site and an adjacent positively charged TC OH site. The O-O interatomic distances for carbonate are 2.22 Å in average. The blue circles denote protons that confer a net positive charge to the vast majority of these sites, across the pH range studied (Figure 3b). The structures were cut from a multiplied goethite unit cell [13] using the VESTA software [14].

In this manner, the proposed complex (Figure 2b) would show an intermediate nature between purely monodentate and bidentate complexes.

Kubicki and collaborators [15] simulated the hematite (α-Fe₂O₃) surface as small edge-sharing dioctahedral Fe³⁺ clusters and predicted formation of stable bidentate (bridged) and monodentate carbonate surface complexes using MO/DFT (Molecular Orbitals/Density Functional Theory) model calculations. In order to accommodate the bidentate (bridged) carbonate configuration, the model predicted large stretching of the bound Fe-O angles. The theoretical calculations were able to predict previous infrared evidence [16] for these complexes. The question remains whether such a large stretching is possible in real larger scale crystal faces with more constraints from surrounding octahedra (both from those that share edges and from those found in rows at close distance, from the occupied SC sites). The complex we propose here most likely yields spectroscopic signals that are close to those of true bidentate nature.

Figure 3. Surface protonation simulations using the CD-MUSIC model for GOE94 in 0.01 mol/L NaNO₃ (from data reported by [6]); proton charge components separating total negatively and positively proton-charged sites, and the net proton charge for: (a) singly-coordinated (SC) sites, also showing the total proton charge (that includes triply-coordinated – TC sites); and (b) the individual triply-coordinated (TC) sites. For (a) the components shown include the corresponding electrolyte-binding complexes, while for (b) all surface species are shown separately. A similar behavior occurs with Cl^-, with a higher contribution of the Cl^- bound complex.

Figure 3. Surface protonation simulations using the CD-MUSIC model for GOE94 in 0.01 mol/L NaNO₃ (from data reported by [6]); proton charge components separating total negatively and positively proton-charged sites, and the net proton charge for: (a) singly-coordinated (SC) sites, also showing the total proton charge (that includes triply-coordinated – TC sites); and (b) the individual triply-coordinated (TC) sites. For (a) the components shown include the corresponding electrolyte-binding complexes, while for (b) all surface species are shown separately. A similar behavior occurs with Cl^-, with a higher contribution of the Cl^- bound complex.

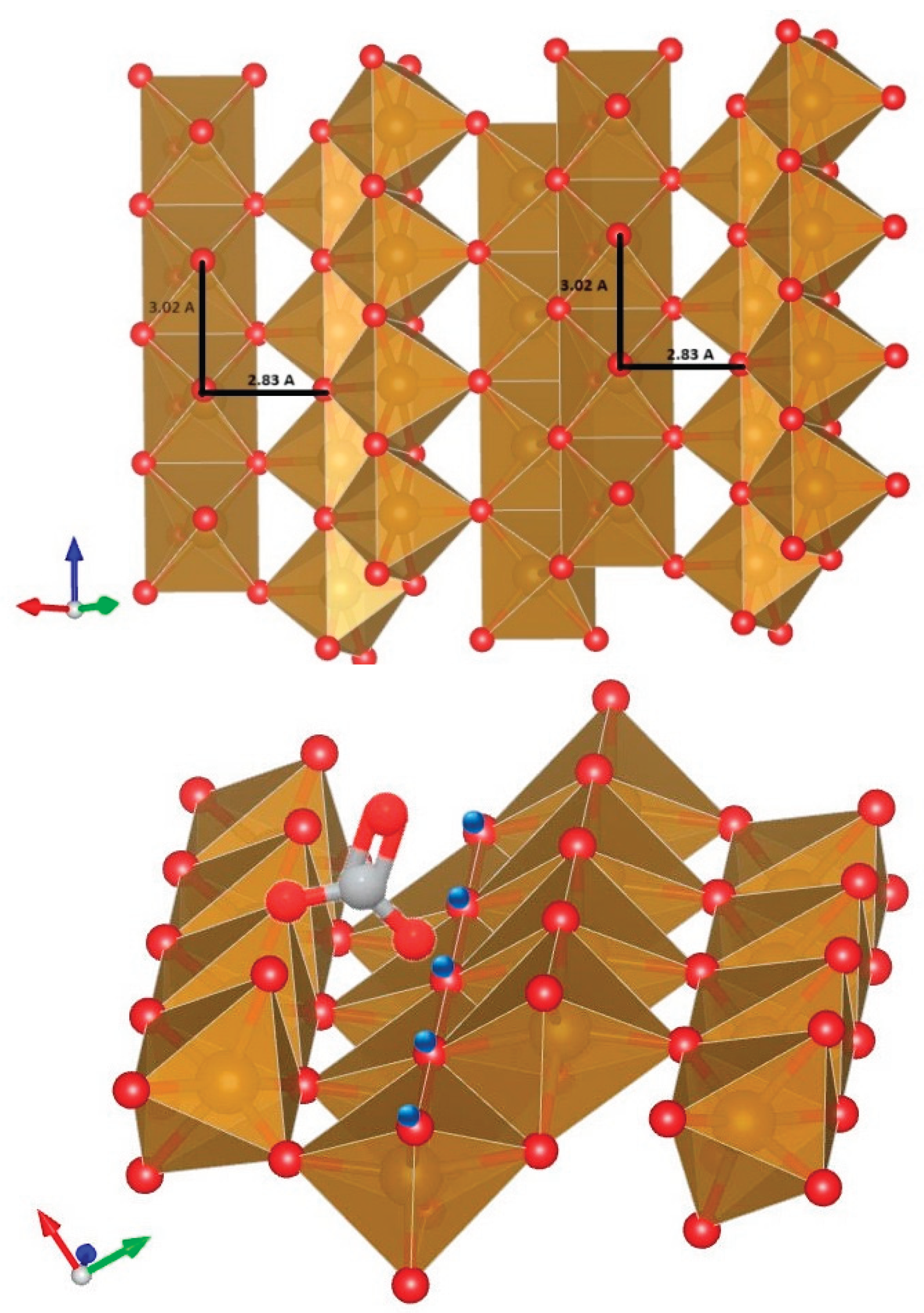
2.3.2. Infrared Evidence

Another line of reasoning that does not support the formation of a bidentate binuclear carbonate complex comes from infrared experimental evidence: The asymmetric OCO stretching band ν₃ at 1390 cm⁻¹ of the aqueous CO₃^2- oxyanion is affected when it binds to other cationic species and to mineral surface sites, because the symmetry of all free oxygens bound in resonance to the central C atom is broken and thus, a split band appears [3,4,17,18]. The magnitude of the difference between the resulting bands (Δν₃) is directly proportional to the binding strength of the carbonate to the moiety in question; therefore, surface monodentate complexes are expected to show a lower split, than bidentate ones [3,4,17,18,19,20]. The particular magnitude difference reported previously for carbonate adsorbed unto the same goethite (76 m²/g) is Δν₃ = 155 cm^-1 [3], which closely coincides with [21,22,23].

Jolivet and collaborators [17] showed that the magnitude of Δν₃ is directly proportional to the polarizing power (=z/r²) of the central cation to which the carbonate moiety binds (with attenuating factors, such as H-bond formation, etc.). Cations with similar polarizing power as Fe(III), such as Co(III) show Δν₃ values in the range of 400 to 750 cm^-1 for bidentate bridged (binuclear) complexes, of 310 to 340 cm^-1 for bidentate mononuclear complexes, and of 80 to 110 cm^-1 for monodentate complexes [17,18,19]. The Δν₃ of 155 cm^-1 lies between the values of the above monodentate and bidentate mononuclear complexes, and the complex we propose (Figure 2b) could be such an intermediate complex. The vast majority of bidentate bridged carbonate compounds yield high values of Δν₃, even for cations with considerably lower polarizing power such as Cu(II) they are ca. 200 cm^-1 [17]. Only in a very exceptional case a solid dehydrated Cu(II)-carbonate compound with bidentate bridged binding yielded lower Δν₃ than its bidentate mononuclear hydrated counterparts [20]. In addition, for carbonate adsorbed on different polymorphs of Ga₂O₃, Ga(III) having a very similar polarizing power as Fe(III), a bridged bidentate carbonate was assigned to a Δν₃ observed of 400 cm^-1, while one with Δν₃ of 262 cm^-1 was assigned to a bidentate mononuclear complex [24]. A monodentate bicarbonate was assigned a Δν₃ of 199 cm^-1.

The above infrared evidence points to a surface carbonate complex on goethite that yields too low a Δν₃ band split to consider it arising from a bidentate bridged (binuclear) complex, so the most likely complex configuration would be an intermediate one between a monodentate and a bidentate mononuclear complex.

2.3.3. CD-MUSIC Model Fitting Procedure

The stoichiometry of the proposed complex is shown in equation (1). This complex is only possible on goethite crystal face {101} because no TC sites occur on the {210} face. The model description required definition of separate reactive SC site densities for the {101} face from those of the {210} face according to Table 1.

$${FeOH}^{-0.5}+{Fe}_3{O}^{-0.5}+{CO}_3^{2-}+2H^{+}\to FeOCO{O}^{..}HO{Fe}_3+H_{2}O$$

(1)

The charge distribution of the complex cannot be placed in the above stoichiometry because both Fe_nO sites should be placed on the same (left) side of the equation. However, -1+ΔZ₀ computes the optimal final charge present at the 0-plane, and ΔZ₁ is directly the final charge on the 1-plane.

All experimental data in NaCl as electrolyte were grouped together to optimize simultaneously log K and ΔZ₀; and all data in NaNO₃ were optimized separately also simultaneously, although the data on GOE76 were optimized separately from the data on GOE94. All other parameters were fixed according to the values given in Table 1 and Table 2.

To unify the three separate sets of log K and ΔZ₀, the average ΔZ₀ was computed and used to reoptimize log K values of each set.

With the three optimized log K values, an iterative optimization procedure was performed for the complete set of data beginning with the highest log K value obtained and evaluating the RMSE (root mean square error) and R² obtained.

The Log K value was decreased by 0.01 log units steps, each time computing the RMSE and R², until reaching the lowest log K value from step 4.

The log K chosen as optimal was the one that that yielded the R² closest to 1 and the lowest RMSE. This is the value reported in Table 3, including the errors for the log K and ΔZ₀ parameters.

3. Results

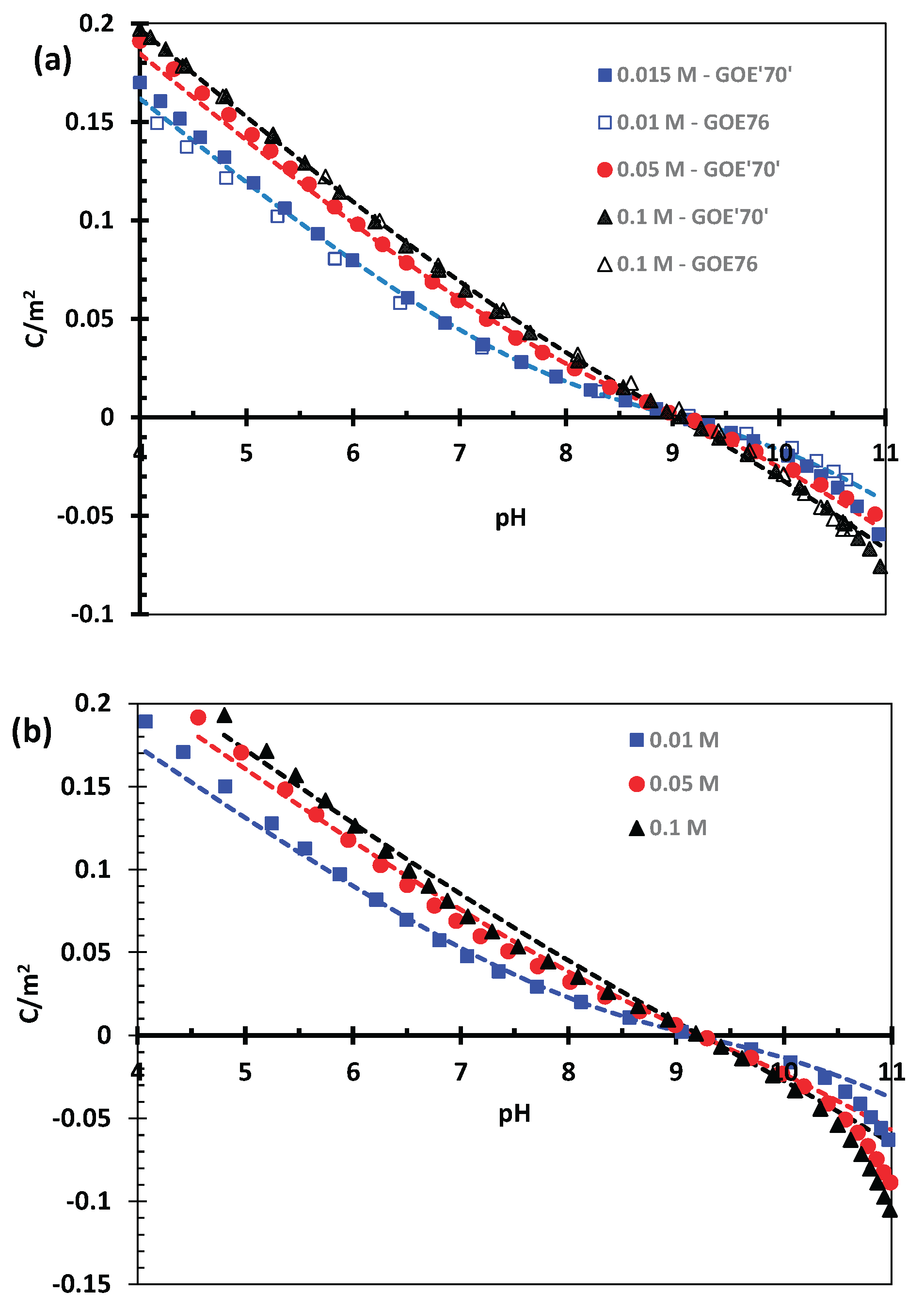
3.1. Goethite Surface Proton Charging in NaCl

The positive surface proton charge of goethite is higher for Cl^- than for NO₃^- at any given pH below the point of zero net proton charge (PZNPC - compare Figure 1a with Figure 1b), and this is evident in the larger intrinsic binding constant obtained for Cl^- of -0.1 log units than for NO₃^- of -0.6 log units (Table 2). This yields a slightly lower symmetry in the electrolyte binding with Na⁺ ions for NaCl, but not large enough that a common intersection point among charging curves of different ionic strengths cannot be found to assign a PZNPC of ca. pH 9.1. The model describes successfully the surface proton charging behavior with pH and ionic strength, but the data are somewhat better simulated in NaNO₃ than in NaCl.

3.2. Carbonate Adsorption Modeling

The proposed complex (Figure 2b) when optimized yielded a global affinity constant of 22.51 logarithmic units, with a relatively low error, below 0.1 log units when simulating all the experimental data (Table 3). Its optimal charge distribution (CD) was -0.28 and -0.72 (=-1+0.72 and =-0.72, cf. ΔZ values in Table 3), for the 0-plane and the 1-plane, respectively. The simulations of the experimental data were very good (Figure 4), but did not perform as well for systems at high ionic strength in NaCl (Figure 4a,b), except for the systems at 5.52 µatm for which performance was excellent for both ionic strengths. Simulations were also excellent for the open systems in nitrate electrolyte at high ionic strength, especially for the 94 m²/g goethite (Figure 4c). The global coefficient of determination, R² was high (0.984 - Table 3). This value is slightly higher than when fitting a non-protonated bidentate complex on adjacent SC sites on both goethite crystal faces (0.980 – not shown).

Figure 4. Carbonate adsorption behavior and CD-MUSIC modeling on a 76 m²/g goethite (previously reported as 70 m²/g [2,3,10]) in NaCl electrolyte on (a) closed systems with gaseous to aqueous volumes of 0.7-0.8 (legends refer to total CO₂ added in µmol/L of suspension); (b) open CO₂ systems; and (c) open CO₂ systems in NaNO₃ electrolyte.

Figure 4. Carbonate adsorption behavior and CD-MUSIC modeling on a 76 m²/g goethite (previously reported as 70 m²/g [2,3,10]) in NaCl electrolyte on (a) closed systems with gaseous to aqueous volumes of 0.7-0.8 (legends refer to total CO₂ added in µmol/L of suspension); (b) open CO₂ systems; and (c) open CO₂ systems in NaNO₃ electrolyte.

The computed proton co-adsorption from the model yielded linear values of [H]_ads/[carbonate]_ads = 1.3-1.6 in NaCl, which compare very closely with those found from the experimental data, of 1.3-1.7 [2]. In NaNO₃ the values also agree exactly: 1.5-1.7 adsorbed protons per adsorbed carbonate, from both sources.

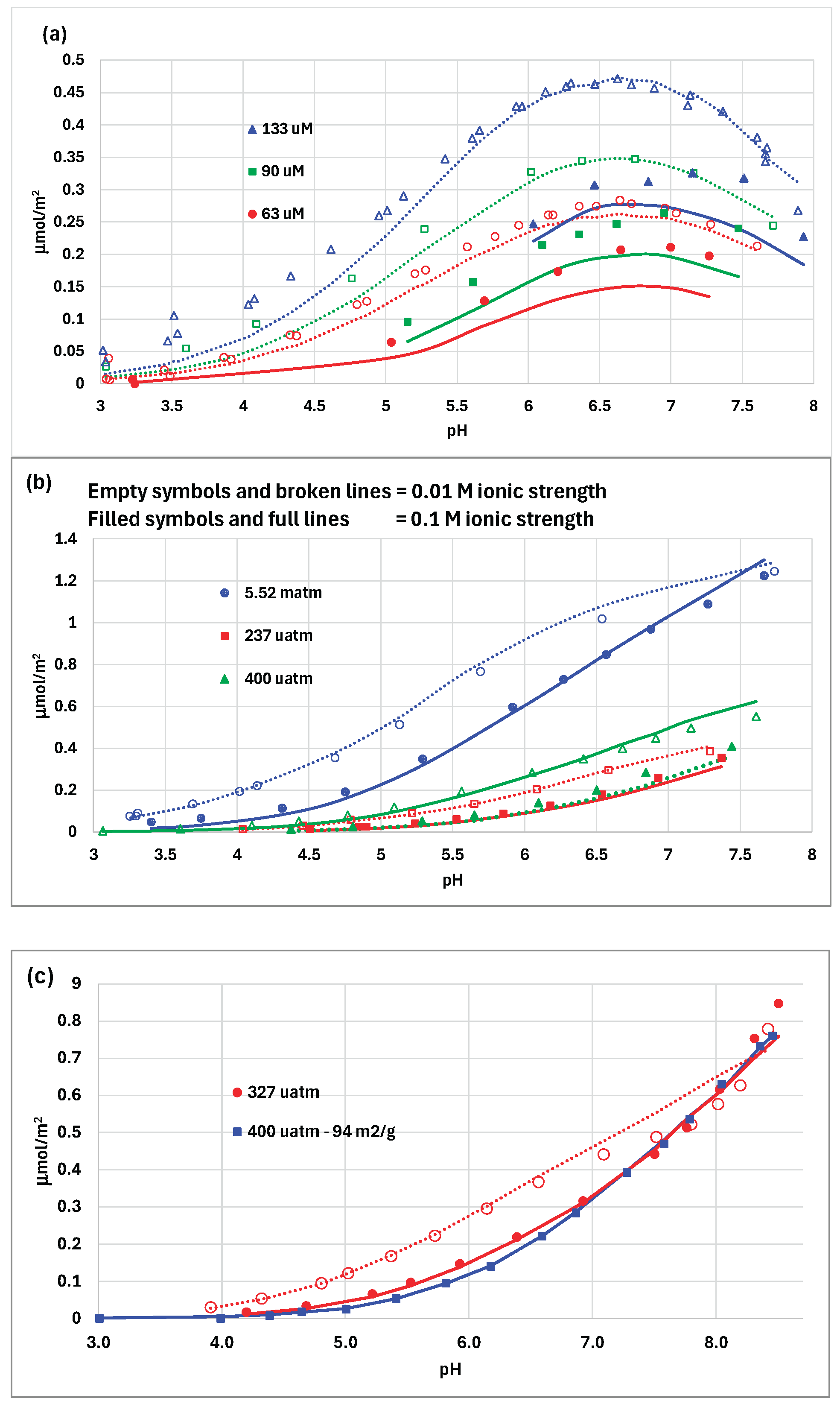
4. Discussion

4.1. Goethite Specific Surface Area and Surface Proton Charging in NaCl

The SSA of the goethite used previously in the carbonate adsorption experiments (and acid-base titrations) in both NaCl and NaNO₃ was reported as 70 m²/g [2,3], but the proton charging data in NaNO₃ coincided with our data for the more recent 76 m²/g goethite [6,9] in the same electrolyte. We speculate that the reason for this comes from the different drying procedures followed for each goethite preparation. The previous goethite was oven-dried, while the more recent goethite was freeze-dried. The decrease in 6 m²/g in the BET determination could be a result of particle aggregation that occurs under oven drying conditions and thus blocking a fraction of SSA, despite the fact that it is later dispersed in a mortar, as compared to the freeze-drying procedure, which is meant to minimize particle aggregation.

Chloride is known to bind more strongly than nitrate to oxide surfaces, this is evident in the experimental proton charging data on goethite (Figure 1), which is also manifested in the optimized intrinsic binding constants of -0.1 log units for Cl^- and -0.60 log units for nitrate (Table 2). A similar difference had been reported previously by Hiemstra and co-workers [4], but their values were -0.5 and -1 log units, respectively, i.e., 0.5 log units lower than our values. This is probably because they approximated the log value of both goethite acidity constants (i.e., to SC and TC sites) to the goethite PZNPC of 9.2. Also, they used a Basic Stern model with an extremely high value of capacitance of 0.9 F/m², whereas our total capacitance value for the Extended Stern CD-MUSIC model is 0.42 = (1/[1/0.93+1/0.75]) (cf. Table 2), in which both capacitance values are close to each other. This latter approach has been later used by Hiemstra and collaborators, e.g., in [25,26] with the corresponding values of their capacitances being 0.85 and 0.75 F/m² [25] or 0.92 F/m² [26] for both (yielding total capacitances of 0.40 and 0.46, respectively). In the latter case, their intrinsic affinity values for Cl^- and for NO₃^- binding were corrected to -0.45 and -0.7 log units, respectively, but still approximating both acidity constants to the PZNPC (this time of 9.0). Finally, their total site density for goethite refers to ideal goethite crystals made of pure face {101} on their elongated section, and pure face {210} at the tips, which yield values of 3.45 SC sites/nm² and 2.7 TC sites/nm². Compare these values with 4.24 and 2.21 sites/nm² (Table 1), respectively according to our calculations [6].

These distinctions in binding strength, capacitances, and site density values are important to confer accurate model descriptions of the goethite/aqueous interface that carry lower error propagations, and may play important roles in describing the competition for surface binding with other ions.

4.2. Carbonate Adsorption

Optimal simulations described the carbonate adsorption data quite well, especially those under open systems, or at low ionic strength (Figure 2). The model reproduces well the large negative effect observed of ionic strength on total carbonate adsorption, which is due to effective competition of the electrolyte anion with carbonate for adsorption sites. This is the result of two contributions: A relatively weak carbonate binding constant of 22.5 log units (Table 3), as compared for example with those obtained using the same model in previous work of this article series for the bidentate complexes of As(V) (29.1 log units [6]) and of phosphate (29.8 log units [7]), combined with the fact that a relatively large absolute negative charge was found at the 1-plane (c.f., ΔZ₁ value in Table 3), i.e., the sample plane where the electrolyte anions reside. The optimized ΔZ values are very close to the theoretical ones, where ΔZ₁ would be -0.67, and this is in agreement with previous CD-MUSIC modeling of the same experimental data [4].

Also, the open system data in 0.1 M NaNO₃ on GOE94 under 400 µatm CO₂ showed slightly lower adsorbed carbonate concentrations in the pH range of ca. 4-7 than the corresponding GOE76 system under 327 µatm CO₂ (despite the former being a higher partial pressure). This illustrates well the higher total capacity (SC site density) of GOE 76 as compared to that of GOE94 (Table 1). The description of these adsorption variations with unified parameters on goethite is one of the main goals of the present article series.

It is noteworthy that the model is able to capture the crossover in adsorption behavior that occurs between ionic strengths for open systems at high pH, e.g., at 327 µatm at pH above 8 (Figure 2c), and especially at 5.52 µatm at pH above 7.5 (Figure 2b). In these regions the data at 0.1 M ionic strength, which below those pH values yields considerably lower carbonate adsorption because of competition with the electrolyte anion, surpass the data at 0.01 M. This may be explained by the fact that in open systems, the total aqueous carbonate concentration present is growing logarithmically with pH after the first carbonic acid pKa (ca. pH of 6.3), and the increase is larger as ionic strength increases in such a way that the dissolved bicarbonate becomes progressively larger with pH at 0.1 M ionic strength than at 0.01 M (cf., Figure 7 in [2]).

The reason for this behavior arises from a chemical activity effect: for the bicarbonate anion, the coefficient (γ), calculated with the extended Debye-Hückel equation, is 0.90 at 0.01 M ionic strength but decreases considerably to 0.77 at 0.1 M ionic strength. Therefore, the corresponding ionic concentrations required to uphold the thermodynamic dissociation constant of carbonic acid (more properly of aqueous hydrated CO₂) at the same activity of aqueous protons, i.e., pH, is larger at higher ionic strength, and the absolute concentration of the total dissolved carbonate is higher at pH values when bicarbonate begins predominating in the aqueous carbonate speciation (pH>6.3) for the higher ionic strength systems. In equation terms, at the same pH above ca. 6.5 (and below 10.3) (γ_HCO3-[HCO₃^-])_{I=0.01 M} = (γ_HCO3-[HCO₃^-])_{I=0.1 M}, or 0.90[HCO₃^-] _{I=0.01 M} = 0.77[HCO₃^-] _{I=0.1 M}. This means that [HCO₃^-] _{I=0.1 M} / [HCO₃^-] _{I=0.01 M} = 0.90/0.77 = 1.17. This increase in dissolved total carbonate concentrations become important at high enough pH values (which are lower as the partial pressure of CO₂ increases) that cause higher adsorption of carbonate at 0.1 M ionic strength, reversing the net negative effect of ionic strength on carbonate adsorption observed at lower pH values, through a sufficient increase in total dissolved carbonate at 0.1 M ionic strength.

When carbonic acid predominates (pH<6.3) no dissolved carbonate difference is calculated between ionic strengths because its activity does not depend on this parameter, since this species has no electrostatic charge.

Finally, our optimized log K of the carbonate complex of 22.51 log units (Table 3) is much larger than the corresponding one obtained previously [4] with the CD-MUSIC model, of 3.90 log units. This is likely the result mainly of the very high total capacitance value they used of 0.9 F/m² as compared to ours of 0.42 F/m² (cf. previous section 4.1). In a later study by the same group [27] using the extended Stern version of the model (with lower total capacitance [26]), they did determine an affinity value much closer to ours (22.01 log units) for a bidentate bridged complex. This value was obtained indirectly from competition experiments with phosphate, but they used extreme conditions meant to mimic very alkaline environments, such as soda lakes: total dissolved carbonate (30-500 mM), pH (7-12), and ionic strengths (mainly of 0.5 M). We believe that obtaining indirect values from ternary systems (with two solutes) may ensue error propagation from the binary system modeling (in their case of phosphate adsorption to goethite). It is always a better choice to ensure accurate values from well-controlled separate single solute (binary) experiments.

They required very high values of total carbonate [27] to observe the competitive adsorption effect of carbonate vs. phosphate (at 0.4 mM total concentration), which shows a much larger affinity for the goethite surface (e.g., K=29.84 log units for the same bidentate configuration, in addition to K=27.48 log units for the monodentate configuration [7] - both required to simulate adequately phosphate adsorption under a wide range of conditions). In these extreme conditions, a Na⁺-outer sphere interaction with the bidentate carbonate surface complex was required, and a significant contribution of an outer sphere carbonate complex, with a CO₃^2- anion, was modeled at the very end of the pH values investigated (ca. pH 11-12) [27]. The justification of the bidentate bridged carbonate complex modeled came from MO/DFT calculations of dioctahedral Fe³⁺ clusters that allowed large bending of the Fe-OH SC octahedral bonds to accommodate the short O-O distances of the bound carbonate moiety (cf. previous section 2.3.1), as in [15].

5. Conclusions

Unified proton charging parameters have been complemented in this third part of the article series by adding the Cl^- affinity to positively charged SC and TC surface sites, with an intrinsic value of -0.1 log units, making it 0.5 log units stronger than NO₃^-. We propose a single carbonate surface complex on goethite that describes the carbonate adsorption behavior in a wide range of conditions, such as pH, carbonate concentrations and ionic strength. This surface complex has a mixed configuration of monodentate binding to SC sites on crystal face {101} and an electrostatic bond to adjacent positively proton-charged TC sites on this face. The O-O distance of carbonate of 2.23 Å is too short to fit as a bidentate complex on adjacent SC sites, because the distances between them range from 2.89 Å to 3.02 Å, depending on the face and assuming no bond relaxation. Even if the C-O-C angle of carbonate were to stretch completely to 180^o the total distance between oxygens would be of 2.56 Å, which makes it impossible to form bidentate (binuclear) bridged complexes. Infrared evidence also supports the formation of a surface complex with a configuration between a monodentate and a bidentate mode.

The formation constant of the surface carbonate complex was optimized to 22.51 log units with a charge distribution of -0.28 and -0.72 valence units, for the 0-plane and the 1-plane, respectively. These parameters describe the carbonate behavior under all conditions studied and unified for goethites of different particle sizes and under different electrolyte anions at different ionic strengths. In this manner, the parameters found may be incorporated in a geochemical speciation database to be applicable for adsorption reactions at any condition with an underlying thermodynamic basis. This is an important step in describing more complex geochemical scenarios when goethite is present as a dominant Fe (hydr-)oxide since carbonate is a ubiquitous anion found as a major component in aqueous geochemical environments.