SAIN: Search-And-INfer, A Mathematical and Computational Framework for Personalised Multimodal Data Modelling with Applications in Health Care

1. Introduction

Multimodal data processing has become a new data science trend with applications in neuro-imaging, health diagnosis and prognosis, environmental modeling, and financial modelling, see [1,2,3].

Methods for searching relevant items in databases have been developed and used for decades, improving their accuracy and speed. These searches are a significant part of personalised modelling (e.g. precision medicine), where an optimal model is created for a given vector of person x data X and a database D of past personalised records with labelled outcomes to predict x behaviour. Most methods (e.g. [3,4]) select a subset $D_X$ of closest vectors to X from the database D (for example, the K-nearest neighbours) and build a machine learning model using this subset $D_X$. To select a subset $D_X$ of the closest vectors to X, the method searches D using predominantly Euclidean or Hamming distances to measure the similarity between the new vector X and the vectors in D. These methods have been applied in many applications and constitute the state-of-the-art in the field (e.g. [5,6,7,8]).

The enormous growth of personal multimodal data worldwide demands more advanced personalisation of search and inference methods. Most methods for multi-modal data represent all modalities of data for one object as a vector and then apply a single machine learning method, such as a deep neural network or a statistical regression (e.g. [9,10]). In these cases, the specificity of each data modality cannot be considered, which negatively impacts the inference results and explanation.

The proposed new method offers new functionality and features for personalised search and model creation in multimodal data, some of which are listed below. The method

• is suitable for multimodal data searches in heterogeneous data sets, e.g. numbers, text, images, sound, and categorical data,
• uses a novel mathematical similarity measure superseding a single (e.g. Euclidean, Hamming) distance used in the existing methods. In this way, inaccurate measurement of similarity on a large number of heterogeneous variables is avoided,
• search is fast even on large data sets, with millions of records and thousands of variables,
• includes advanced personalised searches with multiple parameters and other features,
• facilitates multiple solutions with corresponding probabilities,
• is suitable for unsupervised clustering in multimodal heterogeneous data,
• is suitable for personalised model creation to classify or predict specific outcomes based on multimodal and heterogeneous data.

2. Mathematical Description

In this section, we present the mathematical method.

2.1. Database

We will work with the multidimensional data described as follows:

• $m>1$ objects (samples) $o_1,\dots ,o_m$,
• each object $o_i$ ($1\le i\le m$) is defined by $n>1$ criteria (variables) $c_1,\dots ,c_n$ with values in linearly ordered domains $D_i$ with $min{D}_i$ and $max{D}_i$; if some value $a_{i,j}\in D_i$ ($1\le i\le m$, $1\le j\le n$) is either missing or uncertain, then its value is recorded as ∞,
• $n>1$ weights $w_1,\dots ,w_n$ in $(0,1)$ with ${\sum }_{i=1}^n{w}_i=1$, where each $w_i$ ($1\le i\le n$) quantifies the importance of the criterion $c_i$; if $w_i={\displaystyle \frac{1}{n}}$ for all $1\le i\le n$, then all criteria are equally important; a criterion $c_i$ is ignore if $w_i=0$.

Data of independent variables are organised as follows:

Table 1. Unlabelled database.

Objects/Criteria	${\mathit{c}}_1$	${\mathit{c}}_2$	...	${\mathit{c}}_{\mathit{j}}$	...	${\mathit{c}}_{\mathit{n}}$
$o_1$	$a_{1,1}$	$a_{1,2}$	...	$a_{1,j}$	...	$a_{1,n}$
⋮	⋮	⋮	...	⋮	...	⋮
$o_i$	$a_{i,1}$	$a_{i,2}$	...	$a_{i,j}$	...	$a_{i,n}$
⋮	⋮	⋮	...	⋮	...	⋮
$o_m$	$a_{m,1}$	$a_{m,2}$	...	$a_{m,j}$	...	$a_{m,n}$
w	$w_1$	$w_2$	...	$w_j$	...	$w_n$

Table 1. Unlabelled database.

Objects/Criteria	${\mathit{c}}_1$	${\mathit{c}}_2$	...	${\mathit{c}}_{\mathit{j}}$	...	${\mathit{c}}_{\mathit{n}}$
$o_1$	$a_{1,1}$	$a_{1,2}$	...	$a_{1,j}$	...	$a_{1,n}$
⋮	⋮	⋮	...	⋮	...	⋮
$o_i$	$a_{i,1}$	$a_{i,2}$	...	$a_{i,j}$	...	$a_{i,n}$
⋮	⋮	⋮	...	⋮	...	⋮
$o_m$	$a_{m,1}$	$a_{m,2}$	...	$a_{m,j}$	...	$a_{m,n}$
w	$w_1$	$w_2$	...	$w_j$	...	$w_n$

2.2. Distance Metrics

A distance metric on a space X is a positive real-valued function $d:X\times X\to {\mathbf{R}}_{+}$ satisfying the following three conditions for all $x,y,z\in X$: a) $d(x,y)=0$ if and only if $x=y$, b) $d(x,y)=d(y,x)$, c) $d(x,z)\le d(x,y)+d(y,z)$.

The domains $X=D_i$ can vary greatly: they can be sets of logical values, rational numbers, percentages, digitally codified images, sounds, videos, and many others. We use a bounded distributive complemented lattice $(L,\vee ,\wedge ,\overline{\phantom{x}},0,1)$ to describe uniformly the domains $D_i$, [11,12].

Here is a list with illustrative, but far from exhaustive, examples of domains $D_i$:

• Logical Boolean domain: $(\{0,1\},max,min,\overline{\phantom{x}},0,1)$, where $\overline{x}=1-x,x\in \{0,1\}$.
• Logical non-Boolean domain: $\left(\left\{0,{\displaystyle \frac{1}{N-1}}0.5ex,{\displaystyle \frac{2}{N-1}}0.5ex,\dots ,{\displaystyle \frac{N-2}{N-1}}0.5ex,1\right\},max,min,\overline{\phantom{x}},0,1\right)$, where $x\in \left\{0,{\displaystyle \frac{1}{N-1}}0.5ex,{\displaystyle \frac{2}{N-1}}0.5ex,\dots ,{\displaystyle \frac{N-2}{N-1}}0.5ex,1\right\}$ and $\overline{x}=1-x,$.
• Numerical domain with natural values: $\left(\{0,1,\dots ,N\},max,min,\overline{\phantom{x}},0,1\right)$, where $\overline{x}=N-x,x\in \{0,1,\dots ,N\}$.
• Numerical domain with rational values: $\left(\{x\mid a\le x\le A\},max,min,\overline{\phantom{x}},a,A\right)$, where $\overline{x}=A-x,a\le x\le A$.
• Binary code: $\left({\{0,1\}}^n,max,min,\overline{\phantom{x}},00\dots 0,11\dots 1\right)$, where the domain consists of all binary strings of length n, ${\{0,1\}}^n=\{x_1{x}_2\dots x_n\mid x_i\in \{0,1\}\}$ and for all $x_1{x}_2\dots x_n,y_1{y}_2\dots y_n\in {\{0,1\}}^n$, $max(x_1{x}_2\dots x_n,y_1{y}_2\dots y_n)=max(x_1,y_1)max(x_2,y_2)\dots max(x_n,y_n)$, $min(x_1{x}_2\dots x_n,y_1{y}_2\dots y_n)=min(x_1,y_1)min(x_2,y_2)\dots min(x_n,y_n)$, $\overline{x_1{x}_2\dots x_n}=(1-x_1)(1-x_2)\dots (1-x_n).$

In the lattice $(L,\vee ,\wedge ,\overline{\phantom{x}},0,1)$ we introduce, following [11], the metric:

$$d(x,y)=\left\{\begin{array}{cc}(x\wedge \overline{y})\vee (\overline{x}\wedge y),\hfill & \mathrm{if}\mathrm{x}\ne \mathrm{y},\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

for $x,y\in L$. This metric d can be extended to $L\cup \{\infty \}$ as follows:

$$d_{\infty }(x,y)=\left\{\begin{array}{cc}d(x,y),\hfill & \mathrm{if}\mathrm{x},\mathrm{y}\in \mathrm{L},\hfill \\ \sigma \left(x\right),\hfill & \mathrm{if}\mathrm{x}\in \mathrm{L}\mathrm{and}\mathrm{y}=\infty ,\hfill \\ \sigma \left(y\right),\hfill & \mathrm{if}\mathrm{y}\in \mathrm{L}\mathrm{and}\mathrm{x}=\infty ,\hfill \end{array}0,\mathrm{otherwise},\right.$$

where $\sigma \left(x\right)=max(x,\overline{x})$.

The metrics $d_{\infty ,i}$ on $L_i\cup \{\infty \}$, $1\le i\le n$, can be extended to ${(L_i\cup \{\infty \})}^n$, i.e. to n-dimensional vectors, as follows:

$$d_{\infty }(x_1{x}_2\dots x_n,y_1{y}_2\dots y_n)=\sum _{i=1}^n{d}_{\infty ,i}(x_i,y_i),$$

(1)

where $x_i,y_i\in L_i\cup \{\infty \}$, $1\le i\le n$.

In what follows, we write d for $d_{\infty }$ when the meaning is clear from the context.

2.3. Tasks Specification

Data organised as in Table 2 consists of independent objects augmented with a column of labels, the weights of criteria, and a new unlabelled object, see Table 2 and Table 3.

Additional information associated with data in Table 2 may include the range of each criterion $c_j$ and the associated specific distance, e.g. the Euclidean distance for real numbers and the distance d for binary strings or strings over a non-binary alphabet (e.g. for images or colours).

We consider the following tasks:

Task

1: Calculate the distance (or similarity metric) between the new object and each object in Table 2. If the distance corresponding to $c_i$ is $d_i$, then

$$d(o_j,x)=\sum _{i=1}^n{w}_i·d_i(a_{i,j},x_j).$$

Task

2: Given a threshold $\delta >0$, calculate all objects $o_i$ at a distance at most $\delta$ to x.

Task

3: Calculate the probability of a new object to belong to a labelled class (e.g. low risk vs. high risk) using a threshold $\delta$ and Table 2.

Task

4: Rank the criteria in Table 2 and calculate the marker or markers criterion/criteria, that is the most important one/ones.

Task

5: Assign alternative weights to criteria.

Task

6: Test the accuracy of data and method for Task 4.

2.4. Tasks Solutions

For Task 1 we calculate the distances $d_{\infty }(o_i,x)$ between each object $o_i$ in Table 2 and x in Table 4.

For Task 2, given a threshold $\delta >0$, we calculate all objects in Table 2 at a distance at most $\delta$ to x, that is, the objects which are $\delta$-similar to x:

$$C_{\delta ,x}=\{o_i\mid d(x,o_i)\le \delta ,1\le i\le m\},$$

and its complement $\overline{C_{\delta ,x}}$.

For Task 3 we calculate the probability that x is in class label $l_t$, which is the ratio of the number of objects in $C_{\delta ,x}$ with the label $l_t$ to the size of the cluster $C_{\delta ,x}$:

$$Prob\left(xhaslabel{l}_t\right)={\displaystyle \frac{\#\{o_i\in C_{\delta ,x}\mid l_i=l_t\}}{\#\left(C_{\delta ,x}\right)}},$$

where $\#\{\dots \}$ means the number of elements in the set $\{\dots \}$.

For Task 4, we work with Table 2. Recall that for each criterion $c_i$ we have a domain $D_i$ augmented with information “high" or “low," indicating whether higher or lower values are desirable. Based on this information, we can construct a hypothetical object which has as the most desirable values for each criterion: one could see this object as an “exemplar" one.

Table 5. Hypothetical exemplar object.

Object/Criteria	${\mathit{c}}_1$	${\mathit{c}}_2$	...	${\mathit{c}}_{\mathit{j}}$	...	${\mathit{c}}_{\mathit{n}}$	Class label
$o_E$	$n_1$	$n_2$	...	$n_j$	...	$n_n$	$l_h$

Table 5. Hypothetical exemplar object.

Object/Criteria	${\mathit{c}}_1$	${\mathit{c}}_2$	...	${\mathit{c}}_{\mathit{j}}$	...	${\mathit{c}}_{\mathit{n}}$	Class label
$o_E$	$n_1$	$n_2$	...	$n_j$	...	$n_n$	$l_h$

Sometimes, criteria are interrelated or correlated. This means that in some cases, there is no unique “exemplar object", but a couple of them have to be studied in ranking the importance of criteria.

For example, fix an “exemplar object" $o_E$.

• Compute the distances $d_{\infty }(o_i,o_E)$ between each object $o_i$ in Table 2 and $o_E$, so obtain a vector with n non-negative real components $V_0=(d_1^0,\dots d_n^0)$.
• For each $1\le t\le m$, compute the distances $d_{\infty }(o_i,o_E)$ taking into consideration all criteria in Table 2except$c_t$: obtain the vector $V_t=(d_1^t,\dots d_n^t)$.
• Compute the distances between $dist(V_0,V_t)$, $1\le t\le m$ using the formula

  $$dist(V_0,V_t)=\sum _{i=1}^n|d_{0,i}-d_{t,i}|,$$

  and sort them in increasing order. The criterion $c_t$ is a marker if $dist(V_0,V_t)\ge dist(V_0,V_j)$, for every $1\le j\le m$.

We repeat this procedure for each “exemplar object" and study possible variations.

For Task 5, normalise the distances $dist(V_0,V_t)$ and use these values to construct the weights $w_i^{*}$, $1\le t\le m$.

For Task 6 assume we have weights $\left(w_i\right)$ associated to Table 2 (see Table 1). To test the accuracy of the data and method used for Task 4, compare the original weights $\left(w_i\right)$ with $\left(w_i^{*}\right)$. Serious discrepancies should signal issues either with the data or the choices made in the applications of the method.

2.5. An Example

We illustrate the above tasks with an example of a labelled database in (see Table 6) and a new object (see Table 7), all having the following seven characteristics (the last column has the label classes 1 and 2):

• $c_1$: real number $\{0-100\}$, e.g. age, weight, BMI etc.;
• $c_2$: Boolean value $\{0,1\}$, e.g. gender;
• $c_3$: integer number $\{0-10,000\}$, e.g. gene expression;
• $c_4$: categorical {small, med, large }, e.g. size of tumour, body size, keywords;
• $c_5$: colour {red, yellow, white, black}, e.g. colour of a spot on the body, on the heart;
• $c_6$: spike sequence of $\{-1,0,1\}$ e.g. encoded EEG, ECG;
• $c_7$: black and white image, e.g. MRI, face image.

In this example, for simplicity, we didn’t use weights.

The first step is to code the data in Table 6 and Table 7. The new data is in Table 8 and Table 9.

Then, we normalise the data in Table 8 and Table 9 – the entries in the first, third and fourth columns have been divided by 100, 10,000 and 2, respectively, and the entries in the last three columns have been transformed in reals in the unit interval, and the column of labels has been removed.

In this way, we have obtained Table 10 and Table 11.

Then, we choose an appropriate distance according to each criterion. In this example, we used the Euclidean distance for all criteria.

We can compute $C_{\delta ,x}=\{o_i\mid d(o_i,x)\le \delta \}$ and, accordingly, the probability that x would be labelled in class 1 or class 2.

If $\delta =3.5$, then $C_{3.5,x}=\{o_1,o_2,o_3,o_5,o_6,o_7,o_8\}$ so the probability that x is in class 1 is 2/7 and the probability that x is in class 2 is 5/7. If $\delta =2.5$, then its closest cluster is $C_{2.5,x}=\{o_2,o_3,o_5,o_6,o_7,o_8\}$, so the probability that x is in class 1 is 1/3 and the probability that x is in class 2 is 2/3.

Table 12. Normalised distances from the new object to all objects.

$\mathit{d}({\mathit{o}}_1,\mathit{x})$	0.197	1	0.3889	1	0	0.4	0.11111111	3.09701111
$d(o_2,x)$	0.445	0	0.52321	0.5	0.33333333	0.6	0.22222222	2.62376556
$d(o_3,x)$	0.04	0	0.40079	0	0	0.5	0.22222222	1.16301222
$d(o_4,x)$	0.083	1	0.4559	1	0.66666667	0.45	0.11111111	3.76667778
$d(o_5,x)$	0.222	1	0.36223	0	0.33333333	0.45	0.22222222	2.58978556
$d(o_6,x)$	0.33	0	0.33276	0.5	0	0.45	0.11111111	1.72387111
$d(o_7,x)$	0.082	0	0.23221	1	0.33333333	0.45	0.22222222	2.31976556
$d(o_8,x)$	0.285	1	0.37846	0	0.33333333	0.45	0.22222222	2.66901556
$d(o_9,x)$	0.285	1	0.37846	1	0.33333333	0.45	0.22222222	3.66901556

Table 12. Normalised distances from the new object to all objects.

$\mathit{d}({\mathit{o}}_1,\mathit{x})$	0.197	1	0.3889	1	0	0.4	0.11111111	3.09701111
$d(o_2,x)$	0.445	0	0.52321	0.5	0.33333333	0.6	0.22222222	2.62376556
$d(o_3,x)$	0.04	0	0.40079	0	0	0.5	0.22222222	1.16301222
$d(o_4,x)$	0.083	1	0.4559	1	0.66666667	0.45	0.11111111	3.76667778
$d(o_5,x)$	0.222	1	0.36223	0	0.33333333	0.45	0.22222222	2.58978556
$d(o_6,x)$	0.33	0	0.33276	0.5	0	0.45	0.11111111	1.72387111
$d(o_7,x)$	0.082	0	0.23221	1	0.33333333	0.45	0.22222222	2.31976556
$d(o_8,x)$	0.285	1	0.37846	0	0.33333333	0.45	0.22222222	2.66901556
$d(o_9,x)$	0.285	1	0.37846	1	0.33333333	0.45	0.22222222	3.66901556

Table 13. Ranking of distances in increasing order in Table 12.

$\mathit{d}({\mathit{o}}_3,\mathit{x})$	0.04	0	0.40079	0	0	0.5	0.22222222	1.16301222
$d(o_6,x)$	0.33	0	0.33276	0.5	0	0.45	0.11111111	1.72387111
$d(o_7,x)$	0.082	0	0.23221	1	0.33333333	0.45	0.22222222	2.31976556
$d(o_5,x)$	0.222	1	0.36223	0	0.33333333	0.45	0.22222222	2.58978556
$d(o_2,x)$	0.445	0	0.52321	0.5	0.33333333	0.6	0.22222222	2.62376556
$d(o_8,x)$	0.285	1	0.37846	0	0.33333333	0.45	0.22222222	2.66901556
$d(o_1,x)$	0.197	1	0.3889	1	0	0.4	0.11111111	3.09701111
$d(o_9,x)$	0.285	1	0.37846	1	0.33333333	0.45	0.22222222	3.66901556
$d(o_4,x)$	0.083	1	0.4559	1	0.66666667	0.45	0.11111111	3.76667778

Table 13. Ranking of distances in increasing order in Table 12.

$\mathit{d}({\mathit{o}}_3,\mathit{x})$	0.04	0	0.40079	0	0	0.5	0.22222222	1.16301222
$d(o_6,x)$	0.33	0	0.33276	0.5	0	0.45	0.11111111	1.72387111
$d(o_7,x)$	0.082	0	0.23221	1	0.33333333	0.45	0.22222222	2.31976556
$d(o_5,x)$	0.222	1	0.36223	0	0.33333333	0.45	0.22222222	2.58978556
$d(o_2,x)$	0.445	0	0.52321	0.5	0.33333333	0.6	0.22222222	2.62376556
$d(o_8,x)$	0.285	1	0.37846	0	0.33333333	0.45	0.22222222	2.66901556
$d(o_1,x)$	0.197	1	0.3889	1	0	0.4	0.11111111	3.09701111
$d(o_9,x)$	0.285	1	0.37846	1	0.33333333	0.45	0.22222222	3.66901556
$d(o_4,x)$	0.083	1	0.4559	1	0.66666667	0.45	0.11111111	3.76667778

which induces a ranking of the objects in the Table 8: $o_3,o_6,o_7,o_5,o_2,o_8,o_1,o_9,o_2,$.

For Task 4, assume that the criteria $c_1,\dots ,c_7$ in Table 10 have the additional information $(m,m,m,m,m,M,M)$, where m (M) means that the exemplar value is the minim (maximum) value. Based on this vector, we compute the exemplar object:

Table 14. Exemplar object.

${\mathit{o}}_{\mathit{E}}$

0.2

0

0.00089

0

1

0.1222210012

0.100001001

Table 14. Exemplar object.

${\mathit{o}}_{\mathit{E}}$

0.2

0

0.00089

0

1

0.1222210012

0.100001001

Next we calculate $V_0,\dots ,V_t$, see Table 14, and finally the distances $Dist(V_0,V_t)$, $t=1,2,\dots ,7$ and the weights as their normalised values, see Table 16. The marker, in this case, is the criterion $c_5$.

Table 15. Vectors $V_0,\dots ,V_m$, rounded to two decimals.

${\mathit{V}}_0$	${\mathit{V}}_1$	${\mathit{V}}_2$	${\mathit{V}}_3$	${\mathit{V}}_4$	${\mathit{V}}_5$	${\mathit{V}}_6$	${\mathit{V}}_7$
1.469	0.987	1.469	1.402	1.469	0.669	1.359	1.459
3.709	2.979	2.709	2.730	3.209	3.309	3.609	3.709
3.220	2.975	2.220	3.165	2.220	2.420	3.110	3.210
0.378	0.010	0.378	0.378	0.378	0.378	0.378	0.368
2.167	2.104	2.167	2.073	1.167	1.167	2.167	2.157
3.824	3.209	2.824	3.035	3.324	3.024	3.714	3.814
3.066	2.699	2.066	2.378	3.066	2.066	3.066	3.055
1.487	1.487	1.487	1.410	0.487	1.087	1.477	1.487
1.487	1.487	1.487	1.410	0.487	1.087	1.477	1.487

Table 15. Vectors $V_0,\dots ,V_m$, rounded to two decimals.

${\mathit{V}}_0$	${\mathit{V}}_1$	${\mathit{V}}_2$	${\mathit{V}}_3$	${\mathit{V}}_4$	${\mathit{V}}_5$	${\mathit{V}}_6$	${\mathit{V}}_7$
1.469	0.987	1.469	1.402	1.469	0.669	1.359	1.459
3.709	2.979	2.709	2.730	3.209	3.309	3.609	3.709
3.220	2.975	2.220	3.165	2.220	2.420	3.110	3.210
0.378	0.010	0.378	0.378	0.378	0.378	0.378	0.368
2.167	2.104	2.167	2.073	1.167	1.167	2.167	2.157
3.824	3.209	2.824	3.035	3.324	3.024	3.714	3.814
3.066	2.699	2.066	2.378	3.066	2.066	3.066	3.055
1.487	1.487	1.487	1.410	0.487	1.087	1.477	1.487
1.487	1.487	1.487	1.410	0.487	1.087	1.477	1.487

Table 16. Distances $Dist(V_0,V_t)$ and (normalised) weights.

Distances	2.870	4.00	2.826	5.00	5.60	0.450	0.061
Weights	0.137	0.192	0.135	0.240	0.269	0.021	0.002

Table 16. Distances $Dist(V_0,V_t)$ and (normalised) weights.

Distances	2.870	4.00	2.826	5.00	5.60	0.450	0.061
Weights	0.137	0.192	0.135	0.240	0.269	0.021	0.002

3. Survival Analysis in SAIN

Medical survival analysis evaluates the time until an event of interest occurs, like death or disease recurrence, in a group of patients. This analysis is often used to compare treatment outcomes or predict prognosis.

3.1. Data and Tasks

We are given the following data:

• Table 17 in which the first column lists the patients treated for the same disease with the same method under strict conditions and the last column records the times till the patient’s deaths.
• Table 18, which includes the record of the new patient p.
• A threshold $\delta$ which defines the acceptable similarity between p and the relevant $p_i$’s in the Survival database (i.e. $d(p,p_i)\le \delta$).

We consider the following tasks:

Task 1: What is the life expectancy of p?

Task 2: What is the probability that the life expectancy of p is greater than or equal to a given T?

3.2. Tasks Solutions

Using a standard method of survival analysis

• For Task 1,

  (a)

  Compute the set of patients that are similar up to $\delta$ to p:

  $$C_{\delta ,p}=\{p_i\mid d(p,p_i)\le \delta ,1\le i\le m\}.$$

  (2)

  (b)

  Using $C_{\delta ,p}$, compute the probability that p will survive the time $t_j$:

  $$Pro{b}_{\delta }\left(psurvivestime{t}_j\right)={\displaystyle \frac{\#\{p_i\in C_{\delta ,p}\mid t_i=t_j\}}{\#\left(C_{\delta ,p}\right)}}.$$

  (3)

  (c)

  Compute the life expectancy of p using the formula:

  $$L{E}_{\delta }\left(p\right)=\sum _{j=1,t_j\in C_{\delta ,p}}^m{t}_j\times Pro{b}_{\delta }\left(psurvivestime{t}_j\right).$$

  (4)

• For Task 2, calculate the probability that the life expectancy of p is at least time T:

  $$Pro{b}_{\delta }(LE\left(p\right)\ge T)=\sum _{j=1,t_j\in C_{\delta ,p},t_j\ge T}^{m}Pro{b}_{\delta }\left(psurvivestime{t}_j\right).$$

  (5)

3.3. An Example

We illustrate the above tasks with an example of a database in which columns 2–8 record patients’ medical test results, and the last column records time to death (see Table prec) and a new patient (see Table 20):

Table 19. Patient records.

patients	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$	${\mathit{c}}_5$	${\mathit{c}}_6$	${\mathit{c}}_7$	units of time
$p1$	0.682	0	0.06789	0	0.2	0.012211001	0.110001001	12.3
$p2$	0.93	1	0.98	0.5	0.6	0.022220012	0.100001001	15
$p3$	0.445	1	0.056	1	0.2	0.012121001	0.110101111	68
$p4$	0.568	0	0.00089	0	1	0.122221001	0.110011101	1.4
$p5$	0.263	0	0.09456	1	0	0.122201001	0.110111101	40.5
$p6$	0.815	1	0.78955	0.5	0.2	0.012122001	0.110001111	97.2
$p7$	0.567	1	0.689	0	0	0.122121001	0.111001111	97.2
$p8$	0.2	0	0.07833	1	0.6	0.112211022	0.100001111	55.7
$p9$	0.2	0	0.07833	∞	0.6	0.112211022	0.100001111	63.7

Table 19. Patient records.

patients	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$	${\mathit{c}}_5$	${\mathit{c}}_6$	${\mathit{c}}_7$	units of time
$p1$	0.682	0	0.06789	0	0.2	0.012211001	0.110001001	12.3
$p2$	0.93	1	0.98	0.5	0.6	0.022220012	0.100001001	15
$p3$	0.445	1	0.056	1	0.2	0.012121001	0.110101111	68
$p4$	0.568	0	0.00089	0	1	0.122221001	0.110011101	1.4
$p5$	0.263	0	0.09456	1	0	0.122201001	0.110111101	40.5
$p6$	0.815	1	0.78955	0.5	0.2	0.012122001	0.110001111	97.2
$p7$	0.567	1	0.689	0	0	0.122121001	0.111001111	97.2
$p8$	0.2	0	0.07833	1	0.6	0.112211022	0.100001111	55.7
$p9$	0.2	0	0.07833	∞	0.6	0.112211022	0.100001111	63.7

Table 20. New patient records.

$\mathit{x}\mathit{p}$

0.485

1

0.45679

1

0.2

0.1002121001

0.110001101

Table 20. New patient records.

$\mathit{x}\mathit{p}$

0.485

1

0.45679

1

0.2

0.1002121001

0.110001101

The distance for column 4 is $d(x,y)=|x-y|=$ and $d_{\infty }(x,\infty )=max(x,1-x)$. For example, $d_{\infty }(1,\infty )=max(1,1-1)=1$. For all other columns, the distance is $d(x,y)=|x-y|$. Finally, the total distance is the sum of individual distances (7 terms), with the results in Table 21.

The results for Task 1, (a), (b) and (c) are listed below:

• For $\delta \ge 3.37$, $C_{\delta ,p}=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8,v_9\}$, that is the entire database. Then

  (a)

  $L{E}_{\delta }\left(p\right)=50.11$,

  (b)

  • $Pro{b}_{\delta }(psurvivestime=12.3)=1/9$,
  • $Prob(psurvivestime=15)=1/9$,
  • $Pro{b}_{\delta }(psurvivestime=68)=1/9$,
  • $Pro{b}_{\delta }(psurvivestime=1.4)=1/9$,
  • $Pro{b}_{\delta }(psurvivestime=40.5)=1/9$,
  • $Pro{b}_{\delta }(psurvivestime=97.2)=2/9$,
  • $Pro{b}_{\delta }(psurvivestime=55.7)=1/9$,
  • $Pro{b}_{\delta }(psurvivestime=63.7)=1/9$.

  (c)

  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 1.4)=1$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 12.3)=8/9$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 15)=7/9$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 40.5)=6/9$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 55.7)=5/9$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 63.7)=4/9$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 68)=3/9$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 97.2)=2/9$,

  We can calculate other probabilities, for example, $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 60)=Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 63.7)+Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 68)=3/9+Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 97.2)=2/9=1/9+1/9+2/9=4/9$.
• For $\delta \ge 2.5$, $C_{\delta ,p}=\{v_2,v_3,v_5,v_6,v_7,v_8\}$. Then

  (a)

  $L{E}_{\delta }\left(p\right)=62.27$,

  (b)

  • $Prob(psurvivestime=15)=1/6$,
  • $Prob(psurvivestime=68)=1/6$,
  • $Prob(psurvivestime=40.5)=1/6$,
  • $Prob(psurvivestime=97.2)=2/6$,
  • $Prob(psurvivestime=55.7)=1/6$,

  (c)

  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 15)=1$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 40)=5/6$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 55.7)=4/6$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 68)=3/6$,
  • $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 97.2)=2/6$.

  Similarly, we can calculate the probabilities $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 45)=4/6$, $Pro{b}_{\delta }(L{E}_{\delta }\left(p\right)\ge 100)=0$.

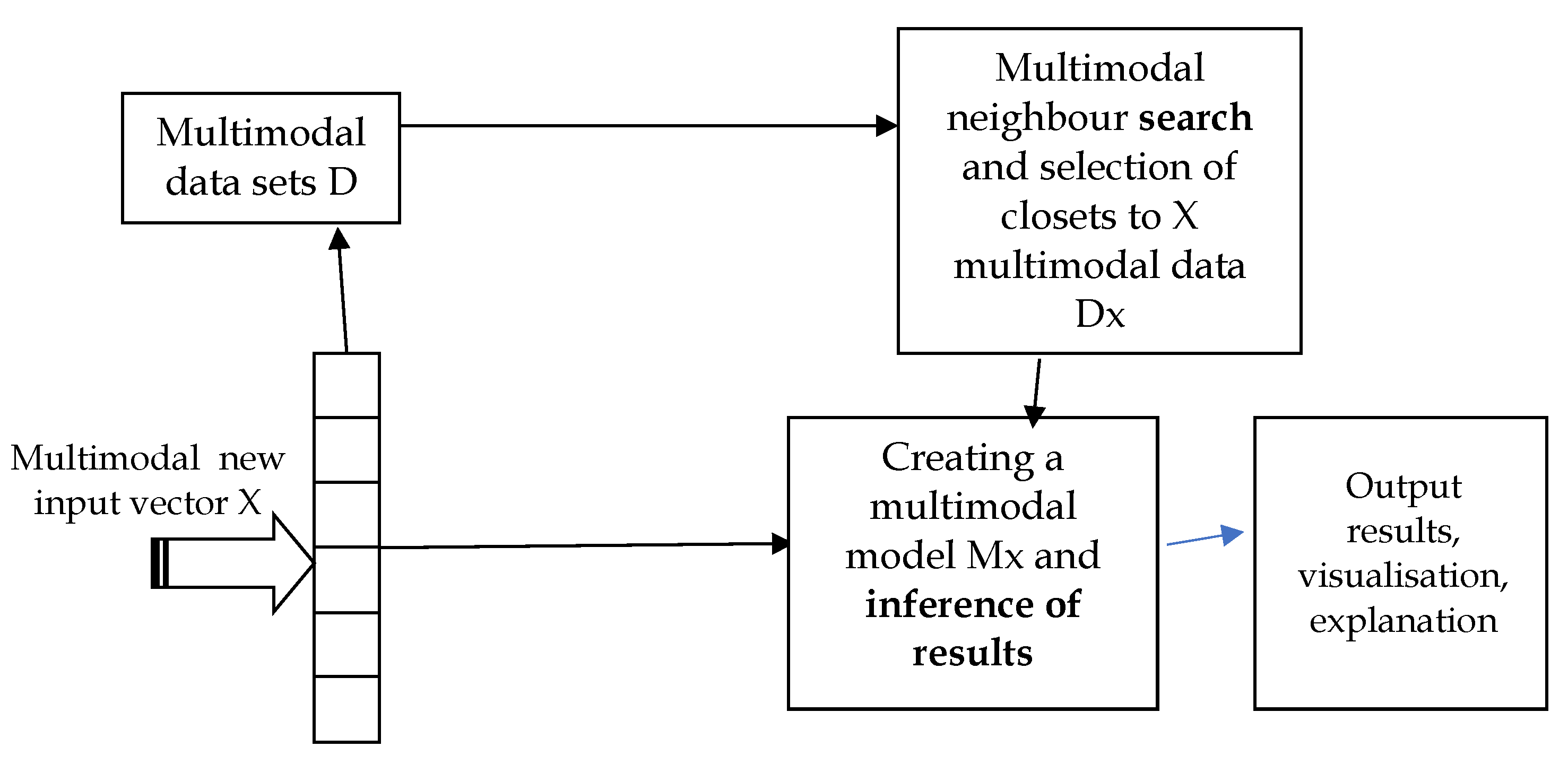
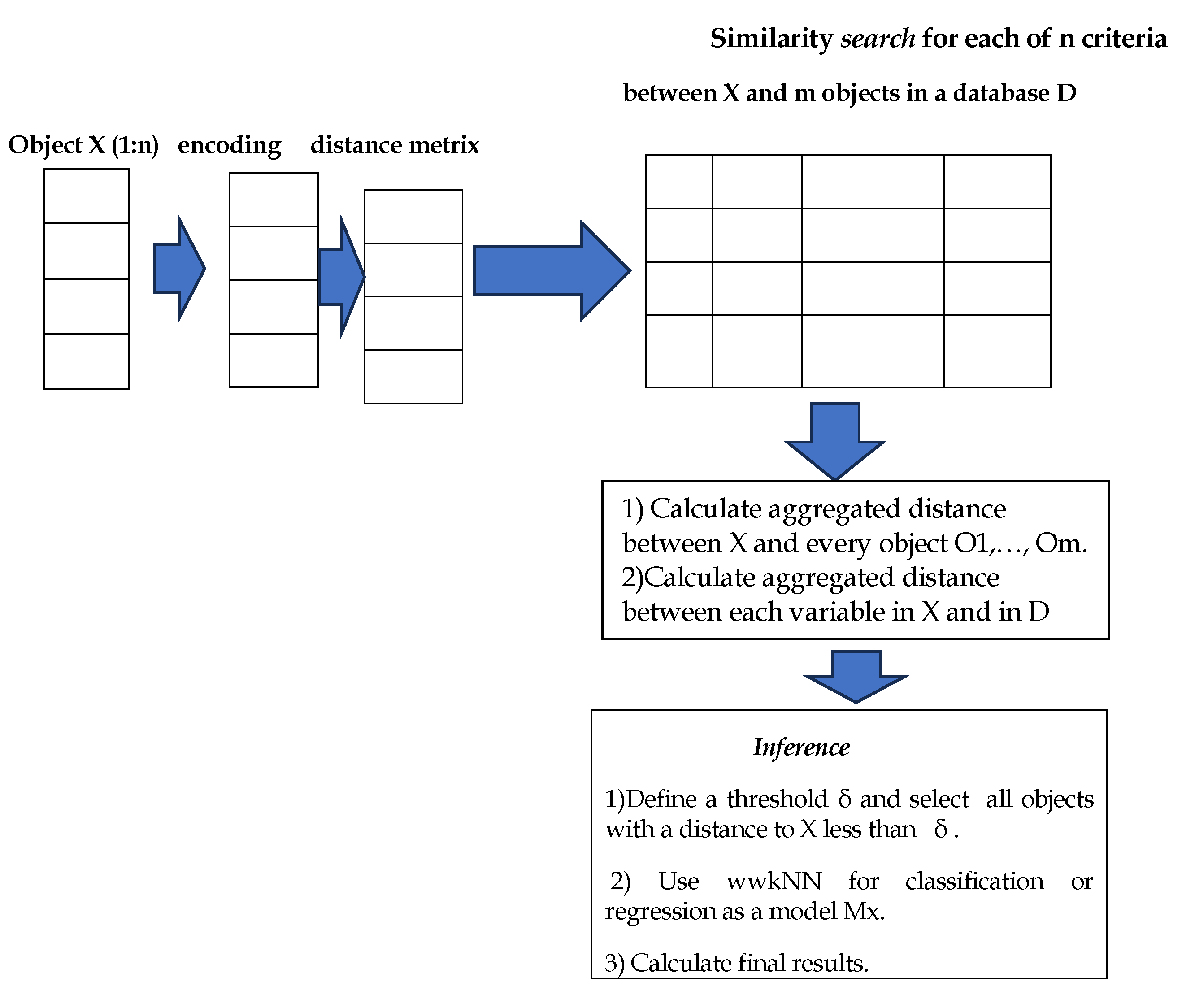
4. SAIN: A Modular Diagram and Functional Information Flow

In Figure 1 and Figure 2, we present the modular diagram and the functional information flow of SAIN.

5. Case Studies for Medical Diagnosis and Prognosis

We present three case studies in which we applied SAIN.

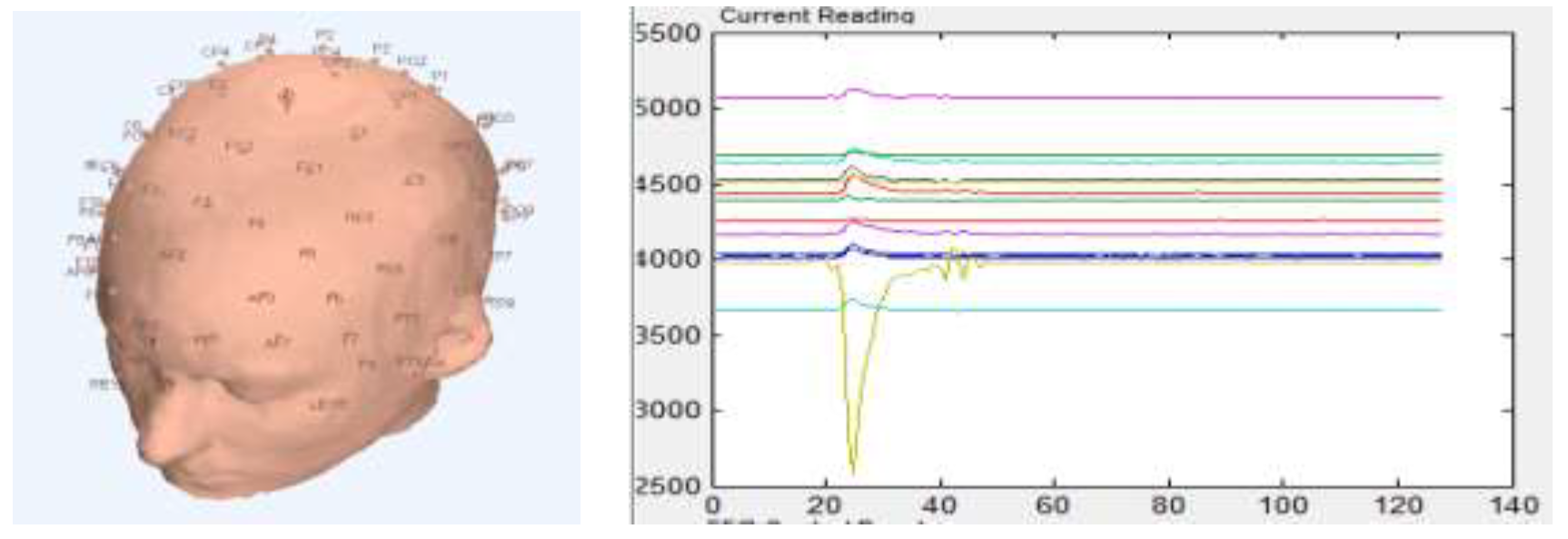
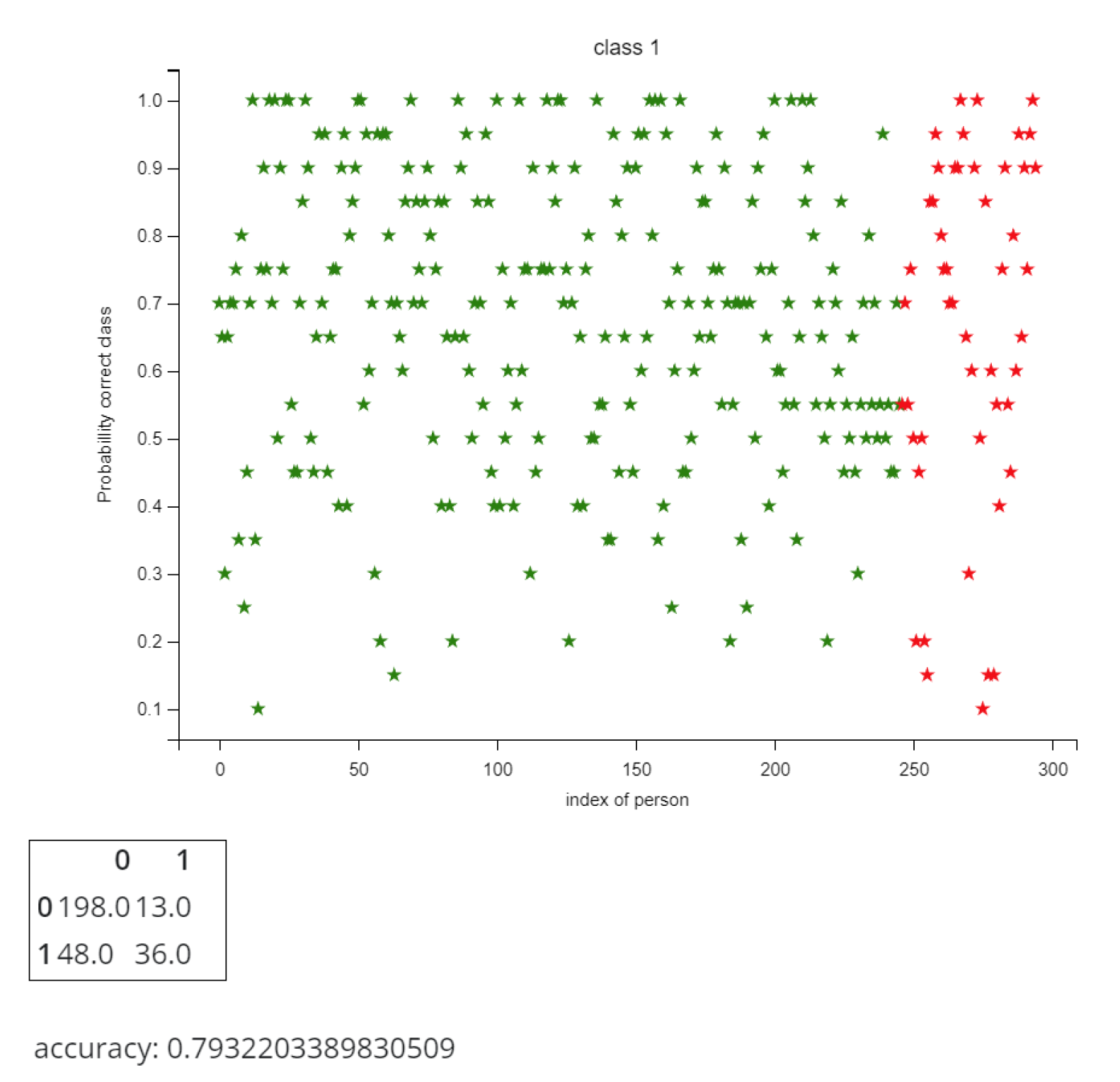
5.1. Heart Disease Diagnosis

We worked with the well-known Cleveland dataset, which contains multiple data types [13]. The UCI Heart Disease data set contains 76 attributes. As in most articles, the attributes in our experiment data were restricted to 14, see Table 22.

The problem is a binary classification on whether the patient has or does not have heart disease.

First, we selected suitable distance metrics and weights to classify the attributes. For binary objects, the distance metric is simply whether they are equal; for non-binary discrete objects such as resting electrocardiographic results, the appropriate distance measure is not obvious and should be informed by an expert. We give electrocardiographic results 0 for normal, 1 for having ST-T wave abnormality, and 2 for showing probable or definite left ventricular hypertrophy following Estes’ criteria.

Many studies with the Cleveland dataset have been tested with different machine learning techniques. For example, [14] lists different algorithms and performances ranging from 47% to 80% accuracy. SAIN achieved an 82% accuracy score. Why SAIN? The search is fast, it uses appropriate distances chosen by a medical expert, it provides explainability at a personal level including probabilities. If offers different scenarious for modelling by experimenting different sets of features, parameters and preferred outcome vizualitations.

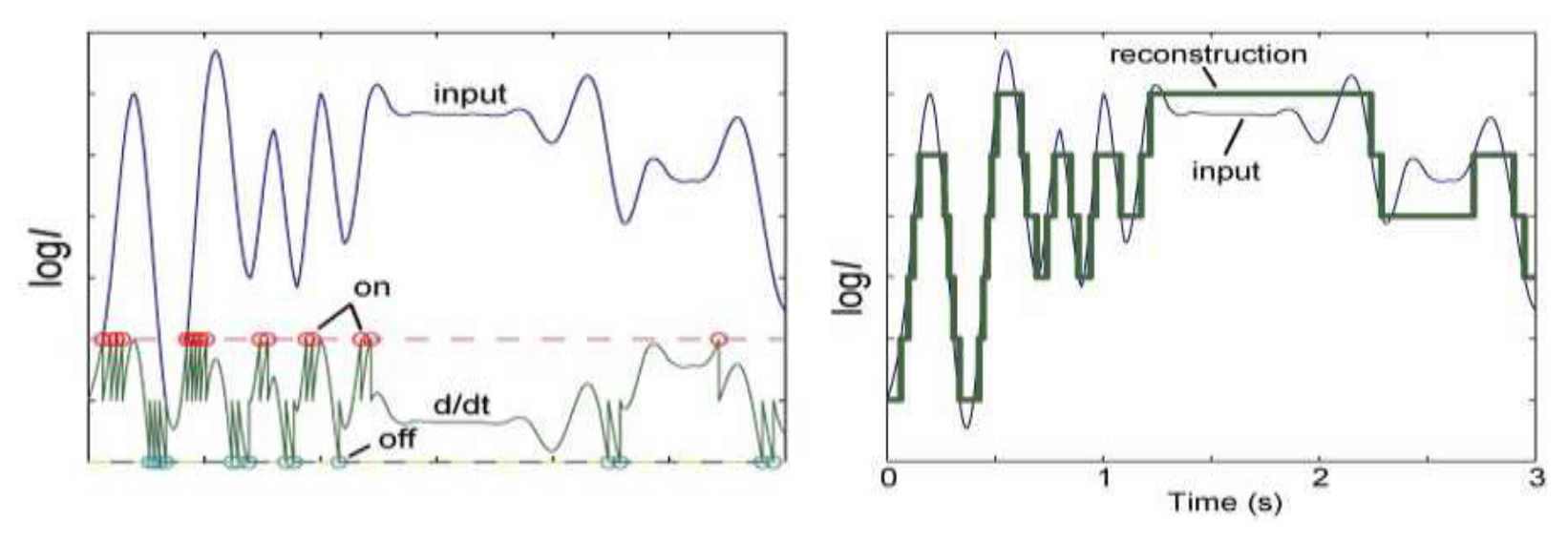
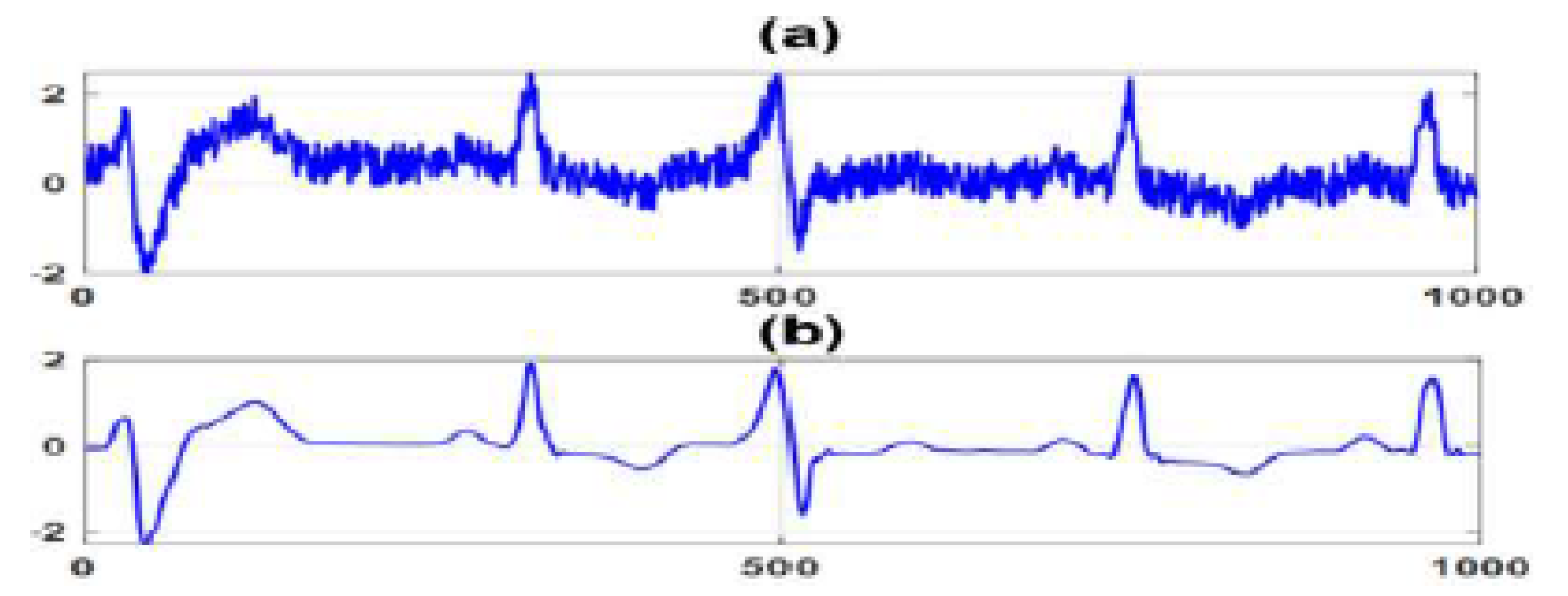
5.2. Time Series Classification

Many data sets for classifying outcomes of events consist of multiple time series. Each variable in a time series may depend on other variables that change in time. The proposed model can deal with this problem by encoding time series (signal) into binary vectors which can be processed for classification in the SAIN framework. The variables for this data set are 14 channels of temporal EEG data channels, located at places of interest on the human scalp.

The signals measured over the same time period are the EEG channels, fMRI voxels, ECG electrodes, seismic sensory signals, financial time series, gene expressions, voice, and music frequency bands [8]. Even when the variable (signal) measurements are independent, the signals may have an impact on each other as they represent the same object/person at the same time period. The number N of these signals can vary from just a few for a short time window T (Figure 3) to hundreds and thousands when the time varies from a few milliseconds to minutes, hours, days, etc.

Figure 4 shows an EEG experiment and Figure 5 shows one cardio-vascular disease signal.

Next we present a simple example how this search can be computed for a new record X consisting of only 3 variables/signals (e.g. EEG channels, ECG electrodes) over a short period of 5 time moments and the data base D constituting of only 6 such records which are labelled by an outcome labels 1,2,3 (e.g. diagnosis, prognosis).

In addition to the record X, a weight vector is supplied with the weighted importance of the signals at different time points, e.g. $W=[0.1,0.2,0.4,0.2,0.1]$, meaning that the most important and informative part of the measurements is at time point 3.

The new record $X=[1,1,-1,0,1]$ (signal, EEG channel 1) 0, 1, 1, 1, -1 (signal, EEG channel 2) 1, 1, -1, -1, 0 (signal, EEG channel 3), $W=[0.1,0.2,0.4,0.2,0.1]$

The database contains records $(Records,R1,R2,R3,R4,R5,LabelsL)$ where:

Table 23. Caption.

Record	Channel 1	Channel 2	Channel 3	Label
R1	(1, 1, -1, 0, 1)	(0, 1, 1, 1, -1)	(1, 1, -1, -1, 0)	1
R2	(1, 0, -1, 0, 1)	( 0, 1, 1, 1, -1)	(1, 0, -1, -1, 1 )	1
R3	(1, 1, -1, 0, 1)	(0, -1, 1, 1, -1)	(1, 1, -1, 0, 1)	2
R4	(1, 1, -1, 0, 1)	(0, -1, 1, 0, -1)	(1, 1, -1, 0, 1)	2
R5	(1, 1, -1, 0, 0)	(0, -1, 0, 1, -1)	(1, 1, -1, 1, 1)	3
R6	(1, -1, -1, 0, 1)	(0, -1, 1, 0, -1)	(1, 1, -1, 0, 1)	3

Table 23. Caption.

Record	Channel 1	Channel 2	Channel 3	Label
R1	(1, 1, -1, 0, 1)	(0, 1, 1, 1, -1)	(1, 1, -1, -1, 0)	1
R2	(1, 0, -1, 0, 1)	( 0, 1, 1, 1, -1)	(1, 0, -1, -1, 1 )	1
R3	(1, 1, -1, 0, 1)	(0, -1, 1, 1, -1)	(1, 1, -1, 0, 1)	2
R4	(1, 1, -1, 0, 1)	(0, -1, 1, 0, -1)	(1, 1, -1, 0, 1)	2
R5	(1, 1, -1, 0, 0)	(0, -1, 0, 1, -1)	(1, 1, -1, 1, 1)	3
R6	(1, -1, -1, 0, 1)	(0, -1, 1, 0, -1)	(1, 1, -1, 0, 1)	3

The new record X of EEG-signals will be classified in class 1 as it is closest according to the Euclidian distance class 1 data samples $R1$ and $R2$.

5.3. Predicting Longevity in Cardiac Patients

We utilised a data set in which we applied a binary classification on whether the patient had an event (e.g. death) and further to those that had an event whether this would occur in the near future (within the next 180 days, e.g. approximately six months). The data set contained a set of 150 variables and an outcome, with 295 patients in the first data set and 49 in the second. The data included a mix of variables that could be grouped as follows:

• demographics, risk factors, disease states, medication and deprivation scores,
• echocardiography, cardiac ultrasound measurements,
• advanced ECG measurements,

The other data includes the days until the event occurred of the censor date for the Cox proportional hazard monitoring.

The objectives are to predict an arrhythmic event or death.

Before running the algorithm, the data was normalised, and to account for the data being unbalanced, we utilised SMOTE data balancing method [15] each time we left one out (ensuring that we did not SMOTE when the true data point was part of the data set). For the event classification data set, the model achieved an accuracy of 79%. This is broken down into classifying no event (198/247, 80%) and an event with (36/49, 73%) accuracy. It is worth noting the confidence of each individual could be explored with a sample of the confidence for classification in Figue Figure 6.

For the second experiment, we normalised the dataset and removed any columns with unknown values. We then applied a genetic algorithm to find the set of features to use for classification. We found a set of 34 variables which would provide an accuracy of $81\%$ with (34/34) for class 0 and (6/15) for class 1. Alternatively, we find that if we apply SMOTE and focus more on the accuracy of class 1, we obtain $69\%$ accuracy, however, more evenly distributed with (24/34) for class zero and (10/15) for class 1.

6. Data and Software Availability

The data has been obtained from the following: UCI Cleveland data available at https://archive.ics.uci.edu/dataset/45/heart+disease EEG data available at https://github.com/KEDRI-AUT/NeuCube-Py/tree/master/example_data Access to the software is available on request.

7. Conclusions

The paper presents a new method for search and inference, called here SAIN, for multi-modal data integration and personalised model creation based on these multi-modal data. The model not only evaluates the outcome for a person more accurately than traditional machine learning methods using a single modality data, but it also explains the proposed solution in terms of probability and visual explanation.

The proposed method is implemented as a computer system and applied to several case studies to illustrate its advantages and applicability. The SAIN method described in Section 4 was implemented as a software system.

The proposed mathematical method and computational framework can be applied to a broad spectrum of applications, such as [15]: a) medical diagnosis based on multimodal data, such as genetic, clinical, cognitive, and ethnical, b) early disease prognosis based on multimodal personalised data modelling, c) multimodal neuroimaging data modelling, d) multisensory spatio-temporal data modelling for pollution level estimation and prediction, e) earthquake prediction based on both seismic and GPS spatio-temporal data.