1. Introduction
During the past decade, the tendency for numerous wireless devices to communicate with each other in a specific area has accelerated the development of wireless network technology. IEEE 802.11 wireless technology is widely deployed in WLANs, and its next generations are rapidly developing to support higher data rates, security enhancement, and an increasing number of users. The Distributed Coordination Function (DCF) method of IEEE 802.11 uses the Carrier Sensing Medium Access with Collision Avoidance (CSMA/CA) protocol to control the process of participating stations entering the channel to transmit their packets [
1]. The protocol is also called a time-frame control protocol because it uses a Binary Exponential Backoff algorithm (BEB) to generate a deferring time for each station to avoid collisions, and to wait for an opportunity to transmit its packets. The BEB algorithm works efficiently in a low-load or an unsaturated network, where the BEB algorithm guarantees that participating stations send their packets without any collision [
2].
However, the BEB implementation causes more collisions when the network becomes dense and hence makes channel access control for stations more challenging [
3]. The problem is that after achieving a successful transmission, it resets the contention window (
CW) to the minimum backoff interval, which accidentally increases collision probability. In addition, the network delay may be affected by the exponential expansion of the
CW size to support packet retransmission after the station suffers a collision [
3,
4]. Many proposed schemes have focused on adjusting the
CW size in the BEB algorithm to improve the CSMA/CA protocol. Even so, finding an optimal
CW size for a dynamic wireless network remains an open problem. Typically, some schemes control the
CW size to increase or decrease depending on the result of each transmission or the history of transmission times that performed better than the BEB algorithm [
5,
6,
7,
8,
9,
10]. Nevertheless, these schemes mostly expand the
CW size after a station which suffered a collision without considering the status of the network load. Therefore, they are ineffective in some cases of rapid change in network loads, and it was difficult for them to reach a theoretical maximum throughput [
10]. Besides, some other schemes collect additional information in the network environment to estimate the density of the stations, and then combine them with the result of each transmission to optimize
CW size [
3,
11]. So, they also outperform the BEB algorithm, reduce collisions, obtain high throughput in a saturated network but the obtained
CW sizes stayed at high values, which might deteriorate network delay [
10]. On the other hand, some research focused on investigating the distribution of random variables in the duration of packet transmission to indicate its influence on network delay [
12,
13,
14].
In this study, we proposed a new scheme to control how to change the size of CW based on the combination of Transmission History and Backoff Probability (named THBP). In our mechanism, the transmission history is expressed by the aggregation of the status (successful or unsuccessful transmission) from two sequent transmissions. In addition, the ratio between the random backoff value (BO) and the CW size defines the backoff probability at the current transmission time. In our scheme, the sizes of CW increase or decrease for subsequent transmissions depends on the transmission history, and the backoff probability.
An internal collision occurs when the BO timers of stations expire simultaneously. The collision is partly due to the CW size, but somehow because of the BO. When a station encounters a collision, the CW size is extended to give the station one more opportunity to retransmit its packet. However, the CW size was at a large value after several times of retransmission, yet the station continues to collide. There are two reasons for this problem: One reason for the CW size was not large enough, and needed to be expanded more, the other reason is that the uniformly random mechanism of BOs leads stations expire simultaneously. In this study, along with using the packet transmission history, we additionally observe the probability of occurrence of the BO in the range of [0, CW - 1] to support the adjustment of CW size more reasonably.
The remaining part of this paper is organized as follows. Section II summarizes the related work. Section III introduces the new scheme. Section IV presents the simulation results are compared to other schemes to evaluate our scheme. Some conclusions are presented in the last section.
2. Related Work
In the CSMA/CA scheme using the BEB algorithm [
1], each station generates a uniformly random backoff value (BO) from [0,
CW – 1], where the BO is an integer in units of slot time and
CW is the size of the contention window. In this algorithm, the
CW size is limited in the range of [
CWmin,
CWmax], and its initial value could be set to
CWmin. The values of
CWmin,
CWmax and slot time are specified in the IEEE 802.11 standard [
1]. BO depends on the channel status, and when the BO counts down to zero, the packet is allowed to be sent. The
CW size is updated to a new value according to the indication in the acknowledgment and recovery procedures of the CSMA/CA scheme. In the BEB algorithm, the new
CW size for the next transmission is obtained in Eq. 1.
where
si is defined as a backoff stage at the
ith transmission time and
, the parameter
smax is the maximum times of retransmission. The default value of
smax is seven, along with the value of
CW corresponding to [16, 32, 64, 128, 256, 512, 1024]. Whenever a station suffers a collision, its
CW size is exponentially increased for a retransmission until it catches the value of
CWmax or the (2)
In the case of a saturated network, the BEB algorithm performed inefficiently, so Song N.-O
et al. proposed a scheme (named exponential increase exponential decrease - EIED) [
5], in which the
CW size was increased the same as the one in the BEB origin after a collision, and the
CW size was divided in half after a successful transmission instead of resetting to
CWmin like in the BEB algorithm as in Eq. 1. The new value of
CW in this scheme was updated in Eq. 2:
In this scheme, after a station achieved a successful transmission, the size of
CW was controlled to gradually decrease to prevent the backoff from falling into a tiny interval. The scheme outperformed the BEB origin. However, in this scheme,
CW size was maintained at a high value after a successful transmission, which may be sensitive to throughput and average delay [
10]. After that, many other schemes were proposed to improve BEB and surmount the limit of this scheme in the case of dynamic and saturated networks. A proposed scheme named the LILD based on the to adjust the
CW size by adding a value of
CWmin after a collision of transmission, and by subtracting a value of
CWmin after a successful transmission [
7]. The speed of changing
CW size is slower than that in the EIED scheme because of linear increase or decrease calculations but the LILD scheme is rather effective when the network was dense. However, the scheme caused a network degradation due to the linear decrease of
CW size when the network rapidly changed into low loads. Therefore, Ke C.
et al. proposed a scheme named SETL to take advantages of the EIED and LILD schemes to improve the BEB algorithm [
15]. They used a value of the
CW size as a threshold and performed the scheme in a combination of the EIED and LILD schemes. The EIED scheme was performed before the threshold and the LILD was performed after it. The performance of the scheme achieved a low collision rate and a high throughput in comparison to the BEB, EIED and LILD schemes. However, it still failed to reach the maximum throughput due to the setting of
CW sizes for networks in saturated condition [
10]. Lin C.-H.
et al. proposed a scheme named RACB in which the optimal CW sizes were obtained basing on the calculation of collision rate, with the optimal value of collision rate was of 0.1 [
10]. The two thresholds of low and high values were pre-defined according to the optimal value in order to combine the performances of the EIED and LILD schemes. The RACB scheme outperformed to the SELT scheme, but many parameters were pre-defined.
Some other proposed schemes presented a new approach to control
CW size. Beside using the result of each packet transmission, they extracted more information from the network environment to estimate the network condition. It is valuable when the coming and leaving stations of a network were unknown. Liang H.-M.
et al. proposed a PCB (Pause Count Backoff) algorithm used the average number of pauses in the countdown duration to estimate the active stations in the network and then aggregate the estimation result with the result of each transmission to set the appropriate
CW size [
11]. The scheme’s performance outperformed to the BEB and EIED, especially in fairness. Recently, Ali R.
et al. introduced a Channel Observation-based Scaled Backoff scheme (COSB) [
3]. In this scheme, they assigned a counter parameter to count the appearance of busy, idle, collision, and success at each slot time in the backoff duration of a station to estimate the channel activities. Then they calculated a collision probability (
pcol) as a ratio between the counter parameters and used to control the
CW size in combination with the result of each transmission for the subsequent transmission. The
CW size was updated in the Eq. 3.
in which
ρ was chosen equals to
CWmin and
pcol is the probability of collision [
3].
At first sight, the COSB scheme looked like the EIED scheme when it updated the CW size according to the result of each transmission. However, it became prominent when adding more information about the network environment through the factor pcol. The scheme performed better than the EIED and BEB algorithms, especially when the network became saturated. However, the scheme also created a variety of CW sizes, and the extraction mechanism of pcol was rather complex. In addition, many of the CW sizes were kept at high values to ensure continuously successful transmission, which was a reason for the average delay degradation.
In the past few years, the machine learning algorithms become prior candidates to enhance the CSMA/CA protocol. D. Lee
et al. used a method based on a hybrid back-off algorithm that was a combination of the LILD and the EIED schemes with a threshold of
CW size to apply the Q-learning algorithm to guarantee the reliability of increasing traffic and to improve the performance in a vehicular network (VANET) [
16]. Ali R.
et al. had built an iQRA paradigm based on a designed scheme to exploit the optimal actions using Q-learning algorithm, and the CW values were then scaled to those optimal actions for the stations [
17]. The performance of the iQRA paradigm was improved in throughput and especially in fairness. However, the trade-off between the exploration and exploitation in Q-learning remains a dilemma [
18]. Besides, the Deep Q-learning technique is also approached to optimize the
CW size, Wydmanski W.
et al. proposed a method called centralized contention window optimization with deep reinforcement learning (CCOD) [
19]. The method predicted the
CW sizes correctly to maximize the saturation throughput of the system, the inputs of the deep neuron network were the history of collision probabilities, and the output were the optimized rewards which maximized network performance. The obtained results presented an outperformance to the original BEB algorithm in a dense network. Similarly, Zuo Z.
et al. employed a Q-learning technique in first phase to obtain the history of collision probabilities, and then a deep neuron network in the second phase to sense the network condition to optimize the
CW sizes with a dynamic adjustment in backoff strategy for different access categorie (AC) in an EDCA mechanism [
20]. The obtained results presented a better performance than other methods in both normalized throughput and collision rate for differentiating ACs. However, designing a deep neuron network to optimize the parameters in IEEE 802.11 DCF is rather complex and it takes a long time to perform.
In this study, besides using the history of packet transmission, we additionally observe the probability of the BO occurrence during the backoff duration to control the CW size more reasonable for the next transmission. The BO was one of the factors which partly affected the packet transmission result due to its uniform random manner. Our proposal scheme ensures to improve throughput and solve the deterioration of the average delay in case of different network loads. Besides, it is simply in calculation and makes a few alterations to the original BEB algorithm in control the CW size.
3. The Proposal Scheme
In the THBP scheme, we initially estimated the density of a dynamic wireless network based on the results of two consecutive transmission states. We defined
Tpc to show ‘previous’ and ‘current’ transmission states, with
p and
c notated with terms ‘0’ and ‘1’ respectively. The term ‘0’ specified a successful transmission, and ‘1’ indicated that the station had experienced a collision. There are four states (
T00,
T01,
T10,
T11), these present the ‘previous’ and ‘current’ transmission states which was successful transmission or collision. Furthermore, we calculate the ratio between the BO value and
CW in the current transmission and use it to support the adjustment of
CW more reasonable in combination with each transmission state. Mathematically, we defined a backoff probability
fi by the ratio
where the BO
i was a random backoff value and the
CWi size at the
ith transmission. We observed the value of
fi in combination with four states to define more suitable
CW size for the next transmission.
In the case of a saturated network, a small
CW size causes more collisions because it increases the probability of the stations falling to the same backoff values. Likewise, if a large
CW size was kept in an unsaturated network, the average delay might be deteriorated [
10]. Although many schemes were proposed to enhance the BEB algorithm basing on the result of each packet transmission or information from network environment but how the
CW size is reasonable to adapt the network condition that is still necessary to investigate and discover. Therefore, we combine the history of two consecutive transmission with the observation of BO through the
fi value to adjust the
CW size appropriately. In this scheme, we defined
si = [0, 1, 2 …, (
smax - 1)] as the backoff stages in which
smax was the maximum number of retransmitted times as in the BEB algorithm. The increment term of
was used to update a new backoff stage after a combination the result of the
Tpc and
fi observation for stations, and it also specifies the speed change of
CW sizes. The backoff stage
si was updated to the backoff stage
sj as below
Then the new contention window
CWj was obtained by:
We observe value of fi to appear in one of three ranges of [0, 0.25), [0.25, 0.5), and [0.5, 1.0]. In the BEB algorithm, the CW is the series of {CWmin, 2 × CWmin, 4 × CWmin, …, CWmax}. At the current CWi, the previous CW are calculated by 0.5 × CWi, 0.25 × CWi, … So, in our scheme, the factors of 1.0, 0.5 and 0.25 were chosen as the upper limit of three ranges above to observe probability fi. It also implies to the BO appearing in any backoff stages of (si - 2), (si - 1) or si. These ranges were normalized in corresponding to BO being small, medium, or large compared to the CW size. Let us discuss the rules for combining Tpc with fi.
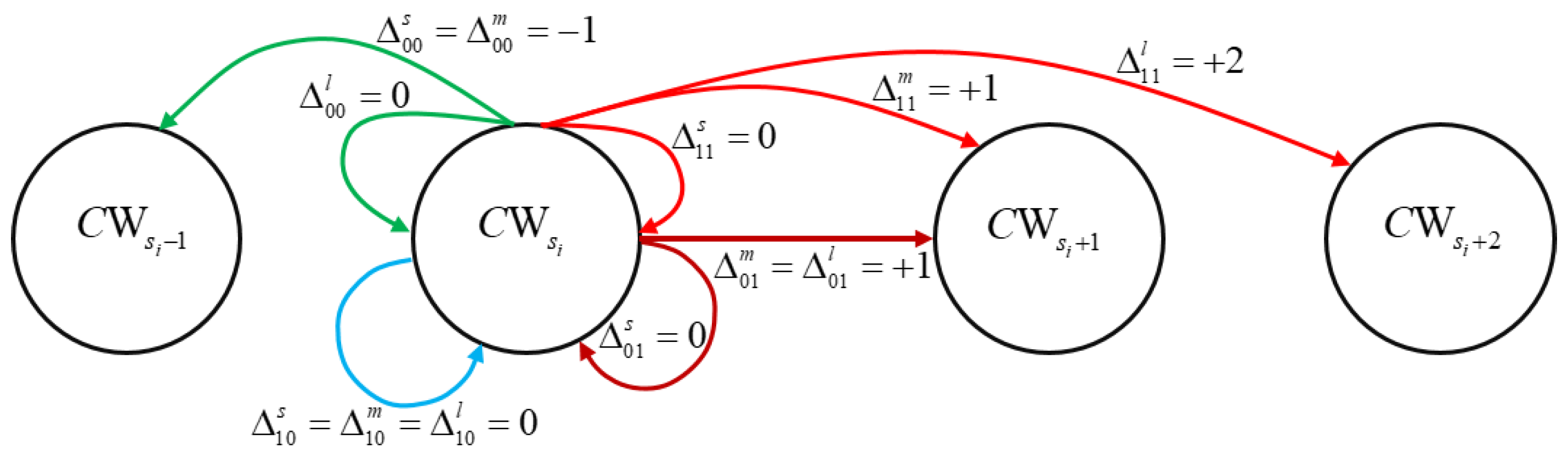
In our mechanism, fi is used to partly support the change of CW in each transmission state. When the transmission state presents two sequent collisions (T11). The CW typically needs to expand to avoid collision for the next transmission. However, if fi is small, BO can be larger in the next round with the current CW size. It means that the collision can be solved without changing the backoff stage, and the CW remains unchanged. If fi is medium, the current CW size is necessary to extend a reasonable amount to support the average delay of the network. If fi is large, it implies that the BO is proportional to the CW size, and we should increase a large amount of the CW size to avoid collision in the subsequent transmission. In the case of the transmission state changes from success to collision (T01), the BEB algorithm increases the CW size by twice to increase the BO value to avoid collision in the next round. However, in our mechanism, if the fi is small, BO can be larger in the next round with the current CW size, thus its size remains at this backoff stage. If the fi is medium or large, the CW is doubled, similar to the BEB algorithm, to support a suitable BO value for the next transmission. Likewise, when the transmission state presents two sequent successes (T00). If fi is large, the CW size is reasonable at this backoff stage and is unchanged. If the fi is small and medium, the CW size decreases a small amount to avoid an unnecessary delay for the backoff duration. In the case of transmission state changes from collision to success (T10), instead of decreasing to the previous backoff stage, CW size still remains at this backoff stage with any values of fi to avoid more collisions in the next round.
The factor Δ
pc in equation (5) was described by
where (
s), (
m), (
l) correspond to small, medium, and large, respectively. The value of factor Δ
pc is used to define the next backoff stage. We present the predicted values of Δ
pc in
Table 1.
Table 1 shows that the state
T00 specifies the transmission state to be successful twice, and the value of
fi < 0.5 refers to a small BO value. Therefore,
CW should be smaller, and the backoff stage
si reduces to
si -1 by the setting
. If
fi > 0.5, it implies that the current
CW size was large enough and should remain unchanged, as
.
In the state T10, which means that the transmission state changes from collision to a success, then the backoff stage si is good enough. So, CW size is kept unchanged with any values of fi and , and are set to zero. Then, the backoff stage si can be changed in the next round.
In the state T01, it refers to a success accompanied by a collision. If fi < 0.25, it implies that the collision of the current transmission time was not due to the size of CW, and the backoff stage si should remain unchanged, and was set to zero. Only if fi > 0.25, the CW size needed to be increased to the CW size at the backoff stage si + 1, so we set both and to equal +1.
In the state of T11, which indicates two consecutive collisions. If fi > 0.5, this means that the CW size and the BO value were rather high, but the station has continuously suffered a collision. Therefore, the CW size needed to be expanded a lot, and here the appropriate factor should be +2, which referred to the CW size at the backoff stage jumped to the backoff stage si + 2. If 0.25 ≤ fi < 0.5, the CW size needed to expand a few, we thus predicted to increase the CW size in the backoff stage si to the backoff stage si + 1 and set the factor to be +1. For the case fi < 0.25, we kept the CW size unchanged and set the factor to be zero.
Likewise, we describe the transition of the
CW among backoff stages according to the factor Δ
pc in the diagram in
Figure 1 with the pseudo-codes in the Algorithm 1.
In
Figure 1, the
CW size is at each retransmission time of the BEB algorithm, which was described in
Section 2. The
CW size is updated in this scheme presented in Equation 8.
| Algorithm 1. The pseudo-codes of THBP scheme. |
| 1: |
Procedure update_contention_window |
| 2: |
fi = BOi/(CWi + 1) // using Eq. (4) |
| 3: |
If (previous_transư is successful AND current_trans is successful) then |
| 4: |
If (fi < 0.25) then |
| 5: |
Deltapc = − 1 |
| 6: |
Elseif (fi ≥ 0.25 AND fi < 0.5) then |
| 7: |
Deltapc = -1 |
| 8: |
Elseif (fi ≥ 0.5) then |
| 9: |
Deltapc = 0 |
| 10: |
ElseIf (previous_trans is successful AND current_trans is failed) then |
| 11: |
If (fi < 0.25) then |
| 12: |
Deltapc = 0 |
| 13: |
Elseif (fi ≥ 0.25 AND fi < 0.5) then |
| 14: |
Deltapc = 0 |
| 15: |
Elseif (fi ≥ 0.5) then |
| 16: |
Deltapc = 0 |
| 17: |
ElseIf (previous_trans is failed AND current_trans is successful) then |
| 18: |
If (fi < 0.25) then |
| 19: |
Deltapc = 0 |
| 20: |
Elseif (fi ≥ 0.25 AND fi < 0.5) then |
| 21: |
Deltapc = 1 |
| 22: |
Elseif (fi ≥ 0.5) then |
| 23: |
Deltapc = 1 |
| 24: |
ElseIf (previous_trans is failed AND current_trans is failed) then |
| 25: |
If (fi < 0.25) then |
| 26: |
Deltapc = 0 |
| 27: |
Elseif (fi ≥ 0.25 AND fi < 0.5) then |
| 28: |
Deltapc = 1 |
| 29: |
Elseif (fi ≥ 0.5) then |
| 30: |
Deltapc = 2 |
| 31: |
Update sj ← si // using Eq. (5) |
| 32: |
Update CWj = CWmin × 2^sj // using Eq. (6) |
| 33: |
Update previous_trans ← current_trans |
| 34: |
END procedure |
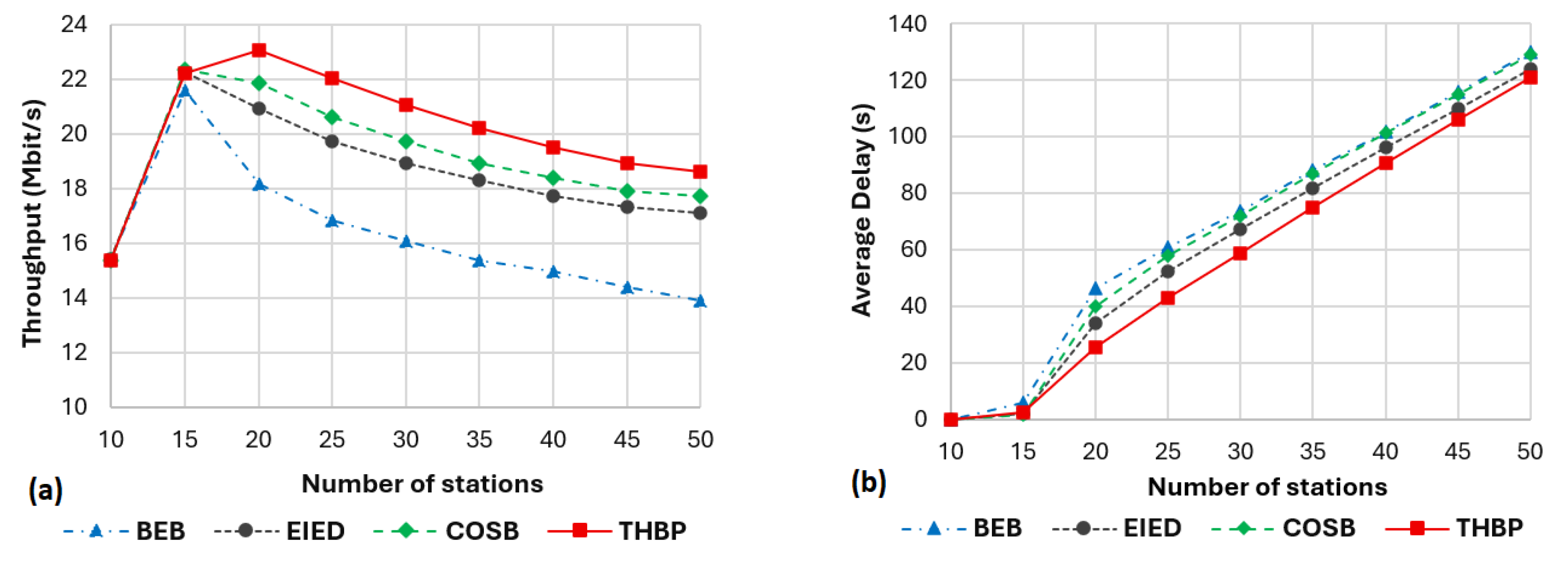
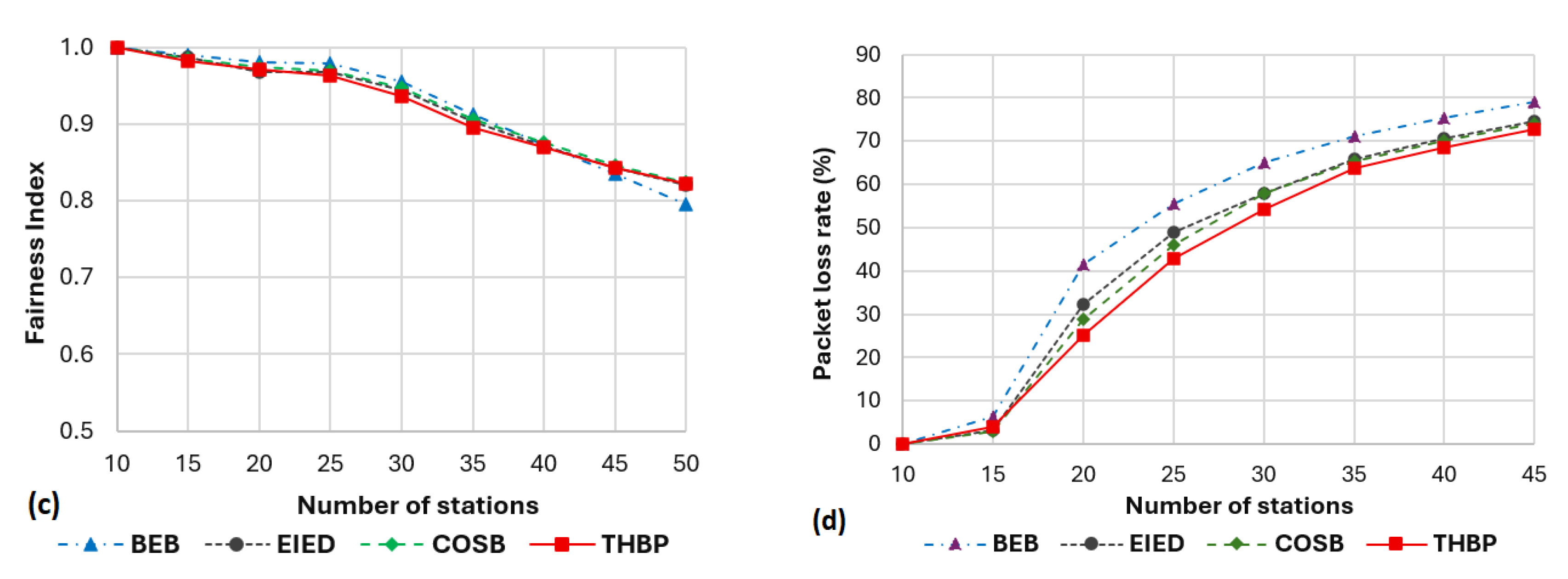
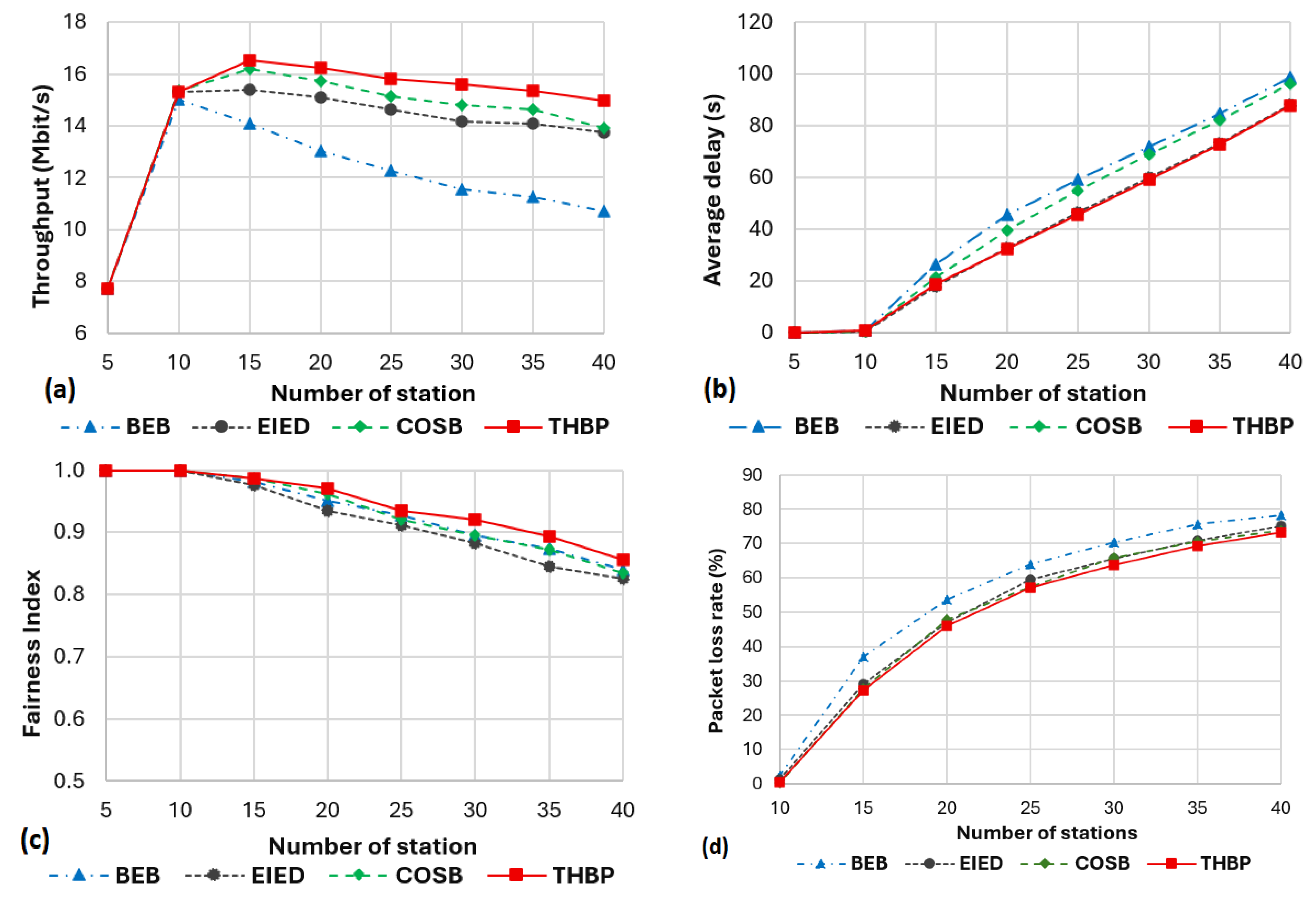
The proposed THBP scheme guarantees to obtain high throughput, low delay, good fairness, and address the sensitive delay that the EIED and COSB schemes encountered. The scheme contributed to minimizing collisions and improving the network performance for different network loads. Moreover, our scheme requests a little computational resource by adding a few conditional statements (see in the pseudo-codes). In comparison to the BEB algorithm, our scheme only uses two new integer variables that are updated after each transmission, the first one is the previous state of transmission which is either 0 or 1, the second one is the transmission stage si ∈ [0, smax - 1] with smax is a tiny integer number. Hence, no overhead traffic is added.