Submitted:
25 June 2025
Posted:
26 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Method
2.1. Materials
2.2. Graphical Method for Extracting Electrical Parameters.
3. Validation of the Proposed Method
4. Conclusions
References
- Kozłowski, Michał & Racewicz, Szymon & Wierzbicki, Sławomir. (2024). Image Analysis in Autonomous Vehicles: A Review of the Latest AI Solutions and Their Comparison. Applied Sciences. 14. 8150. [CrossRef]
- Sun, Yan & Ren, Zhenyun & Zheng, Wenxi. (2022). Research on Face Recognition Algorithm Based on Image Processing. Computational Intelligence and Neuroscience. 2022. [CrossRef]
- Sijo TF, Impact of image and video visual analysis in sports, International Journal of Physiology, Nutrition and Physical Education 2019; 4(1): 1294-1296, 4-1-323-276.
- Fischer, Bernhard. (2003). Loss Analysis of Crystalline Silicon Solar Cells Using Photoconductance and Quantum Efficiency Measurements.
- Kumar M, Kumar A. An efficient parameters extraction technique of photovoltaic models for performance assessment. Solar Energy. 2017;158:192-206.
- Batzelis, Efstratios. (2019). Non-Iterative Methods for the Extraction of the Single-Diode Model Parameters of Photovoltaic Modules: A Review and Comparative Assessment. Energies. 12. [CrossRef]
- Venkateswari, Radhakrishnan & Rajasekar, Natarajan. (2021). Review on parameter estimation techniques of solar photovoltaic systems. International Transactions on Electrical Energy Systems. 31. [CrossRef]
- Ramos, Jose & Martín, J.J. & Belver, I. & Larrañaga Lesaca, JM & Zulueta, Ekaitz & Pérez, E.. (2010). Modelling of Photovoltaic Module. Renewable Energy and Power Quality Journal. 1. 1186-1190. [CrossRef]
- “KC200GT High Efficiency Multicrystalline Photovoltaic Module Datasheet Kyocera,” [Online]. Available: http://www.kyocera.com.
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear minimization algorithm for determiningthe solar cell parameters with microcomputers. Int. J. Sol. Energy 1986, 4, 1–12.
- http://m.sunpropowersky.com/solar-panel/mono-solar-panel/450w-144cells-mono-solar-panel-with-black.html.
- José de Jesús Martínez Basilio, “Desarrollo e Investigación de un Proceso de Fabricación de Celdas Solares Basadas en la Tecnología del c-Si, INAOE”, Tesis de Doctorado, INAOE, 2017.
- Ye, Fan. (2021). Application of Photoshop Graphics and Image Processing in the Field of Animation. Journal of Sensors. 2021. 1-18. [CrossRef]
- Shaltout, Mohamed & Gad, Mohamed. (2021). MATLAB for Modeling, Simulating, Analyzing and Visualizing.
- M. J. Heredia-Rios, L. Hernandez-Matinez, M. Linares-Aranda and M. Moreno-Moreno, "Non-iterative parameter extraction method based on the single diode model (SDM).," 2023 IEEE Latin American Electron Devices Conference (LAEDC), Puebla, Mexico, 2023, pp. 1-5. [CrossRef]
- Heredia-Rios M.J.; Hernandez-Martinez L.; Linares-Aranda M.; Moreno-Moreno M.; Méndez J.F. Analysis of Losses Associated with Series Resistance (Rs) in Simple-Structured c-Si Solar Cells. Energies 2024, 17, 1520. [CrossRef]
- Cubas, Javier & Pindado, Santiago & Sorribes, Felix. (2017). Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point. Applied Sciences. 7. 870. [CrossRef]
- Ben aribia, Houssem & El-Rifaie, Ali & Tolba, Mohamed & Shaheen, Abdullah & Moustaffa, Ghareeb & Elsayed, Fahmi & Elshahed, Mostafa. (2023). Growth Optimizer for Parameter Identification of Solar Photovoltaic Cells and Modules. Sustainability. 15. 7896. [CrossRef]
- Villalva, M.; Gazoli, J.; Filho, E. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208.
- Manuel Jesús Heredia Rios, “Método de extracción de parámetros para el modelado de celdas y paneles solares”, Tesis de Doctorado, INAOE, 2024.
- Breitenstein, J. P. Rakotoniaina, M. H. Al Rifai, and M.Werner, “Shunt types in crystalline silicon solar cells,” Progressin Photovoltaics: Research and Applications, vol. 12, no. 7, pp.529–538, 2004.
- R Singh, Priyanka & Ravindra, Nuggehalli. (2012). Analysis of series and shunt resistance in silicon solar cells using single and double exponential models. Emerging Materials Research. 1. 33–38. [CrossRef]
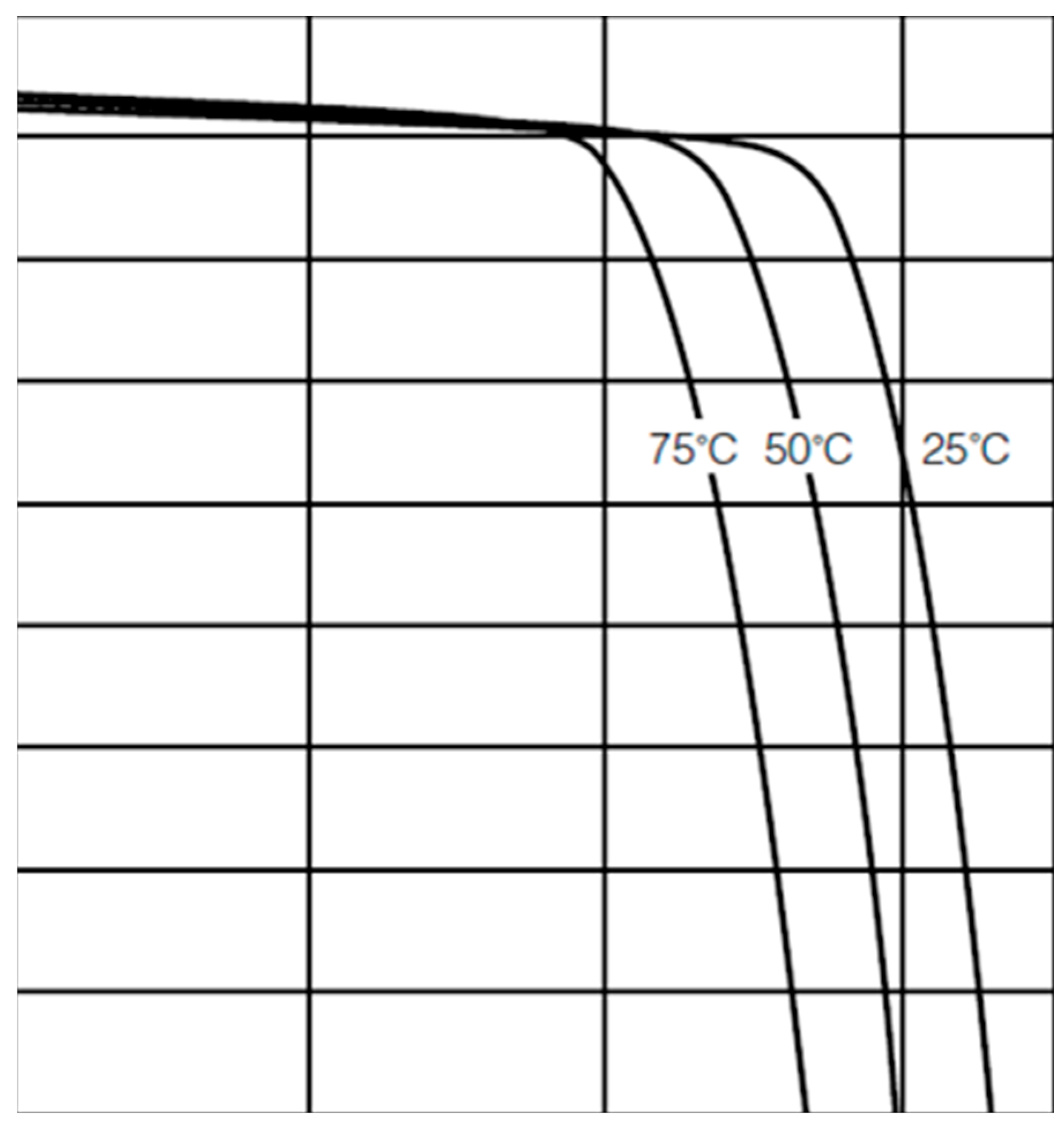
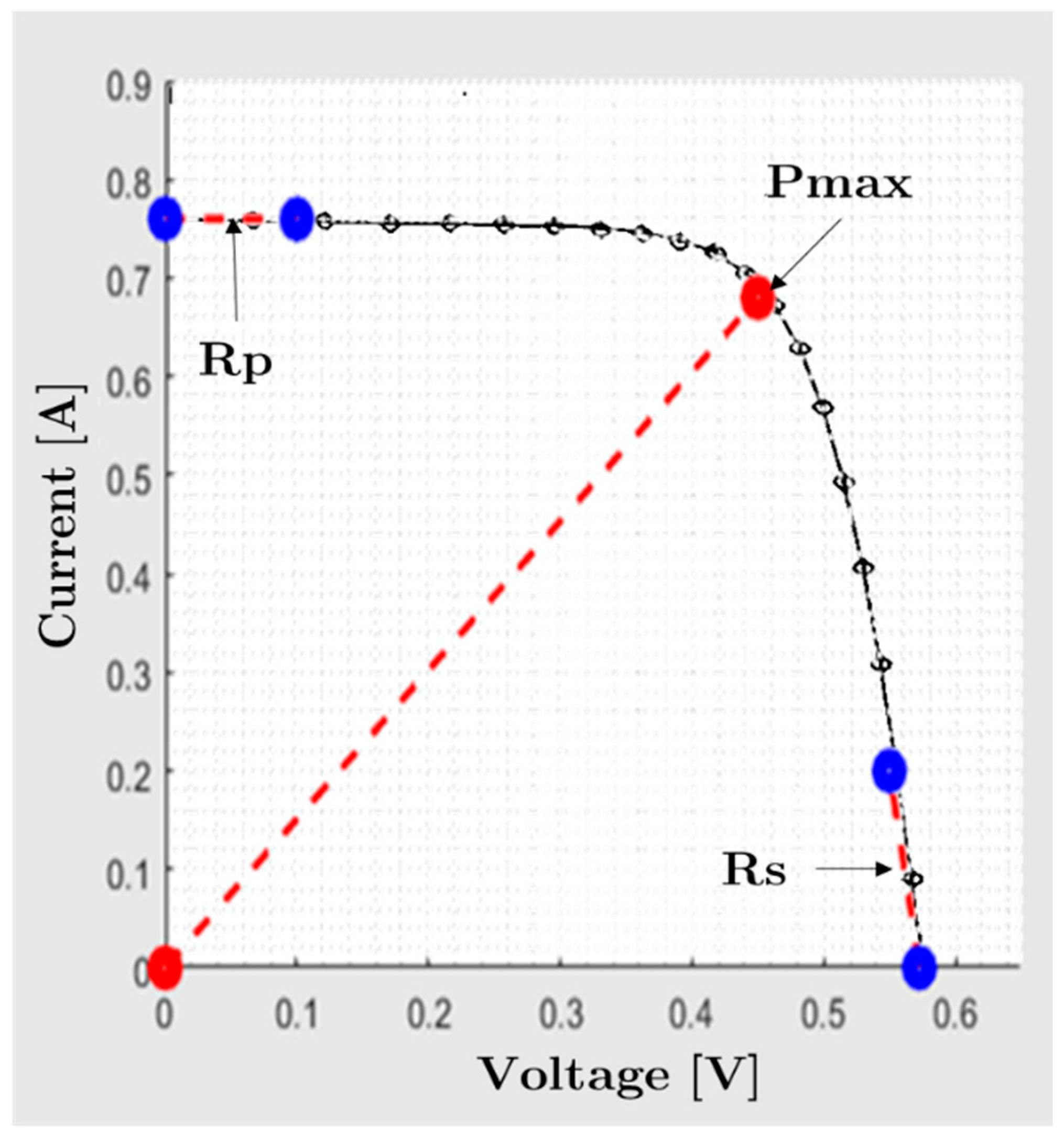
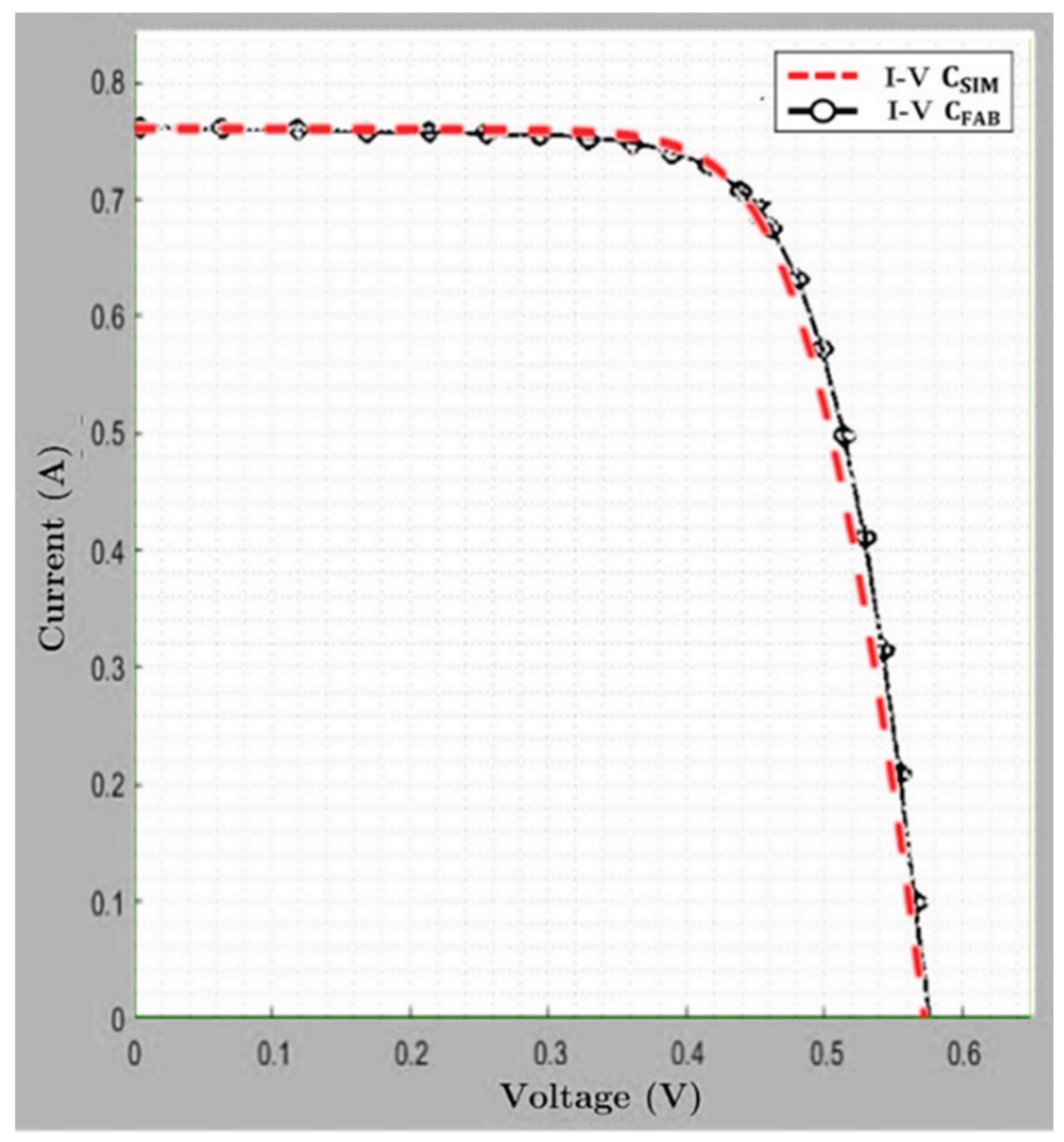
| Name | Type | Technology | Isc (A) | Voc (V) | Im (A) | Vm (V) | Pmax (W) |
|---|---|---|---|---|---|---|---|
| RTC-FRANCE [10] | Cell | Poly-Si | 0.76 | 0.572 | 0.689 | 0.450 | 0.310 |
| INAOE [12] | Cell | c-Si | 28.76e-03 | 0.52 | 0.32 | 2.227e-03 | 7.126e-03 |
| KC200GT [9] | Panel | Poly-Si | 8.21 | 32.9 | 7.63 | 25.6 | 200(+10%/-5%) |
| SP450M [11] | Panel | mono-Si | 11.56 | 49.8 | 10.98 | 41 | 450 |
| Device | Method | Author | IO (A) | IPV (A) | n | RS (Ω) | RP (Ω) |
|---|---|---|---|---|---|---|---|
| RTC-FRANCE | NMA | Easwarakhanthan (1986), [10] | 3.22E-07 | 0.760 | 1.483 | 0.036 | 53.763 |
| ACPSBOP | Cubas (2017) [17] | 2.92E-06 | 0.760 | 1.74 | 0.045 | 246.785 | |
| GO | Ben aribia (2023) [18] | 3.23E-07 | 0.760 | 1.481 | 0.036 | 53.718 | |
| Proposed | Proposed (2025) | 1.04E-08 | 0.760 | 1.154 | 0.075 | 333.333 | |
| KC200GT | NR | Villalva (2009) [19] | 9.82E-08 | 8.210 | 1.300 | 0.221 | 415.405 |
| GO | Ben aribia (2023) [18] | 4.31E-08 | 8.192 | 1.248 | 0.004 | 15.103 | |
| Proposed | Proposed (2025) | 8.78E-08 | 8.212 | 1.293 | 0.114 | 801.5 | |
| INAOE | Proposed | Proposed (2025) | 4.53e-09 | 28.9e-03 | 1.29 | 7.2 | 1000 |
| SP450M | Proposed | Proposed (2025) | 3.22e-07 | 11.195 | 1.853 | 0.700 | 90.909 |
| Device | Parameter extraction | ISC (A) | VOC (V) | PMAX (W) | η (%) | % Difference in η |
|---|---|---|---|---|---|---|
| RTC-FRANCE | Manufacturer | 0.7603 | 0.5728 | 0.3107 | 3.10 | 3.5 |
| Proposed | 0.7600 | 0.5720 | 0.3107 | 2.99 | ||
| KC200GT | Manufacturer | 8.21 | 32.9 | 200.143 | 16 | 0.62 |
| Proposed | 8.21 | 32.9 | 200.14 | 15.9 | ||
| SP450M | Manufacturer | 11.56 | 49.8 | 450 | 20.77 | 1.1 |
| Proposed | 11.56 | 49.8 | 451 | 21 | ||
| INAOE | Manufacturer | 28.76e-03 | 0.520 | 7.126e-03 | 7.125 | 1.14 |
| Proposed | 28.90e-03 | 0.528 | 7.04e-03 | 7.044 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





