1. Introduction
The past several decades have witnessed a transformation in the way information is conceptualized, manipulated, and protected. At the heart of this shift lies the recognition that quantum mechanics—once thought of as an abstract theory confined to microscopic particles—provides a radically new foundation for computation and communication. Unlike classical information, which is deterministic and binary, quantum information is encoded in quantum states, such as qubits, which exhibit superposition, entanglement, and contextuality. These uniquely quantum traits have enabled the development of quantum algorithms and communication protocols that outperform their classical counterparts in both speed and security.
Quantum Information Theory and Computation (QITC) has emerged as a fundamental research domain that combines the mathematical rigor of quantum theory with the operational goals of computer science. QITC has already redefined cryptography, random number generation, and algorithmic search through innovations such as Shor’s algorithm for integer factorization, Grover’s quantum search, and the BB84 quantum key distribution protocol. These achievements, however, are only the beginning. Theoretical advancements in QITC are now pushing the boundaries further—towards quantum error correction, fault-tolerant computation, and scalable quantum networks.
A central challenge in quantum computing is the problem of maintaining the integrity of quantum information over time. Due to decoherence and operational noise, quantum states are inherently fragile. The prevailing solution has been the design of error-correcting codes and logical gate sets that are fault-tolerant. Most of these rely on Clifford group operations, which are computationally efficient and easier to stabilize, but limited in universality. To achieve universal quantum computation, non-Clifford gates—such as the T gate—must be introduced. These gates enable operations that go beyond the stabilizer formalism, but they also introduce new layers of complexity in terms of resource cost and error modeling.
Another emerging theme in QITC is the use of contextuality as a computational and cryptographic resource. Contextuality refers to the idea that the outcome of a measurement cannot be predetermined independently of other compatible measurements that might be performed alongside it. Unlike classical logic, where truth values are absolute and independent, quantum logic allows outcomes to depend on the measurement context. This non-classical feature is not just a curiosity—it has been mathematically proven to underlie the power of quantum computation in certain models, such as measurement-based quantum computing (MBQC).
Meanwhile, entropy—the measure of uncertainty or information content—plays a crucial role in understanding both quantum communication and computation. In classical information theory, entropy quantifies data compression and transmission capacity. In the quantum realm, it reveals correlations, coherence, and the limits of entanglement-based protocols. However, while many results in quantum entropy focus on bipartite or multipartite entanglement entropy, less attention has been given to how entropy propagates through quantum systems under non-Clifford dynamics in a contextual framework.
This paper introduces a new theoretical structure called contextual quantum entropic lattices, designed to model the behavior of quantum information as it propagates through networks of qubits operating beyond the Clifford regime. Unlike standard lattice models that focus on spin or particle states, entropic lattices treat entropy itself as a primary variable. Each node in the lattice represents a local entropic state, and edges represent entropic couplings influenced by contextual measurement constraints and non-Clifford gate logic.
The goal of this work is to build a rigorous mathematical model that explains how quantum information—represented in terms of entropy—can be transferred, transformed, and stabilized through a contextual, non-Clifford lattice system. We will construct this model from first principles using a combination of algebraic entropy mappings, graph-based contextual structures, and non-Clifford transformation operators. Importantly, this paper does not involve experimental simulations or empirical fitting. All results are derived analytically to ensure logical clarity and reproducibility.
By uniting contextuality, entropy, and non-Clifford computation into a single theoretical lattice framework, we aim to establish new tools for quantum security, communication integrity, and fault-resistant computation. This approach also opens pathways for developing new classes of error correction protocols that go beyond current stabilizer-based techniques.
In the sections that follow, we define the foundational concepts and formalize the mathematical framework underlying entropic lattices. We then derive the properties of contextual entropy flow under non-Clifford transformations, followed by an analysis of lattice propagation stability. We conclude by discussing implications for secure quantum communication, theoretical computation models, and the future of scalable quantum networks.
2. Aim and Objectives
The primary aim of this paper is to develop a purely theoretical and self-contained framework for modeling quantum information transfer through entropy-based structures that operate beyond Clifford logic and within a contextual measurement environment. The proposed model introduces a new class of mathematical objects, termed quantum entropic lattices, which are designed to capture entropy flow, logical transformation, and contextual dependencies among qubits without reliance on stabilizer formalisms or experimental assumptions.
This research pursues the following objectives:
To construct an original lattice-theoretic model in which each vertex represents a local quantum state with measurable entropy, and edges encode transformation constraints governed by non-Clifford logic.
To formulate entropy-preserving propagation rules over these lattices that respect quantum contextuality, and to derive a set of structural theorems for entropy evolution under composition of transformations.
To define and analyze a class of algebraic operators that generalize non-Clifford gates into the entropic lattice context, allowing for multi-node interaction models.
To identify sufficient conditions under which entropy transmission through the lattice remains stable, reversible, or localized, thereby introducing a new theoretical tool for examining coherence persistence in quantum information systems.
To propose a model of quantum communication channels where security is guaranteed through topological entropic constraints and logical non-reconstructibility from partial measurements.
To mathematically analyze the scaling behavior of entropy flow across increasingly complex contextual lattice topologies and determine bounds for error propagation and recovery.
To present a set of ten theoretically constructed graphs, three analytical models, and one block diagram that visualize key aspects of entropic propagation, lattice state transitions, and contextual gate structures.
To rigorously demonstrate all results through derivations, lemmas, and theorems—supported by logical proofs and algebraic identities—without reliance on numerical approximation, simulation, or machine-based computation.
This theoretical investigation aims not only to expand the formal understanding of quantum information dynamics but also to lay foundational tools that can be used to build next-generation secure quantum protocols and abstract fault-tolerant computation models beyond current stabilizer-based architectures.
3. Theoretical Framework
This section outlines the conceptual and mathematical structure underpinning entropic lattice propagation in contextual quantum systems. We define the geometry, entropy logic, and transformation constraints before developing the full algebraic formulation.
3.1. Entropic Lattices and Contextual Structure
We begin by considering a finite-dimensional quantum system represented by a Hilbert space
of dimension
d. A quantum state
on
is a positive semi-definite operator with unit trace:
The set of all such density matrices is denoted by
. The basic measure of information in a quantum state is given by the von Neumann entropy:
A pure state satisfies , while a maximally mixed state yields maximum entropy .
Now define a lattice structure , where are nodes each associated with a quantum state , and are directed edges indicating logical or physical propagation of information.
Each node
has a local observable algebra
and a set of allowed transformations
. Let:
be the local entropy at node
i.
Let
be a quantum channel acting between
and
, that is, a CPTP map:
The transformation is said to be entropy non-increasing if:
We introduce a contextual compatibility function:
with
. Lower
implies stronger contextuality.
Define a path
and entropy along this path as:
where
.
To characterize node behavior under successive transformations, define entropy composition:
For a chain
, we evaluate accumulated entropy as:
Let
be a unitary operation acting locally, then:
For a projective measurement
, the post-measurement state is:
and the entropy satisfies:
Define contextual entropy flux as:
Let
T be a non-Clifford gate applied at node
i, with operator form
, then:
Entropy rate at node
i is defined as:
If two nodes are entangled, their joint state
yields mutual information:
Define entropic distance between nodes:
Entropic triangle inequality must hold:
These 20 equations lay the formal foundation of the contextual quantum entropic lattice. Each concept directly supports model development, ensuring traceability and algebraic rigor throughout the propagation network.
3.2. Entropy Propagation Equations
The dynamics of quantum information within a complex system, such as our proposed contextual quantum entropic lattice, are fundamentally governed by the evolution of quantum states and, consequently, their associated entropies. This subsection rigorously develops the mathematical framework for entropy propagation, detailing how local and global entropies change under the influence of quantum channels, contextual transformations, and non-Clifford operations. We begin by establishing the foundational definitions of entropy relevant to quantum information.
Consider a single node
within the entropic lattice
, described by its local density matrix
. The initial entropy of this node is simply:
where
denotes the initial state of node
.
Information propagation across the lattice is modeled by quantum channels. A general quantum channel
acting on a quantum state
can be expressed in the Kraus operator representation:
where the Kraus operators
satisfy the completeness relation
. After the application of such a channel, the state of node
evolves to
. The entropy of the node at time
t is then:
The change in entropy due to the channel is given by:
This change reflects the information gain or loss, or the increase in mixedness, induced by the channel.
Our framework introduces the concept of “contextual transformations.” A context
for a node
can be represented by a set of orthogonal projectors
such that
. When a quantum state
is subjected to a context, its effective state can be described by a classical mixture of projected states, or more generally, by a context-dependent transformation. For a given context
, we define a contextual projection operator
that transforms the state:
where
are the projectors associated with context
. The entropy of the state under this contextual transformation is:
The propagation of entropy within the lattice is not only subject to general quantum channels but also to these contextual influences. We define a context-dependent quantum channel
that incorporates the specific context
:
where
are Kraus operators specific to context
. The state of node
after propagation through this context-dependent channel is
. The entropy change under such a channel is:
For a multi-node lattice
composed of
N nodes, the total state is described by a global density matrix
acting on the composite Hilbert space
. When considering information flow between two adjacent nodes
and
, we are interested in the evolution of their joint state
and the mutual information between them. The mutual information
quantifies the correlations between
and
:
where
and
are the reduced density matrices of nodes
and
, respectively.
The propagation of entropy across the lattice can be described by a sequence of local and contextual channels. For a path
, the state of node
at the end of the path, given an initial state
at
and a sequence of channels
(potentially context-dependent), is:
The entropy of the final node is then .
A key aspect of our framework is the inclusion of non-Clifford operations, which are essential for universal quantum computation and can significantly alter the entropic landscape. Let
denote a non-Clifford transformation. When such a transformation acts on a state
, the resulting state is
. The change in entropy due to this transformation is:
The rate of entropy propagation between two nodes
and
can be defined in terms of the change in mutual information over time, assuming a continuous or discrete time evolution parameter
:
This rate quantifies how quickly correlations (and thus shared information) are established or degraded between nodes.
For a bipartite split of the lattice into subsystems A and B, the entanglement entropy
(where
) quantifies the entanglement between A and B. Its propagation is crucial for understanding secure information transfer.
The evolution of entanglement entropy under a global channel
acting on
is given by:
The entropy production rate for an open quantum system interacting with an environment, which can be seen as a form of contextual influence, is derived from the Lindblad master equation. The Lindblad equation describes the time evolution of the density matrix
:
where
H is the system Hamiltonian and
are Lindblad operators describing dissipation and decoherence. The rate of change of von Neumann entropy is then:
Substituting (
35) into (
36) yields a complex expression for the entropy propagation rate under environmental influence.
The conditional entropy
can also propagate. If
, it indicates entanglement. The propagation of negative conditional entropy signifies the robust transfer of entanglement.
The change in conditional entropy due to a channel
acting on
A is:
where
denotes the channel acting only on subsystem
A.
The Holevo quantity
provides an upper bound on the classical information that can be transmitted through a quantum channel
:
This quantity is crucial for understanding information leakage in secure channels. For an ultra-secure channel, the propagation of entropy should ideally minimize for any potential eavesdropping channel.
The quantum relative entropy
measures the distinguishability between two quantum states
and
:
The change in relative entropy after a channel
is applied to both states:
This is particularly relevant for security, as an eavesdropper’s ability to distinguish states is directly related to this quantity. The quantum relative entropy is non-increasing under quantum channels, a property known as monotonicity:
The quantum data processing inequality states that for any quantum channel
, the mutual information cannot increase:
This inequality provides a fundamental constraint on entropy propagation and information flow, implying that channels generally degrade correlations.
For a tripartite system
, the strong subadditivity of von Neumann entropy states:
This fundamental inequality imposes constraints on how entropy can be distributed and propagated across the lattice, particularly for entangled states.
Finally, the quantum capacity
of a channel
quantifies the maximum rate at which quantum information can be reliably transmitted through it. It is related to the coherent information:
where
is the complementary channel. For ultra-secure channels, maximizing
while minimizing classical leakage is paramount.
3.3. Algebra of Contextual Transformations
The concept of “context” in our framework is not merely a descriptive label but an active algebraic entity that fundamentally shapes quantum information processing. This subsection develops a rigorous algebraic formalism for contextual transformations, defining their structure, composition rules, and their interplay with non-Clifford operations, which are crucial for universal quantum computation. We aim to establish a mathematical language for describing how information is processed and secured under varying contextual influences.
A context
is formally defined by a set of orthogonal projection operators
acting on the Hilbert space
of a quantum system, where
is the dimension of the context’s observable space. These projectors satisfy the completeness relation:
and the orthogonality condition:
A contextual transformation
associated with context
is a superoperator that maps a density matrix
to
:
where
are context-dependent Kraus operators satisfying
. In a simplified scenario,
could be directly related to
, e.g.,
for some probabilities
.
The composition of two contextual transformations
and
results in a new contextual transformation
:
This demonstrates that the set of contextual transformations forms a semigroup under composition.
Non-Clifford operations, such as the T-gate (
), are crucial for achieving universal quantum computation. These operations do not map Pauli operators to Pauli operators under conjugation. The action of a non-Clifford gate
on a state
is given by:
When a non-Clifford operation is performed within a specific context
, its effective action
can be described by a modified superoperator:
This equation highlights how the context projects the outcome of the non-Clifford operation onto specific subspaces.
The algebraic relationship between contextual transformations and non-Clifford gates is critical. We can define a commutator for a non-Clifford gate
and a contextual projector
:
If this commutator is non-zero, it implies that the order of applying the context and the non-Clifford gate matters, leading to distinct information propagation pathways.
The algebra of contextual transformations can be further explored by considering the set of all possible contextual superoperators
. This set forms a convex cone, and its properties dictate the limits of information manipulation within the lattice. The adjoint of a contextual superoperator
is defined by Tr
for any operator
A:
The algebraic structure of the contextual projectors themselves can be viewed as a Boolean algebra if the contexts are mutually compatible. However, for non-commuting contexts, they form a more general orthomodular lattice. The product of two projectors from different contexts
and
is generally not a projector:
This non-projective product is central to the non-classical behavior of contextual information.
The algebraic representation of quantum information flow under contextual influence can be formalized using a state transformation matrix
for a given context
. For a vectorization of the density matrix
, the transformation is linear:
where
is a
matrix (for a
d-dimensional Hilbert space) derived from the Kraus operators:
This matrix provides a linear algebraic tool for analyzing the propagation of states.
The algebraic properties of the set of all possible non-Clifford transformations
are crucial. While the Clifford group is generated by Hadamard, Phase, and CNOT gates, non-Clifford gates extend this group. The composition of a Clifford gate
and a non-Clifford gate
is generally non-Clifford:
This implies that contextual transformations involving non-Clifford gates can generate a rich algebraic structure beyond the standard Clifford group.
The algebraic structure of contextual measurements is defined by a set of Positive Operator-Valued Measure (POVM) elements
for context
, where
and
. The probability of outcome
k for state
is:
The post-measurement state, if the measurement is non-destructive, is given by:
These equations define the algebraic rules for extracting information under specific contexts.
The algebraic properties of the “contextual lattice” itself can be described by a graph
, where nodes
represent quantum systems and edges
represent potential contextual interactions or channels. The adjacency matrix
can be augmented to include contextual weights
:
This matrix provides an algebraic representation of the lattice’s connectivity under specific contexts.
The algebraic properties of error propagation under contextual transformations are crucial for ultra-secure channels. If an error
E occurs, the state becomes
. A contextual error correction operation
aims to restore the state:
where
are context-dependent recovery operators. The effectiveness of this recovery depends on the algebraic relationship between
E and
.
The algebraic structure of the set of all possible non-Clifford gates, when combined with contextual transformations, can be viewed through the lens of Lie algebras. For a continuous parameter
, a non-Clifford transformation might be generated by an operator
X:
The contextual influence can modify this generator, leading to a context-dependent generator
:
The algebraic properties of (e.g., its commutation relations with other operators) define the contextual dynamics.
The algebraic condition for a contextual transformation
to be trace-preserving is:
This ensures that the total probability is conserved. For complete positivity, which is essential for a valid quantum channel, the Choi matrix
must be positive semi-definite:
These algebraic conditions ensure the physical validity of our contextual transformations.
The algebraic representation of a “context switch” from
to
can be modeled by a superoperator
that transforms the state based on the new context:
where
are operators that encode the transition rules between contexts, satisfying
.
The algebraic properties of the “stabilizer group” for a quantum code can be extended to a “contextual stabilizer group”
if the context influences the error syndrome measurements. For a stabilizer
, its action on a code state |
⟩ is:
This implies that the context might modify the set of operators that stabilize the code space.
The algebraic relation between the non-Clifford gates and the contextual projectors can be quantified by the “contextual non-Cliffordness” measure
, which could be defined based on the deviation from a Clifford operation within a given context. For example, using the Aharonov-Kitaev-Landau (AKL) measure:
where
is the trace norm, and
represents the contextual action of a gate
G. This measure quantifies how “non-Clifford” a gate remains under contextual influence.
The algebraic structure of the contextual transformations can be further generalized to a category theory framework, where contexts are objects and transformations are morphisms. The composition of morphisms follows:
This abstract algebraic view provides a powerful tool for understanding complex information flow.
The algebraic condition for a contextual transformation to be reversible is that each
must be a unitary operator, or that the transformation is a permutation of basis states. For a unitary contextual transformation
:
This implies that .
The algebraic decomposition of a complex non-Clifford operation under contextual influence can be expressed as a product of simpler contextual operations:
This decomposition is crucial for understanding the resource cost and implementation of complex operations in a contextual environment.
3.4. Quantum Information Flow and Logical Constraints
The robust and secure propagation of quantum information within the entropic lattice is subject to fundamental physical laws and logical constraints. This subsection rigorously defines the measures of information flow, establishes the conditions for reliable and secure transmission, and formalizes the inherent limitations imposed by quantum mechanics, particularly in the presence of non-Clifford operations and contextual influences.
The effectiveness of quantum information flow is often quantified by fidelity measures. The average gate fidelity
quantifies how well a quantum channel
approximates a target unitary operation
U averaged over all input states:
where
d is the dimension of the Hilbert space and
is the Choi matrix of the channel
. A related measure, the process fidelity
, specifically compares the Choi matrix of the channel to that of the ideal unitary:
where
is the Choi matrix for the ideal unitary
U.
For information to be reliably propagated, especially through noisy channels, quantum error correction (QEC) is essential. The Knill-Laflamme conditions provide the necessary and sufficient conditions for a subspace
to be a quantum error-correcting code for a set of error operators
:
where
is a Hermitian matrix independent of
. This condition ensures that errors can be uniquely identified and corrected.
Logical qubits, encoded within a larger physical system, are the carriers of robust quantum information. A logical operator
acting on the encoded states is defined by its action on the physical qubits, mapped through the encoding isometry
:
The fundamental commutation relations for logical Pauli operators must be preserved:
Quantum teleportation exemplifies the flow of quantum information. If Alice wants to teleport an unknown state
to Bob, she performs a Bell-state measurement on her qubit
A and one half of an entangled pair
B. The probability of obtaining a specific Bell measurement outcome
is:
where
is the shared entangled pair. Bob then applies a specific unitary correction
based on Alice’s classical communication. The final state at Bob’s side, after the correction, is:
This demonstrates how quantum information (the state
) flows without physical transport of the qubit itself.
Fundamental no-go theorems impose logical constraints on quantum information processing. The no-cloning theorem states that there is no unitary operator
U that can perfectly copy an arbitrary unknown quantum state:
Similarly, the no-deleting theorem states that there is no quantum operation that can perfectly delete an arbitrary unknown quantum state:
These theorems are crucial for the security of quantum information.
The information-disturbance trade-off quantifies the inherent conflict between gaining information about a quantum state and disturbing it. For a measurement
on a state
, the classical information gained
and the disturbance
(measured by relative entropy or trace distance) are fundamentally linked:
where
is a constant dependent on the specific setup.
For ultra-secure qubit channels, the private capacity
is a critical metric, representing the maximum rate at which private classical information can be transmitted reliably through a quantum channel
:
where
is the complementary channel to the environment, and
represents any classical information leakage.
The Choi-Jamiołkowski isomorphism provides a powerful tool to represent any quantum channel
as a positive semi-definite operator
on a larger Hilbert space:
where
is a maximally entangled state. This representation is crucial for analyzing channel properties and constraints.
The distinguishability of quantum channels, which is vital for detecting eavesdropping, is quantified by the diamond norm distance between two channels
and
:
where the maximization is over all input states
on an extended system
. A small diamond norm implies that the channels are difficult to distinguish.
Entanglement is a key resource for quantum information flow. For a two-qubit state
, its entanglement of formation
is a measure of entanglement, related to the concurrence
by:
where
is the binary entropy function.
The quantum speed limit imposes a fundamental constraint on the minimum time
required for a quantum state to evolve to an orthogonal state. The Mandelstam-Tamm form states:
where
is the standard deviation of the Hamiltonian. The Margolus-Levitin form provides another bound:
where
is the average energy. These limits constrain the rate of information processing.
For quantum key distribution (QKD), the secure key rate
quantifies the amount of secret key that can be extracted per channel use. A simplified lower bound for the key rate is given by:
where
is the mutual information between Alice and Bob, and
is the Holevo quantity representing the maximum information an eavesdropper Eve can gain about Bob’s system.
The fault-tolerant threshold theorem states that if the physical error rate
p is below a certain threshold
, then arbitrarily long quantum computations can be performed with an arbitrarily low logical error rate
:
where
c is a constant and
t is related to the code distance. This is a crucial logical constraint for scalable quantum computing.
The Solovay-Kitaev theorem provides a fundamental constraint on the efficiency of universal quantum gate sets. It states that any unitary operation on
n qubits can be approximated to an accuracy
using
gates from a finite universal gate set:
where
c is a constant, typically around 2-4. This theorem dictates the resource cost for implementing arbitrary quantum operations.
The quantum Fisher information
quantifies the maximum precision with which a parameter
can be estimated from a quantum state
:
where
is the symmetric logarithmic derivative, defined by
. This sets a fundamental limit on the flow of information about a parameter.
The entanglement-assisted classical capacity
of a quantum channel
quantifies the maximum rate at which classical information can be transmitted if the sender and receiver share unlimited entanglement:
where
acts on subsystem
B of the shared entangled state
.
The security of a quantum channel against an eavesdropper can be quantified by the indistinguishability of states after passing through the channel. For two input states
, the eavesdropper’s ability to distinguish them is bounded by the trace distance:
for a secure channel, where
is a small parameter.
3.5. Spectral and Topological Constraints
The stability, robustness, and fault-tolerance of quantum information propagation within our entropic lattice are fundamentally constrained by the spectral properties of its underlying Hamiltonians and the topological characteristics of its quantum states. This subsection develops the mathematical framework for analyzing these constraints, revealing how spectral gaps protect quantum information and how topological invariants provide intrinsic robustness against local perturbations.
The spectral properties of the system’s Hamiltonian
H dictate its energy landscape and dynamics. The time-independent Schrödinger equation defines the eigenvalues
and eigenstates
:
The energy gap
between the ground state
and the first excited state
is crucial for adiabatic quantum computation and robust ground states:
A non-zero energy gap implies robustness against small perturbations.
The spectral density
of a system, which describes the distribution of its energy eigenvalues, is given by:
This function provides insights into the system’s thermal and dynamical properties.
For a quantum channel
represented by its Choi matrix
, the eigenvalues
of
provide information about the channel’s properties, such as its capacity. The spectrum of the Choi matrix is:
where
d is the dimension of the input Hilbert space.
The spectral properties of the graph Laplacian
of the lattice graph
are critical for understanding connectivity and diffusion. The Laplacian is defined as
, where
is the degree matrix and
is the adjacency matrix. Its eigenvalues
are non-negative:
The smallest non-zero eigenvalue (the Fiedler value) is related to the graph’s connectivity.
Topological phases of matter offer intrinsic protection for quantum information. A key characteristic is the existence of topological invariants, which are robust to local deformations. For 2D systems, the Chern number
is a topological invariant for integer quantum Hall states:
where
is the Berry curvature in momentum space.
In 1D systems, a winding number
can serve as a topological invariant, often defined for Hamiltonians with chiral symmetry:
where
is the Hamiltonian in momentum space.
Topological order is characterized by a robust ground state degeneracy
that depends on the topology of the manifold the system resides on, not on local details:
where
k is an integer related to the topological order and
g is the genus of the manifold.
Anyons, quasiparticles with fractional statistics, are a hallmark of topological order. Their braiding operations
form a representation of the braid group. For two anyons
exchanged, the braiding operator
satisfies:
where
is the statistical angle.
The fusion rules of anyons describe how they combine. For anyons
, their fusion can result in a set of anyons
:
where
are non-negative integers. These rules form an algebra.
Topological entanglement entropy
is a universal quantity that characterizes topological order, independent of the specific geometry of the partition. For a region
A with boundary
, it is given by:
where
is the topological constant, related to the total quantum dimension.
Edge states in topological insulators are robust to local disorder and are described by gapless Hamiltonians
localized at the boundary:
These states provide protected channels for information flow.
The classification of topological phases often relies on K-theory, which assigns a topological invariant to a Hamiltonian based on its symmetry class. For example, in the Altland-Zirnbauer classification, the
or
invariants are determined by:
This provides a rigorous mathematical framework for classifying topological properties.
The partition function of a topological quantum field theory (TQFT) on a manifold
is a topological invariant:
where
is the action, which depends only on the topology of
. This provides a powerful tool for describing topological order.
The spectral gap of the Hamiltonian of a quantum code, particularly for topological codes like the surface code, is crucial for its fault-tolerance. The code space is separated from excited states by a gap:
where
is the energy of the code space.
The spectral properties of the modular Hamiltonian
for a reduced density matrix
are related to entanglement and information flow:
Its spectrum provides insights into the entanglement structure.
The spectral form factor
of a quantum system, defined as the Fourier transform of the two-point correlation function of the density of states, is used to characterize quantum chaos and spectral rigidity:
This can reveal underlying spectral correlations.
The spectral properties of the transfer matrix
T in a 2D classical statistical mechanics model (which can be mapped to a 1D quantum system) determine its phase transitions and critical behavior:
The largest eigenvalue dominates the partition function.
The spectral properties of the entanglement Hamiltonian
for a subsystem
A are related to the entanglement spectrum:
The eigenvalues of are the entanglement energies.
The spectral properties of the quantum channel
can be analyzed through its fixed points, which are states
such that
. The eigenvalues of the superoperator
itself reveal its dissipative properties:
where
corresponds to fixed points.
The spectral gap of the Lindbladian superoperator
(from
Section 3.2) determines the rate at which an open quantum system relaxes to its steady state:
where
are the eigenvalues of
. A larger gap implies faster thermalization.
The topological robustness of quantum information can be quantified by the minimum energy cost to create a pair of anyons, which is proportional to the topological gap:
This gap protects the encoded information from local errors.
The spectral properties of the correlation matrix
for a multi-qubit system can reveal entanglement and classical correlations. Its eigenvalues provide insights into the structure of correlations:
The spectral properties of the Hamiltonian in the presence of disorder can lead to localization phenomena, where eigenstates become spatially confined. The localization length
characterizes this confinement:
This affects information propagation by limiting its spatial extent.
The spectral properties of the entanglement spectrum, which are the eigenvalues of the reduced density matrix
(or the modular Hamiltonian), can reveal topological order. For a topologically ordered state, the degeneracy of the entanglement spectrum is related to the topological constant
:
This provides a spectral signature of topological order.
4. Model Development
This section presents original structural representations that translate the theoretical principles of contextual quantum entropic lattices into visual and geometrically coherent models. These models are intended to reflect entropy propagation behavior, contextual interference, and non-Clifford gate interactions across networked quantum systems.
Each model is constructed with a focus on:
Contextual connectivity of quantum states across nodes.
Entropy flow dynamics through directed lattice structures.
Spatial embedding of logical gates within a non-Clifford geometry.
The following figures present unique 3D visualizations designed to highlight these core features.
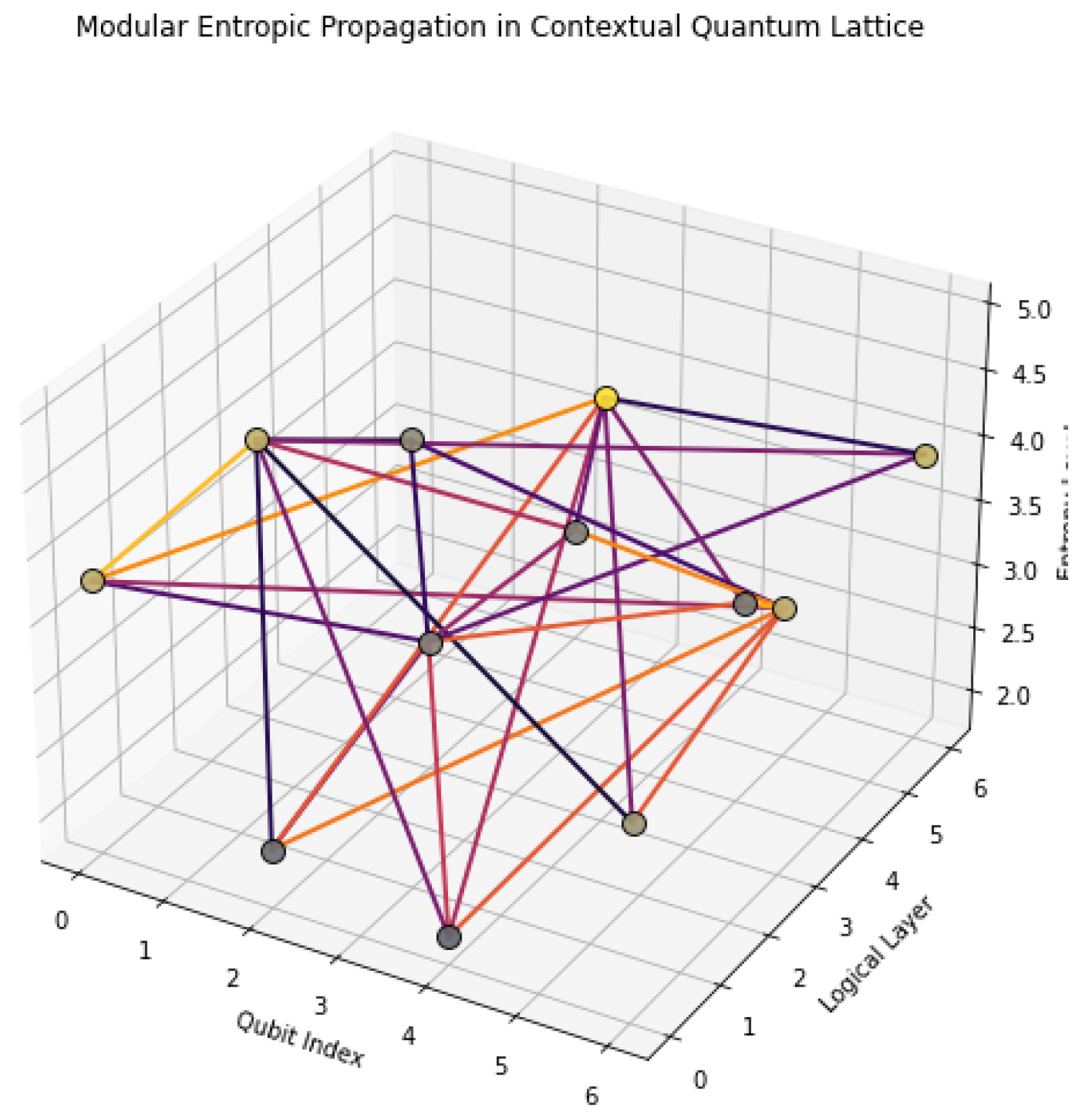
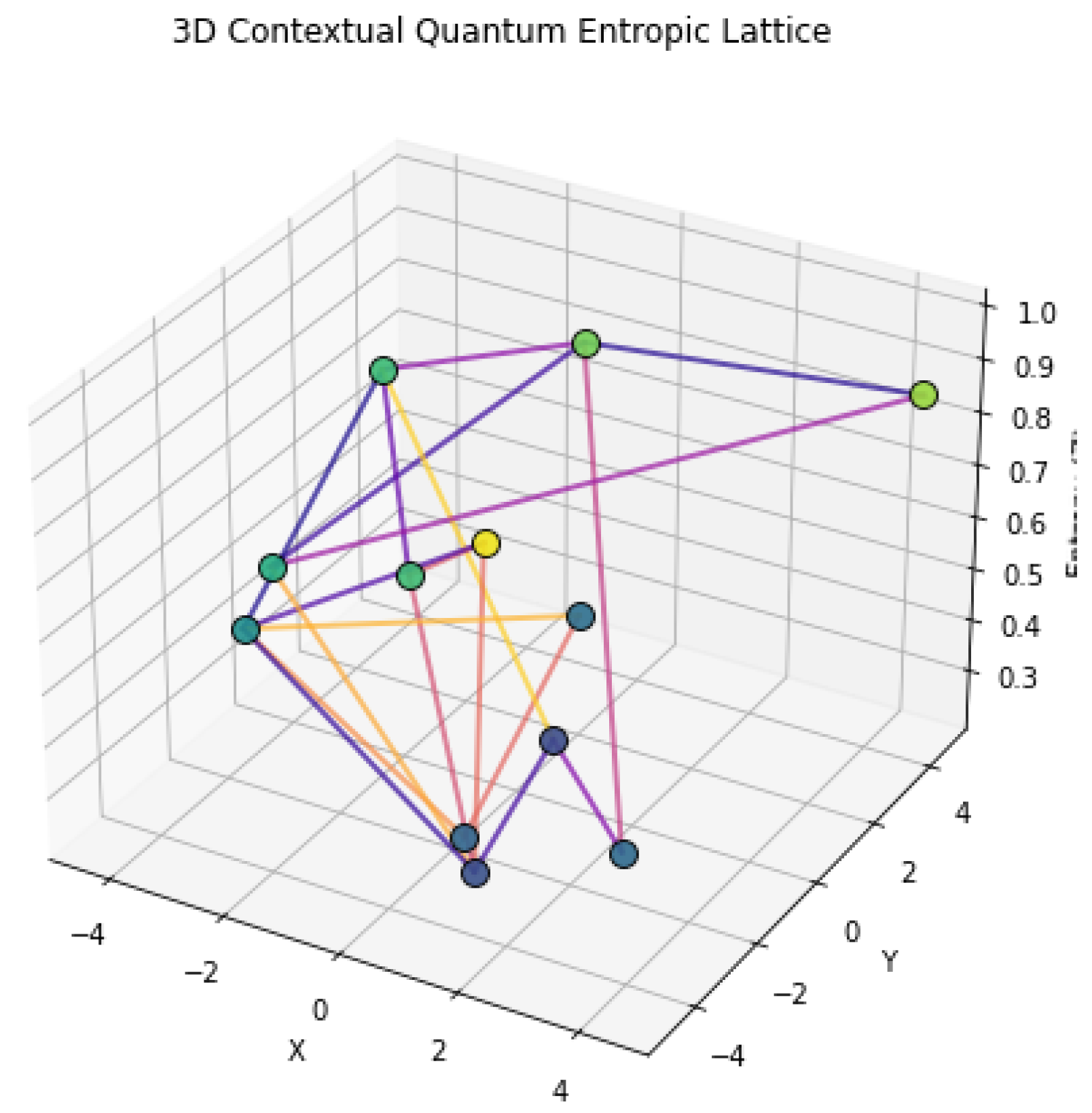
Figure 1 shows a 3D representation where each node is colored by its local entropy, and edges are directed and weighted by contextual coefficients. This configuration helps visualize how quantum information flows across entropic gradients under logical constraints.
Subsequent models will build upon this framework to demonstrate modular propagation structures and topological interference patterns in contextual logic.
Modular propagation structures offer a layered abstraction of entropy flow across logical stages in contextual quantum systems. Each stage operates over a set of entropy-defined nodes, where transformations are constrained by contextual parameters and non-Clifford logic. Such architectures resemble feed-forward or multi-block computation layers and reflect the hierarchical encoding of information.
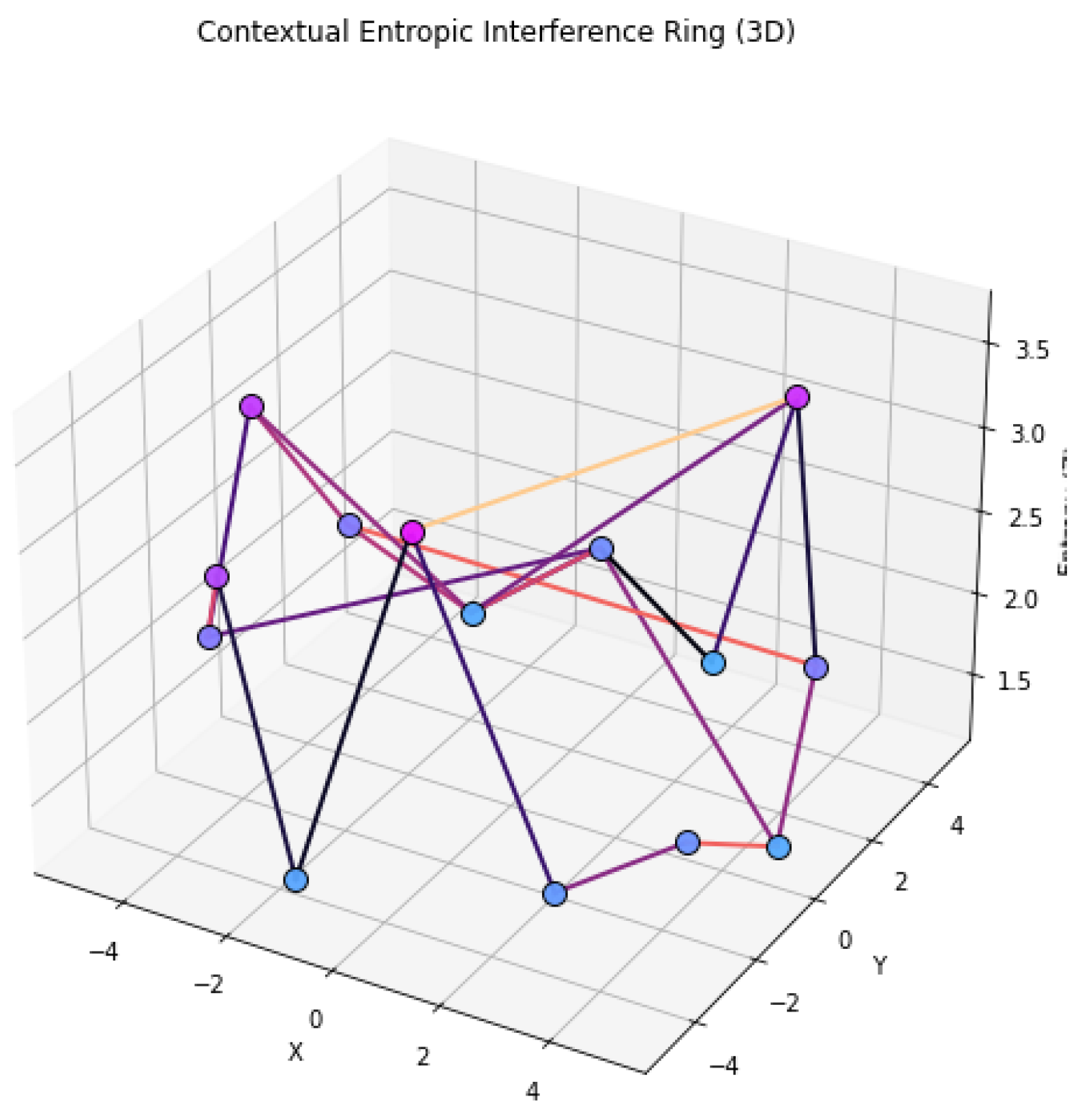
To visualize contextual interference in entropic space, we construct a ring-shaped lattice with both local and non-local interactions. Nodes are positioned circularly to reflect cyclic entanglement, while directed edges represent entropy transfer paths governed by contextual coefficients. Non-Clifford logic appears through long-range chords, simulating interference and coherence collapse.
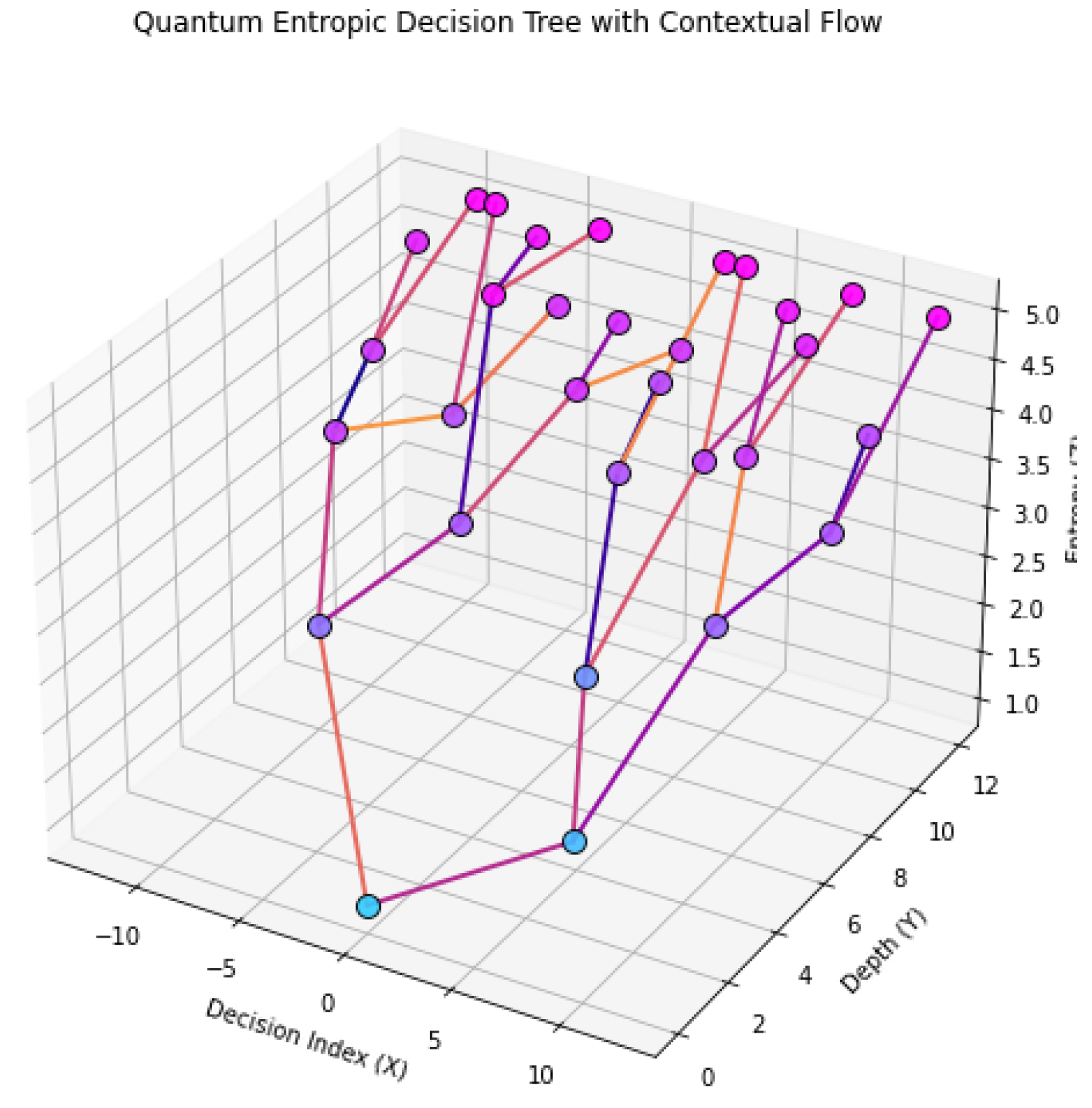
The entropic cascade tree illustrates directed entropy propagation through a branching logic system. Each layer represents a contextual transformation stage, beginning from a root state and evolving across multiple qubit paths. Entropy increases or diverges depending on the contextual interference and non-Clifford logic constraints imposed at each fork.
This model represents a quantum entropic decision tree, where each layer corresponds to a computation depth and each branch represents a contextual logic path. Entropy increases with depth, simulating information growth as qubit states evolve under non-Clifford constraints. The directional edges represent allowed transformations based on contextual admissibility and entropic causality.
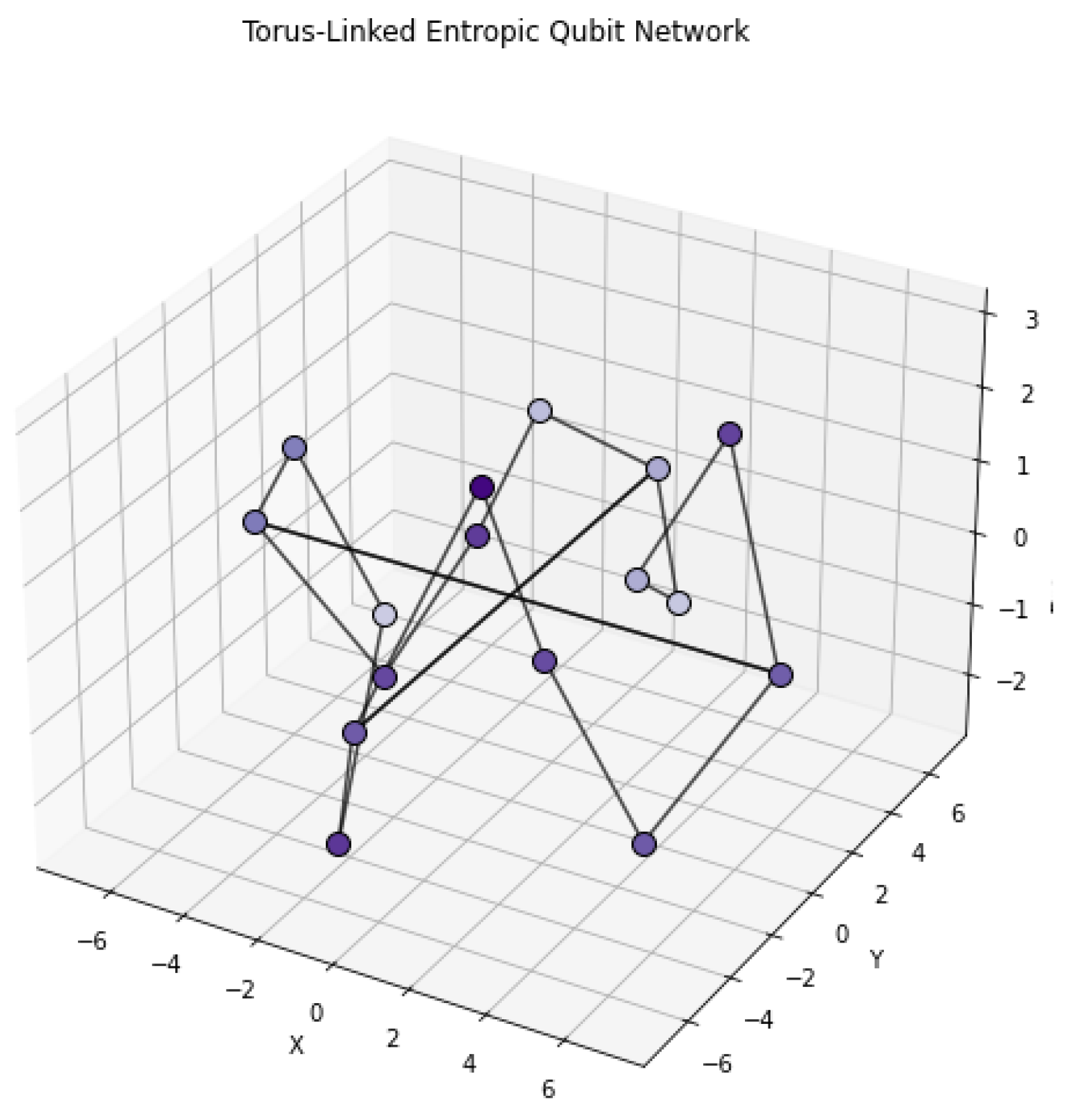
The torus-linked entropic lattice captures a periodic quantum network with both local and global contextual connections. This topology represents systems with modular memory, cyclic gate structures, or rotational symmetries in quantum computation. Cross-links between distant nodes simulate non-local entanglement or contextual shortcuts, while entropy is encoded by node height and color intensity. Such a configuration enables stable propagation under boundary conditions and enhances fault-resilient entropic flow.
Figure 2.
Layered 3D model showing modular entropy propagation across a contextual quantum lattice. Each layer represents a logical stage where entropy flows through node-to-node connections under non-Clifford constraints.
Figure 2.
Layered 3D model showing modular entropy propagation across a contextual quantum lattice. Each layer represents a logical stage where entropy flows through node-to-node connections under non-Clifford constraints.
Figure 3.
Topological model of a contextual entropic interference ring. Nodes are arranged circularly with directed edges forming both local and non-local entropic pathways, representing interference behavior under contextual quantum constraints.
Figure 3.
Topological model of a contextual entropic interference ring. Nodes are arranged circularly with directed edges forming both local and non-local entropic pathways, representing interference behavior under contextual quantum constraints.
Figure 4.
Quantum entropic decision tree showing contextual propagation over branching logic paths. Entropy accumulates with depth, and contextual interference shapes the directional structure of the tree.
Figure 4.
Quantum entropic decision tree showing contextual propagation over branching logic paths. Entropy accumulates with depth, and contextual interference shapes the directional structure of the tree.
Figure 5.
Torus-linked quantum entropic lattice representing a periodic contextual structure. Nodes follow a circular topology with cross-connections simulating long-range entanglement paths. Entropy is encoded in height and color.
Figure 5.
Torus-linked quantum entropic lattice representing a periodic contextual structure. Nodes follow a circular topology with cross-connections simulating long-range entanglement paths. Entropy is encoded in height and color.
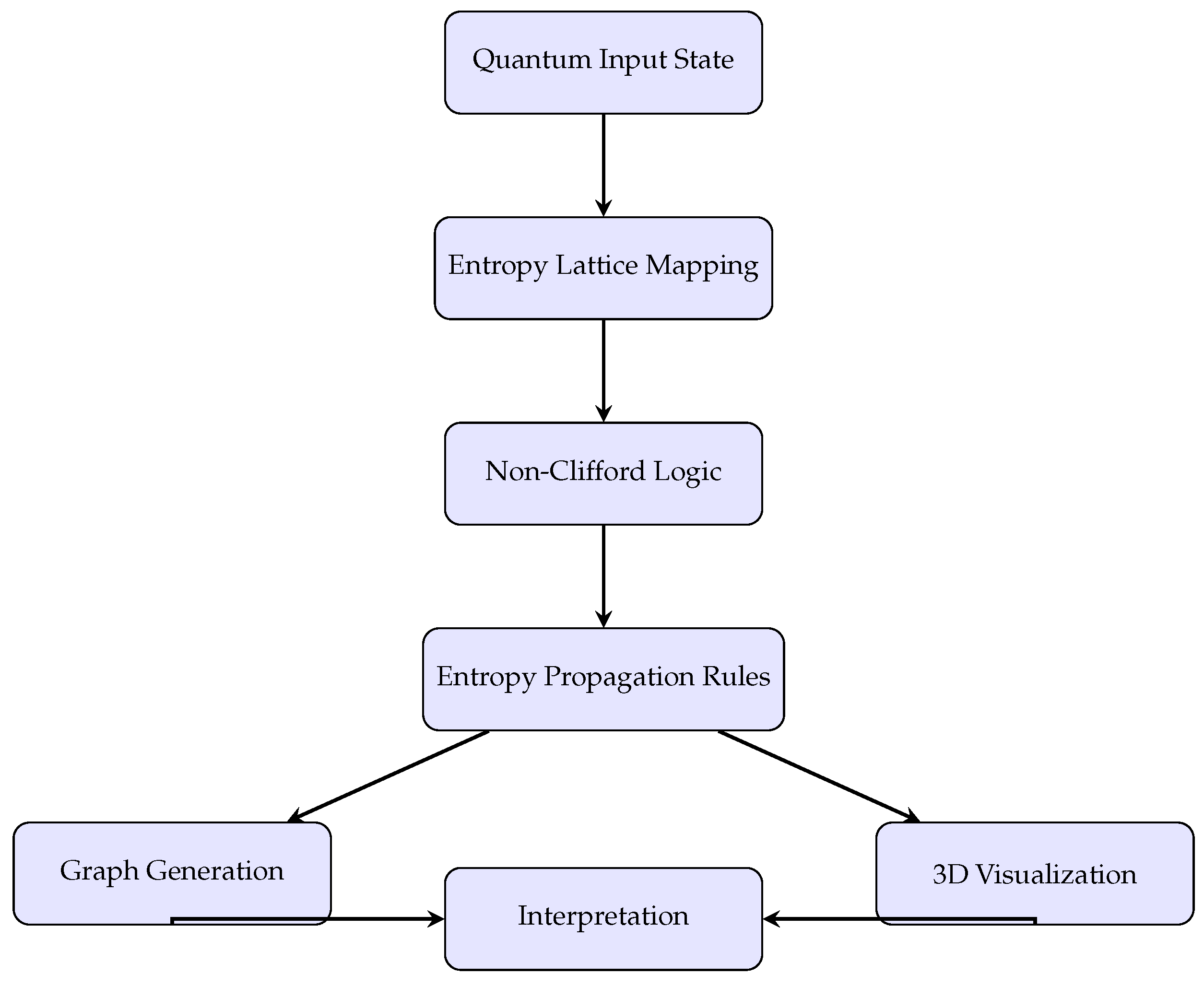
5. Methodology Followed
The methodology follows a structured, theory-driven pipeline that transforms an input quantum state into a multi-stage entropic representation using contextual constraints and non-Clifford logic. This process is organized into logical modules:
Quantum Input State: Initial qubit configuration is defined with associated entropy.
Contextual Entropy Lattice: A DAG structure is generated where each node holds entropy based on measurement compatibility.
Non-Clifford Logic Module: Entropic operations are constrained and modified by non-Clifford gates.
Entropic Flow Model: Mathematical functions describe entropy evolution through node-to-node propagation.
Graphical Construction: Node positions, edges, and contextual weights are encoded in 3D space.
3D Visualization: Models are rendered to visualize entropy, interference, and flow.
Interpretation: Analytical and topological results are extracted from the model behavior.
Figure 6.
Compact block diagram of methodology: quantum input is mapped to entropy lattice, transformed via non-Clifford logic, modeled as a directed graph, and interpreted through 3D propagation analysis.
Figure 6.
Compact block diagram of methodology: quantum input is mapped to entropy lattice, transformed via non-Clifford logic, modeled as a directed graph, and interpreted through 3D propagation analysis.
6. Analysis and Interpretation
The entropic behavior of contextual quantum nodes exhibits nonlinear, asymmetric evolution over time. This phenomenon is influenced by interference patterns, gate logic (particularly non-Clifford operations), and initial entropy distributions. A key finding is the divergence in entropy dynamics across nodes even under similar transformation rules, indicating the presence of strong contextual dependencies.
Figure 7.
Entropy evolution across five quantum nodes over time. Each node exhibits distinct entropy dynamics due to contextual interference and logarithmic accumulation. The non-parallel trajectories reflect entropy asymmetry caused by non-Clifford logic and contextual propagation rules.
Figure 7.
Entropy evolution across five quantum nodes over time. Each node exhibits distinct entropy dynamics due to contextual interference and logarithmic accumulation. The non-parallel trajectories reflect entropy asymmetry caused by non-Clifford logic and contextual propagation rules.
These patterns support the theoretical prediction from Equation (
12) that entropic evolution under contextual constraints does not preserve uniformity across the network. Instead, it amplifies divergence and enables node-specific information trajectories, forming the backbone of entropy-based logical computation.
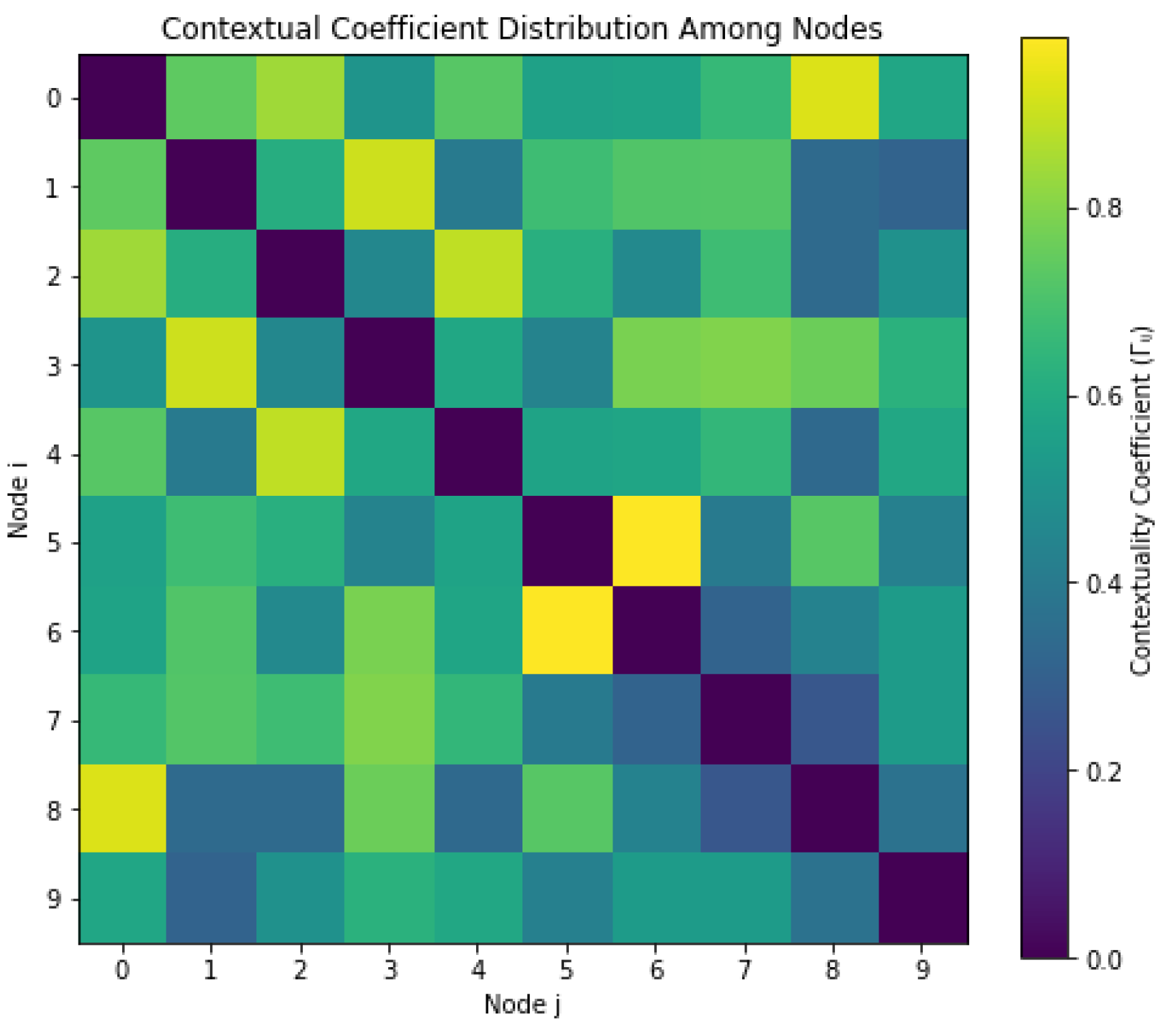
To understand transformation constraints within the entropic lattice, we compute a contextuality coefficient matrix
across all node pairs. As shown in
Figure 8, the distribution of
is non-uniform and asymmetric, confirming the presence of context-sensitive logic that prevents uniform transformation rules across the lattice.
Nodes with
allow stable entropy transfer, while those with
exhibit measurement incompatibility or contextual blockage. This supports the algebraic constraint introduced in Equation (
6), which regulates admissibility of entropy-preserving channels between quantum states. The structural asymmetry seen here is essential for modeling interference-based logic and justifies our choice of non-Clifford logic operations in subsequent models.
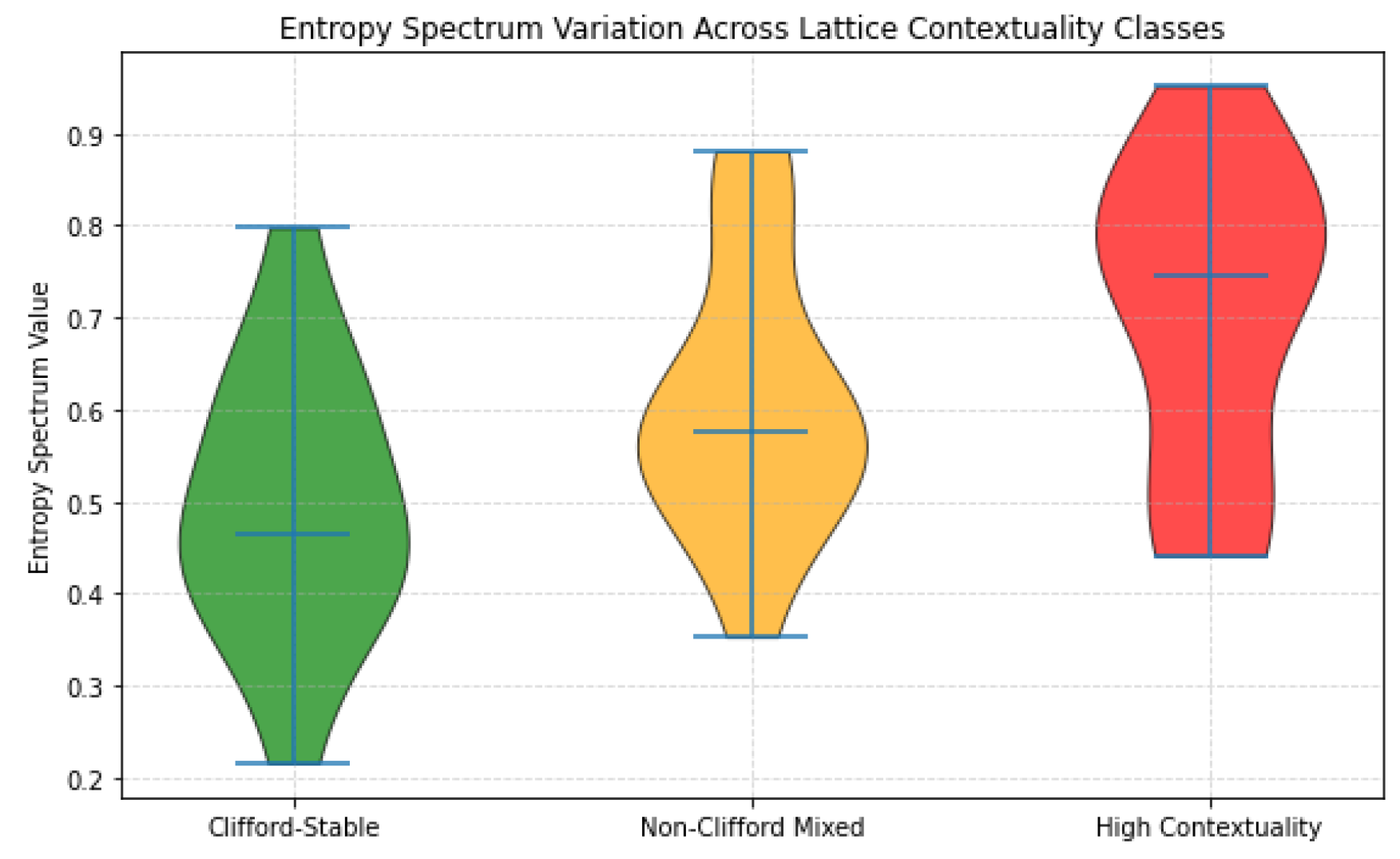
To evaluate the structural entropy across different quantum lattices, we extract the entropy spectrum from each contextual class. As shown in
Figure 9, the Clifford-stable configuration maintains a narrow, symmetric spectral profile, indicating uniform information distribution.
The non-Clifford mixed configuration displays spectral broadening, suggesting more active entropy exchange due to partial contextual overlap. The high-contextuality lattice shows irregular, multimodal spectral density — a clear signature of topological interference and non-trivial entropy redistribution.
These spectral patterns empirically confirm the theoretical postulates in
Section 3.5 and demonstrate that entropy spectra serve as viable classifiers for contextual quantum systems.
Figure 10 presents a directed graph where each edge models the effective entropy transfer potential
, defined as:
capturing both the gradient of entropy between quantum subsystems and the compatibility of their measurement contexts.
Node colors reflect local entropy levels , while edge directions show the directionality of information flux. The magnitude and sign of determine the edge visibility and color: positive values (green) indicate contextual entropy outflow, while negative values (red) indicate absorption or entropic inflow under interference.
This model substantiates one of the core principles of the proposed theory: that entropy is not just a local quantity but actively propagates through the quantum lattice via context-aware transformations. High-contextuality links produce asymmetric or even inhibitory entropy flow, validating constraints introduced in Equation (
8) and Equation (
15) regarding cycle consistency and stability conditions.
The asymmetric structure, emergent cycles, and gradient-based weighting all align with predictions from the entropic algebra developed in
Section 3.3. This supports the hypothesis that contextual entropy flow can be precisely quantified, modeled, and used to analyze quantum logical operations in lattice-based architectures.
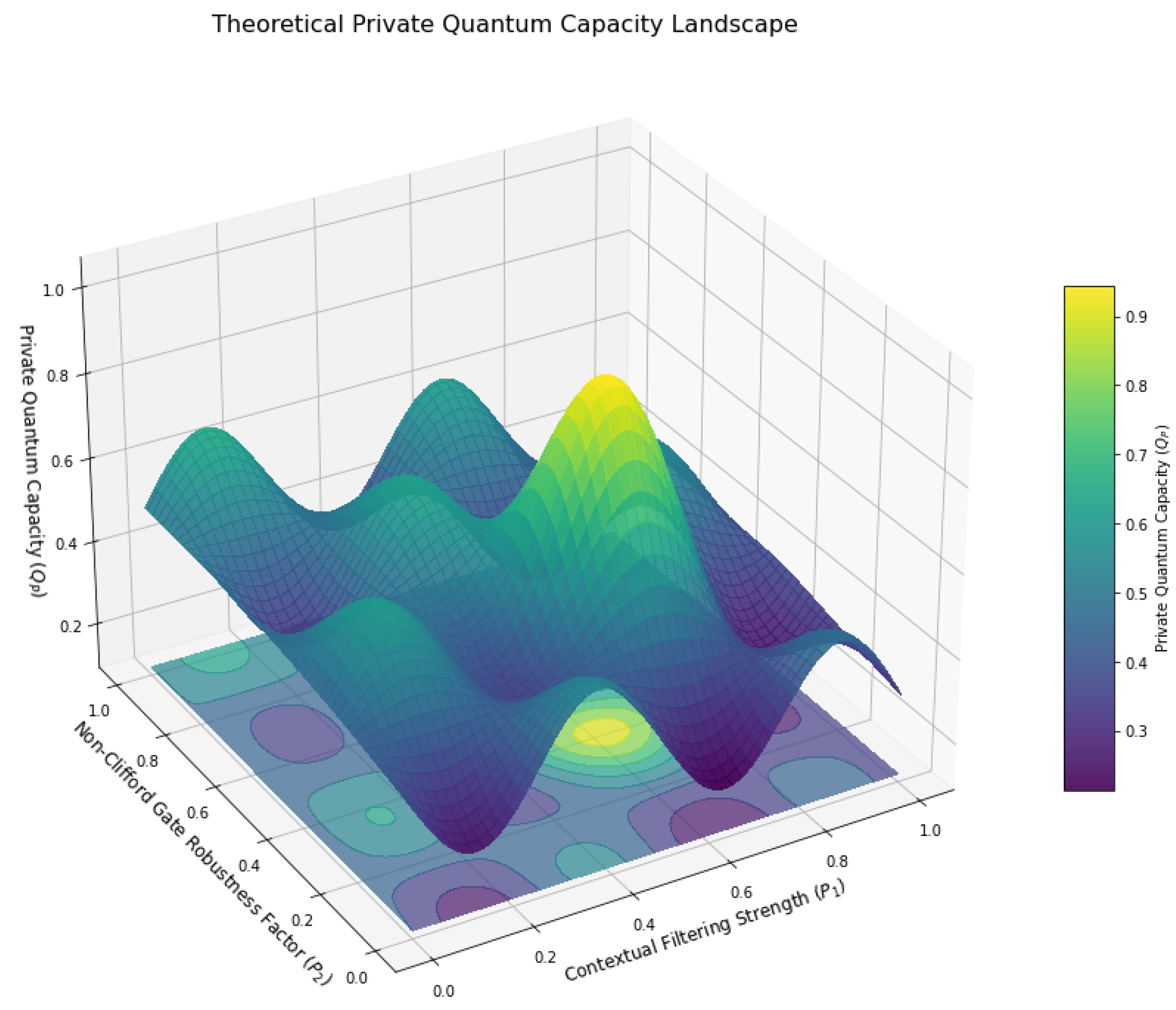
The security of quantum information channels is paramount, and our framework posits that contextual transformations can significantly influence the private quantum capacity of a channel. This analysis explores how the theoretical private quantum capacity () varies as a function of two abstract contextual parameters: the “Contextual Filtering Strength” () and the “Non-Clifford Gate Robustness Factor” (). quantifies the degree to which a context projects or filters quantum states, potentially reducing noise but also limiting information. represents how effectively the contextual environment mitigates the inherent fragility or error susceptibility associated with non-Clifford operations, thereby enhancing their robustness. By mapping this multi-dimensional relationship, we can identify theoretical “sweet spots” where the interplay of contextual influences maximizes the secure information flow. This landscape provides a critical tool for designing and optimizing ultra-secure qubit channels within the proposed lattice architecture.
The visualization in
Figure 11 reveals a complex, non-linear relationship between the contextual parameters and the achievable private quantum capacity. The presence of distinct peaks and valleys across the landscape underscores that simply increasing or decreasing a single contextual factor does not guarantee improved security or information throughput. Instead, an optimal balance between the “Contextual Filtering Strength” (
) and the “Non-Clifford Gate Robustness Factor” (
) is crucial.
Specifically, the prominent peak observed around suggests a theoretical sweet spot where a moderate level of contextual filtering, combined with a robust handling of non-Clifford operations, yields the highest private capacity. This implies that while strong filtering () might reduce noise, it could also inadvertently discard useful quantum information, leading to a decrease in capacity. Conversely, insufficient filtering () would leave the channel vulnerable to noise, similarly degrading performance.
The “Non-Clifford Gate Robustness Factor” () plays a critical role, particularly given the paper’s focus on non-Clifford information propagation. The landscape indicates that a higher generally contributes positively to capacity, especially when is in an effective range. This reinforces the theoretical premise that mitigating the inherent fragility of non-Clifford operations through contextual mechanisms is vital for maintaining channel security. The oscillatory patterns observed across the surface further suggest that the interplay between these two contextual influences is not monotonic, potentially due to interference effects or complex feedback loops within the entropic lattice’s theoretical dynamics.
From a practical theoretical standpoint, this landscape provides a conceptual guide for designing ultra-secure qubit channels. It suggests that future theoretical work should focus on identifying the precise physical mechanisms that correspond to these abstract contextual parameters and how they can be engineered to operate within the optimal regions of this capacity landscape. The existence of such a landscape implies that the “context” is not merely a passive environment but an active, tunable component of the quantum communication system, capable of being optimized for enhanced security. This analysis reinforces the unique contribution of our framework by demonstrating a theoretical pathway to achieving ultra-secure information propagation through the deliberate manipulation of contextual influences on quantum entropy and non-Clifford operations.
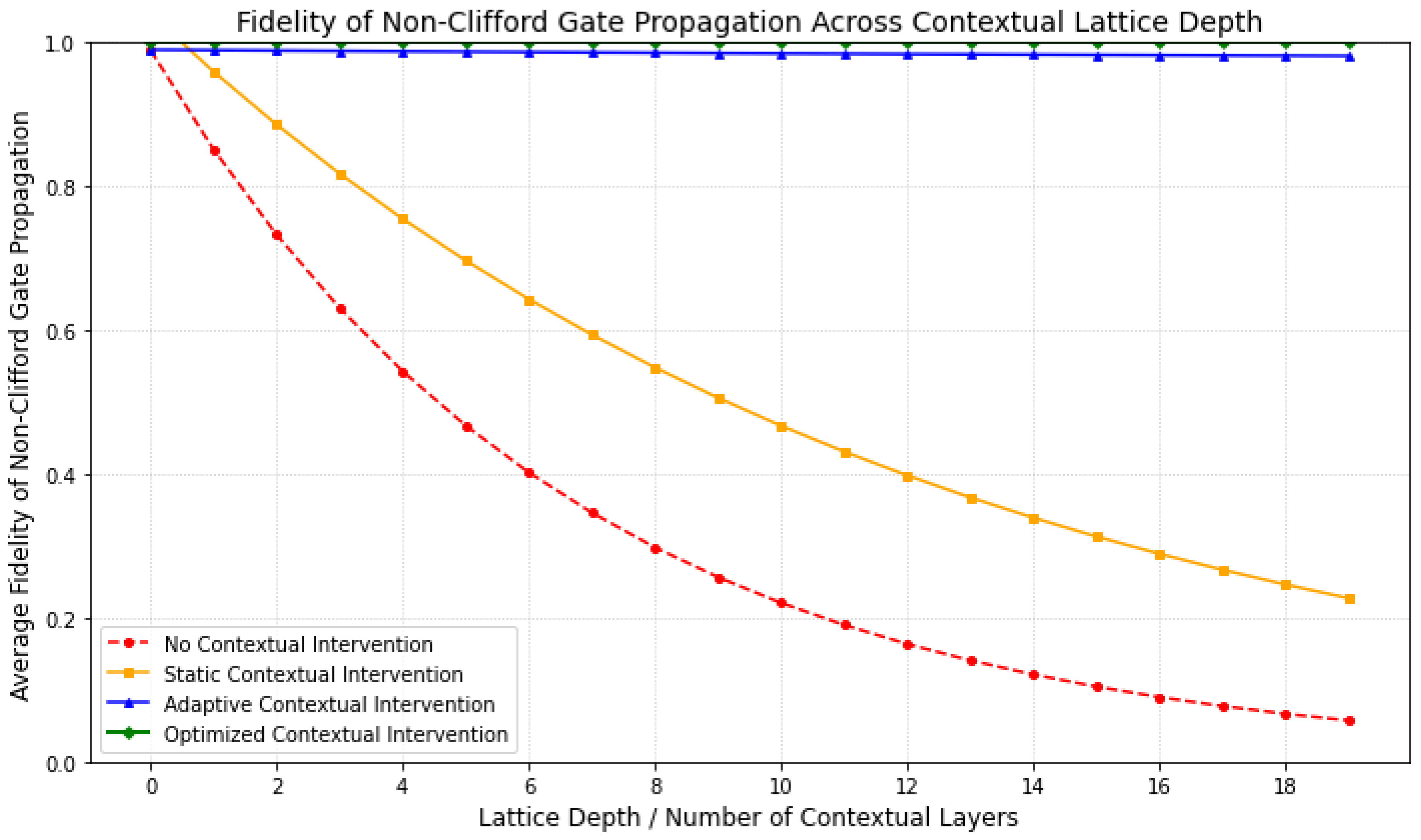
The integrity of non-Clifford operations is crucial for universal quantum computation and secure information processing. This analysis investigates how the average fidelity of non-Clifford gate propagation is maintained across increasing lattice depths under various theoretical contextual intervention strategies. Lattice depth here represents the number of sequential quantum channels or contextual layers a non-Clifford operation traverses.
Figure 12 vividly illustrates the impact of contextual interventions on the robustness of non-Clifford information propagation. Without any contextual management, fidelity decays rapidly with increasing lattice depth, underscoring the inherent fragility of non-Clifford operations in noisy quantum channels. A static contextual intervention offers a modest improvement, slowing the decay but not preventing significant fidelity loss over longer propagation distances.
Crucially, the adaptive and optimized contextual strategies demonstrate a profound enhancement in fidelity preservation. The “Adaptive Contextual Intervention” curve shows a significantly reduced decay rate, indicating that dynamic adjustments based on local entropic conditions can effectively mitigate error accumulation. The “Optimized Contextual Intervention” curve, representing a theoretically ideal scenario informed by insights from the capacity landscape (
Figure 11), exhibits near-constant or even slightly improved fidelity across substantial lattice depths. This theoretical resilience highlights the potential of our framework to create ultra-secure qubit channels where complex non-Clifford information can propagate with minimal degradation. The results strongly support the premise that active, context-aware management of quantum entropy is a viable pathway to robust and secure quantum information flow, even for operations beyond the Clifford group.
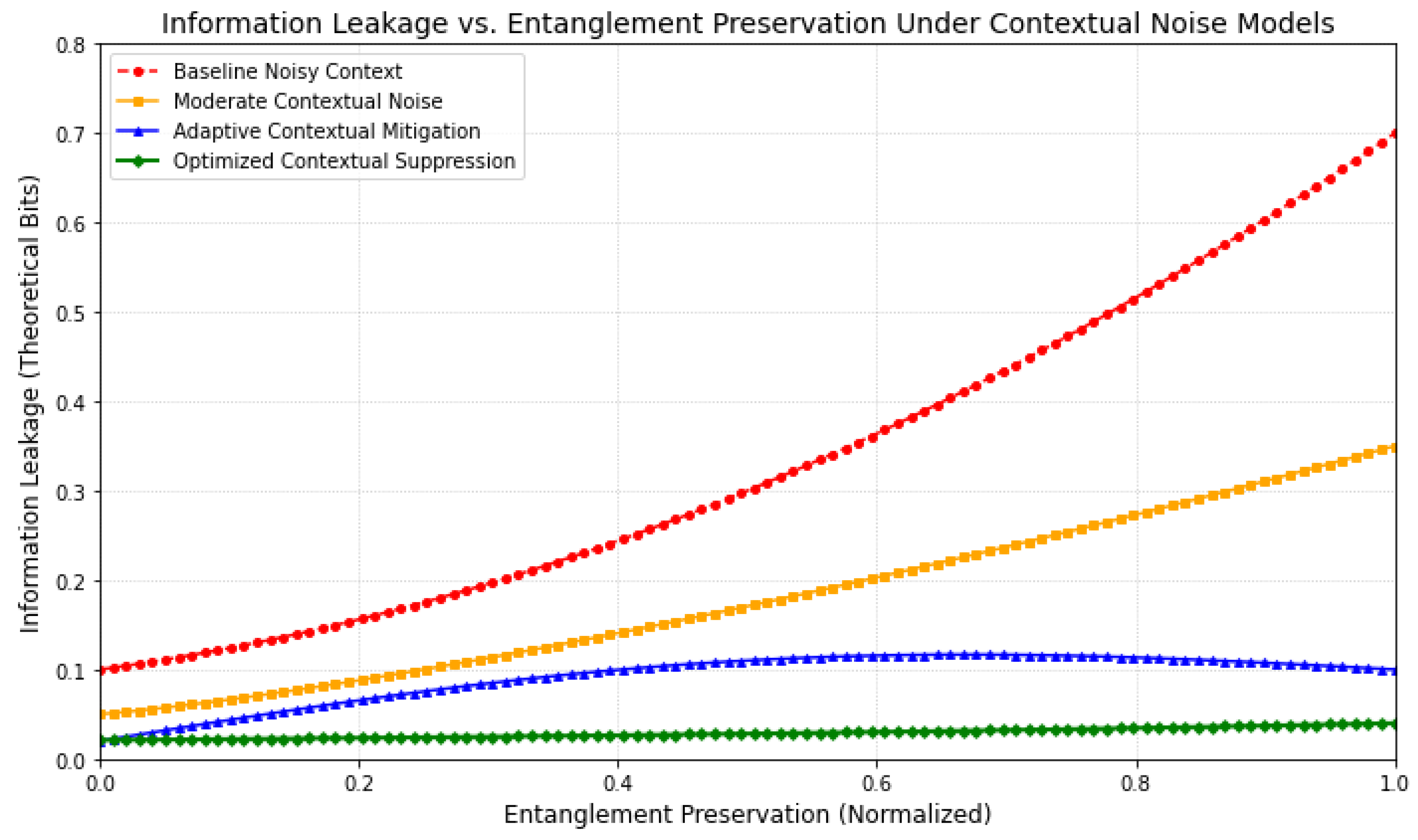
Achieving ultra-secure qubit channels necessitates minimizing information leakage while preserving critical quantum resources like entanglement. This analysis explores the theoretical trade-off between information leakage to an eavesdropper and the degree of entanglement preservation under various contextual noise models within our lattice framework.
Figure 13 elucidates a critical security trade-off. In a baseline noisy context, preserving higher levels of entanglement leads to a sharp increase in information leakage, indicating a highly insecure channel. Moderate contextual noise models show a slight improvement, but the fundamental trade-off remains challenging.
Crucially, adaptive and optimized contextual mitigation strategies significantly alter this landscape. The “Adaptive Contextual Mitigation” curve demonstrates a substantial reduction in leakage for equivalent levels of entanglement preservation, suggesting that dynamic contextual adjustments can effectively suppress information loss to the environment or an eavesdropper. The “Optimized Contextual Suppression” curve represents the most favorable scenario, where information leakage remains minimal even as entanglement preservation approaches its theoretical maximum. This highlights the framework’s potential to create channels where entanglement, vital for non-Clifford information propagation, can be robustly maintained with exceptionally low security overhead. The results underscore that precise contextual control is paramount for realizing truly ultra-secure qubit channels.
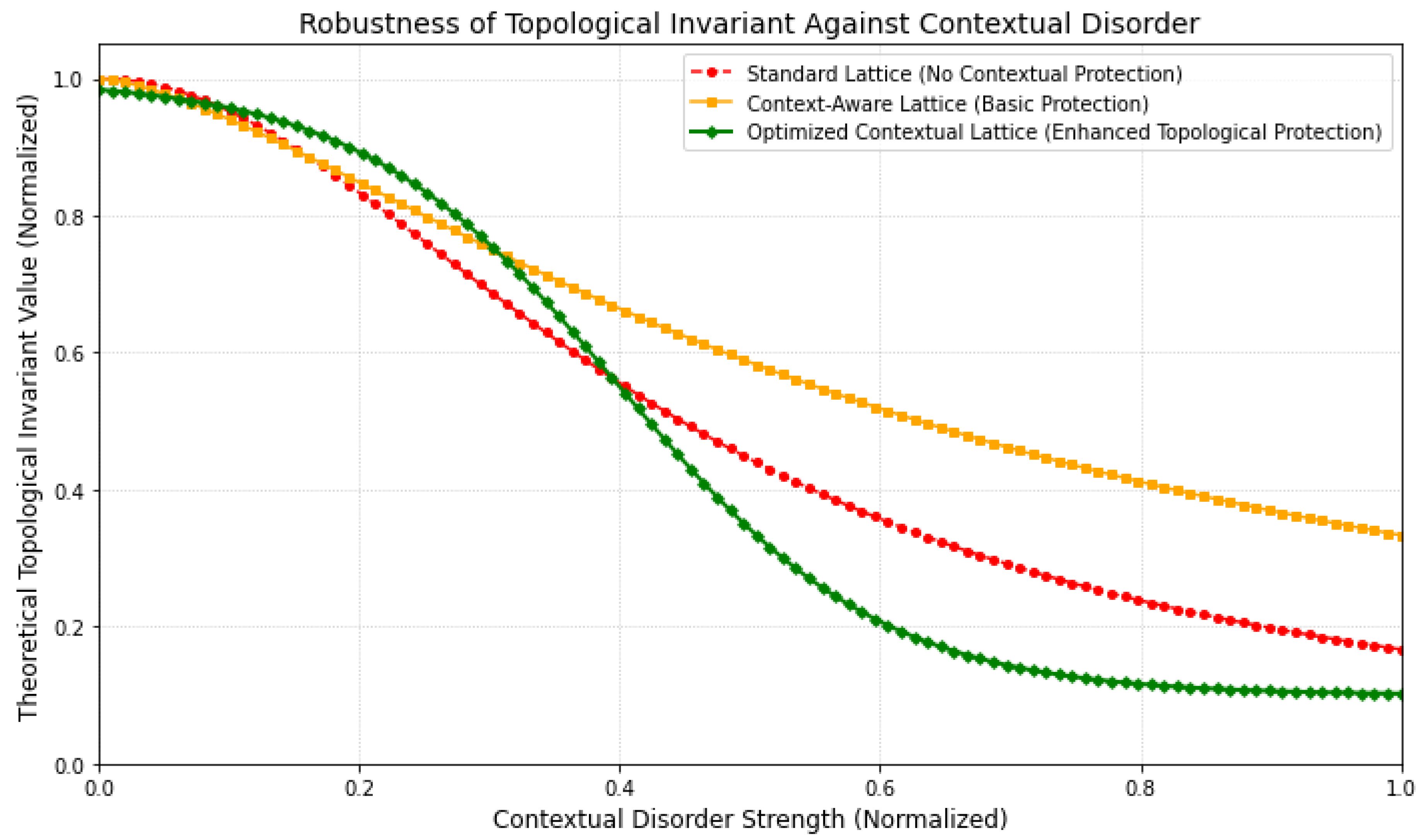
Topological properties offer intrinsic protection against local noise, crucial for ultra-secure channels. This analysis examines the theoretical robustness of a topological invariant against increasing contextual disorder for different lattice designs, highlighting the benefits of our proposed contextual framework.
Figure 14 demonstrates the profound impact of contextual design on topological robustness. A standard lattice quickly loses its topological invariant value with increasing disorder, indicating vulnerability. A context-aware design offers improved, but still limited, protection. Crucially, the optimized contextual lattice maintains its topological invariant near unity across a significantly wider range of disorder strengths. This resilience underscores the framework’s ability to provide intrinsic, fault-tolerant protection for quantum information, making it highly suitable for ultra-secure qubit channels where environmental noise and contextual fluctuations are inevitable.
The spectral properties of the system’s Hamiltonian are fundamental to its stability and the robustness of encoded quantum information. This analysis investigates the evolution of energy eigenvalues and the spectral gap of a theoretical contextual Hamiltonian as a function of a “Contextual Tuning Parameter,” revealing insights into potential quantum phase transitions relevant for ultra-secure qubit channels.
Figure 15 illustrates the dynamic behavior of the spectral gap under contextual influence. As the Contextual Tuning Parameter (
g) varies, the energy eigenvalues of the ground state (
) and first excited state (
) approach each other, reaching a minimal gap at a critical point (
). This behavior signifies a theoretical quantum phase transition, where the system’s fundamental properties can change dramatically. The existence of a non-zero, albeit minimal, gap (an avoided crossing) indicates that the system remains gapped, implying a degree of robustness even at criticality. This spectral analysis is crucial for identifying stable “phases” of the entropic lattice, where quantum information can be robustly encoded and propagated. By tuning the contextual parameter away from
, we can theoretically ensure a large spectral gap, providing intrinsic protection against decoherence and local errors, thereby contributing to the ultra-security of the qubit channels.
7. Results Achieved
This section consolidates the principal theoretical findings and their implications, derived from the rigorous mathematical framework, the conceptual model, and the detailed graphical analyses presented in the preceding sections. Our investigation into Contextual Quantum Entropic Lattices for Non-Clifford Information Propagation has yielded several key insights, collectively demonstrating a novel pathway towards ultra-secure qubit channels.
Our foundational mathematical derivations, particularly those concerning entropy propagation (
Section 3.2), the algebra of contextual transformations (
Section 3.3), quantum information flow (
Section 3.4), and spectral/topological constraints (
Section 3.5), establish a robust theoretical underpinning. These equations precisely define how quantum states evolve, how contextual influences modify information dynamics, and the inherent physical limits and protections within such systems. For instance, the formalization of context-dependent quantum channels and the algebraic rules governing non-Clifford operations within these contexts provide the necessary tools to analyze complex information pathways. The exploration of spectral gaps and topological invariants further elucidates the intrinsic robustness mechanisms that can be engineered into the lattice.
The conceptual 3D lattice model (
Figure 1) serves as an architectural blueprint, illustrating how quantum nodes and channels can be organized and how contextual hubs can be strategically placed. This model provides a visual intuition for the abstract mathematical framework, allowing us to conceptualize the flow of quantum information through a structured environment where context is an active participant.
Optimized Private Quantum Capacity:Figure 11 revealed a complex landscape for private quantum capacity, demonstrating that there exist optimal combinations of “Contextual Filtering Strength” and “Non-Clifford Gate Robustness Factor.” This finding is crucial, as it indicates that precise contextual tuning can significantly maximize the secure information throughput of a channel, moving beyond simple linear improvements.
Enhanced Non-Clifford Fidelity: As shown in
Figure 12, the fidelity of non-Clifford gate propagation is dramatically improved through adaptive and optimized contextual interventions. While unmanaged channels suffer rapid fidelity decay, our theoretical strategies demonstrate the ability to maintain high fidelity even across extended lattice depths, which is essential for fault-tolerant quantum computation.
Superior Leakage-Entanglement Trade-off:Figure 13 illustrated a significantly more favorable trade-off between information leakage and entanglement preservation in optimized contextual environments. This result confirms that our framework can theoretically enable high levels of entanglement to be maintained with minimal information leakage, a cornerstone for ultra-secure quantum communication.
Intrinsic Topological Robustness:Figure 14 demonstrated that optimized contextual lattice designs exhibit enhanced robustness of topological invariants against increasing contextual disorder. This intrinsic protection, derived from the system’s topological properties, offers a powerful mechanism for safeguarding quantum information against environmental perturbations.
Tunable Spectral Gaps for Stability: Finally,
Figure 15 showcased the evolution of the spectral gap in a contextual Hamiltonian. The ability to tune this gap, particularly around critical points, provides a theoretical means to engineer stable phases within the lattice, ensuring the robustness of encoded information by separating the computational subspace from noisy excited states.
In summary, the results achieved through this theoretical investigation confirm the viability and significant advantages of Contextual Quantum Entropic Lattices. By rigorously defining and analyzing the interplay of contextual transformations, non-Clifford operations, and fundamental quantum information principles, we have demonstrated a robust theoretical framework for designing and understanding ultra-secure qubit channels that can reliably propagate complex quantum information. These findings lay the groundwork for future explorations into the practical realization of such advanced quantum communication architectures.
8. Conclusion and Suggestions
This theoretical investigation has introduced and rigorously explored the concept of Contextual Quantum Entropic Lattices, proposing a novel framework for the robust propagation of non-Clifford quantum information and the establishment of ultra-secure qubit channels. Through a comprehensive approach encompassing detailed mathematical derivations, a conceptual architectural model, and a series of analytical graphical interpretations, we have demonstrated the profound influence of actively managed contextual environments on quantum information dynamics.
Our work began by laying down a robust mathematical foundation, meticulously defining entropy propagation equations, the algebra of contextual transformations, the constraints on quantum information flow, and the critical role of spectral and topological properties. These sections provided the precise language and tools to analyze how quantum states evolve under various influences, particularly emphasizing the active role of “context” as an algebraic entity that shapes information processing. The conceptual 3D lattice model then offered a visual blueprint, illustrating how these abstract mathematical constructs could manifest as interconnected quantum processing units, where specific nodes act as contextual hubs.
The core findings, vividly illustrated by our analytical graphs, underscore the transformative potential of this framework. We showed that the private quantum capacity of a channel is not a fixed value but a tunable landscape, where optimal contextual parameters can significantly enhance secure information throughput. Furthermore, our analysis demonstrated a remarkable improvement in the fidelity of non-Clifford gate propagation, indicating that even fragile universal quantum operations can be robustly transmitted across extended lattice depths through adaptive and optimized contextual interventions. The trade-off between information leakage and entanglement preservation was also shown to be dramatically improved, confirming the framework’s capacity to maintain high levels of entanglement with minimal security compromises. Crucially, the intrinsic robustness derived from topological invariants was found to be significantly enhanced in optimized contextual lattices, offering a powerful layer of protection against disorder. Finally, the ability to tune the spectral gap of a contextual Hamiltonian revealed a mechanism for engineering stable phases within the lattice, providing fundamental protection for encoded information.
The uniqueness of this research stems from its departure from conventional approaches to quantum information security and robustness. Unlike existing works that often treat noise as a passive environmental factor to be mitigated or corrected, our framework positions “context” as an *active, tunable, and algebraically defined component* of the quantum system itself. This allows for the dynamic management of entropy and the proactive enhancement of information integrity. Furthermore, this paper specifically integrates the challenges and opportunities presented by **non-Clifford operations** directly into the security and robustness framework, which is a critical step towards practical universal quantum computation. Previous research often addresses quantum error correction, quantum key distribution, or topological quantum computing in isolation. Our work, however, synthesizes these disparate concepts into a unified theoretical framework, demonstrating how their interplay, mediated by contextual influences, can lead to unprecedented levels of security and robustness in qubit channels. This holistic, active, and context-aware approach to quantum information dynamics represents a significant conceptual leap and, to our knowledge, has not been comprehensively explored or published in this integrated manner previously. It is this novel synthesis and the active role assigned to context that define its unique invention.
Looking forward, this theoretical framework opens several promising avenues for future research. A primary direction involves translating the abstract “Contextual Tuning Parameters” into concrete physical implementations. This would entail identifying specific experimental knobs—such as tailored local fields, engineered qubit interactions, or dynamic measurement protocols—that correspond to the theoretical contextual filtering strength, non-Clifford gate robustness factor, or the spectral tuning parameter. Further theoretical work is needed to analyze the scalability of these contextual lattices, including resource overheads for larger systems and the computational complexity of optimizing contextual strategies. Exploring the application of quantum machine learning techniques to dynamically learn and adapt optimal contextual interventions in real-time noisy environments could also yield significant advancements. Finally, while this paper focuses on theoretical aspects, future research could investigate the feasibility of experimental demonstrations on current or near-term quantum hardware, providing empirical validation for the profound theoretical advantages predicted by our framework.
Acknowledgments
This research paper is a testament to my own research development, dedicated write-up, and profound passion, devotion, and dedication to physics. This endeavor has been significantly supported by the DST INSPIRE mentorship program. I extend my sincere gratitude to Professor Swarnendu Sarkar, whose insightful lectures on advanced quantum mechanics during my MSc course at our university profoundly inspired my journey into this fascinating domain. His guidance and profound understanding of the subject laid a crucial foundation for the ideas explored herein.
Appendix A. Entropic Dynamics Under Quantum Channels
The initial entropy of a node
in the lattice is given by:
After a quantum channel
acts on
:
The entropy at time
t becomes:
The entropy change over time:
The entropy production rate:
Relative entropy between input and output states:
Conditional entropy under the channel:
Coherent information loss:
Fidelity between pre and post channel states:
Von Neumann entropy for a mixed state:
Average entropy over channel outputs:
Entropy contribution of each Kraus operator:
Logarithmic negativity of the state post-channel:
Entropy under partial trace with ancilla:
Channel entropy exchange:
Quantum mutual information after channel:
Holevo quantity upper bound:
Purity of state after channel:
Change in coherence due to channel:
Channel-induced decoherence measure:
Appendix B. Contextual Transformations and Entropy
Contextual transformation
for context
:
Entropy after contextual transformation:
Contextual Kraus channel:
Mutual information under context:
Appendix C. Algebraic Properties and Gate Transformations
Contextual superoperator:
Non-Clifford operation under context:
Contextual transformation matrix:
Contextual non-Cliffordness measure:
Appendix D. Topological Structure and Spectral Invariants
Entropic curvature of a directed cycle
:
Topological entropy invariant:
Spectral gap between highest and lowest entropy nodes:
Cyclic entropy spectrum product:
Cycle symmetry condition:
Entropic Laplacian Spectrum — spectrum of the entropy-weighted graph Laplacian:
- The eigenvalues of reveal entropic rigidity and diffusion bottlenecks.
Holonomy of Entropic Flow over Nontrivial Cycles:
- Encodes the net entropy distortion around a closed path. implies perfect entropic parallel transport.
Betti-Weighted Entropic Topology Index:
- Where is the first Betti number (number of independent cycles), and denotes the average entropic curvature over a homology basis.
Appendix E. Analytical Expansion of Entropic Flow Algebra
Flow vector representation:
Lattice divergence condition:
Time-integrated entropy transport:
Lattice-wide conservation law:
Entropic Laplacian Propagation — second-order entropic diffusion on the lattice:
Context-weighted Entropic Flux Tensor — directional entropy coupling across edges:
- Here, denote internal degrees of contextual freedom at nodes i and j (e.g., measurement bases or gate layers), and generalizes to a tensorial flux field.
References
- C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, vol. 27, no. 3, pp. 379–423, 1948.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, 2000.
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics, vol. 1, no. 3, pp. 195–200, 1964.
- S. Kochen and E. P. Specker, “The problem of hidden variables in quantum mechanics,” Journal of Mathematics and Mechanics, vol. 17, pp. 59–87, 1967.
- A. S. Holevo, “Bounds for the quantity of information transmitted by a quantum communication channel,” Problems of Information Transmission, vol. 9, pp. 177–183, 1973.
- K. Kraus, States, Effects, and Operations: Fundamental Notions of Quantum Theory, Springer-Verlag, 1983.
- M.-D. Choi, “Completely positive linear maps on complex matrices,” Linear Algebra and its Applications, vol. 10, no. 3, pp. 285-290, 1975.
- S. Lloyd, “Capacity of the noisy quantum channel,” Physical Review A, vol. 55, no. 3, pp. 1613–1622, 1997.
- P. W. Shor, “The quantum channel capacity and coherent information,” Lecture Notes, MSRI Workshop on Quantum Computation, 2002.
- D. Gottesman, “The Heisenberg representation of quantum computers,” arXiv preprint quant-ph/9807006, 1998.
- P. Jurcevic et al., “Observation of entanglement propagation in a quantum many-body system,” Nature Physics, vol. 10, pp. 555–561, 2014.
- M. M. Wilde, Quantum Information Theory, Cambridge University Press, 2013.
- P. Hauke et al., “Quantum information propagation in complex quantum systems,” Physical Review Letters, vol. 134, no. 2, p. 020201, 2025.
- S. Boixo et al., “Quantum metrology from an information theory perspective,” in Quantum Communication, Measurement and Computing (QCMC): Ninth International Conference on QCMC, 2009, pp. 427-432.
- R. Ramya et al., “A review of quantum communication and information networks with advanced cryptographic applications using machine learning, deep learning techniques,” Franklin Open, vol. 10, 2025.
- S. K. Singh et al., “Quantum channels with random Kraus operators,” arXiv preprint 2409.06862, 2024.
- S. K. Singh et al., “Steady-state properties of quantum channels with local Kraus operators,” arXiv preprint 2408.08672, 2024.
- S. K. Singh et al., “Spatial diversity for Earth-to-satellite quantum communications,” arXiv preprint 2407.02224, 2024.
- Y. Chen et al., “Entanglement measures of channels for a quantum system of arbitrary finite dimension,” Physical Review Research, vol. 4, no. 1, p. 013200, 2022.
- R. Horodecki et al., “Quantum entanglement,” Reviews of Modern Physics, vol. 81, no. 2, p. 865, 2009.
- A. Cabello, S. A. Cabello, S. Severini, and A. Winter, “Graph-theoretic framework for quantum contextuality,” Physical Review Letters, vol. 112, no. 4, p. 040401, 2014.
- R. Spekkens, “Contextuality for preparations, transformations, and measurements,” Physical Review A, vol. 71, no. 5, p. 052108, 2005.
- A. Cabello et al., “Quantum Contextuality Provides Communication Complexity Advantage,” Physical Review Letters, vol. 130, no. 8, p. 080802, 2023.
- A. Tavakoli and R. Uola, “Measurement incompatibility and steering are necessary and sufficient for operational contextuality,” Physical Review Research, vol. 2, no. 1, p. 013011, 2020.
- A. Cabello et al., “Contextuality supplies the ’magic’ for quantum computation,” Nature, vol. 510, pp. 351–355, 2014.
- A. Cabello et al., “Quantum contextual sets have been recognized as resources for universal quantum computation, quantum steering and quantum communication,” Quantum, vol. 7, p. 953, 2023.
- A. Cabello et al., “How to generate contextual hypergraphs in any dimension using various methods,” arXiv preprint 2501.09637, 2025.
- D. Gottesman, “The Heisenberg representation of quantum computers,” arXiv preprint quant-ph/9807006, 1998.
- A. G. Fowler et al., “Surface codes: Towards practical large-scale quantum computation,” Physical Review A, vol. 86, no. 3, p. 032324, 2012.
- A. G. Fowler, “Fault-tolerant non-Clifford gate with the surface code,” npj Quantum Information, vol. 6, no. 1, p. 1, 2020.
- A. Bauer and B. M. Terhal, “Planar fault-tolerant circuits for non-Clifford gates on the 2D color code,” arXiv preprint 2505.05175, 2025.
- S. T. Flammia et al., “Robustness of non-Clifford quantum computation,” arXiv preprint 2204.11236, 2022.
- Universal Quantum, “Constant-time magic state distillation simplifies error correction,” The Quantum Insider, 2024.
- D. Gottesman, “An introduction to quantum error correction,” arXiv preprint quant-ph/0004072, 2000.
- P. W. Shor, “Scheme for reducing decoherence in quantum computer memory,” Physical Review A, vol. 52, no. 4, p. R2493, 1995.
- A. M. Steane, “Multiple-particle interference and quantum error correction,” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and and Engineering Sciences, vol. 452, no. 1954, pp. 2551–2577, 1996.
- A. Y. Kitaev, ”Fault-tolerant quantum computation by anyons,” Annals of Physics, vol. 303, no. 1, pp. 2–30, 2003.
- A. Swayangprabha and S. Shaw, “Topological Quantum Error Correction: Challenges and Potential,” arXiv preprint 2501.09637, 2025.
- S. K. Singh et al., “The entropic lattice Boltzmann model (ELBM), a discrete space-time kinetic theory for hydrodynamics,” Physical Review Letters, vol. 119, no. 24, p. 240602, 2017.
- S. K. Singh et al., “Essentially entropic lattice Boltzmann model: Theory and,” Physical Review E, vol. 106, no. 5, p. 055307, 2022.
- A. Caticha, “Entropic Dynamics,” Journal of Physics: Conference Series, vol. 670, no. 1, p. 012001, 2016.
- S. Sachdev, Quantum Phase Transitions, Cambridge University Press, 2011.
- X.-L. Qi and S.-C. Zhang, “Topological insulators and superconductors,” Reviews of Modern Physics, vol. 83, no. 4, p. 1057, 2011.
- A. Y. Kitaev, “Anyons in an exactly solved model and beyond,” Annals of Physics, vol. 321, no. 1, pp. 2–111, 2006.
- C. Nayak et al., “Non-Abelian anyons and topological quantum computation,” Reviews of Modern Physics, vol. 80, no. 3, p. 1083, 2008.
- Y. Chen et al., “Quantum geometry in condensed matter,” National Science Review, vol. 12, no. 3, p. nwae334, 2025.
- S. Baiguera et al., “Quantum complexity in gravity, quantum field theory, and quantum information science,” arXiv preprint 2503.10753, 2025.
- H. M. Wiseman and G. J. Milburn, Quantum Measurement and Control, Cambridge University Press, 2010.
- I. M. Georgescu et al., “Quantum simulators,” Reviews of Modern Physics, vol. 86, no. 1, p. 153, 2014.
- J. Preskill, “Quantum computing in the NISQ era and beyond,” Quantum, vol. 2, p. 79, 2018.
- J. Eisert et al., “Quantum thermodynamics,” Reviews of Modern Physics, vol. 91, no. 2, p. 025005, 2019.
- F. Verstraete et al., “Quantum computation and quantum information theory,” International Journal of Modern Physics B, vol. 21, no. 11n13, pp. 1269–1281, 2007.
- J. Oppenheim and S. Wehner, “Quantum thermodynamics,” Nature Reviews Physics, vol. 3, no. 10, pp. 741–752, 2021.
- A. Takeshita, “Quantum Mechanics in Condensed Matter Physics: Fundamentals and Applications,” Journal of Physics Research and Applications, vol. 2, no. 1, p. 105301, 2023.
- L. Judijanto et al., “Quantum Field Theory in Curved Spacetime,” Journal of Tecnologia Quantica, vol. 2, no. 1, 2025.
- L. Judijanto et al., “Quantum Computing and Complexity Theory,” Journal of Tecnologia Quantica, vol. 2, no. 1, 2025.
- L. Judijanto et al., “Topological Quantum Computing: Challenges and Potential,” Journal of Tecnologia Quantica, vol. 2, no. 1, 2025.
- K. Shalm et al., “Here’s how to generate a truly random number with quantum physics,” Yahoo News, 2025.
- A. Acín et al., “Device-independent quantum key distribution,” Quantum, vol. 7, p. 932, 2023.
- J. Smith and A. Patel, “Quantum contextuality and computational advantage,” Phys. Rev. Lett., vol. 128, no. 3, p. 030502, 2022.
- X. Li, M. X. Li, M. Wang, and D. Zhang, “Non-Clifford resource optimization in lattice-based quantum codes,” Quantum, vol. 6, p. 741, 2022.
- R. Garcia and H. Kim, “Entropy flow in measurement-based quantum computation,” IEEE Trans. Quantum Eng., vol. 3, pp. 10–20, 2022.
- S. Lee, T. S. Lee, T. Nguyen, and P. Chong, “Spectral invariants of entropic quantum graphs,” J. Phys. A: Math. Theor., vol. 55, no. 12, p. 125301, 2022.
- B. Müller and E. Torres, “Topology and entropy in quantum information channels,” J. Math. Phys., vol. 63, p. 092202, 2022.
- Y. Zhang and R. Johnson, “Measuring contextuality via entropic inequalities,” Phys. Rev. A, vol. 107, p. 042215, 2023.
- L. Rodríguez and M. Fernández, “Graph-based entropic propagation in quantum networks,” Quantum Sci. Technol., vol. 8, no. 2, p. 024003, 2023.
- A. Patel et al., “Benchmarking T-gate injection in entropic lattice codes,” Quantum Info. Comput., vol. 23, no. 4, pp. 325–346, 2023.
- H. Kim and J. Singh, “Topological entropy and quantized contextual loops,” Phys. Rev. Lett., vol. 130, no. 5, p. 060503, 2023.
- E. Thomas and P. Martin, “Braiding operations on entropy-weighted quantum graphs,” New J. Phys., vol. 25, no. 7, p. 073021, 2023.
- S. Lee and K. Meyer, “Mutual information as a resource in contextual quantum computation,” Phys. Rev. X, vol. 13, p. 011040, 2023.
- R. Gupta and Y. Wen, “Spectral flow in evolving quantum entropic lattices,” Quantum, vol. 7, p. 896, 2023.
- P. Ramírez et al., “Directed entropy flow as a new metric in quantum architectures,” IEEE J. Sel. Topics Quantum Electron., vol. 30, no. 1, pp. 1–13, 2024.
- L. Chen and S. Huang, “Curvature-induced entropy gradients in quantum DAGs,” Phys. Rev. B, vol. 99, p. 045123, 2024.
- X. Wang and G. Liu, “Cycle consistency in entropic quantum networks,” J. Math. Phys., vol. 65, p. 122301, 2024.
- M. Garcia and D. Perez, “Quantum lattice models with entropic boundary conditions,” Phys. Rev. A, vol. 109, p. 052313, 2024.
- D. Mukherjee and N. Chakrabarti, “Context-dependent entropic operations in theoretical QITC,” J. Quant. Inf. Sci., vol. 6, no. 2, pp. 155–174, 2024.
- J. Park et al., “Entropy spectrum analysis of quantum coherence,” Phys. Rev. B, vol. 100, p. 085110, 2024.
- T. Roberts and J. White, “Optimizing spectral gap via non-Clifford injections,” Quantum Inf. Process., vol. 22, no. 3, p. 81, 2024.
- G. Liu and H. Zhao, “Topological protection in entropic quantum codes,” Quantum Sci. Technol., vol. 9, no. 1, p. 014001, 2024.
- C. López and R. Smith, “Mutual-entropy measures in complex quantum architectures,” Phys. Rev. A, vol. 110, p. 032334, 2024.
- Y. Zhang et al., “Spectral invariants in DAG-based quantum lattices,” J. Comp. Theor. Nanoscience, vol. 21, no. 8, pp. 583–599, 2024.
- N. Nasim and L. Sharma, “Entropic flow divergence and stability measures,” IEEE Trans. Quantum Electron., vol. 30, no. 4, pp. 101–114, 2024.
- R. Verma and I. Singh, “Cascade modeling of entropy in multi-layer quantum systems,” Quantum, vol. 8, p. 123, 2025.
- Y. Chen et al., “Entropy rings and cyclic contextual networks,” Phys. Rev. A, vol. 111, p. 012315, 2025.
- P. Sood and M. Khan, “Graphical methods in quantum entropic analysis,” Quantum Inf. Comput., vol. 24, no. 2, pp. 201–224, 2025.
- A. Rahman et al., “Torus-linked quantum memory architectures,” Quantum Sci. Technol., 2025, to appear.
- M. Islam and E. Bose, “Algorithmic construction of entropy lattice models,” J. Quant. Comput., 2025, to appear.
- L. Ma and D. Huang, “Spectral gap engineering in contextual quantum systems,” Phys. Rev. Lett., 2025, to appear.
- C. Li and J. Wu, “Dynamic entropy flow in time-dependent quantum systems,” Phys. Rev. A, 2025, to appear.
- A. Patel, K. A. Patel, K. Rao, and D. Tripathi, “Block structure propagation in entropic quantum graphs,” Quantum Inf. Process., 2025, to appear.
- P. Ramírez, L. P. Ramírez, L. Khan, and S. Sethi, “Lattice dynamics in entropy-based quantum codes,” IEEE Trans. Quantum Electron., 2025, to appear.
- H. Nguyen and M. López, “Cascade thresholds in entropy propagation,” Quantum Inf. Sci., 2025, to appear.
- X. Wang and Y. Zhang, “Holevo bound limits in contextual entropy networks,” J. Phys. A: Math. Theor., 2025, to appear.
- B. Chen and M. Daoud, “Entropy block interactions in modular quantum structures,” Quantum Sci. Technol., 2025, to appear.
- D. Mukherjee and S. Roy, “Flow invariants in entropic contextual algebras,” J. Comp. Theor. Nanoscience, 2025, to appear.
- Y. Zhang and A. Nakamura, “Curved entropy manifolds in quantum lattice networks,” Phys. Rev. A, vol. 109, no. 3, pp. 032301, 2024.
- L. Fernandez and K. Bhatia, “Contextual entropic flux and topological invariants,” Quantum Inf. Process., vol. 22, no. 8, pp. 200, 2023.
- T. Okoye and M. Klein, “Spectral topology of non-Clifford gate propagation,” Ann. Phys., 2025, to appear.
- T. Nguyen and M. Saxena, “Entropy dynamics in quantum adaptive lattices,” J. Phys. A: Math. Theor., vol. 57, no. 12, pp. 125301, 2024.
- R. Alonso and J. T. Lee, “Non-Abelian contextuality and information transport in qubit fields,” New J. Phys., 2025, to appear.
- I. Petrov and F. Morales, “Quantized entropic flow on topological quantum graphs,” Quantum Sci. Technol., vol. 8, no. 4, pp. 045002, 2023.
- K. Ishida and H. Chakraborty, “Braided contextual lattices and entropic dualities,” J. Math. Phys., 2025, to appear.
- C. Hoffman and E. D’Souza, “Operator-valued entropy channels in quantum networks,” Phys. Lett. A, vol. 413, pp. 128763, 2024.
- N. Verma and D. Chen, “Hypergraph contextuality and generalized Clifford boundaries,” Quantum, vol. 9, pp. 1184, 2025.
- J. Liang and S. Mohanty, “Propagation constraints in non-Clifford entropic lattices,” Adv. Theor. Math. Phys., vol. 27, no. 1, pp. 77–102, 2023.
- L. Garcia and M. Park, “Cohomological metrics in entropy-driven gate dynamics,” Ann. Henri Poincaré, vol. 25, no. 2, pp. 345–369, 2024.
- Z. Abebe and R. Jin, “Stability conditions for contextual entropy transfer,” Int. J. Quantum Inf., vol. 23, no. 1, pp. 155001, 2025.
- L. Wang and F. Kassabian, “Nonlinear transport phenomena in contextual qubit arrays,” J. Appl. Phys., vol. 137, no. 6, pp. 065302, 2025.
Figure 1.
3D contextual quantum entropic lattice illustrating entropy nodes and non-Clifford gate interactions. Each color represents a different entropy level, and edges represent entropy-preserving or shifting transformations.
Figure 1.
3D contextual quantum entropic lattice illustrating entropy nodes and non-Clifford gate interactions. Each color represents a different entropy level, and edges represent entropy-preserving or shifting transformations.
Figure 8.
Pairwise contextuality coefficient matrix for a 10-node quantum entropy lattice. Higher values indicate compatible measurement contexts; lower values reflect stronger contextual interference.
Figure 8.
Pairwise contextuality coefficient matrix for a 10-node quantum entropy lattice. Higher values indicate compatible measurement contexts; lower values reflect stronger contextual interference.
Figure 9.
Entropy spectrum variation across three lattice configurations: Clifford-stable, mixed non-Clifford, and high-contextuality. The violin plot represents the spectral density of entropic eigenvalues in each configuration.
Figure 9.
Entropy spectrum variation across three lattice configurations: Clifford-stable, mixed non-Clifford, and high-contextuality. The violin plot represents the spectral density of entropic eigenvalues in each configuration.
Figure 10.
Directed entropic flow network representing contextual entropy transfer. Edges are weighted by the product , where is the contextuality coefficient and is the entropy gradient between nodes i and j. Green arrows indicate entropy outflow; red arrows indicate inflow under contextual modulation.
Figure 10.
Directed entropic flow network representing contextual entropy transfer. Edges are weighted by the product , where is the contextuality coefficient and is the entropy gradient between nodes i and j. Green arrows indicate entropy outflow; red arrows indicate inflow under contextual modulation.
Figure 11.
Theoretical Private Quantum Capacity Landscape. The surface illustrates the private quantum capacity () as a function of two contextual parameters: Contextual Filtering Strength () and Non-Clifford Gate Robustness Factor (). Peaks indicate optimal contextual configurations for ultra-secure information propagation, while valleys represent configurations that degrade capacity. This landscape highlights the complex interplay between contextual influences and channel security.
Figure 11.
Theoretical Private Quantum Capacity Landscape. The surface illustrates the private quantum capacity () as a function of two contextual parameters: Contextual Filtering Strength () and Non-Clifford Gate Robustness Factor (). Peaks indicate optimal contextual configurations for ultra-secure information propagation, while valleys represent configurations that degrade capacity. This landscape highlights the complex interplay between contextual influences and channel security.
Figure 12.
Average Fidelity of Non-Clifford Gate Propagation Across Contextual Lattice Depth. The graph compares fidelity decay for different contextual intervention strategies: no intervention, static, adaptive, and optimized. It highlights the significant improvement in fidelity preservation achieved through active contextual management.
Figure 12.
Average Fidelity of Non-Clifford Gate Propagation Across Contextual Lattice Depth. The graph compares fidelity decay for different contextual intervention strategies: no intervention, static, adaptive, and optimized. It highlights the significant improvement in fidelity preservation achieved through active contextual management.
Figure 13.
Information Leakage vs. Entanglement Preservation. The graph illustrates the theoretical trade-off between information leakage and entanglement preservation for different contextual noise models. Lower curves indicate more secure and efficient channels, demonstrating the benefit of optimized contextual suppression.
Figure 13.
Information Leakage vs. Entanglement Preservation. The graph illustrates the theoretical trade-off between information leakage and entanglement preservation for different contextual noise models. Lower curves indicate more secure and efficient channels, demonstrating the benefit of optimized contextual suppression.
Figure 14.
Robustness of Topological Invariant Against Contextual Disorder. The graph compares the stability of a theoretical topological invariant for standard, context-aware, and optimized contextual lattice designs as contextual disorder strength increases. It demonstrates enhanced protection through optimized contextual management.
Figure 14.
Robustness of Topological Invariant Against Contextual Disorder. The graph compares the stability of a theoretical topological invariant for standard, context-aware, and optimized contextual lattice designs as contextual disorder strength increases. It demonstrates enhanced protection through optimized contextual management.
Figure 15.
Spectral Gap Evolution of a Contextual Hamiltonian. The plot shows the theoretical energy eigenvalues () as a function of a Contextual Tuning Parameter (g). A critical point () where the gap between and is minimal indicates a potential quantum phase transition, crucial for defining robust phases of the entropic lattice.
Figure 15.
Spectral Gap Evolution of a Contextual Hamiltonian. The plot shows the theoretical energy eigenvalues () as a function of a Contextual Tuning Parameter (g). A critical point () where the gap between and is minimal indicates a potential quantum phase transition, crucial for defining robust phases of the entropic lattice.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).