Deep Learning 2.0.1: Mind and Cosmos - Towards Cosmos-Inspired Interpretable Neural Networks

1. Introduction

The remarkable success of deep learning is largely built upon a standard model: the dot product for linear interaction, followed by a non-linear activation function. The dot product serves as the primary mechanism for measuring similarity and interaction between neural units, a practice dating back to the perceptron’s introduction in 1958 ([1]). Non-linear activation functions, such as the Rectified Linear Unit (ReLU), are then applied to enable the network to learn complex patterns, as underscored by the universal approximation theorem ([2]). Without such non-linearities, a deep stack of layers would mathematically collapse into an equivalent single linear transformation, severely curtailing its representational capacity.

However, this ubiquitous approach has a significant cost: a loss of geometric fidelity and the need for additional components like normalization layers. The dot product itself is a geometrically impoverished measure, primarily capturing alignment while conflating magnitude with direction and often obscuring more complex structural and spatial relationships. Furthermore, the way current activation functions achieve non-linearity can exacerbate this issue. For instance, ReLU ($f\left(x\right)=max(0,x)$) maps all negative pre-activations—which can signify a spectrum of relationships from weak dissimilarity to strong anti-alignment—to a single zero output. This thresholding, while promoting sparsity, means the network treats diverse inputs as uniformly orthogonal or linearly independent for onward signal propagation. Such a coarse-graining of geometric relationships leads to a tangible loss of information regarding the degree and nature of anti-alignment or other negative linear dependencies. This information loss, coupled with the inherent limitations of the dot product, highlights a fundamental challenge.

This raises a central question: Can we develop a single computational operator that possesses intrinsic non-linearity while being inherently geometrically aware, thereby preserving geometric fidelity without the need for separate activation functions?

This paper proposes an elegant answer: the ⵟ-product (pronounced Yat-product), a novel neural operator. The intuition behind the ⵟ-product is the unification of alignment and proximity, inspired by fundamental principles observed in physical systems, particularly the concept of interaction fields governed by inverse-square laws [5,6]. In physics, the strength of interactions (like gravity or electrostatic force) depends not only on intrinsic properties (like mass or charge) but critically on the inverse square of the distance between entities.

To this end, we introduce the ⵟ-product, defined as:

$$ⵟ(\mathbf{w},\mathbf{x}):={\displaystyle \frac{{\langle \mathbf{w},\mathbf{x}\rangle }^2}{{\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ}}={\displaystyle \frac{{\langle \mathbf{w},\mathbf{x}\rangle }^2}{(\mathbf{w}-\mathbf{x})·(\mathbf{w}-\mathbf{x})+ϵ}}={\displaystyle \frac{{\parallel \mathbf{x}\parallel }^2{\parallel \mathbf{w}\parallel }^2{cos}^2\theta }{{\parallel \mathbf{w}\parallel }^2-2\langle \mathbf{w},\mathbf{x}\rangle +{\parallel \mathbf{x}\parallel }^2+ϵ}}$$

where $\mathbf{w}$ is a weight vector, $\mathbf{x}$ is an input vector, $\langle ·,·\rangle$ denotes the dot product, $\parallel ·\parallel$ signifies the Euclidean norm, $\theta$ is the angle between $\mathbf{w}$ and $\mathbf{x}$, and $ϵ$ is a small positive constant for numerical stability. The numerator, ${\langle \mathbf{w},\mathbf{x}\rangle }^2$, emphasizes strong alignment and scales with vector magnitudes. The denominator, ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ$, incorporates an inverse-square law with respect to the Euclidean distance, penalizing large distances. This ensures the ⵟ-product yields a high response only when $\mathbf{w}$ and $\mathbf{x}$ are well-aligned, significant in magnitude, and spatially proximate. This coupling of directional similarity with an inverse-square proximity term endows the ⵟ-product with inherent non-linearity, potentially obviating the need for separate activation functions and allowing layers to learn complex, non-linear relationships directly.

The ⵟ-product can be naturally extended to convolutional operations for processing structured data like images. The ⵟ-Convolution (Yat-Conv) is defined as:

$${ⵟ}^{*}(\mathbf{W},\mathbf{X}):={\displaystyle \frac{{\left({\sum }_{i,j}{w}_{ij}{x}_{ij}\right)}^2}{{\sum }_{i,j}{(w_{ij}-x_{ij})}^2+ϵ}}$$

where $\mathbf{W}$ and $\mathbf{X}$ represent local patches (e.g., a convolutional kernel and an input patch, respectively), and $w_{ij}$ and $x_{ij}$ are their corresponding elements. This formulation allows for patch-wise computation of the ⵟ-product, integrating its geometric sensitivity into convolutional architectures.

Building upon the ⵟ-product, we propose Neural-Matter Networks (NMNs) and Convolutional NMNs (CNMNs). NMNs are designed to preserve input topology by leveraging the ⵟ-product’s geometric awareness and avoiding aggressive, dimension-collapsing non-linearities typically found in standard architectures. In NMNs, each neuron, through its learned weight vector $\mathbf{w}$, effectively defines an interaction field. It "attracts" or responds to input vectors $\mathbf{x}$ based on the dual criteria of learned alignment and spatial proximity, analogous to how bodies with mass create gravitational fields. This approach aims to maintain critical geometric relationships, fostering more interpretable models and robust learning.

The primary contributions of this work are:

• The introduction of the ⵟ-product, a novel, physics-grounded neural operator that unifies directional sensitivity with an inverse-square proximity measure, designed for geometrically faithful similarity assessment.
• The proposal of Neural-Matter Networks (NMNs), a new class of neural architectures based on the ⵟ-product, which inherently incorporate non-linearity and are designed to preserve input topology.
• The development and pretraining of AetherGPT, a transformer model based on GPT-2 architectural principles incorporating the ⵟ-product, pretrained on the FineWeb 10B dataset, serving as an initial large-scale validation of the proposed concepts.
• A commitment to open science through the release of all associated code and models under the Affero GNU General Public License.

By reconceiving neural computation through the lens of physical interaction fields, this work seeks to bridge the empirical successes of contemporary machine learning with the structural understanding and interpretability afforded by principles derived from physics. The remainder of this paper is organized as follows: Section 2 discusses related work in geometric deep learning and alternative neural operators. Section 4 details the mathematical formulation of the ⵟ-product and NMNs. Section Section 5 presents experimental results, including the AetherGPT model. Section Section 6 provides a discussion of these results, and Section 7 concludes the paper with future directions.

2. Related Work

2.1. Inverse-Square Laws

The inverse-square law, where a quantity or intensity is inversely proportional to the square of the distance from its source, is a fundamental principle observed across numerous scientific disciplines ([19]). This relationship signifies that as the distance from a source doubles, the intensity reduces to one-quarter of its original value.

In classical physics, this law is foundational. Newton’s Law of Universal Gravitation describes the force between two masses ([29]), and Coulomb’s Law defines the electrostatic force between charges ([9]). The intensity of electromagnetic radiation, such as light, and the intensity of sound from a point source also diminish according to this principle. Gauss’s Law offers a unifying mathematical framework for these phenomena in fields like electromagnetism and gravitation, connecting them to the property that the divergence of such fields is zero outside the source ([12]). Similarly, thermal radiation intensity from a point source adheres to this law ([26]).

The inverse-square law’s influence extends significantly into engineering and applied sciences. In health physics, it is critical for radiation protection, governing the attenuation of ionizing radiation ([20]). Photometry applies it to illumination engineering for lighting design ([33]). In telecommunications, it underpins the free-space path loss of radio signals, as described by the Friis transmission equation ([32]), while radar systems experience an inverse fourth-power relationship due to the signal’s two-way travel ([37]). Seismology observes that seismic wave energy attenuates following this law ([1]), and in fluid dynamics, the velocity field from a point source in incompressible, irrotational flow also demonstrates an inverse-square dependence ([3]).

Beyond the physical sciences, analogous concepts are found in information theory, data science, and social sciences. For instance, the Tanimoto coefficient, used in molecular similarity analysis ([39]), and the Jaccard index, a metric for set similarity ([17]), exhibit mathematical properties akin to inverse-square decay when viewed in feature space geometry. In economics, the gravity model of trade frequently employs an inverse-square (or similar power law) relationship to predict trade flows between entities, based on their economic "mass" (e.g., GDP) and the distance separating them ([2]), illustrating how these physical principles can offer insights into complex socio-economic phenomena.

2.2. Learning with Kernels

Learning with kernels has significantly influenced machine learning by enabling algorithms to handle complex, non-linear patterns efficiently. The introduction of Support Vector Machines (SVMs) ([7]) laid the foundation for kernel-based learning, leveraging the kernel trick to implicitly map data into high-dimensional spaces. Schölkopf et al. (1999) formalized kernel methods, expanding their applicability to various tasks ([35]).

Key advancements include Kernel PCA ([36]) for non-linear dimensionality reduction and Gaussian Processes ([43]) for probabilistic modeling. Applications like Spectral Clustering([30]) and One-Class SVM ([34]) highlight the versatility of kernel methods.

To address computational challenges, techniques like the Nyström method ([42]) and Random Fourier Features ([31]) have improved scalability. Recent work, such as the Neural Tangent Kernel (NTK) ([18]), bridges kernel methods and deep learning, offering insights into the dynamics of neural networks.

Furthermore, many prominent kernel functions, such as the Gaussian Radial Basis Function (RBF) kernel ([4]), explicitly define similarity based on the Euclidean distance between data points, effectively giving higher weight to nearby points. This inherent sensitivity to proximity allows models like Support Vector Machines with RBF kernels or Gaussian Processes to capture local structures in the data.

While these methods leverage distance to inform the kernel matrix or model covariance, our research explores a more direct architectural integration of proximity. We propose a novel neural operator where an inverse-square law with respect to feature vector distance is fundamentally incorporated into the neuron’s computation, in conjunction with measures of feature alignment. This approach differs from traditional kernel methods where the kernel function primarily serves to define a similarity measure for algorithms that operate on pairs of samples, rather than defining the intrinsic operational characteristics of individual neural units themselves.

2.3. Deep Learning

The landscape of deep learning is characterized by a continuous drive towards architectures and neural operators that offer enhanced expressivity, computational efficiency, and improved understanding of underlying data structures. Convolutional Neural Networks (CNNs) remain a foundational paradigm, particularly in vision, lauded for their proficiency in extracting hierarchical features ([21]). However, the pursuit of alternative and complementary approaches remains vibrant.

A significant trajectory involves architectures leveraging dot-product mechanisms, most prominently exemplified by the Transformer architecture and its self-attention mechanism ([41]). This has spurred developments like Vision Transformers (ViTs) ([10]), and models such as MLP-Mixer ([40]) and gMLP ([23]) which, while simplifying or eschewing self-attention, still rely on operations like matrix multiplication for feature mixing, demonstrating competitive performance, particularly in computer vision.

The quest for capturing intricate data relationships has also led to renewed interest in Polynomial Neural Networks. These networks incorporate polynomial expansions of neuron inputs, enabling the modeling of higher-order correlations ([16,24]), offering a different inductive bias compared to standard linear transformations followed by activation functions. Concurrently, Fourier Networks, such as FNet ([22]), explore the frequency domain, replacing spatial convolutions or attention with Fourier transforms for token or feature mixing, presenting an alternative for global information aggregation with potential efficiency gains.

Despite these advancements, a persistent challenge in deep learning is interpretability. The complex interplay of numerous parameters and non-linear activation functions (e.g., ReLU ([28]), sigmoid, tanh) often renders the internal decision-making processes of deep models opaque ([27]). These diverse approaches highlight a shared pursuit for more expressive primitives. Our work contributes to this by proposing an operator that achieves non-linearity not through polynomial expansion or frequency-domain transformation, but through a unified measure of geometric alignment and proximity.

3. Theoretical Background

3.1. Revisiting Core Computational Primitives and Similarity Measures

The computational primitives used in deep learning are fundamental to how models represent and process information. This section revisits key mathematical operations and similarity measures—such as the dot product, convolution, cosine similarity, and Euclidean distance—that form the bedrock of many neural architectures. We will explore their individual properties and how they contribute to tasks like feature alignment, localized feature mapping, and quantifying spatial proximity. Furthermore, we will delve into the role of neural activation functions in enabling the non-linear transformations crucial for complex pattern recognition. Understanding these core concepts and their inherent characteristics is crucial for appreciating the motivation behind developing novel operators, as explored in this work, that aim to capture more nuanced relationships within data ([13]).

3.1.1. The Dot Product: A Measure of Alignment

The dot product, or scalar product, remains a cornerstone of neural computation, serving as the primary mechanism for quantifying the interaction between vectors, such as a neuron’s weights and its input. For two vectors $\mathbf{a}=[a_1,a_2,\dots ,a_n]$ and $\mathbf{b}=[b_1,b_2,\dots ,b_n]$, it is defined as:

$$\mathbf{a}·\mathbf{b}=\sum _{i=1}^n{a}_i{b}_i=a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n$$

Geometrically, the dot product is proportional to the cosine of the angle between the vectors and their Euclidean magnitudes: $\mathbf{a}·\mathbf{b}=\parallel \mathbf{a}\parallel \parallel \mathbf{b}\parallel cos\left(\theta \right)$. Its sign indicates the general orientation (acute, obtuse, or orthogonal angle), and its magnitude reflects the degree of alignment scaled by vector lengths. In machine learning, dot product scores are pervasively used to infer similarity, relevance, or the strength of activation. However, as noted in Section 1, its conflation of magnitude and directional alignment can sometimes obscure more fine-grained geometric relationships, motivating the exploration of operators that offer a more comprehensive assessment of vector interactions.

3.1.2. The Convolution Operator: Localized Feature Mapping

The convolution operator is pivotal in processing structured data, particularly in Convolutional Neural Networks (CNNs). It applies a kernel (or filter) across an input to produce a feature map, effectively an operation on two functions, f (input) and g (kernel), yielding a third that expresses how one modifies the shape of the other. For discrete signals, such as image patches and kernels, it is:

$$(f\ast g)\left[n\right]=\sum _{m=-\infty }^{\infty }f\left[m\right]g[n-m]$$

In CNNs, convolution performs several critical roles:

• Feature Detection: Kernels learn to identify localized patterns (edges, textures, motifs) at various abstraction levels.
• Spatial Hierarchy: Stacking layers allows the model to build complex feature representations from simpler ones.
• Parameter Sharing: Applying the same kernel across spatial locations enhances efficiency and translation equivariance.

The core computation within a discrete convolution at a specific location involves an element-wise product sum between the kernel and the corresponding input patch, which is, in essence, a dot product. Consequently, the resulting activation at each point in the feature map reflects the local alignment between the input region and the kernel. If an input patch and a kernel are orthogonal (i.e., their element-wise product sums to zero, akin to a zero dot product if they were vectorized), the convolution output at that position will be zero, indicating no local match for the feature encoded by the kernel. This reliance on dot product-like computations means that standard convolutions primarily assess feature alignment, potentially overlooking other geometric aspects of the data.

3.1.3. Cosine Similarity: Normalizing for Directional Agreement

Cosine similarity refines the notion of alignment by isolating the directional aspect of vector relationships, abstracting away from their magnitudes. It measures the cosine of the angle between two non-zero vectors $\mathbf{A}$ and $\mathbf{B}$:

$$\mathrm{similarity}=cos\left(\theta \right)={\displaystyle \frac{\mathbf{A}·\mathbf{B}}{\parallel \mathbf{A}\parallel \parallel \mathbf{B}\parallel }}={\displaystyle \frac{{\sum }_{i=1}^n{A}_i{B}_i}{\sqrt{{\sum }_{i=1}^n{A}_i^2}\sqrt{{\sum }_{i=1}^n{B}_i^2}}}$$

Scores range from -1 (perfectly opposite) to 1 (perfectly aligned), with 0 signifying orthogonality (decorrelation). By normalizing for vector lengths, cosine similarity provides a pure measure of orientation. This is particularly useful when the magnitude of vectors is not indicative of their semantic relationship, such as in document similarity tasks. While it effectively captures directional agreement, it explicitly discards information about vector magnitudes and, like the dot product, does not inherently account for the spatial proximity between the vectors themselves if they are points in a space ([11,38]).

3.1.4. Euclidean Distance: Quantifying Spatial Proximity

In contrast to measures of alignment, Euclidean distance quantifies the "ordinary" straight-line separation between two points (or vectors) $\mathbf{p}=(p_1,\dots ,p_n)$ and $\mathbf{q}=(q_1,\dots ,q_n)$ in an n-dimensional Euclidean space:

$$d(\mathbf{p},\mathbf{q})=\sqrt{\sum _{i=1}^n{(q_i-p_i)}^2}$$

This metric is fundamental in various machine learning algorithms, including k-Nearest Neighbors and k-Means clustering, and forms the basis of loss functions like Mean Squared Error. Euclidean distance measures dissimilarity based on spatial proximity; a smaller distance implies greater similarity in terms of location within the vector space. Unlike cosine similarity, it is sensitive to vector magnitudes and their absolute positions. However, Euclidean distance alone does not directly convey information about the relative orientation or alignment of vectors, only their nearness.

The distinct characteristics of these foundational measures—alignment (dot product, cosine similarity) versus proximity (Euclidean distance)—highlight an opportunity. These foundational measures force a choice: one can measure alignment (dot product, cosine similarity) or spatial proximity (Euclidean distance), but no single, primitive operator in conventional use effectively unifies both. Neural operators that can synergistically combine these aspects, assessing not only if vectors point in similar directions but also if they are close in the embedding space, could offer a richer, more geometrically informed way to model interactions. This perspective underpins the development of the ⵟ-product introduced in Section 4.

3.2. The Role and Geometric Cost of Non-Linear Activation

While the core computational primitives provide tools to measure similarity and interaction, their inherent linearity limits the complexity of functions they can represent. To overcome this, deep neural networks employ non-linear activation functions. These are the standard method for introducing non-linearity, a necessary step for modeling intricate data patterns. However, this "fix" is imperfect, as it introduces its own set of problems, particularly concerning the preservation of the input data’s geometric integrity. The remarkable expressive power of deep neural networks hinges on their capacity to model complex, non-linear relationships. This ability to approximate any continuous function to an arbitrary degree of accuracy is formally captured by the universal approximation theorem.

Theorem 1

(Universal Approximation Theorem ([8,14,15,25])). Let σ be any continuous, bounded, and nonconstant activation function. Let $I_m$ denote the m-dimensional unit hypercube ${[0,1]}^m$. The space of continuous functions on $I_m$ is denoted by $C\left(I_m\right)$. Then, for any $f\in C\left(I_m\right)$ and any $ϵ>0$, there exists an integer N, real constants $v_i,b_i\in \mathbb{R}$, and real vectors $w_i\in {\mathbb{R}}^m$ for $i=1,\dots ,N$, such that the function $F:I_m\to \mathbb{R}$ defined by

$$F\left(x\right)=\sum _{i=1}^N{v}_i\sigma (w_i^{T}x+b_i)$$

satisfies $\left|F\right(x)-f(x\left)\right|<ϵ$ for all $x\in I_m$. In simpler terms, a single hidden layer feedforward network with a sufficient number of neurons employing a suitable non-linear activation function can approximate any continuous function on compact subsets of ${\mathbb{R}}^m$ to any desired degree of accuracy.

This theorem underscores the critical role of non-linear activation functions. Without such non-linearities, a deep stack of layers would mathematically collapse into an equivalent single linear transformation, severely curtailing its representational capacity. Activation functions are thus not mere auxiliaries; they are the pivotal components that unlock the hierarchical and non-linear feature learning central to deep learning’s success. They determine a neuron’s output based on its aggregated input, and in doing so, introduce crucial selectivity: enabling the network to preferentially respond to certain patterns while attenuating or ignoring others.

3.2.1. Linear Separability and the Limitations of the Inner Product

The fundamental computation within a single artificial neuron (perceptron) is an affine transformation followed by a non-linear activation function $\sigma$:

$$y=\sigma (\langle \mathbf{w},\mathbf{x}\rangle +b),$$

(1)

where $\mathbf{w}$ is the weight vector, $\mathbf{x}$ is the input vector, and b is the bias term. The decision boundary of this neuron is implicitly defined by the hyperplane where the argument to $\sigma$ is zero:

$$\{\mathbf{x}\in {\mathbb{R}}^d\mid \langle \mathbf{w},\mathbf{x}\rangle +b=0\}.$$

(2)

This hyperplane partitions the input space ${\mathbb{R}}^d$ into two half-spaces. Consequently, a single neuron can only implement linearly separable functions. This is a direct consequence of the linear nature of the inner product, which can only define a linear decision boundary. While this allows for efficient computation, it severely restricts the complexity of functions that can be learned.

A classic counterexample is the XOR function, whose truth table cannot be satisfied by any single linear decision boundary. Specifically, for inputs $\mathbf{x}\in \{(0,0),(0,1),(1,0),(1,1)\}\subset {\mathbb{R}}^2$, there exist no $\mathbf{w}\in {\mathbb{R}}^2$ and $b\in \mathbb{R}$ such that $sign(\langle \mathbf{w},\mathbf{x}\rangle +b)$ matches the XOR output (0, 1, 1, 0 respectively). This limitation stems directly from the linear nature of the inner product operation defining the separating boundary ([13]).

3.2.2. Non-Linear Feature Space Transformation via Hidden Layers and Its Geometric Cost

Multi-layer perceptrons (MLPs) overcome this limitation by cascading transformations. A hidden layer maps the input $\mathbf{x}$ to a new representation $\mathbf{h}$ through a matrix-vector product and an element-wise activation function $\varphi$:

$$\mathbf{h}=\varphi (W\mathbf{x}+\mathbf{b}).$$

(3)

Here, $W\in {\mathbb{R}}^{m\times d}$ is the weight matrix, $\mathbf{b}\in {\mathbb{R}}^m$ is the bias vector, and m is the number of hidden neurons. Each row ${\mathbf{w}}_i^{\top }$ of W corresponds to the weight vector of the i-th hidden neuron, computing $h_i=\varphi (\langle {\mathbf{w}}_i,\mathbf{x}\rangle +b_i)$. This transforms the input space ${\mathbb{R}}^d$ into a feature space ${\mathbb{R}}^m$. The introduction of the non-linear activation function $\varphi$ is what allows the network to learn non-linear decision boundaries. However, this gain in expressive power comes at a cost: the potential loss of geometric fidelity.

3.2.3. Topological Distortions and Information Loss via Activation Functions

While hidden layers using the transformation $\mathbf{h}=\varphi (W\mathbf{x}+\mathbf{b})$ enable the learning of non-linear functions, the introduction of the element-wise non-linear activation function $\varphi$, often crucial for breaking linearity, can significantly alter the topological and geometric structure of the data representation, potentially leading to information loss ([13]). This is a critical trade-off: gaining non-linear modeling capability while potentially discarding valuable geometric information.

Consider the mapping $T:{\mathbb{R}}^d\to {\mathbb{R}}^m$ defined by $T\left(\mathbf{x}\right)=\varphi (W\mathbf{x}+\mathbf{b})$. The affine part, $A\left(\mathbf{x}\right)=W\mathbf{x}+\mathbf{b}$, performs a linear transformation (rotation, scaling, shear, projection) followed by a translation. While this affine map distorts metric properties (distances and angles, unless W is proportional to an orthogonal matrix), it preserves basic topological features like connectedness and maps lines to lines (or points) ([13]).

However, the subsequent application of a typical non-linear activation $\varphi$ element-wise often leads to more drastic topological changes:

• Non-Injectivity and Collapsing Regions: Many common activation functions render the overall mapping T non-injective.
  • ReLU ($\varphi \left(z\right)=max(0,z)$): Perhaps the most prominent example. For each hidden neuron i, the entire half-space defined by $\{\mathbf{x}\in {\mathbb{R}}^d\mid \langle {\mathbf{w}}_i,\mathbf{x}\rangle +b_i\le 0\}$ is mapped to $h_i=0$. Distinct points ${\mathbf{x}}_1,{\mathbf{x}}_2$ within this region, potentially far apart, become indistinguishable along the i-th dimension of the hidden space. This constitutes a significant loss of information about the relative arrangement of data points within these collapsed regions. The mapping is fundamentally many-to-one. For instance, consider two input vectors that are anti-aligned with a neuronś weight vector to different degrees—one strongly and one weakly. A ReLU activation function would map both resulting negative dot products to zero, rendering their distinct geometric opposition indistinguishable to subsequent layers. This information is irretrievably discarded.
  • Sigmoid/Tanh: While smooth, these functions saturate. Inputs ${\mathbf{z}}_1=A\left({\mathbf{x}}_1\right)$ and ${\mathbf{z}}_2=A\left({\mathbf{x}}_2\right)$ that are far apart but both fall into the saturation regime (e.g., large positive or large negative values) will map to ${\mathbf{h}}_1\approx {\mathbf{h}}_2$. This ’squashing’ effect can merge distinct clusters from the input space if they map to saturated regions in the hidden space, again losing discriminative information and distorting the metric structure.
• Distortion of Neighborhoods: The relative distances between points can be severely distorted. Points close in the input space ${\mathbb{R}}^d$ might be mapped far apart in ${\mathbb{R}}^m$, or vice-versa (especially due to saturation or the zero-region of ReLU). This means the local neighborhood structure is not faithfully preserved. Formally, the mapping T is generally not a homeomorphism onto its image, nor is it typically bi-Lipschitz (which would provide control over distance distortions).

Figure 1. Illustration of how non-linear activation functions can distort the geometric structure of the input data manifold, leading to potential information loss. The original manifold (left) is transformed into a distorted representation after applying a non-linear activation functions.

Figure 1. Illustration of how non-linear activation functions can distort the geometric structure of the input data manifold, leading to potential information loss. The original manifold (left) is transformed into a distorted representation after applying a non-linear activation functions.

While these distortions are precisely what grant neural networks their expressive power to warp the feature space and create complex decision boundaries, they come at the cost of potentially discarding information present in the original geometric configuration of the data. The network learns which information to preserve and which to discard based on the optimization objective, but the mechanism relies on potentially non-smooth or non-injective transformations introduced by $\varphi$. This highlights the conflation of magnitude and direction in the dot product, the information loss from activation functions, and the lack of a unified measure for proximity and alignment, setting the stage for the ⵟ-product.

4. Methodology: A Framework for Geometry-Aware Computation

4.1. The ⵟ-Product: A Unified Operator for Alignment and Proximity

The methodological innovations presented in this work are fundamentally rooted in the ⵟ-product, introduced in Section 1. This single operator serves as the foundation for subsequent layers and networks.

The ⵟ-product is formally defined as $ⵟ(\mathbf{w},\mathbf{x})={\displaystyle \frac{{\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2}{{\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ}}$. It exhibits a unique form of non-linearity. Unlike conventional activation functions (e.g., ReLU, sigmoid) which are often applied as separate, somewhat heuristic, transformations to introduce non-linearity after a linear operation, the non-linearity in the ⵟ-product arises directly from its mathematical structure. It is a function of the squared dot product (capturing alignment) and the inverse squared Euclidean distance (capturing proximity) between the weight vector $\mathbf{w}$ and the input vector $\mathbf{x}$. This formulation provides a rich, explainable non-linearity based on fundamental geometric and algebraic relationships, rather than an imposed, "artificial" non-linear mapping. The interaction between the numerator and the denominator allows for complex responses that are inherently tied to the geometric interplay of the input vectors.

Figure 2. Visualization of the ⵟ-product’s vector field in 2D and 3D spaces. The heatmaps illustrate how the ⵟ-product, unlike traditional similarity measures, creates a potential well around the weight vector $\mathbf{w}$, reflecting both alignment and proximity. This figure embodies the paper’s philosophy of unifying geometric alignment and spatial closeness within a single neural operator, inspired by physical interaction fields. The resulting landscape demonstrates how the ⵟ-product enables neural units to act as localized fields of influence, supporting our approach to interpretable, geometry-aware neural computation.

Figure 2. Visualization of the ⵟ-product’s vector field in 2D and 3D spaces. The heatmaps illustrate how the ⵟ-product, unlike traditional similarity measures, creates a potential well around the weight vector $\mathbf{w}$, reflecting both alignment and proximity. This figure embodies the paper’s philosophy of unifying geometric alignment and spatial closeness within a single neural operator, inspired by physical interaction fields. The resulting landscape demonstrates how the ⵟ-product enables neural units to act as localized fields of influence, supporting our approach to interpretable, geometry-aware neural computation.

As visualized in Figure 2, the ⵟ-product creates a potential well around the weight vector $\mathbf{w}$, reflecting both alignment and proximity.

To further appreciate the unique characteristics of the ⵟ-product, it is instructive to compare it with other common similarity or distance metrics:

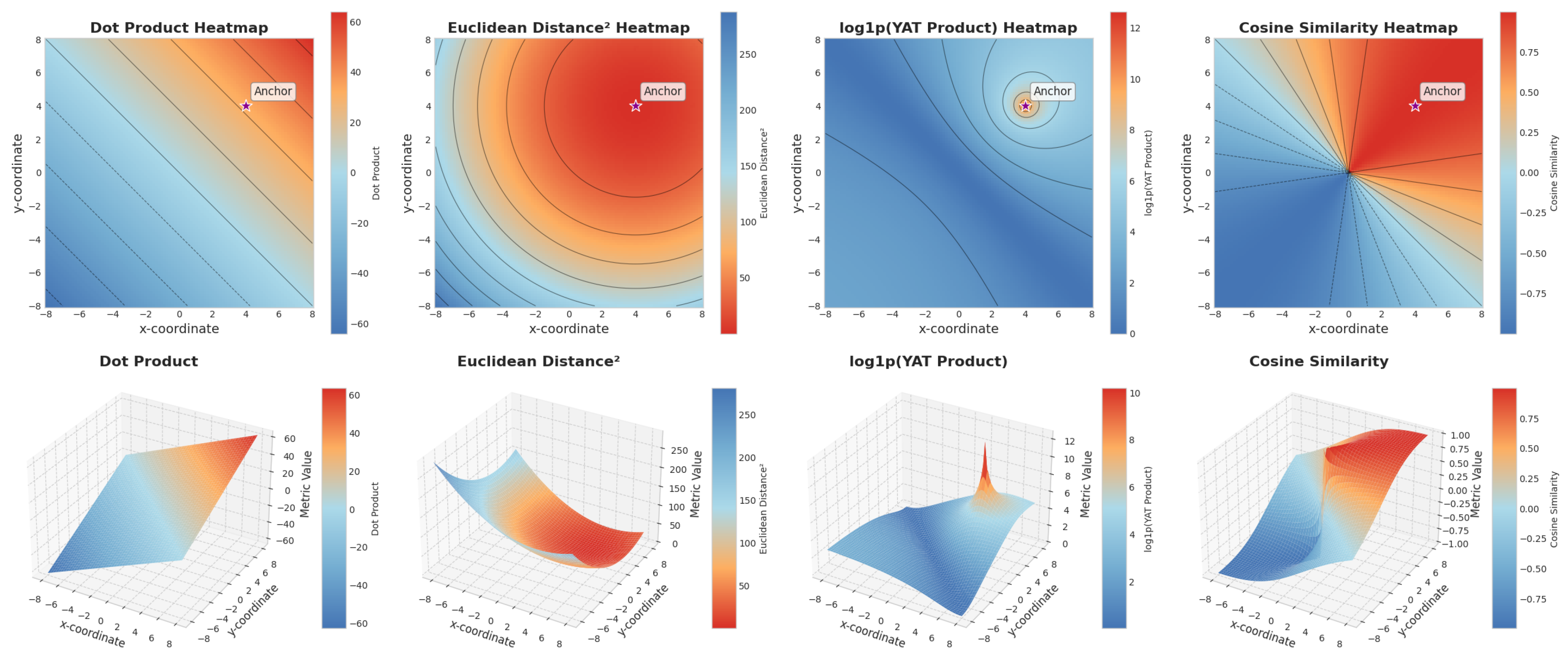
• Dot Product (${\mathbf{w}}^{\top }\mathbf{x}$): The dot product measures the projection of one vector onto another, thus capturing both alignment and magnitude. A larger magnitude in either vector, even with constant alignment, leads to a larger dot product. While useful, its direct sensitivity to magnitude can sometimes overshadow the pure geometric alignment.
• Cosine Similarity (${\displaystyle \frac{{\mathbf{w}}^{\top }\mathbf{x}}{\parallel \mathbf{w}\parallel \parallel \mathbf{x}\parallel }}$): Cosine similarity normalizes the dot product by the magnitudes of the vectors, yielding the cosine of the angle between them. This makes it purely a measure of alignment, insensitive to vector magnitudes. However, as pointed out, this means it loses information about true distance or scale; two vectors can have perfect cosine similarity (e.g., value of 1) even if one is very distant from the other, as long as they point in the same direction.
• Euclidean Distance ($\parallel \mathbf{w}-\mathbf{x}\parallel$): This metric computes the straight-line distance between the endpoints of two vectors. It is a direct measure of proximity. However, it does not inherently capture alignment. For instance, if $\mathbf{w}$ is a reference vector, all vectors $\mathbf{x}$ lying on the surface of a hypersphere centered at $\mathbf{w}$ will have the same Euclidean distance to $\mathbf{w}$, regardless of their orientation relative to $\mathbf{w}$.
• ⵟ-Product (${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})={\displaystyle \frac{{\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2}{{\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ}}$): The ⵟ-product uniquely combines aspects of both alignment and proximity in a non-linear fashion. The numerator, ${\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2$, emphasizes strong alignment (being maximal when vectors are collinear and zero when orthogonal) and is sensitive to magnitude. The denominator, ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ$, heavily penalizes large distances between $\mathbf{w}$ and $\mathbf{x}$. This synergy allows the ⵟ-product to be highly selective. It seeks points that are not only well-aligned with the weight vector $\mathbf{w}$ but also close to it. Unlike cosine similarity, it distinguishes between aligned vectors at different distances. Unlike Euclidean distance alone, it differentiates based on orientation. This combined sensitivity allows the ⵟ-product to identify matches with a high degree of specificity, akin to locating a point with "atomic level" precision, as it requires both conditions (alignment and proximity) to be met strongly for a high output.

The ⵟ-product’s ability to discern between aligned vectors at varying distances, as well as its sensitivity to the angle between vectors, is illustrated in Figure 2 and Figure 3. The vector field generated by the ⵟ-product can be visualized as a potential well around the weight vector $\mathbf{w}$, where the strength of the interaction diminishes with distance, akin to gravitational or electrostatic fields. This visualization underscores how the ⵟ-product captures both alignment and proximity in a unified manner. This combined sensitivity is crucial for tasks where both the orientation and the relative position of features are important.

The ⵟ-product’s non-linearity is not merely a mathematical curiosity; it has practical implications for neural computation. By integrating alignment and proximity into a single operator, the ⵟ-product allows for more nuanced feature learning. It can adaptively respond to inputs based on their geometric relationships with learned weight vectors, enabling the network to capture complex patterns without the need for separate activation functions.

Consider the classic XOR problem, which is not linearly separable and thus cannot be solved by a single traditional neuron (linear perceptron). The inputs are $(0,0)\to 0$, $(0,1)\to 1$, $(1,0)\to 1$, and $(1,1)\to 0$. A single ⵟ-product unit can, however, solve this. Let the weight vector be $\mathbf{w}={[1,-1]}^{\top }$.

For $\mathbf{x}={[0,0]}^{\top }$: ${\mathbf{w}}^{\top }\mathbf{x}=0$, so ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})=0$.

For $\mathbf{x}={[1,1]}^{\top }$: ${\mathbf{w}}^{\top }\mathbf{x}=1-1=0$, so ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})=0$.

For $\mathbf{x}={[0,1]}^{\top }$: ${\mathbf{w}}^{\top }\mathbf{x}=-1$. ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2={\parallel {[1,-2]}^{\top }\parallel }^2=5$. So ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})={\displaystyle \frac{{(-1)}^2}{5+ϵ}}={\displaystyle \frac{1}{5+ϵ}}>0$.

For $\mathbf{x}={[1,0]}^{\top }$: ${\mathbf{w}}^{\top }\mathbf{x}=1$. ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2={\parallel {[0,-1]}^{\top }\parallel }^2=1$. So ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})={\displaystyle \frac{1^2}{1+ϵ}}={\displaystyle \frac{1}{1+ϵ}}>0$.

Thus, the ⵟ-product unit with an appropriate weight vector (such as one where components have opposite signs, reflecting the XOR logic) naturally separates the XOR patterns, effectively acting as a mathematical kernel.

To understand its behavior during learning, let us consider its gradient. The partial derivative of ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})$ with respect to an input component $x_k$ (assuming $\mathbf{x}=(x_1,...,x_d)$ and $\mathbf{w}=(w_1,...,w_d)$) can be expressed. For simplicity, let $N={\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2$ and $D={\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ$. Then, ${\displaystyle \frac{\partial N}{\partial x_k}}=2\left({\mathbf{w}}^{\top }\mathbf{x}\right)w_k$ and ${\displaystyle \frac{\partial D}{\partial x_k}}=-2(w_k-x_k)$. Using the quotient rule, ${\displaystyle \frac{\partial {\mathcal{K}}_{ⵟ}}{\partial x_k}}={\displaystyle \frac{\frac{\partial N}{\partial x_k}D-N\frac{\partial D}{\partial x_k}}{D^2}}$. Substituting the terms:

$${\displaystyle \frac{\partial {\mathcal{K}}_{ⵟ}}{\partial x_k}}={\displaystyle \frac{2\left({\mathbf{w}}^{\top }\mathbf{x}\right)w_k{(\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ)-{\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2(-2(w_k-x_k))}{{(\parallel \mathbf{w}-\mathbf{x}\parallel }^2{+ϵ)}^2}}$$

$$={\displaystyle \frac{2\left({\mathbf{w}}^{\top }\mathbf{x}\right)[w_k{(\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ)+\left({\mathbf{w}}^{\top }\mathbf{x}\right)(w_k-x_k)]}{{(\parallel \mathbf{w}-\mathbf{x}\parallel }^2{+ϵ)}^2}}$$

A key characteristic of this derivative is its continuous nature and the fact that it is generally non-zero, barring specific configurations where ${\mathbf{w}}^{\top }\mathbf{x}=0$ (orthogonal vectors) or pathological cases. The presence of $ϵ$ in the denominator ensures that the derivative remains well-defined and avoids division by zero, contributing to numerical stability. This contrasts with activation functions like ReLU, which have a derivative of zero for negative inputs, potentially leading to "dead neurons." The smooth and generally non-zero gradient of the ⵟ-product is hypothesized to contribute to more stable and efficient learning dynamics, reducing the reliance on auxiliary mechanisms like complex normalization schemes. The non-linearity is thus not an add-on but an intrinsic property derived from the direct mathematical interaction of vector projection (alignment, via the ${\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2$ term) and vector distance (proximity, via the ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ$ term). This provides a mathematically grounded basis for feature learning, as the unit becomes selectively responsive to inputs that exhibit specific geometric relationships—both in terms of angular alignment and spatial proximity—to its learned weight vector $\mathbf{w}$. Consequently, $\mathbf{w}$ can be interpreted as a learned feature template or prototype that the unit is tuned to detect, with the ⵟ-product quantifying the degree of match in a nuanced, non-linear fashion.

The gradient of the ⵟ-product, being responsive across the input space, actively pushes the neuron’s weights away from configurations that would lead to a zero output (neuron death, e.g., at an input of $[0,0]$ for this problem if weights were also near zero). This contrasts with a simple dot product neuron where the gradient might vanish or lead to a global minimum at zero output for certain problems. For instance, when considering gradient-based optimization, the loss landscape "seen" by the ⵟ-product neuron in the XOR context would exhibit a peak or high loss at $[0,0]$ (if that were the target for non-zero outputs), encouraging weights to move towards a state that correctly classifies. Conversely, a simple dot product neuron might present a loss landscape where a gradient-based optimizer could find a stable (but incorrect) minimum at zero output. This ability to avoid such dead zones and actively shape the decision boundary makes it helpful to solve problems like XOR with a single unit, leveraging its inherent non-linearity as a mathematical kernel.

Figure 4. Comparison of the loss landscape for a simple dot product neuron and a ⵟ-product neuron. The dot product neuron has a stable minimum at zero output which doesn’t solve the xor problem and cause the neuron death, while the ⵟ-product neuron resides in a valley of orthogonality, allowing it to avoid dead zones and actively shape the decision boundary. This illustrates the ⵟ-product’s ability to solve problems like XOR with a single unit, leveraging its inherent non-linearity as a mathematical kernel.

Figure 4. Comparison of the loss landscape for a simple dot product neuron and a ⵟ-product neuron. The dot product neuron has a stable minimum at zero output which doesn’t solve the xor problem and cause the neuron death, while the ⵟ-product neuron resides in a valley of orthogonality, allowing it to avoid dead zones and actively shape the decision boundary. This illustrates the ⵟ-product’s ability to solve problems like XOR with a single unit, leveraging its inherent non-linearity as a mathematical kernel.

Conceptually, the decision boundary or vector field generated by a simple dot product neuron is linear, forming a hyperplane that attempts to separate data points. In contrast, the ⵟ-product generates a more complex, non-linear vector field. This field can be visualized as creating a series of potential wells or peaks centered around the weight vector $\mathbf{w}$, with the strength of influence decaying with distance. The condition ${\mathbf{w}}^{\top }\mathbf{x}=0$ defines a "valley" of zero output where vectors are orthogonal to the weight vector. This structure allows for more nuanced and localized responses, akin to a superposition of influences rather than a single linear division, enabling the capture of intricate patterns in the data.

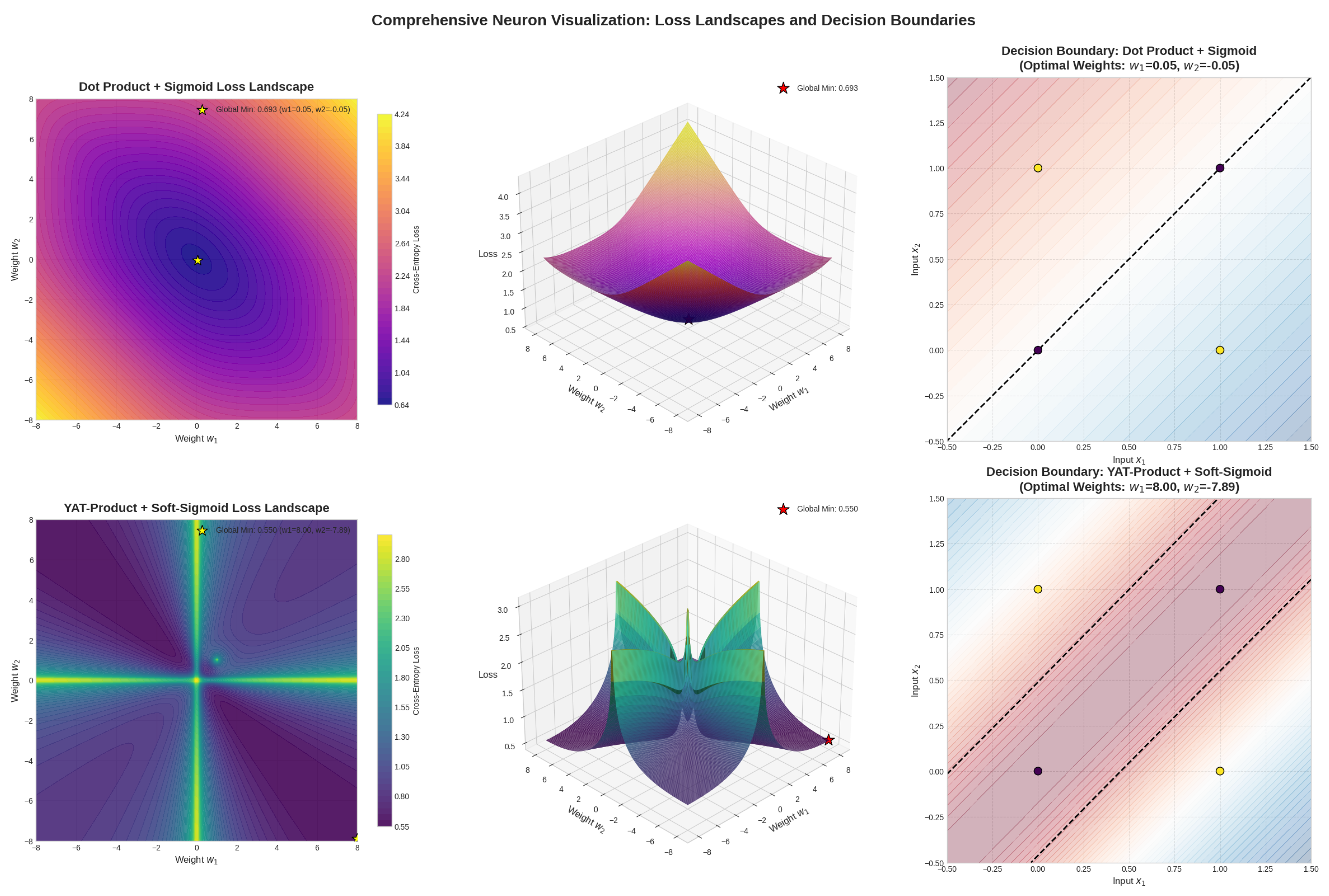
4.2. Design Philosophy: Intrinsic Non-Linearity and Self-Regulation

A central hypothesis underpinning our methodological choices is that the ⵟ-product (Section 1) possesses inherent non-linearity and self-regulating properties that can reduce or eliminate the need for conventional activation functions (e.g., ReLU, sigmoid, GeLU) and normalization layers (e.g., Batch Normalization, Layer Normalization).

This philosophy recontextualizes the fundamental components of neural computation. Neuron weights ($\mathbf{w}$) and input signals ($\mathbf{x}$) are not merely operands in a linear transformation followed by a non-linear activation; instead, they are conceptualized as co-equal vector entities inhabiting a shared, high-dimensional feature manifold. Within this framework, each vector can be viewed as an analogue to a fundamental particle or feature vector, with its constituent dimensions potentially encoding excitatory, inhibitory, or neutral characteristics relative to other entities in the space. The ⵟ-product (Section 1) then transcends simple similarity assessment; it functions as a sophisticated interaction potential, ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})={\displaystyle \frac{{\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2}{{\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ}}$, quantifying the ’field effects’ between these vector entities. This interaction is reminiscent of n-body problems in physics. In machine learning, it draws parallels with, yet distinctively evolves from, learned metric spaces in contrastive learning, particularly those employing a triplet loss framework. While triplet loss aims to pull positive pairs closer and push negative pairs apart in the embedding space, our ⵟ-product seeks a more nuanced relationship: ’positive’ interactions (high ⵟ-product value) require both strong alignment (high ${\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2$) and close proximity (low ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2$). Conversely, ’negative’ or dissimilar relationships are not merely represented by distance, but more significantly by orthogonality (leading to a vanishing numerator), which signifies a form of linear independence and contributes to the system’s capacity for true non-linear discrimination. Crucially, the non-linearity required for complex pattern recognition is not an external imposition (e.g., via a separate activation function) but is intrinsic to this interaction potential. The interplay between the squared dot product (alignment sensitivity) and the inverse squared Euclidean distance (proximity sensitivity) in its formulation directly sculpts a complex, non-linear response landscape without recourse to auxiliary functions.

Furthermore, this conceptualization of the ⵟ-product as an intrinsic interaction potential suggests inherent self-regulating properties. The distance-sensitive denominator, ${\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ$, acts as a natural dampening mechanism. As the ’distance’ (dissimilarity in terms of position) between interacting vector entities $\mathbf{w}$ and $\mathbf{x}$ increases, the strength of their interaction, and thus the resultant activation, diminishes quadratically. This behavior is hypothesized to inherently curtail runaway activations and stabilize learning dynamics by ensuring that responses are localized and bounded. Such intrinsic stabilization contrasts sharply with conventional approaches that rely on explicit normalization layers (e.g., Batch Normalization, Layer Normalization) to manage activation statistics post-hoc. These layers, while effective, introduce additional computational overhead, can obscure direct input-output relationships, and sometimes complicate the theoretical analysis of network behavior. The ⵟ-product’s formulation, therefore, offers a pathway to architectures where regulatory mechanisms are embedded within the primary computational fabric of the network.

The inherent non-linearity of the ⵟ-product, coupled with the self-regulating properties suggested by its formulation, are central to our hypothesis that it can form the basis of powerful and robust neural architectures. These intrinsic characteristics open avenues for simplifying network design, potentially reducing reliance on or even eliminating conventional activation functions and normalization layers.

Figure 5. The Vectoverse: Conceptualizing neural computation where weight vectors ($\mathbf{w}$) and input vectors ($\mathbf{x}$) are akin to fundamental particles (vectoms). The interaction force between them is quantified by the ⵟ-product, which measures their alignment and proximity, defining a field of influence.

Figure 5. The Vectoverse: Conceptualizing neural computation where weight vectors ($\mathbf{w}$) and input vectors ($\mathbf{x}$) are akin to fundamental particles (vectoms). The interaction force between them is quantified by the ⵟ-product, which measures their alignment and proximity, defining a field of influence.

4.3. Core Building Blocks

Now, we show how the ⵟ-product is operationalized into reusable layers.

4.3.1. The Neural Matter Network (NMN) Layer

The first and simplest application of the ⵟ-product is in Neural-Matter Network (NMN) layers. These networks represent a departure from traditional Multi-Layer Perceptrons (MLPs) by employing the non-linear, spatially-aware ${\mathcal{K}}_{ⵟ}$-kernel (derived from the ⵟ-product, see Section 4.1) as the primary interaction mechanism, instead of the conventional linear projection ($\langle \mathbf{w},\mathbf{x}\rangle$).

An NMN layer transforms an input vector ($\mathbf{x}\in {\mathbb{R}}^d$) into an output (here, we consider a scalar output h for simplicity, extendable to vector outputs $\mathbf{h}$ by aggregating the influence of multiple "neural matter" units). Each unit i is defined by a weight vector (${\mathbf{w}}_i\in {\mathbb{R}}^d$) (acting as a positional anchor or prototype) and a bias term ($b_i\in \mathbb{R}$). The layer output is computed as:

$$h\left(\mathbf{x}\right)=\left(s·\sum _{i=1}^n\left({\mathcal{K}}_{ⵟ}({\mathbf{w}}_i,\mathbf{x})+b_i\right)\right)=\left(s·\sum _{i=1}^n\left({\displaystyle \frac{{\left({\mathbf{w}}_i^{\top }\mathbf{x}\right)}^2}{\parallel {\mathbf{w}}_i{-\mathbf{x}\parallel }^2+ϵ}}+b_i\right)\right)$$

where:

• ${\mathbf{w}}_i$ is the weight vector of the i-th NMN unit.
• $b_i$ is the bias term for the i-th NMN unit.
• ${\mathcal{K}}_{ⵟ}({\mathbf{w}}_i,\mathbf{x})$ represents the ⵟ-product between the weight vector ${\mathbf{w}}_i$ and the input $\mathbf{x}$.
• n is the number of NMN units in the layer.
• s is a scaling factor.

This formulation allows each NMN unit to respond based on both alignment and proximity to its learned weight vector.

Furthermore, the representational power of NMNs can be formally stated. We posit the following theorem regarding their approximation capabilities:

Theorem 2

(Universal Approximation for NMNs with ${\mathcal{K}}_{ⵟ}$-Kernel). Let K be a compact subset of ${\mathbb{R}}^d$. Let $C(K,{\mathbb{R}}^m)$ denote the space of continuous functions from K to ${\mathbb{R}}^m$. Let the ${\mathcal{K}}_{ⵟ}$-kernel be defined as ${\mathcal{K}}_{ⵟ}(\mathbf{w},\mathbf{x})={\displaystyle \frac{{\left({\mathbf{w}}^{\top }\mathbf{x}\right)}^2}{{\parallel \mathbf{w}-\mathbf{x}\parallel }^2+ϵ}}$ for some $ϵ>0$. Then, for any function $f\in C(K,{\mathbb{R}}^m)$ and any $\delta >0$, there exist:

• a positive integer n (number of units),
• weight vectors ${\mathbf{w}}_k\in {\mathbb{R}}^d$ for $k=1,\dots ,n$,
• scalar bias terms $b_k\in \mathbb{R}$ for $k=1,\dots ,n$,
• vector coefficients ${\mathbf{c}}_k\in {\mathbb{R}}^m$ for $k=1,\dots ,n$,

such that the NMN layer $h:K\to {\mathbb{R}}^m$ defined by

$$h\left(\mathbf{x}\right)=\sum _{k=1}^n{\mathbf{c}}_k\left({\mathcal{K}}_{ⵟ}({\mathbf{w}}_k,\mathbf{x})+b_k\right)$$

satisfies ${sup}_{\mathbf{x}\in K}\parallel h\left(\mathbf{x}\right)-f\left(\mathbf{x}\right)\parallel <\delta$. This approximation is achieved without recourse to traditional, separate activation functions, relying solely on the inherent non-linearity of the ${\mathcal{K}}_{ⵟ}$-kernel based terms and their linear combination.

This property underscores the potential of the ${\mathcal{K}}_{ⵟ}$-kernel to form the basis of powerful function approximators, distinguishing NMNs from classical MLP architectures that explicitly require non-linear activation functions for universal approximation.

4.3.2. Convolutional Neural-Matter Networks (CNMNs) and the ⵟ-Convolution Layer

To extend the principles of Neural-Matter Networks (NMNs) (Section 4.3.1) and the ⵟ-product (Section 1) to spatially structured data like images, we introduce the ⵟ-Convolution (Yat-Conv) layer. This layer adapts the ⵟ-product to operate on local receptive fields, analogous to standard convolutional layers. The ⵟ-Conv operation is defined as:

$${\left(ⵟ\text{-}\mathrm{Conv}(K,I)\right)}_{i,j}={ⵟ}^{*}(K,I_{i,j})={\displaystyle \frac{{\langle K,I_{i,j}\rangle }^2}{\parallel K-I_{i,j}{\parallel }^2+ϵ}}$$

where K is the convolutional kernel and $I_{i,j}$ is the input patch at location $(i,j)$ corresponding to the receptive field of the kernel.

4.3.3. The ⵟ-Attention Mechanism

To extend the ⵟ-product’s application to sequence modeling, we propose the ⵟ-Attention mechanism. This mechanism serves as an alternative to the standard scaled dot-product attention found in transformer architectures by replacing the dot product used for calculating query-key similarity with the ⵟ-product (Section 4.1). Given Query (Q), Key (K), and Value (V) matrices, ⵟ-Attention is computed as:

$$ⵟ\text{-}\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(s·(QⵟK^T)\right)V$$

where the operation $QⵟK^T$ signifies applying the ⵟ-product element-wise between query and key vectors (e.g., the $(i,j)$-th element is $ⵟ(q_i,k_j)$), and s is a scaling factor.

4.4. Architectural Implementations

The development of architectures like AetherResNet and AetherGPT without standard components (like separate activation and normalization layers) is a deliberate effort to test the hypothesis outlined in Section 4.2. Key architectural distinctions driven by this philosophy include:

• Fundamental Operator Replacement: The standard dot product is replaced by the ⵟ-product. This is manifested as ⵟ-Convolution (Equation ??) in convolutional networks and ⵟ-Attention (Equation 4.3.3) in transformer-based models.
• Feed-Forward Networks (FFNs): The FFNs within are constructed using NMN layers (Section 4.3.1) without explicit non-linear activation functions.
• Omission of Standard Layers: Consistent with this design philosophy, explicit activation functions and standard normalization layers are intentionally omitted.

By minimizing reliance on these traditional layers, we aim to explore simpler, potentially more efficient, and interpretable models where the primary computational operator itself handles these crucial aspects of neural processing. Furthermore, this principle of substituting the dot product with the ⵟ-product is not limited to the architectures presented and holds potential for enhancing other neural network paradigms.

4.4.1. Convolutional NMNs:

AetherResNet is a Convolutional Neural-Matter Network (CNMN) built by replacing all standard convolutions in a ResNet18 architecture with the ⵟ-Convolution layers. Building upon the ⵟ-Conv layer, CNMNs adapt conventional convolutional architectures by employing the ⵟ-Conv layer as the primary feature extraction mechanism. The core idea is to leverage the geometric sensitivity and inherent non-linearity of the ⵟ-product within deep convolutional frameworks. Consistent with the philosophy of Section 4.2, AetherResNet omits Batch Normalization and activation functions. The design relies on the hypothesis that the ⵟ-product itself provides sufficient non-linearity and a degree of self-regulation.

A key architectural adaptation in our CNMN implementation is the removal of the traditional fully connected (FC) classification layer at the end of the network. Instead, classification is performed by appending a final ⵟ-Convolution layer, where the number of output channels is set equal to the number of target classes. This is followed by a global average pooling operation, which aggregates the spatial outputs of each class channel into a single score per class. This approach maintains the geometric and spatial inductive biases of the convolutional framework all the way through to the output, and further simplifies the architecture by eliminating the need for flattening and dense layers. Further details on the specific architectural adaptations of AetherResNet are provided in the experimental setup.

4.4.2. YatFormer: AetherGPT

AetherGPT is a YatFormer model that uses ⵟ-Attention (from Section 4.3.3) for sequence interaction and NMN layers (from Section 4.3.1) in its feed-forward blocks. Building upon the ⵟ-Attention mechanism, which forms its cornerstone, we introduce YatFormer, a family of transformer-based models. As a specific instantiation for our investigations, we developed AetherGPT. This model adapts the architectural principles of GPT-2. Again, following the philosophy of Section 4.2, it omits standard normalization and activation layers.

4.5. Output Processing for Non-Negative Scores

The ⵟ-product and its derivatives, such as the ${\mathcal{K}}_{ⵟ}$-kernel, naturally yield non-negative scores. In many machine learning contexts, particularly when these scores need to be interpreted as probabilities, attention weights, or simply normalized outputs, it is essential to apply a squashing function to map them to a desired range (e.g., [0, 1] or ensuring a set of scores sum to 1).

Traditional squashing functions, however, present challenges when applied to non-negative inputs:

• Standard Sigmoid Function ($\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$): When applied to non-negative inputs ($x\ge 0$), the standard sigmoid function produces outputs in the range $[0.5,1)$. The minimum value of $0.5$ for $x=0$ renders it unsuitable for scenarios where small non-negative scores should map to values close to 0.
• Standard Softmax Function ($\mathrm{softmax}{\left(\mathbf{x}\right)}_i={\displaystyle \frac{e^{x_i}}{{\sum }_j{e}^{x_j}}}$): The use of the exponential function in softmax can lead to hard distributions, where one input value significantly dominates the output, pushing other probabilities very close to zero. While this is often desired for classification, it can be too aggressive if a softer assignment of probabilities or attention is preferred.

Given these limitations and the non-negative nature of ⵟ-product scores, we consider alternative squashing functions more suited to this domain:

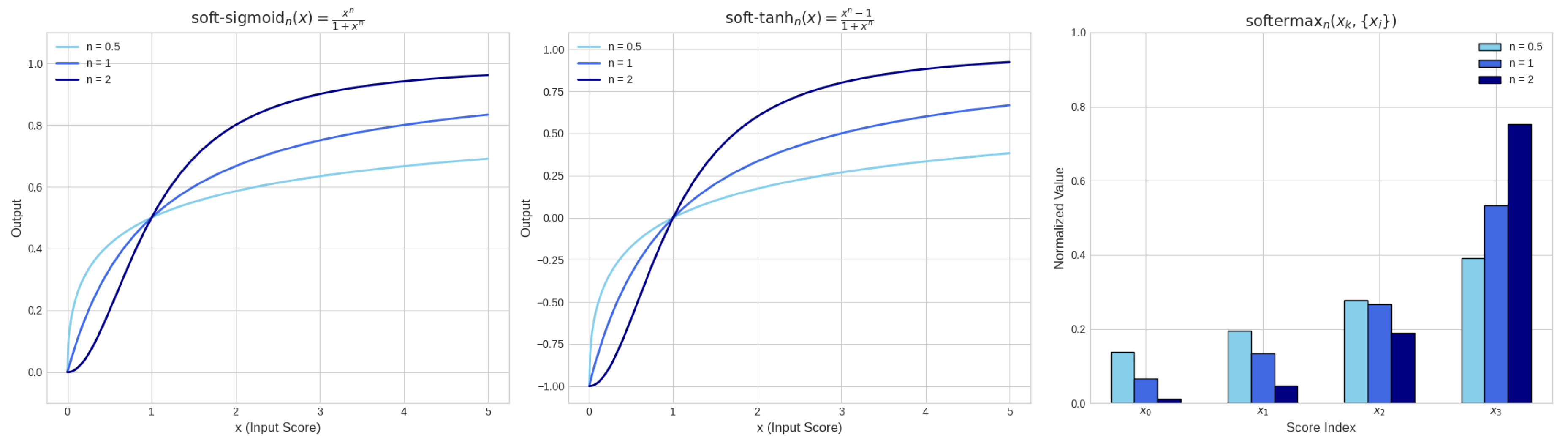
• softermax: This function normalizes a score $x_k$ (optionally raised to a power $n>0$) relative to the sum of a set of non-negative scores $\left\{x_i\right\}$ (each raised to n), with a small constant $ϵ>0$ for numerical stability. It is defined as:

  $${\mathrm{softermax}}_n(x_k,\left\{x_i\right\})={\displaystyle \frac{x_k^n}{ϵ+{\sum }_i{x}_i^n}}$$
  The power n controls the sharpness of the distribution: $n=1$ recovers the original Softermax, while $n>1$ makes the distribution harder (more peaked), and $0<n<1$ makes it softer.
• soft-sigmoid: This function squashes a single non-negative score $x\ge 0$ (optionally raised to a power $n>0$) into the range $[0,1)$. It is defined as:

  $${\mathrm{soft}\text{-}\mathrm{sigmoid}}_n\left(x\right)={\displaystyle \frac{x^n}{1+x^n}}$$
  The power n modulates the softness: higher n makes the function approach zero faster for large x, while $n<1$ makes the decay slower.
• soft-tanh: This function maps a non-negative score $x\ge 0$ (optionally raised to a power $n>0$) to the range $[-1,1)$ by linearly transforming the output of soft-sigmoid. It is defined as:

  $${\mathrm{soft}\text{-}\tan \mathrm{h}}_n\left(x\right)=2·({\mathrm{soft}\text{-}\mathrm{sigmoid}}_n\left(x\right)-\frac{1}{2})={\displaystyle \frac{x^n-1}{1+x^n}}$$
  The power n again controls the transition sharpness: higher n makes the function approach $-1$ more quickly for large x.

  

  Figure 6. Visualization of the softermax, soft-sigmoid, and soft-tanh functions. These functions are designed to handle non-negative inputs from the ⵟ-product and its derivatives, providing appropriate squashing mechanisms that maintain sensitivity across the range of non-negative inputs.

  Figure 6. Visualization of the softermax, soft-sigmoid, and soft-tanh functions. These functions are designed to handle non-negative inputs from the ⵟ-product and its derivatives, providing appropriate squashing mechanisms that maintain sensitivity across the range of non-negative inputs.

  

These functions are particularly well-suited for the outputs of ⵟ-product-based computations, as they maintain sensitivity across the range of non-negative inputs while avoiding the pitfalls of standard activation functions. The softermax function provides a normalized distribution over multiple scores, soft-sigmoid offers a gentle squashing to [0, 1), and soft-tanh maps to [-1, 1) while preserving the non-negative nature of the input.

5. Results and Discussion

In-Progress

6. Explainability

In-Progress

7. Conclusion

Perhaps artificial intelligence’s greatest limitation has been our stubborn fixation on the human brain as the pinnacle of intelligence. The universe itself, governed by elegant and powerful laws, demonstrates intelligence far beyond human cognition. These fundamental laws, which shape galaxies and guide quantum particles, represent a deeper form of intelligence that we have largely ignored in our pursuit of AI.

In this paper, we challenge the conventional AI paradigm. We broke free from biological metaphors by drawing direct inspiration from inverse-square law interactions in physics. The ⵟ-product, with its inherent non-linearity and geometric sensitivity, allows for a more nuanced understanding of vector interactions, capturing both alignment and proximity in a single operation. This approach not only simplifies the architecture of neural networks but also enhances their interpretability and robustness.