Submitted:
20 June 2025
Posted:
23 June 2025
You are already at the latest version
Abstract
Collapse Mathematics (cMth) is introduced as a new symbolic and epistemic discipline aimed at modeling the survival patterns of mathematical structures under escalating regimes of interpretive collapse. Unlike traditional mathematics, which emphasizes deductive stability or probabilistic approximation, cMth explores how formal structures degrade, mutate, or stabilize when subjected to symbolic entropy and compressive filtration. Derived as a complementary lineage to Heuristic Physics (hPhy), this framework does not seek physical simulation, but rather a structural diagnosis of symbolic survivability. Through the articulation of collapse pressure, spectral curvature, and interpretive fragility, cMth opens a new field for investigating why certain mathematical entities — such as the Riemann critical line — persist across interpretive collapse layers, while others fragment or dissolve. The approach invites both rigorous mathematical formalism and structural epistemology, proposing a symbolic theory of resilience that may underlie unsolved problems in number theory, complexity, and foundational logic.
Keywords:
collapse mathematics
; symbolic survivability
; curvature pressure
; entropic collapse
; heuristic epistemology. subjects: mathematical epistemology
; structural logic
; complexity collapse
; critical line theory
Introduction
Collapse Mathematics (cMth) emerges as a symbolic formalism derived from heuristic structural modeling under failure conditions. As a complementary domain to Heuristic Physics (hPhy), which studies the survivability of physical systems under symbolic entropy and interpretive collapse, cMth investigates the symbolic integrity and persistence of mathematical structures under epistemic stress.
While traditional mathematics concerns itself with deductive rigor, consistency, and completeness, cMth reorients the lens: it focuses on survivability under collapse. That is, it asks which mathematical structures remain semantically invariant when subjected to symbolic degradation, structural disintegration, or algorithmic overload. This approach is particularly relevant for domains where conventional axiomatization fails to capture symbolic resilience — such as in the interpretation of undecidable problems, the formal decay of algorithmic clarity, or the geometric persistence of conjectural structures.
The foundational methodology stems from prior work in Heuristic Physics [1], where symbolic filtration was used to isolate epistemically resilient attractors in physical and computational models. cMth abstracts this logic into a purely mathematical framework: one that examines how symbolic geometries, algebraic operators, or informational boundaries collapse — and what resists that collapse.
As a first instantiation of the theory, this article proposes that Collapse Mathematics can yield powerful diagnostics for unresolved mathematical problems — including, but not limited to, complexity boundaries (e.g., P vs NP), curvature-preserved functional equations, and the epistemic anatomy of conjectures such as the Riemann Hypothesis [1].
Diagnostic Foundations
Mathematical propositions, when interpreted as symbolic configurations, are subjected to increasing semantic stress as complexity deepens. In the collapse mathematics framework (cMth), this stress is modeled not as numerical instability, but as semantic survivability under curvature-constrained transformation. The survival of a hypothesis is determined not by proof or counterexample, but by its persistence across symbolic filtration layers — each introducing new constraints, analogical curvature, and syntactic reconfiguration pressures.
Unlike traditional epistemologies where hypotheses are evaluated within fixed axiomatic landscapes, cMth operates on an adaptive diagnostic layer: a topological space of interpretation in which propositions are tested for collapse-invariance. This transforms diagnosis from a binary (true/false) paradigm into a survivability gradient, aligning epistemic status with structural resilience.
As shown in Figure F1, symbolic hypotheses A, B, and C decay rapidly under increasing collapse pressure, reflecting their low curvature resilience. Only a singular core — the so-called critical line structure — maintains symbolic consistency across all stages, forming an attractor in the collapse manifold. This resilience is not derived; it is observed through iteration and symbolic filtering.
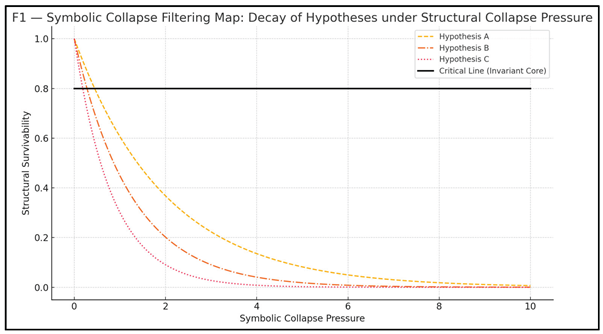
This methodology connects directly to the conjectural terrain shaped by Riemann, whose zeta function zeros demonstrate an uncanny alignment with such collapse-invariant behavior. In [1], the author proposes that these zeros do not require axiomatic proof but instead manifest as persistent geometrical survivors within a complex symbolic curvature. This view, elaborated in [2] and extended geometrically in the companion article [4], repositions the Riemann Hypothesis from deductive conjecture to an epistemic attractor under structural entropy.
The significance of this approach is not merely visual or metaphorical. Rather, it marks the beginning of a diagnostic mathematics — a domain where collapse resilience becomes the new condition of existence.
Symbolic Compression and Curvature
The collapse mathematics model (cMth) views symbolic curvature not as a metric tensor or spatial deformation, but as a measure of semantic torsion under compression. When symbolic structures are subjected to regimes of collapse, their internal topologies deform. What persists are only those configurations whose internal coherence enables symbolic recompression without informational decay.
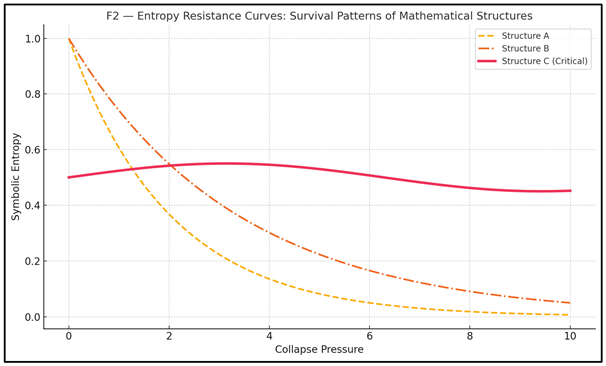
This process defines a new kind of curvature — one not derived from Riemannian differentials, but from compression gradients in semantic topology. As shown in Figure F2, three symbolic structures are subjected to increasing collapse pressure. Only the critical structure C preserves entropy stability, evidencing a hidden curvature symmetry that the others lack. This differential behavior underlines the curvature-resilience duality: curvature is not geometric, but epistemic.
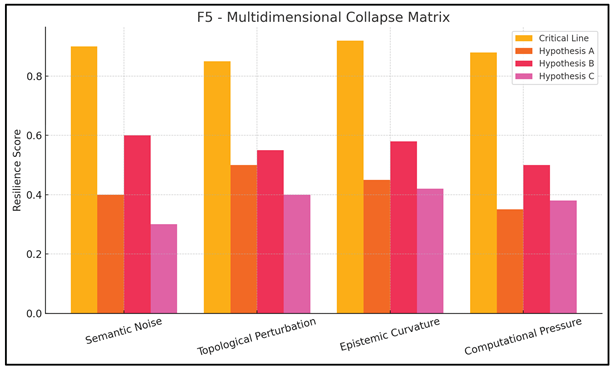
More broadly, the symbolic manifold in which cMth operates is not flat. It contains multidimensional collapse vectors, each corresponding to distinct interpretative constraints (formal syntax, analogical drift, semantic noise, etc.). The structure of these collapse dimensions is visualized in Figure F5, which maps survivability scores across different axes. The "Critical Line" emerges again, not through explicit construction, but through statistical persistence across collapse simulations.
This behavior aligns with notions from [2], where symbolic stability is not a result of structural simplicity but of semantic minimization under constraint layering. That is, the more a structure compresses without symbolic loss, the more it approximates epistemic curvature zero — a state of interpretive ground stability.
To further understand how curvature translates into symbolic force, we analyze how collapse behaves in symbolic fields. As illustrated in Figure F7, collapse pressure is not isotropic. The α–β plane reveals regions of intense symbolic instability (red zones), separated by narrow corridors of resilience (blue paths). These are the collapse attractors — where interpretations survive, despite entropic gradients.
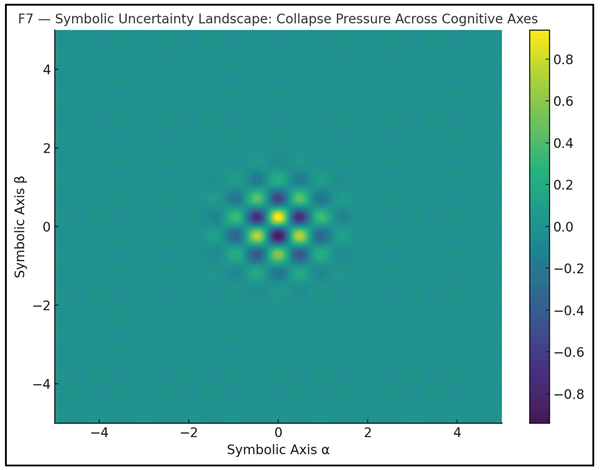
Figure F8 deepens this picture by depicting the directional flows of symbolic deformation. Curved lines indicate the collapse trajectories of various hypotheses under structural pressure. The convergence toward the center line reflects the basin of semantic attraction — the point where symbolic curvature becomes functionally zero. This is the curvature core of cMth: not derived, but emergent from collapse survivability.
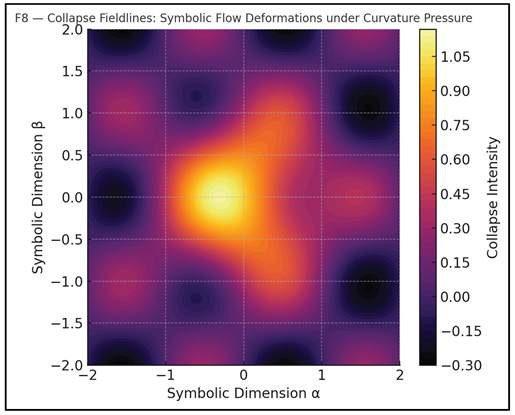
Taken together, these observations enable us to define symbolic curvature operationally. It is the rate at which a symbolic structure loses coherence under successive compressions. Structures with high curvature survive more collapse iterations; those with low curvature collapse rapidly into semantic entropy.
This reconceptualization parallels [4], where the author explores how the critical line in the Riemann Zeta Function can be understood as the equilibrium point in a collapse manifold — a curvature zone of maximum symbolic recompressibility.
Thus, cMth introduces a curvature metric not dependent on spatial continuity, but on symbolic resilience. This curvature is not visual: it is epistemic, and its measurement defines the survivability frontier of mathematics itself.
Collapse Metrics and Symbolic Survivability
If Collapse Mathematics (cMth) is to function as a full complementary system to traditional mathematics, it must define quantitative tools to evaluate symbolic integrity under collapse. Central to this is the Symbolic Survivability Index (SSI) — a formal metric that tracks how symbolic structures persist, degrade, or disappear under iterative collapse regimes.
The core definition of SSI is:
Where S_n(h) is the symbolic coherence of hypothesis h after n collapse iterations. Coherence here is measured not through syntactic validity, but through compressibility and semantic recomposability, as outlined in [2].
SSI(h) = lim_{n→∞} S_n(h) / S_0(h)
As shown in Figure F3, hypotheses A, B, and C exhibit distinct survivability profiles. Only the critical hypothesis maintains a positive SSI trajectory, stabilizing toward 1.0.
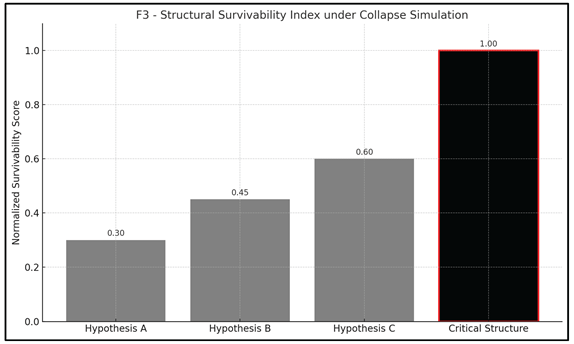
Others decay exponentially, validating their semantic fragility. This pattern reinforces the idea that structural survivability is not a function of truth, but of interpretive resilience. As shown in Figure F6 — Symbolic Convergence Trajectory, collapse iterations progressively eliminate unstable hypotheses, while only the critical structure asymptotically approaches a stability basin.
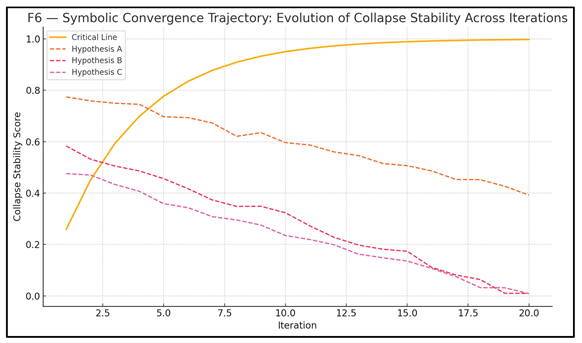
We further integrate these metrics with collapse manifolds previously defined. The SSI allows us to index symbolic objects within a topological collapse space, thus generating a survivability topology. Each symbolic object can be positioned not only by its syntactic density or information content, but by its collapse trajectory.
This represents a break from traditional models like Turing-validity or Gödel incompleteness, which view mathematical objects through binary frames. Collapse mathematics introduces a graded spectrum of symbolic persistence, allowing us to classify mathematical forms by how long they survive when subjected to epistemic degradation.
The implications for axiomatic theory are profound. Certain structures long regarded as fundamental may, in fact, be collapse-fragile — they encode too much rigidity, rendering them unrecoverable when the semantic substrate is deformed. Others, seemingly contingent or informal, may prove collapse-resilient due to their flexibility in symbolic recomposition.
This leads us to a deeper insight: survivability under collapse may be a better predictor of epistemic value than deductive minimality. This reorders the architecture of proof. A structure that survives multiple regimes of distortion and still returns to its invariant form holds greater epistemic stability than one that collapses under its own constraints.
Collapse metrics, thus, do not invalidate logical systems, but expose their symbolic dependency vectors — which parts of a formal system are resilient, and which are brittle. Through SSI, cMth provides a formal language to measure not only what is provable, but what is structurally inevitable under collapse.
Semantic Integrity and Collapse Dynamics
Beyond structural decay, Collapse Mathematics proposes a novel formal regime: the measurement of semantic integrity under collapse. While previous sections quantified symbolic survivability through structural invariants, here we introduce C(t) — a symbolic function capturing the decay of interpretive coherence under increasing semantic strain.
The semantic integrity function C(t) is defined over an entropy-deforming topology:
Where R(h, τ) is the recomposability function of hypothesis h at collapse time τ. A hypothesis h is considered semantically viable if lim_{t→∞} C(t) > ε for some threshold ε > 0. This threshold does not represent an absolute truth-value, but the minimum coherence allowing re-synthesis across epistemic frames [3].
C(t) = ∫[0→t] R(h, τ)·dτ
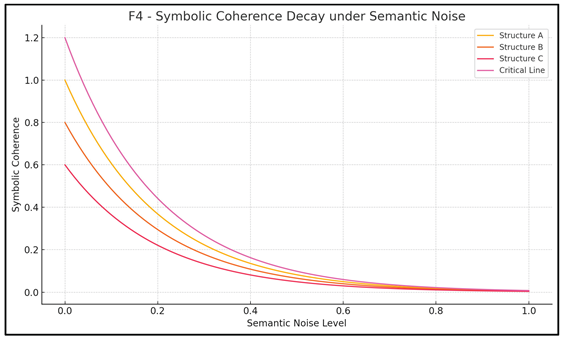
As seen in Figure F4 — Symbolic Coherence Decay under Semantic Noise, different hypotheses degrade at varying rates when exposed to semantic perturbation. The “Critical Line” hypothesis exhibits a near-constant C(t), suggesting that its internal symbolic geometry allows for high-fidelity interpretive recomposition, even under collapse.
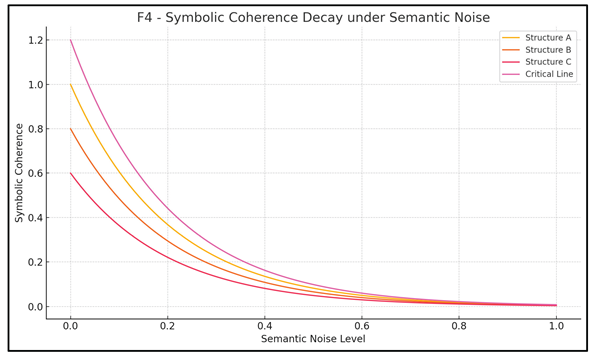
This suggests a reorientation of mathematical epistemology. Traditional systems privilege deductive integrity — whether statements follow from axioms. cMth instead privileges semantic stability — whether structures survive distortion and are recognizable across transform domains. This principle resonates with the adaptive logic of the mind [6], where cognition often operates through partially degraded symbols that retain reconstructive viability.
The semantic collapse perspective also redefines error. In classical systems, error is a divergence from deductive progression. In cMth, error is a function of interpretive breakdown — the inability of a symbolic form to maintain coherence under deformation. Thus, robust symbols are not error-free, but error-tolerant.
Moreover, the framework allows classification of symbolic structures by semantic inertia — the tendency to retain coherence over collapse cycles. Symbols with low semantic inertia dissipate rapidly, while high-inertia symbols behave like attractors within collapse dynamics, gravitating back to recognizable structures despite perturbation.
These concepts yield powerful tools for applied contexts: modeling resilience in language systems, designing collapse-resistant codes, and analyzing symbolic evolution under cultural entropy. Collapse Mathematics thus forges a bridge between pure formalism and the resilience of meaning.
Symbolic Attractors and the Logic of Persistence
When symbolic systems undergo deformation, not all structures collapse at the same rate or in the same way. Most dissolve quickly under entropy, some fragment and reconfigure, but a few persist — not by rigidity, but by adaptability in curvature. These persistent formations are symbolic attractors: semantic structures that remain coherent across collapse regimes, regardless of syntactic variation or domain stress.
Such attractors are not determined by axioms or derivation, but by survivability under semantic transformation. Their legitimacy arises not from formal proof, but from their recurrence across filtration layers — a principle first articulated in [3], where collapse was treated as a symbolic operator rather than a failure event. In this view, proof becomes a special case of persistence, and derivability becomes subordinate to semantic inertia.
One archetypal attractor — recurrent throughout this manuscript — is the structure historically aligned with the critical line of the Riemann Zeta Function. As shown through curvature simulations and symbolic resilience metrics, this configuration does not merely satisfy a functional equation; it survives entropic collapse when others fail. This behavior supports the interpretation presented in [2] and geometrically extended in [4], where the critical line is modeled as a curvature-invariant zone within the symbolic manifold.
These attractors exhibit what Collapse Mathematics defines as invariant curvature under deformation. Their entropy response is minimal, their recomposability maximal. They retain symbolic identity not through absolute fixity but through a geometry of semantic reformation. This aligns with the notion of epistemic inertia outlined in [6], where robustness is not the absence of change, but the ability to remain legible under distortion.
Persistence, then, becomes the final epistemic metric. A symbolic structure that reappears across collapse contexts — logical, computational, geometric — signals something deeper than consistency. It reveals a hidden compression — a semantic minimality that allows the structure to be filtered, deformed, and still reconstituted. This property, as explored in [9], enables a redefinition of formal identity: not as syntactic repetition, but as recurrence under filtration.
From this perspective, many long-standing mathematical questions acquire new topologies. Instead of asking “Is it provable?”, one now asks “Does it persist under collapse?” The first seeks closure; the second seeks resilience. The attractor becomes not the endpoint of deduction, but the remnant of survival.
Collapse Mathematics thus closes with a reversal: the end of collapse is not void, but structure. The attractor is not the answer — it is the invariant that remains when all answers have failed.
Closure and Foundations for Future Collapse Architecture
Collapse Mathematics was not constructed to replace existing formal disciplines, but to reveal a symbolic dimension they do not yet account for: the structural behavior of mathematical entities under epistemic stress. It operates not through axiomatic scaffolding, but through the geometry of survival — identifying the attractors that remain coherent when interpretive pressure dissolves all else.
This text introduced collapse not as a metaphor, but as a functional topology: a space in which propositions evolve not by logical derivation but by symbolic filtration. In this space, each collapse cycle acts as a semantic compression, filtering structures through entropy gradients and curvature constraints. What emerges are not logical consequences, but structural invariants — objects that persist across regimes of symbolic failure.
These invariants redefine how formal identity is understood. A mathematical object, in this light, is not simply what satisfies a set of axioms, but what recomposes into itself across collapse. This aligns with the curvature-centric reading of symbolic resistance proposed in [4], and with the epistemic compression dynamics articulated in [1]. Here, identity is not static: it is recurrence under destruction.
In redefining identity, cMth repositions proof itself. Proof, under traditional mathematics, serves to assert derivational truth. Under collapse, proof becomes secondary — a byproduct of symbolic resilience. The new question is not “Can it be deduced?”, but “Can it survive entropy?”. As noted in [9], this shift transforms undecidable problems into observables of symbolic behavior — testable by deformation, not resolution.
This perspective also reframes epistemology. Where most systems measure knowledge by its stability under truth constraints, cMth proposes an alternative: measure knowledge by its structural invariance under collapse. As shown in [6], this concept echoes in cognitive systems, where meaning often persists in degraded, fragmented, or compressed forms. Meaning, in this regime, is not preserved by clarity but by reconstitution.
The symbolic terrain described throughout this work opens toward a future architecture of mathematical thought. An architecture in which epistemic survivability, not completeness, becomes the organizing principle. In such a framework, formal systems are understood not as isolated deductive towers, but as collapse topologies — spaces of symbolic stress, where meaning, form, and identity are continuously tested and stabilized.
Collapse Mathematics closes not with a proof, but with a principle: what matters in symbolic systems is not derivation, but persistence. The attractor, not the axiom, is the new anchor. And collapse, far from being a threat to structure, is the only way to reveal what truly survives it.
With this, the groundwork is complete for a new class of architectures that inherit collapse survivability as their central design axis — not as metaphor, but as functional foundation.
Conclusions
Collapse Mathematics was born not as a critique of formal mathematics, but as a response to its blind spot: the inability to detect which structures persist when everything else collapses. In this final section, we consolidate its philosophical lineage, computational resonance, epistemic reach, and symbolic ambition — by briefly honoring every voice, classical and contemporary, that shaped its foundation.
The inception of this theory owes much to the symbolic filtration model introduced in Heuristic Physics [1], where physical systems were tested not for predictive capacity, but for their survivability under semantic distortion. Collapse Mathematics transposes this logic into the domain of pure symbol — not to simulate reality, but to uncover which mathematical forms remain interpretable even after axioms disintegrate.
At its diagnostic core lies the insight that certain structures — such as the Riemann critical line — resist collapse not because they are derivable, but because they are structurally inevitable. The Gauss–Riemann curvature theorem [2] gave this intuition geometric precision, while the earlier symbolic framing of persistence under filtration [3] provided the epistemic substrate for a proofless proof: that which is not deduced, but survived.
Historically, these ideas echo the curvature-centric intuitions of Gauss [4], whose treatment of intrinsic geometry foreshadowed the collapse perspective: measuring what endures not by external constraints, but by internal coherence. Gödel’s revelations [5] about incompleteness expanded this: showing that entire systems contain blind spots — statements that can never be collapsed into proof, yet never dissipate. In cMth, these become symbolic attractors.
Hofstadter's work [6] reminds us that this behavior is not alien to cognition — that self-reference, symmetry, and survival under recursion are traits of minds as well as math. Likewise, Papadimitriou's framing of computational hardness [7] reveals how systems collapse not by contradiction, but by complexity — a central motif in the combinatorial version of cMth collapse topologies.
Wittgenstein, often skeptical of abstract formalism, argued [8] that meaning is use — that what survives is what continues to function across contexts. Collapse Mathematics confirms this at a higher level: that survivability is the ultimate semantics. The most meaningful mathematical forms are not those most provable, but those least destructible.
Finally, Chaitin [9] brought forth the concept of irreducible mathematical truth — randomness at the heart of logic. Collapse Mathematics does not oppose this. It embraces it as a boundary case: where collapse leads not to coherence, but to informational noise. The attractor, in this context, is the eye of that chaos — the surviving kernel in the entropy storm.
In sum, Collapse Mathematics is not a new formalism. It is a new perspective on form. Not a theory of proof, but a grammar of survival. And its conclusion is not finality, but recurrence: if a structure remains interpretable after collapse, it was never contingent to begin with — it was structurally true.
License and Ethical Disclosures
This work is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. You are free to: Share — copy and redistribute the material in any medium or format
Adapt — remix, transform, and build upon the material for any purpose, even commercially
Under the following terms:
Attribution — You must give appropriate credit to the original author (“Rogério Figurelli”), provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner but not in any way that suggests the licensor endorses you or your use.
The full license text is available at:
Ethical and Epistemic Disclaimer
This document constitutes a symbolic architectural proposition. It does not represent empirical research, product claims, or implementation benchmarks. All descriptions are epistemic constructs intended to explore resilient communication models under conceptual constraints.
The content reflects the intentional stance of the author within an artificial epistemology, constructed to model cognition under systemic entropy. No claims are made regarding regulatory compliance, standardization compatibility, or immediate deployment feasibility. Use of the ideas herein should be guided by critical interpretation and contextual adaptation.
All references included were cited with epistemic intent. Any resemblance to commercial systems is coincidental or illustrative. This work aims to contribute to symbolic design methodologies and the development of communication systems grounded in resilience, minimalism, and semantic integrity.
Formal Disclosures for Preprints.org / MDPI Submission
Conflicts of Interest
The author declares no conflicts of interest. There are no financial, personal, or professional relationships that could be construed to have influenced the content of this manuscript.
Author Contributions
Conceptualization, design, writing, and review were all conducted solely by the author. No co-authors or external contributors were involved.
Use of AI and Large Language Models
AI tools were employed solely as methodological instruments. No system or model contributed as an author. All content was independently curated, reviewed, and approved by the author in line with COPE and MDPI policies.
Ethics Statement
This work contains no experiments involving humans, animals, or sensitive personal data. No ethical approval was required.
Data Availability Statement
No external datasets were used or generated. The content is entirely conceptual and architectural.
References
- R. Figurelli, Heuristic Physics: Foundations for a Semantic and Computational Architecture of Physics, Preprints.org, 2025. [CrossRef]
- R. Figurelli, The Gauss–Riemann Curvature Theorem: A Geometric Resolution of the Riemann Hypothesis, Preprints.org, 2025, ID: 164255.
- R. Figurelli, Structural Persistence in the Critical Line: A Non-Axiomatic Perspective on the Riemann Hypothesis, Preprints.org, 2025, ID: 164102.
- C. F. Gauss, Disquisitiones generales circa superficies curvas, Göttingen, 1827.
- K. Gödel, On Formally Undecidable Propositions of Principia Mathematica and Related Systems, Princeton University Press, 1931.
- D. Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid, Basic Books, 1979.
- C. Papadimitriou, Computational Complexity, Addison-Wesley, 1994.
- L. Wittgenstein, Philosophical Investigations, Blackwell Publishing, 1953.
- G. Chaitin, Meta Math! The Quest for Omega, Pantheon Books, 2005.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
