A Review of Population Count Algorithms in Binary Sequence: Through a Software Perspective

1. Introduction

The rapid increase in computation devices following their architectural progression has witnessed the need for counting the number of Bit’s High(that is 1) in a binary sequence. Initial discussions in early 1960’s [1] revealed it’s significance in varying fields of Computational Science and Mathematics like those in cryptography, database management, statistical machine learning. The following table reveals the various common terminologies associated with population count in binary sequence.

Table 1. Contextual Description useful in terms related to the population count.

S. No	Synonym	Contextual Description
1	Bit Count	Generic term for counting bits, often implies counting 1s
2	Population Count	Most widely used term in software/hardware literature
3	Hamming Weight	Term used in information theory and coding
4	1’s Count	Number of 1s in the binary sequence
5	Set Bit Count	Bits that are 1
6	Bitwise Weight	Usud in Hardware Literatures , specially related to FPGA

Table 1. Contextual Description useful in terms related to the population count.

S. No	Synonym	Contextual Description
1	Bit Count	Generic term for counting bits, often implies counting 1s
2	Population Count	Most widely used term in software/hardware literature
3	Hamming Weight	Term used in information theory and coding
4	1’s Count	Number of 1s in the binary sequence
5	Set Bit Count	Bits that are 1
6	Bitwise Weight	Usud in Hardware Literatures , specially related to FPGA

Authors specifically E. El-Qawasmeh and Marilyn Mack have contributed significantly in this domain, with their papers having the following titles :

- Papers by Marilyn Mack :

(a) A bit-counting algorithm using the frequency division principle [2]

- Papers by E. El Qawasmeh :

(a) Beating the Popcount [3]

- While both the researchers that is Marilyn Mack and E. El Qawasmeh contributed the following works together:

(a) Increasing the Efficiency of Bit-Counting [4]

(b) Organization of near matching in bit attribute matrix applied to associative access methods in information retrieval. [5]

On comparing with Hardware perspective papers of Daniel Lemire, titled the following (a) introduces Advancement recent in this field for Faster Positional-Population Counts for AVX2, AVX-512, and ASIMD. [6]

(b) Faster Population Counts Using AVX2 Instructions [7]

These emphasizes a lot over the technicality and need to compute mathematically the Population-Count of given Binary Sequence.

2. Case Study

Algorithm 1 Population count using Naive Bitwise Count

def popcount_naive(NUM : int) -> int:            COUNT = 0            while NUM:                        COUNT += NUM & 1                        NUM = NUM >> 1            return COUNT

Algorithm 2 Population count using Brian Kernighan’s Algorithm

def popcount_b_kerninghan(NUM : int) -> int:            COUNT = 0            while NUM:                        NUM = NUM & (NUM - 1)                        COUNT += 1            return COUNT

Algorithm 3 Population count using Lookup Table

bit_Table_256 = [0] * 256 for bit_i in range(256):            bit_Table_256[bit_i] = (bit_i & 1) + bit_Table_256[bit_i >> 1]     def popcount_LookupTable(NUM : int) -> int :             return bit_Table_256[ NUM & 0xff ]        + bit_Table_256[ (NUM >> 8) & 0xff ] +                     bit_Table_256[ (NUM >> 16) & 0xff ] + bit_Table_256[ (NUM >> 24) & 0xff ]

Algorithm 4 Population count using CSA - Carry Save Adder|

from typing import List      def csa(a: int, b: int, c: int) -> (int, int):             total = a ⌃b ⌃c            carry = (a & b) | (b & c) | (a & c)            return carry,total def popcount(x: int) -> int:            x = x - ((x >> 1) & 0x5555555555555555)            x = (x & 0x3333333333333333) + ((x >> 2) & 0x3333333333333333)            x = (x + (x >> 4)) & 0x0F0F0F0F0F0F0F0F            x = x + (x >> 8)            x = x + (x >> 16)            x = x + (x >> 32)            return x & 0x7F    def popcount_csa(data: List[int]) -> int:            ones = twos = fours = eights = 0            i = 0            n = len(data)            while i + 7 < n:                        t1, o1 = csa(data[i], data[i+1], data[i+2])                        t2, o2 = csa(data[i+3], data[i+4], data[i+5])                        f1, t3 = csa(t1, t2, data[i+6])                        f2, ones = csa(o1, o2, data[i+7])                        fours, twos = csa(f1, f2, twos)                        eights, fours = csa(eights, fours, 0)                        i += 8            TOTAL = (                        8 * popcount(eights) +                        4 * popcount(fours) +                        2 * popcount(twos) +                        1 * popcount(ones) )            while i < n:                        TOTAL += popcount(data[i])                        i += 1            return TOTAL

Algorithm 5 Population count using VTPC method

def popcount_VTPC(n : int) -> int :            mask_size = 4            mask = [0,1,1,2]            m = 0            i = 0            $d=\lceil logmask\_size\left(n\right)\rceil$            e = mask_size            r = n            while d ≥ 0 :                        $i=\lfloor (r/e)\times mask\_size\rfloor$                          $r=r-({\displaystyle \frac{e}{mask\_size}}\times i)$   $e={\displaystyle \frac{e}{mas{k}_{s}ize}}$                          $m=m+mask\left[i\right]$                         $d=d-1$            return m

Algorithm 6 Population count using Divide and Conquer adder

def popcount_divconq(NUM : int) -> int :            NUM = (NUM & 0x55555555) + ((NUM >> 1) & 0x55555555)            NUM = (NUM & 0x33333333) + ((NUM >> 2) & 0x33333333)            NUM = (NUM + (NUM >> 4)) & 0x0F0F0F0F            NUM = (NUM * 0x01010101) >> 24            return NUM

Algorithm 7 Population count using RF method

def countRF(N):                TEMP = N                COIN = 2                prev = 1            COUNTER = 0            while TEMP :                       ss = (N+1)//COIN                       v1 = (N+1)%COIN                       if v1 <= prev:                                  REM = 0                       else:                                  REM = (N+1)%prev                       COUNTER += REM + ss*prev                       prev = prev<<1                       COIN = COIN<<1                       TEMP = TEMP >> 1            return COUNTER def RF(N):                return countRF(N) - countRF(N-1)

3. Complexity Comparison

Under this section we discuss and show the complexity analysis of various algorithms, by taking LOG₁₀ OF (N) : Input number, as this value ranges from [1,1000000], it;s imperative to transform it into a scale that’s quite implementable on the graph of Time to compute vs Input Size. He nce we applied the following transformations :

Table 2. The transformation analysis of plotting functions over the graph from old v/s new perspective ,where N : number till we checked Natural numbers for the several algorithms, the results T : Time taken to compute these results (ms).

S.No	Old parameter	Transformed parameter
1	N	Log10 N
2	T	Ln T

Table 2. The transformation analysis of plotting functions over the graph from old v/s new perspective ,where N : number till we checked Natural numbers for the several algorithms, the results T : Time taken to compute these results (ms).

S.No	Old parameter	Transformed parameter
1	N	Log10 N
2	T	Ln T

Table 3. An outline in comparison of several software algorithmic implementations of techniques in computing the population count for binary sequences, where M : Number of bits used to implement the input Number. N : Input Number. L : Number of elements in addressing each element of Lookup Table. S : Size of Mask Vector.

S. No	Method	Average Time	Space
		Complexity	Complexity
1	Naive Approach	O(M)	O(1)
2	Brian Kerninghan	O(${\log }_2$ (N))	O(1)
3	Lookup Table	O(M / L)	O(256)
4	CSA	O(${\log }_2$ (M))	O(M)
5	VTPC	O(${\log }_S$ (N))	O(S)
6	Divide and Conquer	O(${\log }_2$ (M))	O(1)
7	RF Algorithm	O(log2 N)	O(1)

Table 3. An outline in comparison of several software algorithmic implementations of techniques in computing the population count for binary sequences, where M : Number of bits used to implement the input Number. N : Input Number. L : Number of elements in addressing each element of Lookup Table. S : Size of Mask Vector.

S. No	Method	Average Time	Space
		Complexity	Complexity
1	Naive Approach	O(M)	O(1)
2	Brian Kerninghan	O(${\log }_2$ (N))	O(1)
3	Lookup Table	O(M / L)	O(256)
4	CSA	O(${\log }_2$ (M))	O(M)
5	VTPC	O(${\log }_S$ (N))	O(S)
6	Divide and Conquer	O(${\log }_2$ (M))	O(1)
7	RF Algorithm	O(log2 N)	O(1)

Figure 1. The plot of natural LOG T : Time taken against LOG₁₀ (NUMBER) of Natural Numbers till count of population count is taken.

Figure 1. The plot of natural LOG T : Time taken against LOG₁₀ (NUMBER) of Natural Numbers till count of population count is taken.

Table 4. Time Taken to Compute Bit’s population count till given Number - N by various Algorithms, with time taken to compute is in milli seconds (ms).

N	log10N	NAIVE		KERNINGHAN		LOOKUP		CSA		RF
		T	Ln T	T	Ln T	T	Ln T	T	Ln T	T	Ln T
1	0	0.009	-4.711	0.009	-4.711	0.008	-4.828	0.016	-4.135	0.01	-4.605
10	1	0.011	-4.51	0.009	-4.711	0.01	-4.605	0.037	-3.297	0.029	-3.54
100	2	0.084	-2.477	0.051	-2.976	0.07	-2.659	0.409	-0.894	0.426	-0.853
103	3	1.206	0.187	0.776	-0.254	0.389	-0.944	3.403	1.225	5.509	1.706
104	4	15.816	2.761	12.887	2.556	4.616	1.53	22.309	3.105	62.769	4.139
105	5	227.941	5.429	130.344	4.87	29.188	3.374	228.655	5.432	886.574	6.787
106	6	1823.992	7.509	1858.631	7.528	281.325	5.64	3518.617	8.166	12526.57	9.436

Table 4. Time Taken to Compute Bit’s population count till given Number - N by various Algorithms, with time taken to compute is in milli seconds (ms).

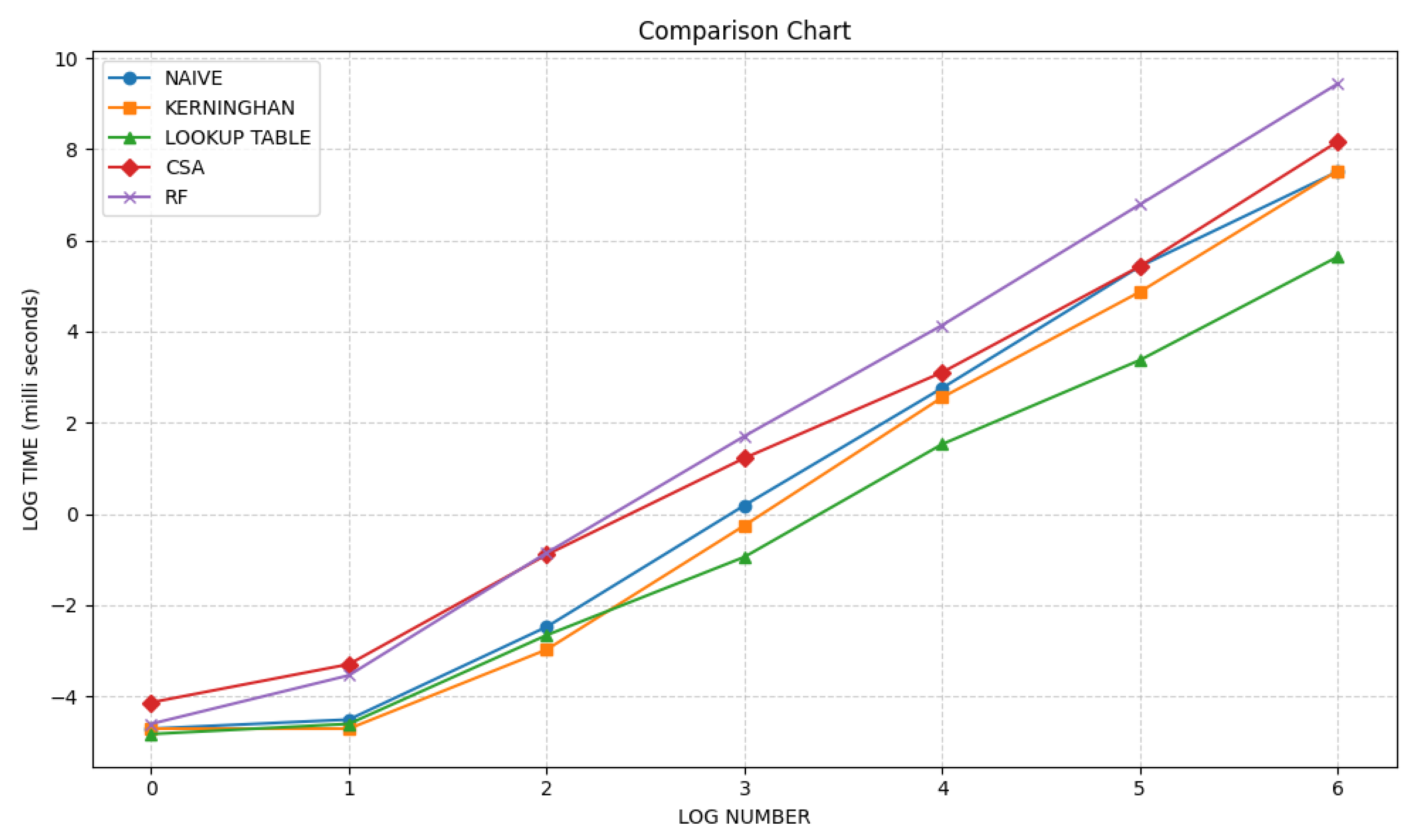
N	log10N	NAIVE		KERNINGHAN		LOOKUP		CSA		RF
		T	Ln T	T	Ln T	T	Ln T	T	Ln T	T	Ln T
1	0	0.009	-4.711	0.009	-4.711	0.008	-4.828	0.016	-4.135	0.01	-4.605
10	1	0.011	-4.51	0.009	-4.711	0.01	-4.605	0.037	-3.297	0.029	-3.54
100	2	0.084	-2.477	0.051	-2.976	0.07	-2.659	0.409	-0.894	0.426	-0.853
103	3	1.206	0.187	0.776	-0.254	0.389	-0.944	3.403	1.225	5.509	1.706
104	4	15.816	2.761	12.887	2.556	4.616	1.53	22.309	3.105	62.769	4.139
105	5	227.941	5.429	130.344	4.87	29.188	3.374	228.655	5.432	886.574	6.787
106	6	1823.992	7.509	1858.631	7.528	281.325	5.64	3518.617	8.166	12526.57	9.436

4. Conclusions

Through the current work, we presented multiple software-oriented algorithms that are pivotal in computing the population count of ones in a binary sequence. The results were developed as a result of and are dependent upon the programming language , compiler/interpreter version, also the server’s memory and priority pooling allocation for the google colab notebook , that was used to run and implement these algorithms.