In this section eight cases where division by zero frequently appears is considered. how the semi-structured complex framework is used to provide a logical, consistent interpretation of division by zero across these eight cases are demonstrated.
3.1. Applications in Classical Mechanics
Case 1: The period of a simple pendulum in the absence of gravity
An experiment conducted by Chinese astronaut Wang Yaping in 2013 during a space lecture on board the Shenzou-10 space mission demonstrated that when a pendulum was released in near zero gravity conditions on a space station orbiting earth the pendulum did not swing. This experiment is significant because it shows that without gravity the pendulum has no period. Note that the period of the simple pendulum cannot be 0 since this would imply that the pendulum swings instantaneously which is not what the experiment shows. The question that arises: “how do you represent this state in the equation of the period of a simple pendulum?”
Consider Equation (8), the equation for the period of a simple pendulum.
where
period of the pendulum;
Length of the pendulum
acceleration due to gravity
Suppose
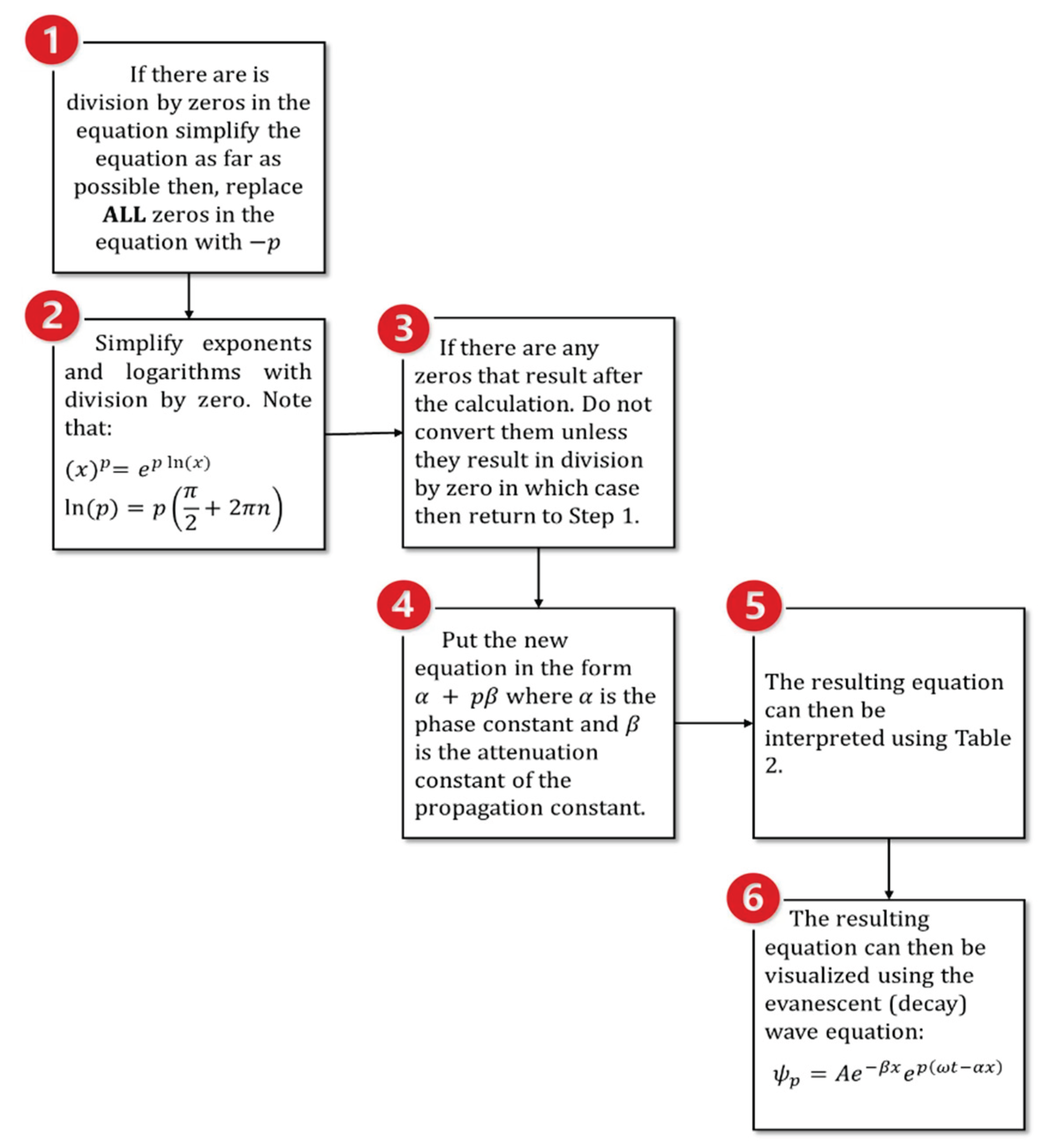
and this value is placed in Equation (8), then by conventional mathematics, the result would be undefined. However, with the application of the semi-structured complex framework, this can easily be resolved in a manner that agrees with experimental results. This is done as follows:
Using the semi-structured complex framework in
Figure 7, Replacing
with p (The semi-structured complex unit. This can be seen in result 2 of
Table 3). The new equation becomes:
Replacing with in the equation implies that the period of the simple pendulum is now being viewed from the perspective of semi-structured complex state space; that is, represents an interpretation of the state of the simple pendulum. The period of the pendulum is now a propagation constant. Since the can have two possible values then the period only has a value with the value having two distinct roots. Note here that length and the square root of length are usually positive, however since we are in semi-structured complex state space both positive and negative values for are accepted.
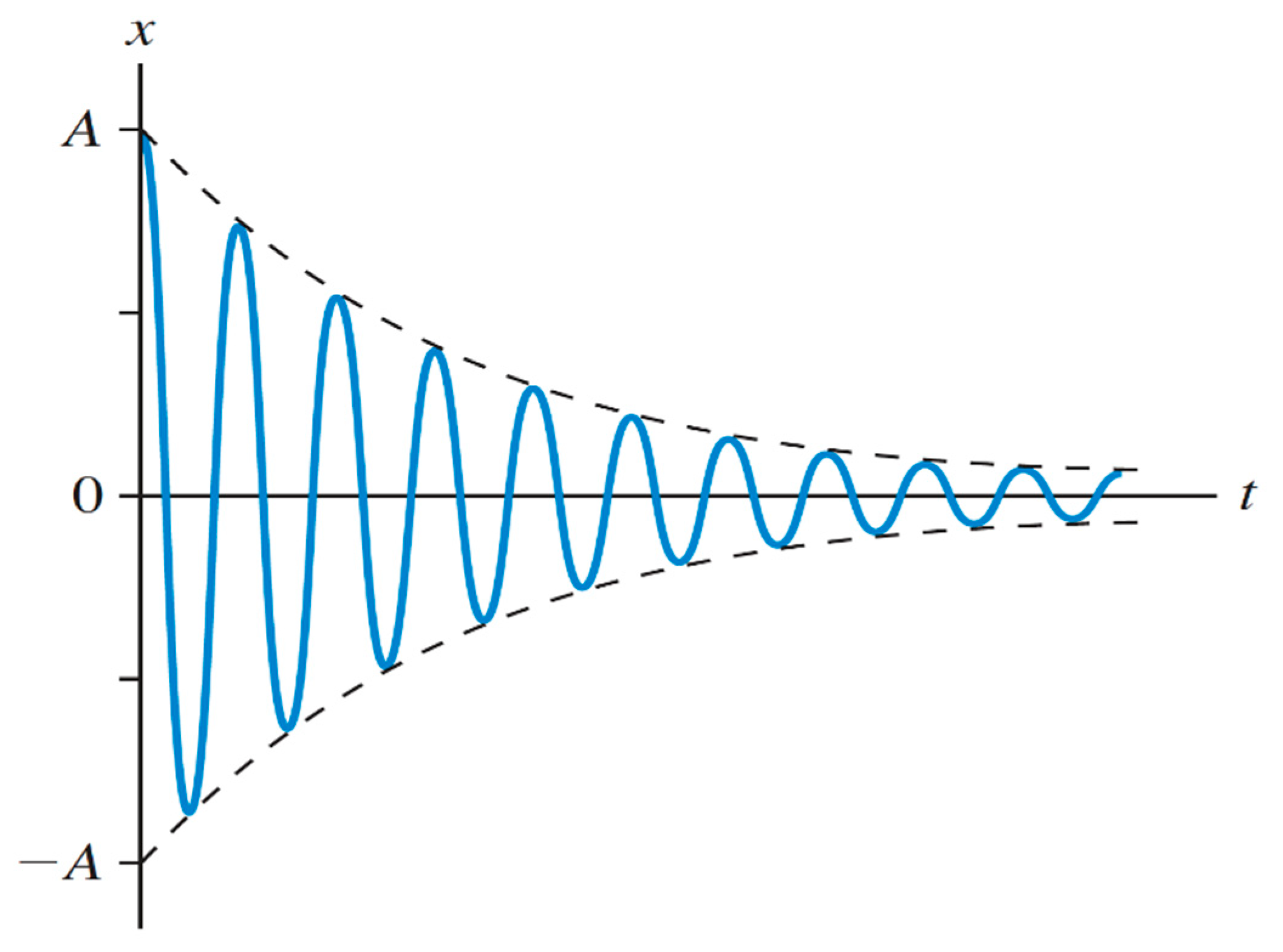
Therefore according to
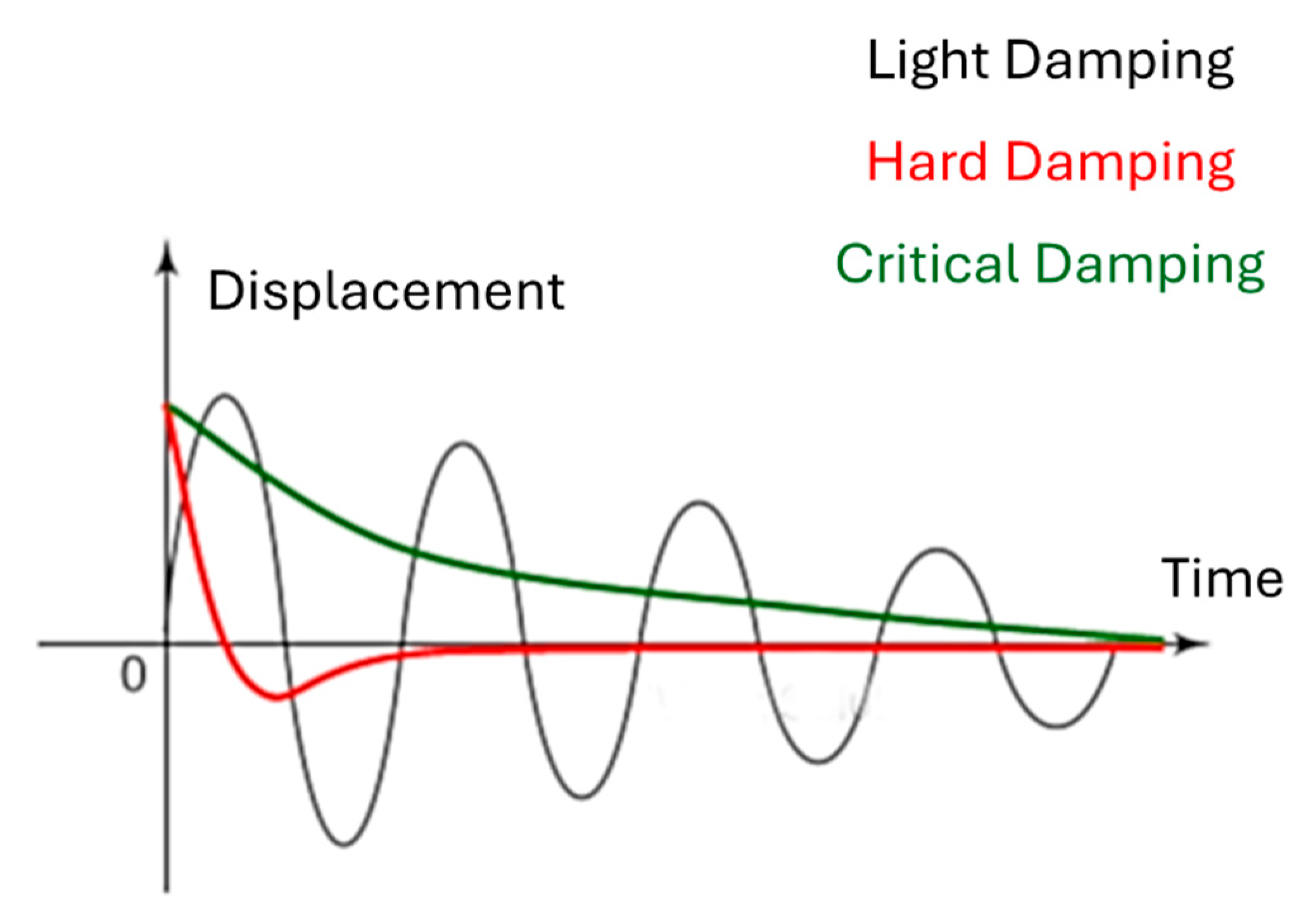
Table 2, this propagation constant implies that the period of the pendulum in the absence of gravity is over dampened. This implies that the pendulum does not swing. This agrees with experimental evidence from the Shenzou-10 space mission. This result also implies that the framework is good in producing correct experimental results in at least this case. More cases from classical mechanics need to be considered to determine the utility of the semi-structured complex framework.
Case 2: Resolving singularities in Friedmann’s cosmological equations:
In the Friedmann equations that describe the expansion of the universe in general relativity, the scale factor
a(
t) is a function of time that tells us how "big" the universe is (or how fast the universe is expanding at a given moment in cosmic time t). One simplified form of the Hubble parameter is shown in Equation (10)
Where
the Hubble parameter at time t representing the rate of expansion.
the time derivative of the scale factor representing how fast it's changing.
the scale factor of the universe describing how distances in the universe change over time.
According to conventional physics, at the Big Bang (at ), . In many models this results in the Hubble constant becoming undefined or as some would put it . This suggest that at the Big Bang (because of many of the cosmology equations result in division by zero): (1) the density and temperature become infinite; (2) the curvature of spacetime diverges; and, (3) time itself becomes undefined. This point is called a singularity, a place where the laws of physics break down due to division by zero in the equations. This does not give any predicable results from which to draw conclusions.
Nevertheless, this issue can be resolved using the semi-structured complex framework proposed in this paper. To do this, consider a radiation-dominated universe, where the scale factor behaves like:
This implies the following:
When t = 0, we apply the steps shown in
Figure 7 (Replacing
with p (The semi-structured complex unit)
The new equation becomes:
This value measures how quickly the universe is expanding per unit distance at the time of the Big Bang (that is at ).
Result (10) is a propagation constant with
and
(a repeated root). According to
Table 2, this propagation constant implies that at the time of the Big Bang the Hubble parameter was critically dampened. This means that the Hubble parameter did not vary or oscillate but decayed very quickly to a single equilibrium value. This also has implications for other parameters that depend on
For example: (1) the age of the universe and (2) distances and redshifts.
The age of the universe is approximated by Equation (11).
Result (10) can be placed in Equation (11) to yield:
Result 14 is still in semi-structured complex state space. It is possible to convert it back to physical space. Note that
according to
Table 3 in Appendix 1. Hence the age of the universe at the point of the Big Bang (that is at time
) is given by Result (15).
Result (15) makes absolute sense because at time the universe does not have an age. Result (15) simply illustrates that the semi-structured complex framework can yield logical consistent results.
In terms of distances and redshifts, the Hubble parameter relates how far away a galaxy is (distance) to how fast it's receding (redshift), via Hubble's Law given in Equation (16).
Result (10) can be placed in Equation (16) to yield:
Result (17) is a propagation constant with
and
(a repeated root). According to
Table 2, this propagation constant implies that at the time of the Big Bang the velocity of receding galaxies
was critically dampened. This means that the velocity did not vary or oscillate but decayed very quickly to a single equilibrium value.
The results in this case implies that the semi-structured complex framework is capable of handling singularities and infinities that may arise in physics equations in a manner that is logical and consistent. This point towards that idea that physics is no longer limited and does not break down in division by zero cases.
Case 3: Newtons law of Gravitation where r = 0
The proposed framework can also be used to interpret Newton’s Law of gravitation (shown in Equation (18)) at
.
Where
Universal Gravitational Constant
mass of body 1 and mass of body 2 respectively
The resultant gravitational force between body 1 and body 2
distance between centre of mass of body 1 and body 2
When
, Equation (18) evaluates to Result (19).
Result (19) is a propagation constant with
and
(a repeated root). According to
Table 2, this propagation constant implies that when the distance between the centre of masses of two objects is zero, the resultant gravitational force between the two objects is critically dampened. This means that the gravitational force did not vary or oscillate in value but decayed very quickly to a single equilibrium value. For example, an object placed at the centre of the earth will experience no resultant force and hence will remain stationary. This is a verifiable result.
Case 4: Curvature at the centre of a non-rotating black whole.
The advantage of being able to resolve singularities in such equations is that one can confidentially resolve singularities (resulting from division by zero) in equations where experimental data is difficult or impossible to obtain. For example, consider the equation of a non-rotating blackhole shown in Equation (20).
Universal Gravitational Constant
Interval between two events
distance from the centre of the blackhole
angular interval
Now according to classical physics the metric exhibits a singularity at the centre of the black hole (), indicating infinite spacetime curvature. However this is not a good interpretation of the situation (infinity is not a quantity and having an infinite curvature does not fit well with the infinite energy associated with spacetime).
Nevertheless, using the semi-structured complex framework a better interpretation of this situation can be obtained. When
, Equation (20) evaluates to Result (21).
then:
Grouping all real and semi-structured terms together gives:
Result (21) is a propagator with and . Result (21) is an interesting situation as it implies that the center of a black hole does not universally settle onto a single state, but rather whether the center is curved or flat depends on the values that and take on. For example if and then the center of a non-rotating black hole would not be flat but would be curved with the value of curvature oscillating. However, if and then this implies that the center of the non-rotating black hole would eventually decay to some flat value.
Case 5: Evaluating the rate constant of a chemical reaction at absolute zero
The rate constant for a chemical reaction (
) measures how quickly a chemical reaction occurs at a given temperature and under certain conditions. The value of K is given by the Arrhenius Equation shown in Equation
Where
the rate constant for a chemical reaction
the pre-exponential factor (frequency of collisions)
the activation energy
the universal gas constant
temperature (in Kelvin) at which the reaction occurs
Suppose it's needed to determine the rate of reaction at
(absolute zero). This yields the following result:
When
, we apply the steps shown in
Figure 7. Hence converting
:
Where and .
Result (29) is a propagation constant. Its value implies that the sort of dampening that occurs at absolute 0 depends on the activation energy . For example, if the activation energy is 0 then the equation becomes . This implies that at the reaction it is not dampened but would proceed to some constant rate. If on the other hand , then . This in turn implies that . This would imply that is critically dampened and the rate of reaction would decrease to zero without oscillating in value. Any other value for the activation energy at would imply that the reaction is expected to be under-dampened decreasing in an oscillatory manner to zero value.
3.2. Application of Framework in Quantum Mechanics
Case 6: A Novel Hamiltonian operator for Evanescent Energy transitions
To show how the semi-structured complex framework can be applied to quantum mechanics, it is necessary to first formalize the semi-structured complex numbers algebra in the realm of quantum mechanics and then show how the proposed framework can be used in this setting. This formalizing involves defining the algebra that will be used in the quantum mechanical setting, defining the norm and inner product produced by this algebra and then defining a -Hilbert space, where is the unstructured unit. All of this is done in Appendix 3.
Suppose there is a Hamiltonian matrix,
, whose matrix elements represents the probability amplitude of transitioning from one quantum state to another under some quantum dynamical process. Also consider that the transition probability amplitude takes the form of an evanescent wave (that is, takes the form of
). The question now stands: “what is the wave function of these two quantum states?”. To To answer this question we define the two state quantum system as follows:
Suppose each state can evanescent (decay) into another and the Hamiltonian matrix are defined as:
The off diagonal elements are transition amplitudes. These transition amplitudes are written with semi-structured complex numbers implying that they are evanescence amplitudes. Assuming that these two quantum states follow the time evolution of the Schrödinger Equation and is still governed by the expression in Equation (26),
the Schrodinger Equation now becomes:
Solving this will involve handling the real, imaginary, and unstructured terms explicitly. The solution to Equation (27) is give in Result (35). The working to arrive at Result (35) is given in Appendix 3.
Where
, Time varying variables.
In Result (35),
where
are constants.
Clearly from Result (35), and are semi-structured complex wave functions. These waves have a complex phase part (the first two terms of the wave function) and an unstructured part (the last term of the wave function). This will enable the tracking of component, potentially modelling "singular" parts of the wavefunction that correspond to infinite energy, vacuum bubbles, or divergent regions.
Case 7: Characterizing Novel Schrödinger Equation for Evanescent waves
Rather than just defining a new Hamiltonian matrix, an extra step can be taken to define a whole new Schrödinger equation for quantum systems that exhibit divergent behavior. Using the characteristic equation Equation (6), a new Schrodinger equation can be developed to find the wave function of quantum system that may contain singularities and infinities. The new time-dependent Schrodinger equation is given in Equation (30).
The derivation of this equation is given in Appendix 4. is the wave function that defines some quantum state that contains a singularity or Infinity. Equation (30) is different from Equation (26) in that it does not assume that the resulting wave has an imaginary part.
An example of how this equation is used is given below:
Consider the time-independent Schrödinger equation in one dimension for a particle of mass m in the potential:
with
, and
. This potential has a singularity at
. The aim is to find the behaviour of solutions at the singularity and discuss under what conditions bound states exist.
Step 1: Schrödinger Equation
Let
and
. This gives:
Step 2: Let us assume a solution
, where s is time value semi-structured value. This means that:
Substitute into the equation:
Let
. Hence A is a semi-structured complex number so that:
Solving the quadratic equation gives:
Hence the wave function becomes:
These wave functions are evanescent wave functions that is capable of providing interpretable results at .
From the example, the singularity that arises for the potential at is structurally dealt with in a manner that would enable proper interpretation of the wave equation at the point of singularity. The final result is an interpretable evanescent wave with a real and unstructured part. Therefore we know that the wave function decays at the point of singularity. Note that the type of decay would depend on the values of and in the equation for .
3.3. Application of Framework in Quantum Field Theory
Case 8: Understanding semi-structured Complex Evanescent Probabilities
In quantum field theory singularities usually arise in Feynman diagrams where regularization and renormalization have to be used to resolve these. Whilst these techniques do provide some solutions these methods are sometimes seen as ad hoc. Nevertheless the semi-structured complex framework can be used to resolve these singularities in a manner that is structured, logical and consistent.
Feynman diagrams are used to calculate the probabilities for relativistic scattering processes. To do so the Lorentz-invariant scattering amplitude needs to be calculated. is the probability scattering amplitude which represents moving from an initial state containing some particles with well-defined momenta to a final state containing (often different) particles also with well-defined momenta.
Consider the one-loop scattering diagram shown in
Figure 8. Each line or loop represents the momentum of a particle. Read from left to right, two particles intersect (two line meet at the first vertex with each line representing the momentum of the particles) and scatter to produce two new particles on the right (represented by two lines that diverge on the right). Each line and vertex in the diagram is given a special name and has associated with it a special equation. The rules for interpreting Feynman diagrams and converting them into equations that can be used to calculate the scattering amplitude of the diagram is given in reference For the above diagram, the scattering amplitude is given as:
Where:
Scattering transition amplitude. This represents the probability amplitude for a quantum particle (like an electron or a photon) to scatter from an initial state i to a final state f. It’s the core quantity calculated from the Feynman diagram using the Feynman rules of a given quantum field theory; Momenta () of incoming particles (1 and 2 respectively) and Momenta () of outgoing particles (3 and 4 respectively). These typically represent the 4-momenta (energy + 3-momentum) of the particles involved in the interaction; Coupling constant. This often denotes the interaction strength in the theory. For example in QED (Quantum Electrodynamics), (the electric charge) and in QCD (Quantum Chromodynamics) g is the strong coupling constant, Typically speed of light, often set to 1 in natural units, Rest masses of the particles involved.
The integral in Equation (31) it's not easy to calculate. Ordinarily this integral would be considered infinite and regularization and renormalization techniques would be required to solve it. However with the semi-structured complex framework developed in this paper the solution is not infinite. The usual first step is to write the four dimensional volume element as:
(where
is the angular part). At large
the integrand is essentially had the form
, the so the
integral has the form:
Where
Solving Equation (33) using the semi-structured complex framework developed in this paper gives:
Let
and
. This implies
According to the results from
Table 3 (
Appendix 1):
and
Where
and
are integer values. Hence:
This final result represents the probability associate with the scattering diagram shown in
Figure 8. At first glance this probability appears strange because it suggests that you have an evanescent wave that is also complex. However this can easily be resolved. Usually the coupling constant that is used in the interpretation of the filament diagram involves an imaginary unit
. However, if we redefine the coupling constant and replace
with
(since the powers of
and
behave the same algebraically), then the meaning of the equation becomes much more clear. The equation becomes:
All that is left at this point is to choose an appropriate value of N that would agree with experimental results.
Equation (41) suggests that the final form of the scattering amplitude depends on the value of . First it can clearly be seen that no decay occurs irrespective of the value of . It is also clear from the form of the scattering amplitude that the value goes to a constant value.
The above example shows how easy it is to use semi-structured complex framework to calculate the scattering amplitude associated with Feynman diagram. There is no need for regularization or renormalization. Moreover the algebraic nature of the solution makes it logical consistent and treats infinity in a very structured manner.
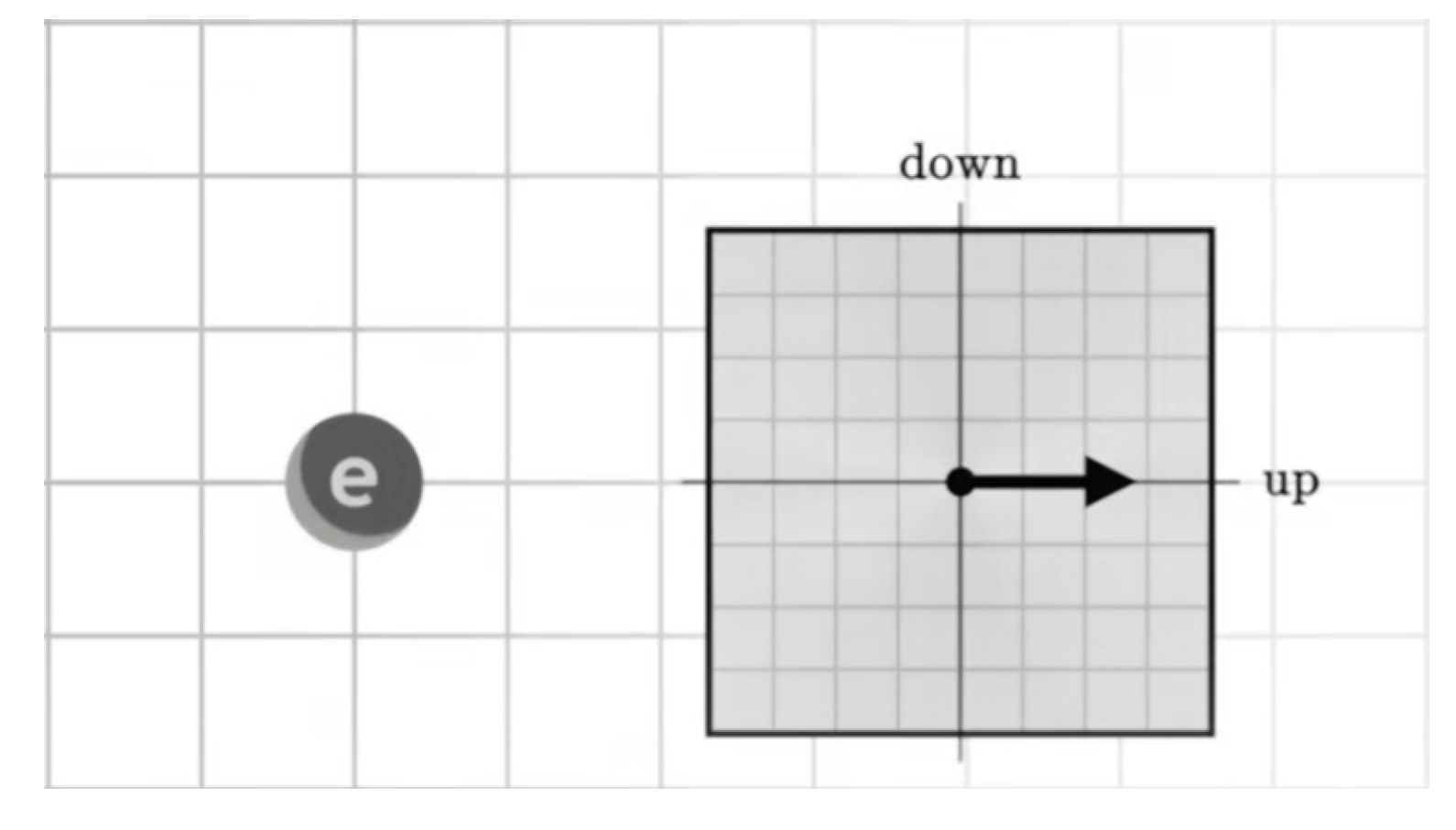
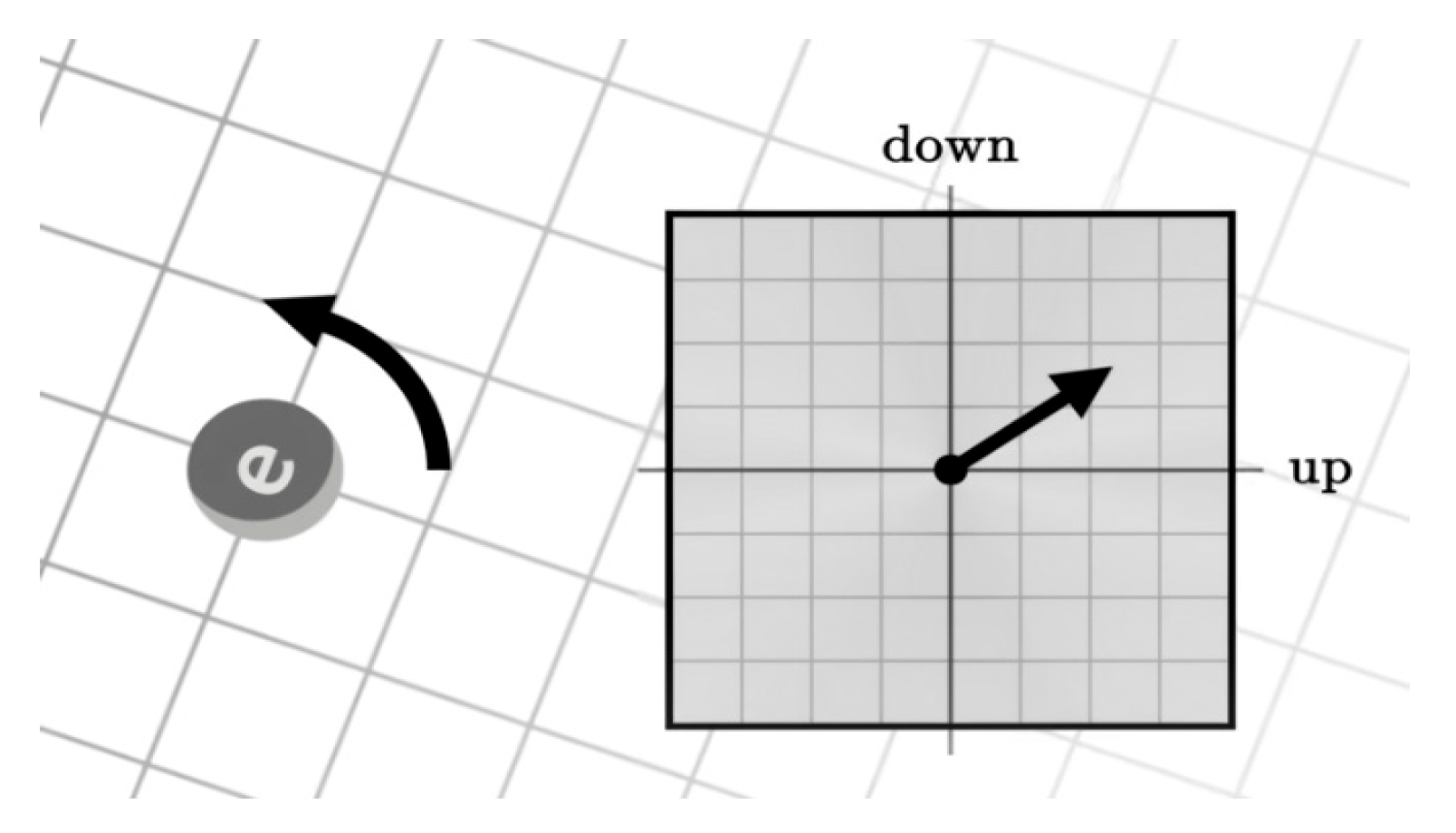
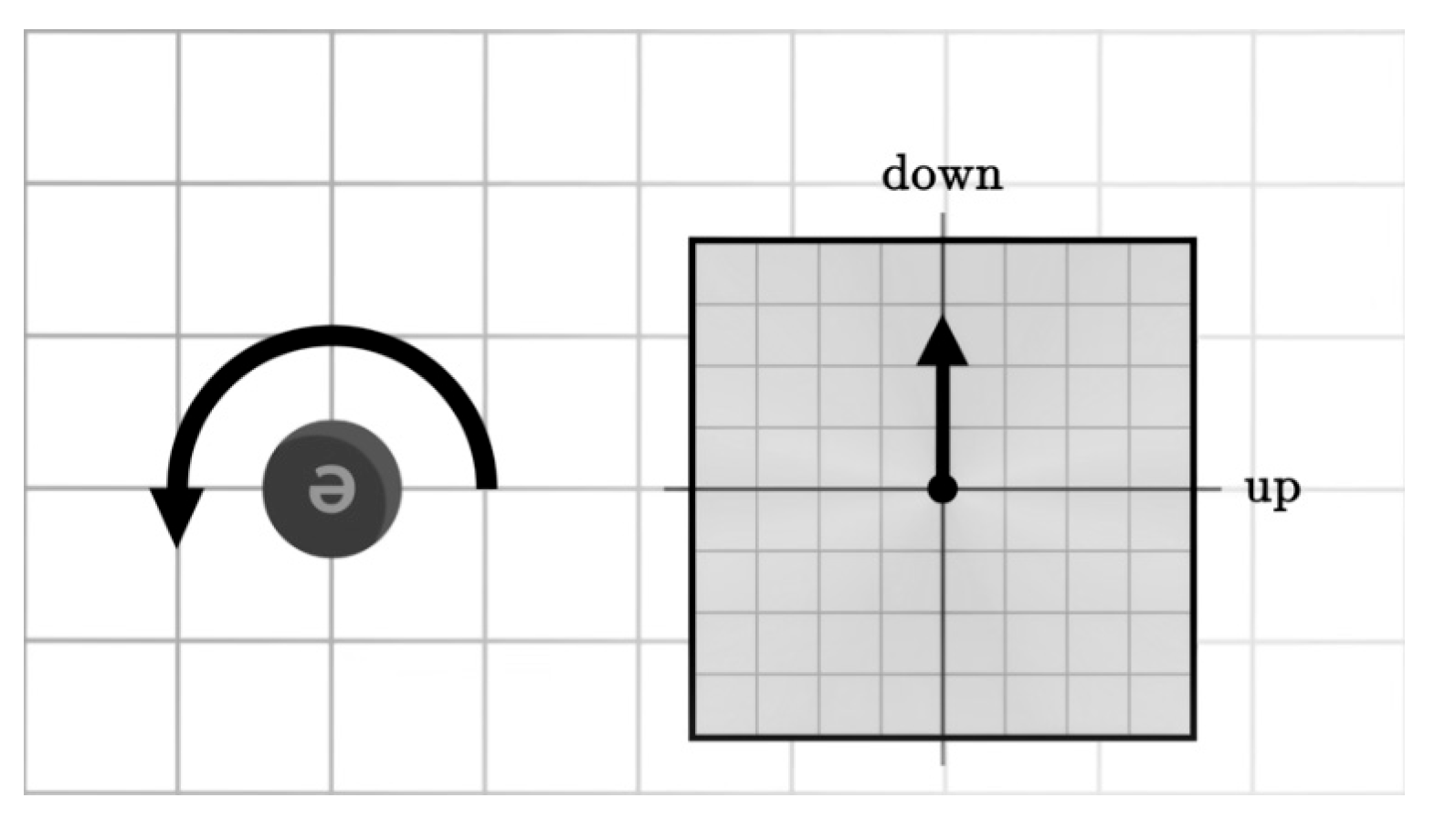
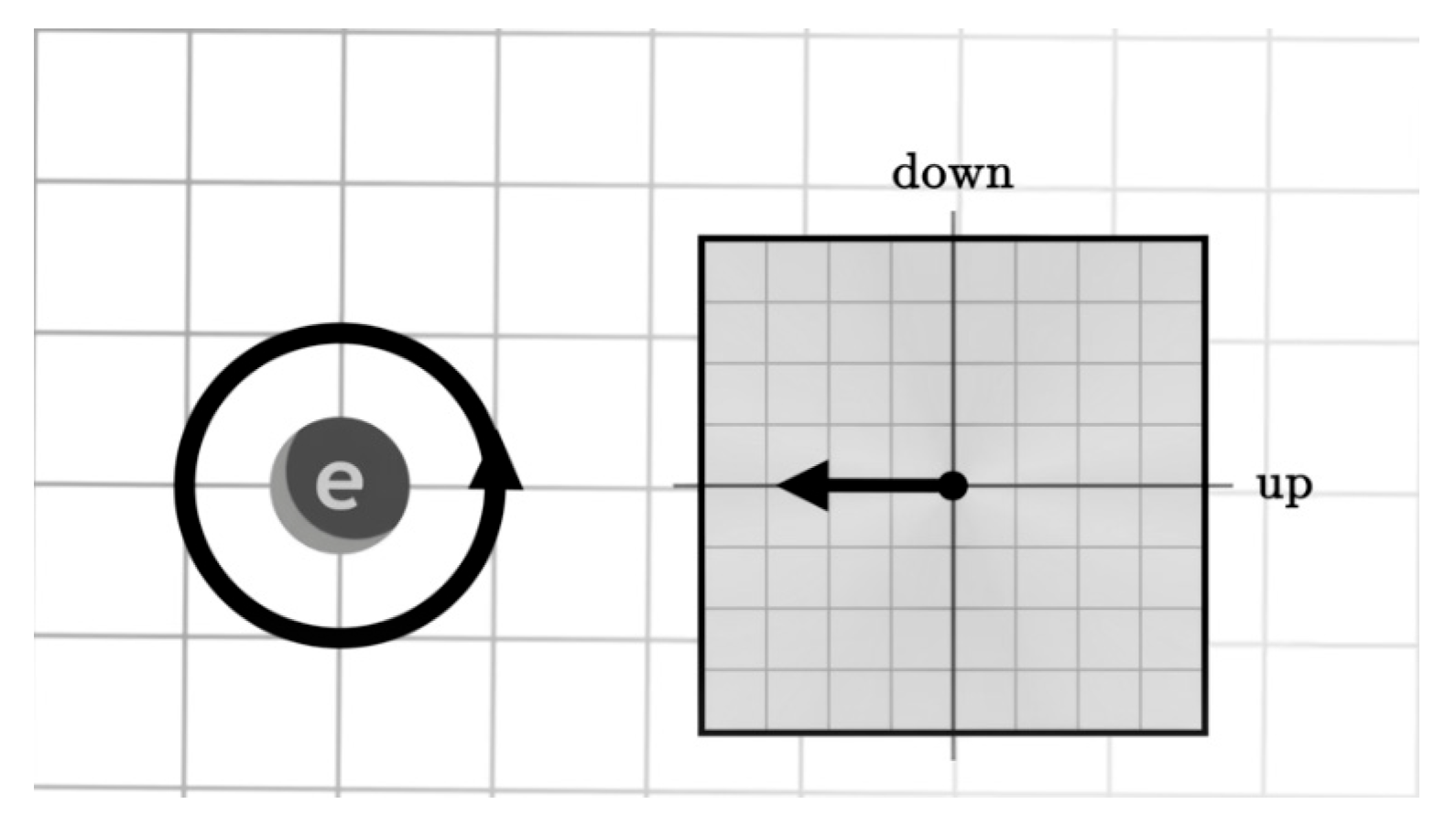

 When combined with the original Euler formula describes the relationship between trigonometric, hyperbolic, and exponential functions for the entire semi-structured complex Euclidean -space.
When combined with the original Euler formula describes the relationship between trigonometric, hyperbolic, and exponential functions for the entire semi-structured complex Euclidean -space.





