A Mathematical View on the Coordinate Distortion Induced by Gravitational Waves

Rohit Dhormare

doi:10.20944/preprints202506.0392.v1

Submitted:

26 May 2025

Posted:

05 June 2025

You are already at the latest version

Abstract

We develop a theoretical framework to analyze how coordinate systems deform under the influence of gravitational waves. This model treats coordinates as nodes in a discrete spatial graph, with inter-node distances perturbed by time-varying distortions due to passing waves. A direct proportionality is proposed between the distortion and the energy density of the wave, analogous to strain measured in interferometric detectors. We also relate this to the geodesic deviation equation from general relativity and propose directions for extending the model with continuous differential geometry and perturbation theory.

Keywords:

Gravitational waves

;

coordinate distortion

;

metric perturbation

;

geodesic deviation

;

strain

;

energy flux

Subject:

Physical Sciences - Theoretical Physics

1. Introduction

Gravitational waves (GWs), predicted by Einstein’s general theory of relativity, are ripples in the curvature of space-time generated by accelerated mass distributions, such as binary black holes or neutron star mergers. As these waves propagate, they cause transient distortions in the geometry of space-time itself, which can manifest as changes in distances between test masses or coordinate markers. These perturbations form the basis of detection in gravitational wave observatories like LIGO and Virgo [1].

In this work, we present a discrete geometric model that captures the coordinate distortions caused by gravitational waves. Unlike the standard continuous tensorial approach, we represent coordinates as discrete points in a spatial graph and investigate how wave-induced metric changes affect the effective “lengths” between these nodes.

2. Discrete Coordinate Framework

Let the spatial domain be discretized as a set of points (nodes):

Σ = \{x^{0}, x^{1}, \dots, x_{n}\}

Define a length functional over this set:

Γ (t) = Σ ||x_{i + 1} (t) - x_{i} (t)||

This length Γ (t)

represents the total path length between boundary coordinates under the influence of a time-dependent gravitational wave field.

3. Metric Perturbations and Time Evolution

In linearized general relativity, gravitational waves are modeled as small perturbations h_μν)to the flat Minkowski metric η_μν:

g_{μ ν} = η_{μ ν} + h_{μ ν}, |h_{μ ν}| ≪ 1

For a transverse-traceless

(T T)

gauge, the only non-zero components are

h_{+} (t)

and

h_{\times} (t),

corresponding to the two GW polarizations.

4. Energy Content of Gravitational Waves

The energy flux carried by gravitational waves per unit area is given by the Isaacson stress-energy tensor in the high-frequency limit:

E_{G W} = (c ³ / 32 π G) ⟨ {ḣ_{+}}^{2} + ḣ_{\times}^{2} ⟩

5. Geodesic Deviation and Physical Interpretation

The distortion of spatial distances under gravitational wave influence can also be understood using the geodesic deviation equation:

D^{2} ξ^{μ} / d τ ² = - R_{ν ρ σ}^{μ} u^{ν} ξ^{ρ} u^{σ}

6. Example: Triplet Configuration

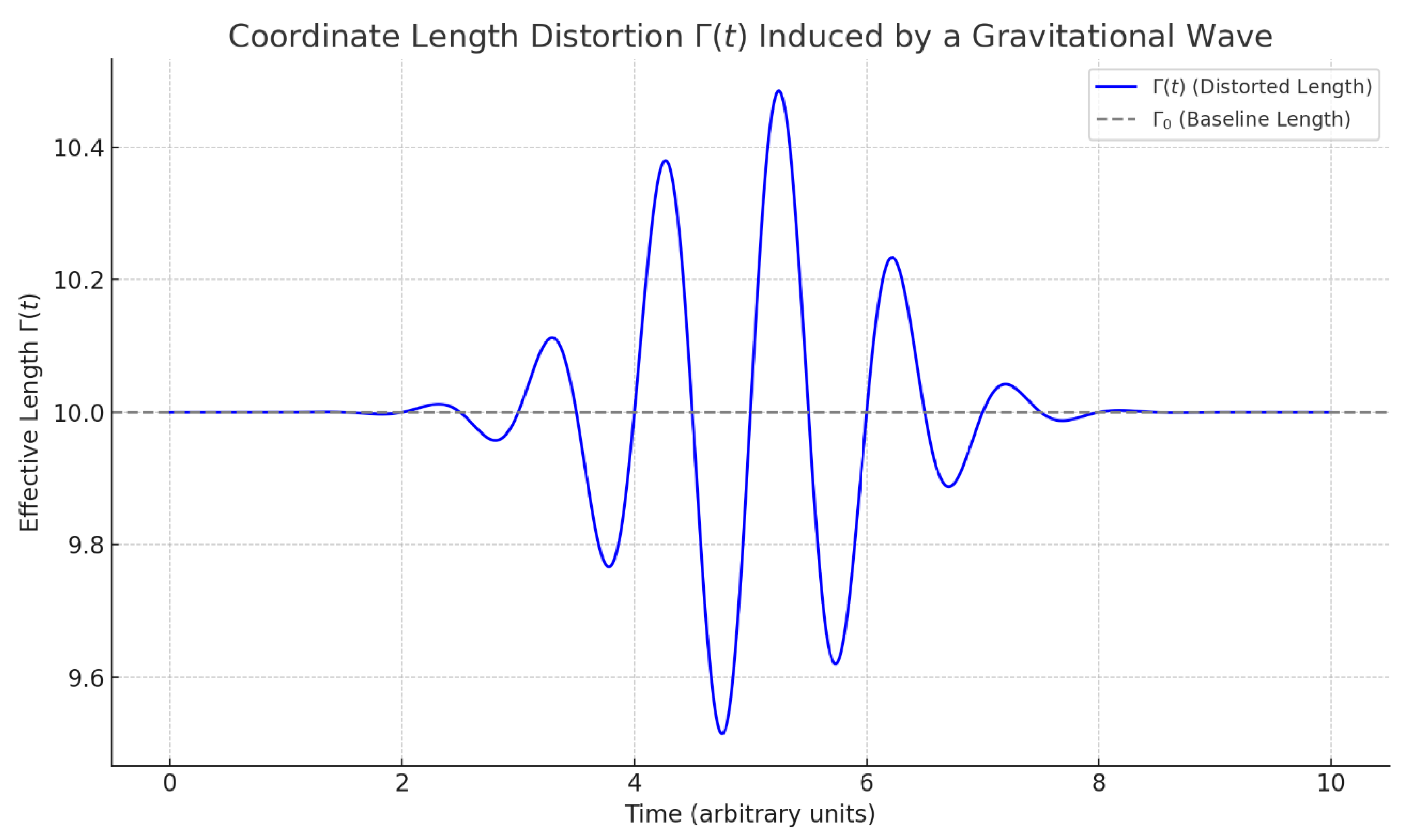
Consider a simple configuration of three spatial points

(x_{0}, x_{1}, x_{2})

. When a gravitational wave passes through, the central point x₁ experiences the maximal displacement at time t′, creating a symmetric distortion.

7. Graph-Based Representation

Let the total event duration be:

τ = \{t_{1}, t_{2}, \dots, x_{k}\}

Then the integrated distortion is:

\partial Γ (τ) = Σ Γ (t_{i}), and Δ Γ_{t o t a l} = \partial Γ (τ) - k Γ^{0}

8. Conclusions and Outlook

We have introduced a graph-based, discrete geometric model for understanding coordinate deformation caused by gravitational waves. This model captures the essence of space-time perturbations in a simplified setting and relates naturally to known physical and mathematical frameworks.

References

B. P. Abbott et al., Observation of Gravitational Waves from a Binary Black Hole Merger,’ Phys. Rev. Lett. 116, 061102 (2016).
Kip S. Thorne, Gravitational Waves, in: 300 Years of Gravitation, eds. S. W. Hawking and W. Israel, Cambridge University Press (1987).
R. A. Isaacson, ‘Gravitational Radiation in the Limit of High Frequency. I. The Linear Approximation and Geometrical Optics,’ Phys. Rev. 166, 1263 (1968).
Misner, C. W., Thorne, K. S., and Wheeler, J. A., Gravitation, W. H. Freeman and Company (1973).
Schutz, Bernard F., A First Course in General Relativity, Cambridge University Press (2009).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.