A Mathematical Comparison of Machine Learning and Deep Learning Models for Automated Fake News Detection

1. Introduction

The rise of the internet and digital communication platforms over the past two decades has fundamentally transformed the production, dissemination, and consumption of news. While these advances have democratized access to information and accelerated the pace of global news delivery, they have also facilitated the spread of fake news—false or misleading information presented as legitimate news content [1]. Fake news poses significant risks to public understanding, democratic institutions, and societal trust. Notable examples include the proliferation of fabricated political stories during the 2016 U.S. presidential election [2], widespread misinformation about COVID-19 vaccines and health policies [3], and manipulated narratives contributing to social unrest in geopolitical conflicts [4].

Fake news propagates through a variety of online channels, including social media platforms (e.g., Twitter, Facebook, Reddit), news aggregation websites, independent blogs, and online forums [5]. Social media, in particular, enables rapid and wide-reaching dissemination, often amplifying the reach of false information through algorithmic recommendation systems and viral user engagement. Automated accounts or bots further compound the problem by artificially boosting the visibility of fake news, distorting public discourse [6].

1.1. Automated Detection of Fake News

Given the overwhelming volume and velocity of digital news content, traditional manual verification approaches are insufficient to ensure information integrity [7]. This has motivated the development of automated fake news detection systems leveraging advances in machine learning (ML) and deep learning (DL). Early ML approaches—such as logistic regression, random forests, and support vector machines—use features extracted from textual content, user metadata, or publication patterns to classify news articles as real or fake [8]. However, these models often depend on hand-engineered features and may struggle to generalize across topics, domains, or evolving deception strategies.

Recent progress in deep learning, particularly in natural language processing (NLP), has enabled more flexible and effective fake news detection. Recurrent neural networks (RNNs), convolutional neural networks (CNNs), and transformer-based architectures (e.g., BERT and ALBERT) can automatically learn complex linguistic and contextual representations from raw text, surpassing traditional approaches in both accuracy and adaptability [9,10,11]. These models have proven especially valuable in identifying nuanced or subtle patterns of deception that may not be captured by surface-level features alone.

1.2. Challenges and Open Problems

Despite these advances, several core challenges persist:

• Linguistic Diversity and Context: Fake news articles often use varied writing styles, rhetorical strategies, and context-dependent cues, complicating detection by automated systems [12,13,14].
• Class Imbalance: In most datasets, genuine news far outnumbers fake news, leading to imbalanced learning scenarios that can bias models toward majority classes [15,16,17].
• Generalization Across Sources and Topics: News data is highly heterogeneous, with content drawn from diverse sources, domains, and time periods. Models trained in one context may not transfer well to others [18].
• Interpretability: While deep models achieve high accuracy, their complex architectures often hinder transparency and interpretability, complicating the justification of automated decisions—an important issue for stakeholders, journalists, and platform administrators.

1.3. Study Motivation and Contributions

This work addresses these challenges by providing a comprehensive, mathematically rigorous comparison of classical and deep learning models for automated fake news detection. Using the WELFake dataset—a large, balanced benchmark that includes both news headlines and full article content [19]—we systematically evaluate the following models:

• Classical machine learning: Logistic Regression, Random Forest, and Light Gradient Boosting Machine (LightGBM);
• Deep learning: A Lite Bidirectional Encoder Representations from Transformers (ALBERT) and Gated Recurrent Units (GRU).

Models are assessed under two input conditions: (i) news headlines only and (ii) combined headlines and article bodies. We report performance across multiple metrics (macro-averaged precision, recall, F1-score, and AUC-ROC), apply robust hyperparameter optimization and McNemar’s statistical significance testing, and analyze model interpretability via feature importance.

The main contributions of this study are:

• A unified, mathematically principled benchmarking of traditional and neural NLP models for fake news detection across diverse input scenarios;
• Empirical insights into how input granularity (headline vs. headline+content) affects model performance and feature utilization;
• A transparent, reproducible experimental protocol with interpretable analysis of model decision criteria.

The remainder of this paper is organized as follows: Section 2 describes data processing, model architectures, and evaluation metrics. Section 3 presents quantitative results, statistical comparisons, and interpretability analyses. Section 4 discusses practical implications, limitations, and future research directions.

2. Methods

This section presents the methodological framework developed to systematically evaluate the effectiveness of classical and deep learning models for fake news detection. We begin by describing the construction and preprocessing of the WELFake dataset, detailing the mathematical techniques used to transform raw text into suitable feature representations. Next, we outline the architectures and optimization procedures for both traditional machine learning and advanced neural models, including hyperparameter tuning strategies grounded in statistical rigor. Finally, we define the quantitative evaluation metrics employed to assess and compare model performance, highlighting the mathematical rationale behind each metric in the context of binary text classification. This comprehensive approach enables a robust, reproducible, and interpretable analysis of fake news identification models across a variety of input and algorithmic scenarios.

2.1. Data Preprocessing and Preparation

In this study, we utilized the WELFake dataset, a large and diverse corpus specifically designed for fake news classification tasks [19]. WELFake integrates four prominent open-access news sources—the Kaggle Fake News Dataset, McIntire Dataset, Reuters Dataset, and BuzzFeed Political News Dataset—resulting in a balanced collection of 72,134 English-language news articles, each annotated with a binary label indicating its authenticity (1: fake, 0: real).

A distinctive feature of the WELFake dataset is the inclusion of two textual columns for each record: the title, corresponding to the news headline, and the content, representing the full article text. This structure allowed us to systematically examine and compare model performance in two experimental settings:

• Title-only models: Trained solely on the title field, emulating scenarios where only headline information is available or where computational efficiency is paramount.
• Title + Content models: Trained on the concatenated output of the title and content fields, leveraging both concise headline cues and the broader semantic context provided by the full article.

For both modeling strategies, we applied a unified text normalization pipeline to all relevant fields, comprising:

• Lowercasing: All text was converted to lowercase to standardize lexical representation.
• Noise removal: URLs, HTML tags, user mentions, hashtags, punctuation, and numerical digits were removed using regular expressions.
• Whitespace normalization: Multiple consecutive spaces were collapsed into a single space, and leading/trailing whitespace was trimmed.
• Stopword removal: Common English stopwords were excluded using the NLTK corpus, retaining only semantically meaningful words.
• Lemmatization: The WordNet lemmatizer was used to reduce each token to its lemma, consolidating morphological variants.

For the Title + Content models, the preprocessed title and content were concatenated prior to feature extraction or tokenization. To ensure data quality and consistency, all entries with missing or duplicate values in either field were removed.

For classical machine learning models, the processed text was transformed into fixed-length feature vectors using the Term Frequency–Inverse Document Frequency (TF-IDF) method. Specifically, for each document d and term t, the TF-IDF score is defined as:

$$\mathrm{TF}-\mathrm{IDF}(t,d)=\mathrm{tf}(t,d)\times log\left({\displaystyle \frac{N}{\mathrm{df}\left(t\right)}}\right)$$

where $\mathrm{tf}(t,d)$ is the frequency of term t in document d, N denotes the total number of documents, and $\mathrm{df}\left(t\right)$ represents the number of documents containing t[20,21]. We extracted up to 1,000 TF-IDF features (including unigrams and bigrams, n-gram range: 1–2) per sample. The TF-IDF vectorizer was fit on the training set and applied to the validation and test sets to prevent information leakage.

The dataset was partitioned into training (60%), validation (20%), and test (20%) subsets using stratified random sampling, preserving the class distribution across splits. Random seeds were fixed for all splitting procedures to guarantee full experimental reproducibility.

This comprehensive and standardized preprocessing framework ensured high data quality and comparability across all models and input configurations, allowing for a rigorous assessment of the incremental value of article context and the mathematical properties of different NLP modeling approaches.

2.2. Machine Learning Models

To systematically assess the predictive capacity of classical algorithms for fake news detection, we implemented and rigorously evaluated a suite of supervised machine learning models. Each method represents a distinct class of mathematical modeling approaches—ranging from linear discriminative models to complex nonlinear ensembles—offering a comprehensive perspective on the strengths and limitations of established techniques within natural language processing (NLP). By applying these models to both title-only and title+content feature sets, we aim to elucidate the mathematical foundations and practical trade-offs that govern model selection and performance in high-dimensional, text-based classification tasks. The following subsections provide detailed descriptions and mathematical formulations of each model considered in this study.

2.2.1. Logistic Regression

Logistic regression is a fundamental statistical model for binary classification and provides an interpretable reference point for more complex algorithms in NLP [22]. In the fake news detection setting, each article is represented as a high-dimensional TF-IDF feature vector $\mathbf{x}\in {\mathbb{R}}^p$, and the probability that a sample belongs to the “fake” class ($y=1$) is modeled as:

$$P(y=1\mid \mathbf{x})=\sigma ({\mathbf{w}}^{\top }\mathbf{x}+b)={\displaystyle \frac{1}{1+exp\left(-({\mathbf{w}}^{\top }\mathbf{x}+b)\right)}}$$

where $\mathbf{w}$ is the coefficient vector, b is a scalar bias, and $\sigma (·)$ denotes the sigmoid activation.

The model parameters are estimated by minimizing the regularized binary cross-entropy loss:

$$\mathcal{L}(\mathbf{w},b)=-{\displaystyle \frac{1}{n}}\sum _{i=1}^n\left[y_{i}log{\widehat{y}}_i+(1-y_i)log(1-{\widehat{y}}_i)\right]+\lambda {\parallel \mathbf{w}\parallel }_2^2$$

where $y_i$ is the ground-truth label for sample i, ${\widehat{y}}_i$ is the model-predicted probability, and $\lambda$ is the ℓ₂ regularization strength. The regularization term discourages overly large weights, promoting model stability and generalizability, especially in high-dimensional settings common in text classification.

To optimize model performance, we conducted a grid search over key hyperparameters using the validation set weighted F1-score as the selection criterion. The parameter grid was defined as follows:

• $\mathtt{penalty}=$ℓ₂, specifying ridge regularization.
• $C\in \{0.01,0.1,1,10,100\}$, where $C=1/\lambda$ is the inverse regularization strength.
• $\mathtt{solver}\in \{\mathtt{liblinear},\mathtt{lbfgs}\}$, where liblinear implements coordinate descent, suitable for sparse, high-dimensional data, and lbfgs is a quasi-Newton method advantageous for larger datasets and faster convergence with ℓ₂ regularization.
• $\mathtt{class}\_\mathtt{weight}\in \{\mathtt{balanced},\mathtt{None}\}$, to optionally adjust weights inversely proportional to class frequencies.

The grid search systematically evaluated all combinations of these hyperparameters to identify the configuration maximizing generalization as measured by the weighted F1-score on held-out validation data.

The linearity and transparency of logistic regression permit direct interpretation of feature coefficients, enabling identification of headline terms most associated with the likelihood of fake news. This mathematical clarity justifies its use as a baseline for comparison against non-linear and ensemble models.

2.2.2. Tree-Based Models

The decision tree is a non-parametric, supervised learning algorithm that partitions the input space into axis-aligned regions, facilitating interpretable and hierarchical decision boundaries for classification. In the context of fake news detection, the tree recursively splits the feature space derived from text representations (such as TF-IDF vectors) to predict the binary authenticity label of each article [23].

At each internal node, the tree selects a feature j and threshold t that partitions the dataset $\mathcal{D}$ into left and right child nodes, maximizing the purity of each subset. The splitting criterion is based on minimizing an impurity function, with common choices including the Gini index and Shannon entropy.

For a node containing N samples with C classes, the Gini impurity is defined as:

$$G=1-\sum _{c=1}^C{p}_c^2$$

where $p_c$ is the proportion of samples belonging to class c at the node. For binary classification ($C=2$), this simplifies to $G=2p(1-p)$, where p is the fraction of one class.

Alternatively, the entropy-based information gain uses the entropy at a node:

$$H=-\sum _{c=1}^C{p}_c{log}_2{p}_c$$

The optimal split at each node is determined by selecting the feature and threshold that maximize the reduction in impurity (Gini or entropy) from the parent node to its children.

The tree construction proceeds recursively, partitioning the data until a stopping condition is met, such as:

• A minimum number of samples required to further split a node,
• A maximum tree depth,
• All samples at a node belong to the same class.

Although decision trees can represent complex and highly nonlinear relationships, their expressiveness often leads to overfitting, especially in high-dimensional, sparse settings such as those encountered in text classification. Overfitting manifests as a tree memorizing idiosyncrasies of the training data, rather than learning generalizable patterns [24].

Despite their limitations, decision trees remain popular for their transparent, rule-based decision structure, which enables users to trace the logic behind each classification through the tree’s branches.

In this work, we constructed decision tree classifiers as mathematical baselines for understanding hierarchical feature interactions. However, due to their known propensity for overfitting—particularly in the context of high-dimensional textual features—we focused our primary analysis on ensemble variants, such as random forest and boosting, which introduce mechanisms to improve generalization performance.

2.2.2.1. Random Forest

Random forest is an ensemble-based classification algorithm that addresses the high variance and overfitting issues commonly associated with single decision trees. By constructing a collection of randomized trees and aggregating their predictions, the random forest achieves robust generalization, especially in high-dimensional text classification tasks [25].

Each tree in the ensemble is built from a bootstrapped sample of the training data. At each node, only a randomly selected subset of features is considered for splitting, promoting diversity among the trees. The prediction for a given sample is determined by a majority vote across all trees.

For a binary classification problem, the random forest seeks to minimize classification error by reducing variance through averaging, while maintaining low bias. Formally, for T trees ${\left\{h_t\right\}}_{t=1}^T$, the predicted class $\widehat{y}$ for an input $\mathbf{x}$ is:

$$\widehat{y}=\mathrm{mode}\left({\left\{h_t\left(\mathbf{x}\right)\right\}}_{t=1}^T\right)$$

where $h_t\left(\mathbf{x}\right)$ is the class prediction from tree t.

We optimized the random forest configuration using a grid search over the following parameter space, selecting the best model based on the weighted F1-score on the validation set:

• n_estimators$\in \{50,100,200\}$: Number of trees in the forest,
• max_depth$\in \{10,20,\mathrm{None}\}$: Maximum allowable depth for each tree,
• min_samples_split$\in \{2,5,10\}$: Minimum number of samples required to split an internal node,
• min_samples_leaf$\in \{1,2,4\}$: Minimum number of samples required to be at a leaf node,
• class_weight$\in \{\mathrm{None},\mathrm{balanced}\}$: Adjusts weights inversely proportional to class frequencies to mitigate class imbalance.

All combinations were exhaustively evaluated to identify the optimal configuration for the task.

Feature importance was assessed by averaging the reduction in impurity across all trees for each feature, offering interpretable insights into which words or phrases most influenced classification. While the random forest sacrifices some transparency relative to a single decision tree, its ensemble structure yields significantly improved predictive accuracy and robustness in text-based settings.

Light Gradient Boosting Machine (LightGBM) — Mathematical Perspective

Gradient boosting machines (GBMs) are additive models that build an ensemble of base learners ${\left\{h_m\right\}}_{m=1}^M$, typically decision trees, in a stage-wise manner. At each boosting round m, the model $F_m$ is updated as:

$$F_m\left(\mathbf{x}\right)=F_{m-1}\left(\mathbf{x}\right)+{\gamma }_m{h}_m\left(\mathbf{x}\right),$$

where $h_m$ is fit to approximate the negative gradient of the loss function $\mathcal{L}$ evaluated at the current model predictions [26].

For a general differentiable loss function $\mathcal{L}$, the optimization at each stage is performed by minimizing the expected loss:

$$\underset{h_m}{min}\sum _{i=1}^n\mathcal{L}\left(y_i,F_{m-1}\left({\mathbf{x}}_i\right)+h_m\left({\mathbf{x}}_i\right)\right).$$

LightGBM utilizes a second-order Taylor expansion of the loss function around $F_{m-1}\left({\mathbf{x}}_i\right)$ to efficiently find the optimal splits:

$$\mathcal{L}(y_i,F_{m-1}\left({\mathbf{x}}_i\right)+h_m\left({\mathbf{x}}_i\right))\approx \mathcal{L}(y_i,F_{m-1}\left({\mathbf{x}}_i\right))+g_i{h}_m\left({\mathbf{x}}_i\right)+{\displaystyle \frac{1}{2}}{h}_i{h}_m{\left({\mathbf{x}}_i\right)}^2,$$

where $g_i=\partial \mathcal{L}(y_i,F_{m-1}\left({\mathbf{x}}_i\right))/\partial F_{m-1}\left({\mathbf{x}}_i\right)$ is the first derivative (gradient), and $h_i$ is the second derivative (Hessian) with respect to $F_{m-1}\left({\mathbf{x}}_i\right)$. This second-order approximation enables LightGBM to select splits based on both the gradient and curvature information, accelerating convergence [27].

For a candidate split that partitions data into left (L) and right (R) child nodes, the split gain (i.e., reduction in loss) is computed as:

$$\mathrm{Gain}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{G_L^2}{H_L+\lambda }}+{\displaystyle \frac{G_R^2}{H_R+\lambda }}-{\displaystyle \frac{{(G_L+G_R)}^2}{H_L+H_R+\lambda }}\right]-\gamma ,$$

where $G_L={\sum }_{i\in L}{g}_i$, $H_L={\sum }_{i\in L}{h}_i$, $G_R$ and $H_R$ are the corresponding sums for the right child, $\lambda$ is the regularization parameter on leaf weights, and $\gamma$ is the penalty for creating a new leaf (to control model complexity). The optimal split maximizes this gain.

Traditional GBMs expand trees level-wise (breadth-first). LightGBM instead uses a leaf-wise strategy: at each step, it identifies the leaf whose split would yield the greatest reduction in the loss (highest gain), resulting in deeper, more adaptive trees that can fit complex patterns in the data.

LightGBM bins continuous features into a finite number of discrete intervals, which reduces the complexity of finding the best split from $O\left(N\right)$ to $O\left(K\right)$ per feature per split, where K is the number of bins ($K\ll N$), improving both speed and memory efficiency.

To avoid overfitting, LightGBM introduces:

• An ℓ₂ penalty on leaf weights ($\lambda$),
• A minimum sum of Hessians per leaf node,
• A penalty $\gamma$ for each additional leaf.

These regularizers help to control tree growth and model complexity.

Through mask-based optimization and efficient memory usage, LightGBM directly supports sparse input matrices (e.g., from TF-IDF vectorization), skipping unnecessary computation and storage for zero-valued features.

Through its mathematically grounded innovations—including second-order optimization, leaf-wise splitting, and histogram-based binning—LightGBM attains a strong balance of accuracy, efficiency, and scalability, making it particularly apt for high-dimensional, sparse-text classification problems such as fake news detection.

2.3. Deep Learning Models

To complement the classical machine learning baselines, we implemented a set of deep learning architectures tailored for sequential and contextual modeling of textual data. Deep learning approaches, particularly those based on neural networks, offer powerful tools for capturing complex dependencies, hierarchical patterns, and semantic nuances in natural language. In this study, we selected two state-of-the-art neural models—A Lite Bidirectional Encoder Representations from Transformers (ALBERT) and Gated Recurrent Units (GRU)—each representing a distinct paradigm in modern NLP: transformer-based contextual encoding and recurrent sequence modeling. The following subsections provide mathematical formulations and methodological details for each model, highlighting their suitability for large-scale fake news detection tasks.

2.3.1. A Lite Bidirectional Encoder Representations from Transformers (ALBERT)

Transformer-based models have revolutionized natural language processing by enabling efficient modeling of contextual and sequential relationships in text. The Bidirectional Encoder Representations from Transformers (BERT) model [28] established a new paradigm by leveraging deep stacks of transformer encoders, each comprising multi-head self-attention and position-wise feedforward layers, to compute bidirectional, context-sensitive token embeddings.

Mathematically, the encoder processes an input sequence ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^L$ through L layers:

$${\mathbf{h}}_i^{(l+1)}=\mathrm{LayerNorm}\left({\mathbf{h}}_i^{\left(l\right)}+\mathrm{MultiHeadAttn}\left({\mathbf{h}}_i^{\left(l\right)}\right)\right),$$

$${\mathbf{h}}_i^{(l+1)}=\mathrm{LayerNorm}\left({\mathbf{h}}_i^{(l+1)}+\mathrm{FFN}\left({\mathbf{h}}_i^{(l+1)}\right)\right),$$

where MultiHeadAttn denotes multi-head self-attention, FFN the feedforward network, and LayerNorm layer normalization.

While BERT achieves strong empirical results, its large parameter count increases both memory usage and computational demand. ALBERT (A Lite BERT) [10] addresses these issues via two principal innovations:

• Factorized Embedding Parameterization: ALBERT factorizes the word embedding matrix, decoupling vocabulary size from hidden dimension, such that $\mathbf{E}={\mathbf{E}}_1{\mathbf{E}}_2$ with ${\mathbf{E}}_1\in {\mathbb{R}}^{V\times k}$ and ${\mathbf{E}}_2\in {\mathbb{R}}^{k\times d}$, for vocabulary size V, bottleneck size k, and hidden size d, where $k\ll d$.
• Cross-layer Parameter Sharing: A single set of encoder weights $\Theta$ is shared across all layers, so

  $${\mathbf{z}}_i^{(l+1)}=\mathrm{TransformerLayer}\left({\mathbf{z}}_i^{\left(l\right)};\Theta \right),l=0,\dots ,L-1,$$

  reducing the total number of trainable parameters and promoting regularization.

Furthermore, ALBERT introduces Sentence Order Prediction (SOP) as an auxiliary pretraining objective to enhance inter-sentence coherence modeling.

In our study, we fine-tuned the pre-trained albert-base-v2 model for binary fake news classification, using either headline-only or concatenated headline+content inputs. Each sequence was tokenized, padded, or truncated to a fixed maximum length, and the [CLS] token’s output embedding was used for classification via a softmax layer.

A randomized search was performed over the following domains:

• Learning rate $\eta$: log-uniformly sampled in $[{10}^{-5},{10}^{-4}]$,
• Number of epochs: integers in $[3,5]$,
• Dropout rate: uniformly sampled in $[0.1,0.5]$.

Ten random hyperparameter configurations were evaluated, with the optimal setting selected based on the validation weighted F1-score.

ALBERT’s parameter-efficient and mathematically grounded design yields robust performance on large-scale text classification, making it particularly suitable for fake news detection across both succinct headlines and full article contexts.

2.3.2. Gated Recurrent Units (GRU)

Recurrent neural networks (RNNs) are foundational models for sequential data analysis in natural language processing, as they can process arbitrary-length sequences and capture dependencies across time steps. Standard RNNs, however, often struggle with learning long-range dependencies due to vanishing or exploding gradients. Gated Recurrent Units (GRUs) [29] address this issue by introducing gating mechanisms that adaptively regulate the flow of information through the network.

Given an input sequence ${\left\{{\mathbf{x}}_t\right\}}_{t=1}^T$, the GRU maintains a hidden state ${\mathbf{h}}_t$ at each time step, updated via:

$${\mathbf{z}}_t=\sigma ({\mathbf{W}}_z{\mathbf{x}}_t+{\mathbf{U}}_z{\mathbf{h}}_{t-1}+{\mathbf{b}}_z),(\mathrm{update}\mathrm{gate})$$

$${\mathbf{r}}_t=\sigma ({\mathbf{W}}_r{\mathbf{x}}_t+{\mathbf{U}}_r{\mathbf{h}}_{t-1}+{\mathbf{b}}_r),(\mathrm{reset}\mathrm{gate})$$

$${\tilde{\mathbf{h}}}_t=tanh({\mathbf{W}}_h{\mathbf{x}}_t+{\mathbf{U}}_h({\mathbf{r}}_t\odot {\mathbf{h}}_{t-1})+{\mathbf{b}}_h),(\mathrm{candidate}\mathrm{state})$$

$${\mathbf{h}}_t=(1-{\mathbf{z}}_t)\odot {\mathbf{h}}_{t-1}+{\mathbf{z}}_t\odot {\tilde{\mathbf{h}}}_t,$$

where $\sigma (·)$ denotes the sigmoid activation, ⊙ is element-wise multiplication, and ${\mathbf{W}}_{*}$, ${\mathbf{U}}_{*}$, and ${\mathbf{b}}_{*}$ are learnable parameters. The update gate ${\mathbf{z}}_t$ interpolates between the previous hidden state and the candidate state, while the reset gate ${\mathbf{r}}_t$ determines how much past information to forget.

For fake news classification, each input text (either title-only or concatenated title+content) was tokenized and mapped to a sequence of embeddings. The GRU-based model consisted of:

• An embedding layer that converts token indices into dense vectors.
• One or more GRU layers to encode sequential dependencies and context.
• A fully connected output layer applied to the final hidden state for binary classification.

Dropout regularization was included to reduce overfitting.

We adopted a randomized search approach, sampling 10 distinct hyperparameter combinations from the following domains:

• Embedding dimension: integers in $[150,250]$,
• Hidden dimension: integers in $[256,768]$,
• Learning rate $\eta$: log-uniformly sampled in $[{10}^{-4},{10}^{-3}]$,
• Number of epochs: integers in $[5,10]$.

Model performance was evaluated using the weighted F1-score on the validation set, and the best configuration was selected accordingly.

The GRU’s gating mechanisms enable the model to retain or forget information dynamically, allowing effective modeling of both local and global dependencies in text. This makes GRUs especially suited to tasks such as fake news detection, where critical information may occur anywhere in the sequence.

Through their mathematically principled gating structure and efficient parameterization, GRU networks provide a strong and scalable approach for sequential modeling in NLP, serving as a competitive neural baseline for our fake news detection experiments.

2.4. Evaluation Metrics

To rigorously assess model performance in the context of fake news identification, we employed several standard classification metrics, each underpinned by a precise mathematical formulation. Let $y_i\in \{0,1\}$ denote the ground-truth label and ${\widehat{y}}_i\in \{0,1\}$ the predicted label for sample i, where 1 represents a fake news article.

$$\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$

Here, $\mathrm{TP}$ (true positives) is the number of fake news articles correctly identified as fake, while $\mathrm{FP}$ (false positives) is the number of real news articles incorrectly labeled as fake. High precision in fake news detection indicates that when the model flags an article as fake, it is highly likely to be truly fake—minimizing false alarms and reducing the risk of wrongly censoring legitimate content.

$$\mathrm{Recall}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$

$\mathrm{FN}$ (false negatives) is the number of fake news articles incorrectly labeled as real. High recall means the model is effective at catching the majority of fake news articles, reducing the chance that misleading information will evade detection and propagate unchecked.

$$\mathrm{F}1=2·{\displaystyle \frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

The F1-score balances the trade-off between precision and recall. In fake news identification, a high F1-score signifies that the model performs well both at accurately flagging fake articles (precision) and at catching as many fakes as possible (recall)—a crucial property in environments where both false positives (wrongly flagged news) and false negatives (missed fake news) are costly.

When classes are imbalanced, as is common in real-world fake news datasets, macro-averaged metrics are used. For a binary case, macro-averaged precision, recall, and F1-score are calculated by computing the metric for each class (fake and real) and then averaging, thereby giving equal weight to both classes regardless of their frequency.

The ROC curve plots the true positive rate (TPR, or recall) versus the false positive rate (FPR) at various probability thresholds:

$$\mathrm{TPR}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}},\mathrm{FPR}={\displaystyle \frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}}}$$

The area under this curve (AUC) reflects the probability that the model will rank a randomly chosen fake article higher than a randomly chosen real article. In fake news detection, a high AUC means the model is consistently good at distinguishing between fake and real news, regardless of the classification threshold.

Weighted F1-score on the validation set was adopted as the primary criterion for hyperparameter tuning and model selection, ensuring both precision and recall are optimized and that the evaluation is robust to any minor class imbalance. All metrics were reported on the held-out test set for final comparison.

This comprehensive, mathematically rigorous evaluation strategy provides nuanced insight into the strengths and weaknesses of each model in addressing the critical societal challenge of fake news identification.

2.5. Statistical Comparison of Classifiers: McNemar’s Test

To formally assess whether differences in classification accuracy between pairs of models were statistically significant, we conducted pairwise hypothesis testing using McNemar’s test [30]. McNemar’s test is a non-parametric method for evaluating the performance of two classifiers on the same sample, specifically testing the null hypothesis that both classifiers have the same error rate on paired observations.

Given two classifiers, A and B, let $n_{01}$ denote the number of samples misclassified by A but correctly classified by B, and $n_{10}$ denote the number of samples correctly classified by A but misclassified by B. McNemar’s test statistic is defined as:

$${\chi }^2={\displaystyle \frac{{(n_{01}-n_{10})}^2}{n_{01}+n_{10}}}$$

Under the null hypothesis of equal error rates, this statistic asymptotically follows a chi-squared distribution with one degree of freedom.

To account for multiple pairwise comparisons, p-values were adjusted using Holm’s method, providing a more stringent control of the family-wise error rate. This approach enables robust inference on the relative superiority of competing classifiers under identical experimental conditions.

3. Results

This section presents a comprehensive evaluation of classical and deep learning models for fake news detection across two distinct input configurations: (i) headline (title) only and (ii) headline combined with article body (title + content). We first summarize the predictive performance of all models using multiple quantitative metrics on the held-out test set, enabling direct comparison of precision, recall, F1-score, and AUC-ROC under both scenarios. Next, we report the results of rigorous pairwise statistical tests to determine the significance of performance differences between models. Finally, we analyze feature importance for each machine learning model, providing interpretability insights into which textual elements most strongly influence classification outcomes. Collectively, these results offer a nuanced understanding of how model architecture and input context affect fake news detection accuracy, robustness, and transparency.

3.1. Model Performance and Model Comparison

Table 1 reports the macro-averaged precision, recall, F1-score, and AUC-ROC for all evaluated models on the test set, stratified by the two input scenarios: title only and title + content.

When restricted to headline information, ensemble and deep learning models consistently outperformed classical linear baselines. Among traditional machine learning approaches, Random Forest exhibited the strongest results (Precision/Recall/F1: 0.85; AUC-ROC: 0.93), marginally exceeding both Logistic Regression (0.84 across metrics, AUC-ROC: 0.92) and LightGBM (0.83 across metrics, AUC-ROC: 0.92). This finding suggests that the Random Forest’s capacity to model nonlinear feature interactions confers a performance advantage, even in concise textual contexts.

Deep learning architectures provided a substantial boost. ALBERT achieved the highest overall accuracy in this setting, with a macro F1-score of 0.93 and an AUC-ROC of 0.98, indicating its strong ability to extract informative patterns from short headlines. The GRU model also demonstrated competitive performance (F1: 0.90, AUC-ROC: 0.96), affirming the value of sequential modeling, although it trailed ALBERT by a moderate margin.

Integrating the full article text with the headline led to marked improvements across all models. Classical machine learning approaches exhibited notable gains: both Logistic Regression and Random Forest achieved F1-scores of 0.93 and AUC-ROC values of 0.98 and 0.99, respectively. LightGBM showed an even greater improvement (F1: 0.94, AUC-ROC: 0.99), highlighting the utility of richer feature sets for boosting ensembles.

Neural models achieved near-perfect accuracy in the combined input scenario. ALBERT reached an F1-score and recall of 0.99 and an AUC-ROC of 1.00, demonstrating exceptional discriminative ability. The GRU model also performed remarkably well (F1: 0.97, AUC-ROC: 1.00), nearly matching ALBERT’s performance and substantially outperforming all classical baselines. These results demonstrate that, when provided with comprehensive textual context, advanced neural networks are capable of synthesizing both local and global features to enable highly accurate fake news detection.

The incremental benefit of incorporating article content is clear for all models, with the most pronounced relative gains seen for LightGBM and GRU. Across both input scenarios, ALBERT consistently outperformed all other models, highlighting the power of transformer-based architectures for both short and long textual classification. Classical machine learning models, while efficient and interpretable, were ultimately surpassed by neural methods—especially when richer input was available. Across all models and configurations, AUC-ROC values remained high, reflecting robust discrimination between fake and real news even under balanced class conditions.

Overall, these findings reinforce the superiority of state-of-the-art neural architectures, particularly ALBERT, for automated fake news detection. The added contextual information from article content led to substantial improvements in performance for all models, with neural networks demonstrating especially strong gains. Classical machine learning methods remain viable for resource-constrained settings or when interpretability is paramount, but their predictive power is outmatched by contemporary deep learning approaches on large-scale, real-world datasets.

To rigorously assess whether observed differences in predictive performance between models were statistically significant, we conducted pairwise McNemar’s tests with Holm correction for multiple comparisons (Table 2) [30]. This non-parametric approach evaluates whether two classifiers differ in their tendency to make errors on the same samples, providing a robust basis for head-to-head significance testing.

For the title-only models, ALBERT consistently and significantly outperformed all classical machine learning baselines (logistic regression, random forest, LightGBM) as well as GRU, with extremely small corrected p-values ($<0.0001$) in all comparisons. GRU also demonstrated significant superiority over all tree-based models. Among the classical methods, random forest outperformed LightGBM and logistic regression, though the margin over LightGBM was particularly pronounced. The only non-significant result in the title-only scenario was between LightGBM and logistic regression ($p=0.33$), indicating comparable performance profiles between these two models in this input setting.

For the title+content models, the advantage of deep learning models became even more pronounced. ALBERT emerged as the top performer, significantly outperforming all other models, including GRU, which itself exhibited a significant advantage over all classical methods. LightGBM outperformed both random forest and logistic regression, while random forest was only marginally better than logistic regression ($p=0.02$). The high frequency of statistically significant results (corrected $p<0.0001$) underscores the clear superiority of transformer-based neural architectures when richer textual context is leveraged.

Collectively, these results provide robust statistical evidence that advanced neural models—especially ALBERT—offer substantial gains over traditional machine learning approaches for fake news detection. This effect is most pronounced when both headline and full article content are available, but remains apparent even with headline-only inputs. These findings highlight the critical role of deep contextual models for text classification in practical misinformation detection pipelines.

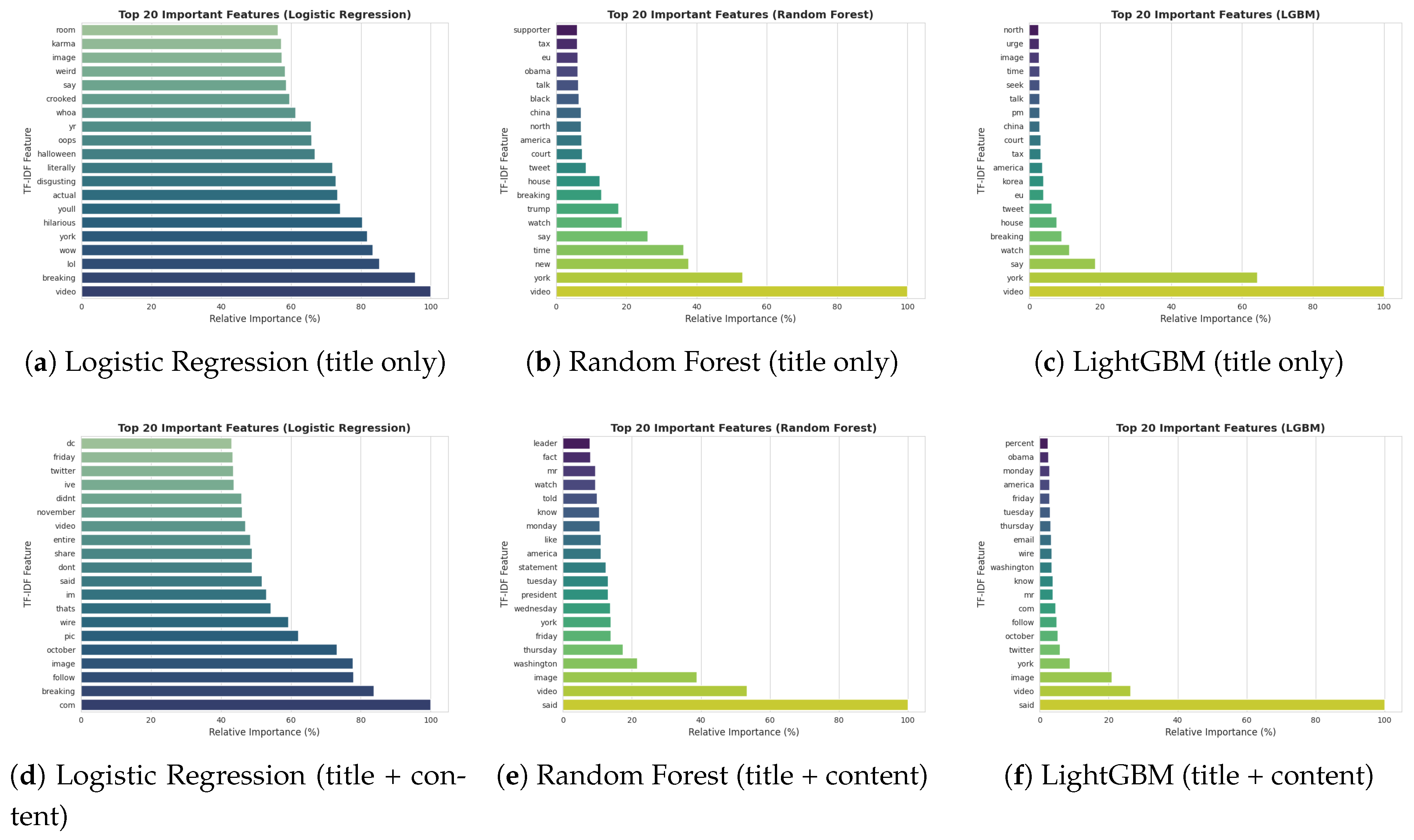
3.2. Model Interpretation: Feature Importance Analysis

To better understand how classical machine learning models distinguish between fake and real news, we analyzed the top 20 most important TF-IDF features as determined by each model in both the title-only and title+content scenarios. Figure 1 displays these feature importance for Logistic Regression, Random Forest, and LightGBM.

Across all models, the term video consistently emerged as the most predictive feature, indicating that video-related content is a salient marker for fake news articles. Location-based words such as york, washington, and temporal or event-driven words (e.g., breaking, friday, president) were also frequently ranked highly, especially by the tree-based models.

For Random Forest and LightGBM, the inclusion of article content led to a shift towards features associated with events, speaker attributions, and dates (e.g., said, image, october), reflecting their ability to exploit broader contextual cues when available.

In contrast, Logistic Regression models, while still highlighting terms like video and breaking, also emphasized stylistic and informal words (e.g., lol, wow, hilarious), which suggests that linear models may be particularly sensitive to expressive or colloquial language features often present in sensational headlines.

Overall, the combination of location, media-related, event-driven, and stylistic cues reflects the multi-faceted nature of language signals that classical machine learning models leverage in fake news detection, and highlights the complementary strengths of linear and non-linear algorithms in modeling different aspects of the input text.

4. Discussion

This study delivers a comprehensive, mathematically principled evaluation of both classical and deep learning models for automated fake news detection, leveraging the large-scale WELFake dataset under both headline-only and headline+content input scenarios. Our findings provide new insights into the relative effectiveness, interpretability, and practical implications of these approaches for text-based misinformation detection in modern digital ecosystems.

4.1. Comparative Model Performance

Our results underscore that both input representation and algorithmic choice exert a profound impact on fake news detection outcomes. In the headline-only scenario, ensemble tree-based models (Random Forest, LightGBM) consistently surpass linear baselines such as Logistic Regression, demonstrating the advantage of capturing nonlinear feature interactions and higher-order relationships even in short textual inputs. However, the adoption of deep neural models—most notably ALBERT, a highly parameter-efficient transformer—produces the most pronounced gains. The superior macro F1-score and AUC-ROC attained by ALBERT indicate that transformer-based architectures are adept at extracting subtle contextual patterns from minimal input, which are otherwise challenging for classical models.

When the full article content is included, all models benefit from the additional semantic context, but the magnitude of improvement is especially dramatic for deep learning approaches. Both ALBERT and GRU models attain near-perfect accuracy (macro F1 $\ge 0.97$, AUC-ROC $\approx 1.00$), decisively outperforming classical methods. These findings validate the exceptional representational power of neural architectures for natural language processing (NLP) tasks and affirm that context-rich features significantly enhance detection of sophisticated fake news.

4.2. Statistical Significance and Model Robustness

To rigorously evaluate the robustness of observed performance differences, we conducted pairwise McNemar’s tests with Holm correction. These statistical results substantiate that the improvements offered by neural models—and especially ALBERT—over classical baselines are both substantial and statistically significant across all settings. This provides strong evidence that, when data and computational resources permit, deep contextual NLP models are the methodological gold standard for fake news detection.

Notably, in the headline-only scenario, differences between Random Forest and LightGBM are minimal and often statistically insignificant, highlighting the competitive nature of these two ensemble approaches for concise inputs. In contrast, the advantage of boosting (LightGBM) becomes more pronounced when more complex and high-dimensional features (title+content) are incorporated. The only statistically non-significant result is between LightGBM and logistic regression for headline-only inputs, suggesting their performance is context dependent.

4.3. Interpretability and Feature Analysis

Interpretability remains an essential consideration, particularly for real-world applications where model transparency and explainability are required. Classical machine learning models offer direct insights into the decision process. Our feature importance analysis reveals that all models consistently prioritize keywords such as “video,” “breaking,” and location names as key indicators of fake news. Linear models, such as logistic regression, tend to elevate expressive or colloquial terms (e.g., “lol,” “hilarious”), suggesting sensitivity to the sensational and stylistic language that often characterizes fake headlines. In contrast, ensemble and boosting models leverage broader contextual and event-related cues, especially with article content (e.g., “said,” “image,” “friday”), demonstrating their capacity to incorporate both local and global signals. These observations point to complementary strengths of linear and nonlinear models for different aspects of fake news detection.

4.4. Practical Implications

Our findings have practical implications for the design and deployment of fake news detection systems:

• For environments requiring computational efficiency and interpretability—such as media monitoring or regulatory compliance—classical ensemble models, particularly Random Forest and LightGBM, offer a robust and transparent option, especially when limited to headline data.
• In mission-critical or high-stakes settings, where detection accuracy is paramount and computational resources are sufficient, transformer-based neural architectures (such as ALBERT) are preferable, particularly when full article content is available.
• The interpretable nature of classical models can facilitate human-in-the-loop systems and explainable AI pipelines, supporting trust, regulatory transparency, and the rapid identification of emerging fake news topics or patterns.

4.5. Limitations and Future Directions

Despite the strengths of this study, several limitations should be considered. First, while the WELFake dataset is large and balanced, real-world fake news distributions are often imbalanced and can shift over time (temporal or topical drift), challenging generalization. Second, our analysis is limited to supervised learning; future research should explore semi-supervised, unsupervised, and domain adaptation approaches, as well as continual learning for dynamically evolving misinformation landscapes. Third, deep learning models, despite their high accuracy, pose ongoing challenges for interpretability. The development and application of model-agnostic interpretability tools and attention-based visualization techniques should be pursued. Finally, while our statistical significance tests provide rigorous comparative validation, future evaluations in operational settings should also consider cost-sensitive metrics, deployment trials, and real-world impact assessments.

Overall, this study demonstrates that, under mathematically rigorous and statistically validated evaluation protocols, transformer-based models—especially ALBERT—offer state-of-the-art performance for fake news detection, especially when leveraging both headline and article content. These findings provide practical guidance for both researchers and practitioners developing automated solutions for misinformation detection in increasingly complex digital media environments.