From Transformer to Transponder: Introducing Contextual Modulation Training for Residual Learning in LLMs

1. Introduction

Transformer architectures deliver state-of-the-art performance across vision, language, and multimodal tasks [1,2,3,4]. In standard designs, information flows through a sequence of linear and nonlinear components—query/key/value projections, attention output projections, and the two feed-forward networks (FFN) linear maps—interleaved with residual connections. After training, the scaling by which these components contribute to the residual stream is effectively static for all the input tokens. Several mechanisms attempt to manipulate residual or path scaling via global reparameterizations (e.g., ReZero [5], DeepNorm/DeepNet [6]) or depth-aware normalization [7,8]. Yet these approaches assign fixed gains in spite of the current token, channel, or depth position.

These designs clash with the core goal of representation learning: the relevance of a component’s output is input-dependent. Rare tokens may call for amplifying specific heads; bursty channels may require attenuation; deeper layers may benefit from different mixing strengths than shallow ones. When scaling is static, the model must implicitly encode such selectivity inside the functional maps themselves—mixing representation (what to compute) with control (how much to pass through).

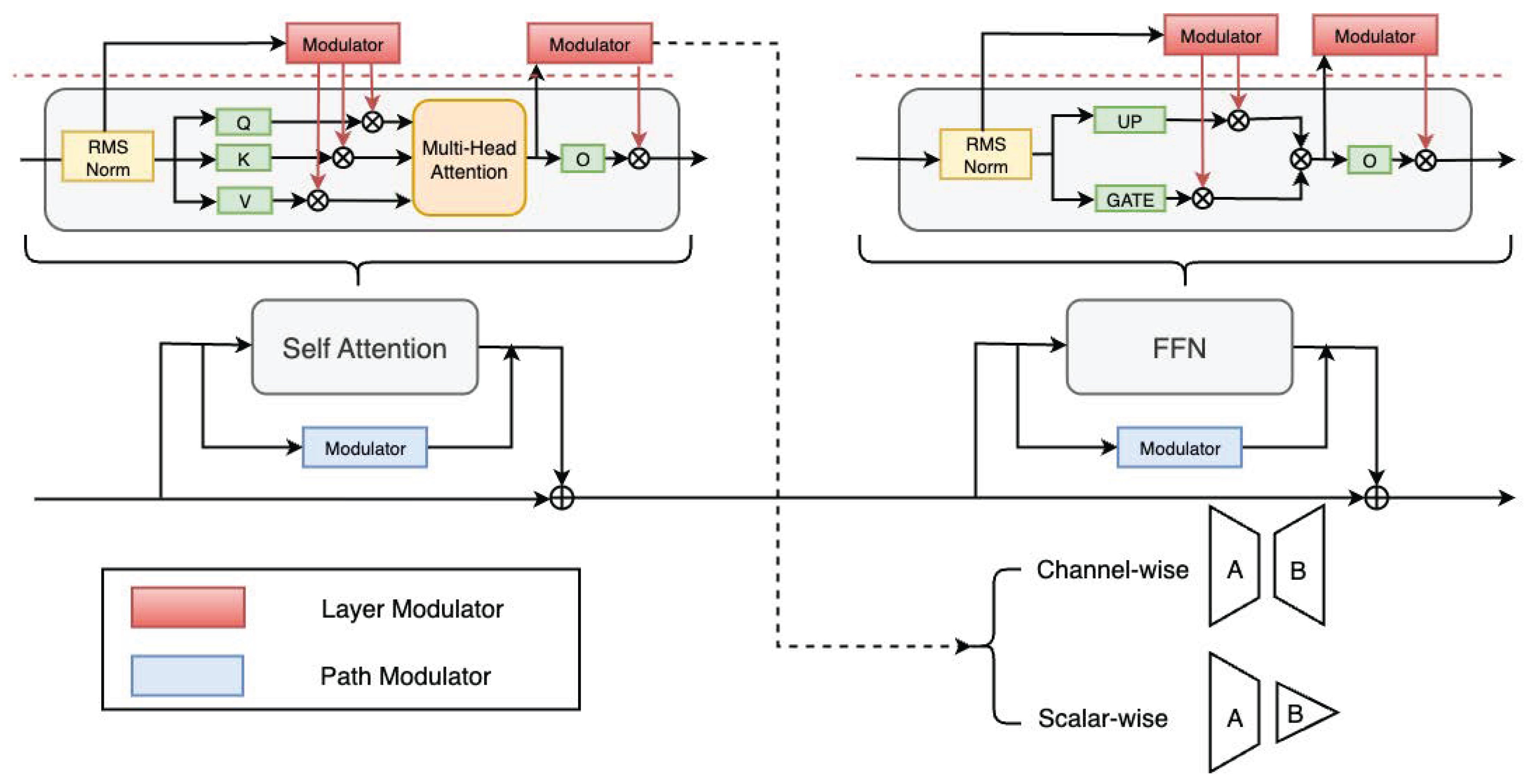
To address this limitation, we introduce Transponder, whose core principle is simple: pair each Transformer component with a contextual, input-aware modulator that explicitly controls its contribution at inference. Specifically, for a component with output $\mathbf{Y}=\mathbf{F}\left(\mathbf{X}\right)$, we attach a lightweight controller $g\left(\mathbf{X}\right)\in [0,1]$ and compute $\tilde{\mathbf{Y}}=\mathbf{F}\left(\mathbf{X}\right)\odot g\left(\mathbf{X}\right)$. This decouples representation from control, turning residual mixing from a static heuristic into a principled, context-sensitive regulation mechanism.

We instantiate this principle with Transponder, designed to be minimally invasive and broadly compatible:

• Input-aware modulation. Modulators calculate the scales that multiply functional-path outputs at use time, yielding context-conditioned scaling factors for each component in Transformer.
• Granularity and placement. We systematically study where to modulate (projection- vs. path-level) and at what resolution (scalar vs. channel-wise), providing a comprehensive view of practical design.
• Low overhead, easy integration.Transponder adds $\le 1\%$ parameters and integrates into standard Transformer blocks via a fused Triton kernel for each modulator to accelerate inference.

Across large-scale language-modeling benchmarks, Transponder delivers consistent gains on LLaMA backbones from 60M to 250M parameters, achieving up to 5.8–15.3% relative perplexity reductions over the LLaMA baselines. Extensive ablations spanning placement, granularity, hidden size, and component coverage (attention and FFN) show the robustness of the design. Analysis of learned modulator values uncover depth-, module-, and token-specific patterns that adapt layer-wise contributions to input semantics, providing direct evidence that residual functional transformations benefit from adaptive, context-aware scaling.

2. Related Work

2.1. Residual Connections and the Transformer Architecture

Residual connections [9] enable very deep models by adding a learned transformation to an identity shortcut, improving gradient flow, preserving signal, and allowing layers to refine rather than reconstruct representations. The Transformer [1] instantiates this principle with a persistent residual stream that carries token-wise state across layers while each block applies a functional path—multi-head self-attention (MHA) followed by a position-wise feed-forward network (FFN). Concretely, each block computes linear projections for queries, keys, and values and an attention output, then applies two FFN linear maps with nonlinearities; the results are mixed back into the residual stream through additive shortcuts. Layer normalization (LayerNorm) is interleaved with these sublayers: the original Post-LN normalizes after each sublayer [1], whereas Pre-LN normalizes before sublayers, improving optimization stability for deeper stacks [10]. This decomposition—identity carryover plus functional updates—yields strong gradient propagation and composability, but it also implicitly fixes the contribution of each subcomponent to the residual stream at inference, motivating methods that explicitly control (or scale) block updates relative to the identity path.

2.2. Scaling the Block: Static Reparameterizations and Normalization Placement

A substantial line of work manipulates the magnitude of each block’s update relative to the residual stream via static, input-agnostic mechanisms. ReZero [5] introduces a zero-initialized, learnable scalar per block that gates the residual branch, effectively starting from an identity mapping and allowing depth to emerge during training. DeepNorm/DeepNet [6] analytically rescales residual and sublayer outputs to maintain stability in very deep Transformers, enabling substantially deeper stacks without divergence. LAuReL [11] generalizes residual/functional mixing with learned coefficients (e.g., RW/LR/PA variants), providing a tunable trade-off between identity flow and the functional path. While these approaches improve training dynamics and depth, their coefficients are typically block-level and input-agnostic at inference time, leaving the strength of updates fixed for any given input.

2.3. Context-Conditioned Gating Methods

In convolutional networks, squeeze-and-excitation (SE) [12] introduces feature-wise, input-conditioned scaling by pooling global context and learning channel gates, improving representational efficiency and accuracy. The core idea—context-aware modulation of features—has influenced architectures beyond convolution. Within Transformers, SDPA-gated mechanisms [13] attach the gating mechanism to scaled dot-product attention, commonly parameterized at the head or channels. These gates selectively modulate attention behavior and can stabilize training, but they often incur heavy additional parameters and computation, and primarily target the attention pathway.

3. Transponder - Contextual Modulation Training

We formalize the Transponder by introducing the lightweight, input-conditioned modulators that scale the functional information flow inside Transformer blocks. The goal is to convert static functional compositions into context-aware modulation while preserving (i) the inductive bias of the base operator (attention/MLP), (ii) training stability, and (iii) negligible parameter/FLOP overhead. We show the main architecture of the Transponder in Figure 1.

3.1. Preliminaries: Residual Functional Composition in Transformers

Let ${\mathbf{Y}}_{l-1}\in {\mathbb{R}}^{T\times d}$ denote the hidden states entering layer l (sequence length T, width d), and let ${\mathcal{F}}_l$ denote a parameterized sublayer (self–attention or FFN). The standard residual formulation composes identity and functional streams additively:

$${\mathbf{Y}}_l={\mathbf{Y}}_{l-1}+{\mathcal{F}}_l\left({\mathbf{Y}}_{l-1}\right).$$

(1)

While Equation (1) ensures stable signal and gradient propagation, the contribution of ${\mathcal{F}}_l$ is typically static at inference time: once trained, the magnitude with which ${\mathcal{F}}_l$ perturbs the skip path does not depend on the current token, channel, or context. Prior work improves optimization via block-wise scalars (e.g., ReZero [5]), depth-aware reparameterizations (e.g., DeepNorm [6]), or by mixing identity and functional streams with learned but input-agnostic coefficients (e.g., LAuReL [11]). Our aim is to endow Equation (1) with contextual modulators applied to, or inside, ${\mathcal{F}}_l$.

3.2. Definition: Transponder Scheme

A Modulator ${\mathcal{G}}_l$ produces a contextual scaling signal that modulates a sublayer at its point of use. For a generic operator ${\mathcal{F}}_l$ acting on $\mathbf{X}$,

$$\mathbf{Y}={\mathcal{F}}_l\left(\mathbf{X}\right)\odot {\mathcal{G}}_l\left(\mathbf{X}\right),$$

(2)

where ⊙ denotes broadcasted Hadamard multiplication. In a residual block,

$${\mathbf{Y}}_l={\mathbf{Y}}_{l-1}+\left[{\mathcal{F}}_l\left({\mathbf{Y}}_{l-1}\right)\odot {\mathcal{G}}_l\left({\mathbf{Y}}_{l-1}\right)\right].$$

(3)

• Modulator parameterization.

We parameterize the modulator ${\mathcal{G}}_l$ with a compact bottleneck applied to each input activation $\mathbf{X}$, followed by a bounded nonlinearity:

$${\mathcal{G}}_l\left(\mathbf{X}\right)={\tilde{\sigma }}_{{\alpha }_l}\left({\mathbf{B}}_l\varphi \left({\mathbf{A}}_l\mathbf{X}\right)\right),{\mathbf{A}}_l\in {\mathbb{R}}^{r\times d_{\mathrm{in}}},{\mathbf{B}}_l\in {\mathbb{R}}^{d_{\mathrm{out}}\times r},$$

(4)

where $d_{\mathrm{in}}$ is the input width of the summary, $d_{\mathrm{out}}$ matches the modulation resolution (one single scalar or channel-wise. $\varphi$ is a pointwise nonlinearity (e.g., Sigmoid), and ${\tilde{\sigma }}_{\alpha }$ is a learnable curvature sigmoid,

$${\sigma }_{\alpha }\left(x\right)={\displaystyle \frac{1}{1+exp(-\alpha x)}},\alpha >0,{\tilde{\sigma }}_{\alpha }\left(x\right)=2{\sigma }_{\alpha }\left(x\right).$$

(5)

The base gate ${\sigma }_{\alpha }$ maps to $[0,1]$ and interpolates between soft scaling (small $\alpha$) and near-binary gating (large $\alpha$). We use the calibrated gate ${\tilde{\sigma }}_{\alpha }\in [0,2]$ so that ${\tilde{\sigma }}_{\alpha }\left(0\right)=1$, preserving the expected residual magnitude at initialization.

3.3. Granularity: Where and at What Resolution to Modulate?

We distinguish where the Modulator is applied (inter–layer) from how finely it is parameterized (intra–layer).

• Inter–layer granularity.

• Projection–level modulation. Apply a modulator after each linear projection inside a functional path:

  $$\underset{\mathrm{projection}}{\underbrace{\mathbf{W}\mathbf{X}}}\mapsto \left(\mathbf{W}\mathbf{X}\right)\odot {\mathcal{G}}_l\left(\mathbf{X}\right).$$

  (6)
  This affords precise control (e.g., on $Q,K,V$ and MLP up/down projections) with minimal additional computation.
• Path–level modulation. Modulate the entire functional path (e.g., self–attention or FFN):

  $${\mathbf{Y}}_l={\mathbf{Y}}_{l-1}+{\mathcal{F}}_l\left({\mathbf{Y}}_{l-1}\right)\odot {\mathcal{G}}_l\left({\mathbf{Y}}_{l-1}\right).$$

  (7)

• Intra–layer granularity.

Let $d_{\mathrm{out}}$ be the dimension of ${\mathcal{F}}_l$’s output at the modulation site. We instantiate:

• Layer–wise (scalar) modulation:${\mathcal{G}}_l\left(\mathbf{X}\right)\in \mathbb{R}$ via ${\mathbf{B}}_l\in {\mathbb{R}}^{1\times r}$. A single scale uniformly modulates the sublayer; parameter and compute overheads are negligible.
• Channel–wise modulation:${\mathcal{G}}_l\left(\mathbf{X}\right)\in {\mathbb{R}}^{d_{\mathrm{out}}}$ via ${\mathbf{B}}_l\in {\mathbb{R}}^{d_{\mathrm{out}}\times r}$, enabling feature–specific modulating with two low–rank matrices.

3.4. Fused Projection for Projection–Level Transponder

For each linear layer, the dominant cost is the matrix product $\mathbf{X}{\mathbf{W}}_{\star }$. When the summary $u_{\star }\left(\mathbf{X}\right)$ is token-wise, we also need $\mathbf{X}{\mathbf{A}}_{\star }^{\top }$. Instead of launching two kernels, we concatenate along the output dimension and perform a single tiled GEMM:

$$\begin{array}{c}\hfill \left[{\mathbf{Z}}_{\star }{\mathbf{U}}_{\star }\right]=\mathbf{X}\underset{{\mathbf{C}}_{\star }\in {\mathbb{R}}^{d_{\mathrm{in}}\times (d_{\mathrm{out}}+r)}}{\underbrace{\left[{\mathbf{W}}_{\star }|{\mathbf{A}}_{\star }^{\top }\right]}},{\mathbf{Z}}_{\star }\in {\mathbb{R}}^{B\times T\times d_{\mathrm{out}}},{\mathbf{U}}_{\star }\in {\mathbb{R}}^{B\times T\times r}.\end{array}$$

(8)

Here ${\mathbf{A}}_{\star }\in {\mathbb{R}}^{r\times d_{\mathrm{in}}}$ is the rank-r bottleneck, ${\mathbf{W}}_{\star }\in {\mathbb{R}}^{d_{\mathrm{in}}\times d_{\mathrm{out}}}$ is the projection, B is batch size, and T is sequence length. After the fused GEMM, we compute the modulator logits and modulate in-register per tile:

$$\begin{array}{c}\hfill {\mathrm{logits}}_{\star }={\mathbf{U}}_{\star }{\mathbf{B}}_{\star }^{\top },{\mathbf{B}}_{\star }\in {\mathbb{R}}^{d_{\mathrm{out}}\times r},{\gamma }_{\star }={\tilde{\sigma }}_{{\alpha }_{\star }}\left({\mathrm{logits}}_{\star }\right)\in \left\{\begin{array}{cc}{\mathbb{R}}^{B\times T\times 1},\hfill & \mathrm{scalar}\mathrm{gate},\hfill \\ {\mathbb{R}}^{B\times T\times d_{\mathrm{out}}},\hfill & \text{channel-wise}\mathrm{gate}.\hfill \end{array}\right.\end{array}$$

(9)

Finally, we apply broadcasted modulation to the projected activations:

$${\widehat{\mathbf{Z}}}_{\star }={\gamma }_{\star }\odot {\mathbf{Z}}_{\star }.$$

(10)

This fusion amortizes the summary computation into the main GEMM and keeps the modulator arithmetic on-chip, yielding precise projection-level control at minimal overhead.

4. Experiments

4.1. Setup

We evaluate Transponder on standard language modeling with LLaMA backbones [4] ranging from $\sim 60$M to $\sim 250$M parameters, trained on the C4 [14] and OpenWebText [15] corpus. All models are optimized with Adam and a base learning rate of $3\times {10}^{-3}$ for Openwebtext dataset and $1\times {10}^{-3}$ for C4 dataset. All the experiments are trained with bfloat16 for all the activations, weights, and optimization states. The hidden dimension of the contextual modulator is set to $r=8$ in the main comparisons to emphasize gains from contextual modulation rather than capacity. For fairness, we keep training data, tokenization, optimizer settings, and learning-rate schedules identical across baselines and Transponder. We report the perplexity (the lower the better) as the standard language-modeling metrics and measure parameter overhead relative to the corresponding backbone. We initialize $A,B$ of the Transponder with Kaiming uniform [16] and zero biases; set $\alpha =1$ initially. Detailed hyperparameter settings can be found in Table A1.

4.2. Baselines

We compare against widely used residual/normalization designs and recent residual-scaling or layer-wise contextual control methods:

• DeepNorm/DeepNet [6]: rescales the residual branch with depth-dependent constants and tailored initialization to stabilize training of very deep Transformers.
• LayerNorm Scaling [8]: multiplies each layer’s normalized output by a depth-aware factor (e.g., $\propto 1/\sqrt{L}$) to curb variance growth across residual connections.
• LAuREL [11]: learns a lightweight mixer that blends the skip and transformed paths (LR/PA variants), improving layer-wise signal routing with minimal extra parameters.
• SDPA-Gate [13]: applies a per-head sigmoid gate to the scaled dot-product attention output to modulate contribution and mitigate attention-sink effects.

To match SDPA-Gate’s mechanism more broadly, we also implement an ALL-Gate variant that applies the same gating scheme to all linear sublayers, including the MLP projections, providing a stronger control baseline.

4.3. Modulator Variants Validation

We instantiate five different variants of the contextual modulator in the framework of the Transponder to probe where and at what resolution modulation helps most:

• Modulator-path-scalar: a single scalar Modulator modulates the entire functional path (attention output or MLP output) per block.
• Modulator-path-channel: a channel-wise Modulator modulates the entire functional path (attention output or MLP output) output channels.
• Modulator-layer-scalar: a single scalar Modulator per linear projection.
• Modulator-layer-channel: a channel-wise Modulator per linear projection.
• Modulator-layer-channel-scalar (Transponder): a channel-wise Modulator per linear projection and a single scalar output Modulator per linear projection.

Table 1 shows two consistent trends across model scales. (i) The functional-path modulator does not aid training and can even destabilize optimization, whereas the layer-wise modulator consistently improves both training dynamics and final performance. (ii) With a layer-wise modulator in place, both channel-wise and scalar modulators further benefit Transponder: the scalar provides coarse, global control, while the channel-wise variant offers finer-grained adjustments. Using both together yields an additional, robust gain with only a modest $\sim 1\%$ parameter overhead.

Given its consistently best validation perplexity under comparable budgets and its favorable integration cost, we adopt Modulator–layer–channel–scalar as the default Transponder configuration for all subsequent comparisons against baseline methods.

4.4. Main Results for Language Modeling.

Table 2 compares validation perplexity (PPL; lower is better) across three LLaMA model scales. From the results, Transponder attains the best PPL wherever reported with only $\sim !1\%$ parameter overhead. Compared to the LLaMA baseline, Transponder reduces PPL on OpenWebText by 15.3% at 60M (26.56→22.50), 9.4% at 130M (19.27→17.45), and 13.6% at 250M (17.28→14.93); on C4 the reductions are 5.8% at 60M (30.31→28.55), 17.4% at 130M (26.73→22.09), and 14.6% at 250M (21.92→18.72). These gains persist through 250M under larger token budgets, indicating strong large-scale behavior.

Capacity-heavy gates (SDPA-Gate, ALL-Gate) improve PPL but require 15–80% extra parameters. In contrast, Transponder matches or exceeds these improvements with only $1\%$ overhead. Among minimal/zero-overhead baselines, LayerNorm Scaling is competitive yet still trails.

Several baselines that attempt to learn the mixing between the residual path and functional blocks exhibit instability at some scales (e.g., DeepNet and LAuReL-LR explode on C4-130M, 143.65 and 106.94 PPL; LAuReL-PA diverges on C4-130M with 1355 PPL and collapses on OpenWebText-250M to 257 PPL), whereas Transponder delivers consistent improvements across all reported settings.

Under comparable budgets, Transponder achieves state-of-the-art PPL with minimal overhead, strong large-scale behavior, and improved robustness, establishing it as our default configuration for subsequent comparisons.

4.5. Stability with Post-LayerNorm

Beyond the Pre-LN setting, we evaluate Transponder under the more delicate Post-LN regime. As shown in Table 3, vanilla LLaMA with Post-LN is unstable at scale: PPL explodes at 250M (1409.79), and even at 130M performance degrades to 26.95 in comparison to the Pre-LN LLaMA. In contrast, Transponder stabilizes training and improves accuracy in both cases, yielding a 4.6% PPL reduction at 130M (26.95$\to$25.71) and preventing divergence at 250M, where it achieves 20.28 PPL instead of catastrophic failure. While Post-LN remains slightly behind strong Pre-LN baselines at a similar scale, these results indicate that Transponder substantially enlarges the viable training regime for Post-LN models with only $\sim 1\%$ overhead, mitigating the well-known optimization fragility of Post-LN Transformers.

4.6. Ablations and Sensitivity Tests

• Contextual vs. Non-Contextual.

To assess the contribution of contextual modulation, we compare Transponder with and without contextual signals. In the non-contextual variant, for each layer l, we replace the contextual pathway with learnable parameters—a layer-wise scalar ${\beta }_1^{\left(l\right)}$ and a channel-wise vector ${\beta }_2^{\left(l\right)}$—and set

$${\mathcal{G}}_l={\tilde{\sigma }}_{{\alpha }_l}\left({\beta }_1^{\left(l\right)}·{\beta }_2^{\left(l\right)}\right),$$

where ${\beta }_1^{\left(l\right)}$ applies uniform scaling and ${\beta }_2^{\left(l\right)}$ provides per-channel modulation.

As shown in Table 4, the non-contextual variant already improves over the LLaMA baseline at certain scales, confirming the utility of the proposed modulator design. However, adding contextual control consistently delivers much larger gains across all model sizes, establishing it as the key driver of performance. This result directly supports our initial motivation: each component benefits from input-aware, contextual control rather than relying solely on static modulation.

• Sigmoid and Learnable Sigmoid.

A key innovation of Transponder is the introduction of a learnable sigmoid. This learnable non-linear modulation mechanism allows each modulator to dynamically adjust its sensitivity to the input, either amplifying or attenuating modulation strength as needed. As shown in Table 4, incorporating the learnable sigmoid consistently improves (except for 250M that is comparable)perplexity across model sizes, validating our design intuition that adaptive nonlinearity provides a crucial layer of flexibility for effective modulation.

• Hidden dimensions.

We further examine the effect of the hidden dimension r in the contextual modulator. Table 5 shows that even with an extremely compact setting ($r=2$), Transponder already delivers large gains over the LLaMA baseline. Scaling up the hidden size from 8 to 32 provides marginal yet consistent improvements. These findings suggest that the modulator does not require a large intermediate capacity to capture input-dependent scaling, underscoring the efficiency of our design: lightweight modulators suffice to model contextual dependencies while adding negligible parameter overhead.

• Contribution of functional components.

We next investigate which functional modules benefit most from modulation by selectively applying the contextual modulators to individual subcomponents (Table 6). Applying modulators to either the self-attention or MLP block alone yields clear improvements, while restricting modulation to partial components (e.g., only_first, only_last, only_qk) provides only limited gains.

We further evaluate the effect of removing the up- and gate-projections. In the original LLaMA design, the gate projection serves as a channel-wise modulator to the up-projection, though implemented as a full-rank matrix. Interestingly, excluding these projections leads to strong performance, second only to the full “all” configuration. This suggests that the gate-projections already play a key role in channel-wise contextual modulation.

Overall, the best results are consistently achieved when all components are modulated jointly (“all”), yielding the lowest PPL on both LLaMA-60M and LLaMA-130M. This confirms that full-path functional modulation is necessary to provide comprehensive control over residual transformations, enabling robust and consistent improvements across scales.

5. Contextual Modulator Values Analysis

The results in Section 4 suggest that, beyond static architectural scaling (e.g., fixed layer-normalization schemes), context-/input-sensitive modulation is a powerful way to improve optimization and expressivity in deep language models. Transponder learns, for each token and sub-layer (self-attention and FFN), both a layer scalar and channel-wise modulation. The question is whether these modulators truly encode context rather than acting as static rescalers.

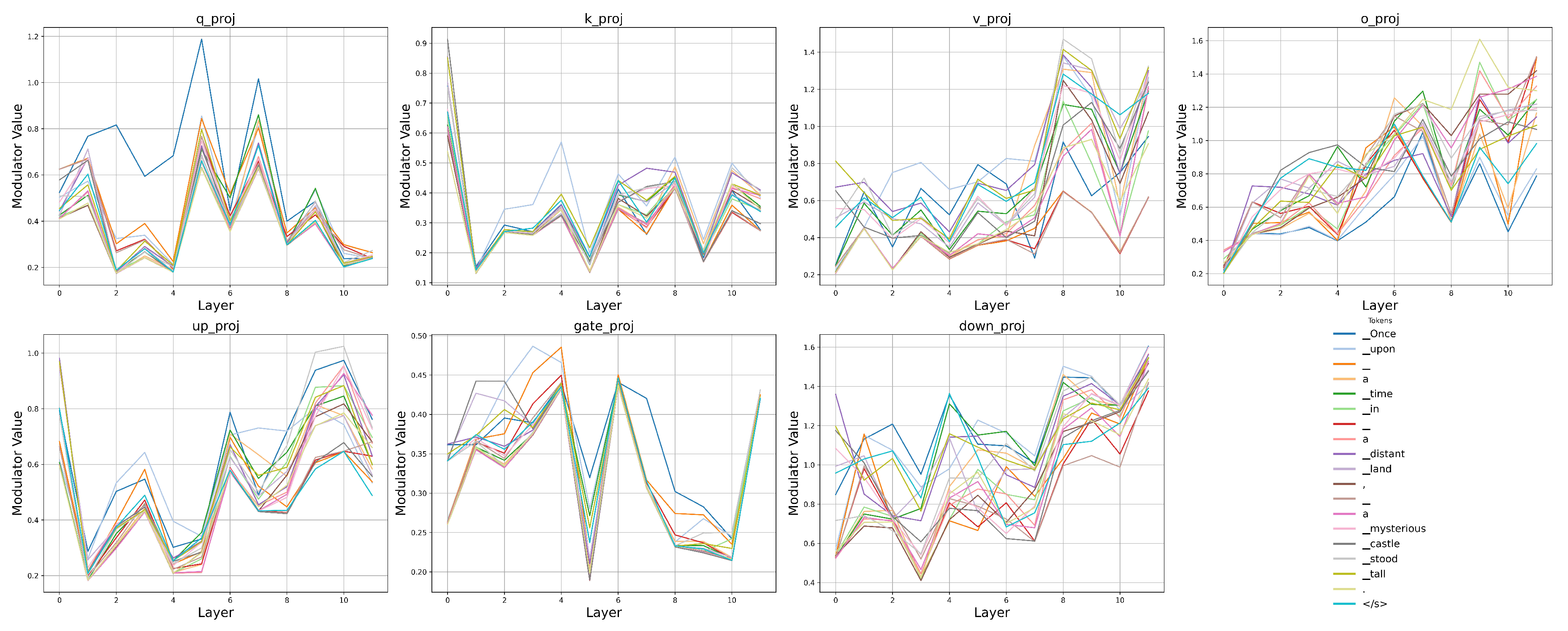
Figure 2 (layer-scalar, per module) shows clear depth- and module-specific structure with token-dependent variation. The traces for different tokens diverge at many layers, indicating context sensitivity. We observe systematic trends across modules: o_proj and down_proj steadily strengthen with depth, consistent with greater late-layer amplification; v_proj exhibits a pronounced surge in upper layers; up_proj follows a U-shaped pattern (early attenuation, late amplification); gate_proj remains in a tighter band with a mid-depth peak; and q_proj/k_proj show early suppression followed by recovery.

Figure A1 further confirms the effectiveness of the channel-wise modulation. Early layers are relatively flat, but mid–late layers develop structured ridges over both tokens and channels, with increasing contrast across depth. In particular, we observe a similar trend at some specific layers. For instance, at the 5th layer, one token exhibits very large modulator values across all channels, whereas in the 11th layer, one channel displays very large modulation values across the tokens.

Taken together, the two views indicate that Transponder learns structured, context-aware gains that evolve with depth and specialize by module and channel—precisely the behavior we would expect if the modulators were encoding useful contextual signals rather than acting as fixed, global scalars.

6. Conclusions

In this article, we proposed Transponder, a simple but effective way to modulate the sub-layers in Transformers context-aware. By pairing key projections and paths with compact modulators that produce scalar- and channel-wise gates, Transponder explicitly controls each component’s contribution at inference, separating representation from control. The design is minimally invasive—$\le 1\%$ parameter overhead—and broadly compatible with standard decoder blocks. Empirically, Transponder consistently improves language modeling quality across LLaMA backbones (60M–250M) on OpenWebText and C4. Under comparable budgets, it surpasses stronger, capacity-heavy gating schemes while remaining far lighter, and it outperforms static depth-aware scaling methods. Ablations map a practical design space. We find (i) layer-wise placement is preferable to coarse functional-path-only control; (ii) combining channel-wise modulator with a single scalar modulator per layer yields the best accuracy-cost trade-off; (iii) modulating all the layers is crucial. Modulator value analyses further show structured, token- and depth-dependent behaviors, providing direct evidence that adaptive scaling learns semantically meaningful control. The limitation of this work can be found in Appendix B.