Submitted:
31 May 2025
Posted:
02 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
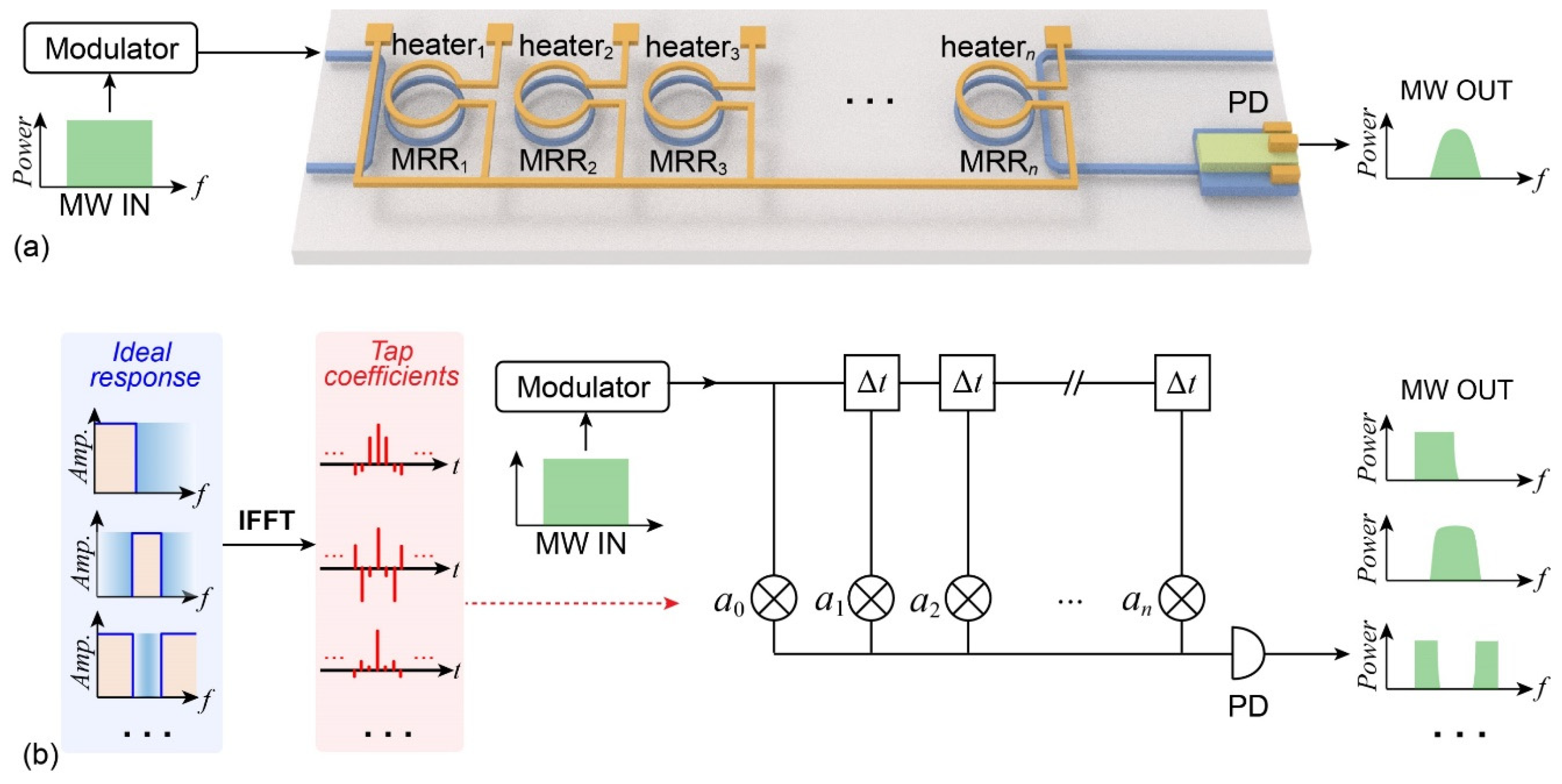
2. Principle
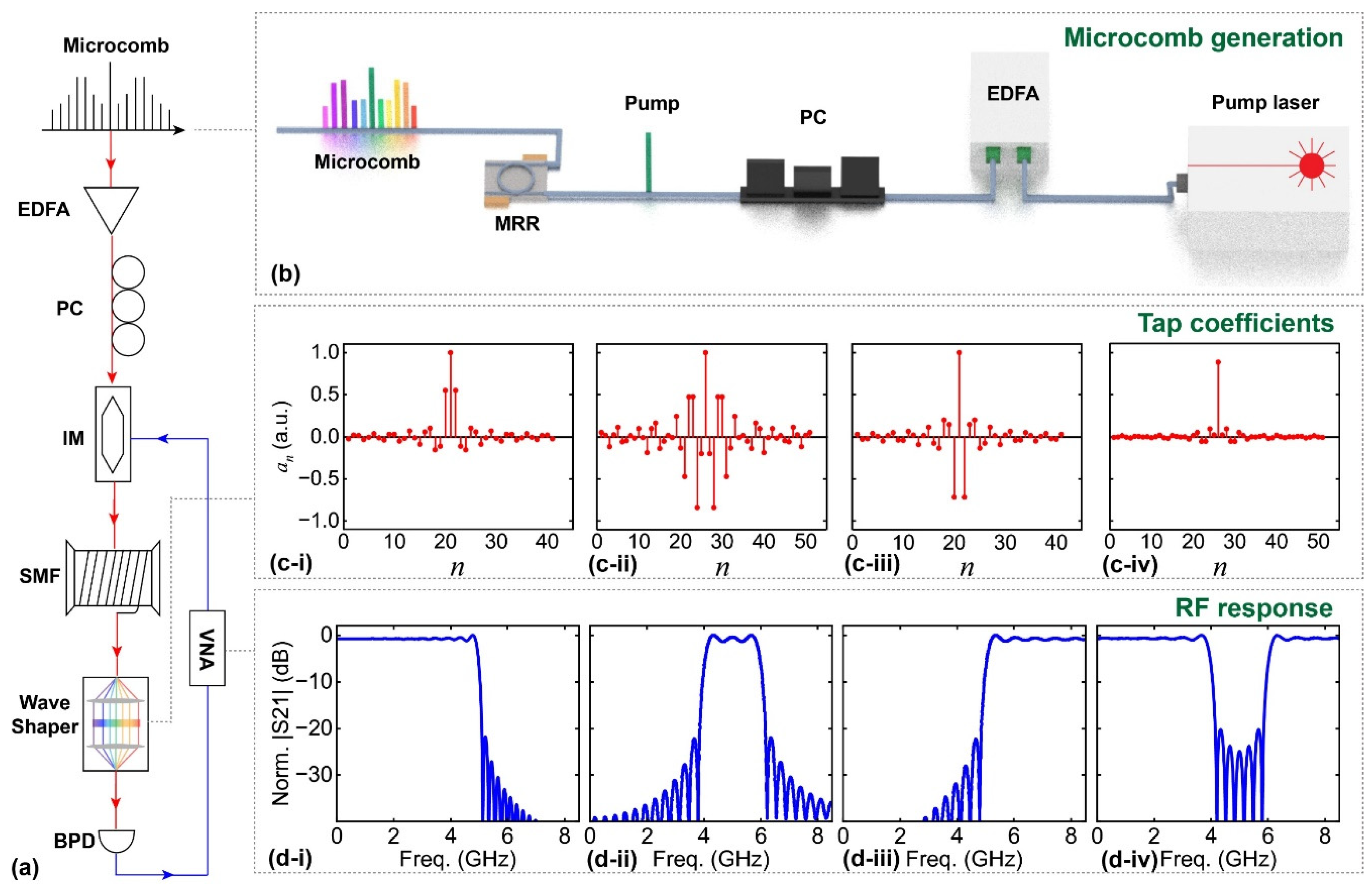
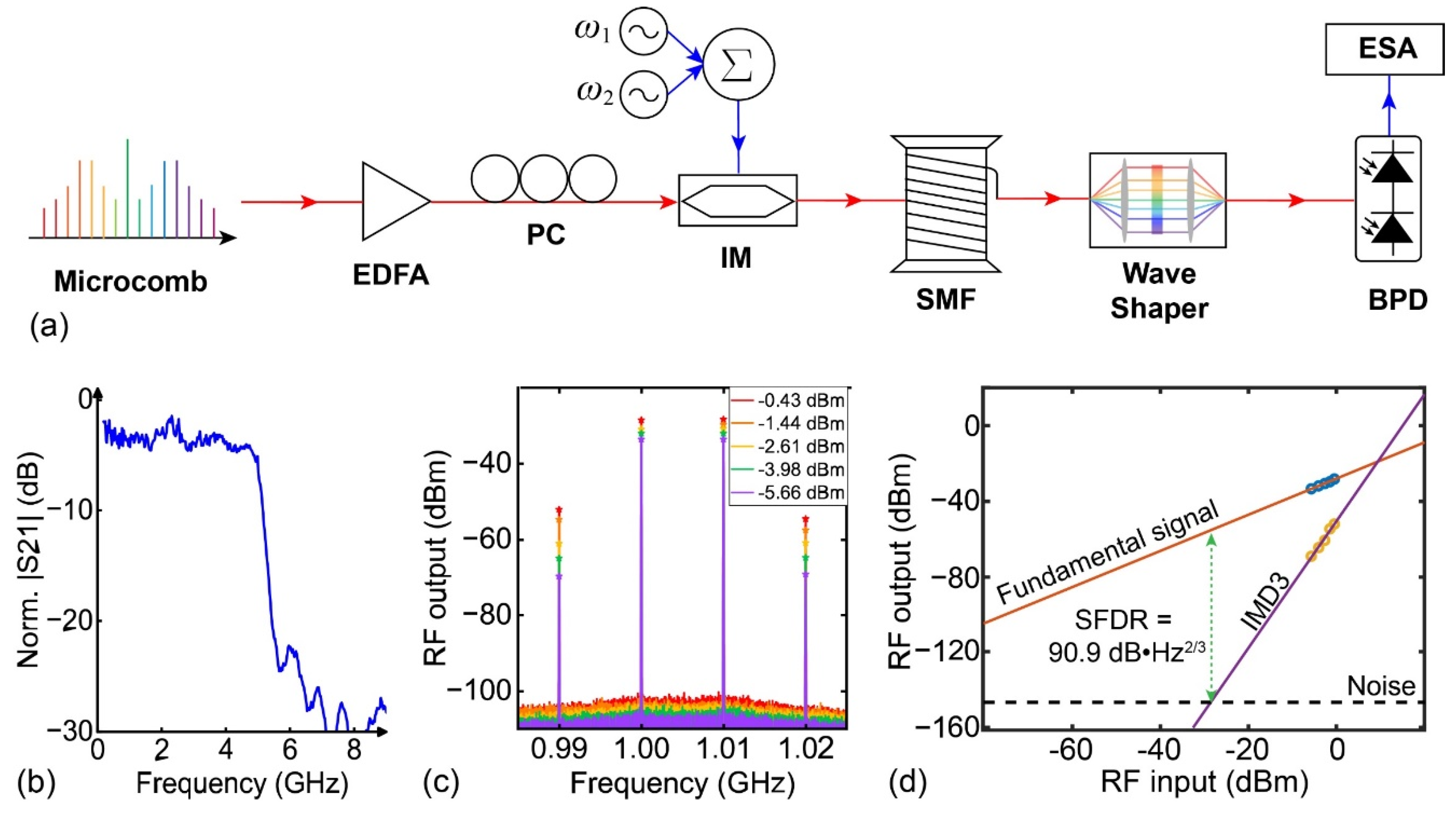
3. Experimental Demonstration
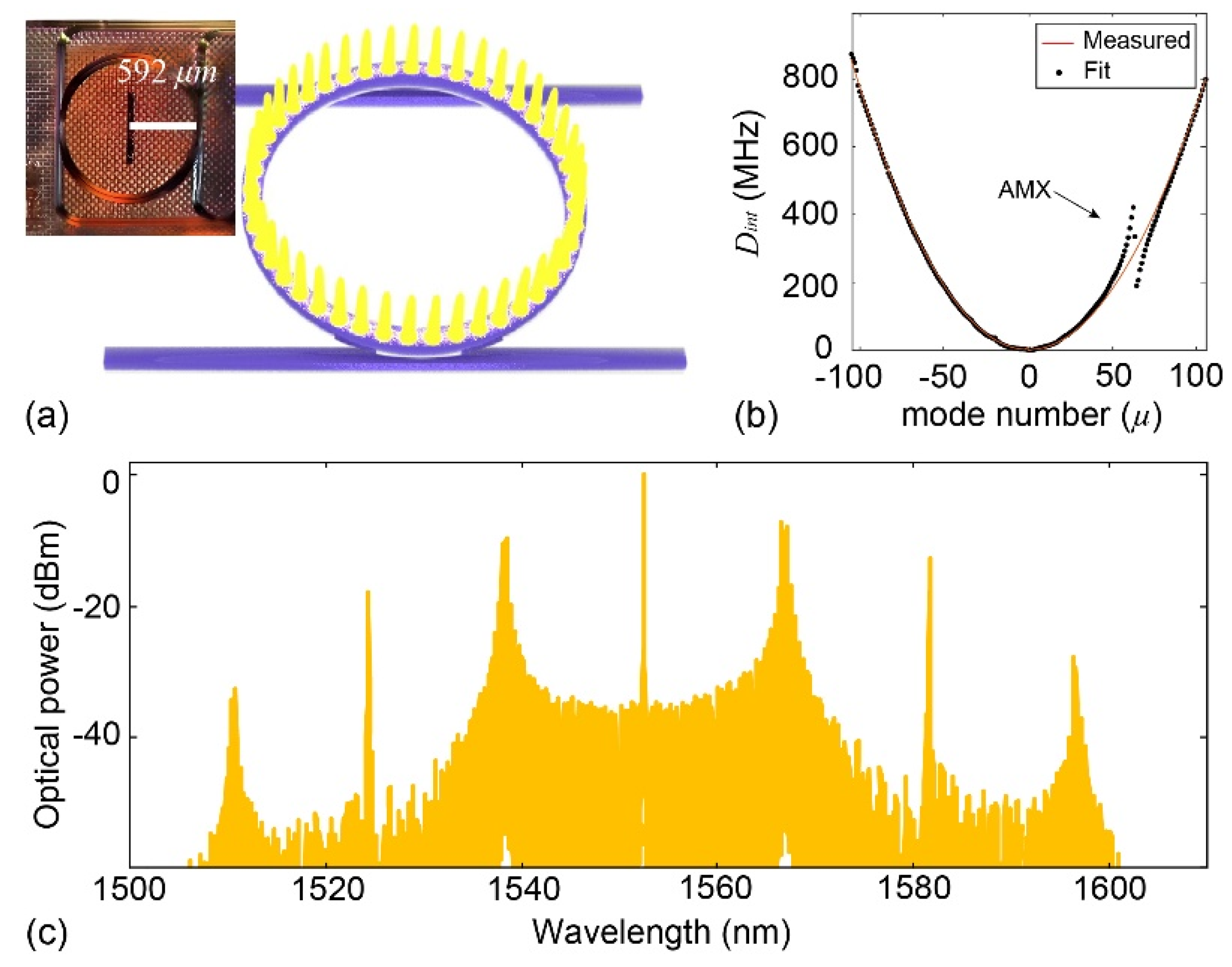
3.1. Soliton Crystal Microcomb
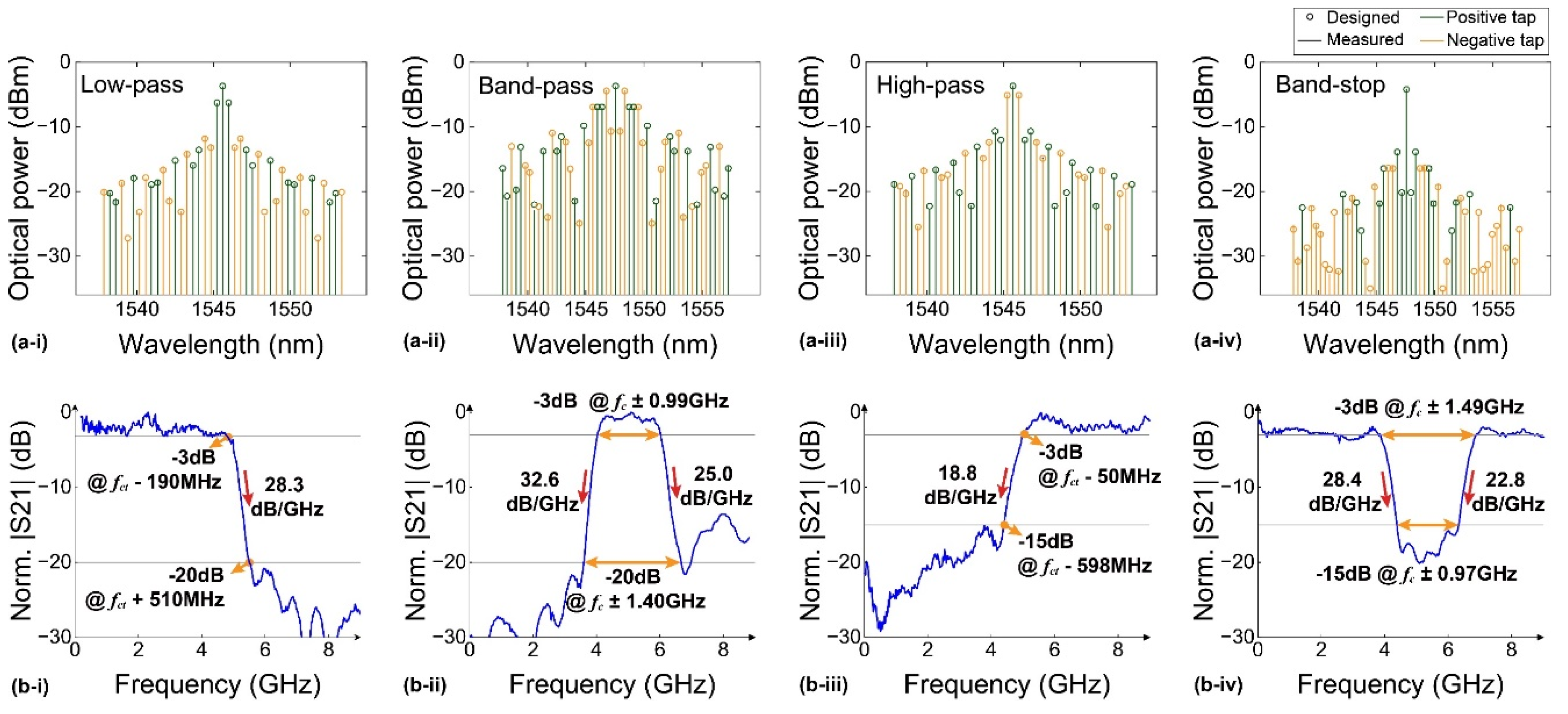
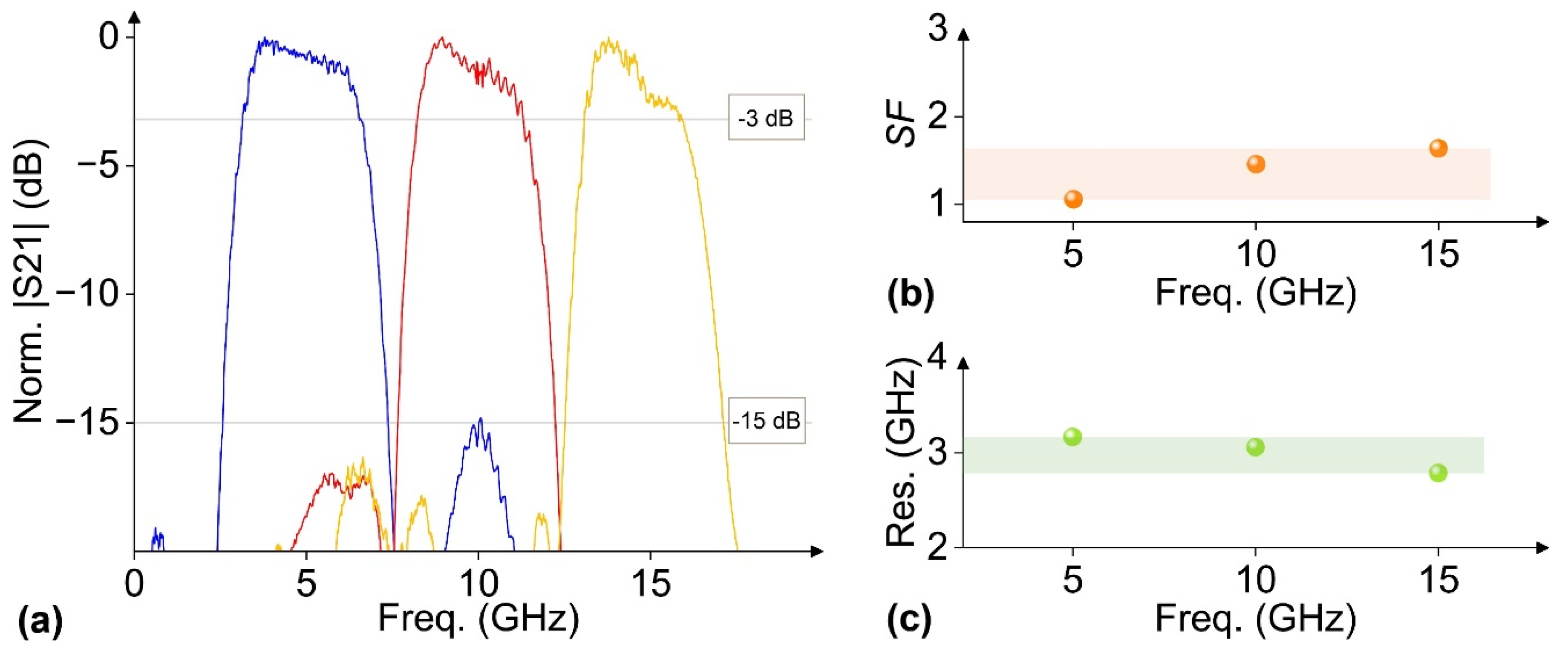
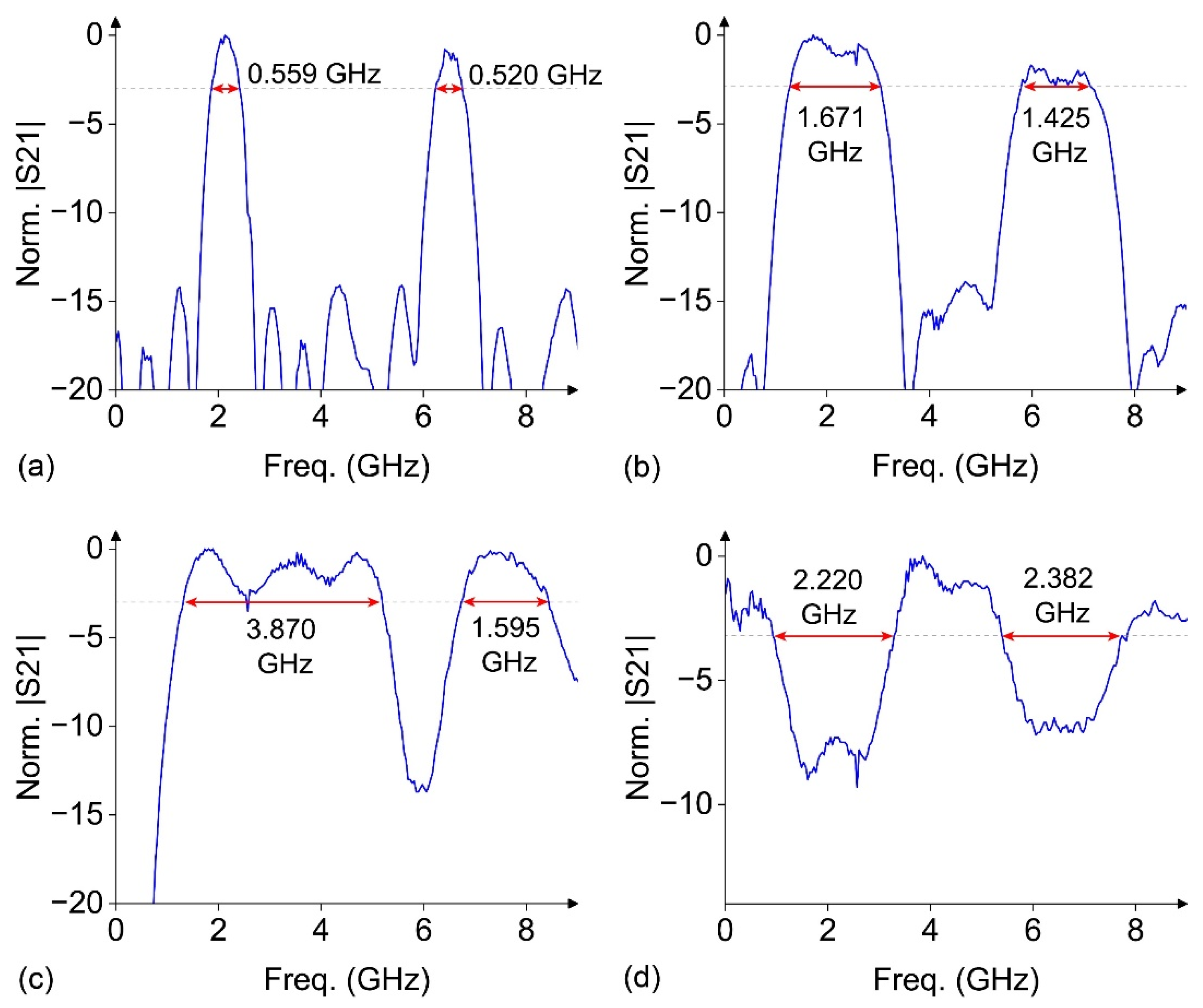
3.2. Ultrahigh-Performance Adaptive MWP Filters
4. Conclusions
Conflicts of Interest
References
- J. Yao, “Microwave Photonic Systems,” Journal of Lightwave Technology, vol. 40, no. 20, pp. 6595-6607, 2022.
- Y. Liu et al., “Integrated microwave photonic filters,” Adv. Opt. Photon., vol. 12, no. 2, pp. 485-555, 2020.
- Q. Zhang et al., “A single passband microwave photonic filter with enhanced flat top and shape factor based on tunable optical bandpass filter and fiber Bragg gratings,” Optics & Laser Technology, vol. 168, pp. 109838, 2024.
- J. Capmany et al., “A Tutorial on Microwave Photonic Filters,” Journal of Lightwave Technology, vol. 24, no. 1, pp. 201, 2006.
- L. Xu et al., “Silicon-on-insulator-based microwave photonic filter with widely adjustable bandwidth,” Photonics Res., vol. 7, no. 2, pp. 110-115, 2019.
- C. Porzi et al., “Silicon-on-Insulator Microwave Photonic Filter With Widely Tunable and Reconfigurable Flat-Top Bandpass Functionality,” Journal of Lightwave Technology, vol. 40, no. 20, pp. 6666-6675, 2022.
- W. Cheng et al., “Tunable bandpass microwave photonic filter with largely reconfigurable bandwidth and steep shape factor based on cascaded silicon nitride micro-ring resonators,” Opt. Express, vol. 31, no. 16, pp. 25648-25661, 2023.
- L. Liu et al., “Ultra-High Peak Rejection, Sub-Gigahertz Narrowband and Bandwidth Tunable Microwave Photonic Filter Based on Silicon Racetrack Resonators,” Journal of Lightwave Technology, vol. 41, no. 18, pp. 5820-5826, 2023.
- Y. Liu et al., “Reconfigurable Microwave Photonic Bandpass Filter Based on CROW,” Journal of Lightwave Technology, vol. 42, no. 5, pp. 1597-1604, 2024.
- L. Huo et al., “IIR Microwave Photonic Filters Based on Homogeneous Multicore Fibers,” Journal of Lightwave Technology, vol. 36, no. 19, pp. 4298-4304, 2018.
- Liu et al., “Ultrahigh-Q microwave photonic filter with tunable Q value utilizing cascaded optical-electrical feedback loops,” Opt. Lett., vol. 38, no. 21, pp. 4304-4307, 2013.
- H. Yan et al., “Wideband-Tunable on-Chip Microwave Photonic Filter with Ultrahigh-Q U-Bend-Mach–Zehnder-Interferometer-Coupled Microring Resonators,” Laser Photon. Rev., vol. 17, no. 11, pp. 2300347, 2023.
- Liu et al., “Si3N4-Based Narrowband and High Peak Rejection Microwave Photonic Filter With Adjustable Bandwidth,” Journal of Lightwave Technology, vol. 42, no. 5, pp. 1580-1585, 2024.
- Garrett et al., “Integrated microwave photonic notch filter using a heterogeneously integrated Brillouin and active-silicon photonic circuit,” Nat. Commun., vol. 14, no. 1, pp. 7544, 2023.
- R. Zhang et al., “Tunable Microwave Photonic Filter with Ultra-Narrow Passband and High Out-of-Band Rejection,” Journal of Lightwave Technology, pp. 1-8, 2024.
- D. B. Hunter et al., “Tunable optical transversal filter based on chirped gratings,” Electronics Letters, 31, 1995. Available online: https://digital-library.theiet.org/content/journals/10.1049/el_19951495.
- Z. Zhu et al., “All-positive-coefficient microwave photonic filter with rectangular response,” Opt. Lett., vol. 42, no. 15, pp. 3012-3015, 2017.
- X. Xu et al., “Advanced Adaptive Photonic RF Filters with 80 Taps Based on an Integrated Optical Micro-Comb Source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288-1295, 2019.
- X. Xu et al., “High performance RF filters via bandwidth scaling with Kerr micro-combs,” APL Phontonics, vol. 4, no. 2, pp. 8, 2019.
- Y. Sun et al., “Applications of optical microcombs,” Adv. Opt. Photon., vol. 15, no. 1, pp. 86-175, 2023.
- Pasquazi et al., “Micro-combs: A novel generation of optical sources,” Physics Reports, vol. 729, pp. 1-81, 2018.
- L. Chang et al., “Integrated optical frequency comb technologies,” Nat. Photonics, vol. 16, no. 2, pp. 95-108, 2022.
- X. Xu et al., “11 TOPS photonic convolutional accelerator for optical neural networks,” Nature, vol. 589, no. 7840, pp. 44-51, 2021.
- S. Chen et al., “High-Bit-Efficiency TOPS Optical Tensor Convolutional Accelerator Using Microcombs,” Laser Photon. Rev., vol. 19, no. 9, pp. 2401975, 2025.
- Bai et al., “TOPS-speed complex-valued convolutional accelerator for feature extraction and inference,” Nat. Commun., vol. 16, no. 1, pp. 292, 2025.
- Xu et al., “Advanced RF and microwave functions based on an integrated optical frequency comb source,” Opt. Express, vol. 26, no. 3, pp. 2569-2583, 2018.
- J. Capmany et al., “Discrete-time optical processing of microwave signals,” Journal of Lightwave Technology, vol. 23, no. 2, pp. 702-723, 2005.
- L. Razzari et al., “CMOS-compatible integrated optical hyper-parametric oscillator,” Nat. Photonics, vol. 4, no. 1, pp. 41-45, 2010.
- D. Moss et al., “New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics,” Nat. Photonics, vol. 7, no. 8, pp. 597-607, 2013.
- X. Xu et al., “Photonic Perceptron Based on a Kerr Microcomb for High-Speed, Scalable, Optical Neural Networks,” Laser Photon. Rev., vol. 14, no. 10, pp. 10, 2020.
- E. Murray et al., “Investigating the thermal robustness of soliton crystal microcombs,” Opt. Express, vol. 31, no. 23, pp. 37749-37762, 2023.
- W. Wang et al., “Robust soliton crystals in a thermally controlled microresonator,” Opt. Lett., vol. 43, no. 9, pp. 2002-2005, 2018.
- Corcoran et al., “Ultra-dense optical data transmission over standard fibre with a single chip source,” Nat. Commun., vol. 11, no. 1, pp. 7, 2020.
- X. Xu et al., “High performance RF filters via bandwidth scaling with Kerr micro-combs,” APL Phontonics, vol. 4, no. 2, pp. 026102, 2019.
- Y. Li et al., “Performance Analysis of Microwave Photonic Spectral Filters based on Optical Microcombs,” Advanced Physics Research, vol. 4, no. 1, pp. 2400084, 2025.
- Y. Li et al., “Feedback Control in Microwave Photonic Transversal Filter Systems Based on Optical Microcombs,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 30, no. 5: Microresonator Frequency Comb Technologies, pp. 1-17, 2024.
- Y. Sun et al., “Optimizing the Accuracy of Microcomb-Based Microwave Photonic Transversal Signal Processors,” Journal of Lightwave Technology, vol. 41, no. 23, pp. 7223-7237, 2023.
- L. Juseop et al., “A dual-passband filter of canonical structure for satellite applications,” IEEE Microwave and Wireless Components Letters, vol. 14, no. 6, pp. 271-273, 2004.
- W. S. Chang et al., “Analytical Design of Microstrip Short-Circuit Terminated Stepped-Impedance Resonator Dual-Band Filters,” IEEE Transactions on Microwave Theory and Techniques, vol. 59, no. 7, pp. 1730-1739, 2011.
- L. Gao et al., “Microwave Photonic Filter With Two Independently Tunable Passbands Using a Phase Modulator and an Equivalent Phase-Shifted Fiber Bragg Grating,” IEEE Transactions on Microwave Theory and Techniques, vol. 62, no. 2, pp. 380-387, 2014.
- Marpaung et al., “Integrated microwave photonics,” Laser Photon. Rev., vol. 7, no. 4, pp. 506-538, 2013.
- V. J. Urick et al., Fundamentals of microwave photonics: John Wiley & Sons, 2015.
- M. Garrett et al., “Multi-Band and Frequency-Agile Chip-Based RF Photonic Filter for Ultra-Deep Interference Rejection,” Journal of Lightwave Technology, vol. 40, no. 6, pp. 1672-1680, 2022.
- Y. Stern et al., “Tunable sharp and highly selective microwave-photonic band-pass filters based on stimulated Brillouin scattering,” Photonics Res., vol. 2, no. 4, pp. B18-B25, 2014.
- M. Nikles et al., “Brillouin gain spectrum characterization in single-mode optical fibers,” Journal of Lightwave Technology, vol. 15, no. 10, pp. 1842-1851, 1997.
- Choudhary et al., “Tailoring of the Brillouin gain for on-chip widely tunable and reconfigurable broadband microwave photonic filters,” Opt. Lett., vol. 41, no. 3, pp. 436-439, 2016.
- J. S. Fandiño et al., “A monolithic integrated photonic microwave filter,” Nat. Photonics, vol. 11, no. 2, pp. 124-129, 2017.
- L. Razzari, et al., “CMOS-compatible integrated optical hyper-parametric oscillator,” Nature Photonics, vol. 4, no. 1, pp. 41-45, 2010.
- J. Moss, R. Morandotti, A. L. Gaeta, and M. Lipson, “New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics,” Nature Photonics, vol. 7, no. 8, pp. 597-607, 2013/08/01, 2013.
- Pasquazi, et al., “Sub-picosecond phase-sensitive optical pulse characterization on a chip”, Nature Photonics, vol. 5, no. 10, pp. 618-623 (2011).
- M Ferrera et al., “On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Optics Express vol. 19 (23), 23153-23161 (2011).
- Bao, C., et al., Direct soliton generation in microresonators, Opt. Lett, 42, 2519 (2017).
- M.Ferrera et al., “CMOS compatible integrated all-optical RF spectrum analyzer”, Optics Express, vol. 22, no. 18, 21488 - 21498 (2014).
- M. Kues, et al., “Passively modelocked laser with an ultra-narrow spectral width”, Nature Photonics, vol. 11, no. 3, pp. 159, 2017.
- M. Ferrera, et al., “Low-power continuous-wave nonlinear optics in doped silica glass integrated waveguide structures,” Nature Photonics, vol. 2, no. 12, pp. 737-740, 2008.
- M.Ferrera et al.“On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Opt. Express, vol. 19, (23)pp. 23153-23161 (2011).
- D. Duchesne, M. Peccianti, M. R. E. Lamont, et al., “Supercontinuum generation in a high index doped silica glass spiral waveguide,” Optics Express, vol. 18, no, 2, pp. 923-930, 2010.
- H Bao, L Olivieri, M Rowley, ST Chu, BE Little, R Morandotti, DJ Moss, … “Turing patterns in a fiber laser with a nested microresonator: Robust and controllable microcomb generation”, Physical Review Research vol. 2 (2), 023395 (2020).
- M. Ferrera, et al., “On-chip CMOS-compatible all-optical integrator”, Nature Communications, vol. 1, Article 29, 2010.
- Pasquazi, et al., “All-optical wavelength conversion in an integrated ring resonator,” Optics Express, vol. 18, no. 4, pp. 3858-3863, 2010.
- A.Pasquazi, Y. Park, J. Azana, et al., “Efficient wavelength conversion and net parametric gain via Four Wave Mixing in a high index doped silica waveguide,” Optics Express, vol. 18, no. 8, pp. 7634-7641, 2010.
- Peccianti, M. Ferrera, L. Razzari, et al., “Subpicosecond optical pulse compression via an integrated nonlinear chirper,” Optics Express, vol. 18, no. 8, pp. 7625-7633, 2010.
- M Ferrera, Y Park, L Razzari, BE Little, ST Chu, R Morandotti, DJ Moss, … et al., “All-optical 1st and 2nd order integration on a chip”, Optics Express vol. 19 (23), 23153-23161 (2011).
- M. Ferrera et al., “Low Power CW Parametric Mixing in a Low Dispersion High Index Doped Silica Glass Micro-Ring Resonator with Q-factor > 1 Million”, Optics Express, vol.17, no. 16, pp. 14098–14103 (2009).
- M. Peccianti, et al., “Demonstration of an ultrafast nonlinear microcavity modelocked laser”, Nature Communications, vol. 3, pp. 765, 2012.
- A.Pasquazi, et al., “Self-locked optical parametric oscillation in a CMOS compatible microring resonator: a route to robust optical frequency comb generation on a chip,” Optics Express, vol. 21, no. 11, pp. 13333-13341, 2013.
- A.Pasquazi, et al., “Stable, dual mode, high repetition rate mode-locked laser based on a microring resonator,” Optics Express, vol. 20, no. 24, pp. 27355-27362, 2012.
- Pasquazi, A. et al. Micro-combs: a novel generation of optical sources. Physics Reports 729, 1-81 (2018).
- H. Bao, et al., Laser cavity-soliton microcombs, Nature Photonics, vol. 13, no. 6, pp. 384-389, Jun. 2019.
- Antonio Cutrona, Maxwell Rowley, Debayan Das, Luana Olivieri, Luke Peters, Sai T. Chu, Brent L. Little, Roberto Morandotti, David J. Moss, Juan Sebastian Totero Gongora, Marco Peccianti, Alessia Pasquazi, “High Conversion Efficiency in Laser Cavity-Soliton Microcombs”, Optics Express Vol. 30, Issue 22, pp. 39816-39825 (2022). [CrossRef]
- Cutrona, M. Rowley, A. Bendahmane, V. Cecconi, L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Nonlocal bonding of a soliton and a blue-detuned state in a microcomb laser”, Nature Communications Physics 6 Article 259 (2023). [CrossRef]
- Aadhi A. Rahim, Imtiaz Alamgir, Luigi Di Lauro, Bennet Fischer, Nicolas Perron, Pavel Dmitriev, Celine Mazoukh, Piotr Roztocki, Cristina Rimoldi, Mario Chemnitz, Armaghan Eshaghi, Evgeny A. Viktorov, Anton V. Kovalev, Brent E. Little, Sai T. Chu, David J. Moss, and Roberto Morandotti, “Mode-locked laser with multiple timescales in a microresonator-based nested cavity”, APL Photonics9 031302 (2024). [CrossRef]
- Andrew Cooper, Luana Olivieri, Antonio Cutrona, Debayan Das, Luke Peters, Sai Tak Chu, Brent Little, Roberto Morandotti, David J Moss, Marco Peccianti, and Alessia Pasquazi, “Parametric interaction of laser cavity-solitons with an external CW pump”, Optics Express 32 (12), 21783-21794 (2024).
- Cutrona, M. Rowley, A. Bendahmane, V. Cecconi, L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Stability Properties of Laser Cavity-Solitons for Metrological Applications”, Applied Physics Letters vol. 122 (12) 121104 (2023). [CrossRef]
- Caitlin E. Murray, Mengxi Tan, Chawaphon Prayoonyong, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, David J. Moss and Bill Corcoran, “Investigating the thermal robustness of soliton crystal microcombs”, Optics Express 31(23), 37749-37762 (2023).
- Yonghang Sun, James Salamy, Caitlin E. Murry, Brent E. Little, Sai T. Chu, Roberto Morandotti, Arnan Mitchell, David J. Moss, Bill Corcoran, “Enhancing laser temperature stability by passive self-injection locking to a micro-ring resonator”, Optics Express 32 (13) 23841-23855 (2024). [CrossRef]
- Yonghang Sun, James Salamy, Caitlin E. Murray, Xiaotian Zhu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, Sai T. Chu, David J. Moss, Bill Corcoran, “Self-locking of free-running DFB lasers to a single microring resonator for dense WDM”, Journal of Lightwave Technology 43, (4) 1995-2002 (2025). [CrossRef]
- X. Xu, J. Wu, M. Shoeiby, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source,” APL Photonics, vol. 2, no. 9, 096104, Sep. 2017.
- Xu, X., et al., Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated micro-comb source, Photonics Research, vol. 6, B30-B36 (2018).
- X. Xu, M. Tan, J. Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “Microcomb-based photonic RF signal processing”, IEEE Photonics Technology Letters, vol. 31 no. 23 1854-1857, 2019.
- Xu, et al., “Advanced adaptive photonic RF filters with 80 taps based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288-1295 (2019).
- X. Xu, et al., “Photonic RF and microwave integrator with soliton crystal microcombs”, IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 12, pp. 3582-3586, 2020. [CrossRef]
- X. Xu, et al., “High performance RF filters via bandwidth scaling with Kerr micro-combs,” APL Photonics, vol. 4 (2) 026102. 2019.
- M. Tan, et al., “Microwave and RF photonic fractional Hilbert transformer based on a 50 GHz Kerr micro-comb”, Journal of Lightwave Technology, vol. 37, no. 24, pp. 6097 – 6104, 2019.
- M. Tan, et al., “RF and microwave fractional differentiator based on photonics”, IEEE Transactions on Circuits and Systems: Express Briefs, vol. 67, no.11, pp. 2767-2771, 2020. [CrossRef]
- M. Tan, et al., “Photonic RF arbitrary waveform generator based on a soliton crystal micro-comb source”, Journal of Lightwave Technology, vol. 38, no. 22, pp. 6221-6226 (2020). [CrossRef]
- M. Tan, X. Xu, J. Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “RF and microwave high bandwidth signal processing based on Kerr Micro-combs”, Advances in Physics X, VOL. 6, NO. 1, 1838946 (2021). [CrossRef]
- X. Xu, et al., “Advanced RF and microwave functions based on an integrated optical frequency comb source,” Opt. Express, vol. 26 (3) 2569 (2018).
- M. Tan, X. Xu, J. Wu, B. Corcoran, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Lowery, A. Mitchell, and D. J. Moss, ““Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb”, Journal of Lightwave Technology vol. 39 (24) 7581-7587 (2021).
- Wu, J. et al. RF Photonics: An Optical Microcombs’ Perspective. IEEE Journal of Selected Topics in Quantum Electronics Vol. 24, 6101020, 1-20 (2018).
- T. G. Nguyen et al., “Integrated frequency comb source-based Hilbert transformer for wideband microwave photonic phase analysis,” Opt. Express, vol. 23, no. 17, pp. 22087-22097, Aug. 2015.
- X. Xu, et al., “Broadband RF channelizer based on an integrated optical frequency Kerr comb source,” Journal of Lightwave Technology, vol. 36, no. 19, pp. 4519-4526, 2018.
- X. Xu, et al., “Continuously tunable orthogonally polarized RF optical single sideband generator based on micro-ring resonators,” Journal of Optics, vol. 20, no. 11, 115701. 2018.
- X. Xu, et al., “Orthogonally polarized RF optical single sideband generation and dual-channel equalization based on an integrated microring resonator,” Journal of Lightwave Technology, vol. 36, no. 20, pp. 4808-4818. 2018.
- X. Xu, et al., “Photonic RF phase-encoded signal generation with a microcomb source”, J. Lightwave Technology, vol. 38, no. 7, 1722-1727, 2020.
- X. Xu, et al., Broadband microwave frequency conversion based on an integrated optical micro-comb source”, Journal of Lightwave Technology, vol. 38 no. 2, pp. 332-338, 2020.
- M. Tan, et al., “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Comm. vol. 465,125563, Feb. 22. 2020.
- X. Xu, et al., “Broadband photonic RF channelizer with 90 channels based on a soliton crystal microcomb”, Journal of Lightwave Technology, Vol. 38, no. 18, pp. 5116 – 5121 (2020). [CrossRef]
- M. Tan et al, “Orthogonally polarized Photonic Radio Frequency single sideband generation with integrated micro-ring resonators”, IOP Journal of Semiconductors, Vol. 42 (4), 041305 (2021). [CrossRef]
- Mengxi Tan, X. Xu, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and David J. Moss, “Photonic Radio Frequency Channelizers based on Kerr Optical Micro-combs”, IOP Journal of Semiconductors Vol. 42 (4), 041302 (2021). [CrossRef]
- Corcoran, et al., “Ultra-dense optical data transmission over standard fiber with a single chip source”, Nature Communications, vol. 11, Article:2568, 2020.
- X. Xu et al, “Photonic perceptron based on a Kerr microcomb for scalable high speed optical neural networks”, Laser and Photonics Reviews, vol. 14, no. 8, 2000070 (2020). [CrossRef]
- X. Xu, et al., “11 TOPs photonic convolutional accelerator for optical neural networks”, Nature vol. 589, 44-51 (2021).
- Xingyuan Xu, Weiwei Han, Mengxi Tan, Yang Sun, Yang Li, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, Kun Xu, and David J. Moss, “Neuromorphic computing based on wavelength-division multiplexing”, IEEE Journal of Selected Topics in Quantum Electronics 29 (2) 7400112 (2023). [CrossRef]
- Yunping Bai, Xingyuan Xu,1, Mengxi Tan, Yang Sun, Yang Li, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, Kun Xu, and David J. Moss, “Photonic multiplexing techniques for neuromorphic computing”, Nanophotonics vol. 12 (5): 795–817 (2023). [CrossRef]
- Chawaphon Prayoonyong, Andreas Boes, Xingyuan Xu, Mengxi Tan, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, David J. Moss, and Bill Corcoran, “Frequency comb distillation for optical superchannel transmission”, Journal of Lightwave Technology vol. 39 (23) 7383-7392 (2021). [CrossRef]
- Mengxi Tan, Xingyuan Xu, Jiayang Wu, Bill Corcoran, Andreas Boes, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Integral order photonic RF signal processors based on a soliton crystal micro-comb source”, IOP Journal of Optics vol. 23 (11) 125701 (2021). [CrossRef]
- Yang Sun, Jiayang Wu, Yang Li, Xingyuan Xu, Guanghui Ren, Mengxi Tan, Sai Tak Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Optimizing the performance of microcomb based microwave photonic transversal signal processors”, Journal of Lightwave Technology vol. 41 (23) pp 7223-7237 (2023). [CrossRef]
- Mengxi Tan, Xingyuan Xu, Andreas Boes, Bill Corcoran, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Jiayang Wu, Arnan Mitchell, and David J. Moss, “Photonic signal processor for real-time video image processing based on a Kerr microcomb”, Nature Communications Engineering 2 94 (2023). [CrossRef]
- Mengxi Tan, Xingyuan Xu, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Communications, vol. 465, Article: 125563 (2020). [CrossRef]
- Yang Sun, Jiayang Wu, Yang Li, Mengxi Tan, Xingyuan Xu, Sai Chu, Brent Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Quantifying the Accuracy of Microcomb-based Photonic RF Transversal Signal Processors”, IEEE Journal of Selected Topics in Quantum Electronics vol. 29 no. 6, pp. 1-17, Art no. 7500317 (2023). [CrossRef]
- Yang Li, Yang Sun, Jiayang Wu, Guanghui Ren, Bill Corcoran, Xingyuan Xu, Sai T. Chu, Brent. E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Processing accuracy of microcomb-based microwave photonic signal processors for different input signal waveforms”, MDPI Photonics 10, 10111283 (2023). [CrossRef]
- Yang Sun, Jiayang Wu, Yang Li, and David J. Moss, “Comparison of microcomb-based RF photonic transversal signal processors implemented with discrete components versus integrated chips”, MDPI Micromachines 14, 1794 (2023). [CrossRef]
- Mengxi Tan, David J. Moss, “The laser trick that could put an ultraprecise optical clock on a chip”, Nature 624, (7991) 256-257 (2023). [CrossRef]
- Weiwei Han, Zhihui Liu, Yifu Xu, Mengxi Tan, Chaoran Huang, Jiayang Wu, Kun Xu, David J. Moss, and Xingyuan Xu, “Photonic RF Channelization Based on Microcombs”, IEEE Journal of Selected Topics in Quantum Electronics 30 (5) 7600417 (2024). [CrossRef]
- Yang Li, Yang Sun, Jiayang Wu, Guanghui Ren, Xingyuan Xu, Mengxi Tan, Sai Chu, Brent Little, Roberto Morandotti, Arnan Mitchell, and David Moss, “Feedback control in micro-comb-based microwave photonic transversal filter systems”, IEEE Journal of Selected Topics in Quantum Electronics Vol. 30(5) 2900117 (2024). [CrossRef]
- Weiwei Han, Zhihui Liu, Yifu Xu, Mengxi Tan, Yuhua Li, Xiaotian Zhu, Yanni Ou, Feifei Yin, Roberto Morandotti, Brent E. Little, Sai Tak Chu, Xingyuan Xu, David J. Moss, and Kun Xu, “Dual-polarization RF Channelizer Based on Microcombs”, Optics Express 32, No. 7, 11281-11295 (2024). [CrossRef]
- Zhihui Liu, Haoran Zhang, Yuhang Song, Xiaotian Zhu, Yunping Bai, Mengxi Tan, Bill Corcoran, Caitlin Murphy, Sai T. Chu, David J. Moss, Xingyuan Xu, and Kun Xu, “Advances in Soliton Crystals Microcombs”, Photonics Vol. 11, 1164 (2024). [CrossRef]
- Mazoukh, L. Di Lauro, I. Alamgir1 B. Fischer, A. Aadhi, A. Eshaghi, B. E. Little, S. T. Chu, D. J. Moss, and R. Morandotti, “Genetic algorithm-enhanced microcomb state generation”, Nature Communications Physics Vol. 7, Article: 81 (2024). [CrossRef]
- Shifan Chen, Yixuan Zheng, Yifu Xu, Xiaotian Zhu, Sirui Huang, Shuai Wang, Xiaoyan Xu, Chengzhuo Xia, Zhihui Liu, Chaoran Huang, Roberto Morandotti, Sai T. Chu, Brent E. Little, Bill Corcoran, Yuyang Liu, Yunping Bai, David J. Moss, Xingyuan Xu, and Kun Xu, “High-bit-efficiency TOPS optical tensor convolutional accelerator using micro-combs”, Laser & Photonics Reviews 19 2401975 (2025). [CrossRef]
- Weiwei Han, Zhihui Liu, Yifu Xu, Mengxi Tan, Yuhua Li, Xiaotian Zhu, Yanni Ou, Feifei Yin, Roberto Morandotti, Brent E. Little, Sai Tak Chu, David J. Moss, Xingyuan Xu, and Kun Xu, “TOPS-speed complex-valued convolutional accelerator for feature extraction and inference”, Nature Communications 16 292 (2025). [CrossRef]
- Yang Li, Yang Sun, Jiayang Wu, Guanghui Ren, Roberto Morandotti, Xingyuan Xu, Mengxi Tan, Arnan Mitchell, and David J. Moss, “Performance analysis of microwave photonic spectral filters based on optical microcombs”, Advanced Physics Research 4 (9) 2400084 (2025). [CrossRef]
- Luigi di Lauro, Stefania Sciara, Bennet Fischer, Junliang Dong, Imtiaz Alamgir, Benjamin Wetzel, Goëry Genty, Mitchell Nichols, Armaghan Eshaghi, David J. Moss, Roberto Morandotti, “Optimization Methods for Integrated and Programmable Photonics in Next-Generation Classical and Quantum Smart Communication and Signal Processing”, Advances in Optics and Photonics Vol. 17 (2) (2025).
- Bill Corcoran, Arnan Mitchell, Roberto Morandotti, Leif K. Oxenlowe, and David J. Moss, “Optical microcombs for ultrahigh-bandwidth communications”, Nature Photonics Volume 19 (5) 451 - 462 (2025). [CrossRef]
- Qihang Ai, Mengxi Tan, Hanxiao Feng, Xinyu Yang, Xingyuan Xu, Roberto Morandotti, Arnan Mitchell, Donglin Su, and David J. Moss, “Photonic real-time signal processing”, Nanophotonics 29 (2025).
- Xingyuan Xu, Jiajia Wang, Xiaotian Zhu, Yifu Xu, Shifan Chen, Haoran Zhang, Shuying Li, Yunping Bai, Zhihui Liu, Roberto Morandotti, Brent E. Little, Arthur J. Lowery, David J. Moss, Sai T. Chu, and Kun Xu, “Microcomb-enabled parallel self- calibration optical convolution streaming processor”, Light Science and Applications (2025).
- Shifan Chen, Yixuan Zheng, Yifu Xu, Xiaotian Zhu, Sirui Huang, Shuai Wang, Xiaoyan Xu, Chengzhuo Xia, Zhihui Liu, Chaoran Huang, Roberto Morandotti, Sai T. Chu, Brent E. Little, Bill Corcoran, Yuyang Liu, Yunping Bai, David J. Moss, Xingyuan Xu, and Kun Xu, “Integrated photonic neural networks”, npj Nanophotonics 2, 28 (2025).
- Aadhi, L. Di Lauro, B. Fischer, P. Dmitriev, I. Alamgir, C. Mazoukh, N. Perron, E. Viktorov, A. Kovalev, A. Eshaghi, S. Vakili, M. Chemnitz, P. Roztocki, B.E. Little, S. T. Chu, D. J. Moss, and R. Morandotti, “Scalable Photonic Reservoir for Parallel Machine Learning Applications”, Nature Communications 16 (2025).
- Hamed Arianfard, Saulius Juodkazis, David J. Moss, and Jiayang Wu, “Sagnac interference in integrated photonics”, Applied Physics Reviews 10 (1) 011309 (2023). [CrossRef]
- Hamed Arianfard, Jiayang Wu, Saulius Juodkazis, and David J. Moss, “Optical analogs of Rabi splitting in integrated waveguide-coupled resonators”, Advanced Physics Research 2 2200123 (2023). [CrossRef]
- Hamed Arianfard, Jiayang Wu, Saulius Juodkazis, and David J. Moss, “Spectral shaping based on optical waveguides with advanced Sagnac loop reflectors”, Paper No. PW22O-OE201-20, SPIE-Opto, Integrated Optics: Devices, Materials, and Technologies XXVI, SPIE Photonics West, San Francisco CA January 22 - 27 (2022). [CrossRef]
- Hamed Arianfard, Jiayang Wu, Saulius Juodkazis, David J. Moss, “Spectral Shaping Based on Integrated Coupled Sagnac Loop Reflectors Formed by a Self-Coupled Wire Waveguide”, IEEE Photonics Technology Letters vol. 33 (13) 680-683 (2021). [CrossRef]
- Hamed Arianfard, Jiayang Wu, Saulius Juodkazis and David J. Moss, “Three Waveguide Coupled Sagnac Loop Reflectors for Advanced Spectral Engineering”, Journal of Lightwave Technology vol. 39 (11) 3478-3487 (2021). [CrossRef]
- Hamed Arianfard, Jiayang Wu, Saulius Juodkazis and David J. Moss, “Advanced Multi-Functional Integrated Photonic Filters based on Coupled Sagnac Loop Reflectors”, Journal of Lightwave Technology vol. 39 Issue: 5, pp.1400-1408 (2021). [CrossRef]
- Hamed Arianfard, Jiayang Wu, Saulius Juodkazis and David J. Moss, “Advanced multi-functional integrated photonic filters based on coupled Sagnac loop reflectors”, Paper 11691-4, PW21O-OE203-44, Silicon Photonics XVI, SPIE Photonics West, San Francisco CA March 6-11 (2021).
- Jiayang Wu, Tania Moein, Xingyuan Xu, and David J. Moss, “Advanced photonic filters via cascaded Sagnac loop reflector resonators in silicon-on-insulator integrated nanowires”, Applied Physics Letters Photonics vol. 3 046102 (2018). [CrossRef]
- J. Wu, H. Lin, D. J. Moss, K. P. Loh, and B. Jia, “Graphene oxide for photonics, electronics and optoelectronics,” Nature Reviews Chemistry, vol. 7, no. 3, pp. 162-183, 2023/03/01, 2023.
- Y. Zhang, J. Wu, L. Jia, Y. Qu, Y. Yang, B. Jia, and D. J. Moss, “Graphene Oxide for Nonlinear Integrated Photonics,” Laser & Photonics Reviews, vol. 17, no. 3, pp. 2200512, 2023/03/01, 2023.
- J. Hu, J. Wu, W. Liu, D. Jin, H. E. Dirani, S. Kerdiles, C. Sciancalepore, P. Demongodin, C. Grillet, C. Monat, D. Huang, B. Jia, and D. J. Moss, “2D graphene oxide: a versatile thermo-optic material,” Advanced Functional Materials, vol. 34, no. 46, pp. 2406799, 2024.
- J. Wu, L. Jia, Y. Zhang, Y. Qu, B. Jia, and D. J. Moss, “Graphene Oxide for Integrated Photonics and Flat Optics,” Advanced Materials, vol. 33, no. 3, pp. 2006415, 2021.
- Y. Zhang, J. Wu, Y. Yang, Y. Qu, L. Jia, T. Moein, B. Jia, and D. J. Moss, “Enhanced Kerr Nonlinearity and Nonlinear Figure of Merit in Silicon Nanowires Integrated with 2D Graphene Oxide Films,” ACS Applied Materials & Interfaces, vol. 12, no. 29, pp. 33094-33103, 2020/07/22, 2020.
- Junkai Hu, Jiayang Wu, Di Jin, Wenbo Liu, Yuning Zhang, Yunyi Yang, Linnan Jia, Duan Huang, Baohua Jia, and David J. Moss, “Integrated waveguide and microring polarizers incorporating 2D reduced graphene oxide”, Opto-Electronic Science 4 240032 (2025). [CrossRef]
- Jin, J. Wu, J. Hu, W. Liu, Y. Zhang, Y. Yang, L. Jia, D. Huang, B. Jia, and D. J. Moss, “Silicon photonic waveguide and microring resonator polarizers incorporating 2D graphene oxide films,” Applied Physics Letters, vol. 125, no. 5, 2024.
- H. Arianfard, S. Juodkazis, D. J. Moss, and J. Wu, “Sagnac interference in integrated photonics,” Applied Physics Reviews, vol. 10, no. 1, 2023.
- Jin, S. Ren, J. Hu, D. Huang, D. J. Moss, and J. Wu, “Modeling of Complex Integrated Photonic Resonators Using the Scattering Matrix Method,” Photonics, vol. 11, no. 12, pp. 1107, 2024.
- J. Wu, Y. Yang, Y. Qu, X. Xu, Y. Liang, S. T. Chu, B. E. Little, R. Morandotti, B. Jia, and D. J. Moss, “Graphene Oxide Waveguide and Micro-Ring Resonator Polarizers,” Laser & Photonics Reviews, vol. 13, no. 9, pp. 1900056, 2019.
- J. Hu, J. Wu, D. Jin, S. T. Chu, B. E. Little, D. Huang, R. Morandotti, and D. J. Moss, “Thermo-Optic Response and Optical Bistablility of Integrated High-Index Doped Silica Ring Resonators,” Sensors, vol. 23, no. 24, pp. 9767, 2023.
- Yunyi Yang, Jiayang Wu, Xingyuan Xu, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Enhanced four-wave mixing in graphene oxide coated waveguides”, Applied Physics Letters Photonics vol. 3 120803 (2018). [CrossRef]
- Wu, J. et al., “Graphene oxide waveguide and micro-ring resonator polarizers”, Laser and Photonics Reviews Vol. 13, 1900056 (2019).
- Jiayang Wu, Yunyi Yang, Yang Qu, Xingyuan Xu, Yao Liang, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Laser and Photonics Reviews vol. 13 (9) 1900056 (2019). [CrossRef]
- Wu, J. et al. “2D layered graphene oxide films integrated with micro-ring resonators for enhanced nonlinear optics”, Small Vol. 16, 1906563 (2020).
- Yang Qu, Jiayang Wu, Yunyi Yang, Yuning Zhang, Yao Liang, Houssein El Dirani, Romain Crochemore, Pierre Demongodin, Corrado Sciancalepore, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced nonlinear four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films”, Advanced Optical Materials vol. 8 (21) 2001048 (2020). arXiv:2006.14944. [CrossRef]
- Jiayang Wu, Yunyi Yang, Yang Qu, Yuning Zhang, Linnan Jia, Xingyuan Xu, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Enhanced nonlinear four-wave mixing in microring resonators integrated with layered graphene oxide films”, Small vol. 16 (16) 1906563 (2020). [CrossRef]
- Jiayang Wu, Yunyi Yang, Yang Qu, Xingyuan Xu, Yao Liang, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Paper 11282-29, SPIE Photonics West, San Francisco, CA, 4 - 7 February (2020). [CrossRef]
- Yuning Zhang, Jiayang Wu, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Design and optimization of four-wave mixing in microring resonators integrated with 2D graphene oxide films”, Journal of Lightwave Technology Vol. 39 (20) 6553-6562 (2021). [CrossRef]
- Yang Qu, Jiayang Wu, Yuning Zhang, Yao Liang, Baohua Jia, and David J. Moss, “Analysis of four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films”, Journal of Lightwave Technology Vol. 39 (9) 2902-2910 (2021). [CrossRef]
- Y. Qu, J. Wu, Y. Zhang, L. Jia, Y. Yang, X. Xu, S. T. Chu, B. E. Little, R. Morandotti, B. Jia, and D. J. Moss, “Graphene oxide for enhanced optical nonlinear performance in CMOS compatible integrated devices”, Paper No. 11688-30, PW21O-OE109-36, 2D Photonic Materials and Devices IV, SPIE Photonics West, San Francisco CA March 6-11 (2021).
- Yuning Zhang, Jiayang Wu, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Optimizing the Kerr nonlinear optical performance of silicon waveguides integrated with 2D graphene oxide films”, Journal of Lightwave Technology Vol. 39 (14) 4671-4683 (2021). [CrossRef]
- Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Linnan Jia, Baohua Jia, and David J. Moss, “Photo thermal tuning in GO-coated integrated waveguides”, Micromachines Vol. 13 1194 (2022). [CrossRef]
- Zhang Y, Wu J, Qu Y, Jia L, Jia B, D.J. Moss, “Graphene oxide-based waveguides for enhanced self-phase modulation”, Annals of Mathematics and Physics Vol. 5 (2) 103-106 (2022). [CrossRef]
- Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Enhanced spectral broadening of femtosecond optical pulses in silicon nanowires integrated with 2D graphene oxide films”, Micromachines Vol. 13 756 (2022). [CrossRef]
- Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Linnan Jia, Houssein El Dirani, Sébastien Kerdiles, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced supercontinuum generated in SiN waveguides coated with GO films”, Advanced Materials Technologies 8 (1) 2201796 (2023). [CrossRef]
- Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Houssein El Dirani, Romain Crochemore, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced self-phase modulation in silicon nitride waveguides integrated with 2D graphene oxide films”, IEEE Journal of Selected Topics in Quantum Electronics Vol. 29 (1) 5100413 (2023). [CrossRef]
- Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Linnan Jia, Houssein El Dirani, Sébastien Kerdiles, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Integrated optical parametric amplifiers in silicon nitride waveguides incorporated with 2D graphene oxide films”, Light: Advanced Manufacturing 4 39 (2023). [CrossRef]
- Jiayang Wu, Yuning Zhang, Junkai Hu, Yunyi Yang, Di Jin, Wenbo Liu, Duan Huang, Baohua Jia, David J. Moss, “Novel functionality with 2D graphene oxide films integrated on silicon photonic chips”, Advanced Materials Vol. 36 2403659 (2024). [CrossRef]
- Di Jin, Jiayang Wu, Junkai Hu, Wenbo Liu, Yuning Zhang, Yunyi Yang, Linnan Jia, Duan Huang, Baohua Jia, and David J. Moss, “Silicon photonic waveguide and microring resonator polarizers incorporating 2D graphene oxide films”, Applied Physics Letters, Vol. 125, 053101 (2024). [CrossRef]
- Yuning Zhang, Jiayang Wu, Linnan Jia, Di Jin, Baohua Jia, Xiaoyong Hu, David Moss, Qihuang Gong, “Advanced optical polarizers based on 2D materials”, npj Nanophotonics 1, 28 (2024). [CrossRef]
- Y. Zhang, J. Wu, Y. Yang, Y. Qu, L. Jia, C. Grillet, C. Monat, B. Jia, and D.J. Moss, “Graphene oxide for enhanced nonlinear optics in integrated photonic chips”, Paper 12888-16, Conference OE109, 2D Photonic Materials and Devices VII, Chair(s): Arka Majmdar; Carlos M. Torres Jr.; Hui Deng, SPIE Photonics West, San Francisco CA, January 27 – February 1 (2024). Proceedings Volume 12888, 2D Photonic Materials and Devices VII; 1288805 (2024). [CrossRef]
- Di Jin, Wenbo Liu, Linnan Jia, Junkai Hu, Duan Huang, Jiayang Wu, Baohua Jia, and David J. Moss, “Thickness and Wavelength Dependent Nonlinear Optical Absorption in 2D Layered MXene Films”, Small Science 4 2400179 (2024).
- Yuning Zhang, Jiayang Wu, Junkai Hu, Linnan Jia, Di Jin, Baohua Jia, Xiaoyong Hu, David J. Moss, Qihuang Gong, “2D material integrated photonics: towards industrial manufacturing and commercialization”, Applied Physics Letters Photonics 10, 000000 (2025). [CrossRef]
- Linnan Jia, Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Baohua Jia, and David J. Moss, “Third-order optical nonlinearities of 2D materials at telecommunications wavelengths”, Micromachines, 14 307 (2023). [CrossRef]
- Linnan Jia, Jiayang Wu, Yuning Zhang, Yang Qu, Baohua Jia, Zhigang Chen, and David J. Moss, “Fabrication Technologies for the On-Chip Integration of 2D Materials”, Small: Methods Vol. 6, 2101435 (2022). [CrossRef]
- Linnan Jia, Dandan Cui, Jiayang Wu, Haifeng Feng, Tieshan Yang, Yunyi Yang, Yi Du, Weichang Hao, Baohua Jia, David J. Moss, “BiOBr nanoflakes with strong nonlinear optical properties towards hybrid integrated photonic devices”, Applied Physics Letters Photonics vol. 4 090802 vol. (2019). [CrossRef]
- Linnan Jia, Jiayang Wu, Yunyi Yang, Yi Du, Baohua Jia, David J. Moss, “Large Third-Order Optical Kerr Nonlinearity in Nanometer-Thick PdSe2 2D Dichalcogenide Films: Implications for Nonlinear Photonic Devices”, ACS Applied Nano Materials vol. 3 (7) 6876–6883 (2020). [CrossRef]
- Kues, M. et al. “Quantum optical microcombs”, Nature Photonics vol. 13, (3) 170-179 (2019). [CrossRef]
- C.Reimer, L. Caspani, M. Clerici, et al., “Integrated frequency comb source of heralded single photons,” Optics Express, vol. 22, no. 6, pp. 6535-6546, 2014.
- Reimer, et al., “Cross-polarized photon-pair generation and bi-chromatically pumped optical parametric oscillation on a chip”, Nature Communications, vol. 6, Article 8236, 2015. [CrossRef]
- L. Caspani, C. Reimer, M. Kues, et al., “Multifrequency sources of quantum correlated photon pairs on-chip: a path toward integrated Quantum Frequency Combs,” Nanophotonics, vol. 5, no. 2, pp. 351-362, 2016.
- Reimer et al., “Generation of multiphoton entangled quantum states by means of integrated frequency combs,” Science, vol. 351, no. 6278, pp. 1176-1180, 2016.
- M. Kues, et al., “On-chip generation of high-dimensional entangled quantum states and their coherent control”, Nature, vol. 546, no. 7660, pp. 622-626, 2017.
- P. Roztocki et al., “Practical system for the generation of pulsed quantum frequency combs,” Optics Express, vol. 25, no. 16, pp. 18940-18949, 2017.
- Y. Zhang, et al., “Induced photon correlations through superposition of two four-wave mixing processes in integrated cavities”, Laser and Photonics Reviews, vol. 14, no. 7, pp. 2000128, 2020. [CrossRef]
- Reimer, et al., “High-dimensional one-way quantum processing implemented on d-level cluster states”, Nature Physics, vol. 15, no.2, pp. 148–153, 2019.
- P.Roztocki et al., “Complex quantum state generation and coherent control based on integrated frequency combs”, Journal of Lightwave Technology vol. 37 (2) 338-347 (2019).
- S. Sciara et al., “Generation and Processing of Complex Photon States with Quantum Frequency Combs”, IEEE Photonics Technology Letters vol. 31 (23) 1862-1865 (2019). [CrossRef]
- Nicola Montaut, Agnes George, Monika Monika, Farzam Nosrati, Hao Yu, Stefania Sciara, Benjamin Crockett, Ulf Peschel, Zhiming Wang, Rosario lo Franco, Mario Chemnitz, William J. Munro, David J. Moss, José Azaña, and Roberto Morandotti, “Progress in integrated and fiber optics for time-bin based quantum information processing”, Advanced Optical Technologies 14 1560084 (2025). [CrossRef]
- Hao Yu, Benjamin Crockett, Nicola Montaut, Stefania Sciara, Mario Chemnitz, Sai T Chu, Brent E Little, David J Moss, Zhiming Wang, José Azaña, And Roberto Morandotti, “Exploiting nonlocal correlations for dispersion-resilient quantum communications”, Physical Review Letters 134 (2025).
- Stefania Sciara, Piotr Roztocki, Bennet Fisher, Christian Reimer, Luis Romero Cortez, William J. Munro, David J. Moss, Alfonso C. Cino, Lucia Caspani, Michael Kues, J. Azana, and Roberto Morandotti, “Scalable and effective multilevel entangled photon states: A promising tool to boost quantum technologies”, Nanophotonics vol. 10 (18), 4447–4465 (2021). [CrossRef]
- L. Caspani, C. Reimer, M. Kues, et al., “Multifrequency sources of quantum correlated photon pairs on-chip: a path toward integrated Quantum Frequency Combs,” Nanophotonics, vol. 5, no. 2, pp. 351-362, 2016.
- H. Yu, S. Sciara, M. Chemnitz, N. Montaut, B. Fischer, R. Helsten, B. Crockett, B. Wetzel, T. A. Göbel, R. Krämer, B. E. Little, S. T. Chu, D. J. Moss, S. Nolte, W.J. Munro, Z. Wang, J. Azaña, R. Morandotti, “Quantum key distribution implemented with d-level time-bin entangled photons”, Nature Communications 16 171 (2025). [CrossRef]
| Mechanism | Structure | Number of functions | Type of functions | Tuning range (GHz) | SFDR (dB·Hz2/3) | ROR (dB/GHz) | Shape factor |
|---|---|---|---|---|---|---|---|
| DRM [7] | Two cascaded MRRs | 1 | B | 4.0 – 21.5 | – | – | 1.23 |
| DRM [9] | Four cascaded MRRs | 1 | B | 4.0 – 36.0 | – | 10.23 | – |
| DRM [47] | RAMZI | 1 | A | 0 – 6.0 | 81.4 | – | – |
| DRM [6] | DFBR waveguide Bragg grating | 1 | B | 10.0 – 67.5 | 95.8 | 7.0 | – |
| DRM [3] | TOBF + FBGs | 1 | B | 6.3 – 22.4 | – | – | 1.88 |
| DRM [40] | EPS-FBG | 1 | E | 0.8 – 7.4 | 89.8 | – | 3.3 |
| SBS [43] | Waveguide | 1 | D | 5.0 – 20.0 | 92.2 | – | – |
| SBS [44] | Optical fibre | 2 | B, E | 1.65 – 2.15 | – | – | 1.35 |
| TFS [26] | Microcomb | 4 | A, B, C, D | 2.0 – 6.0 | – | – | – |
| TFS [34] | Microcomb | 1 | B | 3.28 – 19.4 | – | 5.2 | – |
| This work | Microcomb | 6 | A, B, C, D, E, F | 0 – 25.0 | 90.9 | 32.6 | 1.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




