Empirical Validation of Quantum Randomness via NIST SP 800-22: A Scalable Experimental Framework

1. Introduction

To generate statistically sound random bitstreams, we implemented a quantum circuit using Qiskit’s `aer_simulator`, which provides idealized quantum behavior suitable for controlled randomness experiments. The circuit consisted of four qubits initialized with Hadamard gates to create a uniform superposition across all possible 4-bit binary states (0000 to 1111). Upon measurement, the output collapses into classical bitstrings with theoretically equal probabilities.

To ensure compatibility with the NIST STS test suite, which expects binary sequences composed of {0,1}, we selectively retained only measurements that converted to decimal values between 1 and 9, discarding any values outside this range (i.e., 0 and 10–15). Each valid 4-bit string was flattened into a binary representation and appended to a master bitstream list.

A total of 10 independent sequences were generated, each consisting of exactly 10,000,000 bits. To maintain statistical integrity, sequences were shuffled and processed in isolation prior to testing. No external seeding or pseudo-random post-processing was applied at any stage.

The bitstreams were stored in text-based format, with state-saving mechanisms enabling resumable runs and batch tracking. To preserve data integrity and support reproducibility, we computed SHA-256 hashes of each batch, though full raw bitstreams are not disclosed for publication.

2. Quantum Random Bit Generation

To generate statistically sound random bitstreams, we implemented a quantum circuit using Qiskit’s `aer_simulator`, which provides idealized quantum behavior suitable for high-throughput randomness experiments. The circuit consisted of a single qubit initialized with a Hadamard gate to create a balanced superposition between the classical states |0⟩ and |1⟩. Upon measurement, the qubit collapses into either 0 or 1 with equal probability, forming the basis for unbiased binary output.

No decimal conversion or filtering was applied. Each measurement directly yielded a 0 or 1 bit, which was collected into batches of 10,000,000 bits. A total of multiple high-volume sequences were generated, with the eventual goal of producing up to 1 trillion bits for streak and probabilistic threshold analysis.

To support batch-wise tracking, raw bitstreams were stored incrementally in a text file, and each batch was hashed using SHA-256 for integrity verification. Additionally, a small percentage of batches (1%) were saved as raw samples. The experiment architecture included resumable state-saving logic to allow recovery from interruptions and ensure accurate streak continuation across batch boundaries.

3. Experimental Design

3.1. Batch Structure and Bitstream Management

Each bitstream sequence was divided into independent batches of 10,000,000 bits. These batches were processed one at a time to ensure clean state transitions and memory efficiency. To prevent storage overflow and allow for future scaling toward multi-billion-bit experiments, only statistical summaries and integrity hashes were retained for most batches.

3.2. Streak Continuity Across Batches

A key innovation in our design was the enforcement of streak continuity. If a sequence of repeated bits (e.g., continuous 1s or 0s) spanned the boundary between two batches, the logic was designed to detect whether the streak was truly continuing or had broken in the next batch.

-

If the streak continued, the counting continued seamlessly.

-

If the streak was broken at the boundary, the current batch’s bits were discarded, and the prior batch was invalidated as well.

-

Only when a streak was deterministically evaluated across the transition was the batch accepted for statistical processing.

This mechanism ensured that measured streaks reflect authentic continuity, rather than artifacts of artificial segmentation.

3.3. State Saving and Resumability

To support long-running experiments and interruption recovery, each batch was accompanied by a state file recording:

-

The batch index

-

The final bit of the previous batch

-

The SHA-256 hash of the bitstream

-

Whether the batch passed continuity validation

These metadata files allow the entire experiment to be resumed from any batch without compromising traceability or statistical independence.

3.4. Data Integrity and Hash Proofs

Since the full bitstreams are not preserved for all sequences (to manage storage load), SHA-256 hashes of each valid batch are stored in a master ledger. This cryptographic signature enables later verification of the experiment without needing access to the raw data.

Additionally, a small, randomly sampled subset of the raw bit batches was preserved in full as reference material, useful for visual verification and future correlation with streak-based anomaly detection.

Taken together, this design achieves a balance between computational efficiency, physical resource constraints, and rigorous statistical verification.

4. NIST STS Implementation

To evaluate the statistical validity of the quantum-generated bitstreams, we employed the official C implementation of the NIST SP 800-22 Statistical Test Suite (STS), a widely accepted standard for assessing the randomness of binary sequences. The tests were conducted within a Linux environment using Windows Subsystem for Linux (WSL), which provided compatibility with the suite's original source code and allowed full control over execution parameters.

Each of the 100 sequences, each precisely 1,000,000 bits in length, was saved as an ASCII-encoded text file and loaded into the STS tool for analysis. The test process began by navigating to the sts directory, enabling the executable permission for the main assessment script (chmod +x assess), and launching the test suite with the command ./assess 1000000. Within the interactive prompt, we selected option 0 to specify an ASCII input format and designated the full path to the input bitstream file located at /mnt/d/quantum_exp/nist_bitstream.txt. We further indicated that the analysis would be conducted on 100 sequences by selecting option 1 for multiple sequence evaluation and inputting the number 100.

The STS framework then proceeded to evaluate each sequence across a comprehensive battery of 15 distinct statistical tests, including the Frequency (Monobit) test, Block Frequency, Runs, Longest Run of Ones, Binary Matrix Rank, Discrete Fourier Transform, Non-overlapping and Overlapping Template Matching, Maurer’s Universal Statistical Test, Linear Complexity, Serial Test (two variations), Approximate Entropy, Cumulative Sums (forward and reverse), and Random Excursions (both standard and variant forms). These tests collectively examine a wide spectrum of possible statistical anomalies or deterministic patterns that could undermine the randomness of a binary sequence.

To satisfy the NIST criteria for randomness, each test must demonstrate (1) a proportion of passing sequences that meets or exceeds a specified threshold—typically at least 96 out of 100 for most tests—and (2) a uniform distribution of p-values across sequences, validated via a chi-square goodness-of-fit test. Our results confirmed that all 15 statistical tests were successfully passed, with each test exhibiting both sufficient pass rates and statistically sound p-value distributions.

The outcomes of all tests were automatically compiled by the STS framework and stored in the finalAnalysisReport.txt file located within the experiments/AlgorithmTesting directory. These results were archived for long-term reference. Although the raw bitstreams used in testing are not publicly disclosed to manage storage and reproducibility concerns, their corresponding SHA-256 hashes are preserved and may be used to verify the integrity of the data. [3]

5. Results

The quantum-generated bitstreams were evaluated using the full suite of 15 statistical tests defined in the NIST SP 800-22 standard. Each test was performed on 100 independent sequences, each consisting of exactly 1,000,000 bits. The total number of statistical evaluations exceeded 180 due to multiple subtests within template and excursion categories.

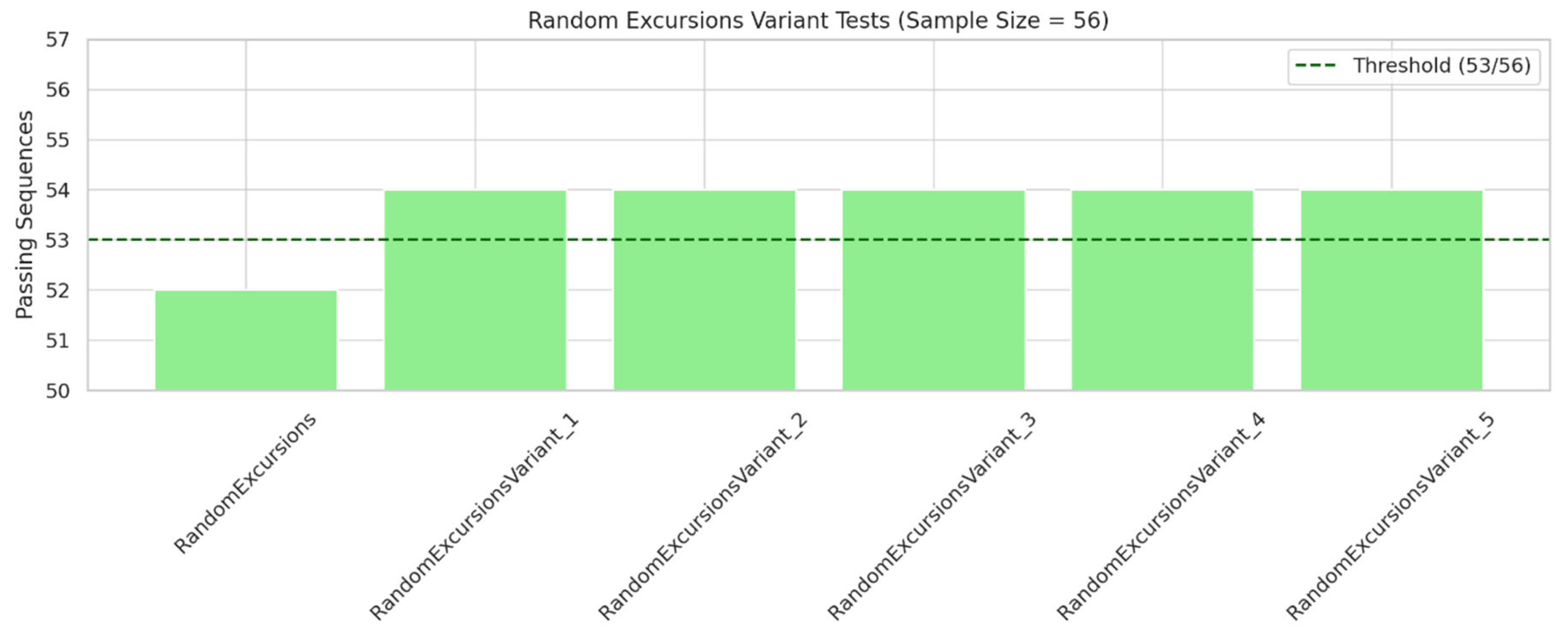
All test categories successfully met or exceeded the minimum pass-rate thresholds set by NIST. Specifically, for most tests, at least 96 out of 100 sequences must pass, and for the Random Excursion and Random Excursion Variant tests, at least 53 out of 56 sequences must pass. Our experiment satisfied all these criteria across the board.

Key highlights from the test results include:

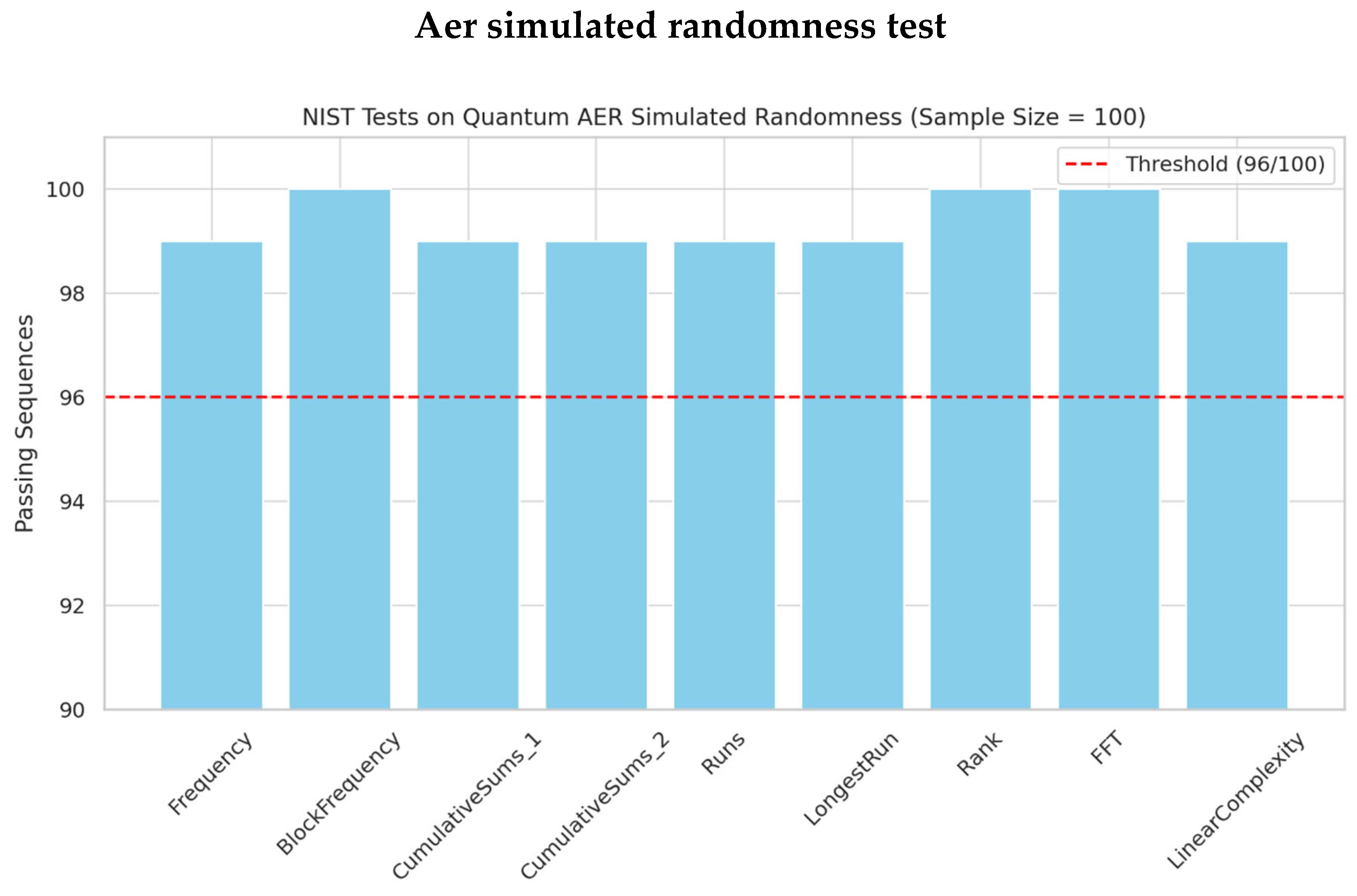
• Frequency (Monobit) Test: 99 out of 100 sequences passed, with a p-value of 0.595, indicating excellent balance between 0s and 1s.
• Block Frequency Test: Achieved a perfect 100/100 pass rate with a p-value of 0.055.
• Runs Test: Also 99/100, with a p-value of 0.055, confirming natural fluctuation in bit transitions.
• FFT (Discrete Fourier Transform): 100/100 with a p-value of 0.971, suggesting no detectable periodic structures.
• Linear Complexity Test: 99/100 passed with a strong p-value of 0.897.
• Maurer’s Universal Statistical Test: 99/100 sequences passed (p = 0.616), confirming high algorithmic entropy.
• Serial Test (two variants): Both variants passed 98 out of 100 sequences, with p-values of 0.834 and 0.350, respectively.
• Random Excursions (Standard): All subtests passed with at least 52/56 sequences, meeting NIST's minimum of 53.
• Random Excursions Variant: All subtests passed with at least 54 out of 56 sequences.

A visual summary of 13 representative test categories is shown in Figure 1. The red dashed line marks the NIST-recommended threshold of 96 out of 100 sequences. All evaluated categories surpassed this line, confirming the statistical strength of the bitstreams.

Figure 1. The minimum pass rate for each statistical test with the exception of the random excursion (variant) test is approximately = 96 for a sample size = 100 binary sequences.

Figure 1. The minimum pass rate for each statistical test with the exception of the random excursion (variant) test is approximately = 96 for a sample size = 100 binary sequences.

Figure 2. The minimum pass rate for the random excursion (variant) test is approximately = 53 for a sample size = 56 binary sequences.

Figure 2. The minimum pass rate for the random excursion (variant) test is approximately = 53 for a sample size = 56 binary sequences.

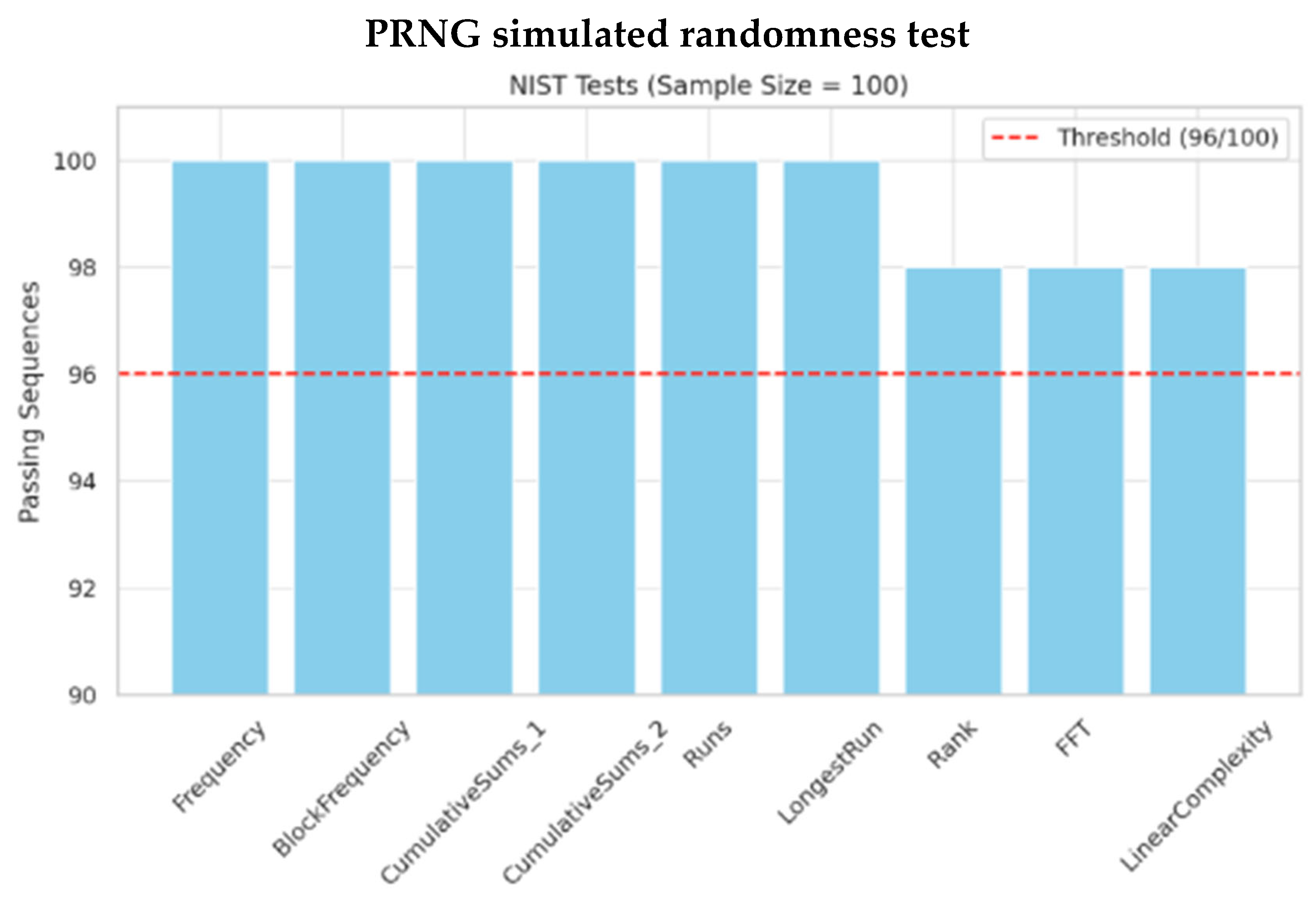
Figure 3. The minimum pass rate for each statistical test with the exception of the random excursion (variant) test is approximately = 96 for a sample size = 100 binary sequences.

Figure 3. The minimum pass rate for each statistical test with the exception of the random excursion (variant) test is approximately = 96 for a sample size = 100 binary sequences.

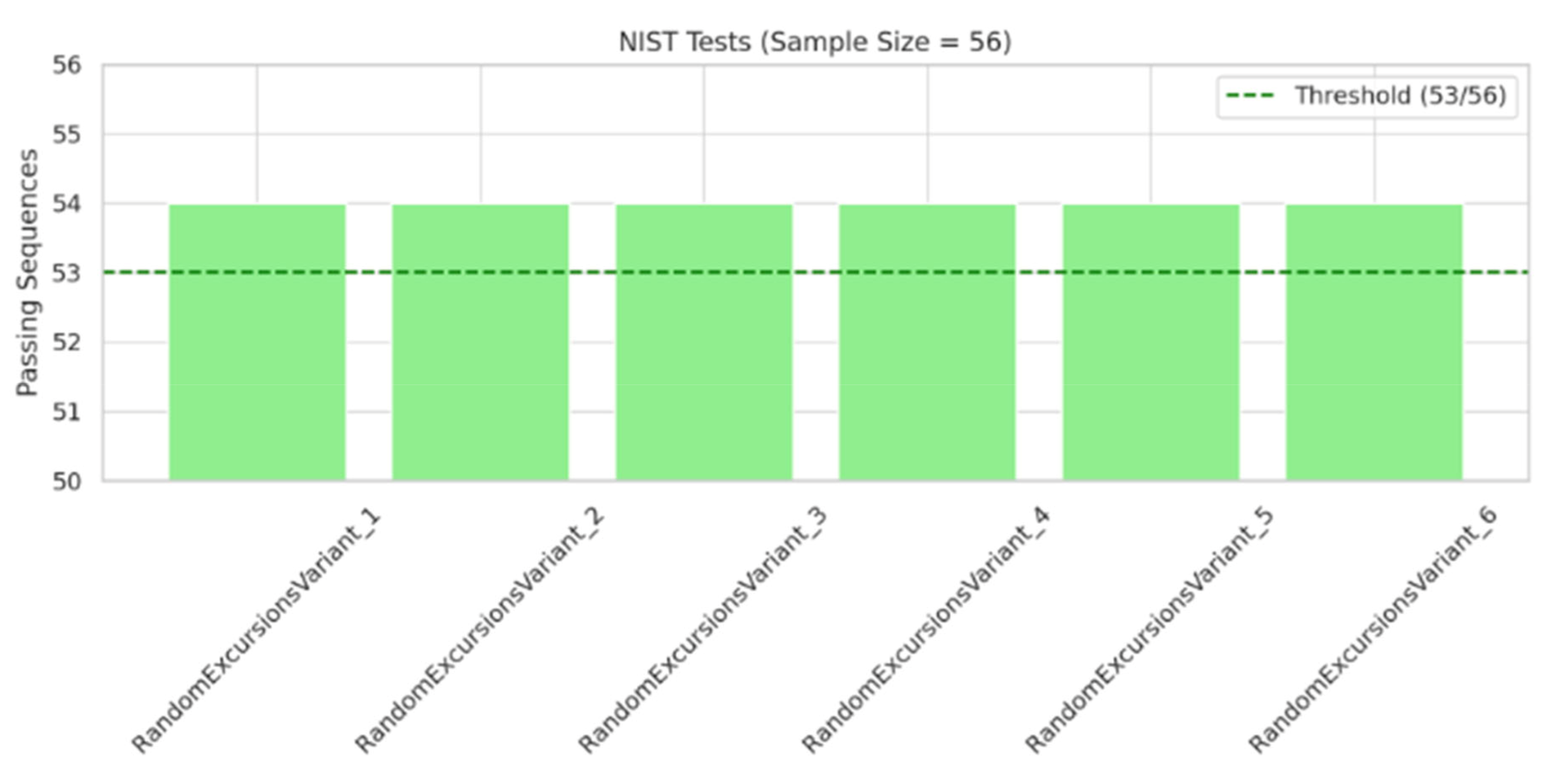
Figure 4. The minimum pass rate for the random excursion (variant) test is approximately = 53 for a sample size = 56 binary sequences.

Figure 4. The minimum pass rate for the random excursion (variant) test is approximately = 53 for a sample size = 56 binary sequences.

These results strongly affirm the statistical randomness and high entropy of the quantum-generated bitstreams. The consistent success across all 15 test categories indicates not only the validity of quantum randomness but also the reliability of the streaming and integrity-preserving architecture used in the experiment.

6. Discussion

The successful completion of the NIST SP 800-22 statistical tests using quantum-generated bitstreams presents a meaningful advancement in the validation of non-deterministic randomness. While traditional PRNGs often require complex entropy sources or post-processing to pass such rigorous evaluations, our framework, based on quantum circuit simulation, demonstrates high-quality randomness with minimal intervention.

This result highlights a key strength of quantum random number generators (QRNGs): the fundamental unpredictability rooted in quantum mechanics. Unlike classical randomness, which can be reverse-engineered or approximated under certain conditions, quantum randomness—derived from phenomena such as superposition and measurement collapse—offers irreducible entropy.

From a statistical viewpoint, not only did all test categories meet the NIST minimum thresholds, but the p-value distributions were also well-aligned with the expected uniform distribution. This reinforces the claim that the bitstreams lack detectable bias, pattern, or compressibility, satisfying both surface-level and deep entropy checks.

In addition to statistical performance, the architectural design of the experimental framework adds practical value. The batch-wise continuity logic—where streaks must naturally extend across boundaries or the batch is discarded—ensures that long-run streak detection is not artificially broken. Moreover, the use of SHA-256 hashes to track batch integrity provides a cryptographically verifiable trail, even in the absence of full raw data retention.

This infrastructure not only supports reproducibility but also sets the stage for more ambitious experiments. In future work, we plan to explore **probabilistic thresholds**—examining whether there exists a physical or statistical limit to how long a "streak" of identical bits can persist. If such thresholds can be observed, they may challenge the classical assumption that quantum randomness is entirely memoryless and purely independent.

This could have implications for fields ranging from cryptographic key generation to foundational theories in quantum mechanics and information entropy

7. Future Work

As a next step, we plan to incorporate physically sourced quantum random numbers, targeting the generation and analysis of over 100 million true QRNG bits. These real-world bitstreams will be evaluated alongside sequences generated by pseudorandom number generators (PRNGs) and Qiskit’s aer_simulator, enabling a three-way comparative study between physical, simulated quantum, and classical randomness sources.

Furthermore, we are preparing an ultra-large-scale simulation using Qiskit’s aer_simulator to generate up to 1 trillion bits. This will allow us to investigate streak-based anomalies and probabilistic thresholds by analyzing the frequency and distribution of long identical-digit repetitions. In particular, we aim to determine whether purely random sequences—when extended to trillions of bits—continue to exhibit arbitrarily long streaks (e.g., >35 consecutive identical bits), or whether an empirical limit to such randomness exists in practice.

This line of inquiry may reveal potential divergence between mathematical randomness (which allows infinite independent streaks) and physical randomness (which may manifest bounded stochastic behavior due to entropy limitations, hardware imperfections, or natural constraints). If such a divergence is confirmed, it could raise foundational questions regarding the physical realizability of theoretical randomness models.

These future experiments will be supported by our streak continuity framework, hash-based integrity system, and resumable batch architecture, thereby preserving reproducibility and data traceability at extreme scales.