1. Introduction
In large-scale distributed environments, recommender systems face challenges of data silos and user privacy, while centralized models pose serious leakage risks due to data aggregation. Federated learning offers a collaborative training paradigm that avoids raw data sharing, enabling privacy-preserving recommendations. However, current federated methods struggle to model complex user–item associations and capture higher-order semantic dependencies within graph structures. Graph Convolutional Networks (GCNs) effectively represent deep topological and feature interactions, making them well-suited for enhancing recommendation quality. Integrating GCNs into the federated framework enables structure-aware personalized modeling while preserving data locality—offering both theoretical and practical value for improving system intelligence and privacy protection.
2. GCN-Based Federal Recommendation Model Design
2.1. Formalized Definition of the Problem
Federated recommender systems aim to collaboratively train a unified model across multiple clients with isolated data. Let U = {u₁, …, uₘ} be the user set and V = {v₁, …, vₙ} the item set. Each client Cₖ holds a local interaction record Rₖ ⊆ Uₖ × Vₖ, forming a bipartite graph Gₖ = (Uₖ ∪ Vₖ, Eₖ), where Eₖ represents user-item interactions [
1]. The goal is to learn a preference prediction function f_θ: U × V → ℝ, with parameters θ updated via federated gradient aggregation. To incorporate graph structural information, each client constructs a neighbor matrix Aₖ ∈ ℝ⁽ᵐ⁺ⁿ⁾×⁽ᵐ⁺ⁿ⁾, and a feature matrix Xₖ, which are input to a graph convolutional network (GCN). Embedding propagation is defined as [
2]:
where Ẽₖ = Aₖ + I, D̃ₖ is the degree matrix, W⁽ˡ⁾ is the l-th layer weight, σ(⋅) the activation function, and H⁽⁰⁾ = Xₖ. As shown in
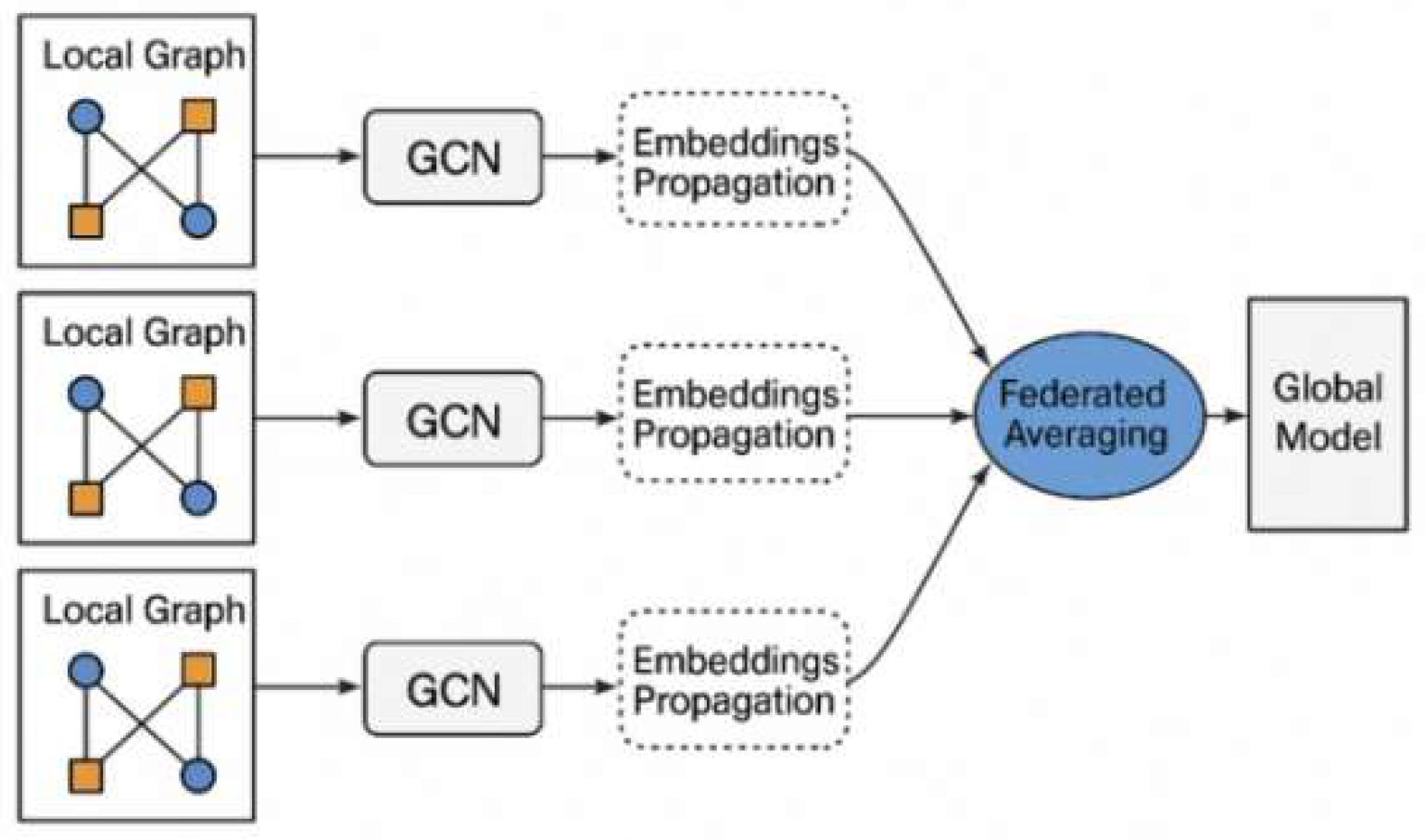
Figure 1, each client maps its bipartite graph to an embedding space and applies FedAvg for global model updates.
2.2. Overall Model Architecture
The overall architecture of the federated recommendation system integrates a modular data flow comprising local graph modeling, GCN-based feature propagation, privacy-preserving parameter perturbation, and global aggregation. Each client maintains its own user-item bipartite graph and initializes a feature matrix Xk based on local interaction histories. The model consists of three main stages:
(1) Local Data Preprocessing and Graph Construction: Clients preprocess raw interaction data to construct an adjacency matrix Ak and normalized feature inputs.
(2) Graph Convolution Embedding: A two-layer Graph Convolutional Network is applied:
With A~k=Ak+I, where node features are updated iteratively to learn high-order interaction semantics.
(3) Embedding Protection and Upload: Before uploading to the server, local embeddings H(L) are perturbed via Gaussian mechanism:
and securely encoded with homomorphic encryption under the Secure Aggregation Protocol (SAP).
(4) Central Aggregation and Model Broadcast: The server performs federated averaging:
without accessing individual model parameters, ensuring structural and statistical privacy. Updated global parameters are broadcasted to clients for the next local round.
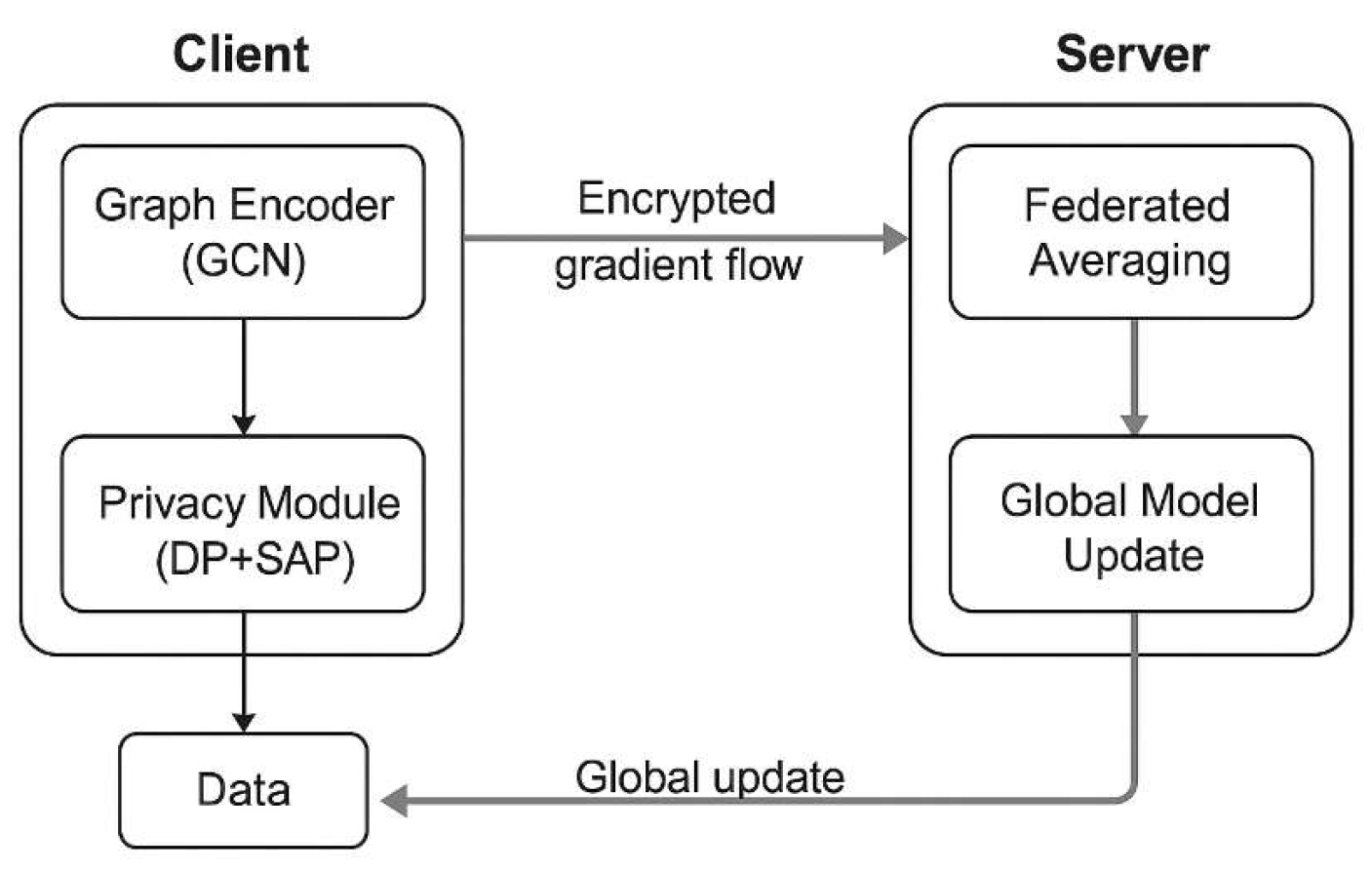
To further clarify the interaction between modules, the revised
Figure 2 is redesigned to explicitly depict the end-to-end flow. The integration of GCN with federated learning not only captures topological user-item relations but also ensures that privacy-sensitive embeddings are never exposed in plaintext, thereby forming a structurally aware and privacy-enhanced recommendation pipeline.
2.3. Graph Convolution Layer Design
To model higher-order dependencies in the user-item graph, the GCN employs a multi-layer structure to improve feature expressiveness while mitigating overfitting and oversmoothing. Each layer performs embedding propagation based on the locally normalized adjacency matrix, using the formula [
4]:
where A~=A+I includes self-loops, D~ is the degree matrix, H(l) is the input at layer ll, W(l) the trainable weights, and σ(⋅) the activation function. A two-layer GCN is adopted. The first layer incorporates edge-type adaptive weights αuv to differentiate interaction strengths (e.g., clicks vs. ratings), with the normalized weighted adjacency matrix formulated as [
5]:
To improve local representation stability, residual connections and batch normalization are added after each convolution layer, and dropout is applied to reduce overfitting.
2.4. Federal Learning Strategies
To ensure efficient cross-client synchronization and model consistency under heterogeneous data distributions, this architecture adopts periodic synchronization, combined with asynchronous fault-tolerant updates and personalized adaptation modules. During training, each client Cₖ conducts multiple rounds of local GCN propagation and gradient-based optimization with the objective function [
6]:
where ℓ(⋅) is the prediction loss, ruv the observed rating, and λ the regularization coefficient. After local updates, model parameters are uploaded via a secure channel, and global aggregation is performed using the FedAvg algorithm:
with nk denoting the number of samples at client Ck. To reduce communication overhead and improve convergence, Partial Participation (PP) and adaptive local step size strategies are employed.
3. Data Privacy Protection Algorithm Design
3.1. Privacy Threat Model Analysis
Federated recommendation systems face multiple privacy risks as clients upload local user interaction data in parameter form for global training. These threats can be analyzed through an explicit threat model [
7]. Attackers include external passive listeners, internal malicious clients, and semi-honest servers. External and internal adversaries may infer attributes via intercepted parameters, embedding reconstruction, or gradient analysis, while servers may perform unauthorized joint analysis at the aggregation stage.
Table 2 summarizes typical attack types, including method, entry point, accessible data, and risk level. In GCN-based models, high-dimensional user-item relationships enable adversaries to infer graph structures through output and gradient reversal. Moreover, due to heterogeneous data, client gradients may leak information across update paths, increasing exposure risk.
3.2. Differential Privacy Protection Mechanisms
To defend against reconstruction and gradient-based attacks, the system applies differential privacy (DP) during local updates, perturbing parameters before each upload. DP limits an attacker’s ability to infer the presence of any single sample by injecting noise into the function output. For neighboring datasets D and D’, a random mechanism M satisfies ϵ-differential privacy if for any output O⊆Range(M) [
8]:
Then M is said to satisfy ϵ-differential privacy. To balance privacy and utility, a Gaussian mechanism perturbs the local gradient vector before upload:
where gk is the original gradient, and σ is the noise scale, dynamically adjusted based on the privacy budget ε, sampling ratio q, and training rounds T.
Table 3 provides recommended noise settings and upload frequencies for different ε values to guide deployment.
3.3. Secure Aggregation Protocol
While differential privacy protects local updates, it remains vulnerable to intermediate reconstruction attacks without secure communication. To address this, the system employs a Secure Aggregation Protocol (SAP) under encryption, ensuring that uploaded parameters remain encrypted and inaccessible to the server before aggregation.
The protocol uses secret sharing and additive homomorphic encoding. Let client Ci’s update be Δθi; the uploaded value is [
9]:
where sij is a shared random mask between clients Ci and Cj. Aggregation removes these masks, so the server only obtains ∑iΔθi and cannot recover individual updates. To assess overhead,
Table 4 presents communication performance under varying encryption rounds and client scales, guiding deployment-level strategy selection.
3.4. Optimization of Privacy Performance Tradeoffs
In federated recommender systems, privacy mechanisms like differential privacy and secure aggregation introduce noise, communication overhead, and potential accuracy loss. To maintain practicality, the framework adopts a dynamic privacy-performance trade-off strategy that adjusts protection strength during training. A privacy budget scheduling function distributes the total budget εmax across T rounds as:
where T is the total number of rounds and β∈(0,1] is a scheduling factor. Early rounds receive smaller budgets for stronger privacy, while later rounds allow more noise relaxation to improve convergence.
To enhance adaptiveness, a gradient sensitivity-aware adjustment is introduced. Let
represent the gradient sensitivity of client k at round t, and S‾ be its exponential moving average. The adjusted privacy budget becomes:
with γ as the adaptation coefficient. This increases noise tolerance during sharp updates and reduces it as learning stabilizes. All strategies conform to moments accountant privacy composition, ensuring the total budget is not exceeded while preserving model utility and robustness.
3.5. Communication Efficiency Optimization
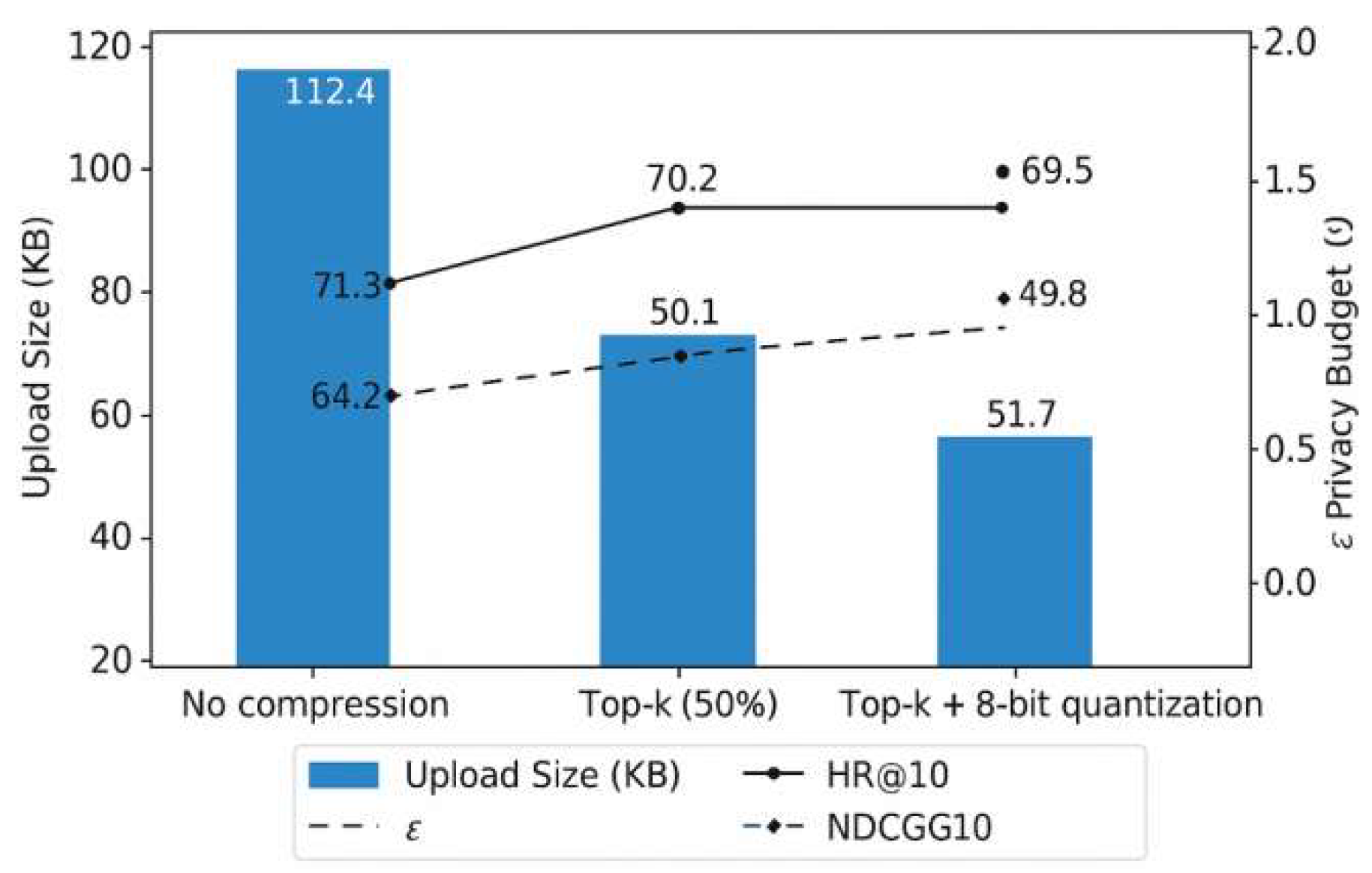
In federated GCN systems, frequent transmission of high-dimensional parameters leads to significant communication overhead, particularly under bandwidth constraints. To mitigate this, the DP-FedGCN framework integrates compression techniques without weakening privacy guarantees. A top-k sparsification strategy is applied, transmitting only the most significant gradients each round, reducing uplink bandwidth by over 70%. This is combined with stochastic quantization, compressing 32-bit gradients to 8-bit integers while preserving convergence. To maintain compatibility with differential privacy and secure aggregation, compressed gradients are perturbed post-compression using the Gaussian mechanism and encoded via secret sharing. The secure aggregation protocol remains valid due to additive homomorphism over quantized vectors. As shown in
Figure 3, with 50% compression, the model retains over 95% of its original accuracy while reducing average upload size from 112.4 KB to 51.7 KB. These results confirm the feasibility of deploying DP-FedGCN in bandwidth-limited environments without compromising robustness or privacy.
4. Experimental Evaluation and Analysis
4.1. Experimental Environment and Data Set
To evaluate the deployment feasibility of the proposed federated recommendation model with graph convolution and privacy mechanisms, experiments are conducted on TensorFlow 2.13 and PySyft 0.6, with the server running Linux on dual Intel Xeon Gold 6226R CPUs (64 cores, 256GB RAM). Federated clients are simulated via containerized nodes. Three benchmark datasets—MovieLens-1M, Amazon-Books, and Yelp-2018—are used, covering movie ratings, e-commerce, and local services. Their statistical details are shown in
Table 5. Each dataset is partitioned by user ID hash to ensure data heterogeneity and privacy isolation. During local graph construction, bipartite adjacency matrices are generated from historical behaviors and converted to sparse tensor formats for GCN input. All features are uniformly encoded and normalized to reduce cross-source embedding bias during training.
4.2. Model Performance Analysis
To evaluate the predictive performance and training efficiency of the proposed DP-FedGCN model, experiments were conducted on MovieLens-1M, Amazon-Books, and Yelp-2018 using metrics HR@10, NDCG@10, and AUC-based convergence curves. Comparisons were made against two baselines: Fed-MF and the non-private Fed-GCN. As shown in
Figure 3, GCN-based models outperform Fed-MF on all datasets, with DP-FedGCN achieving 8.2% higher HR@10 and 6.7% higher NDCG@10 on the sparse Amazon-Books dataset. The GCN structure captures high-order user-item relations, and adding differential privacy does not significantly degrade accuracy. In early training rounds (5–10), Fed-GCN shows parameter instability, while DP-FedGCN converges smoothly, indicating greater robustness under noisy updates and data heterogeneity. Further benchmarking against FedRec, GCN-FedRS, and FedDPSGD (see
Table 7) confirms that DP-FedGCN achieves the best accuracy on MovieLens-1M, with only moderate overhead from encryption and noise. It also offers the lowest reconstruction attack success rate (12.7%), thanks to its tunable ε-DP mechanism. These results verify that the proposed framework balances accuracy, communication efficiency, and privacy, making it well-suited for sensitive, high-risk applications.
Table 6.
Performance comparison on MovieLens-1M.
Table 6.
Performance comparison on MovieLens-1M.
| Model |
HR@10 |
NDCG@10 |
Upload (KB) |
ε-DP |
Attack Rate (%) |
| FedRec |
63.1 |
42.5 |
75.4 |
— |
32.6 |
| GCN-FedRS |
65.7 |
44.9 |
89.2 |
— |
35.2 |
| FedDPSGD |
61.2 |
40.8 |
102.5 |
1.0 |
18.9 |
| DP-FedGCN |
71.3 |
51.6 |
112.4 |
1.0 |
12.7 |
4.3. Analysis of Privacy Protection Effectiveness
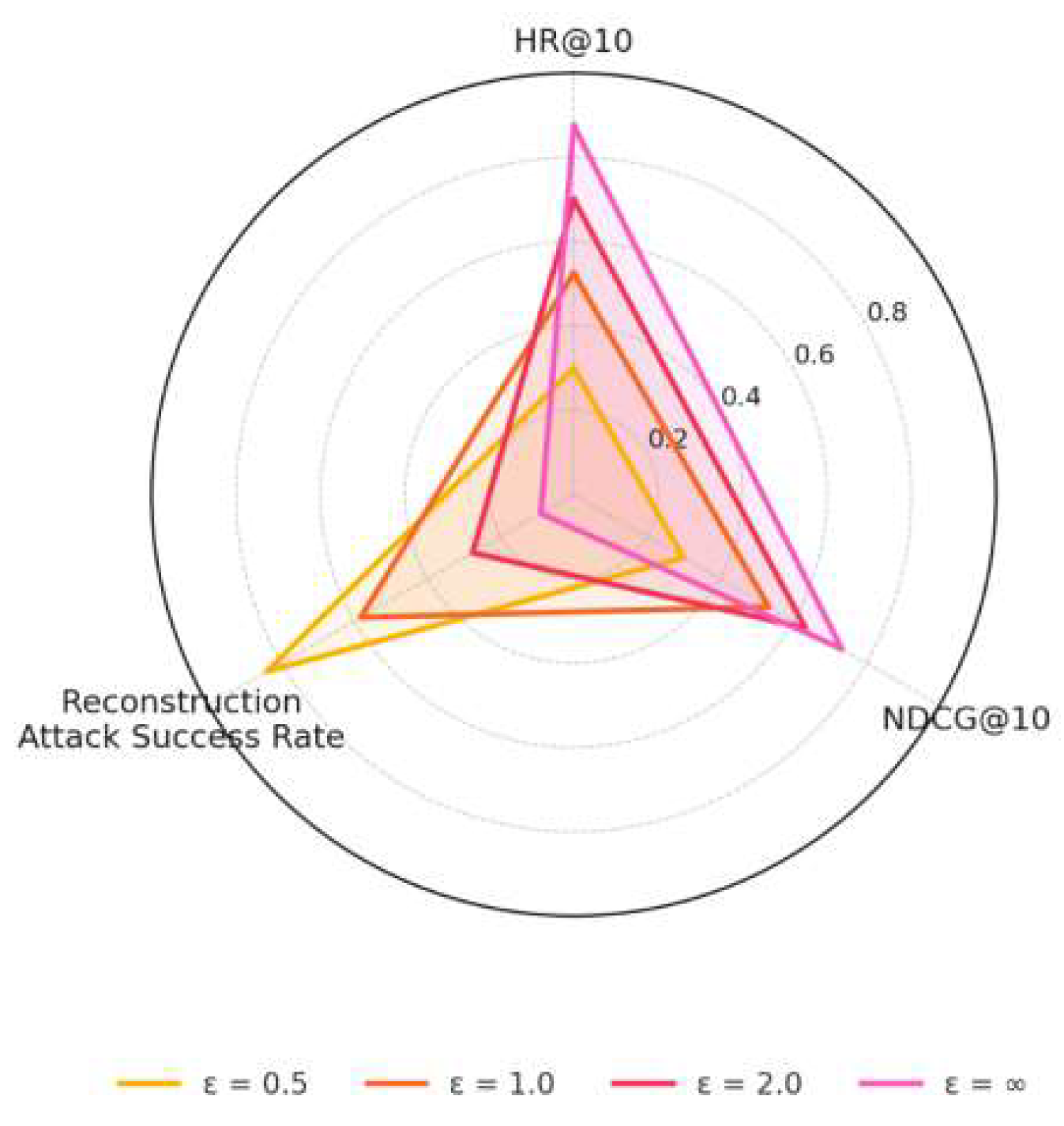
To assess the effectiveness of the proposed differential privacy and secure aggregation mechanisms, experiments focus on three aspects: leakage suppression, performance retention, and attack resistance. DP-FedGCN is evaluated under varying privacy budgets ε, examining its sensitivity to reconstruction and gradient backpropagation attacks. As shown in
Figure 4, higher ε values improve HR@10 and NDCG@10, but reduce privacy strength, illustrating the typical accuracy-privacy trade-off. To quantify robustness,
Table 6 compares reconstruction and gradient leakage rates across models. With Gaussian noise and secure aggregation, DP-FedGCN reduces reconstruction success from 35.2% to 12.7%, effectively limiting exposure of user embeddings. Even under strong noise, DP-FedGCN maintains stable Top-N recommendation performance, confirming its practicality and robustness in privacy-sensitive scenarios.
Table 6.
Comparative analysis of leakage rate of each model in privacy attack scenarios.
Table 6.
Comparative analysis of leakage rate of each model in privacy attack scenarios.
| mould |
Reconfiguration attack success rate (%) |
Gradient leakage reproducibility (%) |
| Fed-GCN |
35.2 |
28.4 |
| Fed-GCN + SAP |
21.6 |
15.2 |
| DP-FedGCN |
12.7 |
9.5 |
5. Conclusion
In this study, from the perspective of fusion of federated learning and graph neural network, a federated recommendation model oriented to data privacy protection is constructed to enhance the effect of personalized recommendation while effectively curbing the potential risk of information leakage. The designed differential privacy mechanism and secure aggregation protocol show high robustness under multi-class attack scenarios, verifying the feasibility and practicality under decentralized data distribution conditions. The model shows some innovations in heterogeneous graph structure modeling, higher-order relationship expression and privacy performance tradeoffs. However, there is still room for optimization in the stability control of federated asynchronous training, adaptive adjustment of differential privacy noise, and communication efficiency in large-scale client scenarios. Future research can further explore the fusion mechanism of graph neural structure and multimodal behavioral data, and introduce personalized privacy budget scheduling strategies to construct a more robust and efficient federated recommender system.
References
- Hu P, Lin Z, Pan W, et al. Privacy-preserving graph convolution network for federated item recommendation[J]. Artificial Intelligence, 2023, 324: 103996. [CrossRef]
- Liu Z, Yang L, Fan Z, et al. Federated social recommendation with graph neural network[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2022, 13(4): 1-24. [CrossRef]
- Ma C, Ren X, Xu G, et al. FedGR: Federated graph neural network for recommendation systems[J]. Axioms, 2023, 12(2): 170. [CrossRef]
- Yin Y, Li Y, Gao H, et al. FGC: GCN-based federated learning approach for trust industrial service recommendation[J]. IEEE Transactions on Industrial Informatics, 2022, 19(3): 3240-3250. [CrossRef]
- Tian C, Xie Y, Chen X, et al. Privacy-preserving cross-domain recommendation with federated graph learning[J]. ACM Transactions on Information Systems, 2024, 42(5): 1-29. [CrossRef]
- Li Z, Bilal M, Xu X, et al. Federated learning-based cross-enterprise recommendation with graph neural networks[J]. IEEE Transactions on Industrial Informatics, 2022, 19(1): 673-682. [CrossRef]
- Wu G, Pan W, Yang Q, et al. Lossless and Privacy-Preserving Graph Convolution Network for Federated Item Recommendation[J]. 2024; arXiv:2412.01141.
- Xu Z, Li B, Cao W. Enhancing federated learning-based social recommendations with graph attention networks[J]. Neurocomputing, 2025, 617: 129045. [CrossRef]
- Yao Y, Kamani M M, Cheng Z, et al. FedRule: Federated rule recommendation system with graph neural networks[C]//Proceedings of the 8th ACM/IEEE Conference on Internet of Things Design and Implementation. 2023: 197-208.
- Yan B, Cao Y, Wang H, et al. Federated heterogeneous graph neural network for privacy-preserving recommendation[C]//Proceedings of the ACM Web Conference 2024. 2024: 3919-3929.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).