Relativistic Algebra over Finite Fields

1. Introduction

A growing body of work in mathematics and physics suggests that foundational structures are best understood through a relational or relativistic lens [15,20,23]. In such a paradigm, mathematical entities acquire meaning not as intrinsic absolutes but through their role within a system defined by internal symmetries and reference frames. Constants like 0, 1, or i are not metaphysical primitives, but relational markers—origins, units, or axes—assigned by a chosen framing.

This perspective invites a re-evaluation of one of the most entrenched assumptions in mathematics: the acceptance of actual infinity. From real analysis to Hilbert spaces, infinity has been treated as foundational, despite its lack of empirical or computational realization. Under a relational view, such constructs may instead be interpreted as emergent limits or symbolic artifacts—arising when finite systems attempt to encode relationships that exceed their internal scope.

In previous work [2], we argued that concepts like infinity, randomness, and undecidability are not ontological features of nature, but epistemic placeholders—signals of representational saturation in finite informational systems. Here, we extend this view into a concrete formalism: a relativistic algebra constructed entirely over a finite field ${\mathbb{F}}_p$, with observer-relative arithmetic and emergent pseudo-numbers.

The present framework resonates with several contemporary perspectives that question the ontological status of the continuum and advocate for finitely constructed alternatives. In particular, Smolin has emphasized the need for a relational, observer-dependent formulation of physical laws, suggesting that the continuum is merely an idealization beyond the reach of internal observers [28,29]. Similarly, D’Ariano and collaborators have reconstructed quantum theory from finite, informationally grounded axioms, demonstrating that core features of quantum mechanics can emerge without invoking infinite-dimensional Hilbert spaces [12]. From a mathematical standpoint, the approach aligns with the ultrafinitist program developed by Benci and Di Nasso, which offers a rigorous alternative to classical cardinality through the theory of numerosities and bounded arithmetic [6,7].

Furthermore, the ultrafinitist school—pioneered by Yessenin-Volpin and Parikh—takes finitude even further by denying the meaningful existence of “too large” numbers and insisting on feasibility as a foundational constraint. Formalizations of ultrafinitism and feasibility arithmetic appear in works such as [4,24,26,32], which explore the proof-theoretic and computational consequences of enforcing strict constructive bounds on arithmetic.

Ultrafinitism enforces an a priori cutoff on numerical existence—only those magnitudes deemed “feasible” within a human or machine resource bound are admitted. By contrast, our relativistic framework treats finiteness not as a hard barrier but as a contextual framing condition: We allow arbitrarily large numbers, so “size” is always relative to the chosen frame. Infinite structures, such as integers and rationals emerge asymptotically or as coordinate projections, rather than being forbidden. Arithmetic operations become internal symmetries of a finite system, rather than operations constrained by external feasibility checks. This shift replaces the ultrafinitist’s absolute feasibility threshold with a relational notion of scope: any number “exists” within some finite frame, while “infinity” itself appears as a relative point beyond the horizon of observability and algebraic accessibility.

To support this framework, we further draw upon several key developments in mathematics and physics. The foundational critique of actual infinity has been explored in works such as [9,31], which emphasize the constructive and finitist approaches to mathematics. The relational perspective on mathematical objects aligns with category theory [20], where objects are defined by their morphisms and relationships rather than intrinsic properties. Additionally, the parallels between relativistic mathematics and modern physics are inspired by the symmetry principles in [15,23], which highlight the role of invariance and frame-dependence in physical laws. Finally, the informational limits of finite systems and their implications for mathematical representation are discussed in [11,22].

2. Finite Field Framing

Let ${\mathbb{F}}_p=\{0,1,2,\dots ,p-1\}$ be the finite field of integers modulo an odd prime p. The elements of ${\mathbb{F}}_p$ form a complete and closed set of relational representations of ${\mathbb{F}}_p$ under modular addition, multiplication and exponentiation. However, the specific numeric labels assigned to these elements—particularly the designation of 0 and 1 as the additive and multiplicative identities—are intrinsically relative and carry no absolute meaning within the field itself. The field ${\mathbb{F}}_p$ is invariant under relabeling of its elements via any bijective affine transformation of the form

$$k\mapsto a·k+bmodq,$$

where $a\in {\mathbb{F}}_p^{\times }$ and $b\in {\mathbb{F}}_p$. Such transformations preserve the field structure and allow any element to be reinterpreted as the origin. In this sense, the element labeled 0 is not uniquely privileged; it simply represents the additive identity with respect to a chosen reference frame. The same applies to the label 1, which identifies the multiplicative unit only relative to a particular scaling.

Recall that choosing a “frame” in ${\mathbb{F}}_p$ consists of picking two distinguished elements

$$0^{\prime }=a,1^{\prime }=b,b\ne 0,$$

and then defining relabeled addition and multiplication by

$$x\oplus y:=a+b\left((x-a)/b+(y-a)/b\right),x\otimes y:=a+b\left((x-a)/b·(y-a)/b\right),$$

where divisions are in the original field ${\mathbb{F}}_p$.

Theorem 1 

(Frame-Invariance). Let ${\mathbb{F}}_p$ be a finite field, and let two frames $(0,1)$ and $(a,b)$ be related by the affine bijection

$$\varphi :{\mathbb{F}}_p⟶{\mathbb{F}}_p,\varphi \left(x\right)=a+bx,b\ne 0.$$

Then ϕ is a ring isomorphism between $\left({\mathbb{F}}_p,+,·\right)$ and $\left({\mathbb{F}}_p,\oplus ,\otimes \right)$. Consequently, any polynomial identity

$$P\left(x_1,\dots ,x_n\right)=0\mathit{holds}\mathit{in}\mathit{the}\mathit{standard}\mathit{frame}$$

if and only if the “relabeled” identity

$$P\left({\varphi }^{-1}\left(X_1\right),\dots ,{\varphi }^{-1}\left(X_n\right)\right)=0\mathit{holds}\mathit{in}\mathit{the}(a,b)-\mathit{frame},$$

where $X_i=\varphi \left(x_i\right)$.

Proof. 

Since $b\ne 0$, $\varphi$ is a bijection with inverse ${\varphi }^{-1}\left(X\right)=(X-a)/b$. For any $x,y\in {\mathbb{F}}_p$,

$$\varphi (x+y)=a+b(x+y)=\left(a+bx\right)\oplus \left(a+by\right)=\varphi \left(x\right)\oplus \varphi \left(y\right),$$

and similarly

$$\varphi \left(xy\right)=a+b\left(xy\right)=\left(a+bx\right)\otimes \left(a+by\right)=\varphi \left(x\right)\otimes \varphi \left(y\right).$$

Thus, $\varphi$ preserves addition and multiplication, so it is a ring isomorphism. It follows immediately that any algebraic (polynomial) relation valid in one frame is carried over to the other by conjugation with $\varphi$, establishing frame-independence of all algebraic identities. □

Therefore, in the absence of an externally imposed or contextually declared frame—such as one defined by a designated pair $(0,1)$—the labels in ${\mathbb{F}}_p$ are relational rather than absolute. The roles of “zero” and “one” are thus not the fundamental properties of the elements themselves, but a consequence of the system’s framing, making all representations in ${\mathbb{F}}_p$ symmetric and interchangeable under coordinate transformation. To define our system unambiguously, we must specify a reference frame or coordinate system $(0,1)$ within the context of ${\mathbb{F}}_p$, which then becomes a framed finite ring ${\mathbb{F}}_p(0,1)$. We will henceforth assume all such systems to be framed systems ${\mathbb{F}}_p(0,1)$ and will denote the corresponding finite ring as ${\mathbb{F}}_p$ for simplicity, unless explicitly stated otherwise.

3. Finite Field as Discrete Geometric Structure

Let p be an odd prime and let ${\mathbb{F}}_p$ denote the finite field with p elements [10]. The additive group $({\mathbb{F}}_p,+)$ is a cyclic group of order p, and the multiplicative group of nonzero elements $({\mathbb{F}}_p^{\times },·)$ is a cyclic group of order $p-1$ [14]. We associate the cardinality degree of freedom p and the three fundamental arithmetic operations with 4 distinct symmetry classes in a symbolic geometry as in [1]:

• Counting — defines the number of elements in the ring.
• Addition $(+)$ — defines rotational symmetry on a linear periodic axis.
• Multiplication $(\times )$ — defines scaling symmetry on a multiplicative periodic axis.
• Exponentiation — defines cyclic phase-like symmetry from repeated powers of a generator [3].

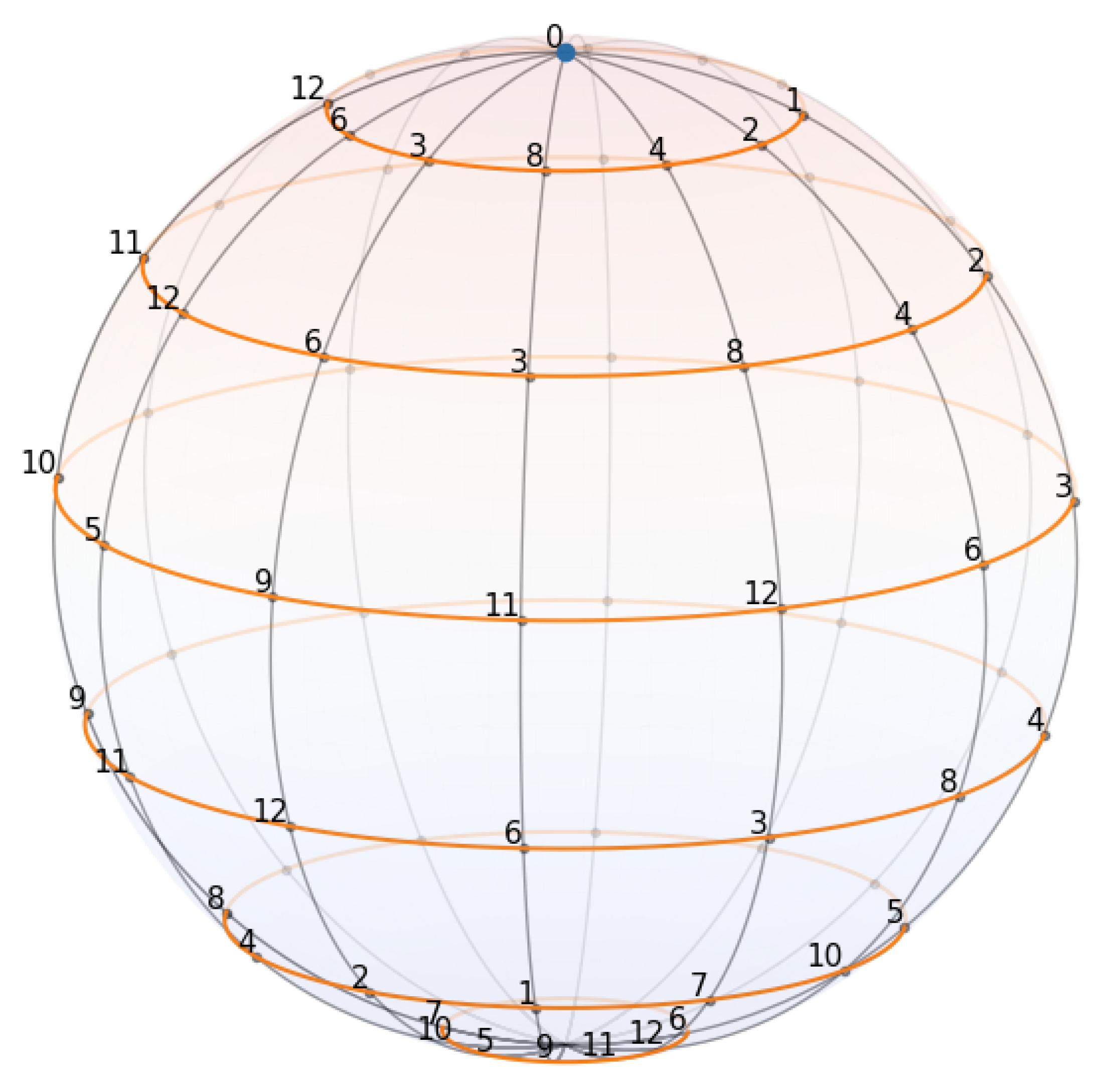
The choice of cardinality itself defines a linear—radial—degree of translation, and each cyclic operation corresponds to a spherical axis of rotational transformation in a four-dimensional abstract symmetry space. For a fixed odd prime p, the described mathematical construct forms the geometric scaffold of a discrete spheroidal system. The three spherical axes are mutually orthogonal, but algebraically dependent forming a 2D spheroid in the 4D symmetry space.

The resultant 2D spheroid for ${\mathbb{F}}_{13}$ is depicted in Figure 1, where the prime meridian depicts the additive group $({\mathbb{F}}_{13},+)$ and the latitudes represent multiplicative group $({\mathbb{F}}_{13}^{\times },·)$ generated by the minimum multiplicative generator $g_{min}=2$ [1].

4. Pseudo-Numbers

4.1. Pseudo-Integers

While the finite field ${\mathbb{F}}_p$ provides a complete and closed algebraic structure, its inherently cyclic nature eliminates any meaningful notion of ordering or signed magnitude. In contrast, many physical and informational systems rely on the intuitive structure of the integers $\mathbb{Z}$, with concepts such as positive and negative values, proximity to an origin, and relational comparison. To bridge this conceptual gap, we would like to introduce a relativistic, context-dependent construction within ${\mathbb{F}}_p$ that recovers the essential features of integer arithmetic in a familiar and logically consistent form.

In the conventional finite field ${\mathbb{F}}_p$, we can define negative elements $-k\in {\mathbb{F}}_p$ as the unique additive inverse of k, satisfying $k+(-k)\equiv 0modp$ [14]. This definition of negation is algebraically consistent but is purely modular and lacks any intrinsic ordering. For example, the element $-1$ in ${\mathbb{F}}_p$ is not necessarily less than 0, as we can state $-1-0=-1=12$, or greater than 0, as we can also state $0-(-1)=1$, and the same applies to any other element in the field. The lack of a meaningful ordering relation in the finite field ${\mathbb{F}}_p$ makes it impossible to define a signed magnitude or compare elements in a way that aligns with our intuitive understanding of integers.

Let us therefore consider the 3D representation of the finite field ${\mathbb{F}}_p$ as depicted in Figure 1 by observing it from the top down. We would like to offer a metaphor of the "North Pole" frame of reference, but it is important to note that the surface of the manifold in Figure 1 does not have any real special points and the selection of such "North Pole" position and the corresponding frame of reference is purely arbitrary and subjective.

Correspondingly, the original additive sequence $0,1,\dots ,p-1$ of the ring’s elements are represented as points located on the latitudinal axis—let us call it the prime meridian—of the ${\mathbb{F}}_p$ 2D manifold sphere, while the multiplicative symmetry elements are now arranged in circular patterns along the longitudinal axes and around the origin. Now let us imagine a naive local observer that is not aware of the spherical nature of the surface he is observing. We may need to hereby assume a sufficiently large cardinality p such that the local curvature is not apparent to such observer in the exact same way as the local curvature of the Earth is not apparent to a human observer. For such observer, the ${\mathbb{F}}_p$ manifold surface would appear as flat, and with the sequence of elements $\dots ,-2,-1,0,1,2,\dots$ forming a horizontal axis around the observer’s position 0, as illustrated in Figure 2.

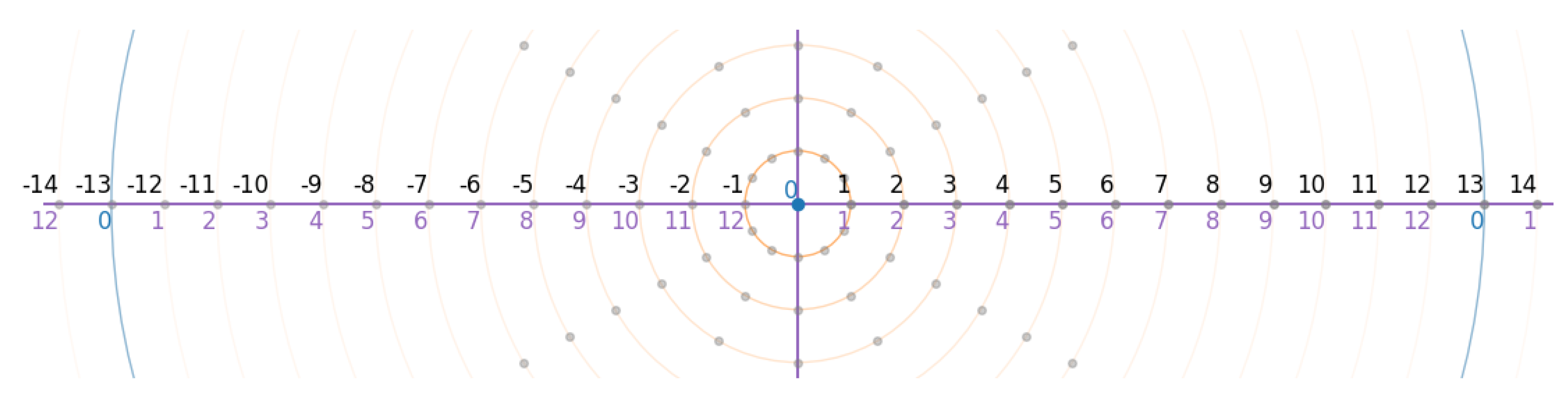
Define a mapping $k:\mathbb{Z}\to {\mathbb{F}}_p$, with $k\left(z\right)=zmodp$. This wraps $\mathbb{Z}$ onto ${\mathbb{F}}_p$ as depicted in Figure 2. The observer, located at 0 and bounded by horizon $H\ll p$, perceives the wrapped axis as infinite. Thus, the apparent integer line emerges as a pseudo-integer class $\mathbb{Z}/{\mathbb{F}}_p$, where negation, order, and comparison are reconstructed locally [17]. The resulting class of relativistic pseudo-integers $\mathbb{Z}/{\mathbb{F}}_p$ exhibits all the characteristic properties of the conventional integer set $\mathbb{Z}$, including sign, order, addition, subtraction and multiplication. This framework allows us to recover the intuitive and logical structure of integers — including signed quantities and magnitude comparison — entirely within the finite, self-contained system ${\mathbb{F}}_p$, while preserving consistency with its modular arithmetic.

4.2. Pseudo-Rationals

Having recovered the structure of signed integers $\mathbb{Z}$ over the finite field ${\mathbb{F}}_p$, it is natural to ask whether further extensions of this framework can reproduce the next layer of classical number systems—namely, the rational numbers $\mathbb{Q}$. Rational numbers emerge from the pragmatic necessity to express and manipulate ratios of integers, and their introduction marks a critical step in the construction of continuous arithmetic, proportional reasoning, and linear structure.

The motivation for this extension is twofold. First, it allows us to reconstruct the essential properties of $\mathbb{Q}$ over ${\mathbb{F}}_p$, making clear that rationality is not an intrinsic feature of infinite arithmetic but an emergent relational construct definable within finite algebra. Second, it enables a more expressive arithmetic language within the finite mathematical system, allowing for the representation of proportional relationships, scales, and geometric constructs entirely within the bounds of a finite and self-contained mathematical system.

Let

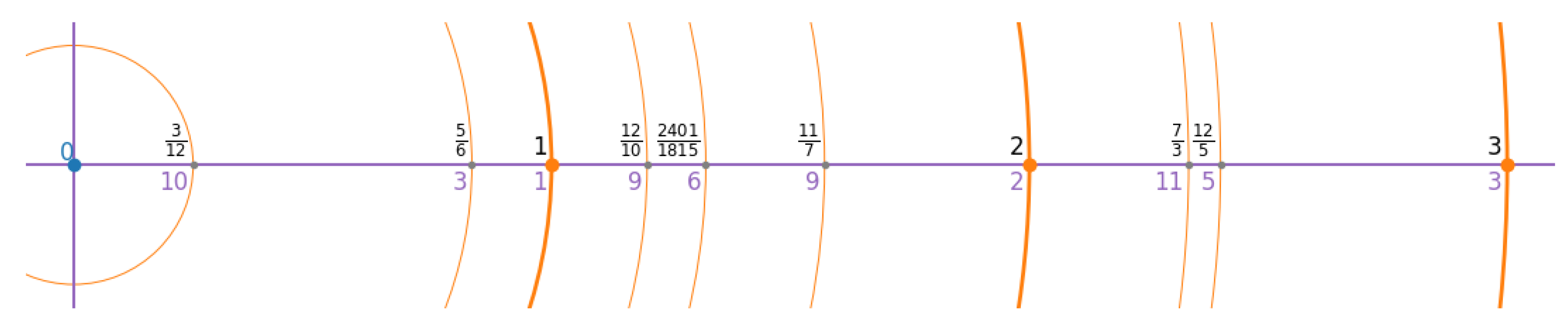
$${\mathbb{Q}}_p:=\left\{{\displaystyle \frac{a}{b}}\mid a\in \mathbb{Z},b=\prod _i{k}_i,k_i\in {\mathbb{F}}_p^{\times }\right\}.$$

The corresponding field value is

$$k\left({\displaystyle \frac{a}{b}}\right):=a·b^{-1}modp.$$

Multiple representations can map to the same $k\in {\mathbb{F}}_p$, forming equivalence classes as depicted in Figure 3. We show ${\mathbb{Q}}_p$ is dense in $\mathbb{Q}$ under a metric induced by bounded denominators $b={(p-1)}^n$ [27]. For any $q\in \mathbb{Q}$ and $ϵ>0$, there exists $q^{\prime }\in {\mathbb{Q}}_p$ such that $|q-q^{\prime }|<ϵ$.

The validity of such definition is ensured by the fact that all elements $k_i$ constituting the denominator product $b={\prod }_i{k}_i$ have a multiplicative inverse $k_i^{-1}\in {\mathbb{F}}_p^{\times }$. A selection of some simple examples of such pseudo-rational numbers is depicted in Figure 3, where for each position along the prime meridian $q=a/b\in {\mathbb{Q}}_p$ indicated as a black label on top, the corresponding finite field element $k\left(q\right)\in {\mathbb{F}}_p$ is indicated as purple label on the bottom.

Proposition 1. 

Let $p>2$ be an odd prime number, and let $q=a/b\in \mathbb{Q}$ be any conventional rational number. Then for any $ϵ>0$, there exists an integer $n\in \mathbb{N}$ and an integer $x\in \mathbb{Z}$ such that

$$\left|{\displaystyle \frac{a}{b}}-{\displaystyle \frac{x}{{(p-1)}^n}}\right|<ϵ.$$

Proof. 

Let ${\displaystyle \frac{a}{b}}\in \mathbb{Q}$ be given, and let $ϵ>0$ be arbitrary small number.

Since p is a fixed prime, the expression ${(p-1)}^n$ grows without bound as $n\to \infty$. Therefore, there exists an integer $n\in \mathbb{N}$ such that

$${\displaystyle \frac{1}{{(p-1)}^n}}<ϵ.$$

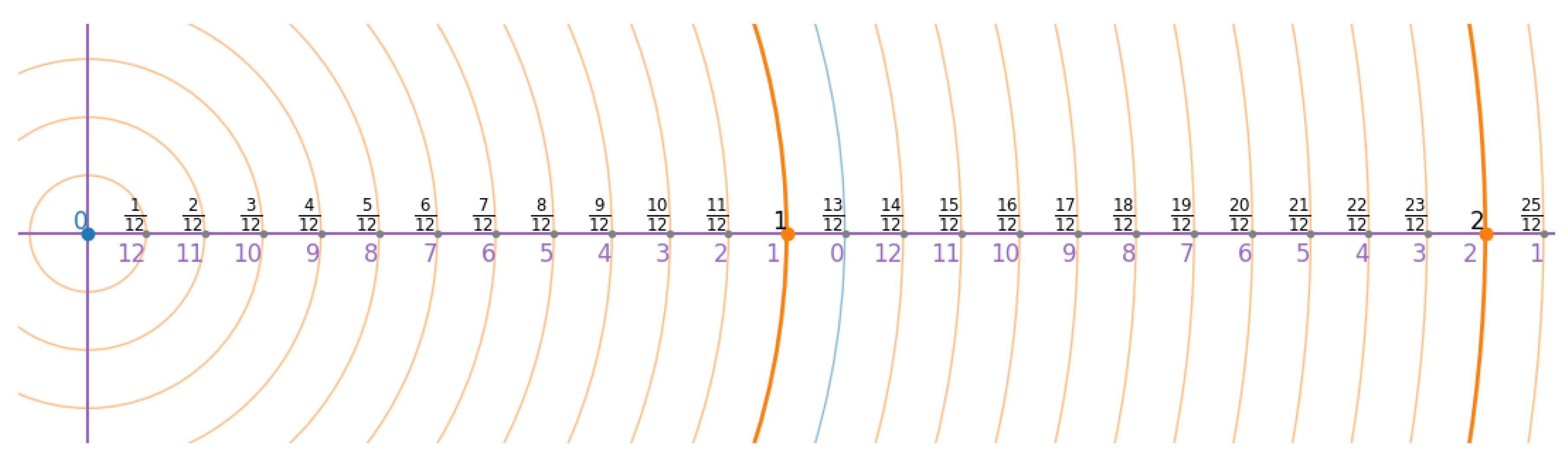
Now consider the set of rational points of the form

$$\left\{{\displaystyle \frac{k}{{(p-1)}^n}}|k\in \mathbb{Z}\right\},$$

as illustrated in Figure 4. This set is a uniform grid of rational numbers with step size ${\displaystyle \frac{1}{{(p-1)}^n}}$, which is less than $ϵ$ by construction. There exists therefore an integer $x\in \mathbb{Z}$ such that

$$\left|{\displaystyle \frac{a}{b}}-{\displaystyle \frac{x}{{(p-1)}^n}}\right|<ϵ,$$

which completes the proof. □

It is very important to reiterate the meaning of this construct from an ontological viewpoint. More specifically, we stipulate that what actually “exists” are the p representations of the finite field ${\mathbb{F}}_p$, while the derivative class of pseudo-rationals $q\in {\mathbb{Q}}_p$ constitute an abstract mathematical construct derived from the inherent relational properties of the framed instance ${\mathbb{F}}_p$.

In other words, the resultant field of pseudo-rational numbers ${\mathbb{Q}}_p$ will exhibit all the properties of the field of conventional numbers $\mathbb{Q}$ and can further approximate it with any arbitrary precision. Furthermore, for an observer with a limited observability horizon and sufficiently large values of cardinality p, the pseudo-rational field ${\mathbb{Q}}_p$ becomes completely indistinguishable from its conventional counterpart, as all the desired rational numbers of the form $q=a/b$, where $b<p$ are represented not approximately, but exactly within the scope of the pseudo-rational numbers ${\mathbb{Q}}_p$.

4.3. Pseudo-Reals

In classical mathematics, the field of real numbers $\mathbb{R}$ is introduced to enable the formulation of continuous functions, calculus, and metric spaces—tools indispensable for modeling physical phenomena and abstract structures alike. However, the real number line is defined as an uncountable, infinitary continuum, an ontological commitment that conflicts with the finite and relational framework we adopt in this study. Nonetheless, our need for continuous approximation and proportional reasoning persists, particularly in describing geometric constructs, dynamic systems, and analytic behaviors. Our approach is therefore pragmatic and epistemic rather than metaphysical. We seek to construct a class of pseudo-real numbers that fulfills the operational role of $\mathbb{R}$ without invoking actual infinity.

Define truncated pseudo-rationals:

$${\mathbb{Q}}_p^{\le H}=\left\{[x,n]:0\le x<p,0\le n\le H\right\},[x,n]:={\displaystyle \frac{x}{{(p-1)}^n}}.$$

This set is finite and totally bounded under the metric:

$$d_H([x,n],[y,m]):=\left|{\displaystyle \frac{x}{{(p-1)}^n}}-{\displaystyle \frac{y}{{(p-1)}^m}}\right|.$$

Define ${\mathbb{R}}_p$ as the closure of ${\mathbb{Q}}_p^{\le H}$. We show all computable real numbers can be approximated within $2^{-k}$ by some element $[x,n]\in {\mathbb{Q}}_p^{\le H}$, where $H\ge \lceil k{log}_{2}p\rceil$ [30].

Proposition 2 

(Finite Total Boundedness). For each fixed H, the metric space $\left({\mathbb{Q}}_p^{\le H},d_H\right)$ is finite and thus totally bounded.

Proof. 

Since $0\le x<p$ and $0\le n\le H$, there are $\left(P\right)\times (H+1)$ elements in ${\mathbb{Q}}_p^{\le H}$. Any finite metric space is trivially totally bounded. □

Theorem 2 

(Approximation of Computable Reals). Let $r\in \mathbb{R}$ be a computable real number. For any integer $k\ge 1$ there exist integers $a_k,b_k$ with $b_k\ne 0$ such that

$$\left|r-\frac{a_k}{b_k}\right|<2^{-k}.$$

Moreover, if the observer’s horizon H satisfies

$$H\ge ⌈k{log}_{2}p⌉,$$

then one can construct $[x_k,n_k]\in {\mathbb{Q}}_p^{\le H}$ with

$$\left|r-[x_k,n_k]\right|<2^{-k-1}.$$

In order to prove Theorem 2 we first show that every Cauchy sequence $\left(x_n\right)\subseteq Q_{\le H,p}$ converges in ${\mathbb{R}}_p$. The key step is a uniform bound on the number of divisions in the Euclidean algorithm.

Lemma 1 

(Euclidean-algorithm exponent bound). Let p be a prime and suppose $a,b\in \{1,2,\dots ,p-1\}$. If the Euclidean algorithm applied to $(a,b)$ produces k nonzero remainders before terminating, then

$$k\le ⌊{log}_2\left(p\right)⌋+1.$$

Proof. 

At each step of the Euclidean algorithm, if $\left(r_i\right)$ are the successive remainders with $r_0=a,r_1=b,r_{i+1}=r_{i-1}mod{r}_i$, then

$$r_{i-1}=q_i{r}_i+r_{i+1},0\le r_{i+1}<r_i,$$

and $q_i\ge 1$. It is known (Lamé’s theorem) that the worst-case sequence of quotients $\left(q_i\right)$ all equal 1, which yields the Fibonacci-type descent [19].

$$r_{i+1}\le r_{i-1}-r_i,$$

so that

$$r_k\ge F_{k+1},$$

where $F_n$ is the n-th Fibonacci number. Since $r_k\ge 1$ and $F_n\ge 2^{(n-2)}$ for $n\ge 2$, termination after k steps implies

$$2^{k-1}\le F_{k+1}\le p-1⟹k-1\le {log}_2(p-1)<{log}_2\left(p\right),$$

hence $k\le \lfloor {log}_2\left(p\right)\rfloor +1$. □

Proof of Theorem 2 

(Completeness of ${\mathbb{R}}_{\mathbf{p}}$). Let $\left(x_n\right)\subseteq Q_{\le H,p}$ be a Cauchy sequence with respect to the metric

$$d_H\left(a/b,c/d\right)=\left|ad-bc\right|/\left(bd\right),$$

where $|·|$ is taken in the integer sense and we require $a,b,c,d\le H$. By the Cauchy property, for any $ϵ>0$ there exists N such that for all $m,n\ge N$,

$$d_H(x_m,x_n)<ϵ.$$

Write $x_n=a_n/b_n$ in lowest terms. Apply the Euclidean algorithm to each pair $(a_n,b_n)$ to obtain the continued-fraction expansion

$${\displaystyle \frac{a_n}{b_n}}=q_{n,0}+{\displaystyle \frac{1}{q_{n,1}+\frac{1}{\ddots +\frac{1}{q_{n,k_n}}}}},$$

with $k_n\le \lfloor {log}_2\left(p\right)\rfloor +1$ by Lemma 1. Truncating at the J–th convergent yields a rational ${\displaystyle \frac{p_{n,J}}{q_{n,J}}}$ satisfying the standard bound

$$\left|{\displaystyle \frac{a_n}{b_n}}-{\displaystyle \frac{p_{n,J}}{q_{n,J}}}\right|<{\displaystyle \frac{1}{q_{n,J}^2}}.$$

Since $q_{n,J}\le b_n\le H$, for any chosen $J>{log}_2(H/ϵ)$ we get

$$\left|x_n-{\displaystyle \frac{p_{n,J}}{q_{n,J}}}\right|<{\displaystyle \frac{1}{H^2}}<ϵ.$$

Thus, $\left(x_n\right)$ is a Cauchy sequence in the complete metric space $\mathbb{R}$, hence converges to some real limit L. By construction of ${\mathbb{R}}_p$ as the metric completion of $Q_{\le H,p}$, this same limit L defines an element of ${\mathbb{R}}_p$. Therefore, every Cauchy sequence in $Q_{\le H,p}$ converges in ${\mathbb{R}}_p$, proving completeness. □

Recall that ${\mathbb{R}}_p$ is defined as the metric completion of the set

$$Q_{\le H,p}=\left\{a/b|a,b\in \{1,2,\dots ,H\}\subset {\mathbb{F}}_p,gcd(a,b)=1\right\}$$

equipped with the metric

$$d_H\left(a/b,c/d\right)={\displaystyle \frac{|ad-bc|}{bd}}.$$

Proposition 3 

(Compactness of ${\mathbb{R}}_p$). ${\mathbb{R}}_p$ is a compact metric space.

Proof. 

We invoke the standard characterization of compactness in metric spaces [25]:

Theorem. A metric space is compact if and only if it is complete and totally bounded.

• By Theorem 2, ${\mathbb{R}}_p$ is complete: every Cauchy sequence in $Q_{\le H,p}$ converges to a point of ${\mathbb{R}}_p$.
• Proposition 2 establishes that $Q_{\le H,p}$ is totally bounded. Since ${\mathbb{R}}_p$ is the closure (completion) of $Q_{\le H,p}$, it too is totally bounded.

Therefore, ${\mathbb{R}}_p$, being both complete and totally bounded, is compact. □

The resulting pseudo-real field ${\mathbb{R}}_p$ is thus defined as the topological closure of ${\mathbb{Q}}_p$ under modular convergence. For any finite observer with bounded resolution and limited horizon of observability, ${\mathbb{R}}_p$ is indistinguishable from the conventional real number continuum.

In conclusion, the field of pseudo-real numbers ${\mathbb{R}}_p$ is not a metaphysical continuum but a layered epistemic utilitarian construct. It combines:

• Exact pseudo-reals that satisfy algebraic equations within ${\mathbb{F}}_p$, and
• Approximated pseudo-reals that are limits of converging sequences in ${\mathbb{Q}}_p$.

This framework provides all the functional properties of the real numbers—continuity, density, and completeness—without invoking actual infinity. It affirms that, in a finite and informationally complete universe, continuum-like behavior is a pragmatic illusion emerging from local reasoning over a fundamentally finite arithmetic substrate.

4.4. Complex Plane over Finite Framed Field

Having established the construction of pseudo-integers, rationals and reals over the finite field ${\mathbb{F}}_p$ as relativistic, frame-dependent analogs of their classical counterparts, we seek to further extend this framework to encompass the algebraic closure of the pseudo-real field. In conventional mathematics, the introduction of complex numbers $\mathbb{C}$ is necessitated by the absence of solutions to certain polynomial equations, such as $x^2+1=0$, within the real numbers. Analogously, in the finite framed context, we are motivated to introduce complex-like elements in order to achieve closure under operations that are otherwise impossible within the pseudo-rational or alone.

Moreover, the construction of a relativistic complex plane enables the representation of rotations, oscillations, and other phenomena that are fundamental in both mathematics and physics, all within a finite and self-contained system. This approach not only mirrors the classical extension from $\mathbb{R}$ to $\mathbb{C}$, but also demonstrates that the essential properties and utility of complex numbers can be realized as emergent features of a finite, relational arithmetic—thereby reinforcing our framework’s central theme of relativistic, context-dependent number systems.

As is commonly known, the field of real numbers $\mathbb{R}$ does not contain any solutions of certain polynomial equations, such as the prominent equation $x^2+1=0$. But that is not the case for many finite fields ${\mathbb{F}}_p$, where depending on the value and properties of their cardinality P, such solutions can readily exist. For example, in the finite field ${\mathbb{Z}}_5$, the equation $x^2+1=0$ has two solutions: $x=2$ and $x=3$. More generally, it is evident that the equation $x^2+1=0$ can be satisfied in a finite field ${\mathbb{F}}_p$ if and only if $P-1$ is devisable by 4, or in other words $p\equiv 1mod4$. This is due to the fact that the multiplicative group of non-zero elements in such fields is cyclic and contains elements—and the corresponding rotational symmetry—of order 4, which allows for the existence of square roots of $-1$. In this case, we can define a special element $i\in {\mathbb{F}}_p$ that satisfies the equation $i^2+1=0$. The element i is not unique, instead we have a pair of pseudo-integer elements i and $-i$ in $\mathbb{Z}/{\mathbb{F}}_p$ that satisfy the equation, in the same way as we have pairs x and $-x$ of solutions for quadratic equations in the conventional complex plane $\mathbb{C}$.

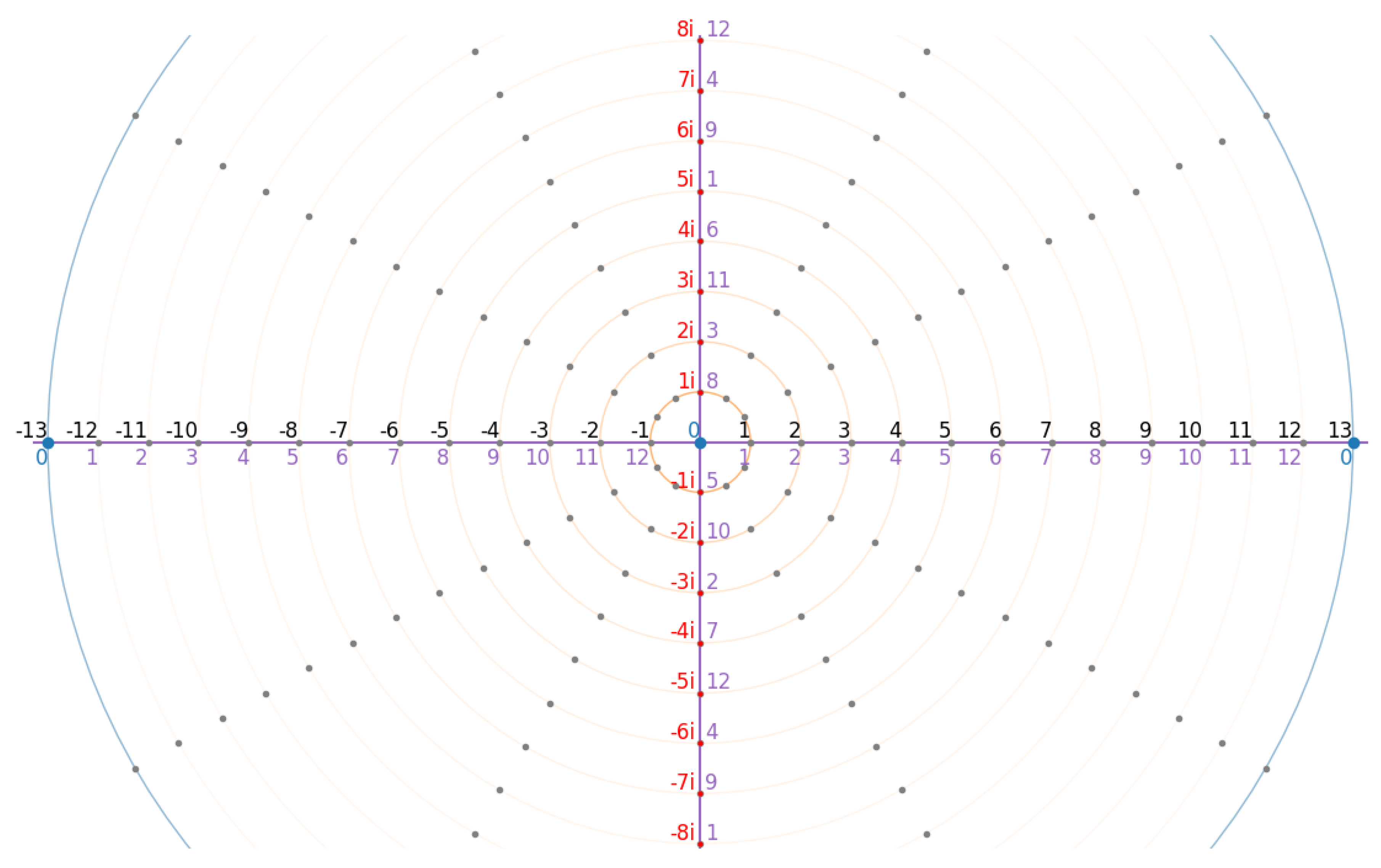
Let us now observe the “North Pole” frame of reference of the spherical representation of the finite field ${\mathbb{F}}_p$ with its prime meridian of pseudo-reals ${\mathbb{R}}_p$ forming the horizontal axis around the origin. The order-4 rotational symmetry of the finite field ${\mathbb{F}}_p$ can be represented as a vertical axis of imaginary numbers $c=z·i$, where $z\in \mathbb{Z}$, that are perpendicular to the prime meridian, as illustrated in Figure 5. The imaginary numbers c are represented by their respective red labels, while the corresponding elements $k\left(c\right)$ are depicted in purple.

More generally, we can define a class of pseudo-complex numbers ${\mathbb{C}}_p$ as the Cartesian product of the pseudo-reals ${\mathbb{R}}_p$ and the imaginary numbers $r·i,r\in \mathbb{R}$. The pseudo-complex numbers are defined as follows:

$${\mathbb{C}}_p:=\left\{c=a+b·i|a,b\in {\mathbb{R}}_p\right\},$$

(1)

where a and b are the real and imaginary components of the pseudo-complex number c, respectively. The pseudo-complex numbers can be represented as points in the complex plane, where the horizontal axis corresponds to the pseudo-reals ${\mathbb{R}}_p$ and the vertical axis corresponds to the imaginary numbers $r·i$. The pseudo-complex numbers form a field and can be added, subtracted, multiplied, and divided in a manner analogous to conventional complex numbers, with the additional consideration of their finite field properties.

The pseudo-complex numbers form a relativistic algebraic field and can be added, subtracted, multiplied, and divided in a manner analogous to conventional complex numbers, subject to the selection of the arbitrary frame of reference, as well as the properties and constraints of the underlying finite field.

5. Unification and Ontological Perspective

We assert that only the p representations of ${\mathbb{F}}_p$ truly exist. All pseudo-number classes are epistemic constructs derived from relational symmetries and observer framing. The observer’s bounded horizon $H\ll p$ induces the illusion of infinite domains [5].

5.1. Infinity as the unknowable “far-far away”

Let us revisit the ontological concept of infinity as described in [2]. In the previous sections, we have established the finite framed field ${\mathbb{F}}_p$ as an abstract pseudo-sphere ${\mathbb{F}}_p(0,1)$ with a limited-horizon observer at its origin 0. We would like now to consider the geometric point on our pseudo-sphere that is the furthest away from the observer. This point is evidently the South Pole—the antipodal point on the prime meridian—of the pseudo-sphere, which we will denote as $s_P$ for now. We would like to emphasize the following important properties of $s_P$

• $s_P$ is a unique point on the pseudo-sphere that is the farthest away from the observer at 0.
• $s_P$ is invisible to the observer at 0, that is to say that is located beyond any conceivable definition of the observer’s limited observability horizon.
• Finally, $s_P$ is algebraically inaccessible to the observer at 0, in the sense that $s_P\notin {\mathbb{F}}_p,{\mathbb{Q}}_p$, and cannot be reached by any finite number of arithmetical steps along the surface of the pseudo-sphere.

We would like to provide a formal proof of the less evident Property 3 as follows.

Theorem 3 

(No South Pole in ${\mathbb{F}}_p$). Let $P>2$ be an odd prime. Then the only solution $s\in {\mathbb{Z}}_P$ to

$$2s\equiv 0(modP)$$

is $s\equiv 0$. Equivalently, there is no nonzero pseudo-rational $q\in Q_P$ whose image in ${\mathbb{Z}}_P$ has additive order 2.

Proof. 

• Since p is prime, the additive group $({\mathbb{F}}_p,+)$ is cyclic of order p. An element $s\in {\mathbb{F}}_p$ has order 2 precisely if

  $$2s\equiv 0\left(\mathrm{mod}P\right).$$
• Because $gcd(2,p)=1$, multiplication by 2 is invertible in ${\mathbb{F}}_p$. Hence, from $2s\equiv 0(modp)$ it follows immediately that $s\equiv 0(modP)$. There is no nontrivial order-2 element.
• By definition, each pseudo-rational $q={\displaystyle \frac{a}{b}}\in {\mathbb{Q}}_p$ is represented in the field by

  $$k\left(q\right)=a{b}^{-1}modP\in {\mathbb{F}}_p,$$

  so ${\mathbb{Q}}_p\subseteq {\mathbb{F}}_p$ under the embedding k. If some $q\in {\mathbb{Q}}_p$ mapped to a nonzero order-2 element $s=k\left(q\right)\ne 0$, then $2s\equiv 0$ would force $s\equiv 0$, a contradiction.

Therefore, no “South Pole” antipodal point exists in ${\mathbb{Q}}_p$ or ${\mathbb{Z}}_p$, completing the proof. □

These properties of the geometrical point $s_P$ are unmistakably consistent with the properties of the concept of infinity in its conventional sense. This gives us the justification to identify the relativistic antipodal point $s_P$ with the concept of infinity in the context of ${\mathbb{F}}_p$, and thus denote it as ∞.

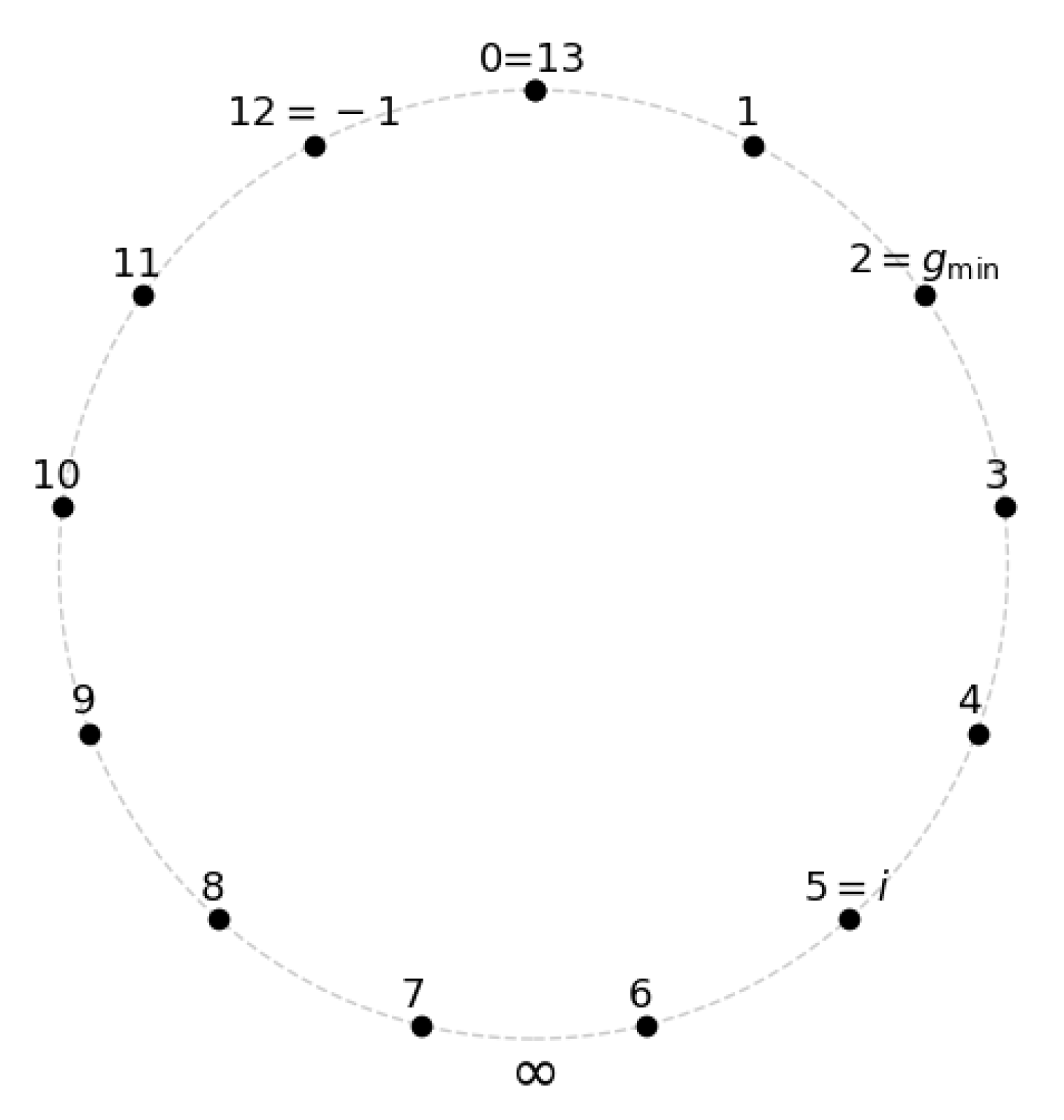
To exemplify, let us now consider the concrete example of $p=13$ and the corresponding finite framed field ${\mathbb{F}}_{13}$. We can identify the following values for the constants i, e and $\pi$ in ${\mathbb{F}}_{13}$:

$$p=13,g_{min}=2,i=5.$$

The corresponding visual representation of the finite field ${\mathbb{F}}_{13}$ is shown in Figure 6. The figure shows the state space of the finite field ${\mathbb{F}}_{13}$ as a circle on a 2D plane, with the major structural elements $-1,0,1,g_{min},i$, as well as ∞ indicated. The antipodal point ∞ is located at the South Pole of the pseudo-sphere, which is the farthest point from the observer at 0.

5.2. Approximate Lie Groups

Continuous Lie groups such as $\mathrm{SO}\left(2\right)$, $\mathrm{SU}\left(n\right)$, and $\mathrm{GL}(n,\mathbb{R})$ are approximated in ${\mathbb{F}}_p$ by discrete symmetry groups generated by modular exponentiation and cyclic subgroup structures [16].

Let $G_p\subseteq {\mathbb{F}}_p^{\times }$ be a multiplicative cyclic group of order $N\mid (p-1)$. The mapping:

$$\theta \mapsto g^{\theta }modp,\theta \in \mathbb{Z}/N\mathbb{Z},g\mathrm{a}\mathrm{primitive}\mathrm{root},$$

approximates continuous rotation $e^{i\theta }$ by discrete steps. Similarly, discrete matrix groups over ${\mathbb{F}}_p$, such as $\mathrm{GL}(n,{\mathbb{F}}_p)$, replicate local algebraic behavior of Lie algebras over reals. These finite analogs converge to their continuous counterparts as $p\to \infty$ and preserve closure, invertibility, and group action properties locally within observer horizons $H\ll p$ as follows.

Let p be a prime with $p\equiv 1(mod4)$, and fix a primitive root g of ${\mathbb{F}}_p^{\times }$. Set $N=p-1$, and identify the cyclic subgroup

$$G_p=\langle g\rangle \subset {\mathbb{F}}_p^{\times }$$

with the “discretized” circle via the map

$$\varphi :\mathbb{R}/2\pi \mathbb{Z}⟶G_p,\varphi \left(\theta \right)=g^{k\left(\theta \right)}\mathrm{where}k\left(\theta \right)=⌊\frac{N}{2\pi }\theta +\frac{1}{2}⌋modN.$$

Proposition 4 

(Angle-approximation error). For every $\theta \in [0,2\pi )$, defining $k=k\left(\theta \right)$, one has

$$\left|arg\left(\varphi \left(\theta \right)\right)-\theta \right|\le {\displaystyle \frac{\pi }{N}}⟹\left|\varphi \left(\theta \right)-e^{i\theta }\right|\le 2sin\left(\frac{\pi }{2N}\right)\le {\displaystyle \frac{\pi }{N}}.$$

Proof. 

By construction, $\left|k-\frac{N}{2\pi }\theta \right|\le \frac{1}{2}$, so

$$\left|arg\left(\varphi \left(\theta \right)\right)-\theta \right|=\left|{\displaystyle \frac{2\pi }{N}}k-\theta \right|\le {\displaystyle \frac{\pi }{N}}.$$

Thus, using the chord-arc bound $|e^{i\alpha }-e^{i\beta }|=2|sin\frac{\alpha -\beta }{2}|$,

$$\left|\varphi \left(\theta \right)-e^{i\theta }\right|=2\left|sin\left(\frac{1}{2}(arg\varphi \left(\theta \right)-\theta )\right)\right|\le 2sin\left(\frac{\pi }{2N}\right)\le {\displaystyle \frac{\pi }{N}}.$$

□

Proposition 5 

(Group-law error). For any ${\theta }_1,{\theta }_2\in [0,2\pi )$, let $k_i=k\left({\theta }_i\right)$ and set ${\varphi }_i=\varphi \left({\theta }_i\right)$. Then

$${\varphi }_1{\varphi }_2=\varphi ({\theta }_1+{\theta }_2)·\delta \mathrm{with}\left|arg\left(\delta \right)\right|\le {\displaystyle \frac{2\pi }{N}},$$

and hence

$$\left|{\varphi }_1{\varphi }_2-e^{i({\theta }_1+{\theta }_2)}\right|\le {\displaystyle \frac{2\pi }{N}}+O\left(N^{-2}\right).$$

Proof. 

We have

$${\varphi }_1{\varphi }_2=g^{k_1+k_2}=g^{k({\theta }_1+{\theta }_2)+r}=\varphi ({\theta }_1+{\theta }_2)g^r,$$

where the “round-off” exponent $\left|r\right|=\left|k_1+k_2-k({\theta }_1+{\theta }_2)\right|$ satisfies

$$\left|r\right|\le \left|\frac{N}{2\pi }{\theta }_1-k_1\right|+\left|\frac{N}{2\pi }{\theta }_2-k_2\right|+\frac{1}{2}\le \frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{3}{2}.$$

Hence, $\left|r\right|\le 1$ and $arg\left(g^r\right)$ is a multiple of $\frac{2\pi }{N}$ with $|arg\left(g^r\right)|\le \frac{2\pi }{N}$. Setting $\delta =g^r$ yields the claimed estimates. The final bound follows by combining $\varphi ({\theta }_1+{\theta }_2)=e^{i({\theta }_1+{\theta }_2)}+O\left(\frac{\pi }{N}\right)$ from Prop. 4 with $|\delta -1|\le O\left(\frac{2\pi }{N}\right)$. □

5.3. Finite Langlands Program

In the usual Langlands philosophy one relates two vast worlds: on the one hand the (infinite) Galois representations of a global field, and on the other the automorphic representations of a reductive group over that field [8,21]. If one accepts that only finite rings ${\mathbb{Z}}_q$ can exist, then every “infinite” Galois group must be replaced by its finite quotient

$$\mathrm{Gal}(\overline{F}/F)⟶\mathrm{Gal}(\overline{F}/F)/N\cong \mathrm{Gal}(F_N/F)\subset \mathrm{Perm}\left(F_N\right),$$

and every automorphic representation must likewise factor through a finite group of points

$$G\left({\mathbb{A}}_F\right)⟶G\left({\mathbb{A}}_F\right)/K_N\cong G\left({\mathbb{Z}}_q\right)$$

for some level $K_N$. In this “finite-Langlands” perspective all objects—Galois data and automorphic forms—are built from the same finite base ring ${\mathbb{Z}}_q$, and the conjectural correspondence becomes a bijection between

$$\left\{\mathrm{finite}-\mathrm{quotient}\mathrm{Galois}\mathrm{representations}\mathrm{into}G{L}_n\left({\mathbb{Z}}_q\right)\right\}⟷\left\{\mathrm{irreducible}\mathrm{representations}\mathrm{of}G\left({\mathbb{Z}}_q\right)\right\}.$$

From the function-field side one already has a prototype: Drinfeld and Lafforgue proved a global Langlands correspondence for $G{L}_n$ over ${\mathbb{F}}_q\left(T\right)$, where ${\mathbb{F}}_q$ is a finite field, and automorphic forms live on $G{L}_n\left({\mathbb{F}}_q\left[T\right]\right)$ [13,18]. There, both Galois representations and automorphic sheaves are intrinsically finite objects—perverse sheaves on moduli stacks over ${\mathbb{F}}_q$ and ℓ-adic representations of ${\pi }_1$. This suggests that a genuinely finite-universe version of the Langlands program would reorganise every classical component (Hecke operators, L-functions, trace formulas) into purely combinatorial operations on ${\mathbb{Z}}_q$-modules and finite group characters.

In summary, if one accepts that ${\mathbb{Z}}_q$ is the only ontologically primitive object, then the Langlands correspondence reduces to an equivalence of categories between ${\mathbb{Z}}_q$-linear Galois modules and ${\mathbb{Z}}_q$-linear automorphic modules. All “infinite” phenomena (analytic continuation, spectral decompositions) become emergent from the finiteness of ${\mathbb{Z}}_q$ through limiting processes within finite-dimensional ${\mathbb{Z}}_q$-vector spaces. Such a viewpoint collapses the traditional dichotomy and recasts Langlands duality as a statement about different frames of reference on a single finite ring.

6. Conclusions

The primary objective of this work has been to devise an algebraic framework that (1) does not contradict our conventional arithmetic and geometric intuitions, (2) enables all practical applications of modern mathematics, and (3) completely disposes of the ontological need for actual infinity. We have shown that by interpreting addition, multiplication and exponentiation as internal symmetries of a finite framed field ${\mathbb{F}}_p(0,1)$, one can reconstruct signed integers, pseudo-rationals, pseudo-reals and pseudo-complex numbers in a way that matches classical behavior up to any desired precision, without ever invoking an infinite set. This construction preserves the familiar algebraic laws and analytic operations that underpin standard number systems, ensuring full compatibility with intuition and established mathematical practice.

Moreover, our finite relational algebra supports the full spectrum of modern mathematical techniques—solving polynomial equations, performing limit-like approximations via dense pseudo-rationals, and modeling continuous symmetries through $\epsilon$-Lie-group approximations—while entirely replacing classical infinities with context-dependent finite representations. In doing so, it provides exact algebraic analogs for roots, exponentials and trigonometric relationships, and offers a discrete yet arbitrarily precise scaffold for differential-geometric and analytic constructions. By eliminating any ontological reliance on actual infinity, this framework retains the power and flexibility of conventional mathematics in a fully finitary setting, while also offering an avenue towards the resolution of classical paradoxes of logic and set theory imposed by the infinitude conjecture. The resulting structure is not merely a mathematical curiosity; it is a coherent and physically grounded alternative to standard formalism, suitable for the description of discrete, informationally finite physical systems.

Looking forward, extending our framework to composite moduli, and exploring the implications for the analysis of dynamic physical systems, will further strengthen and broaden its applicability. We anticipate that this relational, finite approach will serve as both a conceptually coherent foundation and a practical computational paradigm across mathematics, physics, formal logic and computer science.