1. Introduction
In an era where sustainability is no longer optional but imperative, economic decision-making must be equipped to navigate uncertainty with both resilience and foresight. Optimization problems arising in economic, financial, and engineering systems are often plagued by significant uncertainty in their input parameters. Classical optimization techniques typically rely on the assumption of complete and accurate knowledge regarding all relevant data; however, such assumptions rarely hold in practice. Variations in market conditions, model misspecification, and data estimation errors frequently lead to suboptimal or even misleading results when deterministic approaches are applied [
1,
2].
To address these limitations, robust optimization (RO) has emerged as a powerful modeling paradigm for decision-making under uncertainty. Rather than optimizing for a single, potentially inaccurate scenario, RO seeks strategies that perform acceptably across a spectrum of plausible configurations—an approach particularly valuable for sustainable resource allocation and resilient economic planning. Seminal contributions by Ben-Tal and Nemirovski [
3,
4], as well as El Ghaoui and Lebret [
5], have laid the theoretical foundation for robust optimization, introducing duality principles, tractable reformulations, and structured uncertainty sets. These foundations have been widely extended [
6], with applications in portfolio optimization [
4,
7], control systems [
8], logistics [
9], and infrastructure planning [
10,
11].
Traditional RO techniques operate by defining convex uncertainty sets and enforcing worst-case performance guarantees. This idea is exemplified by the robust counterpart formulation [
12], enriched later through polyhedral and ellipsoidal models [
3,
6,
13]. Recent developments have focused on data-driven uncertainty sets [
13,
14], entropy-based robustness metrics [
15], and scalarization methods from multi-objective optimization [
16,
17,
18], thereby improving the flexibility and interpretability of RO in practice.
A key innovation in modern RO theory is the integration of value-driven decision criteria, enabling models to reflect real-world preferences. Scalarizing functionals are central to this evolution: they map multi-scenario evaluations into interpretable scalar indices, facilitating both comparison and optimization [
16,
19]. This aligns with classical economic notions such as risk aversion and supports behavioral interpretations of robustness [
20]. Despite the field’s maturity, a key challenge remains: to construct robust models that are both theoretically rigorous and economically interpretable. In particular, the encoding of investor preferences and structural feasibility through directional scalarization continues to attract interest [
17,
21]. Recent studies have also explored entropy-inspired formulations [
15], behavioral robustness [
22], and automated solution methods [
8,
23], reflecting the demand for robust yet accessible decision-support tools.
As global economic systems face increasing levels of uncertainty, volatility, and structural disruption, the need for robust and adaptable decision-making frameworks has become more pronounced. This is particularly true in contexts where sustainability objectives—such as long-term stability, efficient resource allocation, and risk resilience—intersect with economic planning under ambiguity. In this landscape, robust optimization techniques are not merely mathematical constructs, but essential tools for ensuring that decisions remain feasible, consistent, and aligned with broader sustainability goals across a variety of scenarios. It is within this conceptual space that the present work is situated.
This paper contributes to this growing literature by proposing a scalarization-based robust optimization framework that unifies strict and reliable robustness within a single coherent model. By interpreting robustness as a directional projection within a risk-constrained space, the model preserves feasibility under uncertainty while offering a clear economic interpretation. Rather than seeking to replace existing robust techniques, this approach complements them by offering a versatile and interpretable alternative that captures both structural constraints and behavioral preferences. In doing so, the model bridges geometric robustness and sustainable economic decision-making, contributing to the development of resilient, uncertainty-aware optimization strategies.
The remainder of the paper is structured as follows.
Section 2 presents the scalarization-based formulation, explains the mathematical construction, and illustrates the method using a portfolio selection case study.
Section 3 discusses the numerical results, and
Section 4 offers concluding remarks along with directions for future research, including generalizations to infinite-dimensional settings and the integration of coherent risk measures. Ultimately, this work aims to support sustainable economic decision-making by providing a robust, interpretable, and adaptable optimization framework suited for long-term planning under uncertainty.
2. Materials and Methods
2.1. Statement and Interpretation of the Problem from the Economic Point of View
In the context of financial decision-making, portfolio optimization remains a central concern due to its significance in the efficient allocation of resources under uncertainty. A portfolio of financial assets can be interpreted as a weighted combination of investments across various instruments, with weights representing the proportion of capital allocated to each asset. Let us consider a portfolio composed of n assets, where the investment decisions are represented by a weight vector , indicating the set of proportion of capital allocated to each asset. From a sustainability perspective, portfolio decisions are not only about maximizing returns, but also about ensuring long-term resilience and responsible capital allocation in uncertain environments.
We define the following sets and vectors:
, the set of weight vectors associated with very low-risk investments.
, the set of admissible portfolios, reflecting feasible investment allocations.
k ∈a reference direction vector that represents the profile of profitable investments.
A key assumption is that the low-risk set B satisfies the condition, which intuitively means that any scaled version of the profitable direction k (tk), when added to a low-risk investment (b’) , results in a new investment (b’ + tk ) that still lies within the low-risk set B.
To evaluate the profitability and risk-adjusted quality of a given investment y, we define the scalarizing functional: zB,k(y) = sup / y }.
which represents the maximum scalar multiple of k that can be added to y to belong B. Economically, this captures the degree to which an admissible investment can be "aligned" with the profitable direction k, while remaining within acceptable risk levels.
The optimization problem then becomes: which seeks the admissible portfolio y ∈ F that achieves the highest zB,k(y)
2.2. Optimization Under Uncertainty Using Nonlinear Scalarizing Functionals and Robustness Concepts
Formulation Optimization Problem with Nonlinear Scaling Functionals ()
In real-world financial contexts, data such as expected returns, volatilities, and correlations are rarely known with certainty. These parameters are often estimated from historical data and are subject to errors, structural breaks, and market volatility. To address these challenges, we extend the scalarization-based optimization framework to account explicitly for uncertainty using robust optimization technique.
Let Y be a topological linear space and k ∈ Y \be a fixed direction vector representing the orientation of profitable decisions
Let F ⊂ Y and B ⊂ Y a proper subset of Y. Suppose that (#).
We define ) : Y → R ∪ {±∞}, ) = sup { t ∈ R / y ∈ B - t⋅k }.
We search Formulation of the Optimization Problem Under Uncertainty Using Concepts of Robustness ()
Robust optimization has become very popular in recent years because it is a realistic approach. Usually when we solve an OP, all its parameters are known. However, in most real-world applications, there are certain parameters that are not accurately known and available only estimated or a lot of their possible values.
In this paper we assume that the set of scenarios is an interval
Let U= [ , ] the set of scenarios.
We formulate an optimization problem under uncertainty.
Let f : Rⁿ×U→R, : Rⁿ×U → R, i=1,..,,m.
An optimization problem under uncertainty is defined as an optimization
problem with parameter (OP uncertain) (Q(ξ), ξ ∈ U), where, for ξ₀ ∈ U given, the optimization problem is :
max f ( x, ξ₀ )
Q(ξ₀): At the time of OP uncertain to be solved, it is not known which value ξ ∈ U will take. We call ∈ U the nominal value, i.e. the value of ξ which is assumed to be true at the present time. Q () is called the nominal problem.
In this paper we assume that there are maximum problems will be proposed in the following sections. Next, we will assign optimization problem conditions with an equivalent robust uncertainty. Note:
OP = real-world optimization problem;
= counterpart robust optimization problem;
= the problem formulated with linear scalarizing functionals
In conclusion, the optimization problem can be addressed as follows:
OP (formulated with economic concepts) ↔ ⇔↔OP (under uncertainty), or Financial Market ↔ F of ↔ constraints in Financial Market ↔ k of ↔ x of This unified formulation allows us to interpret robustness, not only as protection against uncertainty but also as a nonlinear projection toward profitability under structural risk constraints. Viewed through the lens of sustainability, this interpretation aligns with the need for resilient and responsible financial strategies that remain viable across a range of uncertain futures.Bottom of Form
Strict Robustness
The convenient than the objective function value is maximized in order to achieve a sufficiently good solution, even in the worst case. It is intended that all restrictions to be checked for each scenario ξ ∈ U.
Then the strictly robust counterpart equivalence robust optimization problem (Q(ξ), ξ ∈ U) is given by
sR : max
( x ) = max
f(x,
)
In [
14], it is demonstrated that (sR) can be characterized through a scaling function z
B,k by appropriately selecting the parameters k and B.
Reliable Robustness
When it is difficult or impossible to find a solution that satisfies all constraints for all scenarios, we introduce reliable robustness. Instead of working with restrictions , in this case we allow the constraints to satisfy a tolerance δi ∈ R₋ provided that the solution to be possible to obtain restriction weak . However, initial nominal constraints must be verified, i.e. , .
The reliable robust optimization problem is:
rR : max
( x ) = max
f(x,
)
In [
14], it is demonstrated that (sR) can be characterized through a scaling function z
B,k by appropriately selecting the parameters k and B.
2.3. Case Studies
To illustrate the theoretical framework developed in the previous sections, we consider a portfolio optimization problem involving three risky assets, denoted by A, B, and C. The investor is tasked with allocating capital among these assets in the presence of uncertainty regarding future market conditions., represented by a finite set of four possible scenarios, denoted by U = {ξ1, ξ2, ξ3, ξ4}. This scenario-based setup also serves as a proxy for sustainable investment planning, where robustness under multiple futures is essential for economic resilience. For any allocation vector x∈R+3, we define:
- f(x,ξ) is the return associated with allocation x under scenario ξ
- μ(x,ξ) represents a risk measure associated with scenario ξ.
- ε is the investor's risk tolerance level
- F(x,ξ) ≥ 0 i.e. the feasibility constraint that must be satisfied in each scenario ξ of U, reflecting regulatory, budgetary, or structural requirements
We define the set Bε ⊂ R4 as the collection of return vectors ( f(x,ξ1),…,f(x,ξ4) ) corresponding to portfolios whose risk remains below the investor’s tolerance level in all scenarios, i.e., μ(x,ξi) < ε for all i = 1,…,4, which corresponds to all portfolios whose associated risk remains below the tolerance level ε in each scenario.
The admissible set F ⊂ R
4 contains all return vectors that satisfy the feasibility condition F(x,ξ) ≥ 0 in every scenario. The reference direction vector is taken as k = (1,1,1,1), representing a uniform preference for increasing returns across all scenarios. We assume the scalarization condition B − t⋅k ⊇ B for all t ≥ 0, ensuring that the nonlinear functional
is well defined and satisfies the structural requirements outlined in
Section 2.2.
The investor’s objective is to identify a portfolio x∈R+3 that maximizes the worst-case return across all scenarios, while remaining feasible. This leads to the robust optimization problem: max f(x, )
. Using the equivalence result established earlier, this robust formulation can be recast into a scalar optimization problem of the form
, where ) is the nonlinear scalarizing functional defined as
) = sup { t ∈ R / y ∈ B - t⋅k }.
Under the stated assumptions, the two problems are equivalent, and the scalarization approach provides a mathematically consistent and computationally tractable method to determine robust investment strategies in the presence of uncertainty.
3. Results and Discussions
The theoretical framework developed in this paper establishes a novel connection between robust optimization and scalarization-based decision-making. By introducing a nonlinear scalarizing functional ), we reinterpret the classical notion of robustness as a geometric alignment between potential decisions and a predefined direction of profitability, constrained by structural risk boundaries. This scalarization transforms the original problem—defined under uncertainty—into a tractable deterministic formulation that avoids the need for explicit probabilistic modeling. Such an approach is particularly valuable in financial domains where data is scarce, volatile, or unreliable, making classical methods difficult to apply with confidence. This makes it especially suitable for sustainable financial planning, where long-term viability must be ensured despite informational gaps, volatile markets, and evolving risk landscapes. By enabling reliable decision-making without relying on fragile distributional assumptions, the proposed framework provides a practical foundation for building resilient investment strategies aligned with sustainability goal
The scalarizing functional plays a dual role in the optimization process. On one hand, it penalizes decisions that deviate from acceptable risk thresholds; on the other, it rewards portfolios that maintain favorable return patterns across multiple scenarios. This dual nature is essential in striking a balance between performance and robustness, especially in contexts where investors aim to optimize returns without sacrificing structural safety.
The key property B − t⋅k ⊇ B ensures that improvements along the preferred direction k do not compromise feasibility, thereby reflecting a natural economic preference: any portfolio that is deemed acceptable should remain so if its performance improves uniformly
In the numerical case study, we applied the proposed model to a portfolio composed of three risky assets evaluated under four discrete market scenarios. Each allocation vector was assessed with respect to both return and risk, using scenario-specific constraints and a fixed investor tolerance level. The direction vector k = (1,1,1,1) was selected to reflect a uniform preference for return improvement across all scenarios. The scalarizing functional ), served as a filter to identify admissible portfolios that align with the desired performance direction while remaining within the tolerated risk region.
The equivalence established between the scalar optimization problem and the strict and reliable robust counterparts provides not only theoretical depth but also practical relevance. In particular, the scalarization approach allows decision-makers to bypass nested constraint formulations and scenario-by-scenario feasibility checks—features that are often computationally demanding in classical robust optimization frameworks. Instead, all uncertainty is embedded within the structure of the functional itself, enabling a compact formulation that is amenable to efficient solution using standard optimization solvers.
From a modeling perspective, the scalarization framework enhances interpretability. Unlike traditional approaches based solely on variance minimization or expected utility maximization, this model can accommodate nonlinear investor preferences, asymmetric risk responses, and feasibility structures defined across discrete or continuous scenarios. This flexibility is critical in modern economic environments where decision-making is shaped by both structural constraints (e.g., regulatory or liquidity limits) and behavioral dimensions (e.g., loss aversion, return targeting).
In the context of sustainable finance, portfolio strategies must not only deliver consistent performance but also withstand structural uncertainty across diverse future conditions. The results obtained in our empirical case study validate the theoretical contributions. Among the evaluated portfolio strategies, those that maintained consistent returns across all four scenarios while respecting the investor's risk threshold achieved higher scalarization scores. This confirms the model’s ability to promote robust yet economically rational decision-making. The scalar framework thus proves to be a useful tool for analysts and practitioners aiming to construct resilient portfolios in uncertain and data-constrained environments.
In summary, the scalarization-based robust optimization model presented here succeeds in bridging theoretical rigor with practical applicability. It offers a coherent decision-making architecture that unifies multiple robustness concepts, supports computational efficiency, and aligns naturally with real-world economic reasoning. The promising results of our study open the door to further applications across a range of financial and economic problems, particularly those involving scenario-based planning, risk-constrained optimization, and behavioral modeling.
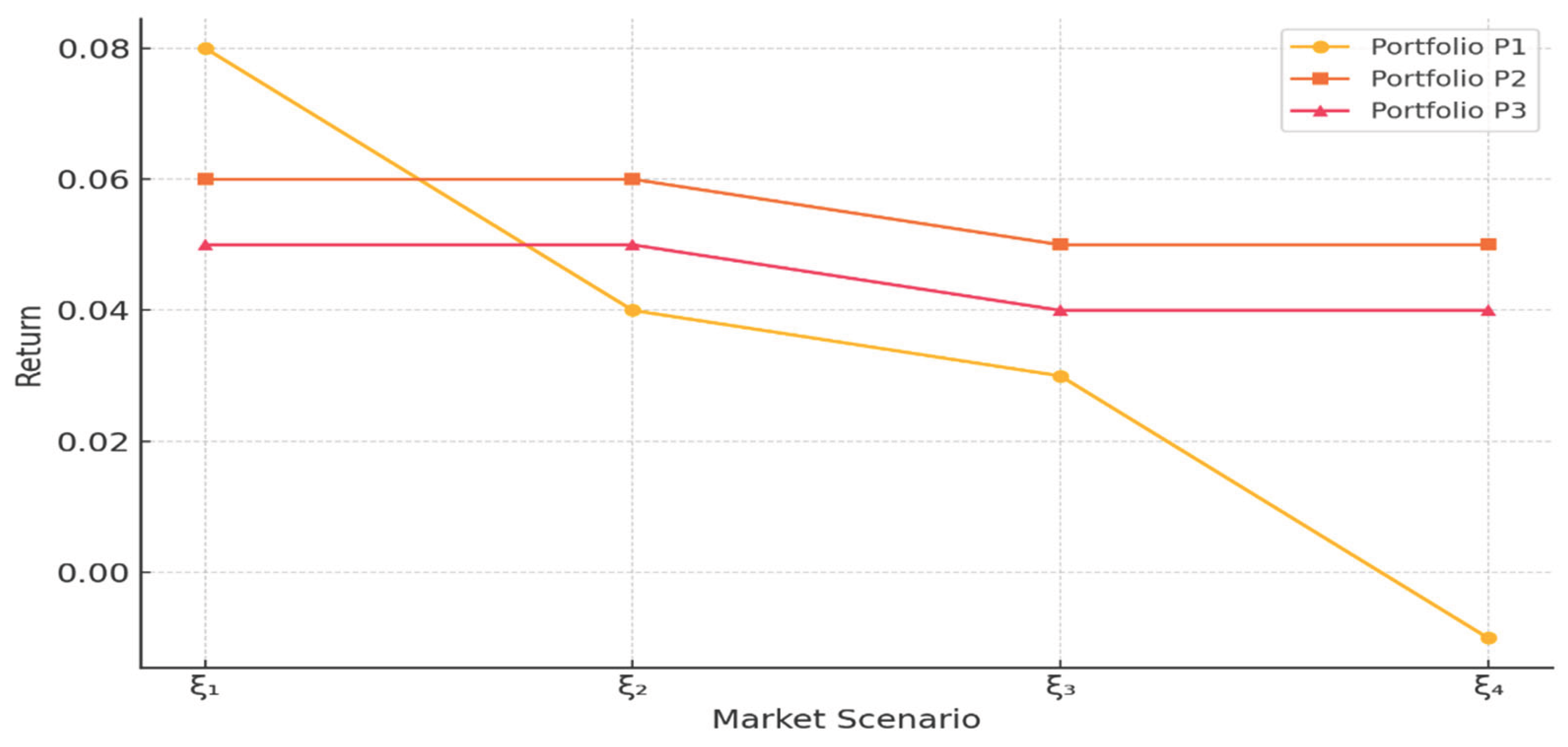
Table 1 presents the simulated returns of three distinct portfolio strategies evaluated across the four considered market scenarios. The scalarizing functional values are included to highlight each portfolio's alignment with robust performance criteria.
Table 1.
Portfolio Returns and Scalarization Values Simulated Portfolio Returns across Market Scenarios.
Table 1.
Portfolio Returns and Scalarization Values Simulated Portfolio Returns across Market Scenarios.
| Portfolio |
Scalarizing Functional z^(B,k)(y) |
| P1 |
0.75 |
| P2 |
0.95 |
| P3 |
1.00 |
| Scenario |
Portfolio P1 |
Portfolio P2 |
Portfolio P3 |
| ξ₁ |
0.08 |
0.06 |
0.05 |
| ξ₂ |
0.04 |
0.06 |
0.05 |
| ξ₃ |
0.03 |
0.05 |
0.04 |
| ξ₄ |
-0.01 |
0.05 |
0.04 |
Figure 1 graphically illustrates the portfolio behaviors under the different scenarios. Portfolio P3 exhibits the most stable performance, with minimal deviation across states and a superior scalarization score, confirming its robustness relative to the other alternatives.
Overall, the results support both the mathematical validity and the practical utility of the proposed approach. By embedding robustness into a scalar performance index, the framework equips decision-makers with a transparent and interpretable methodology for optimization under uncertainty. This dual benefit—rigorous theoretical grounding and intuitive economic applicability—helps bridge the longstanding gap between abstract modeling and real-world decision-making
The findings of our study confirm that scalarization via nonlinear functionals is not only a mathematically sound technique but also a conceptually accessible one. It offers a unified structure for incorporating investor preferences, risk constraints, and scenario variability within a single optimization framework. Theoretical guarantees, combined with the encouraging empirical performance, suggest that the approach holds significant potential for broader applications—including portfolio optimization, resource allocation, financial regulation, and multi-scenario economic planning. In this sense, our framework contributes to sustainability by enabling robust, data-efficient decisions that remain viable across uncertain future scenarios.
4. Conclusions and Future Work
This paper introduced a unified robust optimization framework based on nonlinear scalarizing functionals, offering a fresh perspective on decision-making under uncertainty. By integrating multiple robustness paradigms—specifically strict and reliable robustness—within a single scalarization-based structure, the proposed approach provides both a rigorous theoretical foundation and a practical mechanism for modeling economic decisions affected by ambiguity. One of its core strengths lies in recasting robust formulations into economically meaningful constructs, such as expected returns and risk thresholds, thus facilitating the interpretation and application of robustness in real-world contexts. This interpretability is particularly relevant in sustainability contexts, where decision-makers must align profitability with resilience and long-term feasibility under uncertainty.
The adoption of a multi-scenario planning perspective enables the translation of uncertainty into a coherent risk–return profile. This is particularly valuable in financial environments characterized by volatility and incomplete information. The empirical case study on portfolio optimization demonstrated the model’s dual advantage: mathematical soundness and alignment with investor goals. The ability to identify optimal strategies that balance return maximization with risk control under multiple scenarios confirms the framework’s practical utility and relevance to modern economic decision-making.
Beyond its immediate applicability, the research also reveals deeper conceptual links between scalar robust optimization and other established paradigms. In particular, the proposed model shares structural affinities with multi-objective optimization and scenario-based stochastic programming. The scalarizing functional serves as a bridge between these approaches, offering a unified language through which uncertainty, preference, and feasibility can be integrated. This opens promising avenues for the development of hybrid models that combine robustness with probabilistic or dynamic elements.
Looking ahead, several directions for future research are worth exploring. First, from a theoretical standpoint, we intend to derive necessary optimality conditions for scalar robust optimization problems, especially under differentiability assumptions. Establishing analogues to the Karush–Kuhn–Tucker conditions within this framework would enhance the analytical understanding of robust solutions and their sensitivity to changes in model parameters. Second, we plan to extend the current methodology to address problems involving infinite-dimensional uncertainty. This includes applications where uncertainty evolves over time, such as in continuous-time finance or dynamic economic systems, requiring tools from functional analysis and infinite-dimensional optimization. These future developments could further enhance the framework’s applicability to sustainability-driven domains, where long-term planning under deep uncertainty is a critical requirement.
Moreover, a particularly promising extension involves the integration of coherent risk measures—such as Conditional Value-at-Risk (CVaR)—into the scalarization scheme. Embedding such measures would further enhance the model’s relevance for financial regulation and risk management practice, bringing it closer to established tools in the regulatory landscape.
In conclusion, this work presents a robust optimization paradigm that is conceptually rich, mathematically consistent, and practically oriented. By unifying multiple robustness approaches and grounding them in a scalar functional framework, we contribute a versatile tool for uncertainty-aware decision-making. The theoretical insights and empirical validation presented here lay the foundation for future developments in robust economic modeling, with applications extending from portfolio management to sustainable resource allocation and policy planning under uncertainty.
Author Contributions
Conceptualization, Florentin Șerban and Silvia Dedu; methodology, Florentin Șerban and Silvia Dedu; validation, Florentin Șerban; formal analysis, Florentin Șerban and Silvia Dedu; investigation, Florentin Șerban; resources, Florentin Șerban and Silvia Dedu; data curation, Silvia Dedu; writing—original draft preparation, Florentin Șerban and Silvia Dedu; writing—review and editing, Florentin Șerban and Silvia Dedu; visualization, Florentin Șerban and Silvia Dedu; supervision, Florentin Șerban. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Flores-Siguenza, P., Marmolejo-Saucedo, J.A., & Niembro-Garcia, J. (2023). Robust Optimization Model for Sustainable Supply Chain Design Integrating LCA. Sustainability, 15(19), 14039.
- Li, H., Yu, D., Zhang, Y., & Yuan, Y. (2025). A two-stage robust optimization model for emergency service facilities location-allocation problem under demand uncertainty and sustainable development. Scientific Reports, 15, 2895.
- Ben-Tal, A.; Nemirovski, A. (2000). Robust solutions of linear programming problems contaminated with uncertain data. Mathematical Programming, 88, 411–424.
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. (2009). Robust Optimization. Princeton University Press: Princeton, NJ, USA.
- El Ghaoui, L.; Lebret, H. (1997). Robust solutions to least-squares problems with uncertain data. SIAM Journal on Matrix Analysis and Applications, 18, 1034–1064.
- Ben-Tal, A.; den Hertog, D.; De Waegenaere, A.M.B.; Melenberg, B.; Rennen, G. (2013). Robust solutions of optimization problems affected by uncertain probabilities. Management Science, 59, 341–357.
- Bertsimas, D.; Brown, D.; Caramanis, C. (2011). Theory and applications of robust optimization. SIAM Review, 53, 464–501.
- Bertsimas, D.; Sim, M. (2004). The price of robustness. Operations Research, 52, 35–53.
- Goerigk, M.; Schöbel, A. (2011). A scenario-based approach for robust linear optimization. In Proceedings of the 1st International ICST Conference on Practice and Theory of Algorithms in Computer Systems; Springer: Berlin, Germany, pp. 139–150.
- Ogryczak, W. (2012). Robust decisions under risk for imprecise probabilities. In Managing Safety of Heterogeneous Systems; Springer: Berlin, Germany; Volume 658, pp. 51–66.
- Ogryczak, W. (2013). Tail mean and related robust solution concepts. Scientific International Journal of Systems.
- Eichfelder, G. (2008). Adaptive Scalarization Methods in Multiobjective Optimization. Springer: Berlin, Germany.
- Peng, J.-W., Wei, W.-B., & Kasimbeyli, R. (2025). Linear and Nonlinear Scalarization Methods for Vector Optimization Problems with Variable Ordering Structures. Journal of Optimization Theory and Applications, 206(2).
- Klamroth, K.; Köbis, E.; Schöbel, A.; Tammer, C. (2013). A unified approach for different concepts of robustness and stochastic programming via non-linear scalarizing functionals. Optimization, 62, 649–671.
- Köbis, E.; Tammer, C. (2012). Relations between strictly robust optimization problems and a nonlinear scalarization method. AIP Conference Proceedings, 1479, 2371–2374.
- Lach, L., Fottner, A. W., & Okhrin, Y. (2025). Bridging the Gap Between f-divergences and Bayes Hilbert Spaces. Proceedings of the International Conference on Learning Representations (ICLR).
- Goh, J.; Sim, M. (2011). Robust optimization made easy with ROME. Operations Research, 59, 973–985.
- Löfberg, J. (2012). Automatic robust convex programming. Optimization Methods and Software, 27, 115–129.
- Sayin, S.; Kouvelis, P. (2005). The multiobjective discrete optimization problem: A weighted min-max two-stage optimization approach and a bicriteria algorithm. Management Science, 51, 1572–1581.
- Kouvelis, P.; Sayin, S. (2006). Algorithm robust for the bicriteria discrete optimization problem—Heuristic variations and computational evidence. Annals of Operations Research, 147, 71–85.
- Golub, G.H., & Van Loan, C.F. (2013). Matrix Computations (4th ed.). Johns Hopkins University Press.
- Hansen, L.P., & Sargent, T.J. (2023). Risk, Ambiguity, and Misspecification: Decision Theory, Robust Control, and Statistics. Journal of Applied Econometrics.
- Nemirovski, A. (2009). Lectures on Robust Convex Optimization. Lecture Notes, Georgia Institute of Technology.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).