How the Potential Payback Period (PPP) Extends and Surpasses the Gordon Growth Model (GGM) at the Limits of Financial Theory

1. Introduction

The Gordon Growth Model (GGM), developed by Myron Gordon and Eli Shapiro in 1956, and the Potential Payback Period (PPP), introduced by Rainsy Sam (the author of this article), are two valuation frameworks that integrate assumptions about growth and discounting. The GGM — long a cornerstone of discounted cash flow analysis — estimates the present value of a perpetuity of dividends growing at a constant rate. The PPP, by contrast, is a more recent and evolving concept that estimates the time required for an investor to recover their initial investment through discounted, growing earnings. This paper compares the two models, with a particular focus on their behavior under limiting and edge-case conditions, where traditional valuation methods often break down.

2. Core Formulations

2.1. The Gordon Growth Model Is Expressed as

where:

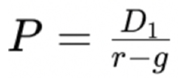
• P is the stock price,
• D₁ is next year's dividend,
• r is the required rate of return,
• g is the expected growth rate of dividends.

2.2. The Potential Payback Period (PPP) Is Defined as

where:

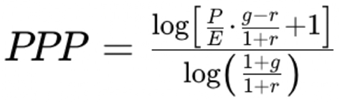
• P is the stock price,
• E is current earnings per share,
• g is the earnings growth rate,
• r is the discount rate.

Both models respond sensitively to the relationship between g and r , but their behavior near critical values diverges sharply.

3. Limit Case: When g → r

In the GGM, as g → r, the denominator approaches zero, causing P to tend toward infinity. This result reflects a scenario in which future dividends are growing just fast enough to offset discounting, but it renders the model practically unusable.

In the PPP model, a similar issue arises: both the numerator and denominator of the formula approach zero, producing an indeterminate form 0/0 . However, applying L'Hôpital's Rule to resolve mathematical limits yields a meaningful and finite expression:

This outcome is intuitive: when growth exactly offsets the discount rate, the time required to recover the investment is equivalent to a discounted P/E ratio.

4. Extreme Case: When g = r = 0

The behavior of the models becomes even more revealing under the condition g = r = 0:

constant earnings is simply:

This is the classic P/E ratio. Hence the PPP reduces exactly and meaningfully to the static multiple it generalizes.

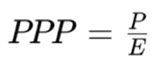
5. Interpretation and Implications

These comparisons yield several insights:

• Both models are built on the same valuation logic: future cash flows adjusted for time and growth.
• However, PPP demonstrates greater mathematical resilience and interpretive clarity near and at critical boundaries.
• The fact that PPP collapses to the P/E ratio when g = r = 0 reinforces its role as a generalization of static valuation multiples.
• Practically, PPP offers usable, consistent outputs in conditions where GGM fails — such as early-stage companies, low-growth environments, or when applying valuation to earnings rather than dividends.

6. Conclusions

While both the Gordon Growth Model and the Potential Payback Period model share a conceptual foundation, their behavior under edge cases reveals a key distinction: PPP remains robust and interpretable where GGM becomes unstable or undefined. This analytical flexibility underscores PPP's potential as a general-purpose valuation tool, particularly in dynamic or constrained financial environments. Its capacity to reduce to traditional metrics under simplifying assumptions further strengthens its theoretical legitimacy and practical appeal.