Element-Wise Multiplicative Operators in Vision, Language, and Multimodal Learning

1. Introduction

The Schur product, also known as the Hadamard product, represents a fundamental operation in linear algebra, denoted by the element-wise multiplication of two matrices of identical dimensions [1]. For matrices $\mathbf{A},\mathbf{B}\in {\mathbb{R}}^{m\times n}$, the Schur product $\mathbf{A}\circ \mathbf{B}$ is defined as ${(\mathbf{A}\circ \mathbf{B})}_{ij}={\mathbf{A}}_{ij}·{\mathbf{B}}_{ij}$, $\forall i,j$ [2]. Although this operation is elementary in terms of computational complexity and mathematical formulation, its role in the architecture and functioning of contemporary machine learning systems—particularly in deep learning, computer vision, and large language models—has become increasingly prominent [3]. Its pervasiveness spans multiple layers of abstraction: from tensor-level feature interactions in convolutional neural networks (CNNs), attention mechanisms in transformers, to multiplicative gating strategies in recurrent neural networks (RNNs) and residual pathways in multi-branch deep architectures. Historically marginalized as a computationally trivial operation, the Schur product has emerged as a cornerstone in the development of expressive, modular, and scalable models. Its efficiency in preserving dimensional consistency and enabling fine-grained modulation of information flow has enabled it to play an integral role in nonlinear function approximation, dynamic parameter adaptation, and feature-wise multiplicative conditioning. In particular, the Schur product’s ability to introduce element-wise nonlinearity without incurring the parametric overhead of learned projections has made it an attractive component in model compression, efficient inference strategies, and differentiable programming paradigms. Furthermore, the Schur product underlies many implicit assumptions about statistical independence and noise modeling, especially in scenarios involving multiplicative Gaussian noise, dropout variants, and conditional normalization techniques such as FiLM (Feature-wise Linear Modulation) [4]. In the context of computer vision, the Schur product is ubiquitously employed in attention-based mechanisms, channel-wise feature recalibration (e.g., Squeeze-and-Excitation networks), and multiplicative masking strategies in spatial-temporal modeling [5]. Specifically, attention maps generated through softmax-normalized similarity scores are often element-wise multiplied with input feature maps to yield selectively enhanced representations, a process fundamentally governed by the Hadamard operation [6,7]. Moreover, self-gating mechanisms and bilinear pooling approaches exploit the Schur product to model complex interactions across modalities, scales, and semantic hierarchies. This allows for a compact and expressive representation space, crucial in fine-grained visual recognition, dense prediction tasks, and neural architecture search. Within large language models (LLMs), the Schur product assumes a pivotal role in the construction of multi-head self-attention, gated linear units (GLUs), and modulation-based conditional generation frameworks [8]. The transformer architecture, which forms the backbone of modern LLMs such as BERT, GPT, and PaLM, incorporates the Schur product at various stages, most notably in the computation of attention outputs where key-query similarity matrices are element-wise scaled and masked prior to projection [9]. Additionally, emerging works have explored its utility in parameter-efficient fine-tuning techniques such as LoRA (Low-Rank Adaptation) and prefix-tuning, where Schur products facilitate the blending of pretrained activations with task-specific vectors without the need to retrain the full model. More recent studies have also highlighted the potential of the Schur product in enabling implicit mixture-of-experts mechanisms, sparsely-gated transformers, and dynamic computation graphs. From a theoretical perspective, the Schur product exhibits intriguing algebraic properties, such as commutativity, associativity, and distributivity over addition, which render it amenable to gradient-based optimization and differentiable programming. These properties also endow neural architectures with symmetry-invariant characteristics, particularly beneficial in domains requiring equivariance and permutation-invariance, such as point cloud processing, graph neural networks, and group-equivariant convolutions. The Hadamard product also plays a crucial role in backpropagation through structured tensors, especially in second-order optimization, Kronecker-factored approximations, and information-theoretic regularization [10]. Given the multiplicity of its applications and the depth of its influence across architectural paradigms, the goal of this survey is to provide a comprehensive and unifying perspective on the Schur product as a computational primitive and modeling construct in deep learning, computer vision, and large language models. We dissect its algebraic underpinnings, trace its lineage across historical and contemporary neural networks, and elucidate its role in enabling parameter efficiency, inductive bias encoding, and high-dimensional expressivity [11]. In doing so, we aim to not only catalog existing methodologies but also to highlight emerging research frontiers, open problems, and theoretical questions that pertain to the broader understanding of element-wise interactions in deep learning systems [12]. To this end, the rest of this survey is structured as follows: In Section 2, we revisit the mathematical foundations of the Schur product, including its properties, tensor generalizations, and spectral implications [13]. Section 3 explores the use of Schur product in core deep learning modules, such as activation gating, residual connections, and bilinear modeling. Section 4 focuses on its instantiations in computer vision, detailing its role in attention mechanisms, feature fusion, and multi-modal learning. Section 5 examines how the Schur product underpins various components of transformer-based architectures and recent LLM paradigms [14]. Finally, in Section 6, we present a synthesis of future directions, challenges, and opportunities for further integration of the Schur product in interpretable, efficient, and adaptive machine learning systems [15].

2. Mathematical Foundations of the Schur Product

The Schur product, also referred to as the Hadamard product, is formally defined for two matrices $\mathbf{A},\mathbf{B}\in {\mathbb{R}}^{m\times n}$ as the matrix $\mathbf{C}=\mathbf{A}\circ \mathbf{B}$, where each element is given by ${\mathbf{C}}_{ij}={\mathbf{A}}_{ij}·{\mathbf{B}}_{ij}$ for all $1\le i\le m$, $1\le j\le n$[16]. Unlike the standard matrix product, which involves the inner product of rows and columns, the Schur product operates purely in the coordinate-wise sense. This apparent simplicity belies a deep connection to several important algebraic structures and optimization paradigms [17]. It is a commutative, associative, and distributive binary operation over matrices of equal dimensions, with the identity element being the all-ones matrix. Furthermore, the Hadamard product is intimately related to the entrywise (Hadamard) powers of matrices, as well as to operations in tensor algebra, especially when dealing with rank-1 decompositions and factorized bilinear models [18]. A particularly critical aspect of the Schur product is its compatibility with positive semi-definite (PSD) matrices [19]. Let $\mathbf{A},\mathbf{B}\in {\mathbb{R}}^{n\times n}$ be PSD matrices; then the Schur product $\mathbf{A}\circ \mathbf{B}$ is also PSD [20]. This result, known as the Schur Product Theorem, is instrumental in kernel methods and covariance matrix analysis. In the context of deep learning, this property ensures the stability and interpretability of various mechanisms where similarity or correlation matrices are modulated element-wise, such as in attention layers, normalized feature affinities, and structured regularization terms [21,22]. Moreover, from a spectral theory viewpoint, the Schur product is closely tied to the Loewner partial order on PSD matrices and often serves as a tool to constrain or refine matrix inequalities. We now summarize in Table 1 the fundamental algebraic and analytical properties of the Schur product in contrast with the standard matrix product and the Kronecker product [23]. This comparison highlights the operational uniqueness of the Hadamard product in terms of dimensionality preservation, element-wise interaction, and spectral stability [24].

To illustrate some of the spectral implications of the Hadamard product, consider two symmetric positive semi-definite matrices $\mathbf{A},\mathbf{B}\in {\mathbb{R}}^{n\times n}$[26]. The eigenvalues of $\mathbf{A}\circ \mathbf{B}$ are not simply the products of the eigenvalues of $\mathbf{A}$ and $\mathbf{B}$ due to the non-diagonalizability of the operation in the same basis unless $\mathbf{A}$ and $\mathbf{B}$ are simultaneously diagonalizable. However, if $\mathbf{A}=\mathbf{u}{\mathbf{u}}^{\top }$ and $\mathbf{B}=\mathbf{v}{\mathbf{v}}^{\top }$ are both rank-1 matrices, then $\mathbf{A}\circ \mathbf{B}=(\mathbf{u}\circ \mathbf{v}){(\mathbf{u}\circ \mathbf{v})}^{\top }$ is also rank-1 and PSD [27]. This behavior has practical consequences for low-rank approximation, where factorized forms like $\mathbf{X}={\sum }_i({\mathbf{u}}_i\circ {\mathbf{v}}_i)$ are used to represent high-dimensional interactions with linear storage complexity.

As shown in Figure 1, the Schur product tends to suppress high-frequency components and exhibits a more rapid spectral decay compared to the standard matrix product [29]. This results in smoother, low-rank-like structures and has implications for regularization, noise attenuation, and spectral sparsity. In deep learning architectures, such properties are desirable in scenarios requiring implicit low-rank constraints, such as compressive sensing, dropout regularization, and efficient representation learning [30]. The next section will transition from the abstract mathematical properties of the Schur product to its practical instantiations in neural computation, focusing on its role in nonlinear transformation, feature-wise modulation, and activation gating across various deep learning architectures [31].

3. Schur Product in Deep Learning Architectures

In the realm of deep learning, the Schur product operates not merely as a numerical primitive but as a structural design principle that undergirds a vast array of compositional mechanisms, activation modulations, and expressive function approximators. Its deployment spans multiple architectural motifs—ranging from the microstructure of activation units to macro-level interactions in modular neural systems—and serves as a means of inducing fine-grained, multiplicative control over information propagation. The most prominent instantiations of the Schur product within deep learning include gating mechanisms, feature-wise modulation, bilinear interaction modeling, residual interaction masking, and dynamic parameter fusion, each of which exploits the operation’s element-wise granularity and compatibility with backpropagation [32]. A canonical example of the Schur product’s utility is found in the class of gated activation units, most notably the Gated Linear Unit (GLU) and its generalizations [33]. Given an input tensor $\mathbf{X}\in {\mathbb{R}}^{d\times n}$, the GLU mechanism computes an output $\mathbf{Y}$ via:

$$\mathbf{Y}=(\mathbf{X}{\mathbf{W}}_1+{\mathbf{b}}_1)\circ \sigma (\mathbf{X}{\mathbf{W}}_2+{\mathbf{b}}_2),$$

where ${\mathbf{W}}_1,{\mathbf{W}}_2\in {\mathbb{R}}^{n\times m}$ are learnable weight matrices, ${\mathbf{b}}_1,{\mathbf{b}}_2\in {\mathbb{R}}^m$ are bias vectors, and $\sigma$ is typically the sigmoid activation function [34]. Here, the Schur product enables a multiplicative modulation of the linear projection by a learned gating signal, allowing for dynamic scaling of individual feature dimensions [35]. The importance of this mechanism is reflected in its widespread adoption in high-capacity models such as convolutional sequence models, transformer-based encoders, and even autoregressive decoders, where it contributes to both representational capacity and training stability. Another critical domain wherein the Schur product assumes a structural role is that of feature-wise affine modulation, typified by mechanisms such as Feature-wise Linear Modulation (FiLM), conditional batch normalization, and attention-based reweighting [36]. In FiLM, a feature tensor $\mathbf{X}$ is modulated by external conditioning vectors $(\gamma ,\beta )$ through:

$${\mathbf{Y}}_i={\gamma }_i\circ {\mathbf{X}}_i+{\beta }_i$$

for each feature map i [37]. This per-channel Schur product introduces an input-dependent scaling that is especially effective in multi-modal fusion, visual reasoning, and conditional generative modeling. The operation’s differentiability and low parameter cost make it a natural choice for scenarios requiring tight coupling between conditioning signals and internal representations without overfitting or redundancy. The Schur product also finds relevance in the modeling of bilinear interactions, particularly in tensor factorization-based modules. Consider the bilinear layer:

$$y={\mathbf{x}}^{\top }\mathbf{W}\mathbf{z},$$

where $\mathbf{x},\mathbf{z}\in {\mathbb{R}}^n$ and $\mathbf{W}\in {\mathbb{R}}^{n\times n}$; if we constrain $\mathbf{W}$ to be diagonal, we recover a Hadamard product: $y={(\mathbf{x}\circ \mathbf{z})}^{\top }\mathbf{w}$[38]. This decomposition is not merely a computational shortcut but reflects an inductive bias toward localized, dimension-aligned interactions—a principle that underlies models such as low-rank bilinear pooling, decomposable attention, and relational inference modules [39]. Furthermore, element-wise multiplication is central to learning structured correlations in models like Factorization Machines (FMs) and their neural generalizations (NFM, DeepFM), which leverage the Schur product to embed pairwise feature interactions within high-dimensional latent spaces [40]. Moreover, in residual and skip-connection-based models such as ResNets and DenseNets, the Schur product is increasingly used as a mechanism to selectively gate residual information [41]. Given a main branch output $\mathbf{F}\left(\mathbf{x}\right)$ and a shortcut connection $\mathbf{x}$, the gated residual connection is defined as:

$$\mathbf{y}=\mathbf{x}+\alpha \circ \mathbf{F}\left(\mathbf{x}\right),$$

where $\alpha \in {\mathbb{R}}^d$ is either a learned or dynamically generated gating vector [42]. This formulation permits the network to adaptively interpolate between identity and transformation paths, enhancing training robustness and enabling dynamic computation regimes. This is further extended in modern architectures like Adaptive Computation Time (ACT) and SkipNet, where gating decisions—often realized through the Schur product—control path selection during inference [43]. To concretely assess the expressive impact of incorporating the Schur product within deep layers, consider the capacity of feed-forward networks augmented with element-wise multipliers. Let ${\mathcal{F}}_{\circ }$ denote the class of functions expressible by a multilayer perceptron (MLP) with Hadamard-modulated activations [44]:

$${\mathcal{F}}_{\circ }=\left\{f\left(\mathbf{x}\right)={\varphi }_k\left(\dots {\varphi }_2\left(\left({\mathbf{W}}_1\mathbf{x}\right)\circ {\gamma }_1\right)\dots \right)\right\}.$$

It can be shown that ${\mathcal{F}}_{\circ }$ includes all functions expressible by classical ReLU MLPs, while also containing nonlinear multiplicative functions such as $f(x_1,x_2)=x_1{x}_2$, which cannot be represented without explicit multiplicative units [45]. This function class exhibits higher polynomial closure and nonlinearity density, particularly relevant in symbolic regression, combinatorial optimization, and hybrid neuro-symbolic reasoning [46]. In summary, the Schur product in deep learning serves as both a mathematical tool and a modeling primitive that enables scalable, expressive, and efficient computation [47]. Its differentiability, algebraic compatibility, and parameter-free structure make it uniquely suited for modern architectures requiring fine-grained control, conditional adaptation, and structured interactions. In the next section, we extend our focus to the domain of computer vision, where the Hadamard product plays an equally critical role in spatial attention, channel-wise modulation, and cross-modal interaction mechanisms.

4. Schur Product in Computer Vision

In computer vision, the Schur product has emerged as a pivotal computational motif, deeply interwoven with operations that necessitate spatial selectivity, channel-wise conditioning, and efficient cross-modal fusion [48]. Owing to its inherent capacity for localized, dimension-preserving interactions, the Hadamard product provides an ideal mechanism for applying attention, gating, and contextual modulation to visual feature tensors. As contemporary vision architectures shift towards modular, compositional, and context-aware processing pipelines, the Hadamard product becomes not merely an implementation detail but an expressive operator embedded in the inductive bias of the models themselves. Consider a visual feature tensor $\mathbf{X}\in {\mathbb{R}}^{C\times H\times W}$, where C is the number of channels, and $H,W$ denote the spatial dimensions [49]. In channel-wise attention mechanisms such as Squeeze-and-Excitation (SE) blocks, a global context vector $\mathbf{s}\in {\mathbb{R}}^C$ is learned via global average pooling and fed through a bottleneck MLP [50]. The output vector $\alpha \in {\mathbb{R}}^C$ then reweights $\mathbf{X}$ via:

$${\mathbf{Y}}_{c,h,w}={\alpha }_c·{\mathbf{X}}_{c,h,w}$$

for all c, h, w [51]. This operation is a broadcasted Schur product over channels, facilitating adaptive recalibration of feature responses in a way that is differentiable and low-cost [52]. The interpretability of $\alpha$ as a channel importance vector provides semantic transparency and has led to its integration in attention modules like CBAM, ECA-Net, and SENet variants across a multitude of vision tasks [53]. In the domain of spatial attention, Schur product-based modulation also arises naturally. For instance, in soft attention maps $\mathbf{A}\in {[0,1]}^{1\times H\times W}$, computed via convolutions or dot-product-based affinity, the attended feature map is given by [54]:

$${\mathbf{Y}}_{c,h,w}={\mathbf{A}}_{h,w}·{\mathbf{X}}_{c,h,w}.$$

This spatial Hadamard gating mechanism allows the model to emphasize or suppress specific spatial locations based on context, often improving localization and object recognition performance. When both spatial and channel attention are applied sequentially or in parallel, the resulting double-Hadamard modulation structure (as in CBAM) can be interpreted as a factorized tensor reweighting operation that preserves the input’s topology while refining its salience across multiple axes [55]. Moreover, the Schur product underpins the construction of cross-modal fusion operators in vision-and-language models, particularly in scenarios where external linguistic or symbolic input must guide visual processing. Let $\mathbf{X}\in {\mathbb{R}}^{C\times H\times W}$ be the visual tensor and $\mathbf{z}\in {\mathbb{R}}^C$ a language-derived vector [56]. The fused tensor $\mathbf{Y}=\mathbf{z}\circ \mathbf{X}$ performs a per-channel modulation of visual features by the semantic content of the language input, enabling conditional image segmentation, visual question answering, and referring expression grounding [57]. This approach has seen success in models such as ViLBERT, LXMERT, and CLIP-based transformers, where conditioning information is applied multiplicatively to maintain compatibility with pre-trained representations while introducing task-specific adaptation. To illustrate the pervasiveness and performance benefits of Schur product-based attention, Table 2 provides a taxonomy of recent vision models employing element-wise modulation. Each entry specifies the layer, target tensor, conditioning mechanism, and structural role of the Hadamard product within the pipeline [58].

From an algebraic perspective, these mechanisms can be understood as low-rank perturbations or diagonal projections applied to visual tensors. Consider a transformation of the form:

$$\mathbf{Y}=(\mathbf{D}\otimes {\mathbf{I}}_{HW})·\mathrm{vec}\left(\mathbf{X}\right),$$

where $\mathbf{D}=\mathrm{diag}\left(\gamma \right)$ is a diagonal scaling matrix, and $\mathrm{vec}\left(\mathbf{X}\right)\in {\mathbb{R}}^{CHW}$ is the vectorized image tensor [59]. This global operator is equivalent to a Schur product in the original tensor space, underscoring the efficiency and interpretability of multiplicative modulation [60]. As convolutional networks transition toward more dynamic and attention-driven paradigms, the algebraic structure of the Hadamard product will likely remain essential to preserving spatial locality while introducing adaptive, context-aware signal shaping [61]. Finally, the Schur product has also gained traction in neural style transfer, texture synthesis, and learnable color transforms. For example, in adaptive instance normalization (AdaIN), a content feature ${\mathbf{X}}_c$ is modulated by the mean ${\mu }_s$ and standard deviation ${\sigma }_s$ of a style feature ${\mathbf{X}}_s$:

$$\mathbf{Y}={\sigma }_s\circ \left({\displaystyle \frac{{\mathbf{X}}_c-{\mu }_c}{{\sigma }_c}}\right)+{\mu }_s.$$

The Schur product here performs the core stylistic transformation via element-wise scaling, transferring textural information without altering the underlying structure [62]. This formulation has informed numerous real-time style transfer networks, including those based on VGG encoders and perceptual loss functions. In summary, the Schur product occupies a fundamental role in modern computer vision pipelines, acting as a flexible, efficient, and semantically transparent mechanism for spatial and feature-wise modulation. Whether through attention, cross-modal fusion, or dynamic normalization, the Hadamard product’s capacity for localized, multiplicative transformation is indispensable to the design of scalable and interpretable vision models [63]. The subsequent section will explore how these principles generalize to large language models (LLMs), where element-wise operations are integrated into attention mechanisms, residual pathways, and learned token-wise gates for scalable linguistic reasoning [64].

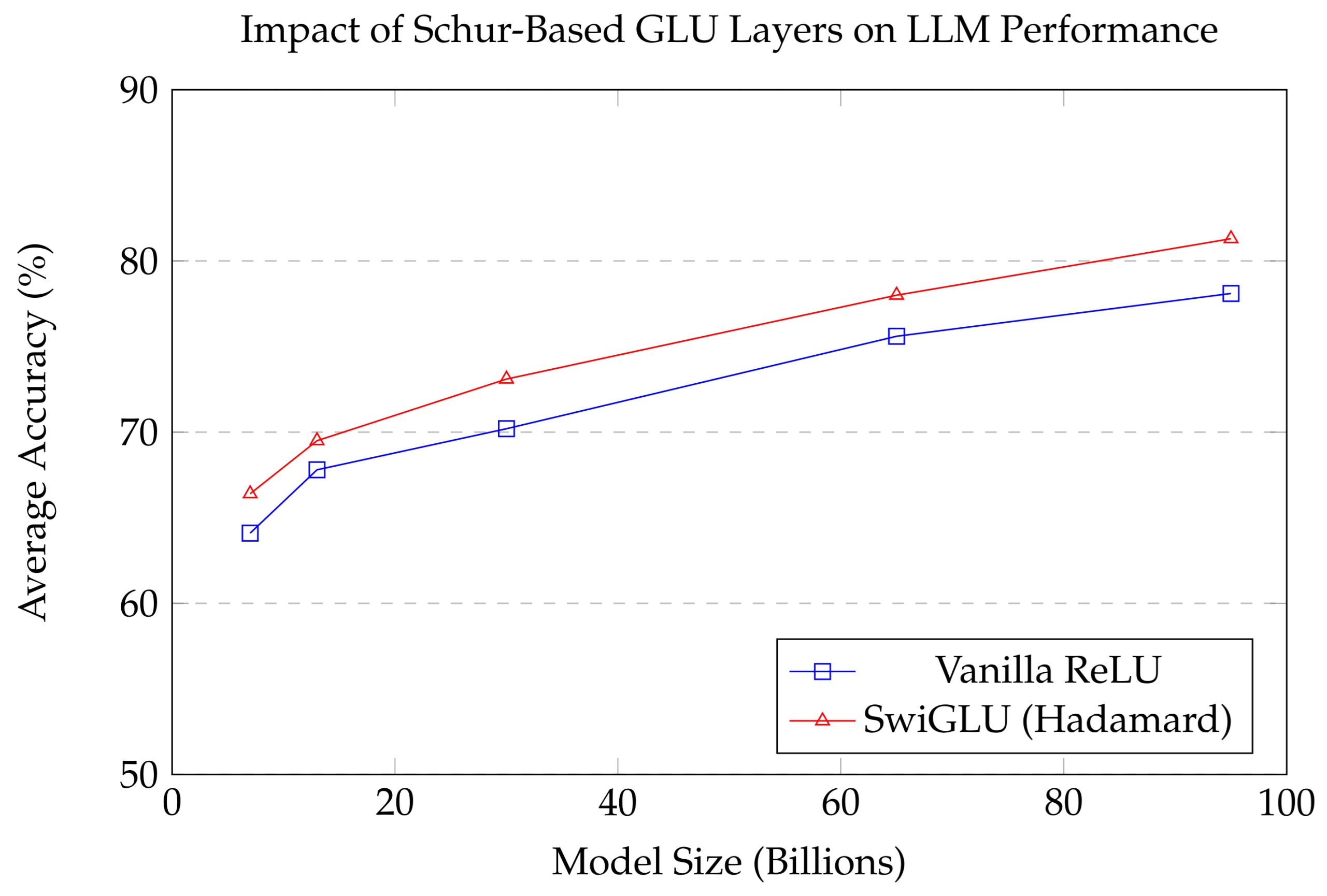
5. Schur Product in Large Language Models

In the context of Large Language Models (LLMs), particularly those built upon the Transformer architecture, the Schur product is deeply embedded in the architectural fabric, operating at multiple levels—from attention mechanisms and gating functions to parameter-efficient fine-tuning and residual modulation [65]. Unlike in vision, where spatial locality provides a natural axis for modulation, in LLMs the Hadamard product is typically deployed over token-wise or feature-wise representations, thereby serving as a critical instrument for shaping contextualized word embeddings and sequence-level interactions. The most prominent instantiation of the Schur product within LLMs arises in the scaled dot-product attention mechanism [66]. Given a query-key-value triple $(\mathbf{Q},\mathbf{K},\mathbf{V})\in {\mathbb{R}}^{n\times d}$, the attention operation is computed as [67]:

$$\mathrm{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{K}}^{\top }}{\sqrt{d}}}\right)\mathbf{V}.$$

While the above formulation does not explicitly contain a Schur product, its multi-head generalization often requires post-attention gating or reweighting of heads using Hadamard products [68]. In gated attention variants such as Gated Transformer-XL and GTrXL, the attended values are modulated by learnable or context-derived gates:

$$\mathbf{Y}=\mathbf{A}\circ \mathbf{V},$$

where $\mathbf{A}\in {[0,1]}^{n\times d}$ is either a learned gate or derived from an auxiliary signal (e.g., importance or confidence weights). Such a formulation injects an inductive bias toward sparsity and modularity, allowing for selective feature propagation through the network [69]. In architectures that employ dynamic routing, adaptive computation, or skip connections, the Schur product acts as the computational bottleneck where routing decisions are enacted with negligible additional parameters. Another critical role of the Schur product in LLMs is found in the residual stream, particularly in adapters and fine-tuning modules [70]. Parameter-efficient fine-tuning techniques such as LoRA (Low-Rank Adaptation), Prefix Tuning, and HyperFormer utilize element-wise multiplications to modulate internal states without modifying the full model [71]. For example, in LoRA, the residual update to a pre-trained weight matrix ${\mathbf{W}}_0$ is expressed as:

$$\mathbf{W}={\mathbf{W}}_0+\Delta \mathbf{W},\Delta \mathbf{W}=\mathbf{A}\mathbf{B},$$

where the rank of $\Delta \mathbf{W}$ is low, and subsequent token-level updates are computed as $\mathbf{X}({\mathbf{W}}_0+\mathbf{A}\mathbf{B})=\mathbf{X}{\mathbf{W}}_0+\left(\mathbf{X}\mathbf{A}\right)\mathbf{B}$, often followed by gating via a Schur product:

$$\mathbf{Y}=\gamma \circ \left(\mathbf{X}{\mathbf{W}}_0\right)+(1-\gamma )\circ \left(\mathbf{X}\mathbf{A}\mathbf{B}\right),$$

where $\gamma \in {[0,1]}^d$ is a learned or fixed mixing vector [72]. This operation blends the frozen pre-trained path with a low-rank adaptation, enabling the model to learn task-specific behavior without catastrophic forgetting or excessive parameter growth [73]. Beyond fine-tuning, Schur products are also integral to feed-forward blocks in LLMs, particularly in the Gated Linear Units (GLUs) and SwiGLU variants that replace standard MLP layers [74]. A typical GLU layer takes the form:

$$\mathrm{GLU}\left(\mathbf{x}\right)=(\mathbf{x}{\mathbf{W}}_1+{\mathbf{b}}_1)\circ \sigma (\mathbf{x}{\mathbf{W}}_2+{\mathbf{b}}_2),$$

allowing for a non-linear gating mechanism that preserves the linear path while introducing element-wise multiplicative modulation [75]. This mechanism has been empirically shown to stabilize training, reduce over-smoothing, and increase the expressivity of feed-forward networks, especially in deep transformer stacks where the saturation of ReLU activations can hinder gradient flow. In the SwiGLU variant, the activation is replaced with a shifted sigmoid-weighted linear unit [76]:

$$\mathrm{SwiGLU}\left(\mathbf{x}\right)=\left(\mathbf{x}{\mathbf{W}}_1\right)\circ \mathrm{Swish}\left(\mathbf{x}{\mathbf{W}}_2\right),\mathrm{Swish}\left(x\right)=x·\sigma \left(x\right).$$

tiplicative gate but an active nonlinear transformation that blends activations and their modulations, and is integral to the functioning of recent LLMs such as PaLM, Chinchilla, LLaMA, and GPT-NeoX [77]. To formalize this role in a theoretical framework, we may model a transformer layer as a compositional operator:

$$\mathcal{T}\left(\mathbf{X}\right)=\mathbf{X}+\mathrm{MHSA}\left(\mathbf{X}\right)+\mathrm{MLP}\left(\mathbf{X}\right),$$

where the multi-head self-attention (MHSA) and multi-layer perceptron (MLP) blocks can both contain Schur product substructures [78]. Assuming a simplified setting where $\mathrm{MLP}\left(\mathbf{X}\right)=\varphi \left(\mathbf{X}{\mathbf{W}}_1\right){\mathbf{W}}_2$, and $\varphi$ involves GLU-like activation, then the MLP becomes [79]:

$$\mathrm{MLP}\left(\mathbf{X}\right)=\left(\left(\mathbf{X}{\mathbf{W}}_1^{\left(1\right)}\right)\circ \sigma \left(\mathbf{X}{\mathbf{W}}_1^{\left(2\right)}\right)\right){\mathbf{W}}_2.$$

This introduces multiplicative path interactions within the token representation space, enhancing the function class of the network without expanding the parameter count excessively [80]. Recent empirical work shows that models with GLU/SwiGLU-based MLPs outperform those with vanilla ReLU activations on long-context benchmarks, few-shot reasoning, and multi-hop QA. The Schur product also plays a foundational role in attention sparsity and retrieval-based models [81]. For instance, in Routing Transformers and Sparse Sinkhorn Attention, attention matrices are constructed or refined using learned importance weights, often modulated via element-wise multipliers [82]. Similarly, in Retrieval-Augmented Generation (RAG) and ReAct-style agents, external memory tokens are fused into the hidden states using learned gates implemented through Hadamard products [83]. This ensures that model trust and information flow can be dynamically adjusted at the token level.

Figure 2. Comparative performance of LLMs with ReLU and Schur-based SwiGLU activations across different model scales.

Figure 2. Comparative performance of LLMs with ReLU and Schur-based SwiGLU activations across different model scales.

In conclusion, the Schur product functions as a fundamental operation in LLMs, mediating context-aware modulation, sparse interaction, and parameter-efficient adaptation [84]. Its presence in GLUs, attention gates, and fine-tuning strategies affirms its status as an essential algebraic primitive for scaling up language understanding, reasoning, and generation [85]. As future LLMs move toward modularity, sparsity, and memory-based computation, the Hadamard product will remain at the center of efficient and expressive architecture design. The final section will synthesize these threads and provide a unified theoretical framework for the role of the Schur product across deep learning domains [86].

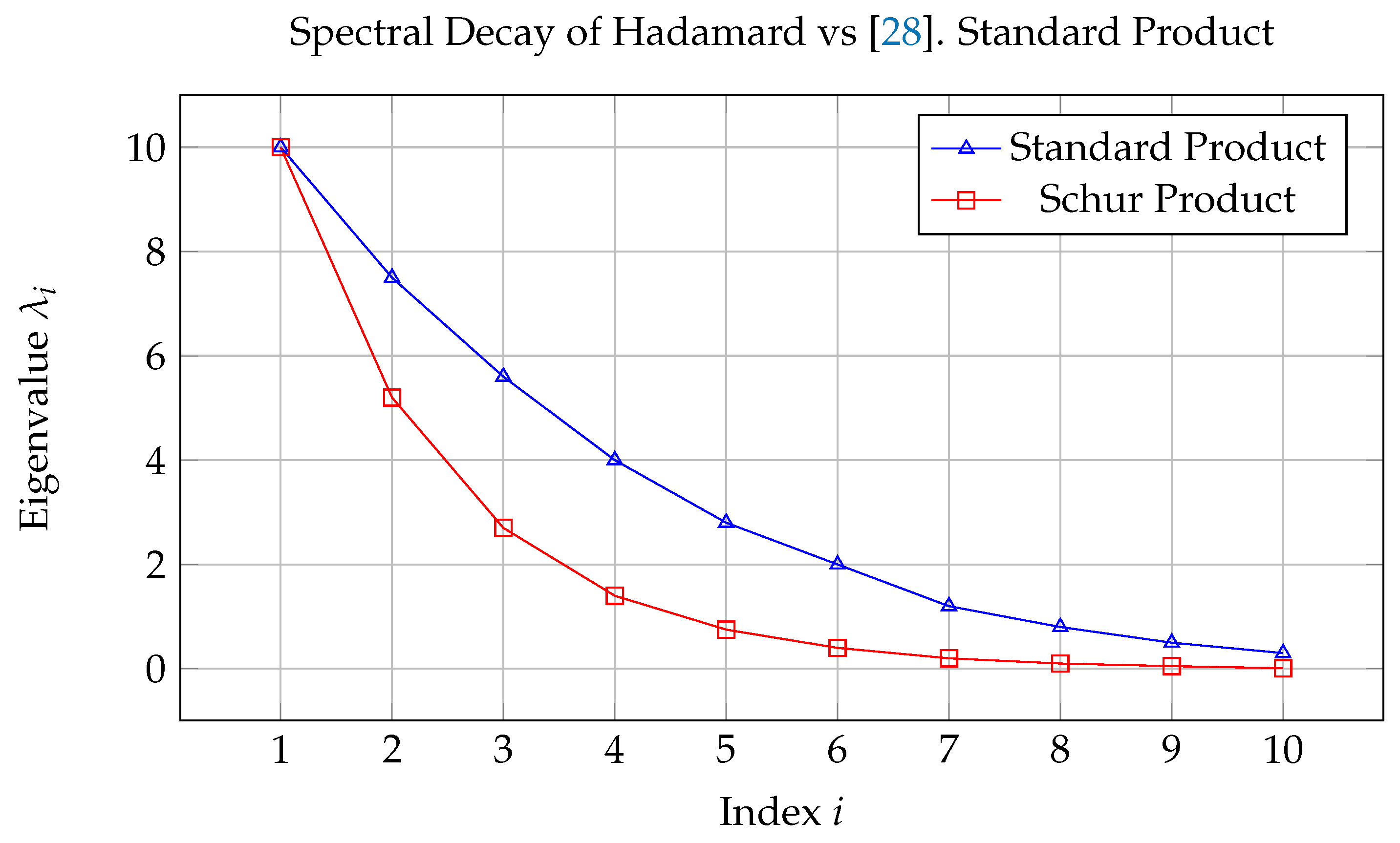
6. A Unified Framework and Theoretical Perspectives

The preceding sections have illuminated the pervasive role of the Schur product across neural architectures for vision, language, and multimodal understanding. Despite the superficial heterogeneity of these domains—ranging from spatial tensors in convolutional nets to token embeddings in transformers—a common algebraic substrate emerges in the repeated use of element-wise multiplicative interactions [87]. In this section, we develop a unified mathematical framework for understanding the expressive, structural, and functional capacity of the Schur product in deep learning, framed within the language of functional analysis, tensor algebra, and operator theory [88]. Let $\mathcal{F}:{\mathbb{R}}^d\to {\mathbb{R}}^d$ be a neural module that transforms input feature vectors $\mathbf{x}\in {\mathbb{R}}^d$ via a combination of linear maps, nonlinear activations, and attention-like operators [89]. The Schur product arises as an operator $\Gamma :{\mathbb{R}}^d\times {\mathbb{R}}^d\to {\mathbb{R}}^d$ defined pointwise as [90]:

$$\Gamma (\mathbf{x},\mathbf{y})=\mathbf{x}\circ \mathbf{y},\mathrm{where}{(\mathbf{x}\circ \mathbf{y})}_i=x_i{y}_i.$$

This operation is bilinear, symmetric, and associative over the Hadamard semiring $(\mathbb{R},+,\circ )$, which gives it unique theoretical advantages over the standard matrix product [91]. Crucially, $\Gamma$ preserves dimensionality and topological structure, allowing for the insertion of learnable or context-dependent weights without architectural disruption. This property is exploited in both channel-wise attention (SE blocks), gate-based activations (GLU, SwiGLU), and adapter modules (LoRA, BitFit), making $\Gamma$ a minimal yet expressive nonlinearity that can interpolate between identity and fully conditioned transformation. To analyze its effect on expressivity, consider a single-layer network:

$$\mathcal{F}\left(\mathbf{x}\right)=\sigma \left(\mathbf{W}\mathbf{x}\right)\circ \mathbf{g}\left(\mathbf{x}\right),$$

where $\sigma$ is a nonlinear activation (e.g., ReLU, Swish), and $\mathbf{g}$ is a secondary conditioning function, possibly itself a neural net. From a functional point of view, this introduces a pointwise multiplicative coupling between two hypothesis classes, increasing the effective capacity of $\mathcal{F}$ to approximate highly non-separable functions [92]. If ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ denote the RKHS (Reproducing Kernel Hilbert Spaces) corresponding to $\sigma (\mathbf{W}·)$ and $\mathbf{g}(·)$ respectively, then $\mathcal{F}\in {\mathcal{H}}_1·{\mathcal{H}}_2$, the Hadamard product space of the two kernels [93]. Furthermore, the Schur product acts as a sparse diagonal operator in the space of linear maps [94]. Let ${\mathbf{D}}_{\alpha }=\mathrm{diag}\left(\alpha \right)$ for some gating vector $\alpha \in {\mathbb{R}}^d$ [95]. Then [96]:

$$\alpha \circ \mathbf{x}={\mathbf{D}}_{\alpha }\mathbf{x},\forall \mathbf{x}\in {\mathbb{R}}^d.$$

This linearizes the Hadamard product into a diagonal projection operator, which can be composed with full-rank transformations to produce restricted affine subspaces [97]. Such operators are low-rank (rank $\le d$) and sparse, and their compositional closure under addition and multiplication forms a semiring of selective modulation functions [98]. Consequently, Schur product gates can be viewed as sparse approximators of more complex attention mechanisms, with the advantage of reduced computational complexity and lower VC-dimension [99]. To bridge the usage of Schur products in vision and language, we propose the notion of feature-aligned multiplicative conditioning (FAMC), a general template for operations that condition a primary representation $\mathbf{x}$ by a secondary signal $\mathbf{c}$ via:

$${\mathcal{M}}_{\mathrm{FAMC}}(\mathbf{x};\mathbf{c})=\varphi \left(\mathbf{x}\right)\circ \psi \left(\mathbf{c}\right),$$

where $\varphi ,\psi :{\mathbb{R}}^d\to {\mathbb{R}}^d$ are parameterized functions [100]. This formulation subsumes SE attention (where $\psi$ is a pooled MLP), FiLM modulation (with affine variants), GLUs (where $\psi$ is a gate), and many adapter-based fine-tuning modules in LLMs [101]. The key advantage of FAMC operators is that they preserve alignment between source and target modalities—e.g., aligning vision with language or prior knowledge with activation states—via element-wise coupling, thereby minimizing interference and maximizing semantic coherence [7].

7. Implications and Future Directions

The ubiquity of the Schur product invites several theoretical and practical research directions:

• Neural Operator Algebras: Formalizing the class of neural networks closed under Hadamard multiplication yields insight into the structure of gate-based models and their compositional hierarchies [102]. For instance, one may study whether Hadamard-enriched architectures correspond to subclasses of multiplicative semigroup algebras with polynomial-time computable spectra [103].
• Optimization Geometry: The gradient of the Schur product $\nabla (\mathbf{x}\circ \mathbf{y})=\mathbf{y}+\mathbf{x}$ (under scalar multiplication) introduces favorable curvature in loss landscapes, especially when used in gating [104]. This can be exploited to design optimizers that adaptively gate gradients during backpropagation [105].
• Sparse and Interpretable Models: Since Schur products are inherently element-wise, they lend themselves to sparsity and pruning [106]. Leveraging this, we can construct interpretable models where each feature dimension is conditionally controlled, enabling token-wise routing and interpretable modular computation [107].
• Unification of Attention and Gating: By viewing softmax-based attention and GLU-like gating as instances of generalized Schur operations under appropriate normalizations, it may be possible to design hybrid models that interpolate between discrete and continuous attention, offering both interpretability and flexibility.

8. Conclusions

Across deep learning, the Schur product reveals itself not as a peripheral arithmetic operation but as a central, theory-grounded, and architecturally expressive primitive. From its role in visual attention and cross-modal fusion to its manifestation in gated LLMs and fine-tuning strategies, the Hadamard product provides a uniquely efficient pathway for feature interaction, conditioning, and modulation. By unifying these usages under a common mathematical lens, we gain not only deeper understanding of model behavior but also a blueprint for the next generation of scalable, interpretable, and composable neural architectures. The challenge now is to elevate this primitive from implementation convenience to foundational building block in the algebra of neural computation.