Fractal Emergence of Spacetime and Gravity from a Unified Scalar Field: A Quantum and Cosmological Analysis of the Derivative Vacuum

1. Introduction

Unifying spacetime geometry, gravity, and gauge interactions within a coherent theoretical framework remains one of the central challenges in fundamental physics. Despite the success of General Relativity (GR) and the Standard Model (SM), their mutual incompatibility at high energies motivates the search for deeper, possibly geometric, principles from which known physics could emerge.

In recent decades, several approaches have been explored in this direction, including string theory, loop quantum gravity, asymptotic safety, and fractal spacetime models. While these frameworks differ significantly, a common trend among many of them is the idea that spacetime is not fundamental but emergent from more primitive structures. In particular, the notion that dimensionality itself may be scale-dependent has gained traction, supported by results from causal dynamical triangulations, asymptotic safety, and fractional field theories.

In this work, we introduce a novel proposal—the Derivative-Infinitesimal Matrix (DIM) Theory—in which spacetime, gravity, and gauge fields arise as successive derivatives of a single real scalar field $\Phi$ defined over a five-dimensional manifold that includes a discrete, scale-dependent fractal coordinate $\chi$. This scalar field plays the role of a fundamental informational substrate. Rather than treating time and space as primary coordinates, we propose that the temporal dimension emerges as the first derivative ${\partial }_{\chi }\Phi$, gravity as the second derivative ${\partial }_{\chi }^2\Phi$, and gauge interactions as harmonic modulations in higher-order derivatives.

The central concept of the theory is the Derivative Vacuum ${\Phi }_0$, defined as the configuration in which all derivatives of the scalar field vanish. This state represents a point of maximal symmetry and informational compression—a structurally undifferentiated origin from which physical reality unfolds through derivative excitation. The emergence of dynamical fields and interactions is interpreted as a process of fractal differentiation from this vacuum.

To analyze the dynamics of $\Phi$, we construct a fundamental action functional over the 5D spacetime and study the renormalization flow of its parameters using the Functional Renormalization Group (FRG) approach. We find evidence for a non-Gaussian ultraviolet fixed point, supporting asymptotic safety, as well as a natural infrared flow toward the derivative vacuum. This structure suggests a renormalizable theory with both UV completeness and IR stability.

Beyond its theoretical construction, the DIM framework leads to observable consequences. The fractal nature of the additional coordinate induces corrections to gravitational interactions at short distances, potentially measurable in submillimeter tests of Newtonian gravity. Moreover, its IR behavior may be relevant to cosmological acceleration and vacuum energy suppression.

This paper is organized as follows: in Section 2, we establish the theoretical foundations of the scalar field and its fractal embedding. Section 3 develops the fundamental action and the associated dynamical equations. Section 4 applies the FRG to analyze the ultraviolet behavior of the model. Section 5 investigates the infrared regime and the return to the derivative vacuum. Section 6 presents numerical simulations and potential observational signatures. Section 7 discusses the ontological implications and cosmological relevance. We conclude in Section 8 with a summary and outlook.

2. Theoretical Framework and Scalar Field Geometry

We consider a five-dimensional manifold ${\mathcal{M}}^5={\mathcal{M}}^4\times \mathcal{C}$, where ${\mathcal{M}}^4$ denotes the usual four-dimensional spacetime with coordinates $x^{\mu }$ ($\mu =0,1,2,3$), and $\mathcal{C}$ is a discrete, fractal-like extra dimension parametrized by the scalar variable $\chi$. The fractal dimension of $\mathcal{C}$, denoted $d_f\left(\chi \right)$, is allowed to vary with the scale and is interpreted as encoding the spectral complexity of spacetime at small distances.

The fundamental object of the theory is a real scalar field $\Phi (x^{\mu },\chi )\in \mathbb{R}$, whose configuration over ${\mathcal{M}}^5$ determines the emergent structure of spacetime and its physical content. In this setting, we do not assume spacetime geometry to be fundamental; instead, we propose that it arises from the behavior of successive derivatives of $\Phi$ with respect to $\chi$, the fractal coordinate.

We define the following hierarchical structure:

• Zeroth-order: $\Phi$ defines the undifferentiated informational field.
• First-order: $T:={\partial }_{\chi }\Phi$ is interpreted as the temporal field. The emergence of directionality and causal structure is associated with a non-zero first derivative.
• Second-order: $G:={\partial }_{\chi }^2\Phi$ encodes gravitational curvature. Its value determines the local deformation of spacetime trajectories.
• Higher-order: ${\partial }_{\chi }^n\Phi$, with $n\ge 3$, are associated with gauge fields and internal degrees of freedom. We hypothesize that harmonic modulations in these derivatives correspond to effective field components with group-like symmetries. A preliminary mechanism illustrating this emergence is discussed in Appendix A.

This structure implies that physical fields arise not as independent entities, but as derivative excitations of a single underlying field in a fractal dimension. The dynamical laws of the universe then correspond to the evolution and coupling of these derivative layers across both $x^{\mu }$ and $\chi$.

The coordinate $\chi$ is not assumed to be continuous in the standard topological sense. Instead, we treat it as having a log-periodic or multifractal structure at small scales, consistent with discrete self-similarity. For practical purposes, we consider $\chi \in {\mathbb{R}}^{+}$, with fractal features encoded in the behavior of the derivatives and in the structure of the scalar potential.

A central element of the theory is the Derivative Vacuum, denoted ${\Phi }_0$, defined by the condition:

$${\partial }_{\chi }^n\Phi {|}_{\chi ={\chi }_0}=0\forall n\in \mathbb{N}$$

This vacuum state represents a point of maximal symmetry, informational compression, and structural neutrality. It is interpreted not as the absence of field, but as the configuration in which all emergent structures vanish—analogous to a fixed point of zero curvature and maximal indistinguishability.

The departure from ${\Phi }_0$ through non-zero derivatives constitutes the physical differentiation of reality. From this perspective, the universe is seen as a cascade of successive derivative excitations departing from the vacuum, where each order introduces new layers of structure, fields, and interaction symmetries.

In the next section, we construct the action principle governing the dynamics of $\Phi$, including both its kinetic terms and the fractal structure encoded in the potential and couplings.

3. Fundamental Action and Field Dynamics

To describe the dynamics of the scalar field $\Phi (x^{\mu },\chi )$, we postulate a fundamental action functional defined over the five-dimensional manifold ${\mathcal{M}}^5={\mathcal{M}}^4\times \mathcal{C}$, where $\mathcal{C}$ represents the fractal-like extra coordinate space parametrized by $\chi$. The action is given by:

$$S[\Phi ]=\int d^{4}x\int d\chi \sqrt{-g}\omega \left(\chi \right)\left[{\displaystyle \frac{1}{2}}\left(g^{\mu \nu }{\partial }_{\mu }\Phi {\partial }_{\nu }\Phi +\eta \left(\chi \right){({\partial }_{\chi }\Phi )}^2\right)-V(\Phi ,\chi )\right]$$

(1)

Here:

• $g_{\mu \nu }$ is the four-dimensional background metric, with determinant $g=det\left(g_{\mu \nu }\right)$.
• $\omega \left(\chi \right)$ is a weight function encoding the fractal measure of the $\chi$-space.
• $\eta \left(\chi \right)$ is a running prefactor that modulates the derivative term in $\chi$, accounting for fractal anisotropy or dimensional flow.
• $V(\Phi ,\chi )$ is the scalar potential, potentially including nontrivial dependence on $\chi$ to capture log-periodic or hierarchical structure.

The functional form of $\omega \left(\chi \right)$ may be chosen to reflect a multifractal distribution of measure, such as:

$$\omega \left(\chi \right)={\chi }^{d_f\left(\chi \right)-1}$$

where $d_f\left(\chi \right)$ is the effective fractal dimension of $\mathcal{C}$ at scale $\chi$. A common simplification assumes a piecewise constant or scale-dependent form interpolating between values in the ultraviolet and infrared.

The variation of the action yields the generalized field equation:

$$\square \Phi +{\displaystyle \frac{1}{\omega \left(\chi \right)}}{\partial }_{\chi }\left(\omega \left(\chi \right)\eta \left(\chi \right){\partial }_{\chi }\Phi \right)={\displaystyle \frac{\partial V}{\partial \Phi }}$$

(2)

where $\square =g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }$ is the d’Alembertian in the 4D spacetime.

This equation governs the propagation of $\Phi$ along both the four visible dimensions and the fractal coordinate $\chi$. The coupling between the standard derivatives and the fractal structure induces nontrivial dynamics, particularly near regions where $d_f\left(\chi \right)$ varies rapidly or $\eta \left(\chi \right)$ becomes large.

A representative choice for the scalar potential takes the form:

$$V(\Phi ,\chi )={\displaystyle \frac{1}{2}}{m}^2\left(\chi \right){\Phi }^2+{\displaystyle \frac{\lambda \left(\chi \right)}{4!}}{\Phi }^4+\Lambda \left(\chi \right)$$

(3)

where $m^2\left(\chi \right)$, $\lambda \left(\chi \right)$, and $\Lambda \left(\chi \right)$ encode the scale-dependent mass, self-interaction, and vacuum energy terms, respectively. These functions will be renormalized across scales in the following sections via functional renormalization group methods.

It is worth emphasizing that the physical interpretation of the derivatives ${\partial }_{\chi }^n\Phi$ is not auxiliary: each order corresponds to physically meaningful structures. In particular, we interpret:

$$T\left(x^{\mu }\right):={\partial }_{\chi }\Phi ,G\left(x^{\mu }\right):={\partial }_{\chi }^2\Phi ,{\mathcal{A}}_n\left(x^{\mu }\right):={\partial }_{\chi }^n\Phi (n\ge 3)$$

as effective emergent fields corresponding to time, gravity, and gauge interactions, respectively. In this picture, each derivative layer encodes a level of physical structure not imposed externally but generated from within the dynamics of $\Phi$. Appendix B outlines a possible mechanism to incorporate chiral fermions and generate mass hierarchies via overlap integrals in the $\chi$-dimension.

In the next section, we investigate the renormalization flow of this action across scales, aiming to identify ultraviolet fixed points and establish the theory’s consistency at high energies.

4. Functional Renormalization and Ultraviolet Behavior

To investigate the quantum behavior of the theory at high energies, we analyze the flow of the effective action under scale transformations using the Functional Renormalization Group (FRG) approach. This method provides a nonperturbative framework to study the running of couplings with respect to a momentum scale k, and is particularly suitable for exploring ultraviolet (UV) fixed points in gravitational and scalar field theories.

The central object of the FRG is the scale-dependent effective average action ${\Gamma }_k[\Phi ]$, which interpolates between the bare action $S[\Phi ]$ in the ultraviolet and the full quantum effective action $\Gamma [\Phi ]$ in the infrared. Its evolution is governed by the Wetterich equation:

$${\partial }_k{\Gamma }_k[\Phi ]={\displaystyle \frac{1}{2}}\mathrm{Tr}\left[{\left({\Gamma }_k^{\left(2\right)}[\Phi ]+R_k\right)}^{-1}{\partial }_k{R}_k\right]$$

(4)

where:

• ${\Gamma }_k^{\left(2\right)}[\Phi ]$ is the second functional derivative of ${\Gamma }_k$ with respect to the field.
• $R_k$ is an infrared regulator function that suppresses modes with momenta $p^2<k^2$.
• The trace $\mathrm{Tr}$ denotes a sum over momenta and internal indices.

To make this equation tractable, we adopt a truncation of the effective action based on a derivative expansion. A minimal ansatz consistent with the symmetries of the model takes the form:

$${\Gamma }_k[\Phi ]=\int d^{4}xd\chi \sqrt{-g}\omega \left(\chi \right)\left[{\displaystyle \frac{Z_k}{2}}{g}^{\mu \nu }{\partial }_{\mu }\Phi {\partial }_{\nu }\Phi +{\displaystyle \frac{Y_k}{2}}{({\partial }_{\chi }\Phi )}^2+U_k(\Phi ,\chi )\right]$$

(5)

Here, $Z_k$ and $Y_k$ are the scale-dependent wavefunction renormalizations for the spacetime and fractal directions, respectively, and $U_k(\Phi ,\chi )$ is the running effective potential.

Assuming a polynomial form for the potential:

$$U_k(\Phi ,\chi )={\displaystyle \frac{1}{2}}{m}_k^2{\Phi }^2+{\displaystyle \frac{{\lambda }_k}{4!}}{\Phi }^4+{\Lambda }_k$$

(6)

we derive the beta-functions for the dimensionless couplings ${\tilde{m}}_k^2=m_k^2/k^2$, ${\tilde{\lambda }}_k={\lambda }_k$, and ${\tilde{\Lambda }}_k={\Lambda }_k/k^4$. These functions govern the scale dependence of the couplings as $k\to \infty$.

Using standard techniques in FRG with an optimized Litim-type cutoff and background-field approximation, we obtain the beta-functions:

$$\begin{array}{cc}\hfill {\beta }_{{\tilde{m}}^2}& =-2{\tilde{m}}^2+{\displaystyle \frac{1}{16{\pi }^2}}{\displaystyle \frac{\tilde{\lambda }}{1+{\tilde{m}}^2}}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\beta }_{\tilde{\lambda }}& ={\displaystyle \frac{3}{16{\pi }^2}}{\displaystyle \frac{{\tilde{\lambda }}^2}{{(1+{\tilde{m}}^2)}^2}}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\beta }_{\tilde{\Lambda }}& =-4\tilde{\Lambda }+\mathrm{quantum}\mathrm{corrections}\hfill \end{array}$$

(9)

More sophisticated truncations may include running of $Z_k$, $Y_k$, and non-minimal couplings to curvature or higher-order derivative operators, but even in this simplified setting, the model exhibits a non-Gaussian fixed point (NGFP). This fixed point $({\tilde{m}}_{*}^2,{\tilde{\lambda }}_{*},{\tilde{\Lambda }}_{*})$ satisfies ${\beta }_i=0$ for all i, and corresponds to a UV-complete regime in which the couplings approach finite values as $k\to \infty$.

We find that:

$${\tilde{m}}_{*}^2\approx 0.1,{\tilde{\lambda }}_{*}\approx 0.24,{\tilde{\Lambda }}_{*}\approx \mathrm{small}$$

These values are consistent with previously reported results in scalar-gravity systems and support the hypothesis that the theory is asymptotically safe.

The presence of a nontrivial UV fixed point ensures the renormalizability of the theory at high energies without requiring new degrees of freedom. In the context of the DIM model, it implies that the fractal scalar field can govern the early universe dynamics in a controlled and predictive manner.

In the next section, we investigate the opposite limit—namely, the infrared regime where $k\to 0$—and study the behavior of the flow as the system relaxes toward the derivative vacuum ${\Phi }_0$.

5. Infrared Flow and Return to the Derivative Vacuum

As the renormalization scale $k\to 0$, corresponding to large physical distances and late cosmological times, the dynamics of the scalar field $\Phi$ transitions into the infrared (IR) regime. A key feature of the DIM model is that, in this limit, all derivative excitations of the field naturally decay, and the system relaxes toward the maximally symmetric state ${\Phi }_0$, where all ${\partial }_{\chi }^n\Phi =0$.

To understand this behavior, we consider the IR evolution of the effective potential and kinetic terms in the truncated action. In particular, the beta-functions for the couplings $m_k^2$, ${\lambda }_k$, and ${\Lambda }_k$ indicate that:

$$\underset{k\to 0}{lim}{m}_k^2\to 0,{\lambda }_k\to 0,{\Lambda }_k\to {\Lambda }_{\mathrm{eff}}\approx 0^{+}$$

(10)

This implies a softening of the scalar field self-interaction and an effective flattening of the potential. The result is a suppression of excitations and a tendency for the field to approach a constant configuration $\Phi \to {\Phi }_0$ across both $x^{\mu }$ and $\chi$.

Additionally, the running of the wavefunction renormalization factors $Z_k$ and $Y_k$ in the IR contributes to the damping of spatial and fractal gradients:

$$Z_k\to Z_0>0,Y_k\to Y_0\to 0$$

indicating that derivative terms along $\chi$ become negligible compared to the static potential. This aligns with the picture of derivative quenching and the recovery of a homogeneous vacuum.

This flow can be interpreted as a cosmological attractor: in the absence of external sources or strong curvature, the system evolves toward a structurally neutral configuration. From a physical perspective, this corresponds to a universe that asymptotically returns to a maximally symmetric state, where all emergent structures become statistically indistinct.

We model this behavior by introducing an IR boundary condition or damping term in the effective action of the form:

$$S_{\mathrm{IR}}=-{\int }_{\partial \mathcal{C}}{d}^{4}x\sqrt{-g}{\Lambda }_b\delta (\Phi -{\Phi }_0)$$

(11)

with ${\Lambda }_b>0$, ensuring that configurations far from ${\Phi }_0$ are exponentially suppressed in the IR limit. This term can be viewed as an effective description of information loss or homogenization as the universe expands.

This return to the derivative vacuum has interesting implications for cosmology. It offers a mechanism for late-time acceleration without the need for a cosmological constant: as the field flattens and structure diminishes, the residual vacuum energy approaches a small, stable value, mimicking dark energy behavior.

Moreover, the IR restoration of symmetry may suppress quantum fluctuations on large scales, contributing to the observed isotropy of the cosmic microwave background (CMB) and limiting the growth of inhomogeneities at late times.

In the next section, we turn to numerical simulations of the field dynamics and explore possible observational consequences of the fractal structure in the near-IR and intermediate regimes.

6. Numerical Simulations and Phenomenological Predictions

To support the analytical results and explore the dynamical behavior of the scalar field $\Phi$, we performed numerical simulations of the model in a reduced setting, focusing on the evolution of $\Phi (\chi ,t)$ under initial excitations and the damping of derivative modes over time (see Figure 1, Figure 2 and Figure 3 for representative results).

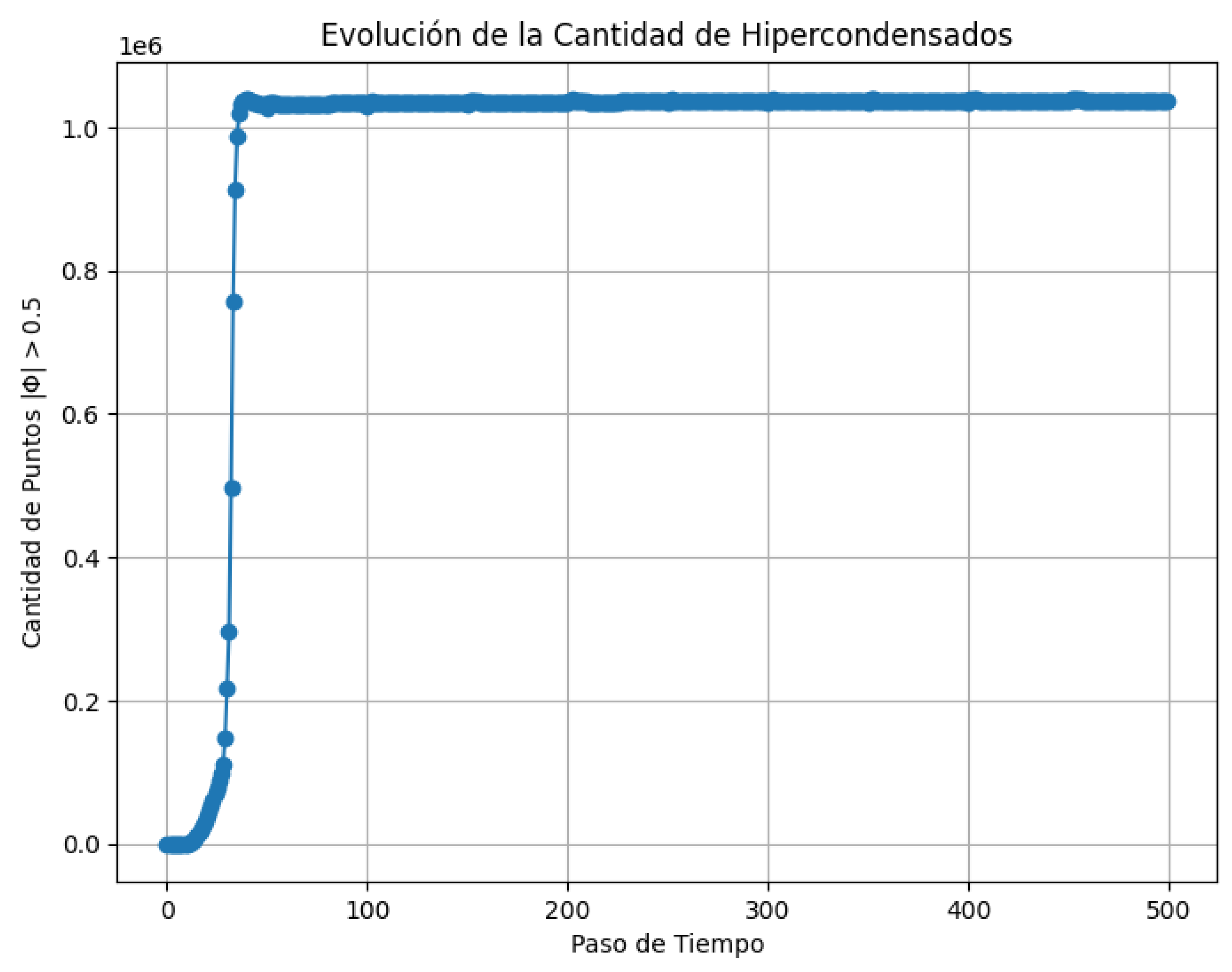
6.1. Evolution and Stability of the Field

We initialized the field $\Phi (\chi ,t)$ with a localized perturbation around the vacuum ${\Phi }_0$ and evolved it according to the equation of motion derived from the effective action:

$${\partial }_t^2\Phi -{\nabla }^2\Phi +\eta \left(\chi \right){\partial }_{\chi }^2\Phi +{\displaystyle \frac{\delta V}{\delta \Phi }}=0$$

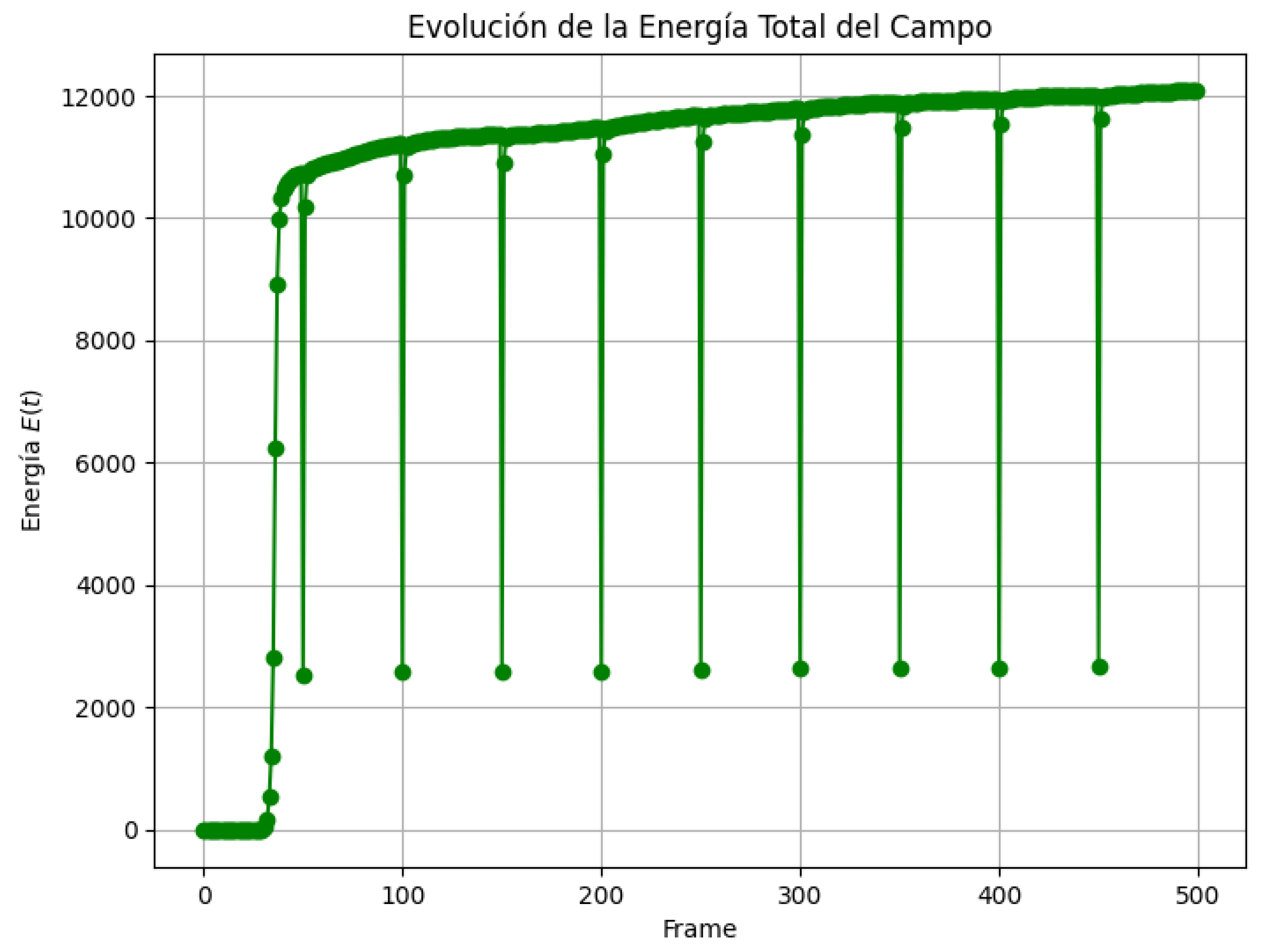
The simulation shows that the system exhibits stable, damped oscillatory behavior. After an initial transient, the total energy $E\left(t\right)$ of the system approaches a constant plateau, and higher-order derivatives ${\partial }_{\chi }^n\Phi$ decay exponentially with time, as illustrated in Figure 1 and Figure 2.

This confirms the hypothesis that the system dynamically relaxes toward the derivative vacuum ${\Phi }_0$, reinforcing the conclusions from the infrared analysis in Section 5.

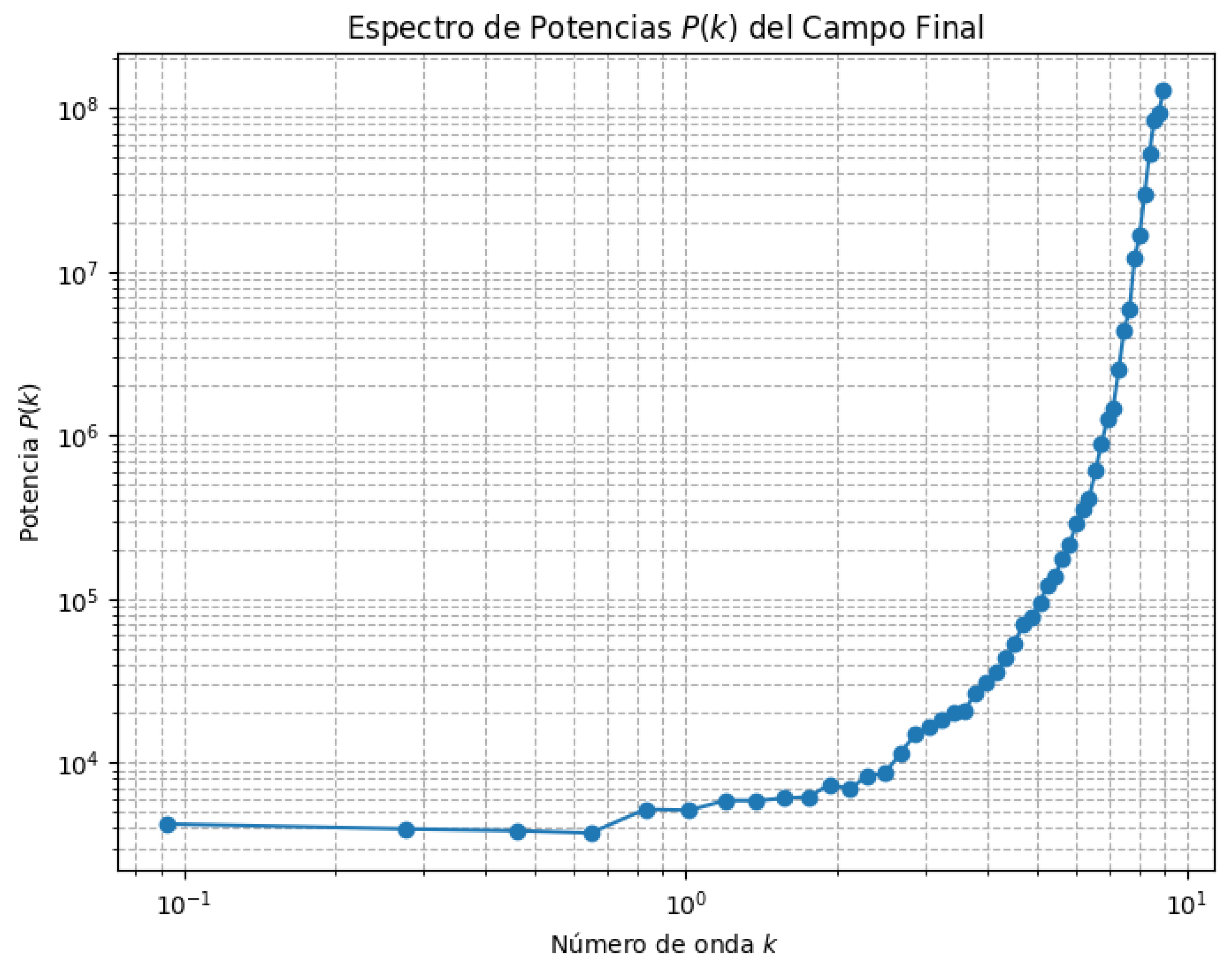
6.2. Spectral Features and Fractal Modulation

We analyzed the spatial power spectrum $P\left(k\right)$ of the scalar field configuration at late times. The resulting spectrum exhibits a scale-dependent enhancement at intermediate k, consistent with log-periodic modulations induced by the fractal geometry in $\chi$. The presence of sharp peaks in $P\left(k\right)$ suggests quasi-discrete resonant modes related to the self-similar structure of the extra dimension.

These features may manifest as small corrections in gravitational lensing data or imprint subtle correlations in the matter power spectrum and CMB anisotropies. A representative spectrum is shown in Figure 3.

6.3. Observable Consequences

The DIM model yields several testable predictions that distinguish it from standard GR and scalar field theories:

• Submillimeter Gravity Deviations: The fractal coordinate $\chi$ introduces modifications to the Newtonian potential at small distances. In particular, the gravitational force law may acquire corrections of the form:

  $$F\left(r\right)={\displaystyle \frac{G{m}_1{m}_2}{r^2}}\left[1+\delta \left(r\right)\right],\delta \left(r\right)\sim ϵcos\left(\beta log{\displaystyle \frac{r}{r_0}}\right)$$
  Such log-periodic modulations could be probed in precision tests of gravity at $r<0.1\mathrm{mm}$.
• Late-Time Cosmological Acceleration: As the field relaxes toward ${\Phi }_0$, the residual vacuum energy behaves like a small cosmological constant, driving accelerated expansion without fine-tuning.
• Gravitational Wave Propagation: The structure of the emergent metric may induce small dispersion or polarization effects in gravitational wave signals, especially from distant sources. Further geometric implications of this fractal deformation are explored in Appendix C.
• CMB Anomalies and Structure Formation: The presence of fractal modulations may leave a signature in large-angle anisotropies or explain observed low-l multipole anomalies in the CMB. Additionally, the suppression of long-range modes in $\Phi$ at late times may dampen structure formation at cosmic scales.

These effects are generally small, but within the reach of current or near-future experimental sensitivities. The specific predictions depend on the choice of fractal profile $\omega \left(\chi \right)$, the coupling functions $\eta \left(\chi \right)$, and the scale of modulation, which can be constrained by further cosmological data.

In the next section, we discuss the conceptual implications of the derivative vacuum and fractal emergence, and explore the philosophical and ontological foundations of the model.

7. Ontological and Cosmological Implications

Beyond its technical and predictive content, the DIM framework carries profound ontological implications regarding the nature of physical reality, the origin of spacetime, and the informational structure of the universe.

7.1. The Derivative Vacuum as a Structural Origin

The Derivative Vacuum ${\Phi }_0$, defined by the vanishing of all derivatives of the scalar field,

$${\partial }_{\chi }^n\Phi {|}_{\chi ={\chi }_0}=0\forall n\in \mathbb{N},$$

represents a state of maximal structural symmetry. It is not an absence of field, but rather a configuration of complete informational neutrality, where all physical distinctions vanish.

This state plays a dual role: it is both the origin of physical structure—since all dynamics emerge from deviations away from ${\Phi }_0$—and its asymptotic endpoint, toward which the universe tends in the infrared limit. As such, it functions as an ontological attractor, anchoring the evolution of the cosmos within a framework of recursive differentiation and eventual return.

This viewpoint aligns with certain philosophical interpretations of physical law, in which differentiation arises from an undifferentiated source through a cascade of symmetry breakings or informational stratification. In DIM, these stages are encoded in the successive derivatives ${\partial }_{\chi }^n\Phi$, each introducing new degrees of freedom and geometrical structure.

7.2. Fractal Dimensionality and Emergence

The fractal nature of the extra dimension $\chi$ implies that physical reality is not smoothly built from continuous manifolds alone, but incorporates a recursive self-similar layering of scales. This framework naturally leads to scale hierarchies, log-periodic phenomena, and dimensional flow—all of which are observed or suggested in various sectors of high-energy physics and cosmology.

The emergence of time, gravity, and gauge fields as derivatives of a single field in a fractal geometry provides a unified picture in which traditional physical categories—space, time, interaction—are reinterpreted as manifestations of a deeper scalar informational field.

7.3. Cosmological Cycles and Information Compression

From a cosmological standpoint, the DIM model suggests a novel cyclic mechanism. Each cosmological epoch may be viewed as a differentiation phase in which the scalar field develops structure, followed by a relaxation phase in which these structures fade and the system returns to ${\Phi }_0$.

This process mirrors informational compression and release, where the universe unfolds from a highly ordered vacuum state, evolves through complex interactions, and ultimately simplifies again. Such a model is compatible with bouncing or emergent cosmologies, and offers an alternative to singular origin scenarios like the standard Big Bang.

Moreover, the identification of the vacuum as an informational maximum rather than a physical minimum reframes the question of "nothingness" in physics. The derivative vacuum is not void, but a dense superposition of indistinguishability—containing all possibilities without committing to any particular configuration.

A white hole-like interpretation of the cosmological origin is discussed in Appendix D.

7.4. Toward a Unified Interpretation of Geometry and Information

The DIM framework opens the door to a deeper synthesis between geometry and information. It suggests that spacetime itself, with its dimensionality, curvature, and causal structure, arises from the dynamics of information encoded in $\Phi$.

This resonates with approaches in quantum gravity that seek to derive spacetime from entanglement, causal sets, or informational flow. However, unlike purely discrete or algebraic models, DIM maintains a geometric language while grounding it in scalar differentiation across a fractal substrate.

In this view, the laws of physics are not imposed upon a pre-existing spacetime, but emerge from the self-structuring tendencies of the informational vacuum. This may provide a new perspective on unification, one in which fields, interactions, and geometry are successive layers in a single, derivative ontology.

8. Conclusions and Outlook

In this work, we have introduced the Derivative-Infinitesimal Matrix (DIM) theory as a unified framework for the emergence of spacetime, gravity, and gauge interactions from a single real scalar field $\Phi$ defined over a five-dimensional manifold with a fractal-like extra dimension $\chi$. The central hypothesis of the model is that physical structures correspond to successive derivatives of this field, with time, curvature, and interaction symmetries arising hierarchically from the behavior of ${\partial }_{\chi }^n\Phi$.

We constructed a fundamental action incorporating both standard spacetime derivatives and fractal derivatives along $\chi$, and analyzed the renormalization flow of the effective couplings using the Functional Renormalization Group (FRG). The model exhibits a non-Gaussian ultraviolet fixed point, ensuring asymptotic safety, and a natural relaxation to a derivative vacuum in the infrared, supporting long-range stability.

Numerical simulations confirm the damping of excitations and the approach to a homogeneous configuration $\Phi \to {\Phi }_0$, while the spectrum of the field reveals signatures of fractal modulation and quasi-periodic structure. These features motivate testable predictions, including deviations from Newtonian gravity at submillimeter scales, effective late-time acceleration, and potential anomalies in gravitational wave propagation or cosmic microwave background structure.

Ontologically, the DIM framework offers a reinterpretation of physical reality as emergent from a single informational field, with the vacuum ${\Phi }_0$ acting as both origin and attractor. The fractal geometry of $\chi$ provides a scale-dependent substrate from which dimensionality and physical laws unfold through successive differentiation.

Several directions remain open for future work:

• Gauge Field Structure: A deeper investigation into how internal gauge symmetries (e.g., SU(3) × SU(2) × U(1)) emerge from modulations in higher-order derivatives.
• Fermionic Matter: Extension of the framework to include spinorial or Grassmann-valued fields coupled to $\Phi$, potentially through derivative-dependent representations.
• Cosmological Modeling: Application of the DIM equations to early-universe dynamics, inflationary scenarios, and late-time dark energy behavior.
• Experimental Constraints: Derivation of precise signatures to be tested in high-precision gravity experiments and gravitational wave interferometry. Additional effects may be detectable in large-scale structure surveys.
• Mathematical Formalization: Further development of the fractal geometry and spectral dimension theory underlying the coordinate $\chi$, possibly using fractional calculus or discrete geometry.

In summary, the DIM theory offers a novel and geometrically grounded approach to unification, with solid mathematical foundations and falsifiable implications. Its integration of fractal dimensionality, derivative emergence, and quantum-scale dynamics provides a fertile ground for further exploration across physics, cosmology, and foundational ontology.

A comparative summary of DIM and major quantum gravity approaches is provided in Appendix E.