Analytic Solutions of the Double Diffusive Convection Equation System

1. Introduction

There is no question that transport processes have extreme importance both for scientific and engineering applications. The simplest ones are heat conduction in solids and the regular diffusion of particles. The existing literature of diffusion (or of heat conduction) is immense; therefore, we mention some recent monographs [1,2,3,4,5,6], only. The development in numerical analysis of diffusion equations made remarkable steps in the last years as well [7]. On the other side the mathematical generalization of the diffusion equation including the p-Laplacean was investigated also [8,9].

Coupling additional transport mechanisms (like fluid flow) to regular diffusion or heat conduction drastically opens the horizon of interesting phenomena and non-linear effects. Nice examples are simplified heated flow systems like heated boundary layers [10] or the Rayleigh-Bènard convection [11]. These are diffusive convection systems where heat is transported together with particle flow which is convection instead of conduction. Such processes are extremely important in the science of meteorology [12] oceanography [13] or in climate change studies [14].

More than half a century ago E.N. Lorenz’s investigated the Rayleigh-Bènard convection [15] and with a truncated Fourier series as a trial function he pioneered the way to a new discipline called chaos theory. On the other way, if we investigate such diffusive convection systems with the self-similar Ansatz we can relatively easily derive analytic solutions which can predict the asymptotic temporal or spatial behavior of such physical phenomena. The self-similar Ansatz is the natural trial function of the regular diffusion equation [16] because the fundamental or Gaussian solution can be derived in a few lines and astonishingly new kind of solutions can be easily obtained as well. This strong performance of this function gives us a strong hint that additional disperse dynamical systems can be successfully analyzed giving insight into the global properties of their solutions. In the last years we successfully investigated such systems like the Rayleigh-Bènard convection [17] or heated boundary layers [18] presenting physically relevant analytic solutions in connection to different special functions like the Kummer’s M and Kummer’s U functions.

We can continue on this path defining more complex (or rather more compound) systems and investigate how they behave. First we analyzed systems where some diffusion equations were coupled in various ways [19].

In the next study we consider the double-diffusive convection which is a fundamental fluid dynamics phenomenon that arises when two scalar quantities with different diffusivities, such as heat and solute concentration, contribute to density gradients within a fluid under the influence of gravity. The interplay between thermal and compositional buoyancy forces gives rise to a rich variety of flow patterns and instabilities, which are often more complex than those observed in single-component convection. Understanding the mathematical structure and behavior of the double-diffusive convection equation system is therefore essential for both theoretical and applied sciences. Therefore a detailed linear stability analysis of double-diffusive convection was performed, laying the groundwork for understanding the onset of instabilities [20]. The low Prandtl number flow behavior which is relevant to astrophysical and geophysical applications was exhaustively studied as well [21]. The sub-microscale dynamics of double-diffusive convection was investigated recently by Radko [22]. Additional effects in homogeneous and heterogeneous porous media are also the subject of current investigations [23].

The literature of this field is remarkable extensive, without completeness we just mention some relevant studies and monographs [24,25,26,27]. Double-diffusion process is an important process in oceanography in general [28], in geophysics understanding the phenomena in magma chambers [29], in astrophysics [30,31,32], or double-diffusive magnetic layering [33]. In hydrology it is meant to describe sediment laden rivers in lakes and the ocean [34,35] in metallurgy [36] or finally even in various engineering applications [37,38]. The formation of salt deposits, under salt density gradient and the presence of solar radiation, have been studied in [39]. The salinity gradient also implies typically a manifestation of bacterial diversity in lakes. Different bacteria may be present in lakes, depending on depth and salinity concentration [40]. Combined effects of salt diffusion, in food industry, have been also studied [41].

After the very first analysis of "an oceanographic curiosity: the perpetual salt fountain" by Henry Stommel and co-workers in 1956 [42], Stern in 1960 firstly described the double-diffusive convection and introduced the concept of salt fingers and their role in oceanographic processes [43].

It is clear that the most studied double-diffusion system is salty fingers. The question of the limits on growing finite–length salt fingers was analyzed and a Richardson number constraint was found by [44]. Planform selection in salt fingers was also studied [45].

Additionally - again without completeness - we mention some references for the interested reader [46,47,48].

This publication aims to contribute to the ongoing exploration of the mathematics of double-diffusive convection by presenting new analytical results that shed light on the system’s behavior across different parameter regimes. By elucidating the underlying mechanisms and mathematical structure of this complex phenomenon, we hope to advance both the theoretical understanding and practical control of double-diffusive systems in nature and industry.

2. Theory and Results

2.1. Double-Diffusion System with No Extra Source Terms

The conservation equations for mass, vertical momentum, heat and salinity equations (under Boussinesq’s approximation) which describes double diffusive salt finger can be formulated in general vector form [46]. We want to perform direct calculations, correspondingly we start with following system of differential equations:

$$\begin{array}{c}\hfill u_x+v_z=0,\end{array}$$

(1)

$$\begin{array}{c}\hfill v_t+u{v}_x+v{v}_z-\nu (v_{xx}+v_{zz})+G(\beta S_{zz}-\alpha T_{zz})=0,\end{array}$$

(2)

$$\begin{array}{c}\hfill T_t+u{T}_x+v{T}_z-k_T(T_{xx}+T_{zz})=0,\end{array}$$

(3)

$$\begin{array}{c}\hfill S_t+u{S}_x+v{S}_z-k_S(S_{xx}+S_{zz})=0,\end{array}$$

(4)

applying the standard notation therefore $u,v,T$ and S denote the dynamical variables of the horizontal and vertical speed components, the temperature and the salinity. The physical parameters $\nu ,G,\alpha ,\beta ,k_T$ and $k_S$ are the kinematic viscosity, the gravitational acceleration, the coefficient of thermal expansion, the haline concentration coefficient at constant pressure and temperature, the molecular diffusivity of heat and the molecular diffusivity of salt [49]. We suppose that all the above mention coefficients are constant for the system studied. There are also cases where the diffusion or heat diffusion coefficient may depend on the parameters of the problem [50,51]. (The complete analysis or the realistic equation-of-state for sea water is a very complicated problem having a large literature. Fortunately these aspects are irrelevant for our forthcoming analysis.) Consider Figure (Figure 1) to fix our system’s geometrical relations.

All five physical parameters should have positive real values. For the better transparency we use the subscripts for the corresponding partial derivatives. The horizontal and the vertical space variables are denoted with x and z, respectively.

In the next we apply the generalization of the self-similar Ansatz [52] for two Cartesian space dimensional dependent dynamical variables in the form of:

$$\begin{array}{ccc}\hfill u(x,z,t)& =t^{-\mu }f\left(\eta \right),v(x,z,t)& =t^{-\gamma }g\left(\eta \right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill T(x,z,t)& =t^{-\delta }h\left(\eta \right),S(x,z,t)& =t^{-ϵ}i\left(\eta \right),\hfill \end{array}$$

(6)

where $\eta ={\displaystyle \frac{x+z}{t^{\lambda }}}$ is the reduced variable. In the next we demand the existence of the corresponding first and second derivatives of the shape functions with adequate smoothness. (We usually use the first two Greek letters $\alpha$ and $\beta$ for the self-similar exponents as well but now these are fixed to physical parameters.) The exponent $\lambda$ is responsible for the spreading of the dynamical variable in time, and all the other four exponents describe the decay or increment of the variable in time. In most of the cases positive exponents mean spreading and decaying solutions in time, which meets our physical intuitions. Existing self-similar symmetry also means that the investigated system has no additional characteristic relaxation time or characteristic length. It is also true that self-similar solutions are defined on infinite horizon and there is no need to introduce dimensionless variable like in the work of [46]. For infinite horizon it is not possible to define reasonable Reynolds or Rayleigh numbers.

After the usual steps of algebraic manipulations we arrive to the ordinary differential equation (ODE) system of

$$\begin{array}{c}\hfill f^{\prime }+g^{\prime }=0,\end{array}$$

(7)

$$\begin{array}{c}\hfill -{\displaystyle \frac{g}{2}}-{\displaystyle \frac{\eta g^{\prime }}{2}}+(f+g)g^{\prime }-2\nu g^{\prime \prime }+G(\beta i^{\prime \prime }-\alpha h^{\prime \prime })=0,\end{array}$$

(8)

$$\begin{array}{c}\hfill -{\displaystyle \frac{h}{2}}-{\displaystyle \frac{\eta h^{\prime }}{2}}+(f+g)h^{\prime }-2k_T{h}^{\prime \prime }=0,\end{array}$$

(9)

$$\begin{array}{c}\hfill -{\displaystyle \frac{i}{2}}-{\displaystyle \frac{\eta i^{\prime }}{2}}+(f+g)i^{\prime }-2k_S{i}^{\prime \prime }=0,\end{array}$$

(10)

where prime means derivation with respect to $\eta$. Additionally we get some constraints among the self-similar exponents:

$$\gamma =\delta =ϵ=\lambda =\mu ={\displaystyle \frac{1}{2}}.$$

(11)

Note, that now all exponents got the same fixed numerical value, which means that the mathematics of the solution is quite restricted. If some exponents remain free then the ODE system and the final solutions contain them as free parameters, too. For the regular diffusion equation if both exponents are fixed to one half we automatically get fundamental Gaussian and error function solutions. It is worth to mention here, that the Rayleigh-Bènard convection model [17] (which in a sense is a far analog) of this systems has slightly different self-similar exponents resulting much richer mathematical structure. Now only, the original physical parameters of the starting dynamical system remain free. As usual the ordinary differential equation of the shape function of the continuity equation Equation (7) can be integrated giving us: $f+g=c$ where c is our first free real integral constant which is proportional to the velocity of the flow. These conditions help us to decouple the heat and the salinity equations from the momentum and the continuity equation. We get even more, the heat conduction and the salinity equations become linear not depending on the products of dynamical variables. Both become independent in the form of

$$\begin{array}{cc}& -{\displaystyle \frac{h}{2}}-{\displaystyle \frac{\eta h^{\prime }}{2}}+c{h}^{\prime }-2k_T{h}^{\prime \prime }=0,\end{array}$$

(12)

$$\begin{array}{cc}& -{\displaystyle \frac{i}{2}}-{\displaystyle \frac{\eta i^{\prime }}{2}}+c{i}^{\prime }-2k_S{i}^{\prime \prime }=0.\end{array}$$

(13)

The solutions can be easily obtained by integrating the ODEs giving:

$$\begin{array}{c}\hfill h\left(\eta \right)=e^{-{\displaystyle \frac{\eta }{2k_T}}({\displaystyle \frac{\eta }{4}}-c)}·\left(c_1\mathrm{erf}\left[{\displaystyle \frac{1}{4}}\sqrt{-{\displaystyle \frac{2}{k_T}}}\eta +{\displaystyle \frac{c}{\sqrt{-2k_T}}}\right]+c_2\right),\end{array}$$

(14)

$$\begin{array}{c}\hfill i\left(\eta \right)=e^{-{\displaystyle \frac{\eta }{2k_S}}({\displaystyle \frac{\eta }{4}}-c)}·\left(c_3\mathrm{erf}\left[{\displaystyle \frac{1}{4}}\sqrt{-{\displaystyle \frac{2}{k_S}}}\eta +{\displaystyle \frac{c}{\sqrt{-2k_S}}}\right]+c_4\right),\end{array}$$

(15)

where erf means the Gaussian error function now with imaginary argument, the real integration constants are notated with $c_i,\{i=1..4\}$. For more information about the properties of the error function consult the handbook of [53]. Figure 2a) presents the shape functions of Equation (15) for some parameter sets. The numerical value of c which is basically the velocity, enhances the maximum of the peak and makes a shift to the right of the peak. The $k_S$ molecular diffusivity of salt is responsible for the half-width at half maximum (FWHM) of the peak. Figure 2b) shows the projection of the $S(x,z,t)$ salinity distribution $(z=0)$. This is very similar to the usual Gaussian solution of diffusion.

Now, if the second derivatives of Equations (14) and (15) are derived and replaced into Equation (16) then the momentum equation of the double diffusive convection problem can be solved. Note that the possible integration of the continuity equation may lead to a linear momentum equation; which will also mean in the next that the linear combination of solutions (superposition) will also give us further solutions. Our experience shows, that fully analytic solutions can be evaluated only for $c_1,c_3\ne 0\&c_2,c_4=0$ in the reverse condition $c_1,c_3=0\&c_2,c_4\ne 0$ the solution contains an additional integration which should be evaluated numerically when all parameters have a given numerical value. No fully analytic solutions exist for the most general case where all integral constants are not zero. We analyze the real solutions only. Therefore the ODE for the velocity shape function contains just the second derivatives of the exponential function and reads as follows:

$$-{\displaystyle \frac{g}{2}}-{\displaystyle \frac{\eta g^{\prime }}{2}}+c{g}^{\prime }-2\nu g^{\prime \prime }+G{(\beta c_4{e}^{-{\displaystyle \frac{\eta }{2k_S}}({\displaystyle \frac{\eta }{4}}-c)}-\alpha c_2{e}^{-{\displaystyle \frac{\eta }{2k_T}}({\displaystyle \frac{\eta }{4}}-c)})}^{\prime \prime }=0,$$

(16)

The solution can be derived with quadrature and has the form of:

$$\begin{array}{c}\hfill g\left(\eta \right)=e^{-{\displaystyle \frac{\eta }{\nu }}\left({\displaystyle \frac{\eta }{4}}-c\right)}\left(c_5·erf\left[{\displaystyle \frac{1}{2}}\sqrt{-{\displaystyle \frac{1}{\nu }}}\eta +{\displaystyle \frac{c}{\sqrt{-\nu }}}\right]+c_6-\right.\\ \hfill {\displaystyle \frac{G{k}_T{k}_S}{k_S{k}_T[2k_S-\nu ][2k_T-\nu ]}}\times \left[\beta c_4\{2k_T-\nu \}{e}^{\left\{{\displaystyle \frac{1}{4\nu }}-{\displaystyle \frac{1}{8k_S}}\right\}{\eta }^2+\left\{-{\displaystyle \frac{c}{\nu }}+{\displaystyle \frac{c}{2k_S}}\right\}\eta }-\right.\\ \hfill \left.\left.\alpha c_2\{2k_S-\nu \}{e}^{\left\{{\displaystyle \frac{1}{4\nu }}-{\displaystyle \frac{1}{8k_T}}\right\}{\eta }^2+\left\{-{\displaystyle \frac{c}{\nu }}+{\displaystyle \frac{c}{2k_T}}\right\}\eta }\right]\right).\end{array}$$

(17)

We analyze the real solutions only, therefore we set $c_5=0$. It is easy to see, that for $c_4=c_2$, $\alpha =\beta$ and $k_T=k_S$ the two exponential functions cancel each other, because of the two opposing competing diffusion effects. The $k_T,k_S$ and $\nu$ are still responsible for the FWHM of the peaks. It is also clear from the formula that for $\nu =2k_s=2k_T$ the velocity function becomes infinite. Large $\nu$ viscosity causes small velocity because it stands in the denominator. Figure 3a) shows us two different $g\left(\eta \right)$ shape functions with different parameter sets. We can see different kind of linear combinations of exponential-type of functions (note that there is the product of a Gaussian and an exponential function in the formula) the results are now so exciting. Either we have a peak with a global maximum or minimum or two peaks with a minimum in between.

Figure 3b) presents the velocity distribution $v(x,z=0,t)=t^{-{\displaystyle \frac{1}{2}}}·g\left(x{t}^{-{\displaystyle \frac{1}{2}}}\right)$ for the parameters of the black curve. Note, that the $\gamma =1/2$ exponent is responsible for the quick temporal decay.

To emphasize the linearity of the velocity distribution Equation (16) Figure 4 presents a linear combination of three real solutions of Equation (17) for different $c_i$ integration constants and when the spatial coordinates are shifted. In principle arbitrary large number of solutions could be summed up resulting very complex velocity distributions in double-diffusive convection systems.

2.2. The Role of Possible Source Terms

We can see, that our obtained self-similar solutions are far from being complicated and have no extra peculiarity. This is due to the fixed numerical values of all self-similar exponents. The Rayleigh- Bénard convection which is also a fluid dynamical system with coupled heat conduction has a much broader self-similar symmetry because one of the self-similar exponents remain free. Groping in this direction to generalize the double-diffusive convection system we may consider addition terms like a source in the temperature convection equation.

A straight forward way is taking a source term which is an arbitrary function of the temperature $n\left(T\right)$, in this sense Equation (3) is changed to:

$$T_t+u{T}_x+v{T}_z-k_T(T_{xx}+T_{zz})=n\left(T\right).$$

(18)

Keeping all exponents fixed to $1/2$ it can be easily shown that the linear source terms should have the form of $n\left(T\right)={\displaystyle \frac{d·T}{t}}$. Here d is the strength of the source (if positive) or sink (when negative) and it fixes the proper physical dimension. The $1/t$ time-dependent factor is needed to have the proper temporal asymptotic. We tried additional power-law dependent source terms as well, only the square root $n\left(T\right)={\displaystyle \frac{d·T^{1/2}}{t^{5/4}}}$ has trivial analytic solution of $h\left(\eta \right)=0.$ (We can easily imagine a periodic driving term as well, but that should assume a traveling wave analysis which could the topic of a possible forthcoming analysis. Such systems usually have Mathieu functions in their solutions.) Interesting reconstructions of initial conditions with possible source in diffusion problems one may find in Ref. [54].

Considering the $\tilde{t}=t-t_0$ transformation the singularity can be shifted having smooth functions. The corresponding ODE for the temperature shape function is now slightly changed to:

$$-{\displaystyle \frac{h}{2}}-{\displaystyle \frac{\eta h^{\prime }}{2}}+c{h}^{\prime }-2k_T{h}^{\prime \prime }=dh,$$

(19)

positive d values mean source The solutions read as:

$$h\left(\eta \right)=c_{1}M\left({\displaystyle \frac{1}{2}}+d,{\displaystyle \frac{1}{2}},-{\displaystyle \frac{{[2c-\eta ]}^2}{8k_T}}\right)+c_{2}U\left({\displaystyle \frac{1}{2}}+d,{\displaystyle \frac{1}{2}},-{\displaystyle \frac{{[2c-\eta ]}^2}{8k_T}}\right),$$

(20)

where $M(,,)$ and $U(,,)$ are the Kummer’s M and Kummer’s U functions with the usual integral constants of $c_1$ and $c_2$. For more information about Kummer’s functions see [53].

As definition consider the series expansion of $M(,,)$

$$M(a,b,z)=1+{\displaystyle \frac{az}{b}}+{\displaystyle \frac{{\left(a\right)}_2{z}^2}{{\left(b\right)}_{2}2!}}+...+{\displaystyle \frac{{\left(a\right)}_n{z}^n}{{\left(b\right)}_{n}n!}},$$

(21)

with the ${\left(a\right)}_n=a(a+1)(a+2)...(a+n-1),{\left(a\right)}_0=1$ which is the so-called rising factorial or Pochhammer’s Symbol [53]. In our present case b has a fix non-negative integer value, so none of the solutions have poles at $b=-n$. For the Kummer’s function M when the parameter a has negative integer numerical values ($a=-m$) the solution is reduced to a polynomial of degree m for the variable z. In other cases $a\ne -m$ we get a convergent infinite series for all values of $a,b$ and z. There is a connecting formula between the two Kummer’s functions, U is defined from M via

$$U(a,b,z)={\displaystyle \frac{\pi }{\sin \left(\pi b\right)}}\left({\displaystyle \frac{M[a,b,z]}{\mathsf{\Gamma }[1+a-b]\mathsf{\Gamma }\left[b\right]}}-z^{1-b}{\displaystyle \frac{M[1+a-b,2-b,z]}{\mathsf{\Gamma }\left[a\right]\mathsf{\Gamma }[2-b]}}\right),$$

(22)

where $\mathsf{\Gamma }\left(a\right)$ is the Gamma function [53]. It is clear that the structure of the irregular Kummer’s U function is much more complicated.

These very nice mathematical formulas do not help us much to visualize and to imagine how these functions look like for different parameters especially for quadratic arguments. Therefore we present them for some parameter values. Figure 5a) presents the regular Kummer’s M function parts of the solution Equation (20) for different d source values. The c former integral constants means just a shift parallel to the x axis, $k_T$ parameter defines the widths of the solutions. All these functions are real and regular in the origin.

It is important to emphasize that there are four parameter ranges exist where the derived solutions behave qualitatively different:

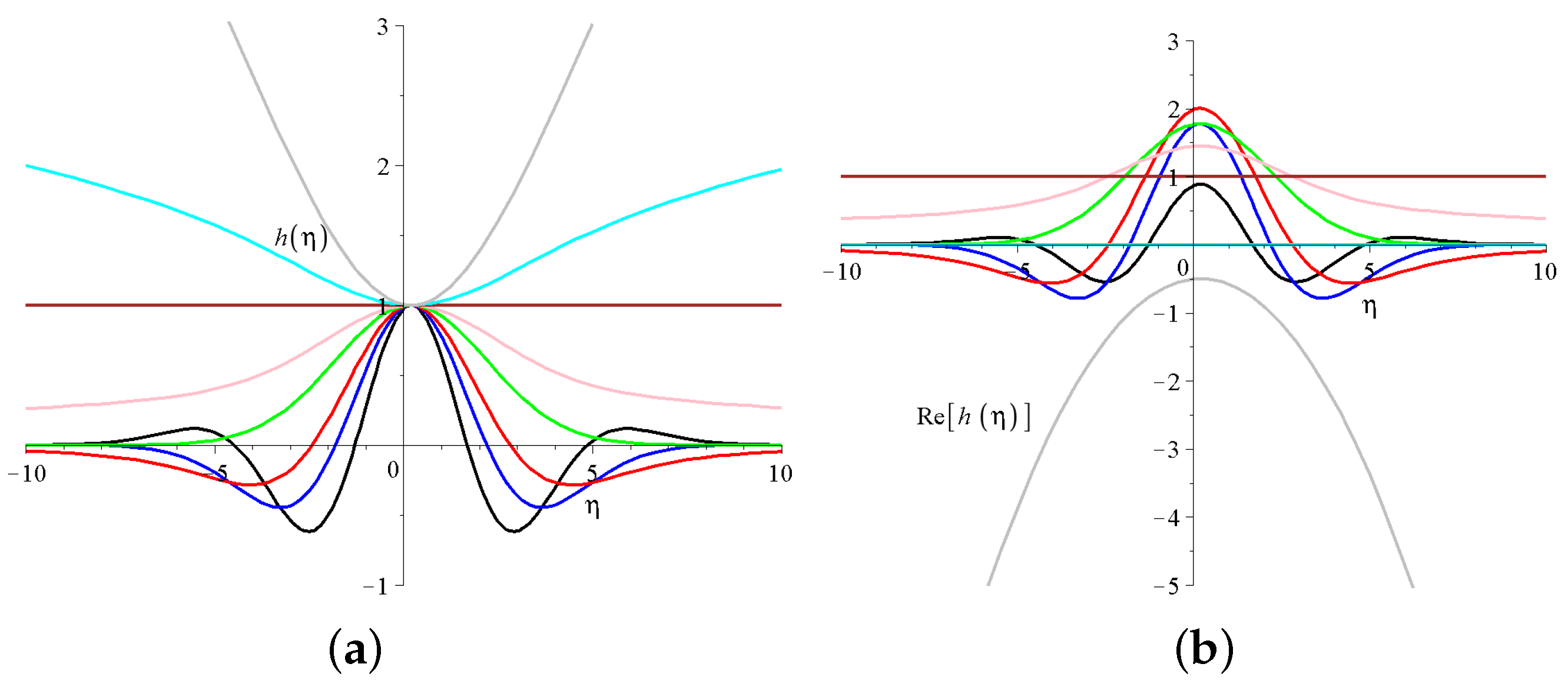
• $d<-1/2,$ where the derived solutions are divergent for large $\eta$s, these are the cyan and the gray lines on Fig 3a). If the first parameter of the Kummer’s M function is a negative integer then the function is a finite order polynomial in $\eta$. A nice example is $d=-{\displaystyle \frac{3}{2}}$ where

  $$M\left(-1,{\displaystyle \frac{1}{2}},-{\displaystyle \frac{{(2c-\eta )}^2}{8k_T}}\right)=M\left(-1,{\displaystyle \frac{1}{2}};-{\displaystyle \frac{c^2}{2k_T}}\right)-{\displaystyle \frac{c}{k_T}}\eta +{\displaystyle \frac{1}{4k_T}}{\eta }^2.$$

  (23)
  Note, that the first term on the right hand side is a constant, (Formally Kummer’s function of the first kind $M(,,)$ is equivalent to the generalized confluent hypergeometric series with the notation of ₁$F_1(,,)$.)
  The smaller the first negative parameter of the Kummer’s function the larger the power of the polynomial. Thank to the $\delta =1/2$ exponent the final $T(x,z,t)$ temperature distribution will be decaying, but we will see that not this parameter regime will attract the largest interest among the solutions.
• $d=-1/2,$ the solution is constant on the whole $\eta$ axis, this is presented by the brown line.
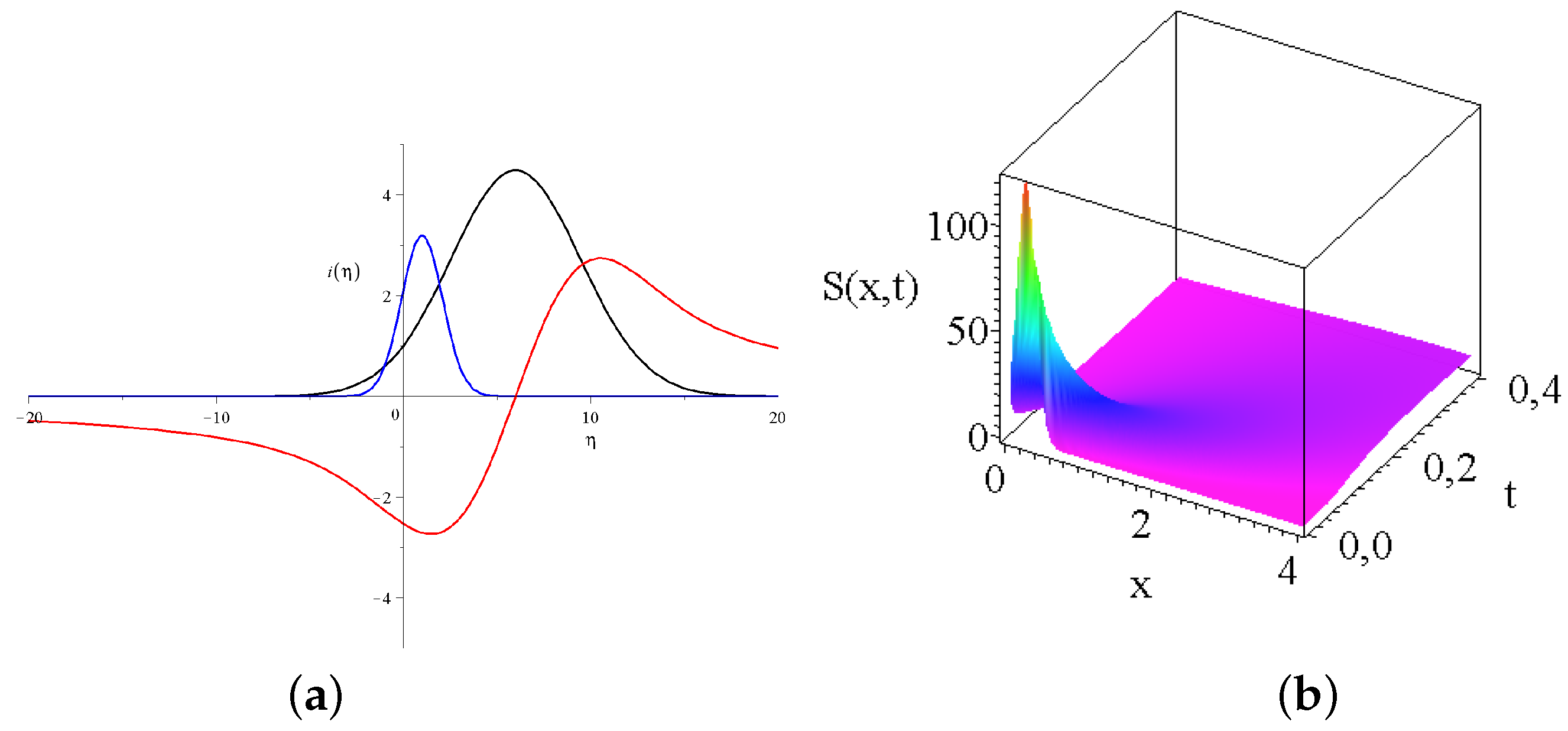
• $-1/2\le d\le 0,$ the solution is positive on the whole axis, and has a decay to zero at large $\eta$s such solutions are plotted with pink and green lines. These are well-behaving solutions with a global maxima in the origin, and in this sense similar to Gaussian solutions.
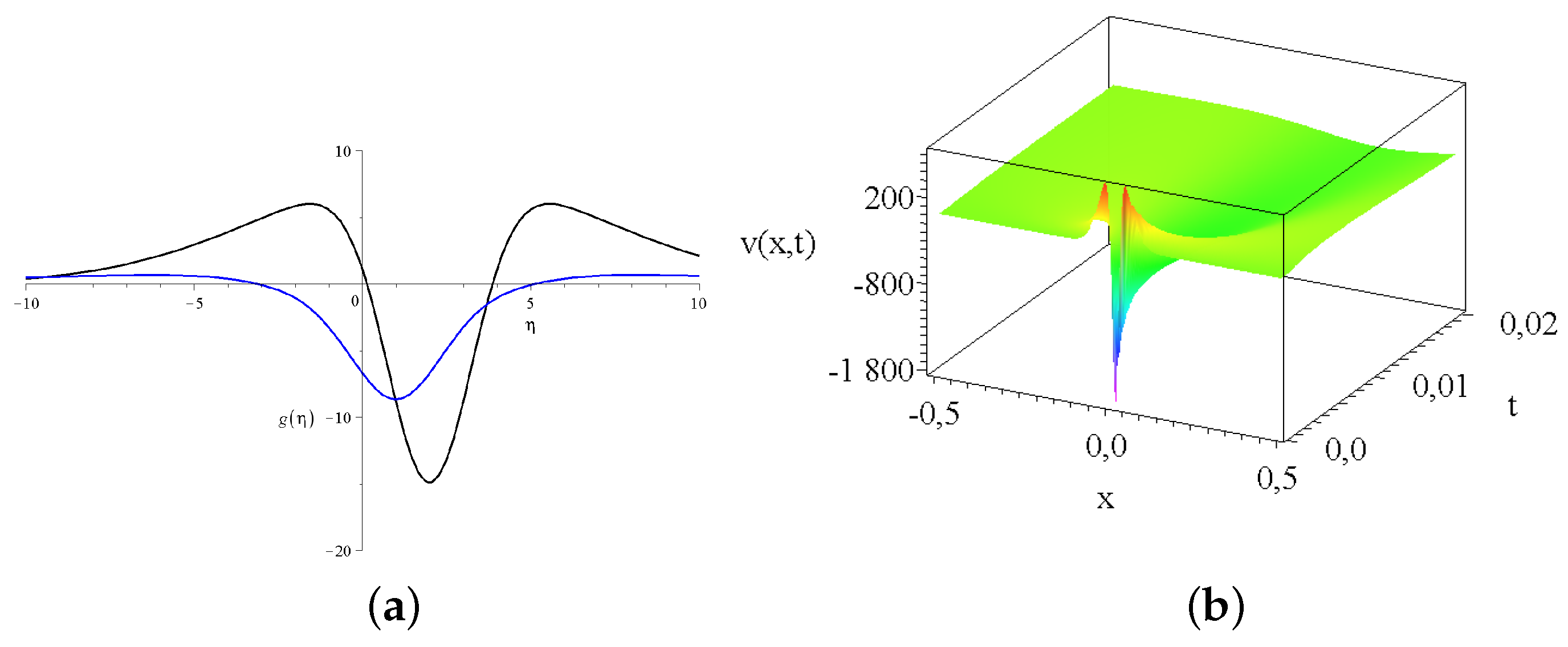
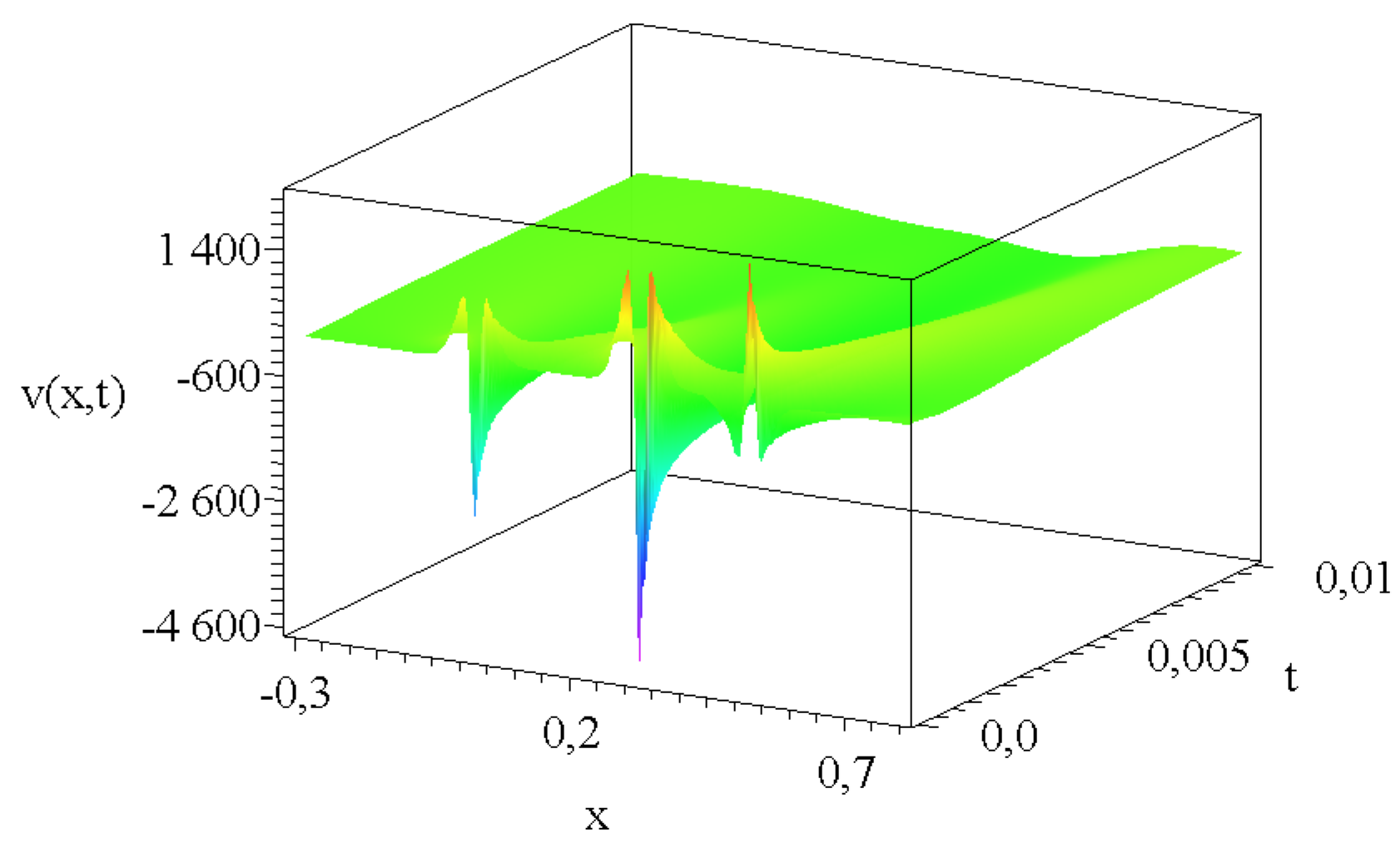
• $1/2<d,$ the solutions has a maxima in the origin following quick oscillatory decay to zero with growing number of zero transitions as d growing. Black, blue and read curves present such solutions. Unfortunately, the defining series of the Kummer’s M function Equation (21) converges very slowly for highly oscillatory functions.
  In some sense these are the most interesting solutions.

For completeness we show on Figure 5b) how the irregular Kummer’s U solutions behave. It can be shown that the Kummer’s U functions with quadratic argument are finite polynomials is the first arguments are negative integer or half integer values. We present only the real part of the solutions. Note, that the general properties are very similar. There are oscillatory and decaying solutions. There are divergent solutions and there is a finite constant and a constantly zero solution as well. To have a complete overview, Figure 6 shows three temperature distributions given with the Kummer’s M functions. We considered, physically relevant decaying solutions in three different parameter regimes.

We gained plenty of experience with the Kummer’s function [16,17,18,19] in the last years. Usually, an additional Gaussian weight functions was involved in the solutions, but the general properties were very similar. The main difference to our former solution is that, in that now a physical parameter (strength of the heat source) works as an index of the solution and additionally we always have a $t^{-1/2}$ prefactor in the final dynamical variable which automatically gives us a temporal decay at infinite times.

To complete our investigations we have to analyze the behavior of the velocity field. Considering only real solutions we take the Gaussian solution for the salinity and the Kummer’s M functions for the heat distribution, we can formulate the final ODE:

$$\begin{array}{c}\hfill -{\displaystyle \frac{g}{2}}-{\displaystyle \frac{\eta g^{\prime }}{2}}+c{g}^{\prime }-2\nu g^{\prime \prime }+G\left[\beta c_4{\left(e^{-{\displaystyle \frac{\eta }{2k_S}}({\displaystyle \frac{\eta }{4}}-c)}\right)}^{\prime \prime }-\right.\\ \hfill \left.\alpha c_{1}M{\left({\displaystyle \frac{1}{2}}+d,{\displaystyle \frac{1}{2}},-{\displaystyle \frac{{[2c-\eta ]}^2}{8k_T}}\right)}^{\prime \prime }-\alpha c_{2}U{\left({\displaystyle \frac{1}{2}}+d,{\displaystyle \frac{1}{2}},-{\displaystyle \frac{{[2c-\eta ]}^2}{8k_T}}\right)}^{\prime \prime }\right]=0,\end{array}$$

(24)

For a better transparency we just marked and not completed the second derivatives in the equation. Unfortunately, we could not find closed form for the solutions for general Kummer’s functions. However, if the power of the series of Kummer’s function is not larger than four then the ODE has an exact solution.

$$\begin{array}{c}\hfill -{\displaystyle \frac{g}{2}}-{\displaystyle \frac{\eta g^{\prime }}{2}}+c{g}^{\prime }-2\nu g^{\prime \prime }+G\left[\beta c_4{\left(e^{-{\displaystyle \frac{\eta }{2k_S}}({\displaystyle \frac{\eta }{4}}-c)}\right)}^{\prime \prime }-\right.\\ \hfill \left.\alpha c_1{\left(a_0+a_1\eta +a_2{\eta }^2+a_3{\eta }^3+a_4{\eta }^4\right)}^{\prime \prime }\right]=0,\end{array}$$

(25)

where the $a_i$ coefficients depend on the parameters of $c,k_T$ in a complicated way. The solution is exhaustive long and contains numerous Gaussian and error function terms. The direct form is given in the Appendix at the end of the study.

3. Summary and Outlook

We investigated the double diffusion convection flow system, which means that two competing diffusion processes are coupled to the momentum equation. Such real processes are heat and salt convection in water. Our self-similar Ansatz easily gave the Gaussian and error functions for the salinity, temperature and flow velocity distributions, which are less than our former expectations. The reason is that all self-similar exponents had a given $+{\displaystyle \frac{1}{2}}$ value. To deepen our analysis we considered an additional cooler or heater source term in the temperature convection equation which drastically opened the horizon of the possible solutions. The heat distribution function becomes the Kummer’s M or Kummer’s U function. The strength of the heat source becomes the first parameter of the temperature distribution which is a well-understood mathematical feature. Unfortunately, the final velocity distribution cannot be evaluated analytically for all temperature distribution parameters, however it was possible up to a considerable order of expansion of the function of the temperature.