On General Covariance

1. Preface

Einstein carried out the equivalence principle after discussing the equivalence of gravitational mass and inertial mass, and then he generalized the equivalent principle to create general relativity [1], which predicts same physics in curve space of gravity geometrization as that in no gravity space, that could be called general covariance. Theoretically, general covariance should include but not be limited in the performances of motion inertia, energy, and momentum conservations as well as equilibrium states in complicated systems. However, we will find that quite amount of observations and evidences perform against general covariance.

It is believed that Riemannian geometry has been employed in general relativity for gravity geometrization [2]. But in fact, a transformation of a space does not really determine physics, what on earth the realities do. It is said that it is not the geometry but only the general covariance that matters. In fact, we could find out plenty of contradictions in classical theory of general relativity. It could be verified that even the motions of matter’s freefalling on the Earth cannot be well interpreted in the frames of the classical theory. So that it is time to sponsor a series of inspections and perceptions to insight into the topics on general covariance.

The gravitational redshift and gravitational acceleration are of the two typical effects that gravity acts on the light rays and massive matters respectively. Hence researches on these topics would be greatly powerful to probe into the investigations and realizations on general covariance.

To discover realities is more important than to carry out new equations and theorems.

2. Contradictions on Gravitational Redshift and Acceleration

2.1. Newtonian Gravitational Redshift

The equation of gravitational redshift can be drawn via Doppler redshift in a thought experiment that a light ray be emitted from the ceiling to the bottom or that is reversely performed from bottom to the ceiling, in a freely falling elevator cabin in a center source field [3]. It could be verified that any observer in the cabin would detect no frequency shift whatever the ways the light emitted. Suppose another observer outside the cabin keeping rest so that to have a relative velocity against the cabin, who will then detect a frequency shift other than the freefalling observer. What I want to say is that whoever freefalling will detect no frequency shift, no matter inside or outside the cabin. It is the relative motion that eliminates the gravitational frequency shift. Once the relative velocities catch up to a relativistic velocity, the gravitational frequency shift will then cannot be eliminated anymore.

As a light ray is down ward emitted from a cabin ceiling and at the same time the cabin is released to freely fall, the light front should spend a time interval to reach the bottom that

$∆t={\displaystyle \frac{∆H}{c}}$                                       (1)

where $∆H$ is the distance that the light travels from the start to the end which may approximately equal to the height of the cabin, $c$ is light speed.

Thus, the cabin velocity increase is

$∆v=a∆t$                                      (2)

where $a$ is gravitational acceleration, which approximately equals to gravity $g$ case velocity does not reach relativistic level. We know it exactly has a minus value as its direction pointing to center source.

Doppler redshift is frequency shift between two observers that one has a relative motion to another, to detect frequency. Here the rest observer outside would have a relative velocity $-∆v$ or $+∆v$ to the cabin so that when they receive light ray at the same time with the inner, the Doppler redshift could be calculated as

$z_D={\displaystyle \frac{∆v}{c}}={\displaystyle \frac{g∆H}{c^2}}={\displaystyle \frac{∆\varnothing }{m{c}^2}}$                                  (3)

With the calculation of Doppler redshift, we know that the gravitational redshift has happened in the same value. Notwithstanding, I prefer to suggest a new methodology to get an equation for gravitational redshift, in which a proposal should be given that every photon at any position in a center source field could be assumed to have experienced a travel from a farthest point to the current position. This attempt may bring about more physical significances and comprehensive understandings.

A photon in one source field at position $r$ with frequency ${{\nu }_0}_{\left(r\right)}$ is set to have a virtual primary frequency ${{\nu }_0}_{(\infty )}$ at a farthest point, so that a so-called primary dynamic energy is

$E_{(\infty )}=h{{\nu }_0}_{(\infty )}$                                    (4)

where $h$ is Planck’s constant. NB, we are not talking about quantum character of photons so that photonic mass momentum we are talking refers to statistic quantities.

The corresponding dynamic mass comes from the mass-energy equation is

$m=E_{(\infty )}{c}^{-2}$                                    (5)

where $c$ is light speed.

Then the gravitational potential at position $r$, especially as is in weak field with $r\gg r^{*}$, could be written as

${\varnothing }_{\left(r\right)}={\int }_{\infty }^r{\displaystyle \frac{GM{m}_r}{r^2}}dr=-{\displaystyle \frac{GM\overline{m}}{r}}\approx -{\displaystyle \frac{GMm}{r}}=-{\displaystyle \frac{r^{*}}{2r}}m{c}^2$ (6)

where $G$ is gravitational constant, $M$ is the mass of the center source with $M\gg m_r$, $m_r$ is photonic mass at position $r$, $\overline{m}$ is the mean mass for the integral and it could be approximately replaced by $m$ case in weak field, and $r^{*}$ is Schwarzschild radius written as $r^{*}={\displaystyle \frac{2GM}{c^2}}$.

The current dynamic energy is the summation of primary dynamic energy and released potential

$E_r=h{{\nu }_0}_{\left(r\right)}=E_{(\infty )}+\left[{\varnothing }_{\left(\infty \right)}-{\varnothing }_{\left(r\right)}\right]\approx m{c}^2+{\displaystyle \frac{r^{*}}{2r}}m{c}^2\approx h{{\nu }_0}_{(\infty )}(1+{\displaystyle \frac{r^{*}}{2r}})$ (7)

Case a light ray travels from positions $r_1$ to $r_2$ , as is shown in Figure 1, gravitational redshift happens.

Gravitational redshift will be defined as

$z_{g\lambda }={\displaystyle \frac{{{\lambda }^1}_{\left(2\right)}-{{\lambda }^1}_{\left(1\right)}}{{{\lambda }^1}_{\left(1\right)}}}={\displaystyle \frac{{{\nu }_0}_{\left(1\right)}-{{\nu }_0}_{\left(2\right)}}{{{\nu }_0}_{\left(2\right)}}}\approx {\displaystyle \frac{r^{*}}{r_{\left(1\right)}}}\bullet {\displaystyle \frac{r_{\left(2\right)}-r_{\left(1\right)}}{2r_{\left(2\right)}+r^{*}}}$ (8)

Considering weak field effects, the gravitational redshift is

$z_{g\lambda }\approx r^{*}\bullet {\displaystyle \frac{r_{\left(2\right)}-r_{\left(1\right)}}{2r_{\left(1\right)}{r}_{\left(2\right)}}}={\displaystyle \frac{r^{*}}{2r_{\left(1\right)}}}-{\displaystyle \frac{r^{*}}{{2r}_{\left(2\right)}}}={\displaystyle \frac{{\varnothing }_{\left(2\right)}-{\varnothing }_{\left(1\right)}}{{mc}^2}}={\displaystyle \frac{∆\varnothing }{m{c}^2}}$ (9)

They are the forms of frequency shift of wave length based expression in weak fields, called redshift, where ${\lambda }^1$ and ${\nu }_0$ are wave length and frequency tensors in contra variant space. Of course, a frequency shift could also be defined based on frequency. But we have been used to the forms based on wave length in traditions. In this equation, redshift may go up to more than 1.0, while blueshift must have been limited in -1 to 0. Case in the form of frequency based equations, one could get blueshift greater than 1.0 but redshift limited in -1 to 0.

We could also carry out new forms of frequency shift for conveniences in special discussions, that a differential of wave length based redshift could be defined as

$d{z}_{\lambda }={\displaystyle \frac{d{{\lambda }^1}_{\left(r\right)}}{{{\lambda }^1}_{\left(r\right)}}}=dln{{\lambda }^1}_{\left(r\right)}$ (10)

So that the integral form for $r_{\left(1\right)}$ to $r_{\left(2\right)}$$z_{\lambda }=ln{{\lambda }^1}_{\left(r\right)}\left|\begin{array}{c}{r}_{\left(2\right)}\\ r_{\left(1\right)}\end{array}\right.=ln{\displaystyle \frac{{{\lambda }^1}_{\left(2\right)}}{{{\lambda }^1}_{\left(1\right)}}}=ln{\displaystyle \frac{{{\nu }_0}_{\left(1\right)}}{{{\nu }_0}_{\left(2\right)}}}$ (11)

Or a differential form of frequency based

$d{z}_{\nu }={\displaystyle \frac{d{{\nu }_0}_{\left(r\right)}}{{{\nu }_0}_{\left(r\right)}}}=dln{{\nu }_0}_{\left(r\right)}$ (12)

So that

$z_{\nu }=ln{{\nu }_0}_{\left(r\right)}\left|\begin{array}{c}{r}_{\left(2\right)}\\ r_{\left(1\right)}\end{array}\right.=ln{\displaystyle \frac{{{\nu }_0}_{\left(2\right)}}{{{\nu }_0}_{\left(1\right)}}}=ln{\displaystyle \frac{{{\lambda }^1}_{\left(1\right)}}{{{\lambda }^1}_{\left(2\right)}}}=-ln{\displaystyle \frac{{{\lambda }^1}_{\left(2\right)}}{{{\lambda }^1}_{\left(1\right)}}}$ (13)

Considering the energy expression of the Eq. (493) in to the Eq. (13), one can gain the redshift result as same as the Eq. (9). But they are based on different definitions of frequency shift so that they would perform physical implications a little different.

It is said that after the definitions of Eq. (11) and Eq. (13) there is

$z_{\lambda }=-z_{\nu }$ (14)

We have seen that they have shown difference from traditional equations. But for small frequency shift, both the two integral equations could be use instead of traditional equation.

Moreover, with Eq. (7), the gravitational frequency differential

$d{{\nu }_0}_{\left(r\right)}\approx d\left[{{\nu }_0}_{(\infty )}\left(1+{\displaystyle \frac{r^{*}}{2r}}\right)\right]=-{\displaystyle \frac{r^{*}}{2r^2}}{{\nu }_0}_{(\infty )}dr$ (15)

Then the differential frequency shift goes

$d{z}_{g\nu }={\displaystyle \frac{d{{\nu }_0}_{\left(r\right)}}{{{\nu }_0}_{\left(r\right)}}}\approx {\displaystyle \frac{-\frac{r^{*}}{{2r}^2}}{1+\frac{r^{*}}{2r}}}dr=-{\displaystyle \frac{r^{*}dr}{r(2r+r^{*})}}$ (16)

This equation will be also taken into further discussions in the next sections. In following sections, the subscripts of frequency shift symbols will be neglected for convenience and in most cases we use the concept redshift to present frequency shifts.

2.2. Errors in the Equation of So-Called Revisit Gravitational Redshift

A thought experiment has ever been employed to present the conception of the so-called revisit gravitational redshift [3,4], in which a pulse of light ray is supposed to be emitted from position 1, lasting for a time interval ${∆t}_{\left(1\right)}$, and be received at position 2 within a time interval ${∆t}_{\left(2\right)}$. The world lines of the of photons are shown in Figure 2. We then know that the two drawn lines are literally the world lines of the first photon and the final photon of the light pulse.

Believing that the two world lines besides the ${∆t}_{\left(1\right)}$ and ${∆t}_{\left(2\right)}$ are parallel, it is known that the time interval ${∆t}_{\left(1\right)}$ equals to that of ${∆t}_{\left(2\right)}$. As the light frequency being inversely proportional to proper time interval $∆\tau$, the proper forms of frequency ratio were written in some textbooks as [3,4]

${\displaystyle \frac{{\nu }_{\left(1\right)}}{{\nu }_{\left(2\right)}}}={\displaystyle \frac{{∆\tau }_{\left(2\right)}}{{∆\tau }_{\left(1\right)}}}={\displaystyle \frac{\sqrt{{g_{00}}_{\left(2\right)}}{∆t}_{\left(2\right)}}{\sqrt{{g_{00}}_{\left(1\right)}}{∆t}_{\left(1\right)}}}={\displaystyle \frac{\sqrt{{g_{00}}_{\left(2\right)}}}{\sqrt{{g_{00}}_{\left(1\right)}}}}\approx 1+{\displaystyle \frac{{\varnothing }_{\left(2\right)}-{\varnothing }_{\left(1\right)}}{m{c}^2}}$ (17)

where ${\nu }_{\left(1\right)}$ and ${\nu }_{\left(2\right)}$ are proper frequencies corresponding to position 1 and position 2, $g_{00}$ is time metric of Schwarzschild. The right hand side of this equation is an approximate result with Schwarzschild solution of metric $g_{00}$ in condition that $r_2>r_1\gg r^{*}$.

Thus, the so-called revisit redshift is

$z_{revisit}={\displaystyle \frac{{\nu }_{\left(1\right)}}{{\nu }_{\left(2\right)}}}-1\approx {\displaystyle \frac{∆\varnothing }{{mc}^2}}$ (18)

It is seemingly that the revisit form of equation for gravitational redshift was worked out.

But there are quite many errors in above equations. (i) The two world lines belong to the first photon and the final photon respectively, thus they might be controlled by emitter, so that the time intervals between the two lines do nothing with any light frequencies. (ii) Any time intervals between neighboring photons could be randomly assigned, so that these intervals also do nothing with any light frequencies. (iii) Frequency of a photon is the reciprocal of its photonic period and is the intrinsic property of a photon, so that it is independent to its positions relating to other photons and any variation of the frequency will not change its position in the pulse of photons. (iv) Detections of frequencies must involve with wave numbers and time intervals together, while this equation has made a mistake by comparing time intervals only. (v) It is said that the time intervals ${∆t}_{\left(1\right)}$ and ${∆t}_{\left(2\right)}$ do nothing with the physical events of frequency shift, they are just the records of the physical event of emission.

2.3. Further Investigation into the Revisit Gravitational Redshift

Following the rules in classical frames, the tensor of light wave period is a tensor with upper index

$T^0={\displaystyle \frac{dt}{dn}}$ (19)

where, $T^0$ is contra variant light period that is described by coordinate time, and $dt$ is coordinate time lasting in which the number of $dn$ waves may have traveled across a specific position. And the proper form of wave period

$T={\displaystyle \frac{d\tau }{dn}}$ (20)

where, $d\tau$ is proper time lasting for $dn$ number of waves to cross the position. So that there is

$T=e_0{T}^0 or T^0=e^{0}T$ (21)

where, $e_0$ is the first component of covariant time base, and it should be noted that the base ${\mathit{e}}_0$ is a vector but the component $e_0$ is not vector even though it is still a tensor. One can get more understandings for these expressions I would sponsor here and in followings.

In this way, we know that different values of the contra variant period and proper period correspond to a same physical issue. Then it leads to a frequency tensor

${\nu }_0={\displaystyle \frac{1}{T^0}}=e_0\nu ={\displaystyle \frac{dn}{dt}}$ (22)

We have seen that, ${\nu }_0$ is called covariant tensor traditionally, and $\nu$ is a proper tensor. This may have brought about confusions in that $\nu$ is actually covariant and yet ${\nu }_0$ has been named the name. I am not going to change the naming methodology thoroughly right now because that may cause more difficulties and sounds more trivial.

Generally, some pure one-order tensors seem to be infinite small quantities such as$dr$, but for ${\nu }_0$, it is $dn$ divided by $dt$, so that it is not an infinite small quantity. As for velocity tensors, they are really mixed tensors.

Theoretically, the covariant derivative of a frequency in a falling process into a center source can be written as

${\displaystyle \frac{D{\nu }_0}{\partial r}}={\displaystyle \frac{\partial {\nu }_0}{\partial r}}-{\Gamma }_{10}^0{\nu }_0$ (23)

where, ${\Gamma }_{\nu \mu }^{\lambda }$ is Christoffel symbols.

We know that, as has been presented in Eq. (15), the contra variant derivative is

${\displaystyle \frac{\partial {\nu }_0}{\partial r}}=-{\displaystyle \frac{r^{*}}{2r^2}}{{\nu }_0}_{(\infty )}$ (24)

Let us calculate the Christoffel symbols in Eq. (23) that

${\Gamma }_{10}^0={\displaystyle \frac{1}{2}}{g}^{0\lambda }({\displaystyle \frac{\partial g_{1\lambda }}{\partial x^0}}+{\displaystyle \frac{\partial g_{0\lambda }}{\partial x^1}}-{\displaystyle \frac{\partial g_{10}}{\partial x^{\lambda }}})$ (25)

The Einstein summation convention has been and will be adopt unless additional declarations.

It is found that only in the condition of $\lambda =0$ there is a nonvanishing item in the bracket of right hand side of Eq. (25), so that with Schwarzschild metrics it turns to be

${\Gamma }_{10}^0={\displaystyle \frac{1}{2}}{g}^{00}{\displaystyle \frac{\partial g_{00}}{\partial x^1}}={\displaystyle \frac{1}{2}}{(-1+{\displaystyle \frac{r^{*}}{r}})}^{-1}{(-1+{\displaystyle \frac{r^{*}}{r}})}^{\text{'}}={\displaystyle \frac{r^{*}}{2r^2}}(1+{\displaystyle \frac{r^{*}}{r-r^{*}}})$ (26)

The covariant derivative will be calculated to be

${\displaystyle \frac{D{\nu }_0}{\partial r}}=-{\displaystyle \frac{r^{*}}{{2r}^2}}{{\nu }_0}_{\left(\infty \right)}-{\displaystyle \frac{r^{*}}{2r^2}}\left(1+{\displaystyle \frac{r^{*}}{r-r^{*}}}\right){\nu }_0$$=-{\displaystyle \frac{r^{*}}{{2r}^2}}{{\nu }_0}_{\left(\infty \right)}-{\displaystyle \frac{r^{*}}{2r^2}}(1+{\displaystyle \frac{r^{*}}{r-r^{*}}})(1+{\displaystyle \frac{r^{*}}{2r}}){{\nu }_0}_{(\infty )}$ (27)

We could get an approximate solution for weak field that

${\displaystyle \frac{D{\nu }_0}{\partial r}}\approx 2{\displaystyle \frac{\partial {\nu }_0}{\partial r}}$ (28)

As we have seen, it shows that the values of covariant redshift doubles that of the contra variant redshift.

2.4. Additional Discussions on the Thought Experiment of Freefalling Elevator Cabin

The thought experiment that observer in freefalling elevator cabin will detect no frequency shift is usually employed to discuss the equivalent principle for the support of general covariance. But in fact, that issue does nothing with covariance. It is just because that the gravitational redshift happens to be offset by Doppler redshift. In fact, this experiment is a comprehensive event that relates both to gravitational redshift and gravitational acceleration.

We know that in a freefalling cabin, freefalling observer will not detect any frequency shift no matter the light ray emitter is on the bottom or on the top to emit up or down to the receiver. Nevertheless, even if the light ray is not vertical, freefalling observer would also observe no frequency shift in the cabin.

For a case that a light ray is emitted to the top with an angle $\theta$ to the vertical line

The time interval for light ray from bottom to the top is

$∆t={\displaystyle \frac{1}{c}}{\displaystyle \frac{∆H}{cos\theta }}$ (29)

And the velocity increase of freefall cabin is

$∆v=a∆t={\displaystyle \frac{g}{c}}{\displaystyle \frac{∆H}{cos\theta }}$ (30)

Then the velocity increase component at the direction of light ray

$∆v_l=∆vcos\theta =g{\displaystyle \frac{∆H}{c}}$ (31)

So that we get the Doppler redshift again as

$z_{\mathrm{D}}={\displaystyle \frac{∆v_l}{c}}={\displaystyle \frac{g∆H}{c^2}}={\displaystyle \frac{∆\varnothing }{m{c}^2}}$ (32)

In fact, the Doppler redshift for the detector in freefalling cabin could eliminate the gravitational frequency shift, even if the emitter is either outside of the cabin or with any low initial velocity. The real reason for non-detectable frequency shift in freefalling cabin is that the relative motion formed Doppler redshift just has a minus approximate value of gravitational frequency shift.

I prefer to put forward the case that the gravitational frequency shift cannot be eliminated by Doppler redshift. In the case that cabin has a relativistic initial velocity, the geometrical acceleration is not the total gravitational acceleration again that

$a=\xi g , \xi <1$ (33)

Thus, for light rays passing across the cabin there is the Doppler velocity of detector

$∆v_l=a∆t=\xi g{\displaystyle \frac{∆H}{c}}$ (34)

so that

$z_{\mathrm{D}}={\displaystyle \frac{∆v_l}{c}}=\xi {\displaystyle \frac{g∆H}{c^2}}=\xi {\displaystyle \frac{∆\varnothing }{m{c}^2}}$ (35)

While the gravitational frequency is still the form

$z_g={\displaystyle \frac{g∆H}{c^2}}={\displaystyle \frac{∆\varnothing }{m{c}^2}}$ (36)

so that in this case

$z_{\mathrm{D}}\ne z_g$ (37)

We now know that in some situations in freefalling cabin one could detect frequency shift again, so that the thought experiment cannot support general covariance thoroughly. Of course, one can continue to argue that relativistic motion may bring about more sophisticated conditions on frequency shift.

2.5. An Investigation into Gravitational Acceleration

For a freefalling massive matter in gravitational field, the component of the velocity at the direction of radius of center source is

$V^1={\displaystyle \frac{d{x}^1}{d\tau }}$ (38)

There is the covariant derivative at one of coordinate direction

${\displaystyle \frac{D{V}^1}{\partial \lambda }}={\displaystyle \frac{\partial V^1}{\partial \lambda }}+{\Gamma }_{\lambda \mu }^1{V}^{\mu }$ (39)

Because $d{x}^0=cdt$, and $dt=e^{0}d\tau$, where $e^0$ is the nonvanishing component of the base ${\mathit{e}}^0$. Thus, the covariant derivative by $\tau$ is

${\displaystyle \frac{D{V}^1}{d\tau }}={\displaystyle \frac{d{V}^1}{d\tau }}+{\displaystyle \frac{d{x}^0}{d\tau }}{\Gamma }_{0\mu }^1{V}^{\mu }=a^1+c{e}^0{\Gamma }_{0\mu }^1{V}^{\mu }$ (40)

where, $a^1={\displaystyle \frac{d{V}^1}{d\tau }}$ is the contra variant acceleration of the matter, $c$ is light speed.

NB, accelerations we have and will discuss refer to geometrical accelerations, which will be something different from gravity $g$, in that the latter sometimes may also be called gravitational accelerations in some writings but in fact matters may not experience accelerating up to that.

With the equation of Christoffel symbols

${\Gamma }_{0\lambda }^1={\displaystyle \frac{1}{2}}{g}^{1\rho }({\displaystyle \frac{\partial g_{0\rho }}{\partial x^{\lambda }}}+{\displaystyle \frac{\partial g_{\lambda \rho }}{\partial x^0}}-{\displaystyle \frac{\partial g_{0\lambda }}{\partial x^{\rho }}})$ (41)

case $\lambda =1$ in this equation, there is ${\Gamma }_{01}^1=0$. Then considering the condition of $\mathsf{\lambda }=0$, it is

${\Gamma }_{00}^1={\displaystyle \frac{1}{2}}{g}^{1\rho }({\displaystyle \frac{\partial g_{0\rho }}{\partial x^0}}+{\displaystyle \frac{\partial g_{0\rho }}{\partial x^0}}-{\displaystyle \frac{\partial g_{00}}{\partial x^{\rho }}})$ (42)

In this condition, only in the case of $\rho =1$ there is the nonvanishing item in the bracket of right hand side, so that

${\Gamma }_{00}^1={\displaystyle \frac{1}{2}}{g}^{11}(-{\displaystyle \frac{\partial g_{00}}{\partial x^1}})={\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{r^{*}}{r}}){(1-{\displaystyle \frac{r^{*}}{r}})}^{\text{'}}={\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{r^{*}}{r^2}}$ (43)

And with $V^0={\displaystyle \frac{d{x}^0}{d\tau }}={\displaystyle \frac{cdt}{d\tau }}=e^{0}c$, Eq. (40) turns to be

${\displaystyle \frac{D{V}^1}{d\tau }}=a^1+c{e}^0{\Gamma }_{00}^1{V}^0=a^1+e^0{e}^0{c}^2(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{r^{*}}{{2r}^2}}$ (44)

As a matter freefalls on to the earth, its acceleration could be calculated to be

$a^1=-e^0{e}^0{\displaystyle \frac{GM}{r^2}}=-e^0{e}^0{c}^2{\displaystyle \frac{r^{*}}{2r^2}}$ (45)

Thus, there is the weak field solution

${\displaystyle \frac{D{V}^1}{d\tau }}\approx 0$ (46)

2.6. Discussions and Controversies

Now we have got more complex results that the revisit gravitational redshift calculated doubles that of contra variant value while covariant acceleration of freefalling goes to zero. The latter seems to fit with general covariance but the previous does not. And there is still a problem that revisit gravitational redshift solved in the way of covariant derivation goes contradictory to classical solution. Moreover, the minus form of $g_{00}$ also involves more matters that have caused the result of zero acceleration, deserving of further discussions in next sections.

It is extraordinary that the covariant derivative of light frequency goes nonvanishing in the view of general covariance. Even more, it is investigated that covariant derivative analysis shows that the classical solution of revisit redshift may be false in that the frequency has been wrong defined. Some ones may argue that the frequency is not a tensor, but that makes no sense because light frequency is the reciprocal of its wave period which involves with time coordinate.

What I urgently want to say is that these discussions are not enough. The most significant problem is that, the item in original covariant differential in Eq. (44) that matter’s velocities multiplied with the base’s differential, has been calculated to do nothing with the realistic velocity. We should know that the multiplied item in Eq. (39) originally indicates a base variation ratio multiplied with the very tensors, but the final equation has given up the effects of initial velocity that does lead to contradictions, and the time speed $V^0$ is a virtual velocity which might have been abused. These contradictions really bothered me until it is occasionally gone through one day, that the real problem is deeply hidden in the equations of Christoffel symbols.

Notwithstanding, a differential of velocity is the differential of that on the trajectory of matter’s motion. Thus, the covariant time derivatives cannot be treated directly as ordinary derivatives anymore as in Eq. (40). We are going to carry out detailed discussions on trajectory derivatives in next sections so that to interpret covariant time derivatives correctly.

3. Theoretical Investigations on Christoffel Symbols

3.1. Classical Equations of Christoffel Symbols

Christoffel symbols have been defined in the equation

${\displaystyle \frac{\partial {\mathit{e}}^{\mu }}{\partial x^v}}=-{\Gamma }_{v\lambda }^{\mu }{\mathit{e}}^{\lambda }$ (47)

There is nothing wrong with the definition in that the derivative of a base must have a direction and so that to be written as a linear combination of the total bases. The key problem is what the Christoffel symbols are.

In this and following sections, all symbols of vectors and matrix would be bold written while their components and that of other quantities may be simplified written, no matter they are tensors or not.

In most conditions, Christoffel symbols could be discussed by the derivation of metrics as

${\displaystyle \frac{\partial g_{\mu \nu }}{\partial x^{\lambda }}}={\displaystyle \frac{\partial }{{\partial x}^{\lambda }}}({\mathit{e}}_{\mu }\bullet {\mathit{e}}_{\nu })={\displaystyle \frac{\partial {\mathit{e}}_{\mu }}{\partial x^{\lambda }}}\bullet {\mathit{e}}_{\nu }+{\mathit{e}}_{\mu }\bullet {\displaystyle \frac{{\partial \mathit{e}}_{\nu }}{{\partial x}^{\lambda }}}={\Gamma }_{\mu \lambda }^{\rho }{\mathit{e}}_{\rho }\bullet {\mathit{e}}_{\nu }+{\Gamma }_{\nu \lambda }^{\rho }{\mathit{e}}_{\rho }\bullet {\mathit{e}}_{\mu }$ (48)

For the derivative forms with alternative indexes mathematically, there will be

${\displaystyle \frac{\partial g_{\mu \nu }}{\partial x^{\lambda }}}-{\Gamma }_{\mu \lambda }^{\rho }{g}_{\rho \nu }-{\Gamma }_{\nu \lambda }^{\rho }{g}_{\rho \mu }=0$ (49)

${\displaystyle \frac{\partial g_{\lambda \nu }}{\partial x^{\mu }}}-{\Gamma }_{\lambda \mu }^{\rho }{g}_{\rho \nu }-{\Gamma }_{\nu \mu }^{\rho }{g}_{\rho \lambda }=0$ (50)

${\displaystyle \frac{\partial g_{\mu \lambda }}{\partial x^{\nu }}}-{\Gamma }_{\mu \nu }^{\rho }{g}_{\rho \lambda }-{\Gamma }_{\lambda \nu }^{\rho }{g}_{\rho \mu }=0$ (51)

In the case the so-called torsions $S_{\mu \lambda }={\Gamma }_{\mu \nu }^{\rho }-{\Gamma }_{\nu \mu }^{\rho }$ is set zero, the summation of the previous two equations minus the last one that

${\displaystyle \frac{\partial g_{\mu \nu }}{\partial x^{\lambda }}}+{\displaystyle \frac{\partial g_{\lambda \nu }}{\partial x^{\mu }}}-{\displaystyle \frac{\partial g_{\mu \lambda }}{\partial x^{\nu }}}-2{\Gamma }_{\mu \lambda }^{\rho }{g}_{\rho \nu }=0$ (52)

Thereafter the equations of Christoffel symbols will be solved as [2,3,5]

${\Gamma }_{\mu \lambda }^{\rho }={\displaystyle \frac{1}{2}}{g}^{\rho \nu }({\displaystyle \frac{\partial g_{\mu \nu }}{\partial x^{\lambda }}}+{\displaystyle \frac{\partial g_{\lambda \nu }}{\partial x^{\mu }}}-{\displaystyle \frac{\partial g_{\mu \lambda }}{\partial x^{\nu }}})$ (53)

Generally, Eq. 49 - Eq. 51 could also be rewritten as the original forms

${\displaystyle \frac{\partial g_{\mu \nu }}{\partial x^{\lambda }}}-{\displaystyle \frac{\partial {\mathit{e}}_{\mu }}{\partial x^{\lambda }}}\bullet {\mathit{e}}_{\nu }-{\displaystyle \frac{\partial {\mathit{e}}_{\nu }}{\partial x^{\lambda }}}\bullet {\mathit{e}}_{\mu }=0$ (54)

${\displaystyle \frac{\partial g_{\lambda \nu }}{\partial x^{\mu }}}-{\displaystyle \frac{\partial {\mathit{e}}_{\lambda }}{\partial x^{\mu }}}\bullet {\mathit{e}}_{\nu }-{\displaystyle \frac{\partial {\mathit{e}}_{\nu }}{\partial x^{\mu }}}\bullet {\mathit{e}}_{\lambda }=0$ (55)

${\displaystyle \frac{\partial g_{\mu \lambda }}{\partial x^{\nu }}}-{\displaystyle \frac{\partial {\mathit{e}}_{\mu }}{\partial x^{\nu }}}\bullet {\mathit{e}}_{\lambda }-{\displaystyle \frac{\partial {\mathit{e}}_{\lambda }}{\partial x^{\nu }}}\bullet {\mathit{e}}_{\mu }=0$ (56)

We will find that in some conditions the torsions do not always equal to zero. It is said that the mixed derivatives of bases ${\displaystyle \frac{\partial {\mathit{e}}_{\mu }}{\partial x^{\nu }}}$ and ${\displaystyle \frac{\partial {\mathit{e}}_{\nu }}{\partial x^{\mu }}}$ do not always equal, and then the Christoffel symbols with mixed subscripts ${\mathsf{\Gamma }}_{\mathsf{\mu }\mathsf{\nu }}^{\mathsf{\rho }}$ and ${\mathsf{\Gamma }}_{\mathsf{\nu }\mathsf{\mu }}^{\mathsf{\rho }}$ do not always equal, so that the Eq. (53) might be invalid in those conditions.

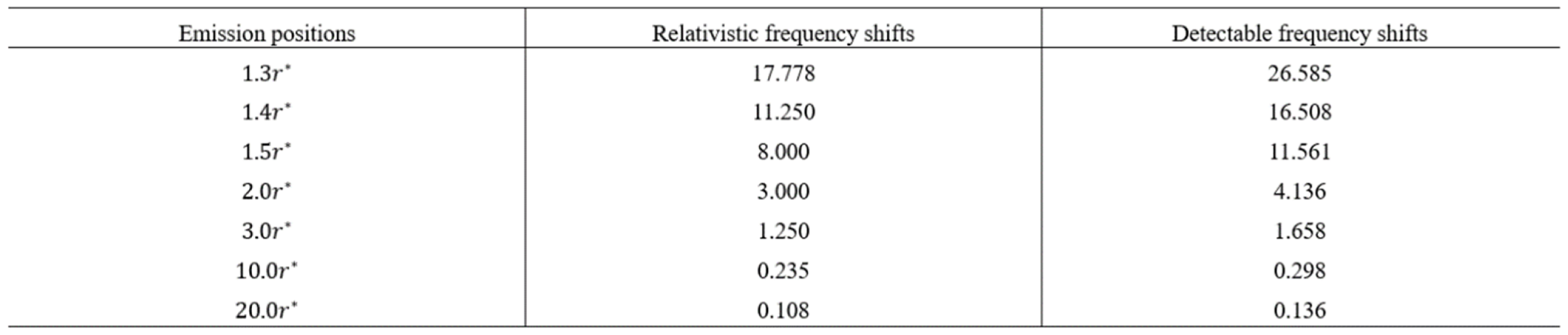
3.2. The Inequality of Christoffel Symbols of Mixed Subscripts

In Riemannian differential geometry, the equality of Christoffel symbols of mixed subscripts is usually adopt the doctrine. But no forceful researches could provide reliable supports. The truth is that the problem of mixed derivatives of bases in a Riemannian space are far different from the problem of normal mixed derivatives of a 3-dimensional surface in Euclidean geometry.

We could find out the truth that in the deduction of ${\Gamma }_{00}^1$ in Eq. (43), ${\displaystyle \frac{\partial g_{00}}{\partial x^1}}$ has been used instead of ${\displaystyle \frac{\partial g_{11}}{\partial x^0}}$ so that to gain ${\Gamma }_{00}^1={\displaystyle \frac{1}{2}}{g}^{11}(-{\displaystyle \frac{\partial g_{00}}{\partial x^1}})$. But we can easily calculate that ${\displaystyle \frac{\partial {\mathit{e}}_0}{\partial x^1}}$ and ${\displaystyle \frac{\partial {\mathit{e}}_1}{\partial x^0}}$ are not equal. It is said that the Eq. (43) could lead to nonvanishing value of ${\Gamma }_{00}^1$, which really relates to time derivatives of bases that must be determined to be zero in rest field. We might have found out the problems.

3.2.1. Coordinate Transformations and Bases

Any points in a Riemannian space of Riemannian manifold of dimension $n$ has a neighborhood homeomorphic to a subset of Euclidean space of dimension $n$, so that there must be probable maps between the neighborhoods and the corresponding subsets. It is just to say that the coordinates of any points in Riemannian space could be expressed with the coordinates of corresponding points of Euclidean space, and reversely. If a part or the entire of a Riemannian space are continuous and differentiable, Euclidean coordinate lines could be drawn in the part or the entire of the Riemannian space. On the other side, coordinate lines of Riemannian space could also be drawn in the corresponding Euclidean space. For convenience, the Riemannian space could be called covariant space, and the corresponding Euclidean space could be called contra variant space. A contra variant space is curved in the view of its covariant space, and the covariant space is also curved in the view of contra variant space.

It is obvious that transformations of spaces are actual coordinate transformations. These transformations could happen between covariant space and contra variant space, as well as they could happen among homeomorphic Riemannian spaces. Coordinate transformations may perform in the way with unequal metrics as well as the way with equal metrics.

The more effective method for coordinate transformation is to define bases and distances for spaces. Two examples would be presented firstly for definitions and for following discussions.

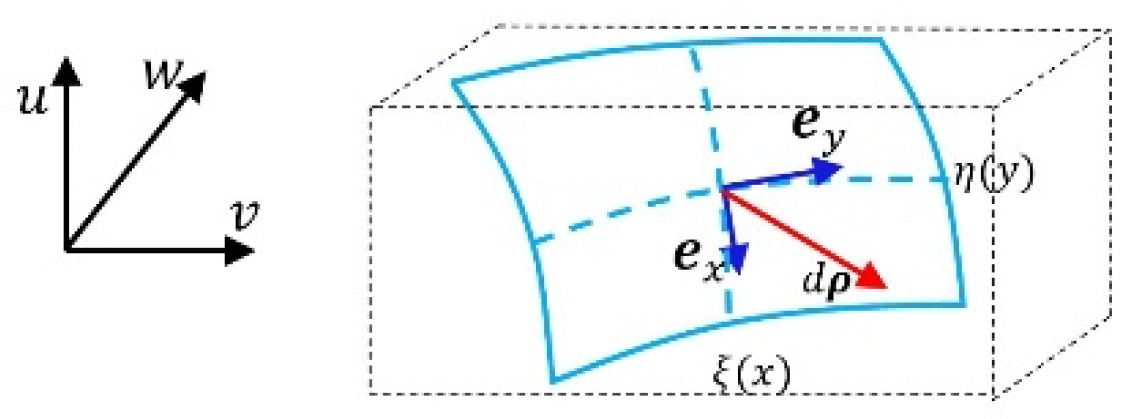
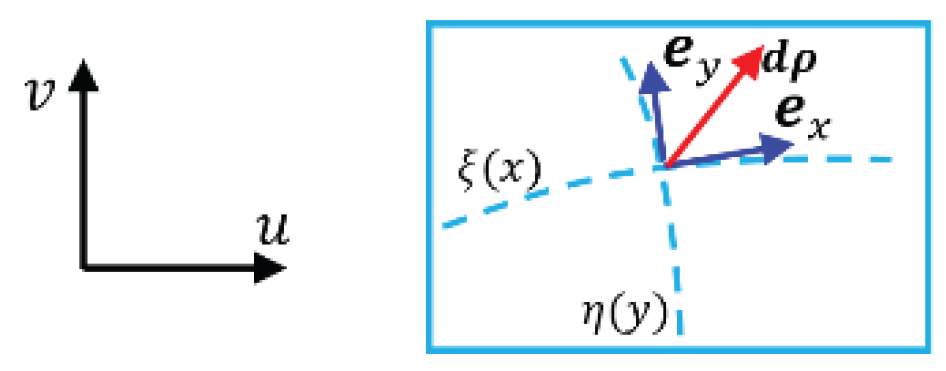
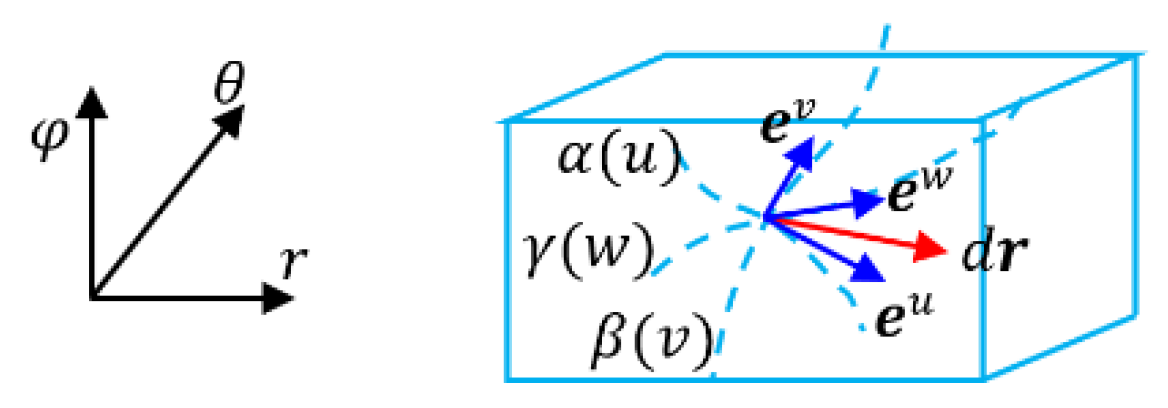
Example 1: Bases of Riemannian manifold of super surface

The derivative vectors of 3-dimensional surfaces were usually employed to form bases in classical differential geometry. The curve space has an extra dimension than a plane space that could be called the super surface. The Riemannian manifold of the super surface in the 3-dimensional space $\left(u,v,w\right)$ would have a homeomorphic Euclidean space $\left(x,y\right)$ in the space $\left(x,y,z\right)$. The coordinate lines $x$ and $y$ in contra variant space could be transformed to be $\xi \left(x\right)$ and $\eta \left(y\right)$ in covariant space, while $u$, $v$ and $w$ in covariant space be transformed to be $\alpha \left(u\right)$, $\beta \left(v\right)$ and $\gamma \left(w\right)$ in the space $\left(x,y,z\right)$ as shown in Figure 3 andFigure 4.

as contra variant space in 3-dimensional space.

The super surface could be determined by a vector function $\mathit{\rho }$$\mathit{\rho }={\left.\mathit{\rho }\left(u,v,w\right)\right|}_{2 of variables independent}$ (57)

And the function could also be written as

$\mathit{\rho }=\mathit{\rho }\left(\xi ,\eta \right)$ (58)

or

$\mathit{\rho }=\mathit{\rho }\left(x,y\right)$ (59)

At the same time, the contra variant space could be defined by $\mathit{r}$$\mathit{r}={\left.\mathit{r}\left(x,y,z\right)\right|}_{z=const.}={\left.\mathit{r}\left(\alpha ,\beta ,\gamma \right)\right|}_{2 of variables independent}=\mathit{r}\left(x,y\right)=\mathit{r}\left(\xi ,\eta \right)$ (60)

There will be varieties of available ways to develop the expressions of bases and distances. I prefer to put forward the followings might as well.

The way in super space:

In super space, the differential $d\mathit{\rho }$ has 3 components

$d\mathit{\rho }=\left(\begin{array}{c}du\\ dv\\ dw\end{array}\right)$ (61)

That of differential $d\mathit{r}$ could be simplified to be 2 dimensional because it just locates in the space $\left(x,y\right)$$d\mathit{r}=\left(\begin{array}{c}dx\\ dy\end{array}\right)$ (62)

To define a set of covariant bases for a position in covariant space by

${\mathit{e}}_x={\displaystyle \frac{\partial \mathit{\rho }}{\partial x}}, {\mathit{e}}_y={\displaystyle \frac{\partial \mathit{\rho }}{\partial y}}$ (63)

It should be pointed out that, in some publications, coordinate and vector symbols have been used reversely like $d\mathit{\rho }$ and $d\mathit{r}$, which would have brought about confusions.

In covariant space, the differential $d\mathit{\rho }$ expressed by $d\mathit{r}$ with covariant bases

$d\mathit{\rho }=dx{\mathit{e}}_x+dy{\mathit{e}}_y$ (64)

Differential distance could be defined as

$d{s}^2=d{u}^2+d{v}^2+d{w}^2=d\mathit{\rho }\bullet d\mathit{\rho }=(dx{\mathit{e}}_x+dy{\mathit{e}}_y)\bullet (dx{\mathit{e}}_x+dy{\mathit{e}}_y)$ (65)

If the bases are orthogonal, there is

$d{s}^2={\mathit{e}}_x\bullet {\mathit{e}}_{x}d{x}^2+{\mathit{e}}_y\bullet {\mathit{e}}_{y}d{y}^2$ (66)

We have seen that the covariant bases are defined in covariant space to help contra variant coordinates to form covariant distances.

There are more complexities for a transformation between a super surface in 3-dimensional space and $R^2$ that the 2 covariant bases would have 3 components

${\mathit{e}}_x=\left(\begin{array}{c}{\displaystyle \frac{\partial u}{\partial x}}\\ {\displaystyle \frac{\partial v}{\partial x}}\\ {\displaystyle \frac{\partial w}{\partial x}}\end{array}\right), {\mathit{e}}_y=\left(\begin{array}{c}{\displaystyle \frac{\partial u}{\partial y}}\\ {\displaystyle \frac{\partial v}{\partial y}}\\ {\displaystyle \frac{\partial w}{\partial y}}\end{array}\right)$ (67)

Define the contra variant bases for a point in the plane that

${\mathit{e}}^u={\displaystyle \frac{\partial \mathit{r}}{\partial u}}, {\mathit{e}}^v={\displaystyle \frac{\partial \mathit{r}}{\partial v}}, {\mathit{e}}^w={\displaystyle \frac{\partial \mathit{r}}{\partial w}}$ (68)

The 3 contra variant bases all have 2 components as

${\mathit{e}}^u=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial u}}\\ {\displaystyle \frac{\partial y}{\partial u}}\end{array}\right), {\mathit{e}}^v=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial v}}\\ {\displaystyle \frac{\partial y}{\partial v}}\end{array}\right), {\mathit{e}}^w=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial w}}\\ {\displaystyle \frac{\partial y}{\partial w}}\end{array}\right)$ (69)

The differential $d\mathit{r}$ expressed by $d\mathit{\rho }$ in contra variant space

$d\mathit{r}=du{\mathit{e}}^u+dv{\mathit{e}}^v+dw{\mathit{e}}^w$ (70)

Of course, one can create transformation matrix to perform the relationship between $d\mathit{r}$ and $d\mathit{\rho }$ directly.

The distance could be defined as

$d{\varsigma }^2=d{x}^2+d{y}^2=d\mathit{r}\bullet d\mathit{r}=(du{\mathit{e}}^u+dv{\mathit{e}}^v+d{\mathit{e}}^w)\bullet (du{\mathit{e}}^u+dv{\mathit{e}}^v+d{\mathit{e}}^w)$ (71)

If the bases are orthogonal

$d{\varsigma }^2={\mathit{e}}^u\bullet {\mathit{e}}^{u}d{u}^2+{\mathit{e}}^v\bullet {\mathit{e}}^{v}d{v}^2+{\mathit{e}}^w\bullet {\mathit{e}}^{w}d{w}^2$ (72)

One could imagine that this condition you cannot give the relationship of metrics that $g_{ii}$ equals to $1/g^{ii}$, in that the covariant bases have 3 components and contra variant bases have 2.

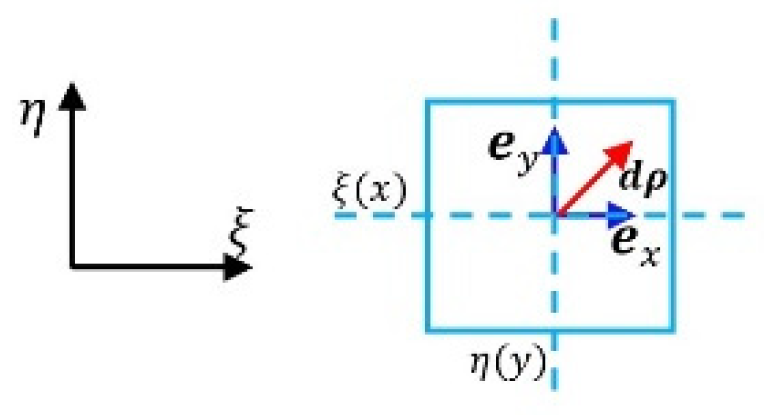
The way in tangent space:

Consequently, the issues could be simplified in tangent spaces. At a position $\mathit{\rho }$ in the covariant space, there is a neighborhood which will be labeled with coordinate lines of $\xi \left(x\right)$ and $\eta \left(y\right)$, at the same time at the position $\mathit{r}$, there is a corresponding neighborhood in contra variant space labeled with coordinate lines of $x$ and $y$, as shown in Figure 5 and Figure 6. Generally, coordinate lines could be set orthogonal. In most of publications, $\xi \left(x\right)$ and $\eta \left(y\right)$ were seen as $x$ and $y$, but one should realize that the difference really matters.

One could define the differential vector in covariant space

$d\mathit{\rho }=\left(\begin{array}{c}d\xi \\ d\eta \end{array}\right)$ (73)

As a result, the bases

${\mathit{e}}_x={\displaystyle \frac{\partial \mathit{\rho }}{\partial x}}=\left(\begin{array}{c}{\displaystyle \frac{\partial \xi }{\partial x}}\\ {\displaystyle \frac{\partial \eta }{\partial x}}\end{array}\right), {\mathit{e}}_y={\displaystyle \frac{\partial \mathit{\rho }}{\partial y}}=\left(\begin{array}{c}{\displaystyle \frac{\partial \xi }{\partial y}}\\ {\displaystyle \frac{\partial \eta }{\partial y}}\end{array}\right)$ (74)

Again, there is the distance

$d{s}^2=d{\xi }^2+d{\eta }^2=d\mathit{\rho }\bullet d\mathit{\rho }={\mathit{e}}_x\bullet {\mathit{e}}_{x}d{x}^2+{\mathit{e}}_y\bullet {\mathit{e}}_{y}d{y}^2$ (75)

The differential $d\mathit{r}$ keep the form as Eq. (62), so that the contra variant bases could be defined as

${\mathit{e}}^{\xi }={\displaystyle \frac{\partial \mathit{r}}{\partial \xi }}=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial \xi }}\\ {\displaystyle \frac{\partial y}{\partial \xi }}\end{array}\right), {\mathit{e}}^{\eta }={\displaystyle \frac{\partial \mathit{r}}{\partial \eta }}=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial \eta }}\\ {\displaystyle \frac{\partial y}{\partial \eta }}\end{array}\right)$ (76)

Also, there is

$d{\varsigma }^2=d{x}^2+d{y}^2=d\mathit{r}\bullet d\mathit{r}={\mathit{e}}^{\xi }\bullet {\mathit{e}}^{\xi }d{\xi }^2+{\mathit{e}}^{\eta }\bullet {\mathit{e}}^{\eta }d{\eta }^2$ (77)

In this case, the relationship of metrics go harmonized that $g_{ii}$ equals to $1/g^{ii}$. It should be pointed out that the ways of expressions of bases are all equivalent except that the substitutions of coordinate lines $\xi$ and $\eta$ might have hidden some information of super surface, so that I would like to make analysis within super space in most cases.

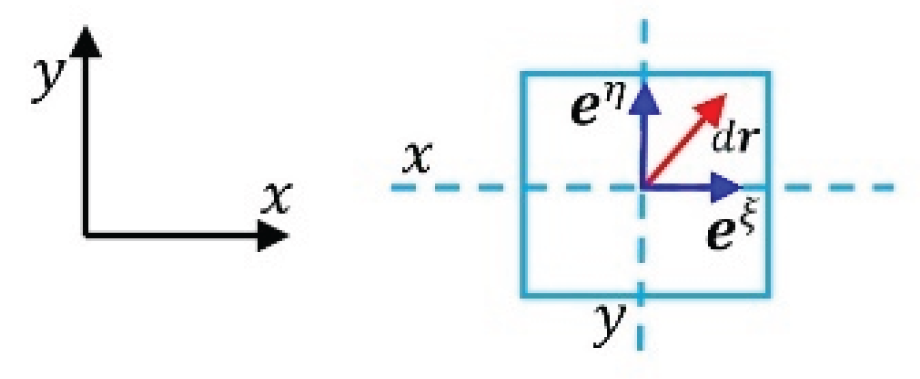
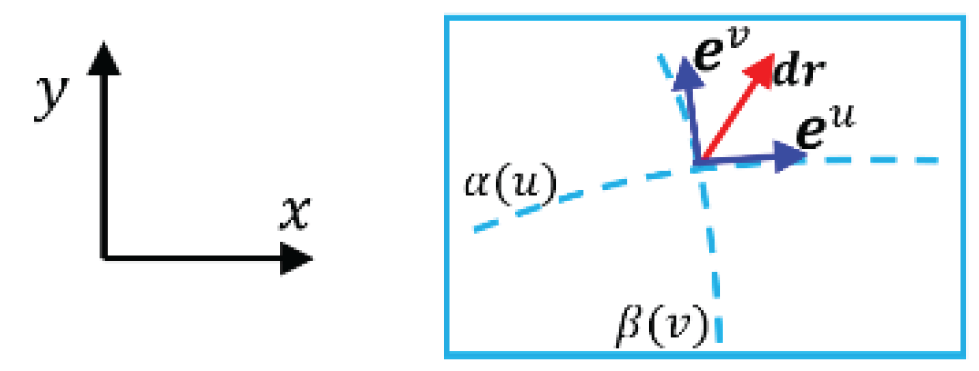
Example 2: Bases of Riemannian manifold of equal dimension

As a Riemanian manifold has equal dimension with its contra variant space, it could be called equal dimension manifold. A plane space $\left(u,v\right)$ maps to a plane space $\left(x,y\right)$ could be taken for granted, as shown in Figure 7 and Figure 8.

A differential vector in covariant space is

$d\mathit{r}=\left(\begin{array}{c}dx\\ dy\end{array}\right)$ (78)

The differential vector in contra variant space is

$d\mathit{\rho }=\left(\begin{array}{c}du\\ dv\end{array}\right)$ (79)

Thus, the definition of contra variant bases could be

${\mathit{e}}^u={\displaystyle \frac{\partial \mathit{r}}{\partial u}}, {\mathit{e}}^v={\displaystyle \frac{\partial \mathit{r}}{\partial v}}$ (80)

To express $d\mathit{r}$ with $d\mathit{\rho }$$d\mathit{r}=du{\mathit{e}}^u+dv{\mathit{e}}^v$ (81)

Also, there is the definition of covariant bases

${\mathit{e}}_x={\displaystyle \frac{\partial \mathit{\rho }}{\partial x}}, {\mathit{e}}_y={\displaystyle \frac{\partial \mathit{\rho }}{\partial y}}$ (82)

So that the expression of $d\mathit{\rho }$ by $d\mathit{r}$ should be

$d\mathit{\rho }=dx{\mathit{e}}_x+dy{\mathit{e}}_y$ (83)

Something different is that a covariant base has 2 components

${\mathit{e}}_x=\left(\begin{array}{c}{\displaystyle \frac{\partial u}{\partial x}}\\ {\displaystyle \frac{\partial v}{\partial x}}\end{array}\right), {\mathit{e}}_y=\left(\begin{array}{c}{\displaystyle \frac{\partial u}{\partial y}}\\ {\displaystyle \frac{\partial v}{\partial y}}\end{array}\right)$ (84)

And a contra variant base also has 2 components

${\mathit{e}}^u=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial u}}\\ {\displaystyle \frac{\partial y}{\partial u}}\end{array}\right), {\mathit{e}}^v=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial v}}\\ {\displaystyle \frac{\partial y}{\partial v}}\end{array}\right)$ (85)

In the case that bases are orthogonal, the distance

$d{s}^2=d{u}^2+d{v}^2=d\mathit{\rho }\bullet d\mathit{\rho }={\mathit{e}}_x\bullet {\mathit{e}}_{x}d{x}^2+{\mathit{e}}_y\bullet {\mathit{e}}_{y}d{y}^2$ (86)

and

$d{\varsigma }^2=d{x}^2+d{y}^2=d\mathit{r}\bullet d\mathit{r}={\mathit{e}}^u\bullet {\mathit{e}}^{u}d{u}^2+{\mathit{e}}^v\bullet {\mathit{e}}^{v}d{v}^2$ (87)

3.2.2. Inequalities of Mixed Derivatives of Bases

Now it is the time to carry out the first discussion on the inequality of mixed derivatives of bases. The mixed derivatives of bases are just special defined for bases alternative derivations. As transformation from contra variant space to covariant space is concerned, the covariant bases could be considered to be derivated by the coordinate lines in chain rule

${\mathit{e}}_x={\displaystyle \frac{\partial \mathit{\rho }}{\partial x}}={\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}{\displaystyle \frac{\partial \xi }{\partial x}}, {\mathit{e}}_y={\displaystyle \frac{\partial \mathit{\rho }}{\partial y}}={\displaystyle \frac{\partial \mathit{r}}{\partial \eta }}{\displaystyle \frac{\partial \eta }{\partial y}}$ (88)

where, ${\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}$ and ${\displaystyle \frac{\partial \mathit{\rho }}{\partial \eta }}$ are the direction derivatives along the coordinate lines $\xi \left(x\right)$ and $\eta \left(y\right)$ in covariant space, and $d\xi$ and $d\eta$ are their differential lengths in covariant space, which could be called the covariant lengths. And there will be a setting that Einstein summation convention does not act on double $d\xi$ and double $d\eta$.

It should be pointed out that, in most mathematics and physics, mixed derivatives being confirmed to be equal is because in the Eq. (88) $dx$ and $dy$ is incorrectly understood to be the differential length in covariant space $\left(u,v,w\right)$, but they are really the lengths in contra variant space $\left(x,y,z\right)$. That is the reason we have carried out the concept of covariant length $d\xi$ and $d\eta$.

Thus, the mixed derivatives will be

${\displaystyle \frac{\partial {\mathit{e}}_x}{\partial y}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \xi \partial \eta }}{\displaystyle \frac{\partial \xi }{\partial x}}{\displaystyle \frac{\partial \eta }{\partial y}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}{\displaystyle \frac{{\partial }^2\xi }{\partial x\partial y}}$ (89)

and

${\displaystyle \frac{\partial {\mathit{e}}_y}{\partial x}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \eta \partial \xi }}{\displaystyle \frac{\partial \eta }{\partial y}}{\displaystyle \frac{\partial \xi }{\partial x}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial \eta }}{\displaystyle \frac{{\partial }^2\eta }{\partial y\partial x}}$ (90)

Consequently 3 conditions could be focused on:

Condition 1:

If there is an equality between the first items of the two equations that

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \xi \partial \eta }}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \eta \partial \xi }}$ (91)

For example, in the super surface, the mixed derivatives of course have the equality just as the equality of normal mixed derivatives of a 3-dimensional surface in a Euclidean space.

In this case and if there is another equality for the last items of the two equations that

${\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}{\displaystyle \frac{{\partial }^2\xi }{\partial x\partial y}}={\displaystyle \frac{\partial \mathit{\rho }}{\partial \eta }}{\displaystyle \frac{{\partial }^2\eta }{\partial y\partial x}}$ (92)

Then that must come to the conclusion

${\displaystyle \frac{\partial {\mathit{e}}_x}{\partial x}}={\displaystyle \frac{\partial {\mathit{e}}_y}{\partial y}}$ (93)

Otherwise, that depends.

It should be pointed out that ${\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}$ and ${\displaystyle \frac{\partial \mathit{\rho }}{\partial \eta }}$ do not equal in general conditions because they have different directions and, in most cases, they are usually set orthogonal, so that if that equality of Eq. (92) happens, it asks for

${\displaystyle \frac{{\partial }^2\xi }{\partial x\partial y}}={\displaystyle \frac{{\partial }^2\eta }{\partial y\partial x}}=0$ (94)

We will see that in some cases it is really well satisfied.

Condition 2:

Most special if

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \xi \partial \eta }}\ne {\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \eta \partial \xi }}$ (95)

that indicate the first items of the two equations are not equal, but at the same time if the total equations are still equal that

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \xi \partial \eta }}{\displaystyle \frac{\partial \xi }{\partial x}}{\displaystyle \frac{\partial \eta }{\partial y}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}{\displaystyle \frac{{\partial }^2\xi }{\partial x\partial y}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \eta \partial \xi }}{\displaystyle \frac{\partial \eta }{\partial y}}{\displaystyle \frac{\partial \xi }{\partial x}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial \eta }}{\displaystyle \frac{{\partial }^2\eta }{\partial y\partial x}}$ (96)

We will still obtain the equality that

${\displaystyle \frac{\partial {\mathit{e}}_x}{\partial x}}={\displaystyle \frac{\partial {\mathit{e}}_y}{\partial y}}$ (97)

Condition 3:

This is the condition after the previous two conditions and else to them. Generally if

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \xi \partial \eta }}{\displaystyle \frac{\partial \xi }{\partial x}}{\displaystyle \frac{\partial \eta }{\partial y}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial \xi }}{\displaystyle \frac{{\partial }^2\xi }{\partial x\partial y}}\ne {\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial \eta \partial \xi }}{\displaystyle \frac{\partial \eta }{\partial y}}{\displaystyle \frac{\partial \xi }{\partial x}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial \eta }}{\displaystyle \frac{{\partial }^2\eta }{\partial y\partial x}}$ (98)

No matter the first items of the two equations are equal or not, the mixed derivatives will perform inequality

${\displaystyle \frac{\partial {\mathit{e}}_x}{\partial x}}\ne {\displaystyle \frac{\partial {\mathit{e}}_y}{\partial y}}$ (99)

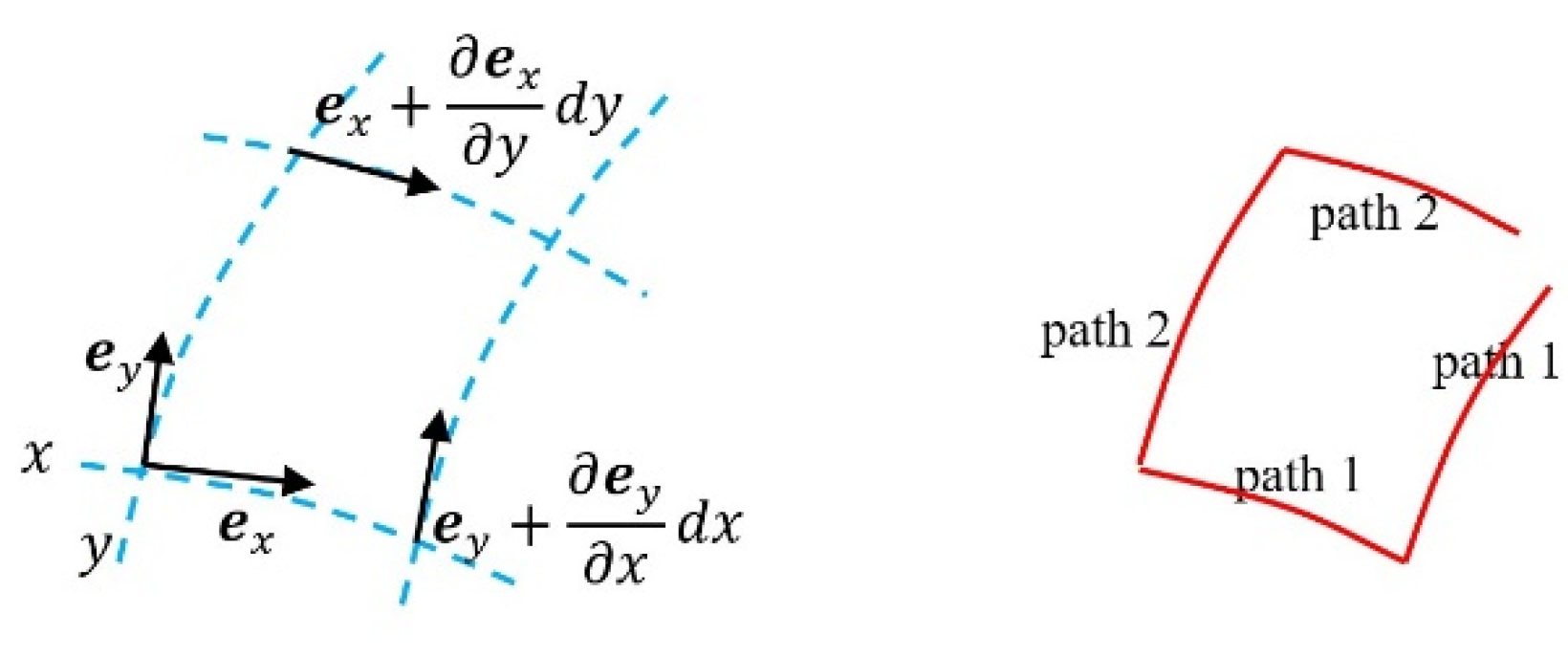
Then, turn to the issue of geometrical influence that the inequality of mixed derivatives will cause closure errors [6,7]. I prefer to give a brief presentation. Consider a differential in a curve line coordinate system expressed by bases along different coordinate paths as shown in Figure 9 that

in path 1,

${\left(d\mathit{\rho }\right)}_1={\int }_x^{x+dx}{\mathit{e}}_{x}dx+{\int }_y^{y+dy}({\mathit{e}}_y+{\displaystyle \frac{\partial {\mathit{e}}_y}{\partial x}}dx)dy$ (100)

The irregular expressions of same symbols of integral variables and integral range could be adopted in special cases.

By Taylor’s approximation, it could be written as

${\left(d\mathit{\rho }\right)}_1\approx {\mathit{e}}_{x}dx+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial {\mathit{e}}_x}{\partial x}}d{x}^2+{\mathit{e}}_{y}dy+{\displaystyle \frac{\partial {\mathit{e}}_y}{\partial x}}dxdy+{\displaystyle \frac{1}{2}}({\displaystyle \frac{\partial {\mathit{e}}_y}{\partial y}}+{\displaystyle \frac{\partial {\mathit{e}}_y}{\partial x\partial y}}dx)d{y}^2$ (101)

We could also get the differential in path 2,

${\left(d\mathit{\rho }\right)}_2\approx {\mathit{e}}_{y}dy+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial {\mathit{e}}_y}{\partial y}}d{y}^2+{\mathit{e}}_{x}dx+{\displaystyle \frac{\partial {\mathit{e}}_x}{\partial y}}dydx+{\displaystyle \frac{1}{2}}({\displaystyle \frac{\partial {\mathit{e}}_x}{\partial x}}+{\displaystyle \frac{\partial {\mathit{e}}_x}{\partial y\partial x}}dy)d{x}^2$ (102)

Trimming off the 3-order infinite small quantities, the difference of ${\left(d\mathit{\rho }\right)}_1$ and ${\left(d\mathit{\rho }\right)}_2$ is

${\left(d\mathit{\rho }\right)}_1-{\left(d\mathit{\rho }\right)}_2\approx ({\displaystyle \frac{\partial {\mathit{e}}_y}{\partial x}}-{\displaystyle \frac{\partial {\mathit{e}}_x}{\partial y}})dydx$ (103)

There will be a closure error in close path if the mixed derivatives of bases do not equal.

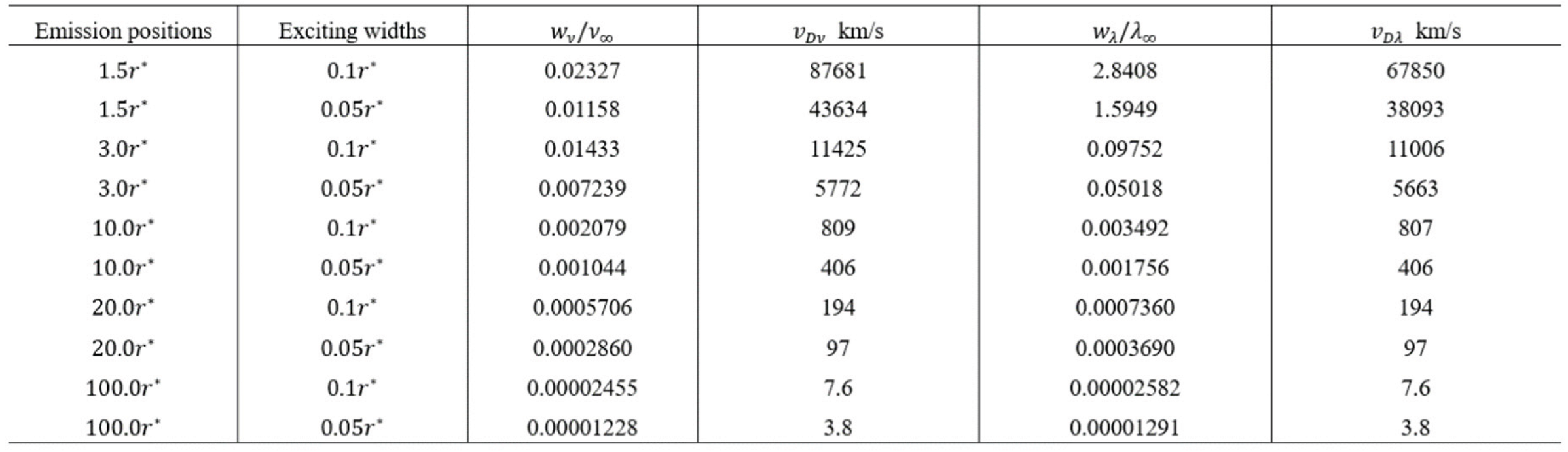
3.2.3. Verifications and Discussions

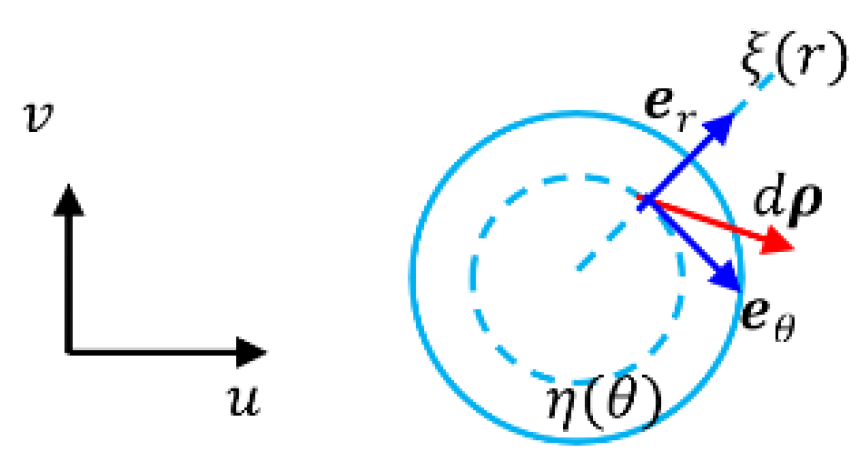
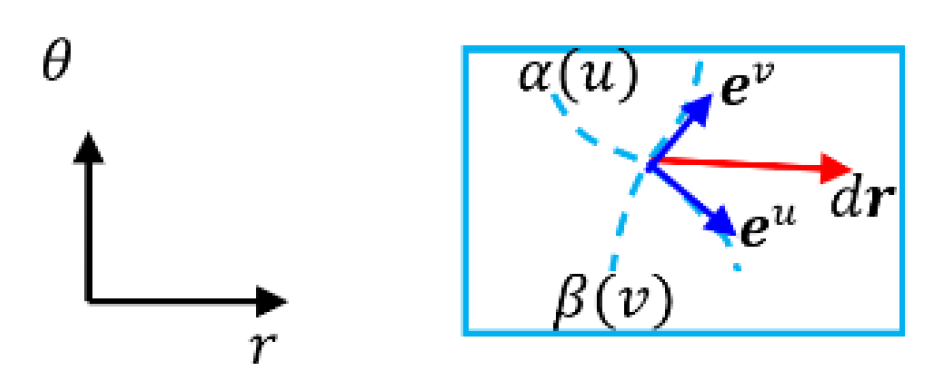
Example 1: Polar coordinate system

Polar coordinate system that we are familiar with is a transformation from its contra variant space $\left(r,\theta \right)$, as shown in Figure 10 and Figure 11.

A position in contra variant space could be expressed by vector

$\mathit{r}=\mathit{r}\left(r,\theta \right)$ (104)

and the differential is

$\mathit{d}\mathit{r}=\left(\begin{array}{c}dr\\ d\theta \end{array}\right)$ (105)

Corresponding position in covariant space, will be expressed by

$\mathit{\rho }=\mathit{\rho }\left(u,v\right)$ (106)

and the differential is

$\mathit{d}\mathit{\rho }=\left(\begin{array}{c}du\\ dv\end{array}\right)$ (107)

In the contra variant space, the differential distance between two positions could be defined as

$d{\varsigma }^2=d\mathit{r}\bullet d\mathit{r}=d{r}^2+d{\theta }^2$ (108)

The system we have used to is the one that has experienced transformation from space $\left(r,\theta \right)$ with

$u=rcos\theta , v=rsin\theta$ (109)

The bases

${\mathit{e}}_r={\displaystyle \frac{\partial \mathit{\rho }}{\partial r}}=\left(\begin{array}{c}cos\theta \\ sin\theta \end{array}\right)$ (110)

${\mathit{e}}_{\theta }={\displaystyle \frac{\partial \mathit{\rho }}{\partial \theta }}=\left(\begin{array}{c}-rsin\theta \\ rcos\theta \end{array}\right)$ (111)

so that

$d\mathit{\rho }={\mathit{e}}_{r}dr+{\mathit{e}}_{\theta }d\theta$ (112)

Thus, there is the covariant distance

$d{s}^2=d{u}^2+d{v}^2=d\mathit{\rho }\bullet d\mathit{\rho }={\mathit{e}}_r\bullet {\mathit{e}}_{r}d{r}^2+{\mathit{e}}_{\theta }\bullet {\mathit{e}}_{\theta }d{\theta }^2=d{r}^2+r^{2}d{\theta }^2$ (113)

The mixed derivatives of bases

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{\partial }{\partial \theta }}\left(\begin{array}{c}cos\theta \\ sin\theta \end{array}\right)=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (114)

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}={\displaystyle \frac{\partial }{\partial r}}\left(\begin{array}{c}-rsin\theta \\ rcos\theta \end{array}\right)=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (115)

We have seen the mixed derivatives got equal

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}$ (116)

It could also be verified in Eq. (89) and Eq. (90) that

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{{\partial }^2{\xi }_{\left(r\right)}}{\partial r\partial \theta }}$ (117)

and

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial r}}$ (118)

The vector $\mathit{\rho }$ is

$\mathit{\rho }=\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{c}rcos\theta \\ rsin\theta \end{array}\right)$ (119)

Because $\mathrm{d}{\xi }_{\left(r\right)}$ is radius length $dr$, and $\mathrm{d}{\eta }_{\left(\theta \right)}$ is arc length $rd\theta$, then

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}={\displaystyle \frac{\partial }{\partial r}}\left(\begin{array}{c}rcos\theta \\ rsin\theta \end{array}\right)=\left(\begin{array}{c}cos\theta \\ sin\theta \end{array}\right)$ (120)

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}={\displaystyle \frac{\partial }{r\partial \theta }}\left(\begin{array}{c}rcos\theta \\ rsin\theta \end{array}\right)=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (121)

Thus, the first item of Eq. (117) is

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}={\displaystyle \frac{\partial }{r\partial \theta }}\left(\begin{array}{c}cos\theta \\ sin\theta \end{array}\right){\displaystyle \frac{\partial r}{\partial r}}{\displaystyle \frac{r\partial \theta }{\partial \theta }}=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (122)

The second item is

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{{\partial }^2{\xi }_{\left(r\right)}}{\partial r\partial \theta }}=\left(\begin{array}{c}cos\theta \\ sin\theta \end{array}\right){\displaystyle \frac{\partial }{r\partial \theta }}{\displaystyle \frac{\partial r}{\partial r}}=\left(\begin{array}{c}0\\ 0\end{array}\right)$ (123)

And the first item of Eq. (118)

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}={\displaystyle \frac{\partial }{\partial r}}\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right){\displaystyle \frac{r\partial \theta }{\partial \theta }}{\displaystyle \frac{\partial r}{\partial r}}=\left(\begin{array}{c}0\\ 0\end{array}\right)$ (124)

The second item

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial r}}=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right){\displaystyle \frac{\partial }{\partial r}}{\displaystyle \frac{r\partial \theta }{\partial \theta }}=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (125)

so that

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)+\left(\begin{array}{c}0\\ 0\end{array}\right)=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (126)

and

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}=\left(\begin{array}{c}0\\ 0\end{array}\right)+\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)=\left(\begin{array}{c}-sin\theta \\ cos\theta \end{array}\right)$ (127)

Obviously there is

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\eta }_{\left(\theta \right)}}}\ne {\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\xi }_{\left(r\right)}}}$ (128)

and

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{{\partial }^2{\xi }_{\left(r\right)}}{\partial r\partial \theta }}\ne {\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial r}}$ (129)

but the mixed derivatives are equal totally that

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}$ (130)

Again, we have got the equality of mixed derivatives. But to our surprise is that this solution really subject to condition 2. It is said that the first items of Eq. (117) and Eq. (118) do not equal. One of the reasons in this case, is that there is no super surface.

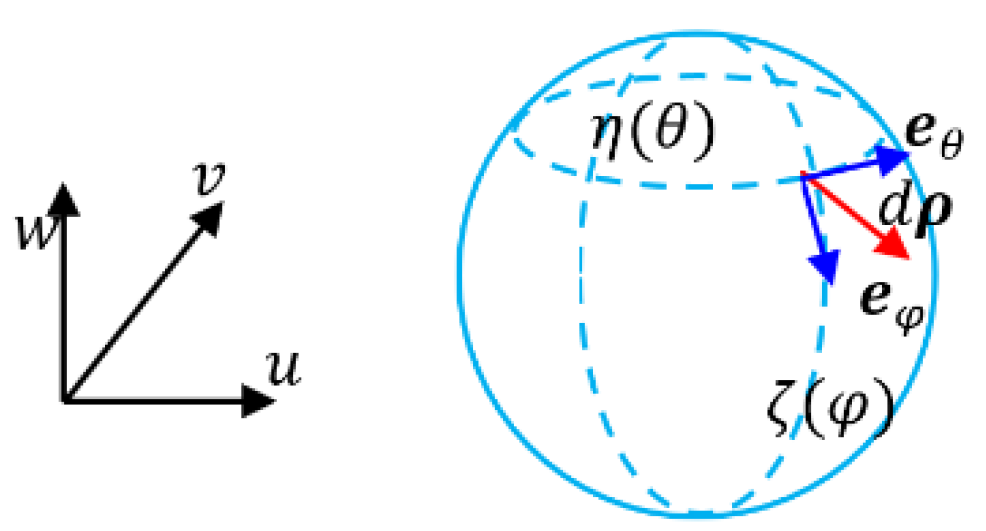
Example 2: Spherical surface coordinate system

A spherical surface coordinate system is also a transformation of the corresponding contra variant space as in Figure 12 and Figure 13, in which

$\mathit{r}={\left.\mathit{r}\left(r,\theta ,\phi \right)\right|}_{r=R}={\left.\left(\begin{array}{c}\theta \\ \phi \end{array}\right)\right|}_{r=R}$ (131)

Differential distance is

$d{\zeta }^2=d\mathit{r}\bullet d\mathit{r}=d{\theta }^2+d{\phi }^2$ (132)

And the coordinates of covariant space will be expressed with

$\mathit{\rho }=\mathit{\rho }\left(u,v,w\right)=\left(\begin{array}{c}u\\ v\\ w\end{array}\right)$ (133)

The spherical coordinates could be transformed to Cartesian coordinates,

$u=Rsin\theta cos\phi , v=Rsin\theta sin\phi , w=Rcos\theta$ (134)

The bases could be defined as

${\mathit{e}}_{\theta }={\displaystyle \frac{\partial \mathit{\rho }}{\partial \theta }}=\left(\begin{array}{c}Rcos\theta cos\phi \\ Rcos\theta sin\phi \\ -Rsin\theta \end{array}\right),{\mathit{e}}_{\phi }={\displaystyle \frac{\partial \mathit{\rho }}{\partial \phi }}=\left(\begin{array}{c}-Rsin\theta sin\phi \\ Rsin\theta cos\phi \\ 0\end{array}\right)$ (135)

and

$d\mathit{\rho }={\mathit{e}}_{\theta }d\theta +{\mathit{e}}_{\phi }d\phi$ (136)

Thus, there is the covariant distance

$d{s}^2=d\mathit{\rho }\bullet d\mathit{\rho }={\mathit{e}}_{\theta }\bullet {\mathit{e}}_{\theta }d{r}^2+{\mathit{e}}_{\phi }\bullet {\mathit{e}}_{\phi }d{r}^2=R^{2}d{\theta }^2+R^2{sin}^2\theta d{\phi }^2$ (137)

The derivatives

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}=\left(\begin{array}{c}-Rcos\theta sin\phi \\ Rcos\theta cos\phi \\ 0\end{array}\right),{\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}=\left(\begin{array}{c}-Rcos\theta sin\phi \\ Rcos\theta cos\phi \\ 0\end{array}\right)$ (138)

so that

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}={\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}$ (139)

It could also be verified in Eq. (89) and Eq. (90) that

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\zeta }_{\left(\phi \right)}}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}{\displaystyle \frac{\partial {\zeta }_{\left(\phi \right)}}{\partial \phi }}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial \phi }}$ (140)

and

${\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{\partial {\zeta }_{\left(\phi \right)}}{\partial \phi }}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}}}{\displaystyle \frac{{\partial }^2{\zeta }_{\left(\phi \right)}}{\partial \phi \partial \theta }}$ (141)

The vector $\mathit{\rho }$ is

$\mathit{\rho }=\left(\begin{array}{c}u\\ v\\ w\end{array}\right)=\left(\begin{array}{c}Rsin\theta cos\phi \\ Rsin\theta sin\phi \\ Rcos\theta \end{array}\right)$ (142)

Because $d{\eta }_{\left(\theta \right)}$ is arc length $Rd\theta$, and $d{\zeta }_{\left(\phi \right)}$ is arc length $Rd\phi$, then

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}={\displaystyle \frac{\partial }{R\partial \theta }}\left(\begin{array}{c}Rsin\theta cos\phi \\ Rsin\theta sin\phi \\ Rcos\theta \end{array}\right)=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right)$ (143)

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}}}={\displaystyle \frac{\partial }{R\partial \phi }}\left(\begin{array}{c}Rsin\theta cos\phi \\ Rsin\theta sin\phi \\ Rcos\theta \end{array}\right)=\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right)$ (144)

Thus, the first item of Eq. (140) is

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\zeta }_{\left(\phi \right)}}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}{\displaystyle \frac{\partial {\zeta }_{\left(\phi \right)}}{\partial \phi }}={\displaystyle \frac{\partial }{R\partial \phi }}\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right){\displaystyle \frac{R\partial \theta }{\partial \theta }}{\displaystyle \frac{R\partial \phi }{\partial \phi }}=\left(\begin{array}{c}-Rcos\theta sin\phi \\ Rcos\theta cos\phi \\ 0\end{array}\right)$ (145)

The second item is

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial \phi }}=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right){\displaystyle \frac{\partial }{\partial \phi }}{\displaystyle \frac{R\partial \theta }{\partial \theta }}=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$ (146)

And the first item of Eq. (141)

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{\partial {\zeta }_{\left(\phi \right)}}{\partial \phi }}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}={\displaystyle \frac{\partial }{R\partial \theta }}\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right){\displaystyle \frac{R\partial \phi }{\partial \phi }}{\displaystyle \frac{R\partial \theta }{\partial \theta }}=\left(\begin{array}{c}-Rcos\theta sin\phi \\ Rcos\theta cos\phi \\ 0\end{array}\right)$ (147)

The second item

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}}}{\displaystyle \frac{{\partial }^2{\zeta }_{\left(\phi \right)}}{\partial \phi \partial \theta }}=\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right){\displaystyle \frac{\partial }{\partial \theta }}{\displaystyle \frac{R\partial \phi }{\partial \phi }}=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$ (148)

With Eq. (145) to Eq. (148) we found that

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\zeta }_{\left(\phi \right)}}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}\partial {\eta }_{\left(\theta \right)}}}$ (149)

and

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial \phi }}={\displaystyle \frac{\partial \mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}}}{\displaystyle \frac{{\partial }^2{\zeta }_{\left(\phi \right)}}{\partial \phi \partial \theta }}$ (150)

so that there is

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}={\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}$ (151)

One can see that this is of condition 1.

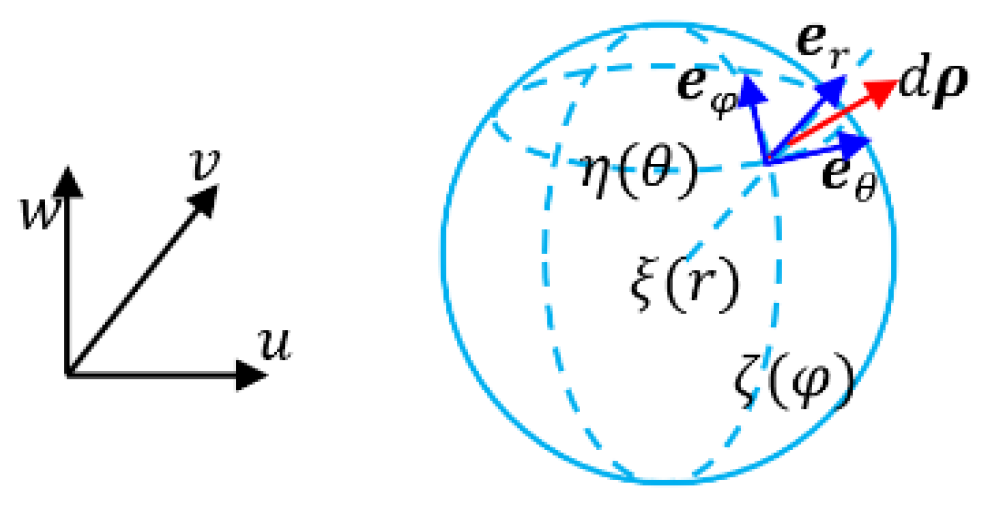
Example 3: Spherical coordinate system

A spherical coordinate system is also a transformation of the corresponding contra variant space as in Figure 14 and Figure 15, in which

$\mathit{r}=\mathit{r}\left(r,\theta ,\phi \right)=\left(\begin{array}{c}r\\ \theta \\ \phi \end{array}\right)$ (152)

Differential distance is

$d{\zeta }^2=d\mathit{r}\bullet d\mathit{r}=d{r}^2+d{\theta }^2+d{\phi }^2$ (153)

And the coordinates of covariant space will be expressed with

$\mathit{\rho }=\mathit{\rho }\left(u,v,w\right)=\left(\begin{array}{c}u\\ v\\ w\end{array}\right)$ (154)

The spherical coordinates could be transformed to Cartesian coordinates,

$u=rsin\theta cos\phi , v=rsin\theta sin\phi , w=rcos\theta$ (155)

The bases could be defined as

${\mathit{e}}_r={\displaystyle \frac{\partial \mathit{\rho }}{\partial r}}=\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right),{\mathit{e}}_{\theta }={\displaystyle \frac{\partial \mathit{\rho }}{\partial \theta }}=\left(\begin{array}{c}rcos\theta cos\phi \\ rcos\theta sin\phi \\ -rsin\theta \end{array}\right),{\mathit{e}}_{\phi }={\displaystyle \frac{\partial \mathit{\rho }}{\partial \phi }}=\left(\begin{array}{c}-rsin\theta sin\phi \\ rsin\theta cos\phi \\ 0\end{array}\right)$ (156)

and

$d\mathit{\rho }={\mathit{e}}_{r}dr+{\mathit{e}}_{\theta }d\theta +{\mathit{e}}_{\phi }d\phi$ (157)

Thus, there is the covariant distance

$d{s}^2=d\mathit{\rho }\bullet d\mathit{\rho }={\mathit{e}}_r\bullet {\mathit{e}}_{r}d{r}^2+{\mathit{e}}_{\theta }\bullet {\mathit{e}}_{\theta }d{\theta }^2+{\mathit{e}}_{\phi }\bullet {\mathit{e}}_{\phi }d{\phi }^2=d{r}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d{\phi }^2$ (158)

The derivatives

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right),{\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right),{\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}=\left(\begin{array}{c}-rcos\theta sin\phi \\ rcos\theta cos\phi \\ 0\end{array}\right)$${\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}=\left(\begin{array}{c}-rcos\theta sin\phi \\ rcos\theta cos\phi \\ 0\end{array}\right),{\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial r}}=\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right),{\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \phi }}=\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right)$ (159)

so that

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}, {\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}={\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}, {\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial r}}={\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \phi }}$ (160)

It could also be verified in Eq. (89) and Eq. (90) that

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{{\partial }^2{\xi }_{\left(r\right)}}{\partial r\partial \theta }}$ (161)

and

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}+{\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial r}}$ (162)

The vector $\mathit{\rho }$ is

$\mathit{\rho }=\left(\begin{array}{c}u\\ v\\ w\end{array}\right)=\left(\begin{array}{c}rsin\theta cos\phi \\ rsin\theta sin\phi \\ rcos\theta \end{array}\right)$ (163)

Because $d{\xi }_{\left(r\right)}$ is radius length $dr$, $d{\eta }_{\left(\theta \right)}$ is arc length $rd\theta$, and $d{\zeta }_{\left(\phi \right)}$ is arc length $rd\phi$, then

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}={\displaystyle \frac{\partial }{\partial r}}\left(\begin{array}{c}rsin\theta cos\phi \\ rsin\theta sin\phi \\ rcos\theta \end{array}\right)=\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right)$ (164)

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}={\displaystyle \frac{\partial }{r\partial \theta }}\left(\begin{array}{c}rsin\theta cos\phi \\ rsin\theta sin\phi \\ rcos\theta \end{array}\right)=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right)$ (165)

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}}}={\displaystyle \frac{\partial }{r\partial \phi }}\left(\begin{array}{c}rsin\theta cos\phi \\ rsin\theta sin\phi \\ rcos\theta \end{array}\right)=\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right)$ (166)

Thus, the first item of Eq. (161) is

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}={\displaystyle \frac{\partial }{r\partial \theta }}\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right){\displaystyle \frac{\partial r}{\partial r}}{\displaystyle \frac{r\partial \theta }{\partial \theta }}=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right)$ (167)

The second item is

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{{\partial }^2{\xi }_{\left(r\right)}}{\partial r\partial \theta }}=\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right){\displaystyle \frac{\partial }{r\partial \theta }}{\displaystyle \frac{\partial r}{\partial r}}=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$ (168)

And the first item of Eq. (162)

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\xi }_{\left(r\right)}}}{\displaystyle \frac{\partial {\eta }_{\left(\theta \right)}}{\partial \theta }}{\displaystyle \frac{\partial {\xi }_{\left(r\right)}}{\partial r}}={\displaystyle \frac{\partial }{\partial r}}\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right){\displaystyle \frac{r\partial \theta }{\partial \theta }}{\displaystyle \frac{\partial r}{\partial r}}=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$ (169)

The second item

${\displaystyle \frac{\partial \mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}}}{\displaystyle \frac{{\partial }^2{\eta }_{\left(\theta \right)}}{\partial \theta \partial r}}=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right){\displaystyle \frac{\partial }{\partial r}}{\displaystyle \frac{r\partial \theta }{\partial \theta }}=\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right)$ (170)

With Eq. (167) and Eq. (170) we found that

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\eta }_{\left(\theta \right)}}}\ne {\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\xi }_{\left(r\right)}}}$ (171)

but there is

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}={\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}$ (172)

One can also calculate that

${\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\eta }_{\left(\theta \right)}\partial {\zeta }_{\left(\phi \right)}}}={\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}\partial {\eta }_{\left(\theta \right)}}}, {\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\zeta }_{\left(\phi \right)}\partial {\xi }_{\left(r\right)}}}\ne {\displaystyle \frac{{\partial }^2\mathit{\rho }}{\partial {\xi }_{\left(r\right)}\partial {\zeta }_{\left(\phi \right)}}}$ (173)

At the end we can obtain

${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial \phi }}={\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial \theta }}, {\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial r}}={\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \phi }}$ (174)

One can see that one of them is of condition 1 and the others of them are of condition 2.

Additional discussion: deformed bases of example 3

If one of the bases in example 3 be set deformed as

${\mathit{e}}_r=f\left(r\right)\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right)$ (175)

where, $f\left(r\right)\ne 1$ is a function of coordinate $r$.

One will find that the derivatives

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}=f\left(r\right)\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right)+{\displaystyle \frac{\partial f\left(r\right)}{\partial \theta }}\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right)=f\left(r\right)\left(\begin{array}{c}cos\theta cos\phi \\ cos\theta sin\phi \\ -sin\theta \end{array}\right)$ (176)

and

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \phi }}=f\left(r\right)\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right)+{\displaystyle \frac{\partial f\left(r\right)}{\partial \phi }}\left(\begin{array}{c}sin\theta cos\phi \\ sin\theta sin\phi \\ cos\theta \end{array}\right)=f\left(r\right)\left(\begin{array}{c}-sin\theta sin\phi \\ sin\theta cos\phi \\ 0\end{array}\right)$ (177)

while ${\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}$ and ${\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial r}}$ will still keep the results as in Eq. (159), that will cause

${\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \theta }}\ne {\displaystyle \frac{\partial {\mathit{e}}_{\theta }}{\partial r}}, {\displaystyle \frac{\partial {\mathit{e}}_{\phi }}{\partial r}}\ne {\displaystyle \frac{\partial {\mathit{e}}_r}{\partial \phi }}$ (178)

This result reminds us that the same performance would have happened in gravitational space time that will be put into discussions in next section.

4. Metrics and Covariant Derivatives in Space Time

4.1. Metrics in Pseudo Riemannian Space

Pseudo Riemannian space is raised for the description of space time for general relativity, after Minkowski space for special relativity [8,9]. Invariant distance for flat space time could be written as

$d{s}^2=-c^{2}d{t}^2+d{x}^2+d{y}^2+d{z}^2$ (179)

We know that there is a minus signal in the equation. The minus signal does not come from transformations of spaces or coordinates. It is a kind of mathematical and physical setting. Former researchers have made efforts on this topic, for example, the concept of plural employed to reform the base ${\mathit{e}}_0$ [6]. But plural bases for relativity is not a good idea. Another treatment is to define $x^0=ict$, which looks like more reasonable [7]. The more important is that the metrics for this condition should be carefully treated so that the metric $g_{00}$ will not be minus.

In general relativity, spherical coordinates are usually suggested for one source problem. So that there will be contra variant space $\left(t,r,\theta ,\phi \right)$ and covariant space $\left(\tau ,\rho ,\theta ,\phi \right)$. The invariant distance of Schwarzschild solution is

$d{s}^2=d\mathit{\rho }\bullet d\mathit{\rho }=-(1-{\displaystyle \frac{r^{*}}{r}}){\left(cdt\right)}^2+{(1-{\displaystyle \frac{r^{*}}{r}})}^{-1}{dr}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d{\phi }^2$ (180)

Most of publications have set the metric [3,4,10,11,12] to be

$g_{00}=-(1-{\displaystyle \frac{r^{*}}{r}})$ (181)

So that there could be a brief expression of invariant distance

$d{s}^2=g_{ij}d{x}^{i}d{x}^j$ (182)

As we have discussed, that will cause plural bases. Anyway, minus metrics is improper. In fact, it is one of the reasons that cause the wrong result of acceleration calculation in Eq. (44).

Considering the above discussions, I prefer to give the invariant distance of one source field as

$d{s}^2=-g_{00}{\left(cdt\right)}^2+g_{11}{dr}^2+g_{22}d{\theta }^2+g_{33}d{\phi }^2$ (183)

Thus, we will prevent from plural items. That doesn’t hurt the expressions of relativity. Metrics and bases defined are just employed for the transformation from Minkowski space time to pseudo Riemannian space time.

It should be highlighted that the bases still would have sophisticated forms that

${\mathit{e}}_0=\left(\begin{array}{c}\begin{array}{c}(1-{\displaystyle \frac{r^{*}}{r}}{)}^{1/2}\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right), {\mathit{e}}_1=\left(\begin{array}{c}\begin{array}{c}0\\ sin\theta cos\phi (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\end{array}\\ \begin{array}{c}sin\theta sin\phi (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\\ cos\theta (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\end{array}\end{array}\right), {\mathit{e}}_2=\left(\begin{array}{c}\begin{array}{c}0\\ rcos\theta cos\phi \end{array}\\ \begin{array}{c}rcos\theta sin\phi \\ -rsin\theta \end{array}\end{array}\right), {\mathit{e}}_3=\left(\begin{array}{c}\begin{array}{c}0\\ -rsin\theta sin\phi \end{array}\\ \begin{array}{c}rsin\theta cos\phi \\ 0\end{array}\end{array}\right)$ (184)

That is because the spherical space we have discussed has already experienced coordinates transformations. The transformed coordinates are not real spherical coordinates, they are the Cartesian coordinates $(u,v,w)$ expressed by parameters of $r,\theta ,\phi$, which could be called parameterized Cartesian coordinates. One can learn from previous section for the reasons.

It could be calculated that

${\displaystyle \frac{\partial {\mathit{e}}_1}{\partial t}}=\left(\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right), {\displaystyle \frac{\partial {\mathit{e}}_1}{\partial \theta }}=\left(\begin{array}{c}\begin{array}{c}0\\ cos\theta cos\phi (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\end{array}\\ \begin{array}{c}cos\theta sin\phi (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\\ -sin\theta (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\end{array}\end{array}\right), {\displaystyle \frac{\partial {\mathit{e}}_1}{\partial \phi }}=\left(\begin{array}{c}\begin{array}{c}0\\ -sin\theta sin\phi (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\end{array}\\ \begin{array}{c}sin\theta cos\phi (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\\ 0\end{array}\end{array}\right)$${\displaystyle \frac{\partial {\mathit{e}}_0}{\partial r}}=\left(\begin{array}{c}\begin{array}{c}{\displaystyle \frac{r^{*}}{{2r}^2}}(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right), {\displaystyle \frac{\partial {\mathit{e}}_2}{\partial r}}=\left(\begin{array}{c}\begin{array}{c}0\\ cos\theta cos\phi \end{array}\\ \begin{array}{c}cos\theta sin\phi \\ -sin\theta \end{array}\end{array}\right), {\displaystyle \frac{\partial {\mathit{e}}_3}{\partial r}}=\left(\begin{array}{c}\begin{array}{c}0\\ -sin\theta sin\phi \end{array}\\ \begin{array}{c}sin\theta cos\phi \\ 0\end{array}\end{array}\right)$ (185)

there are

${\displaystyle \frac{\partial {\mathit{e}}_1}{\partial t}}\ne {\displaystyle \frac{\partial {\mathit{e}}_0}{\partial r}}, {\displaystyle \frac{\partial {\mathit{e}}_1}{\partial \theta }}\ne {\displaystyle \frac{\partial {\mathit{e}}_2}{\partial r}}, {\displaystyle \frac{\partial {\mathit{e}}_1}{\partial \phi }}\ne {\displaystyle \frac{\partial {\mathit{e}}_3}{\partial r}}$ (186)

In general relativity, it could be suggested to simplify the presentation that we only focus on the gravitational transformation. So that the contra variant space is no longer of real spherical coordinates, which could be set as parameterized Cartesian coordinates, and the covariant space could also be the form of parameterized Cartesian. Thus, the invariant distance could be expressed as

$d{s}^2=-g_{00}{\left(cdt\right)}^2+g_{11}{dr}^2+g_{22}{r}^{2}d{\theta }^2+g_{33}{r}^2{sin}^2\theta d{\phi }^2$ (187)

In which, $g_{22}=g_{33}=1$.

These metrics could be called the gravitational metrics, while the metrics previous could be called total metrics and the metrics before gravitational transformation could be called original metrics or pseudo spherical transformation metrics.

For gravitational metrics of Schwarzschild solution, we have the bases

${\mathit{e}}_0=\left(\begin{array}{c}\begin{array}{c}(1-{\displaystyle \frac{r^{*}}{r}}{)}^{1/2}\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right), {\mathit{e}}_1=\left(\begin{array}{c}\begin{array}{c}0\\ (1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right), {\mathit{e}}_2=\left(\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}1\\ 0\end{array}\end{array}\right), {\mathit{e}}_3=\left(\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}0\\ 1\end{array}\end{array}\right)$ (188)

It could be calculated that

${\displaystyle \frac{\partial {\mathit{e}}_0}{\partial r}}=\left(\begin{array}{c}\begin{array}{c}{\displaystyle \frac{r^{*}}{2r^2}}(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right), {\displaystyle \frac{\partial {\mathit{e}}_1}{\partial t}}=\left(\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right)$ (189)

so that

${\displaystyle \frac{\partial {\mathit{e}}_0}{\partial r}}\ne {\displaystyle \frac{\partial {\mathit{e}}_1}{\partial t}}$ (190)

This is of the condition 3 that we have discussed in Section 3.2.2. One can also calculate the inequality of mixed derivatives of bases of total metrics.

That reminds us that the inequality of mixed derivatives of bases will cause closure errors in space time, which would be left for more discussions elsewhere.

4.2. Discussions on Bases, Tensors, and Their Derivatives

Tensors could be recognized as the quantities relating to coordinates in space time. Case a tensor varies in space time, the variation rate could be inspected by derivation. The simplest tensor is position vector $\mathit{\rho }(x0,x1,x2,x3,)$. You have seen that we are going to use middle subscriptions to express coordinates and tensors in covariant space time, though they are rarely mentioned in most of references. To study its variation in space time, one could define the distance variation ratio to form the bases

${\mathit{e}}_i={\displaystyle \frac{\partial \mathit{\rho }}{\partial x^i}}$ (191)

For any tensors involved with bases, such as a proper tensor

$\mathit{A}=A^i{\mathit{e}}_i$ (192)

where, $A^i$ is the number $i$ component of the total contra variant tensor.

The derivatives of the tensor are

${\displaystyle \frac{\partial \mathit{A}}{\partial x^j}}={\mathit{e}}_i{\displaystyle \frac{\partial A^i}{\partial x^j}}+A^i{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^j}}$ (193)

The differential of a proper tensor $d\mathit{A}$ could be defined to be covariant differential labeled as $D\mathit{A}$, and then the derivative ${\displaystyle \frac{\partial \mathit{A}}{\partial x^j}}$ to be covariant derivative ${\displaystyle \frac{D\mathit{A}}{\partial x^j}}$${\displaystyle \frac{D\mathit{A}}{\partial x^j}}={\displaystyle \frac{\partial \mathit{A}}{\partial x^j}}={\mathit{e}}_i{\displaystyle \frac{\partial A^i}{\partial x^j}}+A^i{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^j}}$ (194)

In these equations, the middle subscriptions of proper tensors maybe neglected conventionally so that it is expressed as $\mathit{A}$. And the tensor $\mathit{A}$ could be called proper tensor because $A_i$ has already been named covariant tensor conventionally. Because $A^i$ or $A_i$ is just a component, we could imagine that there must be the total quantity. That will be expressed to be ${\mathit{A}}^{\uparrow }=(A^0,A^1,A^2,A^3)$ or ${\mathit{A}}_{\downarrow }=(A_0,A_1,A_2,A_3)$ for convenience. Sometimes, row forms of expressions of vectors are employed to interpret components which are equivalent to the column forms.

Bases sometimes look like one-order tensors since they have a single index in expressions. But in fact, they really are two-order mixed tensors. For example, a component of contra variant base of collinear transformation，i.e. coordinate lines of contra variant space and covariant space coinciding, could be written as

$e^{\mu }\nu ={\displaystyle \frac{\partial x^{\mu }}{\partial x\nu }}$ (195)

where the contra variant base and proper coordinate differential are all labeled with middle index $\nu$.

So that the base really is

${\mathit{e}}^{\mu }=\left(\begin{array}{c}\begin{array}{c}{e}^{\mu }0\\ e^{\mu }1\end{array}\\ \begin{array}{c}{e}^{\mu }2\\ e^{\mu }3\end{array}\end{array}\right)$ (196)

If $e^{\mu }\nu$=0 case $\mu \ne \nu$, we could use $e^{\mu }$ instead of $e^{\mu }\mu$ for convenience, as it is the only nonvanishing component.

For any one order tensors there is a transformation

$A^{\mu }={\mathit{e}}^{\mu }\bullet \mathit{A} or A_{\mu }={\mathit{e}}_{\mu }\bullet \mathit{A}$ (197)

But for two order tensors, there are some things different. For example, a component of contra variant velocity could be transformed from proper velocity

$V^{\mu }={\displaystyle \frac{d{x}^{\mu }}{d\tau }}={\mathit{e}}^{\mu }\bullet {\displaystyle \frac{d\mathit{\rho }}{d\tau }}={\mathit{e}}^{\mu }\bullet \mathit{V}$ (198)

We know that it may be seen as one-order tensor in practice, but it is really two order tensor.

As for whole contra variant velocity as $V_0^1={\displaystyle \frac{d{x}^1}{dt}}$, that would not be worked out by direct vector product. In fact, it could be composed independently by $d{x}^1$ and $dt$.

$V_0^1={\displaystyle \frac{d{x}^1}{dt}}={\displaystyle \frac{{\mathit{e}}^1\bullet d\mathit{\rho }}{{\mathit{e}}^0\bullet d\mathit{\rho }}}={\displaystyle \frac{e^{1}dx1}{e^{0}d\tau }}=e^1{e}_0{\displaystyle \frac{dx1}{d\tau }}$ (199)

It is impossible to get $e^1{e}_0$ from ${\mathit{e}}^1\bullet {\mathit{e}}_0$ and the latter is zero. Notwithstanding, a velocity is a derivative on matter’s trajectory rather than a direct derivative. That will be further discussed in next sections.

4.3. Derivation via Christoffel Symbols

Christoffel symbols were put forward to perform geometrical relationship that takes similar effects with that of bases. They are defined in the equations [3,13]

${\displaystyle \frac{\partial {\mathit{e}}^{\mu }}{\partial x^{\lambda }}}=-{\Gamma }_{\lambda v}^{\mu }{\mathit{e}}^v or {\displaystyle \frac{\partial {\mathit{e}}_{\mu }}{\partial x^{\lambda }}}={\Gamma }_{\lambda \mu }^v{\mathit{e}}_v$ (200)

Taking the first one for example, the purpose of the equation is to consider the derivatives to be a function of bases, so that the right hand item is really a kind of trivial types. In the summation items, ${\mathit{e}}^v$ just act as direction indicators that would give out whole basic vectors of entire dimensions. And then, ${\Gamma }_{\lambda v}^{\mu }$ provide the coefficients of all directions. It is said, this definition has just provided an error-free frame for the functions of derivatives. It means there may be redundant designs for the coefficients.

Since there is the probability of inequality of mixed derivatives of bases, we should define a specific sequence for subscripts of Christoffel symbols. For the traditional reasons, ${\Gamma }_{\lambda v}^{\mu }$ will be defined as the coefficient of a derivative of ${\mathit{e}}^{\mu }$ that is derivated by $x^{\lambda }$, on a direction of ${\mathit{e}}^v$，that requires unexchangeable subscripts of ${\Gamma }_{\lambda v}^{\mu }$.

We know that a covariant differential is exactly a differential of a proper tensor

${\displaystyle \frac{D\mathit{A}}{\partial x^{\lambda }}}={\displaystyle \frac{\partial \mathit{A}}{\partial x^{\lambda }}}$ (201)

This highlightable concept is essentially carried out to perform general covariance.

The contra variant form also performs the same covariance as that

${\displaystyle \frac{D{A}^{\mu }}{\partial x^{\lambda }}}={\mathit{e}}^{\mu }\bullet {\displaystyle \frac{D\mathit{A}}{\partial x^{\lambda }}}$ (202)

You might have found that the tensor component has been expressed by a total tensor is exactly partial expression. It is just of traditional operations. One can of course carry out whole form expression of ${\mathit{A}}^{\uparrow }$ expressed by $\mathit{A}$ with base matrix $\left[{\mathit{e}}^{\uparrow }\right]$. But too more renovations in a performance will bring about more reading difficulties. So I prefer to present equations in traditional forms as far as possible.

A component of contra variant tensor transformed from covariant one

$A^{\mu }={\mathit{e}}^{\mu }\bullet \mathit{A}$ (203)

Its derivatives is

${\displaystyle \frac{{\partial A}^{\mu }}{\partial x^v}}={\displaystyle \frac{\partial }{\partial x^v}}\left({\mathit{e}}^{\mu }\bullet \mathit{A}\right)={\displaystyle \frac{\partial {\mathit{e}}^{\mu }}{\partial x^v}}\bullet \mathit{A}+{\mathit{e}}^{\mu }\bullet {\displaystyle \frac{\partial \mathit{A}}{\partial x^v}}={\displaystyle \frac{\partial {\mathit{e}}^{\mu }}{\partial x^v}}\bullet \mathit{A}+{\displaystyle \frac{D{A}^{\mu }}{\partial x^v}}$ (204)

so that

${\displaystyle \frac{D{A}^{\mu }}{\partial x^v}}={\displaystyle \frac{\partial A^{\mu }}{\partial x^v}}-{\displaystyle \frac{\partial {\mathit{e}}^{\mu }}{\partial x^v}}\bullet \mathit{A}={\displaystyle \frac{\partial A^{\mu }}{\partial x^v}}+{\Gamma }_{v\lambda }^{\mu }{A}^{\lambda }$ (205)

It is easy to study those covariant derivatives for covariant tensors

${\displaystyle \frac{D{A}_{\mu }}{\partial x^v}}={\displaystyle \frac{\partial A_{\mu }}{\partial x^v}}-{\displaystyle \frac{\partial {\mathit{e}}_{\mu }}{\partial x^v}}\bullet \mathit{A}={\displaystyle \frac{\partial A_{\mu }}{\partial x^v}}-{\Gamma }_{v\mu }^{\lambda }{A}_{\lambda }$ (206)

We have seen that the methodologies of Christoffel symbols and the derivation directly from bases are actually equivalent treatments that present the covariant derivatives. That of course may be use to inspect the problems of equations of Christoffel symbols. Since we have known that part of Christoffel symbols with mixed subscripts do not equal in space time, it is necessary to do more discussions.

It is convenient to discuss the case that a space is defined by orthogonal bases. In practice, metrics are usually taken in to Christoffel connections analysis. For a series of bases ${\mathit{e}}_{0 },{\mathit{e}}_{1 },{\mathit{e}}_{2 },{\mathit{e}}_{3 }$, there is the metric

$g_{ij}={\mathit{e}}_i\bullet {\mathit{e}}_j$ (207)

For whole orthogonal coordinate spaces,

$\left\{\begin{array}{c}{g}_{ij}=0 , i\ne j\\ g_{ij}={\mathit{e}}_i\bullet {\mathit{e}}_i\ne 0 , i=j\end{array}\right.$ (208)

The nonvanishing derivatives

${\displaystyle \frac{\partial g_{ij}}{\partial x^k}}={\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^k}}\bullet {\mathit{e}}_j+{\displaystyle \frac{\partial {\mathit{e}}_j}{\partial x^k}}\bullet {\mathit{e}}_i=2{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^k}}\bullet {\mathit{e}}_{j }, i=j$ (209)

Then the equation could have nonvanishing value, that

${\displaystyle \frac{\partial g_{ij}}{\partial x^{\lambda }}}=2{\Gamma }_{\lambda i}^k{\mathit{e}}_k\bullet {\mathit{e}}_j=2{\Gamma }_{\lambda i}^k{g}_{kj} , i=j$ (210)

Then

${\Gamma }_{\lambda i}^k={\displaystyle \frac{1}{2}}{g}^{kj}{\displaystyle \frac{\partial g_{ij}}{\partial x^{\lambda }}}, i=j$ (211)

This equation could be called revised equation for Christoffel symbols in general relativity. In the equation, it also need $k=i=j$ for the ${\Gamma }_{\lambda i}^k$ to get nonvanishing.

For a result, this equation could be verified in a covariant derivative directly as that in Eq. (206) that

${\Gamma }_{\lambda i}^k{A}_k={\displaystyle \frac{1}{2}}{g}^{kj}{\displaystyle \frac{\partial g_{ij}}{\partial x^{\lambda }}}{A}_k={\displaystyle \frac{1}{2}}({\mathit{e}}^k\bullet {\mathit{e}}^j)(2{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\lambda }}}\bullet {\mathit{e}}_j)A_k=A_k{\mathit{e}}^k\bullet {\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\lambda }}}={\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\lambda }}}\bullet \mathit{A}$ (212)

It should be pointed out that the Christoffel symbols are not necessary because that the issue only started from derivatives of bases, as consequences they surely might be taken the place by the operations of bases.

4.4. Derivatives on Matter’s Trajectory

The calculation of time derivatives may cause to another mathematical abuse in classical theory. For a one source field, it could be seen as rest field in general. Thus, a time derivative of a field quantity should be zero. Case a matter moves in a space, it is the issue that the matter changes its position in a time interval and forms a motion trajectory. In this condition, to learn the acceleration is to study the position variation rather than the field variation. It is one of the reasons that make errors in covariant derivative calculation in Eq. (43), in that the direct derivative has been used instead of trajectory derivative.

It is valuable to reclassify tensors to be field tensors and motion tensors, thus field tensors may vary with field while motion tensors should vary both with field and matter’s motion. For example, the bases only depend on gravitational field, while velocity of a matter may vary due to positions changed. For example, case in one source field, a space derivative of a base may be nonvanishing, but a time derivative of a base must be zero, nevertheless, the base relating to a matter moving in space time would vary because the coordinates varied on trajectory.

A trajectory of motions of a matter should be a directed curve line in a space, from the start to the end. It is said that the trajectory must be single parametrical curve line. Theoretically, the parameter maybe natural i.e. the line it pass through, and as same it could be time that the motion experienced. What worthy of highlight is that these parameters are simultaneous. That is said a record of the parameter corresponds to a sole record of another. The parameter indicates the sequences.

It is no harm to discuss the trajectory vector $\mathit{\lambda }$ as a curve line in contra variant space, in that the trajectory is a function of single variable. There is

$\mathit{\lambda }\left(x^0,x^1,x^2,x^3\right)=\mathit{\lambda }\left(\lambda \right)=\mathit{\lambda }\left(t\right)$ (213)

where $\lambda$ is the length of trajectory.

It is said that the trajectory is of

$x^0=x^0\left(t\right), x^1=x^1\left(t\right), x^2=x^2\left(t\right), x^3=x^3\left(t\right)$ (214)

A tensor variation ratio during a time interval on trajectory could be defined to be trajectory derivative that

${\left({\displaystyle \frac{D\mathit{A}}{d{x}^{\mu }}}\right)}_{tr}={\displaystyle \frac{D\mathit{A}}{d\lambda }}{\displaystyle \frac{d\lambda }{d{x}^{\mu }}}$ (215)

For example

${\left({\displaystyle \frac{D\mathit{A}}{dt}}\right)}_{tr}={\displaystyle \frac{D\mathit{A}}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}$ (216)

where, Einstein summation convention does not act on double $\lambda$ because trajectory is just a single line. The differential length d$\lambda$ is the differential of matter’s trajectory, so that ${\displaystyle \frac{D\mathit{A}}{d\lambda }}d\lambda$ is the covariant differential of tensor $\mathit{A}$ between two neighbourhood positions on the trajectory. Thus, the so-called trajectory derivative is really a kind of line derivative that is derivated by a parameter of trajectory.

It should be noted that a trajectory of matter’s motion indicates time sequences corresponding to positions on the trajectory. There is the substantial difference between trajectory derivatives and primary derivatives. A differential on trajectory is the distance interval that a matter has past across, so that the velocity is a trajectory derivative

${\mathit{V}}_0^{\uparrow }={\left({\displaystyle \frac{d\mathit{\lambda }}{dt}}\right)}_{tr}={\displaystyle \frac{d\mathit{\lambda }}{dt}}=({\displaystyle \frac{d{x}^0\left(t\right)}{dt}},{\displaystyle \frac{d{x}^1\left(t\right)}{dt}},{\displaystyle \frac{d{x}^2\left(t\right)}{dt}},{\displaystyle \frac{d{x}^3\left(t\right)}{dt}})$ (217)

As mentioned above, bases are defined by direct derivatives such as

${\mathit{e}}^{\mu }={\displaystyle \frac{\partial \mathit{r}}{\partial x\mu }}=({\displaystyle \frac{\partial x^0}{\partial x\mu }},{\displaystyle \frac{\partial x^1}{\partial x\mu }},{\displaystyle \frac{\partial x^2}{\partial x\mu }},{\displaystyle \frac{\partial x^3}{\partial x\mu }})$ (218)

where, $dx\mu$ is a proper coordinate differential, so that it is middle labeled.

For the velocity, the differential $d{x}^{\mu }$ is exactly defined on a trajectory of a matter, so that there is the probability that

${\mathit{V}}_0^{\uparrow }\ne 0$ (219)

It is said that velocity tensor itself is literally trajectory derivatives.

Trajectory derivatives of general tensor should be labeled for discrepancy.

For example, the bases along a trajectory in rest field

${\left({\displaystyle \frac{d{e}^i}{dt}}\right)}_{tr}={\displaystyle \frac{d{e}^i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}\ne 0$ (220)

while direct derivatives with $i\ne 0$${\displaystyle \frac{\partial e^i}{\partial t}}=0$ (221)

Eq. (216) could be calculated as

${\left({\displaystyle \frac{D\mathit{A}}{dt}}\right)}_{tr}={\displaystyle \frac{D\left(A^i{\mathit{e}}_i\right)}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}={\mathit{e}}_i{\displaystyle \frac{d{A}^i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}+A^i{\displaystyle \frac{d{\mathit{e}}_i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}$ (222)

and ${\displaystyle \frac{d{A}^i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}$ is also time derivative, and there is

${\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}={\displaystyle \frac{d{A}^i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}$ (223)

where, Einstein summation convention does not act on double $\lambda$.

Thus, we have seen the difference between a trajectory derivative and a primary derivative.

On the other hand, the value of matter’s velocity

$V_0^{\lambda }={\displaystyle \frac{d\lambda }{dt}}$ (224)

so that

${\left({\displaystyle \frac{D\mathit{A}}{dt}}\right)}_{tr}={\mathit{e}}_i{\displaystyle \frac{d{A}^i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}+A^i{\displaystyle \frac{d{\mathit{e}}_i}{d\lambda }}{\displaystyle \frac{d\lambda }{dt}}$$={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i{\displaystyle \frac{d{\mathit{e}}_i}{d\lambda }}{V}_0^{\lambda }$$={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\mu }}}{\displaystyle \frac{\partial x^{\mu }}{\partial x^{\lambda }}}{V}_0^{\lambda }$$={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\mu }}}{\displaystyle \frac{\partial {\mathit{x}}^{\mu }}{\partial x^{\lambda }}}\bullet {\mathit{V}}_0^{\uparrow }$$={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\mu }}}{\mathit{\alpha }}_{\lambda }^{\mu }\bullet {\mathit{V}}_0^{\uparrow }$$={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^{\mu }}}{V}_0^{\mu }$ (225)

where, Einstein summation convention does not act on double $\lambda$, and ${\mathit{\alpha }}_{\lambda }^{\mu }={\displaystyle \frac{\partial {\mathit{x}}^{\mu }}{\partial x^{\lambda }}}$ is the direction cosine on the direction $\mu$ of vector line $\mathit{\lambda }$, so that $V_0^{\mu }={\mathit{\alpha }}_{\lambda }^{\mu }\bullet {\mathit{V}}_0^{\uparrow }$ is of component of ${\mathit{V}}_0^{\uparrow }$ on that direction and ${\mathit{V}}_0^{\uparrow }$ is vector form of $V_0^{\lambda }$ so that it could also be written as ${\mathit{V}}_0^{\lambda }$ equivalently in this equation specially for matter’s motion on the trajectory.

It could be expanded to be

${\left({\displaystyle \frac{D\mathit{A}}{dt}}\right)}_{tr}={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i({\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^0}}{V}_0^0+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^1}}{V}_0^1+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^2}}{V}_0^2+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^3}}{V}_0^3)$ (226)

The expression in component forms could also be worked out as

${\left({\displaystyle \frac{D{A}^{\mu }}{dt}}\right)}_{tr}={\left({\displaystyle \frac{d{A}^{\mu }}{dt}}\right)}_{tr}+A^i({\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^0}}\bullet {\mathit{e}}^{\mu }{V}_0^0+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^1}}\bullet {\mathit{e}}^{\mu }{V}_0^1+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^2}}\bullet {\mathit{e}}^{\mu }{V}_0^2+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^3}}\bullet {\mathit{e}}^{\mu }{V}_0^3)$ (227)

The expression in the way of Christoffel symbols as

${\left({\displaystyle \frac{D{A}^{\mu }}{dt}}\right)}_{tr}={\left({\displaystyle \frac{d{A}^{\mu }}{dt}}\right)}_{tr}+{\Gamma }_{0i}^{\mu }{A}^i{V}_0^0+{\Gamma }_{1i}^{\mu }{A}^i{V}_0^1+{\Gamma }_{2i}^{\mu }{A}^i{V}_0^2+{\Gamma }_{3i}^{\mu }{A}^i{V}_0^3$ (228)

We could find that the first component of 4-dimensional velocity is something special in that it is not true velocity. Generally, a velocity of massive matters in contra variant space is

${\mathit{V}}_0^{\uparrow }=(V_0^0,V_0^1,V_0^2,V_0^3)$ (229)

And velocity composition expressed as

$-{\left|{\mathit{V}}_0^{\uparrow }\right|}^2=-(V_0^0{)}^2+(V_0^1{)}^2+(V_0^2{)}^2+(V_0^3{)}^2$ (230)

where $V_0^0={\displaystyle \frac{cdt}{dt}}=c$.

For light rays, the contra variant velocity will be composed to be nonvanishing

$-{\left|{\mathit{c}}_0^{\uparrow }\right|}^2=-(c_0^0{)}^2+(c_0^1{)}^2+(c_0^2{)}^2+(c_0^3{)}^2\ne 0$ (231)

where $c_0^0={\displaystyle \frac{cdt}{dt}}=c$.

But their velocity composition in covariant space is zero

$-{\left|\mathit{c}\right|}^2=-c^2+(c1/0{)}^2+(c2/0{)}^2+(c3/0{)}^2=0$ (232)

in that the summation of the last 3 items is $c^2$.

We know that invariant light speed is $c$. It is said that a covariant composite velocity does not always perform real velocity, so does a contra variant composite velocity. The velocity of $V_0^0$ or $c_0^0$ is something virtual quantity, and we have found more complexities in kinematics. One can argue that there are still some issues unsolved. That could be expected in next sections.

In rest fields, there will be ${\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^0}}=0$, so that ${\Gamma }_{0i}^{\mu }=0$. It is said that for one source field, a trajectory derivative could be based on a real trajectory that

${\left({\displaystyle \frac{D\mathit{A}}{dt}}\right)}_{tr}={\mathit{e}}_i{\left({\displaystyle \frac{d{A}^i}{dt}}\right)}_{tr}+A^i({\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^1}}{V}_0^1+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^2}}{V}_0^2+{\displaystyle \frac{\partial {\mathit{e}}_i}{\partial x^3}}{V}_0^3)$ (233)

and

${\left({\displaystyle \frac{D{A}^{\mu }}{dt}}\right)}_{tr}={\left({\displaystyle \frac{d{A}^{\mu }}{dt}}\right)}_{tr}+{\Gamma }_{1i}^{\mu }{A}^i{V}_0^1+{\Gamma }_{2i}^{\mu }{A}^i{V}_0^2+{\Gamma }_{3i}^{\mu }{A}^i{V}_0^3$ (234)

It should be highlighted that the trajectory derivatives could also be defined in distance derivatives as

$({\displaystyle \frac{D{A}^{\mu }}{d\lambda }}{)}_{tr}={\displaystyle \frac{D{A}^{\mu }}{d\lambda }}$ (235)

which just performs a special appearance of trajectory derivatives.

For free falling trajectory, it is

$({\displaystyle \frac{D{A}^{\mu }}{dr}}{)}_{tr}={\displaystyle \frac{D{A}^{\mu }}{dr}}$ (236)

Trajectory derivative is derivative on a curve line in space time. Sometimes it is presented with time because that the time variable is used in the parametric equation. Christoffel symbols in the equations owe to derivatives of space differentials rather than trajectory differentials. We will see that the concept of trajectory derivative help to describe frequency shift and acceleration, as well as to falsify the concept of geodesic line in section 8.2.

5. Theoretical Verifications on Gravitational Redshifts and Accelerations

Because of the inequality of Christoffel symbols of mixed subscripts, the classical Christoffel symbol equations could not be used any more in the theory of general relativity. The covariant derivatives in gravitational field should be considered in their correct forms.

5.1. On Gravitational Redshifts

Light rays travelling in gravitational field, are also the issue of matter’s motions. Something special is that we would rather focus more on the frequency derivatives by distance, in that they could perform more specialties of the light ray frequency shift.

Taking light propagation at vertical direction for example, a distance derivative of contra variant frequency is exactly trajectory derivative

$({\displaystyle \frac{D{\nu }_0}{dr}}{)}_{tr}=({\displaystyle \frac{d{\nu }_0}{dr}}{)}_{tr}-{\Gamma }_{10}^0{\nu }_0$ (237)

Where, the first item of right side of the equation is contra variant derivative that has been drawn in Eq. (15).

It is sure to consider the tensor of frequency and its derivative to be vectors, but in traditions it is not of a rare necessity. It has been mentioned that Christoffel symbol ${\Gamma }_{10}^0$ were employed correctly with the form ${\Gamma }_{10}^0={\displaystyle \frac{1}{2}}{g}^{00}{\displaystyle \frac{\partial g_{00}}{\partial x^1}}$ as has been shown in Eq. (26). As a result, it will lead to a real answer

${\Gamma }_{10}^0={\displaystyle \frac{1}{2}}{g}^{00}{\displaystyle \frac{\partial g_{00}}{\partial r}}={\displaystyle \frac{1}{2}}{(1-{\displaystyle \frac{r^{*}}{r}})}^{-1}{(1-{\displaystyle \frac{r^{*}}{r}})}^{\text{'}}={\displaystyle \frac{r^{*}}{2r^2}}(1+{\displaystyle \frac{r^{*}}{r-r^{*}}})$ (238)

The covariant derivative will be calculated to be

$({\displaystyle \frac{D{\nu }_0}{\partial r}}{)}_{tr}=-{\displaystyle \frac{r^{*}}{{2r}^2}}{{\nu }_0}_{\left(\infty \right)}-{\displaystyle \frac{r^{*}}{2r^2}}(1+{\displaystyle \frac{r^{*}}{r-r^{*}}}){(1+{\displaystyle \frac{r^{*}}{2r}}){\nu }_0}_{(\infty )}$ (239)

The approximate solution for weak field is that

$({\displaystyle \frac{D{\nu }_0}{\partial r}}{)}_{tr}\approx 2{\displaystyle \frac{d{\nu }_0}{dr}}$ (240)

It is said that the solution Eq. (27) and Eq. (28) are confirmed again, and they have revealed that the covariant redshift is approximately double of the contra variant one in weak field.

Notwithstanding, one can also make another derivative as

$({\displaystyle \frac{D{\nu }_0}{dt}}{)}_{tr}={\displaystyle \frac{d{\nu }_0}{dr}}{\displaystyle \frac{dr}{dt}}-{\Gamma }_{10}^0{\nu }_0{\displaystyle \frac{dr}{dt}}$ (241)

For light rays at that trajectory, ${\displaystyle \frac{dr}{dt}}=c_0^1$. It becomes

$({\displaystyle \frac{D{\nu }_0}{dt}}{)}_{tr}=({\displaystyle \frac{d{\nu }_0}{dt}}{)}_{tr}-c_0^1{\Gamma }_{10}^0{\nu }_0$ (242)

The first item of right hand side can also be transformed to be

$({\displaystyle \frac{d{\nu }_0}{dt}}{)}_{tr}={\displaystyle \frac{d{\nu }_0}{dr}}{\displaystyle \frac{dr}{dt}}=c_0^1{\displaystyle \frac{d{\nu }_0}{dr}}$ (243)

so that

$({\displaystyle \frac{D{\nu }_0}{dt}}{)}_{tr}=c_0^1({\displaystyle \frac{d{\nu }_0}{dr}}-{\Gamma }_{10}^0{\nu }_0)=c_0^1({\displaystyle \frac{D{\nu }_0}{dr}}{)}_{tr}\approx 2c_0^1{\displaystyle \frac{d{\nu }_0}{dr}}$ (244)

5.2. On Accelerations

One can take matter’s freefalling for example to study the acceleration in gravitational fields. The whole contra variant acceleration is the derivative of whole contra variant velocity as that

$a_{00}^1=({\displaystyle \frac{d{V}_0^1}{dt}}{)}_{tr}={\displaystyle \frac{d^{2}r}{{dt}^2}}$ (245)

And whole covariant acceleration is a pure covariant derivative

$a1/00=({\displaystyle \frac{DV1/0}{d\tau }}{)}_{tr}={\displaystyle \frac{d^2\rho }{{d\tau }^2}}$ (246)

One may find that some tensors have been labeled with detailed middle index hence they may help to provide explicit expressions, in which the symbol / is employed to divide the middle upper and middle lower indexes.

With the relationship between covariant derivatives, it could be drawn that

$e^1{e}_0{e}_{0}a1/00=({\displaystyle \frac{D{V}_0^1}{dt}}{)}_{tr}$ (247)

To study the covariant derivative expression with Christoffel symbols, there is

$({\displaystyle \frac{D{V}_0^1}{dt}}{)}_{tr}=({\displaystyle \frac{d{V}_0^1}{dt}}{)}_{tr}+{\Gamma }_{11}^1{\displaystyle \frac{dr}{dt}}{V}_0^1-{\Gamma }_{10}^0{\displaystyle \frac{dr}{dt}}{V}_0^1$ (248)

With ${\displaystyle \frac{dr}{dt}}=V_0^1$, it becomes

$({\displaystyle \frac{D{V}_0^1}{dt}}{)}_{tr}=({\displaystyle \frac{d{V}_0^1}{dt}}{)}_{tr}+{\Gamma }_{11}^1{\left(V_0^1\right)}^2-{\Gamma }_{10}^0{\left(V_0^1\right)}^2$ (249)

With ${\Gamma }_{11}^1=e^1{\displaystyle \frac{{\partial e}_1}{\partial r}}$, ${\Gamma }_{10}^0=e^0{\displaystyle \frac{{\partial e}_0}{\partial r}}$, $e^0{\partial e}_0=-e_0{\partial e}^0$ and $({\displaystyle \frac{d{V}_0^1}{dt}}{)}_{tr}=a_{00}^1$ there is

$({\displaystyle \frac{D{V}_0^1}{dt}}{)}_{tr}=a_{00}^1+e^1{\displaystyle \frac{{\partial e}_1}{\partial r}}{\left(V_0^1\right)}^2-e^0{\displaystyle \frac{{\partial e}_0}{\partial r}}{\left(V_0^1\right)}^2$$=a_{00}^1+e^1{\displaystyle \frac{{\partial e}_1}{\partial r}}{\left(V_0^1\right)}^2+e_0{\displaystyle \frac{\partial e^0}{\partial r}}{\left(V_0^1\right)}^2$$=a_{00}^1+e^1{e}_0{\displaystyle \frac{\partial }{\partial r}}\left(e_1{e}^0\right){\left(V_0^1\right)}^2$ (250)

With Eq. (247), there is

$a1/00=e^0{e}^0{e}_1({\displaystyle \frac{D{V}_0^1}{dt}}{)}_{tr}=e^0{e}^0{e}_1{a}_{00}^1+e^0{\displaystyle \frac{\partial }{\partial r}}(e_1{e}^0){\left(V_0^1\right)}^2$ (251)

One can find that we have use ${\Gamma }_{11}^1$ and ${\Gamma }_{10}^0$ in the calculation of $a1/00$, rather than ${\Gamma }_{00}^1$ that has been used in Eq. (44). As we have discussed, the value of ${\Gamma }_{00}^1$ is really of zero.

As has been said that covariant derivatives could also be developed in a direct way without Christoffel symbols

$a1/00=({\displaystyle \frac{DV1/0}{d\tau }}{)}_{tr}=({\displaystyle \frac{d^2\rho }{{d\tau }^2}}{)}_{tr}=\left[{\displaystyle \frac{d}{\partial \tau }}\right({\displaystyle \frac{e_{1}dr}{e_{0}dt}}){]}_{tr}=[{\displaystyle \frac{d}{e_{0}dt}}\left({\displaystyle \frac{e_{1}dr}{e_{0}dt}}\right){]}_{tr}$$=e^0{\displaystyle \frac{e_1}{e_0}}\left[{\displaystyle \frac{d}{dt}}\right({\displaystyle \frac{dr}{dt}}){]}_{tr}+e^0{\displaystyle \frac{dr}{dt}}[{\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{e_1}{e_0}}\right){]}_{tr}$$=e^0{e}^0{e}_1{a}_{00}^1+e^0{V}_0^1[{\displaystyle \frac{d}{dt}}\left(e^0{e}_1\right){]}_{tr}$$=e^0{e}^0{e}_1{a}_{00}^1+e^0{V}_0^1{\displaystyle \frac{\partial }{\partial r}}\left(e^0{e}_1\right){\displaystyle \frac{dr}{dt}}$$=e^0{e}^0{e}_1{a}_{00}^1+e^0{\displaystyle \frac{\partial }{\partial r}}\left(e^0{e}_1\right){\left(V_0^1\right)}^2$ (252)

It could be found that this equation has been far different from the Eq. (44), because errors in Christoffel symbol equation have been eliminated and at the same time the concept of trajectory derivate help to calculate an acceleration in right way. These discussions have presented further verifications for the revised equation of Christoffel symbols of Eq. (211).

By the way, it is interesting to take some discussions on some trivial concepts such as $a_{00}^0$ and the covariant form$a0/00$ of massive matters. Since $V_0^0$ and $V0/0$ are the velocities of contra variant time and proper time but not the real velocity of light

$V_0^0={\displaystyle \frac{d{x}^0}{dt}}={\displaystyle \frac{d\left(ct\right)}{dt}}=c$ (253)

and

$V0/0={\displaystyle \frac{e_{0}d{x}^0}{d\tau }}={\displaystyle \frac{e_{0}d\left(ct\right)}{d\tau }}=c$ (254)

Then their derivatives are just the accelerations of time coordinates that

$a_{00}^0=({\displaystyle \frac{d{V}_0^0}{dt}}{)}_{tr}=0$ (255)

while

$({\displaystyle \frac{D{V}_0^0}{dt}}{)}_{tr}=({\displaystyle \frac{d{V}_0^0}{dt}}{)}_{tr}+{\Gamma }_{10}^0{V}_0^0{V}_0^1-{\Gamma }_{10}^0{V}_0^0{V}_0^1=0$ (256)

so that

$a0/00=0$ (257)

As light propagation at a direction of a radius is concerned, we know that light speed $c$ keeps invariant in covariant space, so that there is

${\displaystyle \frac{Dc}{d\tau }}=0$ (258)

Case discussing the performance of contra variant light speed, with invariant distance, there is

$\mathrm{d}{\mathrm{s}}^2=-g_{00}{c}^{2}d{t}^2+g_{11}d{r}^2=0$ (259)

and then the light speed in contra variant space will be

$c_0^1={\displaystyle \frac{dr}{dt}}=\sqrt{{\displaystyle \frac{g_{00}}{g_{11}}}}c=e_0{e}^{1}c$ (260)

where, positive $g_{00}$ is set instead of a minus $g_{00}$ as has suggested previous.

Then the acceleration

$a_{00}^1=({\displaystyle \frac{d{c}_0^1}{dt}}{)}_{tr}=[{\displaystyle \frac{d}{dt}}(e_0{e}^1{c\left)\right]}_{tr}=c{\displaystyle \frac{\partial }{\partial r}}\left(e_0{e}^1\right){\displaystyle \frac{\partial r}{\partial t}}=c{c}_0^1{\displaystyle \frac{\partial }{\partial r}}\left(e_0{e}^1\right)=c^2{e}_0{e}^1{\displaystyle \frac{\partial }{\partial r}}\left(e_0{e}^1\right)$ (261)

With Eq. (250) the covariant derivative is

$({\displaystyle \frac{D{c}_0^1}{dt}}{)}_{tr}=({\displaystyle \frac{d{c}_0^1}{dt}}{)}_{tr}-e_1{e}^0{\displaystyle \frac{\partial }{\partial r}}\left(e^1{e}_0\right){\left(c_0^1\right)}^2$$=a_{00}^1-e_1{e}^0{\displaystyle \frac{\partial }{\partial r}}\left(e^1{e}_0\right){\left(c_0^1\right)}^2$$=c^2{e}_0{e}^1{\displaystyle \frac{\partial }{\partial r}}\left(e_0{e}^1\right)-c^2{e}_0{e}^1{\displaystyle \frac{\partial }{\partial r}}\left(e^1{e}_0\right)=0$ (262)

Of course, with Eq. (260) and Eq. (247), we could obtain the result only by a judgment that

$({\displaystyle \frac{D{c}_0^1}{dt}}{)}_{tr}=e^1{e}_0{e}_0{\displaystyle \frac{Dc}{d\tau }}=0$ (263)

6. Experimental Verifications on Gravitational Redshifts and Accelerations

Every tensor involved with measurable quantities could have probabilities to be performed in practice with measured quantities to verify their theoretical expressions. In space time, space intervals and time intervals are all measurable quantities so that they surely could be employed to perform the space and time dependent tensors.

The methodology of the so-called revisit gravitational redshift encourages me to sponsor a realistic analysis method to further verify the general covariance, which will present solutions all based on physical events of realities. Physical events always have substantial existence so that they can help to create irrefutable conclusions. We know that physical events may be record both in contra variant space and covariant space that might provide different values for physical quantities, but both of them actually represent the same physical realities.

6.1. On Measurable Experiments

Measurable quantities could be used to describe physical events, which may be coordinate independent or not. Coordinate independent quantities of course show invariance in physical events in different spaces, such as wave numbers, which could be record as images or texts at specific times and positions. However, coordinate dependent quantities measured in site may really depend. For examples, distance measurements not only depend on in-site space intervals but also depend on the in-site rulers, so as well, time measurements also depend on both in-site time intervals and the in-site clocks. We imagine that the space rulers and clocks their selves maybe also vary. Logically, records of these quantities are recognizable even if they are in farthest distance to the bystanders.

Case a measurement equipment varies with time space, whether the measurement quantity measured is in contra variant space quantity or covariant space quantity? With general covariance, it has been believed that rulers will shrink when they go closer to the center source corresponding to the space interval to become shorter. And also, it has been expected that clocks will go variant corresponding to their dynamic conditions.

However, after those inspections in previous sections, we know that general covariance does not work in some circumstances. Energy and momentum of a matter may not keep covariant in covariant space, while light speed may keep covariant spectacularly. On another side, our discussions may have led to a theoretical inference that matters may experience relativistic emission when they go to a center source and then shrink because of the variation of energy structure. That could be called covariant deformations.

Once we measure space and time intervals at a position, maybe they are not committed to be contra variant quantities or covariant quantities, because our rulers may vary uncommitted. But we could do made measurements anyway. In another word, we could indeed measure something so that they will correspond to any others. Thus, it is not harmful to suppose one of the series of measurable quantities could be measured in following discussions, for example, the contra variant distances or contra variant time intervals. And then they will be valid to be transformed from one to another. That will help us to do more analysis for comparisons and discussions.

6.2. Measurable Verifications for Gravitational Redshift

For the issue of redshift, we are going to sponsor the physical events of wave number counting. It is known that light frequency investigation should be accomplished by indirect techniques and sometimes it may come out with deviations. But it is supposed here that the wave number of the light is countable, or it is believed that light wave could be seen and record. This assumption actually may not do harm to our understanding to the realities, because that indeed will not change the realities and the events of wave counting in that the measurements themselves are also physical processes.

The event of wave number counting could be specified as the record of a number of waves to past a position in a time interval, and it could also be simplified to be one wave corresponding to a time lasting of the light ray propagating a wave length distance. On another side indirectly, one can get wave number by measuring wave length, based on the assumption of invariant light speed. But the apparent light speed might be variable so that the indirect method is not a good idea.

If there is a photon propagating from position 1 to position 2 in a one source field as shown in Figure 16, which correspond to coordinates $r_{\left(1\right)}$and $r_{\left(2\right)}$,

The wave number counting events should be carried out at the time that the photon passes the position 1 and position 2. In very short time $∆t_{\left(1\right)}$ and $∆t_{\left(2\right)}$, we will count the corresponding wave number $∆n_{\left(1\right)}$ and $∆n_{\left(2\right)}$. It should be pointed out that the time intervals here do nothing with the time intervals in Figure 2 in Section 2.2, in that they belong to different physical events that the ones we are talking are of the records of wave counting events and the ones in Figure 2 are of the records of pulse emission and receiveing events.

Since the frequencies should be calculated as

${{\nu }_0}_{\left(1\right)}={\displaystyle \frac{∆n_{\left(1\right)}}{∆t_{\left(1\right)}}} and {{\nu }_0}_{\left(2\right)}={\displaystyle \frac{∆n_{\left(2\right)}}{∆t_{\left(2\right)}}}$ (264)

Redshift has been defined as

$z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}={\displaystyle \frac{{{\nu }_0}_{\left(1\right)}-{{\nu }_0}_{\left(2\right)}}{{{\nu }_0}_{\left(2\right)}}}$ (265)

With the measurable records, redshift in contra variant space is

$z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}={\displaystyle \frac{∆n_{\left(1\right)}∆t_{\left(2\right)}}{∆n_{\left(2\right)}∆t_{\left(1\right)}}}-1$ (266)

In the event of wave counting, wave numbers are invariant in both contra variant space and covariant space, but the time intervals $∆t_{\left(1\right)}$ and $∆t_{\left(2\right)}$ will vary to be $∆{\tau }_{\left(1\right)}$ and $∆{\tau }_{\left(2\right)}$. In fact, every physical event keeps the only one event, whereas the different describing metrics lead to different results in the different spaces.

Naturally, gravitational redshift in covariant space is

$z_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{t}}={\displaystyle \frac{{\nu }_{\left(1\right)}-{\nu }_{\left(2\right)}}{{\nu }_{\left(2\right)}}}={\displaystyle \frac{∆n_{\left(1\right)}∆{\tau }_{\left(2\right)}}{∆n_{\left(2\right)}∆{\tau }_{\left(1\right)}}}-1$ (267)

where, this redshift symbol labeled with revisit is because it corresponds to that one named in classical equations.

As we know,

$∆\tau =e_0∆t$ (268)

It turns to be

$z_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{t}}={\displaystyle \frac{e_{0\left(2\right)}}{e_{0\left(1\right)}}}{\displaystyle \frac{∆n_{\left(1\right)}∆t_{\left(2\right)}}{∆n_{\left(2\right)}∆t_{\left(1\right)}}}-1$ (269)

As in a field of center source, the metric takes the forms of Schwarzschild solution, it is drawn that

$z_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{t}}=(1+{\displaystyle \frac{{\varnothing }_2-{\varnothing }_1}{c^2}}+o){\displaystyle \frac{∆n_{\left(1\right)}∆t_{\left(2\right)}}{∆n_{\left(2\right)}∆t_{\left(1\right)}}}-1$ (270)

We know that the $z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}$ in Eq. (266) could have been measured in the physical event of wave number counting that of course equals to that in Eq. (9), so that

${\displaystyle \frac{∆n_{\left(1\right)}∆t_{\left(2\right)}}{∆n_{\left(2\right)}∆t_{\left(1\right)}}}=(1+{\displaystyle \frac{{\varnothing }_2-{\varnothing }_1}{c^2}}+o)$ (271)

Thus, the covariant redshift in weak field is obtained

$z_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{t}}={(1+{\displaystyle \frac{{\varnothing }_2-{\varnothing }_1}{c^2}}+o)}^2-1\approx 2{\displaystyle \frac{∆\varnothing }{m{c}^2}}\approx 2{\left(z\right)}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}$ (272)

It is said that, the revisit gravitational redshift is double of that of contra variant one.

As the equation of contra variant redshift is concerned, we know that it could be of course drawn by counting two wave numbers in two equivalent specified time intervals. For example, set $∆t_{\left(1\right)}=∆t_{\left(2\right)}=∆t$ which are measured at positions of $r_{\left(1\right)}$ and $r_{\left(2\right)}$, then $∆n_{\left(1\right)}$ and $∆n_{\left(2\right)}$ should represent the difference of frequency without time intervals. So that

$z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}={\displaystyle \frac{∆n_{\left(1\right)}∆t}{∆n_{\left(2\right)}∆t}}-1={\displaystyle \frac{∆n_{\left(1\right)}}{∆n_{\left(2\right)}}}-1$ (273)

We know that $∆n_{\left(1\right)}$ and $∆n_{\left(2\right)}$ present the wave numbers with respect to $∆t_{\left(1\right)}=∆t$ and $∆t_{\left(2\right)}=∆t$.

As for revisit redshift, one will still get different covariant time intervals because the metrics go varied. Thus it is always doubled of the previous.

$z_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{t}}={\displaystyle \frac{∆n_{\left(1\right)}}{∆n_{\left(2\right)}}}{\displaystyle \frac{e_{0\left(2\right)}}{e_{0\left(1\right)}}}{\displaystyle \frac{∆t}{∆t}}-1\approx 2{\left(z\right)}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}$ (274)

It should be pointed out that in some experiments on gravitational redshift, only one timing clock was designed for time interval measurement. In this case, a wrong setting of proper time intervals may be taken into consideration, for example some sole clock timing experiments, so that the experimental redshift may be presented as

$z_{\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}}={\displaystyle \frac{∆n_{\left(1\right)}∆{\tau }_{\left(2\right)}}{∆n_{\left(2\right)}∆{\tau }_{\left(1\right)}}}-1={\displaystyle \frac{∆n_{\left(2\right)}}{∆n_{\left(1\right)}}}{\displaystyle \frac{e_{0\left(\mathrm{x}\right)}}{e_{0\left(\mathrm{x}\right)}}}{\displaystyle \frac{∆t_{\left(2\right)}}{∆t_{\left(1\right)}}}-1={\left(z\right)}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}$ (275)

where, $e_{0\left(\mathrm{x}\right)}$ is base component at clock position of $r_{\left(1\right)}$ or $r_{\left(2\right)}$ or any position others to them.

We can find out those completed experiments observations [14,15,16] on gravitational redshift will be easy to be verified to have only worked out the results of contra variant frequency shift.

Of course, one can calculate the real proper time intervals by time interval transformation between sole timing position and frequency shift positions. That will finaly help to work out revisit gravitational redshift as have discussed.

6.3. Measurable Verifications for Acceleration

6.3.1. Measurable Quantities and Measurable Acceleration

Firstly, I prefer to rise a controversy of a free falling on the Earth that if a matter freefalls from rest with velocity ${V_0^1}_{\left(1\right)}=0$ as well as ${V1/0}_{\left(1\right)}=0$ by nature, we do know that it will move quite faster with velocity ${V_0^1}_{\left(2\right)}$ after traveling a distance in a time interval because of gravity. In traditional theory, we know that the proper velocity ${V1/0}_{\left(2\right)}=e_0{e}^1{V_0^1}_{\left(2\right)}$. Considering the weak field effect, there is $e_0{e}^1\approx 1$. Hence comes the controversy that the covariant acceleration must be great than zero because the matter has started from rest to a quite apparent motion. That is really contradicted with the principle of general covariance with a requirement of zero covariant acceleration. Nevertheless, considering that ${V_0^1}_{\left(2\right)}$ and ${V1/0}_{\left(2\right)}$ are still non-relativistic velocities, it is easy to estimated that the accelerations are also approximately equal that $a1/00\approx a_{00}^1$. The following works of so-called realistic verifications in this section are exactly to be sponsored to solve these controversies thoroughly.

A freefalling test with initial velocity is going to be put forward, in which a matter freely falls to source center from a position $r_{\left(1\right)}$ to a position $r_{\left(2\right)}$ as shown in Figure 17. Once the velocities at the two positions are measured, the average values could be estimated with the velocities difference and the interval distance. Considering the condition on the surface of the Earth, a freefalling with a rarely big velocity and a rarely small traveling would be performed. For example, a velocity of more than 10000 m/s, could be seen as a constant accelerating motion even in covariant space, in that a covariant derivative is expected to be linear with velocity.

It is supposed that contra variant distances and time intervals are measurable. Based on the measurements, velocity at position 1 could be written as

${V_0^1}_{\left(1\right)}={\displaystyle \frac{∆r_{\left(1\right)}}{∆t_{\left(1\right)}}}$ (276)

where the $∆r_{\left(1\right)}$ and $∆t_{\left(1\right)}$ are measured distance and time intervals when the matter goes by the position $r_{\left(1\right)}$, so that they are both tensors of contra variant space. For reasons of convenience their bracketed sub indexes here are only employed to represent positions.

As well as that at position 2

${V_0^1}_{\left(2\right)}={\displaystyle \frac{∆r_{\left(2\right)}}{∆t_{\left(2\right)}}}$ (277)

Because the velocity at position 2 is the result of acceleration, it could be written in integral form

${V_0^1}_{\left(2\right)}={V_0^1}_{\left(1\right)}+{\int }_{t_{\left(1\right)}}^{t_{\left(2\right)}}{a}_{00}^{1}dt$$={V_0^1}_{\left(1\right)}+\overline{a_{00}^1}[t_{\left(2\right)}-t_{\left(1\right)}]$ (278)

where, the mean acceleration $\overline{a_{00}^1}$ is the integral point value, and $t_{\left(2\right)}-t_{\left(1\right)}$ is time interval for the matter traveling from $r_{\left(1\right)}$ to $r_{\left(2\right)}$.

So that the mean acceleration is

$\overline{a_{00}^1}={\displaystyle \frac{{V_0^1}_{\left(2\right)}-{V_0^1}_{\left(1\right)}}{t_{\left(2\right)}-t_{\left(1\right)}}}$ (279)

On the other hand, with covariant bases there are the relationships of contra variant quantities and proper ones

$∆{\rho }_{\left(1\right)}={e_1}_{\left(1\right)}∆r_{\left(1\right)}, ∆{\tau }_{\left(1\right)}={e_0}_{\left(1\right)}∆t_{\left(1\right)}, ∆{\rho }_{\left(2\right)}={e_1}_{\left(2\right)}∆r_{\left(2\right)}, ∆{\tau }_{\left(2\right)}={e_0}_{\left(2\right)}∆t_{\left(2\right)}$ (280)

One can use the mean metric to calculate the proper time intervals from position 1 to positon 2

${\tau }_{\left(2\right)}-{\tau }_{\left(1\right)}={\int }_{t_{\left(1\right)}}^{t_{\left(2\right)}}{e}_{0}dt=\overline{e_0}(t_{\left(2\right)}-t_{\left(1\right)})$ (281)

where the $\overline{e_0}$ is the value at integral point, and it is suggested to be evaluated approximately as following in weak field

$\overline{e_0}\approx 0.5({e_0}_{\left(1\right)}+{e_0}_{\left(2\right)})$ (282)

The proper velocities

${V1/0}_{\left(1\right)}={\displaystyle \frac{∆{\rho }_{\left(1\right)}}{∆{\tau }_{\left(1\right)}}}$ (283)

${V1/0}_{\left(2\right)}={\displaystyle \frac{∆{\rho }_{\left(2\right)}}{∆{\tau }_{\left(2\right)}}}$ (284)

And the integral relationship in covariant space that

${V1/0}_{\left(2\right)}={V1/0}_{\left(1\right)}+{\int }_{{\tau }_{\left(1\right)}}^{{\tau }_{\left(2\right)}}a1/00d\tau$$={V1/0}_{\left(1\right)}+\overline{a1/00}({\tau }_{\left(2\right)}-{\tau }_{\left(1\right)})$ (285)

And also, we get the mean covariant acceleration with Lagranian mean value theorem of integration that

$\overline{a1/00}={\displaystyle \frac{{V1/0}_{\left(2\right)}-{V1/0}_{\left(1\right)}}{{\tau }_{\left(2\right)}-{\tau }_{\left(1\right)}}}$ (286)

So that the mean covariant derivative

$\overline{a1/00}={\displaystyle \frac{\frac{{e_1}_{\left(2\right)}∆r_{\left(2\right)}}{{e_0}_{\left(2\right)}∆t_{\left(2\right)}}-\frac{{e_1}_{\left(1\right)}∆r_{\left(1\right)}}{{e_0}_{\left(1\right)}∆t_{\left(1\right)}}}{\overline{e_0}(t_{\left(2\right)}-t_{\left(1\right)})}}={\displaystyle \frac{\frac{{e_1}_{\left(2\right)}}{{e_0}_{\left(2\right)}}{V_0^1}_{\left(2\right)}-\frac{{e_1}_{\left(1\right)}}{{e_0}_{\left(1\right)}}{V_0^1}_{\left(1\right)}}{\overline{e_0}(t_{\left(2\right)}-t_{\left(1\right)})}}$ (287)

It is of course the measuring forms of an acceleration of a freefalling. And then it could be compared to that of contra variant one.

We would like substitute the equation of contra variant velocity 2 of Eq. (278) into this equation. That is

$\overline{a1/00}=\overline{e^0}{\displaystyle \frac{\frac{{e_1}_{\left(2\right)}}{{e_0}_{\left(2\right)}}\left[\right(t_{\left(2\right)}-t_{\left(1\right)})\overline{a_{00}^1}+{V_0^1}_{\left(1\right)}]-\frac{{e_1}_{\left(1\right)}}{{e_0}_{\left(1\right)}}{V_0^1}_{\left(1\right)}}{t_{\left(2\right)}-t_{\left(1\right)}}}$$=\overline{e^0}{\displaystyle \frac{{e_1}_{\left(2\right)}}{{e_0}_{\left(2\right)}}}\overline{a_{00}^1}+\overline{e^0}{\displaystyle \frac{\frac{{e_1}_{\left(2\right)}}{{e_0}_{\left(2\right)}}-\frac{{e_1}_{\left(1\right)}}{{e_0}_{\left(1\right)}}}{t_{\left(2\right)}-t_{\left(1\right)}}}{V_0^1}_{\left(1\right)}$$=\overline{e^0}{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}\overline{a_{00}^1}+\overline{e^0}{\displaystyle \frac{{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}-{e_1}_{\left(1\right)}{e^0}_{\left(1\right)}}{t_{\left(2\right)}-t_{\left(1\right)}}}{V_0^1}_{\left(1\right)}$ (288)

It could be transformed to be

$\overline{a1/00}=\overline{e^0}{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}\overline{a_{00}^1}+\overline{e^0}{\displaystyle \frac{{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}-{e_1}_{\left(1\right)}{e^0}_{\left(1\right)}}{t_{\left(2\right)}-t_{\left(1\right)}}}{V_0^1}_{\left(1\right)}{\displaystyle \frac{r_{\left(2\right)}-r_{\left(1\right)}}{r_{\left(2\right)}-r_{\left(1\right)}}}$$=\overline{e^0}{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}\overline{a_{00}^1}+\overline{e^0}{\displaystyle \frac{{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}-{e_1}_{\left(1\right)}{e^0}_{\left(1\right)}}{r_{\left(2\right)}-r_{\left(1\right)}}}{V_0^1}_{\left(1\right)}\overline{V_0^1}$ (289)

Here we have got the transformed form of covariant acceleration of freefalling.

Nevertheless, with Lagrangian differential mean value theorem, we can write down the differential form as

$\overline{a1/00}=\overline{e^0}{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}\overline{a_{00}^1}+\overline{e^0}\overline{{\displaystyle \frac{\partial }{\partial r}}\left(e_1{e}^0\right)}{V_0^1}_{\left(1\right)}\overline{V_0^1}$ (290)

Or the form of reverse bases

$\overline{a1/00}=\overline{e^0}{e_1}_{\left(2\right)}{e^0}_{\left(2\right)}\overline{a_{00}^1}-\overline{e^0}{e_1}_{\left(2\right)}{e_1}_{\left(1\right)}{e^0}_{\left(2\right)}{e^0}_{\left(1\right)}\overline{{\displaystyle \frac{\partial }{\partial r}}\left(e^1{e}_0\right)}{V_0^1}_{\left(1\right)}\overline{V_0^1}$ (291)

Thus, by the way, another kind of proof of differential analysis of the Eq. (252) and Eq. (249) has been completed, in the way of measurable experiment.

6.3.2. Examples

Some terrestrial experiments are going to be put forward, that matters with initial velocity freefall in vacuum circumstance with in 1000m height to the ground. Both at the start point position 1 and end point position 2, the matter’s velocities will be measured. And of course, the space and time intervals between position 1 and 2 that depend on the so-called geodesic line will be measured together so that to calculate the mean accelerations.

Some basic data of the Earth have already been tested certainly, so that we can take the standard value for our experiments, such as the total mass of the Earth $M=5.97237\times {10}^{24}kg$, and the position on the ground could be assigned to have a radial coordinate $R_{⨁}=6.371393\times {10}^{6}m$. We could also take the gravitational constant $G=6.67259\times {10}^{-11}N{m}^2/k{g}^2$, with the light speed $\mathrm{c}=299792458 m/s$ thus the gravitational radius will be calculated as

$r^{*}={\displaystyle \frac{2GM}{c^2}}=8.8680827\times {10}^{-3}m$ (292)

With Newtonian equation and Schwarzschild’s solution, some positional data could be listed in following table.

Table 1. Base components, derivatives and gravity at experimental positions.

Table 1. Base components, derivatives and gravity at experimental positions.

So far as we have discussed, the accelerations $a_{00}^1$ and $a1/00$ are really geological quantities, and now it is necessary to make an extending study. We know that all kinds of interactions could be seen as momentum exchanges between matters, as that

$dP=d\left(mv\right)=vdm+mdv$ (293)

For the convenience, some quantities discussed in this section will not be marked with tensor index anymore.

In conditions of low velocity motions, the theory of special relativity indicates small mass variations, thus

$dP\approx mdv$ (294)

For the cases of high velocity motions, one should take a total analysis. Now the total acceleration could be defined

$\mathsf{\Lambda }={\displaystyle \frac{d\left(mv\right)}{mdt}}={\displaystyle \frac{vdm}{mdt}}+{\displaystyle \frac{dv}{dt}}$ (295)

It is said, the total acceleration includes mass variant acceleration and velocity variant acceleration, and the latter also could be called geometrical acceleration.

With a momentum variation, kinetic energy will vary a difference

$d{E}_k=vdP=v^{2}dm+mvdv$ (296)

At the same time, the mass energy equation of differential form is

$d{E}_k=c^{2}dm$ (297)

Thus, there will be

$c^{2}dm=v^{2}dm+mvdv$ (298)

To be divided by time differential, that will lead to the expression of acceleration

$a_{00}^1={\displaystyle \frac{dv}{dt}}={\displaystyle \frac{c^2-v^2}{mv}}{\displaystyle \frac{dm}{dt}}$ (299)

Now one can define a coefficient of geometrical acceleration

$\eta ={\displaystyle \frac{\frac{dv}{dt}}{\mathsf{\Lambda }}}={\displaystyle \frac{\frac{c^2-v^2}{mv}\frac{dm}{dt}}{\frac{vdm}{mdt}+\frac{c^2-v^2}{mv}\frac{dm}{dt}}}=1-{\displaystyle \frac{v^2}{c^2}}$ (300)

In one source field, single acting gravitational geometrical acceleration is

$a_{00}^1=\eta {\displaystyle \frac{GM}{r^2}}=\eta g$ (301)

where $g$ is the total acceleration of gravity.

We will see that geometrical acceleration declines as velocity goes up to a relativistic level, and it goes to zero as velocity closely catches up to light speed.

If a matter is accelerated from rest, the total energy includes rest part and kinetic part

${mc}^2=m_0{c}^2+\xi m{v}^2$ (302)

where $m$ is relativistic mass and $m_0$ is rest mass.

We know that in special relativity there is

$m={\displaystyle \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}}$ (303)

Back to Eq. (302), there is

$\xi =(1-\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}){\displaystyle \frac{c^2}{v^2}}$ (304)

Then the total kinetic energy

$E_k=\xi m{v}^2=(1-\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}){\displaystyle \frac{c^2}{v^2}}m{v}^2$ (305)

Case $v/c$ is a small value, $\xi$ would be close to 0.5, so that

$E_k\approx {\displaystyle \frac{1}{2}}m{v}^2$ (306)

On the occasion of freefalling the variation of kinetic energy

${\xi }_2{m}_2{v}^2-{\xi }_1{m}_1{v}_1^2={\int }_{r_{\left(1\right)}}^{r_{\left(2\right)}}mgds=\overline{m}\overline{g}s$ (307)

Again with Eq. (298) the energy difference in an experiment

$∆{mc}^2\approx ∆{mv}^2+m_{1}v∆v$ (308)

Thus, there is

$∆m=m_1{\displaystyle \frac{v∆v}{c^2-v^2}}$ (309)

Considering ${\eta }_1\approx {\eta }_2$ in experiments, the difference of kinetic energy could be written as

$∆E_k={\xi }_2{m}_2{v}^2-{\xi }_1{m}_1{v}_1^2={\xi }_2\left(m_1+∆m\right)({v_1+∆v)}^2-{\xi }_1{m}_1{v}_1^2$$\approx {\xi }_1\left(m_1+∆m\right)(v_1^2+2v_1∆v)-{\xi }_1{m}_1{v}_1^2$$={\xi }_1(∆m{v}_1^2+2m_1{v}_1∆v)$$={\xi }_1{m}_1({\displaystyle \frac{v_1∆v}{c^2-v_1^2}}{v}_1^2+2v_1∆v)$$\approx m_{1}gs$ (310)

so that

$∆v\approx {\displaystyle \frac{gs}{{\xi }_1{v}_1(\frac{v_1^2}{c^2-v_1^2}+2)}}$ (311)

Thus,

$t_{\left(2\right)}-t_{\left(1\right)}=∆t=∆v/\overline{a_{00}^1}$ (312)

Unfortunately, this solution cannot come up with a higher accuracy than that

$∆t={\displaystyle \frac{s}{v_1+0.5∆v}}$ (313)

After then, we are going to sponsor series of freefalling experiments. Contra variant accelerations and covariant accelerations for every position are easy to calculate. While measurable covariant acceleration $\overline{a1/00}$ could be obtained with measured distances and time intervals via Eq. (287). But it is convenient to calculate with Eq. (289), in that the latter is just a transformation of the previous. And in this equation, space intervals would be gained with Newtonian equations and time intervals $t_{\left(2\right)}-t_{\left(1\right)}$ with Eq. (313) for convenience. One may argue that the measured quantities might come from calculation. That doesn’t matter, because the equation has been verified for hundreds of years, therefore it is sure that the calculated quantities have equal value with that by measuring. And then the mean covariant acceleration will be taken to compare with the contra variant acceleration $a_{00}^1$ calculated with Eq. (301) and covariant acceleration $a1/00$ calculated with Eq. (249) or Eq. (252). Calculation results have been listed in Table 2 and Table 3.

7. Conclusions and Inferences and Their Applications

7.1. Conclusions

Previous discussions will lead to two conclusions for matters’ motions in gravitational fields:

1) For light: Light speed keeps general covariance, but light frequency keeps conservation in contra variant space.

2) For massive matters: Massive matter’s velocity does not perform general covariance.

These two conclusions have been drawn based on three items, which are light speed invariance, gravitational redshift measurement and acceleration measurement. Among these items, light speed invariance is a theoretical setting. This setting is come from special relativity and observational verifications. Gravitational redshifts and accelerations could be measured in realistic events that guarantees the conclusions in a very high reliability.

It is only the general covariance of light speed that has been observed. That relates to the inacceleratablity of light rays even in contra variant space, which is one of the performances of light speed invariance.

7.2. Inferences

These conclusions are really different from classical theory of general relativity and they will then lead to natural inferences. I prefer to focus on the inferences on kinematics and relativistic release:

1) For kinematics: General covariance goes break by a large range. During the motions in gravitational field, all matters, including light rays, will keep energy and momentum conservation in contra variant space rather than that in covariant space. Only for light rays they may keep velocity invariant in covariant space, but their energy and momentum will still keep conservation in contra variant space. Energy momentum conservations are the conservations under the condition of gravitational potential conversions. It is said that there is only one exception in realities, the light speed invariance, which will lead to the validity of light ray propagation Lagrangian. While for massive matters, Lagrangian goes invalid. At any positions in gravity fields, massive matters always have opportunities to be accelerated up to and keep velocities close to absolute-light-speed.

2) For relativistic release: Since apparent light speed may vary in gravitational field, that will bring changes to interaction ratio in particles of massive matters to influence fine structures. For electromagnet force there will be of variation of momentum exchange. It is also reasonable to predict that the speed of gluons relating to the strong interactions is general covariant like that of photons. On the other side, these interactions keep energy momentum conservations at the same time. Therefore, case massive matters inflow enough intervals in gravitational fields, they might get an excited state and release, which could be called relativistic release, just as excited electrons might do. The difference is that relativistic releases may experience thoroughly exciting in whole intrinsic structures, including exciting of electrons. Matters may also experience covariant deformation after relativistic release because of equivalent state. Moreover, relativistic emissions and absorptions may reveal the mystery of intrinsic structures.

7.3. Applications

Detailed discussions on some applications will be sponsored consequently that will greatly support the conclusions and inferences.

1) On kinematics: General covariance and conservation principle are the two key handles to rectify the classical equations, especially the principle of mass energy conservation. It would be seen that those efforts to employ the geodesic equation or covariant derivatives to build kinetic equations have already gone failed, in that covariant derivatives may be actually nonvanishing.

2) On relativistic release: The concept of equivalent state would be carried out to estimate the energy exceeding for inflow matters so that to discuss energy release, which will then lead to relativistic redshift of emission and absorption. Equivalent state also relates to relativistic deformation that might perform another kind of covariance.

8. Kinematics and Dynamics

8.1. The Most Important

The second Newtonian law interprets the mechanism of accelerative motions of massive matters so that to form the dynamics. Case in the conditions that matters have relativistic velocities, forces acting on matters will cause not only the variations of velocities but also the variations of matter’s mass. It should be pointed out that a force really is of a statistic quantity rather than an essential physical quantity. In fact, a force is just a performance of exchange of momentum, as well as mass energy. Thus, that physics could be called the relativistic dynamics.

But for light propagations, the second Newtonian law will not take effects anymore. Even in the case that a force is vertical to a light ray, we will see that the second Newtonian law remains invalid. That is the reason we suggest the concept of kinematics that others to the concept of dynamics. If we persistently employ the concept of dynamics, it should be a new one.

No matter the space time been determined by what kind of metrics and labeled by what kind of coordinates, it is just a methodology for descriptions for physical events. None of them would have priorities. Physics is on earth depends on its nature rather on spaces. The most important is the conservation principles in realities.

It is easy to imagine that geodesic line could be employed for the solution of kinematic trajectories of matters, because general relativity expects conservations in curve space. But we will find out that geodesic equation or covariant derivatives have not really taken effect in the solving of the kinematics in the past century. We know the reason is that covariant derivatives may be nonvanishing so that those imposed settings of vanishing covariant derivatives might cause discrepancies to realities.

Most of methodologies for kinematic trajectories published were based on the so-called Lagrangian. Besides these conditions, contra variant angular momentum conservation has been used in all of those solutions. One can imagine that this condition is apparently contradicted with general covariance. In fact, it is always the greatest reason for me to persist in this issue with more efforts.

Finally, the Lorentz covariance is also a kind of constraint condition, since it has been involved in the settings of Minkowski space and pseudo Riemannian space.

8.2. Falsification of the Employment of Geodesic Line for Kinematic Equation

We have drawn the conclusion that covariant accelerations of matters in gravitational fields may be nonvanishing so that the geodesic lines which ask for zero value of the covariant derivatives cannot be employed to be the kinematic equation for matter’s motions. We will find faults in those equations with which they declare the kinematic equations coming from geodesic lines.

The geodesic line equations presented by Weinberg [17] with metrics given by

$d{s}^2=B\left(r\right){dt}^2-A\left(r\right){dr}^2-r^2{d\theta }^2-r^2{sin}^2\theta d{\phi }^2$ (314)

is

${\displaystyle \frac{d^2{x}^{\mu }}{{d\tau }^2}}+{\Gamma }_{\nu \lambda }^{\mu }{\displaystyle \frac{d{x}^{\nu }}{d\tau }}{\displaystyle \frac{d{x}^{\lambda }}{d\tau }}=0$ (315)

That has been calculated to perform as components as [17]

$0={\displaystyle \frac{d^{2}r}{{d\tau }^2}}+{\displaystyle \frac{A^{\text{'}}\left(r\right)}{2A\left(r\right)}}({\displaystyle \frac{dr}{d\tau }}{)}^2-{\displaystyle \frac{r}{A\left(r\right)}}({\displaystyle \frac{d\theta }{d\tau }}{)}^2-r{\displaystyle \frac{{sin}^2\theta }{A\left(r\right)}}({\displaystyle \frac{d\phi }{d\tau }}{)}^2+{\displaystyle \frac{B^{\text{'}}\left(r\right)}{2A\left(r\right)}}({\displaystyle \frac{dt}{d\tau }}{)}^2$ (316)

$0={\displaystyle \frac{d^2\theta }{{d\tau }^2}}+{\displaystyle \frac{2}{r}}{\displaystyle \frac{d\theta }{d\tau }}{\displaystyle \frac{dr}{d\tau }}-sin\theta cos\theta ({\displaystyle \frac{d\phi }{d\tau }}{)}^2$ (317)

$0={\displaystyle \frac{d^2\phi }{{d\tau }^2}}+{\displaystyle \frac{2}{r}}{\displaystyle \frac{d\phi }{d\tau }}{\displaystyle \frac{dr}{d\tau }}+2cot\theta {\displaystyle \frac{d\phi }{d\tau }}{\displaystyle \frac{d\theta }{d\tau }}$ (318)

$0={\displaystyle \frac{d^{2}t}{{d\tau }^2}}+{\displaystyle \frac{B^{\text{'}}\left(r\right)}{B\left(r\right)}}{\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{dr}{d\tau }}$ (319)

And then, with $\theta =\pi /2$, the so-called kinematic equation, were finally drawn as

$A\left(r\right)({\displaystyle \frac{dr}{d\tau }}{)}^2+{\displaystyle \frac{L^2}{r^2}}-{\displaystyle \frac{1}{B\left(r\right)}}=-E$ (320)

where, $L=r^2{\displaystyle \frac{d\phi }{d\tau }}$ and $E$ are set constants.

It seems that the kinematic equation has been created by covariant derivatives. But it should be pointed out that Eq. (315) to Eq. (320) have gone wrong. Because we have discussed that the covariant derivatives could be nonvanishing in some occasions, so that there must be something wrong involved.

We are going to sponsor investigations in two ways for a comparison. Firstly, a transformation from the tangent space defined as $\left(dt,dr,d\theta ,d\phi \right)$ to that defined as $\left(d\tau ,d\rho ,rd\theta ,rsin\theta d\phi \right)$, just as the same as previous discussions, will be put into considerations. For convenience, the invariant distance should be rewritten as

$d{s}^2=-B\left(r\right){dt}^2+A\left(r\right){dr}^2+r^2{d\theta }^2+r^2{sin}^2\theta d{\phi }^2$$=-g_{00}{dt}^2+g_{11}{dr}^2+g_{22}{d\theta }^2+g_{33}d{\phi }^2$ (321)

where, signs in the equation have been modified to traditional forms and the metrics would be defined as $g_{00}=B\left(r\right)$, $g_{11}=A\left(r\right)$, $g_{22}=r^2$, $g_{33}=r^2{sin}^2\theta$, in which metrics should be positive as has been discussed.

The Eq. (228) could be employed for the solution, so that the derivative components could be performed with and then

${\left({\displaystyle \frac{D{V}^1}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{\partial \tau }}{\displaystyle \frac{dr}{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^1}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^1{V}^i{V}^0+{\Gamma }_{1i}^1{V}^i{V}^1+{\Gamma }_{2i}^1{V}^i{V}^2+{\Gamma }_{3i}^1{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^1}{d\tau }}\right)}_{tr}+{\Gamma }_{01}^1{V}^1{V}^0+{\Gamma }_{11}^1{V}^1{V}^1+{\Gamma }_{21}^1{V}^1{V}^2+{\Gamma }_{31}^1{V}^1{V}^3$$={\left({\displaystyle \frac{d{V}^1}{d\tau }}\right)}_{tr}+{\Gamma }_{11}^1{V}^1{V}^1$$={\displaystyle \frac{d^{2}r}{{d\tau }^2}}+{\displaystyle \frac{A^{\text{'}}\left(r\right)}{2A\left(r\right)}}({\displaystyle \frac{dr}{d\tau }}{)}^2$ (322)

${\left({\displaystyle \frac{D{V}^2}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{d\tau }}{\displaystyle \frac{d\theta }{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^2}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^2{V}^i{V}^0+{\Gamma }_{1i}^2{V}^i{V}^1+{\Gamma }_{2i}^2{V}^i{V}^2+{\Gamma }_{3i}^2{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^2}{d\tau }}\right)}_{tr}+{\Gamma }_{02}^2{V}^2{V}^0+{\Gamma }_{12}^2{V}^2{V}^1+{\Gamma }_{22}^2{V}^2{V}^2+{\Gamma }_{32}^2{V}^2{V}^3$$={\left({\displaystyle \frac{d{V}^2}{d\tau }}\right)}_{tr}+{\Gamma }_{12}^2{V}^2{V}^1$$={\displaystyle \frac{d^2\theta }{{d\tau }^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\theta }{d\tau }}{\displaystyle \frac{dr}{d\tau }}$ (323)

${\left({\displaystyle \frac{D{V}^3}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{d\tau }}{\displaystyle \frac{d\phi }{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^3}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^3{V}^i{V}^0+{\Gamma }_{1i}^3{V}^i{V}^1+{\Gamma }_{2i}^3{V}^i{V}^2+{\Gamma }_{3i}^3{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^3}{d\tau }}\right)}_{tr}+{\Gamma }_{03}^3{V}^3{V}^0+{\Gamma }_{13}^3{V}^3{V}^1+{\Gamma }_{23}^3{V}^3{V}^2+{\Gamma }_{33}^3{V}^3{V}^3$$={\left({\displaystyle \frac{d{V}^3}{d\tau }}\right)}_{tr}+{\Gamma }_{13}^3{V}^3{V}^1+{\Gamma }_{23}^3{V}^3{V}^2$$={\displaystyle \frac{d^2\phi }{{d\tau }^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\phi }{d\tau }}{\displaystyle \frac{dr}{d\tau }}+cot\theta {\displaystyle \frac{d\phi }{d\tau }}{\displaystyle \frac{d\theta }{d\tau }}$ (324)

${\left({\displaystyle \frac{D{V}^0}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{d\tau }}{\displaystyle \frac{dt}{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^0}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^0{V}^i{V}^0+{\Gamma }_{1i}^0{V}^i{V}^1+{\Gamma }_{2i}^0{V}^i{V}^2+{\Gamma }_{3i}^0{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^0}{d\tau }}\right)}_{tr}+{\Gamma }_{00}^0{V}^0{V}^0+{\Gamma }_{10}^0{V}^0{V}^1+{\Gamma }_{20}^0{V}^0{V}^2+{\Gamma }_{30}^0{V}^0{V}^3$$={\left({\displaystyle \frac{d{V}^0}{d\tau }}\right)}_{tr}+{\Gamma }_{10}^0{V}^0{V}^1$$={\displaystyle \frac{d^{2}t}{{d\tau }^2}}+{\displaystyle \frac{B^{\text{'}}\left(r\right)}{2B\left(r\right)}}{\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{dr}{d\tau }}$ (325)

where, $V^{\mu }={\displaystyle \frac{d{x}^{\mu }}{d\tau }}$ is number $\mu$ component of contra variant velocity.

We have seen that some errors in the Eq. (316) to Eq. (320) have been rectified. In fact, it is easy to find out calculation errors. If any $i\ne j$ the Christoffel symbol of ${\Gamma }_{\mu i}^j$=0, in that the bases we discussed are orthogonal.

Secondly, we are going to study another condition that the tangent spaces from $\left(dt,dr,rd\theta ,rsin\theta d\phi \right)$ to $\left(d\tau ,d\rho ,rd\theta ,rsin\theta d\phi \right)$. The invariant distance could be written as

$d{s}^2=-B\left(r\right){\left(dt\right)}^2+A\left(r\right){dr}^2+(rd\theta {)}^2+(rsin\theta d\phi {)}^2$ (326)

Thus, $g_{00}=B\left(r\right)$, $g_{11}=A\left(r\right)$, $g_{22}=1$, $g_{33}=1$.We can see that only gravitational metrics has been considered in the expression, as has been mentioned. This kind of settings would easily help us to verify the calculation previous. One may argue that this transformation has overcome Riemannian manifold definition because the contra variant space is not a $R^4$. But on earth in mathematics, that doesn’t matter because we know that the space could map to a $R^4$ at all. The derivation regulars are still available. Then the derivatives should be performed with Eq. (228) that

${\left({\displaystyle \frac{D{V}^1}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{\partial \tau }}{\displaystyle \frac{dr}{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^1}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^1{V}^i{V}^0+{\Gamma }_{1i}^1{V}^i{V}^1+{\Gamma }_{2i}^1{V}^i{V}^2+{\Gamma }_{3i}^1{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^1}{d\tau }}\right)}_{tr}+{\Gamma }_{01}^1{V}^1{V}^0+{\Gamma }_{11}^1{V}^1{V}^1+{\Gamma }_{21}^1{V}^1{V}^2+{\Gamma }_{31}^1{V}^1{V}^3$$={\left({\displaystyle \frac{d{V}^1}{d\tau }}\right)}_{tr}+{\Gamma }_{11}^1{V}^1{V}^1$$={\displaystyle \frac{d^{2}r}{{d\tau }^2}}+{\displaystyle \frac{A^{\text{'}}\left(r\right)}{2A\left(r\right)}}({\displaystyle \frac{dr}{d\tau }}{)}^2$ (327)

${\left({\displaystyle \frac{D{V}^2}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{d\tau }}{\displaystyle \frac{rd\theta }{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^2}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^2{V}^i{V}^0+{\Gamma }_{1i}^2{V}^i{V}^1+{\Gamma }_{2i}^2{V}^i{V}^2+{\Gamma }_{3i}^2{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^2}{d\tau }}\right)}_{tr}+{\Gamma }_{02}^2{V}^2{V}^0+{\Gamma }_{12}^2{V}^2{V}^1+{\Gamma }_{22}^2{V}^2{V}^2+{\Gamma }_{32}^2{V}^2{V}^3$$={\left({\displaystyle \frac{d{V}^2}{d\tau }}\right)}_{tr}+0$$=r{\displaystyle \frac{d^2\theta }{{d\tau }^2}}+{\displaystyle \frac{d\theta }{d\tau }}{\displaystyle \frac{dr}{d\tau }}$ (328)

${\left({\displaystyle \frac{D{V}^3}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{d\tau }}{\displaystyle \frac{rsin\theta d\phi }{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^3}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^3{V}^i{V}^0+{\Gamma }_{1i}^3{V}^i{V}^1+{\Gamma }_{2i}^3{V}^i{V}^2+{\Gamma }_{3i}^3{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^3}{d\tau }}\right)}_{tr}+{\Gamma }_{03}^3{V}^3{V}^0+{\Gamma }_{13}^3{V}^3{V}^1+{\Gamma }_{23}^3{V}^3{V}^2+{\Gamma }_{33}^3{V}^3{V}^3$$={\left({\displaystyle \frac{d{V}^3}{d\tau }}\right)}_{tr}+0$$=rsin\theta {\displaystyle \frac{d^2\phi }{{d\tau }^2}}+sin\theta {\displaystyle \frac{d\phi }{d\tau }}{\displaystyle \frac{dr}{d\tau }}+rcos\theta {\displaystyle \frac{d\phi }{d\tau }}{\displaystyle \frac{d\theta }{d\tau }}$ (329)

${\left({\displaystyle \frac{D{V}^0}{\partial \tau }}\right)}_{tr}={\left({\displaystyle \frac{D}{d\tau }}{\displaystyle \frac{dt}{d\tau }}\right)}_{tr}={\left({\displaystyle \frac{d{V}^0}{d\tau }}\right)}_{tr}+{\Gamma }_{0i}^0{V}^i{V}^0+{\Gamma }_{1i}^0{V}^i{V}^1+{\Gamma }_{2i}^0{V}^i{V}^2+{\Gamma }_{3i}^0{V}^i{V}^3$$={\left({\displaystyle \frac{d{V}^0}{d\tau }}\right)}_{tr}+{\Gamma }_{10}^0{V}^0{V}^1$$={\displaystyle \frac{d^{2}t}{{d\tau }^2}}+{\displaystyle \frac{B^{\text{'}}\left(r\right)}{2B\left(r\right)}}{\displaystyle \frac{dt}{d\tau }}{\displaystyle \frac{dr}{d\tau }}$ (330)

In comparisons of the last two calculations, we could find subtle nuance in that they are settled by different $x^{\mu }$ and $V^{\mu }$. But they have really given the equivalent results, in that both of them could be transformed to uniform covariant derivatives ${\displaystyle \frac{D\mathit{V}}{\partial \tau }}$. Because the latter calculation is very easy to be done, it is also a kind of verification to the previous. And moreover, the most important, the comparison calculations have verified the conclusions on inequality of mixed subscript Christoffel symbols, because the last result is easily worked out and approved to be right, and then one could find that the simplified expression of the second step could be used to verified the solution of the first step. That will finally indicate the errors in classical theory, as well as that in Weinberg’s calculations on geodesic equations.

Many efforts [11,12,17] have been made to attempt to prove the conservation principles after the equation of geodesic equations that it is expected

$r^2{\displaystyle \frac{d\phi }{d\tau }}=const. and (1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{dt}{d\tau }}=const.$ (331)

coming from the Eq. (318), and the Eq. (319).

It is easy to find that all of the works involve with errors. In comparison on the results of ${\left({\displaystyle \frac{D{V}^2}{\partial \tau }}\right)}_{tr}$ and ${\left({\displaystyle \frac{D{V}^3}{\partial \tau }}\right)}_{tr}$ in previous two kinds of strategies, we will find that the two derivatives do nothing with gravity influence, and they are just come from transformation of spherical coordinates so that any doctrines after that to form angular momentum conservation principle would be lack of supports. We will make further verifications in next sections that these two equations are all false. In fact, the first equation in (331) is not a correct form of angular momentum, and the last in (331) does nothing with energy. We will see that, motion trajectories cannot be calculated based on zero covariant derivatives, in that trajectories are not the geodesic lines.

8.3. Classical Equations of Light Ray Deflection

It is indicated in some books that the Lagrangian relates to Euler-Lagrangian equation and geodesic equation [3,4]. It is trivial to continue the discussions on whatever of the origins. I will say that the Lagrangian for light rays is absolutely correct, because we will see that it is just the expression of composition of light speed components in covariant space. It is the reason that the Lagrangian is employed for the equation of matter’s trajectories in most publications. In fact, velocity composition equation could be easily employed to solve the trajectory of Newtonian problems. But it should be pointed out that the Lagrangian equation is not proper for massive matters, which will be presented in following discussions.

Incomprehensibly, classical solving processes for Lagrangian equations seem like to do nothing with geodesic line equation and covariant differentials. On the other side, we could find that those solved trajectories all involved with contra variant angular momentum conservation, which also indicates that the solved trajectories may be not real geodesic lines.

To take the problem of the light rays passing across the Sun for granted, as shown in Figure 18.

It is expected in classical theories that for the motion of light rays, the Lagrangian is zero

$\mathcal{L}=-(1-{\displaystyle \frac{r^{*}}{r}})c^2{\dot{t}}^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=0$ (332)

where, Schwarzschild metrics has been concerned. Thereby, derivatives by proper time have been special expressed for conveniences as $\dot{t}={\displaystyle \frac{dt}{d\tau }}$, $\dot{r}={\displaystyle \frac{dr}{d\tau }}$ and $\dot{\phi }={\displaystyle \frac{d\phi }{d\tau }}$, which will also be employed in following expressions.

Thereafter, two items were always set to be constant in most publications [3,4] as

${\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial \mathcal{L}}{\partial \dot{\phi }}}=r^2\dot{\phi }=L$ (333)

${\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial \mathcal{L}}{\partial \dot{t}}}=(1-{\displaystyle \frac{r^{*}}{r}})c^2\dot{t}=c^{2}E$ (334)

NB, because of the multiplier $r^2$ used, $L$ is really an equivalent contra variant angular momentum rather than a covariant one, so that this setting seems like to insert the contra variant conservation in. It is said that the setting of $L$ does not coincide with general covariance. Even so, we will find out that it is exactly wrong setting together with the setting of constant $E$ to give not bad results, which perform two negatives making a positive.

Then the Lagrangian would be treated to be

$c^2{E}^2-{\dot{r}}^2-(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{L^2}{r^2}}=0$ (335)

Setting $r\mathrm{\text{'}}={\displaystyle \frac{dr}{d\phi }}={\displaystyle \frac{\dot{r}}{\dot{\phi }}}$, $u={\displaystyle \frac{1}{r}}$, and then $r\mathrm{\text{'}}={\displaystyle \frac{dr}{d\phi }}=-{\displaystyle \frac{u\mathrm{\text{'}}}{u^2}}$, there is

${\displaystyle \frac{c^2{E}^2}{L^2}}-{u\text{'}}^2-(1-r^{*}u)u^2=0$ (336)

Derivated by $\phi$, it is

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3}{2}}{r}^{*}{u}^2$ (337)

At a farthest position the right hand item goes to zero, then the equation will have a solution $u=sin\phi /b$, where $b$ is a distance from solar center to the asymptotic line, that could be called asymptotic distance. Replacing the very small right hand item with the solution, there is

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3r^{*}}{2b^2}}{sin}^2\phi$ (338)

There is a particular solution

$u_1={\displaystyle \frac{3r^{*}}{4b^2}}(1+{\displaystyle \frac{1}{3}}cos2\phi )$ (339)

Then the approximate solution of Eq. (337) is obtained

$u={\displaystyle \frac{sin\phi }{b}}+{\displaystyle \frac{3r^{*}}{4b^2}}(1+{\displaystyle \frac{1}{3}}cos2\phi )$ (340)

For an infinite large $r$, the $u$ is infinitesimal one, there is

${\phi }_{\mathrm{\infty }}=-{\displaystyle \frac{r^{*}}{b}}$ (341)

Observational deflection case $b\approx R_{⨀}$ is

$∆=2\left|{\phi }_{\mathrm{\infty }}\right|=1.75\text{'}\text{'}$ (342)

where $R_{⨀}$ is the radius of the Sun.

At the position $\phi ={\displaystyle \frac{\pi }{2}}$ and $r=R$, there is

${\displaystyle \frac{1}{R}}={\displaystyle \frac{1}{b}}+{\displaystyle \frac{3r^{*}}{4b^2}}(1-{\displaystyle \frac{1}{3}})$ (343)

or

$b\approx R+{\displaystyle \frac{r^{*}}{2}}$ (344)

That will bring about contradictions for the setting of Eq. (333) that at peak point there is

$L_R=r^2\dot{\phi }=Rc$ (345)

while at a very far point, there is

$L_{\infty }=r_{\infty }^2\dot{\phi }=bc=(R+{\displaystyle \frac{r^{*}}{2}})c\ne L_R$ (346)

It is said that the equations have been solved incorrectly. Might as well, we could find out an inevitable solution after the inappropriate setting of Eq. (333) in next section.

8.4. Revisit Equations of Light Ray Deflection

8.4.1. Errors Hidden in Classical Equations

It is obvious that a wrong setting has been made in Eq. (335), because in gravitational field, $(1-{\displaystyle \frac{r^{*}}{r}})c^2\dot{t}$ really varies with $r$. In fact, the Eq. (332) could be solved directly as following.

Considering $\dot{t}={\displaystyle \frac{dt}{d\tau }}=(1-{\displaystyle \frac{r^{\mathrm{*}}}{r}}{)}^{-1/2}$, the Lagrangian really is

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=0$ (347)

or

$-c^2+{\dot{\rho }}^2+r^2{\dot{\phi }}^2=0$ (348)

It is really the composition of light speed in covariant space.

Transform the equation as

$(1-{\displaystyle \frac{r^{*}}{r}})c^2-{\dot{r}}^2-(1-{\displaystyle \frac{r^{*}}{r}})r^2{\dot{\phi }}^2=0$ (349)

If setting peak point radius as $R$ and the angular moment at that point $L=Rc=r^2\dot{\phi }=const$, with $u={\displaystyle \frac{1}{r}}$, it becomes

$(1-r^{*}u)c^2-{u\text{'}}^2{R}^2-(1-r^{*}u)u^2{R}^2=0$ (350)

To be derivated by $\phi$, it is

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3}{2}}{r^{*}u}^2-{\displaystyle \frac{r^{*}}{2R^2}}$ (351)

With ${\displaystyle \frac{3r^{\mathrm{*}}}{2b^2}}{sin}^2\phi$ instead of ${\displaystyle \frac{3}{2}}{r^{\mathrm{*}}u}^2$, it becomes

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3r^{*}}{2b^2}}{sin}^2\phi -{\displaystyle \frac{r^{*}}{2R^2}}$ (352)

Because$R\approx b$, it could be solved as

$u={\displaystyle \frac{sin\phi }{b}}+{\displaystyle \frac{r^{*}}{4b^2}}(1+cos2\phi )$ (353)

One will obtain the solution of the equation as

${\phi }_{\mathrm{\infty }}=-{\displaystyle \frac{r^{*}}{2b}}$ (354)

At the peak point as $\phi ={\displaystyle \frac{\pi }{2}}$, we will get the constant $b$ that

${\displaystyle \frac{1}{R}}={\displaystyle \frac{1}{b}}+{\displaystyle \frac{r^{*}}{4b^2}}(1-1)$ (355)

so that

$b=R$ (356)

And the setting of Eq. (333) has been well kept that

$L_R=r^2\dot{\phi }=Rc$ (357)

and

$L_b=r^2\dot{\phi }=bc=Rc=L_R$ (358)

This is really the inevitable solution for classical equations but it is not a true result for realities. We have seen that the classical equations to have been solved to an answer Eq. (340) accurately up to the observation results is just caused by the wrong settings of energy momentum conservations of Eq. (333) and Eq. (334). It is said the classical equations do involve with problems while the wrong settings being set.

8.4.2. Momentum, Energy, and Angular Momentum Conservations

We have drawn the conclusion that light momentum keeps conservation in contra variant space rather than covariant space, and then of course, so does the light mass energy. In fact, apparent light speed or so-called contra variant light speed may varies in contra variant space, but light momentum and energy will not be affected by apparent speeds. In fact, neither geodesic equation nor the derivations of Lagrangian could help proving the Eq.(333) and Eq.(334), in that Eq.(333) and Eq.(334) are substantially not correct.

Considering a light ray goes a vertical distance on the Earth, one could gain the mass variation as

$m_r={\displaystyle \frac{h{{\nu }_0}_{\left(\infty \right)}}{c^2}}(1+{\displaystyle \frac{r^{*}}{2r}})=m_{\infty }(1+{\displaystyle \frac{r^{*}}{2r}})$ (359)

It could be called simplified equation of mass in gravitational field.

Light momentum could be expressed as

$P={\displaystyle \frac{h{\nu }_0}{c}}=m_{r}c$ (360)

or the momentum square

$P^2=m_r^2{c}^2$ (361)

Case in contra variant space, apparent light speed varies with position so that that speed cannot be used in expressions of light momentum directly. The invariant light speed $c=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.$ could be seen as absolute light speed. Eq. (360) performs full variation with gravity by $m_r$, which is the performance of momentum conservation. In fact, light momentum depends on frequency, just as $m_r$ does. If we ask more for a deep reason, that should be mass energy equation.

Case in covariant space, if light momentum will also be expressed by frequency, that will vary with bases additionally.

We know the Lagrangian

$c^2=(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2$ (362)

With Lagrangian substituted in conservative momentum square, it turns to be

$P^2=m_r^2\left[\right(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2]$ (363)

or

$P^2=m_r^2\left[\right(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-2}({\displaystyle \frac{dr}{dt}}{)}^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{r}^2\left({\displaystyle \frac{d\phi }{dt}}{)}^2\right]$ (364)

As we have discussed, light speed cannot be directly composed in contra variant space but can be done in covariant space. This is a reason the Lagrangian is employed in conservative momentum square.

In one source fields, the momentum vector could be discomposed to be components of centripetal and tangent

$\mathit{P}={\mathit{P}}_c+{\mathit{P}}_t$ (365)

or

$P^2=P_c^2+P_t^2$ (366)

Obviously, the tangent momentum relates to tangent velocity and centripetal momentum relates to centripetal velocity. It could also be inferred that the tangent component varies with the corresponding velocity, and so does the centripetal one.

So that there must be

$P_c^2=m_r^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2=m_r^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-2}({\displaystyle \frac{dr}{dt}}{)}^2$ (367)

and

$P_t^2=m_r^2{r}^2{\dot{\phi }}^2=m_r^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{r}^2({\displaystyle \frac{d\phi }{dt}}{)}^2$ (368)

In one source field, the angular moment conservation could be expressed as

$L^2=r^2{P}_t^2=m_r^2{r}^4{\dot{\phi }}^2=m_r^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{r}^4({\displaystyle \frac{d\phi }{dt}}{)}^2=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.$ (369)

It should be highlighted that we are talking about the moment conservation in contra variant space. It is amazing that the angular momentum should be expressed in the form of $r^2{m}_r\dot{\phi }$ or $r^2{m}_r{\displaystyle \frac{d\phi }{d\tau }}$ rather than the form of $r^2{m}_r{\displaystyle \frac{d\phi }{dt}}$, or we have seen that contra variant light momentum could be only directly composed in covariant form. The real reason is that the invariant light speed $c$ is just employed for the expressions by invariance.

The issues of light momentum have always been one of the controversies in physics for more than a hundred years [18]. The problem is the difficulty of assessing the light momentum in transparent materials between Minkowski’s equation [19] and Abraham’s equation [20]. To one’s surprise, we would have made the conclusion different from both of them, after the discussions in previous sections, because of Lorentz covariance.

Nevertheless, angular momentum brings about new surprises on it. We will find that the surprises not only have been picked up from the expressions, but also hide behind the kinematics of light propagations in gravitational fields. These efforts might bring about tiny contributions for the attempt to answer the question of Einstein about 'What are light quanta?' [21] I appreciate what Leonhardt has said that light continues to surprise [22].

8.4.3. Revisit Equations for Light Ray Trajectory

We have recognized that it is conservation principle that really controls the solutions. In fact, light rays in gravitational field may experience mass energy variation.

As has mentioned previous, the light mass at the peak point is

$m_R={\displaystyle \frac{h{{\nu }_0}_{\left(\infty \right)}}{c^2}}(1+{\displaystyle \frac{r^{*}}{2R}})$ (370)

And it varies at position $r$$m_r={\displaystyle \frac{h{{\nu }_0}_{\left(\infty \right)}}{c^2}}(1+{\displaystyle \frac{r^{*}}{2r}})$ (371)

These two equations involve the energy conservation in contra variant space rather than that in covariant space.

For a light ray passing by a one source field, there is the angular momentum conservation as

$L=r^2{m}_r\dot{\phi }=R{m}_{R}c=const.$ (372)

It should be highlighted again that the contra variant light momentum has been expressed by $c$ and $\dot{\phi }$ which are of covariant space quantities rather than $c_0^{\mu }$ and ${\displaystyle \frac{d\phi }{dt}}$ of contra variant ones. In fact, it could be proved that $c_0^{\mu }$ and ${\displaystyle \frac{d\phi }{dt}}$ cannot be taken to form momentum conservation, if one takes efforts to have a try. That is because momentum variation depends on $m_r$ that perform the effect of gravity, or in another words, the gravity input energy into the $m_r$. The invariant light speed $c$ employed reveals that light momentum variation really depends on frequency rather than real velocity, just as that light propagates in transparent materials. That perhaps is really surprise.

Considering the Eq. (370) and Eq. (371), Eq. (372) will lead to

$\dot{\phi }={\displaystyle \frac{{Rm}_{R}c}{m_r{r}^2}}={\displaystyle \frac{Rc}{r^2}}{\displaystyle \frac{1+\frac{r^{*}}{2R}}{1+\frac{r^{*}}{2r}}}={\displaystyle \frac{\tilde{L}}{r^2(1+\frac{r^{*}}{2r})}}$ (373)

where $\tilde{L}=\left(R+{\displaystyle \frac{r^{\mathrm{*}}}{2}}\right)c$. In weak field, the item $1/(1+{\displaystyle \frac{r^{\mathrm{*}}}{2r}})\approx (1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})$, thus

$\dot{\phi }={\displaystyle \frac{1}{r^2}}(1-{\displaystyle \frac{r^{*}}{2r}})\tilde{L}$ (374)

I prefer to present the Lagrangian again

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=0$ (375)

Define $r\mathrm{\text{'}}={\displaystyle \frac{dr}{d\phi }}$, so that $\dot{r}={\displaystyle \frac{dr}{d\phi }}{\displaystyle \frac{d\phi }{d\tau }}=r\mathrm{\text{'}}\dot{\phi }$. There is

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{r\text{'}}^2{\dot{\phi }}^2+r^2{\dot{\phi }}^2=0$ (376)

Insert the Eq. (374) into it, so that

$-c^2+(1-{\displaystyle \frac{{\mathrm{r}}^{\mathrm{*}}}{\mathrm{r}}}{)}^{-1}{\mathrm{r}\mathrm{\text{'}}}^2[{\displaystyle \frac{1}{r^2}}(1-{\displaystyle \frac{r^{*}}{2r}})\tilde{L}{]}^2+{\mathrm{r}}^2\left[{\displaystyle \frac{1}{r^2}}\right(1-{\displaystyle \frac{r^{*}}{2r}})\tilde{L}{]}^2=0$ (377)

With ${(1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})}^2\approx 1-{\displaystyle \frac{r^{\mathrm{*}}}{r}}$, it is

$-c^2+{r\text{'}}^2{\displaystyle \frac{{\tilde{L}}^2}{r^4}}+(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (378)

With $u={\displaystyle \frac{1}{r}}$, and $r\mathrm{\text{'}}={\displaystyle \frac{dr}{d\phi }}=-{\displaystyle \frac{u\mathrm{\text{'}}}{u^2}}$ it turns to be

$-{\displaystyle \frac{c^2}{{\tilde{L}}^2}}+{u\text{'}}^2+(1-u{r}^{*})u^2=0$ (379)

We have seen the similar form of Eq. (336), but this equation comes from the settings of the real conservation principles.

Differentiation results in

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3}{2}}{r}^{*}{u}^2$ (380)

Case $r$ is very big value, the equation could be simplified as

$u^{\text{'}\text{'}}+u=0$ (381)

It could be solved to be

$u={\displaystyle \frac{sin\phi }{b}}$ (382)

It is a horizontal line with a perpendicular distance $b$ to the center of the Sun.

The right item of Eq. (380) could be replaced with the simple solution, because the deviation is also very small. So that the equation could be reformed to be

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3r^{*}}{2b^2}}{sin}^2\phi$ (383)

Once again, we could obtain the solution

$u={\displaystyle \frac{sin\phi }{b}}+{\displaystyle \frac{3r^{*}}{4b^2}}(1+{\displaystyle \frac{1}{3}}cos2\phi )$ (384)

And then the deflection angle

${\phi }_{\mathrm{\infty }}=-{\displaystyle \frac{r^{*}}{b}}$ (385)

Case $\phi ={\displaystyle \frac{\pi }{2}}$, there is

${\displaystyle \frac{1}{R}}={\displaystyle \frac{1}{b}}+{\displaystyle \frac{r^{*}}{2b^2}}$ (386)

Because $b\gg r^{*}$ it becomes

$R\approx b-{\displaystyle \frac{r^{*}}{2}}$ (387)

or

$b=R+{\displaystyle \frac{r^{*}}{2}}$ (388)

To verify the momentum conservation that

$L_R=m_{R}Rc$ (389)

At a position $r\gg R$$L_b=m_{b}bc={\displaystyle \frac{1+\frac{r^{*}}{2r}}{1+\frac{r^{*}}{2R}}}{m}_{R}bc\approx {\displaystyle \frac{1}{R+\frac{r^{*}}{2}}}R{m}_{R}bc=m_{R}Rc=L_R$ (390)

It seems that we have got the same results as that of classical equations. But the truth is that the solution is the results after the conclusions of momentum and mass conservations which completely others to that of classical theory and at the same time the assumptions of Eq. (333) and Eq. (334) are thoroughly given up.

The most important is that the real kinematics of light propagation has been worked out.

8.5. More Discussions

The trajectories of light ray in gravitational fields have more details behind the previous solution. More discussions may help to discover more realities.

8.5.1. Detailed Discussions on the Coordinates of the Light Ray Trajectory

Further discussions are going to be sponsored to make more detailed analysis for understanding of two items, positions and angles.

Item 1 is to recognize various kinds of lines. The most important line is the real light ray that is emitted from a farthest star to the observers on the Earth. This line should be curved as it goes closely to the sun. Prolonging the straight parts of the light ray, one will gain the crossed straight lines, the asymptotic lines of light trajectory. They will be parallel to the two radial coordinate vectors $r_{\mathrm{\infty }}$ left and $r_{\mathrm{\infty }}$ right. There is another important line is the straight line from farthest star to the observer, that will present the real star direction from observer to the star.

Item 2 is to recognize those angles. ${\phi }_{\mathrm{\infty }}$ is the second coordinate of farthest point on the light ray. Because the Earth is far enough to the Sun, the elevation angle of observer view line could be seen as ${\phi }_{\mathrm{\infty }}$. And because the star is very very far from the sun, the angle between straight line to the star and horizontal line could be also seen as ${\phi }_{\mathrm{\infty }}$. Thus the total deflect angle of ${∆}_{Observe}$ is approximate $2{\phi }_{\mathrm{\infty }}$. They could be shown in Figure 19.

For the coordinate of the Earth, $u=1/A_u$, where $A_u$ is astronomical unit, the simple solution could be used

${\displaystyle \frac{1}{A_u}}\approx {\displaystyle \frac{{\phi }_{\oplus }}{b}}$ (391)

where, ${\phi }_{\oplus }$ is second coordinate of the Earth.

Thus, there is

${\phi }_{\oplus }\approx {\displaystyle \frac{b}{A_u}}$ (392)

Because we know that $\mathrm{b}\approx R_{\odot }$, where $R_{\odot }$ is solar radius, so that

${\phi }_{\oplus }\approx 0.004654478\mathrm{r}\mathrm{a}\mathrm{d}$ (393)

The height of the horizon line to light ray

$CE=R-A_{u}sin{\phi }_{\oplus }$ (394)

It is difficult to get a not bad accurate solution. However, we can turn to discuss the value of $h=BC$ instead. For the approximate of ${\phi }_{\mathrm{\infty }}\approx {\displaystyle \frac{1}{2}}{∆}_{\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{r}}$, it could be gain

$h\approx A_{u}sin{\phi }_{\mathrm{\infty }}\approx 635\mathrm{k}\mathrm{m}$ (395)

in the upper height $h=CF$.

There is a very small difference between real ray trajectory and asymptotic line, the $\delta =EF$. For the condition that light rays run from farthest position to the position they pass by the Sun, there is the equation after angular momentum conservation

$(1+{\displaystyle \frac{r^{*}}{2r_{\mathrm{\infty }}}})b=(1+{\displaystyle \frac{r^{*}}{2R}})R$ (396)

NB, $\mathrm{b}$ is perpendicular length to asymptotic line, which is the moment distance for farthest positions, and only in approximate cases, it could be seen as $R+\delta$. $R$ is peak point radius, and it need not be determined to be $R_{\odot }$ in these discussions theoretically.

Then it is easy to obtain

$b=R+{\displaystyle \frac{r^{*}}{2}}$ (397)

Peak difference between $R$ and $b$ is

(398)

It is more difficult to investigate such a fine distance in practice that not only because of the observational accuracy but also due to the coordinating of the peak point of light ray. The development of very-long-baseline interferometry have the capability of measuring angular separations and changes in angles as small as 10^-4 seconds of arc [23]. That shows probabilities for the quite good accuracy for fine angle measuring. This issue perhaps cannot be solved easily.

We can study the right branch of asymptotic line with an overplayed ${\phi }_{\mathrm{\infty }}$ as shown in Figure 20.

There is the asymptotic line equation as

$rsin(\phi +\left|{\phi }_{\mathrm{\infty }}\right|)=b$ (399)

or

$rsin(\phi +{\displaystyle \frac{r^{*}}{b}})=b$ (400)

Case $\phi ={\displaystyle \frac{\pi }{2}}$, we will see that the top point is just a little bit higher than horizontal line

$r=b/sin({\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{r^{*}}{b}})\approx b$ (401)

Case $\phi$ is not very close to ${\displaystyle \frac{\pi }{2}}$, considering ${\displaystyle \frac{r^{*}}{b}}$ is very small, an approximate form of sine function is

(402)

Thus, the deformed equation of asymptotic line could be written as

$r={\displaystyle \frac{b}{sin\phi +r^{*}cos\phi /b}}$ (403)

It should be pointed out that the equation

or $rsin\phi =b$ is a horizontal line with an asymptotic distance $b$ to the Sun center.

For the case that a light passes closely by the edge of the sun, there might be some influences from solar corona. It is a good idea to left a distance from the edge, for example, the position of ${1.5R}_{⨀}$ or even further. But this idea is only for theoretical discussions. Hitherto, we could only observe light deflections in the conditions that light rays pass by the sun edge just fine, because otherwise, peak point could not be coordinated at all.

8.5.2. The Invalidity of Newtonian Second Law in Light Propagation

It is the most interesting that perhaps there is the probability to carry out new numerical method to calculate the light trajectories or close-to-light-speed motions in gravitational field, which could be called ballistic trajectory method. Considering that the gravity component parallel to the motion trajectory will not bring about changes to further motion, we could only consider the calculation on motion variation due to vertical component of gravity so that to determine a differential coordinate on the trajectory. Thus, in the way incremental, the trajectory could be solved at last.

Firstly, it is proficient to take a motion of close-to-light-speed massive particle in one source field into discussion, as shown in Figure 21.

It is believed that for a massive particle in weak field, the vertical deviation could be solved by Newtonian second law

$∆s={\displaystyle \frac{1}{2}}{g}_v∆t^2$ (404)

where, $g_v$ is the component of gravity vertical to the velocity of the particle.

The coordinates at position $A$ are known to be $(r_{\mathrm{A}},{\phi }_{\mathrm{A}})$ or $(x_{\mathrm{A}},y_{\mathrm{A}})$. As well, the trajectory will have a direction with angle ${\mathsf{\alpha }}_{\mathrm{A}}$. Then, the distance in a time interval $∆t$ the particle travelling is

$AB=c∆t$ (405)

The deviation angle of $AB$ to $AC$ is

$\mathsf{\delta }\approx ∆s/AB$ (406)

and

$\mathsf{\gamma }={\mathsf{\alpha }}_{\mathrm{A}}+\mathsf{\delta }$ (407)

Thus, the coordinates at position $B$ could be calculated as

$x_{\mathrm{B}}=x_{\mathrm{A}}+ABcos\mathsf{\gamma }$ (408)

$y_{\mathrm{B}}=y_{\mathrm{A}}+ABsin\mathsf{\gamma }$ (409)

or

$r_{\mathrm{B}}=\sqrt{x_B^2+y_B^2}$ (410)

${\phi }_{\mathrm{B}}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}{\displaystyle \frac{x_{\mathrm{B}}}{r_{\mathrm{B}}}}$ (411)

It should be pointed out that the angle $\mathsf{\gamma }$ is not the direction angle ${\mathsf{\alpha }}_{\mathrm{B}}$. The ${\mathsf{\alpha }}_{\mathrm{B}}$ could be calculated by angular momentum conservation.

$(1+{\displaystyle \frac{r^{*}}{2R}})R=(1+{\displaystyle \frac{r^{*}}{2r_{\mathrm{B}}}})r_{\mathrm{B}}sin{\beta }_B$ (412)

where, ${\beta }_B={\mathsf{\alpha }}_{\mathrm{B}}+{\phi }_{\mathrm{B}}$.

Now back to the fly of light ray from position A to position B. It might be imagined to calculate the deviation $∆s$ also by Newtonian second law. That sounds naturally to see the photons as light speed particles with dynamic mass so that to deviate in the same way as massive particles do. Unfortunately, it is impossible in that that kind of calculation will lead to the result very close to that of massive particles. It seems like that the Newtonian second law sounds invalid in light propagation even at the vertical direction. Perhaps one can propose a double gravity for a simulation on light propagation with respect to that of massive particles and it could be imagined that the results would be of not bad precisions. But the truth is that they are really not of a same issue in that they would have different asymtotic distance $b$. An interesting clue is that light rays are un-accelerable even at the direction vertical to the motion. Maybe that could be employed to interpret the invalidity of Newtonian second law.

Anyway, there is still an opportunity to explore the ballistic trajectory method for them. That is to perform by trial methodologies. We can imagine that after point A there will be a wave front after Huygens’ postulation, then, some points on it may be selected for further considerations. With angular momentum conservation and Lagrangian, one can calculate the velocity and angle ${\mathsf{\alpha }}_{\mathrm{B}}$, as well as coordinates as shown in Figure 22. Thus, the deviations of the points could be estimated to help for further trials. I have made more efforts to try but not done, although I still believe the probabilities.

8.5.3. A Wrong Treatment for Light Propagations

If the covariant angular momentum conservation would be insisted for light propagations as

$L=R{m}_{\mathrm{R}}c=r^2{m}_r{\displaystyle \frac{d\phi }{dt}}$ (413)

It is seemingly that ${\displaystyle \frac{d\phi }{dt}}$ presents the contra variant angular velocity of photons which is expected to correspond to contra variant angular momentum. And moreover, it could be argued to take $R{m}_{\mathrm{R}}{c}_0^{\mu }$ as expressions of contra variant angular momentum, that will exactly lead to conservation break as gravitational redshift is concerned.

Now for the equation Eq. (413), there is

${\displaystyle \frac{d\phi }{dt}}={\displaystyle \frac{{Rm}_{\mathrm{R}}c}{m_r{r}^2}}={\displaystyle \frac{Rc}{r^2}}{\displaystyle \frac{1+\frac{r^{*}}{2R}}{1+\frac{r^{*}}{2r}}}={\displaystyle \frac{\tilde{L}}{r^2(1+\frac{r^{*}}{2r})}}$ (414)

where $\tilde{L}=(R+{\displaystyle \frac{r^{\mathrm{*}}}{2}})c$. In weak field, the item $1/(1+{\displaystyle \frac{r^{\mathrm{*}}}{2r}})\approx (1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})$, and ${(1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})}^2\approx 1-{\displaystyle \frac{r^{\mathrm{*}}}{r}}$, thus

${\displaystyle \frac{d\phi }{dt}}={\displaystyle \frac{(1-\frac{r^{*}}{2r})\tilde{L}}{r^2}}$ (415)

Because the Lagrangian with coordinate time is

$-c^2+{(1-{\displaystyle \frac{r^{*}}{r}})}^{-2}{\left({\displaystyle \frac{dr}{dt}}\right)}^2+{(1-{\displaystyle \frac{r^{*}}{r}})}^{-1}{r}^2{\left({\displaystyle \frac{d\phi }{dt}}\right)}^2=0$ (416)

It could be transformed to be

$c^2-{(1-{\displaystyle \frac{r^{*}}{r}})}^{-1}{r\text{'}}^2{\displaystyle \frac{{\tilde{L}}^2}{r^4}}-{\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (417)

or

$(1-{\displaystyle \frac{r^{*}}{r}})c^2-{r\text{'}}^2{\displaystyle \frac{{\tilde{L}}^2}{r^4}}-(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (418)

Consider $\tilde{L}\approx bc$ again

$(1-r^{*}u)-{u\text{'}}^2{b}^2-(1-r^{*}u)u^2{b}^2=0$ (419)

To be derivated to be

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3}{2}}{r^{*}u}^2-{\displaystyle \frac{r^{*}}{2b^2}}$ (420)

It could be solved as

$u={\displaystyle \frac{sin\phi }{b}}+{\displaystyle \frac{r^{*}}{4b^2}}+{\displaystyle \frac{r^{*}}{4b^2}}cos2\phi$ (421)

One will gain obtain that

${\phi }_{\mathrm{\infty }}=-{\displaystyle \frac{r^{*}}{2b}}$ (422)

One can verify the peak point on the case of $\phi =\pi /2$, and $r=R$, and then will gain

$b=R$ (423)

That has broken that principle of angular momentum conservation. Of course, it is a wrong answer for light ray propagations, because of a wrong setting.

8.5.4. Equations of Close-to-Light-Speed Massive Particles

We have known that massive particles will not run with general covariance. They run with Newtonian laws. The velocity composition for close-to-light-speed massive particles really is

$-c^2+{\left({\displaystyle \frac{dr}{dt}}\right)}^2+r^2{\left({\displaystyle \frac{d\phi }{dt}}\right)}^2=0$ (424)

The conservation of angular momentum

L=$R{m}_{\mathrm{R}}c=r^2{m}_r{\displaystyle \frac{d\phi }{dt}}$ (425)

One will find that ${\displaystyle \frac{d\phi }{dt}}$ is used here is because the velocity composition equation Eq. (424), which is rare different from the Lagrangian for light. The constant $c$ is not the speed of light while it really is the approximate speed of massive matter. So that the $c$ in Eq. (424) is just a velocity composition of close-to-light-speed motion. The Eq. (424) and Eq. (425) perform the differences of conservation between light fly and the motion of massive matter. We will see these differences in the equations of low velocity motions of massive matters in next sections.

The angular velocity

${\displaystyle \frac{d\phi }{dt}}={\displaystyle \frac{{Rm}_{\mathrm{R}}c}{m_r{r}^2}}={\displaystyle \frac{Rc}{r^2}}{\displaystyle \frac{1+\frac{r^{*}}{2R}}{1+\frac{r^{*}}{2r}}}={\displaystyle \frac{\tilde{L}}{r^2(1+\frac{r^{*}}{2r})}}$ (426)

where $\tilde{L}=(R+{\displaystyle \frac{r^{\mathrm{*}}}{2}})c$. In weak field, the item $1/(1+{\displaystyle \frac{r^{\mathrm{*}}}{2r}})\approx (1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})$, and ${(1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})}^2\approx 1-{\displaystyle \frac{r^{\mathrm{*}}}{r}}$, thus

${\displaystyle \frac{d\phi }{dt}}={\displaystyle \frac{1}{r^2}}(1-{\displaystyle \frac{r^{*}}{2r}})\tilde{L}$ (427)

Together with ${\displaystyle \frac{dr}{dt}}={\displaystyle \frac{dr}{d\phi }}{\displaystyle \frac{d\phi }{dt}}=r\mathrm{\text{'}}{\displaystyle \frac{d\phi }{dt}}$, the Eq. (424) turns to be

$c^2-(1-{\displaystyle \frac{r^{*}}{r}}){r^{\text{'}}}^2{\displaystyle \frac{{\tilde{L}}^2}{r^4}}-(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (428)

or

$(1+{\displaystyle \frac{r^{*}}{r}})c^2-{r\text{'}}^2{\displaystyle \frac{{\tilde{L}}^2}{r^4}}-{\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (429)

With $u={\displaystyle \frac{1}{r}}$, and $r\mathrm{\text{'}}={\displaystyle \frac{dr}{d\phi }}=-{\displaystyle \frac{u\mathrm{\text{'}}}{u^2}}$, and considering $\tilde{L}\approx bc$, there is

$(1+r^{*}u)-{u\text{'}}^2{b}^2-u^2{b}^2=0$ (430)

To be differentiated as

$u^{\text{'}\text{'}}+u={\displaystyle \frac{r^{*}}{2b^2}}$ (431)

It could be solved as

$u={\displaystyle \frac{sin\phi }{b}}+{\displaystyle \frac{r^{*}}{2b^2}}$ (432)

Obviously, there is

${\phi }_{\mathrm{\infty }}=-{\displaystyle \frac{r^{*}}{2b}}$ (433)

It is easy to calculate in Eq. (432) that at the peak point, $\phi =\pi /2$, and $r=R$, so that

$b=R+{\displaystyle \frac{r^{*}}{2}}$ (434)

Or with angular momentum conservation there is

$(1+{\displaystyle \frac{r^{*}}{2r_{\mathrm{\infty }}}})b=(1+{\displaystyle \frac{r^{*}}{2R}})R$ (435)

Again, we obtain

$b=R+{\displaystyle \frac{r^{*}}{2}}$ (436)

The asymptotic line

$r={\displaystyle \frac{b}{sin\phi +r^{*}cos\phi /b/2}}$ (437)

It is said that the trajectories of light rays and close-to-light-speed particles present different ${\phi }_{\mathrm{\infty }}$ but the same peak difference $\mathsf{\delta }$. The same peak difference is just the result of momentum conservation.

In fact, these studies have help to create the dynamics of close-to-light-speed particles in gravitational field. By the way, one can compare this solution with that in section 8.4.1 that they have both given the same result of ${\phi }_{\mathrm{\infty }}$, but they gave different value of $b$.

8.5.5. Comparisons of Numerical Solutions and Algebraic Solutions

To make comparisons with numerical and algebraic solutions is not only a kind of further verification but also a further support to the conclusion of energy moment conservation, and at last, a surprise of light propagation. As has discussed previous, ballistic trajectory method could be developed to calculate the trajectories of close-to-light massive particles. It could be applied by dividing trajectory to finite segments and calculating coordinates with Eq. (404) to Eq. (412) step by step. The invalidity of Newtonian second law for light propagation is actual another kind of support to the inferences of kinematics.

Notwithstanding, difference method for all differential equations could also be employed for more comparisons. Difference method has shown great advantages in scientific calculations and many excellent schemes have been developed to serve for more complex requirements.

For the equation of light rays

$u^{\text{'}\text{'}}+u={\displaystyle \frac{3}{2}}{r^{*}u}^2$ (438)

The simple central difference scheme could be suggested that

$u^{\text{'}\text{'}}={\displaystyle \frac{u\left(\phi +∆\phi \right)-2u\left(\phi \right)+u(\phi -∆\phi )}{(∆\phi {)}^2}}$ (439)

Thus, the difference equation could be built as

${\displaystyle \frac{u\left(\phi +∆\phi \right)-2u\left(\phi \right)+u(\phi -∆\phi )}{(∆\phi {)}^2}}+u\left(\phi \right)={\displaystyle \frac{3}{2}}{r}^{*}{u}^2\left(\phi \right)$ (440)

Pre-exercises show that if step intervals defined by $∆\phi <0.1°$, the calculations would get quite good accuracy.

As for the equation of close-to-light massive particles, the differential equation

$u^{\text{'}\text{'}}+u={\displaystyle \frac{r^{*}}{2b^2}}$ (441)

could also be built simply as

${\displaystyle \frac{u\left(\phi +∆\phi \right)-2u\left(\phi \right)+u(\phi -∆\phi )}{(∆\phi {)}^2}}+u\left(\phi \right)={\displaystyle \frac{r^{*}}{2b^2}}$ (442)

Thus, we would sponsor a comparison with the analytical solutions, difference method solutions and the ballistic trajectory method solutions mentioned previously, together with the asymptotic lines and horizontal line for references.

Numerical methods of difference and ballistic were carried in office computer and others were completed by the calculator of my mobile phone, in that the phone calculator could provide 8 floating point precisions more than that of the Fortran software in the computer.

It is shown in Table 4 that difference method and ballistic method still perform not bad precisions in the results of upper parts of the trajectories. Of course, both of the two methods are of step by step arithmetic so as to accumulate quite amount of deviations at the rear parts of the trajectories. Anyway, the two numerical methods are reliable, that greatly supports the inferences of kinematics.

It is easy to develop more optimal schemes for difference method and the way of optimal secant seeking instead of the tangent seeking for ballistic method or any other effective technologies to improve the precisions of numerical analyses. That will confirm the conclusions and inferences that have been drawn previous.

8.6. Time Delay of Radar Echoes

For a light ray passing by the Sun, the apparent light speed varies with the positions and directions on the trajectory. There should be a difference between the real time interval and that calculated via invariant light speed instead of apparent light speed. Shapiro proposed new tests of time delay of radar signals which transmitted from the Earth to pass by the edge of the Sun to another planet or satellite and then they would be reflected back to the Earth [24,25]. The observations on time delay of radar echoes would forcefully support the theory of general relativity as well as that of light ray deflect.

However, the solutions of time delay must have involved in the problems with light trajectory, that the solution process has inherited the errors in classical equations of light trajectory, so that it is necessary to make a detailed discussion to rectify.

8.6.1. Classical Solution

In classical procedure, with the assumptions of $\dot{t}(1-{\displaystyle \frac{r^{*}}{r}})=E$ and $r^2\dot{\phi }=L$, the Lagrangian could be transformed to be

${\dot{r}}^2=c^2{E}^2-(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{L^2}{r^2}}$ (443)

as that in Eq. (335).

And also with

$\dot{r}={\displaystyle \frac{dr}{dt}}\dot{t}={\displaystyle \frac{dr}{dt}}E(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}$ (444)

The Lagrangian becomes

$(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-3} ({\displaystyle \frac{dr}{dt}}{)}^2=c^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}-{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{L^2}{E^2}}$ (445)

At the peak point, ${\displaystyle \frac{dr}{dt}}=0$ so that there is

${\displaystyle \frac{L^2}{E^2}}=c^2{R}^2(1-{\displaystyle \frac{r^{*}}{R}}{)}^{-1}$ (446)

Where, $R$ is the coordinate of the peak point.

Taking it back into the Eq. (445), there is

$(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-3} ({\displaystyle \frac{dr}{dt}}{)}^2-c^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}+c^2{\displaystyle \frac{R^2}{r^2}}(1-{\displaystyle \frac{r^{*}}{R}}{)}^{-1}=0$ (447)

or

$({\displaystyle \frac{dr}{dt}}{)}^2=c^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^2-c^2{\displaystyle \frac{R^2}{r^2}}(1-{\displaystyle \frac{r^{*}}{r}}{)}^3(1-{\displaystyle \frac{r^{*}}{R}}{)}^{-1}$ (448)

The differential relationship could be integrated that

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}{\int }_R^r(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}[1-(1-{\displaystyle \frac{r^{*}}{r}}\left)\right(1-{\displaystyle \frac{r^{*}}{R}}{)}^{-1}{\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}dr$ (449)

Because ${\displaystyle \frac{r^{*}}{r}}$ and ${\displaystyle \frac{r^{*}}{R}}$ are very small, it could be written as

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}{\int }_R^r(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}[1-(1-{\displaystyle \frac{r^{*}}{r}}+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}dr$ (450)

It has an approximate form [4] as

${\left.t\right|}_R^r\approx {\displaystyle \frac{1}{c}}{\int }_R^r(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-1/2}[1+{\displaystyle \frac{r^{*}}{r}}+{\displaystyle \frac{r^{*}R}{2r\left(r+R\right)}}]dr$$={\displaystyle \frac{1}{c}}[\sqrt{r^2-R^2}+r^{*}\mathit{ln}\left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)+{\displaystyle \frac{r^{*}}{2}}\sqrt{{\displaystyle \frac{r-R}{r+R}}}]$ (451)

8.6.2. Errors in

We have known that the assumption in classical equations is incorrect. In fact, the equation could be solved without the assumption. Such as the Lagrangian

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=0$ (452)

With $L=Rc=r^2\dot{\phi }=const.$ it is

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+{\displaystyle \frac{c^2{R}^2}{r^2}}=0$ (453)

And we know that

$\dot{r}={\displaystyle \frac{dr}{dt}}\dot{t}={\displaystyle \frac{dr}{dt}}{\displaystyle \frac{dt}{d\tau }}={\displaystyle \frac{dr}{dt}}(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1/2}$ (454)

so that

$({\displaystyle \frac{dr}{dt}}{)}^2=c^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^2-c^2(1-{\displaystyle \frac{r^{*}}{r}}{)}^2{\displaystyle \frac{R^2}{r^2}}$ (455)

The differential relationship could be integrated that

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}{\int }_R^r(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-1/2}dr$ (456)

Approximate solution is

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}[\sqrt{r^2-R^2}+r^{*}\mathit{ln}\left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)]$ (457)

One can find that this treatment has just brought about a little deviation from the previous. That is because the trajectory is only a little different from that one at deflect angle.

8.6.3. Revisit Solution for Radar Echoes

The revisit equation of trajectory may help to get new performances of the issue.

For the Lagrangian

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=0$ (458)

In previous section, we have got the angular velocity expression based on energy momentum conservation as discussed in previous sections that $R{m}_{\mathrm{R}}c=r^2{m}_r\dot{\phi }$ and $\dot{\phi }={\displaystyle \frac{{Rm}_{R}c}{m_r{r}^2}}={\displaystyle \frac{Rc}{r^2}}{\displaystyle \frac{1+\frac{r^{*}}{2R}}{1+\frac{r^{*}}{2r}}}={\displaystyle \frac{\tilde{L}}{r^2(1+\frac{r^{*}}{2r})}}$, where

$\tilde{L}=(R+{\displaystyle \frac{r^{*}}{2}})c$ (459)

In weak field, the item $1/(1+{\displaystyle \frac{r^{\mathrm{*}}}{2r}})\approx (1-{\displaystyle \frac{r^{\mathrm{*}}}{2r}})$, thus

$\dot{\phi }={\displaystyle \frac{1}{r^2}}(1-{\displaystyle \frac{r^{*}}{2r}})\tilde{L}$ (460)

Then the Lagrangian becomes

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+{\displaystyle \frac{1}{r^2}}(1-{\displaystyle \frac{r^{*}}{r}}){\tilde{L}}^2=0$ (461)

A transformation could be made as

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-2}({\displaystyle \frac{dr}{dt}}{)}^2+(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (462)

With Eq. (459) it becomes

$-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-2}({\displaystyle \frac{dr}{dt}}{)}^2+(1-{\displaystyle \frac{r^{*}}{r}})(1+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2{c}^2}{r^2}}=0$ (463)

so that there is

$({\displaystyle \frac{dr}{dt}}{)}^2=c^2[(1-{\displaystyle \frac{r^{*}}{r}}{)}^2-(1-{\displaystyle \frac{r^{*}}{r}}{)}^3(1+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}]$ (464)

or

$(dt{)}^2={\displaystyle \frac{1}{c^2}}[(1-{\displaystyle \frac{r^{*}}{r}}{)}^2-(1-{\displaystyle \frac{r^{*}}{r}}{)}^3(1+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1}(dr{)}^2$ (465)

or

$dt={\displaystyle \frac{1}{c}}\left[\right(1-{\displaystyle \frac{r^{*}}{r}}{)}^2-(1-{\displaystyle \frac{r^{*}}{r}}{)}^3(1+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}dr$ (466)

Integrate above differential to be

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}{\int }_R^r(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}(1-{\displaystyle \frac{R^2}{r^2}}+{\displaystyle \frac{r^{*}}{r}}{\displaystyle \frac{R^2}{r^2}}{-{\displaystyle \frac{r^{*}}{R}}{\displaystyle \frac{R^2}{r^2}})}^{-1/2}dr$ (467)

or

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}{\int }_R^r(1+{\displaystyle \frac{r^{*}}{r}})[1-{\displaystyle \frac{R^2}{r^2}}+({\displaystyle \frac{r^{*}}{r}}-{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}dr$ (468)

By building a function

$f\left(x\right)=x^{-1/2}$ (469)

where, $x=1-{\displaystyle \frac{R^2}{r^2}}$. The derivative

$f^{\text{'}}\left(x\right)=-{\displaystyle \frac{1}{2}}{x}^{-3/2}$ (470)

Considering ${\displaystyle \frac{r^{*}}{r}}$ is very small, the rear part in the integral could be simplified as

$[1-{\displaystyle \frac{R^2}{r^2}}+({\displaystyle \frac{r^{*}}{r}}-{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}\approx (1-{\displaystyle \frac{R^2}{r^2}}{)}^{-{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-3/2}({\displaystyle \frac{r^{*}{R}^2}{r^3}}-{\displaystyle \frac{r^{*}R}{r^2}})$ (471)

Then the integration could be gain as

${\left.t\right|}_R^r\approx {\displaystyle \frac{1}{c}}{\int }_R^r\left[\right(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-1/2}(1+{\displaystyle \frac{r^{*}}{r}})-{\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-3/2}({\displaystyle \frac{r^{*}{R}^2}{r^3}}-{\displaystyle \frac{r^{*}R}{r^2}}\left)\right]dr$ (472)

where in the last item, a $(1+{\displaystyle \frac{r^{*}}{r}})$ has been simplified to be 1.

The first part of the integration could be calculated to be

$\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}1={\displaystyle \frac{1}{c}}{\int }_R^r(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-1/2}(1+{\displaystyle \frac{r^{*}}{r}})dr={\displaystyle \frac{1}{c}}[\sqrt{r^2-R^2}+r^{*}\mathit{ln}\left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)]$ (473)

and the last part is done as

$\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}2=-{\displaystyle \frac{1}{c}}{\int }_R^r{\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-3/2}({\displaystyle \frac{r^{*}{R}^2}{r^3}}-{\displaystyle \frac{r^{*}R}{r^2}}\left)\right]dr={\displaystyle \frac{r{r}^{*}}{2\sqrt{r^2-R^2}}}-{\displaystyle \frac{r^{*}R}{2\sqrt{r^2-R^2}}}$ (474)

so that the total integration is

${\left.t\right|}_R^r\approx {\displaystyle \frac{1}{c}}[\sqrt{r^2-R^2}+r^{*}\mathit{ln}\left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)+{\displaystyle \frac{r^{*}}{2}}\sqrt{{\displaystyle \frac{r-R}{r+R}}}]$ (475)

8.6.4. Solution for Close-to-Light-Speed Particles

Now let’s discuss another kind of no delay time spend, the time spend of close-to-light-speed particles. The velocity composition of close-to-light-speed particles could be expressed as

$-c^2+({\displaystyle \frac{dr}{dt}}{)}^2+r^2({\displaystyle \frac{d\phi }{dt}}{)}^2=0$ (476)

With angular momentum conservation, there is

$-c^2+({\displaystyle \frac{dr}{dt}}{)}^2+(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{{\tilde{L}}^2}{r^2}}=0$ (477)

or

$-c^2+({\displaystyle \frac{dr}{dt}}{)}^2+(1-{\displaystyle \frac{r^{*}}{r}}\left)\right(1+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2{c}^2}{r^2}}=0$ (478)

so that the integration could be built

${\left.t\right|}_R^r={\displaystyle \frac{1}{c}}{\int }_R^r[1-(1-{\displaystyle \frac{r^{*}}{r}}\left)\right(1+{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}dr$$={\displaystyle \frac{1}{c}}{\int }_R^r[1-{\displaystyle \frac{R^2}{r^2}}-({\displaystyle \frac{r^{*}}{r}}-{\displaystyle \frac{r^{*}}{R}}){\displaystyle \frac{R^2}{r^2}}{]}^{-1/2}dr$$\approx {\displaystyle \frac{1}{c}}{\int }_R^r\left[\right(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-1/2}-{\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{R^2}{r^2}}{)}^{-3/2}({\displaystyle \frac{r^{*}{R}^2}{r^3}}-{\displaystyle \frac{r^{*}R}{r^2}}\left)\right]dr$$={\displaystyle \frac{1}{c}}[\sqrt{r^2-R^2}+{\displaystyle \frac{r^{*}}{2}}\sqrt{{\displaystyle \frac{r-R}{r+R}}}]$ (479)

8.6.5. Equations of Time Delay

We have found that the revisit solution of time spend is the same with classical. The reality is that the classical treatment has got the same trajectory by additional settings, so that it is undoubtful to gain a same time spend with. In fact, the problem of time delay of radar echoes is just a kind of performance of light deflection. The results in these discussions are also just extensions of that in the problem of light deflection. The classical equation for time delay is to defined the difference between time interval of light rays and that of an imaginary motion of absolute light speed, and the length of the trajectory has been coarsely set to be

$l=\sqrt{r^2-R^2}$ (480)

So that the classical equation of half branch time delay could be calculated as

$∆t={\displaystyle \frac{1}{c}}[r^{*}\ln \left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)+{\displaystyle \frac{r^{*}}{2}}\sqrt{{\displaystyle \frac{r-R}{r+R}}}]$ (481)

But the half branch time delay of light rays, with respect to the time interval of close-to-light-speed particles Eq. (479), will be a little different

${∆t}_p\approx {\displaystyle \frac{r^{*}}{c}}\ln \left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)$ (482)

One may argue that the trajectory of close-to-light-speed particles will be different to light rays. In fact the real length of the light trajectory also does not equal to $\sqrt{r^2-R^2}$. One can easily take measures to work out the real length of that trajectory. I prefer to give a more accurate value than Eq. (480) that could be estimated by geometrical relationship while $r\gg R\approx b$ that

$l_{accurate}=\sqrt{r^2-R^2}+Rsin(-{\phi }_{\mathrm{\infty }})\approx \sqrt{r^2-R^2}+r^{*}$ (483)

where, ${\phi }_{\mathrm{\infty }}=-r^{*}/b$ is deflect angle of light ray.

So that a real half branch time delay of light rays with respect to an absolute motion on the very trajectory is

${∆t}_{real}={\displaystyle \frac{1}{c}}\left[r^{*}\mathrm{l}\mathrm{n}\right({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}})+{\displaystyle \frac{r^{*}}{2}}\sqrt{{\displaystyle \frac{r-R}{r+R}}}-r^{*}]\approx {\displaystyle \frac{1}{c}}[r^{*}\ln \left({\displaystyle \frac{r+\sqrt{r^2-R^2}}{R}}\right)-{\displaystyle \frac{r^{*}}{2}}]$ (484)

We know that the time delay has been verified to be very high accurate value with respect to the classical equation, that is because the trajectory length has always been set to be $\sqrt{r^2-R^2}$, which is indeed not accurate length of trajectory line.

If consider the close-to-light-speed particles, the real length of its trajectory line could be estimated to be

$l_p=\sqrt{r^2-R^2}+Rsin\left(-{\phi }_{\mathrm{\infty }}\right)=\sqrt{r^2-R^2}+{\displaystyle \frac{r^{*}}{2}}$ (485)

where, ${\phi }_{\mathrm{\infty }}=-r^{*}/\left(2b\right)$ is deflect angle of particles.

With Eq. (479), the half branch time delay of close-to-light-speed particles is

${∆t}_p=0$ (486)

This is a substantial zero delay calculation. This result of close-to-light-speed particles is a spectacular inevitability of kinematics rather than occasionality.

Something different from trajectory investigation, the test of time delay of light and close-to-light-speed particle propagation might allow a quite big separation to the Sun edge thereby to provide not bad accuracy. Furthermore, it could be expected to sponsor an experiment to emit light rays and massive particles on a straight line from a point not very close to the Sun at the same time for time delay verification.

8.7. Equations for Un-Close-to-Light-Speed Massive Particles

Let us investigate an un-close-to-light-speed motion for massive particles from specific position $R$ to another position $r$. Considering a variable mass $m_r$, the gravity

$F=-{\displaystyle \frac{GM{m}_r}{r^2}}=-m_r{c}^2{\displaystyle \frac{r^{*}}{2r^2}}$ (487)

Dynamic energy converted from gravitational potential by a motion from $R$ to $r$ is

$E_{conv}=-{\int }_R^r{m}_{\rho }{c}^2{\displaystyle \frac{r^{*}}{{2\rho }^2}}d\rho$ (488)

and the total energy

$E=m_r{c}^2=m_R{c}^2+E_{conv}$ (489)

The function of total energy could be written as

$m_r{c}^2=m_R{c}^2-{\int }_R^r{m}_{\rho }{c}^2{\displaystyle \frac{r^{*}}{{2\rho }^2}}d\rho$ (490)

Setting energy at position $R$ as a known quantity, it could be differentiated that

${m_r}^{\text{'}}=-m_r{\displaystyle \frac{r^{*}}{{2r}^2}}$ (491)

It could be integrated to be

$\mathit{ln}{m}_r-\mathit{ln}{m}_R={\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}}$ (492)

Then we gain the expression of variable mass that

$m_r=m_R{e}^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}=m_{\mathrm{\infty }}{e}^{{\displaystyle \frac{r^{*}}{2r}}}$ (493)

where, $m_{\mathrm{\infty }}$ is the mass at a farthest position with respect to the Eq. (359). This equation could be called general mass equation in gravitational field.

And we would like to carry out the expanded expression of gravity equation that

$F=-m_r{c}^2{\displaystyle \frac{r^{*}}{2r^2}}=-m_R{c}^2{\displaystyle \frac{r^{*}}{2r^2}}{e}^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}=-m_{\mathrm{\infty }}{c}^2{\displaystyle \frac{r^{*}}{2r^2}}{e}^{{\displaystyle \frac{r^{*}}{2r}}}$ (494)

One could find that the relativistic mass may not keep mass conservation any more that may surprise us, but it really has been revealed in realities. This is another kind of comprehensive physics which I will not make further discussions in this section. Mass of matter does matter [26]. The truths stay in realities.

Dynamic energy will be converted as

$E_{conv}=m_r{c}^2-m_R{c}^2=m_R{c}^2[e^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}-1]$ (495)

It should be pointed out that the expression of exponential equations of mass variation of course could be used for light ray propagations and close-to-light-speed massive particles for higher accuracy analysis case in strong fields.

For massive matters, with special relativity, the equation of dynamic energy at a position $r$ is

$E_k=\xi m_r{V}_r^2$ (496)

where, $\xi =(1-\sqrt{1-{\displaystyle \frac{V_r^2}{c^2}}}){\displaystyle \frac{c^2}{V_r^2}}$, see Eq. (304).

In gravitational field the dynamic energy varies with position that

$E_k={\xi }_r{m}_r{V}_r^2={\xi }_R{m}_R{V}_R^2+E_{conv}={\xi }_R{m}_R{V}_R^2+m_R{c}^2[e^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}-1]$ (497)

Conversion energy $E_{conv}$ could be positive case potential release or negative case potential withdrawn. However, dynamic energy $E_k$ will be always greater than zero, so that the variable $r$ will be limited in some specific cases that depends on initial conditions.

NB, for the convenience of expressions, the tensors of velocities, frequencies or the components maybe not written in tensor format anymore case they may not bring about confusions for understandings, for examples, $V_r$ and $V_R$ refer to the velocity at position $r$ and $R$.

It should be further discussed here that we have seen dynamic mass energy may come from the release of gravitational potential. That will then perform as inertial mass and gravitational mass. If in two source system, they move closer or farther will cause mass increase or lose in that we incline to realize that potential does not act as mass. We are not sure that in this condition mass conservation is available or not. I am inclining to say no. Maybe this discussion involves with new physics. In this section, this controversy does not really matter. This discussion just presents the issue for more focus.

We now prefer to study the conditions of irrelativistic velocities so that ${\xi }_r\approx {\xi }_R\approx 0.5$, and after Eq. (493) and Eq. (497), there is the velocity square

$V_r^2=e^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}{V}_R^2+2e^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}[e^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}-1]c^2$$=e^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}{V}_R^2+2[1-e^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}]c^2$ (498)

As we have discussed, Lagrangian could no longer be employed for analysis on the motion of massive particles. In some publications, the so-called Lagrangian for massive particles is classically defined to be $-c^2$ [3,10] as

$\mathcal{L}=-(1-{\displaystyle \frac{r^{*}}{r}})c^2{\dot{t}}^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=-c^2$ (499)

In fact, it could be easily deformed to be

$\mathcal{L}=-c^2+(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=-c^2$ (500)

That will lead to obvious errors that

$(1-{\displaystyle \frac{r^{*}}{r}}{)}^{-1}{\dot{r}}^2+r^2{\dot{\phi }}^2=0$ (501)

That means a zero velocity composition. It is impossible to interpret realities with. We know that in classical equations, the assumption of $\dot{t}(1-{\displaystyle \frac{r^{*}}{r}})=E$ has still been employed to solve the problem. One might be involved with more errors to solve one more error.

After conclusions and inferences previous, for a massive particle in one source gravitational field, the velocity composition could be expressed as

$-V_r^2+({\displaystyle \frac{dr}{dt}}{)}^2+r^2({\displaystyle \frac{d\phi }{dt}}{)}^2=0$ (502)

This equation could also be performed for that of close-to-light-speed massive particles as $V_r\to c$, as Eq. (424) and Eq. (476), where these discussions have not been released because of consideration of reducing arguments.

With angular momentum conservation, there is

${{r^{2}m}_r{\displaystyle \frac{d\phi }{dt}}=Rm}_R{V}_R=const.$ (503)

Of course, the angular momentum conservation for lower velocity motion will be the same as that of close-to-light-speed massive particles. But they are really different from that of light rays.

So that

${\displaystyle \frac{d\phi }{dt}}={\displaystyle \frac{\mathrm{R}}{r^2}}{\displaystyle \frac{m_R}{m_r}}{V}_R={\displaystyle \frac{\mathrm{R}}{r^2}}{V}_R{e}^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}$ (504)

In which $V_R$ and $m_R$ are velocity and mass at peak point, where $r=R$.

Together with the Eq. (498) and ${\displaystyle \frac{dr}{dt}}={\displaystyle \frac{dr}{d\phi }}{\displaystyle \frac{d\phi }{dt}}=r^{\text{'}}{\displaystyle \frac{d\phi }{dt}}$, the Eq. (502) becomes

$-e^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}{V}_R^2-2[1-e^{({\displaystyle \frac{r^{*}}{2R}}-{\displaystyle \frac{r^{*}}{2r}})}]c^2+(r\text{'}{)}^2{\displaystyle \frac{1}{r^4}}{e}^{({\displaystyle \frac{r^{*}}{R}}-{\displaystyle \frac{r^{*}}{r}})}{R}^2{V}_R^2+{\displaystyle \frac{1}{r^2}}{e}^{({\displaystyle \frac{r^{*}}{R}}-{\displaystyle \frac{r^{*}}{r}})}{R}^2{V}_R^2=0$ (505)

or

$-e^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}{V}_R^2-2[e^{({\displaystyle \frac{r^{*}}{r}}-{\displaystyle \frac{r^{*}}{R}})}-e^{({\displaystyle \frac{r^{*}}{2r}}-{\displaystyle \frac{r^{*}}{2R}})}]c^2+(r\text{'}{)}^2{\displaystyle \frac{1}{r^4}}{R}^2{V}_R^2+{\displaystyle \frac{1}{r^2}}{R}^2{V}_R^2=0$ (506)

Setting $u={\displaystyle \frac{1}{r}}$, it is

$-e^{({\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}})}{V}_R^2-2[e^{(u{r}^{*}-{\displaystyle \frac{r^{*}}{R}})}-e^{({\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}})}]c^2+(u\text{'}{)}^2{R}^2{V}_R^2+u^2{R}^2{V}_R^2=0$ (507)

To be derivated by $\phi$, it becomes

$-{\displaystyle \frac{r^{*}}{4}}{e}^{({\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}})}{V}_R^2-[r^{*}{e}^{(u{r}^{*}-{\displaystyle \frac{r^{*}}{R}})}-{\displaystyle \frac{r^{*}}{2}}{e}^{({\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}})}]c^2+u\text{'}\text{'}{R}^2{V}_R^2+u{R}^2{V}_R^2=0$ (508)

To take the one-order approximation for those exponent functions, the equation becomes

$-{\displaystyle \frac{r^{*}}{4}}(1+{\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}})V_R^2-\left[r^{*}\right(1+u{r}^{*}-{\displaystyle \frac{r^{*}}{R}})-{\displaystyle \frac{r^{*}}{2}}(1+{\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}}\left)\right]c^2+u\text{'}\text{'}{R}^2{V}_R^2+u{R}^2{V}_R^2=0$ (509)

One can also get this equation in simplified ways, but that will also experience comprehensive complexities while the way above seems more physically explicit. The exponent function forms used here is also to present more primary expressions of mass energy. In the conditions of strong fields, the exponent forms may take effects. One could imagine that the kinematics of light or close-to-light particles could also be expressed in more primary ways.

In weak fields, those very small items in Eq. (509) will be neglected. That becomes

$-{\displaystyle \frac{3}{4}}{r}^{*2}{c}^{2}u-{\displaystyle \frac{1}{2}}{r}^{*}{c}^2+u\text{'}\text{'}{R}^2{V}_R^2+u{R}^2{V}_R^2=0$ (510)

or

$u^{\text{'}\text{'}}+(1-{\displaystyle \frac{3}{4}}{\displaystyle \frac{r^{*2}{c}^2}{R^2{V}_R^2}})u={\displaystyle \frac{1}{2}}{\displaystyle \frac{r^{*}{c}^2}{R^2{V}_R^2}}$ (511)

Setting

${\omega }^2=1-{\displaystyle \frac{3}{4}}{\displaystyle \frac{r^{*2}{c}^2}{R^2{V}_R^2}}$ (512)

For planets in solar system, the last item in Eq. (512) is far less than 1.0, so that

$\omega \approx 1-{\displaystyle \frac{3}{8}}{\displaystyle \frac{r^{*2}{c}^2}{R^2{V}_R^2}}$ (513)

For planet trajectory, the equation could be solved as [27]

$u=A[1-\epsilon sin(\omega \phi \left)\right]$ (514)

With this solution substituted back into Eq. (511)

$\mathrm{A}={\displaystyle \frac{1}{2}}{\displaystyle \frac{r^{*}{c}^2}{R^2{V}_R^2}}{\omega }^{-2}$ (515)

One-order approximation of Eq. (507) is

$-(1+{\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}})V_R^2-2\left[\right(1+u{r}^{*}-{\displaystyle \frac{r^{*}}{R}})-(1+{\displaystyle \frac{r^{*}}{2}}u-{\displaystyle \frac{r^{*}}{2R}}\left)\right]c^2+(u\text{'}{)}^2{R}^2{V}_R^2+u^2{R}^2{V}_R^2=0$ (516)

Neglecting very small items, it is

$-V_R^2+{\displaystyle \frac{r^{*}}{R}}{c}^2-r^{*}u{c}^2+(u\text{'}{)}^2{R}^2{V}_R^2+u^2{R}^2{V}_R^2=0$ (517)

With Eq. (514), it becomes

$-V_R^2+{\displaystyle \frac{r^{*}}{R}}{c}^2-r^{*}A{c}^2+r^{*}A\epsilon sin\left(\omega \phi \right)c^2+A^2{\omega }^2{\epsilon }^2\left[cos\right(\omega \phi ){]}^2{R}^2{V}_R^2+{(A-A\epsilon sin(\omega \phi \left)\right)}^2{R}^2{V}_R^2=0$ (518)

Case $\phi =0$ there is

$-V_R^2+{\displaystyle \frac{r^{*}}{R}}{c}^2-r^{*}A{c}^2+A^2{\omega }^2{\epsilon }^2{R}^2{V}_R^2+A^2{R}^2{V}_R^2=0$ (519)

So that the eccentricity is

$\epsilon \approx [{\displaystyle \frac{(1-A^2{R}^2)V_R^2-(1-AR)\frac{r^{*}}{R}{c}^2}{A^2{\omega }^2{R}^2{V}_R^2}}{]}^{-2}$ (520)

Some publications have given the following expression for eccentricity

$L^2=a(1-{\epsilon }^2)GM$ (521)

where, $L$ has been set the angular momentum.

But this is not a real solution for eccentricity, because that the Eq. (514) shows $a=A^{-1}(1-{\epsilon }^2{)}^{-1}$.

We will then prefer to present the perihelion precession of

$∆\phi \approx {\displaystyle \frac{3}{8}}{\displaystyle \frac{r^{*2}{c}^2}{R^2{V}_R^2}}\phi$ (522)

or the precession per revolution

$∆{\phi }_{2\pi }\approx {\displaystyle \frac{3\pi }{4}}{\displaystyle \frac{r^{*2}{c}^2}{R^2{V}_R^2}}$ (523)

The most surprising is that this solution of perihelion precession is really irrelativistic. It is a half of the value of the classical solution. It is practicable to carry out more experiments of motions closely around the Sun to verified the conclusions of Eq. (522).

One can focus on more sophisticated conditions for massive matters traveling in gravitational fields, based on the Eq. (508) or the Eq. (511), especially for those motions in strong fields and with high velocities.

Perhaps this result is the only one in which we have focused on that is in contradictions with the observations that have declared perihelion precessions of planets in solar system [17]. But some observations on PSR J0737-3039A/B [28,29] have shown quite big deviations from classical predictions, which had been expected to have perihelion precession together with geodetic precession. Nevertheless, the experiment of Gravity Probe B [30] shows that geodetic item has got accurate results while frame-dragging item hasn’t, in which it could be recognized that the geodetic item is really the effect of special relativity. Observations on S2 [31] and PSR 1913+16 [32] also cannot provide positive supports for the predictions of perihelion precession of classical theory.

8.8. Additional Discussions on Geodesic Line, Inertial Motion, and General Covariance

We have discussed those derivatives theoretically in section 4, section 5 and section6 that in covariant space the acceleration of a massive matter could not be really calculate to be zero and even revisit light frequency shift will perform double of that of contra variant space. There is only the light speed that always serve the general covariance as the result the acceleration of a light ray may perform nonvanishing in covariant space in any conditions. These conclusions would have then challenged the theory of geodesic lines, because geodesic lines ask for thoroughly nonvanishing solutions for covariant derivatives. We also have proved that geodesic equation cannot be really employed for the solutions of massive matter’s motions as well as the motions of light rays in section 8.

Now it is the time to make additional discussions on the tips between matter’s trajectories, inertial motions, and geodesic lines.

General covariance asks for matters in covariant space to perform inertial motions just as they perform in no gravity fields. That requires trajectories of matters stay on the lines of geodesic lines in gravitational fields.

Geodesic lines are of the so-called straight lines of a covariant space that present the geometrical properties of the space. But inertial motions must ask for more. For example, an inertial trajectory must serve for any matters to run on, either the massive matters or light rays. The more important is that inertial trajectory must be run on by any matters with any velocities with same direction. It could be said that inertial motions share trajectories.

Back to the massive matter’s trajectories, it is no doubt that any two matters with different velocities in gravitational field with same initial positions and directions, will fly apart, so that to fly on two trajectories, just as matter’s motions in solar system. These trajectories of course correspond to two lines in covariant space. It is said that the matters with different velocities may not share trajectory in covariant space so that the motions are not inertial motions in covariant space and the trajectories are not geodesic lines.

As for light rays, due to the consequence of invariant light speed, they will come up to zero accelerations in covariant space and we might have seen that light rays could share trajectories in different frequencies, that really performs general covariance. But the trajectories of light rays are not that of real inertial motions or geodesic lines yet, in that light rays do not share trajectories with massive matters.

The motions of close-to-light-speed particles are something special, in that they would have zero acceleration approximately just as light rays, but they do not share trajectories with light rays and un-close-to-light-speed particles as have discussed.

9. Relativistic Release and Relativistic Frequency Shift

It is predicted that in one source field, the inflow of matters may cause relativistic release. Sole matters moving into the source center for a separation is of course exactly a kind of inflow. But I want to point out that the inflows of accretions of active galactic nuclei are of normal performances in celestial evolutions. As the matter of facts, they have not been well investigated, so that it is necessary to cast a few concentrations on.

9.1. Dynamics of Active Galactic Nuclei Accretions

9.1.1. Galactic Nuclei Accretions and Planet Rings

The discovery of active galactic nuclei is one of the greatest advancing of the astronomy in the 1960s [33,34]. Active galactic nuclei are of the most spectacular extragalactic objects not only because of their extraordinary giant radiations [35] but also due to the complicated spectra and very high redshifts. The emission spectra of active galactic nuclei are really non-thermal continuum [36]. Those issued models for active galactic nuclei in the past decades, such as the so-called standard model [37] or unified model [38], have not really interpreted the mechanism of accretion inflow and energy release. This is the reason that I want to sponsor a brief discussion on the dynamics of active galactic nuclei accretions.

Active galactic nuclei accretion disks exactly experience resemblant kinematics with planet ring systems in that both of them are of surrounding dusts revolving the center source, loosely inside the Roche limit [39]. I am going to sponsor a study firstly with respect to the planet ring systems so that to renovate those recognitions upon the evolution and fueling mechanism of active galactic nuclei accretions.

Planet rings are not static structures [40,41]. Their evolutions involve with numerous internal and external processes in which Keplerian shear acts the key role. It causes rings to spread [42] in all process. As we have seen, Saturn rings usually have that striking refined structures.

In the condition that ring particles are small enough, the electromagnet interactions will then overcome the inertials so that to control the motion within the rings. Such particles or together with gases getting to form colloid, will as a whole to perform fluid behaviors so as to bear pressure. Under the driving effects from outer boundaries, a fluid ring may go bolder cubically because pressure increasing helps particles to move deviate vertically to the ring plane, such as the Halo ring of Jupiter [43]. Spectrum observations predict that the particles in Halo ring are less than submicron. Optical observations also show that Halo ring seems blue and gray with respect to that the main rings show red color [43]. It is because that the fine particles scatter more blue rays, just like our sky does, while coarse particles scatter more red.

Firstly, I want to make a discussion based on a fluid ring in the condition that the center velocity equals to Keplerian velocity.

9.1.2. The Dynamic Models of Fluid Rings

For Keplerian motions of matters around center object, there is

$mr{\omega }_k^2={\displaystyle \frac{GMm}{r^2}}$ (524)

where, $m$ is mass of a particle,$G$ is gravitational constant, $M$ is the mass of center source, $r$ is distance to the center and ${\omega }_k={\displaystyle \frac{v_k}{r}}$ is angular velocity while $v_k$ is tangent velocity.

The tangent velocity and angular velocity will increase as radius getting smaller that

$v_k={\displaystyle \frac{{\left(GM\right)}^{0.5}}{r^{0.5}}} and {\omega }_k={\displaystyle \frac{{\left(GM\right)}^{0.5}}{r^{1.5}}}$ (525)

Keplerian kinetic energy could be expressed as

$E_k={\displaystyle \frac{1}{2}}m{v}_k^2={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r}}$ (526)

Keplerian motion determines constant angular momentum for a particle at specific position.

$L_k=rm{v}_k=m{r}^{0.5}{\left(GM\right)}^{0.5}$ (527)

Namely, there is Keplerian shear at the specific position, and the shearing rate can be derived to be

${\displaystyle \frac{{dv}_k}{dr}}=-{\displaystyle \frac{{\left(GM\right)}^{0.5}}{2r^{1.5}}} and {\displaystyle \frac{{d\omega }_k}{dr}}=-{\displaystyle \frac{{3\left(GM\right)}^{0.5}}{2r^{2.5}}}$ (528)

I do not think that the dynamics of planet rings is very easy to be built in that the evolutions of the rings must be rarely sophisticated. I prefer to suggest three simplified models that may reveal a little bit of probabilities.

Model 1: Central Keplerian motion with driving front and resistant front

It is imagined that a ring keeps Keplerian velocity at its center position while outer part has velocity lower than Keplerian velocity so that to form driving force, and inner part has velocity higher than Keplerian velocity so that to form resistant force. In this way, the driving force and resistant force could help to form fluid pressure to bolder the ring at vertical dimension as shown in Figure 23. That really others to the flat rings as that of Saturn.

For example, in the outer part of a fluid ring, if the velocity is lower to form driving force, the pressure could be calculated as

$p={\int }_{r_o}^r(\rho {\displaystyle \frac{GM}{x^2}}-\rho x{\omega }^2)dx$ (529)

where, $\rho$ is density of fluid, $r_o$ is radius from source center to the outer edge of fluid ring, and the angular velocity $\omega$ is less than Keplerian angular velocity ${\omega }_k$ of the very point so that to give driving force. If a linear function is assumed for an element of outer part

${\omega }^2=({\omega }_k^2-{\displaystyle \frac{r-r_c}{r_o-r_c}}∆{\omega }_o^2)$ (530)

where, $r_c$ refers to radius of pressure center and $∆{\omega }_o^2$ represents the angular velocity square difference with respect to ${\omega }_k^2$, which is the Keplerian angular velocity square at the very position $r$.

This equation presents an active falling of the outer part particles because of losing of energy and velocity.

Concern that at every position there is the relationship

$\rho {\displaystyle \frac{GM}{r^2}}=\rho r{\omega }_k^2$ (531)

The Eq. (529) becomes

$p={\int }_{r_o}^r\rho x{\displaystyle \frac{x-r_c}{r_o-r_c}}∆{\omega }_o^2 dx$ (532)

Giving the pressure of inner edge and outer edge equal to zero, and constant density, and $r_o-r_c\ll r_c$, there will be an approximate solution of center pressure

$p_c\approx {\displaystyle \frac{1}{2}}\rho r_c\left(r_o-r_c\right)∆{\omega }_o^2={\displaystyle \frac{1}{2}}\rho r_{c}b∆{\omega }_o^2$ (533)

where, $b=r_o-r_c$ represents the outer radius of the fluid ring.

On another side, the resistant force determined by the higher velocity of inner parts, with velocity as

${\omega }^2=({\omega }_k^2+{\displaystyle \frac{r_c-r}{r_c-r_i}}∆{\omega }_i^2)$ (534)

In which ${\omega }^2$ is greater than ${\omega }_k^2$ so that to form a passive resistant force.

There will be the center pressure

$p_c\approx {\displaystyle \frac{1}{2}}\rho r_{c}a∆{\omega }_i^2$ (535)

where, $a=r_c-r_i$ represents inner radius of fluid ring.

On the direction vertical to the plane, it is easily to calculate [35] that

$p_c\approx {\int }_0^h\rho r{\omega }_{ck}^2{\displaystyle \frac{y}{r}}dy={\displaystyle \frac{\rho h^2}{2}}{\omega }_{ck}^2$ (536)

where, $h$ represents vertical height from top or the bottom to the center of the ring, $y$ is the distance to pressure center and ${\omega }_{ck}$ is Keplerian angular velocity at pressure center.

Thus, the relationships between semi axes are

$a\approx {\displaystyle \frac{b∆{\omega }_i^2}{∆{\omega }_o^2}}$ (537)

$a\approx {\displaystyle \frac{h^2{\omega }_{ck}^2}{r_c∆{\omega }_i^2}}$ (538)

$b\approx {\displaystyle \frac{h^2{\omega }_{ck}^2}{r_c∆{\omega }_o^2}}$ (539)

The outer edge of the ring may be called driving front, depending on a random falling of outer particles, that forms an ambiguous boundary. The inner edge of the ring comes from passive driving, may be called driven front, so that to form a sharp edge as seen in Halo ring [43], just like curved water surface in an accelerated container. Of course, fluid rings also can be flattened and split to be refined structures so that to perform more complicated than Halo ring.

Model 2: Driving condition with no shear motion in inner part

It is assumed that the driving force will form a pressure gradient in inner part that just fit the gravity difference coming from Keplerian velocity difference so that to form no shear motion as shown in Figure 24.

There will be

${\omega }_{ik}={\omega }_i={\omega }_c$ (540)

It is said that any differential slice in the inner part may be accelerated by outer squeezing to catch up the velocity ${\omega }_{ik}$.

That indicates an increase of the angular velocity square to meet the force equilibrium

$∆{\omega }^2={\omega }_{ik}^2-{\omega }_k^2={\displaystyle \frac{GM}{{r_i}^3}}-{\displaystyle \frac{GM}{r^3}}$ (541)

Thus the ring pressure could be written as

$p={\int }_{r_i}^r\rho x∆{\omega }^2 dx={\int }_{r_i}^r\rho x({\displaystyle \frac{GM}{{r_i}^3}}-{\displaystyle \frac{GM}{x^3}}) dx$ (542)

Assume a constant density, the central pressure is about

$p_c\approx \rho {\displaystyle \frac{GM}{{r_i}^2}}\left(r_c-r_i\right)-\rho {\displaystyle \frac{GM}{r_i{r}_c}}\left(r_c-r_i\right)$$\approx \rho {\displaystyle \frac{GM}{{r_i}^2}}(1-{\displaystyle \frac{r_i}{r_c}}{)}^2$ (543)

That will lead to a special state that inner part of the ring has no Keplerian shear. But this state may need strict conditions and may be destroyed by further evolution in a long term.

Model 3: Momentum conversion and ring split

After then, I want to discuss the split of a ring under the condition of developed Keplerian shear. If a fluid ring is well Keplerian sheared, it could be predicted that the ring will go thinner. We know that there may be Keplerian shear at any position in the ring. But we can make an analysis on the angular momentum conversion in the middle point which could then at last split the ring to two parts. For convenience, it could be defined as two rings originally, the ring $i$ and the ring $i+1$ as shown in Figure 25. They will have their own Keplerian velocity points at $r_i$ and $r_{i+1}$. In a time interval, the two rings will complete quite amount of angular momentum conversion because of the Keplerian shear, which is just like viscous friction acts in the interface that makes the conversion.

Setting the mass of rings $m_i=m_{i+1}=m$, the relative angular momentum difference between two neighboring rings could be estimated as

$rm∆v=-m{\displaystyle \frac{{\left(GM\right)}^{0.5}}{2r^{0.5}}}∆r$ (544)

where $∆r=r_{i+1}-r_i$ and $r\approx 0.5(r_{i+1}+r_i)$The exchange of angular momentum may be expressed as

$∆L=-\beta m{\displaystyle \frac{{\left(GM\right)}^{0.5}}{2r^{0.5}}}∆r$ (545)

where, momentum exchange ratio $0\le \beta \le 1$.

It is said that after a Keplerian shear, the outer one should get increase of angular momentum and the inner one should get that decline. For the reasons of kinetic mechanism, both the inner ring and outer ring will be driven apart from original position. If inner ring goes a difference $\delta r$, the difference of Keplerian angular momentum could be calculated as

${\delta L}_k=m{\displaystyle \frac{{\left(GM\right)}^{0.5}}{2r^{0.5}}}\delta r$ (546)

Let ${\delta L}_k$ equals to $∆L$, it is obtained that

$\delta r=\beta ∆r$ (547)

For the inner ring, it goes to shrink by falling a (minus) $\delta r$ separation so that to form a new state. And for the outer ring, it expands by going up to a (positive) $\delta r$ separation.

We have seen that this is not a whole dynamic analysis because that the pressure in the ring has also taken the effect of angular momentum conversion directly, but that does no harm for the conclusion that Keplerian shear, i.e. the viscous shear in the ring, leads to angular momentum conversion and rings split. One can make detailed study with Navier Stokes equations or the renovated ones.

A process of ring spreading around a source center is an irreversible process with entropy production.

9.1.3. Shearing Dissipation in Fluid Rings

This issue is carried out to estimate the shearing dissipation so that to discuss the evolution by Keplerian shear. Of course, the evolution would involve together with momentum conversion and ring split. But in the way of theoretical methodology, it is better to be investigated in two steps, the angular momentum conversion by Keplerian shear, and the energy momentum conservation during rings split.

Angular momentum conversion must be done across the interface between the two rings, so that the first step analysis is reasonable. I prefer to focus on the states before and after momentum conversion of two neighboring rings as has been shown in Figure (25). Before conversion, the neighboring rings have been separated by $∆r=r_{i+1}-r_i,(r_{i+1}>r_i)$, with velocities

$v_i={\displaystyle \frac{{\left(GM\right)}^{0.5}}{r_i^{0.5}}} and v_{i+1}={\displaystyle \frac{{\left(GM\right)}^{0.5}}{r_{i+1}^{0.5}}}$ (548)

The difference between $v_i$ and $v_{i+1}$ could be written after Eq. (528)

$∆v=-{\displaystyle \frac{{\left(GM\right)}^{0.5}}{2r^{1.5}}}∆r$ (549)

where, $r\approx 0.5(r_{i+1}+r_i)$, $∆v$ is defined as minus quantity while $∆r$ as plus. Namely,

$v_{i+1}=v_i+∆v$ (550)

Considering ring mass equals to each other, two conditions would be taken into study.

As angular momentum conversion happens, there are

$v_{i,after}=v_i+\beta ∆v and v_{i+1,after}=v_i+∆v-\beta ∆v$ (551)

As $∆v$ has been defined minus, the inner ring is really slowed down and the outer ring is accelerated. Because of $0\le \beta \le 1.0$, kinetic energy may not keep conservation. With original kinetic energy of

$E_{before}={\displaystyle \frac{1}{2}}m{v}_i^2+{\displaystyle \frac{1}{2}}m{(v_i+∆v)}^2$ (552)

and the kinetic energy after conversion of

$E_{after}={\displaystyle \frac{1}{2}}m{\left(v_i+\beta ∆v\right)}^2+{\displaystyle \frac{1}{2}}m{\left(v_i+∆v-\beta ∆v\right)}^2$ (553)

Thus, there is the dissipation energy without considering potential variations

${Dissipation}_1=E_{before}-E_{after}=\beta m{∆v}^2-{\beta }^{2}m{∆v}^2$ (554)

Considering the Eq. (549), it turns to be

${Dissipation}_1=\beta (1-\beta )m{\displaystyle \frac{GM}{4r^3}}{∆r}^2$ (555)

Then go to the second step that after the first step of angular momentum conversion, the outer part of inner ring loses momentum so that provides driving force to drive the inner ring to inflow and the inner part of outer ring will be accelerated to higher momentum so that to squeeze the outer ring to outflow. This evolution will perform a little sophisticated in that the inflow ring should be accelerated by gravity and the outflow ring should be slow down by gravity. We know that the inflow of a ring will cause half potential release surplus with respect to the Keplerian energy requirement and the outflow will experience potential withdraw. And also, we know that the gravity is perpendicular to statistic velocity of the ring. These issues could be solved in fluid flow anyway, even though that must involve with the evolution of vortexes.

Now we are going to check the energy conservation of final state. After the inner ring inflows a separation $\delta r$ and the outer ring outflows a sepration $\delta r$, they come to a new state of Keplerian balance. Taking the inner ring for granted, before Keplerian shear, its total energy involves with Keplerian kinetic energy and potential

$E_{i,before}={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i}}+0$ (556)

After Keplerian shear and inflowing a separation $\delta r$, total energy becomes

$E_{i,after}={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i-\delta r}}-m{\displaystyle \frac{GM}{r_i^2}}\delta r$ (557)

and for outer ring, the energy before

$E_{i+1,before}={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}}}+0$ (558)

The energy of final state

$E_{i+1,after}={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}+\delta r}}+m{\displaystyle \frac{GM}{r_{i+1}^2}}\delta r$ (559)

Total energy difference before and after the two steps could be estimated by

$E_{i,before}-E_{i,after}+E_{i+1,before}-E_{i+1,after}$$=({\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i}}-{\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i-\delta r}})+({\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}}}-{\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}+\delta r}})+({\displaystyle \frac{GM}{r_i^2}}\delta r-{\displaystyle \frac{GM}{r_{i+1}^2}}\delta r)$ (560)

The first two items could be transformed as

$({\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i}}-{\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i-\delta r}})$ $={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_i}}-{\displaystyle \frac{1}{2}}mGM({\displaystyle \frac{1}{r_i}}+{\displaystyle \frac{1}{r_i^2}}\delta r+{\displaystyle \frac{1}{r_i^3}}{\delta r}^2)$$=GMm(-{\displaystyle \frac{1}{2r_i^2}}\delta r-{\displaystyle \frac{1}{2r_i^3}}{\delta r}^2)$ (561)

The middle two items could be transformed as

$({\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}}}-{\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}+\delta r}})$$={\displaystyle \frac{1}{2}}m{\displaystyle \frac{GM}{r_{i+1}}}-{\displaystyle \frac{1}{2}}mGM({\displaystyle \frac{1}{r_{i+1}}}-{\displaystyle \frac{1}{r_{i+1}^2}}\delta r-{\displaystyle \frac{1}{r_{i+1}^3}}{\delta r}^2)$$=GMm({\displaystyle \frac{1}{{2r}_{i+1}^2}}\delta r+{\displaystyle \frac{1}{{2r}_{i+1}^3}}{\delta r}^2)$$=GMm[{\displaystyle \frac{1}{2(r_i+∆r{)}^2}}\delta r+{\displaystyle \frac{1}{2r_{i+1}^3}}{\delta r}^2]$$=GMm\left[{\displaystyle \frac{1}{2r_i^2}}\right(1-{\displaystyle \frac{2∆r}{r_i}})\delta r+{\displaystyle \frac{1}{2r_{i+1}^3}}{\delta r}^2]$ (562)

so that the previous four items are

$-GMm{\displaystyle \frac{∆r\delta r}{r_i^3}}=-GMm\beta {\displaystyle \frac{{∆r}^2}{r_i^3}}$ (563)

The last two items are

$({\displaystyle \frac{GMm}{r_i^2}}\delta r-{\displaystyle \frac{GMm}{r_{i+1}^2}}\delta r)$$={\displaystyle \frac{GMm}{r_i^2}}\delta r-{\displaystyle \frac{GMm}{(r_i+∆r{)}^2}}\delta r$$={\displaystyle \frac{GMm}{r_i^2}}\delta r-{\displaystyle \frac{GMm}{r_i^2}}\delta r(1-{\displaystyle \frac{2∆r}{r_i}})$$=2{\displaystyle \frac{GMm}{r_i^3}}∆r\delta r$$=2GMm\beta {\displaystyle \frac{{∆r}^2}{r_i^3}}$ (564)

The energy difference is total energy dissipation

$Dissipation=E_{i,before}-E_{i,after}+E_{i+1,before}-E_{i+1,after}$$=\beta GMm{\displaystyle \frac{{∆r}^2}{r_i^3}}$ (565)

One can calculate the gravitational potential release of a single ring inflowing, although it does not sound reasonable for a comparison with dissipations because there is another ring outflowing. Anyway, that is

$dW=m{\displaystyle \frac{GM}{r^2}}\delta r=\beta m{\displaystyle \frac{GM}{r^2}}∆r$ (566)

Thus, we get the ratio of dissipation and potential release

${\displaystyle \frac{Dissipation}{dW}}={\displaystyle \frac{∆r}{r}}$ (567)

Or the ratio of dissipation-1 and potential release

${\displaystyle \frac{{Dissipation}_1}{dW}}={\displaystyle \frac{(1-\beta )∆r}{4r}}$ (568)

where $\beta \ne 0$.

Ring evolution dynamics indicates that the inner half of an accretion inclines to inflow and outer half inclines to outflow by and large. Additionally, the process of vortex evolution would dissipate, even though the two dissipations are not independent.

${Dissipation}_2=Dissipation-{Dissipation}_1={\displaystyle \frac{1}{4}}\beta (3+\beta )m{\displaystyle \frac{GM}{r^3}}{∆r}^2$ (569)

It shows that the dissipation in vortex evolution might be greater than that in momentum exchange between rings.

We know that inter-ring separation $∆r$ would be far less than the radius $r$ of relative rings. It is said that in the condition of Keplerian shear, the dissipative energy is a higher rank infinitesimal quantity of that of potential release of inflow, no matter that inner ring potential release will support the outer ring potential withdrawing. Classical quasars could have luminosities of 10⁴⁵ erg s^-1 to 10⁴⁶ erg s^-1 [44]. It is unimaginable that those releases completely come from gravitational potential energy.

9.1.4. On Particle Rings

For solid particle rings, it is difficult to make a simple analysis on angular momentum conversions and on ring’s evolutions. In fact, any head-to-head collisions, and partial collisions of edge-by-edge that might form additional rotations, between two particles, might cause great changes to their trajectories. It could be imagined that for numerous particles in neighboring rings, assuming very small velocity difference between any two Keplerian collision particles, we can predict quasi fluid behavior for Keplerian shear acting on neighboring rings, that in a whole, Keplerian shear help to make angular momentum conversion and ring split. One can also write down those equations of energy momentum just as that of fluid rings. But all in all, particle rings cannot form pressure so that they will only spread as a very thin disk with perfect and refined structures in the equator plane, unlike the fluid rings, which could form a bold 3-dimensional torus structures. I believe that numerical method could be expected for quasi fluid behavior simulation for Keplerian shear of particle rings, as the effects of the rings of Saturn have shown us.

9.2. Relativistic Release

Any efforts to conceiving the mechanism of relativistic release would encounter great difficulties, because of two reasons that relativistic release has not been well recognized and we still know less about the intrinsic structures of fundamental particles that might be revealed relativistic emissions. But on the other hand, tremendous of observations have shown incredible probabilities for intrinsic emissions and correlated pseudo redshifts, as well as intrinsic redshift of absorptions, which are so intensely corresponding to the inference of relativistic release that I cannot help to make a try.

A direct realization on this issue is that the conservation of electromagnetic momentum and invariance of electromagnetic wave speed will lead to the variation of proficiency of light moment transportation, then the interactions or so-called the forces between particles, especially that in intrinsic structures. The most complicated is that these variations would be anisotropic so that the dynamics must be even profound and comprehensive.

Despite the complexities of relativistic release for a massive matter inflow into the center source, I suggest a mathematic analysis based on an assumption of continuum release. It is still not a true expression of realities, but that may help for more understandings on that topic.

The apparent light speed ${\mathrm{c}}_0^1$ could be employed to describe the concept of equivalent state in gravitational fields. It may be a state after relativistic release, although this state should be not really stable because there should be energy deficiency in the other two dimensions.

One can discuss the momentum exchange efficiency under the conditions of different apparent light speeds so that to talk about the variation of equivalent state. Another important clue that indicates equivalent state is the fine structure constant. We know that fine structure constant determines the dimensions of condensed matters, of course that may determine the dimensions of intrinsic structures. We can imagine that the variation of apparent light speed could bring about the variation of fine structure constant so that to bring about the variation of the energy of equivalent state.

I don’t think all of energy of a matter would take part in the relativistic release, for example, the most fundamental particles may be expected to be made of quasi photons, in common recognitions, they might not be split anymore. Thus, we would rather define the concept of releasable mass $\tilde{m}$. I cannot give an estimation whether the maximum releasable mass should be up to $0.9m_0$ or not, but it could be believed to be quite amount, where $m_0$ is total rest mass of original equivalent state, which corresponding to the state that the matters do not experience relativistic release.

Now for a center source field, equivalent state of matters is proposed to be

$\tilde{E}=\tilde{m}{\left(c_0^1\right)}^2$ (570)

Matters located at different positions in the gravitational field perform different equivalent states. As a matter goes a separation $dr$ along the radial direction, the expression of exceeding energy is

$d\tilde{E}=2\tilde{m}{c}_0^1\left(c_0^1\right)\text{'}dr$ (571)

As a matter goes from the farthest point to the position of radius$r$, the relativistic released energy could be integrated to be

${\tilde{E}}_{released}={\int }_r^{\mathrm{\infty }}d\tilde{E}=\tilde{m}{c}^2-\tilde{m}{\left(c_0^r\right)}^2={\tilde{m}{c}^2[1-(1-{\displaystyle \frac{r^{*}}{r}})}^2]$ (572)

Thereafter, we could also define a corresponding concept of the relativistic residual energy that, at a position, matters keep an amount of energy for subsequent releases,

${\tilde{E}}_{residual}={\tilde{m}{c}^2(1-{\displaystyle \frac{r^{*}}{r}})}^2$ (573)

It seems that the residual energy may go zero as matters reaches $r^{*}$. It is just a solution of theoretical model. In practice, relativistic release will be intermittent, and matters perhaps to experience flattenizations as they close to $r^{*}$ so that to bring about instabilities. As results, residual energy may not go zero at the end in practice. This effort is just to manage to perform kind of probabilities of relativistic release.

It can be calculated that most part of energy is kept before $10r^{*}$${\tilde{E}}_{residual}\left(10r^{*}\right)=0.81\tilde{m}{c}^2$ (574)

Now it is naturally to define the release rate by derivative of release energy along the radial direction to the center source. Released energy could be the integration of release distribution function from a position farthest to the position $r$ or the minus inversely

${\tilde{E}}_{released}={\int }_{\mathrm{\infty }}^{r}edr={\int }_r^{\mathrm{\infty }}-edr$ (575)

On the other hand, the residual energy could also be defined as an integration of release distribution from position $r^{*}$ to position $r$ or the minus form

${\tilde{E}}_{residual}={\int }_{r^{*}}^{r}edr={\int }_r^{r^{*}}-edr$ (576)

Thus, the release distribution could be derivated to be

$e=2\tilde{m}{c}^2(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{r^{*}}{r^2}}$ (577)

It is easy to calculate that the peak value locates at the position

$r_{emax}={\displaystyle \frac{3}{2}}{r}^{*}$ (578)

with the maximum release distribution

$e_{max}={\displaystyle \frac{8}{27}}{\displaystyle \frac{\tilde{m}{c}^2}{r^{*}}}$ (579)

One can calculate the release intensity of accretion inflow. Setting equivalent mass for every single ring in an accretion, the luminosity could be derived as

$l=2{\tilde{\rho }}^{*}v{c}^2(1-{\displaystyle \frac{r^{*}}{r}}){\displaystyle \frac{{r^{*}}^2}{r^3}}$ (580)

where, ${\tilde{\rho }}^{*}$ is matter’s assuming density at the position $r^{*}$ and $v$ is inflow velocity.

Suppose the accretion spreading sufficiently, it can be calculated that the most luminous area is at the position

$r_{lmax}={\displaystyle \frac{4}{3}}{r}^{*}$ (581)

As well as maximum luminosity

$l_{max}={\displaystyle \frac{27}{128}}{\displaystyle \frac{m{\tilde{\rho }}^{*}v{c}^2}{r^{*}}}$ (582)

Release distribution and accretion luminosity could be shown in Figure 26.

The Eq, (580) represents intensity of release at a specific position in an accretion disk. It is revealed that the peak luminosity should not happen at the edge of horizon event, but at a little outer position, just as that was shown in the event-horizon-scale images of M87 taken by the Event Horizon Telescope Collaboration with wavelength of 1.3mm [45].

9.3. Relativistic Emission Lines and Relativistic Redshift

Eyeing on the stimulated release of electrons in atoms, we could carry out a concept of exceeding ratio for relativistic release of an energy structure.

$\sigma ={\displaystyle \frac{{\tilde{E}}_{excited}-{\tilde{E}}_{ground}}{{\tilde{E}}_{ground}}}$ (583)

where ${\tilde{E}}_{excited}$ and ${\tilde{E}}_{ground}$ are energy of excited state and ground state of specific structure. Exceeding ratios for relativistic release may be more different from that of stimulated release of electrons, probably, they might be quite small or big. We know less about that.

In one source field, exceeding ratio would be variable with position as the so-called equivalent state has shown.

$\sigma ={\sigma }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^2$ (584)

Thus, frequencies of specific emission rays could be written as

${\nu }_r={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^2$ (585)

Case $r\gg r^{*}$ it could be simplified to be

${\nu }_r={\nu }_{\infty }(1-{\displaystyle \frac{2r^{*}}{r}})$ (586)

These emissions of course include but not limit to electron transition emissions that we are more familiar to that could be easily certificated comparing to stimulated release on the Earth. This kind of frequency will be quite different with which we have known well in weak field, in that it looks like redshifted after photons reach the Earth. But it is just a pseudo redshift because the emissions have not experienced real redshift at the emission time. The fact is that it is only verified to be redshifted by comparing to the spectrum characteristics of a matter in weak fields. In this case, it is just redshift seemingly. It could be called relativistic redshift.

In practice, emission lines will experience gravitational redshift to arrive a farthest position. The Eq. (493) could also be employed to interpret light mass energy variation in gravitational field, so that the detectable frequency could be expressed as

${\nu }_{r\to d}={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2r}}}$ (587)

Case $r\gg r^{*}$ it could be simplified to be

${\nu }_{r\to d}\approx {\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^2{(1+{\displaystyle \frac{r^{*}}{2r}})}^{-1}$$={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^{2.5}\approx {\nu }_{\infty }(1-2.5{\displaystyle \frac{r^{*}}{r}})$ (588)

Propose a definition of relativistic frequency shift based on frequency

$z_{rel}={\displaystyle \frac{{\nu }_{\infty }-{\nu }_r}{{\nu }_r}}={(1-{\displaystyle \frac{r^{*}}{r}})}^{-2}-1$ (589)

Case $r\gg r^{*}$ it could be simplified to be

$z_{rel}={\displaystyle \frac{{\nu }_{\infty }-{\nu }_r}{{\nu }_r}}={\displaystyle \frac{2r^{*}}{r}}$ (590)

It is an intrinsic frequency shift rather than cosmological redshift. Note that ${\nu }_r$ keep invariant during propagation process if neglect the effect of gravitational redshift. ${\mathsf{\nu }}_{\infty }$ is the comparative frequency of equivalent radiation in no gravity condition.

Detectable redshift should be calculated as

$z_{r\to d}={\displaystyle \frac{{\nu }_{\infty }-{\nu }_{r\to d}}{{\nu }_{r\to d}}}={(1-{\displaystyle \frac{r^{*}}{r}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2r}}}-1$ (591)

Case $r\gg r^{*}$ it could be simplified to be

$z_{r\to d}={(1-{\displaystyle \frac{r^{*}}{r}})}^{-2.5}-1\approx {\displaystyle \frac{2.5r^{*}}{r}}$ (592)

Relativistic frequency shift and detectable frequency shift could be calculated for comparison in Table 5.

The highest redshift we have observed on quasars is up to 16.4 [46,47]. It could be expected that higher redshift would be seen to be up to more than 20.0 in recent future. Perhaps higher redshifts have already been observed but not certificated.

Perhaps, up to now, we have found the probable way by which the accretions of active galactic nuclei release energy. It has been pointed out that the giant radiations of active galactic nuclei are not of thermal continuum. It has ever been believed that the radiations come from the energy of gravitational potential conversion [35], but we know that the energy of gravitational potential conversion must release radiation by the way of thermal black-body radiation. This will then lead to a contradiction. And in previous section, the dissipation of potential conversion of an accretion has been proved to be an infinitesimal of total conversion, that furtherly deduces the probabilities of potential origin of accretion radiation.

It is carried out that the detectable redshift is just the property of relativistic emissions, which obviously rises against the cosmic original theory. The distribution statistics of observational high redshifts [48,49] might have indicated the redshifts are of property of the emissions rather than that of cosmic reasons.

Theoretically, it will be rarely probable that emission lines of multiple redshifts might be verified in some special observations in that the mechanism implies the probabilities although some of them may be ambiguous perhaps one of them dominates others as has been discussed. In fact, observations on frequency shift and line width and some other aspects of emissions might have present the performances of multiple redshifts. Celestial observations have always brought us surprises, multiple redshift emission might be the new one.

9.4. Broad Lines and Narrow Lines

In the emissions of quite amount of continuous inflow matters, the exciting width that the inflow involved sustains at radial direction may cause specific continuous emission distribution. As a result, that could be certificated to be a broadened line in spectrum diagram. For a massive accretion around a galactic nucleus, the Kepler shear may be employed to interpret the mechanism of inflow of a ring. If there is an inflow of a ring at position $r$ with exciting width of $∆r$, the emission frequency might be distributed from ${\nu }_r$ to ${\nu }_{r+∆r}$. Considering the effect of gravitational redshift, one can get a line width expressed by frequency after Eq. (587) that

$w_{\nu }={\nu }_{r+∆r\to d}-{\nu }_{r\to d}=\left[\right({1-{\displaystyle \frac{r^{*}}{r+∆r}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2(r+∆r)}}}-\left({1-{\displaystyle \frac{r^{*}}{r}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2r}}}\right]{\nu }_{\infty }$ (593)

Case $r\gg r^{*}$ and $r\gg ∆r$ it could be simplified to be

$w_{\nu }\approx (1-{\displaystyle \frac{2.5r^{*}}{r+∆r}}-1+{\displaystyle \frac{2.5r^{*}}{r}}){\nu }_{\infty }=({\displaystyle \frac{1}{r}}-{\displaystyle \frac{1}{r+∆r}})2.5r^{*}{\nu }_{\infty }\approx {\displaystyle \frac{2.5∆r{r}^{*}}{r^2}}{\nu }_{\infty }$ (594)

or by wave length

$w_{\lambda }={\lambda }_r-{\lambda }_{r+∆r}=c/{\nu }_{r\to d}-c/{\nu }_{r+∆r\to d}$$=\left[\right({1-{\displaystyle \frac{r^{*}}{r}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2r}}}-\left({1-{\displaystyle \frac{r^{*}}{r+∆r}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2(r+∆r)}}}\right]{\lambda }_{\infty }$ (595)

Case $r\gg r^{*}$ and $r\gg ∆r$ it could be simplified to be

$w_{\lambda }\approx (1+{\displaystyle \frac{2.5r^{*}}{r}}-1-{\displaystyle \frac{2.5r^{*}}{r+∆r}}){\lambda }_{\infty }\approx {\displaystyle \frac{2.5∆r{r}^{*}}{r^2}}{\lambda }_{\infty }$ (596)

which could also be amount to a so-called Doppler velocity by frequency as

$v_{D\nu }={\displaystyle \frac{w_{\nu }}{{\nu }_r}}c$ (597)

or Doppler velocity by wave length as

$v_{D\lambda }={\displaystyle \frac{w_{\lambda }}{{\lambda }_r}}c$ (598)

where, $c$ is light speed.

Case $r\gg r^{*}$ it could be simplified to be

$v_{D\nu }\approx v_{D\lambda }$ (599)

These equations show that in the regions near to $r^{*}$, relativistic emissions should have broader line widths, and in the regions far off the $r^{*}$, relativistic emissions should have more narrow line widths. Calculations on line widths of various conditions will be presented in Table 6.

This result forcefully matches the observational dimensions of broad line regions and narrow line regions. It is said that line widths depend on inflow exciting width, but in totally analysis, they highly relate to the inflow positions. The regions close to $r^{*}$ may emit lines broader than that of farther regions. Observations show that the sizes of broad line regions are estimated within 0.01 or 0.1pc and line widths are about 1000 kms^-1 to 10000 kms^-1, while the sizes of narrow line regions are about 0.1pc to 1kpc [48,50,51]. In fact, those certificated narrow lines incline to have been certificated as lower redshift lines. For radio emissions, some of them were observed to have compact cores and extended components [50]. The compact cores could be interpreted that equivalent state in inner areas of accretions would have lower equivalent energy to release lower frequency emissions, while some of the giant extended components of emission pictures might be the jet outflow who emit radio lines.

Relativistic release must perform in sophisticated conditions. The most probable condition is that the release in one of the rings could overwhelming all the others, especially that of the most inner ring. Thus, in most cases, releases of an active galactic nucleus might be certificated by the emissions of the sole ring. One can find that most of narrow lines have been certificated lower redshift, such as NGC 4151 with z=0.0033 [52] and MCG-5-23-16 with z=0.00849 [53] have narrow Fe Kα lines. But on the other hand, their spectra both involve with broad lines [54], that indicate controversies in emission line certifications.

The variability, asymmetry, wave length shift and so much as line broadening of active nuclei emissions [49] indicate more sophisticated dynamic conditions than imagine.

9.5. Relativistic Absorption

Most of active galactic nuclei have giant accretion bodies spreading around their equatorial planes. Case a pulse of light ray goes through some parts of an accretion body, that light ray may experience different absorptions due to their passing positions. If a pulse of light crosses several separate rings or blocks of an accretion, it might experience multiple absorptions. Absorption frequencies depend on equivalent state of the matters that have experienced relativistic release, so that the absorption frequencies could be expressed as

${\nu }_r={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^2$ (600)

and the detectable frequency is

${\nu }_{r\to d}={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2r}}}$ (601)

where, ${\nu }_r$ is the frequency of absorption line in that the light rays cross throughout a ring located at a position of $r$, and ${\nu }_{\infty }$ is the absorption frequency case that structure would absorb in no-gravity fields. One can of course calculate the widths of absorption lines just like that of emission lines.

$w_{\nu }=\left[\right({1-{\displaystyle \frac{r^{*}}{r+∆r}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2(r+∆r)}}}-\left({1-{\displaystyle \frac{r^{*}}{r}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2r}}}\right]{\nu }_{\infty }$ (602)

or

$w_{\lambda }=\left[\right({1-{\displaystyle \frac{r^{*}}{r}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2r}}}-\left({1-{\displaystyle \frac{r^{*}}{r+∆r}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2(r+∆r)}}}\right]{\lambda }_{\infty }$ (603)

where, $∆r$ is absorption width of a ring that the light ray passes across.

or expressed by Doppler velocity in frequency as

$v_{D\nu }={\displaystyle \frac{w_{\nu }}{{\nu }_r}}c$ (604)

or Doppler velocity in wave length as

$v_{D\lambda }={\displaystyle \frac{w_{\lambda }}{{\lambda }_r}}c$ (605)

But more different from emissions, absorption spectra must have more narrow lines and lower redshift than emissions, because the absorption rings are mostly at more outer regions with respect to the inner shining emission source, otherwise they would be difficult to be detected.

As has been discussed above, the inflow of inner rings of accretion may act as key role of entire emissions. So, we can image that brighter inner rings emit light rays, and on our view line, they go through some surrounding rings to be absorbed. It is said that, absorbing dusts might be the matters located at surrounding outer positions rather than those so-called insert bodies far away from the emission areas. This image may lead to the so-called relative blueshift, with respect to that of emission lines. Of course, there might be still seldom absorptions happening in inner areas so that we will also observe relative redshift absorption lines occasionally. Given a separation $∆r$ between emission position and absorption position more exterior, the emission frequency could be calculated as

${\nu }_{em\to d}={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r_{em}}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2r_{em}}}}$ (606)

with redshift of the line

$z_{em\to d}={\displaystyle \frac{{\nu }_{\infty }-{\nu }_{em\to d}}{{\nu }_{em\to d}}}$ (607)

and absorption frequency varies because a separation $∆r$ between absorption and emission positions

${\nu }_{ab\to d}={\nu }_{\infty }{(1-{\displaystyle \frac{r^{*}}{r_{ab}}})}^2{e}^{-{\displaystyle \frac{r^{*}}{2(r_{ab}+∆r)}}}$ (608)

so that the redshift of absorption line is

$z_{ab\to d}={\displaystyle \frac{{\nu }_{\infty }-{\nu }_{ab\to d}}{{\nu }_{ab\to d}}}$ (609)

And then, there is a blueshift of an absorption line

$∆z=z_{ab\to d}-z_{em\to d}={(1-{\displaystyle \frac{r^{*}}{r_{ab}}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2(r_{ab}+∆r)}}}-{(1-{\displaystyle \frac{r^{*}}{r_{em}}})}^{-2}{e}^{{\displaystyle \frac{r^{*}}{2r_{em}}}}$ (610)

Given $r_{em}=2.5r^{*}$ and $∆r=0.5r^{*}$, it can be calculated that $z_{em}=2.39$ and $z_{ab}=$

1.66. Here, the absorption lines may show a blueshift of $0.73$

with respect to the emission lines.

It was found that there are both absorption broad line region and absorption narrow line region [55] in single system in which those absorption lines are all corresponding to that of emission lines.

Case a continuum spectrum of light rays passes across multiple rings and arrive at an observatory on the Earth, one can then get a set of multiple frequency shift of absorptions. It is because absorptions only depend on the positions in accretions. This does interpret the multiple redshift absorption lines in tremendous of observations [48,49,50] in those active galactic nuclei. Especially for that of so-called Lyman-alpha forest [56], a series of regular Lyman-alpha absorption lines, with descending order of redshifts, queue up amazingly at the left side of the great main emission line.

There is a special condition for a matter out flowing from center source, for example the center jet outflow. When a matter at ground state moves a separation toward outer direction, its structural energy should experience energy deficiency in that the energy of equivalent state gets increasing. We then see that the matter is in the state lack of energy, and generally, the state should be kept until surrounding environment happens to emit amount of specific light rays across, so as the result, the matter gets absorptions. It is said that, this kind of absorptions would be far different from normal relativistic absorptions as that have been discussed above, so that they could be called the super relativistic absorption. As for the mentioned absorption energy, it depends on the position it getting absorbing as well as the position it has ever been in ground state. Note that this kind of absorptions really distinguish from the general relativistic absorptions in that the super relativistic absorption energy depends on the difference between the final emission position and specific absorption position, while the general relativistic absorption is due to property of structure state. It could be calculated as

$∆\nu ={\nu }_{ab}-{\nu }_{gr}$ (611)

where, ${\nu }_{ab}={(1-{\displaystyle \frac{r^{\mathrm{*}}}{r_{ab}}})}^2{e}^{{\displaystyle \frac{-r^{\mathrm{*}}}{2r_{ab}}}}{\nu }_{\mathrm{\infty }}$, ${\nu }_{gr}={(1-{\displaystyle \frac{r^{\mathrm{*}}}{r_{gr}}})}^2{e}^{{\displaystyle \frac{-r^{\mathrm{*}}}{2r_{gr}}}}{\nu }_{\mathrm{\infty }}$, $r_{ab}$ is the radius at absorption position, and $r_{gr}$ is the radius of the position of equivalent ground state before outflow. This kind of absorption might need greater absorption energy than that of general relativistic absorption. Therefore, it should be called the super relativistic absorption.

To the observer at a farthest position, the absorption line will also perform special frequency shift that

$z_{super}={\displaystyle \frac{{\nu }_{\infty }-∆\nu }{∆\nu }}={\displaystyle \frac{1}{{(1-\frac{r^{*}}{r_{ab}})}^2{e}^{\frac{-r^{*}}{2r_{ab}}}-{(1-\frac{r^{*}}{r_{gr}})}^2{e}^{\frac{-r^{*}}{2r_{gr}}}}}-1$ (612)

Case the jet flow particles of an active galactic nucleus are assigned in a broad area, it could cause a broader absorption pit for a crossing light ray. One can calculate the average redshift and the width of absorption pit.

Additionally speaking on the topic of jet flow, massive particles may be easily accelerated up and keep approaching absolute light speed so as to escape from inner event horizon. On the other hand, apparent light speed may be at lower level in the nearby $r^{*}$ area so that to form pseudo super luminal motions. A high pseudo super luminal motion may cause Cherenkov radiation, which could generally show polarized propagation. That might also be the reasons for some high energy light rays. One can imagine that the events of γ-ray burst detection delay in observations on SN1987A [57] and GW170817 [58] might be interpreted by pseudo super luminal propagations of neutrinos and gravitational waves.