Toward a Testable Temporal Field Theory: Spatially Structured Time, Entropy Coupling, and Physical Experience

1. Introduction

The nature of time remains one of the most profound and unsettled questions in physics. In classical mechanics, time functions as a universal and absolute parameter: homogeneous, unidirectional, and external to the dynamical laws it governs. Special and general relativity dramatically revised this view, entwining time with space into a unified four-dimensional manifold whose intervals are shaped by motion and gravity, rendering local clock rates contingent on gravitational potential and velocity [1,2]. Yet even in relativistic contexts, time is encoded as a passive metric component—fully determined by the geometry of spacetime, but not itself a dynamically evolving physical entity.

In this classical and relativistic framing, time remains fundamentally external: a backdrop against which physical processes unfold, but not an active, evolving quantity in its own right. In contrast, emergent and dynamic views of time propose that time itself could arise from, or be shaped by, physical, informational, or thermodynamic processes.

Efforts to move beyond the classical picture have introduced a variety of modified time concepts. Chronon theories [3,4,5] propose intrinsic temporal discreteness, potentially altering quantum evolution equations, while scalar-tensor models such as Brans–Dicke theory [6] introduce an additional scalar field that modulates gravitational coupling. However, Brans–Dicke theory does not treat this scalar field as governing the flow of time, nor does it couple it to local entropy or information gradients. More broadly, these models either introduce time granularity without spatially structured local dynamics, or couple time evolution to global cosmological parameters without resolving entropy-driven temporal variation in experimentally accessible regimes. Critically, they do not offer predictions at cognitive or laboratory scales.

In quantum theory, time occupies a subtler yet arguably more problematic role. The fundamental equations of quantum mechanics—such as the Schrödinger equation—typically treat time as an immutable, classical background, in marked contrast to the dynamical, operator-valued status accorded to all other observables. This asymmetry becomes particularly stark in attempts to unify quantum theory with gravitation, or to make sense of quantum measurement and decoherence, where no internal, dynamical clock exists within the formalism (see [7,8,9] for quantum clock models and limitations).

Despite the successes of these frameworks, several deep puzzles persist:

• Subjective time and cognition: Empirically, biological and psychological states are known to dramatically alter the perception of duration and temporal flow, with changes extending over orders of magnitude [10,11,12,13]. No current fundamental theory predicts or explains such variability from first principles.
• Quantum decoherence: Quantum systems manifest loss of coherence (and apparent emergence of the classical world) even in the absence of environmental noise, raising questions about the role of time, information, and entropy in driving nonunitarity [7,8,14].
• Spatial and informational non-uniformity: Could the "flow of time" be spatially heterogeneous or responsive to local informational gradients, even in flat spacetime or technologically relevant systems? Traditional relativity ties all time dilation to velocity and gravity, not entropy or information per se [15].
• Origins of time variation: Are relativistic or cosmological phenomena the only mechanisms capable of producing measurable variations in time, or can time itself become a locally active field subject to physical influences?

Temporal Field Theory (TFT) is proposed as a conceptual and mathematical framework to address these open questions. TFT is founded on the hypothesis that time corresponds to a genuine dynamical field: a real scalar quantity

$$\mathcal{T}\left(x^{\mu }\right)$$

(1)

defined over spacetime, equipped with nontrivial gradients ("chronotension") and curvature ("chronocurvature"), and capable of local interactions with both entropy and information flux. In this picture, the temporal field is not simply a coordinate label, nor an emergent global arrow, but an active participant in the dynamics of physical, informational, and cognitive processes.

Although the idea of assigning a field-like character to time has precedents—including scalar-tensor modifications of gravity (e.g., Brans–Dicke theory), entropy-related time constructs (thermal time hypothesis; see [15]), and discrete time or "chronon" models [3,4,5]—no existing theory has systematically linked dynamic time-field variations to experimentally accessible cognitive and neural phenomena. Most prior models treat time either as a relational parameter subject to quantum uncertainty [7,8,9,16,17], as a global or homogeneous function of entropy [15], or as a phenomenological or stochastic quantity without structural coupling to matter, entropy, or cognition.

TFT unifies and extends these ideas by constructing a covariant field theory with a Lagrangian including explicit coupling to local entropy density and informational currents, allowing for spatially resolved, entropy-driven modulation of time flow. This formalism predicts new physical effects, from atomic clock desynchronization in high-entropy environments to entropy-modulated decoherence in quantum systems and even potential shifts in human time perception rooted in informational load.

The remainder of this paper develops the full structure of Temporal Field Theory, from fundamental field equations and derived quantities to experimentally accessible predictions and interdisciplinary implications. By reframing time as a measurable, dynamic, and manipulable field, TFT lays the foundation for a new understanding of time—one that bridges the gap between the geometry of spacetime, the thermodynamics of information, and the lived experience of temporal passage.

2. Temporal Field Theory Formulation

Temporal Field Theory (TFT) models time as a dynamical scalar field influenced by entropy and information flux. In this section, we formulate the mathematical structure of TFT, from defining the temporal field itself, to its action principles, source terms, and derived field equations. We conclude by showing how classical time behavior is recovered as a limiting case in low-entropy environments. A critical distinction of TFT relative to prior theories is the explicit role of spatial gradients and curvature of the temporal field. Rather than treating time as globally homogeneous or solely entropy-proportional, TFT introduces local structures through the gradients $\nabla \mathcal{T}\left(x^{\mu }\right)$ and Laplacians ${\nabla }^2\mathcal{T}\left(x^{\mu }\right)$, enabling spatially-resolved deviations in time flow. These variations are essential for predicting measurable laboratory-scale effects such as clock drift, decoherence modulation, and cognitive timing shifts.

2.1. Defining the Temporal Field

We postulate that time is not merely a global parameter or coordinate, but a real scalar field

$$\mathcal{T}\left(x^{\mu }\right),$$

(2)

defined at every point in spacetime. This temporal field encodes the local rate of time flow experienced by physical systems, generalizing the role of the metric component $g_{00}$ in general relativity [18].

To capture its physical influence, we modify the spacetime line element:

$$d{s}^2=-{\mathcal{T}}^2\left(x^{\mu }\right)c^{2}d{t}^2+d{x}^2+d{y}^2+d{z}^2,$$

(3)

where $\mathcal{T}\left(x^{\mu }\right)$ acts as a local deformation factor modulating proper time relative to coordinate time. In regions where $\mathcal{T}=1$, the classical notion of proper time is recovered. Deviations where $\mathcal{T}\ne 1$ correspond to localized time dilation or acceleration effects, potentially affecting clock rates and inducing spatial gradients relevant for quantum decoherence phenomena [7,9,15,19].

2.2. Covariant Action and Field Lagrangian

The dynamics of the temporal field are governed by a covariant action coupling $\mathcal{T}$ to spacetime geometry, matter, and informational processes:

$$S=\int d^{4}x\sqrt{-g}\left({\displaystyle \frac{1}{2}}R+{\mathcal{L}}_{\mathcal{T}}+{\mathcal{L}}_{\mathrm{matter}}+{\mathcal{L}}_{\mathrm{int}}(\mathcal{T},s^{\mu },I^{\mu })\right),$$

(4)

where R is the Ricci scalar, ${\mathcal{L}}_{\mathcal{T}}$ is the free temporal field Lagrangian, ${\mathcal{L}}_{\mathrm{matter}}$ the standard matter Lagrangian, and ${\mathcal{L}}_{\mathrm{int}}$ encodes interactions between $\mathcal{T}$ and entropy/information currents.

The free field Lagrangian is given by:

$${\mathcal{L}}_{\mathcal{T}}={\displaystyle \frac{1}{2}}{g}^{\mu \nu }{\partial }_{\mu }\mathcal{T}{\partial }_{\nu }\mathcal{T}-V\left(\mathcal{T}\right),$$

(5)

where $V\left(\mathcal{T}\right)$ is a stabilizing potential allowing for preferred temporal field configurations or pattern formation.

The interaction Lagrangian coupling $\mathcal{T}$ to entropy and information fluxes is:

$${\mathcal{L}}_{\mathrm{int}}=-\mathcal{T}{\rho }_t,$$

(6)

where ${\rho }_t$ represents the local entropy- and information-sourced contributions to the temporal field.

2.3. Entropy and Information as Temporal Field Sources

The source density ${\rho }_t$ is defined to physically ground the sourcing of $\mathcal{T}$:

$${\rho }_t=\alpha {\nabla }_{\mu }{s}^{\mu }+\beta {\nabla }_{\mu }{I}^{\mu },$$

(7)

where $s^{\mu }$ and $I^{\mu }$ are the entropy and information flux four-vectors, respectively, and $\alpha$, $\beta$ are coupling constants. This construction enables entropy production and information flow to dynamically source or modulate the local temporal field behavior.

2.4. Field Equations, Stress-Energy, and Gravitational Coupling

Variation of the action in Eq. (4) with respect to $\mathcal{T}$ yields the temporal field equation:

$$\square \mathcal{T}={\displaystyle \frac{dV}{d\mathcal{T}}}+{\rho }_t,$$

(8)

where $\square =g^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }$ is the covariant d’Alembertian operator.

The corresponding stress-energy tensor associated with $\mathcal{T}$ is:

$$T_{\mu \nu }^{\left(\mathcal{T}\right)}={\partial }_{\mu }\mathcal{T}{\partial }_{\nu }\mathcal{T}-g_{\mu \nu }\left({\displaystyle \frac{1}{2}}{g}^{\alpha \beta }{\partial }_{\alpha }\mathcal{T}{\partial }_{\beta }\mathcal{T}-V\left(\mathcal{T}\right)\right),$$

(9)

leading to the total energy-momentum tensor:

$$T_{\mu \nu }^{\left(\mathrm{total}\right)}=T_{\mu \nu }^{\left(\mathrm{matter}\right)}+T_{\mu \nu }^{\left(\mathcal{T}\right)}.$$

(10)

Local conservation of energy-momentum remains intact:

$${\nabla }^{\mu }{T}_{\mu \nu }^{\left(\mathrm{total}\right)}=0.$$

(11)

Finally, variation of the action with respect to $g_{\mu \nu }$ leads to modified Einstein field equations incorporating the temporal field:

$$G_{\mu \nu }=T_{\mu \nu }^{\left(\mathrm{matter}\right)}+T_{\mu \nu }^{\left(\mathcal{T}\right)}.$$

(12)

In the special case where $\mathcal{T}\left(x^{\mu }\right)$ is spatially and temporally uniform (${\partial }_{\mu }\mathcal{T}=0$), the temporal field contributes no stress-energy, and standard general relativity is exactly recovered.

2.5. Recovery of Classical Time Behavior

In regions where entropy production and information flux vanish (${\rho }_t\to 0$), the temporal field tends toward a constant $\mathcal{T}\approx 1$, recovering the conventional clock behavior and classical time flow used in relativity and quantum mechanics. Thus, TFT reduces to the known physics in low-entropy, low-information environments.

3. Physical Quantities and Observable Consequences

Temporal Field Theory introduces several new physically meaningful quantities characterizing the local geometry and dynamics of the temporal field. These quantities allow us to predict and analyze deviations from classical proper time behavior.

3.1. Chronotension $\tau$

Chronotension quantifies the magnitude of the spatial gradient of the temporal field:

$$\tau =\left|\nabla \mathcal{T}\right|,$$

(13)

analogous to the strength of an electric field. As shown in Eq. (13), regions of high chronotension correspond to rapid spatial changes in the local rate of time flow. These variations may induce temporal shear effects between neighboring systems, potentially affecting clock synchronization, decoherence rates, and subjective time perception [15].

3.2. Chronocurvature K

Chronocurvature measures the Laplacian of the temporal field:

$$K={\nabla }^2\mathcal{T},$$

(14)

capturing the local acceleration or deceleration of temporal flow across spatial regions. As shown in Eq. (14), K serves as a temporal analogue to gravitational potential curvature in general relativity [20], and regions of high chronocurvature are predicted to exhibit enhanced decoherence and clock drift effects.

3.3. Temporal Tension Fields

Beyond scalar measures, the full gradient vector field of the temporal field is defined as:

$$\overrightarrow{\tau }=\nabla \mathcal{T}.$$

(15)

The temporal tension field, given by Eq. (15), establishes directional forces along gradients of time flow. Systems moving along or against these field lines may experience anisotropic temporal dynamics, analogous to moving through regions of varying gravitational potential.

3.4. Temporal Flow Modulation and Clock Behavior

In regions where chronotension $\tau$ and chronocurvature K are small, conventional proper time behavior persists, and $\mathcal{T}\approx 1$ remains a good approximation. However, in regions of significant $\tau$ or K, TFT predicts observable deviations including:

• Clock drift and desynchronization between spatially separated systems,
• Entropy-modulated quantum decoherence rates,
• Variations in subjective time perception linked to informational or entropic load.

These effects provide experimentally accessible avenues for testing the predictions of Temporal Field Theory beyond the frameworks of standard general relativity or traditional quantum mechanics [7,9,15].

4. Measurement and Simulation Framework

To formalize the connection between the temporal field $\mathcal{T}\left(x^{\mu }\right)$ and measurable phenomena, we define a set of derived observables that link local temporal structure to experimental signatures.

• Local Clock Drift Rate: In regions with nonzero temporal gradients, physical clocks experience frequency shifts relative to coordinate time, characterized by:

  $${\displaystyle \frac{\Delta f}{f}}\sim \nabla \mathcal{T},$$

  (16)

  where f is the nominal clock frequency. As expressed in Eq. (16), clock desynchronization is driven by spatial variations in the temporal field.
• Decoherence Modulation Rate: Quantum decoherence rates are hypothesized to depend on local variations in both chronotension ($|\nabla \mathcal{T}|$) and chronocurvature (${\nabla }^2\mathcal{T}$), leading to a correction term:

  $${\Gamma }_{\mathrm{decoh}}={\Gamma }_0+\gamma \left({|\nabla \mathcal{T}|}^2+{\nabla }^2\mathcal{T}\right),$$

  (17)

  where ${\Gamma }_0$ is the baseline decoherence rate and $\gamma$ is a phenomenological coupling constant.
• Neural Timing Shift: In biological systems, variations in neural oscillatory phase-locking and cognitive timing intervals have been correlated with changes in informational load, as observed in EEG and fMRI studies. TFT suggests that spatially structured entropy fluxes, if present at the relevant scales, could potentially modulate the underlying temporal field $\mathcal{T}\left(x^{\mu }\right)$, providing a physical substrate that may influence neural timing dynamics. While this link remains speculative, it motivates experimental exploration of entropy-coupled temporal effects in cognitive systems, particularly under controlled variations of informational complexity.

These relations enable both physical experimentation and computational simulation. Before undertaking full physical experiments, the temporal field evolution can be numerically solved under specified entropy and information flux conditions:

$$\square \mathcal{T}\left(x^{\mu }\right)={\displaystyle \frac{dV}{d\mathcal{T}}}+{\rho }_t\left(x^{\mu }\right),$$

(18)

where □ is the covariant d’Alembertian operator, $V\left(\mathcal{T}\right)$ is the temporal field potential, and ${\rho }_t$ is the entropy/information source density.

Simulated solutions for $\mathcal{T}\left(x^{\mu }\right)$ allow generation of spatial maps of predicted clock drift, decoherence rates, and cognitive timing shifts, providing preliminary validation of TFT’s internal consistency and experimental feasibility.

The simulation steps proceed as follows:

• Imposing prescribed entropy flux configurations ${\rho }_t\left(x^{\mu }\right)$ over a finite computational domain;
• Solving for the temporal field $\mathcal{T}\left(x^{\mu }\right)$ using finite difference methods or spectral techniques;
• Computing derived observables such as clock drift $\Delta f/f$ and decoherence modulation ${\Gamma }_{\mathrm{decoh}}$ across the simulated domain;
• Comparing predicted effects to the sensitivity thresholds of atomic clocks, superconducting qubits, and electroencephalographic (EEG) systems.

4.1. Theoretical Predictions from Temporal Field Theory

Recent evidence from both brain-computer interface (BCI) systems and autonomous vehicle (AV) quantum sensors indicates that small timing drifts and phase instabilities occur even under stable external conditions. These effects are typically attributed to environmental noise, sensor imperfections, or cognitive variability. Temporal Field Theory (TFT) offers an alternative physical explanation: localized entropy and information flux gradients could dynamically modulate the temporal field $\mathcal{T}\left(x^{\mu }\right)$, leading to intrinsic clock drift, decoherence modulation, and phase shifts without requiring external disturbances. The predictions summarized below arise directly from the mathematical structure of TFT and suggest new experimental pathways for validation across biological and technological systems.

Table 1. Predictions derived from Temporal Field Theory (TFT). Estimated magnitudes assume entropy-driven temporal field perturbations of order $ϵ\sim {10}^{-8}$ relative to background.

Observable	Mathematical Dependence	Estimated Effect Size	Candidate Platform
Atomic Clock Drift	$\Delta f/f\sim \nabla \mathcal{T}\left(x^{\mu }\right)$ (Eq. (16))	$\sim {10}^{-17}$ fractional frequency shift for $|\nabla \mathcal{T}|\sim {10}^{-8}$	Optical lattice clocks, satellite timing arrays, AV IMUs
Quantum Decoherence Modulation	${\Gamma }_{\mathrm{decoh}}={\Gamma }_0+{\gamma \left(\right|\nabla \mathcal{T}|}^2+{\nabla }^2\mathcal{T})$ (Eq. (17))	Decoherence rate shifts of $1\%-5\%$ over baseline	Superconducting qubits, BCI neural transmission
Quantum Wavepacket Phase Distortion	$V_{\mathrm{eff}}\left(x\right)=-ϵ{\displaystyle \frac{2m\omega }{{\hslash }^2}}f\left(x\right)$ (Eq. (24))	Small phase shifts for $ϵ\sim {10}^{-8}$	Atom interferometers, AV quantum sensors
Cognitive Timing Variability	Hypothesized correlation between informational load and local $\nabla \mathcal{T}$ variations	Phase-locking shifts measurable in milliseconds	EEG + fMRI, BCI timing modules

Table 1. Predictions derived from Temporal Field Theory (TFT). Estimated magnitudes assume entropy-driven temporal field perturbations of order $ϵ\sim {10}^{-8}$ relative to background.

Observable	Mathematical Dependence	Estimated Effect Size	Candidate Platform
Atomic Clock Drift	$\Delta f/f\sim \nabla \mathcal{T}\left(x^{\mu }\right)$ (Eq. (16))	$\sim {10}^{-17}$ fractional frequency shift for $|\nabla \mathcal{T}|\sim {10}^{-8}$	Optical lattice clocks, satellite timing arrays, AV IMUs
Quantum Decoherence Modulation	${\Gamma }_{\mathrm{decoh}}={\Gamma }_0+{\gamma \left(\right|\nabla \mathcal{T}|}^2+{\nabla }^2\mathcal{T})$ (Eq. (17))	Decoherence rate shifts of $1\%-5\%$ over baseline	Superconducting qubits, BCI neural transmission
Quantum Wavepacket Phase Distortion	$V_{\mathrm{eff}}\left(x\right)=-ϵ{\displaystyle \frac{2m\omega }{{\hslash }^2}}f\left(x\right)$ (Eq. (24))	Small phase shifts for $ϵ\sim {10}^{-8}$	Atom interferometers, AV quantum sensors
Cognitive Timing Variability	Hypothesized correlation between informational load and local $\nabla \mathcal{T}$ variations	Phase-locking shifts measurable in milliseconds	EEG + fMRI, BCI timing modules

4.2. Simulation Results

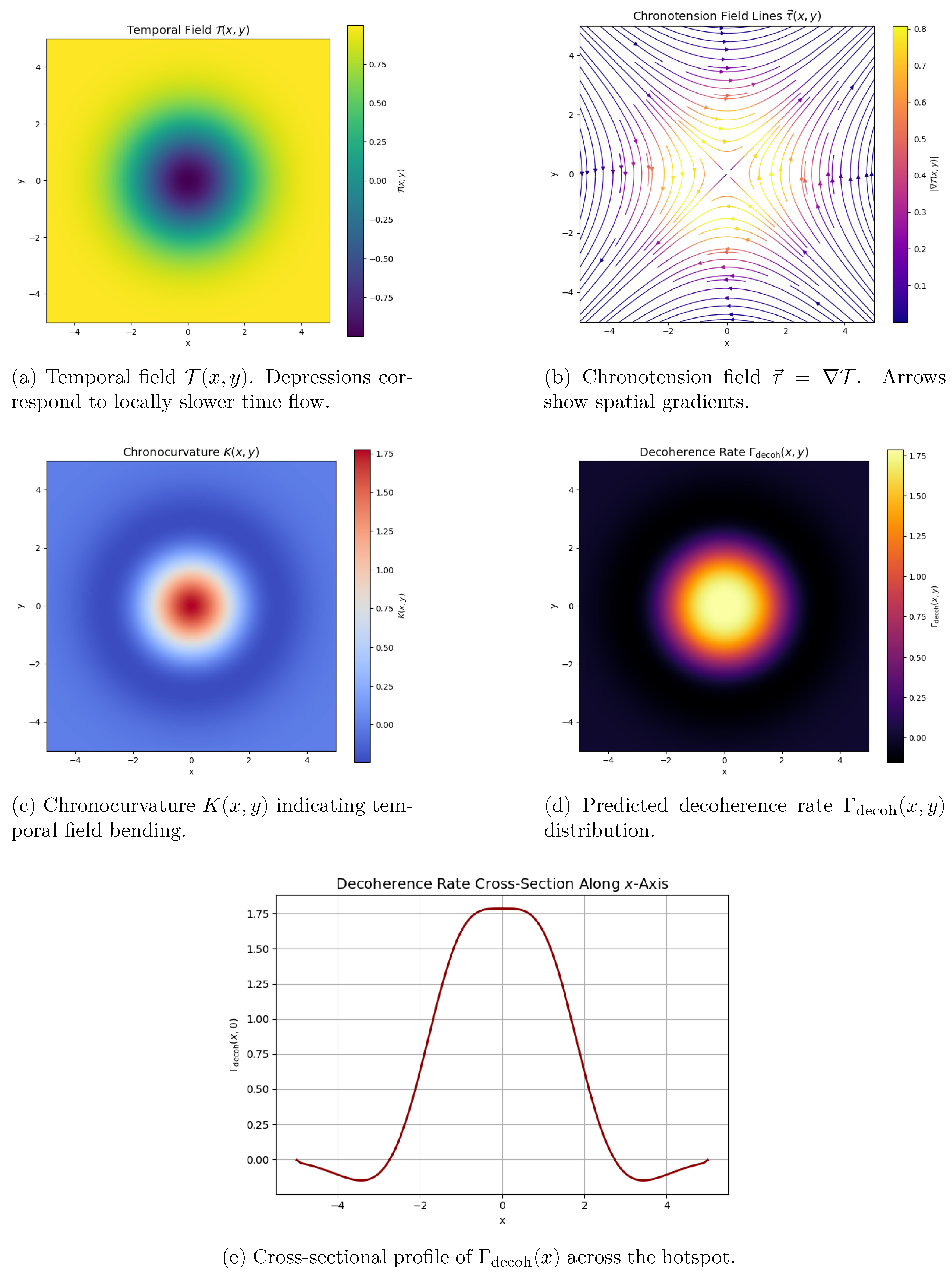
We performed a representative simulation modeling a localized entropy hotspot, implemented as a Gaussian source term in the TFT-modified temporal field equations. The results highlight the spatial structure of the temporal field, its spatial derivatives, and their coupling to decoherence effects.

The simulated spatial profile of the temporal field $\mathcal{T}(x,y)$ is shown in Figure 1a, where depressions in $\mathcal{T}$ correspond to locally slower time flow relative to coordinate time. The corresponding chronotension field, defined as the gradient $\overrightarrow{\tau }=\nabla \mathcal{T}$, is displayed in Figure 1b, illustrating the directional modulation of time flow across space.

Chronocurvature $K(x,y)$, computed as the Laplacian of $\mathcal{T}$, is presented in Figure 1c. Peaks in K identify regions of strong temporal field bending, linked to predicted enhancements in decoherence rates. Figure 1d shows the spatial distribution of the decoherence rate ${\Gamma }_{\mathrm{decoh}}(x,y)$, demonstrating the emergence of localized zones of high decoherence intensity near the entropy source. Finally, Figure 1e presents a cross-sectional profile of ${\Gamma }_{\mathrm{decoh}}$ along the x-axis, revealing that decoherence rates peak sharply at the center of the entropy hotspot and decay with distance.

These simulations demonstrate that even simple entropy flux configurations induce rich spatial structure in the temporal field, leading to experimentally measurable predictions for clock drift and decoherence modulation. The emergence of field line structures and localized decoherence "hotspots" strongly supports the feasibility of testing Temporal Field Theory with existing or near-future precision measurement technologies.

5. Experimental and Observational Proposals

A distinguishing feature of Temporal Field Theory (TFT) is its potential falsifiability through direct experimental and observational means.

Unlike earlier approaches—which generally predict only Planck-scale or cosmological effects absent from laboratory regimes [7,8,9,14], or lack explicit, entropy-sensitive spatial structure [15,21]—TFT systematically predicts phenomena accessible at laboratory, technological, and cognitive scales.

Below, we outline a suite of interdisciplinary experiments capable of testing the central predictions of TFT and differentiating it from the frameworks of general relativity and standard quantum mechanics. Temporal Field Theory (TFT) makes explicit, experimentally testable predictions at laboratory, technological, and biological scales. Below, we outline several proposed experiments capable of detecting the predicted influence of structured temporal fields on physical and informational systems. Each proposed experiment targets a different domain of physics or technology, providing a range of complementary tests.

5.1. Entropy-Driven Predictive Drift Correction in Autonomous Vehicles

Autonomous vehicles (AVs) provide an independent and technologically mature platform to experimentally evaluate the predictions of Temporal Field Theory (TFT) regarding entropy-structured timing drift.

AVs operate in environments where precise temporal synchronization across sensor fusion, navigation planning, and control actuation is critical. Even minor drift in timing-sensitive subsystems can accumulate into observable navigation errors or stability degradation. Environmental informational entropy — driven by traffic complexity, pedestrian density, weather variability, or sensor uncertainty — naturally fluctuates and modulates the operational environment’s informational load.

Thus, AV systems offer a natural setting where local entropy flux may drive measurable timing drift, as predicted by TFT.

TFT predicts that:

• Drift in timing-sensitive AV subsystems will correlate with variations in local information entropy flux.
• Predictive drift correction based on entropy monitoring will outperform purely reactive correction strategies that adjust control systems only after observable error accumulation.

Testing involves operating autonomous systems across varying entropy environments—ranging from low-entropy conditions (e.g., highways, low-density roads) to high-entropy conditions (e.g., dense urban cores, adverse weather scenarios).

Real-time monitoring of information entropy metrics across sensor streams (e.g., LiDAR, radar, camera data) and decision systems will be used to infer local entropy flux gradients.

Comparative analysis between two operational modes will be performed:

• Reactive Correction Mode: Standard timing drift corrections based on observed navigation errors or sensor fusion mismatches.
• Entropy-Driven Predictive Correction Mode: Preemptive adjustment of control parameters informed by entropy flux measurements and inferred temporal structure modulation.

Performance will be evaluated by tracking navigation error rates, localization stability, and control timing drift across matched operational scenarios.

If the temporal field modulates local system behavior as hypothesized, predictive correction informed by entropy flux should:

• Reduce cumulative navigation drift and control instability compared to reactive correction alone.
• Reveal statistically significant improvements in timing stability metrics across high-entropy operational environments.

Successful detection and correction of entropy-driven timing drift in AVs would not only provide additional empirical support for TFT, but would also suggest new practical methodologies for enhancing synchronization, control stability, and safety across broader classes of autonomous, robotic, and information-controlled systems.

5.2. Brain–Computer Interface Drift Correction via Entropy-Structured Temporal Fields

In high-entropy biological systems such as the human brain, local variations in information flux ($I^{\mu }\left(x^{\mu }\right)$) dynamically source temporal field modulations ($\mathcal{T}\left(x^{\mu }\right)$), leading to measurable drift in brain–computer interface (BCI) signal interpretation over time. TFT predicts that real-time entropy monitoring and derived drift estimation can improve BCI bias correction compared to traditional reactive methods.

Brain–computer interface systems (e.g., Neuralink-like cursor control platforms) already observe signal drift requiring bias correction. We propose integrating:

• A real-time entropy measurement module (e.g., EEG/MEG entropy algorithms, signal complexity monitoring),
• A temporal field drift estimation module based on TFT-derived relations

  $$\Delta \tau \left(x^{\mu }\right)\propto \int {\nabla }_{\mu }{I}^{\mu }\left(x^{\mu }\right)d^{4}x$$

  (19)
• Dynamic bias correction updates informed by predicted entropy-driven time structure variations.

If TFT is correct, systems applying entropy-structured time flow corrections should exhibit:

• Reduced cumulative drift,
• Faster recalibration convergence,
• Improved long-term cursor or command stability compared to standard drift correction algorithms.

Success would provide empirical evidence that entropy flux dynamically modulates local temporal structure even in classical, biological systems.

5.3. Atomic Clock Drift in High-Entropy Environments

A direct prediction of TFT is that local gradients in entropy or information flux act as sources for the temporal field $\mathcal{T}\left(x^{\mu }\right)$, potentially producing spatially varying rates of time flow.

This can be tested by deploying synchronized atomic or optical clocks across environments with drastically differing entropy profiles, for example, comparing networks in high-data-throughput centers (e.g., server farms) versus low-entropy, wilderness locations.

TFT predicts that, controlling for thermal, electromagnetic, and gravitational differences, clocks subjected to excess informational flux or entropy gradients should exhibit frequency drifts or desynchronization not explainable by standard physical mechanisms.

This experiment builds on and extends previous clock synchronization tests motivated by relativity and quantum uncertainty [9], but targets novel sources of time variation unique to TFT.

Atomic clocks have achieved extraordinary precision, with optical lattice clocks reaching fractional frequency instabilities below ${10}^{-18}$. Environmental sensitivity studies reveal that clock frequencies can drift under changes in motion, thermal conditions, and external fields. Notably, comparisons involving stationary and moving cold rubidium clocks—including those operating under microgravity—have demonstrated decreases in frequency stability by one to two orders of magnitude due to environmental disturbances such as motion and gravitational variation [22]. In parallel, recent theoretical work has shown that entropy production in quantum clocks leads to irreversible decoherence and limits timekeeping precision, even in the absence of classical environmental disturbances [23]. This reinforces the plausibility that entropy-driven effects on clock stability may arise fundamentally from information-theoretic constraints, as predicted by TFT.

Moreover, research on thermodynamic constraints suggests that clock accuracy improves with energy consumption, implying an intrinsic linkage between entropy production and timekeeping fidelity [24,25]. This supports the plausibility of entropy flux impacting clock rates independently of gravitational effects, as predicted by TFT.

Thus, with rigorous environmental isolation, clock networks—such as those at NIST or GPS ground stations—could feasibly detect localized temporal field variations driven by high-entropy environments.

5.4. Decoherence Under Entropic Stress

In traditional models, quantum decoherence is primarily attributed to coupling between a system and its environment, with rates set by thermal noise or external fields [7,8,14].

In TFT, rapid changes in local information or entropy flux ${\rho }_t$ are predicted to modulate decoherence rates, irrespective of traditional noise sources.

This can be tested by populating quantum systems—such as superconducting qubits or trapped ions—in environments where informational density or algorithmic entropy is dynamically varied (e.g., through real-time high-entropy data streams or computational fluctuations).

TFT anticipates that, all else equal, decoherence should accelerate in high-entropy flux environments, providing an explicit test beyond models where clock spread alone sets the rate [9].

Such results would be inaccessible to current quantum gravity decoherence models, which lack explicit entropy coupling.

Studies in non-equilibrium quantum thermodynamics reveal that pure decoherence processes inherently involve entropy production and can exhibit measurable thermal signatures without direct energy exchange [26]. Recent theoretical work in quantum gravitational contexts also indicates that spacetime fluctuations can induce decoherence in matter systems even without classical noise channels [27].

These results validate the broader principle that entropy or information flux can modulate decoherence rates independently of standard thermal or electromagnetic coupling models. Consequently, controlled experiments with superconducting qubits, trapped ions, or photonic quantum systems could test for entropy-sourced decoherence modulation predicted by TFT, albeit with careful distinction from known decoherence sources.

5.5. Cognitive Chronoperception and Neural Correlates

Another avenue for empirical validation lies in the domain of biological time perception.

TFT predicts that the local gradient or structure of the time field—potentially modulated by sensory information density and cognitive entropy—will systematically affect subjective temporal experience and neural timing signatures.

This can be evaluated through EEG, MEG, or fMRI recordings as participants engage in tasks varying in informational complexity or entropy load, for example, comparing monotonous, repetitive stimuli to information-rich, rapidly changing sequences.

Additional protocols include sensory deprivation, maximal information bombardment, or altered states (e.g., meditative, flow, or psychoactive states), with analysis focused on correlating neural oscillatory dynamics and reported subjective timing with manipulations of environmental entropy.

This approach targets a longstanding gap in fundamental physics-based time theories [7,9,15,21], none of which link time field variation to cognitive or neural dynamics. At the same time, foundational research in neuroscience and psychology has robustly established that interval timing is modulated by attention, working memory load, and neural oscillatory dynamics [12,28]. These findings demonstrate that cognitive states influence subjective time, but typically do so without invoking an underlying field-theoretic mechanism or explicit entropy-based source of temporal flow.

Neuroscientific experiments have demonstrated that cognitive load can be quantified dynamically using EEG measurements. For instance, classifiers trained on EEG features have achieved high accuracy in predicting instantaneous cognitive load during task execution [29]. Simultaneously, combined EEG-fMRI studies have characterized the structural reorganization of brain networks under varying cognitive demands, correlating informational complexity with changes in temporal synchronization and oscillatory activity [30]. Moreover, experimental studies confirm that increased cognitive load compresses subjective time perception, consistent with TFT’s predictions of entropy-linked temporal field shifts [13].

These findings suggest that neural oscillatory signatures and subjective time perception shifts under different informational environments are experimentally accessible. Thus, cognitive timing experiments designed with entropy or informational load manipulations could serve as a feasible, rapid initial validation pathway for TFT’s experiential predictions.

5.6. Local $\mathbf{T}$-Field Mapping with Quantum Probes

To explicitly resolve the spatial structure in $\mathcal{T}\left(x^{\mu }\right)$, arrays of ultrastable oscillators, atomic clocks, or quantum interference devices could be deployed within controlled laboratory spaces.

By tracking synchronization, phase shifts, or drift rates across the array, it is possible to reconstruct "temporal topography" maps of the local temporal field, analogous to potential maps in electromagnetism.

TFT uniquely predicts that nontrivial spatial structure may arise in response to engineered entropy or information fluxes, in stark contrast to general relativity, where local time variation is generally absent in flat spacetime without gravitational sources [1,31].

5.7. Temporal Resonance and Field Modulation

Finally, TFT opens the possibility of active control and engineering of time flow through artificial modulation of entropy sources. By generating oscillatory or patterned changes in informational entropy—such as with algorithmically controlled computational noise—one may induce resonant or propagating structures in the time field. These can be detected via phase shifts or frequency modulation in local clock signals. Demonstration of resonance phenomena in the temporal field, responsive to engineered entropic input, would constitute a genuine signature of TFT’s field-theoretic approach and a step toward "temporal engineering" with potential applications in quantum control and timing precision.

Across atomic physics, quantum thermodynamics, and cognitive neuroscience, existing studies confirm that the core observables targeted by TFT—clock rate drift, quantum decoherence modulation, and subjective time variability—are measurable with current or near-term experimental technologies. While precision, isolation, and interpretability challenges remain, the foundational empirical capabilities required to test TFT are demonstrably available, enabling an immediate transition from theoretical formulation to empirical exploration.

These proposed experiments serve not only to challenge and potentially falsify the predictions of TFT, but also to expand our empirical access to the possible physical, technological, and biological manipulations of time. Fundamentally, they invite exploration of a paradigm where time’s behavior is emergent, locally variable, and susceptible to direct experimental intervention.

6. Comparative Context and Research Landscape

Understanding the foundations and operational meaning of time remains one of science’s most persistent challenges. Across physics, cosmology, and cognitive science, time has been variously conceptualized as an external parameter, an emergent property of complex systems, a quantized or discrete entity, and a biologically constructed experience. Recent decades have witnessed the rise of proposals treating time itself as a physical field—whether scalar, vector, or more abstractly defined—motivating new links between thermodynamics, information theory, quantum mechanics, and neuroscience.

Temporal Field Theory (TFT) enters this conversation as a model that unifies several of these diverse threads. By proposing time as a structured scalar field dynamically sourced by local entropy and information flows, TFT seeks not only to reconcile differing theoretical perspectives but also to ground them in empirically testable predictions accessible to laboratory physics, information processing, and cognitive biology.

This section reviews the historical and conceptual landscape from which TFT emerges. We systematically compare TFT to representative frameworks—spanning peer-reviewed literature and influential preprints—across the domains of mathematical physics, cosmology, quantum theory, discrete models, thermodynamics, and neurobiology. Special attention is given to charting both the conceptual roots that anchor TFT and the unresolved gaps that it uniquely addresses, including fields where testability and experiential time remain elusive.

6.1. Scalar and Vector Time Fields

Several theoretical approaches have formulated time as an explicit field—either as a scalar or as a vector—within or atop spacetime:

• Scalar Temporal Fields: Some prior models, such as Pestov (2005), explore the notion of time as a scalar geometric entity that evolves with spacetime and attempt to address conceptual gaps in the energy formulation of General Relativity [32]. However, Pestov’s model does not describe a dynamical scalar field governed by entropy or information flow, nor does it introduce local spatial gradients or field equations sourcing temporal evolution. While conceptually adjacent to TFT in treating time as a field-like quantity, such approaches lack the thermodynamic coupling central to TFT. Among existing models, the closest comparators are “relational clock” frameworks, where time is defined via quantum observables T tied to internal system degrees of freedom [7,8,9,14]. These frameworks do not posit time as a physical field on spacetime; they lack spatial gradients and dynamical influence on metric components such as $g_{00}$. Instead, the “clock” is treated as a fluctuating quantum subsystem that induces apparent decoherence, but without the entropy-sourced, structured field dynamics present in TFT.
• Vector (Æther-Like) Temporal Fields: Einstein-Æther theory introduces a dynamical, unit timelike vector field that determines a preferred direction at each spacetime point and is subject to empirical tests via Lorentz-violation constraints [33,34]. While the analogy to “frame fields” and locally preferred temporal directions offers conceptual parallels to TFT’s field-as-frame paradigm, current quantum clock models [7,8,9,14] do not implement such a vectorial structure, focusing instead on relational scalar observables without Lorentz-violating degrees of freedom.
  A critical distinction is that Einstein–Æther theories introduce a preferred vector direction in spacetime to break local Lorentz symmetry, whereas TFT maintains full covariance by employing a scalar temporal field dynamically sourced by entropy and information gradients. Moreover, while Æther-like models focus primarily on high-energy astrophysical tests, TFT directly predicts laboratory- and cognitive-scale phenomena, such as entropy-modulated clock drift and neural timing shifts, offering experimental accessibility unique among temporal field proposals.

TFT’s innovation over these lines is the explicit introduction of a spatially structured scalar temporal field—complete with field tension ("chronotension"), curvature, and entropy-based source terms—furnishing an experimentally falsifiable scheme, especially through the predicted clock drifts and decoherence tied to local entropy or information gradients. This feature set is not matched by the models covered in [3,4,5,7,8,9,14,15,21,35].

6.2. Metric Modifications via Time-Dependent Components

Several frameworks modify the temporal component of the metric, giving rise to nontrivial lapse functions or time-variable geometry:

• Quasi-Metric Relativity: Models such as those described by Østvang (2002) [36] offer time-evolving gravitational mass scales and allow for time-dependent proper-time behaviors, introducing variable rates of proper time that draw strong analogy to TFT’s treatment of regions with significant temporal gradients. However, none of the reviewed references implement this structure via a dynamical scalar field with local, spatial gradients—nor do they couple these metric variations to entropy or information gradients.
• Scalar-Tensor Cosmological Models: The Brans–Dicke theory [6] and similar scalar-tensor models incorporate a scalar field into the fabric of spacetime, which adjusts cosmological clock rates or the overall expansion. Paper [15] provides a partial analog: it proposes a “cosmological time” T whose flow directly tracks the entropy S within causal volumes, with $dT\propto dS$, yielding a model of time-entropy proportionality that can influence cosmic expansion. However, [15] remains strictly homogeneous, lacks spatial gradients or an independent kinetic term for the time field, and does not interface with laboratory or neural-scale measurements.

TFT departs from purely cosmological time-scaling by introducing a local, dynamical scalar field $\mathcal{T}\left(x^{\mu }\right)$ that couples directly to entropy and information flux. This approach conceptually extends information-theoretic models—such as the Connes–Rovelli thermal time hypothesis, where time emerges from the modular flow of a statistical state $\rho$, and Jacobson’s thermodynamic gravity [37,38]—but differs fundamentally by assigning a spatially structured, field-based ontological status to time applicable across scales, including atomic laboratory setups and cognitive systems.

6.3. Chronons and Time Quantization

Discrete models of time posit a minimal unit (chronon), which fundamentally alters the character of time evolution and can introduce intrinsic decoherence:

• Classical Chronon Theories: Chronon models such as those by Caldirola [39] and Recami/Farias [40] suggest temporal discreteness $\Delta \tau$, leading to modified quantum evolution equations and providing a built-in, non-environmental source of decoherence and potential friction.
• Discretized Quantum Gravity Models: Relational clock constructions in loop quantum gravity [7,8,9,14,35] employ discretization at the Planck scale, defining clock variables on spacetime lattices and deriving a fundamental (though typically unobservable) decoherence rate. The resultant Lindblad-type decoherence always scales with the quantum uncertainty associated with the clock, not with field curvature or entropy sourcing.

TFT generalizes and potentially unifies granular and continuous approaches by allowing chronons to emerge as quantized excitations (or lumps) of the temporal field—meaning that the effective discretization scale is set by local field curvature rather than imposed by hand. Unlike traditional chronon models, TFT predicts a fully spatially structured scalar field dynamically sourced by entropy and information flux, not merely discrete time steps without spatial or thermodynamic grounding. This perspective remains unaddressed in the reviewed works.

6.4. Entropic and Information-Theoretic Time

Recent approaches tie the direction and flow of time to entropy and information properties:

• Thermal Time Hypothesis (Connes & Rovelli): Time is emergent from the statistical state of a physical system, with the modular flow (generated by $log\rho$) defining a "thermal clock" [41]. While elegant, this framework does not propose a local or dynamical time field, nor does it involve entropy or information gradients as explicit sources of temporal structure.
• Thermodynamic Gravity (Jacobson): Einstein’s equations themselves can be derived from local entropy balance at causal horizons, suggesting a foundational linkage between thermal/entropic flux and spacetime geometry. However, this structure is not realized in the surveyed models, although the theme appears conceptually in the cosmological time–entropy model proposed by [15].
• Spacetime Entropy Action (Bianconi 2025): Bianconi introduces a spacetime action principle modified by entropy, proposing novel metric-like “G-fields” that extend general relativity through entropic considerations [42].

Building on these ideas, Temporal Field Theory (TFT) extends the thermodynamic perspective by proposing that local entropy gradients do not merely influence large-scale spacetime geometry, as in Jacobson’s causal horizon analysis, but actively source measurable variations in the temporal field at laboratory and cognitive scales. In TFT, entropy and information flux directly modulate local clock rates and quantum coherence properties, predicting spatial gradients in decoherence that are accessible through precision timing and quantum experiments.

Moreover, TFT expands the conventional view of quantum decoherence. In traditional models, decoherence arises from environmental noise or system–bath interactions, while unitary evolution is preserved for isolated systems. In contrast, TFT predicts that intrinsic fluctuations in the temporal field—sourced by local entropy production—can themselves drive deviations from unitary evolution, even without an external environment. This intrinsic decoherence stems from spatial variations in the time field, leading to measurable effects such as clock drift, coherence loss, and phase distortion that correlate directly with entropy gradients.

Prior theoretical models addressing time and entropy exhibit important conceptual gaps relative to TFT:

• Cosmological Entropic Time: Only [15] attempts a time–entropy proportionality, with $T\propto S$, but does so globally without local field structure, spatial gradients, or dynamic entropy-driven effects at laboratory or technological scales.
• Relational Quantum Time: Relational clock models [7,9,14,35] induce an arrow of time and decoherence through the quantum uncertainty of clocks but do not dynamically couple time evolution to local entropy flows, nor do they introduce spatially structured fields.

TFT differs by positing that local entropy gradients or information flux directly source the structured geometry of the temporal field—that is, time’s local rate, curvature, or tension is determined by actual physical entropy flows. These effects can, in principle, be measured directly via clock drift or decoherence at laboratory and cognitive scales. None of the identified models [3,4,5,15,21] provide this explicit entropy–field geometry link or its experimental accessibility.

6.5. Biological and Cognitive Time Models

Most physical models of time focus solely on fundamental or cosmological scales, with few attempting to address time perception in biological or cognitive systems. TFT seeks to bridge this gap by positing a unified temporal field substrate that could underpin both objective (physical) and subjective (experiential) time phenomena.

In this context, TFT invites comparison to several influential models and approaches:

• Entropy and Developmental Timing: Elewa (2020) proposes that changes in information entropy within gene regulatory networks modulate developmental trajectories during embryogenesis [43]. Higher genetic entropy is associated with reduced network plasticity and slower developmental rates, suggesting that informational complexity may influence biological timing. While compelling, this approach remains phenomenological and does not conceptualize time flow as a structured field or provide a mechanism for direct coupling to physical clocks or discrete quantum events.
• Quantum Events and Conscious Time (Orch-OR): The Penrose–Hameroff [44,45] orchestrated objective reduction (Orch-OR) model hypothesizes that quantum collapse in cytoskeletal microtubules forms the basis for conscious moments—discrete "time-steps"—within the brain. Although Orch-OR leverages quantum physical phenomena, it does not construct time as a continuous or spatially structured field, nor does it formulate a coupling between entropy/information and the timing of quantum events. The model remains speculative, with debates over the biological plausibility and experimental verifiability of such quantum coherence in the brain.
• Relational Quantum Decoherence in the Brain: Gambini and Pullin (2006–2009) develop relational decoherence models [8,9,35], where the imprecision of any physical clock (including those potentially implemented in biological systems) induces decoherence and an emergent arrow of time. These models are not specific to neural substrates or subjective time, and they do not posit any underlying field structure or spatial gradients governing temporal behavior. Their implication is that all observers—biological or engineered—are subject to fundamental limits on time resolution and coherence loss, but without linking these effects to locally measurable informational or entropic dynamics.

TFT builds upon and extends these ideas by:

• Proposing a dynamical, spatially structured temporal field substrate that may underlie and mediate both physical (objective) time measurements and biological (subjective) time experiences.
• Postulating that local information entropy gradients or fluxes influence the geometry of this field, thereby providing a potential bridge from objective physical processes to their neural and experiential correlates.
• Offering explicit, testable predictions for how biological signals—such as EEG phase-locking, heart-rate variability, or measures of neural quantum coherence—might shift in response to controlled manipulations of local entropy or information flow (e.g., pharmacological interventions, task complexity modulation).
• Aiming for empirical falsifiability at the intersection of physics and neuroscience, moving beyond analogy to measurable experimental predictions—a gap not addressed by the other referenced models.

However, it should be noted that no model in the provided reference set [3,4,5,7,8,9,14,15,21,35] explicitly implements a dynamical time field with cognitive or biological testability. Although Gambini and Pullin’s framework [8,9] is the closest in spirit, their relational models lack spatially structured field dynamics and entropy-coupled mechanisms that could produce experimentally accessible gradients or cognitive timing shifts.

6.6. Comparative Summary

Biological and cognitive models of time—such as informational time dilation in development or quantum-collapse-based accounts of consciousness—rarely supply a mathematically explicit, physically structured temporal field, and most do not embed entropy or information coupling at the neural or experiential level.

Among the surveyed literature [3,4,5,7,8,9,14,15,21,35], only the relational clock paradigm [7,8,9,14,35] provides a partial physical substrate for the perception and flow of time. These models rigorously establish that introducing non-ideal (quantum) clocks induces decoherence and a physical arrow of time, grounding TFT’s core assumptions in a well-developed quantum and gravitational context.

The linkage between entropy and time’s flow, as formalized in cosmological models and the thermal time hypothesis [15], further anchors TFT within existing theoretical traditions.

To our knowledge, no existing model in the literature combines a spatially structured temporal field with local entropy or information coupling. This is precisely where Temporal Field Theory advances the frontier: by positing that measurable temporal gradients and field curvature are locally sourced by entropy flux or informational flow, with direct implications for both physical and cognitive systems.

See Table 2 for a structured comparison of existing temporal field approaches and the distinguishing features of TFT.

Most importantly, unlike cosmological or Planck-scale proposals, TFT is constructed to deliver testable predictions at the scale of atomic clocks, neural oscillations, and entropy-rich laboratory or technological environments—making it uniquely amenable to empirical validation. This pragmatic focus enables TFT to serve as a bridge between foundational physics, information theory, and the science of perception, and provides a unifying substrate for investigating the alignment between physical, informational, and subjective time.

Table 2. Comparative summary of temporal models based on their use of time fields, spatial dynamics, entropy/information coupling, decoherence mechanisms, lab-scale predictions, and experiential modeling. TFT integrates all categories uniquely.

Model or Theory	Explicit Temporal Field	Spatial Gradients or ${\mathit{g}}_{00}$	Entropy / Info Coupling	Decoherence Mechanism	Lab / Cognitive Predictions	Experiential Time Modeled?
Scalar/Vector Field Theories	Yes (scalar/vector)	Sometimes	No	Sometimes; not entropy-based	Occasional Lorentz-violation predictions	No
Relational Quantum Clocks [7,8,9,14,21,35]	Yes (quantum clock)	No	No	Yes; clock uncertainty-driven	Theoretical Rabi oscillation damping	No
Chronon / Discrete Time [3,4]	Yes (discrete steps)	No	No	Yes; discretization-induced nonunitarity	No direct predictions	No
Entropy-Proportional Cosmological Models [15]	No (global T)	No	Yes (cosmic S)	No	No	Conceptual only
Biological & Cognitive Models [8,9,35]	Sometimes (event-linked)	No	Sometimes (informational)	Sometimes (e.g., collapse)	Generally phenomenological; not predictive	Sometimes (not field-based)
TFT (This work)	Yes ($\mathcal{T}\left(x^{\mu }\right)$)	Yes (local gradients)	Yes (entropy / information driven)	Yes (entropy-sourced; quantum + classical decoherence)	Yes; EEG, clocks, heart rate, neural load	Yes; proposed structured field bridge

Table 2. Comparative summary of temporal models based on their use of time fields, spatial dynamics, entropy/information coupling, decoherence mechanisms, lab-scale predictions, and experiential modeling. TFT integrates all categories uniquely.

Model or Theory	Explicit Temporal Field	Spatial Gradients or ${\mathit{g}}_{00}$	Entropy / Info Coupling	Decoherence Mechanism	Lab / Cognitive Predictions	Experiential Time Modeled?
Scalar/Vector Field Theories	Yes (scalar/vector)	Sometimes	No	Sometimes; not entropy-based	Occasional Lorentz-violation predictions	No
Relational Quantum Clocks [7,8,9,14,21,35]	Yes (quantum clock)	No	No	Yes; clock uncertainty-driven	Theoretical Rabi oscillation damping	No
Chronon / Discrete Time [3,4]	Yes (discrete steps)	No	No	Yes; discretization-induced nonunitarity	No direct predictions	No
Entropy-Proportional Cosmological Models [15]	No (global T)	No	Yes (cosmic S)	No	No	Conceptual only
Biological & Cognitive Models [8,9,35]	Sometimes (event-linked)	No	Sometimes (informational)	Sometimes (e.g., collapse)	Generally phenomenological; not predictive	Sometimes (not field-based)
TFT (This work)	Yes ($\mathcal{T}\left(x^{\mu }\right)$)	Yes (local gradients)	Yes (entropy / information driven)	Yes (entropy-sourced; quantum + classical decoherence)	Yes; EEG, clocks, heart rate, neural load	Yes; proposed structured field bridge

TFT is explicitly anchored in relational quantum clock and entropy/time linkage theories [7,8,9,14,15,35], but advances the field by uniquely unifying spatial field structure, local entropy and information sourcing, and accessible laboratory and cognitive predictions.

This novelty, far from a liability, provides an opportunity for practical and conceptual breakthroughs in both physics and the life sciences.

7. Literature Gap Analysis: Time as a Scalar Field Coupled to Entropy

A review of existing theoretical models in quantum gravity, chronodynamics, and decoherence indicates that while several frameworks elevate time from a background parameter to an operator or stochastic variable, none develop a full scalar field theory of time with spatial structure, entropy coupling, and experimental accessibility.

Relational quantum clock models (e.g., Gambini and Pullin [9]) define time via internal quantum degrees of freedom, inducing decoherence through clock imprecision. Though mathematically elegant, these models lack an explicit field structure or entropy-sourced dynamics. Stochastic or chronodynamic theories (e.g., Krolikowski [3], Rozonoer [4]) introduce time deviations or noise fields but do not couple to curvature or a metric component, nor do they model entropy as a field source.

Conceptual approaches (e.g., Poulin [21]) often invoke time emergence in Page–Wootters-style frameworks or mixed state decoherence [16], but without field-theoretic formalism or measurable consequences. Even where time asymmetry or decoherence is derived, the effect stems from randomness or limited resolution—not a dynamic scalar field.

Moreover, the intersection of physical time fields and subjective time perception remains virtually unexplored in these models. None propose field-driven alignment with cognitive or biological systems, nor do they suggest neural or perceptual experiments. While entropy-based emergence of time is hinted at in thermal time hypotheses, these remain untied to localized field behavior.

In contrast, Temporal Field Theory (TFT) introduces a covariant scalar field, sourced by entropy or information flux, with curvature (chronocurvature), gradients (chronotension), and testable predictions. It bridges physical and experiential time through proposed lab-scale and neurocognitive measurements. This literature gap reinforces TFT’s role as a novel and necessary addition to contemporary theoretical physics.

Table 3. Comparison of Temporal Field Theory (TFT) with selected earlier frameworks proposing modified or emergent conceptions of time.

Model	Key Features	Limitations Compared to TFT
Thermal Time Hypothesis (Connes, Rovelli)	Time flow emerges from modular flow of statistical state $log\rho$; no physical field introduced	No spatially structured time; lacks entropy/information sourcing
Relational Quantum Clocks (Gambini, Pullin)	Time is relational; internal degrees of freedom act as clocks	No dynamical temporal field; no local gradients or entropy sourcing
Einstein-Aether Theories	Introduce a dynamical unit timelike vector field; preferred frame	Vectorial structure but no entropy/information coupling; focus on Lorentz violation tests
TFT (This Work)	Dynamical scalar field $\mathcal{T}\left(x^{\mu }\right)$; sourced by entropy/information flux; predicts spatially-local clock drift, decoherence modulation	Requires further development of kinetic terms, coupling constants for full quantitative predictions

Table 3. Comparison of Temporal Field Theory (TFT) with selected earlier frameworks proposing modified or emergent conceptions of time.

Model	Key Features	Limitations Compared to TFT
Thermal Time Hypothesis (Connes, Rovelli)	Time flow emerges from modular flow of statistical state $log\rho$; no physical field introduced	No spatially structured time; lacks entropy/information sourcing
Relational Quantum Clocks (Gambini, Pullin)	Time is relational; internal degrees of freedom act as clocks	No dynamical temporal field; no local gradients or entropy sourcing
Einstein-Aether Theories	Introduce a dynamical unit timelike vector field; preferred frame	Vectorial structure but no entropy/information coupling; focus on Lorentz violation tests
TFT (This Work)	Dynamical scalar field $\mathcal{T}\left(x^{\mu }\right)$; sourced by entropy/information flux; predicts spatially-local clock drift, decoherence modulation	Requires further development of kinetic terms, coupling constants for full quantitative predictions

8. Limitations and Open Questions

While Temporal Field Theory (TFT) aspires to provide a unified framework linking physical, informational, and experiential aspects of time, several significant limitations and unresolved questions remain. These define both the current boundaries of the theory and the principal directions for future research.

8.1. Experimental Limitations

We first outline the practical and observational challenges that may impact the empirical verification of Temporal Field Theory.

8.1.1. Mathematical Formalization and Source Ambiguity

Although TFT takes inspiration from well-established scalar-tensor field theories, its mathematical structure is not yet fully developed. In particular, the precise coupling of the temporal field to matter, entropy, or information flux ${\rho }_t$ lacks a unique and rigorously defined prescription. Establishing explicit forms for this coupling term—whether in terms of thermodynamic entropy, algorithmic information, or neurophysiological activity—will be essential to ensure both empirical precision and internal consistency. Furthermore, the compatibility of TFT’s field equations with the full structure of Einstein’s equations and requirements such as renormalizability remains to be thoroughly demonstrated.

8.1.2. Experimental Isolation and Confounding Effects

The experimental paradigms proposed for detecting TFT effects involve manipulating entropy gradients, information flux, or cognitive load in highly sensitive systems. In practice, precisely isolating contributions attributable solely to the $\mathcal{T}$ field from confounding variables, such as thermal noise, electromagnetic interference, and classical stochastic processes, will be difficult. Many of the predicted TFT effects could be masked or mimicked by conventional physical phenomena, demanding exceptionally rigorous experimental controls and new standards of reproducibility.

8.1.3. Detection, Resolution, and Instrumental Challenges

Direct detection of spatial gradients, curvature, or topologies in the temporal field would require timing instrumentation and synchronization at levels of precision beyond current technologies. Until such devices are developed and validated, empirical testing may be limited to indirect inference, detecting anomalies that are consistent with TFT but not strictly unique to it.

8.1.4. Philosophical and Interpretational Limits

A core ambition of TFT is to bridge objective, physical time with subjective, experiential time. Yet, the relationship between consciousness, perception, and physical field dynamics remains deeply philosophical and contested. It is uncertain whether subjective time perception can truly be modeled by a physical field, or if such a bridge risks conflating phenomenological and physical categories. Care must be taken not to impose anthropocentric interpretations on what are, fundamentally, physical quantities.

8.2. Integration with Quantum Gravity and Discreteness

TFT is formulated as a classical, covariant field theory, but does not yet incorporate quantum gravitational effects or naturally emerge from frameworks such as loop quantum gravity, causal set theory, or string-based approaches [5,7,8,9,14,35]. It remains an open question whether a spatially continuous scalar temporal field is compatible with the intrinsic discreteness posited at the Planck scale in leading quantum gravity models, or how it might be consistently quantized within such frameworks.

Nevertheless, scalar fields already play a prominent role in various approaches to quantum gravity—appearing as dilaton fields, scalar-tensor couplings, or effective low-energy degrees of freedom in semiclassical limits. This suggests that a dynamical temporal field $\mathcal{T}\left(x^{\mu }\right)$ could, in principle, be incorporated as an emergent or effective structure arising from deeper quantum geometric or informational substrates.

Future research must address whether $\mathcal{T}$ should be treated as a fundamental quantum field subject to fluctuations, as a coarse-grained emergent field derived from underlying discrete structures, or as a semiclassical limit of a more granular quantum time network. Exploring the quantization of $\mathcal{T}$, its interaction with gravitational degrees of freedom, and its compatibility with Planck-scale discreteness will be critical for advancing TFT beyond its classical formulation.

8.3. Theoretical Extensions and Modifications

8.3.1. Quantum Evolution Under a Structured Temporal Field

Standard non-relativistic quantum mechanics treats time as an external, universal, and homogeneous parameter t, unaffected by physical processes. In contrast, Temporal Field Theory (TFT) postulates that time corresponds to a real scalar field $\mathcal{T}\left(x^{\mu }\right)$, spatially structured and dynamically sourced by entropy and information flux. This extension has significant consequences for quantum evolution, even in isolated systems independent of environmental interactions.

TFT predicts that local variations in $\mathcal{T}\left(x^{\mu }\right)$ directly modulate quantum phase evolution, modifying the structure of the Schrödinger equation itself. Specifically, we propose that quantum systems evolve according to a TFT-modified Schrödinger equation of the form:

$$i\mathcal{T}\left(x^{\mu }\right){\displaystyle \frac{\partial }{\partial t}}\psi \left(x^{\mu }\right)=\widehat{H}\psi \left(x^{\mu }\right),$$

(20)

where $\psi \left(x^{\mu }\right)$ is the quantum wavefunction, $\widehat{H}$ is the system Hamiltonian, and $\mathcal{T}\left(x^{\mu }\right)$ modulates the local flow of proper time relative to coordinate time.

It is important to distinguish the decoherence effects predicted by TFT from conventional environmental decoherence. In standard models, decoherence arises from entanglement between a system and its external environment, leading to loss of coherence due to uncontrolled degrees of freedom. In contrast, TFT proposes that spatial gradients and curvature in the temporal field $\mathcal{T}\left(x^{\mu }\right)$ intrinsically distort quantum phase evolution, inducing decoherence-like effects even in the absence of environmental coupling. These effects originate from structured variations in time flow itself, not from classical noise sources, offering a fundamentally different mechanism linked to entropy and information fluxes.

In regions where $\mathcal{T}\left(x^{\mu }\right)\approx 1$, standard quantum mechanical evolution is recovered. However, when $\mathcal{T}\left(x^{\mu }\right)$ exhibits gradients or curvature, quantum phase evolution deviates from standard Schrödinger dynamics.

As a concrete example, consider a free particle in one spatial dimension, with Hamiltonian:

$$\widehat{H}=-{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}.$$

(21)

Assuming a separable solution of the form $\psi (x,t)=\varphi \left(x\right)e^{-i\omega t}$, substitution into Eq. (20) reduces the problem to a spatial differential equation:

$${\displaystyle \frac{d^2\varphi }{d{x}^2}}+{\displaystyle \frac{2m\omega }{{\hslash }^2}}\mathcal{T}\left(x\right)\varphi \left(x\right)=0.$$

(22)

Equation (22) resembles a wave equation with an effective spatially dependent "potential" determined by $\mathcal{T}\left(x\right)$. Small variations in $\mathcal{T}\left(x\right)$ induce perturbative effects analogous to weak potentials in conventional quantum mechanics. For small deviations $ϵ\ll 1$, writing:

$$\mathcal{T}\left(x\right)=1+ϵf\left(x\right),$$

(23)

the effective perturbation becomes:

$$V_{\mathrm{eff}}\left(x\right)=-ϵ{\displaystyle \frac{2m\omega }{{\hslash }^2}}f\left(x\right),$$

(24)

where $V_{\mathrm{eff}}\left(x\right)$ represents a time-field induced scattering potential.

Thus, spatial variations in the temporal field induce effective scattering, phase shifts, and wavepacket distortions, even in the absence of external physical potentials or environmental decoherence.

This structure introduces a second mechanism—independent of traditional decoherence—by which entropy or information-driven spatial inhomogeneities in $\mathcal{T}\left(x^{\mu }\right)$ affect quantum behavior:

• Quantum interference patterns could exhibit phase shifts dependent on underlying entropy gradients.
• Wavepackets could spread asymmetrically or acquire effective mass shifts. These effects are predicted to depend on local chronotension and chronocurvature gradients in the temporal field.
• Decoherence-like effects could emerge purely from structured temporal fields without requiring environmental coupling.

These predictions are distinct from standard environment-induced decoherence, offering a new window into quantum behavior in high-entropy or high-information environments. In particular, transporting quantum systems across engineered entropy gradients could experimentally probe the predictions of Temporal Field Theory.

TFT thus not only provides an intrinsic mechanism for entropy-coupled decoherence but also introduces a novel correction to quantum mechanical evolution itself. The spatial structure of time modulates quantum dynamics directly, suggesting new experimental regimes where TFT effects could be isolated, measured, and quantitatively compared against standard quantum mechanical predictions.

8.3.2. TFT and the Unification of Gravity and Quantum Mechanics

A longstanding challenge in theoretical physics is the lack of a unified framework connecting general relativity, which governs gravity and spacetime curvature, with quantum mechanics, which describes the probabilistic behavior of matter and fields at microscopic scales. Central to this incompatibility is the treatment of time: general relativity endows time with a dynamic, geometry-dependent structure, whereas quantum theory typically assumes a fixed, absolute background time parameter.

Temporal Field Theory (TFT) offers a natural bridge to address this divide. By promoting time itself to a dynamical scalar field $\mathcal{T}\left(x^{\mu }\right)$, TFT introduces a common structure that evolves alongside both gravitational and quantum phenomena. In this framework:

• The gravitational field, through the spacetime metric $g_{\mu \nu }$, continues to shape spatial geometry and causal structure as in general relativity.
• The temporal field $\mathcal{T}\left(x^{\mu }\right)$ dynamically modulates the local flow of proper time, influenced by both mass-energy distributions and entropy/information fluxes.
• Quantum systems evolve not against an external, immutable time parameter, but relative to the locally structured field $\mathcal{T}\left(x^{\mu }\right)$, allowing quantum evolution to remain consistent under conditions of spacetime curvature and entropy variation.

The evolution of the temporal field follows a covariant wave equation sourced by both self-interactions and informational currents:

$$\square \mathcal{T}={\displaystyle \frac{dV}{d\mathcal{T}}}+{\rho }_t\left(x^{\mu }\right),$$

(25)

where □ is the covariant d’Alembertian operator, $V\left(\mathcal{T}\right)$ is the stabilizing potential, and ${\rho }_t\left(x^{\mu }\right)$ encodes entropy and information sourcing.

As shown in Eq. (25), this evolution ensures compatibility with relativistic causality while permitting localized deviations from uniform time flow. Quantum states, in turn, evolve according to a modified Schrödinger-like equation where the local lapse function governing evolution is dynamically determined by $\mathcal{T}\left(x^{\mu }\right)$.

This structure allows TFT to offer a pathway toward the unification of gravity and quantum mechanics by:

• Embedding quantum dynamics within an evolving temporal field shaped by spacetime geometry,
• Preserving local covariance and energy-momentum conservation,
• Enabling smooth transitions between classical and quantum regimes without assuming a fixed background time.

Further development—including the quantization of the temporal field itself and its deeper integration into a full quantum gravitational theory—remains an open and profound direction for future research. Nevertheless, TFT provides a foundational step by explicitly modeling time as a dynamic field, resolving the most fundamental conceptual mismatch between general relativity and quantum theory.

8.3.3. Modification of Quantum Field Evolution Under TFT

In conventional quantum field theory (QFT), fields extend globally across spacelike hypersurfaces, evolving over a fixed, externally supplied time parameter t. This framework assumes a uniform, absolute flow of time, independent of local conditions or field configurations.

Temporal Field Theory (TFT) alters this foundational assumption by promoting time itself to a dynamical, spacetime-dependent scalar field $\mathcal{T}\left(x^{\mu }\right)$. As a result, the local rate of temporal evolution is modulated by the structure of the temporal field, leading to important modifications in quantum field behavior:

• Quantum fields continue to extend across space globally, preserving relativistic covariance.
• However, the effective evolution rate at each spacetime point is governed by the local value of $\mathcal{T}\left(x^{\mu }\right)$.
• The standard time evolution equation for quantum states,

  $$i\hslash {\displaystyle \frac{\partial \Psi }{\partial t}}=\widehat{H}\Psi ,$$

  (26)

  becomes locally modified under TFT to:

  $$i\hslash \mathcal{T}\left(x^{\mu }\right){\displaystyle \frac{\partial \Psi }{\partial t}}=\widehat{H}\Psi ,$$

  (27)

  where $\mathcal{T}\left(x^{\mu }\right)$ acts as a dynamic modulation factor.

As shown by the modification from Eq. (26) to Eq. (27), local temporal modulation introduces several key physical consequences:

• Quantum coherence between distant regions becomes sensitive to spatial variations in $\mathcal{T}\left(x^{\mu }\right)$, leading naturally to scale-dependent decoherence without requiring external noise or measurement interactions.
• The effective Hamiltonian dynamics at each point are modulated by local entropy and information fluxes, as encoded in the sourcing of $\mathcal{T}\left(x^{\mu }\right)$.
• In the limit where $\mathcal{T}\left(x^{\mu }\right)\to 1$ globally, conventional QFT is fully recovered, ensuring consistency with established physics in low-entropy environments.

Thus, TFT provides a framework in which quantum fields remain globally defined, but their temporal evolution is locally structured and dynamically responsive to gravitational, thermodynamic, and informational influences. This modification offers a new route toward resolving the tensions between fixed-time quantum dynamics and dynamic spacetime curvature, and further suggests natural mechanisms for emergent decoherence at large scales.

8.4. Theoretical Consistency Requirements

8.4.1. Compatibility with Special Relativity and Lorentz Invariance

Another longstanding foundational challenge is the tension between standard non-relativistic quantum mechanics and special relativity. Ordinary quantum theory assumes a global, absolute time parameter, incompatible with the relativistic structure of spacetime.

Temporal Field Theory addresses this inconsistency by introducing a dynamical scalar field $\mathcal{T}\left(x^{\mu }\right)$ governing local time flow, without introducing preferred frames or violating Lorentz invariance. Because $\mathcal{T}\left(x^{\mu }\right)$ is a scalar under coordinate transformations, the modified Schrödinger equation remains compatible with causal structure and relativistic covariance.

Nonetheless, further detailed formalization—including possible extensions to a fully relativistic quantum field theory incorporating $\mathcal{T}\left(x^{\mu }\right)$—remains an important open area for future research.

These limitations do not undermine the conceptual novelty or exploratory value of TFT but instead illuminate critical avenues for theoretical refinement and empirical validation. Progress will depend on advances in mathematical rigor, experimental sensitivity, and cross-disciplinary engagement—each essential to test and, if necessary, revise the foundations of temporal physics.

8.5. Emergent Temporal Phenomena

8.6. Temporal Field Turbulence, Quantization, and Chronon Excitations

A natural extension of Temporal Field Theory (TFT) concerns the behavior of the temporal field $\mathcal{T}\left(x^{\mu }\right)$ under nonlinear, fluctuating, or stochastic entropy and information flux conditions. In environments with highly non-uniform or rapidly varying ${\rho }_t\left(x^{\mu }\right)$ sources, the temporal field equations predict the emergence of complex spatial and temporal structures, analogous to turbulence in classical fluid systems.

In such regimes, $\mathcal{T}\left(x^{\mu }\right)$ may exhibit chaotic gradients, localized eddies in the flow of time, and spatial intermittency—leading to observable effects such as stochastic clock drifts, unpredictable decoherence rate modulation, and variability in neural timing dynamics. While $\mathcal{T}\left(x^{\mu }\right)$ is not directly observable, its influence on quantum systems, clocks, and cognitive processes provides an experimental pathway for detecting signatures of temporal turbulence.

Furthermore, if the temporal field is quantized in future formulations of TFT, a wave–particle duality naturally emerges. The classical field $\mathcal{T}\left(x^{\mu }\right)$ would support propagating excitations analogous to phonons in condensed matter systems or gravitational waves in spacetime. Quantized excitations—temporal quanta or "chronons"—would carry energy, momentum, and possibly interact with matter fields, inducing clock rate shifts, decoherence, or localized phase changes.

This perspective positions TFT not only as a theory of modified time flow but as a candidate framework for an entirely new sector of physics: the study of dynamic, structured, and quantized temporal fields. Future work will aim to formalize the second-quantized version of TFT, develop the corresponding particle content, and explore experimental scenarios capable of detecting chronon excitations or temporal turbulence signatures.

8.6.1. Toward Chronon Excitations: Quantization of the Temporal Field

While the current formulation of Temporal Field Theory (TFT) treats $\mathcal{T}\left(x^{\mu }\right)$ as a classical, covariant scalar field, a natural extension involves its quantization, in analogy with established procedures in quantum field theory. If $\mathcal{T}\left(x^{\mu }\right)$ is promoted to a dynamical quantum field, localized excitations—quanta of the temporal field—would emerge.

We designate these hypothetical quanta as chronons: discrete, particle-like excitations corresponding to localized distortions or fluctuations in the flow of time. This is conceptually parallel to how photons emerge as quanta of the electromagnetic field, or how the Higgs boson arises as an excitation of the Higgs field.

Chronon properties would depend on the form of the temporal field potential $V\left(\mathcal{T}\right)$ and the dynamics of entropy or information flux sourcing ${\rho }_t$. In general, one might expect chronons to:

• Carry energy and momentum associated with local variations in $\mathcal{T}\left(x^{\mu }\right)$,
• Interact weakly with standard matter fields, potentially modulating clock rates, decoherence, and quantum phase evolution,
• Be produced in regions of strong temporal field curvature, high entropy gradients, or rapidly fluctuating informational environments,
• Affect early-universe cosmology, black hole environments, or laboratory setups involving ultra-sensitive timing measurements.

Detecting chronons would be extraordinarily challenging, requiring instruments capable of resolving temporal anomalies at scales far below current clock or coherence precision. Nevertheless, the conceptual possibility that time itself could possess quantum excitations represents a radical extension of the standard view, opening new theoretical and experimental directions.

Developing a second-quantized, relativistic version of TFT incorporating chronon dynamics, interactions, and phenomenology constitutes a key long-term research avenue emerging from this framework.

9. Potential Applications and Future Directions

While the primary aim of Temporal Field Theory (TFT) is to offer a new conceptual and mathematical framework for understanding time as a dynamical field, the theory also suggests several important potential applications across diverse technological domains. These implications arise naturally from TFT’s predicted modulation of local time flow by entropy and information flux, and are aligned with ongoing advances in quantum systems, brain–computer interfaces, precision metrology, and artificial intelligence.

Brain–Computer Interfaces: If TFT-based entropy-driven drift correction succeeds experimentally, it could dramatically improve the stability and performance of brain–computer interfaces. Systems like Neuralink would benefit from proactive timing corrections, reducing recalibration needs, increasing control precision, and enabling longer-term implanted operation. Real-time entropy monitoring and temporal field adjustment could become a standard for future high-fidelity brain–machine communication systems.

Quantum Clocks and Quantum Networks: TFT predicts measurable clock drift correlated with local entropy conditions. Future quantum clock networks, quantum communication systems, and gravitational wave observatories could incorporate entropy flux monitoring and dynamic temporal field corrections to enhance timing synchronization, stability, and sensitivity beyond general relativistic adjustments alone.

Entropy-Structured Computing and AI Systems: As computational systems scale toward quantum and neuromorphic architectures, understanding and controlling entropy-driven timing drift may become critical. TFT-informed entropy management could enable more stable learning dynamics, better timing in large AI/ML models, and ultimately the design of "time-optimized" computing environments where entropy flux structuring enhances performance.

Temporal Field Engineering: In the long term, TFT opens the conceptual possibility of engineering environments to shape local time flow intentionally. By controlling entropy and information fluxes, systems could "sculpt" temporal gradients for specialized applications in quantum technology, neuroscience, space exploration, or even future forms of communication based on modulated time structures.

These future directions invite interdisciplinary collaboration across physics, neuroscience, information theory, and engineering. The experimental proposals outlined earlier represent first steps toward validating TFT in accessible systems, and if successful, could open a fundamentally new frontier at the intersection of time, information, and technology.

10. Conclusion and Call to Collaboration

Temporal Field Theory (TFT) advances a new paradigm in the conceptualization of time—transforming it from an external, background parameter to a dynamic, physically actionable field. By formulating time as a real scalar field, TFT systematically integrates ideas from relativity, quantum theory, thermodynamics, and neuroscience. This unified framework posits that local variations in the temporal field, sourced by entropy and information flow, can shape phenomena as diverse as gravitational time dilation, quantum decoherence, atomic clock drift, and subjective time perception.

We have presented explicit field equations, novel physical quantities such as chronotension and chronocurvature, and a logically coherent Lagrangian framework capturing the interplay between the temporal field, matter, and informational dynamics. A distinctive strength of TFT is its predictive power: it enables a range of laboratory, technological, and cognitive experiments—from atomic clock networks in high-entropy environments, to quantum decoherence under informational flux, to mapping neural correlates of time under varying cognitive loads. These proposals lay the groundwork for empirical tests that could distinguish TFT from established theories such as general relativity or quantum mechanics.

At the same time, important challenges remain. Fundamental questions regarding the precise definition of temporal sourcing, experimental isolation of effects, quantification of coupling constants, and compatibility with quantum gravity frameworks require further development. Addressing these challenges will be crucial for advancing TFT from a compelling theoretical hypothesis into a rigorously tested framework within modern physics.

Temporal Field Theory thus offers a potential resolution of two longstanding foundational problems: first, by dynamically coupling time flow to entropy and information gradients, TFT provides an intrinsic mechanism for decoherence independent of environmental noise; second, by endowing time with a spatially structured scalar field character, it naturally corrects quantum mechanical evolution near relativistic regimes, where naive time assumptions traditionally fail. These dual contributions suggest that the spatial structure and sourcing of the temporal field may underpin both the emergence of classicality and the reconciliation of quantum behavior with relativistic dynamics.

The open questions and technological frontiers identified here offer significant opportunities for collaborative research across physics, information science, neuroscience, and philosophy. We specifically invite:

• Experimental physicists to design and implement precision tests involving atomic clocks, quantum probes, and entropic modulation;
• Quantum information scientists to explore how entropy-driven decoherence manifests in engineered systems;
• Neuroscientists and psychologists to empirically correlate subjective time perception and cognitive function with environmental and informational variables, leveraging existing knowledge of neural timing while testing TFT’s unique prediction that such effects reflect gradients in an underlying entropy-coupled temporal field;
• Theoretical physicists and mathematicians to formalize TFT’s coupling mechanisms, ensure consistency with fundamental field theories, and investigate avenues for quantization and integration with quantum gravity approaches;
• Philosophers of science to engage with the conceptual innovations raised by the theory and their implications for the philosophy of time.

By bridging expertise and perspectives across these domains, we can collectively explore the possibility that time itself is an active field—seeking both new physical phenomena and a deeper scientific understanding of temporality. We invite all researchers interested in testing, critiquing, and extending TFT to join this effort, as progress in this domain promises not only foundational insights but also practical advances in precision timekeeping, quantum technologies, and cognitive science.