Submitted:
07 May 2025
Posted:
08 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Multi-Robot Task Allocation (MRTA)
1.2. Coalition Formation (CF)
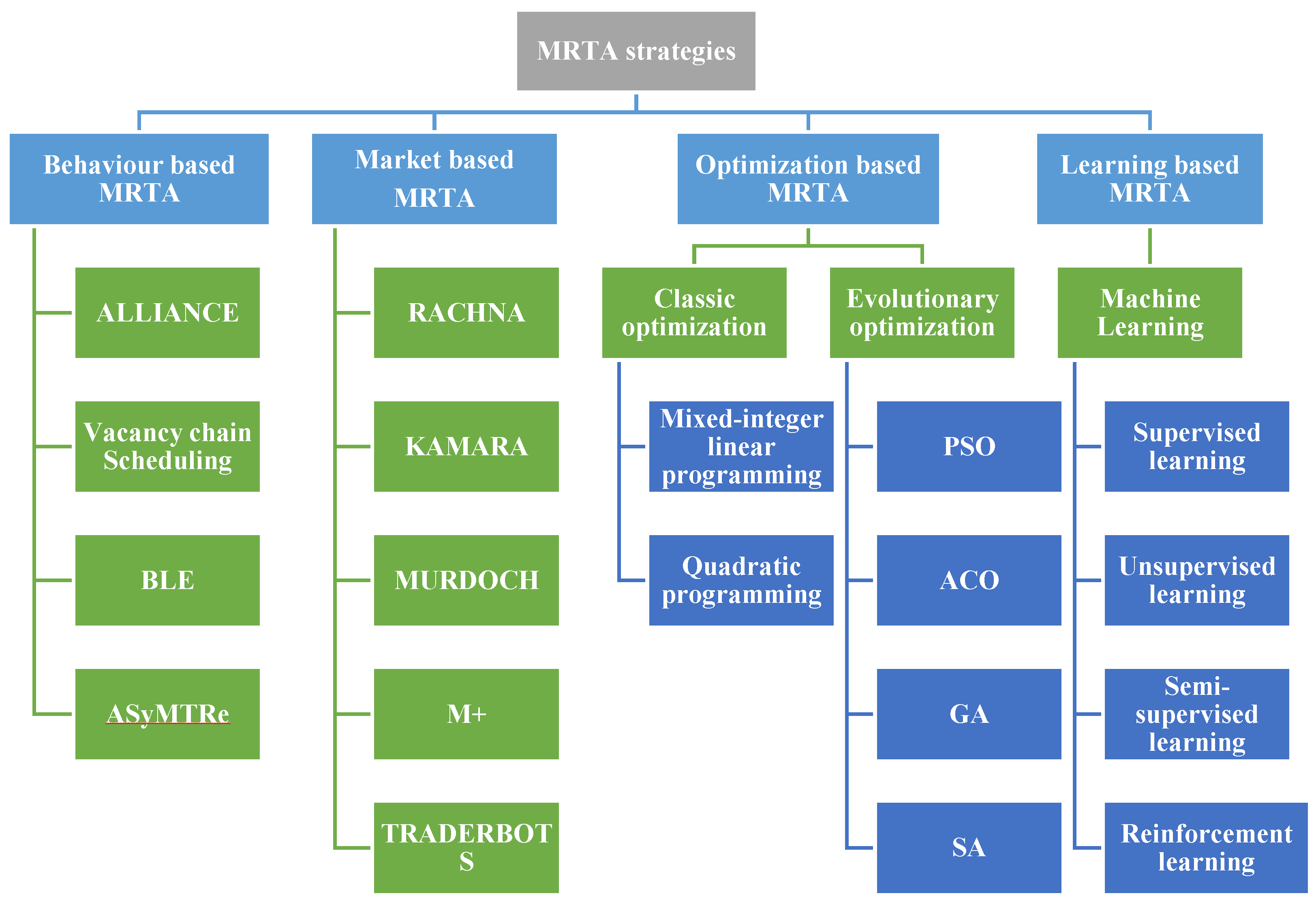
2. MRTA Classification
2.1. Behavior-Based MRTA
2.1.1. Alliance
2.1.2. Vacancy Chain Scheduling
2.1.3. Broadcast of Local Eligibility (BLE)
2.1.4. Automated Synthesis of Multi-Robot Task Solutions through Software Reconfiguration (ASyMTRe)
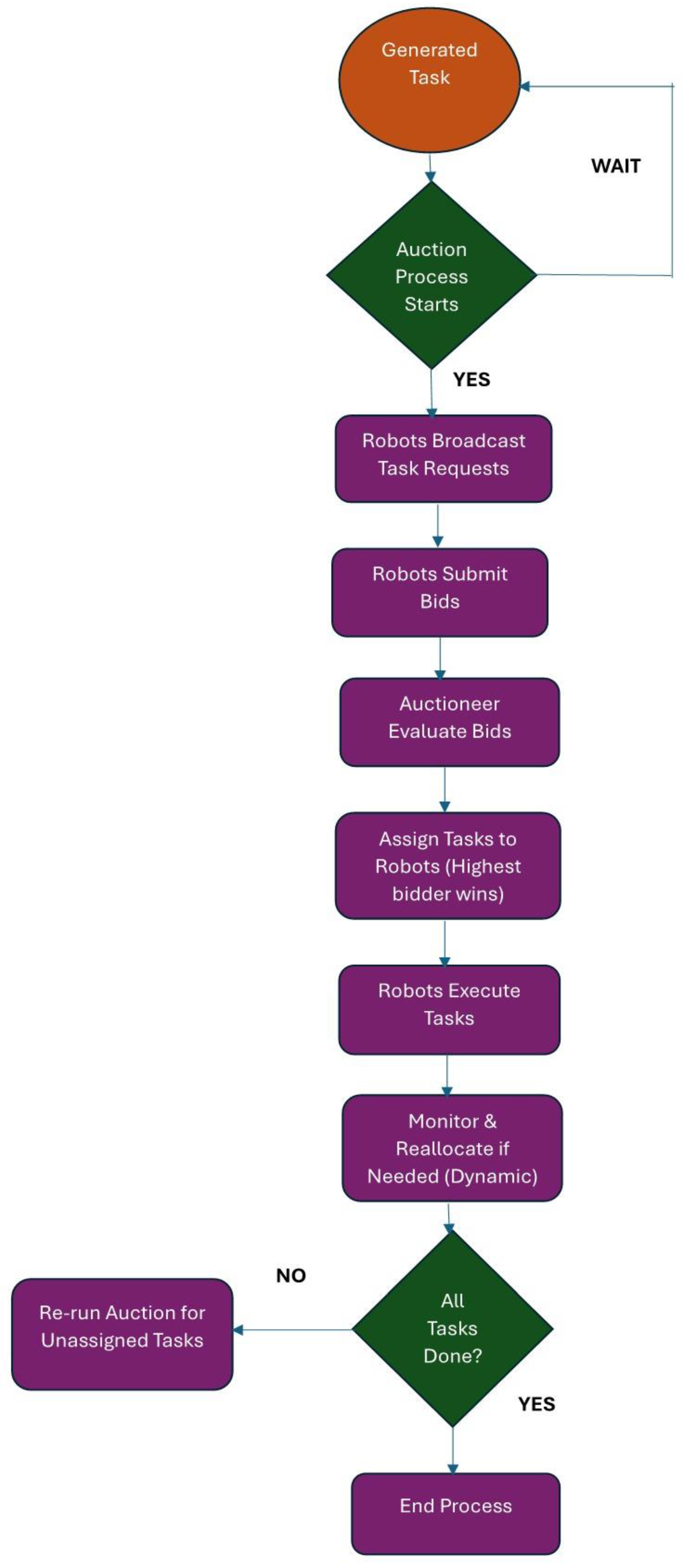
2.2. Market-Based MRTA
2.2.1. RACHNA
2.2.2. KAMARA (KAMRO’s Multi-Agent Robot Architecture)
2.2.3. MURDOCH
2.2.4. M+
2.2.5. TraderBots
2.3. Optimization-Based MRTA
2.3.1. Traditional Optimization
2.3.2. Evolutionary Optimization
- PSO seeks global optima while navigating exploration and exploitation trade-offs.
- ACO emphasizes pheromone-guided exploration and solution construction.
- GA balances diversity through mutation and convergence via crossover.
- SA transitions from high-temperature exploration to low-temperature exploitation.
- LP targets linear relationships, and QP handles quadratic ones, both optimized for resource allocation.
2.4. Learning-Based MRTA
2.4.1. Machine Learning
2.5. Comparison with Different MRTA Approaches
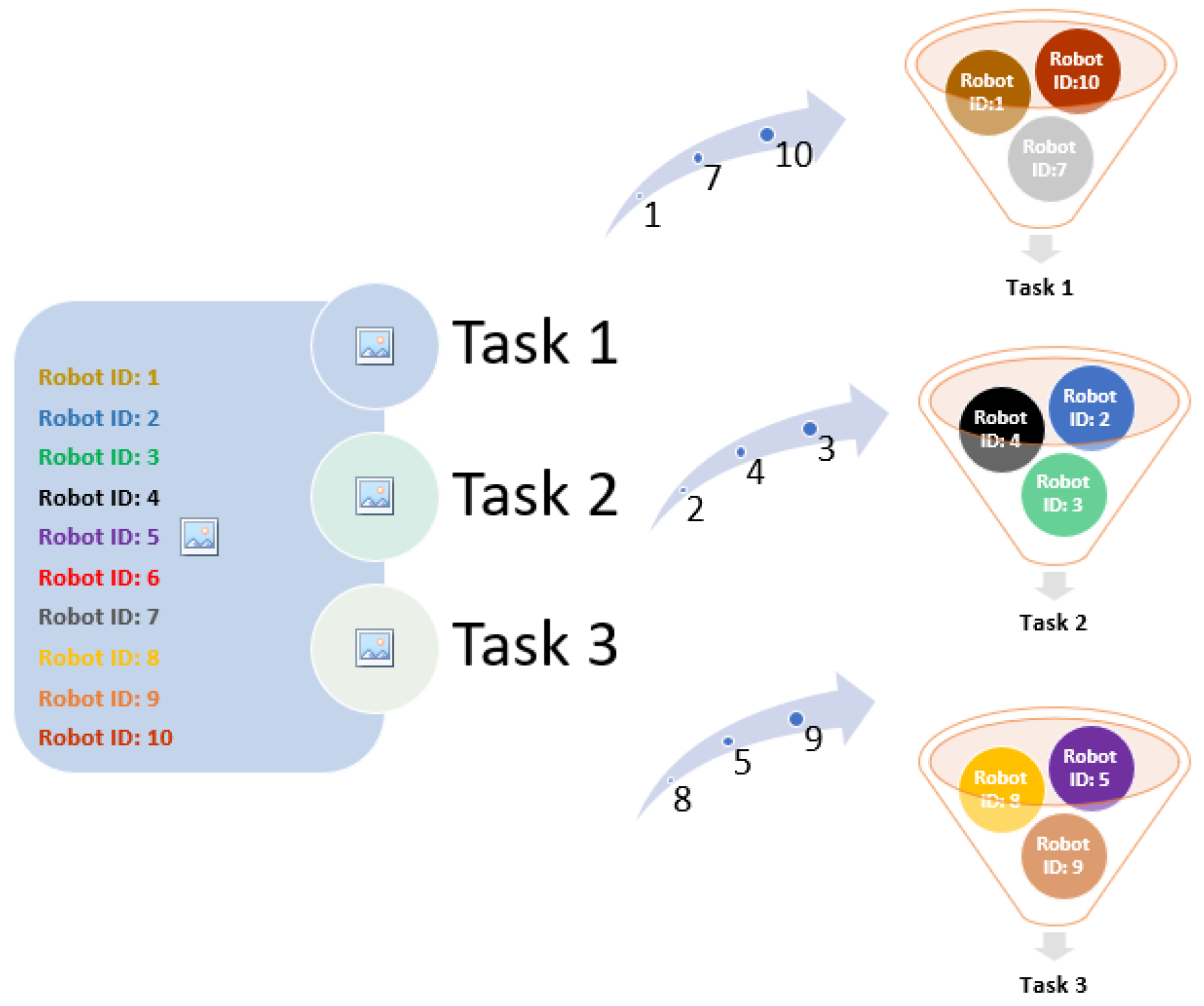
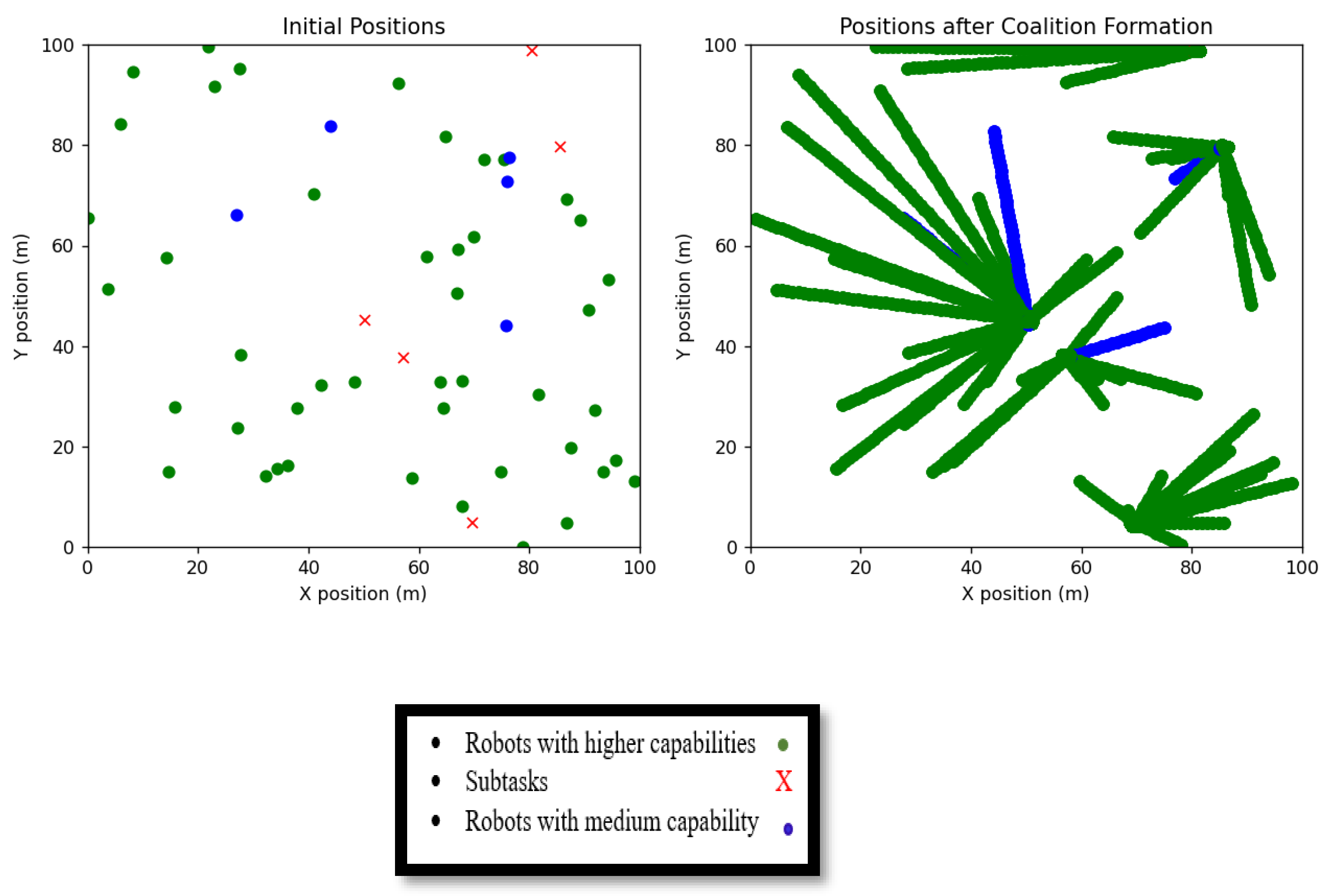
3. Simulation and Results
- Robots are aware of the values of M (the total number of objects) and N (the total number of robots).
- Robots possess knowledge of both the current and desired positions of all M objects.
- Robots are capable to communicate with each other as needed.
- We assume that all robots are operating within a workspace where communication between robots is feasible.
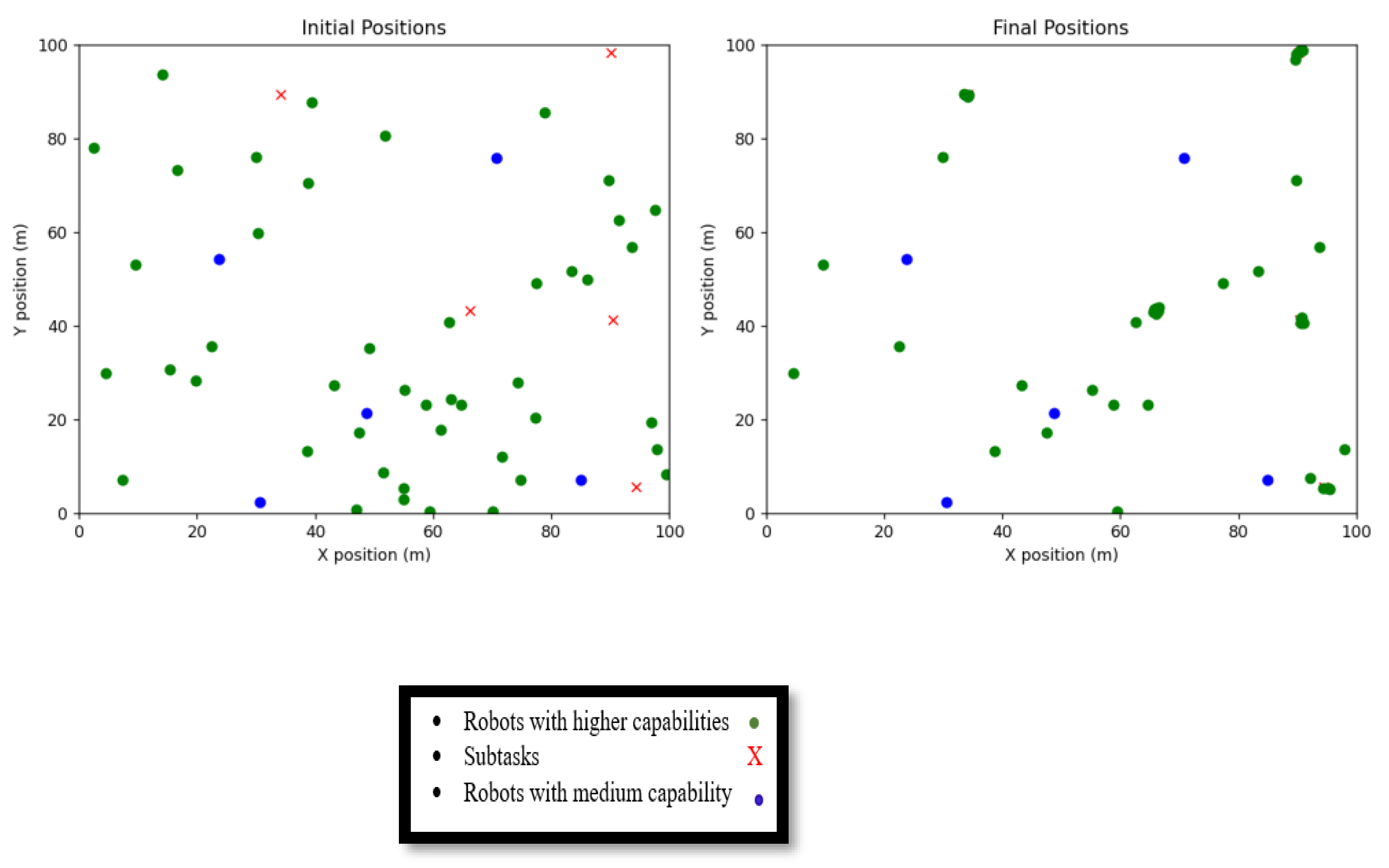
3.1. Behaviour-Based: Alliance Architecture
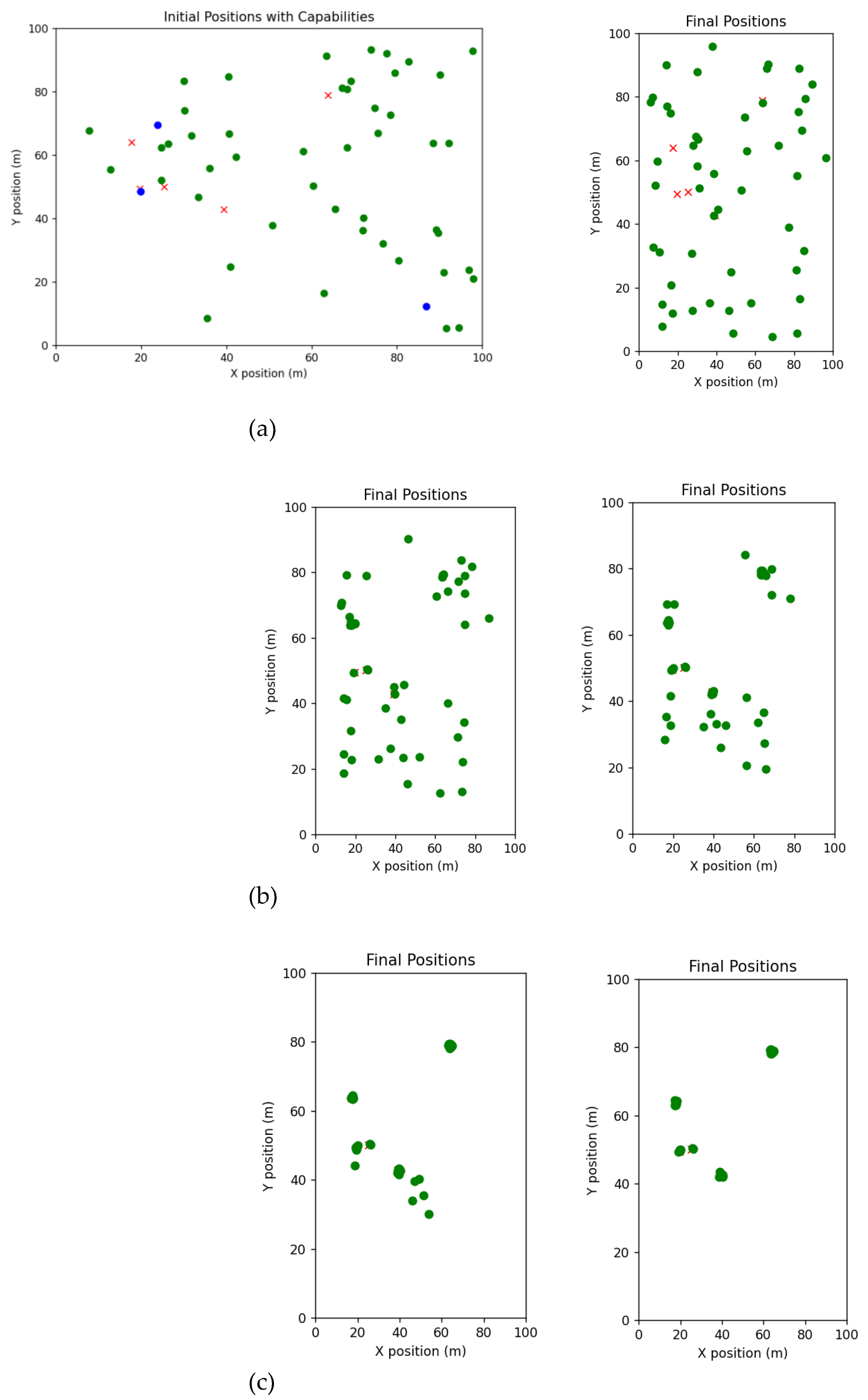
3.2. Market-Based: M+ Algorithm
3.3. Optimization-Based: PSO Algorithm
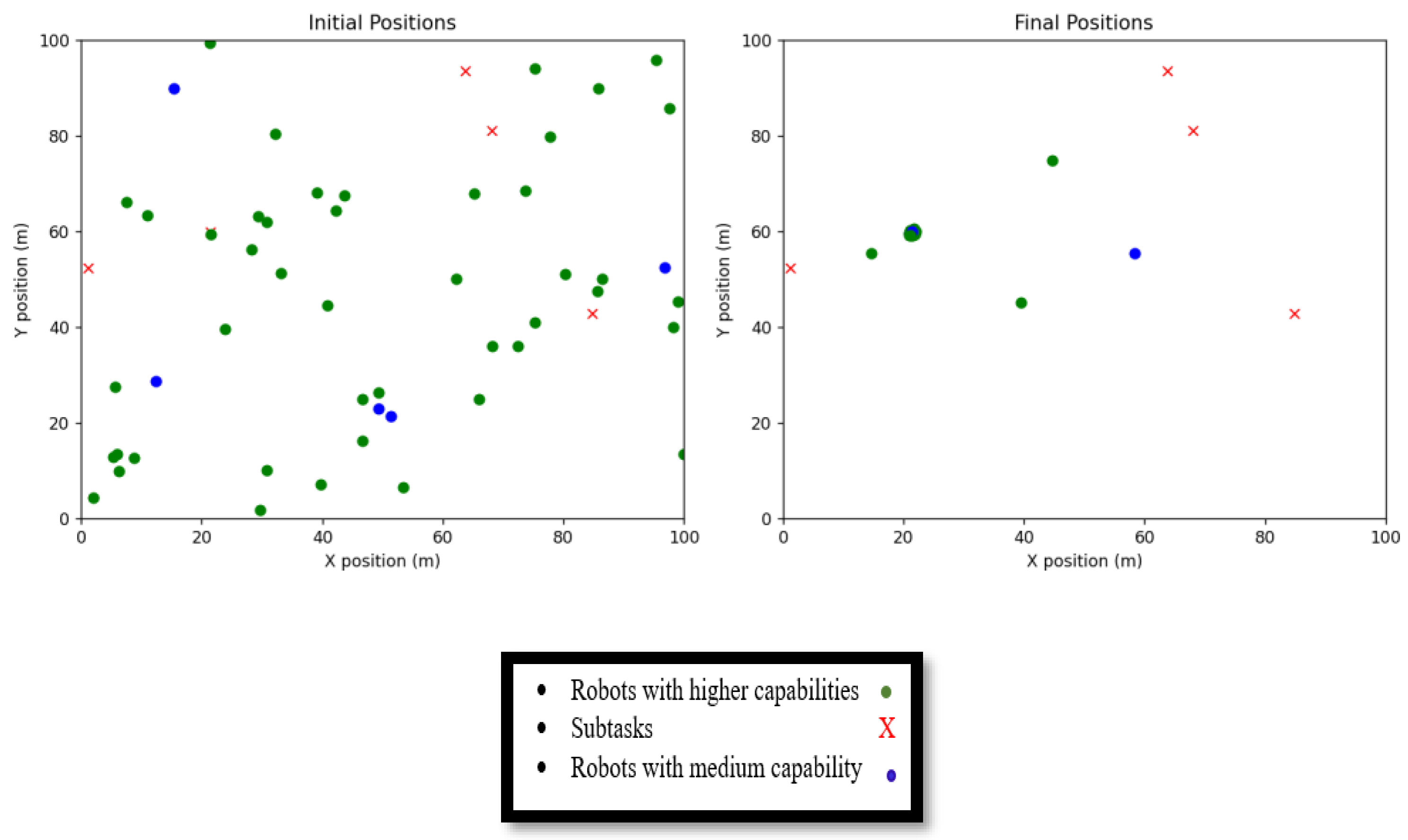
3.4. Learning-Based: Reinforcement Learning
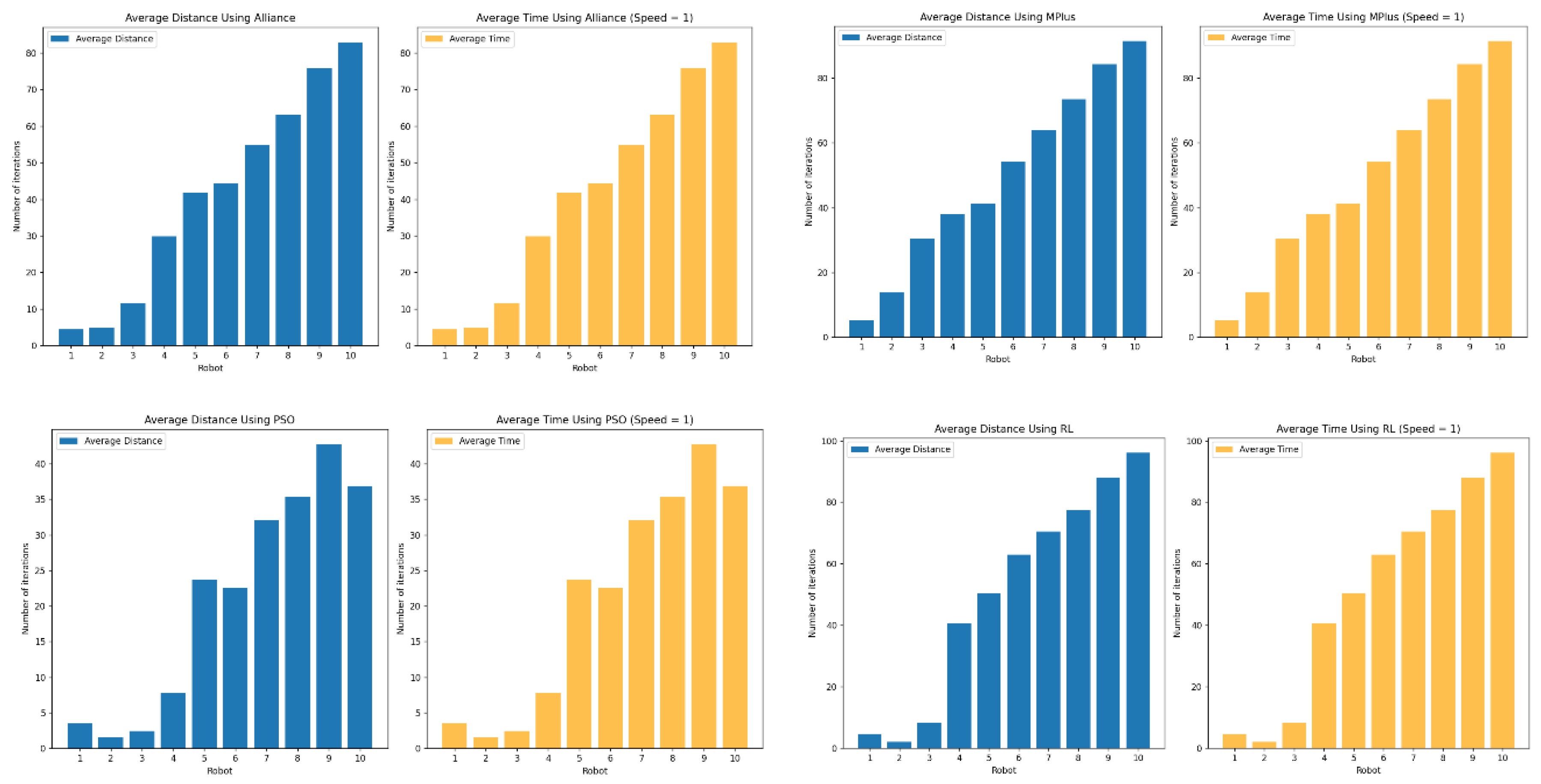
3.5. Statistical Analysis
4. Discussion
5. Conclusion
References
- Gautam, A. and S. Mohan. A review of research in multi-robot systems. in 2012 IEEE 7th International Conference on Industrial and Information Systems (ICIIS). 2012.
- Parker, L.E. Distributed intelligence: overview of the field and its application in multi-robot systems. J. Phys. Agents (JoPha) 2008, 2, 5–14. [Google Scholar] [CrossRef]
- Arai, T. and L. Parker, Editorial: advances in multi-robot systems. 2003.
- Roldán-Gómez, J.J.; Barrientos, A. Special Issue on Multi-Robot Systems: Challenges, Trends, and Applications. Appl. Sci. 2021, 11, 11861. [Google Scholar] [CrossRef]
- Khamis, A., A. Hussein, and A. Elmogy, Multi-robot task allocation: a review of the state-of-the-art. 2015. p. 31-51.
- Gerkey, B.P. and M.J. Mataric. Multi-robot task allocation: analyzing the complexity and optimality of key architectures. in 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422). 2003.
- Gerkey, B.P.; Matarić, M.J. A Formal Analysis and Taxonomy of Task Allocation in Multi-Robot Systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Korsah, G.A.; Stentz, A.; Dias, M.B. A comprehensive taxonomy for multi-robot task allocation. Int. J. Robot. Res. 2013, 32, 1495–1512. [Google Scholar] [CrossRef]
- Saravanan, S., K. C. Ramanathan, R. Mm, and M.N. Janardhanan, Review on state-of-the-art dynamic task allocation strategies for multiple-robot systems. Industrial Robot, 2020.
- Wen, X. and Z.G. Zhao. Multi-robot task allocation based on combinatorial auction. in 2021 9th International Conference on Control, Mechatronics and Automation (ICCMA). 2021.
- Chakraa, H.; Guérin, F.; Leclercq, E.; Lefebvre, D. Optimization techniques for Multi-Robot Task Allocation problems: Review on the state-of-the-art. Robot. Auton. Syst. 2023, 168. [Google Scholar] [CrossRef]
- dos Reis, W.P.N.; Lopes, G.L.; Bastos, G.S. An arrovian analysis on the multi-robot task allocation problem: Analyzing a behavior-based architecture. Robot. Auton. Syst. 2021, 144. [Google Scholar] [CrossRef]
- Agrawal, A., A. Bedi, and D. Manocha, RTAW: an attention inspired reinforcement learning method for multi-robot task allocation in warehouse environments. 2023. 1393-1399.
- Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the Multiple Traveling Salesman Problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 40. [Google Scholar] [CrossRef]
- Deng, P.; Amirjamshidi, G.; Roorda, M. A vehicle routing problem with movement synchronization of drones, sidewalk robots, or foot-walkers. Transp. Res. Procedia 2020, 46, 29–36. [Google Scholar] [CrossRef]
- Sun, Y.; Chung, S.-H.; Wen, X.; Ma, H.-L. Novel robotic job-shop scheduling models with deadlock and robot movement considerations. Transp. Res. Part E: Logist. Transp. Rev. 2021; 149. [Google Scholar] [CrossRef]
- Santana KA, Pinto VP, Souza DAd, Torres JLO, Teles IAG, editors. New GA applied route calculation for multiple robots with energy restrictions. 2020.
- Jorgensen, R.M.; Larsen, J.; Bergvinsdottir, K.B. Solving the Dial-a-Ride problem using genetic algorithms. J. Oper. Res. Soc. 2007, 58, 1321–1331. [Google Scholar] [CrossRef]
- Hussein, A. and A. Khamis. Market-based approach to multi-robot task allocation. in 2013 International Conference on Individual and Collective Behaviors in Robotics (ICBR). 2013. [Google Scholar]
- Ramanathan, K.C., M. Singaperumal, and T. Nagarajan, Cooperative formation planning and control of multiple mobile robots. 2011.
- Aziz, H.; Pal, A.; Pourmiri, A.; Ramezani, F.; Sims, B. Task Allocation Using a Team of Robots. Curr. Robot. Rep. 2022, 3, 227–238. [Google Scholar] [CrossRef]
- Zitouni, F.; Harous, S.; Maamri, R. A Distributed Approach to the Multi-Robot Task Allocation Problem Using the Consensus-Based Bundle Algorithm and Ant Colony System. IEEE Access 2020, 8, 27479–27494. [Google Scholar] [CrossRef]
- Rauniyar, A. and P.K. Muhuri. Multi-robot coalition formation problem: task allocation with adaptive immigrants based genetic algorithms. in 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC). 2016. [Google Scholar]
- Kraus, S. Negotiation and cooperation in multi-agent environments. Artif. Intell. 1997, 94, 79–97. [Google Scholar] [CrossRef]
- Tosic, P. and C. Ordonez, Distributed protocols for multi-agent coalition formation: a negotiation perspective. 2012.
- Selseleh Jonban, M., A. Akbarimajd, and M. Hassanpour, A combinatorial auction algorithm for a multi-robot transportation problem. 2014.
- Capitan J, Spaan MTJ, Merino L, Ollero A. Decentralized multi-robot cooperation with auctioned POMDPs. The International Journal of Robotics Research. 2013;32(6): p. 650-71.
- Hernandez-Leal P, Kaisers M, Baarslag T, Munoz de Cote E. A survey of learning in multiagent environments: dealing with non-stationarity. 2017.
- Vig, L.; Adams, J. Multi-robot coalition formation. IEEE Trans. Robot. 2006, 22, 637–649. [Google Scholar] [CrossRef]
- Guerrero, J.; Oliver, G. Multi-robot coalition formation in real-time scenarios. Robot. Auton. Syst. 2012, 60, 1295–1307. [Google Scholar] [CrossRef]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Cooperative Heterogeneous Multi-Robot Systems. ACM Comput. Surv. 2019, 52, 1–31. [Google Scholar] [CrossRef]
- Chetty, R.K.; Singaperumal, M.; Nagarajan, T. Behaviour based planning and control of leader follower formations in wheeled mobile robots. Int. J. Adv. Mechatron. Syst. 2010, 2, 281. [Google Scholar] [CrossRef]
- Schillinger, P.; Bürger, M.; Dimarogonas, D.V. Simultaneous task allocation and planning for temporal logic goals in heterogeneous multi-robot systems. Int. J. Robot. Res. 2018, 37, 818–838. [Google Scholar] [CrossRef]
- Parker, L.E. , ALLIANCE: an architecture for fault tolerant multirobot cooperation. IEEE Transactions on Robotics and Automation, 1998. 14(2): p. 220-240.
- Parker, L.E. ALLIANCE: an architecture for fault tolerant, cooperative control of heterogeneous mobile robots. in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS'94). 1994. [Google Scholar]
- Parker, L.E. , L-ALLIANCE: task-oriented multi-robot learning in behavior-based systems. Advanced Robotics, 1996. 11(4): p. 305-322.
- Parker, L. , L-ALLIANCE: a mechanism for adaptive action selection in heterogeneous multi-robot teams. 1996.
- Parker, L.E. Evaluating success in autonomous multi-robot teams: experiences from ALLIANCE architecture implementations. J. Exp. Theor. Artif. Intell. 2001, 13, 95–98. [Google Scholar] [CrossRef]
- Parker, L.E. On the design of behavior-based multi-robot teams. Adv. Robot. 1995, 10, 547–578. [Google Scholar] [CrossRef]
- Parker, L.E. Task-oriented multi-robot learning in behavior-based systems. in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. IROS '96. 1996. [Google Scholar]
- Mesterton-Gibbons, M.; Gavrilets, S.; Gravner, J.; Akçay, E. Models of coalition or alliance formation. J. Theor. Biol. 2011, 274, 187–204. [Google Scholar] [CrossRef] [PubMed]
- Dahl, T.S.; Matarić, M.; Sukhatme, G.S. Multi-robot task allocation through vacancy chain scheduling. Robot. Auton. Syst. 2009, 57, 674–687. [Google Scholar] [CrossRef]
- Lerman, K.; Galstyan, A.; Martinoli, A.; Ijspeert, A. A Macroscopic Analytical Model of Collaboration in Distributed Robotic Systems. Artif. Life 2001, 7, 375–393. [Google Scholar] [CrossRef]
- Jia, X. and M.Q.H. Meng. A survey and analysis of task allocation algorithms in multi-robot systems. in 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO). 2013.
- Werger, B. and M. Mataric, Broadcast of local eligibility: behavior-based control for strongly cooperative robot teams. 2000.
- Werger, B. and M. Mataric, Broadcast of local eligibility for multi-target observation. 2000. p. 347-356.
- Faigl, J., M. Kulich, and L. Preucil, Goal assignment using distance cost in multi-robot exploration. 2012. p. 3741-3746.
- Tang, F. and L. Parker, ASyMTRe: automated synthesis of multi-robot task solutions through software reconfiguration. 2005. p. 1501-1508.
- Fang, T. and L.E. Parker. Coalescent multi-robot teaming through ASyMTRe: a formal analysis. in ICAR '05. Proceedings., 12th International Conference on Advanced Robotics, 2005.
- Fang, G., G. Dissanayake, and H. Lau, A behaviour-based optimisation strategy for multi-robot exploration. 2005. 2: p. 875-879.
- Trigui, S.; Koubaa, A.; Cheikhrouhou, O.; Youssef, H.; Bennaceur, H.; Sriti, M.-F.; Javed, Y. A Distributed Market-based Algorithm for the Multi-robot Assignment Problem. Procedia Comput. Sci. 2014, 32, 1108–1114. [Google Scholar] [CrossRef]
- Badreldin, M.; Hussein, A.; Khamis, A. A Comparative Study between Optimization and Market-Based Approaches to Multi-Robot Task Allocation. Adv. Artif. Intell. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Service, T.C., S.D. Sen, and J.A. Adams. A simultaneous descending auction for task allocation. in 2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC). 2014.
- Vig, L. and J. Adams, A framework for multi-robot coalition formation. 2005. p. 347-363.
- Vig, L. and J. Adams, Market-based multi-robot coalition formation. 2007. p. 227-236.
- Vig, L.; Adams, J.A. Coalition Formation: From Software Agents to Robots. J. Intell. Robot. Syst. 2007, 50, 85–118. [Google Scholar] [CrossRef]
- Lueth, T. and T. Längle, Task description, decomposition, and allocation in a distributed autonomous multi-agent robot system. 1994.
- Längle, T., T. Lueth, and U. Rembold, A distributed control architecture for autonomous robot systems. 1994. p. 384-402.
- Gerkey, B.; Mataric, M. Sold!: auction methods for multirobot coordination. IEEE Trans. Robot. Autom. 2002, 18, 758–768. [Google Scholar] [CrossRef]
- Guidotti, C.F., A. T. Baião, G.S. Bastos, and A.H.R. Leite. A murdoch-based ROS package for multi-robot task allocation. in 2018 Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE). 2018.
- Lagoudakis, M. , et al., Auction-based multi-robot routing. 2005. p. 343-350.
- Liu, L. and Z. Zhiqiang. Combinatorial bids based multi-robot task allocation method. in Proceedings of the 2005 IEEE International Conference on Robotics and Automation. 2005.
- Sheng, W.; Yang, Q.; Tan, J.; Xi, N. Distributed multi-robot coordination in area exploration. Robot. Auton. Syst. 2006, 54, 945–955. [Google Scholar] [CrossRef]
- Gerkey, B. and M. Matari, MURDOCH: publish/subscribe task allocation for heterogeneous agents. 2000.
- Alami, R.; Fleury, S.; Herrb, M.; Ingrand, F.; Robert, F. Multi-robot cooperation in the MARTHA project. IEEE Robot. Autom. Mag. 1998, 5, 36–47. [Google Scholar] [CrossRef]
- Botelho, S. and R. Alami, M+: a scheme for multi-robot cooperation through negotiated task allocation and achievement. 1999. 2: p. 1234-1239.
- Botelho, S.C. and R. Alami. A multi-robot cooperative task achievement system. in Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065). 2000.
- Smith, The contract net protocol: high-level communication and control in a distributed problem solver. IEEE Transactions on Computers, 1980. C-29(12): p. 1104-1113.
- Dias, M. B., Zlot, R., Zinck, M., Gonzalez, J. P., & Stentz, A. (2018, June 29). A versatile implementation of the traderbots approach for multirobot coordination. Carnegie Mellon University. [CrossRef]
- Dias, M.B. and A. Stentz. A free market architecture for distributed control of a multirobot system. 2000.
- Zlot, R., A. Stentz, M.B. Dias, and S. Thayer. Multi-robot exploration controlled by a market economy. in Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292). 2002.
- Dias, M.B. and A. Stentz, Traderbots: a new paradigm for robust and efficient multirobot coordination in dynamic environments. 2004, Carnegie Mellon University.
- Hussein, A.; Marín-Plaza, P.; García, F.; Armingol, J.M. Hybrid Optimization-Based Approach for Multiple Intelligent Vehicles Requests Allocation. J. Adv. Transp. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Shelkamy, M., C. M. Elias, D.M. Mahfouz, and O.M. Shehata. Comparative analysis of various optimization techniques for solving multi-robot task allocation problem. in 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES). 2020.
- Atay, N. and B. Bayazit, Mixed-integer linear programming solution to multi-robot task allocation problem. 2006.
- Bouyarmane, K., J. Vaillant, K. Chappellet, and A. Kheddar, Multi-robot and task-space force control with quadratic programming. 2017.
- Pugh, J. and A. Martinoli. Inspiring and modeling multi-robot search with particle swarm optimization. in 2007 IEEE Swarm Intelligence Symposium. 2007.
- Imran, M.; Hashim, R.; Khalid, N.E.A. An Overview of Particle Swarm Optimization Variants. Procedia Eng. 2013, 53, 491–496. [Google Scholar] [CrossRef]
- Li, X. and H.x. Ma. Particle swarm optimization based multi-robot task allocation using wireless sensor network. in 2008 International Conference on Information and Automation. 2008.
- Nedjah, N., R. Mendonc¸a, and L. Mourelle, PSO-based distributed algorithm for dynamic task allocation in a robotic swarm. Procedia Computer Science, 2015. 51: p. 326-335.
- Pendharkar, P.C. An ant colony optimization heuristic for constrained task allocation problem. J. Comput. Sci. 2015, 7, 37–47. [Google Scholar] [CrossRef]
- Dorigo, M., M. Birattari, and T. Stützle, Ant colony optimization: artificial ants as a computational intelligence technique. IEEE Computational Intelligence Magazine, 2006. 1: p. 28-39.
- Agarwal, M.; Agrawal, N.; Sharma, S.; Vig, L.; Kumar, N. Parallel multi-objective multi-robot coalition formation. Expert Syst. Appl. 2015, 42, 7797–7811. [Google Scholar] [CrossRef]
- Dorigo, M. and G.D. Caro. Ant colony optimization: a new meta-heuristic. in Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406). 1999.
- Wang, J.; Gu, Y.; Li, X. Multi-robot Task Allocation Based on Ant Colony Algorithm. J. Comput. 2012, 7, 2160–2167. [Google Scholar] [CrossRef]
- Jianping, C., Y. Yimin, and W. Yunbiao, Multi-robot task allocation based on robotic utility value and genetic algorithm. 2009. p. 256-260.
- Rauniyar, A. and P. Muhuri, Multi-robot coalition formation problem: task allocation with adaptive immigrants based genetic algorithms. 2016. p. 137-142.
- Haghi Kashani, M. and M. Jahanshahi, Using simulated annealing for task scheduling in distributed systems. Computational Intelligence, Modelling and Simulation, International Conference on, 2009. p. 265-269.
- Mosteo, A. and L. Montano, Simulated annealing for multi-robot hierarchical task allocation with flexible constraints and objective functions. 2006.
- Chakraborty, S. and S. Bhowmik, Job shop scheduling using simulated annealing. 2013.
- Elfakharany, A.; Yusof, R.; Ismail, Z. Towards multi robot task allocation and navigation using deep reinforcement learning. Journal of Physics: Conference Series 2020, 1447, 012045. [Google Scholar] [CrossRef]
- Dahl, T., M. Mataric, and G. Sukhatme, A machine learning method for improving task allocation in distributed multi-robot transportation. 2004.
- Wang, Y. and C. Silva, A machine-learning approach to multi-robot coordination. Engineering Applications of Artificial Intelligence, 2008. 21: p. 470-484.
- Cunningham, P., M. Cord, and S. Delany, Supervised learning. 2008. p. 21-49.
- Sermanet, P., C. Lynch, J. Hsu, and S. Levine. Time-contrastive networks: self-supervised learning from multi-view observation. in 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW). 2017.
- Teichman, A. and S. Thrun, Tracking-based semi-supervised learning. The International Journal of Robotics Research, 2012. 31(7): p. 804-818.
- Xu, J.; Zhu, S.; Guo, H.; Wu, S. Automated Labeling for Robotic Autonomous Navigation Through Multi-Sensory Semi-Supervised Learning on Big Data. IEEE Trans. Big Data 2019, 7, 93–101. [Google Scholar] [CrossRef]
- Bousquet, O., U. Luxburg, and G. Rätsch, Advanced lectures on machine learning. ML Summer Schools 2003, Canberra, Australia, February 2-14, 2003, Tübingen, Germany, August 4-16, 2003, Revised Lectures. 2004.
- Arel, I.; Liu, C.; Urbanik, T.; Kohls, A. Reinforcement learning-based multi-agent system for network traffic signal control. IET Intell. Transp. Syst. 2010, 4, 128–135. [Google Scholar] [CrossRef]
- Verma, J. and V. Ranga, Multi-robot coordination analysis, taxonomy, challenges and future scope. Journal of Intelligent & Robotic Systems, 2021. 102.
- Wang, Y. and C.W.D. Silva. Multi-robot box-pushing: single-agent Q-learning vs. team Q-learning. in 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2006.
- Guo, H. and Y. Meng. Dynamic correlation matrix based multi-Q learning for a multi-robot system. in 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2008.
- Ahmad, A. , et al. Autonomous aerial swarming in GNSS-denied environments with high obstacle density. in 2021 IEEE International Conference on Robotics and Automation (ICRA). 2021. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9561284.
- Team CERBERUS wins the DARPA Subterranean Challenge. Autonomous robots lab. https://www.autonomousrobotslab.com/.
- Autonomous Mobile Robots (AMR) For Factory Floors: Key Driving Factors.2021. roboticsbiz. https://roboticsbiz.com/autonomous-mobile-robots-amr-for-factory-floors-key-driving-factors/.
- Different Types Of Robots Transforming The Construction Industry.2020. roboticsbiz. https://roboticsbiz.com/different-types-of-robots-transforming-the-construction-industry/.
- Robocup soccer small-size league. Robocup. https://robocupthailand.org/services/robocup-soccer-small-size-league/.
- Robots in agriculture and farming. 2022. Cyber-weld robotic system integrators. https://www.cyberweld.co.uk/robots-in-agriculture-and-farming.
- Arjun, K. Parlevliet, D. Wang, H. Yazdani, A. Analyzing multi-robot task allocation and coalition formation methods: A comparative study. in 2024 International Conference on Advanced Robotics, Control, and Artificial Intelligence. 2024.
| Algorithm | Efficiency | Advantages | Disadvantages |
|---|---|---|---|
| Alliance | High | Scalable, adaptable to dynamic environments, provide a higher degree of stability in coalition. |
Requires effective communication and coordination |
| Vacancy Chain | Medium | Low communication overhead, stable coalitions |
Limited scalability, sensitive to changes in the team |
| Broadcast Local Eligibility | Medium to high | Efficient, distributed, Low communication |
Tends to form smaller coalitions |
| ASyMTRE | High | Adaptive, efficient task allocation | Requires sophisticated negotiation mechanisms |
| Characteristics | Alliance | Vacancy chain | BLE | ASyMTRE | |||
|---|---|---|---|---|---|---|---|
| Homogenous/ Heterogenous |
Heterogeneous | Homogeneous robots |
Heterogeneous | Heterogeneous | |||
| Optimal allocation |
Guarantee optimal allocation |
Guarantee (Minimal) |
Does not Guarantee | Guarantee (Minimal) |
|||
| Cooperation | Strongly cooperative | Weak cooperation |
Strongly cooperative | Strongly cooperative | |||
| Communication | Strong | Limited | Limited | ||||
| Strong | |||||||
| Hierarchy | Fully distributed | Not fully distributed |
Fully distributed | Not fully distributed |
|||
| Task reassignment |
Possible through coalition reconfiguration) |
Possible (via vacancy announcement) |
(Possible based on dynamic eligibility) |
(Possibly based on genetic optimization) | |||
| Characteristics | RACHNA | KAMARA | MURDOCH | M+ | TraderBots |
|---|---|---|---|---|---|
| Market-based | Negotiation based | Market-based | Market-based | Negotiation based | Auction based |
| Bidding method | Uses a genetic algorithm to optimize bids | Bids are based on utility functions that consider the cost and quality of the task | Bids based on a simple cost function |
Form coalitions to bid on tasks together | Bids are based on a reinforcement learning algorithm |
|
Homogenous/ 9Heterogenous |
Heterogeneous | Heterogeneous | Heterogeneous | Heterogeneous | Homogeneous robots |
| Fault tolerance | Not fault-tolerant | Fault-tolerant | Not fault-tolerant | Fault-tolerant | Fault-tolerant |
| Optimal allocation | Can guarantee depending on the fitness function | Can guarantee based on the utility function | Not Guaranteed | Can guarantee based on the coalition formation algorithm | Can guarantee |
| Cooperation | Cooperative | Cooperative | Strong cooperation | Cooperative | Strongly cooperative |
| Communication | Limited (Global communication) | Limited (Local communication) | Strong (Global communication) | Strong (Local communication) | Strong (Local communication) |
| Hierarchy | Distributed | Hybrid | Distributed (Loosely coupled) |
Fully distributed | Combination of a distributed and centralized approach |
| Task reassignment | Not Possible | Possible | Not possible | Possible | Possible |
| Complexity | Moderate | Moderate | Simple | High | High |
| Cost | Moderate | Moderate | Low | High | High |
| Scalability | Limited | Highly scalable | Limited | Highly scalable | Highly scalable |
| Coalition formation | Yes | Possible | Yes, and dynamically adaptable | Yes, and dynamically adaptable | Yes |
| Approach | Optimization technique | Advantages | Disadvantages |
|---|---|---|---|
| PSO [75,76,77,78] | Swarm intelligence |
|
|
| ACO [79,80,81,82,83] | Swarm intelligence |
|
|
| GA [84,85] | Evolutionary |
|
|
| SA [86,87,88] | Stochastic |
|
|
| MILP [72,73] | Mathematical Programming |
|
|
| QP [74] | Mathematical Programming |
|
|
| Characteristics | Particle Algorithm (GA)/Simulated Annealing (SA) | Mixed Integer Linear Programming (M ILP) | Quadratic Programming (QP) |
|---|---|---|---|
| Fault tolerance | Robust to individual robot failures but not to system-wide failures | Not inherently fault tolerant | Not inherently fault tolerant |
| Optimal allocation | May converge to local optima and be able to handle multiple objectives | Can find globally optimal solutions, but computational complexity may increase with problem size. | Can find globally optimal solutions, but computational complexity may increase with problem size. |
| Scalability | Can handle significant problems efficiently but require extensive parameter tuning. | Small-medium sized problems | Can handle significant problems efficiently but require extensive parameter tuning |
| Task reassignment | Can handle by updating the objective functions and constraints | Can handle by updating the objective functions and constraints | Can handle by updating the objective functions and constraints |
| Coalition formation | Can handle by adding appropriate terms to the objective functions and constraints | Can handle by adding appropriate terms to the objective functions and constraints | Can handle by adding appropriate terms to the objective functions and constraints |
| Complexity | Can handle complex optimization problems with non-linearities and multiple objectives | Can handle linear and non-linear constraints. | Can handle linear and non-linear constraints. |
| Cost | It can be less expensive than MILP and QP but require extensive parameter tuning. | It can be expensive due to the computational complexity | It can be expensive due to the computational complexity |
| Factors | Supervised learning | Unsupervised learning | Semi supervised learning | Reinforcement learning |
|---|---|---|---|---|
| Fault tolerance | Low, sensitive to errors in the labels as it relies on labeled data for training | Low, may handle noise and outliers better as it does not require labels. | More fault tolerant by leveraging both labeled and unlabeled data. | Medium, through exploration-exploitation trade-offs |
| Optimal allocation | Can achieve optimal allocation by learning from labeled data and mapping inputs to correct outputs. | No, mostly aims to discover patterns and relationships in the data. | Partially, it may require more specialized approaches | Partially, it may require more specialized approaches |
| Scalability | High, may face challenges due to the need for labeled data and computational complexity. | High as it does not require labeled data. | High, by utilizing both labeled and unlabeled data. | Medium-high, may face challenges due to the need for labeled data and computational complexity. |
| Task reassignment | Difficult, not inherently designed for it, may require additional mechanisms. | Yes, it naturally clusters data into groups. | Yes, can leverage both labeled and unlabeled data to handle task reassignment. | Yes, equipped to handle task reassignment in sequential decision-making problems. |
| Coalition formation | Not specifically tailored, may need additional considerations and adaptations. | Same as Supervised learning | Same as Supervised learning and Unsupervised Learning | Possible in situations where agents make sequential decisions in coalition formation tasks. |
| Complexity | Lower, but based on the specific algorithm and techniques used within | Same as Supervised learning | Same as Supervised learning and Unsupervised Learning | Higher due to the need to learn policies for sequential decision making. |
| Cost | Lower for simple models but varies depending on the complexity of the model and size of the data. | Same as Supervised learning | Same as Supervised learning and Unsupervised Learning | High due to learning and exploration process. |
| Method | Efficiency | Advantages | Disadvantages |
| Supervised Learning | Low- Medium |
|
|
| Semi-Supervised learning | Low- Medium |
|
|
| Unsupervised learning | Low- Medium |
|
|
| Reinforcement learning | Medium- High |
|
|
| Factors | Behavior-based Methods | Market-based Method | Optimization-based Methods | Learning-based Methods |
|---|---|---|---|---|
| Scalability | Scalable for small to moderate size systems | Scalable for small to moderate size systems | Scalable for large systems | Can scale to large and complex systems |
| Complexity | Can handle simple to moderate complex tasks | Can handle complex tasks and heterogeneous robots | Can handle complex tasks and constraints | Can handle complex tasks, constraints, and heterogeneous robots |
| Optimality | May not always achieve optimality | Can achieve Pareto efficiency under certain conditions | Can achieve optimality under certain conditions. | Can achieve optimality under certain conditions. But guaranteed for good optimal allocation all the time. |
| Flexibility | Limited flexibility to adapt to new tasks or situations | Can be flexible and adaptable to changing market conditions | May be flexible depending on the optimization method used | Can be flexible and adaptable to changing environment |
| Robustness | May be robust to some degree of uncertainty or failures | Can be robust to some degree of market uncertainty and failures | May not be robust to uncertainty or failures. | Can improve robustness through learning from experience and failures. |
| Communication | Local communication among neighbour robots. | Multiple times broadcasting of winner robot details after bidding | Local communication among neighbour robots. | Local/Global communication |
| Objective function | Single/multiple objectives Implicit or ad-hoc |
Single/multiple objectives Optimization |
Single/multiple objectives Mathematical |
Single/multiple objectives Learning from data |
| Coordination type | Centralized/ distributed | Centralized/ distributed | Centralized/ distributed | Decentralized |
| task reallocation method | Heuristics ruled searching/Bayesian Nash equilibrium | Iterative auctioning methods | Iterative searching and allocation | Reinforcement learning |
| Uncertainty handling techniques | Game theory/probabilistic predictive modelling | Iterative auctioning methods | Difficult to handle uncertainty | Adaptive models |
| Constraints | Can be handled in a collective manner | Difficult to conduct auctions | Complex and difficult to solve due to multiple decision variables | Varies based on learning algorithms |
| Computational cost | Higher than optimization-based strategy | Lower than optimization strategy | Higher than market-based strategy | High; need large amount of data |
| Coalition formation | Low efficiency as the approach is based on local rules without a global optimization perspective. | Moderate efficiency due to negotiation and market mechanisms | High efficiency through global optimization approaches | Moderate efficiency as it relies on learning and adaptive algorithms. |
| Task reallocation | Limited ability to perform task reallocation dynamically as it relies on predefined rules. | Efficient task reallocation due to negotiation and the market mechanism | Efficient reallocation due to optimization algorithms and centralized coordination | Adaptive due to learning algorithms and flexible decision making |
| Collision avoidance | Limited capability due to lack of sophisticated coordination mechanism | Effective collision avoidance due to price-based mechanisms and negotiations. | Effective due to optimized task allocation and coordination | Adaptive due to learning and sensor-based approaches |
| Dynamic decision making | Limited adaptability due to its rule-based and reactive characteristic | Limited adaptability as it relies on predefined market rules. |
Flexible due to mathematical optimization and modeling | Flexible through adaptive learning algorithms |
| Temporal constraints | Limited support due to a lack of coordinated decision making | Moderate support due to negotiation and the market mechanism | Highly support handling temporal constraints through optimization techniques and advanced scheduling algorithms. | Highly support handling temporal constraints through learning and scheduling algorithms. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).






