Global Population Growth, Carrying Capacity, and High-Quality Foods in Industrial Revolutions Epoch

1. Introduction

Twelve thousand years ago, the last Ice Age - lasting ~100,000 years - terminated. Global Warming freed Eurasia and North America from the ice sheets. The mild climate and, vast uninhabited areas, rich food resources yielded exceptional opportunities for hunter-gatherers. The Anthropocene epoch began [1]. During only 12 millennia, the global population rose from $~2millions$ (10 000 BCE) to $~8.23billions$ in May 2025 [2,3,4]. This population success was significantly due to the access to ‘infinite’ food resources for an ever-increasing population.

Food is a source of energy and health. Providing it for oneself, family, group, … was and still is the goal and challenge of every person, every day. So, the question arises about the impact of this essential resource on the global population in the Anthropocene.

The answer might seem extremely puzzling due to the huge and multidimensional scope of changes and heterogeneity. However, such data can be hidden in the global population growth scaling patterns, significantly shaped by access to food resources.

Over the millennia, the exponential pattern of global population growth dominated. It is also called geometric growth, with the growth rate directly proportional to its current size or alternatively related to the same relative percentage in each time following time period [2,3,4]. Recently, explicit evidence for such a trend was shown even in a period that was particularly significant for the modern world, from the mid-medieval times till the onset of the Enlightenment. However, ca. 2 centuries ago, the qualitatively new ’boosted’ scaling pattern emerged, namely [2,3]:

$$P\left(t\right)=P_{0}exp\left(rt\right)=P_{0}exp\left({\displaystyle \frac{t}{\tau }}\right)\Rightarrow P\left(t\right)=P_{0}exp\left({\displaystyle \frac{bt}{t_C-t}}\right)=P_{0}exp\left(b{T}^{-1}\right)$$

(1)

$$~1100-1720\left(\text{'}M{althus}^{\text{'}}\right)\Rightarrow ~1720-2024(‘\mathit{constrained}\text{-}\mathit{critical})$$

where $P\left(t\right)$ is for the global population, $t$ is the time since the Anthropocene epoque dawn, 12 000 BCE; $b=const$, $t_C\approx 2216$ is the extrapolated singular ‘Dooms-year’, $T=\left(t_C-t\right)/t$ is the relative distance form $T_C$ metric; $r=const$ is for the Malthus population growth parameter, and $\tau =1/r$ means the relaxation time.

Sojecka and Drozd-Rzoska obtained the above result by introducing the Super-Malthus scaling equation and the distortions-sensitive analysis, briefly discussed below [2,3,4]. Notably, exponential dynamics is common in nature, from microbiology [5,6,7,8] and biology [9,10,11] to dynamics of physical processes [12,13,14], chemical reactions [15,16], nuclear reactions, and nuclear fission reactors. [17,18,19]. For the latter, the name ‘chain reaction’ is used to describe the rising impact of neutrons in subsequent steps [20]. However, in the last two centuries, the growth of the human global population has been essentially stronger, as shown in Eq. (1) and refs. [2,3,4].

Providing food for a growing population has been a source of concern and a challenge for millennia [21,22]. Despite the global population boost over the past 200 years, the growing needs have been met qualitatively, and an abundance previously unknown has also emerged. It can be linked to the Industrial Revolutions epoch, which began two centuries ago [23,24,25,26]. Its essence is the development and mass implementation of groundbreaking technological innovations, in feedback assistance of socio-economic ‘innovations’ supporting and organizing the development. This progress was so rapid that the world changed beyond recognition during one man's lifetime. An example is the qualitative changes in the world during the reign of two symbolic figures: Emperor of Austria Franz Josef I (1848–1916) and Queen of the United Kingdom Victoria I (1837–1901) [27].

In agriculture, productivity was greatly increased due to innovative processing and logistics technologies. The rising amount and assortment influenced demands. But it is 'elastic' only to a certain level. Finally, a relative decrease in food prices and lower expenditure have to appear. The funds of consumers released in this way could be spent on other goods and services, stimulating broader economic development. These processes also caused a qualitative decrease in employment. In highly developed countries, only about 10% of all employees work in agriculture [28,29,30]. A further significant decrease can be expected, e.g., due to using Artificial Intelligence (AI) for fieldwork. For instance, the future can be associated with autonomous agricultural machines, cultivating fields and controlled with the support of Artificial Intelligence. Such a picture of the future is shown, for example, in Christopher Nolan's phenomenal film 'Interstellar' (2014). The recalled ‘feedback mechanism’ between science, technology, and socio-economy, is specific to the Industrial Revolutions times. In this innovations-driven epoch, the development of methods to ensure health safety and extended shelf-life of food, with the minimum possible impact on products' native forms, was essential. Of particular importance are the works of Louis Pasteur (1863), who recognized spontaneously developing parasitic microorganisms as a crucial hazardous factor to health and product quality [31]. He solved the problem by discovering ‘thermal pasteurization’, i.e., heating the product to $~85°C$, for a few minutes [32]. In the second half of the 19th century, also chemical preservation additives started to be broadly implemented for preserving long-term microbiological safety [33]. In those times, the foundations of refrigerators and coolers were also developed, so their mass-scale implementation was possible in the first half of the 20th century [34]. The pioneering works of Pierre Curie and Marie Curie-Skłodowska led to the use of irradiation as a physical factor destructive for microorganisms,…. [35,36,37].

These food preservation methods have led to an extraordinary abundance and diversity of foodstuffs on hypermarket shelves. The development was essential for extending the logistics chain, often reaching a global scale.

However, in recent decades, the dark side of these innovative methods of food preservation has been revealed. The accumulation of parasitic side effects has even led to dangerous and harmful global-scale pandemics related to obesity, numerous allergies, and certain types of cancer [38,39,40,41,42,43,44].

This problem is closely associated with the rich offer of so-called ultra-processed food, which contains few or no wholesome ingredients, often chemically modified and with artificial additives to make it edible, tasty, and addictive. Their list is huge. These include numerous carbonated drinks, sweet or salty packaged snacks, ice cream, chocolate, sweets (confectionery), mass-produced bread and rolls, margarine and spreads, cookies (biscuits), numerous energy cakes and bars, energy drinks, milk drinks, ‘fruit’ yogurts and ‘fruit’ drinks, cocoa drinks, meat, and chicken extracts and prepared sauces, infant formula, milk substitutes and other products for children, ‘quasi-healthy’ and ‘slimming’ products such as powdered or ‘fortified’ meals and meal substitutes, as well as many ready-to-heat products, including pre-prepared cakes, pasta dishes and pizza, poultry and fish ‘nuggets’ and ‘sticks’, sausages, burgers, hot dogs and other reconstituted meat products, and powdered and packaged ‘instant’ soups, dumplings and desserts. is an offer of products at surprisingly low prices, which may immediately raise suspicions of a connection with the so-called ‘junk food’ [45].

This type of ‘food’ is often supplemented by a large addition of chemical preservatives mentioned above. Studies have shown that ultra-processed foods increase the risk of obesity by 55%, sleep disorders by 41%, anxiety disorders by 53%, type 2 diabetes by 40%, and depression and premature death by 20%. It also presents strong evidence of a 50% increase in the risk of death from cardiovascular disease. It is estimated that 70% of all food in the US is ultra-processed. Its consumption is responsible for ~6% in Brazil or Chile but ~14% in the US or England [45,46]. Then, it is not surprising that food waste reaches $>40\%$ globally [47,48].

Reducing these losses is the simplest and environment-friendly way to increase the global food supply. Avoiding catastrophic impacts of ‘junk food’ and food preservatives side effects is also essential for the health and well-being of societies. All these can also mean incalculable benefits for the world economy.

In the current times of the 5th Industrial Revolutions, it is not important only to ensure quantity and variety of foods, and support logistic requirements. Offering food without mentioning harmful ‘side effects’ has become essential.

The answer to these challenges and even civilizational needs is the concept of 'High Quality Foods' defined as 'food produced using specific agricultural production methods, in particular in terms of food safety, traceability, authenticity, labeling, nutritional and health values, as well as respect for the environment and animal welfare, the sustainability of agricultural production and distinctive qualities, in particular quality and taste' [49,50,51]. The fundamental problem is the implementation of these impressive expectations in practice.

Such hope can be provided by innovative methods of preserving and processing food using a different conceptual basis than the abovementioned canon.

Below, high-pressure preservation/processing (HPP) for foods is presented. It is also called ’cold pasteurization‘ or ‘radicalization.’ It has already passed the market test and seems to meet all expectations as the next-generation technology for high-quality foods [7,8,52,53,54,55,56,57,58,59,60,61,62,63]. Original solutions for the next-generation HPP sterilization are also shown.

The preliminary first part of the report shows the conceptual background of the above issues through a new discussion regarding food needs and requirements developed in the Anthropocene. It focuses on the carrying capacity concept as its key metric, including some new interpretations.

2. Materials and Methods

This report recalls the results of recent authors’ studies regarding global population growth since the Anthropocene onset. They explored the essentially new set of population data based on the collection from a few sources, followed by numerical filtering to obtain an analytic set for which the derivative analysis was possible. The latter revealed subtle local features hidden when using direct data analysis [2,3,4,7,8,12,13]. This part of the report focuses on the Malthus, Verhulst, and Super-Malthus approaches [12,13]. These reports do not discuss other approaches to the global population challenge; these topics are discussed in refs. [2,3,4]. The given report supplements the reasonings presented in refs. [2,3], focusing on conclusions regarding food resources in subsequent periods. The hallmarks of the Industrial Revolutions epoch uniqueness are indicted, with a particular focus on innovative methods of food preservation and processing, focused on sustainable society requirements.

High-Pressure Preservation/Processing (HPP) features are presented It includes possible next-generation solutions, introduced and feasibility–tested by the authors: HPP – ‘hot’ and ‘cold’ sterilization [7,8]. It is related to the authors’ research and development experiences in the given field [see: https://young4softmatter.pl/].

3. Results

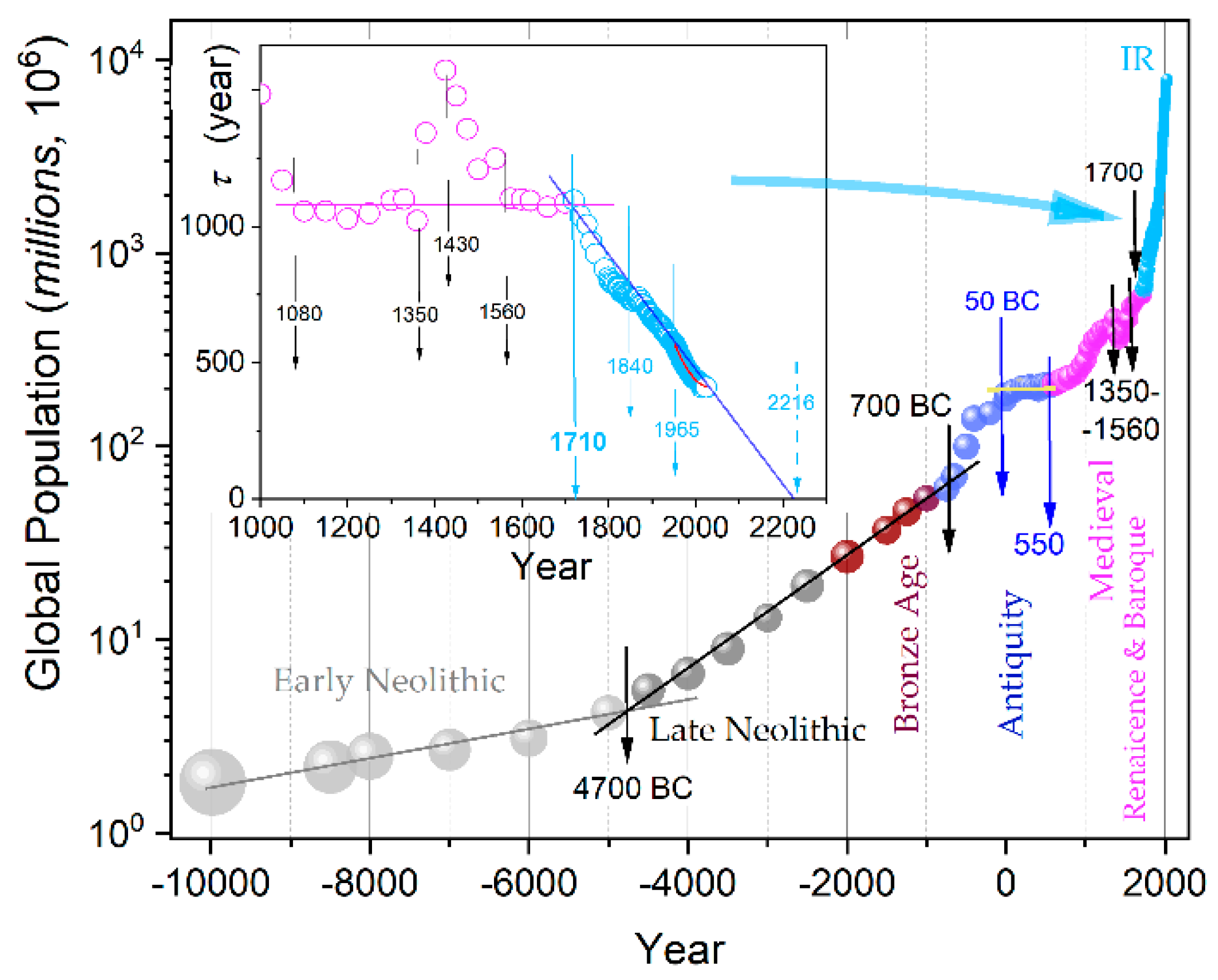
3.1. Global Population, Carrying Capacity, and Condorcet Criterion

The 17th century was the time of the Scientific Method shaping [64,65], the conceptual base of the emerging Industrial Revolution epoch. It stresses the meaning of critically analyzed observations, hypotheses formulation, experimental verifications, output data analysis expressed via analytic equations, and critical conclusions. Isaac Newton's great works significantly supported its universal recognition [65,66]. He used it to discover impressive universal laws of nature expressed by functional scaling equations. An example can be the Laws of Dynamics or the Law of Gravity in physics. The latter links seemingly distant phenomena such as an apple falling from a tree and movements of planets or comets ‘in the sky’. Isaac Newton introduced differential analysis to show in-depth model assumptions and derive final scaling equations [65,66].

In 1798, Thomas Malthus recalled Isaak Newton grand legacy inspiration when introducing the first analytic model describing human populations growth ($P\left(t\right))$ [67]):

$${\displaystyle \frac{dP\left(t\right)}{dt}}=rP\left(t\right)\Rightarrow G_P\left(t\right)={\displaystyle \frac{1}{P\left(t\right)}}{\displaystyle \frac{dP\left(t\right)}{dt}}={\displaystyle \frac{dlnP\left(t\right)}{dt}}=r$$

(2)

$$P\left(t\right)=P_{0}exp\left(rt\right)$$

(3)

where $r=const$ is the Malthus growth rate parameter, $t$ is the time since the onset and the prefactor $P_0$ is related to $t=0$.

Equation (2) presents differential equations showing the Malthus model base. Its left part is for the original dependence, and the right part shows it via the per capita relative growth rate (RGR) $G_P$ [3,4]. Malthus also indicated the meaning of available food resources $F\left(t\right)$ for the population growth, introduced via a supplementary equation that assumes a linear growth [67]:

$$F\left(t\right)=A+Bt$$

(4)

Finally, Malthus concluded [67]: ‘The population increases in geometrical ratio and the subsistence rises only linearly, which finally leads to times of vice and misery’, leading to the Malthus Trap (Catastrophe), when the quantity of food becomes increasingly insufficient for the growing population. Malthus advised population constraints or extra rise in subsistence (food) to escape the trap disaster. Unfortunately, the simplistic escape concept, namely robbery or conquest of other countries, has often been implemented [68,69,70].

A few decades later, Pierre François Verhulst (1838) introduced another scaling relation in which food is explicitly included in the basic model dependence, namely [71,72,73]:

$${\displaystyle \frac{dP\left(t\right)}{dt}}=rP-s{P}^2\Rightarrow G_P={\displaystyle \frac{1}{P\left(t\right)}}{\displaystyle \frac{dP\left(t\right)}{dt}}=r-sP=r\times \left({\displaystyle \frac{K-P\left(t\right)}{K}}\right)$$

(5)

$$P\left(t\right)={\displaystyle \frac{1}{1+Cexp\left(-rt\right)}}$$

(6)

where the parameter $C=1/P_0-s$; $s$ is the Verhulst parameter showing the impact of necessary resources, originally food, and the carrying capacity: $K=s/r$.

Equation (5) is for the derivative-based presentation of model assumptions: the left part recalls original Verhulst works and the right-hand part shows it via RGR parameter, with carrying capacity $K=r/s$ concept, introduced a century ago by Pearl and Reed [72,73]. It can be interpreted as the maximal population in a given system, allowed for available resources. Equation (6) shows the Verhulst model equation for population growth description, resulting from Equation (5).

The comparison of Equations (2) and (5) can suggest that one can consider the apparent growth rate: $r^{\text{'}}\left(r,t\right)=r\left(1-P\left(t\right)/K\right)$. It shows that for the Verhulst model behavior, $P\left(t\right)$ first follows the Malthus pattern (Equations (2) and (3)); next the continuous decrease of the apparent growth rate $r’$ occurs. Finally, the stationary phase related to $r^{\text{'}}\left(r,t\right)0$ and $P\left(t\right)K$ takes place. It is often noted the bimodal behavior [74,75].

Note that the above behavior is valid for systems with constant resources (food) amount despite population growth. This is a system with renewable resources. For systems with non-renewable resources, their amount decreases with the population's growth. In such a case, there is $P\left(t\right)$ maximum instead of the stationary phase, and subsequently, the population diminishes.

There are numerous population growth models [74,75,76,77,78,79,80,81,82,83,84,85], critically discussed in refs. [2,3]. In this report, we focus on the Malthus and Verhulst models, remaining a significant reference [86,87,88,89,90,91,92,93,94], and yielding a possibility to the distortions-sensitive analysis detecting subtle, local $P\left(t\right)$ changes [2,3,4].

Figure 1 presents global population evolutions since the Anthropocene onset. It is based on data developed by the authors [2,3] recently. They have been obtained via numerical filtering of global population data from a few sources. The plot is explores a semi-log scale, for which the basic Malthus behavior is visualized via a linear dependence, namely following Eq. (2): $lnP\left(t\right)=ln{P}_0+rt=ln{P}_0+\left(1/\right)t$ , and ${log}_{10}P\left(t\right)\approx 0.434lnP\left(t\right)$.

The plot reveals the simple Malthus's behavior for the enormous period of the first 9 millennia in the Anthropocene. It means that the global population has risen following a simple ‘geometric’ growth pattern, as described by the Malthus model (Equations (2) and (3)). It also suggests no food/resources restrictions, following the Malthus model discussion.

The Malthusian growth accelerates, ca. 4.6x, when passing the crossover correlated with the transition from the Early to the Late Neolithic epoch, as shown by changes in the slope of lines in Figure 1. It happened soon after the Doggerland flood and the North Sea formation [95], which has to be coupled with s a rise in sea levels, a further retreat of ice sheet remnants, and climate warming. Figure 1 shows that this pattern extends even beyond the Bronze Age, i.e., the times of the first great civilizations in ancient Egypt, the Middle East, the Mediterranean, China, and India.

Significant irregularities in $P\left(t\right)$ changes appear in Antiquity times. For the authors, this should not be linked to food shortages. This was the time of the formation of great empires, of which the Roman Empire was the most famous. Almost 1/3 of the global population lived there at the time. For $~500years$, from Julius Caesar's epoch to the Western Empire fall, the global population remained constant at $~200million$ [96,97]. It might suggest reaching the above-mentioned 'stationary phase' in the Verhulst model scaling, related to the limited available food. For the authors, the dominant cause was different and probably unique in history. The Empire's economy was primarily based on exploring slaves as a 'human energy source', on an enormous scale. For example, in the giant silver mines in the La Tinto region (present-day Spain), where tens of thousands of slaves worked. Their average survival time was only $~3months$ [97,98]. The Empire's weakening and 'barbarian' neighbors civilizational progress effectively limited the 'supply' of this 'raw material', so cruelly exploited. The global population began to grow again after the fall of the Roman Empire.

Starting with the advent of the Medieval times, permanent population growth occurred, as visible in Figure 1. For portraying the visible nonlinear pattern, the Super-Malthus (S-M) relation with time-dependent growth rate $r\left(t\right)$ was proposed in ref. [2]. It is given in the left-hand part of the relation below:

$$P\left(t\right)=P_{0}exp\left(r\left(t\right)\times t\right)=P_{0}exp\left({\displaystyle \frac{t}{\left(t\right)}}\right)\Rightarrow \tau \left(t\right)=t\times ln\left({\displaystyle \frac{P_0}{P\left(t\right)}}\right)$$

(7)

Notable that for $r\left(t\right)=r=const$ the S-M relation simplifies to the basic Malthus Equation (3). The next unique feature of this S-M relation is the time-dependent relaxation time, $\tau \left(t\right)=1/r\left(t\right)$. This magnitude, commonly used for testing dynamics in physics [12,13,14], enables a direct estimation of the time required for 50% changes from the population at a given moment, namely: $t_{1/2}=\tau \times ln2$. Nevertheless, direct parameterization of $P\left(t\right)$ changes via this S-M Equation (7) (left part) can be puzzling, since it requires in prior knowledge of $r\left(t\right)$ or $\tau \left(t\right)$ evolutions.

Nevertheless, one can use it for calculating temporal changes of the relaxation, as shown in the right-hand part of Equation (7). The evolution of this magnitude is shown in the inset in Figure 1. For such a plot the horizontal line is related to the basic Malthus Equation (3), with $r\left(t\right)=r=const$, or $\tau \left(t\right)=\tau =const$. Such behavior has been visible since the middle of Medieval times (~1100) till the Enlightenment period onset (~1700), with a distortion coinciding with the Black Death pandemic impact times [2,3,4]. For the authors, the extension of this ‘distortion’ into the 16th century can be related to the enormous population catastrophe in South America resulting from the Spanish conquest.

Since the year ~1710 till nowadays, emerges the linear trend described via $\tau \left(t\right)=a-bt$, as evidenced in the inset in Figure 1. Substituting it to S-M Equation (7) (left part), one obtains the unique crossover to the constrained critical scaling equation, given in Equation (1) (right part). It has been derived and extensively discussed in refs. [2,3].

How did food resources and their availability influence the population development during this period?

Generally, such discussion over a long period has to be puzzling due to huge civilization changes, cultural diversity, wars, and conquests, … However, the Malthus-type trend for the first period indicated in the inset in Figure 1 (1100 – 1719) suggests no essential global food availability problem, following the above discussion regarding the Malthus and Verhulst model. Of course, numerous famines or local population catastrophes are known during this period, but their global impact is relatively weak.

The measure of food availability can be the standardized income of a well-defined but relatively numerous group of employees, optimally in a country where such distortive factors as wars, conquest, and changes of borders … are negligible. Such conditions can be considered in England, for which almost constant earnings of building workers from $~1200$ to $~1840$ is evidenced Only later does a systematic increase in earnings appear [99,100,101]. For the authors, this can suggest a large 'rent of benefits' for industrialists in the 1^st Industrial Revolution epoch since the enormous increase in productivity in those times had a negligible impact on wages, the relative size of which had remained unchanged since the Middle Ages.

The Verhulst model approach might seem beyond the global population growth shown in Figure 1. However, one may consider a Verhulst-type equation associated with a set of $(r,s)$ associated with crossing subsequent barriers, occurring well before approaching the stationary phase. The effective portrayal of global population data since the Anthropocene onset was considered by Lehman et al. [102], who linked the crossover of subsequent eco- and bio-barriers. The problems and challenges of such an approach were further discussed in ref. [3]. Worth recalling here is the report by Cohen [79], who suggested that the basic Verhulst model dependence (left side of Equation 5) can indicate the following link between population growth and carrying capacity (metric of available resources). He named it the Condorcet equation [79]:

$${\displaystyle \frac{dK\left(t\right)}{dt}}=c\left(t\right){\displaystyle \frac{dP\left(t\right)}{dt}}=\left({\displaystyle \frac{L}{P\left(t\right)}}\right){\displaystyle \frac{dP\left(t\right)}{dt}}$$

(8)

where the coefficient ‘$c$’ is for the Condorcet parameter.

The above relation also contains the next Cohen’s suggestion to explain time dependence of the Condorcet parameter, namely $c\left(t\right)=L/P\left(t\right)$, where $L=const$, via the ‘dilution’ of the system-characteristic constant by the rising population. Cohen suggested that $L$ can be a metric of the total available resources, for instance. Starting from$c=1$, the parameter decreases in each subsequent time $t$, i.e., $c<1$. Finally, it reaches $c=0$, yielding the Verhulst model's stationary state. For $c<0$ carrying capacity, food resources, and consequently population diminishes. When $c>1$, each additional person in the population introduces additional values to the system carrying capacity above their own needs, thus yielding conditions to accelerate population growth, even a boost to infinity. Here, Cohen [79] tried to provide a link to von Foerster et al. Doomsday equation suggests an infinite global population 2026 (!) [74]. When publishing in 1960 it offered an impressing simple scaling equation of $P\left(t\right)$ changes since 400 BCE [76]. However, this scaling failed when more past data became available and when approaching the hypothetical Doomsday in 2026 [2,3,75].

Cohen in ref. [79] It offers an inspiring picture, although it is still heuristic since the basic premise of Equation (8) related to determining a numerical value of the Condorcet parameter c in subsequent stages of population growth remained challenging.

A preliminary response to this problem can be concluded from the recent reports of the authors devoted to the critical discussion of Verhulst-type scaling for the global population growth [3,4]. First, following ref. [102] by Lehman et al., and the discussion of its analytic counterpart in refs. [3,4], the general prevalence of the model analysis focused on the per capita relative growth rate (RGR) $G_P\left(t,P\right)=\left(1/P\right)\left(dP/dt\right)$ was shown [3,4]. Next the analysis directly resulted from the Verhulst model reference derivative Equation (5), explored via the plot $G_P\left(t,P\right)$ vs. $P$, revealed significant inconsistencies between model expectations and ‘empirical’ global population data [3,4]. It led to showing the prevalence of portrayal via the empowered Super Malthus relation introduced in ref. [2]:

$$P\left(t\right)=P_{0}exp{\left(t/\tau \right)}^{\beta }$$

(9)

It can be considered as the alternative to the S-M relation discussed above (Equations (1) and (7), which better estimates general trends. The distortions-sensitive analysis, in fact recalling $G_P\left(t\right)vs.t$ test focused on Equation (9), enables more subtle insight. It enabled insight into a subtle ‘bending up’ discrepancy from the general trend visible in the inset in Figure 1. Finally, it has been shown that in Industrial Revolutions epoch, the following behavior took place: from $~1710$ till $~1965-1968$: $\beta >1$, and later, till nowadays: $\beta <1$. At the indicated crossover the transition from $\beta \approx 1.5$ to still lasting domain described by $\beta \approx 0.85$ took place. [2,4]. This unique crossover even stronger manifests for $G_P\left(P\right)$ dependence, linking it to the global population $P\left(t\right)=3bilions$ [3,4]. Notable that the empowered exponential behavior is relatively common for complex physical systems, where the exponent $\beta >1$ is related to the ‘amplified’ development, associated with the ‘ordered nucleation centers’ and ‘internal energy’ creation. The stretched-exponential case $\beta <1$ is related to multichannel energy dissipation and is observed dominantly disordered system [2].

Considering these, we can see that the basic Cohen’s equation (8) contains the RGR factor. Following this, one can consider the following generalized Condorcet equation linking carrying capacity and population changes:

$${\displaystyle \frac{dK\left(t\right)}{dt}}=L\left(t\right){\displaystyle \frac{dP\left(t\right)/P\left(t\right)}{dt}}=L\left(t\right){\displaystyle \frac{dlnP\left(t\right)}{dt}}=L\left(t\right)G_P\left(t\right)$$

(10)

where $L\left(t\right)$ is the general effective metric of the system carrying capacity i.e., the new Condorcet parameter. For instance it is expressed via the exponent $\beta$ for $P\left(t\right)$ portrayal via the empowered Super-Malthus Equation (9).

The above discussion allows for a discussion of the planetary carrying capacity necessary for the development of the global population based on the values of exponent $\beta$, which have been given since the beginning of the Anthropocene in ref. [2]. Over the millennia until $~1700$ the dominant trend is described by the exponent $\beta =1$. This means that both population and resources increase ‘geometrically’, according to the simplest scaling relation of the Malthus model (Equations (2) and (3)). This may indicate that from the Neolithic Times to the Enlightenment onset, the most important resource remained food resources, and on a global average, each new member of the global population was able to introduce into the system as many new resources as needed. The ‘disruption’ in $P\left(t\right)$ changes in Antiquity times is commented in more detailed in ref. [2].

Since the Industrial Revolution's onset, the boosted population growth, which follows the Condorcet relation, is associated with boosted carrying capacity, related to $c,L,\beta >1$. In this unique epoch, subsequent groundbreaking technological innovations solve cumulated problems that could hinder further development. The scientific and technological breakthroughs opened up areas of exploitation of previously unexploited raw materials, significantly increasing global carrying capacity. An example is the 1st Industrial Revolution period, the Steam Age. It was first driven by wood as an energy source until large areas of Europe were deforested. The problem was solved by the exploitation of hard coal. When it turned out to be insufficient for new and necessary applications, from the mid-19th century, the use of oil and electricity as an energy source became important. The latter again increased the demand for coal as the most essential raw material for generating electricity. Within the years 1965-1968, the scaling of the global population changes has changed associated with the qualitative change of the Condorcet parameters $c,L,\beta <1$. This may mean a spontaneous reaction of the complex system of the global population to the global-scale constraints associated with approaching total carrying capacity limits. During this period, the world became a ‘global village’, and immediate contact between any two places on Earth became possible. There appeared to be a tangible limitation of available space for everyone, and the consequences of massively violated ecological constraints led to the already ongoing ecological catastrophe, including the great catastrophe of Global Warming. The answer to this great challenge, perhaps the greatest in human history, seems to be the tasks of the 5th Industrial Revolution.

The 5th Industrial Revolution is currently underway [23,24]. It is most often defined descriptively as a period of incorporating concepts of (i) sustainability, (ii) human-centeredness, and (iii) concern for the environment…. matched with AI development. This is a descriptive definition and different from the earlier stages of IR, where dominant breakthrough technology and/or scientific innovations were explicitly addressed. However, the term sustainability seems to include issues (ii) and (iii). Maybe the term 5th Industrial Revolution – sustainable development via new generation energy sources, material engineering, and AI implementation would better agree with the subsequent IR stages names.

Although the successive stages of the Industrial Revolution era opened up new ‘raw material’ resources or ‘carrying capacity’ [3,79] without recalling the dominant food resource in previous eras, it remained critically important, and its growth was also created by technological progress. This is the implementation of new technologies in agriculture, directly producing food, but also new food preservation technologies ensuring the health and safety of products and solving the great problem of increasingly complex logistics with a dramatically growing population. This was related to the discovery and mass implementation of new food preservation and processing methods. Of particular importance here were the great discoveries of Louis Pasteur [31], who identified the microbiological source of health hazards in food or beverages related to the presence of parasitic bacteria, fungi, or Yeats and indicated a way to reduce the hazard to a safe level by heating to a temperature of $~85°C$ [32]. Then came various chemical preservatives added to products [33], cooling and freezing [34], and radiation [35,36]. Therefore, the response to the great challenge of the gigantic population growth was characteristic of the New Brave World [103] of the Industrial Revolutions times: mass implementation of innovative technologies. Nowadays, the food problem may seem to be solved globally. The supermarket shelves show previously unknown assortment at prices accessible to the typical consumer. But this great success also has a dark side. New methods of food preservation and processing have proven to be the source of the pandemic on a global scale. New food preservation and processing methods can also be considered a significant cause of food waste, reaching $>40\%$ globally [49,50,51]. Reducing it is the simplest and most environmentally beneficial way to significantly increase available food resources and carrying capacity.

For the Industrial Revolutions epoch, the fundamental response to the following significant challenges is the implementation of breakthrough technologies. [23,24,25,26,27,28]. Below, we present the current state of the art and emerging possibilities for solving the food quality challenge and creating high-quality foods with explicit pro-health properties and pro-environment features. This is the high-pressure reservation/processing (HPP), which nowadays enables ‘cold’ pressure-assisted pasteurization, and for emerging innovations[5,7,8,52,53,54,55,56,57,58,59,60,61,62,63], sterilization is also used [7,8].

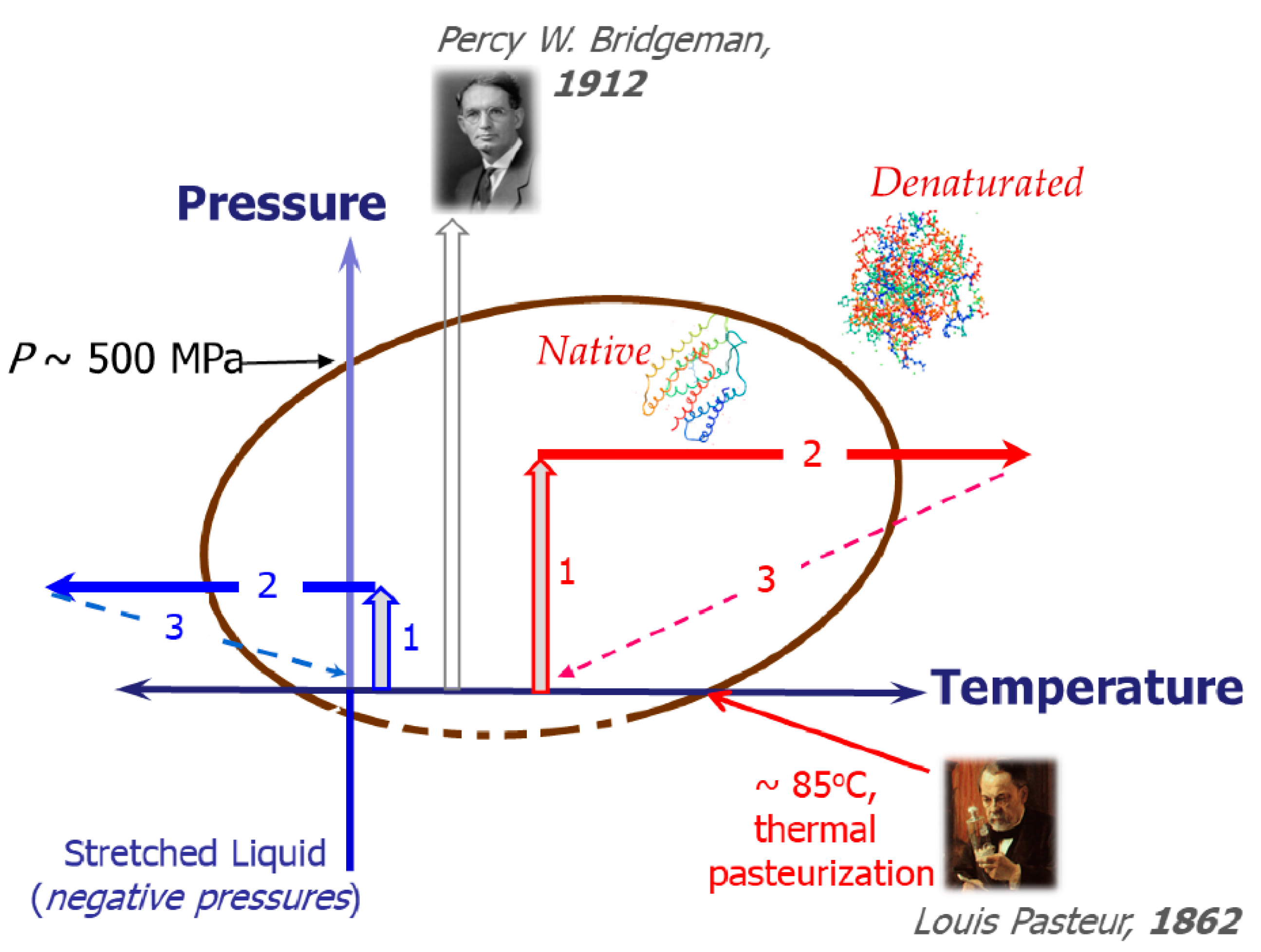
3.2. High Pressure Preservation / Processing of Food

Already in the Middle Pleistocene, pre-humans began to prepare food using fire [104,105]. This improved digestive properties but also reduced the impact of harmful microorganisms or worms. It, therefore, had a pro-health effect. It also extended durability, i.e., the time of consumption. These are the basic goals of all food preservation methods up to today. In subsequent times, increasingly complex methods appeared. This was probably fumigation and then pre-smoking [104,105]. Then, probably methods using natural environmental conditions such as low temperatures (freezing) or wind and low humidity (pre-freeze-drying) [106]. In the Anthropocene, more complex methods of food preservation appeared, mainly related to the processing of its form. For milk, it was sour milk, yogurts, butter, and buttermilk or cheeses, for which records appear as early as $~7000BCE$ [106,107,108]. Then, it was pickling, marinating, using salt and honey (sugar), … Increasingly complex recipes were also developed for the long-term use of meat in the form of hams or sausages [108]. It is also, in fact, the result of implementing ‘innovative technologies’ developed by generations of trial-error approaches and the extraordinary talents of generations of cooks. This huge set of products shapes today’s cuisine, which can be included in the category of ‘high-quality foods’ without exception, as long as natural products are used, as in the old days.

The Industrial Revolution began only 2 centuries ago. During that time, the global population has increased from $~600million$ to $~8.3billion$. It was also a time of previously unknown growth in agricultural productivity resulting from implementing broadly understood technological, biotechnological, and socio-economic innovations. On a global scale, a significant surplus of food appeared, and in the majority of countries, stores with previously unknown abundance and variety of products. Numerous and massive centers related to the implementation of new technologies have appeared. For this ‘New Brave World’, the supply of food, in adequate quantities and at least acceptable quality, has become a particularly significant task. In addition to the direct increase in agricultural production, it has become important to extend the product's shelf life and safety in increasingly complex logistics conditions. There has also been an increasing range of new and highly processed food products. There has been a need for a new generation of food preservation methods that ensure the health safety of the product with minimal impact on its ‘native’ form. They are thermal pasteurization and sterilization, a wide range of chemical preservatives, cooling and freezing [32,33,34,35,36,37,38]. These methods, whose references date back to the 19th century, are important factors in the current ‘abundance’ of food. However, these methods have become increasingly obvious over the past few decades that their mass implementation has led to new and dangerous problems on a global scale, namely [38,39,40,41,42,43,44,45,46]:

✓

Thermal pasteurization ensures microbiological safety, but at the same time, it often reduces the nutritional, vitamin, and bioactive properties of the products

✓

Chemical additives appeared to be directly related to pandemics of obesity, some types of cancer, allergies, skin problems, and intestinal problem

✓

Cooling and freezing are excellent preservation methods, but using technological solutions supports Global Warming.

✓

irradiation can effectively extend shelf life and improve safety by killing pathogens and insects. However, there are problems related to nutrient degradation and changes in taste and texture.

High-pressure preservation (HPP) technology, implemented for over 3 decades, offers a positive impact on the product without the above negative impacts, namely [7,8,52,53,54,55,56,57,58,59,60,61,62,63]:

• shelf-life extension to even up to 180 days!
• high microbiological safety
• fresh product taste, flavor, and texture
• fresh product vitamin composition
• bioactive and nutritional properties maintenance
• no chemical preservatives
• activation/deactivation of selected enzymes
• salt- and sugar limited/free products
• for ‘fluid’ and ‘solid foods
• application to packed food, reducing the risk of secondary contamination
• environment-friendly technology: (i) limited requirements for electric energy- (ii) practical lack of waste during processing, (iii) reduction of ‘expired products’ amount, and then disposal problems
• ‘clean label’, innovative technology

The HPP technology implemented on the market consists of the impact of high-pressure $P=300-600MPa$ for 3 to 15 minutes, generally at room temperature. Figure 2 shows HPP facility with the pressure chamber working volume $V=50L$ operating at arbitrary pressure up to $P=600MPa$. It shows the main pressure chamber body and automated system for closing and opening the chamber and loading the product. The pressure is supplied from an external high-pressure large-volume pump. The automated system is controlled from a panel in an adjacent, safety-isolated room.

Figure 3 shows the conceptual basis of HPP technology, showing an elliptical curve in the pressure-temperature ($P-T$) plane describing the limits of protein denaturation. The first point on this curve was observed by Louis Pasteur (1863), which gave rise to the technology of thermal pasteurization of food. It consists of reaching the denaturation limit (‘clumping’) of protein structures, which occurs at a temperature of $~85°C$. Such thermal treatment of the product leads to the denaturation of proteins in the parasitic organisms present, from worms to microorganisms. Today, the denaturation curve is associated with a 5-decade (${10}^{-5}$) reduction in the number of microorganisms [32] when presented on a logarithmic scale leads to the jargon term 5-log reduction.

The next point in the above curve can be linked to Percy W. Bridgeman compressing of the egg albumin under room temperature [109,110]. Smeller and Heremans plotted the denaturation via modeling using the Clausius-Clapeyron equation [111,112,113,114], implemented for the given process [115,116]:

$${{\displaystyle \frac{d{T}_D}{dP}}=T}_D{\displaystyle \frac{V}{L}}={\displaystyle \frac{V}{S}}$$

(11)

where $T_D$ is for the denaturation temperature at the given pressure and $L,V,S$ is for the latent heat, volume change and entropy change when passing $T_D\left(P\right)$ curve.

In ref. [116] the eliptic curve was obtained by assuming pressure-dependent evolution of $T_D\left(P\right)$, $V\left(P\right)$, $S\left(P\right)$. It is worth recalling here that the Clausius-Clapeyron equation was originally introduced for the melting-freezing discontinuous transition, i.e., $T_m\left(P\right)$. Thus, Smeller and Heremans essentially considered denaturation as a specific discontinuous phase transition.

The vertical arrows in Figure 3 shows standard paths related to HPP technology. Most often it is related to near-room temperature compressing, but generally operations in the range from $~4°C$ to $~50°C$ are considered. Notable that the thermal processing, recalled the thermal pasteurization, is related exclusively to passing the denaturation curve under atmospheric pressure.

The effect of pressure on food and unwanted microorganisms is more complex. At room temperature, compression to $300-400MPa$ usually causes rupture of cell membranes surrounding microorganisms and/or organelles inside, associated with relatively weak intra-structural interactions. This is the most commonly used mechanism in HPP technology. It leads to a 3-5 decades (3-5 log) reduction of parasitic microorganisms while maintaining all the special advantages of this technology listed above [7,52]. An example here is the thermal pasteurization of milk, creating a product with a different taste than native milk and reduced bio-nutritional values. 'Cold' pressure pasteurization at room temperature, with compressing to $~400MPa$ creates pasteurized milk with the taste and all the advantages of 'native' milk. The compression of milk to $~600MPa$, associated with achieving the denaturation curve and subsequent decompression, leads to a deeper reduction in the number of microorganisms, a change in taste, and a reduction in bio-nutritional values but a significantly lesser extent than in the case of thermal treatment at atmospheric pressure [7,52].

Thermal pasteurization, which is commonly used today, significantly reduces but does not eliminate unwanted microorganisms. A pasteurized product, therefore, has a naturally limited shelf life related to microbiological safety.

For many food products, technological sterilization is used [32], which consists of heating the product for the shortest possible time - optimally a few/a dozen seconds - to temperatures in the range of $120-150°C$. This is not full sterilization, as it requires much higher temperatures and times and is used, for example, in medicine. However, technological sterilization of food allows for extending the product's shelf life that is safe for health to a year or more. It is also possible and used to 'support' this shelf life by minimizing the addition of chemical preservatives or the appropriate pH of the product [32].

3.3. Compression – Related Sterilization

Sterilization with the support of high-pressure compression is a problematic issue for HPP processors on a pilot or industrial scale (see Figure 2). Commercially available is a solution where the food product after heating to $~90°C$ is placed in a thermally insulated container (adiabatic conditions), which is then moved to a high-pressure chamber where compression to $P~600MPa$ takes place. This is adiabatic compression, leading to a change in the internal energy of the product and, as a consequence, a temperature increase of $~30°C$. The product under pressure reaches an effective temperature of $~120°C$ and after $10-15minutes$ decompression occurs, which lowers its temperature again to $~90°C$ and at this temperature the product is removed from the chamber [117,118].

For such a technological concept, significantly deeper 'technological sterilization' should be expected than with the standard thermal procedure described above. However, for the ‘pressure assisted sterilization’ technology described above, the product is at an elevated temperature for a very long time, above the denaturation limit determined by the $T_D\left(P\right)$ curve. Together with the compression and decompression time in the high-pressure chamber, this can be even several dozen minutes. Therefore, a significant reduction in nutritional value and bioactivity must occur. This is no longer mild HPP technology like for ‘cold, pressure’ pasteurization, with the avoided features mentioned above.

Recently, the authors of this paper have presented two innovative concepts that limit or even eliminate the above disadvantages and give hope for pressure-assisted sterilization with ‘mild-impact’ features. It involves using the so-called Colossal Barocaloric Effect (CBE) [119,120] ], recently discovered in some materials from the Soft Matter family, especially the so-called Plastic Crystals. A strongly discontinuous phase transition is described by the Clausius-Clapeyron relation (Equation (10)), with colossal latent heat value. In adiabatic conditions (thermally insulated container), in the standard situation of the system where $d{T}_m/dP>0$, this means the release of heat into the interior of the adiabatic container where the $T_m\left(P\right)$ line is exceeded due to compression. As a result, there is a strong increase in temperature in the container where the element containing the material exhibiting the CBE phenomenon is placed. Upon decompression, there is a corresponding immediate decrease in temperature. This process is shown in Figure 3 with two red arrows, showing subsequent stages of the innovative CBE-assisted compression-related sterilization. There are also Soft Matter systems with the strongly discontinuous phase transition where compressing decreases the transition temperature, i.e., they are related to $d{T}_m/dP<0$ condition: this is the base of the inverse barocaloric effect [121]. For such systems, compression causes the absorption of heat energy from the environment under adiabatic conditions, which means a decrease in temperature. Decompression of course means the release of heat to the environment, when passing the $T_m\left(P\right)$ line of discontinuous phase transitions, and an increase in its temperature. Such a ‘reversed CBE’ process creates a unique possibility of crossing the $T_D\left(P\right)$ denaturation line when the temperature is reduced, and therefore a new type of ‘truly cold’ pasteurization or sterilization of food. The stages of this process are shown by two perpendicular blue arrows in Figure 3.

The feasibility analysis of the above CBE-assisted HPP solutions is given in refs. [7,8]. Notable that they offer a precisely controlled, solely by the applied pressure value, time of acting the process-significant (high or low) temperature. Moreover, it can be implemented in existing HPP industrial-scale processors. For product operations, the significant fact is that the product introduced to the chamber can be at near–room temperature, and it is the same when the product is removed.

4. Conclusions

12 thousand years ago, the Anthropocene began. Thanks to increasingly favorable climatic conditions, homo sapiens gained extraordinary development opportunities. People exhibit exceptional inclinations towards strong and multidimensional mutual interactions. Consequently, and, as for any non-homogeneous complex system with such characterizations, one can expect the spontaneous appearance of 'heterogenic structures,' which in this case can only mean the organized clusters of people. Recent discoveries in ​​Göbekli Tepe and Çatalhöyük (​​present-day Turkey) revealed surprisingly large and highly developed quasi-urban centers could dated even to ~ 9,000 BCE.

For every person, both in the Neolithic era and today, the most crucial goal of each subsequent day is to provide food for themselves and their family. The answer to the question of how these needs were shaped in the Anthropocene, the ‘era’ of humans, is puzzling and ambiguous due to variable geographical, climatic, and cultural conditions… However, one may expect that such a message can be indirectly deduced from an appropriate scaling description of global population changes.

This issue is discussed in the first part of this paper from the perspective of Malthus [67], Verhulst [71], the super-Malthusian extension modeling [2,3], and the concept of carrying capacity introduced by Pearl and Reed [72,73]. Attention is drawn to its use via the 'Condorcet' relation concept, proposed by Cohen (1995) [79] - linking carrying capacity with global population changes. In this report, the extension of this relation is proposed, using the results of the authors' recent work, which allows for the direct estimation of the Condorcet coefficient metric with the support of the Super-Malthusian description [2,3,4]. The presented analysis indicates that from the beginning of the Anthropocene to the end of the 17th century a simple geometric growth of the global population dominated, although with a variable time constant ($r,$) in different periods. Disturbances appear in the times of Antiquity or the Black Death times. they are commented on in refs. [2,3,4] and above in the given report.

The analysis using the 'Condorcet model' suggests that the resources (food) needed for the Malthus-type growth increase at the same rate as the population.

Two centuries ago, an extraordinary acceleration in the global population growth has started. Despite this boost, no Malthusian Catastrophe, or a generic global food shortage occurred. On the contrary, there a kind of food surplus took place. Moreover, food prices began to fall, and employment in agriculture was reduced even below 10% of the total number of employees in many countries.

The last 200 years are the times of a new era of Industrial Revolutions. For the first time in history, massively implemented breakthrough inventions and technologies, supported by modern science based on the conceptual-philosophical basis of the Scientific Method, solved civilizational challenges. This would not be possible without feedback interactions with the subsequently implemented ‘socio-economic innovations’ changing societies and managers.

At that time, the concept of carrying capacity ceased to be dominated by food, an energy source directly addressed to every person. Also, raw materials and energy sources became important for the increasingly pervasive ‘technology’ of subsequent Industrial Revolution epochs. There was also a huge impact of a resource rarely considered in earlier eras: shortages of raw materials, energy, or pollution permanently devastating the planet, its climate, and biosphere. The discussion in recent reports [2,3,4,7,8], briefly recalled above, shows that the complex system of the global population has been spontaneously sensing and reacting to this existential problem since the mid-1960s.

However, the current abundance of the most important resource for humans – food, might be illusory. It is mainly based on food preservation methods that have a devastating, even pandemic, effect on society. There is also an exceptionally unfavorable connection with popular industrial highly processed food, referred to as ‘junk food.’

However, it is possible to answer these civilizational challenges within the general scheme of the Industrial Revolution era – development and implementation of Innovative Technologies.

This paper presents the basics of such a technology: High Pressure Preservation/Processing (HPP). The currently existing version of High Pressure ‘Cold’ Pasteurization has already passed the market validation test. It is a market for HPP products worth ~600 million USD, based on several hundred industrial-scale HPP processors and the industry offering solutions in this area [122]. The characteristics of products after HPP processing show a surprising coincidence of customer and producer needs, namely the quality of the fresh product, without preservatives, with extended durability. The inherent waste reduction is important for the environment, as are the disposal costs. There is also an option to extend this technology HPP – pressure assisted sterilization, with CBE concept support – discussed above and in refs. [7,8] It seems possible, therefore, to offer food in a scheme perfectly in keeping with the goals of a ‘sustainable society’ and even to fulfill the great desire of the father of medicine, Hippocrates of Kos (460-375 BCE) [123]: ‘Let food be thy medicine and medicine be thy food’.