Ordinal Random Processes

1. Introduction

1.1. Contents of the Paper

In this introductory section, we introduce the basic concepts in a brief manner. For more detail and background, we refer to ([1] Section II) and [2,3,4,5,6,7]. A new point is the visualization of the distribution of ordinal patterns as refining ordinal histogram in Section 1.4. The main topic of the paper is explained in Section 1.6. Order-related properties of processes, in particular order self-similarity, are introduced in Section 1.7.

Section 2 deals with a paradigmatic example of an ordinal process which has no numerical values. The construction is algorithmic and intuitive, and the probabilities for patterns of length 3 are the same as for Brownian motion. Unfortunately, the example is not self-similar and not relevant for applications. We conjecture that there is a self-similar modification.

The final Section 3 gives a more technical outline of a possible theory of ordinal processes. We construct stationary ordinal processes without using numerical values. Order self-similarity remains an open problem.

1.2. Permutations as Patterns in Time Series

A permutation $\pi$ of length m is a one-to-one mapping from the set $\{1,2,...,m\}$ onto itself. We write ${\pi }_k$ for $\pi \left(k\right)$ and $\pi ={\pi }_1{\pi }_2...{\pi }_m.$ Thus $\pi =231$ means $\pi \left(1\right)=2,\pi \left(2\right)=3,\pi \left(3\right)=1.$ However, we do not need mapping properties of permutations like composition. We just consider the graph of $\pi$ as a geometric pattern - an ordinal pattern.

With $x=x_1,x_2,...,x_T$ we denote a time series of length $T.$ It is also a mapping, assigning to the time points $t=1,...,T$ the values $x_t=x\left(t\right).$ For m time points $t_1<t_2<...<t_m$ between 1 and T we consider the pattern of corresponding values. We define

$$(x_{t_1},x_{t_2},...,x_{t_m}) \mathrm{shows} \mathrm{pattern} \pi \mathrm{when}{x}_{t_i}<x_{t_j}\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} {\pi }_i<{\pi }_j.$$

(1)

In other words, the correspondence $x_{t_j}\to {\pi }_j,j=1,...,m$ is strictly monotonous. This is very intuitive. The pattern $\pi$ can be determined from the time series by calculating ranks: ${\pi }_k$ is the number of time points $t_j$ for which $x_j\le x_k.$

1.3. Pattern Frequencies in Time Series

Instead of arbitrary $t_j,$ we study equally spaced time points $t<t+d<t+2d<...<t+(m-1)d.$ We call m the length and d the delay or lag of the pattern. We always take $m\le 6$ and mainly consider $m=3$ and $m=4.$ However, we vary d as much as possible.

Ordinal pattern analysis is a statistical method. We fix a length m and determine relative frequencies of all patterns $\pi$ of length $m,$ for various delays $d.$ We divide the number of occurences of $\pi$ by the number of time points where $\pi$ could occur.

$$p_{\pi }\left(d\right)={\displaystyle \frac{1}{T-(m-1)d}}\#\left\{t\right|1\le t\le T-(m-1)d,(x_t,x_{t+d},...,x_{t+(m-1)d}) \mathrm{shows} \mathrm{pattern} \pi \}.$$

(2)

These frequencies are the basic parameters of ordinal time series analysis. They can be combined to calculate permutation entropy, persistence, and other important parameters [1,2,3,4,5,6,7].

1.4. Visualization of Pattern Frequencies by an Ordinal Histogram

This paper is not about parameters like entropy. It studies models for all pattern frequencies together. For this reason, we here introduce a graphical method to subsume the pattern frequencies for fixed d in a kind of density function. The permutations $\pi$ are assigned subintervals $I_{\pi }$ of $[0,1]$ as follows: $I_{12}=[0,{\displaystyle \frac{1}{2}}],I_{21}=[{\displaystyle \frac{1}{2}},1].$ We draw bars over $I_{\pi }$ which have area $p_{\pi }\left(d\right).$ For $m=3,$ we note that $p_{12}=p_{123}+p_{132}+p_{231}$ (neglecting a possible tiny error due to the last value for $p_{12}\left(d\right)$ in (2)). We choose $I_{123}=[0,{\displaystyle \frac{1}{6}}],I_{132}=[{\displaystyle \frac{1}{6}},{\displaystyle \frac{1}{3}}],I_{231}=[{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{2}}]$ so that their union is $I_{12}.$ Then we again draw bars with area $p_{\pi }\left(d\right).$ The same is done for $\pi =213,312,321.$ In this way, the histogram for $m=3$ is a refinement of the histogram for $m=2.$ Sukzessive refinements can be obtained for $m=4,5,...$ although the length of the time series will rarely allow reliable estimates for $m>4.$ This arrangement of permutations is called hierarchical order. Details will be given in Section 3.4. As Figure 1 shows for a simulated time series, all pattern frequencies of a time series for a fixed d can be subsumed in this way by a sequence of refining histograms, or in the limit $m\to \infty$ by a kind of density function.

The process chosen for Figure 1 is an AR(1) model with exponential noise: $X_{t+1}={\displaystyle \frac{1}{2}}{X}_t-log{U}_t,$ where the $U_t$ are independent uniformly distributed random numbers in $[0,1].$ Due to the asymmetry of the noise distribution, $p_{21}\left(1\right)\approx 0.58>{\displaystyle \frac{1}{2}}.$ Sukzessive decreasing steps are frequent: $p_{321}\left(1\right)\approx 0.3$ and $p_{4321}\left(1\right)\approx 0.13.$ We cannot explain why 2143 is the permutation with the second largest frequency. However, an AR(1) model with coefficient ${\displaystyle \frac{1}{2}}$ has a short memory. For $d=3$ the patterns already have almost uniform frequencies. The models considered below are more uniform for $m=2$ and 3, but they provide interesting behavior also for large $d.$

The problem of this paper is to find typical ordinal histograms from a theoretical viewpoint. An important question is to find models where the histograms agree for all $d.$ Two such models are known ([1] Section II.C): white noise, where the histogram is a constant function for all $m,$ and Brownian motion, see Figure 3 below. We are looking for other models.

1.5. Stationary and Order Stationary Processes

In time series analysis, we do always assume that the given time series is an instance of a larger ensemble, called a stochastical process. The process represents the mechanism which generates the given time series and many other ones. We want to know the laws of this process. Formally, a stochastical process X is a sequence $X=X_1,X_2,...$ of real random variables on a probability space $(\mathsf{\Omega },P).$ The time series x is a random choice from the ensemble $X.$

To find the laws of X from one single time series, we must assume that the distributions and dependencies of the $X_k$ do not change in time. Usually X is required to be stationary. That is, the m-dimensional distribution of $(X_t,X_{t+1},...,X_{t+m})$ does not depend on $t,$ for all $m.$ This assumption is very strong. When we study autocorrelation, we assume weak stationarity. That is, the mean $M\left(X_t\right)$ and the covariance $Cov(X_t,X_{t+k})$ do not depend on t [8]. When we consider ordinal patterns, we assume a similar very weak stationarity assumption. It will be required throughout this paper.

Order stationarity. For a given pattern $\pi$ with length m and delay $d,$ let

$$P_{\pi }\left(d\right)=P\left\{(X_t,X_{t+d},...,X_{t+(m-1)d}) \mathrm{shows} \mathrm{pattern} \pi \right\}$$

(3)

denote the probability that the process X shows pattern $\pi$ just after time $t.$ We say that the process X is order stationary for patterns of length m if $P_{\pi }\left(d\right)$ is the same value for all $t.$ This should hold for all patterns $\pi$ of length m and all delays $d=1,...,d_{\max }$ where $d_{\max }$ is chosen much smaller than the length T of our time series.

Brownian motion (where $X_0=0$ and $X_{t+1}-X_t$ are independent increments with standard normal distribution for $t=0,1,...$) is an order stationary process which is not even weakly stationary. It is a basic model for financial time series. Note that the process X and the pattern probabilities $P_{\pi }\left(d\right)$ are theoretical objects. The observed frequency $p_{\pi }\left(d\right)$ is an estimate for $P_{\pi }\left(d\right),$ and from the viewpoint of theory, the estimator formula (2) has nice properties [9,10,11,12,13]. The practical success of ordinal patterns indicates that the assumption of order-stationarity is at least approximately fulfilled in applications.

1.6. The topic of this paper.

There are plenty of well-studied stochastic processes: Gaussian processes, random walks, ARMA and GARCH processes, processes with long-range dependence [11,14] etc. Most of them are either stationary or have stationary (multidimensional) increments and so are order stationary. They are defined by arithmetical operations, however. This makes the rigorous study of ordinal pattern frequencies difficult although various interesting theorems could be derived [9,10,11,15,16]. Even for Brownian motion, exact frequencies of patterns can be determined only for $m\le 4$ [17]. Some of them are rational, some irrational. Frequencies for length 5 lead to integrals which can be only numerically calculated. On the whole, the impression is that ordinal patterns do not fit into the established theory of stochastic processes.

The only proper theoretical model for pattern frequencies is white noise, a process of independent and identically distributed random variables $X_i.$ For each $m,$ all permutations have the same probability $p_{\pi }=1/m!$ for any delay $d.$ This model was repeatedly used as null hypothesis for testing serial dependence of time series [1,12,13,18,19,20,21]. A greater variety of models is needed.

In this paper, we try to define ordinal random processes in a combinatorial way, directly by their ordinal pattern frequencies. We do not require normal distribution, we require no arithmetics, and we even do not need numerical values to compare objects $X_i$ and $X_j.$ An algorithmic example in the next chapter will show that this is possible. In Section 3, we outline some technical concepts and basic statements for a theory of ordinal processes. This could be a first step towards finding more applicable ordinal models. Note that possible equality of values, an important problem in practice [21], plays no role in this paper: our models will only allow $X_s<X_t$ or $X_s>X_t$ but not $X_s=X_t.$

1.7. Symmetry and Independence Properties of Ordinal Processes

Of course it is not enough to just postulate pattern frequencies. Our models should also have nice properties. Here we list the ordinal version of some of the most common process properties. We start with symmetry in time and space [9].

A process X is reversible if the distributions of $(X_1,...,X_m)$ and $(X_m,...X_1)$ agree for every $m.$ In the ordinal version, it is reversible if the permutations $\pi ={\pi }_1{\pi }_2...{\pi }_m$ and ${\pi }_m{\pi }_{m-1}...{\pi }_1$ have the same pattern probability for every $\pi .$ The process X is invariant under reversal of values if the distributions of $(X_1,...,X_m)$ and $(-X_1,...-X_m)$ agree for every $m.$ The ordinal version states that the permutations $\pi ={\pi }_1{\pi }_2...{\pi }_m$ and $(m+1-{\pi }_1)(m+1-{\pi }_2)...(m+1-{\pi }_m)$ have the same pattern probability for every $\pi .$

In both cases, the ordinal versions of symmetry are much weaker and much easier to check. These symmetry properties are often met in applications. As a consequence, the distribution of ordinal patterns of length 3 often has only one degree of freedom, since $p_{123}=p_{321},$ and the probabilities of the other four permutations agree. All Gaussian processes are symmetric in space and time [9,11,17].

A process X is said to be Markov if for any t and fixed $X_t,$ the distributions of $(X_1,...,X_{t-1})$ and $(X_{t+1},X_{t+2},...)$ are independent. In the ordinal version, this means that the appearance of patterns $\pi ,{\pi }^{\prime }$ at times $t_1<...<t_m\le t$ and $t\le t_1^{\prime }<...<t_m^{\prime },$ respectively, are independent. Again, the ordinal property is weaker and easier to check. The Markov property appears in theory rather than in applications. It implies that $P_{12...m}={\left(P_{12}\right)}^m$ which is too large to occur in practice, even in financial data.

Order self-similarity. The most important symmetry property in this paper is order self-similarity ([22] Section 6). A random process in continuous time, $Y_t,t>0$ is said to be self-similar if there is an exponent $H>0$ such that $Y_{rt}=r^H{Y}_t$ in distribution, for each positive number r [23]. Such a process cannot be stationary, it must look similar to Brownian motion. The ordinal concept is weaker and much simpler.

A process X is said to be order self-similar for patterns π of length m if

$$P_{\pi }\left(d\right) \mathrm{is} \mathrm{the} \mathrm{same} \mathrm{value} \mathrm{for} \mathrm{all} d.$$

(4)

This should hold for all patterns $\pi$ of length m and all delays $d=1,...,d_{\max }$ where $d_{\max }$ is chosen much smaller than the length T of our time series.

Order self-similarity was verified in financial time series [22] and EEG measurements [1]. Our paper is motivated by the desire for models of this behavior.

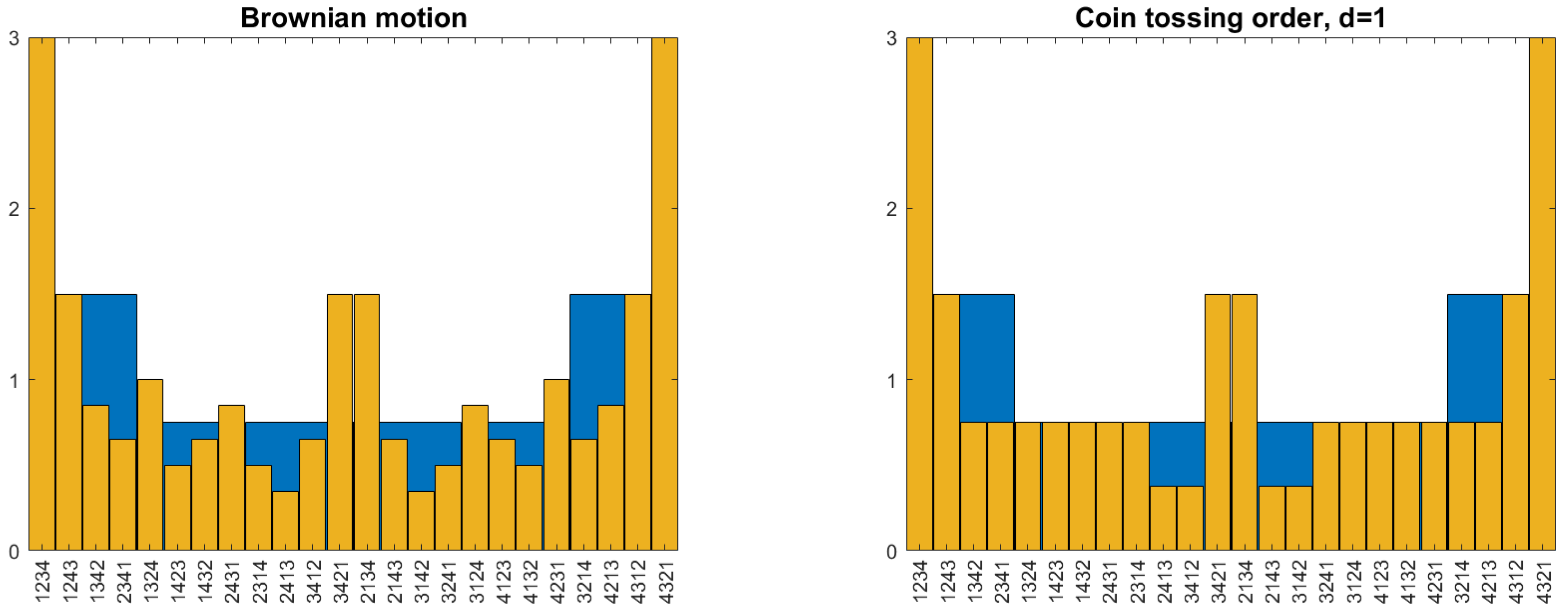
2. The Coin-Tossing Order—An Ordinal Process Without Values

2.1. Ranking Fighters by Their Strength

Ordinal patterns were derived from numerical values of a time series. Now we go the opposite way, as in the world of tennis or chess where players first pairwise compare each other and afterwards are assigned a rank or ELO score. Suppose there are four players $A,B,C,D$ in a tennis club. We design an algorithm to order them by strength. First B plays against $A.$ Let us assume B wins. Then we write $A<B.$ Now the next player C plays against the previous player $B.$ If C wins, then $A<B<C$ by transitivity of order. If C loses, however, C must still play against $A.$ Depending on the result, either $A<C<B$ or $C<A<B.$ Now the last player D comes and plays first against the previous player $C,$ and then against B and/or $A,$ if the comparison is not yet determined by previous games and transitivity.

This procedure will be turned into a mathematical model. We want to construct a random order between objects $X_1,X_2,...$ which are not numbers. We follow the algorithm for tennis players, and replace each match by the toss of a fair coin. As a result we obtain a stochastic process like white noise or Brownian motion, on ordinal level only. It will be possible to determine pattern probabilities much better than for Brownian motion.

2.2. Definition of the Coin Tossing Order

Repeated toin cossing is a standard way to represent randomness. Take a simple random walk, for example, and write $X_n$ for our position at time $n=0,1,2,...$ Then $X_0=0,$ and either $X_{n+1}=X_n+1$ or $X_{n+1}=X_n-1$ depending on the result of a coin throw at time $n.$ In the present case, $X_1,X_2,X_3,...$ will denote objects, not necessarily numbers. We define a random order between the $X_i.$ We throw a fair coin $c_{ji}$ to decide whether $X_i<X_j$ or $X_i>X_j,$ for any pair of integers $i<j.$ Let us write 1 for `head’ and 0 for `tail’. Then our basic probability space $\mathsf{\Omega }$ is the space of all 0-1-sequences, where each coordinate is 0 or 1 with probability ${\displaystyle \frac{1}{2}},$ independently of all other coordinates. Formally,

$$\mathsf{\Omega }=\left\{(c_{21},c_{32},c_{31},c_{43},c_{42},...)\right|c_{ji}\in \{0,1\} \mathrm{for} j>i\ge 1\}$$

where $c_{ji}=0$ means $X_i<X_j,$ and $c_{ji}=1$ means $X_i>X_j,$ for $1\le i<j.$ The important point is that $c_{ji}$ will be disregarded when the order of $X_i$ and $X_j$ is already fixed by previous comparisons and transitivity.

The first coin $c_{21}$ decides the ordering of $X_1$ and $X_2.$ Now suppose $X_1,...,X_{j-1}$ are already ordered. Then $X_j$ is compared to $X_{j-1},X_{j-2},...,X_1$ by considering the random numbers $c_{ji}.$ However, when the comparison is fixed by transitivity from the already defined ordering, then $c_{ji}$ is disregarded - that coin need not be thrown.

The resulting random order will be called coin tossing order. It can be easily simulated. Figure 2 shows rank numbers of 500 consecutive objects $X_j$ in the middle of a simulated series of length $T=10000.$ The global rank numbers have strange discontinuities. Local rank numbers, obtained by comparing with the next 20 objects on the left and right, show a more familiar picture.

Problem. Is there a stochastic process with stationary increments which generates the coin tossing order?

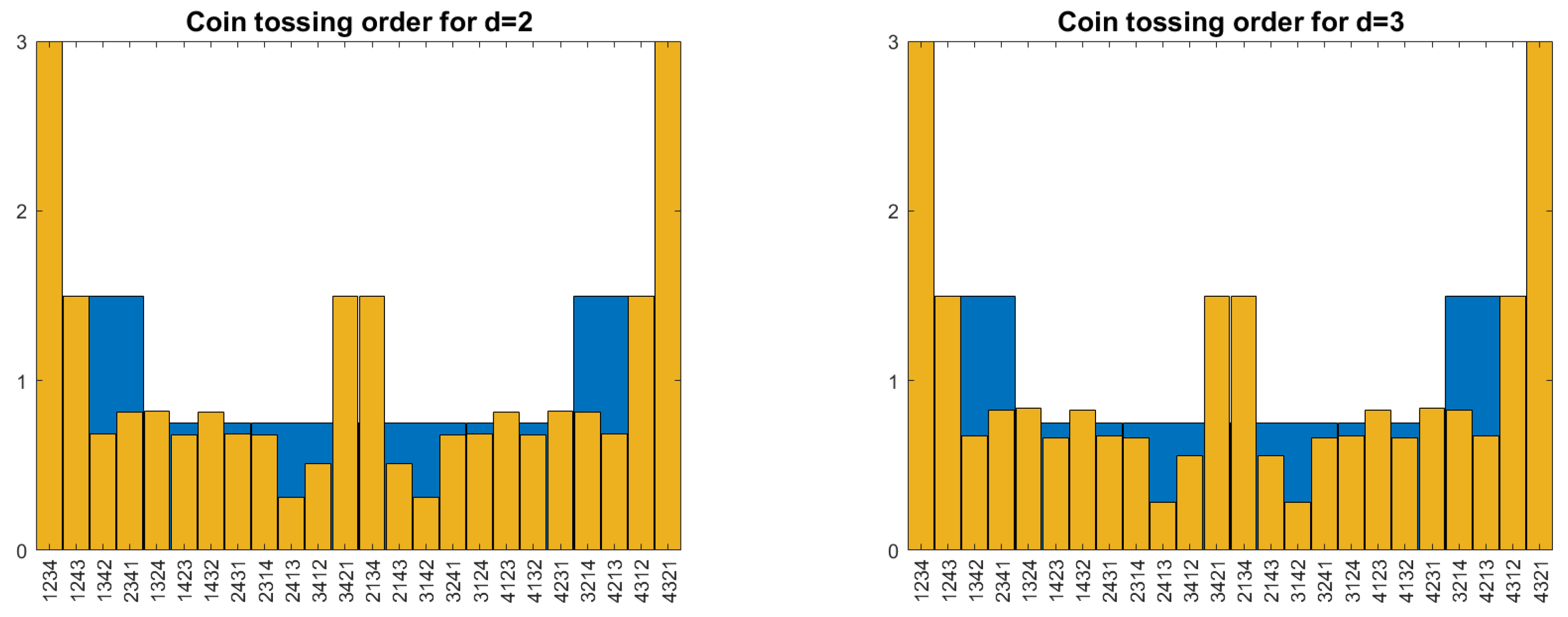
2.3. Basic Properties of the Coin Tossing Order

Despite the erratic view of trajectories in Figure 2, it turns out that the coin-tossing order has the same ordinal pattern frequencies for length 3 as Brownian motion, for arbitrary $d.$ In particular, it is order self-similar for patterns of length 3.

Theorem 1 

(Basic properties of the coin tossing order).

(i) 

The coin tossing order is stationary and has the ordinal Markov property.

(ii) 

For any permutation π of length $m,$ the pattern probability is $P_{\pi }\left(1\right)=2^{-u}$ with

$$u=u\left(\pi \right)=\#\left\{(i,j)\right|1\le i<j\le m, if i<k<j then {\pi }_k is not between {\pi }_i and {\pi }_j\}.$$

(5)

(iii) 

The pattern probabilities $P_{\pi }\left(d\right)$ are invariant under time reversal and reversal of the values.

(iv) 

For $d=1,2,....$ we have $P_{12}\left(d\right)={\displaystyle \frac{1}{2}},P_{123}\left(d\right)=P_{321}\left(d\right)={\displaystyle \frac{1}{4}},$ and $P_{\pi }\left(d\right)={\displaystyle \frac{1}{8}}$ for the other permutations of length 3.

Proof. (i): The order of $(X_t,X_{t+1},...,X_{t+m-1})$ depends on the random numbers $c_{ji},t+m-1\ge j>i\ge t,$ in the same way as the order of $(X_1,X_2,...,X_m)$ depends on the $c_{ji},m\ge j>i\ge 1.$ Since both collections of random numbers have the same distribution, the pattern probabilities do not depend on $t,$ and the defined random order is stationary. Moreover, the comparisons of $X_s$ with $s\ge t$ depend on random numbers $c_{ji}$ with $j>t$ while the comparisons of $X_s$ with $s\le t$ depend on $c_{ji}$ with $j\le t.$ Since different $c_{ji}$ are independent, this implies the ordinal Markov property.

(ii): $u\left(\pi \right)$ is the number of coin flips needed to determine $\pi .$ Given a permutation $\pi ,$ we determine the $c_{ji}$ which are needed to define the occurence of $\pi$ in $(X_1,X_2,...,X_m).$ Of course $m\ge j>i\ge 1,$ and j runs in increasing order. For fixed $j,$ the number $c_{j,j-1}$ is always used, and the other i are considered in decreasing order. Now consider some k with $i<k<j.$ If ${\pi }_i<{\pi }_k<{\pi }_j,$ this was determined by the random numbers $c_{ki}$ and $c_{jk}$ which were drawn before $c_{ji}.$ In that case $c_{ji}$ is disregarded since ${\pi }_i<{\pi }_j$ follows from the transitivity of the order. Similar for ${\pi }_i>{\pi }_k>{\pi }_j.$ However, if there is no ${\pi }_k$ between ${\pi }_i$ and ${\pi }_j,$ then $c_{ji}$ is needed to determine $\pi .$ We shall call $u\left(\pi \right)$ the energy of $\pi .$

(iii): First we consider $d=1.$ Given $\pi ,$ we have to show that the time-reversed and spatially reversed permutations have the same energy $u\left(\pi \right).$ For spatial reversal this directly follows from the definition (5) with `between’. For time reversal, we show that $P_{\pi }\left(1\right)$ can also be determined backwards by considering the $c_{ji}$ with decreasing $i=m-1,m-2,...,1,$ and for fixed $i,$ with increasing $j=i+1,...,m.$ The point is that when we compare places $i<j,$ we have already compared both j and i with all k between. So $c_{ij}$ is needed only if no ${\pi }_k$ is between ${\pi }_i$ and ${\pi }_k.$ Otherwise the order between ${\pi }_i$ and ${\pi }_j$ is already fixed, and $c_{ij}$ is disregarded. This proves reversibility for $d=1.$

Now consider $d>1$ and some $\pi$ of length m which appears as pattern of $(X_1,X_{1+d},...,X_{1+(m-1)d}).$ The probability of this event is $P_{\pi }\left(d\right)$ which may be different from $P_{\pi }\left(1\right).$ We have to calculate $P_{\pi }\left(d\right)$ from all `atom permutations’ of length $M=1+(m-1)d$ for $(X_1,X_2,...,X_{1+(m-1)d})$ for which the order among the special m places agrees with the order of $\pi .$ This would be a lot of work. However, since the reversed permutation of $\pi$ is composed of the reversed `atom permutations’, both in space and in time, we shall get the same pattern probability.

(iv): The spatial reversal invariance implies $P_{12}\left(d\right)=P_{21}\left(d\right)={\displaystyle \frac{1}{2}}.$ Then $P_{123}\left(d\right)=P_{321}\left(d\right)={\displaystyle \frac{1}{4}}$ follows from the Markov property. The equality of the four other pattern frequencies is a consequence of the invariance under time and space reversal. □

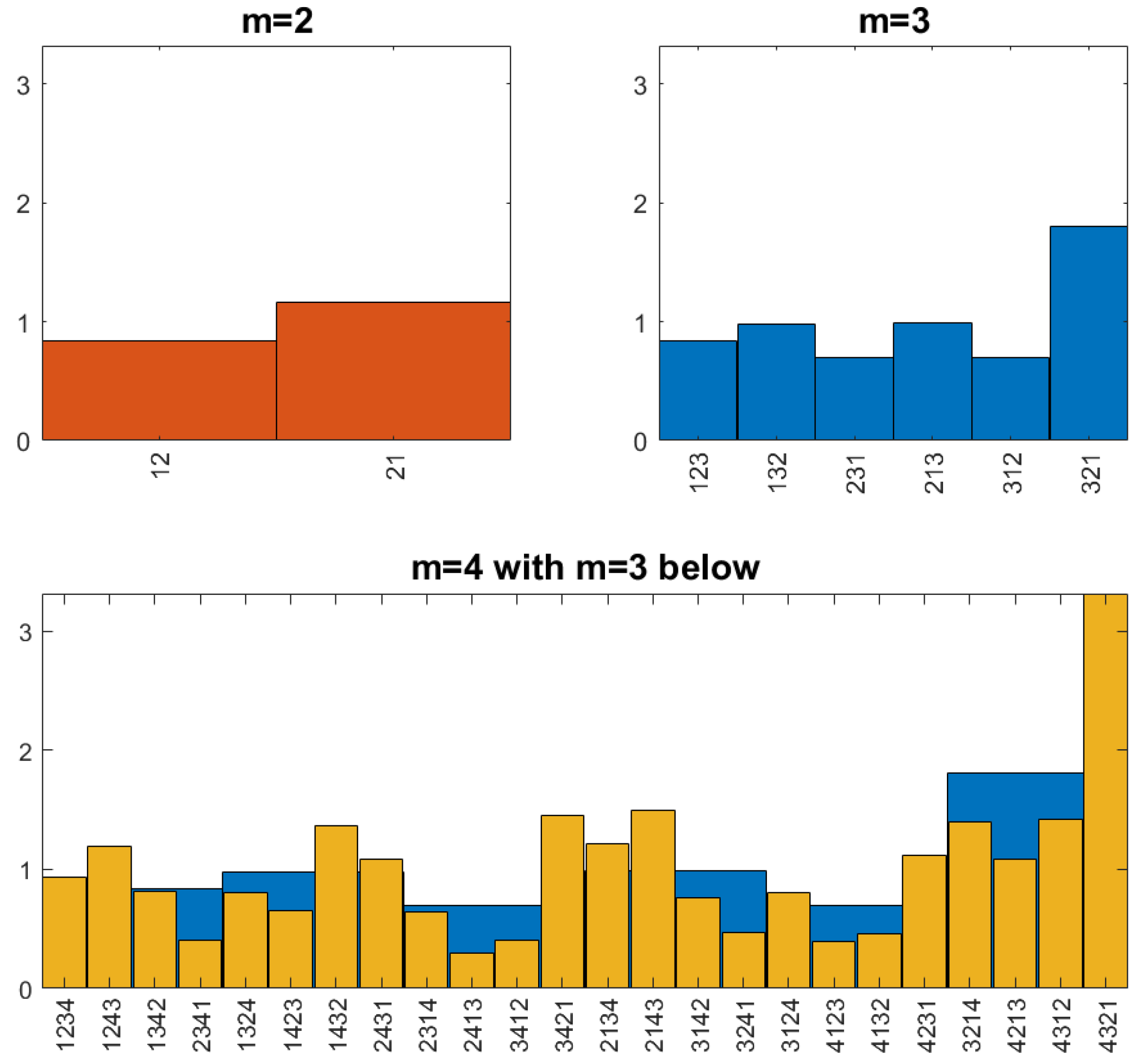
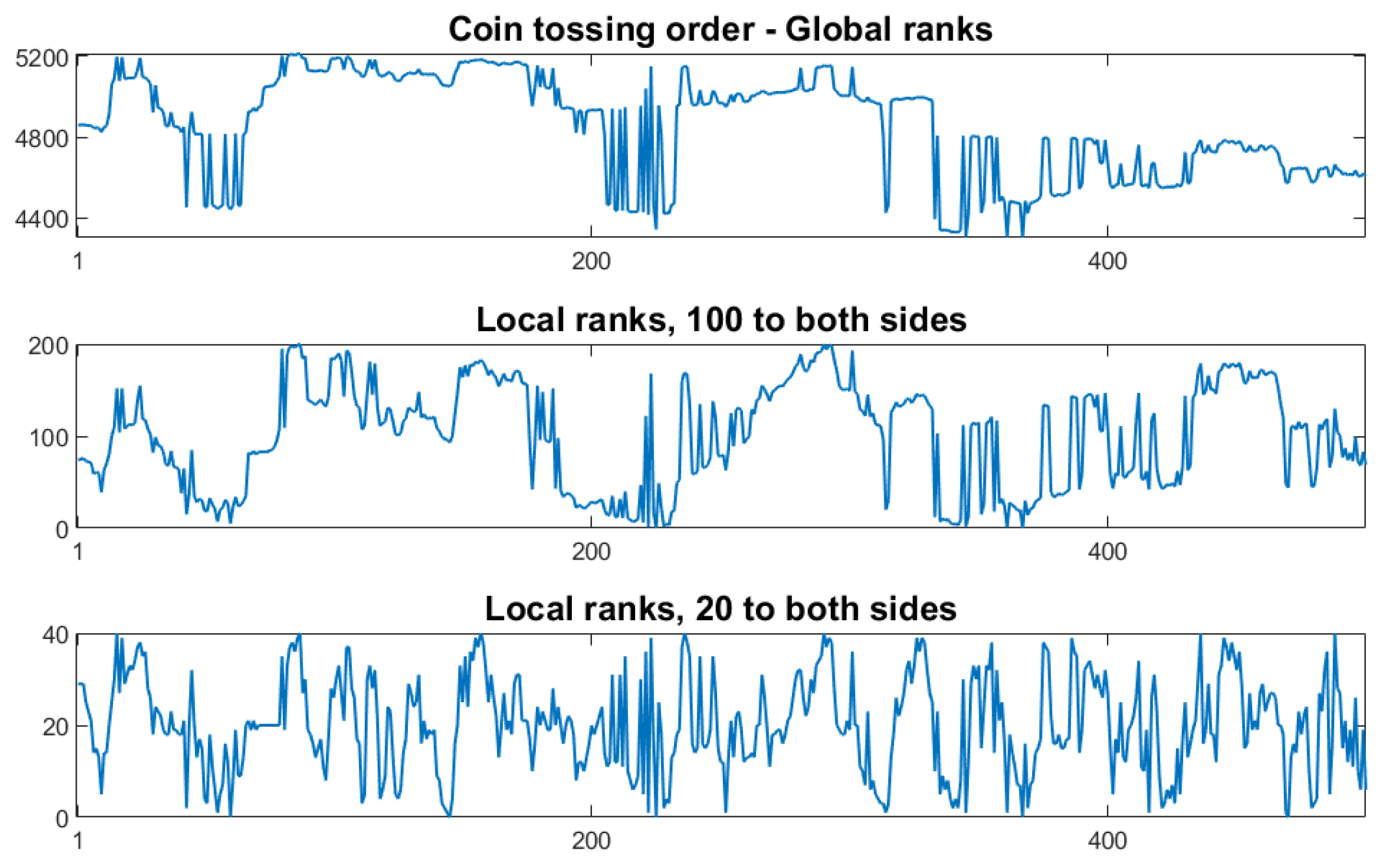
2.4. Computer Work and Breakdown of Self-Similarity

In Figure 3 we compare pattern probabilities of length 4 for Brownian motion and coin tossing order. Brownian motion looks more interesting since coin-tossing allows only the probabilities $2^{-k}.$ Our model is a first attempt, not recommended for applications. For length 3, the $P_{\pi }\left(d\right)$ of the two processes agree and do not depend on $d,$ according to Theorem 1. The figure shows that we must investigate patterns of length $\ge 4$ if we want to distinguish processes like these two. Moreover, Brownian motion is perfectly self-similar so that the probabilities $P_{\pi }\left(d\right)$ of any length do not depend on d [23]. Is that also true for the coin tossing order?

Figure 3. Probabilities of patterns of length 4 (brown) on top of those of length 3 (blue) for Brownian motion (left) and coin tossing order with $d=1$ (right). For length 3, the probabilities coincide.

Figure 3. Probabilities of patterns of length 4 (brown) on top of those of length 3 (blue) for Brownian motion (left) and coin tossing order with $d=1$ (right). For length 3, the probabilities coincide.

The Equation (5) allows fast calculation of all pattern probabilities for $d=1$ and $m\le 10.$ So we can determine $P_{\pi }\left(d\right)$ for all permutations of length 4 and $d=2$ and 3 by adding the probabilities of `atom permutations’ of length 7 and 10, respectively, as sketched in the proof of Theorem 1, (iii). For $d=3$ we have to add $10!/4!=151200$ cases for each permutation.

The result is shown in Figure 4. Unfortunately, order self-similarity breaks down for patterns of length 4. For $\pi =1324$ we have $P_{\pi }\left(1\right)={\displaystyle \frac{1}{32}}\approx 3.12\%$ while $P_{\pi }\left(2\right)\approx 3.42\%$ and $P_{\pi }\left(3\right)\approx 3.49\%.$ However, the probabilities for $d=2$ or 3 can be taken as a new model which is nearer to self-similarity and looks not as artificial as coin tossing in Figure 3.

Problem. Let us define new pattern probabilities $Q_{\pi }\left(1\right)=P_{\pi }\left(d\right)$ for $d=2,3,...$ What are the properties of Q ? Is there a limit for $d\to \infty$ ?

The small difference between $d=2$ and $d=3$ in Figure 4 indicates fast convergence. The mere existence of an order self-similar limit would be interesting but not yet helpful. Brownian motion is already available as an order self-similar process. The merit of the coin tossing order is its algorithmic flavour, its connection with ranking. We look for an order self-similar model with an intuitive explanation.

Finally, let us consider the interpretation of $u\left(\pi \right)$ as an energy function. Let $d=1,$ and let $S_m$ denote the set of all permutations of length $m.$ Let P denote the probability measure on $S_m$ given by the probabilities $P_{\pi }=2^{-u\left(\pi \right)}$ of coin tossing order. The permutation entropy [24] of $P,$ using logarithms with base 2, is just the mean energy with respect to $P.$

$$H\left(P\right)=-\sum _{\pi }{P}_{\pi }{log}_2{P}_{\pi }=\sum _{\pi }{P}_{\pi }u\left(\pi \right)=M_P\left(u\right).$$

For all other probability measures Q on $S_m,$ the permutation entropy is smaller than the mean energy, see ([25] Chapter 1). Thus P is a so-called Gibbs measure on $S_m.$

Problem. Are there other meaningful energy functions for permutations, perhaps even parametric families of Gibbs measures on $S_m$ ?

3. Rudiments of a Theory of Ordinal Processes

3.1. Random Stationary Order

Having studied one example, we turn to discuss a possible theory of ordinal random processes. As above, $X_1,X_2,...$ will not be numbers, only objects which are ordered. We have the discrete time domain $\{1,...,T\}$ for time series and $\mathbb{N}=\{1,2,...\}$ for models. An order will be a relation < on the time domain such that $x\neg <x,$ and $x<y$ implies $y\neg <x,$ and $x<y$ plus $y<z$ implies $x<z$. Of course, the order does not apply to the time points $t,$ but to the corresponding objects $x_t.$ Then the property that $x_t,...,x_{t+m-1}$ shows pattern $\pi$ has a meaning for every $\pi \in S_m$ – it is either true or false. When an order on $\mathbb{N}$ or $\{1,...,T\}$ is given, we can determine pattern frequencies, permutation entropy and so on. In the following, we always have $d=1.$

We want to construct models of ordinal processes, like the coin tossing algorithm. For this purpose we need the concept of random order. To keep things simple, a random order is defined as a probability measure on the set of all orders on the time domain. For the finite time domain $\{1,...,T\},$ a random order is just a probability measure $P_T$ on the set $S_T$ of permutations of length $T.$ For $m\le T$ and $\pi \in S_m$ and $1\le t\le T+1-m$ the random order allows to determine the probability

$$P_{\pi }^t=P\{x_t,...,x_{t+m-1}\mathrm{shows} \mathrm{pattern}\pi \}$$

(6)

The random order will be called stationary if the $P_{\pi }^t$ do not depend on the time point $t,$ for any pattern $\pi$ of any length $m<T.$ In other words, the numbers $P_{\pi }^t$ must be the same for all admissible $t.$ This is exactly the order stationarity which we defined for numerical processes in (3).

3.2. The Problem to Find Good Models

The infinite time domain $\mathbb{N}$ is considered in the next section. Using classical measure theory, that will be easy. The real problem appears already for finite $T,$ even for $T=20.$ We have an abundance of probability measures on $S_T$ since we can prescribe $P_{\pi }$ for every $\pi .$ When we require stationarity, we have $(T-1)!$ equations for these $T!$ parameters, as shown below, which is still too much choice.

The problem is to select realistic $P_{\pi }.$ Most of the patterns $\pi$ for $m=20$ will never appear in any real time series, and we could set $P_{\pi }=0.$ But we do not know for which $\pi .$ There are three types of properties which we should require for our model.

• Independence: Markov property or k-dependence of patterns (cf. [12]).
• Self-similarity: $P_{\pi }\left(d\right)$ should not depend on $d.$ For processes with short-term memory, like Figure 1, this could be replaced by the requirement that the $P_{\pi }\left(d\right)$ converge to the uniform distribution, exponentially with increasing $d.$ There must be a law connecting the $P_{\pi }\left(d\right)$ for different $d.$ Otherwise, how can we describe them all?
• Smoothness: There should not be too much zigzag in the time series. Patterns like 3142 should be exceptions. This can perhaps be reached by minimizing certain energy functions.

Problem. Does there exist on $S_{100}$ a stationary random order which is Markov and self-similar (for admissible d and $\pi$) and has parameters different from white noise and Brownian motion? For instance $P_{12}\ne {\displaystyle \frac{1}{2}},$ or ${\displaystyle \frac{1}{3}}<P_{123}+P_{321}<{\displaystyle \frac{1}{2}}$ ?

3.3. Random Order on $\mathbb{N}$

The infinite time domain $\mathbb{N}$ has its merits. Order stationarity, for instance, is very easy to define since every pattern can be shifted to the right as far as we want. It is enough to require

$$P_{\pi }^t=P_{\pi }^{t+1}\mathrm{for} \mathrm{all} \mathrm{finite} \mathrm{patterns} \pi \mathrm{and} t=1,2,...$$

(7)

It is even enough to require $P_{\eta }^1=P_{\eta }^2$ for all patterns $\eta$ of any length. (To prove that this implies (7) for a fixed t and a pattern $\pi$ of length $k,$ consider all patterns $\eta$ of length $m=t+k-1$ which show the pattern $\pi$ on their last k positions. The sum of their probabilities $P_{\eta }^1$ equals $P_{\pi }^t$ since P is a measure. And shifting all $\eta$ from 1 to 2 means shifting $\pi$ from t to $t+1.$)

On the other hand, infinite patterns require a limit $T\to \infty .$ Actually, there are lots of recent papers on infinite permutations, that is, one-to-one mappings of $\mathbb{N}$ onto itself. An overview is given in Pitman and Tang [26]. However, an order on $\mathbb{N}$ is a much wider concept than a permutation on $\mathbb{N}.$ An infinite permutation ${\pi }_1,{\pi }_2,...$ defines an order on $\mathbb{N},$ with the special property that below a given value ${\pi }_k$ there are only finitely many other values, for any $k.$

For an order on $\mathbb{N},$ however, there rarely exists a smallest object. Usually each object has infinitely many other objects below and above. Nevertheless, an order on $\mathbb{N}$ is uniquely defined by patterns ${\pi }^m\in S_m$ which represent the order of the first m elements, for $m=2,3,...$ For example $12-231-3412-45132-...$

Theorem 2 

(Approximating random order on $\mathbb{N}$).

(i) 

A sequence of permutations ${\pi }^m\in S_m$ defines an order on $\mathbb{N}$ if for $m=2,3,...,$ the pattern ${\pi }^m$ is represented by the first m values of the pattern ${\pi }^{m+1}.$

(ii) 

A sequence of probability measures $P^m$ on $S_m$ defines a random order P on $\mathbb{N}$ if for $m=2,3,...,$ for $\pi \in S_m$ and ${\pi }^{m+1}\in S_{m+1}$ holds

$$P_{m+1}\left\{{\pi }^{m+1} shows pattern \pi at its first m positions\right\}=P_m\left(\pi \right).$$

(iii) 

The random order P defined by the $P_m$ is stationary if and only if for $m=2,3,...,$ for $\pi \in S_m$ and ${\pi }^{m+1}\in S_{m+1}$ holds

$$P_{m+1}\left\{{\pi }^{m+1} shows pattern \pi at its last m positions\right\}=P_m\left(\pi \right).$$

Proof. (i): The condition says that the pattern of the first m objects, defined in step $m,$ will not change during successive steps. So the construction is straightforward. The rank numbers, however, may change in each step, and they may converge to ∞ for $m\to \infty .$

(ii): The condition says that the probability for a pattern $\pi \in S_m$ to appear for the first m objects, defined by $P_m,$ will remain the same for $P_{m+1}$ and successive probability measures. So we can define

$$P\left\{\mathrm{the} \mathrm{objects} \mathrm{with} \mathrm{numbers} 1,...,m \mathrm{show} \mathrm{pattern} \pi \right\}=P_m\left(\pi \right)$$

in a consistent way, and the $P_m$ determine $P.$ Actually, P is an inverse limit of the measures $P_m.$ Below, we provide a more elementary argument.

(iii): Together with (ii), this condition says that $P_{\pi }^1=P_{\pi }^2$ for all patterns $\pi$ of any length $m.$ As noted above, this is just the definition (7) of order stationarity. □

3.4. The Space of Random Orders

Resuming the discussion in Section 1.4, we show that the set of all orders on $\mathbb{N}$ can be represented by the unit interval, using a numeration system similar to our decimal numbers. We first assign subintervals of $I=[0,1]$ to the permutations of length $2,3,...$ The pattern 12 will correspond to $[0,{\displaystyle \frac{1}{2}}],$ and 21 to $[{\displaystyle \frac{1}{2}},1].$ The permutations 123, 132, and 231, which show the pattern 12 at their first two places, will correspond to $[0,{\displaystyle \frac{1}{6}}],[{\displaystyle \frac{1}{6}},{\displaystyle \frac{1}{3}}],$ and $[{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{2}}],$ respectively. For intervals of length 4, see Figure 3.

Instead of lexicographic order, we define a hierarchical order of permutations, with respect to the patterns shown by the first 2,3,... elements. For any permutation $\pi ={\pi }_1...{\pi }_m$ of length m and any k with $2\le k\le m$, let $r_k\left(\pi \right)$ denote the number of $j<k$ with ${\pi }_j>{\pi }_k.$ This is a kind of rank number of ${\pi }_k$ with values between 0 and $k-1.$ For example $r_3\left(123\right)=0,r_3\left(132\right)=1,$ and $r_3\left(231\right)=2$ while $r_2=0$ for these three patterns. Now we assign to the permutation $\pi$ of length m the following interval:

$$I\left(\pi \right)=[x\left(\pi \right),x\left(\pi \right)+{\displaystyle \frac{1}{m!}}]withx\left(\pi \right)=\sum _{k=2}^m{\displaystyle \frac{r_k}{k!}}.$$

(8)

It is easy to check that the patterns ${\pi }^{\left(k\right)}={\pi }_1...{\pi }_k$ of the first $k<m$ items of $\pi$ are assigned to larger intervals:

$$I\supset I\left({\pi }^{\left(2\right)}\right)\supset I\left({\pi }^{\left(3\right)}\right)\supset ...\supset I\left({\pi }^{\left(m\right)}\right)$$

where ${\pi }^{\left(m\right)}=\pi .$ Actually, $\pi$ need not be a permutation, just a pattern - it could also be a numerical time series. Only the ordering of the ${\pi }_j$ is used for defining $r_k$ and $I\left(\pi \right).$

When we extend the pattern to the right, we get smaller nested subintervals, and for $m\to \infty$ a single point $x={\sum }_{k=2}^{\infty }{\displaystyle \frac{r_k}{k!}}$ which characterizes the limiting order of infinitely many objects. Thus each order on $\mathbb{N}$ corresponds to a unique point x in $[0,1].$ This is very similar to decimal expansions where we subdivide an interval into 10 subintervals. In case of patterns, the $r_k$ are the digits, and we subdivide first into 2, then 3, 4, 5,... intervals. The endpoints of intervals represent two orders on $\mathbb{N},$ but this is an exception, as 0.5 and $0.4999...$ for the decimals.

Once we have represented all orders on $\mathbb{N}$ as points in $[0,1],$ we can better understand the probability measures $P_2,P_3,...$ of Theorem 2 and the limiting probability measure P which is called random order on $\mathbb{N}.$ We start with the function $F_1\left(x\right)=1$ which denotes uniform distribution on $[0,1].$ The function $F_m$ will represent the measure $P_m,$ for $m=2,3,...$ For patterns $\pi$ of length m it is defined as histogram of $P_m:$

$$F_m\left(x\right)=m!·P_m\left(\pi \right)forx\in I\left(\pi \right).$$

(9)

See Figure 3. The rectangle over $I\left(\pi \right)$ has area $P_m\left(\pi \right).$ In case of white noise, $F_m=1$ for all $m,$ and the $lim{F}_m=F=1$ is the uniform distribution. We now show that such limit exists for all sequences $F_2,F_3,...$ for which the $P_2,P_3,...$ fulfil condition (ii) of Theorem 2. We reformulate (ii) as

$${\int }_{I\left(\pi \right)}{F}_{m+1}\left(x\right)dx=m!·P_m\left(\pi \right)={\int }_{I\left(\pi \right)}{F}_m\left(x\right)dx.$$

(10)

The second equation is obvious, and the first is best shown by example, for $m=3$ and $\pi =312.$ We have $r_2=r_3=1,$ so $I\left(\pi \right)=[{\displaystyle \frac{4}{6}},{\displaystyle \frac{5}{6}}].$ The possible extensions ${\pi }^4$ of $\pi$ are 3124, 4123, 4132, and 4231. Their intervals of length ${\displaystyle \frac{1}{24}}$ partition $I\left(\pi \right).$ Condition (ii) says that $P_4\{3124,4123,4132,4231\}=P_3\left\{312\right\}.$ Thus the four rectangles of $F_4$ over $I\left(\pi \right)$ together have the same area as the one rectangle of $F_3.$ This is expressed in (10).

Equation (10) says that the $F_m$ form a martingale. The martingale convergence theorem implies that there is a limit function $F,$ in the sense that ${\int }_0^1|F_m-F|dx$ converges to zero for $m\to \infty .$ This limit function is integrable and $\int F=1.$ As a density function, it defines the probability measure P on all orders on $\mathbb{N}.$

Our argument indicates that random orders on $\mathbb{N}$ belong to the realm of classical analysis and probability. Of course, the density function F will be terribly discontinuous and can hardly be used to discuss stationarity. (Open problem for experts: find examples for which the $F_m$ converge in $L_2.$)

3.5. Extension of Pattern Distributions

We conclude our paper with an optimistic outlook for practitioners. When you find a distribution of pattern probabilties of length 3 or 4, from data say, you need not care for an extension to longer finite and infinite patterns. Such an extension will always exist.

Theorem 3 

(Markov extension of pattern probabilities). Any stationary probability measure $P_m$ on $S_m$ can be extended to a stationary probability measure $P_{m+1}$ on $S_{m+1}$, and hence also to a stationary probability measure P on the space of random orders.

Proof. 

To show that $P_{m+1}$ is stationary, we need only verify condition (iii) of Theorem 2: Any pattern within $\{1,...,m\}$ can be shifted to the right, without changing its probability, until its maximum reaches $m,$ by assumption of stationarity of $P_m.$ It remains to shift the maximum from m to $m+1,$ and this is condition (iii).

In the following extension formula, we use the convention that probability measures on permutations also apply to patterns, by replacing a pattern with its representing permutation. Let $\pi ={\pi }_1{\pi }_2...{\pi }_m{\pi }_{m+1}$ be a permutation in $S_{m+1}.$

$$P_{m+1}\left(\pi \right)={\displaystyle \frac{P_m({\pi }_1...{\pi }_m)·P_m({\pi }_2...{\pi }_{m+1})}{P_m({\pi }_2...{\pi }_m)}}$$

(11)

This formula will be used whenever there exists some ${\pi }_k$ with $2\le k\le m$ between ${\pi }_1$ and ${\pi }_{m+1}.$ However, if ${\pi }_1$ and ${\pi }_{m+1}$ are neighboring numbers, then the right-hand side of (11) cannot distinguish $\pi$ and ${\pi }^{\prime }={\pi }_{m+1}{\pi }_2...{\pi }_m{\pi }_1.$ In such cases, both $\pi$ and ${\pi }^{\prime }$ are assigned half of the value of the right-hand side, in order to avoid double counting.

The denominator on the right refers to a pattern ${\pi }_2...{\pi }_m$ which has a representing permutation $\kappa ={\kappa }_1...{\kappa }_{m-1}$ in $S_{m-1}$ and can be extended in m ways to a permutation $\eta ={\eta }_1...{\eta }_m\in S_m.$ Indeed, ${\eta }_m$ can be chosen from $\{1,...,m\}.$ For $j<m$ then either ${\kappa }_j<{\eta }_m$ and ${\eta }_j={\kappa }_j,$ or ${\kappa }_j\ge {\eta }_m$ and ${\eta }_j={\kappa }_j+1.$ Let us write

$$P_m\left(\kappa \right)=P_m\left\{\eta \right|{\eta }_1...{\eta }_{m-1} \mathrm{shows} \mathrm{pattern} \kappa \}\sum _{\eta }{P}_m\left(\eta \right).$$

In the numerator, ${\pi }_1...{\pi }_m$ is also a pattern which has a representing permutation $\lambda ={\lambda }_1...{\lambda }_m$ in $S_m.$ This term is $P_m\left(\lambda \right).$

We now prove that the defined $P_{m+1}$ fulfils condition (ii) of Theorem 2. We calculate

$$p=P_{m+1}\{{\pi }_1...{\pi }_{m+1}|{\pi }_1...{\pi }_m\mathrm{is} \mathrm{represented} \mathrm{by} \lambda \}$$

using the definition (11) of $P_{m+1}.$ There are $m+1$ permutations $\pi \in S_{m+1}$ which fulfil the condition, differing in the value ${\pi }_{m+1}.$ For each case ${\pi }_2...{\pi }_{m+1}$ is represented by one of the permutations $\eta$ introduced above. However, the two cases $\pi$ with $|{\pi }_1-{\pi }_{m+1}|=1$ belong to the same $\eta .$ That is why we consider them together and divide their probability by two. Now

$$p={\displaystyle \frac{P_m\left(\lambda \right)}{P_m\left(\kappa \right)}}·\sum _{\eta }{P}_m\left(\eta \right)=P_m\left(\lambda \right).$$

This proves that $P_{m+1}$ extends $P_m.$ For the stationarity, the same proof has to be performed with extension to the left and condition (iii). We have to care that now $P_m\left(\kappa \right)$ refers to ${\eta }_2...{\eta }_m.$ However, since we assumed that $P_m$ is stationary, this is the same number, and the proof runs as above. □

We called this a Markov extension since (11) says that ${\pi }_{m+1}$ does not depend on ${\pi }_1.$ Since we do not assume any independence properties of $P_m,$ we cannot expect more. However, if we start with $P_2\left(12\right)=P_2\left(21\right)={\displaystyle \frac{1}{2}}$ and extend successively to $m=3,4,...$ we obtain the coin tossing order.

There are many other extensions. Just to give an example, we can divide the double cases in an asymmetric way. A careful study of extensions may lead to a better model than coin tossing. But we have to stop here.

4. Conclusions

Established models of stochastic processes do not say much about probabilities of ordinal patterns. It is suggested that models for ordinal pattern analysis can be found by algorithms for comparison and ranking of objects rather than by arithmetical operations. A paradigmatic example of an ordinal process without numerical values shows that this is possible. Properties like stationarity and self-similarity can be formulated in a weak and very natural way for ordinal processes. As a starting point for further work, we proved a representation theorem and an extension theorem for stationary orders.