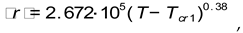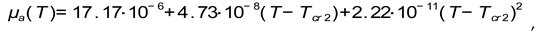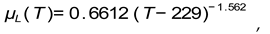Introduction
Microwave technologies are widely used in industrial processes, such as drying (textiles, wood, paper and ceramics), heat treatment of metals (hardening), disposal (recycling or disposal) of radioactive waste. In medicine, they are used to restore frozen tissues, warm blood, and treat tumors. The greatest consumer interest in microwave technologies arises in the food preparation industry, namely the processes of baking, pasteurization, dehydration and sterilization. Volumetric heating of the material by microwave irradiation (internal dielectric heating) refers to accelerated methods of heat exchange and removal of moisture from the material. For various methods of dielectric heating, the prediction (forecasting) of heat and mass transfer (transport) processes is extremely important in terms of equipment development, optimization processes, and product quality improvement. Direct experimental measurement of temperature and moisture content in porous material is a complex and troublesome process. Therefore, a significant amount of scientific research was carried out to model the transport (diffusion) processes of heat and mass transfer for such heterogeneous materials. Several different techniques or methods of numerical calculations, which are based on the use of the finite difference method [
1,
2], finite elements [
3] or the line transfer matrix method [
4] have been used to simulate microwave heating with varying degrees of success. In fact, when performing these calculations, it is necessary to know [
5,
6,
7,
8,
9,
10] the constant dielectric or thermal properties of the material.
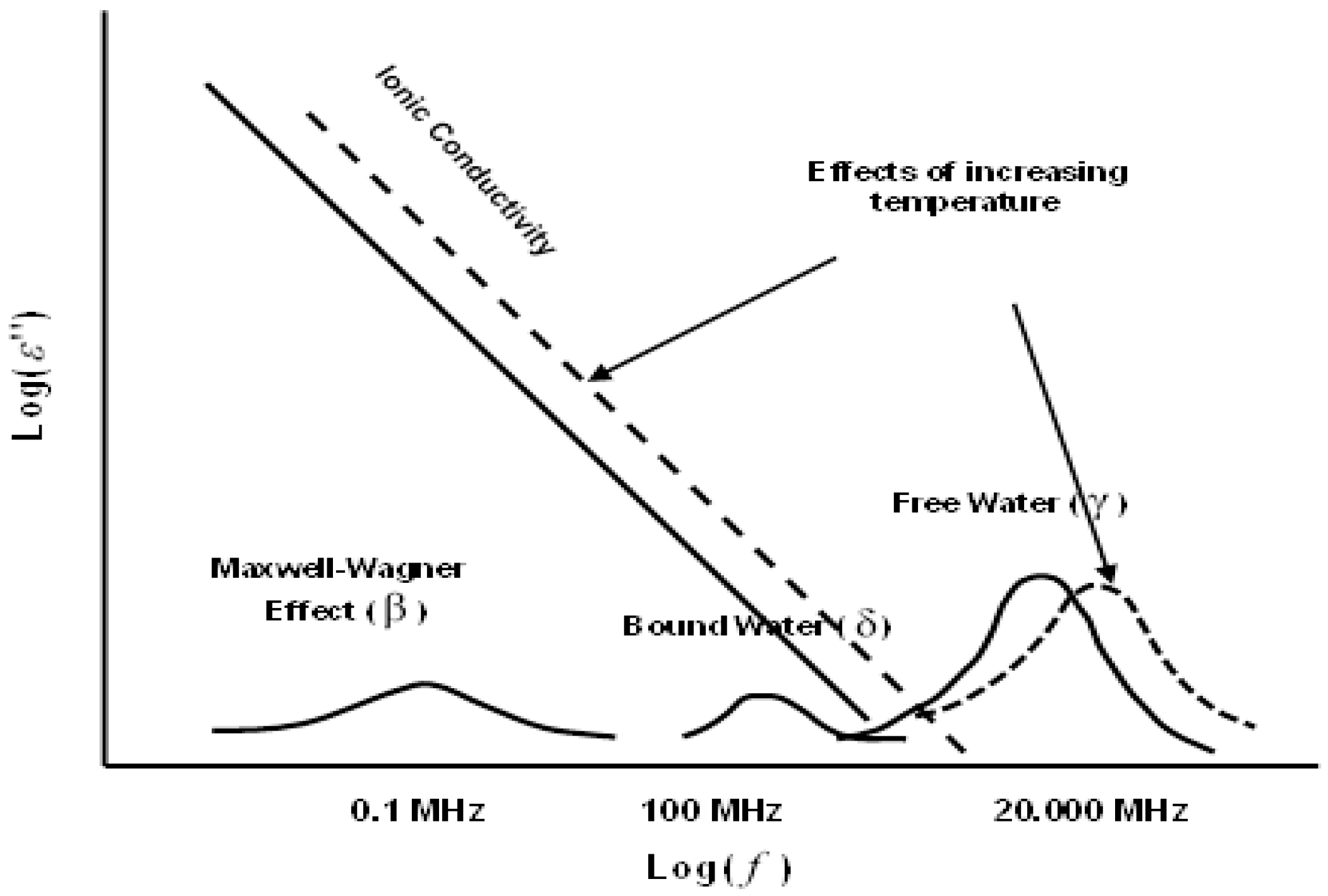
A lot of research has been done in the modeling of microwave heating of materials [
11], but we have little progress in modeling the transfer of heat and mass during microwave drying. Since under influence of dielectric heating or drying in an electromagnetic field, the material with dielectric loss of power of microwave irradiation has no permanent electro-physical properties, for most materials the dielectric properties change as a function of moisture content and temperature. Therefore, during microwave heating (drying), the distribution of the electromagnetic field in the body (material) is strongly related to the processes of heat and mass transfer. Changes in the local moisture content and temperature affect to the dielectric properties of the material, including the distribution of the electromagnetic field. The size of the load (material) relative to the waveguide or the drying cavity, the effect of the wave resistance (impedance) of the cavity, the amount of the radiation power that is reflected from the inner walls of the cavity (resonator) in the direction of the on magnetron determine the quality of the microwave equipment.
Since the detailed distribution of the power of the electromagnetic field (internal heat sources) within the material loading is quite difficult to model [
4], most studies assume that the lines of force of the electromagnetic field during microwave irradiation on the surface of the material are uniform and normal to the surface. It is also assumed that the power of the external irradiation in the body decays in accordance [
12] with the exponential law. Such approach was happy applied to modeling of heat and mass transport of dielectric the heated product of food [
13,
14]. A simple reflection was expressed according to investigation [
15], where heat sources under dielectric losses of microwave irradiation in the range of solid product is assumed uniform. In reality into the mentioned theoretical works the understanding of drying processes is limited, because under description of humidity transfer in porous media at isothermal conditions is used in general. For more developed models a law of molecular diffusion [
16] is applied and assumed [
17,
18], that heat gradient is the main division force into processes of mass transport or transfer. Its need to pointed, that results of numerical modeling according to mentioned above models for humidity diffusion as rule do not agree with experimental measured [
19] in the more cases.
Same researcher development of the models [
20] into approach, when diffusion of water vapor is main mechanism of humidity transport during of drying processes. For too refined methods for describing of drying (microwave heating) the two area transport models [
21,
22,
23] are treated. In this models is assumed, that two different area (region) for describing of humidity transport during drying (wetted and dried area) is existed. In the wetted area moisture content is grate as maximal sorption value for water vapor and basic mechanism for transport (transfer) of humidity is movement of liquid. In sorption region the movement of adsorbed (bounded) water and water vapor is basic reason of mass transport. The applying of this model is limited, because during the long (limited) process of drying the division (boundary) between wetted and sorption areas (regions) is conventional.
A reference review is showed [
24] that main progress was made into development of transport (diffusion) models under investigation of physics of ground, where main interest was concentrated on the utilization of nuclear remains and management of water resources. The basic formulation was development for interconnected processes of heat and mass transfer into works [
25,
26,
27]. The main approaches are based on assumption, that general transport potential consist on the two components: temperature and capillary potential.
During microwave drying an induces by thermal (microwave) heating increment in density of water vapor and humidity potential is calling of movement for humidity from more heated into cooled area. A general restriction or deficiency of mentioned isothermal models is absence of the thermal induced changing of humidity. First of all, this is due to a significant difference in the distribution of moisture in the porous material, which is caused by the processes of evaporation or condensation.
In fact, in the context of drying processes, reformulation of the problem in terms of moisture content and temperature is desirable for a fundamental understanding of drying processes, especially when modeling diffusion (transport) processes under conditions of intense internal microwave heating. First of all, this is due to a significant difference in the distribution of moisture in the porous material, which is caused by the processes of evaporation or condensation.
The nature of stresses in porous materials that arise during microwave heating, as a result of changes in temperature and moisture distribution, also remains insufficiently researched. For example, despite the fact that the hydrothermal behavior of concrete under thermal (radiation) heating is described in detail in the work [
28], the author is aware of only one scientific work [
29], where the maximum values of thermal stresses caused by internal microwave heat sources were calculated in the specified material. Some attempts at computer simulation of the stressed state of the specified material under microwave irradiation were carried out in works [
30,
31], where only the energy (thermal) balance equation was used to calculate the thermal and elastic properties of the material.
Special attention should be paid to the study of the properties of thermal and moisture stresses during microwave irradiation under conditions of phase transformation (evaporation or condensation) and changes in the pressure of the gas medium into the pores of the moistened material. Theoretical models for describing the dependence of microwave heating sources on the distribution of moisture and temperature in a porous medium also need improvement and development, especially in view of modeling effective (measured) characteristics due to the corresponding properties of phases or components in the studied wetted porous sample.
Comparing to Convective Drying we can Poit to Advantage of Microwave or Dilectric Drying
1. High energy efficiency in the period of falling speed, which is a consequence of the concentration of the energy of heat release in places of liquid concentration; 2. A significant increase in fluid mobility with an increase in the internal pressure of water vapor due to the effect of liquid evaporation; 3. Significant improvement or preservation of the quality of the drying product due to the near-uniform distribution of heat sources, which corresponds to the insignificant distribution of stresses along the thickness of the body; 4. Significant improvement or preservation of the quality of the drying product due to the near-uniform distribution of heat sources, which corresponds to the insignificant distribution of stresses along the thickness of the body; 5. The duration of convective drying can be significantly reduced in accordance with the expediency of saving energy costs.
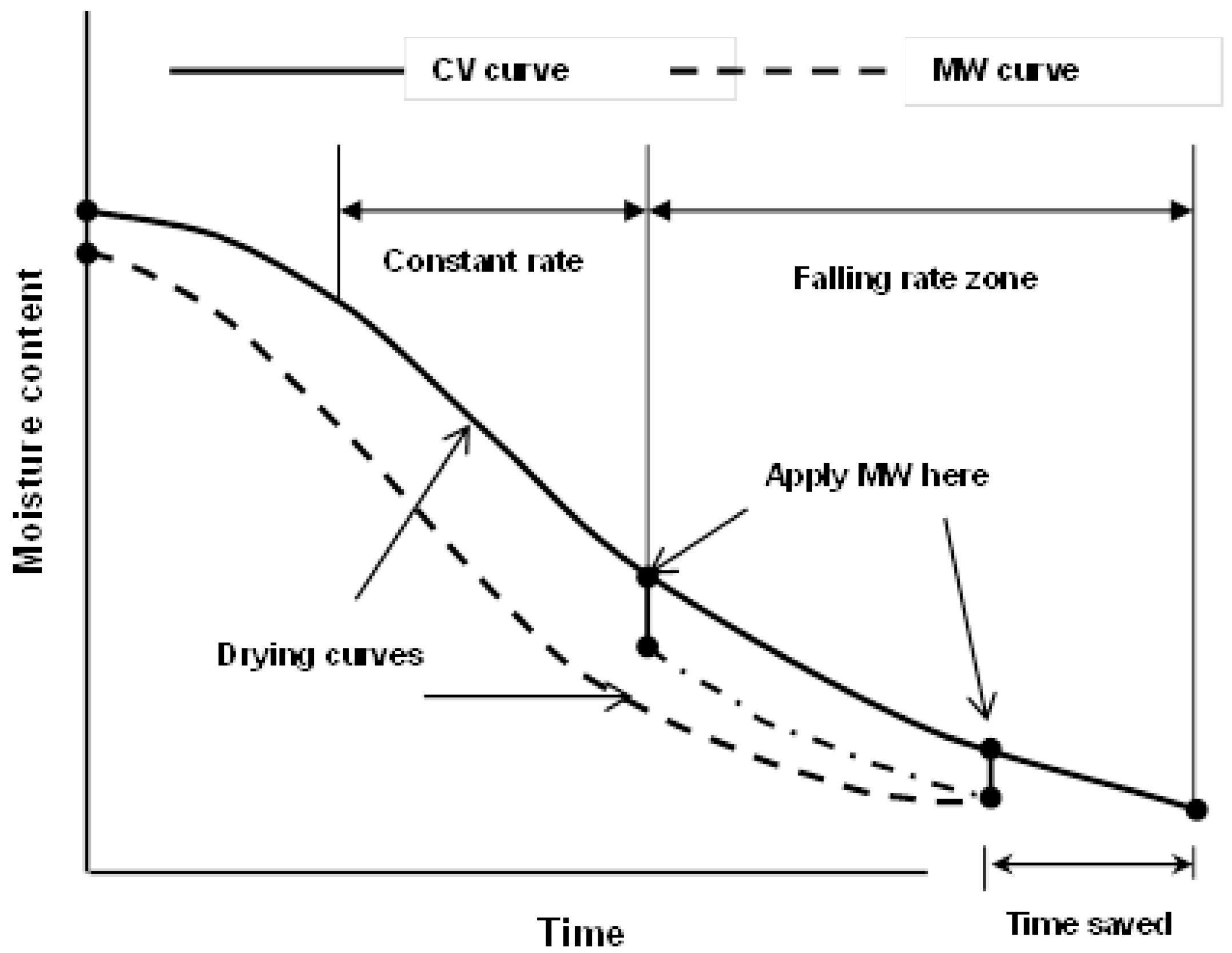
The acceleration of convective drying applying microwave is demonstrated on the
Figure 4 below. There is the significant time saving in drying according to time point of applying microwave. In other word it's possible to combine convective and microwave drying for reduction of drying period.
Figure 4.
Curves of mixed convective and microwave drying.
Figure 4.
Curves of mixed convective and microwave drying.
There are also differences into nature of destruction for investigate porous material, as
its depicted on the Figure 5 below
Figure 5.
Examples of destruction of ceramics under convective (A) and microwave (B) drying.
Figure 5.
Examples of destruction of ceramics under convective (A) and microwave (B) drying.
The main goal of this work to divide of mechanical, electro-magnetical and diffusional processes to correct describes of mentioned physical properties of wetted or humidified porous material under influence of symmetric microwave irradiation for the one-dimensional case into approach of continues media. In general, allow me to characterize and name these phenomena as mechanical thermo-diffusion in the proposed terminology.
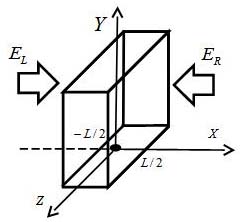
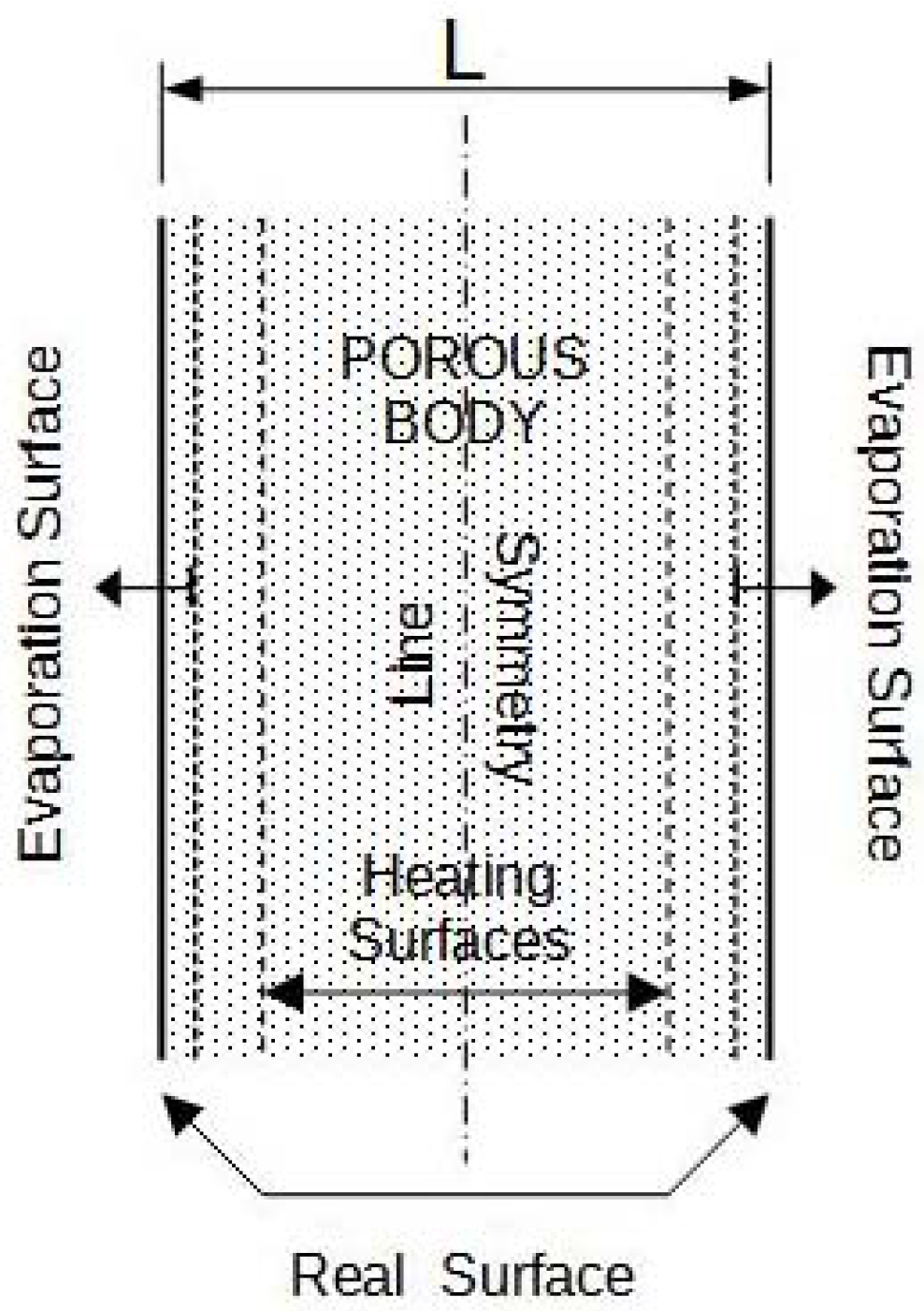
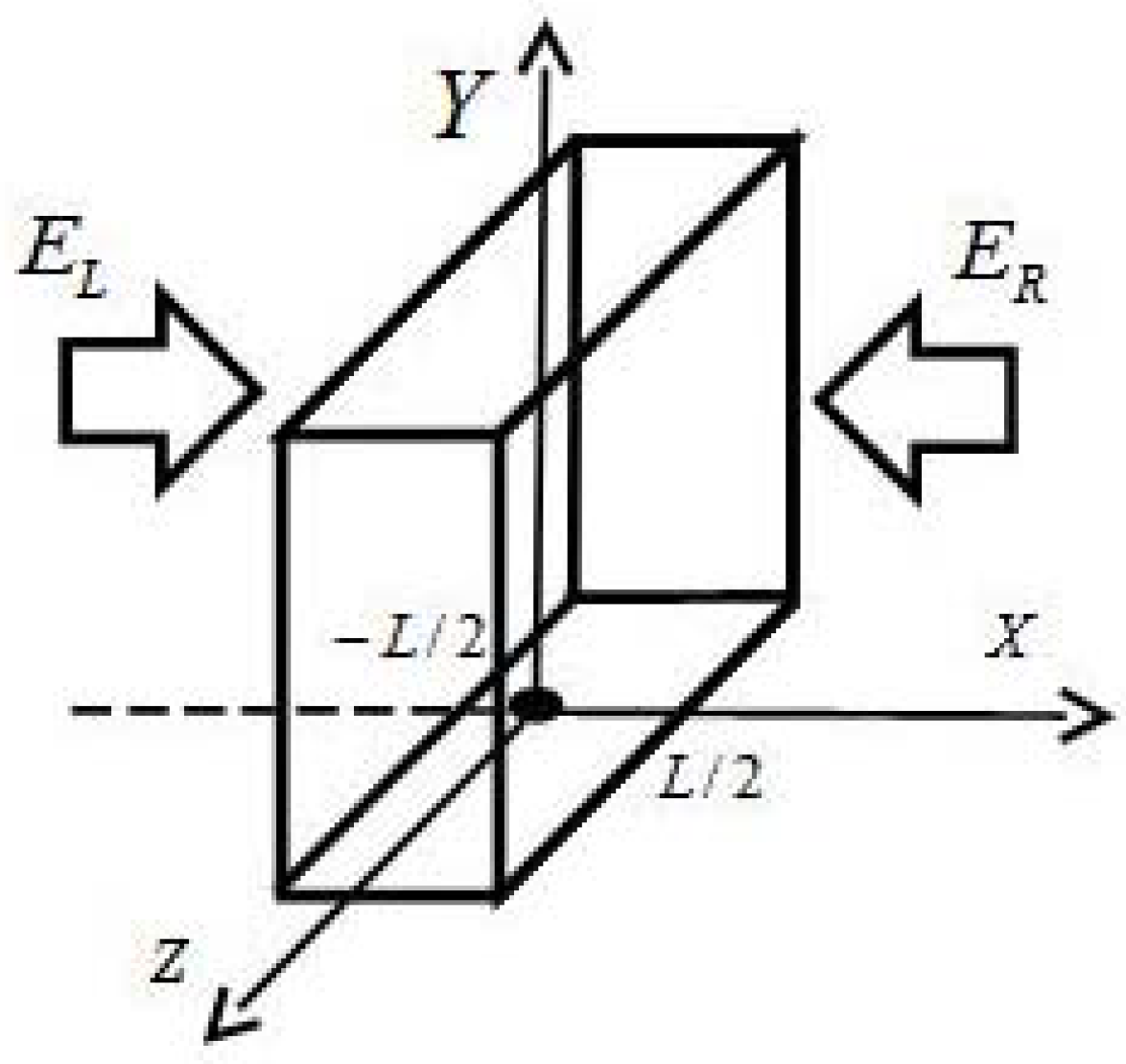
The object of studies Let's define the object of
studies. This is one dimensional porous wetted plate length of (Figure 1) which is under influence of
symmetrical microwave irradiation of the fixed power. The constant convective
flow by the hot air at the surfaces of plate is also additionally applied
during all time of microwave treatment, so in general it is can be classified
as the mixed microwave-convective drying.
Figure 1.
Modeling of microwave treatment of porous sample under symmetric conditions.
Figure 1.
Modeling of microwave treatment of porous sample under symmetric conditions.
We are modeling such drying system mathematically via introduction of
dynamical boundary conditions. There is confirmed by other authors [21–23] that conditionally it is possible to highlight the two zones during of
microwave treatment for porous sample: wetted and heated zone. The term zone is
meaning as a one dimensional area from the internal surface to the real hard
boundaries of body into the direction of external environment. The moving that
zones is interconnected due to dependence of diffusion coefficients in the internal volume of sample from
humidity as well as the time dependences of surface heat and mass transfer
coefficients on the real physical boundaries of mentioned porous sample.
To describe the diffusion
processes in a porous plate, the well-known [32,33] averaged heat and mass transport equations written in general
form are used
where
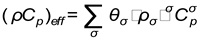
and
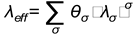
, here
are the effective
thermal characteristics of porous material,
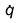
and
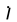
are the heat and
mass surfaces intensity correspondingly,
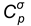
and
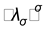
are the specific
capacity and thermo conduction of σ-phase
accordingly and
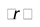
a is the latent
heat of vaporization.
There are the expressions for
concentrations
,
,
and flows of phases (components) in
the porous media
,
,
here and , where and , a the intrinsic permeability of
skeleton and liquid phase correspodingly, , , where a is the corresponding densities
of liquid phase and components of gas mixture, and a is dynamical viscosity, is model diffusion coefficient, and a is the valueas of pressures in
liquid and gas phases, is a capillary pressure, and a is the molar mass of water vapor
and dry air respectively.
Constitutive or material equations:
1. Pressure balance into liguid and gass phase:
, where
a is capillary pressure,
is dimensionless characteristic of
porous material named as J-Laverett [34]
function; 2. The Daltone’s law:
, where
is the partial pressures of gas
mixture components (
, here
a is the molar mass of mixture);
3. Equation of sorption equilibrium
, where
is the relative humidity and
is the partial pressure of water
vapor into the gas phase.
Modification of heat and mass
equations: 1. A transition from variables has been made from to according to Rault’s law [32] (), where is molar fraction of components,
the intensity of evaporation sources in the internal volume and at the surface
of the plate is determined in the different ways
2. An expression for the effective Burger[
35] diffusion coefficient of the gas mixture in the pores of the material is proposed
, (5)
where
a is the diffusion coefficient of
water vapor into dry air,
a is the tortosity factor.
3.For the internal volume
(6)
and surface of plate
the systems of heat and mass
transport equations are separated.
Modeling of microwave treatment
processes: Let`s define the real body surfaces as
(see Figure 1
), heating and
evaporation surfaces as
and
respectively.at the initial moment
of time. The near-surface zones of wetting and heating of the material are
considered, delimited by the surfaces
and
, within which the solutions of the
system of equations and the power of the microwave heating sources are assumed
to be constant.
Internal diffusion processes: The
modified system of equations (6) and (7) with a defined effective diffusion
coefficient (5) of the gas mixture in the pores of the moistened material with
corresponding expanded expressions for the flows is considered
The thicknesses of the surface
zones are determined by the ratios
,
where and are the constant surface mass and
heat exchange coefficients under convective heating conditions, is a surface of symmetry of the
porous plate.
Flow balances: Is defined by
equalities for liquid and components and of gas mixture .
Boundary conditions: Are defined relative to transport flows of mass on the surface under additional conditions: 1. There is no liquid flow () and the transformation of the liquid into water vapor on the boundary surfaces , of constant wetting occurs instantly; 2. Heat sources in the near surface areas of plate heating are uniform.
Than
,
here
and
are the variable with time heat and mass
transfer coefficients,
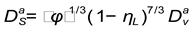
is the known Millington-Quirk [36] coefficient of diffusion for dry air component in the pores of
material at surface
of evaporation.
Electromagnetic interaction As was described in the paper [
37] for a flat plate into the electric field strengths, the wave equation will have the form
here
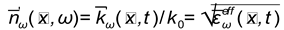
is
the complex refractive index,
is the wave vector into the porous (inhomogenius) media,
(where
is the light velocity in vacuum) is the wave vector of electromagnetic irradiation in the vacuum,
a is the corner frequency electromagnetic field (
is the linial frequency),
and
are the magnetic and electric constants in the vacuun correspondengly.
We are finding the solution of the wave equation as it is specified into the work [
37] according to the method of W.K.B. (Wentzel-Kramers-Brillouin) [
38] in the form
where are the constant values of the refractive index on the edges of porous plate, and are the unknown functions of time.
Under applying of boundary conditions [
37] to the components and derivatives of EMF at the edges of the plate we get the time-varying coefficients
where and (here is the index, which corresponds to and edged of plate), are respectively the coefficients of transmission and reflection of a plane wave at the boundaries of the plate in the accepted notations.
In the approximation of large plate
thicknesses acording to [
37] for the power of microwave irradiation into the porous plate we have
where is the power of external microwave irradiation, and are the boundary values of refractive index and transmission coefficient for electromagnetic wave correspondingly.
The poser of heat sources of electromagnetic (microwave) heating is obtained by the relation
and is gets the following view
,
where is the same equal notation.
Given the ratio , where and are the indicators of adsorbtion and transmission of plane electromagnetic wave, we obtain the effective quantities of wave length and penetration depth for such wave process
,
under conditions of executing of this rationed relation, where is tangent of dielecric loss angle.
Figure 2.
Schematic depiction of porous plate under microwave irradiation.
Figure 2.
Schematic depiction of porous plate under microwave irradiation.
Thermal stress under moisture loads For a spatially isotropic homogeneous solid phase (framework or skeleton) in a porous medium under the condition of the absence of external force loads, the quasi-static problem of linear thermo-elasticity is formulated in the form of the ratios
, ,
where is the leading stress tensor, is the components of internal (pondermotore) forces due to gas pressure , capillary pressure and liquid pore saturation under averaged constant porosity of body and is diagonal tensor.
In the case of a one-dimensional plate (
Figure 2), which is under influence of internal microwave heating according to conditions of compatibility of Saint-Venant deformations [
39], the system of equations for the stress component of the tensor has the following form
Force loads in the internal volume of the plate are determined as
, (9)
where
and
are the quantity of humidity and thermal stress and their corresponding constant values
and
on the internal surface of symmetry (see
Figure 2 is the surface
at
) for the porous plate.
According to the symmetry conditions, the boundary conditions for a plate of finite thickness are applied: 1. There are no internal forces along the plane of symmetry of a plate; 2. The boundary surfaces of the plate are free from the external loads ; 3. The derivative of stresses along a plane of symmetry is equal to zero.
Then the solution of the equations of the quasi linear thermo-elastic problem under the action of internal (moisture and thermal) loads has the form of stresses
and deformation
correspondingly, where is an expression for the total internal forces, and and are the corresponding averaged effort values.
The main mechanical thermo-diffusion equations In such way, we obtain the system of closed equations of heat and moisture diffusion
,
,
with the corresponding boundary conditions described above, the solutions of which can be found according to the obtained expression for the heat sources
and may determine the stress-strain state of the body with values the calculated relative to the plane of symmetry
humidity and thermal forces loadings.
The closed system of equations is obtained by fulfilling the conditions of weak variability of volume (phase), dielectric (wave) properties of an investigated three-phase porous wetted body
and
as well as conditions
,
which are determines the possibility of applying the approximation of the effective macroscopic field in the study (determination) of the effective electro-physical properties of the porous body according to the method of local spatial averaging.
Here and wave vector and phase velocity of electromagnetic (TEM) wave propagation in the simulated environment, is the effective value of refractive index, is the volume fraction of - phase (here a is the angle frequencyand 1 is the characteristic (REV) length of averaged volume).
Analysis and Discussion
Numerical simulation of the stress state of a flat unbounded plate under symmetric microwave irradiation was carried out for the selected porous material: historic ceramic brick. The sorption and capillary properties of the studied material are described in detail into the paper [
40]. In particular, according to a comparative analysis of semi-empirical models of moisture release or retention, it was established, than at defined averaged porosity
the internal permeability of porous skeleton is
and empirical parameter in the model of relative permeabilities for fluid (liquid and gas) phase by van Genuchen [
41]
. Also into the work [
40] the relative permeability of liguid
and gas
phases are defined. Its pointed, that capillary properties of porous material is identically determined by the use of dimensionless
- Leverett function , which takes a form
,
here is effective pore saturation by liquid, and are residual and critical pore saturation by liquid for the mentioned material accordingly.
The beginning or initial equilibrium wetting
of porous material is defined by the know [
40] relation
, (10)
where and are pressure and temperature of the vapor like mixture in surrounding equipment accordingly, and is coefficient of surface tension.
At calculation of matrix elements in the generalized form of heat and mass equation according to known expressions (8) for phase and component flows the following values of molar mass for dry air and water vapor in two component gas mixture are used. Than the expression for density of gas mixture in the approximation of light solution has been view
where
a is partial pressure of unsuturatedwater vapor,
a is relative humidity of air,
is the equilibrium pressure of saturated water vapor, for this value a temperature approximation [
42] is satisfied
here is termodynamic temperature.
Because relative humidity is defined according to the known for investigated material dependence of capilary pressure from temperature and pore saturation by the liquid, in such case the eqvilibrium (initial) value of water vapor molar fraction in wetted porous material is
where
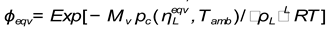
is
the initial value of relative humidity,
is the corresponding equilibrium (beginning) value of wetting, which has been defined according to relation (10) above.
Effective thermal characteristics of the composite material have been calculated according to known [
43,
44] experimental propertied of phases, as it depicted in the
Table 1.
For the defined effective
electro physical properties (11) in the investigated material, including dielectric loss tangent
, the numerical calculations were performed in the approximation of the effective medium (EMA) [
45], according to the relation
. (11)
The last cubical equation is solved relatively to effective dielectric constant of composite
, were coefficients are defined by known dielectric constant
and volume fraction
of porous media component with usage of experimental data, as it is depicted into
Table 2.
At calculation it is taken into account, that density of solid skeleton and incompressible liquid .
A surface tension coefficient
and latent heat (enthalpy) of the vaporization
[
46] has been reviewed in the form of approximated temperature dependencies
and
where is the critical temperature (triple point).
The dynamical viscosity of binary gas mixture has been modeled according to Wilke [
47] theory, when for clear components of water vapor
and dry air
it is selected the following [
48] numerical approхimations
,
here is the fixed (critical) temperature of water freezing, also
where
a is the dynamical viscosity approximation according to data [
49].
Diffusion properties of components of vapor-air mixture in the pores have been defined with usage of introduced by the extended through the author of research the diffusion coefficient
,
where is the diffusion coefficient of water vapor into the dry air.
Conclusions
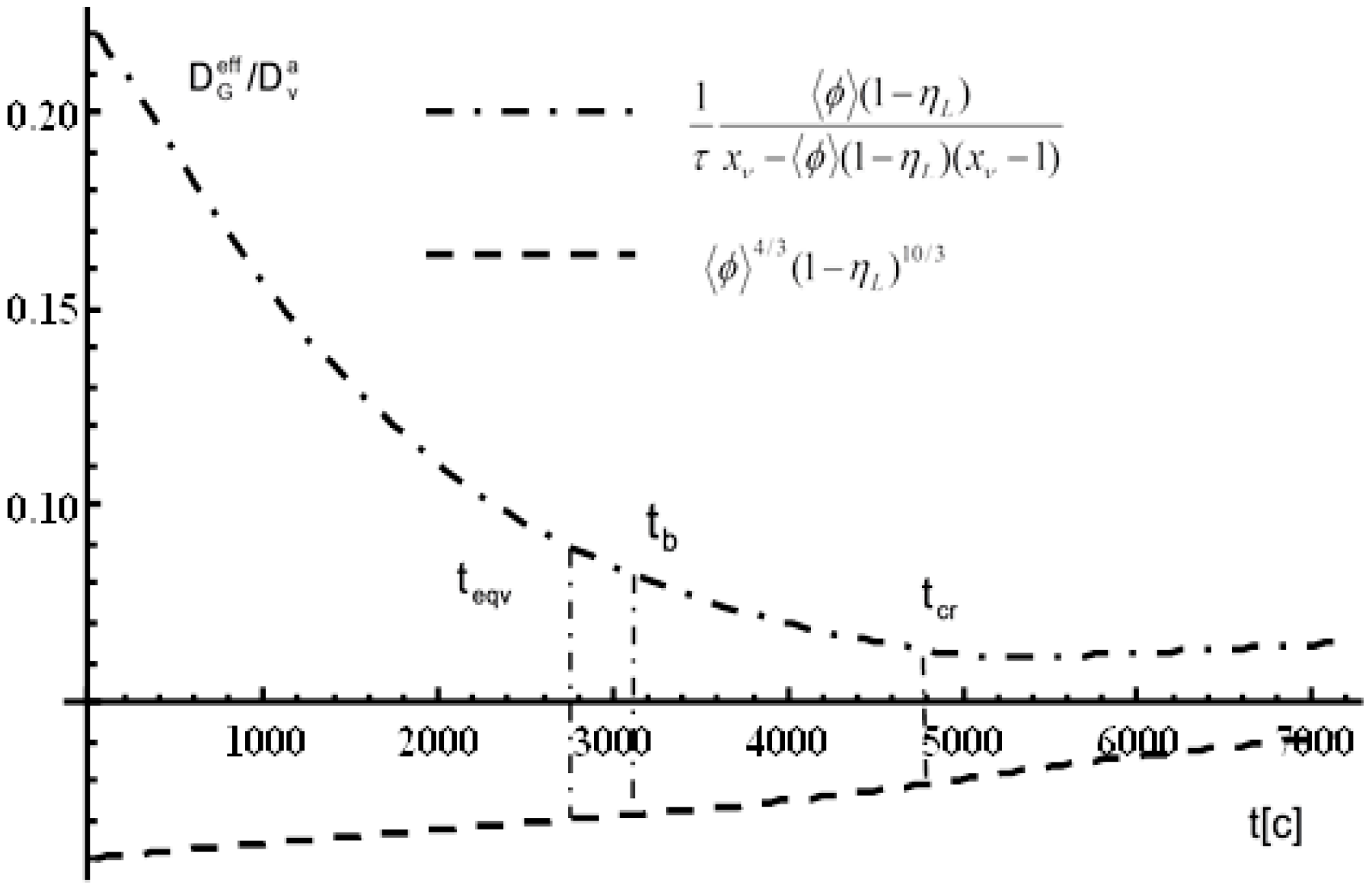
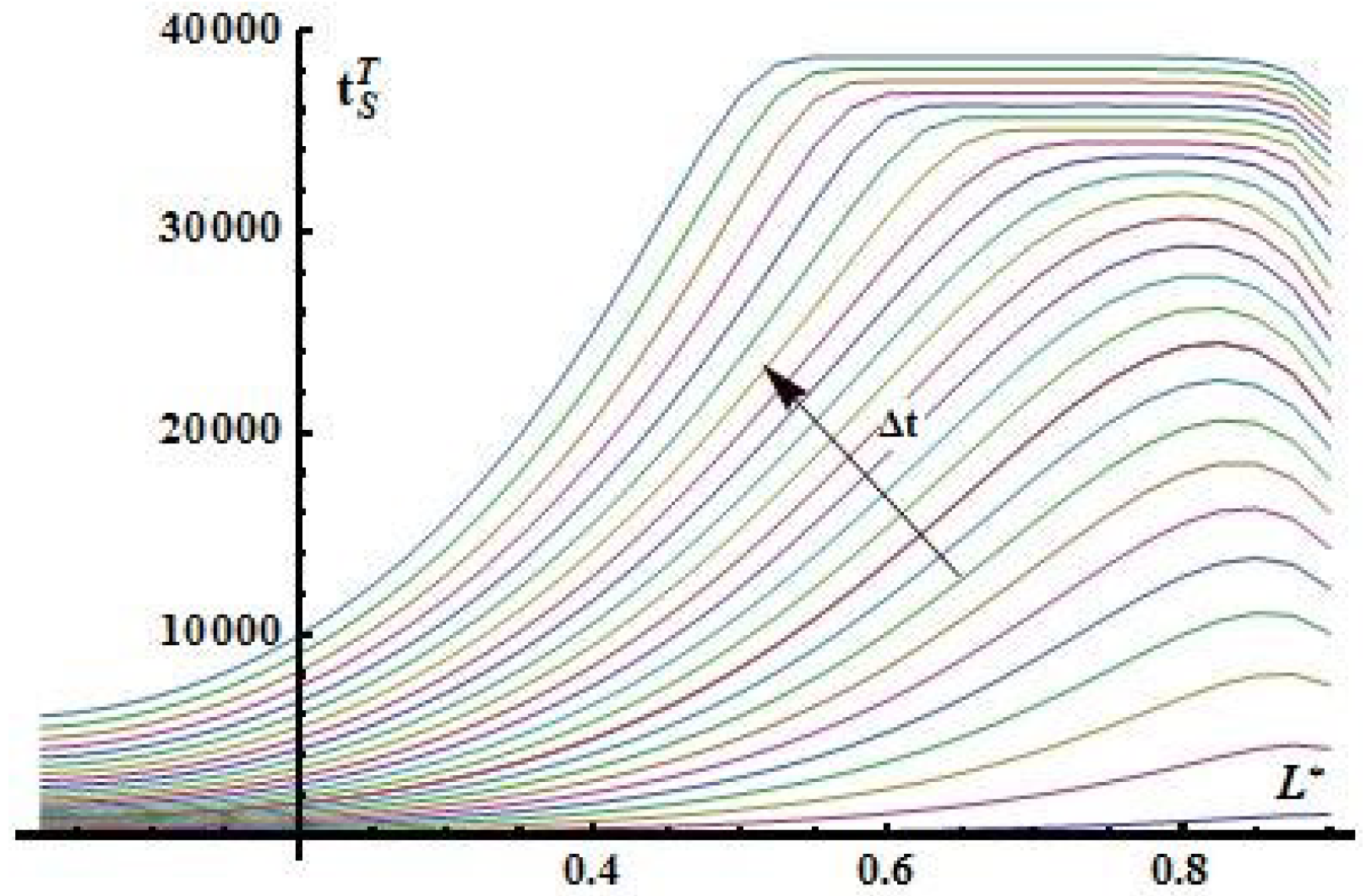
According to results of heat and mass process numerical simulation the time shift of near surface wetted and heated zones which are separated by the surfaces
and
is obtained due to distribution of dimensiomless sickness
and
as it depicted on the (
Figure 3) and (
Figure 4) relatively to surface
of plate symmetry.
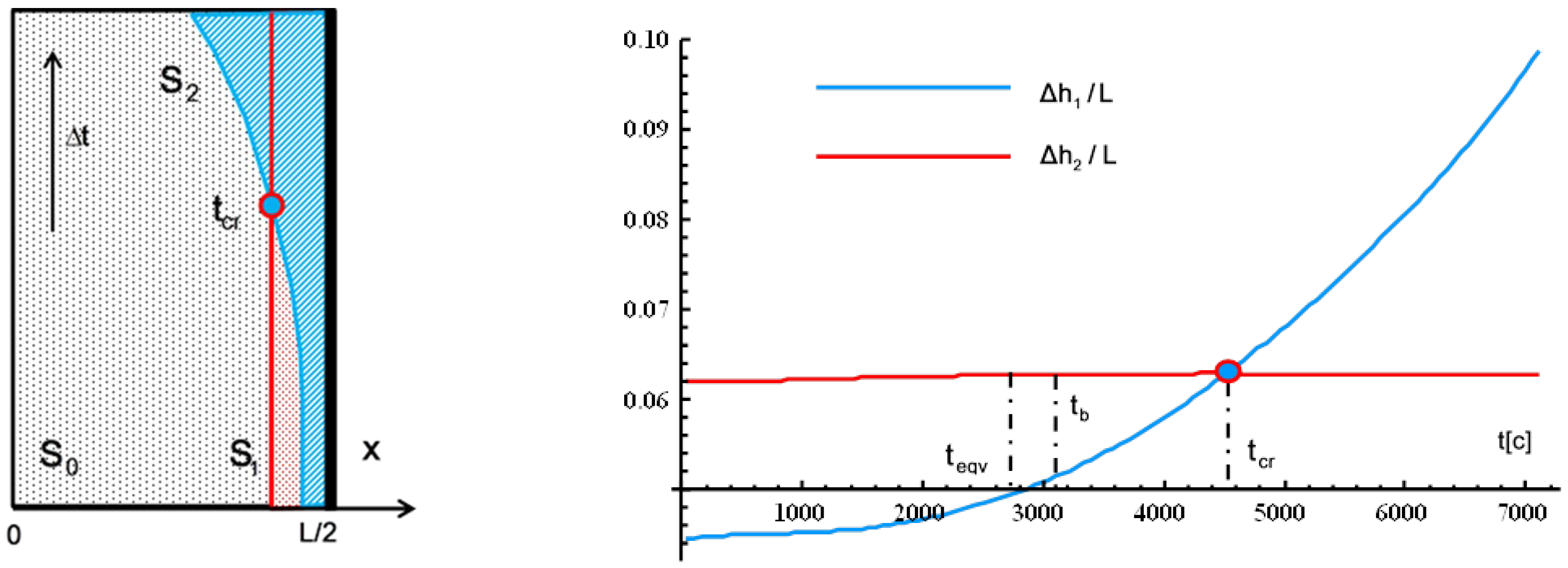
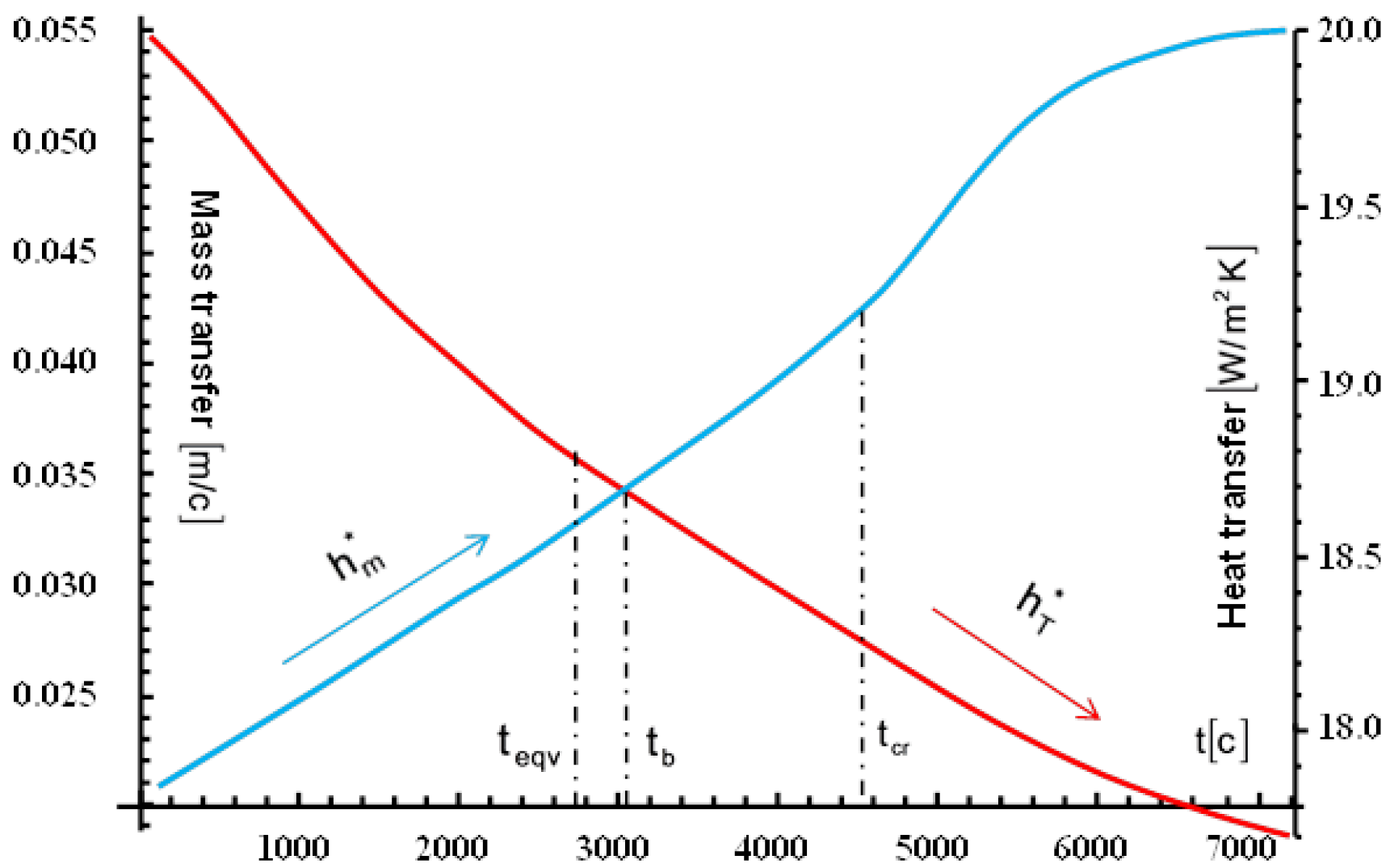
Conclusion I: 1. Its fixed a critical value of time
there is a point of the crossaver surfaces
and
about that the surface mass transfer coefficient
(
Figure 5) increase nonlinially. It is joined with beginning of processes of intensity liquid evaporation at the near surface wetted zone;
2. It's also not significal nonlinear behaviour of surface heat transfer coefficient is delivered
(
Figure 5) along the surface
, which is joined with deviation of averaged liquid pore saturation
from equvilibrium values at surface of symmetry
of plate.
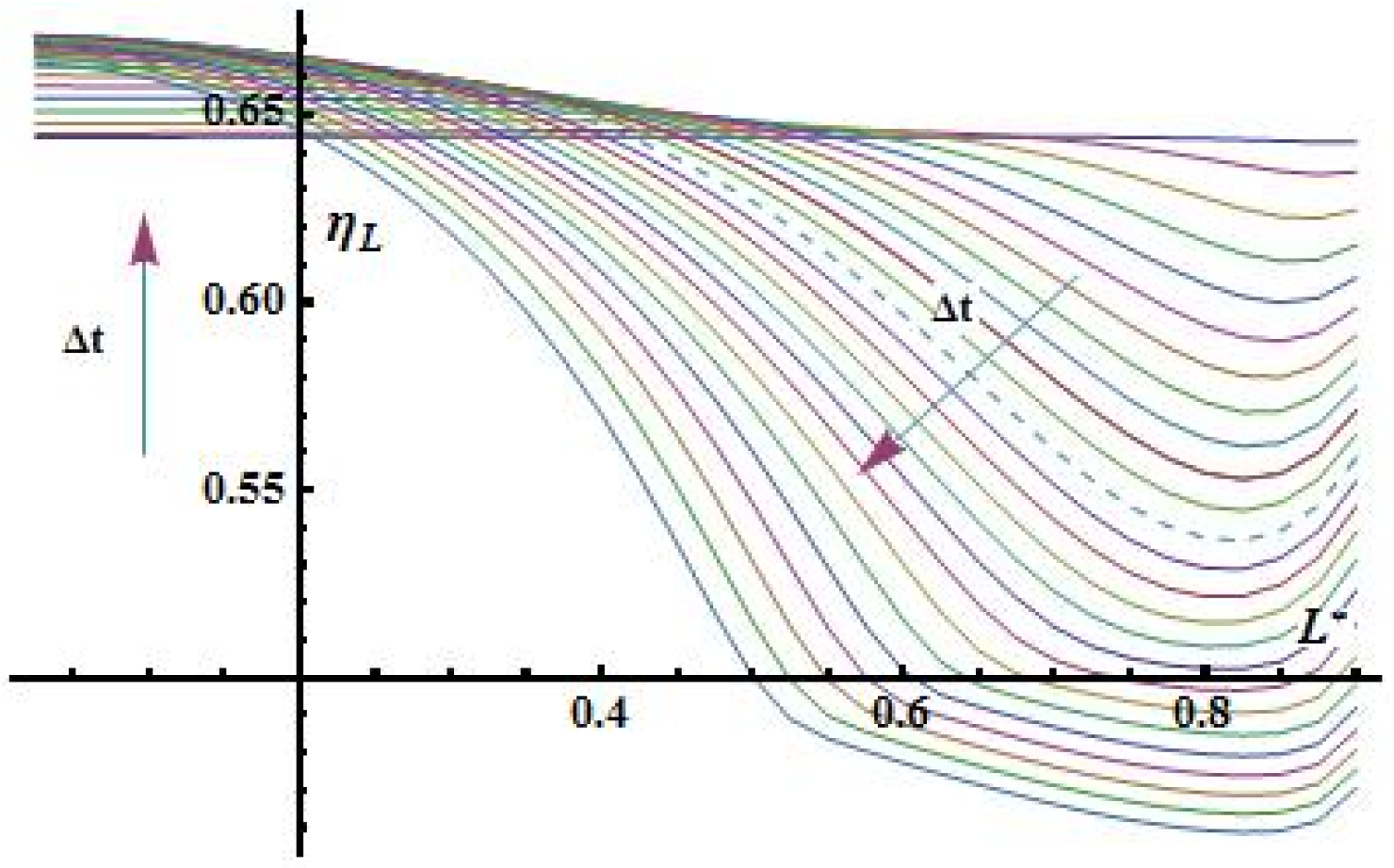
Figure 5.
The surface emission coefficient for heat and mass transfer.
Figure 5.
The surface emission coefficient for heat and mass transfer.
Figure 6.
The values of internal and surface diffusion coefficients at the evaporation surface.
Figure 6.
The values of internal and surface diffusion coefficients at the evaporation surface.
Conclusion II: 1. In the neighborhood of time value an equilibrium state of two component mixture of water vapor and dry air is fixed (), abouve it the dry air is gradually displaced through the surface of wetted and molar fraction of water vapor in critical point of time follows to maximum value of saturation. 2. Diffusivity of gas mixture in pores of material for the internal volume of plate and at the evaporation surface are defined in various way, but over time in the region the calculated values ( at a this model tortosity factor) of difusion coefficiens on the surface is aligned.
Solutions of modified system of heat and mass balance for material of historical ceramic brick are represented in the form of graphical dependencies as its showing below, here is dimensionless half thicknes of plate.
Figure 7.
The distribution of the pore saturation by liquid.
Figure 7.
The distribution of the pore saturation by liquid.
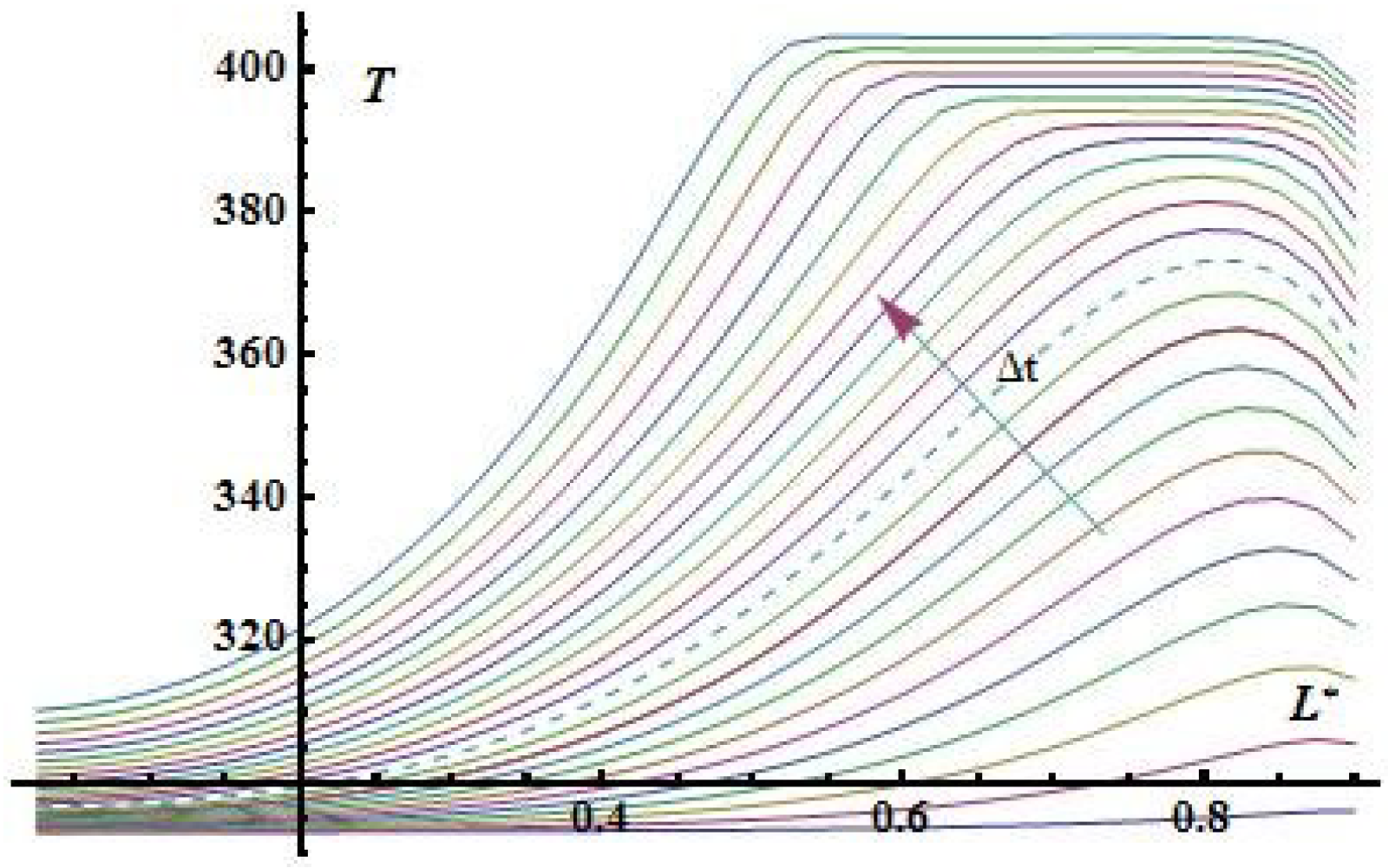
Figure 8.
The distribution of the temperature fiel.
Figure 8.
The distribution of the temperature fiel.
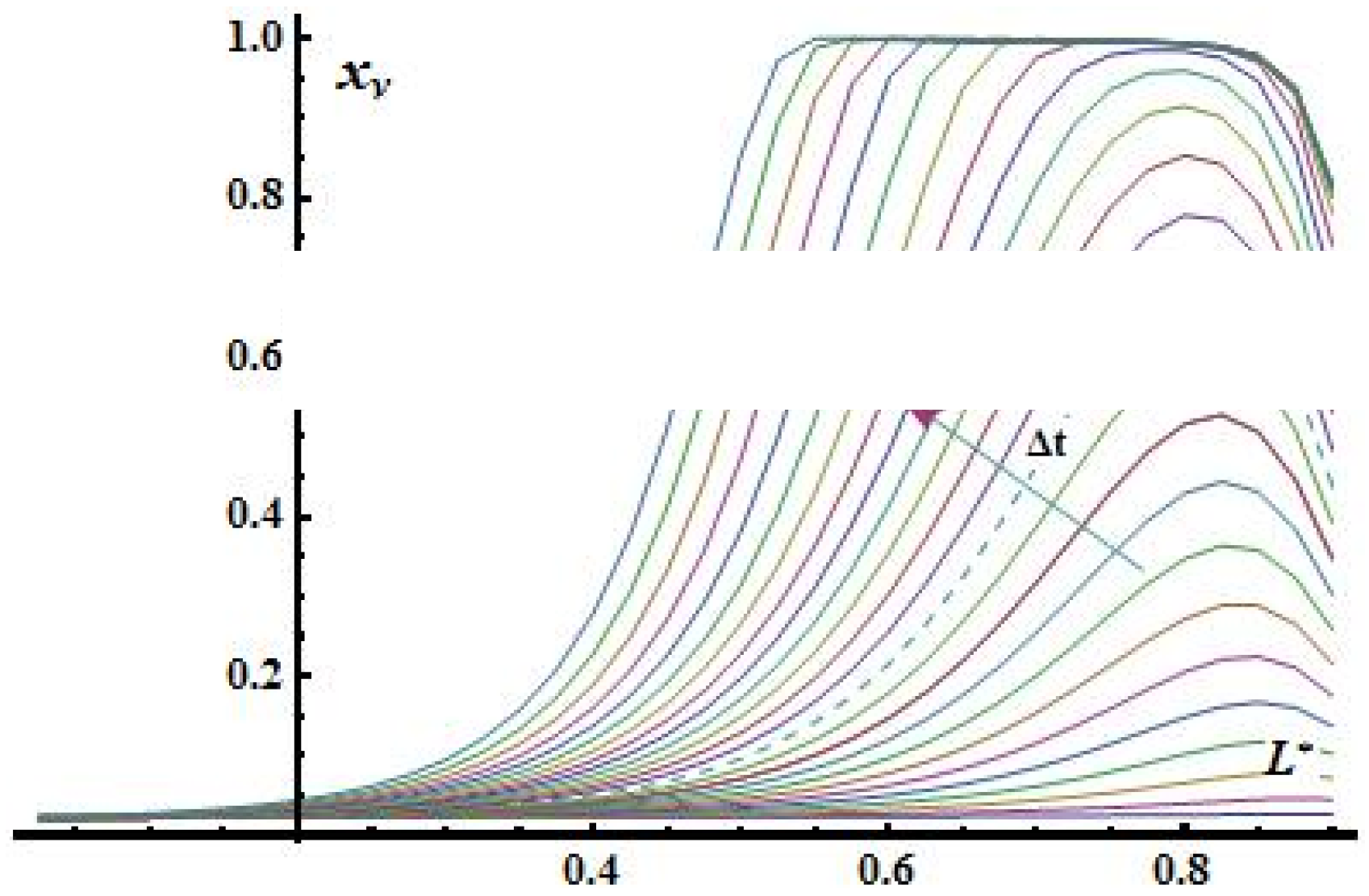
Figure 9.
The distribution of the molar fraction for water vapor.
Figure 9.
The distribution of the molar fraction for water vapor.
Conclusion III: Decreasing of moisture content is caused by increasing of evaporation sources that as a result of inhomogeneous microwave heating of plate and change of thermodynamic state of two component mixture.
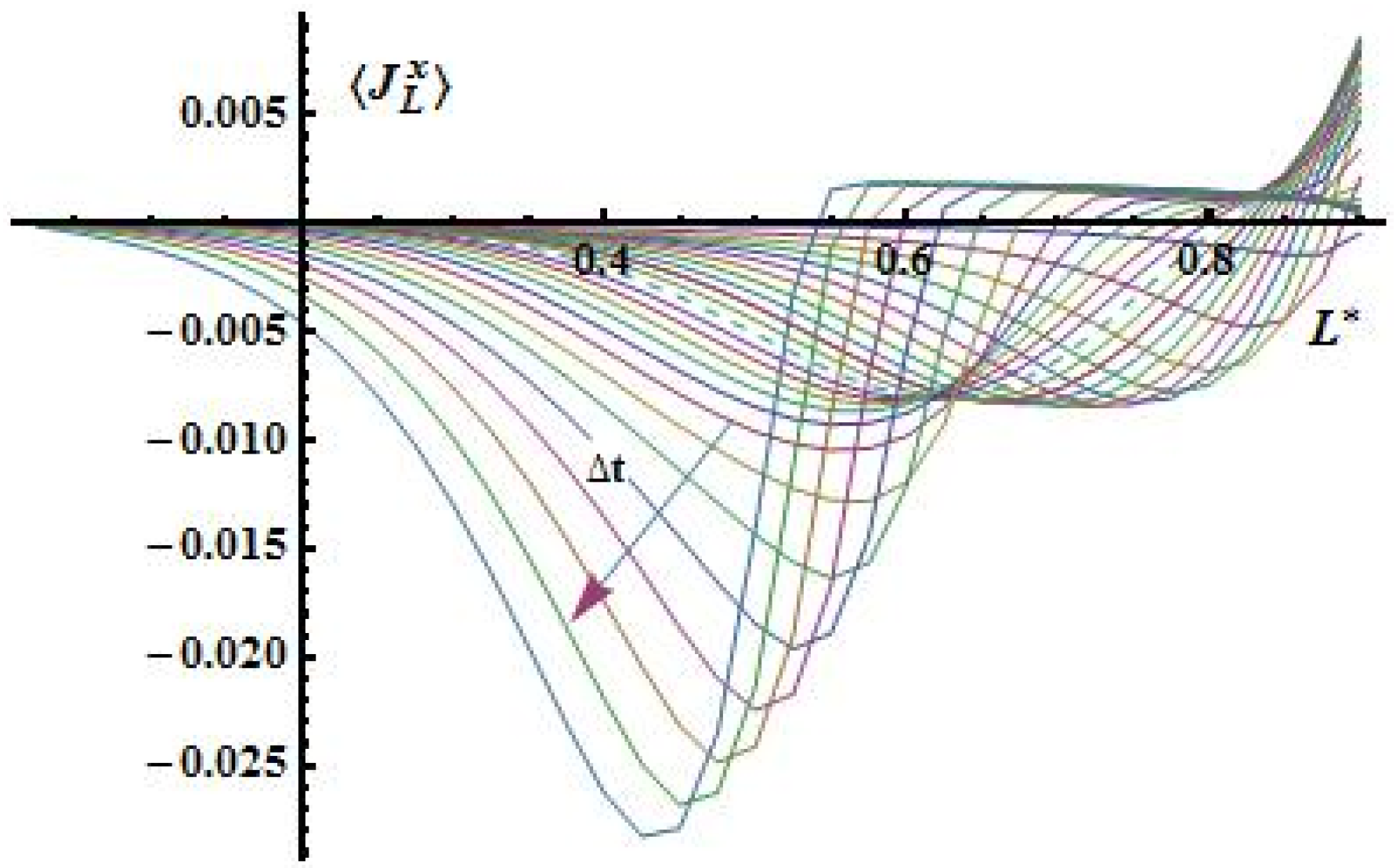
On the pictures below its depicted the distribution of flows by liquid (
Figure 10), water vapor (
Figure 11) and dry air (
Figure 14) along half thickness of plate in the different time intervals.
Figure 10.
Distribution of the liquid flow.
Figure 10.
Distribution of the liquid flow.
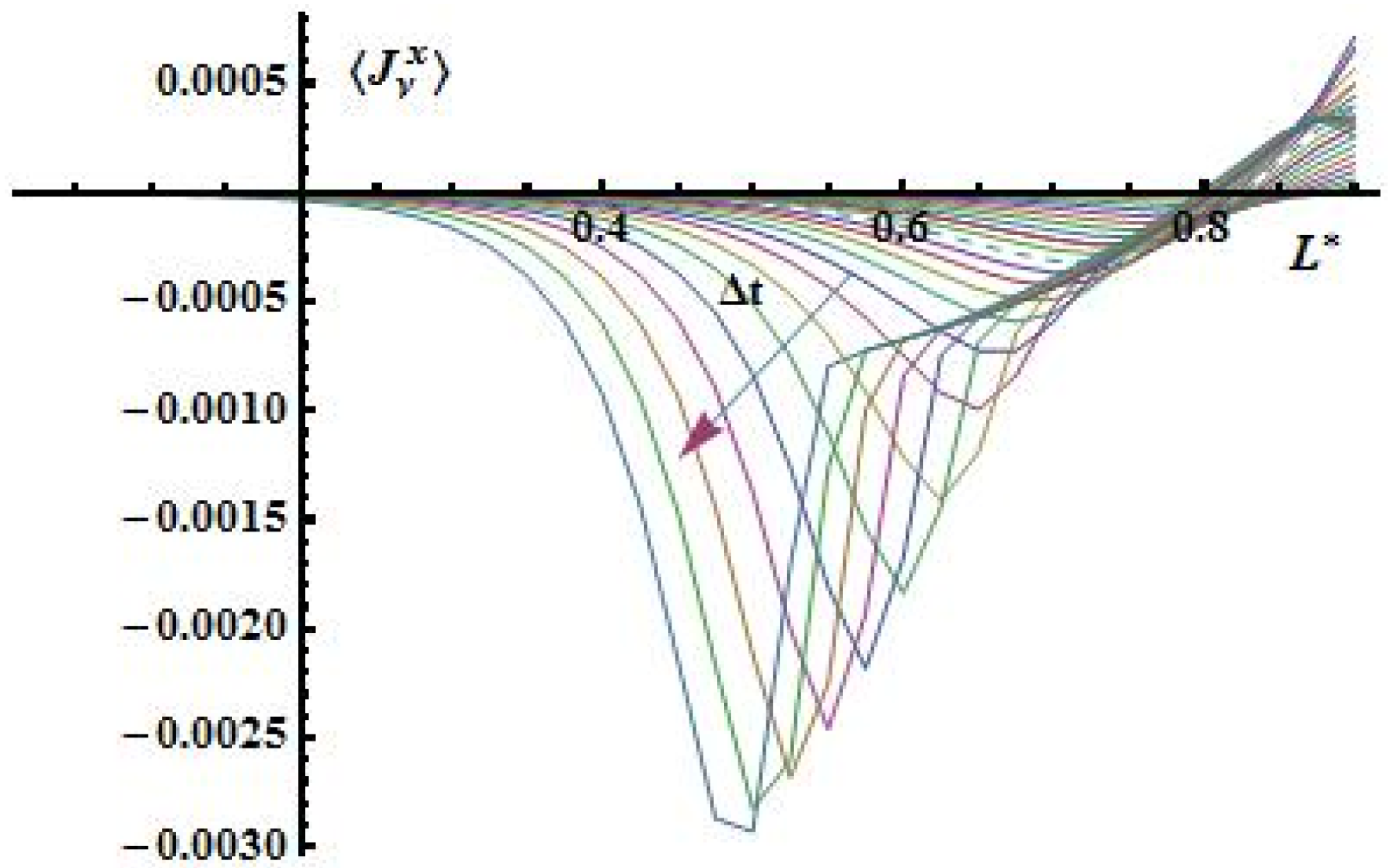
Figure 11.
Distribution of the water vapor flow.
Figure 11.
Distribution of the water vapor flow.
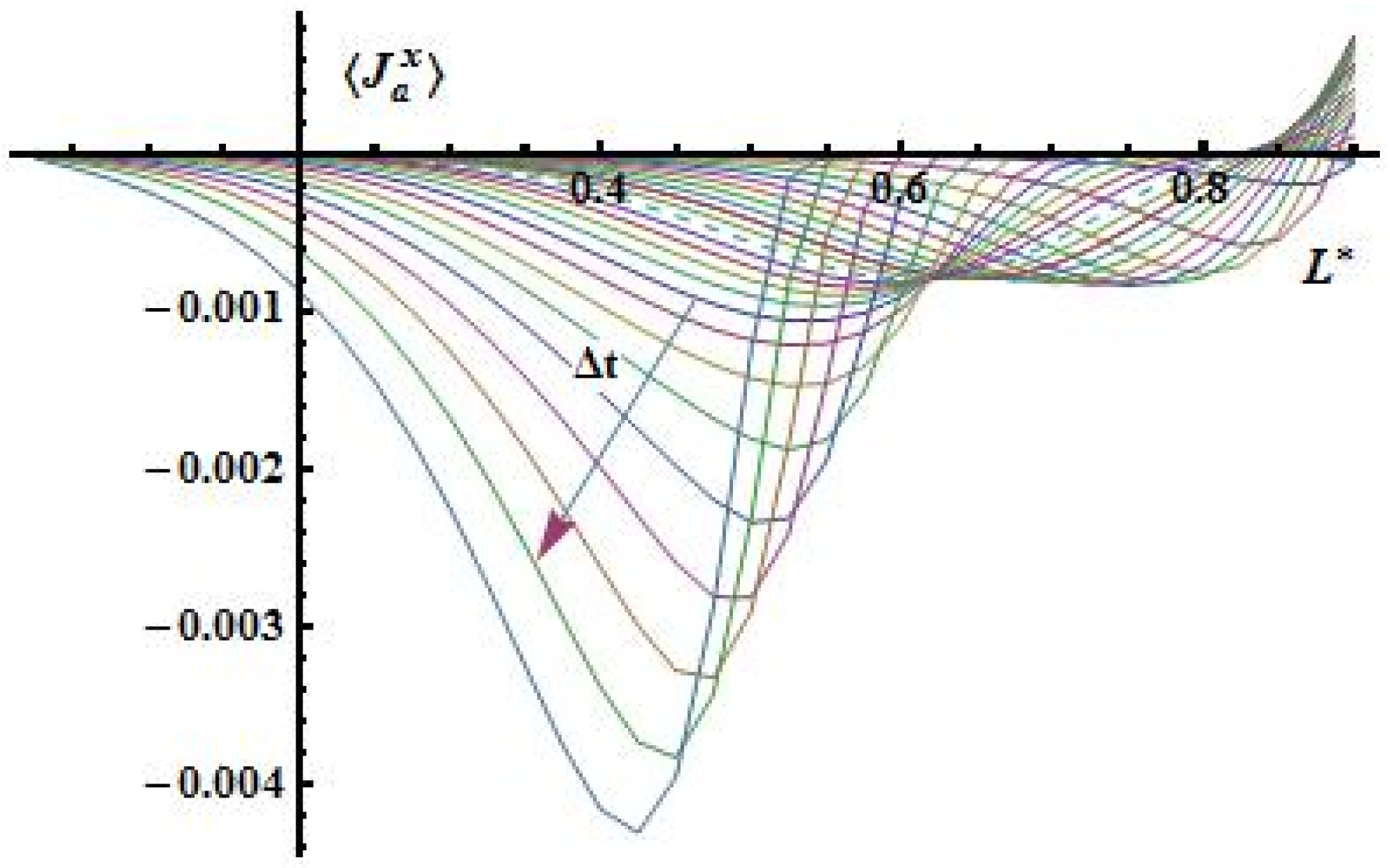
Figure 12.
Distribution of the dry air flow.
Figure 12.
Distribution of the dry air flow.
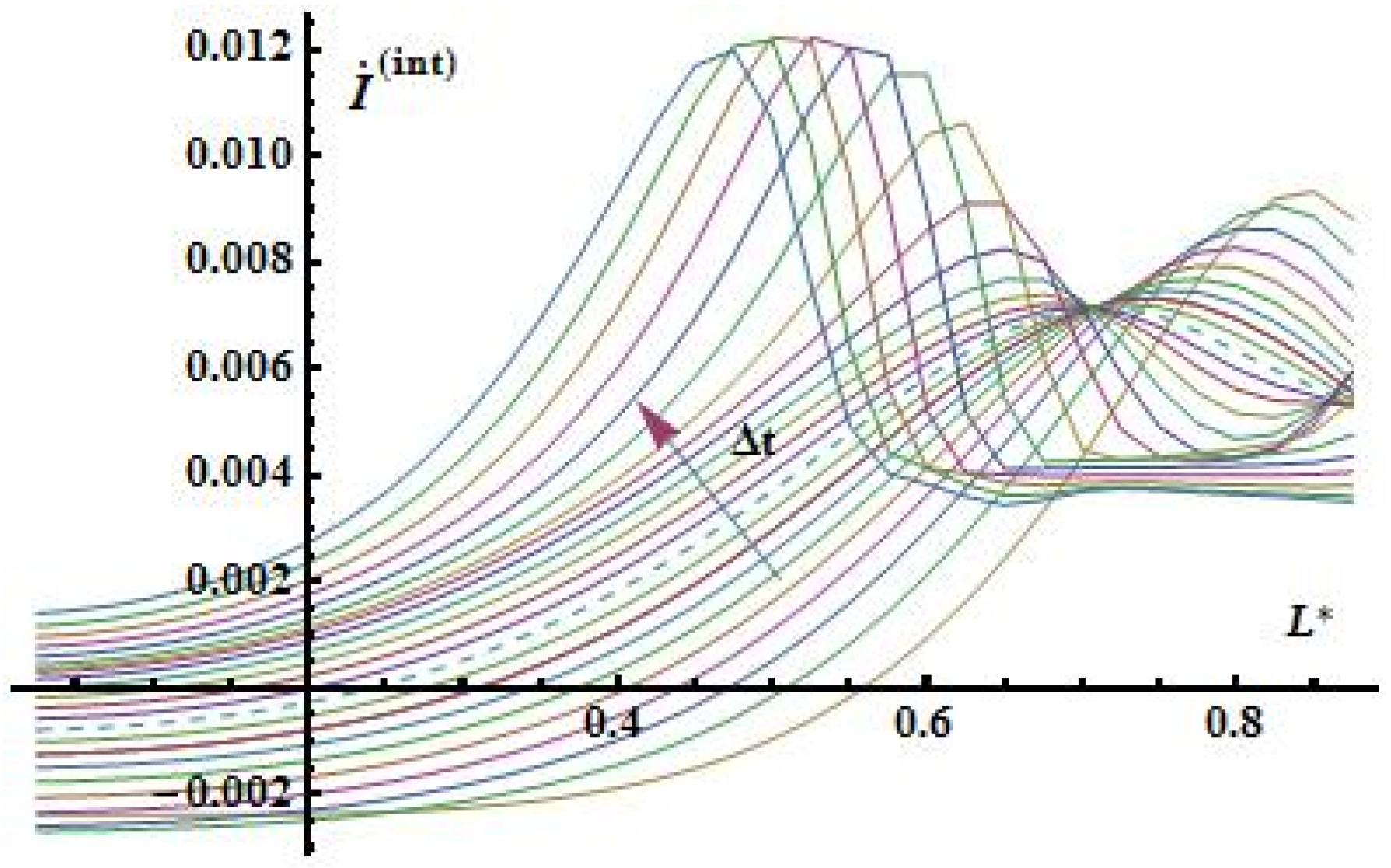
Figure 13.
Distribution of an internal evaporation sources.
Figure 13.
Distribution of an internal evaporation sources.
Conclusion IV: In the neighborhood of time point
, which corresponts to achievement of boiling temperature at normal conditions its fixed chane of flows distributionfor liquid and gas mixture components by thickness of plate (dashed line). This is due to the increase in the intensity (
Figure 13) of internal sources of evaporation
along the thickness of the plate.
The distribution of specific stresses (
Figure 14) and (
Figure 15) and small deformations (
Figure 16) and (
Figure 17) in a solid matrix (frame or skeleton) over the half-thickness of the plate is shown by the following graphical dependencies.
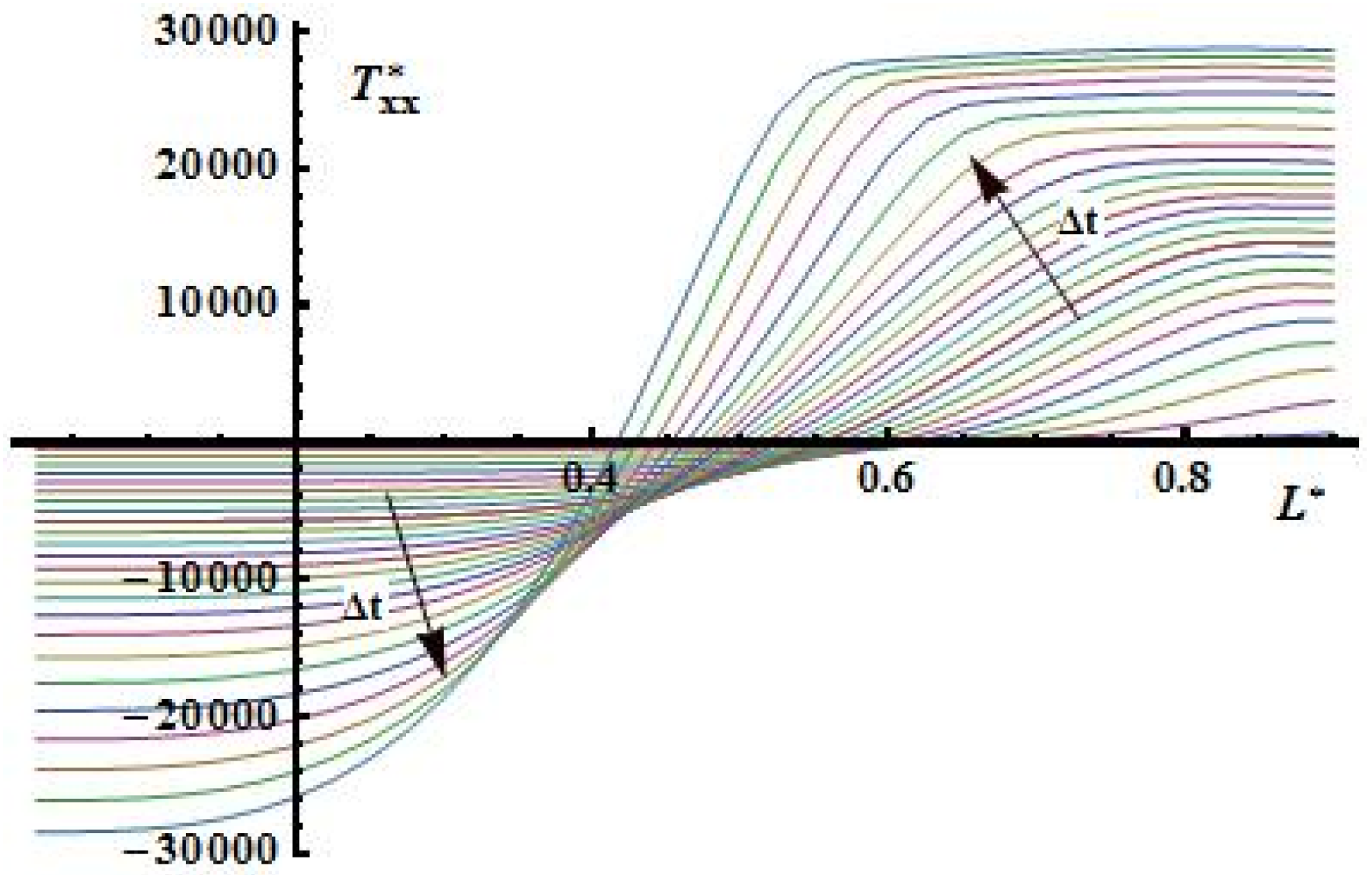
Figure 14.
Distribution of stress in longitudinal direction.
Figure 14.
Distribution of stress in longitudinal direction.
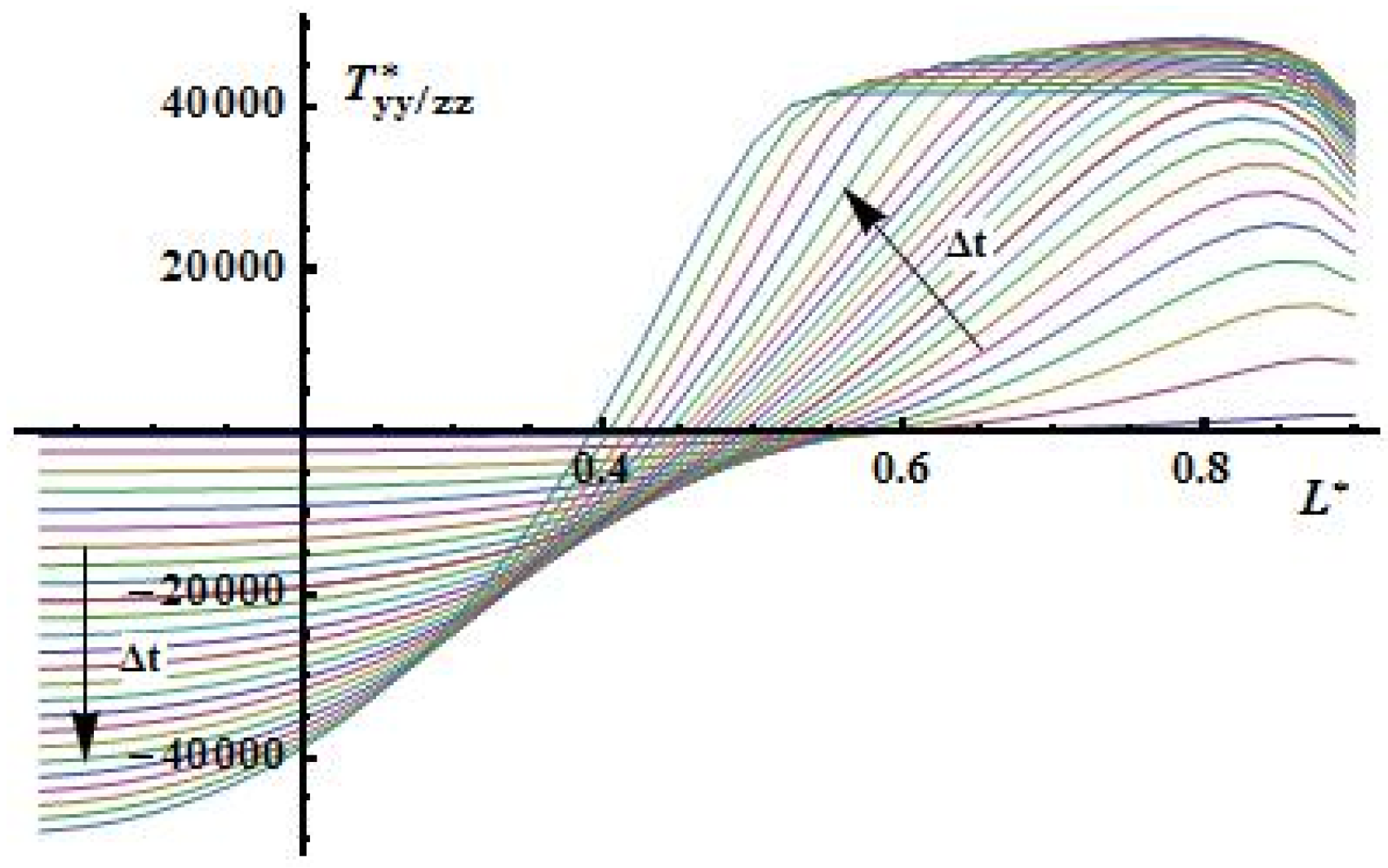
Figure 15.
Distribution of stress in tangential direction.
Figure 15.
Distribution of stress in tangential direction.
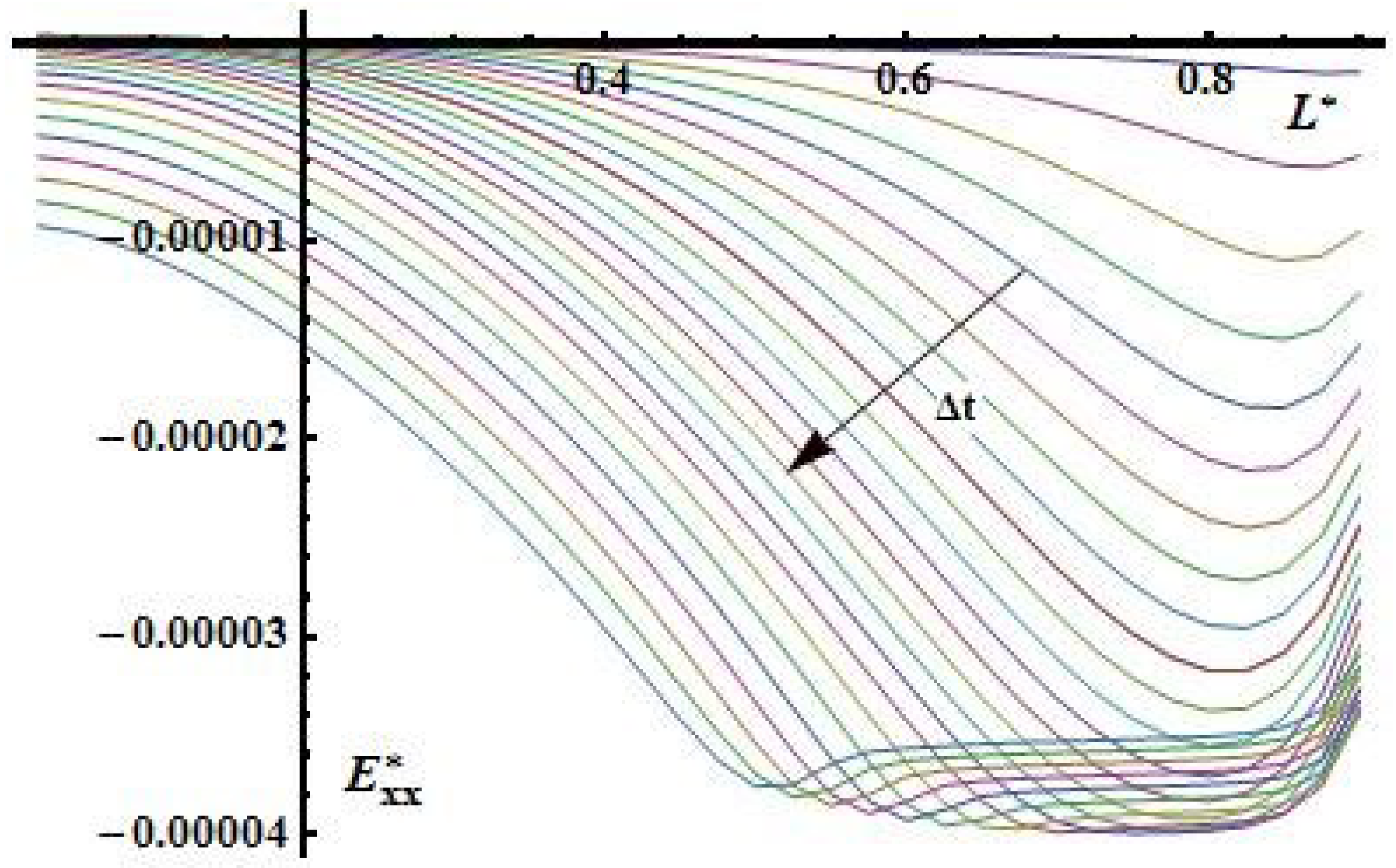
Figure 16.
Distribution of strains in longitudinal direction.
Figure 16.
Distribution of strains in longitudinal direction.
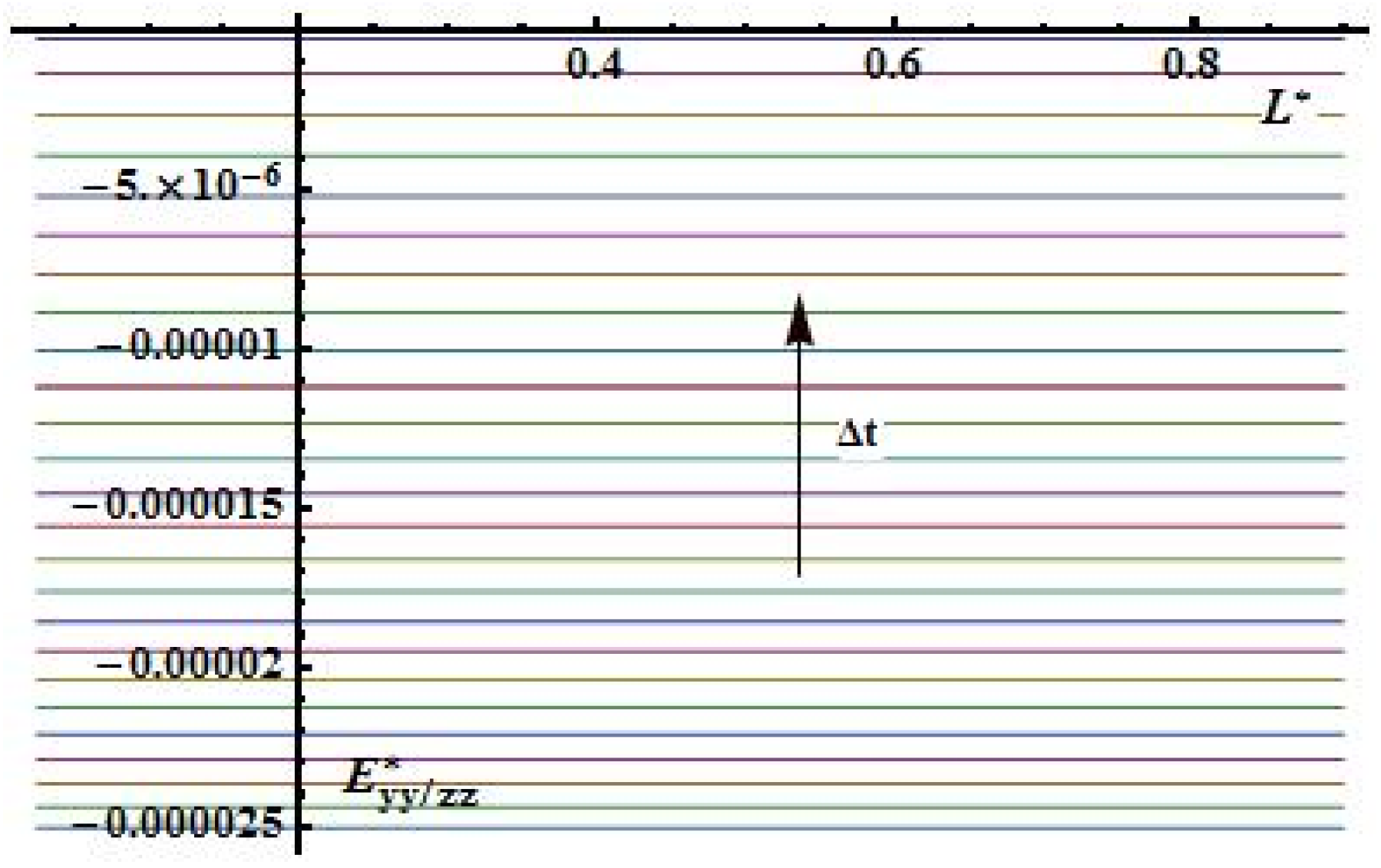
Figure 17.
Distribution of strains in tangential direction.
Figure 17.
Distribution of strains in tangential direction.
The dynamics of thermal stress distribution (
Figure 19) along the thickness of the plate is also shown in the form of the corresponding graphical dependence:
Figure 19.
Distribution of thermal stress in porous skeleton.
Figure 19.
Distribution of thermal stress in porous skeleton.
Form the pictures below (
Figure 14 and
Figure 15) it is shown that longitudinal components of stress tension is joined first with distribution of the temperature field (see
Figure 8) and nonlinear behavior of tangential component of stress tension is results of influence of nonlinear evaporation processes (see
Figure 7) especially near surface of sample.

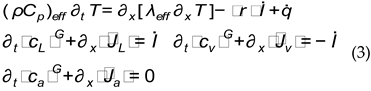
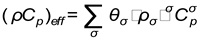 and
and 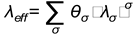 , here
, here  are the effective
thermal characteristics of porous material,
are the effective
thermal characteristics of porous material,  and
and 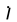 are the heat and
mass surfaces intensity correspondingly,
are the heat and
mass surfaces intensity correspondingly, 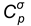 and
and 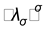 are the specific
capacity and thermo conduction of σ-phase
accordingly and
are the specific
capacity and thermo conduction of σ-phase
accordingly and  a is the latent
heat of vaporization.
a is the latent
heat of vaporization.
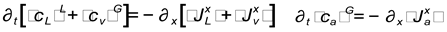
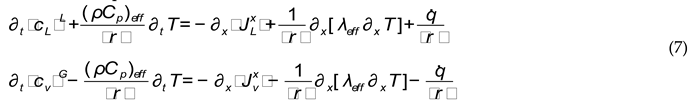
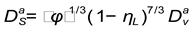 is the known Millington-Quirk [36] coefficient of diffusion for dry air component in the pores of
material at surface of evaporation.
is the known Millington-Quirk [36] coefficient of diffusion for dry air component in the pores of
material at surface of evaporation.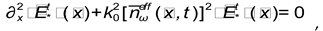
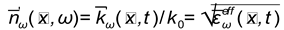 is
the complex refractive index, is the wave vector into the porous (inhomogenius) media, (where is the light velocity in vacuum) is the wave vector of electromagnetic irradiation in the vacuum, a is the corner frequency electromagnetic field ( is the linial frequency), and are the magnetic and electric constants in the vacuun correspondengly.
is
the complex refractive index, is the wave vector into the porous (inhomogenius) media, (where is the light velocity in vacuum) is the wave vector of electromagnetic irradiation in the vacuum, a is the corner frequency electromagnetic field ( is the linial frequency), and are the magnetic and electric constants in the vacuun correspondengly.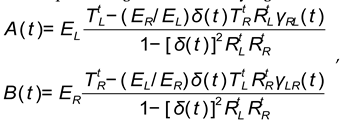
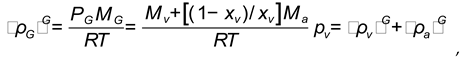
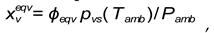
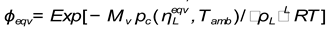 is
the initial value of relative humidity, is the corresponding equilibrium (beginning) value of wetting, which has been defined according to relation (10) above.
is
the initial value of relative humidity, is the corresponding equilibrium (beginning) value of wetting, which has been defined according to relation (10) above.