Submitted:
30 April 2025
Posted:
30 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Two-Photon Excitation Principle in Vapor Cell Optical Clocks
3. Conventional Vapor Cell Optical Clocks
3.1. Rubidium Two-Photon Optical Clock
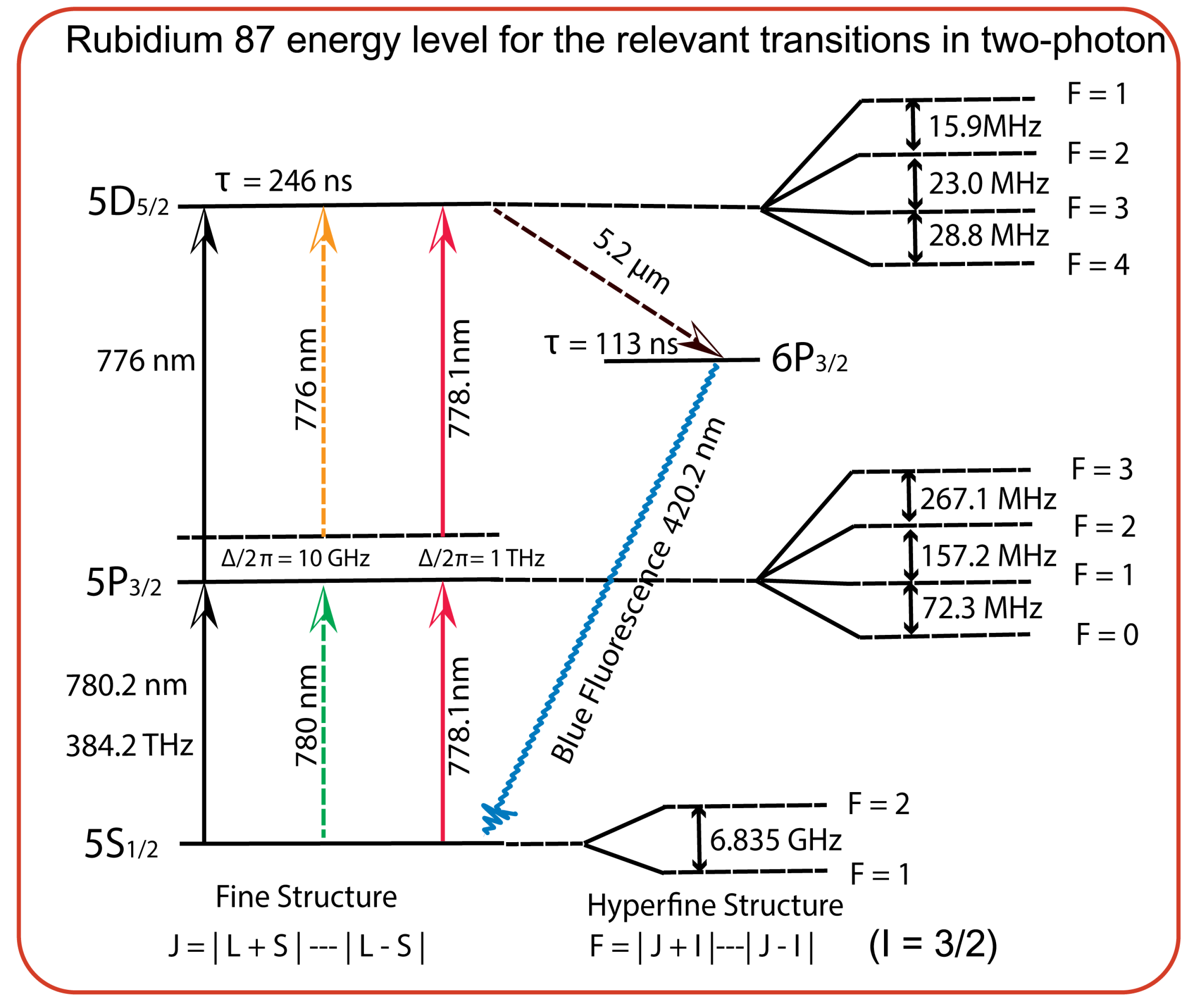
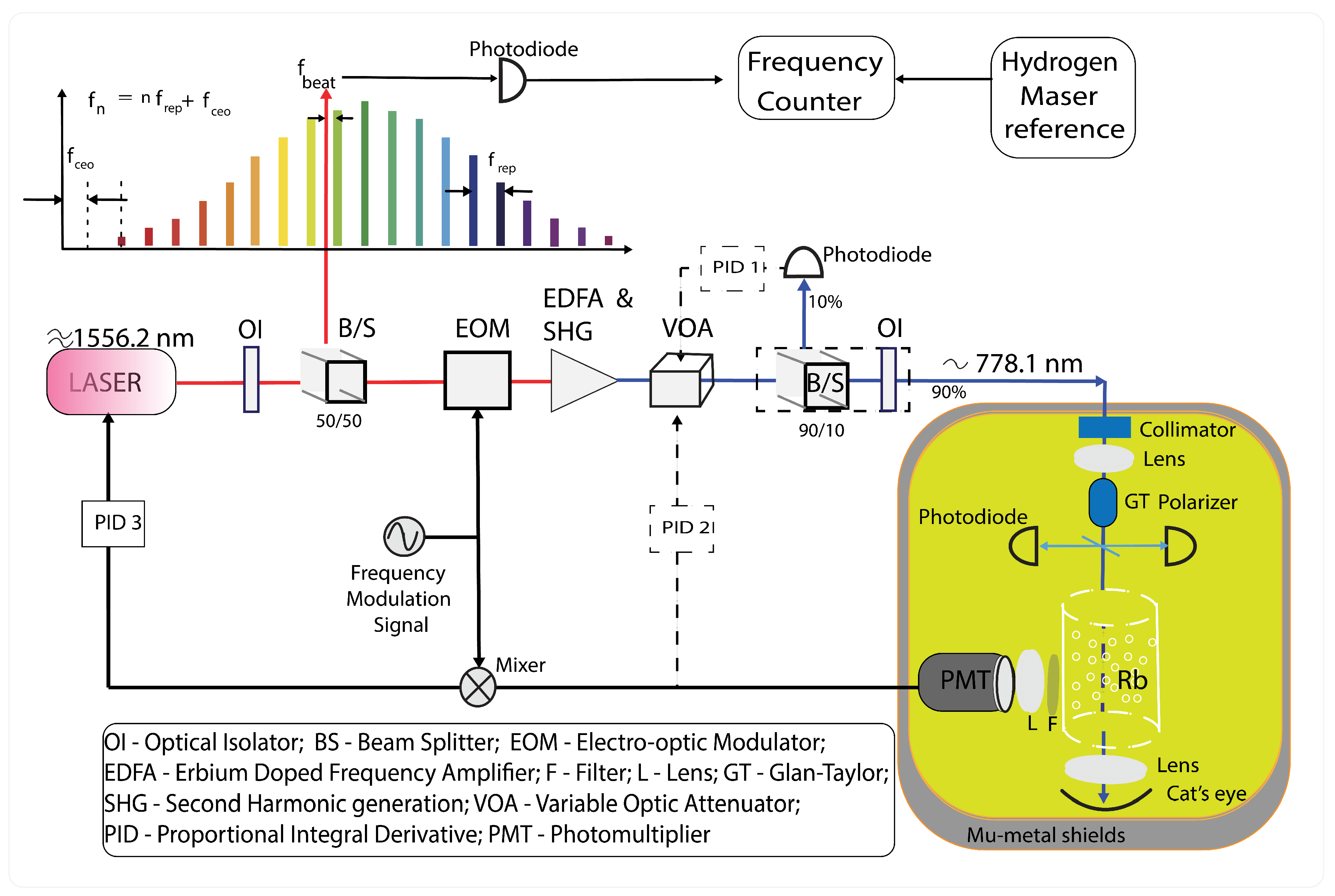
3.1.1. Two-Photon Single-Color Excitation
3.1.2. Difference in Experimental Schemes
| Articles | Signal Linewidth (kHz) | Cell Temperature (C) | Vapor Cell Dimension (mm) | Beam Radius (m) | Fractional Light Shift (per mW) | Reported Fractional Frequency Instability (1/) |
|---|---|---|---|---|---|---|
| Callejo et al. 2024 [114] | 450 | 110 | 25 diameter, 70 length cell | 100 | ||
| Erickson 2024 [171] | 774 | 100 | 1/2" diameter, 1/2" length fill stem, 5 active length | 230 | ||
| Li et al. 2024 [161] | 618 | 100 | ‡ | 800 | † | † |
| Beard et al. 2024 [116] | 106 | 5 | 490 | |||
| Lemke et al. 2022 [117] | 550 | 100 | 50 diameter, 10 length | 2100 | ||
| Maurice et al. 2020 [109] | 2200 | 80 | ‡ | Horizontal 200, Vertical 100 | ||
| Zachary et al. 2019 [110] | 1000 | 100 | ‡ | |||
| Gerginov et al. 2018 [118] | 795 | 90 | 25 diameter, 25 length | 400 | ** | |
| Martin et al. 2018 [119] | 609 | 100 | Rectangular prism of | 0.66(5) | ||
| Poulin et al. 2002 [120] | 410 | 90 | ‡ | 420 |
3.1.3. Two-Photon Two-Color Excitation
3.1.4. Experimental Schemes Discussion
3.2. Comparison and Drawbacks of the Single-Color and Two-Color Rb Schemes
3.3. Cesium Two-Photon Vapor Cell Optical Clock
3.3.1. Experimental Procedure
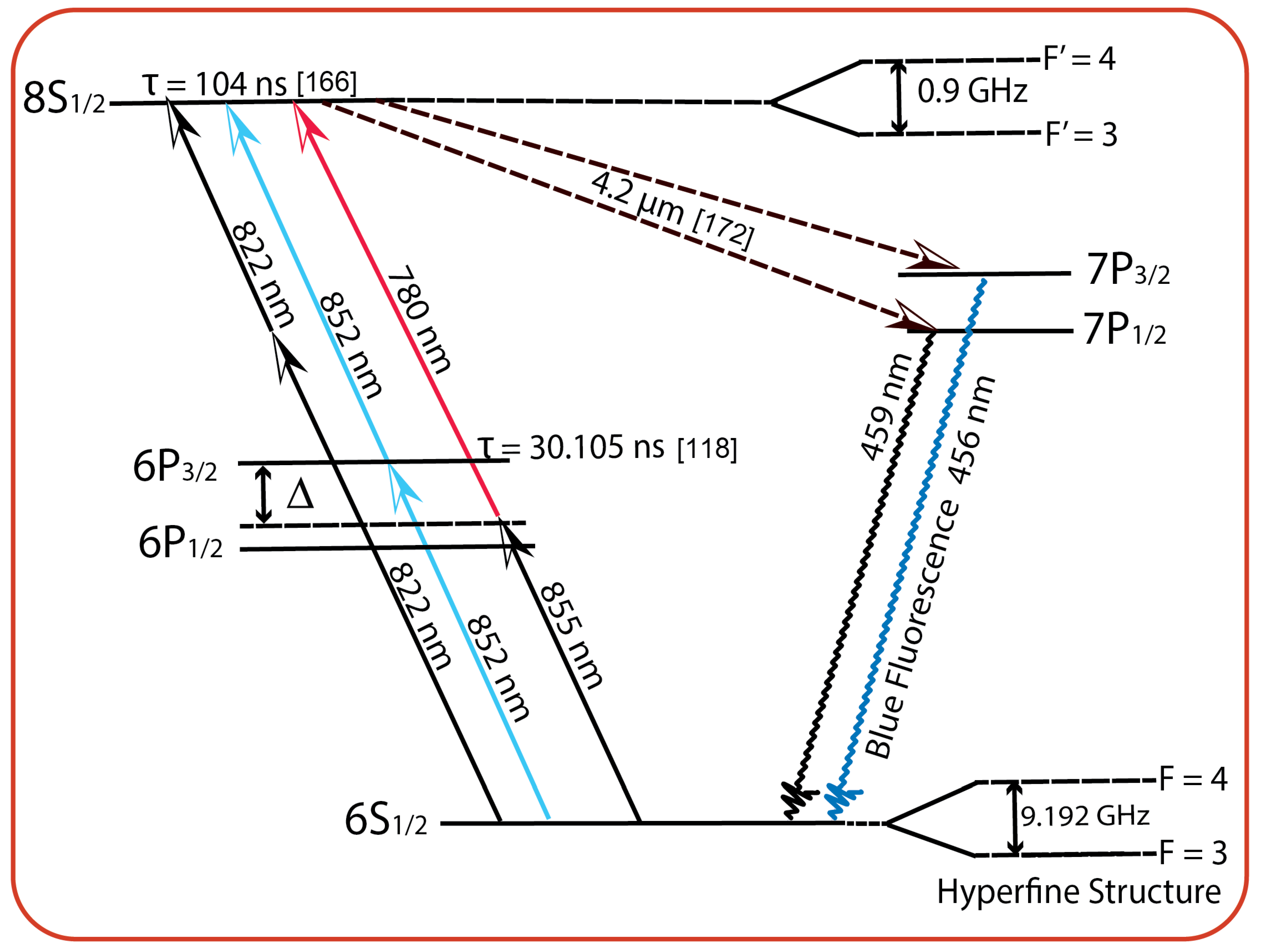
| Article | Signal Linewidth (MHz) | Beam waist (mm) | Cell Temperature( | Light Shift (Hz/mW) | Pressure Shift (kHz/Pa) | longest reported Fractional Frequency Instability |
|---|---|---|---|---|---|---|
| Shi et al. 2024 [143] | 0.03995 | ‡ | 35 | 30000 | ‡ | at s |
| Gusching et al. 2021 [142] | 14.2 | 2 | 62 | ‡ | ‡ | at s |
| Wu et al. 2013 [187] | 1.398 | 0.2 | 81 | -76.92 | ‡ | ‡ |
| Chen et al. 2011 [188] | 1.2 | ‡ | ‡ | ‡ | -290 | @ 400 s |
| Cheng et al. 2007 [190] | ‡ | 0.15 | 95 | -179 | -475 | ** @ 60 s |
| Fendel et al. 2007[195] | 1.2 | 0.72 | 22 | -12.89 | ‡ | |
| Hagel et al. 1999 [191] | 1.89 | 0.38 | <110 | -54 | -90 | @ 60 s |
3.4. Microcell-Based Optical Frequency Standards
4. Short-Term-Performance Metrics and Limitations
4.1. Photon Shot-Noise
4.2. Intermodulation Effect
4.2.1. Background Noise
5. Long-Term Performance Limiting Effects
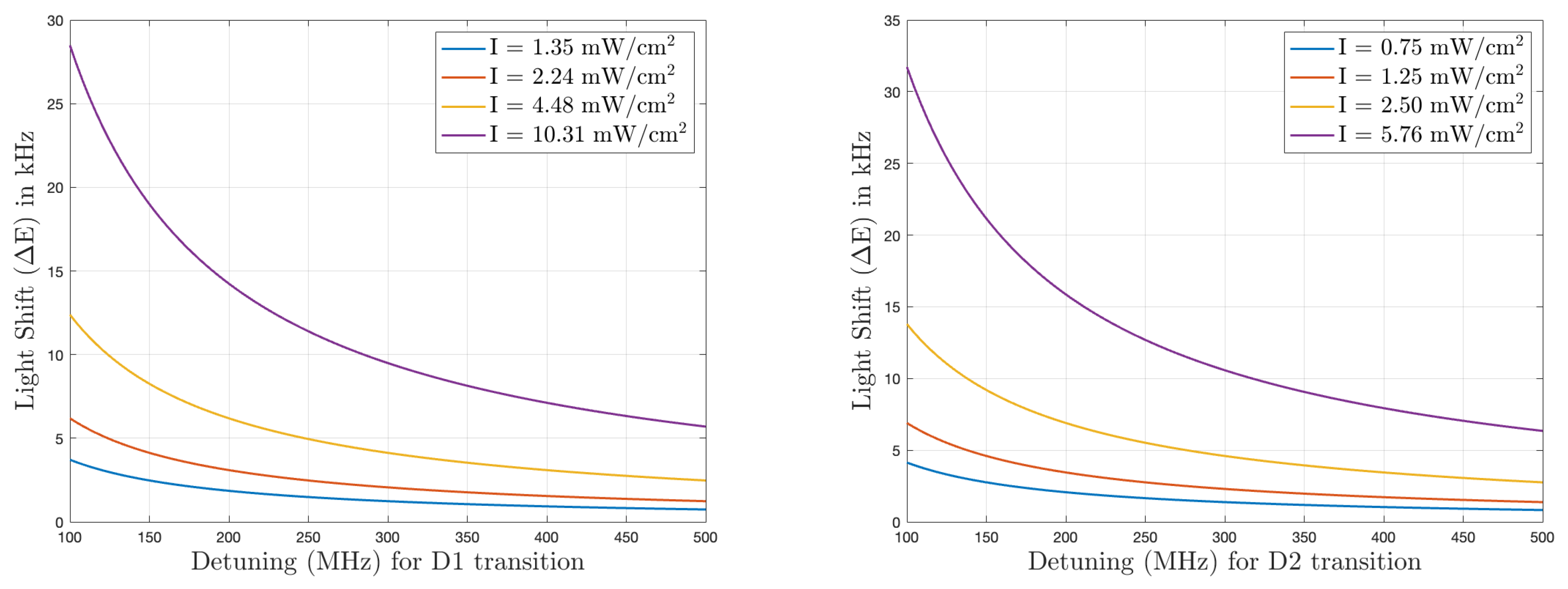
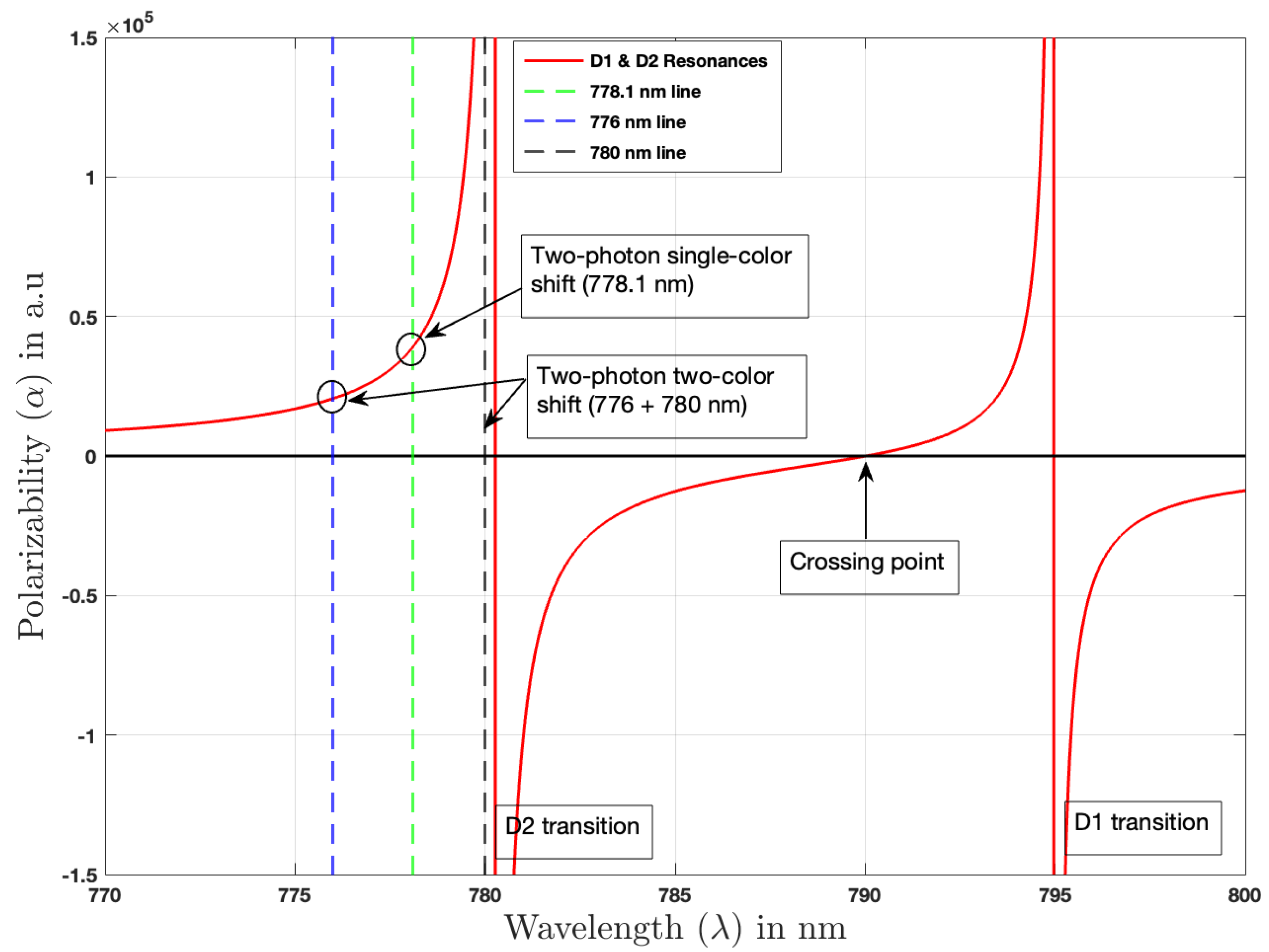
5.1. Light Shift Theory and Discussion
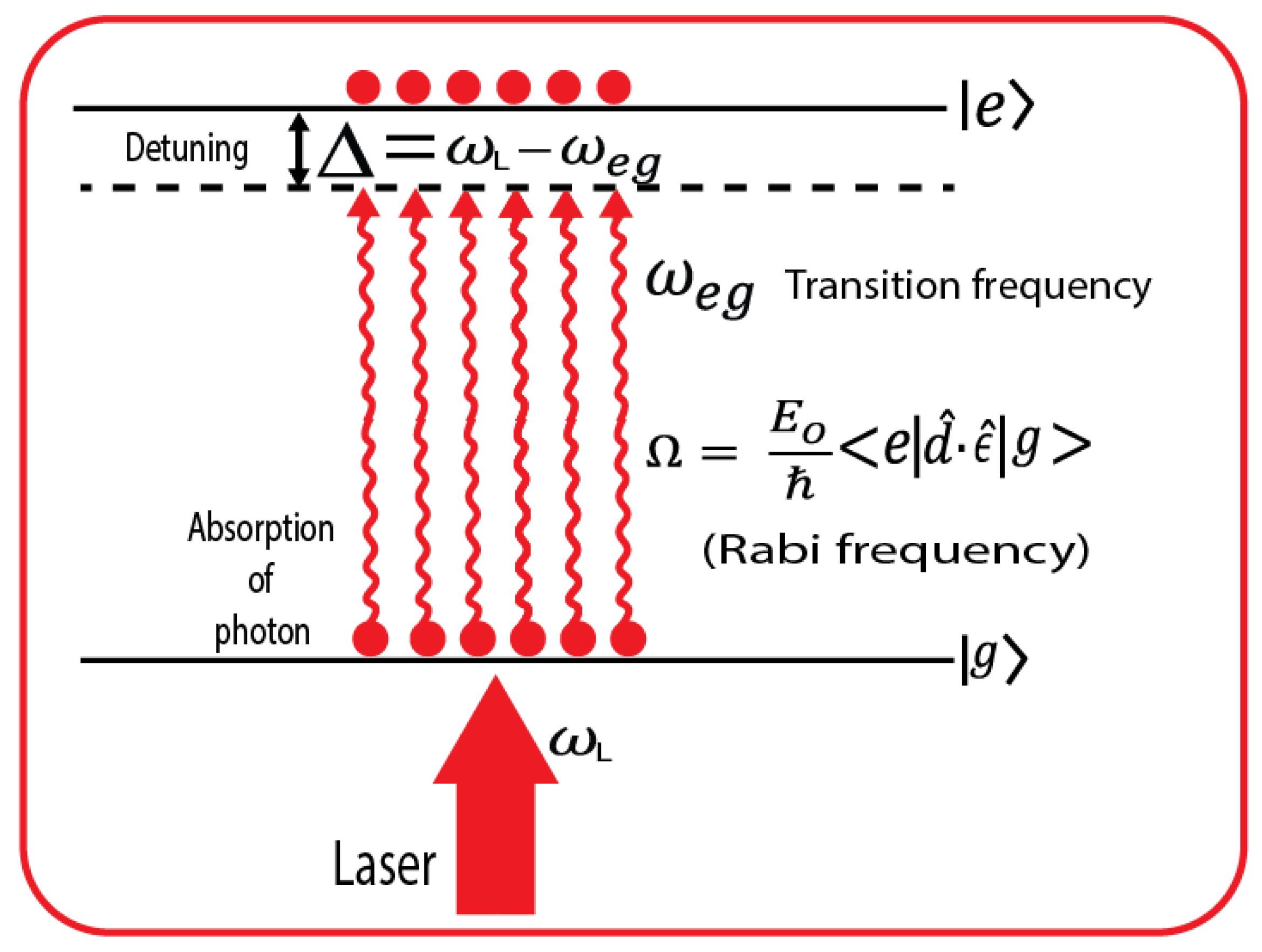
5.1.1. Beyond Two-Level System
5.2. Vapor Cell Temperature Fluctuation and Drift
6. Other Performance Limiting Effects
6.1. The Stochastic Nature of the Laser-Field
6.2. Vapor Cell Design and Functionality
6.2.1. The Signal Detection System
6.3. Density Effects and Impact Due to Spatial Inhomogeneities
6.4. Geometrical Broadening
6.5. Power Broadening
6.6. Second-Order Doppler Effect
6.7. Blackbody Radiation (BBR) Shift
6.8. Atomic Collisions
6.9. DC Stark Shift Contribution
7. Methods for Suppressing the Light-Shift Effects
7.1. Resonance-Offset Locking (ROL)
7.2. Combined Error Signal Method
7.3. Counter-Propagating Beam Approach
8. Conclusion and Prospects
Author Contributions
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Essen, L.; Parry, J.V. An atomic standard of frequency and time interval: a cesium resonator. Nature 1955, 176, 280–282. [Google Scholar] [CrossRef]
- Lombardi, M.A. A Historical Review of US Contributions to the Atomic Redefinition of the SI Second in 1967. Journal of Research of the National Institute of Standards and Technology 2017, 122, 1. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, N.F. History of early atomic clocks. Metrologia 2005, 42, S1. [Google Scholar] [CrossRef]
- Riley, W.J. A history of the rubidium frequency standard. IEEE UFFC-S History 2019, p. 2.
- Gill, P. When should we change the definition of the second? Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2011, 369, 4109–4130. [Google Scholar] [CrossRef]
- Margolis, H. Optical frequency standards and clocks. Contemporary Physics 2010, 51, 37–58. [Google Scholar] [CrossRef]
- Aeppli, A.; Kim, K.; Warfield, W.; Safronova, M.S.; Ye, J. Clock with 8× 10-19 systematic uncertainty. Physical Review Letters 2024, 133, 023401. [Google Scholar] [CrossRef]
- of Standards, N.I.; Technology. World’s most precise and accurate atomic clock pushes new frontiers in Physics. Available online: https://www.nist.gov/news-events/news.
- Wang, B.; Li, B.; Xiao, Q.; Mo, G.; Cai, Y.F. Space-based optical lattice clocks as gravitational wave detectors in search for new physics. Science China Physics, Mechanics & Astronomy 2025, 68, 249512. [Google Scholar]
- Bothwell, T.; Hunt, B.D.; Siegel, J.L.; Hassan, Y.S.; Grogan, T.; Kobayashi, T.; Gibble, K.; Porsev, S.G.; Safronova, M.S.; Brown, R.C.; et al. Lattice Light Shift Evaluations in a Dual-Ensemble Yb Optical Lattice Clock. Physical Review Letters 2025, 134, 033201. [Google Scholar] [CrossRef]
- Bothwell, T.; Brand, W.; Fasano, R.; Akin, T.; Whalen, J.; Grogan, T.; Chen, Y.J.; Pomponio, M.; Nakamura, T.; Rauf, B.; et al. Deployment of a transportable Yb optical<? pag∖break?> lattice clock. Optics Letters 2025, 50, 646–649. [Google Scholar]
- Liao, T.Y.; Liu, H.; Meng, F.; Wang, Q.; Yang, T.; Tian, H.C.; Lu, B.K.; Zhu, L.; Li, Y.; Lin, B.K.; et al. Remote comparison of two Sr optical lattice clocks through a 58 km fiber link. Chinese Physics Letters 2025. [Google Scholar] [CrossRef]
- Shinkai, H.; Takamoto, M.; Katori, H. Transportable optical lattice clocks and general relativity. arXiv preprint arXiv:2502.06104, arXiv:2502.06104 2025.
- Kale, Y.B.; Singh, A.; Gellesch, M.; Jones, J.M.; Morris, D.; Aldous, M.; Bongs, K.; Singh, Y. Field deployable atomics package for an optical lattice clock. Quantum Science and Technology 2022, 7, 045004. [Google Scholar] [CrossRef]
- Ohmae, N.; Takamoto, M.; Takahashi, Y.; Kokubun, M.; Araki, K.; Hinton, A.; Ushijima, I.; Muramatsu, T.; Furumiya, T.; Sakai, Y.; et al. Transportable strontium optical lattice clocks operated outside laboratory at the level of 10- 18 uncertainty. Advanced Quantum Technologies 2021, 4, 2100015. [Google Scholar] [CrossRef]
- Hobson, R.; Bowden, W.; Vianello, A.; Silva, A.; Baynham, C.F.; Margolis, H.S.; Baird, P.E.; Gill, P.; Hill, I.R. A strontium optical lattice clock with 1× 10- 17 uncertainty and measurement of its absolute frequency. Metrologia 2020, 57, 065026. [Google Scholar] [CrossRef]
- Kong, D.H.; Wang, Z.H.; Guo, F.; Zhang, Q.; Lu, X.T.; Wang, Y.B.; Chang, H. A transportable optical lattice clock at the National Time Service Center. Chinese Physics B 2020, 29, 070602. [Google Scholar] [CrossRef]
- Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.L.; Ye, J.; Kennedy, C.J. JILA SrI optical lattice clock with uncertainty of 2.0×10-18. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
- Bloom, B.; Nicholson, T.; Williams, J.; Campbell, S.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.; Ye, J. An optical lattice clock with accuracy and stability at the 10- 18 level. Nature 2014, 506, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Poli, N.; Schioppo, M.; Vogt, S.; Falke, S.; Sterr, U.; Lisdat, C.; Tino, G. A transportable strontium optical lattice clock. Applied Physics B 2014, 117, 1107–1116. [Google Scholar] [CrossRef]
- Takamoto, M.; Hong, F.L.; Higashi, R.; Katori, H. An optical lattice clock. Nature 2005, 435, 321–324. [Google Scholar] [CrossRef]
- McGrew, W.; Zhang, X.; Fasano, R.; Schäffer, S.; Beloy, K.; Nicolodi, D.; Brown, R.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87–90. [Google Scholar] [CrossRef]
- Koller, S.; Grotti, J.; Vogt, S.; Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Transportable optical lattice clock with 7×10-17 uncertainty. Physical review letters 2017, 118, 073601. [Google Scholar] [CrossRef]
- Origlia, S.; Pramod, M.S.; Schiller, S.; Singh, Y.; Bongs, K.; Schwarz, R.; Al-Masoudi, A.; Dörscher, S.; Herbers, S.; Häfner, S.; et al. Towards an optical clock for space: Compact, high-performance optical lattice clock based on bosonic atoms. Physical Review A 2018, 98, 053443. [Google Scholar] [CrossRef]
- Vogt, S.; Häfner, S.; Grotti, J.; Koller, S.; Al-Masoudi, A.; Sterr, U.; Lisdat, C. A transportable optical lattice clock. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2016, Vol. 723, p. 012020.
- Hausser, H.; Keller, J.; Nordmann, T.; Bhatt, N.; Kiethe, J.; Liu, H.; Richter, I.; von Boehn, M.; Rahm, J.; Weyers, S.; et al. In+ 115-Yb+ 172 Coulomb Crystal Clock with 2.5× 10-18 Systematic Uncertainty. Physical Review Letters 2025, 134, 023201. [Google Scholar] [CrossRef] [PubMed]
- King, S.A.; Spieß, L.J.; Micke, P.; Wilzewski, A.; Leopold, T.; Benkler, E.; Lange, R.; Huntemann, N.; Surzhykov, A.; Yerokhin, V.A.; et al. An optical atomic clock based on a highly charged ion. Nature 2022, 611, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Gao, K. The 40Ca+ ion optical clock. National science review 2020, 7, 1799–1801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Huang, Y.; Zhang, H.; Hao, Y.; Zeng, M.; Guan, H.; Gao, K. Progress on the 40Ca+ ion optical clock. Chinese Physics B 2020, 29, 074209. [Google Scholar] [CrossRef]
- Diddams, S.A.; Udem, T.; Bergquist, J.; Curtis, E.; Drullinger, R.; Hollberg, L.; Itano, W.M.; Lee, W.; Oates, C.; Vogel, K.; et al. An optical clock based on a single trapped 199Hg+ ion. Science 2001, 293, 825–828. [Google Scholar] [CrossRef]
- Zeng, M.; Huang, Y.; Zhang, B.; Hao, Y.; Ma, Z.; Hu, R.; Zhang, H.; Chen, Z.; Wang, M.; Guan, H.; et al. Toward a transportable Ca+ optical clock with a systematic uncertainty of 4.8×10-18. Physical Review Applied 2023, 19, 064004. [Google Scholar] [CrossRef]
- Huntemann, N.; Sanner, C.; Lipphardt, B.; Tamm, C.; Peik, E. Single-ion atomic clock with 3×10-18 systematic uncertainty. Physical review letters 2016, 116, 063001. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Zeng, M.; Hao, Y.; Ma, Z.; Zhang, H.; Guan, H.; Chen, Z.; Wang, M.; Gao, K. Liquid-nitrogen-cooled Ca+ optical clock with systematic uncertainty of 3×10-18. Physical Review Applied 2022, 17, 034041. [Google Scholar] [CrossRef]
- Marshall, M.C.; Castillo, D.A.R.; Arthur-Dworschack, W.J.; Aeppli, A.; Kim, K.; Lee, D.; Warfield, W.; Hinrichs, J.; Nardelli, N.V.; Fortier, T.M.; et al. High-Stability Single-Ion Clock with 5.5×10-19 Systematic Uncertainty. arXiv preprint arXiv:2504.13071, arXiv:2504.13071 2025.
- Huntemann, N.; Okhapkin, M.; Lipphardt, B.; Weyers, S.; Tamm, C.; Peik, E. High-accuracy optical clock based on the octupole transition in Yb+ 171. Physical Review Letters 2012, 108, 090801. [Google Scholar] [CrossRef]
- Beeks, K.; Sikorsky, T.; Schumm, T.; Thielking, J.; Okhapkin, M.V.; Peik, E. The thorium-229 low-energy isomer and the nuclear clock. Nature Reviews Physics 2021, 3, 238–248. [Google Scholar] [CrossRef]
- Kraemer, S.; Moens, J.; Athanasakis-Kaklamanakis, M.; Bara, S.; Beeks, K.; Chhetri, P.; Chrysalidis, K.; Claessens, A.; Cocolios, T.E.; Correia, J.G.; et al. Observation of the radiative decay of the 229Th nuclear clock isomer. Nature 2023, 617, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; von der Wense, L.; Doyle, J.F.; Higgins, J.S.; Ooi, T.; Friebel, H.U.; Ye, J.; Elwell, R.; Terhune, J.; Morgan, H.; et al. 229ThF4 thin films for solid-state nuclear clocks. Nature 2024, 636, 603–608. [Google Scholar] [CrossRef] [PubMed]
- Thirolf, P. Shedding Light on the Thorium-229 Nuclear Clock Isomer. Physics 2024, 17, 71. [Google Scholar] [CrossRef]
- Scott, J.P.; Potvliege, R.; Carty, D.; Jones, M.P. Trap induced broadening in a potential hydrogen lattice clock. Metrologia 2024, 61, 025001. [Google Scholar] [CrossRef]
- Baker, C.; Bertsche, W.; Capra, A.; Carruth, C.; Cesar, C.; Charlton, M.; Christensen, A.; Collister, R.; Mathad, A.C.; Eriksson, S.; et al. Laser cooling of antihydrogen atoms. Nature 2021, 592, 35–42. [Google Scholar] [CrossRef]
- Lane, I.C. Production of ultracold hydrogen and deuterium via Doppler-cooled Feshbach molecules. Physical Review A 2015, 92, 022511. [Google Scholar] [CrossRef]
- Gabrielse, G.; Glowacz, B.; Grzonka, D.; Hamley, C.; Hessels, E.; Jones, N.; Khatri, G.; Lee, S.; Meisenhelder, C.; Morrison, T.; et al. Lyman-α source for laser cooling antihydrogen. Optics letters 2018, 43, 2905–2908. [Google Scholar] [CrossRef]
- Burkley, Z.; Yost, D. Proposal for loading hydrogen into a magic wavelength optical lattice. Bulletin of the American Physical Society 2018, 63. [Google Scholar]
- Liu, Y.; Zhu, X.; Chen, C. Millisecond pulsar augmented atomic clock ensemble timescale algorithm. Measurement 2025, p. 117033.
- Zheng, Z.H.; Liu, Y.; Shen, D.; Feng, F.; Liu, J.L.; Ma, Y.X.; Zhu, X.W. Research on Pulsar Time Steered Atomic Time Algorithm Based on DPLL. Research in Astronomy and Astrophysics 2024, 24, 035019. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Z.; Zhao, C.; Li, B.; Tong, M.; Gao, Y.; Yang, T. Research on establishing a joint time-scale of pulsar time and atomic time based on a wavelet analysis method. Monthly Notices of the Royal Astronomical Society 2024, 529, 1082–1090. [Google Scholar] [CrossRef]
- Critchley-Marrows, J.; Wu, X.; Ambatali, C.; Nakasuka, S. Pulsar Timing for Clock Stability–Exploring an Autonomous and Resilient Approach to Timing Using Radio Pulsars. In Proceedings of the Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), 2023, pp. 3175–3189.
- Hobbs, G.; Guo, L.; Caballero, R.; Coles, W.; Lee, K.; Manchester, R.; Reardon, D.; Matsakis, D.; Tong, M.; Arzoumanian, Z.; et al. A pulsar-based time-scale from the International Pulsar Timing Array. Monthly Notices of the Royal Astronomical Society 2020, 491, 5951–5965. [Google Scholar] [CrossRef]
- Taylor, J.H. Millisecond pulsars: Nature’s most stable clocks. Proceedings of the IEEE 1991, 79, 1054–1062. [Google Scholar] [CrossRef]
- Kim, M. Design and Analysis of High-Stability THz Molecular Clock System. PhD thesis, Massachusetts Institute of Technology, 2022.
- Leung, K.; Iritani, B.; Tiberi, E.; Majewska, I.; Borkowski, M.; Moszynski, R.; Zelevinsky, T. Terahertz vibrational molecular clock with systematic uncertainty at the 10-14 level. Physical Review X 2023, 13, 011047. [Google Scholar] [CrossRef]
- Hanneke, D.; Kuzhan, B.; Lunstad, A. Optical clocks based on molecular vibrations as probes of variation of the proton-to-electron mass ratio. Quantum Science and Technology 2020, 6, 014005. [Google Scholar] [CrossRef]
- Roslund, J.D.; Cingöz, A.; Lunden, W.D.; Partridge, G.B.; Kowligy, A.S.; Roller, F.; Sheredy, D.B.; Skulason, G.E.; Song, J.P.; Abo-Shaeer, J.R.; et al. Optical clocks at sea. Nature 2024, 628, 736–740. [Google Scholar] [CrossRef] [PubMed]
- Döringshoff, K.; Gutsch, F.B.; Schkolnik, V.; Kürbis, C.; Oswald, M.; Pröbster, B.; Kovalchuk, E.V.; Bawamia, A.; Smol, R.; Schuldt, T.; et al. Iodine frequency reference on a sounding rocket. Physical Review Applied 2019, 11, 054068. [Google Scholar] [CrossRef]
- Ye, J.; Ma, L.S.; Hall, J.L. Molecular iodine clock. Physical review letters 2001, 87, 270801. [Google Scholar] [CrossRef]
- Day, C. New Accuracy Record for Molecular Lattice Clock. Physics 2023, 16, 36. [Google Scholar] [CrossRef]
- Mawdsley, J.P. Terahertz frequency synthesis in CMOS for a chip-scale molecular clock. PhD thesis, Massachusetts Institute of Technology, 2019.
- Wang, C.; Yi, X.; Mawdsley, J.; Kim, M.; Hu, Z.; Zhang, Y.; Perkins, B.; Han, R. Chip-scale molecular clock. IEEE Journal of Solid-State Circuits 2018, 54, 914–926. [Google Scholar] [CrossRef]
- Fortier, T.; Baumann, E. 20 years of developments in optical frequency comb technology and applications. Communications Physics 2019, 2, 153. [Google Scholar] [CrossRef]
- Hall, J.L. Optical frequency measurement: 40 years of technology revolutions. IEEE Journal of Selected Topics in Quantum Electronics 2000, 6, 1136–1144. [Google Scholar] [CrossRef]
- Sinclair, L.C.; Coddington, I.; Swann, W.C.; Rieker, G.B.; Hati, A.; Iwakuni, K.; Newbury, N.R. Operation of an optically coherent frequency comb outside the metrology lab. Optics Express 2014, 22, 6996–7006. [Google Scholar] [CrossRef]
- Jana, S.; Sahoo, B.; Sharma, A. Progress towards the development of a portable all-optical atomic clock based on a two-photon transition in warm atomic vapor. In Proceedings of the 2022 URSI Regional Conference on Radio Science (USRI-RCRS). IEEE, 2022, pp. 1–4.
- Gill, P. Optical frequency standards. Metrologia 2005, 42, S125–S137. [Google Scholar] [CrossRef]
- Bandi, T.N. A comprehensive overview of atomic clocks and their applications. Demo Journal 2024, 1, 40–50. [Google Scholar] [CrossRef]
- Strangfeld, A.; Kanthak, S.; Schiemangk, M.; Wiegand, B.; Wicht, A.; Ling, A.; Krutzik, M. Prototype of a compact rubidium-based optical frequency reference for operation on nanosatellites. Journal of the Optical Society of America B 2021, 38, 1885–1891. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. Atomic-Clock Detection of CNO-Based Dark Matter; IntechOpen, 2024.
- Safronova, M.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Reviews of Modern Physics 2018, 90, 025008. [Google Scholar] [CrossRef]
- Dimarcq, N.; Gertsvolf, M.; Mileti, G.; Bize, S.; Oates, C.; Peik, E.; Calonico, D.; Ido, T.; Tavella, P.; Meynadier, F.; et al. Roadmap towards the redefinition of the second. Metrologia 2024, 61, 012001. [Google Scholar] [CrossRef]
- Lodewyck, J. On a definition of the SI second with a set of optical clock transitions. Metrologia 2019, 56, 055009. [Google Scholar] [CrossRef]
- Kristen Cote, S.J.; Ryan Zazo, L.M.; Vutha, A.C. The Stratospheric Optical Rubidium Clock Experiment. In Proceedings of the 70th International Astronautical Congress (IAC), Washington D.C., United States, 21-25 October, 2019.
- Jackson, S.; Vutha, A.C. Magic polarization for cancellation of light shifts in two-photon optical clocks. Physical Review A 2019, 99, 063422. [Google Scholar] [CrossRef]
- Riehle, F. Towards a redefinition of the second based on optical atomic clocks. Comptes Rendus. Physique 2015, 16, 506–515. [Google Scholar] [CrossRef]
- Yasuda, M.; Inaba, H.; Kohno, T.; Tanabe, T.; Nakajima, Y.; Hosaka, K.; Akamatsu, D.; Onae, A.; Suzuyama, T.; Amemiya, M.; et al. Improved absolute frequency measurement of the 171Yb optical lattice clock towards a candidate for the redefinition of the second. Applied Physics Express 2012, 5, 102401. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.; Leopardi, H.; Fasano, R.; Nicolodi, D.; Beloy, K.; Yao, J.; Sherman, J.A.; Schaeffer, S.A.; Savory, J.; et al. Towards the optical second: verifying optical clocks at the SI limit. Optica 2019, 6, 448–454. [Google Scholar] [CrossRef]
- Yadav, S.; Aswal, D.K. Redefined SI units and their implications. Mapan 2020, 35, 1–9. [Google Scholar] [CrossRef]
- Le Targat, R.; Lorini, L.; Le Coq, Y.; Zawada, M.; Guéna, J.; Abgrall, M.; Gurov, M.; Rosenbusch, P.; Rovera, D.; Nagórny, B.; et al. Experimental realization of an optical second with strontium lattice clocks. Nature communications 2013, 4, 2109. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Reviews of Modern Physics 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Kitching, J. Chip-scale atomic devices. Applied Physics Reviews 2018, 5. [Google Scholar] [CrossRef]
- Arimondo, E. V coherent population trapping in laser spectroscopy. In Progress in optics; Elsevier, 1996; Vol. 35, pp. 257–354.
- Shah, V.; Kitching, J. Advances in coherent population trapping for atomic clocks. In Advances in atomic, molecular, and optical physics; Elsevier, 2010; Vol. 59, pp. 21–74.
- Petit, G.; Wolf, P.; Delva, P. Atomic time, clocks, and clock comparisons in relativistic spacetime: a review. Frontiers in relativistic celestial mechanics 2014, 2, 249–279. [Google Scholar]
- Kang, S.; Gharavipour, M.; Affolderbach, C.; Gruet, F.; Mileti, G. Demonstration of a high-performance pulsed optically pumped Rb clock based on a compact magnetron-type microwave cavity. Journal of Applied Physics 2015, 117. [Google Scholar] [CrossRef]
- Kang, S.; Gharavipour, M.; Gruet, F.; Affolderbach, C.; Mileti, G. Compact and high-performance Rb clock based on pulsed optical pumping for industrial application. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum. IEEE, 2015, pp. 800–803.
- Godone, A.; Micalizio, S.; Levi, F. Pulsed optically pumped frequency standard. Physical Review A—Atomic, Molecular, and Optical Physics 2004, 70, 023409. [Google Scholar] [CrossRef]
- Gozzelino, M.; Micalizio, S.; Calosso, C.E.; Belfi, J.; Sapia, A.; Gioia, M.; Levi, F. Realization of a pulsed optically pumped Rb clock with a frequency stability below 10-15. Scientific Reports 2023, 13, 12974. [Google Scholar] [CrossRef]
- Pei, H.; Pang, H.; Quan, W.; Fan, W.; Yuan, L.; Zhang, K.; Fang, C. Pulsed optical pumping in electron spin vapor. Measurement 2024, 231, 114619. [Google Scholar] [CrossRef]
- Hao, Q.; Yang, S.; Zheng, S.; Yun, P.; Ruan, J.; Zhang, S. A 44-cm3 physics package for the high-performance pulsed optically pumped atomic clock. Review of Scientific Instruments 2024, 95. [Google Scholar] [CrossRef]
- Hao, Q.; Yang, S.; Ruan, J.; Yun, P.; Zhang, S. Integrated pulsed optically pumped Rb atomic clock with frequency stability of 10- 15. Physical Review Applied 2024, 21, 024003. [Google Scholar] [CrossRef]
- Micalizio, S.; Levi, F.; Godone, A.; Calosso, C.; Francois, B.; Boudot, R.; Affolderbach, C.; Kang, S.; Gharavipour, M.; Gruet, F.; et al. Pulsed optically pumped Rb clock. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2016, Vol. 723, p. 012015.
- Micalizio, S.; Godone, A.; Calosso, C.; Levi, F.; Affolderbach, C.; Gruet, F. Pulsed optically pumped rubidium clock with high frequency-stability performance. IEEE transactions on ultrasonics, ferroelectrics, and frequency control 2012, 59, 457–462. [Google Scholar] [CrossRef]
- Dong, G.; Deng, J.; Lin, J.; Zhang, S.; Lin, H.; Wang, Y. Recent improvements on the pulsed optically pumped rubidium clock at SIOM. Chinese Optics Letters 2017, 15, 040201. [Google Scholar] [CrossRef]
- Shen, Q.; Lin, H.; Deng, J.; Wang, Y. Pulsed optically pumped atomic clock with a medium-to long-term frequency stability of 10- 15. Review of Scientific Instruments 2020, 91. [Google Scholar] [CrossRef]
- Wang, K.M.; Du, Z.J.; Liu, Y.Y.; Yu, Z.J.; Yan, S.B.; Liu, T.; Dong, R.F.; Zhang, S.G. Pulsed vapor cell atomic clock with a differential Faraday rotation angle detection. Optics Express 2021, 29, 38527–38539. [Google Scholar] [CrossRef]
- Baryshev, V.N.; Aleynikov, M.S.; Osipenko, G.V.; Blinov, I.Y. Technique of pulsed optical pumping and pulsed excitation of microwave resonances using the Ramsey scheme in a 87Rb cell with a buffer gas. Quantum Electronics 2018, 48, 443. [Google Scholar] [CrossRef]
- Choi, I.; Lee, S.; Kwon, T.; Park, S. Improvement of short-term stability of pulsed optically pumped rubidium atomic clock. In Proceedings of the CPEM 2010. IEEE; 2010; pp. 432–433. [Google Scholar]
- Lin, H.; Deng, J.; Lin, J.; Zhang, S.; Wang, Y. Frequency stability of a pulsed optically pumped atomic clock with narrow Ramsey linewidth. Applied Optics 2018, 57, 3056–3060. [Google Scholar] [CrossRef]
- Knappe, S.; Shah, V.; Schwindt, P.D.; Hollberg, L.; Kitching, J.; Liew, L.A.; Moreland, J. A microfabricated atomic clock. Applied Physics Letters 2004, 85, 1460–1462. [Google Scholar] [CrossRef]
- Venkatraman, V.; Kang, S.; Affolderbach, C.; Shea, H.; Mileti, G. Optical pumping in a microfabricated Rb vapor cell using a microfabricated Rb discharge light source. Applied Physics Letters 2014, 104. [Google Scholar] [CrossRef]
- Liew, L.A.; Knappe, S.; Moreland, J.; Robinson, H.; Hollberg, L.; Kitching, J. Microfabricated alkali atom vapor cells. Applied Physics Letters 2004, 84, 2694–2696. [Google Scholar] [CrossRef]
- Abdullah, S.; Affolderbach, C.; Gruet, F.; Mileti, G. Aging studies on micro-fabricated alkali buffer-gas cells for miniature atomic clocks. Applied Physics Letters 2015, 106. [Google Scholar] [CrossRef]
- Nishino, H.; Hara, M.; Yano, Y.; Toda, M.; Kanamori, Y.; Kajita, M.; Ido, T.; Ono, T. A reflection-type vapor cell using anisotropic etching of silicon for micro atomic clocks. Applied Physics Express 2019, 12, 072012. [Google Scholar] [CrossRef]
- Maurice, V.; Rutkowski, J.; Kroemer, E.; Bargiel, S.; Passilly, N.; Boudot, R.; Gorecki, C.; Mauri, L.; Moraja, M. Microfabricated vapor cells filled with a cesium dispensing paste for miniature atomic clocks. Applied Physics Letters 2017, 110. [Google Scholar] [CrossRef]
- Knappe, S.; Schwindt, P.; Gerginov, V.; Shah, V.; Liew, L.; Moreland, J.; Robinson, H.; Hollberg, L.; Kitching, J. Microfabricated atomic clocks and magnetometers. Journal of Optics A: Pure and Applied Optics 2006, 8, S318. [Google Scholar] [CrossRef]
- Kitching, J.; Knappe, S.; Shah, V.; Schwindt, P.; Griffith, C.; Jimenez, R.; Preusser, J.; Liew, L.A.; Moreland, J. Microfabricated atomic magnetometers and applications. In Proceedings of the 2008 IEEE International Frequency Control Symposium. IEEE, 2008, pp. 789–794.
- HOLLBERG, L.; KITCHING, J. MICROFABRICATED ATOMIC CLOCKS AND MAGNETOMETERS. LASER SPECTROSCOPY PY, p. 337.
- Venkatraman, V.; Pétremand, Y.; de Rooij, N.; Shea, H. Reliability characteristics of microfabricated Rb mini-lamps for optical pumping in miniature atomic clocks and magnetometers. In Proceedings of the Reliability, Packaging, Testing, and Characterization of MOEMS/MEMS and Nanodevices XII. SPIE, 2013, Vol. 8614, pp. 27–33.
- Carlé, C.; Callejo, M.; Mursa, A.; Hafiz, M.A.; Tanguy, Q.; Vicarini, R.; Millo, J.; Maurice, V.; Klinger, E.; Passilly, N.; et al. Microfabricated vapor cell atomic clocks at FEMTO-ST. In Proceedings of the Hot Vapor Workshop, 2024.
- Maurice, V.; Newman, Z.L.; Dickerson, S.; Rivers, M.; Hsiao, J.; Greene, P.; Mescher, M.; Kitching, J.; Hummon, M.T.; Johnson, C. Miniaturized optical frequency reference for next-generation portable optical clocks. Optics Express 2020, 28, 24708–24720. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Drake, T.; Stone, J.R.; Briles, T.C.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; et al. Architecture for the photonic integration of an optical atomic clock. Optica 2019, 6, 680–685. [Google Scholar] [CrossRef]
- Gellesch, M.; Jones, J.; Barron, R.; Singh, A.; Sun, Q.; Bongs, K.; Singh, Y. Transportable optical atomic clocks for use in out-of-the-lab environments. Advanced Optical Technologies 2020, 9, 313–325. [Google Scholar] [CrossRef]
- Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of general relativity by a pair of transportable optical lattice clocks. Nature photonics 2020, 14, 411–415. [Google Scholar] [CrossRef]
- Grotti, J.; Koller, S.; Vogt, S.; Häfner, S.; Sterr, U.; Lisdat, C.; Denker, H.; Voigt, C.; Timmen, L.; Rolland, A.; et al. Geodesy and metrology with a transportable optical clock. Nature Physics 2018, 14, 437–441. [Google Scholar] [CrossRef]
- Callejo, M.; Mursa, A.; Vicarini, R.; Klinger, E.; Tanguy, Q.; Millo, J.; Passilly, N.; Boudot, R. Short-term stability of a microcell optical reference based on the Rb atom two-photon transition at 778 nm. Journal of the Optical Society of America B 2024, 42, 151–159. [Google Scholar] [CrossRef]
- Erickson, S.E.; Tooley, D.P.; Weerasinghe, K.; Zhu, X.; Chavez-Pirson, A.; Jason Jones, R. Atomic frequency standard based on direct frequency comb spectroscopy. Optics Letters 2024, 49, 5340–5343. [Google Scholar] [CrossRef] [PubMed]
- Beard, R.; Martin, K.W.; Elgin, J.D.; Kasch, B.L.; Krzyzewski, S.P. Two-photon rubidium clock detecting 776 nm fluorescence. Optics Express 2024, 32, 7417–7425. [Google Scholar] [CrossRef]
- Lemke, N.D.; Martin, K.W.; Beard, R.; Stuhl, B.K.; Metcalf, A.J.; Elgin, J.D. Measurement of optical rubidium clock frequency spanning 65 days. Sensors 2022, 22, 1982. [Google Scholar] [CrossRef] [PubMed]
- Gerginov, V.; Beloy, K. Two-photon optical frequency reference with active ac Stark shift cancellation. Physical Review Applied 2018, 10, 014031. [Google Scholar] [CrossRef]
- Martin, K.W.; Phelps, G.; Lemke, N.D.; Bigelow, M.S.; Stuhl, B.; Wojcik, M.; Holt, M.; Coddington, I.; Bishop, M.W.; Burke, J.H. Compact optical atomic clock based on a two-photon transition in rubidium. Physical Review Applied 2018, 9, 014019. [Google Scholar] [CrossRef]
- Poulin, M.; Latrasse, C.; Touahri, D.; Têtu, M. Frequency stability of an optical frequency standard at 192.6 THz based on a two-photon transition of rubidium atoms. Optics Communications 2002, 207, 233–242. [Google Scholar] [CrossRef]
- Ahern, E.J.; Scholten, S.K.; Locke, C.; Bourbeau-Hebert, N.; White, B.; Luiten, A.N.; Perrella, C. Tailoring the Stability of a Two-Color, Two-Photon Rubidium Frequency Standard. arXiv preprint arXiv:2410.16654, arXiv:2410.16654 2024.
- Perrella, C.; Light, P.; Anstie, J.; Baynes, F.; White, R.; Luiten, A. Dichroic two-photon rubidium frequency standard. Physical Review Applied 2019, 12, 054063. [Google Scholar] [CrossRef]
- Lab, Q. Tempo Compact Rubidium Optical Clock. Available online: https://quantxlabs.com/wp-content/uploads/2024/09/TEMPO.pdf.
- Report, C.Q.C. Infleqtion Sells First Tiqker Quantum Clock in he UK. Available online: https://quantumcomputingreport.com/infleqtion-sells-first-tiqker-quantum-clock-in-the-uk/.
- McGuyer, B.H. Atomic physics with vapor-cell clocks. PhD thesis, Princeton University, 2012.
- Camparo, J. The rubidium atomic clock and basic research. Physics today 2007, 60, 33–39. [Google Scholar] [CrossRef]
- McGuyer, B.; Jau, Y.Y.; Happer, W. Simple method of light-shift suppression in optical pumping systems. Applied Physics Letters 2009, 94. [Google Scholar] [CrossRef]
- Affolderbach, C.; Breschi, E.; Schori, C.; Mileti, G. Gas-cell atomic clocks for space: new results and alternative schemes. In Proceedings of the International Conference on Space Optics—ICSO 2006. SPIE, 2017, Vol. 10567, pp. 694–700.
- Göppert-Mayer, M. Über elementarakte mit zwei quantensprüngen. Annalen der Physik 1931, 401, 273–294. [Google Scholar] [CrossRef]
- Biraben, F. The first decades of Doppler-free two-photon spectroscopy. Comptes Rendus. Physique 2019, 20, 671–681. [Google Scholar] [CrossRef]
- Abella, I. Optical double-photon absorption in cesium vapor. Physical Review Letters 1962, 9, 453. [Google Scholar] [CrossRef]
- Roy, R.; Condylis, P.C.; Johnathan, Y.J.; Hessmo, B. Atomic frequency reference at 1033 nm for ytterbium (Yb)-doped fiber lasers and applications exploiting a rubidium (Rb) 5 S 1/2 to 4 D 5/2 one-colour two-photon transition. Optics Express 2017, 25, 7960–7969. [Google Scholar] [CrossRef]
- Khripunov, S.; Radnatarov, D.; Kobtsev, S. Atomic clock based on a coherent population trapping resonance in 87Rb with improved high-frequency modulation parameters. In Proceedings of the Slow Light, Fast Light, and Opto-Atomic Precision Metrology VIII. SPIE, 2015, Vol. 9378, pp. 8–13.
- Sharma, A.; Kolkowitz, S.; Saffman, M. Analysis of a cesium lattice optical clock. arXiv preprint arXiv:2203.08708, arXiv:2203.08708 2022.
- Zameroski, N.D.; Hager, G.D.; Erickson, C.J.; Burke, J.H. Pressure broadening and frequency shift of the 5S1/2-5D5/2 and 5S1/2-7S1/2 two photon transitions in 85Rb by the noble gases and N2. Journal of Physics B: Atomic, Molecular and Optical Physics 2014, 47, 225205. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Schibli, T.R. Temperature-shift-suppression scheme for two-photon two-color rubidium vapor clocks. Physical Review A 2022, 106, 053104. [Google Scholar] [CrossRef]
- Hassanin, K.; Federsel, P.; Karlewski, F.; Zimmermann, C. 5S - 5D two-photon transition in rubidium vapor at high densities. Physical Review A 2023, 107, 043104. [Google Scholar] [CrossRef]
- Nez, F.; Biraben, F.; Felder, R.; Millerioux, Y. Optical frequency determination of the hyperfine components of the 5S1/2-5D3/2 two-photon transitions in rubidium. Optics communications 1993, 102, 432–438. [Google Scholar] [CrossRef]
- Kiran Kumar, P.; Suryanarayana, M. Precision two-photon spectroscopy of alkali elements. Pramana 2014, 83, 189–219. [Google Scholar] [CrossRef]
- Martin, K.W.; Lemke, N.D.; Phelps, G.; Burke, J.H.; Stuhl, B. The Optical Stark Shift on a Two-Photon Transition in Rubidium. In Proceedings of the 2018 IEEE International Frequency Control Symposium (IFCS). IEEE, 2018, pp. 1–2.
- Nguyen, T.N. Degenerate and Non-Degenerate Two-Photon Rubidium Frequency Standard. PhD thesis, University of Colorado at Boulder, 2024.
- Gusching, A.; Petersen, M.; Passilly, N.; Brazhnikov, D.; Abdel Hafiz, M.; Boudot, R. Short-term stability of Cs microcell-stabilized lasers using dual-frequency sub-Doppler spectroscopy. Journal of the Optical Society of America B 2021, 38, 3254–3260. [Google Scholar] [CrossRef]
- Shi, T.; Wei, Q.; Qin, X.; Liu, Z.; Chen, K.; Cao, S.; Shi, H.; Liu, Z.; Chen, J. Dual-frequency optical-microwave atomic clocks based on cesium atoms. Photonics Research 2024, 12, 1972–1980. [Google Scholar] [CrossRef]
- Kitching, J.; Knappe, S.; Hollberg, L. Miniature vapor-cell atomic-frequency references. Applied physics letters 2002, 81, 553–555. [Google Scholar] [CrossRef]
- Kazakov, G.; Matisov, B.; Litvinov, A.; Mazets, I. Coherent population trapping in a finite-size buffer-less cell. Journal of Physics B: Atomic, Molecular and Optical Physics 2007, 40, 3851. [Google Scholar] [CrossRef]
- Erhard, M.; Helm, H. Buffer-gas effects on dark resonances: Theory and experiment. Physical Review A 2001, 63, 043813. [Google Scholar] [CrossRef]
- Khan, S.; Kumar, M.P.; Bharti, V.; Natarajan, V. Coherent population trapping (CPT) versus electromagnetically induced transparency (EIT). The European Physical Journal D 2017, 71, 1–9. [Google Scholar] [CrossRef]
- Batori, E.; Affolderbach, C.; Pellaton, M.; Gruet, F.; Violetti, M.; Su, Y.; Skrivervik, A.K.; Mileti, G. μ POP clock: A microcell atomic clock based on a double-resonance Ramsey scheme. Physical Review Applied 2022, 18, 054039. [Google Scholar] [CrossRef]
- Knappe, S.; Schwindt, P.; Shah, V.; Hollberg, L.; Kitching, J.; Liew, L.; Moreland, J. A chip-scale atomic clock based on 87Rb with improved frequency stability. Optics express 2005, 13, 1249–1253. [Google Scholar] [CrossRef]
- Bandi, T.; Affolderbach, C.; Stefanucci, C.; Merli, F.; Skrivervik, A.K.; Mileti, G. Compact high-performance continuous-wave double-resonance rubidium standard with 1.4× 10- 13 τ- 1/2 stability. IEEE transactions on ultrasonics, ferroelectrics, and frequency control 2014, 61, 1769–1778. [Google Scholar] [CrossRef]
- Gharavipour, M.; Affolderbach, C.; Kang, S.; Bandi, T.; Gruet, F.; Pellaton, M.; Mileti, G. High performance vapour-cell frequency standards. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2016, Vol. 723, p. 012006.
- Affolderbach, C.; Droz, F.; Mileti, G. Experimental demonstration of a compact and high-performance laser-pumped rubidium gas cell atomic frequency standard. IEEE Transactions on Instrumentation and Measurement 2006, 55, 429–435. [Google Scholar] [CrossRef]
- Chen, K.H.; Wu, C.M.; Wu, S.R.; Yu, H.H.; Liu, T.W.; Cheng, W.Y. Influence of atmospheric helium on secondary clocks. Optics Letters 2020, 45, 4088–4091. [Google Scholar] [CrossRef]
- Moreno, W. Rubidium Vapour-cell Frequency Standards: Metrology of Optical and Microwave Frequency References. PhD thesis, Université de Neuchâtel, 2019.
- Terra, O.; Hussein, H. An ultra-stable optical frequency standard for telecommunication purposes based upon the 5S1/2-5D5/2 two-photon transition in Rubidium. Applied Physics B 2016, 122, 1–12. [Google Scholar] [CrossRef]
- Martin, K.W. Compact Optical Frequency Standards for Future Applications beyond the Laboratory. PhD thesis, The University of New Mexico, 2019.
- Li, D.; Liu, K.; Wang, P.; Kang, S. Dual-interrogation method for suppressing light shift in Rb 778 nm two-photon transition optical frequency standard. Optics Express 2024, 32, 2766–2773. [Google Scholar] [CrossRef] [PubMed]
- Edwards, C.; Barwood, G.; Margolis, H.; Gill, P.; Rowley, W. Development and absolute frequency measurement of a pair of 778 nm two-photon rubidium standards. Metrologia 2005, 42, 464. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Fredrick, C.; Fortier, T.; Leopardi, H.; Hollberg, L.; Diddams, S.A.; Kitching, J.; Hummon, M.T. High-performance, compact optical standard. Optics Letters 2021, 46, 4702–4705. [Google Scholar] [CrossRef]
- Perrella, C. Demonstration of a Two-Photon Atomic Clock with Light Shift Suppression using Two-Colour Magic Wavelengths. Technical report, The University of Adelaide North Terrace, SA, 5005 AUS, 2022.
- Li, D.; Liu, K.; Zhao, L.; Kang, S. A frequency shift compensation method for light shift and vapor-cell temperature shift in atomic clocks. arXiv preprint arXiv:2405.14281, arXiv:2405.14281 2024.
- Plocki, A.; Nguyen, T.N.; Schibli, T. Two-color Rubidium clock with AC Stark Shift Suppression. Bulletin of the American Physical Society 2023. [Google Scholar]
- Phelps, G.; Lemke, N.; Erickson, C.; Burke, J.; Martin, K. Compact optical clock with 5× 10- 13 instability at 1 s. Navigation: Journal of The Institute of Navigation 2018, 65, 49–54. [Google Scholar] [CrossRef]
- Olson, A.J.; Carlson, E.J.; Mayer, S.K. Two-photon spectroscopy of rubidium using a grating-feedback diode laser. American Journal of Physics 2006, 74, 218–223. [Google Scholar] [CrossRef]
- Bigelow, M.S.; Martin, K.W.; Phelps, G.; Lemke, N.D. A high performance clock laser for two-photon frequency stabilized optical clocks. In Proceedings of the CLEO: Science and Innovations. Optica Publishing Group, 2018, pp. JW2A–163.
- Manurkar, P.; Perez, E.F.; Hickstein, D.D.; Carlson, D.R.; Chiles, J.; Westly, D.A.; Baumann, E.; Diddams, S.A.; Newbury, N.R.; Srinivasan, K.; et al. Fully self-referenced frequency comb consuming 5 watts of electrical power. OSA Continuum 2018, 1, 274–282. [Google Scholar] [CrossRef]
- Xu, D.R., June 2022. White Paper: Non-linear Optical Crystals Used for Quantum Technology.
- Terra, O. Architecture for the photonic integration of an optical atomic clock: supplementary material. Optica 2019, 144, 83–87. [Google Scholar]
- Nikogosyan, D.N. Nonlinear optical crystals: a complete survey; Springer Science & Business Media, 2006.
- Cutler, T.F.; Hamlyn, W.J.; Renger, J.; Whittaker, K.A.; Pizzey, D.; Hughes, I.G.; Sandoghdar, V.; Adams, C.S. Nanostructured alkali-metal vapor cells. Physical Review Applied 2020, 14, 034054. [Google Scholar] [CrossRef]
- Erickson, S.E. An Optical Atomic Clock Based on Frequency Comb Spectroscopy. PhD thesis, The University of Arizona, 2024.
- Martin, K.W.; Stuhl, B.; Eugenio, J.; Safronova, M.S.; Phelps, G.; Burke, J.H.; Lemke, N.D. Frequency shifts due to Stark effects on a rubidium two-photon transition. Physical Review A 2019, 100, 023417. [Google Scholar] [CrossRef]
- Bjorkholm, J.; Liao, P. Line shape and strength of two-photon absorption in an atomic vapor with a resonant or nearly resonant intermediate state. Physical Review A 1976, 14, 751. [Google Scholar] [CrossRef]
- Egidi, A.; et al. Review of main optical retroreflectors. Istituto Nazionale di Ricerca Metrologica, Turin, Italy, Tech. Rep. RT 31 2018, 31, 2018. [Google Scholar] [CrossRef]
- Mungan, C. The cat’s Eye Retroreflector. Technical report, United States Naval Academy, Spring 2001.
- Snyder, J. Paraxial ray analysis of a cat’s-eye retroreflector. Applied optics 1975, 14, 1825–1828. [Google Scholar] [CrossRef]
- Hamilton, R.; Roberts, B.M.; Scholten, S.K.; Locke, C.; Luiten, A.N.; Ginges, J.S.; Perrella, C. Experimental and Theoretical Study of Dynamic Polarizabilities in the 5 S 1/2–5 D 5/2 Clock Transition in Rubidium-87 and Determination of Electric Dipole Matrix Elements. Physical Review Applied 2023, 19, 054059. [Google Scholar] [CrossRef]
- Hilico, L.; Felder, R.; Touahri, D.; Acef, O.; Clairon, A.; Biraben, F. Metrological features of the rubidium two-photon standards of the BNM-LPTF and Kastler Brossel Laboratories. The European Physical Journal-Applied Physics 1998, 4, 219–225. [Google Scholar] [CrossRef]
- NEWMAN, Z.L.; MAURICE, V.; DRAKE, T.; STONE, J.R.; BRILES, T.C.; SPENCER, D.T.; FREDRICK, C.; LI, Q.; WESTLY, D.; ILIC, B.; et al. Architecture for the photonic integration of an optical atomic clock: supplementary material. Optica 2019.
- True, T.M.; Pitz, G.A.; Rice, C.A.; Perram, G.P. Resonant enhancement of two-photon absorption in rubidium with crossed polarizations. Optics Communications 2022, 510, 127943. [Google Scholar] [CrossRef]
- Perrella, C.; Light, P.; Anstie, J.; Baynes, F.; Benabid, F.; Luiten, A.N. Two-color rubidium fiber frequency standard. Optics Letters 2013, 38, 2122–2124. [Google Scholar] [CrossRef]
- Locke, C.; Ng, S.; Scarabel, J.; O’Connor, M.; Luiten, A.; Scholten, S.; Ahern, E.; Hebert, N.; Perrella, C. Portable Optical Atomic Clock Based on a Dichroic Two-Photon Transition in Rubidium. In Proceedings of the 2023 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS). IEEE, 2023, pp. 1–2.
- Miao, J.; Chen, J.; Yu, D.; Yang, Q.; Pan, D.; Chen, J. Single-Atomic-Ensemble Dual-Wavelength Optical Standard. arXiv preprint arXiv:2411.02107, arXiv:2411.02107 2024.
- Kulatunga, P.; Busch, H.; Andrews, L.; Sukenik, C. Two-color polarization spectroscopy of rubidium. Optics Communications 2012, 285, 2851–2853. [Google Scholar] [CrossRef]
- Caracas Núñez, M.; Gonzalez, M.A.; Núñez Portela, M. Theoretical and experimental study of the 6S-8S two-photon absorption cross-section in cesium atoms. Optics Express 2023, 31, 31749–31759. [Google Scholar] [CrossRef] [PubMed]
- Uehara, T.; Sugiyama, K.; Kitano, M. Frequency measurement of the 6S-8S two-photon transition in cesium. In Proceedings of the Conference on Lasers and Electro-Optics/Pacific Rim. Optica Publishing Group, 2013, p. WPF_3.
- Wu, C.M.; Liu, T.W.; Wu, M.H.; Lee, R.K.; Cheng, W.Y. Absolute frequency of cesium 6 S–8 S 822 nm two-photon transition by a high-resolution scheme. Optics letters 2013, 38, 3186–3189. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.H.; Liu, T.W.; Wu, C.M.; Lee, C.C.; Lee, C.K.; Cheng, W.Y. High-resolution Cs 133 6 S–6 D, 6 S–8 S two-photon spectroscopy using an intracavity scheme. Optics letters 2011, 36, 76–78. [Google Scholar] [CrossRef]
- Wu, C.M.; Cheng, W.Y.; Lee, R.K.; et al. Cesium 6S 1/2→ 8S 1/2 two photon-transition stabilized 822. In 5 nm diode laser. In Proceedings of the 2008 Conference on Precision Electromagnetic Measurements Digest. IEEE; 2008; pp. 318–319. [Google Scholar]
- Cheng, C.Y.; Wu, C.M.; Liao, G.B.; Cheng, W.Y. Cesium 6 S 1/ 2→ 8 S 1/ 2 two-photon-transition-stabilized 822.5 nm diode laser. Optics letters 2007, 32, 563–565. [Google Scholar] [CrossRef]
- Hagel, G.; Nesi, C.; Jozefowski, L.; Schwob, C.; Nez, F.; Biraben, F. Accurate measurement of the frequency of the 6S–8S two-photon transitions in cesium. Optics communications 1999, 160, 1–4. [Google Scholar] [CrossRef]
- Lee, Y.C.; Chui, H.C.; Chen, Y.Y.; Chang, Y.H.; Tsai, C.C. Effects of light on cesium 6S–8S two-photon transition. Optics communications 2010, 283, 1788–1791. [Google Scholar] [CrossRef]
- Sieradzan, A.; Havey, M.; Safronova, M. Combined experimental and theoretical study of the 6 p 2 P j→ 8 s 2 S 1/2 relative transition matrix elements in atomic Cs. Physical Review A 2004, 69, 022502. [Google Scholar] [CrossRef]
- Kim, K.t.; Ahn, J. Direct frequency-comb spectroscopy of 6S_{1/2}-8S_{1/2} transitions of atomic cesium. arXiv preprint arXiv:1707.06424, arXiv:1707.06424 2017.
- Fendel, P.; Bergeson, S.; Udem, T.; Hänsch, T. Two-photon frequency comb spectroscopy of the 6 s–8 s transition in cesium. Optics letters 2007, 32, 701–703. [Google Scholar] [CrossRef]
- Bertinetto, F.; Cordiale, P.; Galzerano, G.; Bava, E. Frequency stabilization of DBR diode laser against Cs absorption lines at 852 nm using the modulation transfer method. IEEE Transactions on Instrumentation and Measurement 2001, 50, 490–492. [Google Scholar] [CrossRef]
- Nakazawa, M.; Suzuki, K. Cesium optical atomic clock: an optical pulse that tells the time. Optics Letters 2001, 26, 635–637. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuka, T.; Nishimiya, N.; Fukuda, T.; Suzuki, M. Doppler-Free Two-Photon Spectroscopy of 6S1/ 2–6D3/ 2, 5/ 2 Transition in Cesium. Journal of the Physical Society of Japan 2005, 74, 2487–2491. [Google Scholar] [CrossRef]
- Bandi, T.; Affolderbach, C.; Mileti, G. Laser-pumped paraffin-coated cell rubidium frequency standard. Journal of Applied Physics 2012, 111. [Google Scholar] [CrossRef]
- Pétremand, Y.; Affolderbach, C.; Straessle, R.; Pellaton, M.; Briand, D.; Mileti, G.; de Rooij, N.F. Microfabricated rubidium vapour cell with a thick glass core for small-scale atomic clock applications. Journal of Micromechanics and Microengineering 2012, 22, 025013. [Google Scholar] [CrossRef]
- Knappe, S.; Gerginov, V.; Schwindt, P.; Shah, V.; Robinson, H.; Hollberg, L.; Kitching, J. Atomic vapor cells for chip-scale atomic clocks with improved long-term frequency stability. Optics letters 2005, 30, 2351–2353. [Google Scholar] [CrossRef]
- Kazakin, A.; Kleimanov, R.; Komarevtsev, I.; Kondrateva, A.; Enns, Y.; Shashkin, A.; Glukhovskoy, A. Microfabrication of Alkali Vapor MEMS Cells for chip-scale atomic clock. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2021, Vol. 2103, p. 012188.
- Di Gaetano, E.; Keliehor, B.; Gallacher, K.; Griffin, P.; Sorel, M.; Riis, E.; Paul, D. 778.1 nm distributed feedback lasers for Rb two-photon atomic systems with sub-4 kHz linewidths. APL Photonics 2024, 9. [Google Scholar] [CrossRef]
- Hou, D.; Wu, J.; Zhang, S.; Ren, Q.; Zhang, Z.; Zhao, J. A stable frequency comb directly referenced to rubidium electromagnetically induced transparency and two-photon transitions. Applied Physics Letters 2014, 104. [Google Scholar] [CrossRef]
- Abdel Hafiz, M.; Carlé, C.; Passilly, N.; Danet, J.; Calosso, C.; Boudot, R. Light-shift mitigation in a microcell-based atomic clock with symmetric auto-balanced Ramsey spectroscopy. Applied Physics Letters 2022, 120. [Google Scholar] [CrossRef]
- Lin, J.; Deng, J.; Ma, Y.; He, H.; Wang, Y. Detection of ultrahigh resonance contrast in<? A3B2 show [pmg: line-break justify=" yes"/]?> vapor-cell atomic clocks. Optics letters 2012, 37, 5036–5038. [Google Scholar]
- Camparo, J.; Frueholz, R. Fundamental stability limits for the diode-laser-pumped rubidium atomic frequency standard. Journal of applied physics 1986, 59, 3313–3317. [Google Scholar] [CrossRef]
- Audoin, C.; Candelier, V.; Dimarcq, N. A limit to the frequency stability of passive frequency standards due to an intermodulation effect. IEEE transactions on instrumentation and measurement 1991, 40, 121–125. [Google Scholar] [CrossRef]
- Brezinski, M. Noise and system performance with td-oct and sd-oct. Optical coherence tomography. Academic Press, Burlington.
- Duspayev, A.; Owens, C.; Dash, B.; Raithel, G. An optical atomic clock using 4D_J states of rubidium. Quantum Science and Technology 2024, 9, 045046. [Google Scholar] [CrossRef]
- Haas, M.; Jentschura, U.D.; Keitel, C.H. Comparison of classical and second quantized description of the dynamic Stark shift. American journal of physics 2006, 74, 77–81. [Google Scholar] [CrossRef]
- Kaplan, A.; Andersen, M.F.; Davidson, N. Suppression of inhomogeneous broadening in rf spectroscopy of optically trapped atoms. Physical Review A 2002, 66, 045401. [Google Scholar] [CrossRef]
- Grynberg, G.; Cagnac, B. Doppler-free multiphotonic spectroscopy. Reports on Progress in Physics 1977, 40, 791. [Google Scholar] [CrossRef]
- Levi, F.; Camparo, J.; Francois, B.; Calosso, C.; Micalizio, S.; Godone, A. Precision test of the ac Stark shift in a rubidium atomic vapor. Physical Review A 2016, 93, 023433. [Google Scholar] [CrossRef]
- Miletic, D.; Bandi, T.; Affolderbach, C.; Mileti, G. ac Stark shift in double resonance and coherent population trapping in a wall-coated cell for compact Rb atomic clocks. Physica scripta 2012, 2012, 014012. [Google Scholar] [CrossRef]
- Camparo, J.; Frueholz, R.; Volk, C. Inhomogeneous light shift in alkali-metal atoms. Physical Review A 1983, 27, 1914. [Google Scholar] [CrossRef]
- Radnatarov, D.A.; Kobtsev, S.M.; Andryushkov, V.A.; Basalaev, M.Y.; Taichenachev, A.V.; Radchenko, M.D.; Yudin, V.I. Active Suppression of the Light Shift in an Atomic Clock Based on Coherent Population Trapping in 87Rb Vapor Using the Phase Jump Technique. JETP Letters 2023, 117, 504–508. [Google Scholar] [CrossRef]
- Bergquist, J.C. Doppler-free spectroscopy. In Experimental Methods in the Physical Sciences; Elsevier, 1996; Vol. 29, pp. 255–272.
- Formichella, V.; Camparo, J.; Tavella, P. Influence of the ac-Stark shift on GPS atomic clock timekeeping. Applied Physics Letters 2017, 110. [Google Scholar] [CrossRef]
- Jones, M. Atom-light interactions. 2015, Archived lecture notes, Durham University.
- Steck, D.A. Rubidium 87 D line data. Available online: http://steck.us/alkalidata/.
- Arora, B.; Safronova, M.; Clark, C.W. Magic wavelengths for the np-ns transitions in alkali-metal atoms. Physical Review A—Atomic, Molecular, and Optical Physics 2007, 76, 052509. [Google Scholar] [CrossRef]
- Gallagher, J.; Perram, G. Determining the Two-Photon Absorption Cross-Section for the 52S1/2-->52D5/2 Transition in Naturally Occurring Rubidium. In Proceedings of the 42nd AIAA Plasmadynamics and Lasers Conference in conjunction with the 18th International Conference on MHD Energy Conversion (ICMHD), 2011, p. 4005.
- Sakurai, J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press, 2021.
- Le Kien, F.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: general theory and application to cesium. The European Physical Journal D 2013, 67, 1–16. [Google Scholar] [CrossRef]
- Mitroy, J.a.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. Journal of Physics B: Atomic, Molecular and Optical Physics 2010, 43, 202001. [Google Scholar] [CrossRef]
- Sheng, D.; Pérez Galván, A.; Orozco, L. Lifetime measurements of the 5 d states of rubidium. Physical Review A—Atomic, Molecular, and Optical Physics 2008, 78, 062506. [Google Scholar] [CrossRef]
- Safronova, M.; Williams, C.J.; Clark, C.W. Relativistic many-body calculations of electric-dipole matrix elements, lifetimes, and polarizabilities in rubidium. Physical Review A 2004, 69, 022509. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, J.; Xie, L.Y.; Zhang, D.H.; Dong, C.Z. Polarizabilities and tune-out wavelengths of the hyperfine ground states of Rb 87, 85. Physical Review A 2016, 94, 052510. [Google Scholar] [CrossRef]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Applied optics 2010, 49, 4801–4807. [Google Scholar] [CrossRef]
- Zhu, M.; Hall, J.L. Stabilization of optical phase/frequency of a laser system: application to a commercial dye laser with an external stabilizer. Journal of the Optical Society of America B 1993, 10, 802–816. [Google Scholar] [CrossRef]
- Camparo, J. Conversion of laser phase noise to amplitude noise in an optically thick vapor. Journal of the Optical Society of America B 1998, 15, 1177–1186. [Google Scholar] [CrossRef]
- Drullinger, R.E.; Szekely, C.; Camparo, J.C. Diode-laser-pumped, gas-cell atomic clocks. In Proceedings of the Proceedings of the 1992 IEEE Frequency Control Symposium. IEEE, 1992, pp. 104–107.
- Robinson, H.; Johnson, C. Narrow 87Rb hyperfine-structure resonances in an evacuated wall-coated cell. Applied Physics Letters 1982, 40, 771–773. [Google Scholar] [CrossRef]
- Knappe, S.; Robinson, H.G. Double-resonance lineshapes in a cell with wall coating and buffer gas. New Journal of Physics 2010, 12, 065021. [Google Scholar] [CrossRef]
- Seltzer, S.; Michalak, D.; Donaldson, M.; Balabas, M.; Barber, S.; Bernasek, S.; Bouchiat, M.A.; Hexemer, A.; Hibberd, A.; Kimball, D.; et al. Investigation of antirelaxation coatings for alkali-metal vapor cells using surface science techniques. The Journal of chemical physics 2010, 133. [Google Scholar] [CrossRef] [PubMed]
- Bandi, T.; Affolderbach, C.; Mileti, G. Study of Rb 0-0 hyperfine double-resonance transition in a wall-coated cell. In Proceedings of the EFTF-2010 24th European Frequency and Time Forum. IEEE; 2010; pp. 1–8. [Google Scholar]
- Singh, G.; Dilavore, P.; Alley, C.O. A technique for preparing wall coated cesium vapor cells. Review of Scientific Instruments 1972, 43, 1388–1389. [Google Scholar] [CrossRef]
- Chu, C.H.; Chang, P.C.; Shih, Y.J.; Luh, D.A.; Chang, M.S.; Liu, T.W.; Lin, Y.T.; Chen, B.W.; Cheng, W.Y. Measurement of the 5S1/2 to 5D5/2 two-photon clock transition frequency of rubidium-85 in high vacuum. Optics Letters 2023, 48, 5984–5987. [Google Scholar] [CrossRef]
- Straessle, R.; Pellaton, M.; Affolderbach, C.; Pétremand, Y.; Briand, D.; Mileti, G.; de Rooij, N.F. Microfabricated alkali vapor cell with anti-relaxation wall coating. Applied Physics Letters 2014, 105. [Google Scholar] [CrossRef]
- Stoicheff, B.; Weinberger, E. Doppler-free two-photon absorption spectrum of rubidium. Canadian Journal of Physics 1979, 57, 2143–2154. [Google Scholar] [CrossRef]
- Camparo, J. The semiclassical stochastic-field/atom interaction problem. In Frequency Standards And Metrology; World Scientific, 2009; pp. 109–117.
- Kraft, S.; Deninger, A.; Trück, C.; Fortágh, J.; Lison, F.; Zimmermann, C. Rubidium spectroscopy at 778–780 nm with a distributed feedback laser diode. Laser Physics Letters 2004, 2, 71. [Google Scholar] [CrossRef]
- Calosso, C.E.; Godone, A.; Levi, F.; Micalizio, S. Enhanced temperature sensitivity in vapor-cell frequency standards. IEEE transactions on ultrasonics, ferroelectrics, and frequency control 2012, 59, 2646–2654. [Google Scholar] [CrossRef]
- Mishra, N.S. Frequency modulation of Rydberg states by radio frequency electromagnetic fields. In Proceedings of the Quantum Sensing and Nano Electronics and Photonics XX. SPIE, 2024, Vol. 12895, pp. 193–198.
- Delone, N.B.; Krainov, V.P. AC Stark shift of atomic energy levels. Physics-Uspekhi 1999, 42, 669. [Google Scholar] [CrossRef]
- Lodewyck, J.; Bilicki, S.; Bookjans, E.; Robyr, J.L.; Shi, C.; Vallet, G.; Le Targat, R.; Nicolodi, D.; Le Coq, Y.; Guéna, J.; et al. Optical to microwave clock frequency ratios with a nearly continuous strontium optical lattice clock. Metrologia 2016, 53, 1123. [Google Scholar] [CrossRef]
- Rębilas, K. Light-induced atomic desorption dynamics: Theory for a completely illuminated cell. Physical Review A—Atomic, Molecular, and Optical Physics 2009, 80, 014901. [Google Scholar] [CrossRef]
- Talker, E.; Arora, P.; Zektzer, R.; Sebbag, Y.; Dikopltsev, M.; Levy, U. Light-induced atomic desorption in microfabricated vapor cells for demonstrating quantum optical applications. Physical Review Applied 2021, 15, L051001. [Google Scholar] [CrossRef]
- Graf, M.T.; Kimball, D.F.; Rochester, S.M.; Kerner, K.i.; Wong, C.; Budker, D.; Alexandrov, E.B.; Balabas, M.V.; Yashchuk, V.V. Relaxation of atomic polarization in para+n-coated alkali-metal vapor cells. Physical Review A 2005, 72. [Google Scholar] [CrossRef]
- Yano, Y.; Gao, W.; Goka, S.; Kajita, M. Theoretical and experimental investigation of the light shift in Ramsey coherent population trapping. Physical Review A 2014, 90, 013826. [Google Scholar] [CrossRef]
- Yudin, V.; Basalaev, M.Y.; Taichenachev, A.; Pollock, J.; Newman, Z.; Shuker, M.; Hansen, A.; Hummon, M.; Boudot, R.; Donley, E.A.; et al. General methods for suppressing the light shift in atomic clocks using power modulation. Physical Review Applied 2020, 14, 024001. [Google Scholar] [CrossRef]
- Abdel Hafiz, M.; Coget, G.; Petersen, M.; Rocher, C.; Guérandel, S.; Zanon-Willette, T.; de Clercq, E.; Boudot, R. Toward a high-stability coherent population trapping Cs vapor-cell atomic clock using autobalanced Ramsey spectroscopy. Physical Review Applied 2018, 9, 064002. [Google Scholar] [CrossRef]
- Aumiler, D.; Ban, T.; Pichler, G. High-resolution measurements of the pressure broadening and shift of the rubidium 5 S 1/ 2 2–6 P 3/ 2 2 line by argon and helium. Physical Review A—Atomic, Molecular, and Optical Physics 2004, 70, 032723. [Google Scholar] [CrossRef]
| Category | Authors | Beam radius ( m) | Laser Power (mW) | Detuning (GHz) | Signal Linewidth (kHz) | Fractional Frequency Instability | Light Shift (per mW) | Rb-Rb Shift (kHz) | Cell Temperature C |
|---|---|---|---|---|---|---|---|---|---|
| Experimental studies | Ahern et al 2024 [121] | 600 | , | 1.5 | 340000 | at s | at 780 nm, at 776 nm | ‡ | 70 |
| Perrella et al. 2019 [122] | 1500 | , | 1.5 | at s | at 780 nm, at 776 nm | 90 | |||
| Gerginov and Beloy 2018 [118] | 2000 | , | 10 | 3480 | † at 1 s | ‡ | 90 | ||
| Perrella et al. 2013 [181] | ‡ | , | 2 | 10400 | at 10 s | at 780, at 776 nm | |||
| Theoretical studies | Rhona et al. 2023 [177] | 1500 | , | 667 | for 50 s | ‡ | ‡ | ||
| Nguyen et al. 2022 [136] | 1000 | , | 0 | ‡ | ‡ | ‡ | ‡ | 79.5 |
| Author | Temperature Shift () | Helium Collision Shift (Torr)−1 | 2nd Order Doppler Shift () | Quadratic Zeeman Shift () | Blackbody Radiation () |
|---|---|---|---|---|---|
| Martin et al. 2018 [119] | |||||
| Zachary et al. 2019 [110] | ‡ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





