YOLO-SCNet: A Framework for Enhanced Detection of Small Lunar Craters

1. Introduction

Craters are among the most prominent features on the lunar surface and hold significant value for understanding planetary evolution and geological processes. In particular, the study of small craters is crucial as they provide insights into the impact history of smaller celestial bodies and contribute to reconstructing the Moon's geological timeline [1,2]. However, detecting small craters on a globally scale poses considerable challenges due to the power-law distribution of crater sizes [3,4] and the complexity of the lunar terrain. These challenges are further compounded by varying lighting conditions and the diverse morphological characteristics of craters.

Traditional methods for crater detection primarily rely on manual feature extraction and predefined parameters. While these approaches have been somewhat effective, they struggle with the Moon's complex topography and variable lighting conditions, resulting in inconsistent outcomes. The reliance on fixed parameters also limits their adaptability to diverse lunar terrains, making them less robust in real-world applications, particularly in regions with challenging surface features and illumination variations [5,6]. In contrast, deep learning techniques have shown significant promise in overcoming these limitations. Advanced models such as Mask R-CNN and Cascade Mask R-CNN excel in detecting craters across varied lunar landscapes by automatically learning intricate patterns and adapting to topographical and lighting variations. These methods have demonstrated remarkable accuracy and adaptability, proving their potential to enhance planetary terrain analysis and autonomous navigation systems [9,10,11,12].

Many studies have classified craters based on their size, categorizing them into large (≥2 km) [13,14,15,16], medium (400 m – 2 km) [17,18,19], and small (100 m – 400 m) craters [20,21]. Despite these advancements, detecting small craters remains a significant challenge. The Moon's diverse terrain, coupled with the varying shapes and sizes of craters, complicates the task of achieving high precision and recall simultaneously. Additionally, the need for large-scale annotated datasets, efficient model transferability, and computationally efficient algorithms further complicates small crater detection [22,23,24]. These challenges are especially pronounced in regions with extreme terrain and lighting conditions, such as the lunar poles, highlands, and mare regions. Historically, crater detection efforts across the entire Moon have primarily focused on craters larger than 1 km in diameter. Recent studies have expanded the scope to include craters as small as 400 meters in diameter. These efforts have led to the creation of three lunar crater catalog databases: RobbinsDB (≥ 1 km) [25], LU1319373 (≥ 1 km) [26], and LU5M812TGT (≥ 0.4 km) [19]. However, smaller craters (less than 400 m) remain underrepresented in global crater databases, and efforts to expand this coverage are crucial. This gap in coverage limits our understanding of the Moon's impact history and geological evolution.

To address these challenges, this study proposes an innovative approach YOLO-SCNet based on the YOLOv11 model, tailored specifically for detecting craters in the 200m–2km range. While our method is adaptable to detecting craters across a wide range of sizes, we focus on this range to complement existing crater catalogs that predominantly include craters ≥1 km and to fill the gaps in small crater detection. The proposed YOLO-SCNet introduces several key enhancements, including a Transformer module for improved feature representation, multi-scale feature extraction for better adaptability to varying crater sizes, and an optimized detection head for increased detection precision and efficiency. These advancements enable robust and high-precision small crater detection, even in complex terrains and lighting conditions.

In addition to model innovation, we propose a custom sample dataset construction method that incorporates advanced data augmentation techniques, such as Poisson Image Editing. This method generates a diverse and high-quality dataset from a relatively small set of manually annotated samples, significantly reducing the manual workload while ensuring consistent and accurate labeling. The dataset covers a wide variety of lunar geomorphological features, including polar regions, high-latitude highlands, mid-latitude highlands, and lunar mare regions, thereby enhancing the model’s generalization ability and robustness under diverse and extreme conditions.

The contributions of this study are three-folded:

A scalable multi-scale crater detection framework: Although this study focuses on detecting craters ranging from 200 meters to 2 kilometers in size, the proposed method demonstrates excellent scalability and adaptability, allowing it to be applied to other size ranges through the use of custom datasets. This flexibility lays the foundation for the future construction of a global multi-scale lunar crater catalog and provides strong support for a wide range of planetary geological research.

A novel sample dataset generation method: By collecting craters and background images and applying image enhancement techniques, this method rapidly generates a sufficient quantity of diverse and context-rich sample data. It effectively addresses the challenge of manually annotating craters in the complex lunar environment, eliminating the need for extensive human labor. The generated sample data is highly accurate, diverse, and closely aligned with real-world application scenarios, helping the model better learn target features and background information, thereby improving detection accuracy, robustness, and generalization ability.

A high-performance small crater detection model: To achieve the target for small craters detection, we modify the Yolov11 by adding a small-object detection layer and supported by a custom-built sample dataset, excels in detecting small craters, especially in complex lunar terrains, with diverse crater morphologies, and under challenging lighting conditions. Extensive experiments validate the robustness, adaptability, and efficient performance of the method, highlighting its significant potential in generating global lunar crater catalogs and supporting future planetary geological research.

The remainder of this paper is organized as follows. Section 2 provides a detailed description of the sample dataset generation method we proposed, as well as the approach for constructing a deep learning-based automatic detection model for small impact craters across the entire lunar surface using lunar region partitioning. Section 3 presents the experimental results of impact crater detection using three types of test data. Section 4 offers an analysis and discussion of these results. Finally, Section 5 concludes the paper and outlines potential directions for future research.

2. Materials and Methods

2.1. Study Regions

2.1.1. Lunar Image Classification

In this study, We utilized high-resolution global lunar imagery data from the CE-2 mission, with a 7-meter resolution [27]. This dataset, which covers the entire lunar surface, is publicly available in a map sheet format [28] and consists of 844 sheets, divided into 12 zones labeled C through N [29]. Its high spatial resolution makes it particularly suitable for detecting small craters with diameters ranging from 200 m to 2 km.

To ensure comprehensive coverage of the lunar surface and enhance the diversity of the training dataset, we categorized the map sheets into four representative regional groups based on their geomorphological and geological characteristics:

• Polar Regions (I): Complex terrain with rugged mountains and abundant craters, many of which are circular or elliptical. These areas exhibit varying albedo, with lower reflectivity near the poles and brighter surfaces in surrounding areas.
• High-Latitude Highlands (II): Characterized by dramatic topographic changes, including mountains, canyons, and slopes, with higher reflectivity compared to mare regions. Craters in these areas are relatively larger and exhibit complex shapes.
• Mid-Low Latitude Highlands (III): Defined by undulating terrain influenced by lava eruptions, volcanic activity, and magma intrusion, leading to altered crater morphology.
• Lunar Mare Regions (IV): Flat regions covered by extensive basaltic lava flows, with relatively low reflectivity. Craters in these areas are generally circular or elliptical with distinct outer walls, lacking significant central peaks or hills.

Each region was further divided into sub-regions to capture finer variations in geomorphology and illumination. This region-based classification ensures flexibility and scalability in dataset creation and model training. By sampling representative sections from these areas, we created a diverse and varied dataset that exposes the model to a wide range of surface conditions during training, significantly enhancing the model's adaptability and generalization capabilities for global lunar crater detection tasks. Table 1 summarizes the regional classification and characteristics of the Chang’E-2 dataset, while Figure 1 illustrates the regional classifications.

2.1.2. Crater Annotation Rules

Detecting small lunar craters presents several challenges, particularly in creating precise annotations. The complex terrain and texture of the lunar surface often obscure small craters, making them difficult to distinguish from the background. Additionally, variations in lighting conditions and viewing angles introduce shadow effects that blur crater edges, further complicating detection. Geological processes such as lava infill, fracturing, and collapse can distort crater shapes, leading to stacked or conjoined craters. Moreover, similar geological features like mountains, valleys, and cliffs can introduce ambiguity in accurate annotation.

To address these challenges, we developed detailed annotation guidelines encompassing crater definitions, boundary determination, and specific annotation criteria to ensure a high-quality dataset of small lunar craters. Craters were categorized into three classes (Figure 2):

• Class A (Definite craters): Craters with clear boundaries and well-preserved morphology.
• Class B (Probable craters): Craters with ambiguous boundaries, requiring subjective interpretation.
• Class C (Non-craters): Geological features that are definitively not craters.

To minimize variability and improve consistency in annotations, we focused exclusively on Class A craters, eliminating potential inconsistencies caused by subjective labeling. This approach ensured reliable and consistent data to enhance the accuracy and efficiency of model training.

The process of crater annotation usually involves the following steps: First, representative images were divided into smaller tiles of 1280×1280 pixels, with approximately 900 tiles generated from each image. Next, high-density crater images with clear boundaries and diverse crater types were selected and categorized into four groups: polar regions, high-latitude highlands, mid-low latitude highlands, and lunar mare regions, with no fewer than 500 images per group. Finally, only craters with diameters between 25 and 300 pixels were annotated using the Labelme software, and detailed information about their size and location was recorded.

2.1.3. Sample Synthesis and Data Augmentation

In deep learning, data augmentation serves as an effective strategy to overcome the challenges posed by limited training data, data imbalance, and low-quality data, ultimately enhancing model accuracy [30,31,32]. The key innovation of this study lies in synthesizing a diverse and high-quality training dataset from a limited number of manually labeled samples. By combining manual annotations with advanced image processing techniques, such as Poisson Image Editing [33] and the Copy-Paste data augmentation method [34], we significantly expanded the dataset size and effectively improved the model’s generalization ability.

In the data augmentation strategy, annotated lunar crater images were utilized to generate a set of lunar crater images (denoted as L), while images with fewer craters were employed to form the background image set (denoted as B). This segmentation approach ensures the diversity of the background, capturing a wide range of lunar terrains. Subsequently, Poisson image editing was applied, where craters from the set L were extracted as source objects, and regions from the background set B provided the varied lunar terrains for the target. The gradient field for each crater was computed using the Poisson equation, capturing the texture and intensity variations. This gradient field was then fused with the target background's gradient field, ensuring seamless transitions between the crater's edges and the surrounding terrain. The fused gradient field was solved using least-squares optimization, producing augmented images with minimal visual discontinuities. This methodology effectively generates realistic augmented images that closely resemble real-world lunar scenarios. Both Poisson Image Editing and Image Segmentation methods are used for data augmentation. Poisson Image Editing is particularly employed to ensure a seamless transition between the target object and the background after replacement, avoiding visible boundary artifacts. As shown in the Figure 3 below.

Our comparative experiments showed that Poisson Image Editing significantly outperforms other augmentation strategies [12,35,36], such as CutMix and MixUp, in terms of improving model robustness and generalization, the results are listed in Section 4.3.2.

2.1.4. Dataset Construction and Partitioning

Ensuring reliable evaluation of a model’s generalization ability is a critical aspect of deep learning-based crater detection, especially when working with a diverse and complex dataset. To address challenges such as data leakage, inconsistent sample distribution, and potential overfitting, we implemented a rigorous and transparent dataset partitioning strategy. This approach ensures reproducibility while reflecting the model’s true performance in detecting craters under varied lunar conditions.

Unique Identifier Assignment. Each image in the dataset was assigned a unique identifier derived from its metadata, including region code, resolution, and acquisition time. This ensured a consistent and structured organization of the dataset while facilitating traceability across all subsets.

Hash-Based Partitioning. To achieve reproducible dataset partitioning, we calculated an MD5 hash value for each unique identifier. Based on the computed hash values, the dataset was split into training, validation, and testing subsets at a fixed ratio of 8:1:1. This hash-based approach minimizes bias in the partitioning process and ensures uniform distribution of samples across subsets.

Augmented Data Management. Augmented images, generated during the data augmentation process, were explicitly linked to their source images. These derived samples were restricted to the same subset as their original images, thereby eliminating the risk of cross-contamination between subsets. This step ensures that the evaluation metrics accurately reflect the model's generalization ability without artificially inflating performance due to data leakage.

Independent Subset Verification. A comprehensive validation process was conducted to confirm that no image, including its augmented variants, was duplicated across subsets. This independent verification guarantees the integrity and exclusivity of each subset, further strengthening the reliability of the reported results.

Automated Implementation. The entire partitioning and verification process was implemented using Python scripts, ensuring complete reproducibility and transparency. By automating these steps, we established a robust framework that can be easily adapted for future studies in lunar crater detection or similar planetary research.

This rigorous dataset partitioning strategy eliminates the risk of data leakage, enhances the transparency and reproducibility of the research, and ensures that the reported evaluation metrics provide an accurate measure of the model’s true generalization ability. By addressing common pitfalls in dataset preparation, such as subset contamination and overfitting risks, this methodology provides a robust foundation for reproducible and trustworthy crater detection studies.

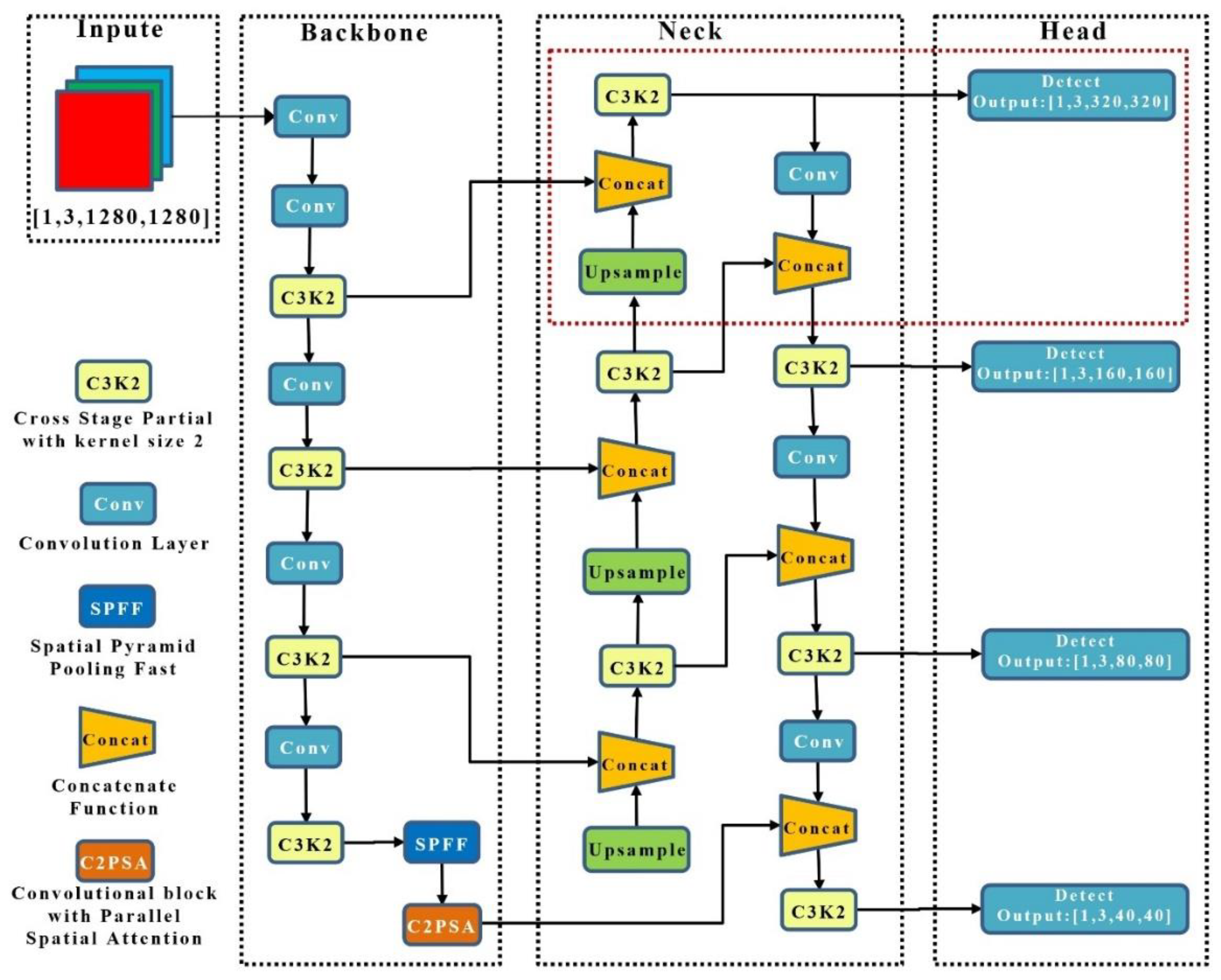
2.2. YOLO-SCNet Detection Method

2.2.1. YOLO-SCNet Architecture and Key Features

YOLOv11 is the latest iteration of the YOLO (You Only Look Once) [37] series, optimized for s complex tasks. YOLOv11 builds upon the core architecture of YOLOv5 [38] and integrates several innovative improvements that enhance detection accuracy and adaptability.

YOLOv11 [39,40] introduces several key technologies to improve performance compare with previous work based on Yolov5 and Yolov8 [41]. Firstly, YOLOv11 replaces the C2f module from YOLOv5 with the C3K2 module. C3K2 is a custom CSP bottleneck layer that includes two smaller convolutional layers, significantly boosting processing speed, particularly for high-resolution images and real-time detection tasks. YOLOv11 also retains the Spatial Pyramid Pooling (SPPF) module from YOLOv8, which further strengthens the model's ability to extract multi-scale features. Additionally, YOLOv11 incorporates the C2PSA module, which combines channel and spatial information along with multi-head attention mechanisms to improve feature extraction efficiency, especially when dealing with targets with rich details in complex backgrounds.

At the same time, YOLOv11 employs a Transformer module for global feature modeling, enhancing the model's ability to capture long-range dependencies in complex backgrounds. Furthermore, YOLOv11 implements multi-scale feature fusion, allowing the model to effectively detect targets of various sizes [42].

Based on the YOLOv11 architecture, we introduce an innovative small object detection head, specifically designed to enhance the model's ability to recognize small objects. The improved YOLO-SCNet network structure is shown in Figure 4. This small object detection head extracts high-resolution fine-grained spatial information from shallow feature maps, significantly enhancing the model’s perception and localization capabilities for small objects.

2.2.2. Design and Optimization of the Small Object Detection Head

The small object detection head works by incorporating shallow feature maps into the YOLOv11 model, preserving more spatial resolution information, which allows the model to capture fine details of small objects. This head specifically focuses on the spatial information of small objects and fuses it with deeper semantic information, significantly improving the precision of localization and classification for small objects. Through this design, YOLO-SCNet can effectively detect small lunar craters and other targets within complex backgrounds.

To further enhance the detection of small objects, we have designed optimized anchor boxes tailored for small targets. By adjusting the size and aspect ratio of the anchor boxes, we ensure they are better suited for detecting smaller objects, allowing for better alignment with the model’s predictions. This optimization process dynamically adjusts the anchor boxes during training to accommodate different sizes of small targets, improving the model’s adaptability and accuracy for small object detection.

In the YOLO-SCNet, the size and aspect ratio of the anchor boxes are dynamically adjusted based on the size and shape of the targets. The adaptive anchor box optimization technique allows YOLO-SCNet to better accommodate targets of various sizes and shapes, particularly excelling in small object detection. During training, YOLO-SCNet automatically adjusts the anchor boxes to better match the actual size and shape of the targets, improving detection accuracy. This optimization process focuses on dynamically adjusting the anchor boxes to align more precisely with different target characteristics. As a result, YOLOv11 is more effective at detecting irregularly shaped or smaller targets, particularly in complex backgrounds. This technique offers significant advantages in detecting small lunar craters and other similar targets, enhancing the model's adaptability and accuracy for small object detection.

For small object detection, we employ a weighted loss function that assigns higher weights to the classification loss, localization loss, and confidence loss for small objects. This weighted mechanism ensures the model prioritizes small object detection during training, thereby improving detection accuracy. Specifically, it includes classification loss, localization loss, and confidence loss. The specific formula for the loss function is as follows:

$$Loss={\lambda }_1{L}_{cls}+{\lambda }_2{L}_{loc}+{\lambda }_3{L}_{conf}$$

(1)

where:

• Classification loss (Lcls): Measures the discrepancy between predicted and true class labels.
• localization loss (Lloc): Evaluates the difference between predicted and true bounding box coordinates.
• confidence loss (Lconf): Assesses the accuracy of the model’s confidence predictions for bounding boxes.
• λ1, λ2, λ3 are dynamically adjusted weight coefficients.

These weighted strategies adjust the weights in the loss function to ensure that small objects are prioritized during training, ultimately improving the model’s performance in detecting small objects.

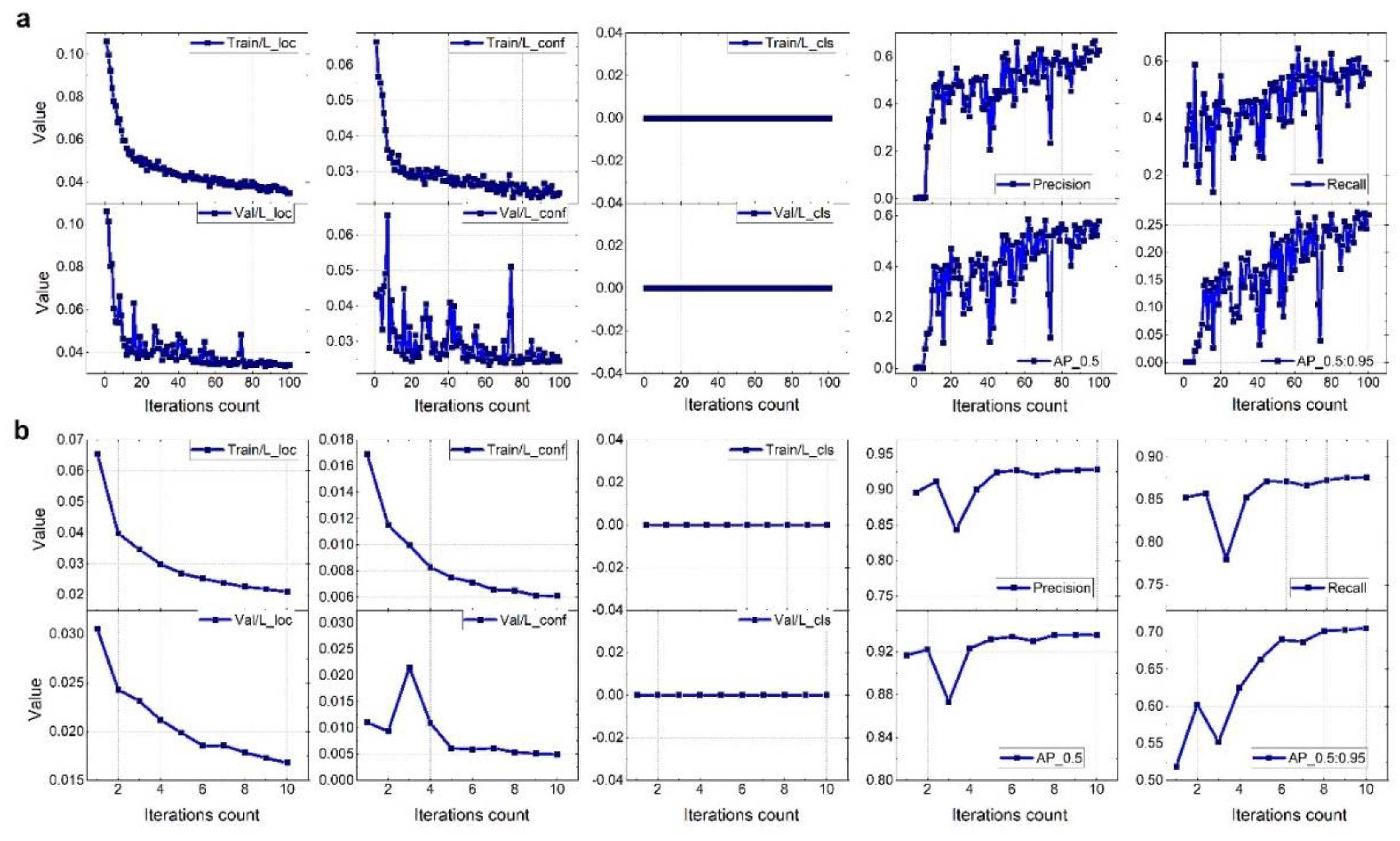
2.2.3. Model Training and Optimization

This section describes the training and optimization process of the YOLO-SCNet, covering training environment, dataset partitioning, and post-processing techniques.

• Model Configuration and Training Environment: Experiments were conducted using PyTorch 1.12 on a robust, high-performance computing system. This system equipped with two Intel 6346 Xeon 16-core processors, two NVidia GeForce RTX 3090 Ti 24 GB GPUs, and 256 GB of memory, all operating under Ubuntu 20.04.5. Key parameters included an input size of 1280×1280, batch size of 8, initial learning rate of 0.01, momentum of 0.937, and weight decay of 0.0005.
• Dataset Partitioning: To ensure fairness in training, validation, and testing, we ultimately constructed a dataset consisting of 80,607 samples, which were collected from four distinct lunar regions (polar region, high-latitude highlands, mid-low latitude highlands, and lunar mare). This dataset was partitioned into training, validation, and testing sets in an 8:1:1 ratio. This partitioning ensures that each dataset represents different lunar terrains and lighting conditions, providing a comprehensive test of the model's generalization capability.
• Training Strategies: To ensure optimal adaptation to lunar crater detection tasks, the following strategies were employed: 1) Fine-Tuning Pre-Trained Weights: The model was fine-tuned with pre-trained weights from ImageNet to adapt to the specific features of lunar craters.2) Adaptive Learning Rate Scheduling: A dynamic learning rate adjustment strategy was employed to accelerate convergence and reduce the risk of overfitting. 3) k-Fold Cross-Validation: A 10-fold cross-validation approach was used to evaluate the stability of the model across different data partitions and reduce the potential bias introduced by a single dataset split. 4) Robustness Validation with Augmented Data: The model's robustness was tested using augmented datasets with variations in noise, contrast, and lighting to simulate real-world imaging conditions. 5) Focused Small Crater Detection: Special attention was given to craters with diameters smaller than 200 meters to ensure the model's suitability for global lunar mapping and planetary geological studies.
• Post-Processing and Result Optimization: During detection, post-processing techniques were applied, including thresholding and Non-Maximum Suppression (NMS), to refine the model's predictions. By setting confidence thresholds, low-confidence detections were filtered out, while NMS was used to eliminate overlapping bounding boxes, retaining only the highest-confidence predictions.

2.2.4. Performance Evaluation

The model’s performance was evaluated using several metrics to comprehensively assess its accuracy, consistency, and generalization ability:

• Precision (P): Measures the proportion of correctly identified craters among all predictions.
• Recall (R): Indicates the proportion of true craters detected by the model.
• F1-Score (F1): The harmonic mean of precision and recall, providing a balanced measure of performance.
• Average Precision (AP): Represents the area under the precision-recall curve across various IoU thresholds, reflecting localization and classification accuracy
• Area Under the Curve (AUC): Assesses the model’s ability to distinguish between true and false detections across different confidence levels.

The formulas for these metrics are provided in Equations (2) to (5):

$$P={\displaystyle \frac{TP}{TP+FP}}$$

(2)

$$R={\displaystyle \frac{TP}{TP+FN}}$$

(3)

$$F1={\displaystyle \frac{2\ast P\ast R}{P+R}}$$

(4)

$$\mathrm{A}\mathrm{P}=\sum _n(R_n-R_{n-1})P_n$$

(5)

Where TP (True Positive) represents the number of correctly identified craters, FP (False Positive) is the number of incorrectly identified craters, and FN (False Negative) is the number of craters that were missed in detection. n represents different threshold points on the PR curve, ${\mathit{R}}_{\mathit{n}}$ represents the recall at threshold n, and $P_n$ denotes the corresponding precision at threshold n.

A critical IoU threshold of 50% was set to classify predictions as true positives. This threshold was chosen because it strikes an appropriate balance between precision and recall, ensuring that the model does not produce excessive false positives. 50% IoU is a widely adopted threshold in object detection tasks, particularly in small object detection. It provides a reliable benchmark for evaluating detection performance while maintaining robust detection of smaller or partially occluded targets. Given the complex lunar surface and small, irregularly shaped lunar craters, a 50% IoU threshold ensures the model's precision and reliability while minimizing false negatives and false positives. This threshold also proved effective in ensuring that the model's detections were reliable without being too lenient, which is important for ensuring the quality of lunar crater catalogs.

In addition to IoU, we also used other evaluation metrics, including confidence levels and crater diameter errors, to provide a comprehensive assessment of the model’s detection capability across various lunar terrains.

3. Experimental Results

This section presents the experimental evaluation of the proposed YOLO-SCNet for lunar crater detection, focusing on its performance across diverse terrains, varying crater sizes, and comparisons with existing crater databases. The experiments were designed to comprehensively assess the model's generalization ability, robustness, and potential to expand existing lunar crater catalogs.

3.1. Ground Truth Data Preparation and Independent Regional Testing

To ensure a rigorous evaluation, accurate ground truth data were prepared to enable direct comparisons between the model's predictions and reference annotations. Six representative regions were selected (Figure 5), encompassing diverse geomorphological and illumination conditions, such as polar regions, high-latitude highlands, mid-low latitude highlands, and lunar mare regions. This selection ensured the model's broad applicability to the lunar surface. The test regions include:

• I-1 (N021, North Pole): Bright surfaces near the polar region with abundant small craters exhibiting black-and-white wart-like structures.
• I-2 (S014, South Pole): Low-albedo areas with dim illumination and larger craters containing central stacks.
• II-1 (C1-02, Northern High-Latitude Highlands): Darker surface with the lowest albedo among similar regions, characterized by dramatic topographic variations.
• III-2 (F1-04, Mid-Low Latitude Highlands): Bright ejecta material with higher reflectivity, featuring craters altered by volcanic activity and lava flows.
• IV-2 (D2-13, Lunar Near-Side Mare): Darker near-side regions with low reflectivity and distinct circular craters.
• IV-3 (K1-36, Lunar Far-Side Mare): Far-side regions with moderate albedo and circular craters with smooth edges.

Three types of labeled datasets were prepared to evaluate the model's performance across various crater sizes:

• Medium-sized craters (400m–2km) Annotated across the entire extent of the six regions to assess the model's ability to detect craters of moderate size.
• Small craters (200m–2km): Fine-grained annotations in specific areas to evaluate the model’s precision in detecting smaller craters.
• Large craters (400m–2km): Extracted from the RobbinsDB [25], LU1319373 catalogs [26] and LU5M812TGT (≥ 0.4 km) [19] in two regions to validate the model's performance in detecting larger craters.

The rigorous partitioning strategy ensured that the selected regions were excluded from the training and validation datasets, simulating independent testing conditions. This approach evaluates the model’s generalization ability under unseen environmental conditions, ranging from rugged polar terrains to flat lunar mare regions. It is important to highlight that previous studies have largely overlooked small craters. In this work, we specifically selected part of the small craters to validate the universality and scalability of our approach across craters of varying sizes.

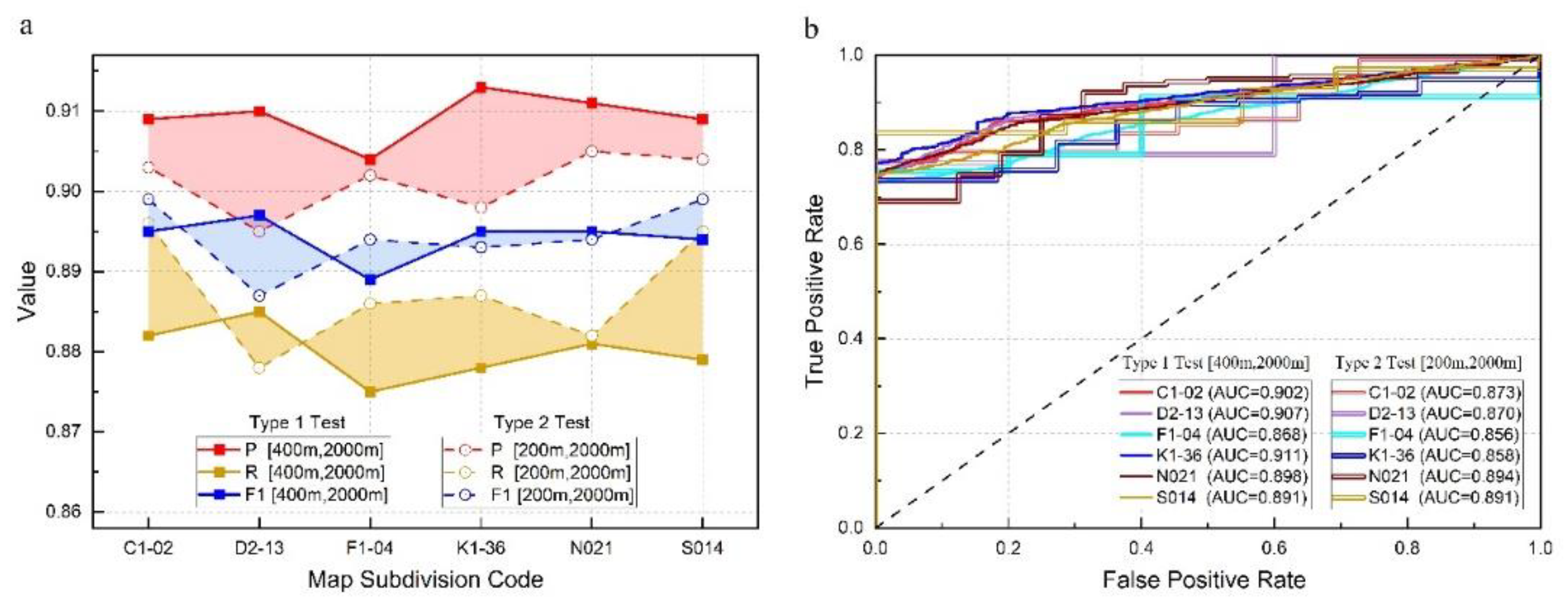
3.2. Type 1 Test: Detection of Medium-Sized Craters (400m—2km)

The first test evaluated the ability of the YOLO-SCNet to detect medium-sized craters (400m–2km) across six test regions. The experimental results demonstrate that YOLO-SCNet performed excellently in all regions, with an average precision of 90.9%, recall of 88.0%, and F1 score of 89.4% (Table 2). This highlights its robust performance under diverse lunar terrains, complex lighting conditions, and topographical variations.

Specifically, the YOLO-SCNet 's adaptability in each region is as follows:

• Highlands (including C1-02 and F1-04): In high-latitude highland regions with significant terrain variations and higher reflectance, the model still demonstrated exceptional adaptability. In the C1-02 northern high-latitude highland, where the reflectance was low and the terrain complex, the model successfully detected most craters, with a precision of 90.9% and recall of 88.2%. In the F1-04 mid-latitude highlands, influenced by volcanic activity and lava flows, which caused alterations in crater morphology, the model achieved a precision of 90.4% and recall of 87.5%, fully reflecting its robustness in complex terrains.
• Maria Regions (including D2-13 and K1-36): In the maria regions, YOLO-SCNet also demonstrated strong detection capabilities. In the D2-13 maria region, where the craters were mostly round or elliptical with clear edges, the model achieved a precision of 91.0% and recall of 88.5%. In the K1-36 maria region, with similar crater features, the model's precision was 91.3% and recall 87.8%. These results indicate that YOLO-SCNet can accurately identify craters even in low reflectance and flat terrains.
• Polar Regions (including N021 and S014): In extreme environments, the model exhibited outstanding adaptability. In the N021 polar region, despite the low reflectance, the model was able to accurately identify a large number of craters, achieving a precision of 90.9% and recall of 88.1%. In the S014 Antarctic region, under high contrast and complex lighting conditions, YOLO-SCNet also performed excellently, with a precision of 90.9% and recall of 87.9%, demonstrating its stability in polar environments.

Despite the high detection precision, YOLO-SCNet maintained efficiency in processing time, with an average processing time of 2 minutes and 52 seconds per region and an average test area of 43,794.96 km². These results further demonstrate that the model can achieve high-precision and efficient crater detection in diverse lunar terrains. Figure 6 presents the detection results for selected regions, emphasizing the model's precise localization ability in complex terrain and environmental conditions.

3.3. Type 2 Test: Detection of Small Craters (200m—2km)

The goal of the Type 2 test was to evaluate the ability of the YOLO-SCNet model to detect smaller craters in the 200m–2km range, including craters as small as 200m, which present additional challenges due to their subtle features, reduced visibility, and the difficulty in distinguishing them from surrounding terrain. Compared to the Type 1 test (400m–2km), this test specifically addresses the detection of even smaller craters, which require more refined detection capabilities. While the regions tested are the same as in the Type 1 test, the smaller crater sizes pose increased difficulty for accurate detection. Across all six regions, the model achieved an overall precision of 90.2% and an F1-score of 89.4%, demonstrating strong performance despite the challenges posed by the smaller craters.

Highlands (including F1-04 and C1-02): In the highland regions, the reduced crater size presented additional challenges in terms of visibility and detection. In the F1-04 mid-low latitude highlands, the smaller craters were often difficult to distinguish from the surrounding terrain features, yet the model maintained a precision of 90.2% and recall of 88.6%. Similarly, in the C1-02 northern high-latitude highlands, the smaller craters, which are more susceptible to being obscured by complex terrain, still achieved a precision of 90.9% and recall of 88.2%, highlighting the model’s robustness in detecting small craters under challenging conditions.

Maria Regions (including D2-13 and K1-36): In the maria regions, smaller craters presented unique challenges related to the lack of prominent crater edges. Despite this, YOLO-SCNet continued to demonstrate effective detection. In the D2-13 maria region, the model maintained a precision of 91.0% and recall of 88.5%, successfully identifying smaller craters with subtle features. In the K1-36 maria region, where the craters are often faint and closely resemble surrounding terrain, the model achieved a precision of 91.3% and recall of 87.8%, indicating its strong ability to detect small craters in smooth, low-reflectance areas.

Polar Regions (including N021 and S014): In the polar regions, the smaller craters were more challenging due to their reduced size and the extreme lighting conditions. However, the model demonstrated its ability to maintain high performance under these conditions. In the N021 polar region, despite the low reflectance and subtle features of the smaller craters, the model achieved a precision of 90.9% and recall of 88.1%. In the S014 Antarctic region, where lighting and contrast further complicated the detection of smaller craters, the model performed excellently with a precision of 90.9% and recall of 87.9%.

These results emphasize YOLO-SCNet’s ability to detect small craters, even in challenging lunar environments. The average processing time per region was 2 minutes and 52 seconds, with an average test area of 43,794.96 km². The high precision and recall values in detecting smaller craters (200m–2km) further demonstrate the model's robustness and adaptability. Detailed performance metrics for the small crater detection test are provided in Table 3, with Figure 7 visually illustrating the detection results across varying terrains.

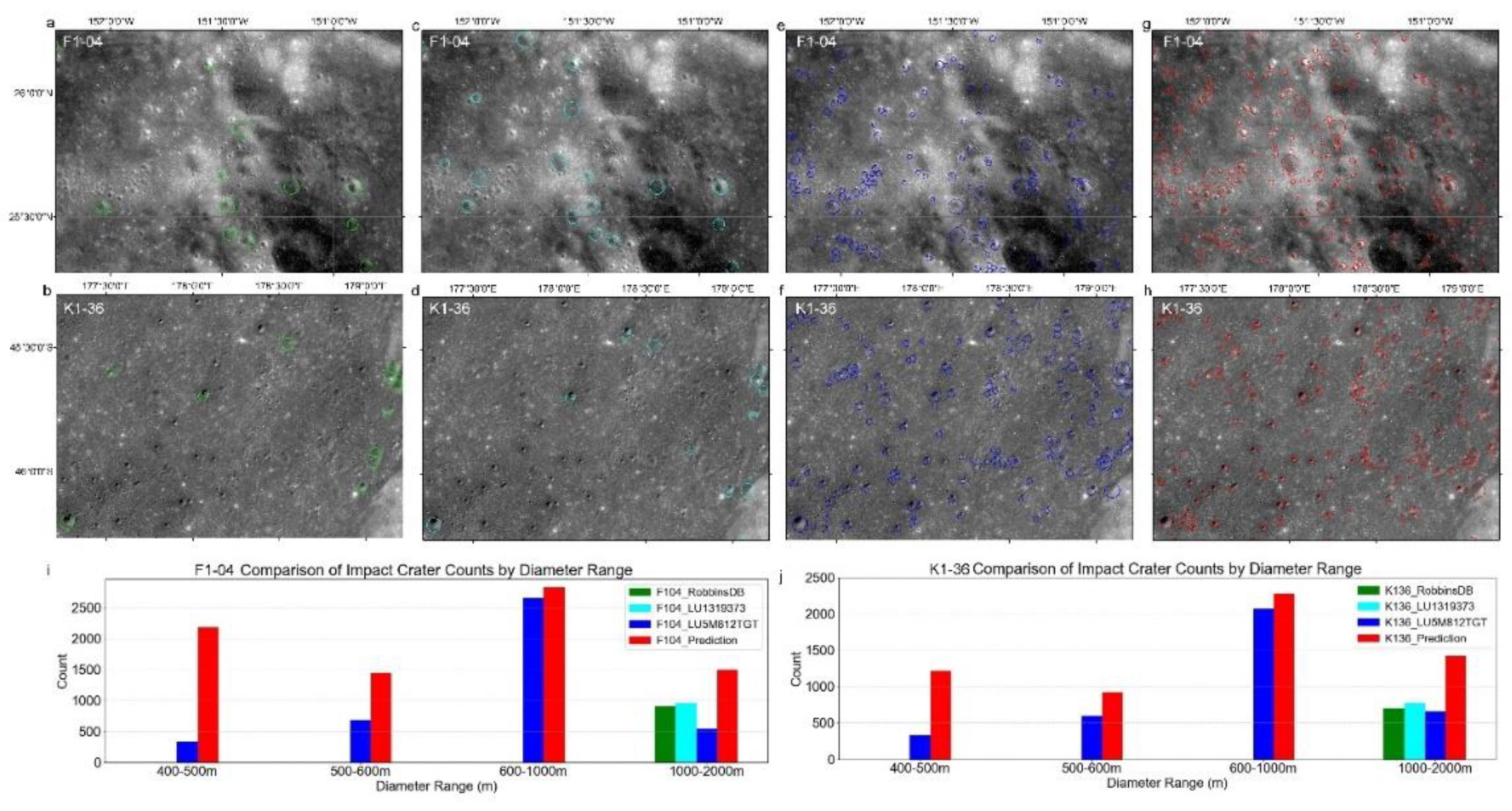
3.4. Type 3 Test: Database Comparison and Detection Expansion (400m—2km)

In this Type 3 test, we compared the detection results of YOLO-SCNet with existing lunar crater catalogs, selecting the F1-04 and K1-36 regions for testing. First, we compared the model with craters from the RobbinsDB and LU1319373 catalogs, with crater diameters ranging from 1 km to 2 km. The results (Table 4) show that the model achieved average recall rates of 97.1%, indicating that the model has high sensitivity in detecting craters already present in the catalogs, with almost no missed detections. However, the average precision was relatively low, at 72.3%. The low precision was primarily due to the model detecting additional craters in several regions, most of which were indeed real impact craters (as shown in Figures 8(a) and 8(b)), but since these craters were not included in the existing database, they were misclassified as false positives, resulting in lower precision.

Additionally, we compared YOLO-SCNet with the LU5M812TGT catalog, which includes craters with diameters ranging from 0.4 km to 2 km. The comparison revealed that the model achieved average recall rate of 97.6% (Table 4), further confirming the efficiency of YOLO-SCNet in lunar crater detection. Furthermore, the model successfully detected numerous craters not recorded in the catalog, which were subsequently verified to be genuine impact craters, particularly in the 400m-600m diameter range (Figure 8). This result not only highlights the advantages of YOLO-SCNet in detecting small lunar craters, but also demonstrates the model's significant potential for expanding existing crater catalogs, providing new data for future lunar geological studies.

These tests demonstrate that YOLO-SCNet is capable not only of validating existing databases but also of identifying newly discovered impact craters. To address the issue of lower detection precision, increasing the number of craters in the existing databases can effectively improve detection accuracy. This result further underscores the importance of expanding current databases to enhance the model's accuracy and comprehensiveness.

3.5. Summary of Experimental Results

Across all three test types, YOLO-SCNet demonstrated better performance in detecting craters of varying sizes and under diverse terrain conditions comparing with existing methods. The experiment results proved that the proposed YOLO-SCNet proves its high accuracy and versatility to adapt to different conditions. Key results include:

• An average Precision of 90.9%, Recall of 88.0% and F1-score of 89.4% for medium-sized craters (400m–2km).
• An overall Precision of 90.2%, Recall of 88.7% and F1-score of 89.4% for small craters (200m–400m), demonstrating adaptability to subtle topographical features.
• A high Recall (97.2%) for database comparison tests, with the model identifying additional craters likely to refine and expand existing catalogs.

The experimental results validate YOLO-SCNet as a reliable and effective tool for lunar crater detection, capable of adapting to complex terrains and varying crater sizes. As the dataset becomes more refined and diverse, the model’s performance is expected to improve further, enhancing its potential for planetary surface analysis and high-resolution geological surveys.

4. Analysis and Discussion

4.1. Performance and Evaluation of the Proposed Model

4.1.1. Overall Performance in Crater Detection

The experimental results demonstrate that the YOLO-SCNet developed in this study excels in detecting small lunar craters across diverse terrains and lighting conditions. The model achieves high Precision, Recall, and F1-scores, highlighting its strong adaptability to the complex lunar surface environment. Figure 9a illustrate the model's detection performance, effectively mitigating the impact of variable lighting and intricate geological features.

Additionally, the model’s Area Under the Curve (AUC) values, shown in Figure 9b, further emphasize its outstanding performance, providing valuable insights into its accuracy at various confidence thresholds. A high AP indicates the model's ability to accurately detect craters under different conditions, while a strong AUC reflects its robust performance in distinguishing between crater presence and absence at varying confidence levels.

Beyond its high accuracy, the model demonstrates excellent computational efficiency. Runtime evaluations across multiple test regions show an average processing speed of averaging 2 minutes and 52 seconds per region with an average area of 43,794.96 km² (Table 2), making it ideal for large-scale applications. This balance of computational efficiency and detection accuracy positions YOLO-SCNet as a powerful tool for generating high-resolution lunar crater catalogs and advancing future planetary geological studies.

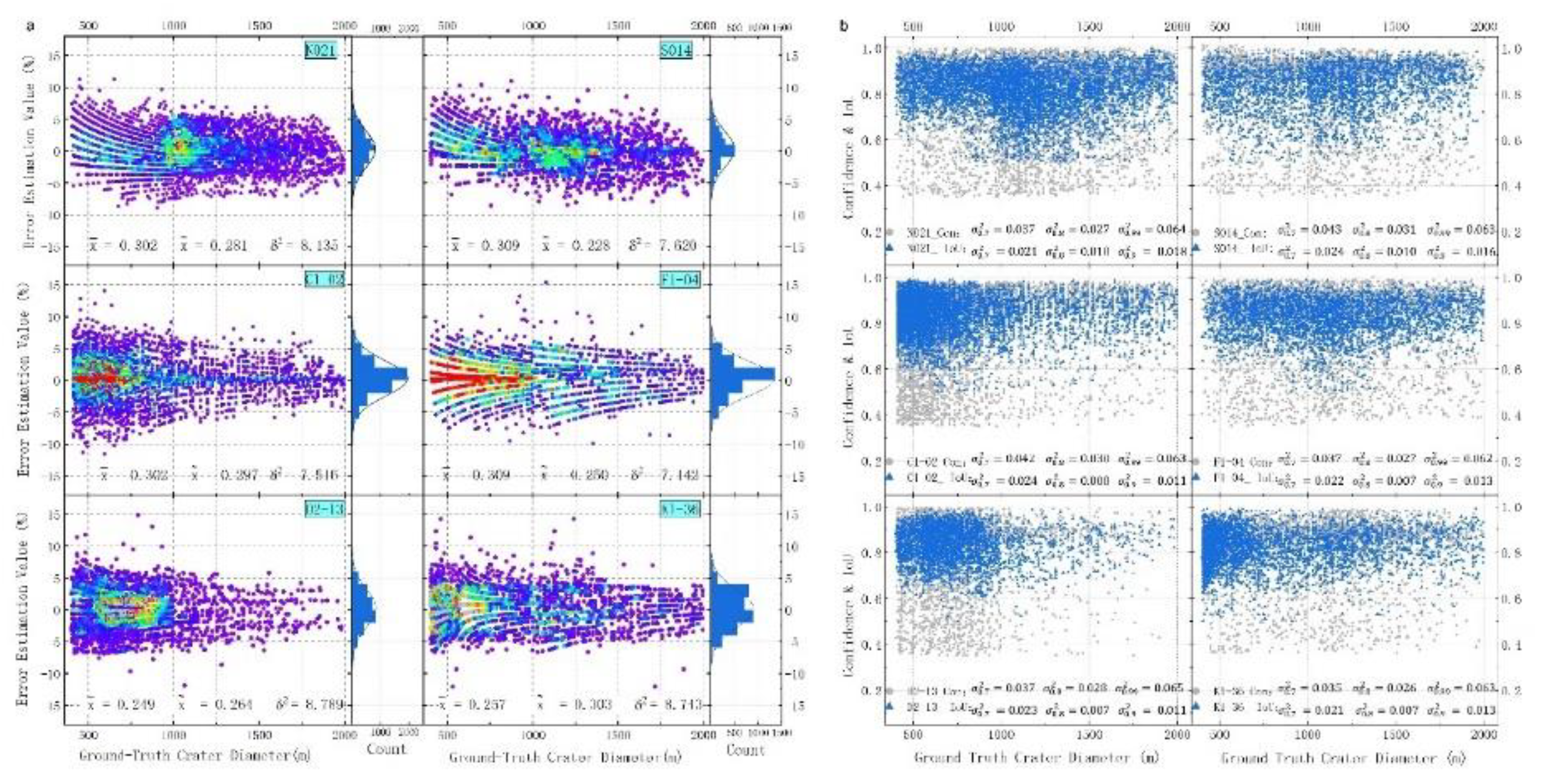
4.1.2. Implications of Regional Diversity in Model Evaluation

The division of the Chang’E-2 dataset into six representative regions allowed for a comprehensive evaluation of YOLO-SCNet’s performance under diverse geomorphological and lighting conditions. These regions simulate the challenges encountered in global lunar crater detection tasks, encompassing:

• Polar regions (e.g., N021, S014): Extreme lighting conditions and shadow effects make detecting small craters particularly challenging.
• High-latitude highlands (e.g., C1-02): Rugged terrain, steep slopes, and dramatic topographic variations test the model’s ability to adapt to complex geological features.
• Mid-low latitude highlands and mare regions (e.g., F1-04, D2-13, K1-36): Contrasting features such as volcanic alterations, flat basaltic plains, and low reflectivity require the model to generalize across varied surface types.

YOLO-SCNet consistently achieved high performance across these diverse regions, with an average Precision of 0.909 and Recall of 0.88 (Table 2). This demonstrates its robustness and adaptability, even in the most challenging conditions. Notably, the high accuracy in polar regions highlights the effectiveness of the model’s feature extraction and detection head optimizations in handling extreme contrasts and shadowed areas.

While external datasets such as LROC or SLDEM could further complement the evaluation, the Chang’E-2 dataset provides a reliable standalone benchmark due to its comprehensive coverage and high-resolution annotations. Future studies could expand this work by incorporating additional datasets or applying the model to other planetary surfaces to further validate its generalization capability.

4.2. Comprehensive Model Performance and Stability Analysis

4.2.1. Crater Detection Accuracy Analysis

To evaluate the model’s accuracy and stability, key metrics such as crater diameter error, confidence levels, and IoU thresholds were analyzed. The diameter error ($\delta \mathrm{\%}$) was calculated using the following formula:

$$\delta \mathrm{\%}=\left({\displaystyle \frac{D_{TP}-D_{GT}}{D_{TP}}}\right)\times 100$$

Where $D_{GT}$ is the ground truth diameter of the annotated crater and $D_{TP}$​ is the predicted diameter. Craters with an IoU value of 50% or greater were considered true positives (TP). The 50% IoU threshold is widely used in target detection tasks, especially for small and partially occluded objects. This threshold was chosen to balance accuracy and recall, ensuring that the model could effectively detect lunar craters without introducing an excessive number of false positives. By using this threshold, the model demonstrated stable performance across various detection conditions.

The average diameter error across all test regions was 0.239, with minimal bias or outliers (Figure 10a). This demonstrates that YOLOv11 accurately predicts crater sizes, providing a reliable foundation for generating high-precision lunar crater catalogs. Furthermore, the model showed low variance across different confidence levels (e.g., 0.7, 0.8, 0.9) and IoU thresholds (e.g., 0.5, 0.7, 0.9), as shown in Figure 10b. These results demonstrate consistent and stable detection performance, even under challenging surface conditions.

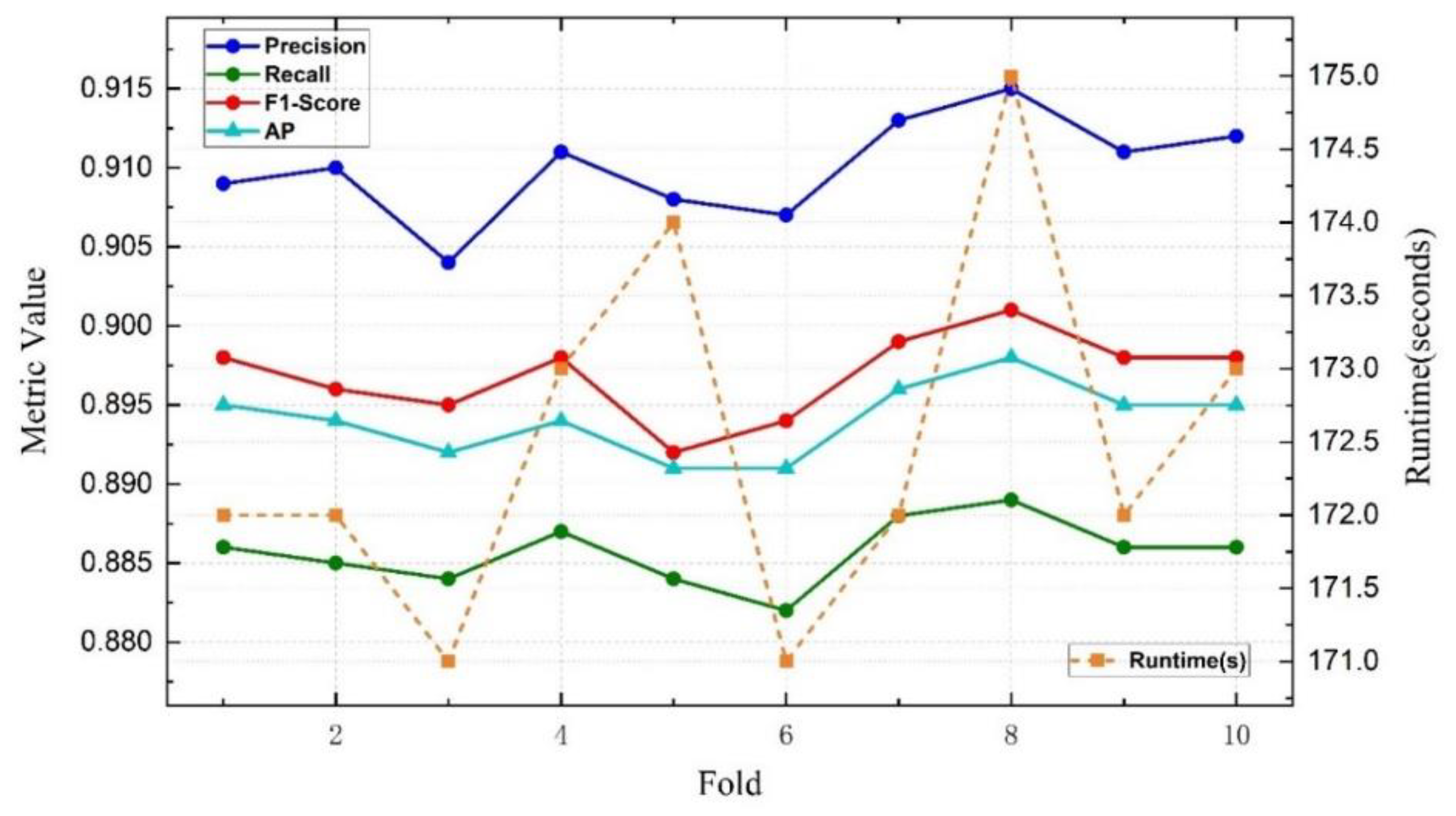
4.2.2. Robustness Evaluation via Cross-Validation

A 10-fold cross-validation experiment was conducted to assess the robustness and generalization capability of YOLO-SCNet. The dataset was divided into 10 approximately equal subsets, with one subset designated as the validation set in each iteration. The results, summarized in Table 5, show that the model achieved an average Precision of 0.909, Recall of 0.886, F1-Score of 0.897, and AP of 0.894, with standard deviations all below 0.003. These low variances highlight the model’s stability across different data splits. Additionally, the average runtime per validation fold was 172 seconds, demonstrating the computational efficiency of YOLOv11.

Figure 11 visually presents the results of the 10-fold cross-validation, where the minimal variance in Precision (±0.003), Recall (±0.003), and F1-Score (±0.003) underscores the robustness and generalization capability of the model. The average runtime per validation fold is 172 seconds (≈2 minutes 52 seconds), highlighting the computational efficiency of the model. This consistent performance across folds further validates YOLOv11's adaptability to diverse lunar surface conditions.

4.2.3. Discussion of Combined Results

The robustness of YOLO-SCNet is strongly supported by the rigorous data partitioning strategy described in Section 2.1.4. The use of hash-based dataset splitting and metadata tracking ensured that the training, validation, and testing datasets were entirely independent, eliminating data leakage risks and enabling reliable performance assessments on unseen data.

The model's high Precision and Recall can be attributed to the quality of the custom-built dataset, which provided diverse and representative samples from polar regions, highlands, and mare areas. Rigorous annotation guidelines and the exclusion of ambiguous samples further enhanced the ground truth accuracy, enabling the model to generalize effectively to unseen lunar terrains.

Finally, the balanced trade-off between Precision and Recall, evidenced by high F1-Score and AP values, demonstrates YOLO-SCNet’s capability to adapt to challenging conditions, such as extreme lighting contrasts in polar regions or low-reflectivity surfaces in mare areas. This balance is critical for accurate crater detection in global lunar mapping tasks and underscores the potential for expanding YOLO-SCNet 's application to other planetary surfaces or integrating additional data types (e.g., multispectral or topographic data) for broader planetary geological studies.

Finally, YOLO-SCNet consistently achieved a balanced trade-off between Precision and Recall, as evidenced by its high F1-Score and AP values. This balance is critical for accurate crater detection in regions with extreme lighting contrasts, such as polar areas, or low-reflectivity regions, such as lunar mare. The cross-validation results confirm that YOLO-SCNet is well-suited for global lunar crater detection tasks, providing a robust foundation for large-scale, high-precision lunar mapping projects. Furthermore, the model’s demonstrated performance underscores its potential applicability to other planetary surfaces and the integration of additional data types, such as multi-spectral or topographic information, to enhance detection performance in broader planetary exploration tasks.

4.3. Dataset Construction and Augmentation Methods in Lunar Crater Detection

4.3.1. Importance of Dataset Construction and Its Role in Performance Improvement

In this study, we focused on constructing a high-quality dataset to address the challenges of small lunar crater detection. The proposed dataset construction method, which separates craters from the background and applies advanced data augmentation techniques, significantly enhanced the model's performance. These methods proved particularly effective in improving detection accuracy for craters within the 200m-2km diameter range.

The rationale for focusing on this range stems from two primary considerations:

• Filling Existing Database Gaps: The current lunar impact crater databases, such as RobbinsDB and LU1319373, primarily include craters with diameters ≥1 km. In contrast, the newly released LU5M812TGT database contains craters with diameters ≥0.4 km. While smaller craters (<200m) are of interest, their detection and annotation often face significant challenges due to terrain complexity and resolution limitations. By targeting the 200m-2km range, our study addresses a critical gap in lunar crater datasets, providing new insights into medium-sized crater distributions.
• Reducing Annotation and Computational Workload: Annotating craters <200m requires extremely high-resolution imagery and significant manual effort, while >2km craters are typically well-documented in existing databases. The chosen range thus balances scientific value and practical feasibility.

Experimental results demonstrate that the newly constructed dataset not only improves detection accuracy but also accelerates model convergence. Figure 12 shows that within 100 iterations, the model trained on the newly constructed dataset achieved stable high precision and recall rates, significantly outperforming traditional datasets. This result highlights the critical role of high-quality datasets in unlocking the full potential of deep learning models for lunar crater detection tasks.

4.3.2. Application and Effectiveness of Data Augmentation Strategies

To further enhance the diversity and representativeness of the dataset, this study introduced Poisson Image Editing as a key data augmentation strategy. Unlike traditional augmentation methods (e.g., rotation, scaling, flipping) or advanced techniques like CutMix, Poisson Image Editing seamlessly blends crater features into diverse lunar backgrounds, preserving gradient continuity and realistic lighting conditions. This approach generates augmented samples that closely resemble real-world scenarios, enabling the model to achieve improved generalization across various lunar terrains.

Table 6 summarizes the comparative performance of Poisson Image Editing and other augmentation methods. Key findings include:

• Highest Precision and F1-Score: Poisson Image Editing achieved the highest Precision (0.915), Recall (0.882), and F1-Score (0.898), outperforming all other methods.
• Faster Convergence: The method required only 1000 iterations to achieve stable training, significantly faster than other methods (e.g., CutMix: 1300 iterations, rotation: 1500 iterations).
• Better Stability: Poisson Image Editing exhibited the lowest variance in metrics (±0.003), indicating consistent performance across validation folds.

These results demonstrate that Poisson Image Editing not only enhances training efficiency but also generates high-quality augmented samples, which are crucial for small lunar crater detection tasks.

4.3.3. Advantages and Scalability of Poisson Image Editing

The experimental results underscore the unique advantages of Poisson Image Editing for lunar crater detection within the 200m–2km range, primarily by preserving gradient continuity to capture subtle boundary features and complex lighting variations that enhance detection precision. By seamlessly blending craters into diverse lunar terrains, Poisson Image Editing generates samples that increase the model’s robustness and generalization ability, even in polar areas and high-latitude highlands where geological and lighting conditions can be extreme. The method also excels in integrating craters into challenging terrains like shadowed polar regions or steep slopes, outperforming simpler augmentation approaches. Although this study focuses on the 200m–2km range, the underlying dataset construction and augmentation strategies can be applied to other crater size ranges: craters smaller than 200m would require higher-resolution imagery and refined annotations, while larger craters (>2km) can be handled with minimal modifications. This scalability establishes Poisson Image Editing as a promising tool for expanding lunar crater databases and addressing broader scientific questions.

4.3.4. Discussion and Future Directions

The proposed dataset construction and augmentation strategies significantly improve the model's performance in lunar crater detection. While the focus of this study is on the 200m-2km range, the methods demonstrate strong scalability, with potential applications in detecting smaller (<200m) or larger (>2km) craters. Future studies could:

1) Expand the dataset to include more diverse regions and crater sizes, particularly for <200m craters.

2) Integrate Poisson Image Editing with other advanced techniques, such as CutMix or domain adaptation, to further enhance data diversity and model robustness.

3) Explore applications beyond lunar craters, such as crater detection on Mars or other planetary surfaces, to validate the method’s generalization ability.

In conclusion, the dataset construction and augmentation methods proposed in this study effectively address the challenges of small lunar crater detection, providing a robust foundation for high-precision lunar mapping and planetary exploration.

4.4. Comparison with Existing Methods

4.4.1. Performance Comparison

This study presents a comparative analysis of crater detection results with recent research in the field, as summarized in Table 7. Most existing studies primarily utilize datasets of craters with diameters greater than 1 km, derived from established crater catalogs, for model training. However, the significant differences in morphology and characteristics between large and small craters often lead to suboptimal results when applied to smaller craters. Additionally, the complexity of lunar terrain makes accurate crater boundary annotation challenging, resulting in inevitable inconsistencies in labeled datasets, which can negatively impact model convergence and detection performance.

4.4.2. Comparative Analysis of Detection Methods

In contrast to previous methods, the advanced YOLO-SCNet trained on a high-quality sample dataset achieves notably higher detection performance, as evidenced by its Recall of 88.7%, surpassing La Grassa et al. 2025 (85.2%) and Grassa et al. (87.2%), largely due to tailored data augmentation strategies that enhance small crater detection [0.2–2 km]. Unlike many earlier approaches focused on craters ≥0.4 km, our study specifically targets the 0.2–2 km range, demonstrating strong adaptability across diverse lunar terrains, including shadowed polar regions and rugged highlands. Our approach remains computationally efficient and highly scalable for large-scale detection tasks, easily extending to crater sizes outside the 0.2–2 km range. Finally, while La Grassa et al. 2025 relies solely on manual annotations, our dataset construction integrates both manual annotations and advanced augmentation (e.g., Poisson Image Editing), thus enriching the data and reducing annotation workload for a more efficient training pipeline.

4.4.3. Key Advantages of Our Approach

By achieving an F1-score of 89.4%—underpinned by high precision (90.9%) and recall (88.0%)—our method ensures reliable crater detection in even the most complex lunar terrains, such as shadowed polar areas and steep highlands. This robustness stems from our advanced dataset construction, which combines manually annotated samples with augmented samples generated through Poisson Image Editing to enhance texture variation and maintain gradient continuity. Consequently, the model performs consistently well across diverse lunar regions, including rugged highlands and low-reflectivity mare areas, making it ideal for global lunar mapping. In contrast, many previous methods are optimized for more uniform terrains (e.g., those in SLDEM datasets). Moreover, while LU5M812TGT uses an IoU threshold of 0.3—which may inflate recall at the expense of precision—our stricter IoU threshold of 0.5 ensures more reliable and accurate detections.

4.5. Analysis of False Positives, False Negatives, and Future Improvements

In all the testing experiments of this study, we observed recurring patterns in the occurrence of false positives (Type I errors) and false negatives (Type II errors) in the model’s detection results. False positives primarily occurred in three situations: (1) due to the complex topography of the detection area, local regions exhibited crater-like geological features (e.g., depressions or dark patches caused by ridges), leading the model to incorrectly classify these features as craters (see Figures 13(a) and 13(b)); (2) the complex morphology of lunar craters caused discrepancies in defining crater boundaries among different annotators, resulting in inconsistencies between the training samples and the labeled data used for testing. Additionally, when craters exhibited multiple morphological types simultaneously, the model misclassified their boundaries, resulting in an Intersection over Union (IoU) ≤ 0.5, and thereby categorized them as false positives (see Figures 13(c) and 13(d)); (3) some craters were detected by the model but were missed in the manual annotation process (see Figures 13(e) and 13(f)). Although this occurrence was rare, it was still observed due to the reliance on manual labeling for the testing data.

False negatives primarily occurred under three circumstances: (1) low contrast between the crater imagery and the background, where many craters blended with the lunar surface and were difficult to distinguish (see Figure 13(g)); or craters were eroded, covered by radial cracks, or obscured by lava flows, making their boundaries unclear and difficult to detect (see Figure 13(h)). These situations occurred more frequently as the crater size decreased; (2) complex crater morphologies such as deformation, collapse, overlapping, or adhesion with other craters (see Figure 13(i)) made it challenging to discern their shapes (see Figure 13(j)); (3) craters with shapes that were less common in a given region and differed significantly from the majority of craters in that area (see Figure 13(k)), or small craters (especially those on the hectometer scale) with morphological differences from larger craters (see Figure 13(l)). These cases were typically attributed to insufficient or neglected sampling of such crater types during the sample production process. Although data augmentation techniques can assist in recognizing craters with similar morphologies but different sizes, the lack of sufficient samples and information on craters with significant morphological differences also limited the model’s ability to detect them.

Through testing, we found that creating a more diverse and refined training dataset was a more effective and significant approach to improving detection accuracy compared to adjusting algorithm parameters or switching models. The method proposed in this study, which combines sample data creation with deep learning model construction, has shown remarkable effectiveness in improving detection accuracy for different regions and smaller craters. In future work, one approach is to improve the quality of data labeling by standardizing the labeling process, performing data validation, and cleaning (i.e., checking labeled sample data to exclude possible errors and outliers), thereby enhancing the model’s detection accuracy and minimizing false positives. Another approach is to selectively collect and enrich sample data that includes various types of craters and background information from different regions. This aims to optimize regional models, allowing them to learn more comprehensive crater features and thus improve detection capabilities.

Despite the promising results achieved in this study, several limitations remain and provide opportunities for future improvement. First, the model occasionally produces false positives or misses true craters in complex terrains or challenging lighting conditions, where geological features such as crater-like formations or shadows may lead to misclassifications, while erosion or ejecta may obscure crater boundaries (see Figures 13(a)–13(j)). Future work can address these issues by enhancing the model’s ability to distinguish between real craters and ambiguous features, potentially incorporating multi-spectral and topographic data. Second, although manual annotation adhered to strict guidelines, inconsistencies and omissions persist due to the complexity of lunar landscapes (see Figures 13(e)–13(f)), suggesting the potential benefit of automated annotation strategies such as semi-supervised learning or Generative Adversarial Networks (GANs) to reduce human error and expand the dataset more efficiently. Finally, although Poisson Image Editing has significantly improved detection accuracy, its high computational cost limits its scalability for large-scale planetary mapping. Therefore, future efforts should explore hybrid augmentation techniques and model optimization strategies (such as pruning and quantization) to reduce computational overhead.

5. Conclusions

This study proposes an innovative sample creation method and develops a deep learning framework for small target detection, YOLO-SCNet, for detecting small lunar craters in the 0.2-2 km diameter range. By combining a high-quality, diversified sample dataset generated using image enhancement techniques such as Poisson Image Editing with the improved YOLOv11 architecture of YOLO-SCNet, we successfully addressed key challenges in lunar crater detection. YOLO-SCNet demonstrates outstanding detection performance, with a precision of 90.2%, recall of 88.7%, and an F1 score of 89.4%, highlighting its reliability across various lunar terrains. Additionally, YOLO-SCNet excels in handling complex lunar environments, effectively managing extreme lighting, shadow effects, and morphological variations, ensuring its broad applicability. Currently, YOLO-SCNet is being applied to detect small craters across the entire lunar surface, contributing to the creation of a global, high-precision lunar crater catalog. Future research will focus on extending this framework to other planets, such as Mars and Mercury, to support broader planetary exploration efforts.