Submitted:
23 April 2025
Posted:
24 April 2025
You are already at the latest version
Abstract
The universe can be described with both real and so-called imaginary numbers - it’s logical to assume reality is like Quantum Gravity. Either Quantum Mechanics or General Relativity could be the more useful description of the universe in different circumstances, with their union in a theory of Quantum Gravity being more complete and better than both. In the same way, descriptions using Complex numbers would be more complete than either Real or Imaginary ones alone. The Kakeya conjecture has been proven for 1, 2, and 3 dimensions. Maybe that proof can be extended to the 4th and imaginary dimensions by the Mobius strip being a fundamental component of the universe, and the Complex Plane’s Wick rotation being built into the Mobius and acting as a timepiece whose real and imaginary components record the passage of time.
Keywords:
Kakeya conjecture
; deltoid curve
; Perron tree
; Wick rotation
; Riemann hypothesis
; other dimensions
; harmonic analysis
; complex numbers
; imaginary time
; holographic principle
; electric dipole moment
; hidden variables
; binary digits
; topology
; photon
; graviton
; quark
; mobius strip
; figure‐8 Klein bottle
; Higgs boson
Article
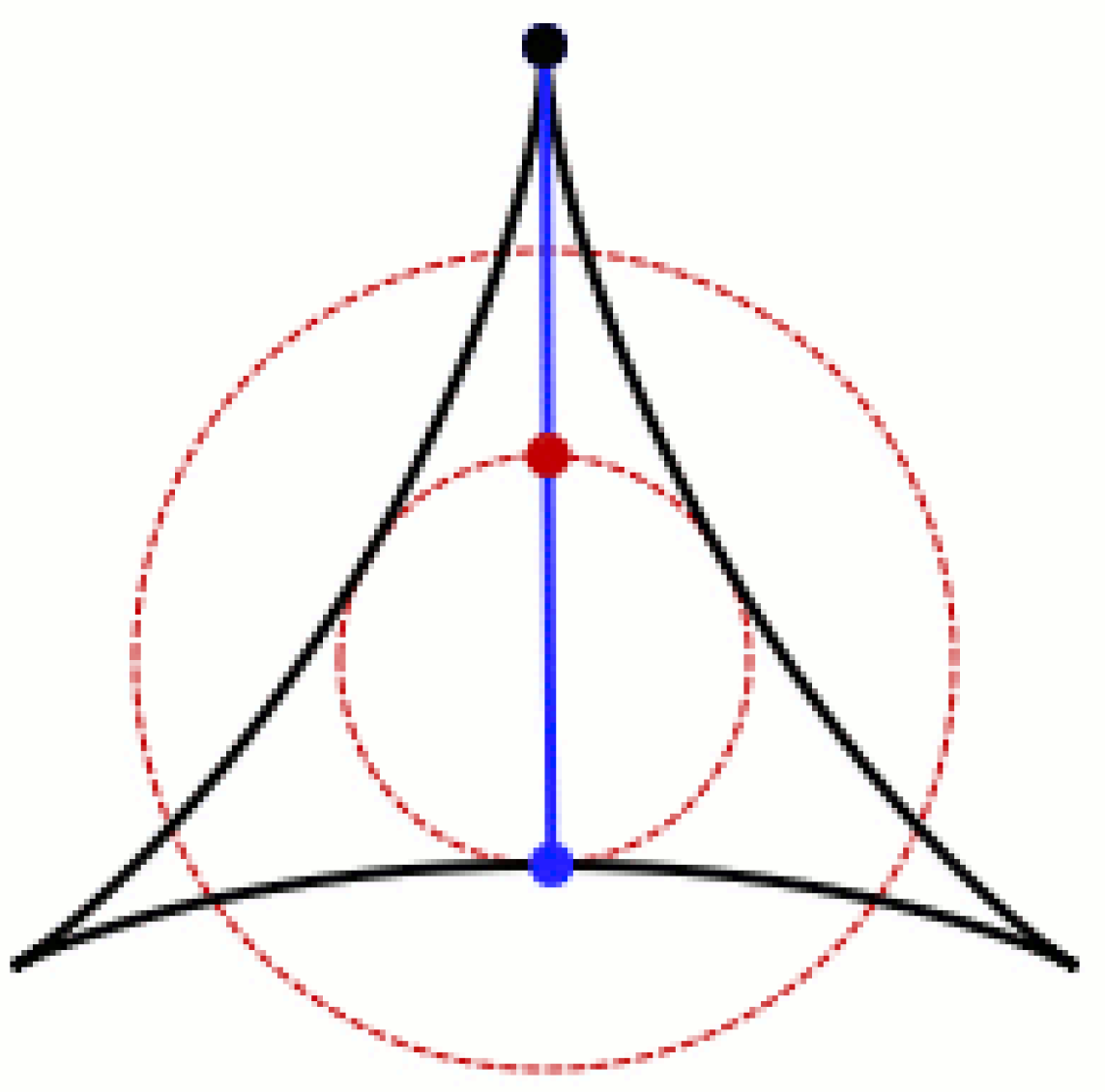
The first thing thought of when reading about the Kakeya conjecture [1] was Georg Riemann. The conjecture has its origin in 1917, when Japanese mathematician Soichi Kakeya asked how small a shape you would need to rotate a needle through 360 degrees, if you’re allowed to move the needle back and forth in any direction. The simplest shape traced out by a spinning needle is a circle. In Figure 1 below, the needle (blue) is shown in the vertical y-axis. When the needle’s centre (red) revolves 90 degrees, the needle would be in the horizontal x-axis. Coupling the circular rotation with these two axes is reminiscent of Wick rotation. In turn, Wick brings to mind the 1859 hypothesis by the German mathematician Georg Friedrich Bernhard Riemann.
Figure 1.
Kakeya needle (blue) rotating inside deltoid (black).
Figure 2.
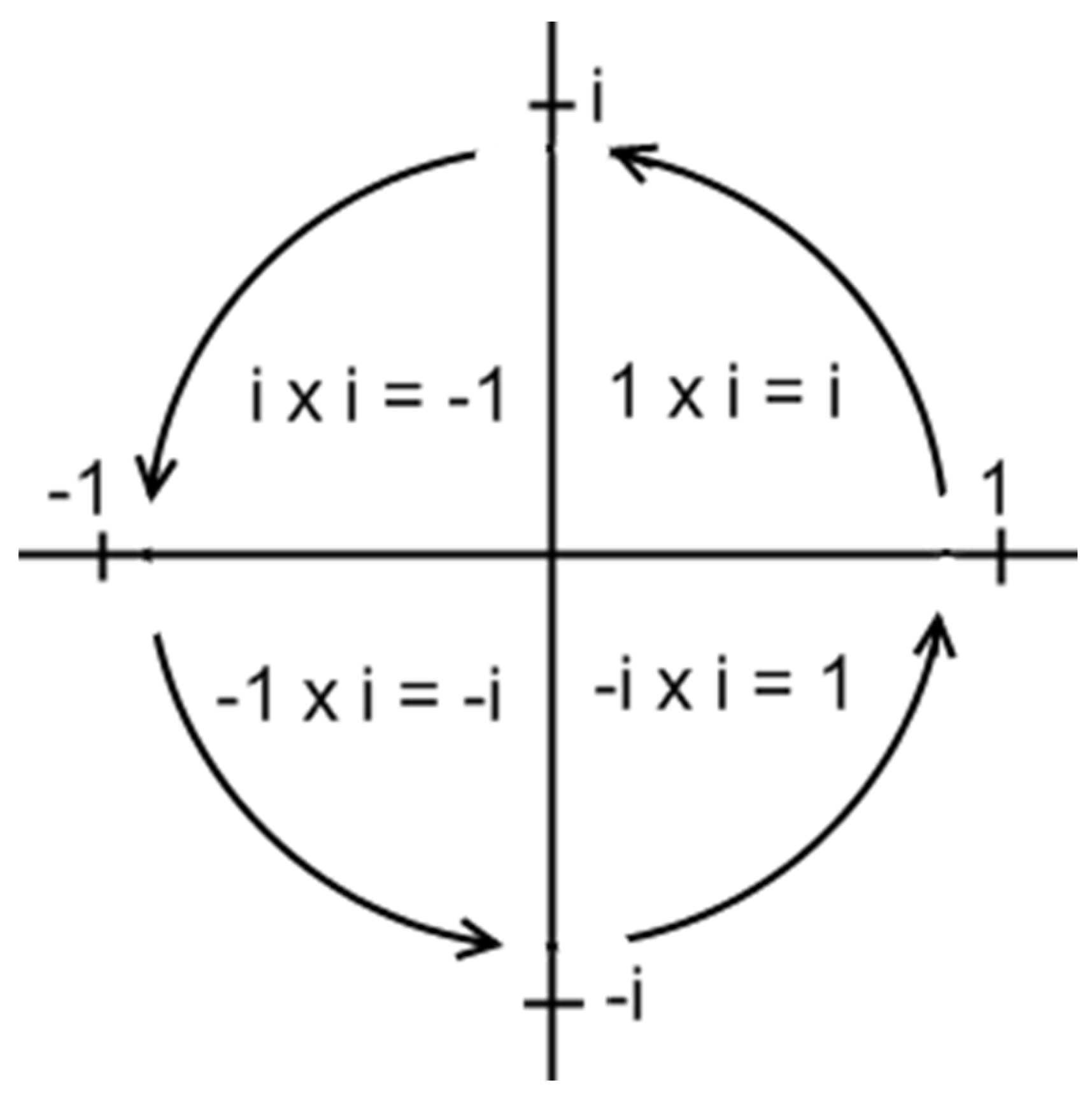
WICK ROTATION: “The complex plane reveals i’s special relationship with cycles via the circle of i, also known as Wick rotation. Whenever a point on the complex plane is multiplied by i, it moves a quarter rotation around the origin or center of the plane.” [2].
Figure 2.
WICK ROTATION: “The complex plane reveals i’s special relationship with cycles via the circle of i, also known as Wick rotation. Whenever a point on the complex plane is multiplied by i, it moves a quarter rotation around the origin or center of the plane.” [2].
The Riemann hypothesis deals with the distribution of prime numbers and is concerned with “nontrivial zeros” on the “critical line”, stating that these zeros lie on the vertical axis of the Complex Plane i.e., on the y-axis in then-undiscovered Wick rotation. The simplest shape traced out by a rotating needle is a circle. Manoevring the needle in complicated ways—similar to what the New Scientist article calls “wiggling a car back and forth to get into a tight parking spot”—in order to produce other, strange, shapes recalls another essential feature of Wick rotation. Its use of real and imaginary numbers to form the Complex Plane is comparable to the back and forth motion in the sense that Wick continually rotates (wiggles) between the real x-axis and the imaginary y-axis. Another possible example of the car wiggling back and forth is the matrix-style transition between 90+90=180 and 90+90=90 described in the next paragraph.
Figure 3.
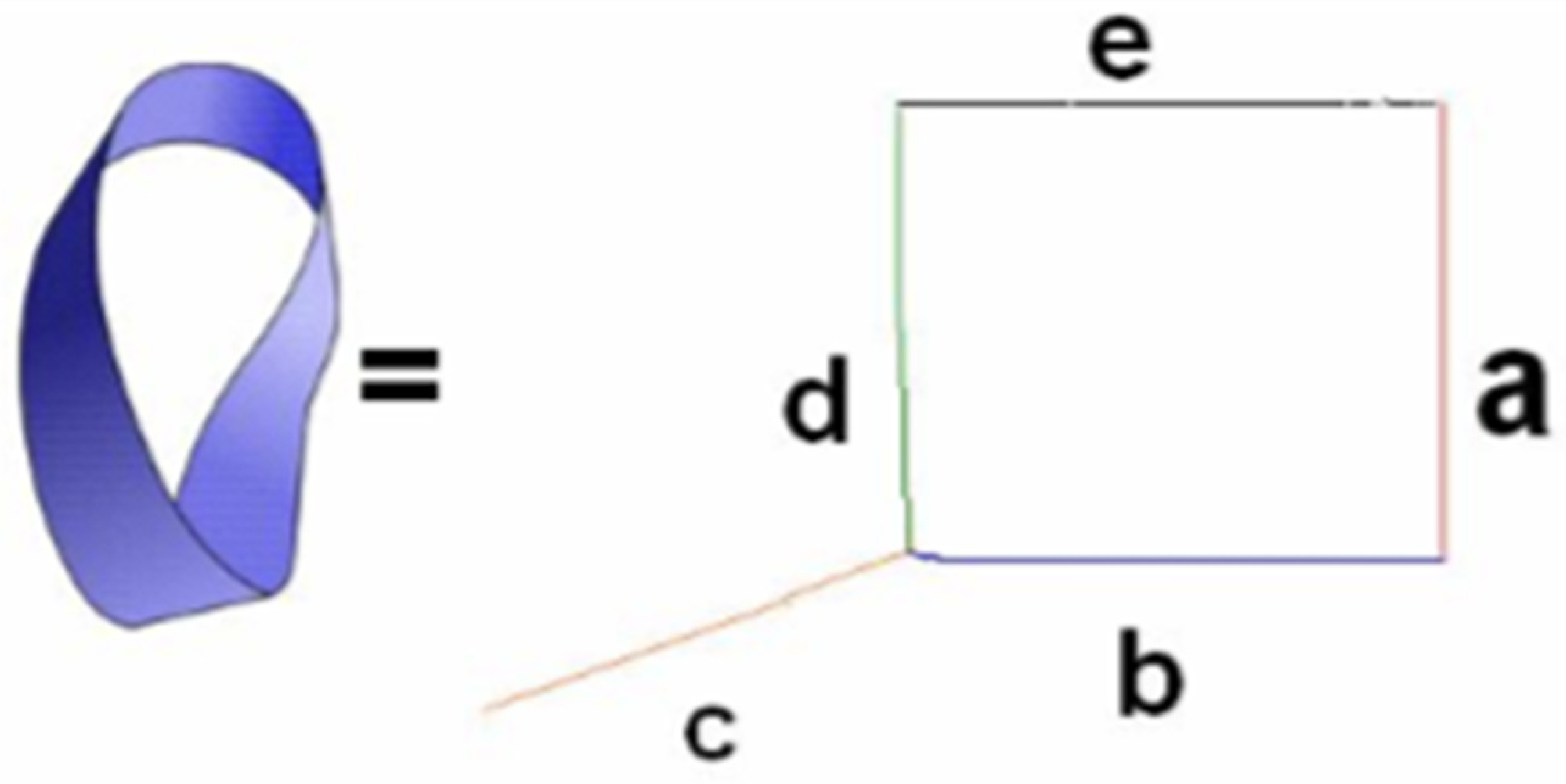
MOBIUS MATRIX (Mobius equals a,b,c,d,e array).
Width a is perpendicular to the length (b or e) which is perpendicular to height c. How can a line be drawn perpendicular to c without retracing b’s path? By positioning it at d, which is then parallel to (or, it could be said, at 180 degrees to) a. d is already at 90 degrees to length b and height c. d has to be at right angles to length, width and height simultaneously if it’s going to include the Complex Plane’s vertical “imaginary” axis in space-time (the “imaginary” realm is at a right angle to the 4 known dimensions of space-time, which all reside on the horizontal real plane). In other words, d has to also be perpendicular to (not parallel to) a. This is accomplished by a twist, like on the right side of the Mobius strip, existing in the particles of matter composing side a. In other words, a fundamental composition of matter is mathematics’ topological Mobius, which can be depicted in space by binary digits creating a computer image. The twist needs to be exaggerated, with the upper right of the Mobius descending parallel to side “a” then turning perpendicular to it at approximately the level of the = sign, then resuming being parallel. Thus, 90+90 (the degrees between b & c added to the degrees between c & d) can equal 180, making a & d parallel. But 90+90 can also equal 90, making a & d perpendicular. (Saying 90+90=90 sounds ridiculous, but it has similarities to the Matrix [of mathematics, not the action-science fiction movie] in which X multiplied by Y does not always equal Y times X. The first 90 plus the second 90 does not always equal the second 90 plus the first 90 because 90+90 can equal either 180 or 90).
Regarding “a fundamental composition of matter (being) mathematics’ topological Mobius”: this makes sense because you have to go around the endless loop of a Mobius strip twice to reach your starting point, and any particle of matter must undergo two complete revolutions (must be turned through 720 degrees) to attain the previous quantum state. Professor Stephen Hawking made statements about imaginary time that are also relevant to time’s partner, topological space -
“In real time, the universe has a beginning and an end at singularities that form a boundary to space-time and at which the laws of science break down. But in imaginary time (time described with imaginary numbers), there are no singularities or boundaries.” “A scientific theory is just a mathematical model we make to describe our observations: it exists only in our minds. So it is meaningless to ask: Which is real, ‘real’ or ‘imaginary’ time? It is simply a matter of which is the more useful description.”[3]
The real and imaginary both exist—so it’s logical to assume reality is like Quantum Gravity. Either Quantum Mechanics or General Relativity could be the more useful description of the universe in different circumstances, with their union in a theory of Quantum Gravity being more complete and better than both. In the same way, descriptions using Complex numbers would be more complete than either Real or Imaginary ones alone. The Kakeya conjecture has been proven for 1, 2, and 3 dimensions. Maybe that proof can be extended to the 4th and imaginary dimensions by the Mobius strip being a fundamental component of the universe, and the Complex Plane’s Wick rotation being built into the Mobius and acting as a timepiece whose real and imaginary components record the passage of time.
When mathematicians explored the Kakeya conjecture, they found the thickness of a real needle would become important. Because of this, they considered an infinitely thin needle, and found that the smallest shape Soichi Kakeya sought was zero despite the needle having a defined length. The critical line in the Riemann hypothesis pertains to zeros—so the distances in space-time (including the needle’s defined length) might equal zero, shocking everybody by making time travel to both the past and future possible as well as making instant intergalactic travel feasible. This seems to be related to the Holographic Principle stating that the 3rd dimension may be a projection of information from the 2nd dimension. Distance in the 3rd dimension can be circumvented by reprogramming the ones and zeros in the precise, merely superficially probabilistic Quantum Mechanics proposed here. Exact calculations can be attained by considering the BITS or binary digits of 1 and 0 as resulting from every fermion and boson possessing Electric Dipole Moment (both positive and negative charges, which can totally or partially cancel). The digits would obey Chaos theory’s principle of concealed order existing in apparent disorder and would function as Hidden Variables not confined to one locality but compatible with quantum entanglement.
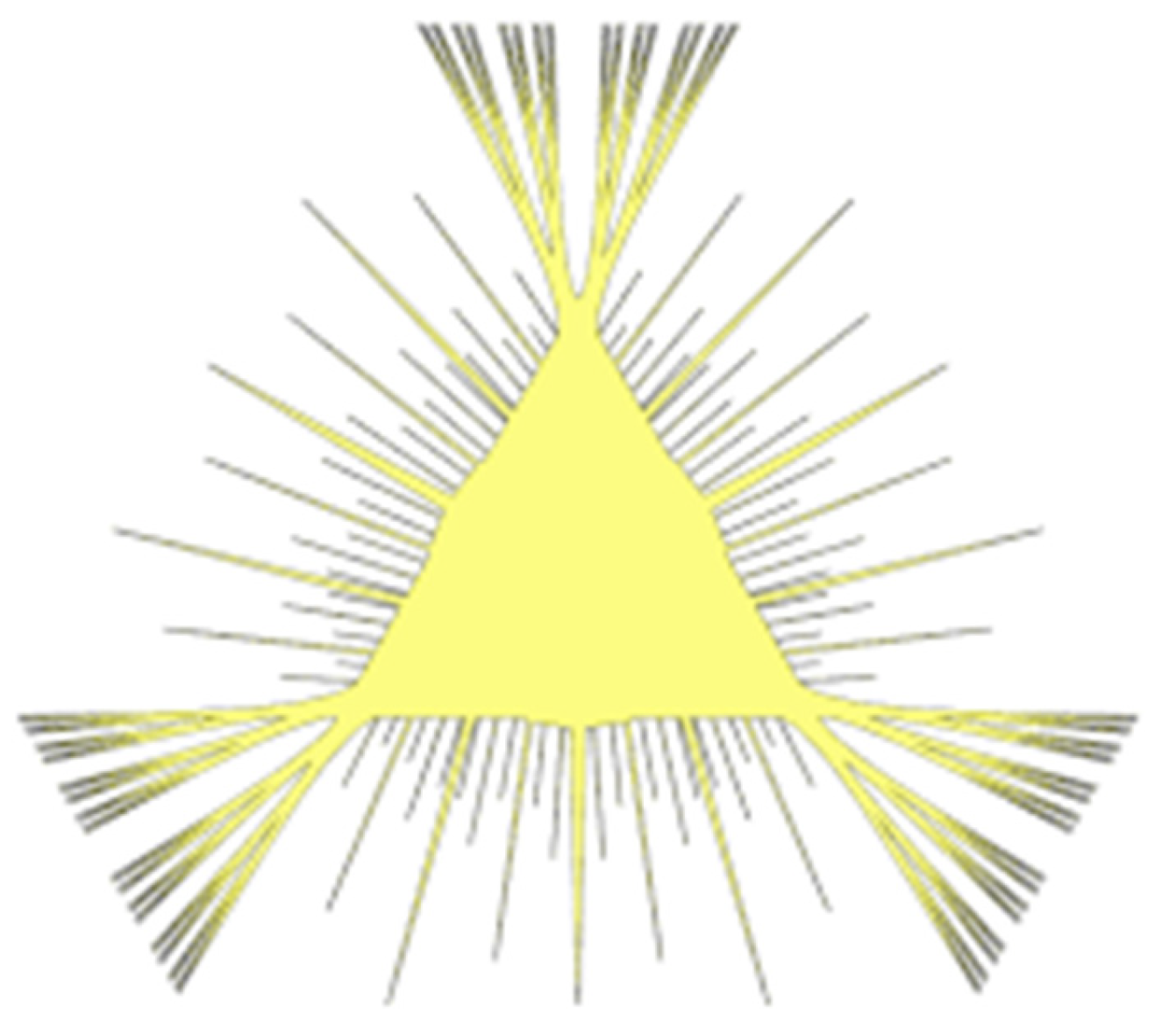
Relating the Perron tree and deltoid through harmonic analysis (the mathematical study of how waves behave)—a Perron tree is formed by repeatedly dividing an equilateral triangle into halves then sliding adjacent triangles so they overlap slightly. Complicated periodic waves formed by some regular repeating motion can be expressed as sine waves using Fourier analysis. Suppose the lines sprouting from the central triangle in Figure 4 are periodic waves subject to Fourier analysis. The triangular appearance of the lines might then correspond to the 3-pointed curved black lines of Figure 1’s deltoid. The Perron tree’s triangle, and the deltoid’s small inner circle, could be thought of as a particle while the sprouts of Figure 4 and black curved lines of Figure 1 could be considered as representing periodic electromagnetic / gravitational waves. Because the waves are united with particles, they travel as gravitons and photons possessing curved trajectories. There are many sprouts (waves) associated with each particle, meaning a boson or fermion can appear in many positions (sproutings) at once. The Perron and deltoid would be diagrams of wave-particle duality and would support Albert Einstein’s paper “Do gravitational fields play an essential role in the structure of elementary particles? [4] Specifically, Einstein was suggesting interactions of gravitons and photons produce electrons, muons, neutrinos, the bosons of the strong and weak nuclear forces, the Higgs boson, and quarks.
The quark model was independently proposed by Murray Gell-Mann and George Zweig in 1964. Owing to a phenomenon called Colour Confinement, quarks can never exist in isolation—they’re found combined within protons, neutrons, and mesons. Stephen Hawking and Leonard Mlodinow state,
“The question of whether it makes sense to say quarks really exist if you can never isolate one was a controversial issue in the years after the quark model was first proposed.” “It is certainly possible that some alien beings would make the same experimental observations that we do, but describe them without quarks.”[5]
If those extraterrestrial beings adopted the ideas proposed in this Article, they might describe their experimental observations with binary digits, topology, the Complex Plane’s combination of real and imaginary numbers, and photon-graviton interaction. The graviton and photon are also classified as elementary particles by today’s science. Like the quark, they are also subject to purely mathematical description and might be composed of binary digits, topology, and Wick rotation.
This connection of the photon and graviton is consistent with the following proposal concerning the fundamental composition of what is called spacetime—the Mathematical Universe Hypothesis (MUH) is a speculation put forward by physicist and cosmologist Max Tegmark. [6,7] It speaks of “altogether different equations and mathematical structures”. This Article could use such structures in the following way—one dimensional (1D) electrical pulses could form binary digits that could encode 2D Mobius strips which would be the next level up in particles’ structure. The 3rd dimension we normally perceive could be thought of as composed of figure-8 Klein bottles ie it could be thought of as the union of pairs of Mobius strips [8] or as projection of the information inherent in particles’ constituent strips. A deltoid curve is formed by a circle of radius 1 rolling inside a larger circle of radius 3. [9] This produces the red doughnut shape in Figure 1—and that shape resembles the outlne of a figure-8 Klein bottle. Since so-called “imaginary” numbers are essential in quantum mechanics, the 4th dimension of time might be described by the Complex Plane’s Wick Rotation which is often regarded as nothing more than mathematical convenience. Adapting a paper by Albert Einstein—if electromagnetism’s photon and gravitation’s graviton are respectively composed of trillions of Mobius strips and trillions of pairs of Mobius strips, electromagnetic and gravitational interactions could produce the mass and quantum spin of every other particle, including the bosons of an atom’s strong nuclear force, weak nuclear force, and even the Higgs boson (the possibility of excitation of the Higgs field resulting from photon-graviton interaction would mean the field is a union of electromagnetic and gravitational fields).
Figure 5.
Mobius Band (left) and figure-8 Klein Bottle (right). The bottle may be called a Mobius Doublet since it’s formed from the union of two bands.
Figure 5.
Mobius Band (left) and figure-8 Klein Bottle (right). The bottle may be called a Mobius Doublet since it’s formed from the union of two bands.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Alex Wilkins. Whole new world of maths unlocked. New Scientist. March 15, 2025. pp. 8-9. https://www.newscientist.com/article/2471211-amazing-spinning-needle-proof-unlocks-a-whole-new-world-of-maths/.
- Kerri Welch.The Meaning of Imaginary Time: Creativity’s Dialog with Timelessness.
- https://textureoftime.wordpress.com/2015/07/15/the-meaning-of-imaginary-time/.
- Stephen Hawking. 1988. “A Brief History of Time”. pp. 139, 143. Bantam Press.
- Einstein, Albert (1919). “Spielen Gravitationfelder im Aufbau der Elementarteilchen eine Wesentliche Rolle?” [Do gravitational fields play an essential role in the structure of elementary particles?]. Sitzungsberichte der Preussischen Akademie der Wissenschaften, [Math. Phys.], 349-356, Berlin.
- Hawking, S., Mlodinow, L. The Grand Design. Bantam Press. p.49 (2010).
- Tegmark, Max (November 1998). “Is ‘the Theory of Everything’ Merely the Ultimate Ensemble Theory?”. Annals of Physics. 270 (1): 1–51.
- arXiv:gr-qc/9704009. [CrossRef]
- Tegmark, M. Our Mathematical Universe. Random House/Knopf, January 2014.
- Polthier, Konrad. “Imaging maths—Inside the Klein bottle”.
- http://plus.maths.org/content/os/issue26/features/mathart/index.
- Virtual Math Museum. Deltoid. https://virtualmathmuseum.org/docs/Deltoid.pdf.
Figure 4.
Kakeya needle set constructed from Perron tree.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
