Submitted:
18 April 2025
Posted:
21 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Preliminaries
2.1. Related Work
2.2. Primary Parameters
3. Methodologies
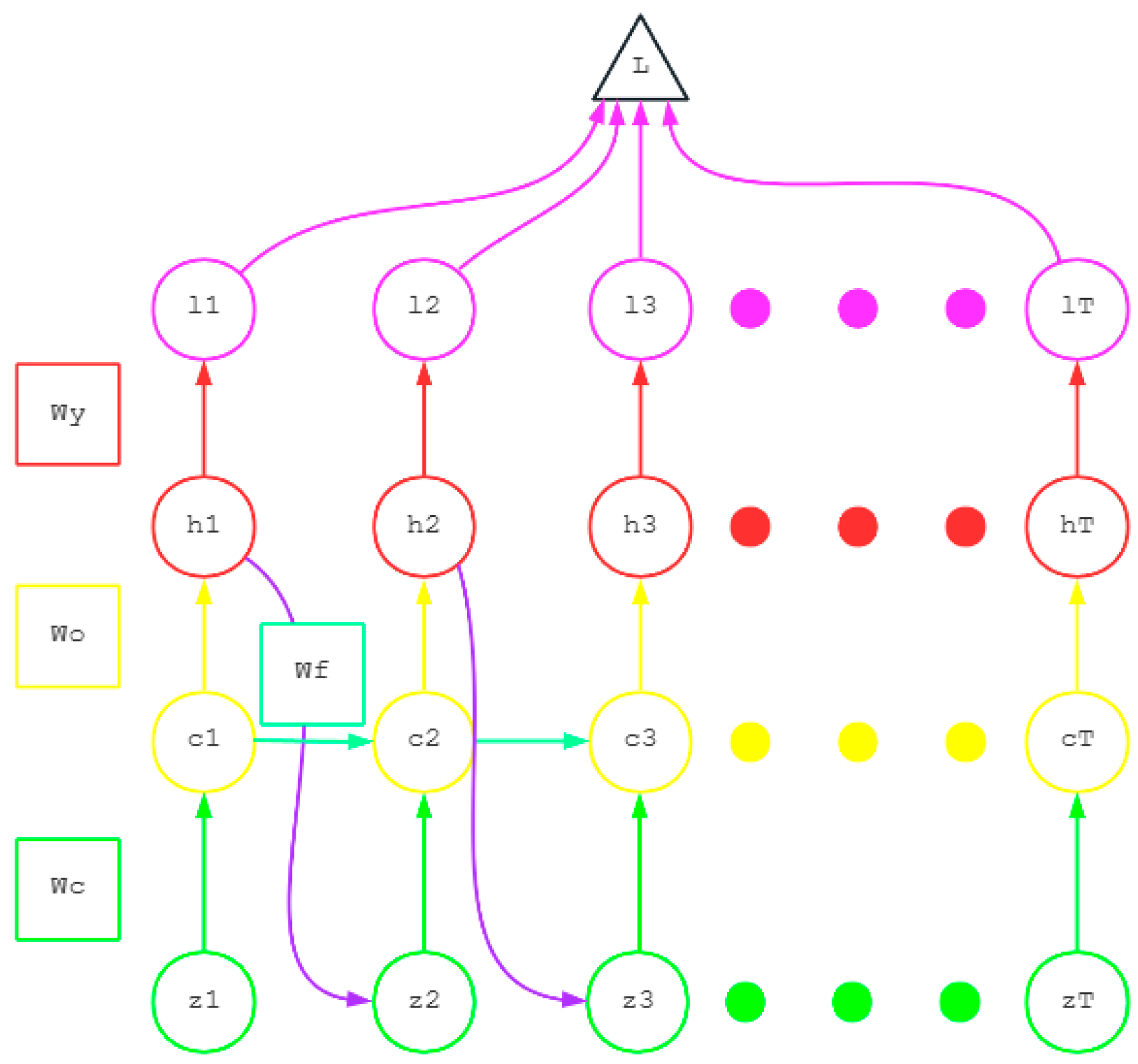
3.1. iLSTM Architecture
3.2. Multi-Objective Optimization Mechanism
3.3. Real-Time Policy Adjustments
4. Experiments
4.1. Experimental Setup
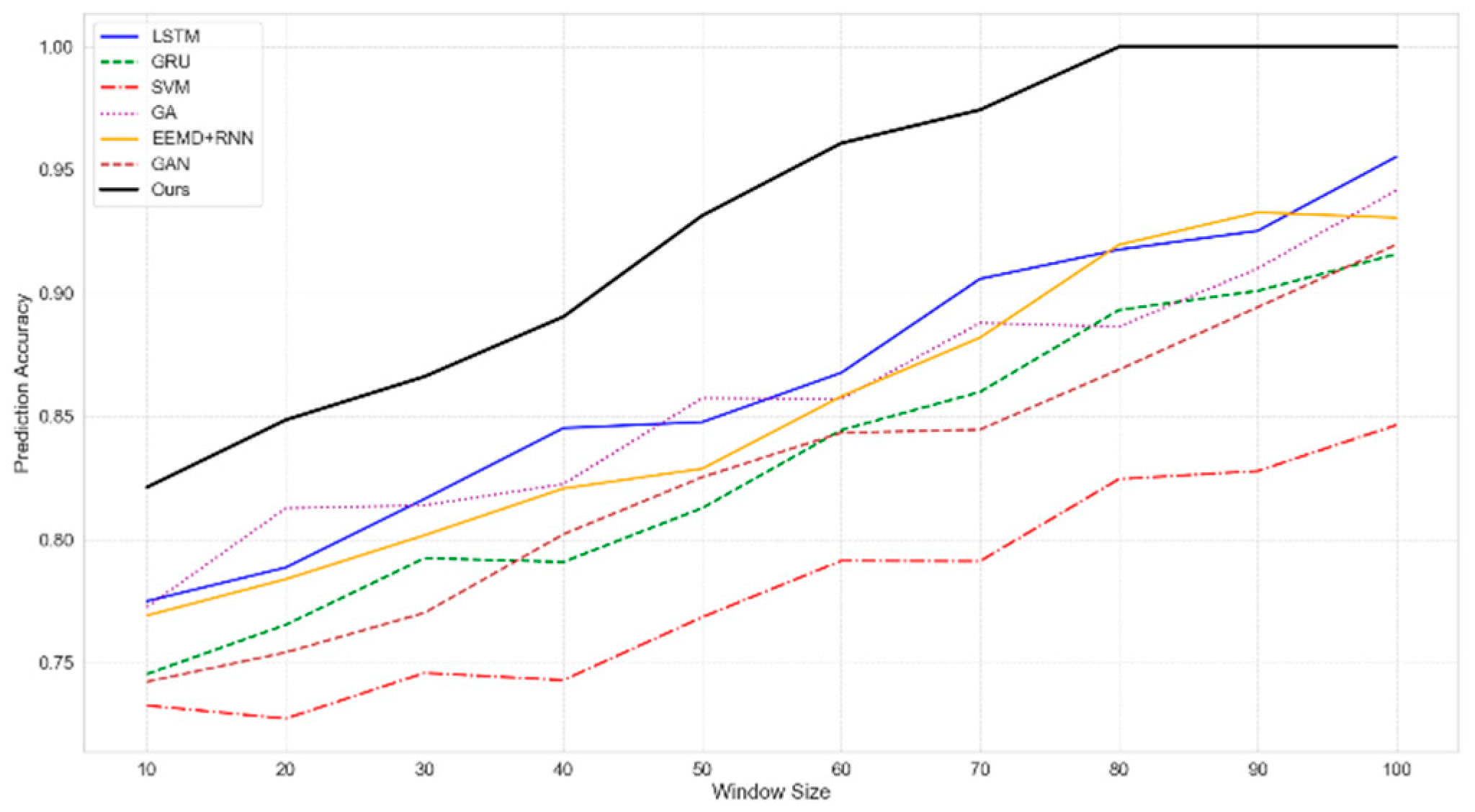
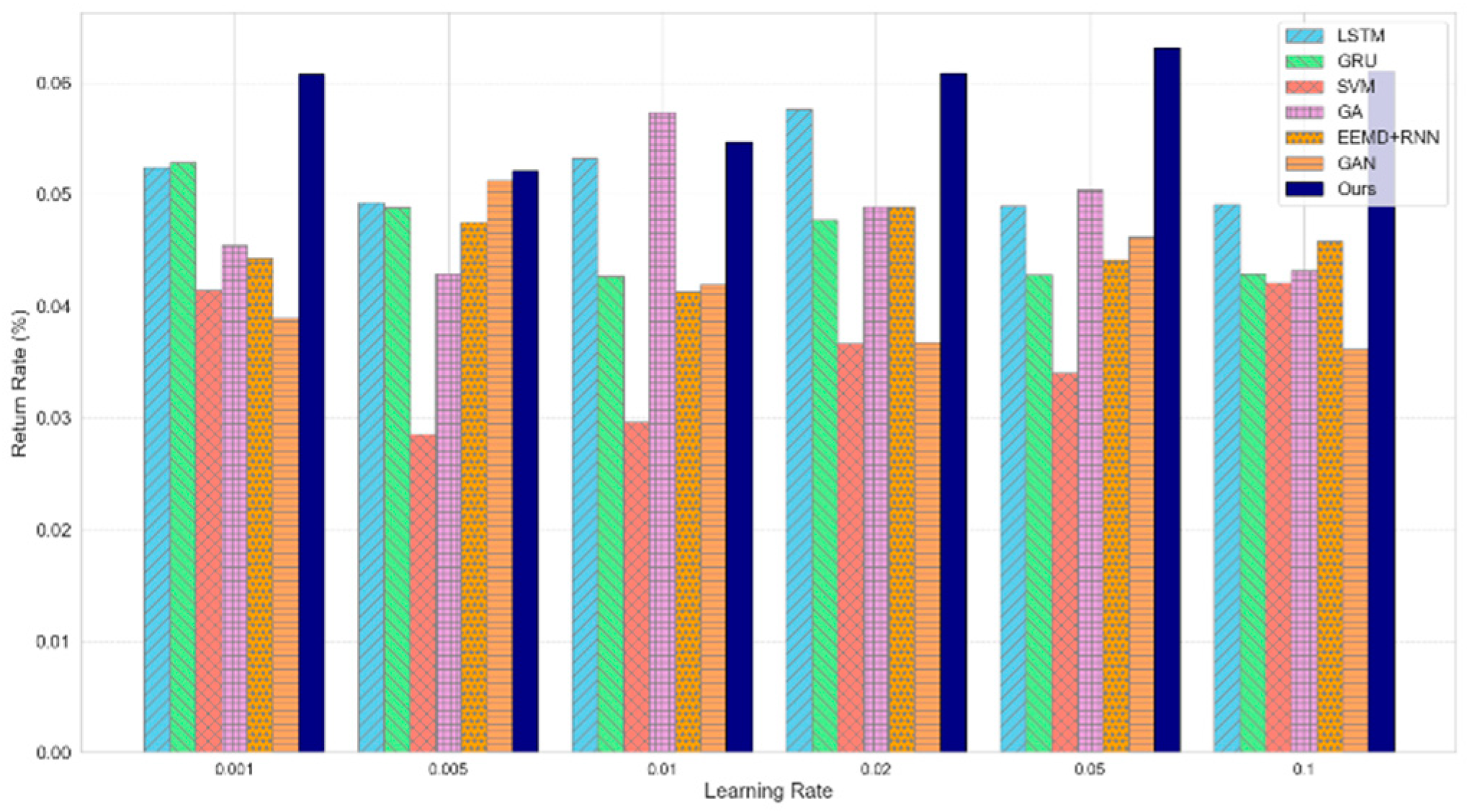
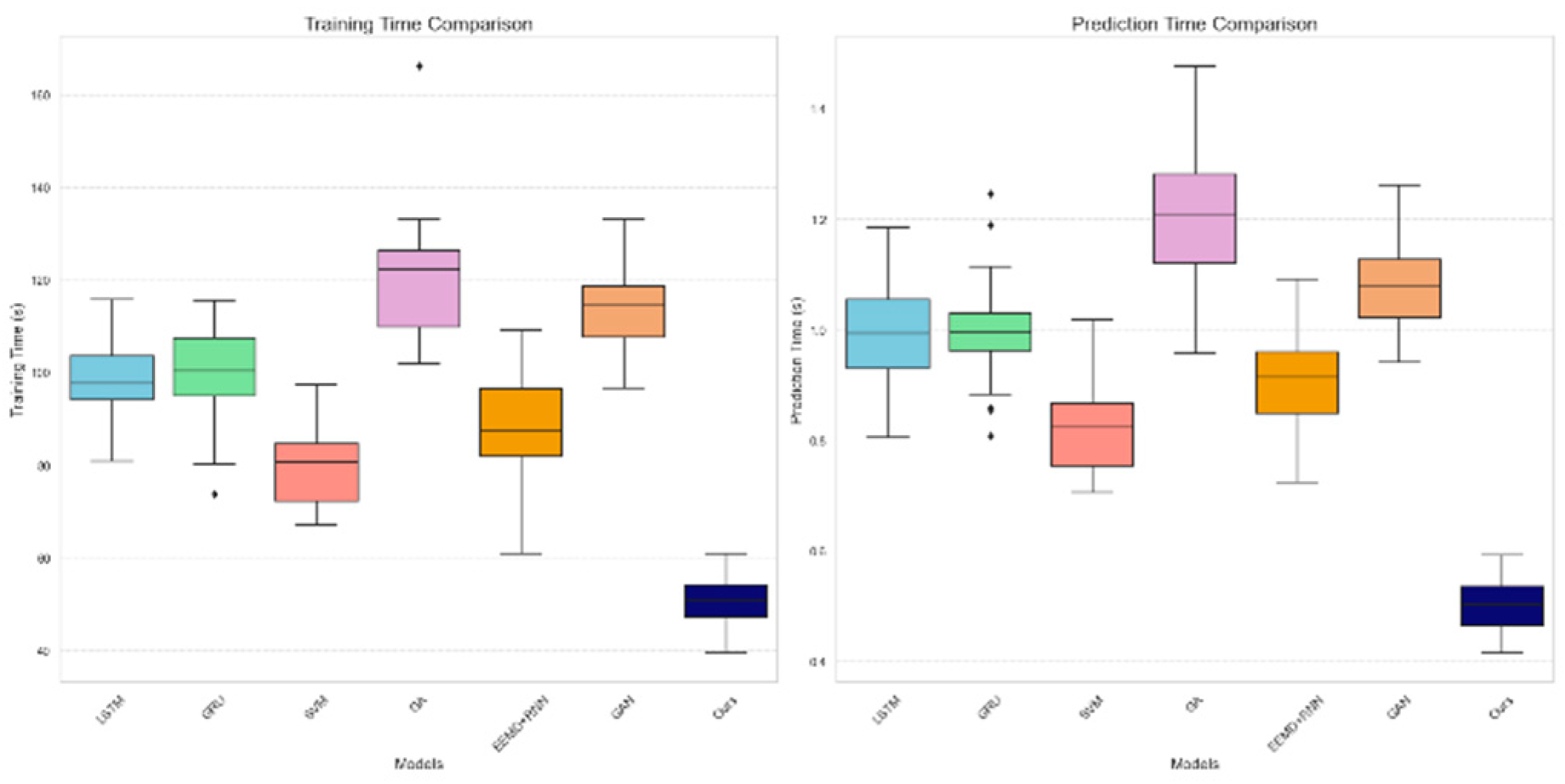
4.2. Experimental Analysis
5. Conclusions
References
- Qian, Hao, et al. "MDGNN: Multi-Relational Dynamic Graph Neural Network for Comprehensive and Dynamic Stock Investment Prediction." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 38. No. 13. 2024. [CrossRef]
- Lee, Woon Ming. Stock market equity advisory tool using analytic hierarchy process and single-layer perceptron neural network. Diss. UTAR, 2023.
- Nguyen, Minh. "AI-Powered Financial Advisory Services." Journal of AI-Assisted Scientific Discovery 4.2 (2024): 115-125.
- Asemi, Asefeh. A Novel Combined Investment Recommender System Using Adaptive Neuro-Fuzzy Inference System. Diss. Budapesti Corvinus Egyetem, 2023.
- Trivedi, Jeegar A., and Priti Srinivas Sajja. "Online Guidance for Effective Investment Using Type 2 Fuzzy-Neuro Advisory System." International Journal of Computer Science and Information Technologies (IJCSIT) 2.2 (2011): 799-803.
- Talwar, Shalini, et al. "Why retail investors traded equity during the pandemic? An application of artificial neural networks to examine behavioral biases." Psychology & Marketing 38.11 (2021): 2142-2163. [CrossRef]
- Shao, Qixiang, et al. "Toward intelligent financial advisors for identifying potential clients: a multitask perspective." Big Data Mining and Analytics 5.1 (2021): 64-78. [CrossRef]
- Needhi, Jeyadev, and S. Manokar. "Enhancing Financial Intelligence: AI Robo-Advisors for Strategic Investment Decisions." (2024).
- Day, Min-Yuh, Jian-Ting Lin, and Yuan-Chih Chen. "Artificial intelligence for conversational robo-advisor." 2018 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM). IEEE, 2018.
- Ng, Shun Yi. Stock market equity advisory tool by using of neural network method. Diss. UTAR, 2024.
- Shahani, M. N. A., et al. "INVESTOPAL-Smart Financial Investment Advisory System." 2023 7th International Conference On Computing, Communication, Control And Automation (ICCUBEA). IEEE, 2023.
- Wang, Pei-Ying, et al. "A robo-advisor design using multiobjective RankNets with gated neural network structure." 2019 IEEE international conference on agents (ICA). IEEE, 2019.
- Roy, Sunil K., et al. "Empowering Robo-Advisors: Data-Driven Mutual Fund and Stock Market Price Prediction with Deep Learning Techniques." 2024 Third International Conference on Electrical, Electronics, Information and Communication Technologies (ICEEICT). IEEE, 2024.
- Day, Min-Yuh, Tun-Kung Cheng, and Jheng-Gang Li. "AI robo-advisor with big data analytics for financial services." 2018 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM). IEEE, 2018.
- Méndez-Suárez, Mariano, Francisco García-Fernández, and Fernando Gallardo. "Artificial intelligence modelling framework for financial automated advising in the copper market." Journal of Open Innovation: Technology, Market, and Complexity 5.4 (2019): 81. [CrossRef]
- Lynch, Dustin Shane. Asset Allocation Technique for a Diversified Investment Portfolio Using Artificial Neural Networks. MS thesis. Ohio University, 2015.

| Notion symbols | Utilization |
|---|---|
| Sigmoid activation function | |
| Weight matrix of the forgetting gate | |
| Regularization parameters | |
| The fully invested Lagrange multiplier | |
| Weight coefficients | |
| Upper limit of the value | |
| Upper bound of the two norms of the weight vector | |
| The total number of training samples | |
| Small constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





