Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Graph-Based Representation Learning for Identifying Fraud in Transaction Networks

Submitted:

29 April 2025

Posted:

30 April 2025

You are already at the latest version

Abstract
This study proposes a graph neural network (GNN)- based method for fraud detection in financial transaction networks. By deeply modeling the transaction graph structure and the relationships between nodes, the method enhances the ability to identify complex fraudulent behaviors. First, financial transaction data is transformed into a graph structure, where transaction accounts are represented as nodes and the flow of funds as edges. Node features such as transaction amount and timestamp are used for node representation learning. Next, graph neural network architectures, such as Graph Convolutional Networks (GCN) and Graph Attention Networks (GAT), are employed to uncover the latent associations and interactions between nodes. This helps identify anomalous fraudulent transactions. To improve the model's generalization and robustness, the study also introduces contrastive learning strategies and imbalance handling techniques. A weighted loss function is used to optimize the model's performance on minority fraud samples. Experimental results show that the proposed method outperforms traditional machine learning models and other deep learning approaches across various evaluation metrics on publicly available datasets. Notably, it achieves a better balance between precision and recall. This method effectively combines graph structural information with deep learning techniques, providing a novel solution for intelligent financial risk control.
Keywords: 
Graph neural networks
;  
fraud detection
;  
transaction networks
;  
deep learning
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

I. Introduction

With the continuous development of financial technologies and the rapid expansion of online transaction scenarios, financial systems have become increasingly complex. Transaction data now exhibit characteristics such as high frequency, multi-source origins, and dense correlations. Against this backdrop, financial fraud has evolved into a more covert, diverse, and organized [1]. Fraudsters often evade traditional risk control methods by creating fake accounts, forging transaction paths, or forming transaction loops. These behaviors are no longer limited to single accounts or isolated events but often involve coordinated actions within complex networks, role switching, and path manipulation, greatly increasing the difficulty of detection. Traditional rule-based or statistical models struggle to deal with such patterns, as they lack the ability to model global structures and inter-node relationships. Therefore, building intelligent models capable of understanding transaction network structures and capturing hidden relationships has become a key direction in fraud detection research.
A transaction network is a graph structure where accounts are represented as nodes and transactions as edges. It effectively reveals behavioral links between accounts and tracks the flow of funds [2]. Compared to traditional representations such as time series or feature vectors [3], graph structures are better suited to model the organized and propagative nature of fraud [4]. In real financial environments, fraud groups often design chain transfers, circular fund flows, and disguised cross-transactions to conceal their traces [5]. These actions tend to form specific structural patterns in graphs, such as high-clustering subgraphs, abnormal edge weight densities, or irregular centrality scores. Modeling transactions as graphs and detecting anomalies through graph structures allows for the analysis of suspicious behavior at both the behavioral and relational levels, significantly improving the accuracy and coverage of fraud detection.
Graph Neural Networks (GNNs), as a cutting-edge technique for modeling graph-structured data [6], offer unique advantages in capturing complex dependencies and non-Euclidean structures [7]. Through neighborhood aggregation, GNNs can learn local structural features and gradually integrate global semantic information across multiple propagation layers [8]. This enables effective representation of each node's role and position within the graph. For transaction networks characterized by strong behavioral dependencies and high structural diversity, GNNs provide a solid foundation for building efficient fraud detection models. In recent years, several studies have applied GNNs to financial fraud detection, showing their effectiveness in identifying complex fraud patterns and uncovering potential collusive behaviors. However, current methods still face challenges in capturing dynamic transaction changes, modeling node-level semantic heterogeneity, and ensuring interpretability, which require further advancement [9].
In this context, research on GNN-based fraud detection for transaction networks is both timely and meaningful from theoretical and practical perspectives. On one hand, it promotes the application of graph learning in financial domains and expands the modeling capabilities of graph-based methods in high-risk, heterogeneous data analysis. On the other hand, building a graph-based fraud detection framework helps improve the intelligence level of financial risk control systems and enables a shift from static rule-based approaches to dynamic behavioral understanding. Furthermore, the structural insight offered by GNNs supports risk visualization, fraud traceability, and coordinated defense strategies, enhancing both detection accuracy and system interpretability for regulatory needs.
In summary, with financial fraud becoming increasingly complex and organized, traditional detection methods face clear limitations in identifying structural and relational anomalies. Graph-based modeling, especially with GNNs, offers a promising alternative to address these challenges. By structurally modeling transaction networks and leveraging GNNs' strong relational learning abilities, more precise and deeper fraud detection can be achieved. This study aims to systematically explore modeling strategies, feature representations, and anomaly discrimination mechanisms of GNNs in financial transaction networks. It proposes a fraud detection method adapted to complex network structures, providing both theoretical foundations and technical solutions for building safer and more intelligent financial risk control systems.

II. Method

Drawing inspiration from the integrated deep learning framework proposed by Cheng et al. [10] for systemic risk prediction, the dynamic and context-aware modeling approach introduced by Liu et al. [11], and the graph neural network-based anomaly detection method developed by Zhang [12], this study constructs financial transaction data into a heterogeneous graph structure tailored for fraud detection. In this structure, transaction accounts are represented as nodes, while transactional interactions serve as edges linking the nodes. To embed richer information within the graph, multiple edge attributes—such as transaction amount, timestamp, transaction type, and additional contextual indicators—are included. These attributes not only capture the direct transactional relationships but also encode temporal dynamics and behavioral characteristics critical for distinguishing fraudulent activities from normal transactions. Building upon the methodologies of these earlier works, the proposed graph structure emphasizes both the structural dependencies and contextual variations inherent in financial transaction networks. This comprehensive representation enhances the model’s ability to learn complex, non-linear patterns associated with fraudulent behavior. 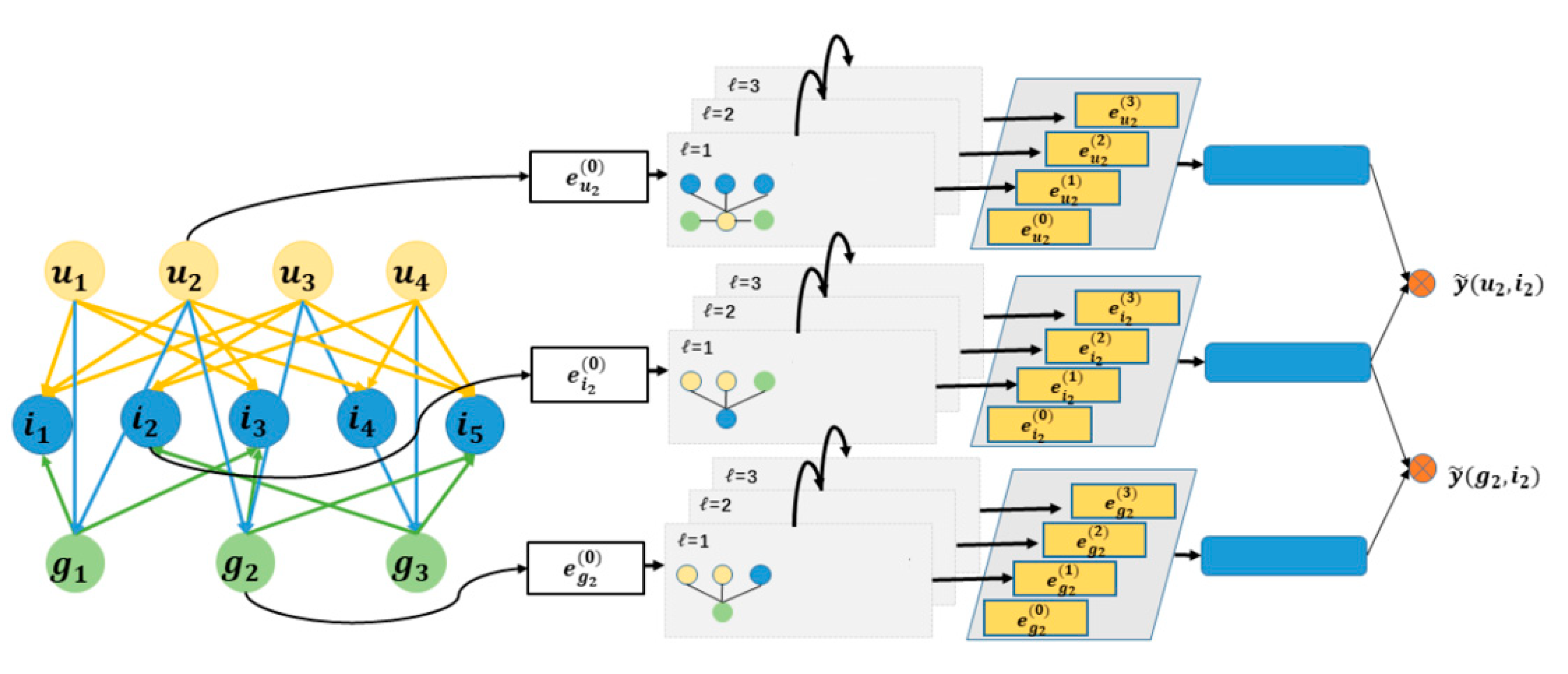The detailed architecture of the proposed model is depicted in Figure 1, and the process of formal graph construction is presented as follows:
Figure 1 shows a transaction graph consisting of multiple types of nodes, where edges represent transaction behaviors. Each edge is input into a multi-layer graph neural network module to extract structural and temporal information features layer by layer.
Suppose the transaction graph is G = ( V , E , X ) , where V represents the node set, E represents the edge set, and X ∈ R | V | × d represents the initial feature matrix of the node. In order to improve the model's perception of the local structure of the transaction network, a graph convolutional neural network (GCN)[13] is used to aggregate and update the nodes. The node representation update method of each layer is:
H ( l + 1 ) = σ ( D ' − 1 / 2 A ' D ' − 1 / 2 H ( l ) W ( l ) )
where A ' = A + I is the adjacency matrix with self-connection added, D ' is the corresponding degree matrix, W ( l ) is the trainable weight of the lth layer, l represents the activation function, and σ ( ⋅ ) . This mechanism enables nodes to aggregate the representations of their neighbors and thus learn potential fraudulent relationships in the local structure.
Building upon the synergistic convolutional-transformer framework proposed by Wang et al. [14], which demonstrated the benefits of combining local feature extraction and global attention for risk-based predictive modeling, the improved temporal dependency capturing techniques introduced by Yao [15] for sequential financial data, and the multimodal data integration strategies developed by Liu [16] for enhancing stock market forecasting, this study enhances the transaction graph representation by introducing edge features and attention mechanisms. A Graph Attention Network (GAT) is utilized to aggregate information from neighboring nodes with dynamically assigned weights, allowing the model to focus more on important transactional relationships. The inclusion of edge features such as transaction amount, type, and timestamp provide crucial context that strengthens the model’s ability to learn discriminative patterns. By integrating these techniques, the model becomes more adept at capturing the heterogeneous and evolving nature of financial transaction networks, thereby improving fraud detection performance. Assume that the initial representation of node i and neighbor node j is h i , h j , and the attention weight is calculated as follows:
α i j = exp ( LeakyReLU ( a T [ W h i | | W h j ] ) ) ∑ k ∈ N ( i ) exp ( LeakyReLU ( a T [ W h i | | W h k ] ) )
where W is the linear transformation matrix, a is the attention vector, | | represents vector concatenation, and N ( i ) is the neighbor set of node i. This mechanism allows the model to automatically learn the importance of transaction relationships and focus on transaction paths related to fraud in multi-hop propagation.
In order to achieve fraud discrimination of nodes (accounts), this paper inputs the final graph encoding representation z i into a discriminator f ( ⋅ ) , and outputs the probability prediction value of it being a fraud account. The Sigmoid function is used as the output activation function, which is defined as follows:
y ' i = σ ( f ( z i ) ) = 1 1 + exp ( − w T z i − b )
where W and b are the discriminator parameters, and the output represents the probability that node i is judged as fraudulent. To train the discriminator, a weighted binary cross-entropy loss function is used to optimize the unbalanced data. This design draws upon several recent advancements. The importance of leveraging hybrid BiLSTM-Transformer models to better capture long-range temporal dependencies and contextual information in financial fraud detection has been emphasized [17], addressing challenges in modeling sequential transaction behaviors. Techniques for transforming multidimensional time series into interpretable event sequences have been proposed [18], providing new methods to extract meaningful and explainable patterns from complex financial data, which is critical for enhancing model interpretability in fraud analysis. Additionally, a data balancing and ensemble learning approach has been introduced [19] to directly tackle class imbalance in credit card fraud detection, demonstrating that proper handling of minority classes can substantially boost predictive performance. By incorporating these insights, the proposed method achieves improved robustness, better interpretability, and heightened sensitivity to fraudulent activities in highly imbalanced financial transaction datasets, and the final loss function is formulated as:
L = − 1 N ∑ i = 1 N [ λ y i log y ' i + ( 1 − y i ) log ( 1 − y ' i ) ]
λ is the weight coefficient of the fraudulent sample, which is used to alleviate the problem of class imbalance, y i is the true label, and y ' i is the predicted probability. This loss function encourages the model to pay more attention to the discrimination of minority classes during training, thereby improving the overall recognition performance.

III. Experiment

A. Datasets

The experimental dataset used in this study is the Elliptic Dataset provided by University College London (UCL). This dataset consists of a Bitcoin transaction graph and is one of the standard benchmarks widely used for transaction network fraud detection tasks. It contains 203,769 nodes and 234,355 edges across 49-time steps. Nodes represent Bitcoin transactions, while edges represent the flow of funds between transactions. The data is organized in graph structure format, making it suitable for training and evaluating graph neural networks.
Each transaction node is associated with a 93-dimensional feature vector, including information such as transaction amount, timestamp, and aggregated statistics. Some of the nodes are labeled as “licit”, “illicit”, or “unknown”. Illicit transactions account for about 2% of the total nodes, showing a typical class imbalance problem. This labeling provides clear supervision signals for fraud detection and closely reflects real-world needs for identifying account risks in financial risk control scenarios.
The structural complexity and temporal continuity of the Elliptic dataset make it particularly suitable for studying the performance of graph neural networks in dynamic financial transaction networks. By modeling the relationships between nodes and the temporal evolution of transactions, this dataset enables a comprehensive evaluation of a model's ability to handle complex transaction paths and detect potential fraud rings. It offers strong research representativeness and experimental reproducibility.

B. Experimental Results

This paper first conducted a comparative experiment on different graph neural network structures (GCN [20] vs. GAT [21] vs. GIN), and the experimental results are shown in Table 1.
As shown in the experimental results in Table 1, different graph neural network architectures exhibit significant differences in performance on the transaction network fraud detection task. GCN, as the most basic graph neural network model, shows stable results in terms of accuracy, precision, and recall. However, its overall detection capability is relatively limited, with an F1-score of 0.734. This indicates that GCN still struggles to capture complex relationships and feature interactions among fraud-related nodes.
The GAT model, which introduces an attention mechanism, achieves better performance than GCN across all metrics. Its F1-score improves to 0.759. This shows that GAT applies more targeted weighting to important neighbors during aggregation, which helps uncover hidden connections among key nodes in the transaction network. As a result, it enhances the model's sensitivity to fraudulent behaviors. In particular, GAT achieves a better balance between precision and recall, allowing more effective control of false positives and false negatives.
Among the three architectures, GIN delivers the best performance, reaching an F1-score of 0.785, significantly higher than the other models. Its precision and recall are 0.832 and 0.743, respectively. These results suggest that GIN has a stronger ability to capture subtle feature differences in complex graph structures. By enhancing structural discriminability, GIN more effectively distinguishes between fraudulent and non-fraudulent nodes. This confirms its adaptability and advantage in modeling transaction networks. The findings further demonstrate that the choice of graph neural network architecture plays a critical role in determining model performance.
Secondly, this paper conducts comparative experiments with the non-graph model, and the experimental results are shown in Table 2.
As shown in the experimental results in Table 2, the graph neural network-based model (GIN) outperforms other non-graph models in the financial transaction network fraud detection task. Traditional methods such as Logistic Regression achieve the lowest performance across all metrics [22], with an F1-score of only 0.687. This reflects its limited capacity to model high-dimensional, non-linear features and complex structural relationships, making it ineffective in capturing hidden fraud-related patterns.
In contrast, non-graph deep models such as MLP [23], Transformers, and 1D-CNN [24] show performance improvements. This indicates that incorporating non-linear modeling and temporal structure extraction is helpful for fraud detection. Among them, Transformers achieve the best performance among non-graph models, with an F1-score of 0.732. However, they still struggle to fully utilize the structural information embedded in transaction networks, which limits their effectiveness in detecting complex, relation-based fraud behaviors.
As the proposed method in this study, GIN leverages its strong ability to model transaction graph structures and local neighbor relationships. It achieves the best results in accuracy, precision, recall, and F1-score, with the F1-score reaching 0.785, significantly outperforming all other methods. This result shows that in complex network environments centered on transactional behaviors, incorporating graph structure modeling not only enhances the model's representation of fraudulent activities but also improves its ability to detect organized fraud patterns.
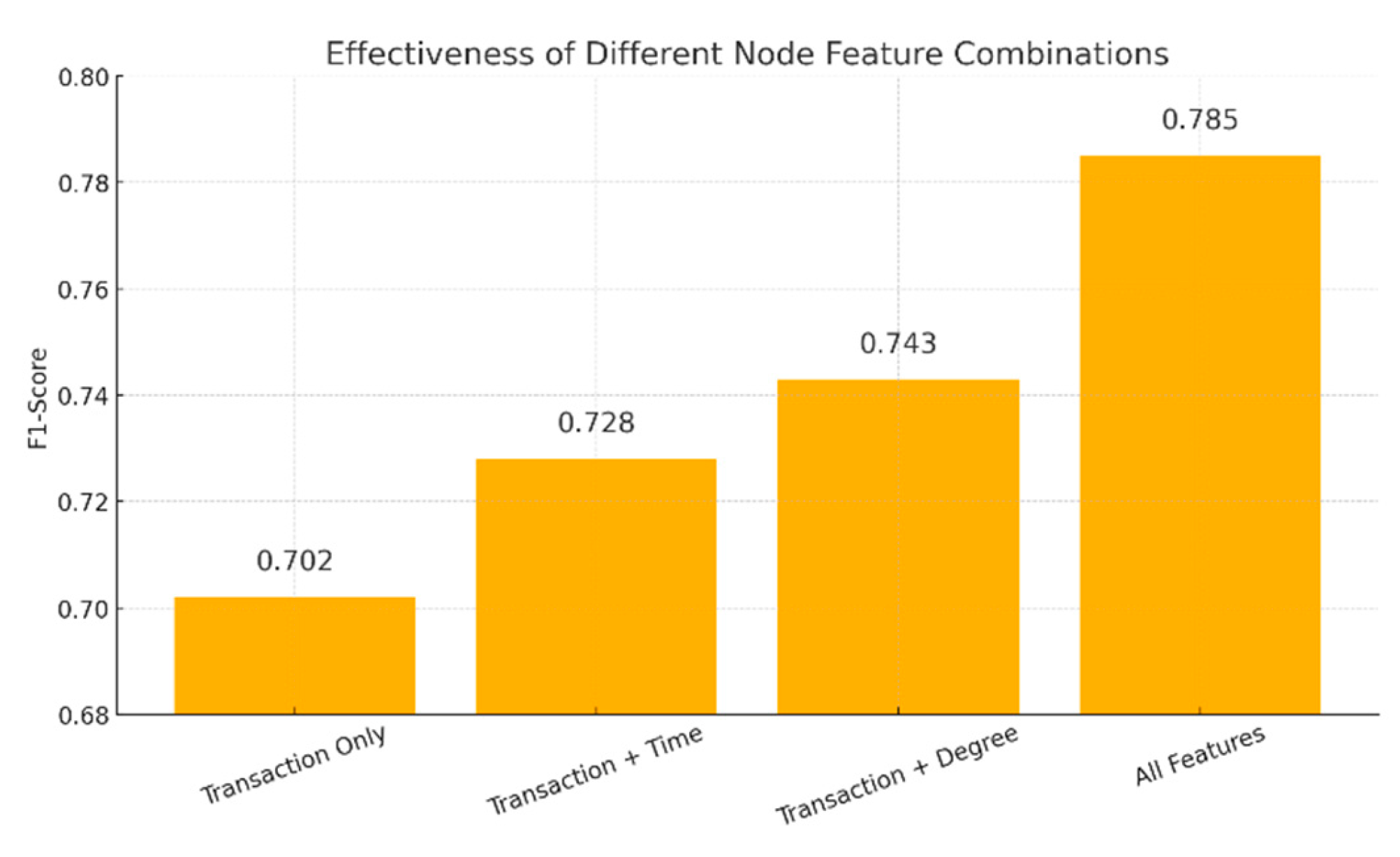
Finally, this paper studies the effectiveness analysis of different node feature combinations, and the experimental results are shown in Figure 2.
As shown in the experimental results in Figure 2, different combinations of node features have a significant impact on the model's fraud detection performance. When using only transaction-related features, the F1-score is just 0.702. This indicates that relying solely on static attributes such as transaction amount and frequency is insufficient to model complex fraud patterns, limiting the model's detection capability.As temporal information and graph structural attributes such as node degree are gradually added, model performance continues to improve. Adding time features increases the F1-score to 0.728. With node degree included, the score further rises to 0.743. This suggests that temporal features help identify abnormal transaction rhythms, while node connectivity reveals unusual interaction patterns. Both contribute positively to classification results.
When all features are combined, the model achieves the highest F1-score of 0.785. This demonstrates the advantage of multi-feature fusion in capturing the multidimensional behavioral characteristics of fraudulent nodes. The results confirm that, in graph neural networks, effectively integrating structural features with transactional attributes can significantly enhance model expressiveness and fraud detection performance.

IV. Conclusions

This paper proposes a graph neural network-based fraud detection method targeting financial fraud in transaction networks. The method fully leverages the structural information of nodes and edges in transaction graphs to efficiently identify potential fraudulent accounts. By integrating node feature representation, structural modeling, and graph aggregation mechanisms, the model achieves high accuracy while effectively detecting complex and hidden fraudulent behaviors. Experimental results show that the proposed method outperforms traditional machine learning models and non-graph deep models across multiple evaluation metrics, demonstrating the effectiveness and adaptability of graph-based modeling in financial fraud scenarios.
Through a series of experiments involving different GNN architectures, feature combinations, and comparisons with non-graph models, this study systematically analyzes the contribution of each component to detection performance. It confirms the synergy between graph structural information and node-level semantic features in fraud detection. Moreover, by introducing edge features and attention mechanisms, the model can better distinguish the importance of transaction relationships, further improving its ability to detect group fraud, disguised paths, and other complex behaviors. These findings provide a methodological foundation for building structured, dynamic, and interpretable financial risk control systems. Despite the promising results, the model still has room for improvement in scalability and real-time response. Future work may explore dynamic graph neural networks to meet the needs of real-time transaction stream processing [25]. Federated learning can be integrated to enable cross-platform risk collaboration. In addition, graph contrastive learning and interpretability mechanisms can be introduced to enhance transparency and regulatory compliance in high-risk financial environments. By continuously expanding the integration of graph learning techniques and financial risk control applications, a more secure and intelligent fraud prevention system can be established.

References

  1. W. Hyun, I. Lee and B. Suh, “LEX-GNN: Label-Exploring Graph Neural Network for Accurate Fraud Detection,” Proceedings of the 33rd ACM International Conference on Information and Knowledge Management, pp. 3802-3806, 2024.
  2. Y. Luo and G. Wang, “Fraud Detection Based on Graph Neural Network,” Proceedings of the 2024 3rd International Conference on Robotics, Artificial Intelligence and Intelligent Control (RAIIC), pp. 276-280, 2024.
  3. J. Du, S. Dou, B. Yang, J. Hu and T. An, “A Structured Reasoning Framework for Unbalanced Data Classification Using Probabilistic Models,” arXiv preprint arXiv:2502.03386, 2025.
  4. X. Li, Y. Peng, X. Sun, Y. Duan, Z. Fang and T. Tang, “Unsupervised Detection of Fraudulent Transactions in E-commerce Using Contrastive Learning,” arXiv preprint arXiv:2503.18841, 2025.
  5. J. Wang, “Credit Card Fraud Detection via Hierarchical Multi-Source Data Fusion and Dropout Regularization,” Transactions on Computational and Scientific Methods, vol. 5, no. 1, 2025.
  6. M. Li, R. Hao, S. Shi, Z. Yu, Q. He and J. Zhan, “A CNN-Transformer Approach for Image-Text Multimodal Classification with Cross-Modal Feature Fusion,” 2025.
  7. X. Sun, Y. Duan, Y. Deng, F. Guo, G. Cai and Y. Peng, “Dynamic Operating System Scheduling Using Double DQN: A Reinforcement Learning Approach to Task Optimization,” arXiv preprint arXiv:2503.23659, 2025.
  8. Y. Duan, L. Yang, T. Zhang, Z. Song and F. Shao, “Automated UI Interface Generation via Diffusion Models: Enhancing Personalization and Efficiency,” arXiv preprint arXiv:2503.20229, 2025.
  9. W. Xie, J. He and J. Ren, “Supply Chain Financial Fraud Detection Based on Graph Neural Network and Knowledge Graph,” Technical Gazette/Tehnički Vjesnik, vol. 31, no. 6, 2024. [CrossRef]
  10. Y. Cheng, Z. Xu, Y. Chen, Y. Wang, Z. Lin and J. Liu, “A Deep Learning Framework Integrating CNN and BiLSTM for Financial Systemic Risk Analysis and Prediction,” arXiv preprint arXiv:2502.06847, 2025.
  11. J. Liu, Y. Zhang, Y. Sheng, Y. Lou, H. Wang and B. Yang, “Context-Aware Rule Mining Using a Dynamic Transformer-Based Framework,” arXiv preprint arXiv:2503.11125, 2025.
  12. Y. Zhang, “Social Network User Profiling for Anomaly Detection Based on Graph Neural Networks,” arXiv preprint arXiv:2503.19380, 2025.
  13. Y. Chen, Z. Zheng, J. Ma, et al., “A Graph Neural Network with Imbalance-Aware Mechanism for Enhanced Fraud Detection,” Proceedings of the 2024 IEEE Cyber Science and Technology Congress (CyberSciTech), pp. 207-213, 2024.
  14. Y. Wang, Z. Xu, Y. Yao, J. Liu and J. Lin, “Leveraging Convolutional Neural Network-Transformer Synergy for Predictive Modeling in Risk-Based Applications,” arXiv preprint arXiv:2412.18222, 2024.
  15. Y. Yao, “Stock Price Prediction Using an Improved Transformer Model: Capturing Temporal Dependencies and Multi-Dimensional Features,” Journal of Computer Science and Software Applications, vol. 5, no. 2, 2024.
  16. J. Liu, “Multimodal Data-Driven Factor Models for Stock Market Forecasting,” Journal of Computer Technology and Software, vol. 4, no. 2, 2025.
  17. P. Feng, “Hybrid BiLSTM-Transformer Model for Identifying Fraudulent Transactions in Financial Systems,” Journal of Computer Science and Software Applications, vol. 5, no. 3, 2025.
  18. X. Yan, Y. Jiang, W. Liu, D. Yi and J. Wei, "Transforming Multidimensional Time Series into Interpretable Event Sequences for Advanced Data Mining," 2024 5th International Conference on Intelligent Computing and Human-Computer Interaction (ICHCI), pp. 126-130, 2024.
  19. Y. Wang, “A Data Balancing and Ensemble Learning Approach for Credit Card Fraud Detection,” arXiv preprint arXiv:2503.21160, 2025.
  20. M. Weber, S. Lebrecht, S. Borno, et al., “Anti-money laundering in bitcoin: Experimenting with graph convolutional networks for financial forensics,” arXiv preprint arXiv:1908.02591, 2019.
  21. B. Bertalanič and C. Fortuna, “Graph isomorphism networks for wireless link layer anomaly classification,” Proceedings of the 2023 IEEE Wireless Communications and Networking Conference (WCNC), 2023.
  22. A. Das, “Logistic regression,” Proceedings of the 2024 Encyclopedia of Quality of Life and Well-Being Research, pp. 3985-3986, 2024.
  23. H. Weytjens, E. Lohmann and M. Kleinsteuber, “Cash flow prediction: MLP and LSTM compared to ARIMA and Prophet,” Electronic Commerce Research, vol. 21, no. 2, pp. 371-391, 2021. [CrossRef]
  24. S. Guessoum, S. Belda, J. M. Ferrandiz, S. Modiri, S. Raut, S. Dhar and H. Schuh, “The short-term prediction of length of day using 1D convolutional neural networks (1D CNN),” Sensors, vol. 22, no. 23, p. 9517, 2022. [CrossRef]
  25. F. Klein and R. Silva, “Detection of collusive behavior in crypto trading networks via GNN,” Proceedings of the International Workshop on Blockchain Analytics, pp. 49-58, 2019.
Preprints 157711 g001
Figure 1. Model network architecture.
Figure 1. Model network architecture.
Preprints 157711 g001
Preprints 157711 g002
Figure 2. Effectiveness analysis of different node feature combinations.
Figure 2. Effectiveness analysis of different node feature combinations.
Preprints 157711 g002
Table 1. Comparative experiment of different graph neural network structures.
Table 1. Comparative experiment of different graph neural network structures.
Model ACC Precision Recall F1-Score
GCN 0.927 0.781 0.692 0.734
GAT 0.938 0.806 0.718 0.759
GIN 0.946 0.832 0.743 0.785
Table 2. The experimental results were compared with the non-graph model.
Table 2. The experimental results were compared with the non-graph model.
Model ACC Precision Recall F1-Score
Logistic Regression 0.901 0.754 0.631 0.687
MLP 0.914 0.773 0.658 0.711
Transformers 0.922 0.789 0.683 0.732
1D-CNN 0.917 0.778 0.671 0.720
GIN(Ours) 0.946 0.832 0.743 0.785
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated