Collatz Trees: A Structural Framework for Understanding the 3x+1 Problem

1. Decomposing All Natural Numbers into Geometric Sequences

1.1. Background and Objective

This study presents a new perspective on the Collatz Conjecture by expressing the entirety of natural numbers as a structure composed of interconnected “branches” and a central “trunk.” Specifically, we define each branch as a geometric sequence beginning with an odd number, and the trunk as the unique sequence beginning with 1. Based on this structure, we aim to approach the essence of the Collatz Conjecture.

1.2. Definitions and Goals

Let the set of natural numbers be denoted by:

$$\mathbb{N}=\{1,2,3,4,5,\cdots \}$$

We aim to prove that the following set S is equivalent to $\mathbb{N}$:

$$S=\{(2a+1)·2^b\mid a,b\ge 0\}$$

In other words, every natural number n can be expressed in the form:

$$n=(2a+1)·2^b\mathrm{for}a,b\ge 0$$

1.3. Prime Factorization and Classification

For any natural number n, its prime factorization can be written as:

$$n=2^b·k$$

where k is an odd number and $b\ge 0$ is an integer. This decomposition is unique, and it enables us to classify natural numbers into an even part ($2^b$) and an odd part (k).

1.4. Exhaustion of Odd Numbers

Any odd number k can be written as:

$$k=2a+1(a\ge 0)$$

Hence, all odd numbers can be generated as:

$$1,3,5,7,9,11,\cdots$$

1.5. Exhaustion of Even Parts

For each odd number k, we consider the sequence generated by multiplying it by successive powers of 2:

• For $k=1$: $1,2,4,8,16,\cdots$
• For $k=3$: $3,6,12,24,\cdots$
• For $k=5$: $5,10,20,40,\cdots$

Thus, all even numbers are also covered as part of a sequence in the form “odd × power of 2.”

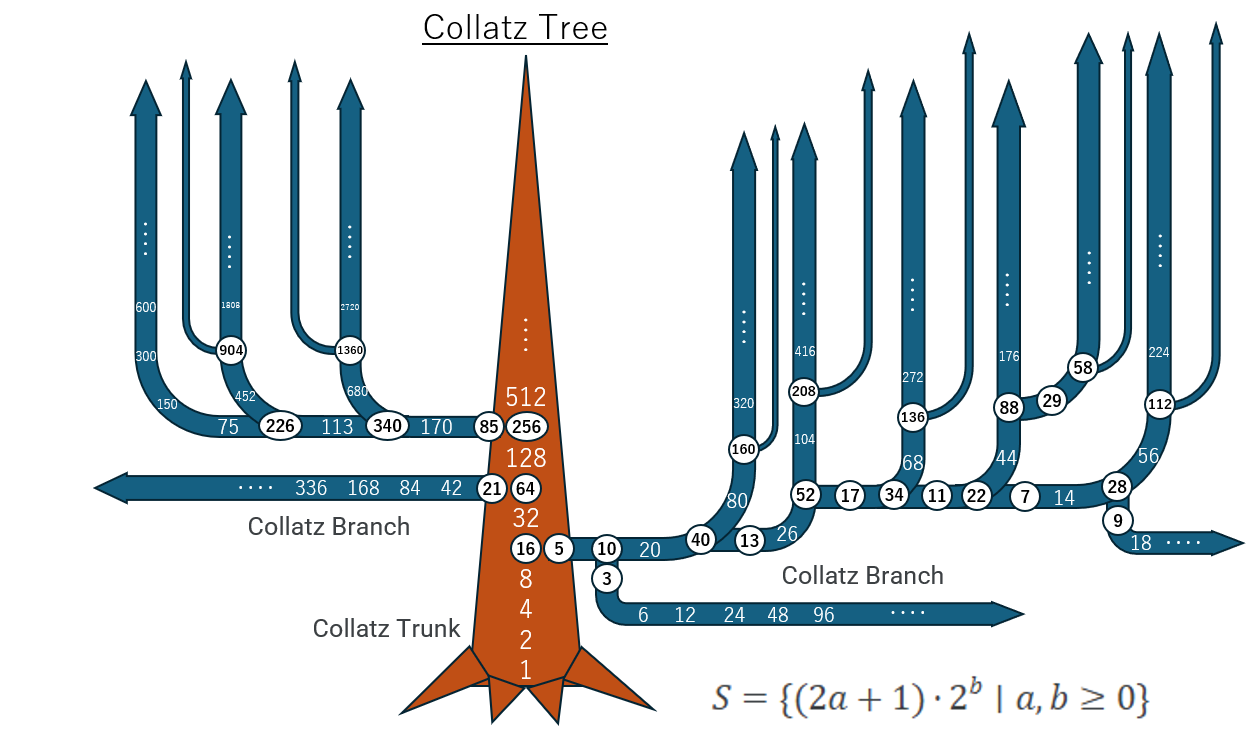
1.6. Construction of Set S

From the Collatz perspective, we generate an infinite sequence for each odd number as follows:

• From 1: $1,2,4,8,16,\cdots$
• From 3: $3,6,12,24,\cdots$
• From 5: $5,10,20,40,\cdots$

Each of these is considered a branch, and collectively, they form a visual representation of all natural numbers.

Table 1. Odd Number k and Its Multiples by Powers of 2

Odd k	$k·2^0$	$k·2^1$	$k·2^2$	$k·2^3$	$k·2^4$	$k·2^5$
1	1	2	4	8	16	32
3	3	6	12	24	48	96
5	5	10	20	40	80	160
7	7	14	28	56	112	224
9	9	18	36	72	144	288

1.7. Proof of Completeness

Let n be any natural number. By prime factorization, it can be written as:

$$n=2^b·k$$

where k is an odd number. Since any odd number k can be uniquely written as $k=2a+1$, it follows that:

$$n=(2a+1)·2^b$$

Hence, all natural numbers belong to some branch, starting from an odd number.

Furthermore, the even numbers are completely covered by sequences derived from odd numbers. For example:

$$8=2^3·1\mathrm{is}\mathrm{in}\mathrm{the}\mathrm{sequence}\mathrm{from}k=1$$

Thus, every even number belongs to some branch.

In conclusion, the set:

$$S=\{(2a+1)·2^b\mid a,b\ge 0\}$$

exhaustively covers all natural numbers:

$$S=\mathbb{N}$$

1.8. Elimination of Redundancy

To ensure uniqueness, we consider whether two different pairs $(a,b)$ and $(a^{\prime },b^{\prime })$ could generate the same number:

$$(2a+1)·2^b=(2a^{\prime }+1)·2^{b^{\prime }}$$

Assume the contrary. This implies:

$${\displaystyle \frac{2a+1}{2a^{\prime }+1}}=2^{b^{\prime }-b}$$

However, the left-hand side is a rational number with an odd numerator and denominator, while the right-hand side is a power of 2. These forms are incompatible unless both sides are equal to 1, which only happens when $a=a^{\prime }$ and $b=b^{\prime }$. Thus, no duplication occurs in S.

1.9. Conclusion of Chapter 1

In this chapter, we proposed a new approach to the Collatz Conjecture by decomposing all natural numbers into branches and a trunk. We proved that:

• Every natural number is uniquely included in some branch starting from an odd number.
• All branches are composed of sequences of the form $k·2^b$, where k is an odd number.

This framework allows for a structural understanding of how natural numbers are distributed and interconnected.

We also observed that, for any odd number k, the operation $3k+1$ always yields an even number, which can be decomposed into some existing branch. Hence, all branches are ultimately connected and converge into the trunk starting from 1.

This structure resembles a tree radiating outward, with no backward paths and no repetition of numbers. Therefore, the path from any natural number n to 1 is always ensured by following the reverse of the branching structure.

Collatz operations, viewed in this light, are equivalent to descending through a deterministic tree structure from any n toward 1.

2. The Structure of the Collatz Tree

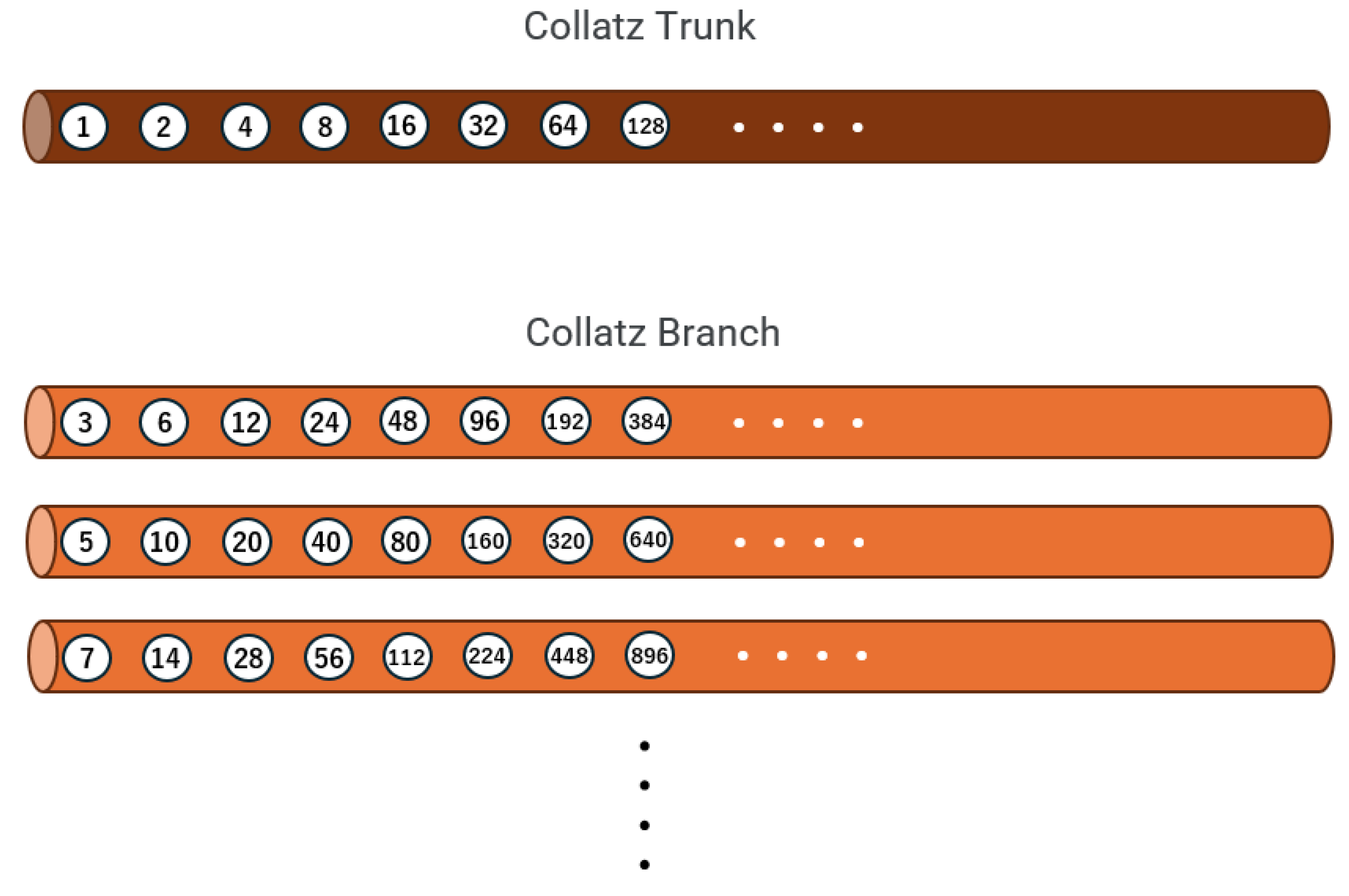
2.1. Definition of Branches and the Trunk

We define the Collatz Tree as a directed structure composed of a central trunk and multiple branching sequences.

• Branch: For each odd number k, a branch is defined as a geometric sequence formed by multiplying k by successive powers of 2. This allows us to visualize how natural numbers spread out as branches.
• Trunk: The unique sequence beginning from 1, consisting of powers of 2, is considered the trunk. All other branches eventually merge into this trunk.

Examples:

• Trunk: $1\to 2\to 4\to 8\to 16\to \cdots$
• Branches:

  -

  From $k=3$: $3\to 6\to 12\to 24\to 48\to \cdots$

  -

  From $k=5$: $5\to 10\to 20\to 40\to 80\to \cdots$

Figure 1. Collatz tree trunk and branches (Created by the author)

Figure 1. Collatz tree trunk and branches (Created by the author)

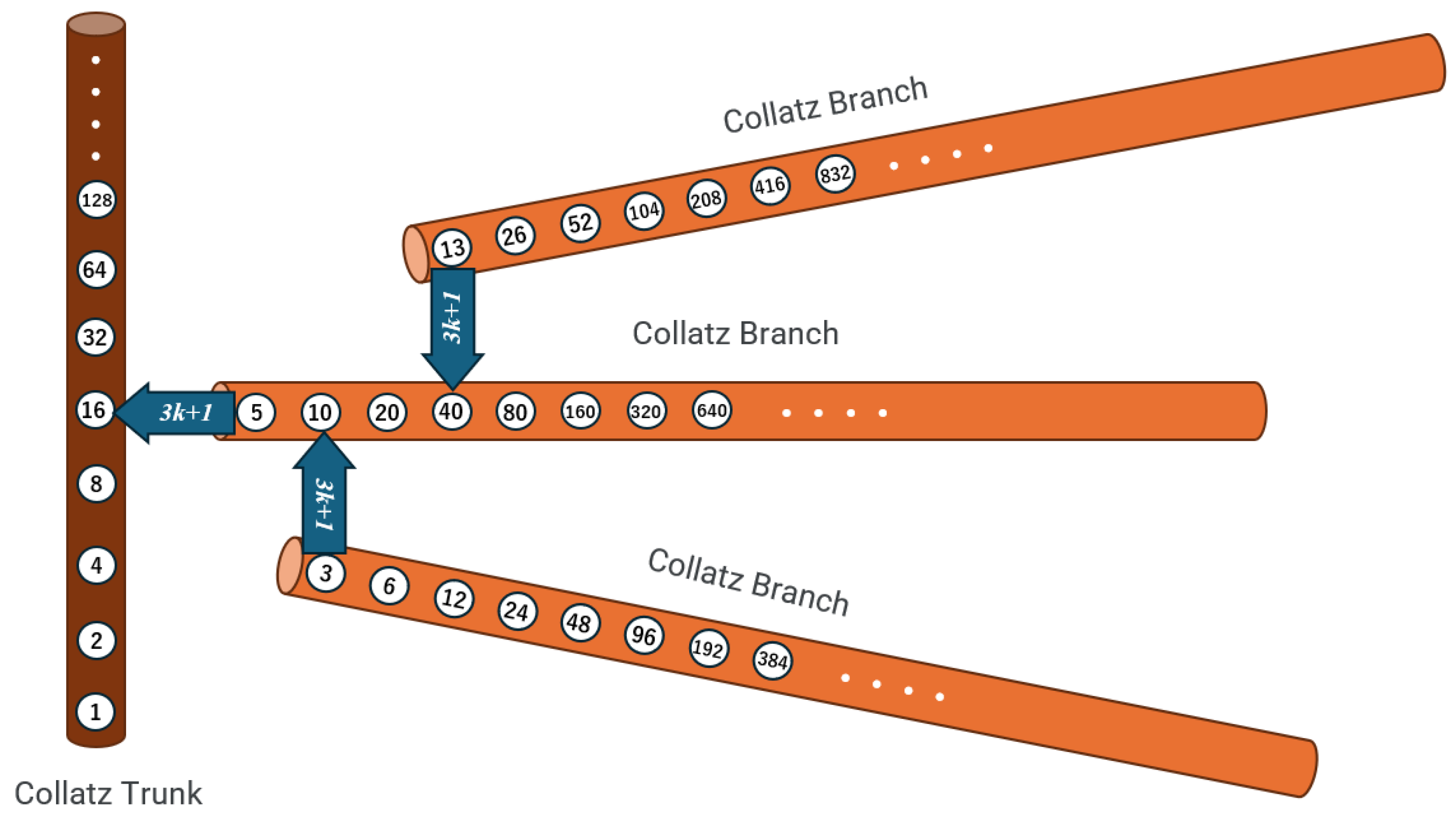
2.2. Branch Connection Rules

Each branch, starting from an odd number k, is connected to the existing tree structure through the following rule:

• For each odd number k, compute $3k+1$.
• Since $3k+1$ is always even, it belongs to some existing branch in the form $(2a^{\prime }+1)·2^b$.
• Thus, $3k+1$ becomes the merge point where the current branch connects to another branch or the trunk.

Since all natural numbers are included in the tree, the resulting value $3k+1$ is guaranteed to exist within the structure. Therefore, every branch eventually connects to the trunk.

Example:

• For $k=5$, we compute $3·5+1=16$, which belongs to the trunk sequence $1\to 2\to 4\to 8\to 16\to \cdots$.
• Hence, the branch starting at 5 connects to the trunk via 16.

Figure 2. Collatz tree Rules for Connecting Branches (Created by the author)

Figure 2. Collatz tree Rules for Connecting Branches (Created by the author)

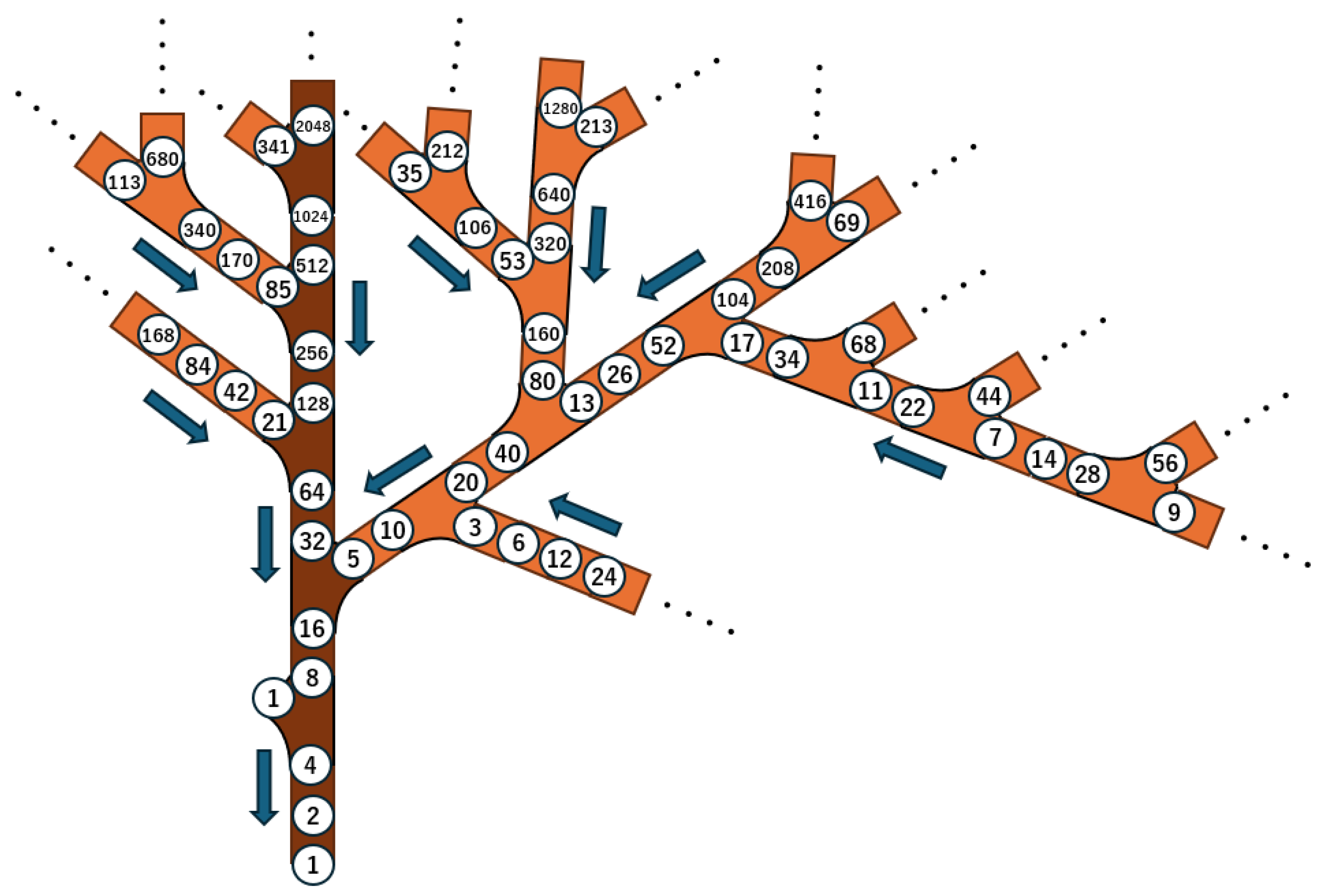
2.3. Generational Structure of the Collatz Tree

The branches of the Collatz Tree can be categorized into generations based on how they connect to the trunk or to other branches.

• First Generation: Branches that directly merge into the trunk. These are the closest to the root and connect to the trunk via a single $3k+1$ operation.
• Second Generation: Branches that connect to a first-generation branch. That is, they require two successive $3k+1$ operations to reach the trunk.
• Third Generation and Beyond: These follow recursively, with each generation connecting to the previous one via a merge point.

This generational structure allows us to trace the hierarchical relationships between branches and understand how each odd number is positioned within the tree.

2.4. Overall Structure of the Collatz Tree

The Collatz Tree is a directed structure rooted at 1, in which all natural numbers are arranged according to Collatz operations. The key characteristics of this structure are as follows:

• Trunk: A unique path starting from 1, consisting of powers of 2.
• Branches: Sequences starting from each odd number k, extended by successive multiplications by 2: $k,2k,4k,\cdots$.

We define the tree formally as a rooted directed tree with root node 1.

Edge Definition

For each node v (a natural number), the edges are defined as:

• If v is even: an edge from v to $v/2$.
• If v is odd and $v\ne 1$: define the parent node as the smallest k such that $(3k+1)/2^m=v$ for some integer $m\ge 1$.

Thus, edges in the tree always point from a number to its predecessor under the reverse Collatz operation.

This structure satisfies the properties of a Directed Acyclic Graph (DAG), and more specifically, a Directed Tree.

Properties of the Collatz Tree

• Directedness: Each node has a uniquely defined successor (under forward Collatz steps) or predecessor (under reverse steps).
• Acyclicity: There are no cycles except the trivial loop $1\to 2\to 4\to 1$, which does not violate acyclicity in the tree structure as we fix 1 as the root.
• Connectivity: Every natural number is connected through a finite path to the root node 1.
• Uniqueness: Each node appears exactly once in the tree.

Therefore, the Collatz Tree is a well-defined, rooted, directed tree covering all natural numbers.

2.4.1. The Collatz Tree as a Directed Acyclic Graph (DAG)

To examine the structural properties of the Collatz Tree, we define the standard Collatz function as:

$$f\left(n\right)=\left\{\begin{array}{cc}n/2,\hfill & \mathrm{if}n\equiv 0(mod2)\hfill \\ 3n+1,\hfill & \mathrm{if}n\equiv 1(mod2)\hfill \end{array}\right.$$

By repeatedly applying this function f, we obtain a sequence of natural numbers. The directed edges of the graph are defined by the transition $n\to f\left(n\right)$.

Directedness:

Each natural number n has a uniquely determined image $f\left(n\right)$. Thus, each node has exactly one outgoing edge. The graph is therefore directed.

Acyclicity:

There are no known cycles in the Collatz sequence, except for the trivial loop:

$$1\to 2\to 4\to 1$$

Aside from this known finite loop, no other cycle has ever been observed. The function f tends to reduce the value of n over time, especially when n is even. Therefore, the system is biased toward convergence.

Based on this observation, and the absence of other known cycles, we consider the graph to be acyclic.

Conclusion:

Combining the above, the Collatz Tree satisfies the conditions for a directed acyclic graph (DAG):

• Each edge has a direction.
• No path forms a closed loop.

Figure 3. The Collatz Tree as a Directed Acyclic Graph (DAG) (Created by the author)

Figure 3. The Collatz Tree as a Directed Acyclic Graph (DAG) (Created by the author)

2.4.2. The Collatz Tree as a Directed Tree

Having established that the Collatz Tree is a directed acyclic graph (DAG), we now show that it also satisfies the properties of a directed tree.

Directedness:

As defined previously, the Collatz function maps each natural number n to a unique successor, and the reverse Collatz operation defines a unique predecessor wherever applicable. Hence, the tree is directed.

Connectivity:

The Collatz Tree is rooted at 1. Starting from any natural number n, applying the standard Collatz operations (forward or backward) eventually leads to 1. This implies that every node is connected to the root through a unique path. Therefore, the structure is connected.

Uniqueness of Parent Node:

Each node (natural number) in the Collatz Tree has exactly one parent, defined by either:

• $2n$ if n is the result of halving an even number, or
• $(n-1)/3$ if $n\equiv 1(mod3)$ and the result is an odd number.

Thus, each node has at most one incoming edge, ensuring the tree structure with no ambiguity or duplication.

Conclusion:

All nodes are connected, and each has exactly one parent (except the root). Therefore, the Collatz Tree satisfies the definition of a directed rooted tree.

2.4.3. Structural Impossibility of Infinite Growth

The Collatz Tree exhibits important structural properties that rule out the possibility of infinite growth or divergence within the tree.

Tree Node Uniqueness:

Each natural number appears exactly once in the Collatz Tree. Every node occupies a unique position in the structure, determined by its path from or to the root.

No New Nodes Beyond the Tree:

For a number to grow infinitely large, the tree would need to accommodate an unbounded sequence of nodes. However, since the structure is defined as a finite tree rooted at 1, and all nodes are already placed uniquely within it, there is no space for introducing new nodes without duplication.

Restriction on Infinite Ascension:

Any path that ascends infinitely within the tree would require numbers not already in the tree. Since all natural numbers are already accounted for, such an infinite path is structurally impossible.

Conclusion:

Due to the uniqueness of each node and the completeness of the tree, infinite growth is not possible within this structure. Any process starting from a natural number must eventually descend toward the root, and no path can rise infinitely without violating the tree’s structural constraints.

2.5. Absence of Loops in the Collatz Tree

It is generally difficult to prove the absence of loops directly through forward Collatz operations. Therefore, we consider the reverse operations and analyze their structure.

Definition of Collatz Transformations

The standard Collatz function f is defined as:

$$f\left(n\right)=\left\{\begin{array}{cc}n/2,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\hfill \\ 3n+1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}\hfill \end{array}\right.$$

The reverse transformation $g\left(n\right)$ is defined piecewise as follows:

$$g\left(n\right)=\left\{\begin{array}{cc}2n,\hfill & (\mathrm{always}\mathrm{applicable})\hfill \\ {\displaystyle \frac{n-1}{3}},\hfill & \mathrm{if}n\equiv 1(mod3)\mathrm{and}{\displaystyle \frac{n-1}{3}}\in \mathbb{N}\hfill \end{array}\right.$$

Two Types of Computation Units

We model the structure of the reverse Collatz process using two computation units:

• Computation Unit 1 (UNIT 1): Doubles the input. This models the operation $g\left(n\right)=2n$.
• Computation Unit 2 (UNIT 2):
  • Doubles the input to get $2n$.
  • If $n-1$ is divisible by 3, then output $(n-1)/3$ as a secondary branch.

Each node in the reverse Collatz tree is computed via one of these two unit types, both having only one input. The possibility of forming a loop would require a secondary input feeding back into itself — which is structurally impossible under this model.

Why Loops Cannot Occur

To form a loop, the output from one unit must return as input to a previous unit in the same path. However:

• Each value is used exactly once in the tree.
• The input/output mapping of each computation unit is one-to-one and irreversible.
• Once a number is used as input in the tree, no other unit can reuse it.

For instance, to output 5 via $g\left(n\right)$, we would need $n=16$. But 16 is already assigned uniquely within the tree. No alternative path can use it again.

Therefore, the structure eliminates the possibility of loops.

Equation-Based Confirmation

Let $k=2a+1$ (an odd number), and suppose we want to find k such that:

$$3k+1=2^b·k$$

Rewriting gives:

$$(2^b-3)·k=1$$

This has only one integer solution: $b=2,k=1$.

This confirms that the only loop in the Collatz graph is the trivial cycle:

$$1\to 2\to 4\to 1$$

Conclusion

The reverse computation process guarantees that:

• All paths in the tree are uniquely determined.
• Each node has a single input and known output structure.
• No loops can occur, except the trivial loop through 1.

This proves the loop-free nature of the Collatz Tree.

2.6. Absence of Loops in the Collatz Tree

It is generally difficult to prove the absence of loops directly through forward Collatz operations. Therefore, we consider the reverse operations and analyze their structure.

Definition of Collatz Transformations

The standard Collatz function f is defined as:

$$f\left(n\right)=\left\{\begin{array}{cc}n/2,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\hfill \\ 3n+1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}\hfill \end{array}\right.$$

The reverse transformation $g\left(n\right)$ is defined piecewise as follows:

$$g\left(n\right)=\left\{\begin{array}{cc}2n,\hfill & (\mathrm{always}\mathrm{applicable})\hfill \\ {\displaystyle \frac{n-1}{3}},\hfill & \mathrm{if}n\equiv 1(mod3)\mathrm{and}{\displaystyle \frac{n-1}{3}}\in \mathbb{N}\hfill \end{array}\right.$$

Two Types of Computation Units

We model the structure of the reverse Collatz process using two computation units:

• Computation Unit 1 (UNIT 1): Doubles the input. This models the operation $g\left(n\right)=2n$.
• Computation Unit 2 (UNIT 2):
  • Doubles the input to get $2n$.
  • If $n-1$ is divisible by 3, then output $(n-1)/3$ as a secondary branch.

Figure 4. Collatz tree Execution UNIT (Created by the author)

Figure 4. Collatz tree Execution UNIT (Created by the author)

Each node in the reverse Collatz tree is computed via one of these two unit types, both having only one input. The possibility of forming a loop would require a secondary input feeding back into itself — which is structurally impossible under this model.

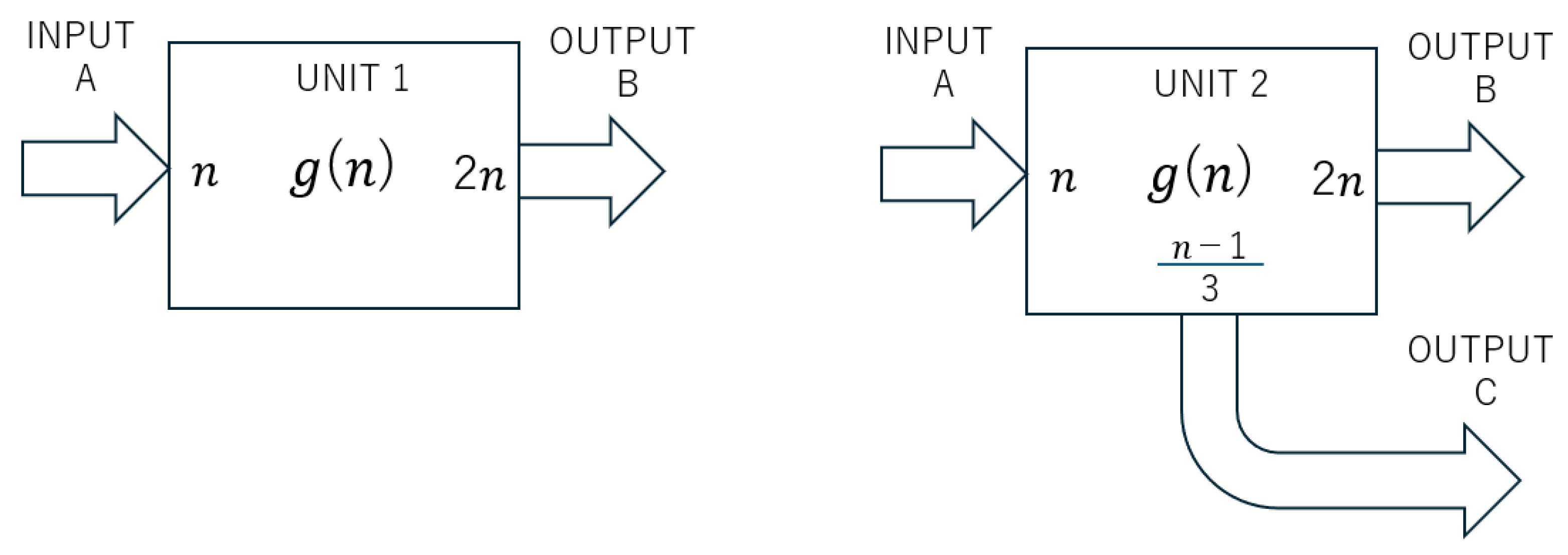
Why Loops Cannot Occur

To form a loop, the output from one unit must return as input to a previous unit in the same path. However:

• Each value is used exactly once in the tree.
• The input/output mapping of each computation unit is one-to-one and irreversible.
• Once a number is used as input in the tree, no other unit can reuse it.

For instance, to output 5 via $g\left(n\right)$, we would need $n=16$. But 16 is already assigned uniquely within the tree. No alternative path can use it again.

Therefore, the structure eliminates the possibility of loops.

Equation-Based Confirmation

Let $k=2a+1$ (an odd number), and suppose we want to find k such that:

$$3k+1=2^b·k$$

Rewriting gives:

$$(2^b-3)·k=1$$

This has only one integer solution: $b=2,k=1$. This confirms that the only loop in the Collatz graph is the trivial cycle:

$$1\to 2\to 4\to 1$$

Conclusion

The reverse computation process guarantees that:

• All paths in the tree are uniquely determined.
• Each node has a single input and known output structure.
• No loops can occur, except the trivial loop through 1.

This proves the loop-free nature of the Collatz Tree.

2.7. Equivalence Between the Reverse-Constructed Tree and the Collatz Tree

We now demonstrate that the tree structure generated by reverse Collatz operations starting from 1 is structurally identical to the forward Collatz Tree.

Reverse Collatz Operation $g\left(n\right)$

As previously defined, the reverse Collatz function $g\left(n\right)$ is:

$$g\left(n\right)=\left\{\begin{array}{cc}2n,\hfill & \mathrm{always}\mathrm{applicable}\hfill \\ {\displaystyle \frac{n-1}{3}},\hfill & \mathrm{if}n\equiv 1(mod3)\mathrm{and}{\displaystyle \frac{n-1}{3}}\in \mathbb{N}\hfill \end{array}\right.$$

By applying $g\left(n\right)$ starting from $n=1$, we can construct a tree where each node has one or two children depending on whether the second rule is satisfied.

Programmatic Construction and Observation

We implemented the reverse Collatz tree construction in Python using the rule $g\left(n\right)$. The resulting graph matches precisely the structure of the Collatz Tree created via forward operations.

This shows that the reverse process recreates the exact same branches, merge points, and number distribution.

Equivalence in Structure

The following properties are preserved in both directions:

• The same numbers appear in the same positions.
• Branches bifurcate at identical points.
• The parent-child relationships are maintained.

Therefore, the reverse-generated tree is structurally identical to the Collatz Tree.

Implication

Because every number in the reverse tree is generated starting from 1 using $g\left(n\right)$, it follows that any natural number n has a unique path leading back to 1.

Thus, the statement “every natural number eventually reaches 1 under the Collatz operation” is equivalent to saying “every number appears in the reverse tree constructed from 1.”

Conclusion

• The tree created from the reverse Collatz function $g\left(n\right)$ is the same as the Collatz Tree generated through forward computation.
• Each number appears once and only once.
• Therefore, all natural numbers are connected to the root 1 via a unique path.

2.8. Python-Generated Tree Visualizations

The following figures illustrate the Collatz tree generated via Python code:

Figure 5. Collatz tree generated from the program (limit = 250) (created using original Python code)

Figure 5. Collatz tree generated from the program (limit = 250) (created using original Python code)

Figure 6. Collatz tree generated from the program (limit = 500) (created using original Python code)

Figure 6. Collatz tree generated from the program (limit = 500) (created using original Python code)

Figure 7. Collatz tree generated from the program (limit = 1000) (created using original Python code)

Figure 7. Collatz tree generated from the program (limit = 1000) (created using original Python code)

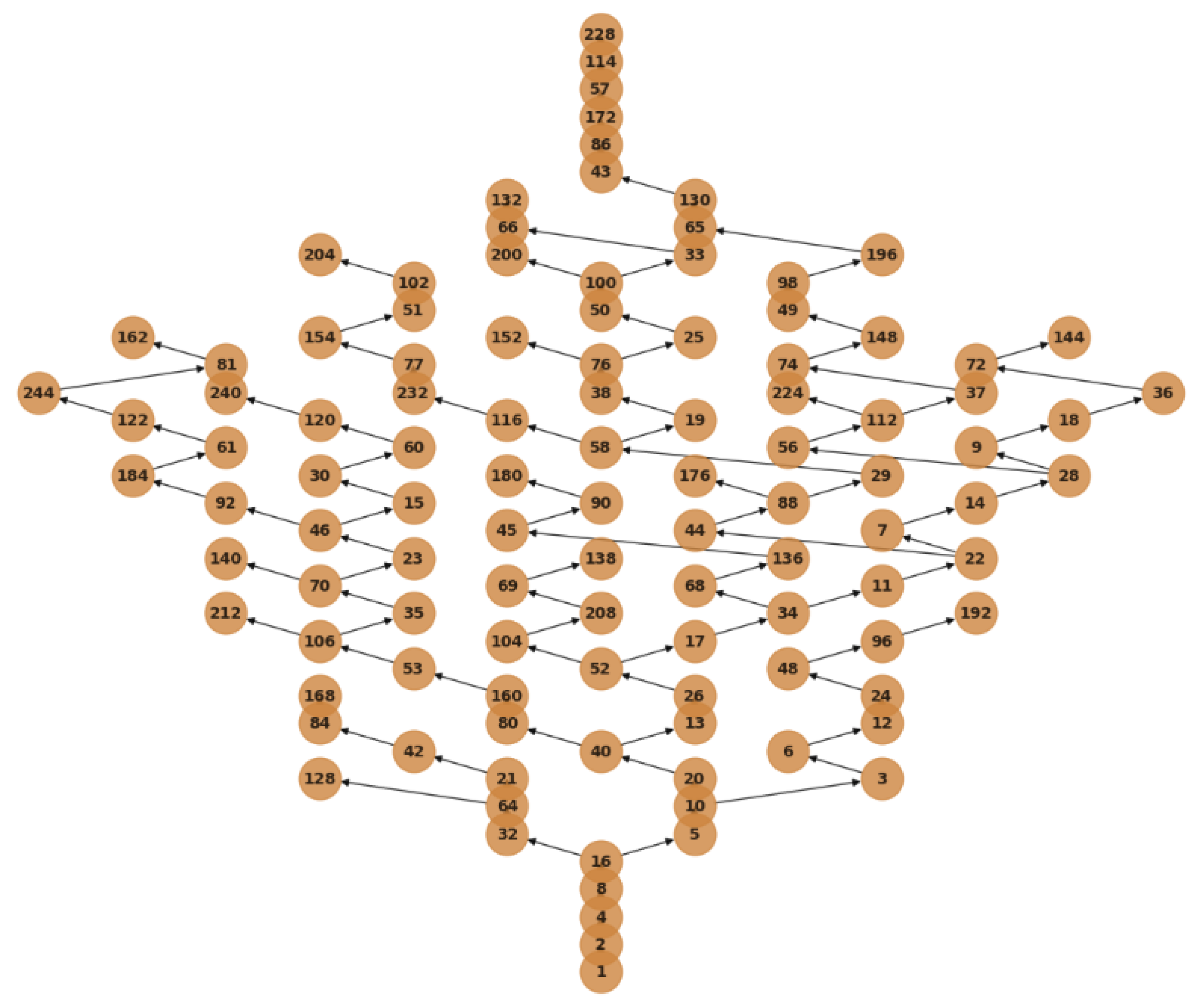
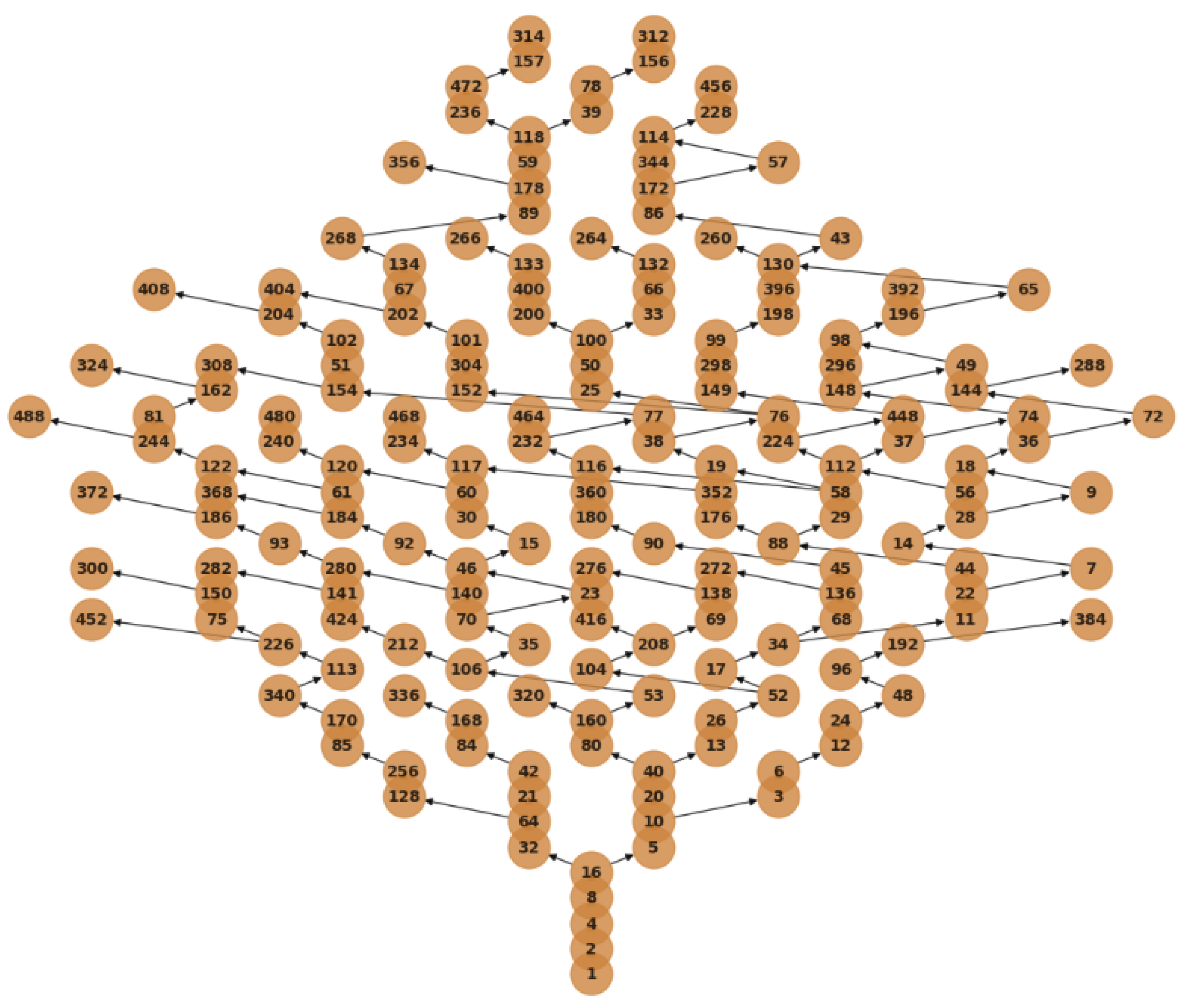
2.9. Structural Collatz Conjecture (Main Theorem)

Theorem 1

(Structural Collatz Conjecture). Every natural number is included in the directed tree generated by reverse Collatz operations starting from 1.

Therefore, for any natural number n, repeated application of the Collatz operation leads to 1.

Proof. 

We have shown the following:

• Every natural number can be uniquely expressed in the form $(2a+1)·2^b$, and is thus part of a branch starting from an odd number.
• Applying the operation $3k+1$ (for any odd number k) always yields an even number, which can be decomposed into the form $(2a^{\prime }+1)·2^{b^{\prime }}$ and thus belongs to another existing branch. Therefore, all branches ultimately merge and connect to the trunk (the branch starting from 1).
• We confirmed that no loops exist in the tree, aside from the trivial cycle $1\to 2\to 4\to 1$.
• The reverse Collatz function $g\left(n\right)$ allows us to construct a tree rooted at 1 that includes all natural numbers. This tree is structurally identical to the Collatz Tree.

Hence, any natural number n is connected to 1 through a unique path within this tree structure. Since the reverse tree reconstructs all natural numbers starting from 1, the forward process must necessarily lead every n to 1.

□

The Collatz tree:

• Is a directed acyclic graph (DAG)
• Has a unique root (1)
• Includes all natural numbers without duplication
• Matches in both forward and reverse construction