Submitted:
07 April 2025
Posted:
08 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Observations and Data Reduction
| Exposure ID | Start MJD | Exposure Time(s) | QPO Frequency (Hz) | RMS | Q-value |
|---|---|---|---|---|---|
| P61433800108 | 60182.28 | 2504 | |||
| P61433800109 | 60182.41 | 2240 | |||
| P61433800110 | 60182.55 | 2670 | |||
| P61433800111 | 60182.68 | 1290 | |||
| P61433800112 | 60182.81 | 1118 | |||
| P61433800201 | 60183.05 | 164.6 | |||
| P61433800202 | 60183.20 | 2784 | |||
| P61433800203 | 60183.34 | 1775 | |||
| P61433800204 | 60183.48 | 2453 | |||
| P61433800205 | 60183.61 | 119.7 | |||
| P61433800206 | 60183.74 | 527.7 | |||
| P61433800207 | 60183.87 | 418.9 | |||
| P61433800208 | 60184.00 | 359.1 | |||
| P61433800209 | 60184.14 | 2034 | |||
| P61433800210 | 60184.26 | 2271 | |||
| P61433800211 | 60184.40 | 2095 | |||
| P61433800212 | 60184.53 | 1727 | |||
| P61433800301 | 60185.30 | 3292 | |||
| P61433800302 | 60185.46 | 2555 | |||
| P61433800303 | 60185.59 | 2691 | |||
| P61433800304 | 60185.72 | 2118 | |||
| P61433800305 | 60185.85 | 359.1 | |||
| P61433800306 | 60185.99 | 435.9 | |||
| P61433800307 | 60186.12 | 2753 | |||
| P61433800308 | 60186.24 | 2394 | |||
| P61433800309 | 60186.38 | 2366 | |||
| P61433800310 | 60186.51 | 2006 | |||
| P61433800311 | 60186.65 | 2514 | |||
| P61433800312 | 60186.78 | 179.5 | |||
| P61433800314 | 60187.04 | 1473 | |||
| P61433800401 | 60187.15 | 2152 | |||
| P61433800402 | 60187.30 | 2423 | |||
| P61433800403 | 60187.44 | 359.1 | |||
| P61433800404 | 60187.57 | 943.6 | |||
| P61433800405 | 60187.70 | 1910 | |||
| P61433800407 | 60187.97 | 777.1 | |||
| P61433800408 | 60188.10 | 2493 | |||
| P61433800409 | 60188.22 | 1017 | |||
| P61433800410 | 60188.36 | 2419 | |||
| P61433800411 | 60188.50 | 1796 | |||
| P61433800412 | 60188.63 | 463.8 | |||
| P61433800413 | 60188.76 | 778.1 | |||
| P61433800414 | 60188.89 | 920.7 | |||
| P61433800501 | 60189.07 | 3148 | |||
| P61433800502 | 60189.22 | 1179 | |||
| P61433800503 | 60189.35 | 2274 | |||
| P61433800504 | 60189.49 | 2019 | |||
| P61433800505 | 60189.62 | 2329 | |||
| P61433800506 | 60189.75 | 718.2 | |||
| P61433800507 | 60189.88 | 225.4 | |||
| P61433800508 | 60190.02 | 2214 | |||
| P61433800509 | 60190.15 | 1013 | |||
| P61433800511 | 60190.41 | 1197 | |||
| P61433800512 | 60190.54 | 2029 | |||
| P61433800513 | 60190.68 | 1717 | |||
| P61433800515 | 60190.94 | 1421 | |||
| P61433800601 | 60191.06 | 3231 |
| Exposure ID | Start MJD | Exposure Time(s) | QPO Frequency (Hz) | RMS | Q-value |
|---|---|---|---|---|---|
| P61433800602 | 60191.20 | 2191 | |||
| P61433800603 | 60191.34 | 2153 | |||
| P61433800604 | 60191.47 | 1712 | |||
| P61433800605 | 60191.60 | 1463 | |||
| P61433800606 | 60191.73 | 538.7 | |||
| P61433800607 | 60191.87 | 359.1 | |||
| P61433800608 | 60192.00 | 2394 | |||
| P61433800611 | 60192.39 | 1855 | |||
| P61433800612 | 60192.53 | 1736 | |||
| P61433800613 | 60192.66 | 1666 | |||
| P61433800615 | 60192.92 | 1377 | |||
| P61433800616 | 60193.06 | 2734 | |||
| P61433800617 | 60193.19 | 1436 | |||
| P61433800618 | 60193.32 | 1774 | |||
| P61433800801 | 60194.03 | 2753 | |||
| P61433800802 | 60194.17 | 1878 | |||
| P61433800803 | 60194.31 | 1496 | |||
| P61433800804 | 60194.44 | 1496 | |||
| P61433800805 | 60194.71 | 1407 | |||
| P61433800807 | 60194.84 | 335.2 | |||
| P61433800808 | 60194.97 | 2392 | |||
| P61433800901 | 60195.09 | 1975 | |||
| P61433800902 | 60195.23 | 1609 | |||
| P61433800903 | 60195.37 | 1541 | |||
| P61433800904 | 60195.50 | 1458 | |||
| P61433800905 | 60195.63 | 538.7 | |||
| P61433800906 | 60195.76 | 114.7 | |||
| P61433800907 | 60195.90 | 2748 | |||
| P61433801001 | 60196.08 | 1938 | |||
| P61433801002 | 60196.22 | 1652 | |||
| P61433801003 | 60196.36 | 1604 | |||
| P61433801004 | 60196.49 | 1255 | |||
| P61433801005 | 60196.62 | 299.2 | |||
| P61433801006 | 60196.76 | 167.6 | |||
| P61433801007 | 60196.89 | 2936 | |||
| P61433801101 | 60197.07 | 1842 | |||
| P61433801102 | 60197.21 | 1496 | |||
| P61433801103 | 60197.35 | 1768 | |||
| P61433801104 | 60197.48 | 1287 | |||
| P61433801105 | 60197.62 | 239.4 | |||
| P61433801106 | 60197.75 | 239.4 | |||
| P61433801107 | 60197.88 | 2022 |

3. Data Analysis and Results
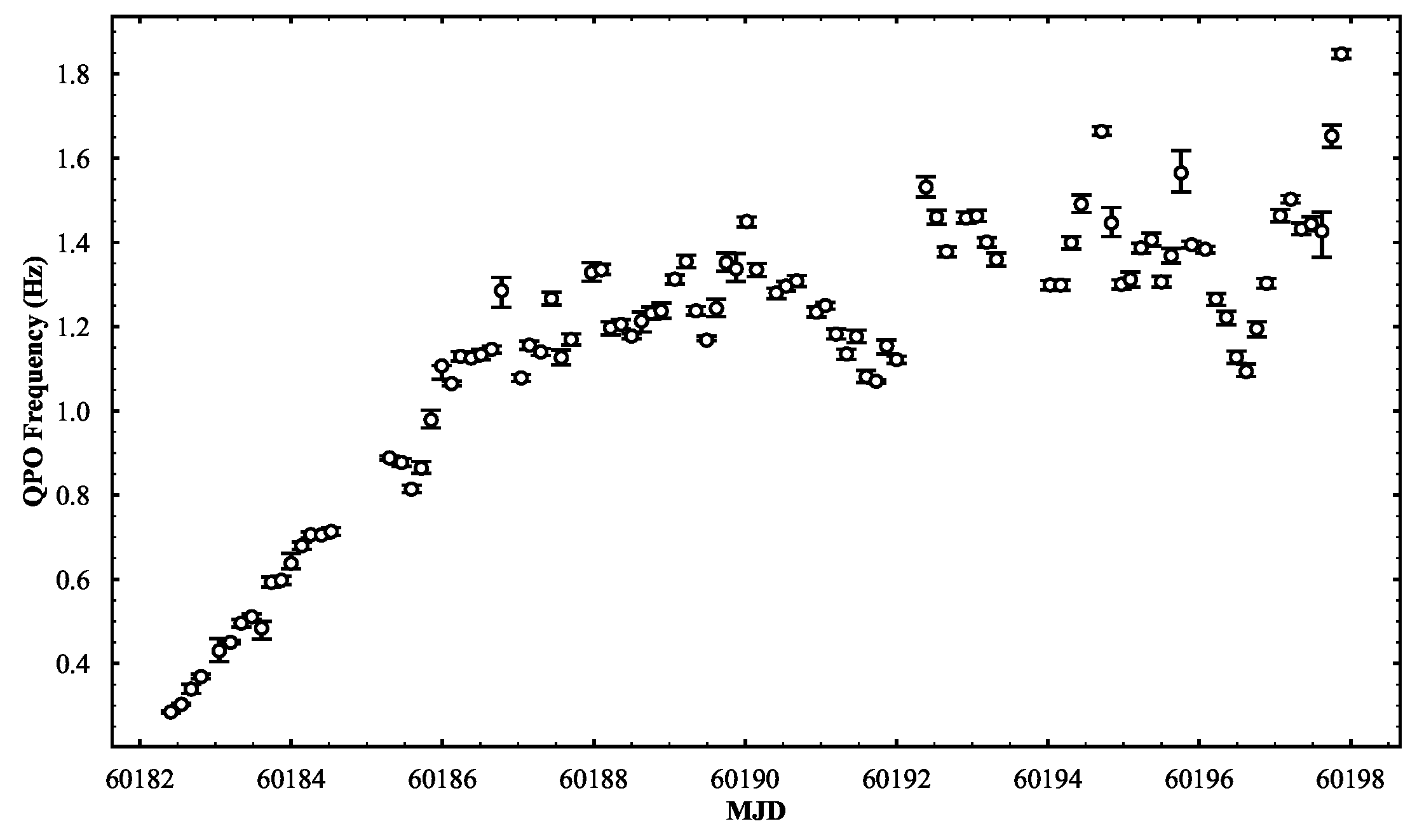

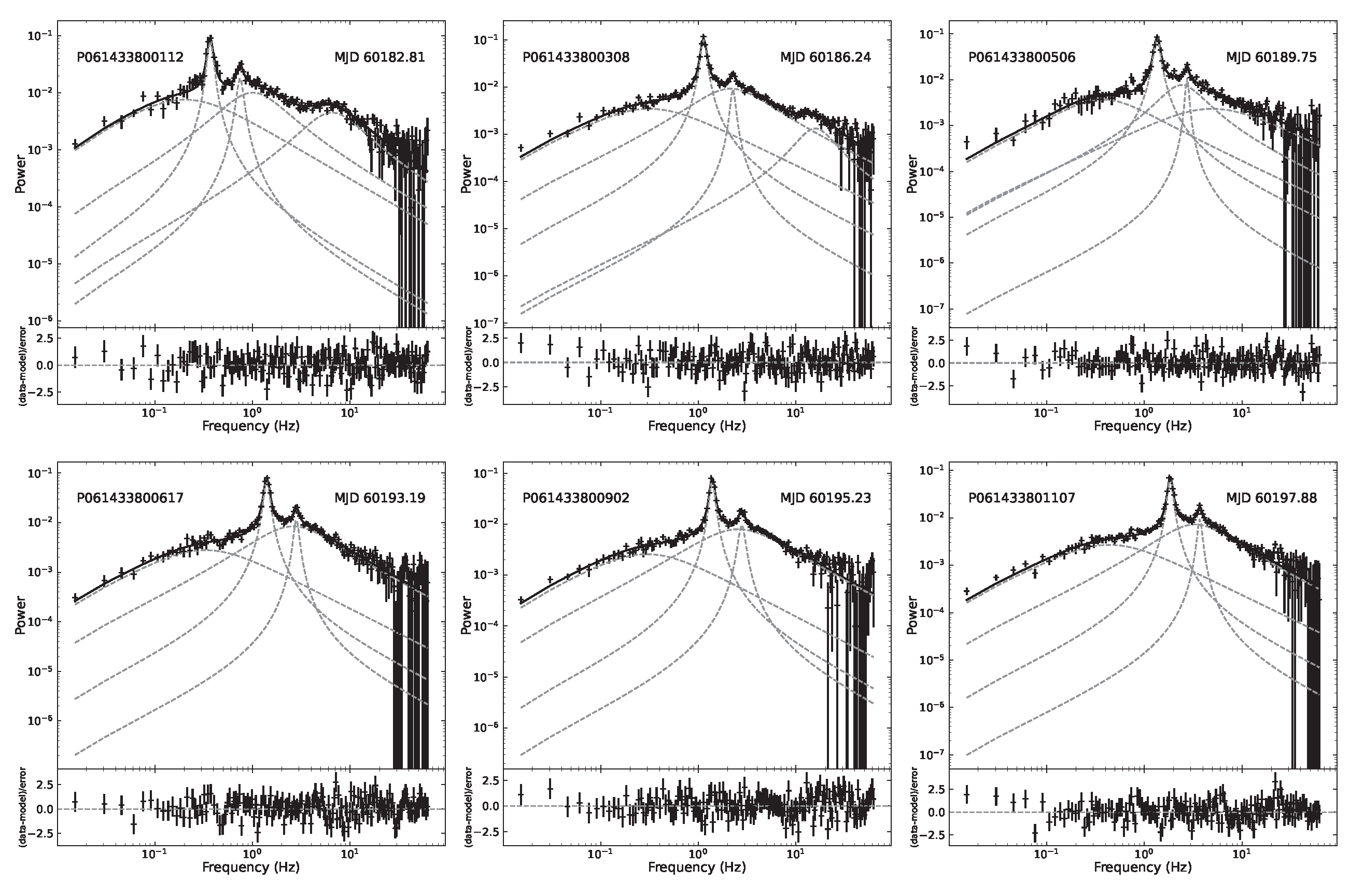
4. Discussion and Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shakura, N. I.; Sunyaev, R. A. . Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337. [Google Scholar]
- Peng, J.-Q.; Zhang, S.; Shui, Q.-C.; Zhang, S.-N.; Kong, L.-D.; Chen, Y.-P.; et al. . NICER, NuSTAR, and Insight-HXMT views to the newly discovered black hole X-ray binary Swift J1727.8-1613. Astrophys. J. Lett. 2024, 960, 17. [Google Scholar] [CrossRef]
- Lasota, J.P. . The disc instability model of dwarf novae and low-mass X-ray binary transients. New Astron. Rev. 2001, 45, 449. [Google Scholar] [CrossRef]
- Belloni, T.; Homan, J.; Casella, P.; van der Klis, M.; Nespoli, E.; Lewin, W.H.G.; et al. . The evolution of the timing properties of the black-hole transient GX 339–4 during its 2002/2003 outburst. Astron. Astrophys. 2005, 440, 207. [Google Scholar] [CrossRef]
- Motta, S.; Belloni, T.; Homan, J. . The evolution of the high-energy cut-off in the X-ray spectrum of GX 339–4 across a hard-to-soft transition. Mon. Not. R. Astron. Soc. 2009, 400, 1603. [Google Scholar] [CrossRef]
- Reig, P.; Kylafis, N. . The origin of the hard X-ray tail in neutron-star X-ray binaries. Astron. Astrophys. 2016, 591, 24. [Google Scholar] [CrossRef]
- McClintock, J.E.; Remillard, R.A. Black hole binaries. In Compact stellar X-ray sources; Lewin, W.H.G.; van der Klis, M., Eds.; Cambridge University Press: Cambridge, UK, 2006, 39, 157.
- Homan, J.; Belloni, T. . The Evolution of Black Hole States. Astrophys. Space Sci. 2005, 300, 107. [Google Scholar] [CrossRef]
- Peng, J.-Q.; Zhang, S.; Shui, Q.-C.; Chen, Y.-P.; Zhang, S.-N.; Kong, L.-D.; et al. . Insight-HXMT, NICER, and NuSTAR Views to the Newly Discovered Black Hole X-Ray Binary Swift J151857.0 –572147. Astrophys. J. Lett. 2024, 973, 7. [Google Scholar] [CrossRef]
- Ingram, A.R.; Motta, S.E. . A review of quasi-periodic oscillations from black hole X-ray binaries: Observation and theory. New Astron. Rev. 2019, 85, 101524. [Google Scholar] [CrossRef]
- Ingram, A.; Done, C.; Fragile, P.C. . Low-frequency quasi-periodic oscillations spectra and Lense-Thirring precession. Mon. Not. R. Astron. Soc. 2009, 397, 101. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, L.; Tao, L.; Bu, Q.C.; Qu, J.L.; Zhang, S.N.; et al. . A Detailed View of Low-frequency Quasi-periodic Oscillation in the Broadband 0.2-200 keV with Insight-HXMT and NICER. Astrophys. J. 2023, 948, 116. [Google Scholar] [CrossRef]
- Belloni, T.M. States and Transitions in Black Hole Binaries. In Lecture Notes in Physics, Berlin Springer Verlag; Belloni, T., Ed.; Springer: Berlin, Germany, 2010, 794, 53.
- Wijnands, R.; Homan, J.; van der Klis, M. . The Complex Phase-Lag Behavior of the 3-12 Hz Quasi-Periodic Oscillations during the Very High State of XTE J1550-564. Astrophys. J. Lett. 1999, 526, 33. [Google Scholar] [CrossRef]
- Casella, P.; Belloni, T.; Stella, L. . The ABC of Low-Frequency Quasi-periodic Oscillations in Black Hole Candidates: Analogies with Z Sources. Astrophys. J. 2005, 629, 403. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. . Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. Lett. 1998, 492, 59. [Google Scholar] [CrossRef]
- Tagger, M.; Pellat, R. . An accretion-ejection instability in magnetized disks. Astron. Astrophys. 1999, 349, 1003. [Google Scholar]
- Shui, Q.C.; Zhang, S.; Chen, Y.P.; Zhang, S.N.; Kong, L.D.; Wang, P.J.; et al. . Tracing the Accretion Geometry of H1743-322 with Type C Quasiperiodic Oscillations in Multiple Outbursts. Astrophys. J. 2023, 943, 165. [Google Scholar] [CrossRef]
- Mata Sánchez, D.; Muñoz-Darias, T.; Armas Padilla, M.; Casares, J.; Torres, M.A.P. . Evidence for inflows and outflows in the nearby black hole transient Swift J1727.8-162. Astron. Astrophys. 2024, 682, 1. [Google Scholar] [CrossRef]
- Svoboda, J.; Dovčiak, M.; Steiner, J.F.; Kaaret, P.; Podgorný, J.; Poutanen, J.; et al. . Dramatic Drop in the X-Ray Polarization of Swift J1727.8–1613 in the Soft Spectral State. Astrophys. J. Lett. 2024, 966, 35. [Google Scholar] [CrossRef]
- Shui, Q.-C.; Zhang, S.; Peng, J.-Q.; Zhang, S.-N.; Chen, Y.-P.; Ji, L.; et al. . Phase-resolved Spectroscopy of Low-frequency Quasiperiodic Oscillations from the Newly Discovered Black Hole X-Ray Binary Swift J1727.8-1613. Astrophys. J. 2024, 973, 59. [Google Scholar] [CrossRef]
- Yu, W.; Bu, Q.-C.; Zhang, S.-N.; Liu, H.-X.; Zhang, L.; Ducci, L.; et al. . Timing analysis of the newly discovered black hole candidate Swift J1727.8-1613 with Insight-HXMT. Mon. Not. R. Astron. Soc. 2024, 529, 4624. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, W. . Energy Dependence of the Low-frequency Quasiperiodic Oscillations in Swift J1727.8 –1613. Astrophys. J. 2024, 968, 106. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, F.J.; Zhang, S.N.; Li, T.P. Introduction to the hard x-ray modulation telescope. In Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray; Takahashi, T.; den Herder, J.-W.A.; Bautz, M., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 2014, 9144, 914421.
- Zhang, S.; Zhang, S.N.; Lu, F.J.; Li, T.P.; Song, L.M.; Xu, Y.P.; et al. The insight-HXMT mission and its recent progresses. In Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray; den Herder, J.-W.A.; Nikzad, S.; Nakazawa, K., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 2018, 10699, 106991U.
- Zhang, S.-N.; Li, T.-P.; Lu, F.-J.; Song, L.-M.; Xu, Y.-P.; Liu, C.-Z.; et al. Overview to the Hard X-ray Modulation Telescope (Insight-HXMT) Satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249502. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, W.-W.; Li, W.; Wang, J.; Xu, Y.-P.; Lu, F.-J.; et al. The Low Energy X-ray telescope (LE) onboard the Insight-HXMT astronomy satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249505. [Google Scholar] [CrossRef]
- Cao, X.; Jiang, W.; Meng, B.; Zhang, W.; Luo, T.; Yang, S.; et al. . The Medium Energy X-ray telescope (ME) onboard the Insight-HXMT astronomy satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249504. [Google Scholar] [CrossRef]
- Liu, C.-Z.; Zhang, Y.-F.; Li, X.-F.; Lu, X.-F.; Chang, Z.; Li, Z.-W.; et al. The High Energy X-ray telescope (HE) onboard the Insight-HXMT astronomy satellite. Sci. China Phys. Mech. Astron. 2020, 63, 249503. [Google Scholar] [CrossRef]
- Chatterjee, K.; Mondal, S.; Singh, C. B.; Sugizaki, M. . Insight-HXMT View of the Black Hole Candidate Swift J1727.8–1613 during Its Outburst in 2023. Astrophys. J. 2024, 977, 148. [Google Scholar] [CrossRef]
- Long, Q. C.; Dong, A. J.; Zhi, Q. J.; Shang, L. H. , Revisiting the Fundamental Planes of Black Hole Activity for Strong Jet Sources. Astrophys. J., 2025, 980, 187. [Google Scholar] [CrossRef]
- Dong, A. J.; Wu, Q. and Cao, X. F., A New Fundamental Plane for Radiatively Efficient Black-hole Sources, Astrophys. J. lett., 2014, 787, 20. [Google Scholar]
- Dong, A. J. and Liu, C. ; Ge, K.; Liu, X. and Zhi, Q. J. and You, Z. Y., A study on the hysteresis effect and spectral evolution in the mini-outbursts of balck hole X-ray binary XTE J1550-564. Front. Astron. Space Sci, 2021, 8, 37. [Google Scholar]
- Ingram, A.; van der Klis, M.; Middleton, M.; Done, C.; Altamirano, D.; Heil, L.; et al. A quasi-periodic modulation of the iron line centroid energy in the black hole binary H1743-322. Mon. Not. R. Astron. Soc. 2016, 461, 1967–1980. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Méndez, M.; Chen, L.; Qu, J.; Altamirano, D.; Belloni, T. . The Evolution of the Phase Lags Associated with the Type-C Quasi-periodic Oscillation in GX 339-4 during the 2006/2007 Outburst. Astrophys. J. 2017, 845, 143. [Google Scholar] [CrossRef]
- Huang, Y.; Qu, J. L.; Zhang, S. N.; Bu, Q. C.; Chen, Y. P.; Tao, L.; et al. . INSIGHT-HXMT Observations of the New Black Hole Candidate MAXI J1535-571: Timing Analysis. Astrophys. J. 2018, 866, 122. [Google Scholar] [CrossRef]
- Kubota, A.; Done, C.; Tsurumi, K.; Mizukawa, R. . Disc corona radii and QPO frequencies in black hole binaries: testing Lense–Thirring precession origin. Mon. Not. R. Astron. Soc. 2024, 528, 1668. [Google Scholar] [CrossRef]
- Ma, W. Q.; Gao, Z. F.; Li, B. P.; Niu, C. H.; Yao, J. M.; Wang, F. Y. . Reinvestigation of Fast Radio Burst Host Galaxy and Event Rate Density. Astrophys. J. 2025, 981, 24. [Google Scholar] [CrossRef]
- Wen, Z. G.; Yuan, J. P.; Wang, N.; Li, D.; Chen, J. L.; and Wang, P.; et al. . A Single-pulse Study of the Subpulse Drifter PSR J1631+1252 Discovered at FAST. Astrophys. J. 2022, 929, 71. [Google Scholar] [CrossRef]
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





