1. Introduction
Floodplains are defined as the flat area (slope less than 3 %) surrounding the active channel of a river, which are flooded during high discharge events, every one or two years [
1]. Within these floodplains are deltas and valleys [
2,
3]. These are areas conducive to economic development, agriculture, and community settlement [
4]. In recent decades, growth in population in floodplains [
5], together with more extreme and intense rainfall events caused by phenomena such as EL NIÑO/LA NIÑA [
6], have increased the risk of flooding in many of these places around the world [
5]. Faced with this scenario, it is necessary to implement risk reduction strategies, which require good quality geo-spatial inputs and the use of modelling tools that generate useful information for decision-making [
6].
One of the most important inputs for land use planning and risk management applications is the altimetrically reliable Digital Elevation Model (DEM) [
7], particularly challenging in flat terrain where low precision global models cannot represent the terrain configuration in enough detail [
8]. Applications like flood zone mapping, river delineation, and definition of restoration zones rely heavily on accurate DEMs due to their direct impact on model reliability [
9,
10].
Currently, DEMs are mainly created by remote sensing techniques, due to the ability to map large areas with low personnel requirements and at lower cost [
11]. Among the remote sensing techniques are photogrammetry, Interferometric Synthetic Aperture Radar (In-SAR), and Light Detection and Ranging (LIDAR) [
7]. These types of elevation models have vertical errors, with LIDAR having the lowest vertical errors (generally <1 m) [
7] while models derived from In-SAR techniques, such as SRTM, ASTER, FABDEM, and ALOS, have errors ranging from 1.12 m to 10 m [
12,
13,
14,
15]
Additionally, these models contain attributes from different objects present in the terrain, both natural (vegetation) and man-made (buildings, communication towers, among others), that need to be removed to have the bare terrain. This is why multiple filtering and classification techniques have been developed and applied to extract terrain points to generate the corrected DEM [
16,
17,
18]. Despite these efforts, none of these techniques is 100% effective in removing all objects that do not belong to the terrain, which makes further editing necessary to generate a DEM suitable for the application of modeling tools [
19]. Additionally, global models do not have sufficient spatial resolution to be able to represent small terrain structures, such as connecting channels between the main river and floodplains, roads and levees [
20], which are necessary for flood mapping [
21].
Different techniques have been developed and applied to perform corrections to global DEMs and improve their accuracy, among the most commonly used techniques for DEM correction are: data fusion (hybridization) [
22], masking of water bodies [
23], gap filling [
24], channel burning [
25] and vegetation removal [
8,
26]. More recently, the application of machine learning techniques to perform DEM enhancement has been explored [
7,
15,
27,
28].
The methodologies presented above have proven effective in improving the vertical accuracy of global DEMs. However, there are certain limitations of these methodologies to achieve the levels of DEM accuracy and detail required for different land use planning and risk management applications. Among these limitations, a common one is the scale of application of these methodologies; most have been applied at a regional or quasi-global scale, and the field information included in the methodological flow is not enough, which does not allow for an optimal level of detail at a local scale of the resulting product, taking into account that land-use planning and risk management exercises are done at local scales, this is a very important aspect.
Based on the above, this article proposes a methodology that combines satellite and remote sensing with surveyed field information to improve the vertical accuracy of digital elevation models in flat areas with limited information. The Rancheria river delta (La Guajira, Colombia) will be used as a case of application of the proposed methodology.
2. Materials and Methods
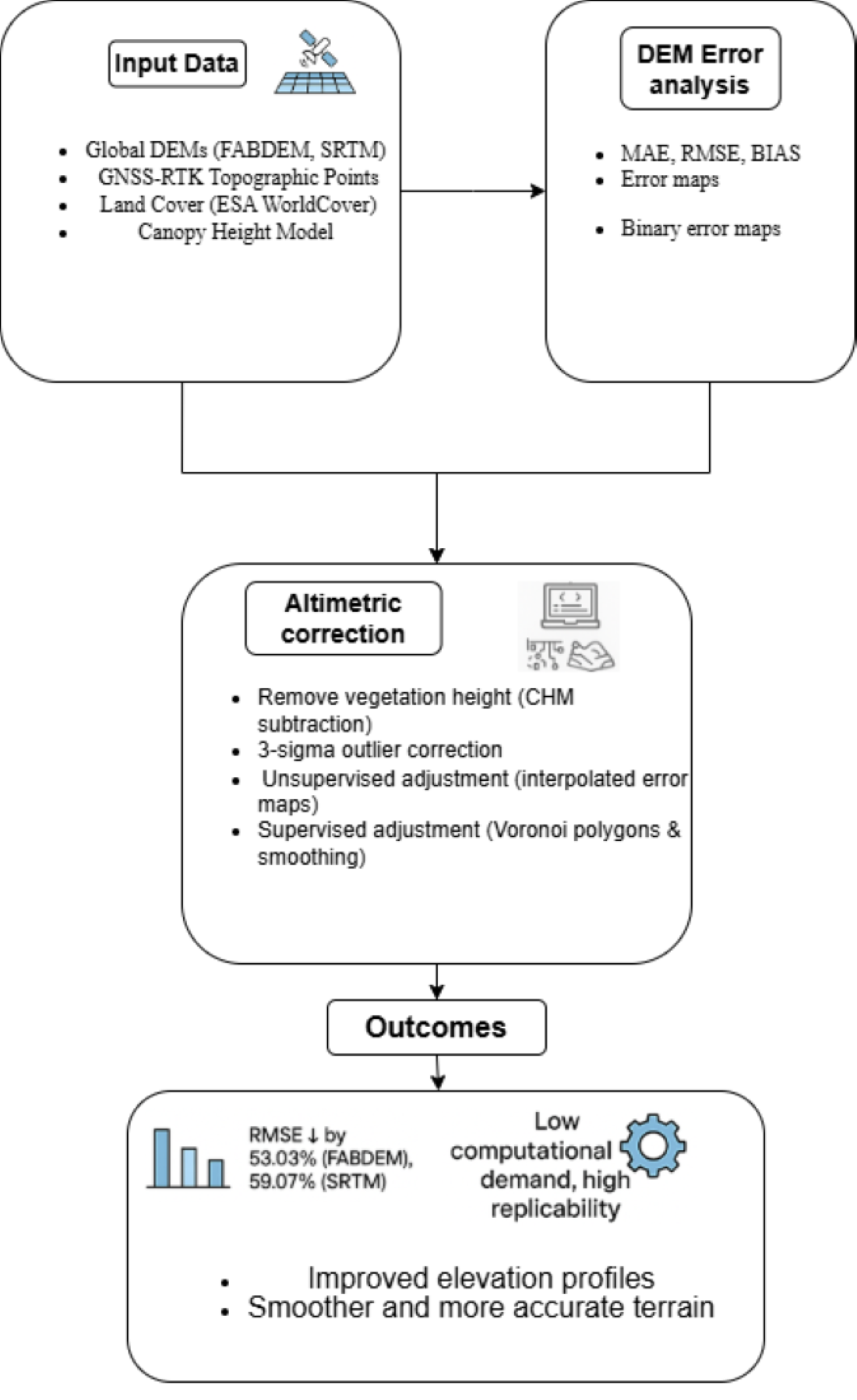
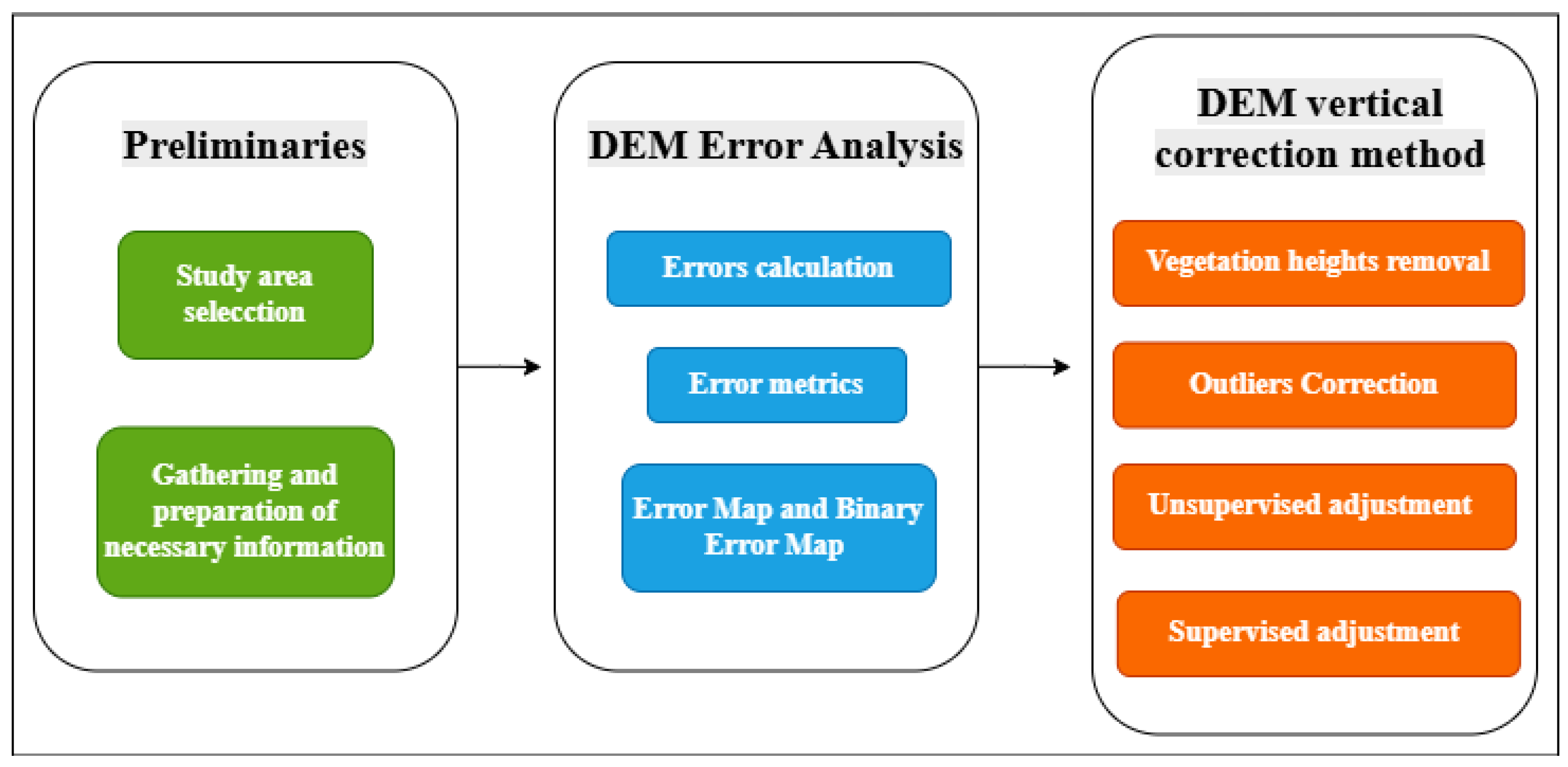
The correction method proposes the use of information derived from remote sensors (land cover, tree height) combined with information acquired in the field (topographic points) to perform the altimetry correction of global digital elevation models. This methodology is proposed in a sequential flow, starting with a preliminary stage in which the study area is selected and all the necessary information is collected and prepared to perform the DEM correction; then an error analysis of the DEMs is performed; then the correction is performed. A summary of the stages of the method is presented in
Figure 1, and each of these stages will be developed in the following sections.
2.1. Preliminaries
2.1.1. Criteria for Study Area Selection
The study area should be one of the plain areas, such as alluvial plains, valleys, deltas, which suffer from periodic flooding due to the overflow of an active river channel, defined by [
1,
2], where terrain variations are less than one meter in several thousand meters of extension, slopes less than 3% [
29]. These areas must have the presence of an active river that causes periodic flooding.
2.1.2. Gathering and Preparation of Input Data
The following are the minimum information requirements for the application of the proposed methodology:
Digital Elevation Models (DEM) at least medium resolution (between 10 and 30 m) are required, such as global models (SRTM, ASTER, ALOS, FABDEM- COPERNICUS);
Land Cover information is necessary to identify the presence of structures such as houses, buildings, roads, vegetation zones, and water bodies in the study area;
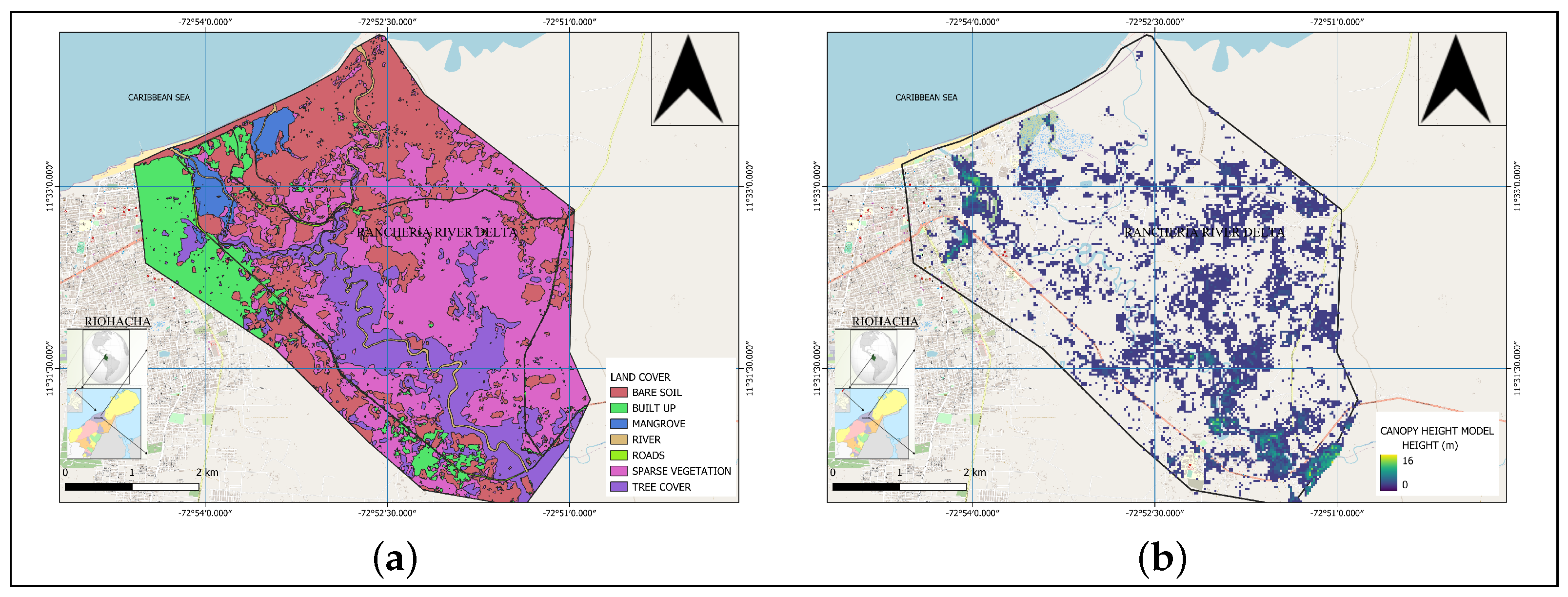
Tree height information (Canopy Height Model) to perform altimetric correction of global models, due to the fact that these models, being surface models, take into account the heights of elements on the ground, such as vegetation and buildings. Several global CHM products can be used to correct tree elevations in global [
30,
31,
32]
Thematic vector information such as roads, streets, buildings and rivers is very important to identify key terrain elements, this information is available through
OpenStreetMap;
-
Topographic information is required for both the flood plains and the riverbed, collected in the field with precision equipment such as GNSS-RTK or Total Station, with which an accuracy (<10 cm) can be obtained, to adjust and validate the elevation models. Requirements of the topographic survey to be carried out are detailed below.
Topographic survey should collect as much information and detail of the configuration and elements of the study area as possible. The survey should be well planned, the method and equipment for the survey should be chosen, and the equipment should be tested for performance and accuracy. Perform an analysis of the land cover in the study area (classified image) to locate the terrain elements that are important for the accuracy of the terrain models and for land use planning and modeling purposes, such as: vegetation, infrastructure, roads, dams, rivers, canals, etc. This is to plan the survey campaigns and to be able to represent these terrain elements.
In the case of GNSS-RTK surveys, the base point must be identified, which must be a point of known coordinates, such as those belonging to the national geodetic or leveling networks. The points close to the study area should be identified, and the point where the base station will be located should be chosen, taking into account the reception conditions. The base station should be located in an area preferably higher than the area where the points are going to be surveyed, to improve the reception of the equipment and its communication with the ROVER. The base station should not be located near tall trees or between buildings, and the base should not be located under high-voltage power transmission lines or very close to radio antennas, since these generate waves that can interfere with the communication radius between the base and the ROVER. Site safety considerations must also be considered when selecting the base station.
2.2. DEM Error Analysis
2.2.1. Error Calculation
The selected DEMs must be evaluated to determine their fit in respect to the topography points surveyed. It begins with the extraction of elevation from the DEM to the point location. Then points must be divided into a data set to evaluate the model errors and make the adjustment, and another set for validation of the performance of the applied correction method [
7,
27]. There is no unique relation to divide the evaluation and validation data of the elevation models; different distributions of the quantities must be tested, depending on the amount of data available, evaluating the results obtained to be able to determine the most optimal in each case. Finally, the differences between the surveyed points and the elevation models must be obtained.
2.2.2. Error metrics
Error metrics are used to evaluate the performance or fit of the models with respect to the observed data. To evaluate the fit of DEMs, the following metrics are commonly used: MAE (Mean Absolute Error) [
15,
33] (equation
1), RMSE [
7,
26,
27,
28] (equation
2), and BIAS (equation
3), this measures the average tendency of the model data to overestimate or underestimate the true value (field data) [
27].
where:
: Elevation of the surveyed point;
: Elevation of the point extracted from the DEM;
n: Number of points evaluated.
2.2.3. Error Map
Metrics can give an averaged measure of the model’s fit to the field data; however, metrics cannot determine the spatial distribution of these errors, which is important when applying DEM correction procedures. In order to appreciate the spatial distribution of the errors, error maps must be generated. The error map is the surface generated from the errors between the terrain points and the DEM. They are made by interpolating the differences to create a grid of data; this grid is converted to a raster format (GeoTiff) to be comparable with the DEMs. Several spatial interpolation methods must be tested to generate the error maps, such as IDW, Kriging, Natural Neighbor, Nearest Neighbor, among others, which are available in different GIS tools [
34,
35].
2.2.4. Binary Error Map
Because negative and positive differences can occur, it is necessary to be able to clearly identify in which areas the DEM is above and in which areas it is below the points. To have more clarity on this behavior, the error maps should be classified to generate a binary map of 0 and 1, in which 0 indicates negative differences, i.e., the DEM pixel value is greater than the terrain points, and 1 indicates positive differences, where the terrain point value is greater than the DEM pixel value.
2.3. DEM Vertical Correction Method
Once the models have been evaluated, they are corrected. The DEM altimetry correction process is divided into 4 steps, which will be presented below.
Vegetation heights removal. This step consists of subtracting from the DEM the vegetation heights of the CHM. This operation is done by means of a raster calculator tool, subtracting the CHM from the DEM. In this step, a DEM with removed vegetation heights is obtained.
Outliers Correction.This process is done to eliminate outliers in the distribution of elevations from the DEMs. This correction is done by applying the
3-sigma criterion. This criterion states that all values of a data distribution must be located between the limits:
average - 3 standard deviations to
average + 3 standard deviations, and any value located outside these limits is considered an
outlier [
36]. This criterion has been applied in multiple DEM correction cases [
37,
38,
39]. In the present methodology, this criterion is applied to correct outliers in DEMs after performing the subtraction of vegetation heights, using an algorithm that goes through the DEM pixel by pixel comparing the value with the
3-sigma calculated for that DEM, where it finds a pixel with a higher value, that value is replaced by the
3-sigma value;
-
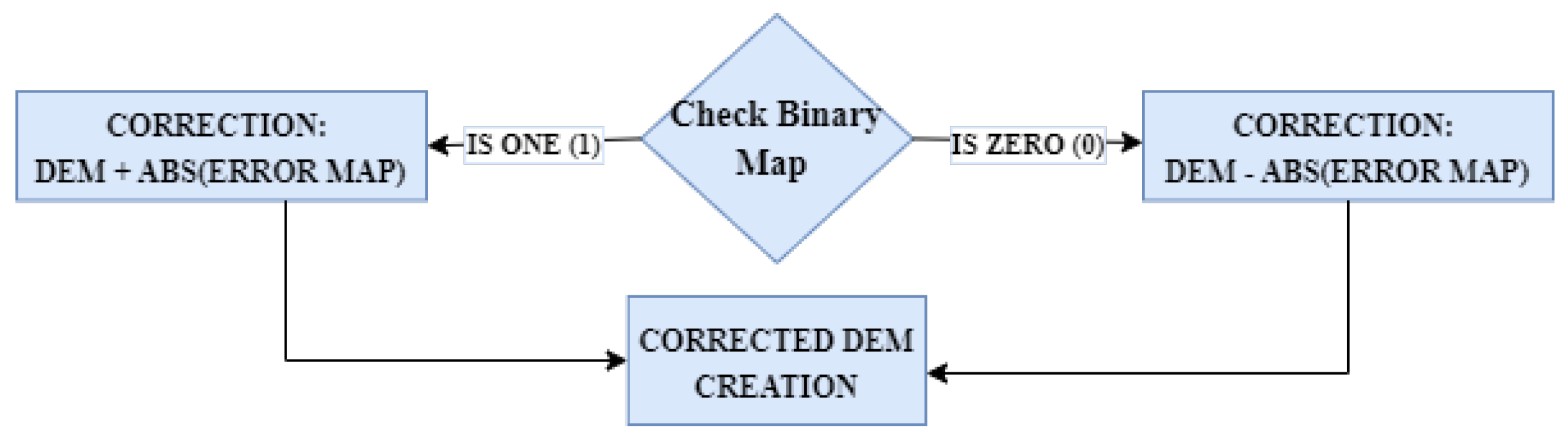
Unsupervised adjustment. With the DEM resulting from the previous step, the adjustment of the DEM with the surveyed terrain points is performed. This stage is called unsupervised because it is performed by error maps generated with different interpolation methods. In which more of the parameters that can be adjusted of the interpolation method, there is no total control of the result that these interpolations will generate, but they constitute a good approximation of the surface adjustment.
The process begins evaluating the binary map, if it is 0 the correction is to subtract from the DEM the absolute value of the error map at the corresponding pixel, if it is 1 the correction is to add the absolute value of the error map to the DEM. In each case, a raster grid is generated containing the adjusted value in the corresponding pixels and the other pixels are left without values. Then the two generated raster are joined to create the final DEM. This process can be seen schematically in
Figure 2;
Supervised adjustment. This step becomes necessary due to the errors that may be left over from the interpolation process performed to generate the error maps, and that consequently propagate to the DEM adjustment. The process starts with the creation of Voronoi polygons [
40,
41] from the terrain points. Once generated, the polygons are sorted and grouped by elevation ranges to create homogeneous elevation zones. Then, each polygon is assigned a value that is going to establish an elevation limit for each zone. These polygons are then rasterized, taking the established elevation limit value. Taking the raster of the Voronoi polygons as a mask, the DEM is traversed with a moving window of
3x3 (9 pixels), this amount is taken to have enough information to recalculate the pixels that will be used in the DEM. The value of each DEM pixel is compared with the value of the polygon raster, if a DEM pixel (i,j) is found to exceed the limit value established by the mask, that pixel is eliminated and recalculated with the average of the 8 surrounding pixels (Equation
4), this process is done iteratively until no more values are found within the DEM that exceed the corresponding elevation limit in each zone indicated by the polygon mask.
3. Results
3.1. Preliminaries
3.1.1. Study Area
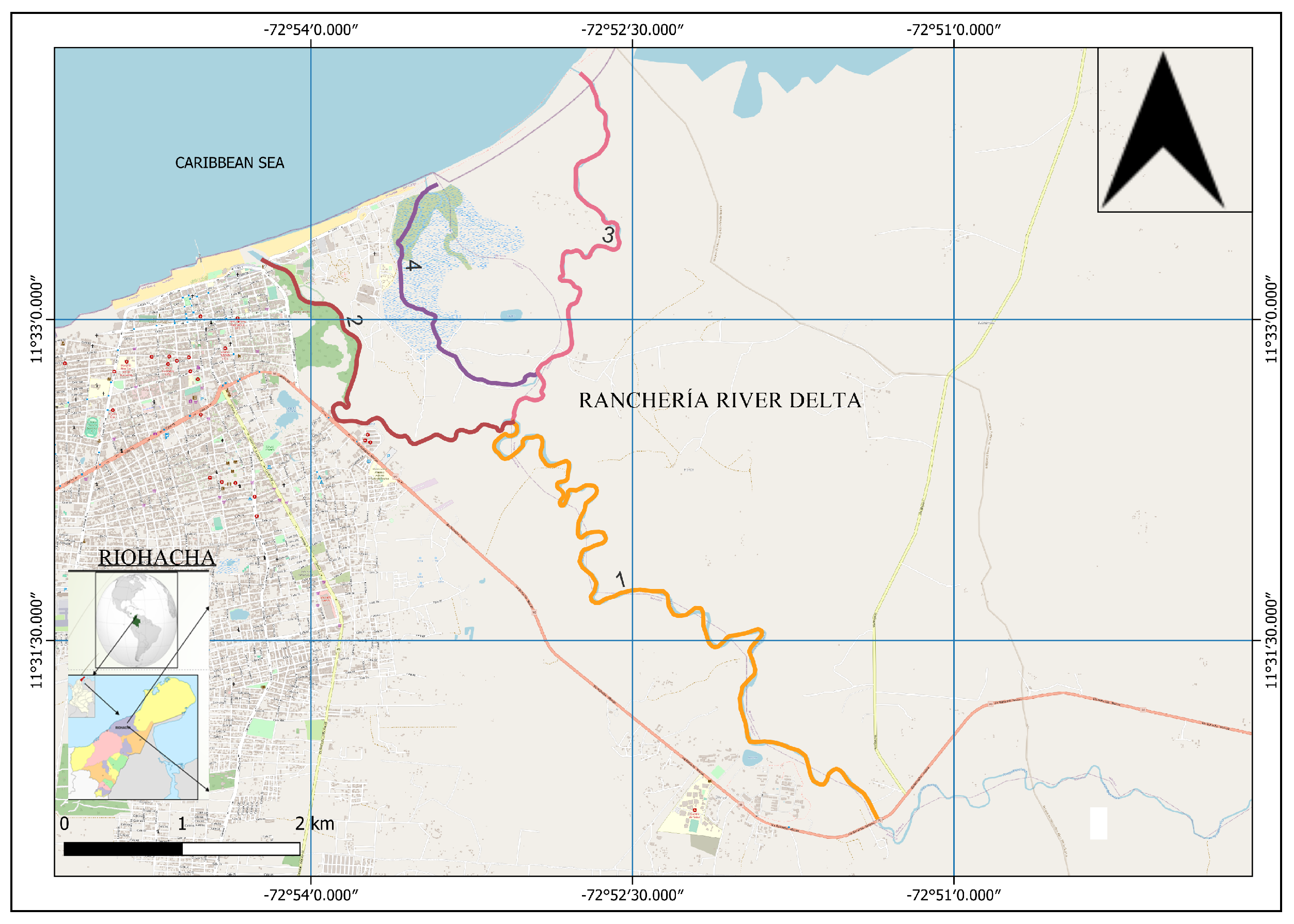
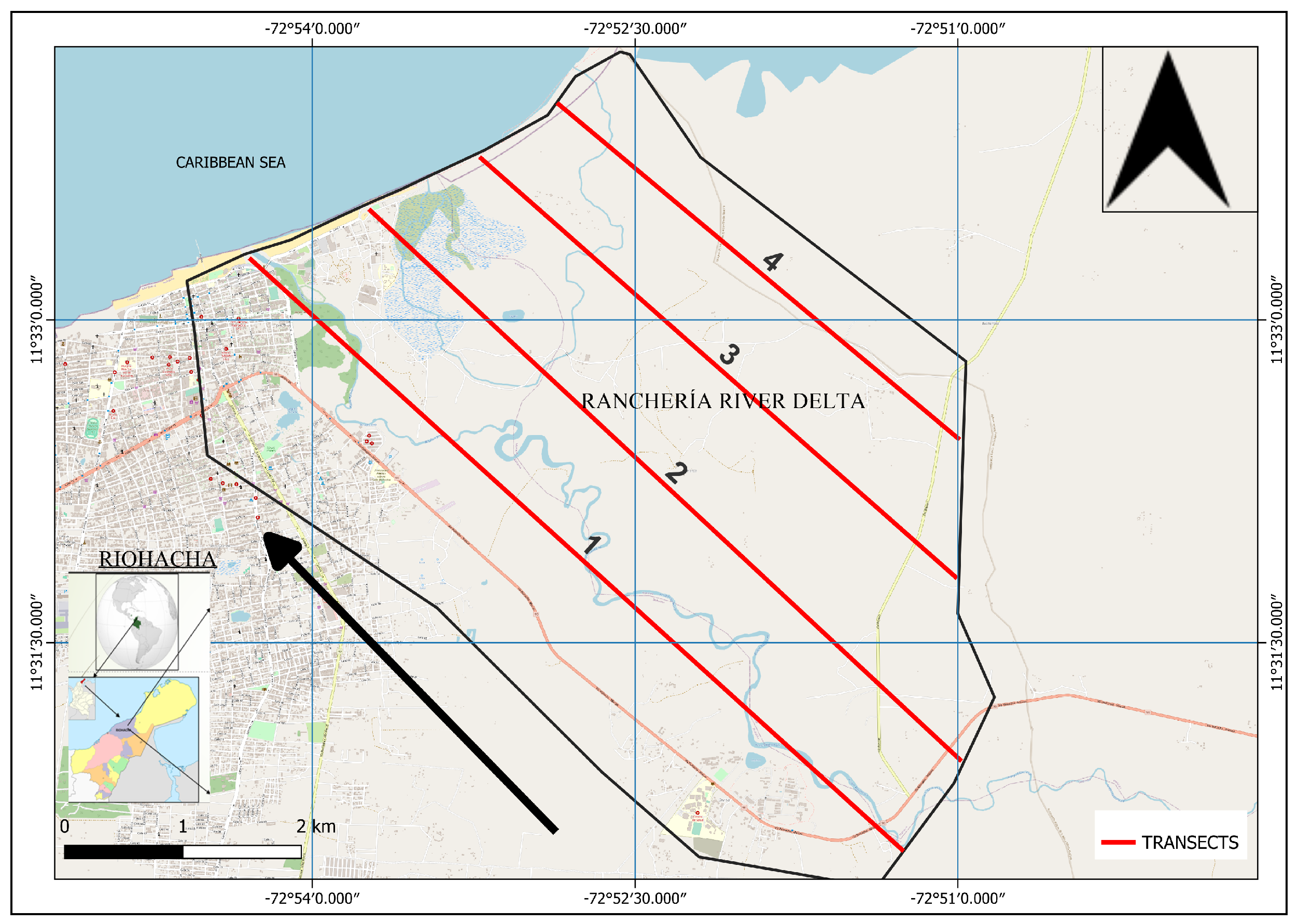
The chosen study area corresponds to the Rancheria river delta, in the city of Riohacha, La Guajira, Colombia. The Rancheria river delta is located northeast of the city.
Figure 3 shows the general location, the layout of the main channel of the Rancheria river (1) that bifurcates close to the coastline, giving rise to two branches that form the delta, El Riito (2) and Santa Rita (3), the latter bifurcating again to give rise to the Calancala branch (4) [
42].
3.1.2. Information Gathered and Processed
Information used for the methodology is presented below.
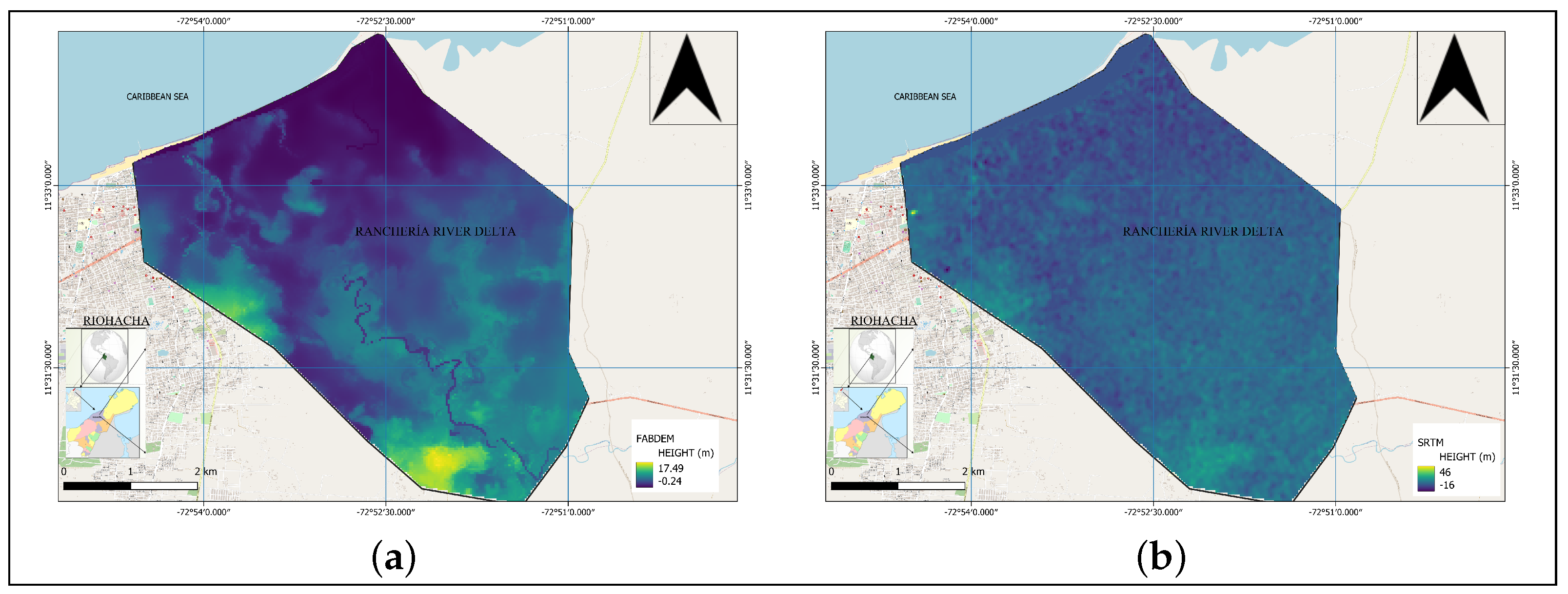
Digital Elevation Models (DEM’s), SRTM
Figure 4 b (Shuttle Radar Topographic Mission), which is the most widely used global distribution model for hydrodynamic modeling exercises [
37,
43], and the FABDEM (Forest And Building Removed DEM) [
15], which has been gaining great popularity for application in hydrodynamic modeling exercises, because it has a significant improvement in vertical accuracy, concerning global models of similar resolution such as SRTM, ASTER, ALOS [
15,
44], were used.
Figure 4 shows the cropping of the DEMs in the study area;
The European Space Agency (ESA)
ESA WorldCover 2021 v200 [
45] was used as a basis to generate a classified map of the study area. The land cover map can be seen in
Figure 5 a;
-
The field topographic information was surveyed in two campaigns carried out in the study area, one in September 2022 and the other in March 2023. The topographic points were surveyed with GNSS-RTK in dynamic mode, with
TOPCON Hyper V equipment, which has a horizontal accuracy of 0.005 m and vertical accuracy of 0.01 m [
46].
For the location of the base station, the database with the points belonging to the national active and passive leveling network of Colombia of the Instituto Geográfico Agustín Codazzi (IGAC). This points can be viewed through the data portal
Colombia en Mapas. The points near the study area were located, and the point belonging to the MAGNA ECO ACTIVE NETWORK (11°30’47.58123"N -72°52’10.95231"W) located at University of La Guajira, this point was chosen because it is located on the roof of a building, which offers an advantage in terms of the signal range of the base equipment and its link with the
ROVER, also at this point there were security conditions to leave the equipment without the need for a person in charge of its security, while the survey of the points was being carried out.
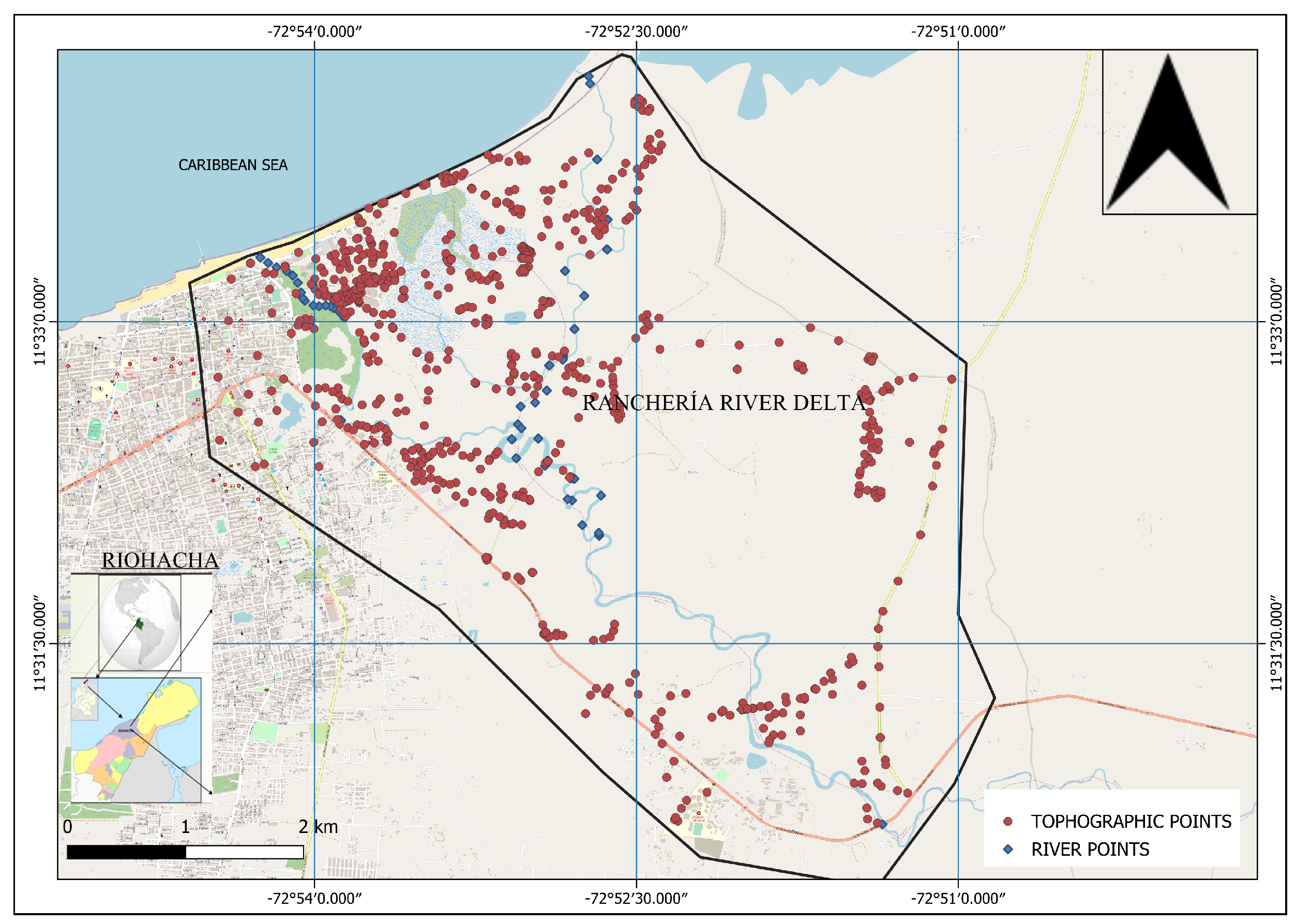
The location of the points was determined in the planning of the survey, where the land cover identified in the area was taken into account, and the aim was to have points in all the identified zones. A series of points were located on the classified map, covering all land cover categories, and that these were equidistant from each other. However, in the execution of the survey it was not always possible to follow what was planned, so the location was quasi-random due to accessibility limitations due to flooded areas, public order situations in the territory, and vegetation conditions, which limited the reception of the GNSS-RTK equipment. The survey was done by traveling through the study area, depending on the accessibility conditions, in some areas by vehicle (motorcycle) and in others by walking. Points were surveyed in areas of interest (i.e. plains, near areas of thick vegetation, embankments, roads, housing areas, elevated areas), trying to capture with the best possible detail the terrain configuration. The ROVER equipment was constantly checked to ensure that it was operating under optimal conditions of satellite reception and connection with the base station.
Figure 6 shows the points surveyed in the study area, which totaled 1016, including terrain points, elevation points of terrain structures, and river points.
3.2. DEM error spatial analysis
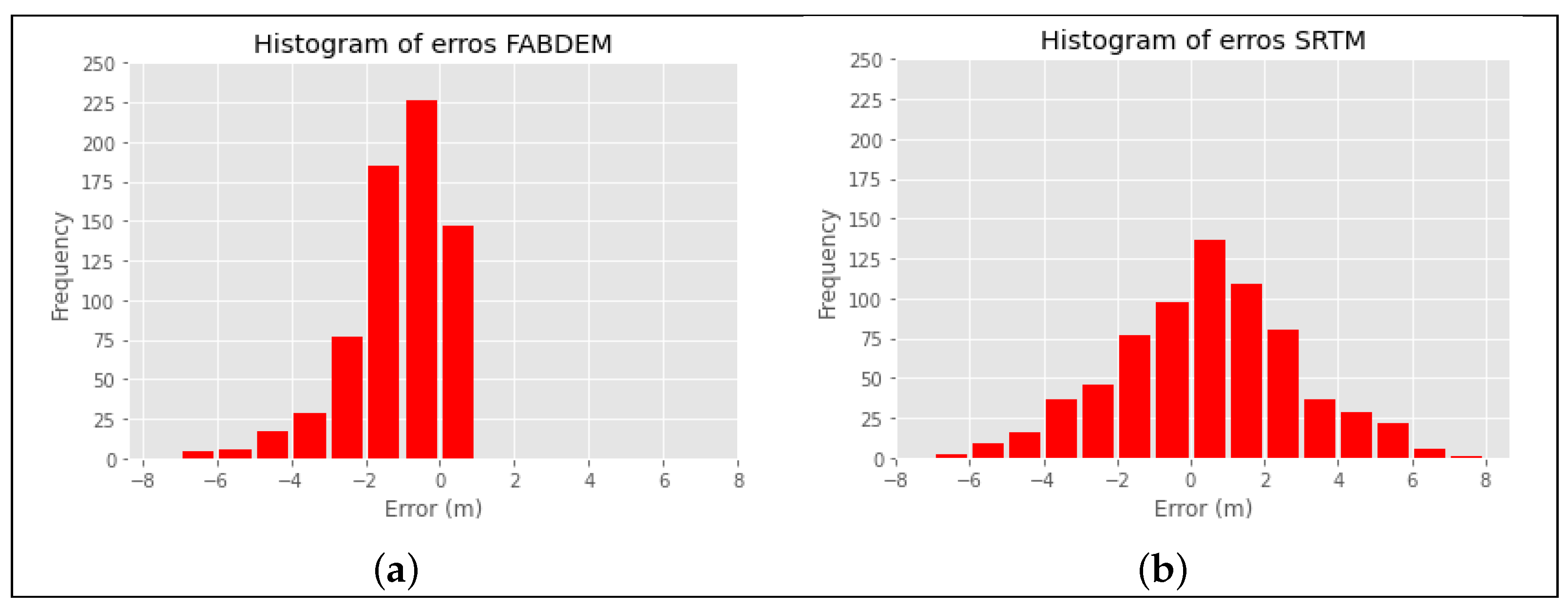
From surveyed points, only the terrain points were selected for the analysis of DEMs. 707 terrain points were used, which were divided into 75% (530) for the adjustment and 25% (177) for the validation of results. The elevation of the DEMs was extracted for each of the points and the error concerning their elevation was determined. The errors in the FABDEM are in the range between
to
m with an average error of
m and for the SRTM between
to
m with an average error of
m. The magnitude of the errors in the two DEMs are very similar; however, the tendency of these is different, as can be seen in the histograms in
Figure 7, the errors in the FABDDEM are mostly negative, while in the SRTM are mores distributed between positive and negative. This trend can be evidenced with the BIAS shown in
Table 1, in the SRTM it is positive because it has a tendency to underestimate the terrain heights represented by the points, while in the FABDEM it is negative, indicating that it is overestimating. The RMSE in the FABDEM DEM is
and in the SRTM is
, which are within the expected range for these models [
15,
47].
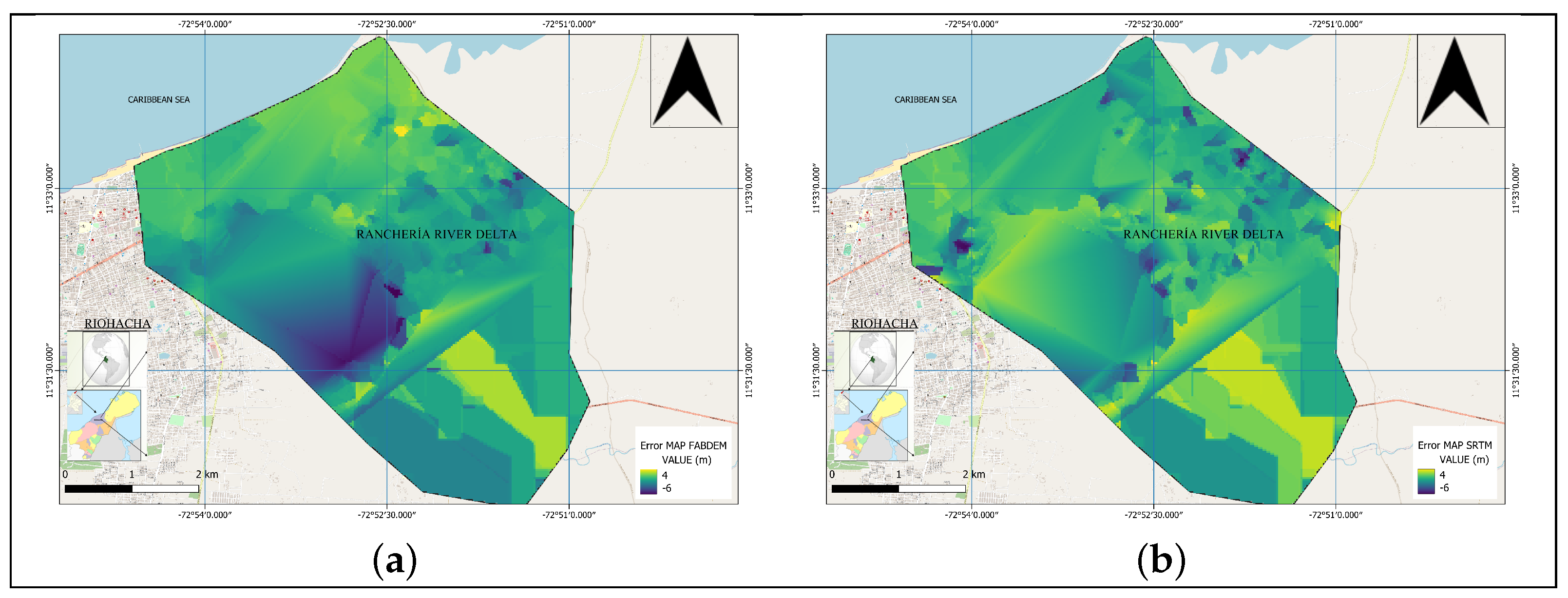
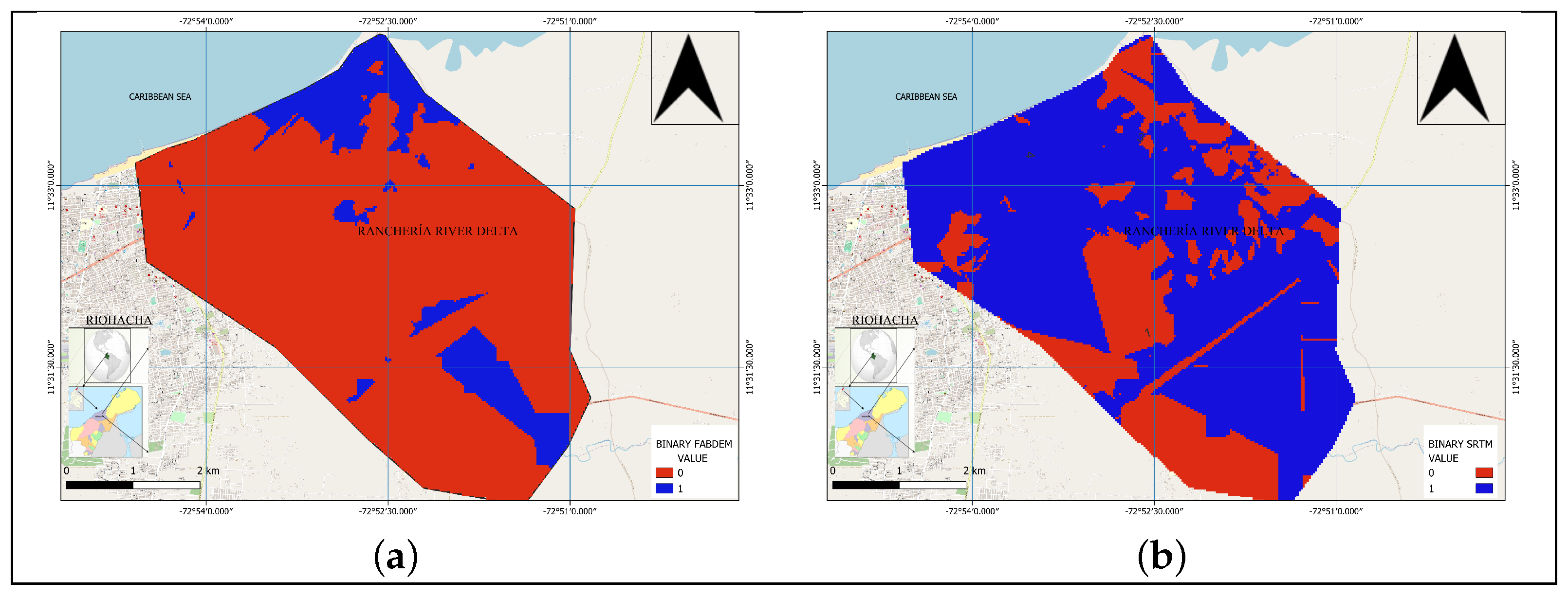
These metrics results demonstrate the importance of not using only one measure for the errors. As can be seen, if only the mean error or mean absolute error (MAE) were taken into account, it could be concluded that the SRTM is better than the FABDEM; however, when the RMSE is analyzed, that of the FABDEM is lower, indicating that it has a better fit to the field data. The metrics, being measurements of specific points, can give an erroneous estimate of the true fit of the models, and also do not allow observing the spatial distribution of the errors. For this purpose, error maps and binary maps of these errors were generated, which can be seen in
Figure 8 and
Figure 9.
The error maps show that they are in the same range of values for the two DEMs; however, as observed in
Table 1, the trend of the errors is different. This behavior spatially can be better observed with the binary maps of the errors, as shown in
Figure 9. For the FABDEM, it is mostly 0, while for the SRTM, the binary map is mostly 1. This coincides with the results of the BIAS that indicate the DEM trend concerning the real value surveyed in the field.
3.3. Output of Proposed Method
The procedure described in
Section 2.3 of the methodology was applied to obtain the altimetrically adjusted DEM. The result of the correction was evaluated by the error metrics described in
Section 2.2.
Table 2 presents the results of the error metrics taken from the DEMs after applying the correction process, comparing them with the metrics taken from the DEMs in the initial evaluation.
According to the results in
Table 2, the correction method achieves a significant reduction of the error in the two DEMs, as can be seen in the different metrics. For the RMSE, which is one of the most used metrics, a reduction of the error is
% in the FABDEM and
% in the SRTM, as for the other metrics it can be observed that the MAE is the one with the highest percentage decrease, being
% in the FABDEM and
% in the SRTM. The BIAS also shows an important reduction, going from
to
in the FABDEM, also showing a change in the trend, while in the SRTM it went from
to
.
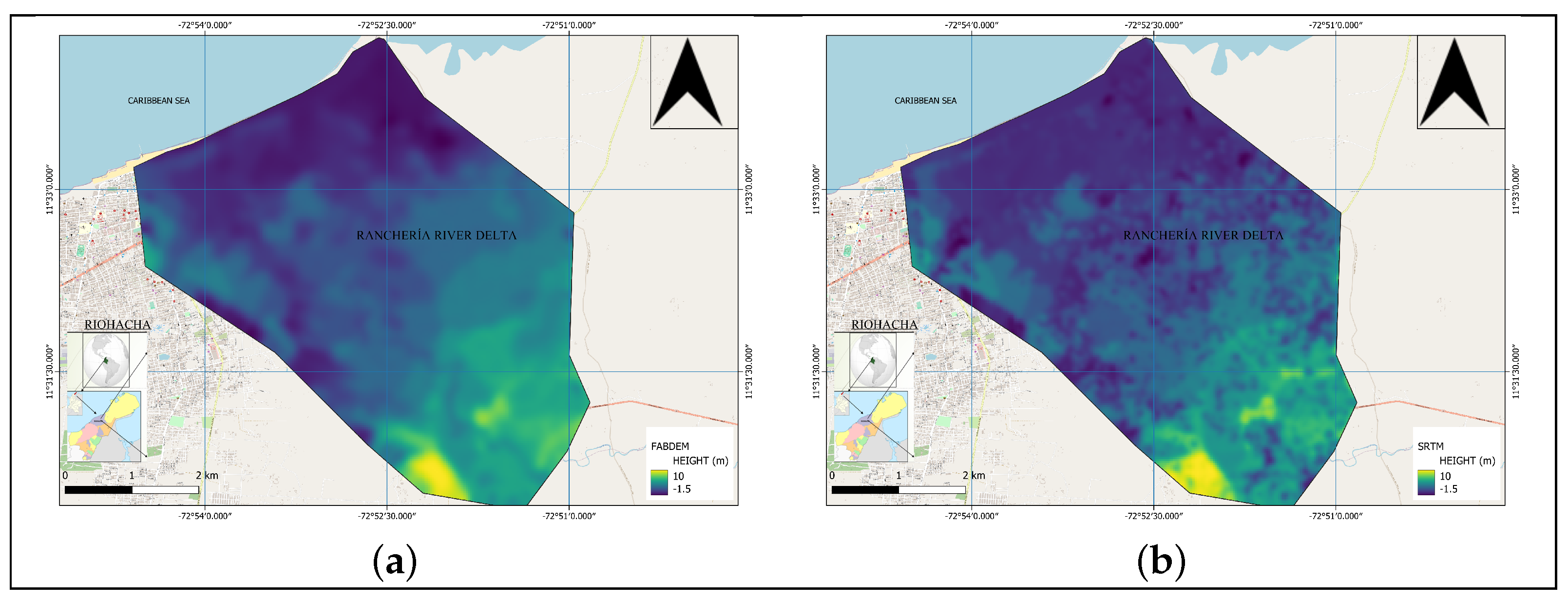
Figure 10 shows the DEMs corrected altimetrically.
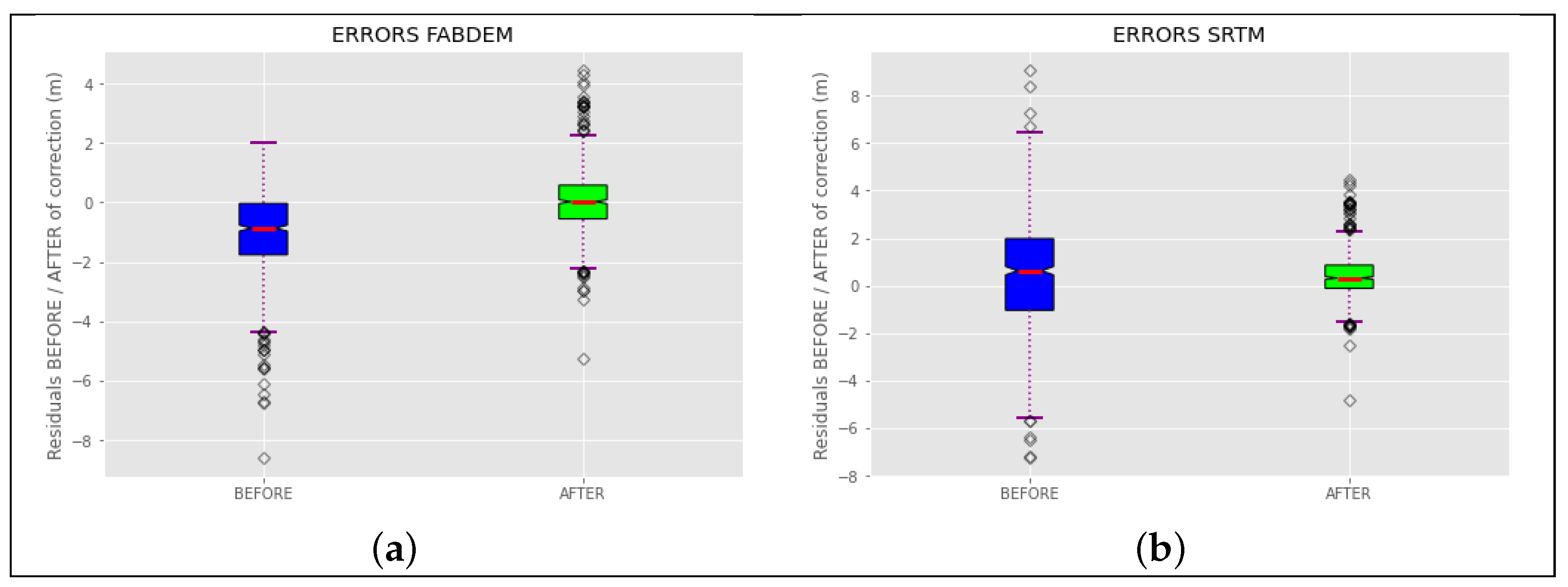
The metrics shown above present a global behavior of the errors and their reduction using the adjustment method; however, it is convenient to analyze the behavior of these errors in a more particular way. To analyze this behavior, box plots of the residual errors in each of the models before and after applying the correction method were made.
Figure 11 shows the box plots for the two DEMs used.
Box plots show how the correction method adjusts the distribution of the residuals in the two DEMs and brings the median closer to zero. At the beginning, the outliers are considerably separated from the extremes of the graph. When the adjustment is applied, the variability of the residuals decreases, and it can be observed how the extremes become wider and closer to the center, and the outliers also become closer to the extremes of the graph.
Another way to appreciate the change in DEMs with the application of the correction is by using profiles or transects in the terrain to see the difference in elevations between the original DEM and the adjusted DEM.
Figure 12 shows the used transects; the arrow indicates the direction in which the profile is drawn.
Figure 13 and
Figure 14 show the profiles obtained in the two DEMs before and after applying the correction process. Likewise, profiles were made to compare one DEM with another before and after the application of the correction process. These comparison profiles between the two DEMs are shown in
Figure 15 and
Figure 16.
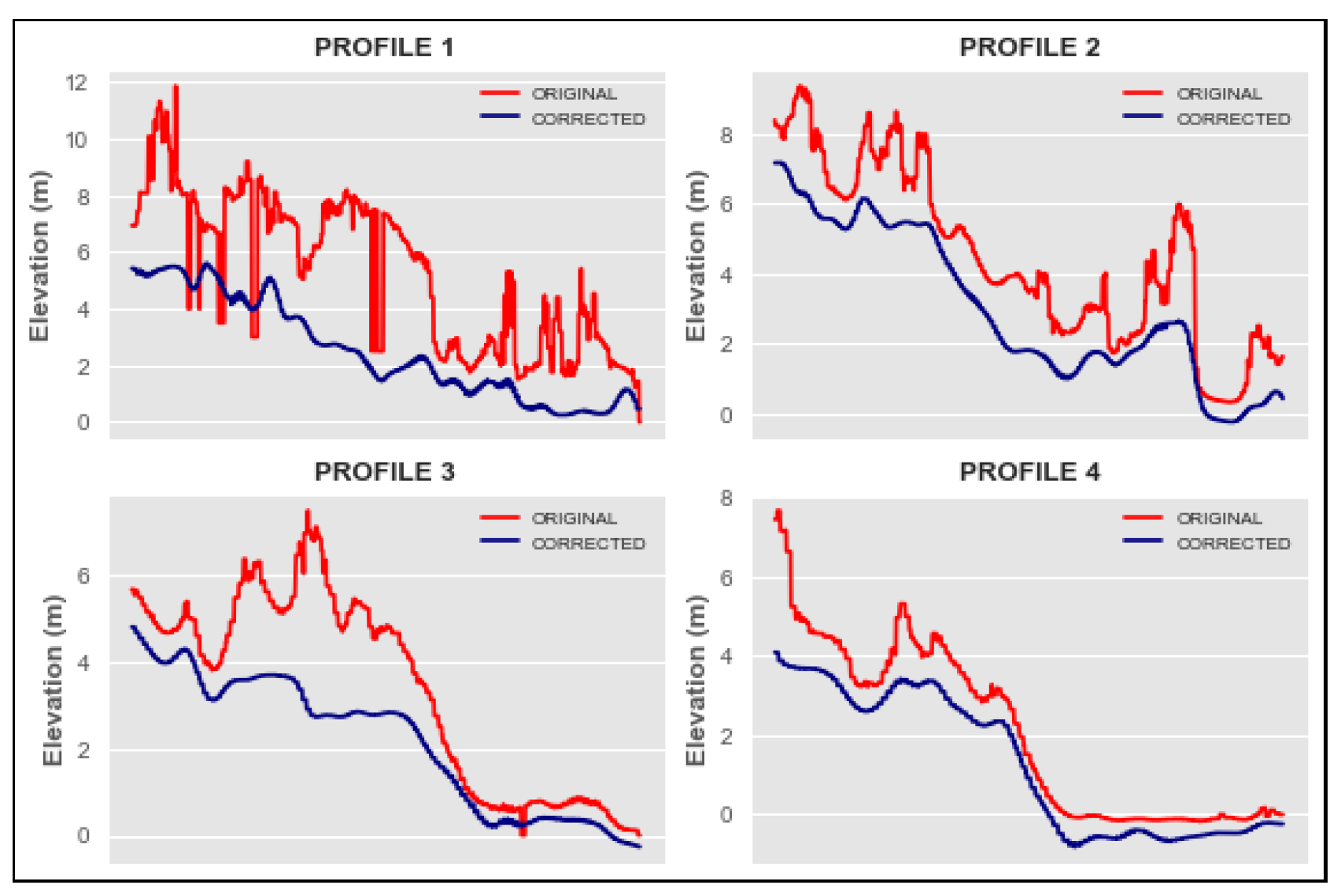
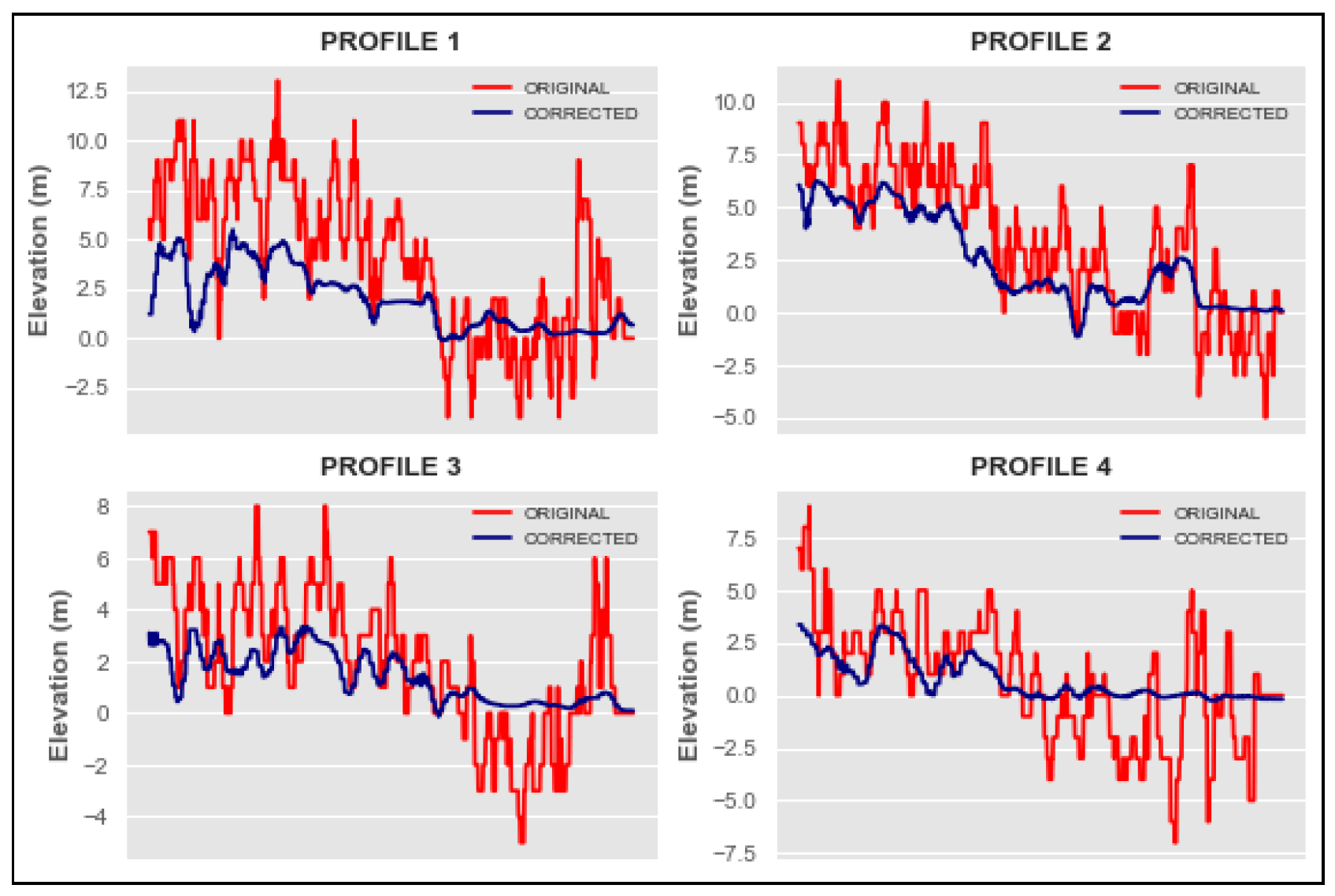
Figure 13 and
Figure 14 show the effect of applying the correction method. Before applying the correction, both DEM´s have great variability and have extreme elevation changes, mostly on SRTM than FABDEM. After applying the correction, profiles show a significant reduction in elevation and present a smoother distribution of elevation along the longitudinal profiles. This last detail is more appreciated for SRTM, as before applying the method it presents a hysterical behavior. SRTM presents poorer results in metrics than FABDEM, because while the latter is a derivative product from the original Copernicus DEM and has certain corrections in elevation [
15], the SRTM is the original product without any additional correction process [
12].
Longitudinal profiles demonstrate that the method is effective in generating a soften surface in the DEM, and eliminating random peacks, and outliers in elevation.
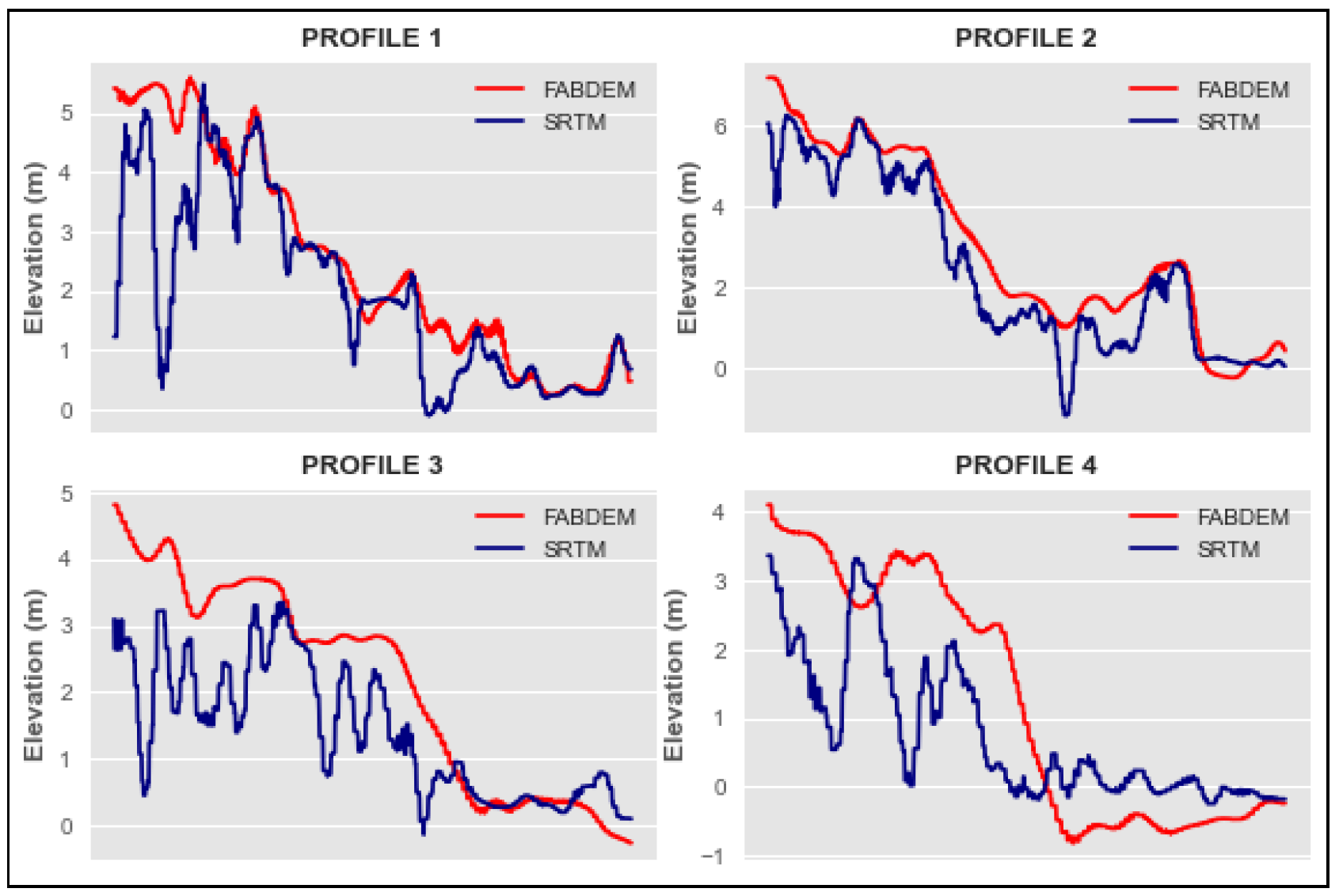
As can be seen in
Figure 15 before the application of the correction method, the two DEMs present a great difference between them, this coincides with the results of the evaluation of the error of the DEMs before the application of the correction method, which shows the difference in the trend of the errors between the FABDEM and the SRTM concerning the field data.
The FABDEM tends to overestimate the real elevation data, while the SRTM tends to underestimate the real elevation. This can be seen in the profiles, where it can be observed that in most cases the FABDEM is above the SRTM, except in some points where the SRTM presents elevation peaks. With the application of the correction, it is possible to reduce the differences between the two DEMs.
This has already been observed with the result of the BIAS presented, which shows a decrease in its dimension for both FABDEM and SRTM. Also, in FABDEM, the tendency of the errors is inverted. Also, the profiles in
Figure 16 show how, after the application of the correction, the difference between the two DEMs is reduced; however, it can be observed that the SRTM still has extreme peaks at some points, but the difference between it and FABDEM is reduced.
4. Discussion
The results presented suggest that the proposed methodology has the capacity to correct a large percentage of the error presented by the digital elevation models. However, although the methodology is shown to be simple, it is convenient to discuss a series of aspects that are involved around it and the results, the discussion is given in a first instance on the aspects to consider in the preparation and analysis of the input information and in a second instance on the results shown in the correction of the DEM.
4.1. Input Data Used and Processing
The methodology presented here has an advantage over other more complex methods in terms of the amount and variety of information needed for its application. In this methodology, the main input of information are the topographic points, and it is very important to be clear about the quantity and density of these in the study area. Regarding these, there are no references in the literature that can indicate precise and applicable values for all cases, being this a determination of each investigation, according to the needs and objectives that are had.
In this study, the number of points and their location was initially defined in the planning of the field campaigns according to the identified land covers, seeking to have points in the different zones; later, at the time of conducting the campaigns, other factors specific to the field were taken into account, such as accessibility, security conditions and environmental conditions that influenced the execution of the field campaigns. The number of points finally obtained was based on the weighting of all these conditions and the criteria of the research team, taking into account the characteristics of the study area, an optimum number was considered for the DEM adjustment process. In order to be able to apply the methodology to other study zones with similar characteristics and based on the results of error reduction, it was determined that a minimum density of 25 points per square kilometer of study area should be used. In addition to considering that, the points should be located in the different classes of land cover identified. However, it should be taken into account that this value is not an absolute standard; the density of points that can be obtained depends on all the factors mentioned above, which vary in each case.
On the other hand, the number of points used for the adjustment process and validation are also values that can vary from one case to another, and there is no exact value that is applicable to all [
7,
27]. Different combinations of the distribution of points were tested, evaluating the results in decreasing the error in the DEMs, finding that with the distribution that was used, it was possible to obtain the best results. Obtains a higher reduction percentage is with the 75 % for the adjustment and 25 % for the validation, which was the distribution used, as presented in
Section 3.2. These percentages of division of the points allow avoiding over-fitting and to have an optimal number of points for validation [
15].
4.2. DEM Correction and Error Evaluation
The removal of tree heights by means of the Canopy Height Model (CHM), and the removal of outliers by the 3-sigma criterion, constitute a good first approximation to the DEM correction; however, altimetry errors that do not come from the vegetation will prevail in the DEM, which makes necessary the application of the subsequent process proposed in this article. With respect to this, it should be kept in mind the possible errors due to the methods used, mainly the interpolations made to generate the error maps, which were used as a DEM correction surface, it was tried to minimize these errors using different interpolation methods to obtain an averaged surface between them. This strategy allowed reducing the appearance of artifacts coming from the interpolation in the surfaces; however, it is kept in mind that they cannot be completely avoided, and the remaining errors presented in the final DEMs are influenced by these errors inherent to the interpolation methods.
The error metrics used in this study agree with those widely used in the scientific community to evaluate the performance of altimetry correction methodologies of DEMs, the most widely used being the RMSE [
15,
28,
48]. Both RMSE and MAE are scale-dependent metrics, i.e. they show the error in the same unit as the studied variable, the main advantage of these metrics is their easy calculation and interpretation [
49,
50]. However, these metrics, being averaged, can be limited to identify trends in the errors, so it was necessary to use the BIAS, which is a metric that indicates the tendency of the model to overestimate or underestimate the real values, it can take negative or positive values and ranges between -1 and 1, with values closer to zero indicating less deviation or error of the model with respect to the real data [
27].
The results show that a significant reduction in the error of DEMs is achieved, taking the RMSE as the error metric, a reduction of between 53% and 59% is achieved. These results show the effectiveness of the method, considering the amount of information needed and its low complexity, compared to other methodologies that require much more information and, therefore, higher computational and processing capacities. Such as methodologies that apply machine learning algorithms [
7,
15,
27,
28], with which reductions of up to 71% of the RMSE are achieved. However, these methodologies require large amounts of information, in addition to extensive knowledge in programming these algorithms, which may limit their application. The methodology proposed in this article is offered as a less complex alternative to be applied, which offers a greater potential to be replicated in similar areas.
5. Conclusions
This study presents the development of a methodology for DEM correction in floodplain areas. The methodology uses global DEM’s of medium resolution (30 m), remote sensing information such as land cover and tree height model, and field topographic information surveyed with GNSS-RTK. The correction methodology allows obtaining a significant improvement between 53% and 59% of the RMSE with respect to the initial error between the DEM and the field points.
Specifically, an RMSE of 0.838 m is acchieved in the FABDEM, which is a great improvement for this type of DEM of global coverage, considering the initial RMSE of 1.785 m. In the SRTM DEM, a reduction of the RMSE from 2.550 to 1.044 m is achieved.
Error maps and binary maps are a very useful tool to spatially analyze the error in digital elevation models. Against the metrics, which only show an average estimation of errors, error maps and binary maps allow for observation of the spatial distribution of errors and their tendency around the study area.
The developed methodology is presented as an easy-to-apply alternative and with low information and processing requirements compared to other methodologies, which offers an advantage for the altimetry correction of the DEM, and is optimal for the required applications. This situation is common in areas with lack of information. The results show the improvement obtained in the elimination of vegetation and building heights.
The product generated using the developed methodology can later be subjected to a hydrological-hydraulic conditioning process to make it optimal for these applications. As a future work of the methodology presented in this article, it is proposed to apply a hydraulic conditioning process to the DEM, to make it optimal for applications that require, in addition to vertical accuracy, a good bathymetric representation, such as those that apply hydrodynamic modeling.
The proposed method offers a technically and operationally feasible solution for improving DEM accuracy in data-scarce floodplains, supporting local authorities, environmental agencies, and researchers involved in local-scale flood risk assessment and land use planning.
Acknowledgments
This research has been carried out and funded under the PhD project of Jose Fragozo that has been funded by the Ministry of Science, Technology and Innovation "Minciencias" of Colombia. We thank the Universidad de La Guajira for their support in the logistical planning of the field campaigns and for funding the APC for this article. To the professor of the Universidad de La Guajira, Johnny Pérez Montiel, for the support provided in the planning and logistics of the field campaigns, and during the different stages of the research. We also thank the Pontificia Universidad Javeriana for providing the necessary equipment for the topographic survey.
Conflicts of Interest
Authors declare no conflict of interest.
References
- Wohl, E. An Integrative Conceptualization of Floodplain Storage. Reviews of Geophysics 2021, 59, e2020RG000724. [CrossRef]
- Carling, P.A.; Hargitai, H. Floodplain. Encyclopedia of Planetary Landforms 2021, pp. 1–5. [CrossRef]
- Leal Filho, W.; Azul, A.M.; Brandli, L.; Lange Salvia, A.; Wall, T. Floodplain. In Life Below Water; Leal Filho Walter}and Azul, A.M.; Luciana, B.; Amanda, L.S.; Tony, W., Eds.; Springer International Publishing: Cham, 2022; p. 419. [CrossRef]
- Hoitink, A.J.; Nittrouer, J.A.; Passalacqua, P.; Shaw, J.B.; Langendoen, E.J.; Huismans, Y.; van Maren, D.S. Resilience of River Deltas in the Anthropocene. Journal of Geophysical Research: Earth Surface 2020, 125, e2019JF005201. [CrossRef]
- Mazzoleni, M.; Mård, J.; Rusca, M.; Odongo, V.; Lindersson, S.; Di Baldassarre, G. Floodplains in the Anthropocene: A Global Analysis of the Interplay Between Human Population, Built Environment, and Flood Severity. Water Resources Research 2021, 57, e2020WR027744. [CrossRef]
- Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the effects of Digital Elevation Model resolution in urban fluvial flood modelling. Journal of Hydrology 2021, 596, 126088. [CrossRef]
- Meadows, M.; Wilson, M. A Comparison of Machine Learning Approaches to Improve Free Topography Data for Flood Modelling. Remote Sensing 2021, 13, 275. [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophysical Research Letters 2017, 44, 5844–5853. [CrossRef]
- Neal, J.; Schumann, G.; Bates, P. A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas. Water Resources Research 2012, 48. [CrossRef]
- O’Loughlin, F.E.; Paiva, R.C.; Durand, M.; Alsdorf, D.E.; Bates, P.D. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sensing of Environment 2016, 182, 49–59. [CrossRef]
- Hawker, L.; Bates, P.; Neal, J.; Rougier, J. Perspectives on Digital Elevation Model (DEM) Simulation for Flood Modeling in the Absence of a High-Accuracy Open Access Global DEM. Frontiers in Earth Science 2018, 6, 233. [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Reviews of Geophysics 2007, 45, 2004. [CrossRef]
- Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.; Oimoen, M.; Zhang, Z.; Danielson, J.; Krieger, T.; Curtis, B.; Haase, J.; et al. ASTER Global Digital Elevation Model Version 2 – Summary of validation results, 2011.
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. GENERATION OF THE 30 M-MESH GLOBAL DIGITAL SURFACE MODEL BY ALOS PRISM. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2016, XLI-B4, 157–162. [CrossRef]
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m global map of elevation with forests and buildings removed. Environmental Research Letters 2022, 17, 24016. [CrossRef]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS Journal of Photogrammetry and Remote Sensing 2004, 59, 85–101. [CrossRef]
- Özcan, A.H.; Ünsalan, C.; Reinartz, P. International Journal of Remote Sensing Ground filtering and DTM generation from DSM data using probabilistic voting and segmentation Ground filtering and DTM generation from DSM data using probabilistic voting and segmentation 2018. [CrossRef]
- Deng, X.; Tang, G.; Wang, Q. A novel fast classification filtering algorithm for LiDAR point clouds based on small grid density clustering. Geodesy and Geodynamics 2022, 13, 38–49. [CrossRef]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Progress in Physical Geography 2008, 32, 31–49. [CrossRef]
- Yamazaki, D.; Baugh, C.A.; Bates, P.D.; Kanae, S.; Alsdorf, D.E.; Oki, T. Adjustment of a spaceborne DEM for use in floodplain hydrodynamic modeling. Journal of Hydrology 2012, 436-437, 81–91. [CrossRef]
- Zhang, K.; Gann, D.; Ross, M.; Robertson, Q.; Sarmiento, J.; Santana, S.; Rhome, J.; Fritz, C. Accuracy assessment of ASTER, SRTM, ALOS, and TDX DEMs for Hispaniola and implications for mapping vulnerability to coastal flooding. Remote Sensing of Environment 2019, 225, 290–306. [CrossRef]
- Patel, A.; Katiyar, S.K.; Prasad, V. Performances evaluation of different open source DEM using Differential Global Positioning System (DGPS). The Egyptian Journal of Remote Sensing and Space Science 2016, 19, 7–16. [CrossRef]
- Abrams, M. ASTER Global DEM Version 3, and new ASTER Water Body Dataset. Remote Sensing and Spatial Information Sciences 2016, pp. 12–19. [CrossRef]
- Wu, Q.; Lane, C.R.; Wang, L.; Vanderhoof, M.K.; Christensen, J.R.; Liu, H. Efficient Delineation of Nested Depression Hierarchy in Digital Elevation Models for Hydrological Analysis Using Level-Set Method. JAWRA Journal of the American Water Resources Association 2019, 55, 354–368. [CrossRef]
- Lindsay, J.B. The practice of DEM stream burning revisited. Earth Surface Processes and Landforms 2016, 41, 658–668. [CrossRef]
- Zhao, X.; Yanjun, S.; Tianyu, H.; Chen, L.; Gao, S.; Wang, R.; Jin, S.; Guo, Q. A global corrected SRTM DEM product for vegetated areas. Remote Sensing Letters 2018, 9, 393–402. [CrossRef]
- Kasi, V.; Yeditha, P.K.; Rathinasamy, M.; Pinninti, R.; Landa, S.R.; Sangamreddi, C.; Agarwal, A.; Dandu Radha, P.R. A novel method to improve vertical accuracy of CARTOSAT DEM using machine learning models. Earth Science Informatics 2020, 13, 1139–1150. [CrossRef]
- Liu, Y.; Bates, P.D.; Neal, J.C.; Yamazaki, D. Bare-Earth DEM Generation in Urban Areas for Flood Inundation Simulation Using Global Digital Elevation Models. Water Resources Research 2021, 57, e2020WR028516. [CrossRef]
- Mitsch, W.J.; Gosselink, J.G. Wetlands 2015. p. 736.
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. Journal of Geophysical Research: Biogeosciences 2011, 116, 4021. [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sensing of Environment 2021, 253, 112165. [CrossRef]
- Lang, N.; Jetz, W.; Schindler, K.; Wegner, J.D. A high-resolution canopy height model of the Earth. Nature Ecology & Evolution 2023, 7, 1778–1789. [CrossRef]
- Wang, W.; Lu, Y. Analysis of the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) in Assessing Rounding Model. IOP Conference Series: Materials Science and Engineering 2018, 324, 012049. [CrossRef]
- Ajvazi, B.; Czimber, K. A comparative analysis of different DEM interpolation methods in GIS: case study of Rahovec, Kosovo. Geodesy and Cartography 2019, 45, 43–48. [CrossRef]
- Habib, M. Evaluation of DEM interpolation techniques for characterizing terrain roughness. CATENA 2021, 198, 105072. [CrossRef]
- Patel, V.; Kapoor, A.; Sharma, A.; Chakrabarti, S. Taxonomy of outlier detection methods for power system measurements. Energy Conversion and Economics 2023, 4, 73–88. [CrossRef]
- Ettritch, G.; Hardy, A.; Bojang, L.; Cross, D.; Bunting, P.; Brewer, P. Enhancing digital elevation models for hydraulic modelling using flood frequency detection. Remote Sensing of Environment 2018, 217, 506–522. [CrossRef]
- Yap, L.; Ludovic, H.; Kandé, R.; Nouayou, J.; Kamguia, N.; Abdou, N.; Makuate, M.B.; Kandé, H.; Nouayou, R.; Kamguia, J.; et al. Vertical accuracy evaluation of freely available latest high-resolution (30 m) global digital elevation models over Cameroon (Central Africa) with GPS/leveling ground control points. International Journal of Digital Earth 2019, 12, 500–524. [CrossRef]
- Han, H.; Zeng, Q.; Jiao, J. Quality Assessment of Three Digital Elevation Models with 30 M Resolution by Taking 12 M TanDEM-X DEM as Reference. International Geoscience and Remote Sensing Symposium (IGARSS) 2020, pp. 5155–5158. [CrossRef]
- Okabe, A.; Satoh, T.; Furuta, T.; Suzuki, A.; Okano, K. Generalized network Voronoi diagrams: Concepts, computational methods, and applications. International Journal of Geographical Information Science 2008, 22, 965–994. [CrossRef]
- Kastrisios, C.; Tsoulos, L. Voronoi tessellation on the ellipsoidal earth for vector data. International Journal of Geographical Information Science 2018, 32, 1541–1557. [CrossRef]
- Pérez, J.I.; Escobar, J.R.; Fragozo, J.M. Modelación Hidráulica 2D de Inundaciones en Regiones con Escasez de Datos. El Caso del Delta del Río Ranchería, Riohacha-Colombia. Información tecnológica 2018, 29, 143–156. [CrossRef]
- Chen, H.; Liang, Q.; Liu, Y.; Xie, S. Hydraulic correction method (HCM) to enhance the efficiency of SRTM DEM in flood modeling. Journal of Hydrology 2018, 559, 56–70. [CrossRef]
- Marsh, C.B.; Harder, P.; Pomeroy, J.W. Validation of FABDEM, a global bare-earth elevation model, against UAV-lidar derived elevation in a complex forested mountain catchment. Environmental Research Communications 2023, 5, 031009. [CrossRef]
- Zanaga, D.; Van De Kerchove, R.; Daems, D.; De Keersmaecker, W.; Brockmann, C.; Kirches, G.; Wevers, J.; Cartus, O.; Santoro, M.; Fritz, S.; et al. ESA WorldCover 10 m 2021 v200, 2022. [CrossRef]
- TOPCON CORPORATION. Hiper V Receptor GNSS de Doble Frecuencia, 2017.
- Courty, L.G.; Soriano-Monzalvo, J.C.; Pedrozo-Acuña, A. Evaluation of open-access global digital elevation models (AW3D30, SRTM, and ASTER) for flood modelling purposes. Journal of Flood Risk Management 2019, 12, e12550. [CrossRef]
- Baugh, C.A.; Bates, P.D.; Schumann, G.; Trigg, M.A. SRTM vegetation removal and hydrodynamic modeling accuracy. Water Resources Research 2013, 49, 5276–5289. [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. International Journal of Forecasting 2006, 22, 679–688. [CrossRef]
- Botchkarev, A. Performance Metrics (Error Measures) in Machine Learning Regression, Forecasting and Prognostics: Properties and Typology. Interdisciplinary Journal of Information, Knowledge, and Management 2018, 14, 45–76. [CrossRef]
Figure 1.
Methodology summary diagram.
Figure 1.
Methodology summary diagram.
Figure 2.
Unsupervised DEM adjustment.
Figure 2.
Unsupervised DEM adjustment.
Figure 3.
Location of the Rancheria river delta with respect to the urban area of Riohacha and its discharge to the Caribbean Sea.
Figure 3.
Location of the Rancheria river delta with respect to the urban area of Riohacha and its discharge to the Caribbean Sea.
Figure 4.
DEMs used a)FABDEM, b) SRTM.
Figure 4.
DEMs used a)FABDEM, b) SRTM.
Figure 5.
Land Cover Map (a) and Canopy Height Model (b).
Figure 5.
Land Cover Map (a) and Canopy Height Model (b).
Figure 6.
Topographic points surveyed in the study area.
Figure 6.
Topographic points surveyed in the study area.
Figure 7.
Error histograms for the FABDEM and SRTM digital elevation models
Figure 7.
Error histograms for the FABDEM and SRTM digital elevation models
Figure 8.
Error Maps. a) FABDEM, b)SRTM.
Figure 8.
Error Maps. a) FABDEM, b)SRTM.
Figure 9.
Binary error maps. a)FABDEM, b)SRTM.
Figure 9.
Binary error maps. a)FABDEM, b)SRTM.
Figure 10.
DEM adjusted altimetrically. a) FABDEM, b) SRTM.
Figure 10.
DEM adjusted altimetrically. a) FABDEM, b) SRTM.
Figure 11.
Box plot of the errors in DEMs.
Figure 11.
Box plot of the errors in DEMs.
Figure 12.
Transects to evaluate DEM elevations.
Figure 12.
Transects to evaluate DEM elevations.
Figure 13.
FABDEM elevation profiles.
Figure 13.
FABDEM elevation profiles.
Figure 14.
SRTM elevation profiles
Figure 14.
SRTM elevation profiles
Figure 15.
Comparative profiles between DEMs, before applying the correction.
Figure 15.
Comparative profiles between DEMs, before applying the correction.
Figure 16.
Comparative profiles between DEMs, after applying the correction.
Figure 16.
Comparative profiles between DEMs, after applying the correction.
Table 1.
DEM Error Metrics.
Table 1.
DEM Error Metrics.
| METRICS |
DEM |
| |
FABDEM |
SRTM |
| MAE |
1.031 |
0.595 |
| RMSE |
1.785 |
2.550 |
| BIAS |
-0.602 |
0.365 |
Table 2.
Comparison of error metrics, before and after applying the correction process.
Table 2.
Comparison of error metrics, before and after applying the correction process.
| METRICS |
DEM |
| FABDEM |
SRTM |
| ORIG |
CORR |
% |
ORIG |
CORR |
% |
| MAE |
1.031 |
0.260 |
74.793 |
0.595 |
0.240 |
59.612 |
| RMSE |
1.785 |
0.838 |
53.028 |
2.550 |
1.044 |
59.075 |
| BIAS |
-0.602 |
0.021 |
|
0.365 |
0.149 |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).