1. Introduction
For critically ill patients in the intensive care unit with severe bacterial infections, the rapid and targeted initiation of adequate antibiotic therapy is of utmost importance for the patient’s outcome. Antibiotic resistance has an increasingly important influence on the effectiveness of therapy and the chances of clinical recovery. The current worldwide increase in antibiotic-resistant bacteria has therefore been defined by the World Health Organization (WHO) as one of the 10 greatest global health threats to humanity, which requires decisive action through differentiated measures.
Antibiotic resistance is mainly caused by overuse or misuse of antibiotics. The choice of substance used plays the major role here, but dosage aspects and the resulting low antibiotic levels in the blood or the target organ system are also relevant, as this can lead to the selection of resistant subpopulations of pathogens under antibiotic therapy. The appropriate dosage of antibiotics is therefore not only important for patient outcome, but also for the development of resistance itself. In addition to choosing the individual substance for the patient, the physician must therefore keep an eye on the sufficient dosage and also the so-called “resistance pressure” that he/she automatically exerts on the individual patient but also on the entire cohort of the corresponding ward and hospital through the choice of antibiotic.
The representation of the local resistance situation in the form of resistance statistics should therefore also be taken into account when selecting the respective substance. As these dimensions are usually not given sufficient consideration in the medical decision-making process for antibiotic therapy, structured optimization measures against antibiotic resistance are of utmost medical importance. Specifically, in addition to the pharmacological development of new substances/antibiotic classes by the pharmaceutical industry, the rational and responsible use of antibiotics is particularly important. This preventive approach to avoiding resistance is subsumed under the term Antibiotic Stewardship (ABS) and includes the following aspects, among others:
the initially broadly calculated antibiotic therapy for critical illnesses (e.g. sepsis), taking into account local resistance situations,
detection of the (bacterial) pathogen causing the infection by means of suitable microbiological diagnostics,
selection of the appropriate antibiotic based on the antibiogram of the identified pathogen(s) (as well as de-escalation in the case of calculated prior therapy),
the adjustment of the duration of therapy,
and the dosage and form of antibiotic administration.
The aim of ABS is to treat patients in the best possible way and at the same time prevent selection processes and resistance from occurring in the bacteria. To this end, it would be desirable to regularly evaluate and optimize the rational use of antimicrobial substances with an integrative approach that combines routine intensive care and microbiological data from the clinic with mathematical and methodological analyses: a clinical decision support system. To establish such a system, however, the above-mentioned hurdles arising from the complexity of the clinical situation must be overcome. Reflection is now required and the natural next step is to first better understand the given complexity.
Even though Germany still has relatively low incidences of resistant bacterial pathogens compared to other (southern and eastern) European countries, the trend in this country is also increasing alarmingly, particularly with certain Gram-negative pathogens. In contrast to Gram-positive pathogens, this group of multi-resistant Gram-negative bacteria poses the greatest challenge, as several hundred different resistances with a pleiotropic pool of different resistance mechanisms have already been identified. Frequent basic principles of antibiotic resistance are the inactivation of
-lactam antibiotics by means of chemical cleavage by so-called
-lactamases, as well as the reduction of the antibiotic in the bacterial periplasm through the expression of efflux pumps or the loss of porins. In particular, the large number of very different
-lactamases influences the efficacy of the largest antibiotic class of
-lactams. Special
-lactamases (so-called carbapenemases) can give rise to the fact that no
-lactam antibiotic, including the group of carbapenems as reserve substances, still has clinical efficacy against corresponding pathogens [
1]. However, multiresistance also affects structurally and functionally unrelated antimicrobial active substances, as will be discussed again below in the context of cross-resistance.
The number of substances available for multi-resistant Gram-negative pathogens is still limited and newly developed antibiotic classes are the exception rather than the rule. Major innovations in the development of antibiotics for Gram-negative pathogens therefore primarily consist of the combination of a “new”
-lactamase inhibitor with an existing substance.
-lactamase inhibitors are able to inactivate
-lactamases produced by bacteria, allowing the antibiotic that was previously ineffective due to inactivation to become effective again. However, there is already resistance to these “new” antibiotics. On the one hand,
-lactamase inhibitors are only effective against certain
-lactamases. On the other hand, their use can lead to the selection of subpopulations of the treated pathogen that are resistant to this combination of active substances [
2]. The use of new antibiotics is therefore strictly limited to cases in which other substances are no longer effective and will not be able to solve the antibiotic resistance problem in the long term.
Preventive concepts such as ABS are therefore of crucial importance in preventing the development of resistance. In addition to the actual microbiological identification of the pathogen, this includes in particular the selection of the appropriate antibiotic, including pharmacokinetic and pharmacodynamic aspects. Clinically, the efficacy of a substance is determined by measuring the minimum inhibitory concentration (MIC). The MIC is the lowest effective concentration of an antibiotic that still prevents the replication of a pathogen in a culture. Clinical threshold values defined for the respective pathogens (in Europe by the EUCAST - “European Committee on Antimicrobial Susceptibility Testing”) then identify a pathogen as resistant (R) or susceptible (S) to the respective antibiotic tested and support clinicians in selecting the correct substance in the form of the so-called antibiogram [
3].
Regarding resistance development, however, the aspect of the active substance concentration achieved in the target compartment is also of decisive importance. It is currently assumed that a pathogen population that triggers an infection has different subpopulations with different MICs [
4]. It is therefore assumed that an antibiotic tested sensitive
per se leads to the selection of subpopulations of the treated pathogen with a higher MIC if blood or target organ levels are inadequate, resulting in the clinical manifestation of resistance. This development can occur either within a patient (e.g. in the case of recurrent antibiotic episodes during long courses of intensive care), but also across patient boundaries in the entire ward or hospital cohort over a longer period of time, as there is inevitably also an exchange of the microbiome between patients (direct and indirect/iatrogenic) [
5].
As a countermeasure, attempts are made by ensuring sufficiently high antibiotic levels and thus a sufficient dosage. This has recently been done, for example, by determining the blood or tissue levels of a substance as part of therapeutic drug monitoring (TDM) and any resulting dose adjustments [
6,
7]. However, a third category “I” in susceptibility testing (English for “susceptible for increased exposure”) also addresses the requirement for sufficient antibiotic levels, which clinically means that the substance has been tested as sensitive but requires an increased dosage. With regard to the overall cohort, the local resistance situation in the form of ward and/or hospital-specific resistance statistics also plays a relevant role.
Another possible ABS strategy proposed and analyzed by numerous authors is the cyclical allocation of antibiotics or so-called mixing (other terms are in circulation). These are strategies at hospitals with the aim of contributing to a reduction in the prevalence of resistant germs by means of spatial (between departments, mixing) or cyclical (temporal) variations in the proportions of consumption of different antibiotic groups. According to a recent systematic review [
8], there is only one randomized controlled trial (RCT) on the effectiveness of such strategies. However, there are some studies that at least compared systematic cyclical administration strategies and standard administration between clinics or carried out before-and-after comparisons (cross-over) [
8,
9].
Meta-analyses report a small effect (on average), with individual studies reporting a clinically relevant effect [
8,
9]. In the RCT study, cycling performed worse than the control ABS [
8]. In numerous studies, “mixing” was chosen as the control strategy, i.e. an alternating exchange between departments. Cycling, i.e. a temporal periodic change simultaneously across all departments, showed no difference to the mixing procedure, which is not surprising from a theoretical point of view if one assumes sufficiently isolated conditions between the departments. Nevertheless, all studies (RCT and cohort studies) including the cross-over studies were considered together in the meta-analyses, regardless of whether they tested against “mixing” or “without strategy”, which must be viewed very critically and neglects the important separate consideration of mixing and cycling. However, in the meta-analysis by [
9], a distinction was made between the two control strategies as part of a secondary analysis. In Gram-positive bacteria, the cycling strategy showed a slightly stronger effect in terms of avoiding resistance. It appears that there is no general evaluation independent of other biological and medical boundary conditions. It is therefore possible that the cycling concept itself is not well thought out. The question of whether cycling or mixing contributes to the “rational and responsible use of antibiotics” has therefore not been conclusively clarified.
“Scheduled cycling” according to a fixed scheme means that the informed, i.e. rational use of antibiotics is deliberately avoided, so that conceptually a control or zero strategy rather than a verum strategy is defined here. In a seminal cycling study published by [
10], the authors investigated interrupted time series in the administration of aminoclycosides. These irregular antibiotic prescriptions followed an observed pattern in the emergence of resistant germs and by no means a fixed periodic cycling scheme. In retrospect, it appears that the authors intuitively used the method that is now referred to as “clinical cycling” and which is actually superior to scheduled cycling because it is based on clinical evidence for the necessity of a switching strategy. Unsurprisingly, scheduled cycling strategies have not yet found any clinical application in practice. Moreover, cycling is explicitly not recommended in a German S3 guideline [
11]. Noteworthy, the validity already expired on 2024-01-31, so an update has been overdue for more than a year, i.e. the S3 guideline does not currently provide any valid orientation for ABS.
The latest insights into the genesis of cross-resistance and delay phenomena in this genesis make the strictly timed cyclical variation appear particularly naive in retrospect [
12,
13,
14]. Cross-resistance can arise due to genetic changes in the bacterial strain. They can acquire resistance via gene transfer - via conjugation or transformation - from other bacteria. Transmission via bacteriophages (transduction) is also possible (e.g. [
15]). However, it has also been clear for some time that multi-resistance must actually be interpreted as cross-resistance
per se, since multidrug resistance is a term that refers to mechanisms of resistance by chromosomal genes. In this case, as [
12] points out, an exposure to a single drug leads to cross-resistance to many other structurally and functionally unrelated drugs. As mentioned above, an important mechanism identified for multidrug resistance in bacteria is drug efflux by membrane transporters.
Results such as those by [
16] show that current strategies for the use of critical antibiotics are not sufficient to avoid unexpected antibiotic cross-resistance. They found that cross-resistance to daptomycin occurred in vancomycin-resistant
Enterococcus faecium when rifaximin was used. Resulting resistance formation has been shown not only for antibiotic use, but also for antiviral drugs: bacteria exposed in vitro to antiviral drugs with antibacterial properties can develop multiple resistance mutations associated with cross-resistance to antibiotics [
16].
In another cross-correlation study, it was shown that considering the previous consumption as well as the incidence density of strains during the previous quarter proved to be the best model to explain Carbapenem resistance of
P. aeruginosa strains based on meropenem consumption during a given quarter [
17]. Furthermore, a correlation was found between antibiotic consumption and the occurrence of multidrug-resistant organisms [
18]. Also worth mentioning is the meta-analysis on the effect of combination therapies on the development of resistance, which shows mixed results. In some cases, the prognosis is better with combinations, but in others the opposite effect is seen [
19].
Arguably, despite the aforementioned counterarguments, the poor performance of “scheduled cycling” does no speak against cycling per se, but rather against cycling that is not carried out intelligently. One could even say that conceptually, scheduled cycling corresponds more to a “placebo-like” (control) ABS, whereas clinical cycling based on clinical expertise corresponds to the verum group. In the context of this interpretation, the many studies on cycling are in fact rather evaluation procedures for assessing whether the respective “clinical cycling” is viable on the basis of implicit clinical knowledge in comparison to a non-informed cycling strategy. In other words, despite the clinically contra-indicated settings of scheduled cycling programs, these strategies represent a kind of basic model structure whose quantitative explanation is the basis for the description of more complex switching strategies (clinical cycling).
In our own preliminary work [
20], we have created and published a mathematical framework that is suitable for adequately quantifying the effect of clinical cycling and, in borderline cases, scheduled cycling. It is worth mentioning that in most of the studies conducted, no quantification of the degree of mixing or cyclic variation was used. An exception is the study by [
21], in which an antibiotic heterogeneity index (AHI) was used. However, it turns out that AHI is completely unsuitable for the intended task. It is a global measure that is invariant to swapping the antibiotic classes. This means that if the consumption shares of two antibiotics are swapped, AHI remains unchanged.
We therefore developed a mathematical method to correctly calculate temporal and spatial heterogeneities in the consumption of antibiotics and in the prevalence of pathogens. Subsequent correlation analyses revealed a relationship between the heterogeneity of antibiotic consumption and the prevalence of resistant pathogens, indicating a reduction in the prevalence of resistant germs. The heterogeneity changes on the pathogen side follow the changes on the consumption side.
Diversity measures, which are frequently used in ecological studies in particular, were used to calculate “mixing”, i.e. the degree of heterogeneity. These measures are related to entropies, which are used in information theory and especially in statistical physics for the quantitative description of mixing processes (dispersions) and similar phenomena. There is a larger class of such entropies or diversities, whereby the concrete choice depends on the specific problem. However, the Shannon entropy known from information theory is, like AHI, a global entropy, i.e. invariant to permutations of the species. Local heterogeneity measures must therefore be used in order to be able to record changes over time. The Kullback-Leibler entropy is such a local entropy and has proven its worth in our preliminary work in the context of ABS as well as of spatio-temporal epidemic patterns [
20,
22]. However, the concrete choice of the final form of the analysis algorithms depends on specific conditions. The estimated values of some entropies from a larger class of theoretically allowed diversity measures are inaccurate when very small consumption fractions are involved.
It must be mentioned that adaptive model-based optimization in everyday clinical practice is not readily possible on the basis of our preliminary work. Theoretically, it would be conceivable to extrapolate the observed mixing states, i.e. to create possible interaction scenarios, in such a way that an “optimal cycling regime” is achieved, but this extrapolation would take place without any “constraints”, such as those imposed by biological and clinical framework conditions and regulations. However, we note that the foundation for such an optimization has been laid by our preliminary work, also taking into account clinical constraints (antibiogram, pharmacokinetics and microbiological parameters, guidelines) [
6,
7,
20,
22,
23].
As mentioned, the clinical requirements of ABS also include careful and appropriate microbiological diagnostics. A comprehensive prevalence and mortality study recently addressed which pathogens are the biggest problem children [
24]. In summary, in 2019, approximately 14% of all deaths were due to a bacterial infection, based on the 33 most important pathogens. Furthermore, 56% of sepsis-associated deaths died as a result of these 33 infections. It is also noteworthy that 55% of deaths from the 33 bacterial species were due to infections of
Previously, the 6 pathogens from the so-called ESKAPE series
Enterococcus faecium
Staphylococcus aureus
Klebsiella pneumoniae
Acinetobacter baumannii
Pseudomonas aeruginosa
Enterobacter
were discussed as particularly critical with the highest clinical relevance [
25]. It almost goes without saying that successful ABS must keep an eye on the prevalence of these pathogens, which are classified as particularly dangerous, especially with regard to the development of resistance. In this context, we also refer to the studies by [
26,
27,
28], that specifically address mortality due to antibiotic resistance in ICUs.
The obvious preparatory step for such a clinical decision support system in form of an adaptive optimization is therefore the precise descriptive representation of the clinical conditions and requirements, i.e. the representation of the local resistance situation in the form of resistance statistics. A first attempt towards such statistics will be made in the present work for the intensive care unit of a German hospital, located in Bochum.
4. Discussion
The central message of this work is twofold, namely that firstly, the integration of clinical expertise, especially in the field of intensive medical care, with the expertise from the microbiology laboratory, but also with the expertise of the mathematical and statistical modeler, represents a tremendous challenge, but secondly, that there is no time to lose in tackling it. Although we limited our descriptive or semi-quantitative analysis to a few problem areas in the field of the development of resistance of microbiological organisms to antimicrobial treatment, we can still report an overwhelming complexity of the clinical situation regarding nosocomial infections and antimicrobial resistance. Needless to say, due to the nature of any observational study, the evaluation presented is also full of limitations. Although we presented a reasonably comprehensive basket of analyses, the study is far from exhaustive. Many fundamental questions remain unanswered, nevertheless, we are tackling the task of structuring the clinical data and processes required for the structured optimization of ABS.
We would like to convey the insight that overcoming the resistance crisis should not be demanded with a raised index finger against the clinicians, but rather that the undoubtedly existing clinical expertise should not only be recognized, but should even be the basis for deriving expert systems within the framework of mathematical support systems. The main direction of impact should be the optimization of actions on the basis of both explicit and implicit clinical knowledge through coordination in a complex environment, in which statistical optimization methods, possibly also AI-based systems, can unfold their advantages. It should have become clear that the interdependence of global and local fields of action and impact, i.e. a synergistic perspective, is crucial.
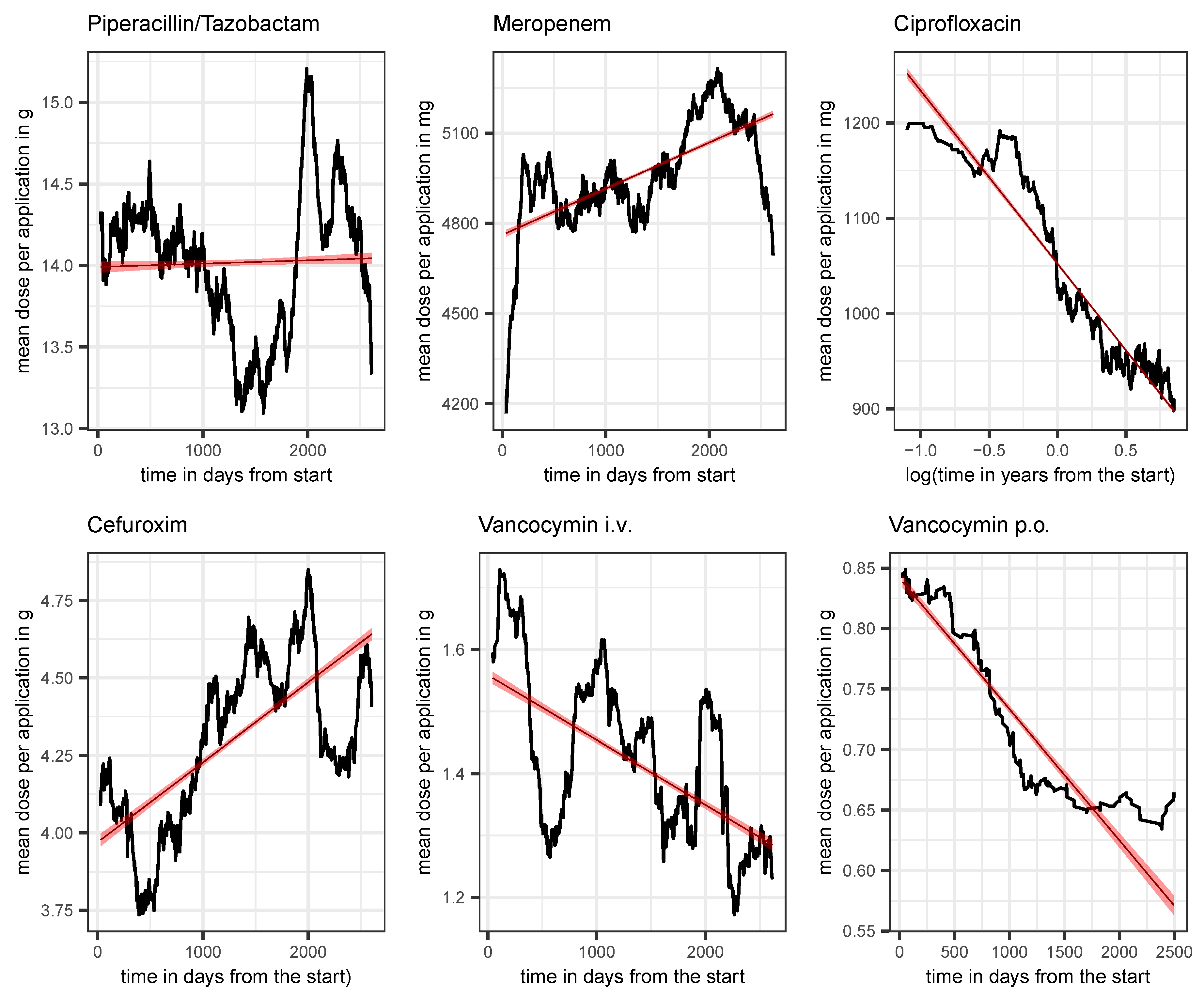
To be specific, we demonstrated, perhaps surprisingly, that the secular increase in resistance is quite moderate for most antibiotics, whereas the dependence on total consumption is strikingly high. But also here there are two counterintuitive observations, namely for vancomycin as well as for cefuroxim we obtain a decreasing proportion of resistance with increasing total consumption. An explanation based on the changing dose per application over time is initially obvious, but the fact that the dose for cefuroxim shows a clearly increasing trend, but the dose for vancomycin shows a markedly decreasing trend, requires a more precise analysis of the blood and tissue concentrations of the respective substance, i.e. precise drug monitoring.
It would be presumptuous to draw far-reaching conclusions from this, but the aforementioned observations make us confident that it is indeed feasible to curb resistance both through intelligent variations in consumption and adaptations in dose per application. This ambitious project is, of course, made more difficult by cross-resistance, which is indicated by the results of time lag cross-correlations. Thus, increasing overall consumption of antibiotics in the population increases the risk of resistance development, but what about low overall consumption but frequent intraindividual repeated use, i.e. an overuse on the individual level? Our provisionally derived results point to a positive correlation between the number of consecutive AB treatments within patients and share of inefficiency of treatment due to resistance.
Less surprising than secular shift and dependance of total consumption is the observation that mortality is higher among AB treated patients, where we assume “AB treated” as a surrogate for “infected”. In addition, length of ICU stay and, more general, duration of hospitalization turned out to be significantly prolonged within the AB treated cohort. A fatal effect of AB treatment itself cannot be ruled out, but is beyond the scope of what can be investigated here.
The assumption that mortality would be even higher without AB treatment seems plausible, but can at best be answered indirectly retrospectively on the basis of the available data set. For an indirect conclusion, for example, a presumably ineffective or at least less effective treatment due to resistance could be interpreted as a control in comparison with susceptible cases. For this purpose, we analyzed the epidemiological characteristics of the patients within the AB treatment stratum, including deaths and duration of hospitalization, stratified by assigned sensibility class using summary tables. The observed effect sizes differ among the 8 common antibiotics studied individually, but they all have in common at least a moderate increase in mortality with ineffective treatment, i.e. the presence of resistance, as well as a significant increase in the duration of hospitalization. Once again, there is a somewhat puzzling exception, namely the cohort of patients treated with ampicillin. The resistance rate for ampicillin is huge anyway, but the increase in deaths in the cohort under treatment with given susceptibility of the pathogen, is somewhat astonishing, to say the least. The assumption that suceptible germs could be more harmful and that the therapy is too slow to respond is, of course, just one of the possible speculations that must now be urgently reviewed. Or are there other or further synergistic or antagonistic interactions between pathogen variants and host, such as a disruption of the microbiome in the case of “successful” treatment of susceptible bacterial variants? It is clear that future research must be open in all directions.
In the population of patients treated with any of the 8 main antibiotic agents, the same picture emerges, namely a lower mortality in the subgroup that was treated inefficiently. However, if the ampicillin-treated patients are excluded, there is no sensibility-specific difference in mortality. The prolonged hospitalization time is the only constant result. No need to be emphasized that the length of stay is in a conditional relationship to the death event, but modeling competitive outcomes is far beyond feasibility here.
In summary, a number of hypotheses can be generated from the analyses carried out that still need to be tested, but unfortunately only a few concrete conclusions can be drawn. The obvious conclusion is that as long as precise knowledge of the dynamics is lacking, an equal distribution of the total consumption of the individual antibiotics should be aimed for, as the concentration of consumption on a small number of antibiotics increases the proportion of resistance. This is mainly due to the fact that hardly any antibiotic has a significantly lower proportion of ineffectiveness.
However, a closer look at the dynamics reveals that there are cyclical variations in resistance shares with approximately annual periods, which ultimately actually suggest a cyclical allocation strategy adapted to these cycles. Furthermore, we found evidence that these cycles associated with each antibiotic are systematically shifted in pairs, possibly indicating retarded cross-correlations. It is obvious that these transfer processes obey nonlinear dynamics.
That said, we draw attention to our observation that both multiple infections, often enough even with all known pathogens classified as particularly dangerous, and multiple antimicrobial therapies are the norm rather than the exception. Far-reaching interactions, which of course also include cross-relationships, can hardly be underestimated. Simply switching from one mainly used antibiotic to another main application does not really help here.
It need not be emphasized that any ABS strategy is limited by clinical indications that per se restrict the use to a few antibiotics. However, it must be warned against preferential allocation that is not based on well-founded evidence, which could be the case with piperacillin, for example. Let us then summarize our observations and obvious conclusions regarding the use of fluoroquinolones. The fact is that in the ICU studied, the use of these substances, which is strongly warned against in a red hand letter, was reduced to almost zero in the course of the observation period. Resistance to these substances also strongly suggests that they should not be reintroduced.
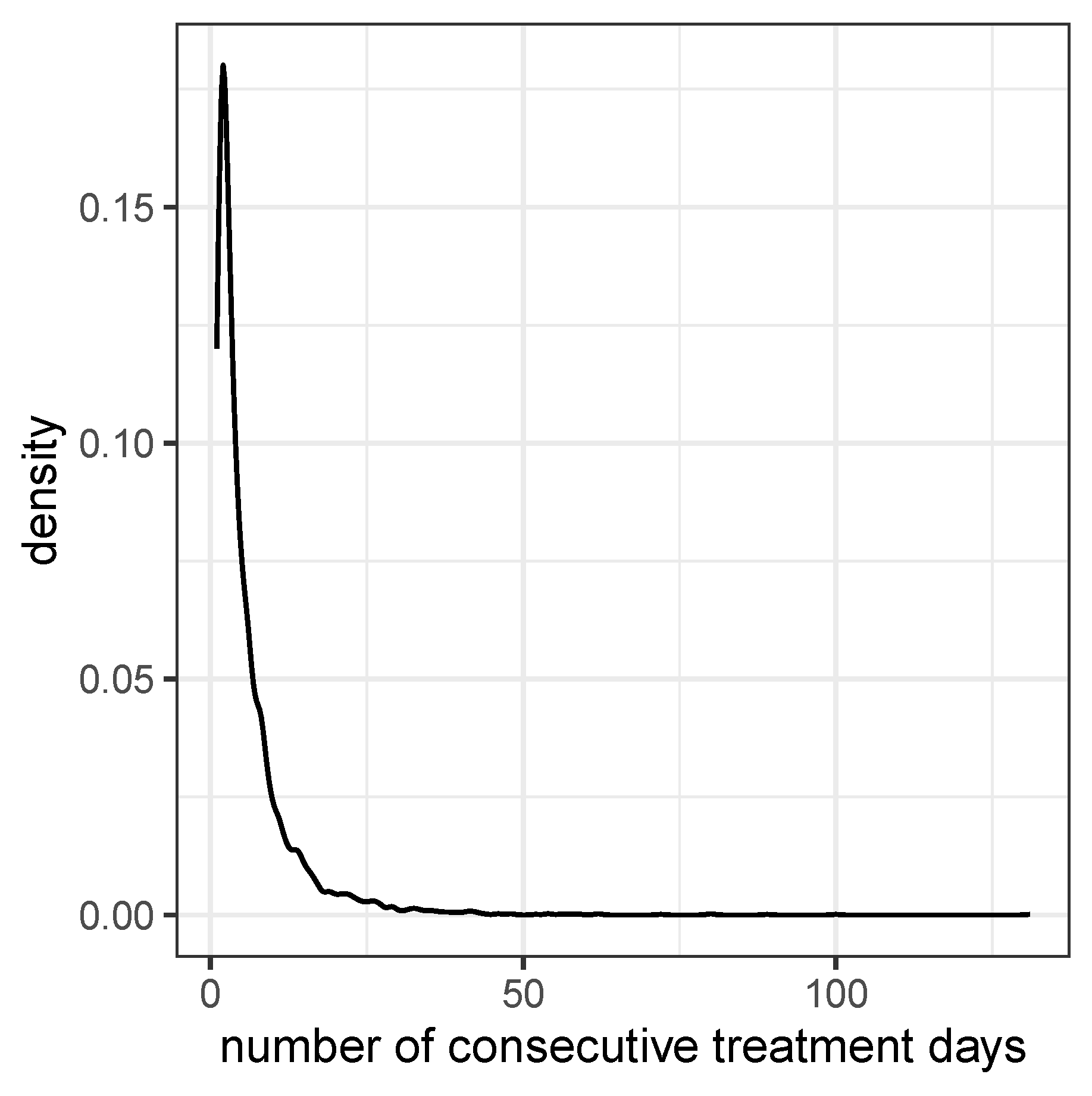
Figure 1.
Density Curve for the duration of treatment sequences (i.e. number of consecutive treatment days)
Figure 1.
Density Curve for the duration of treatment sequences (i.e. number of consecutive treatment days)
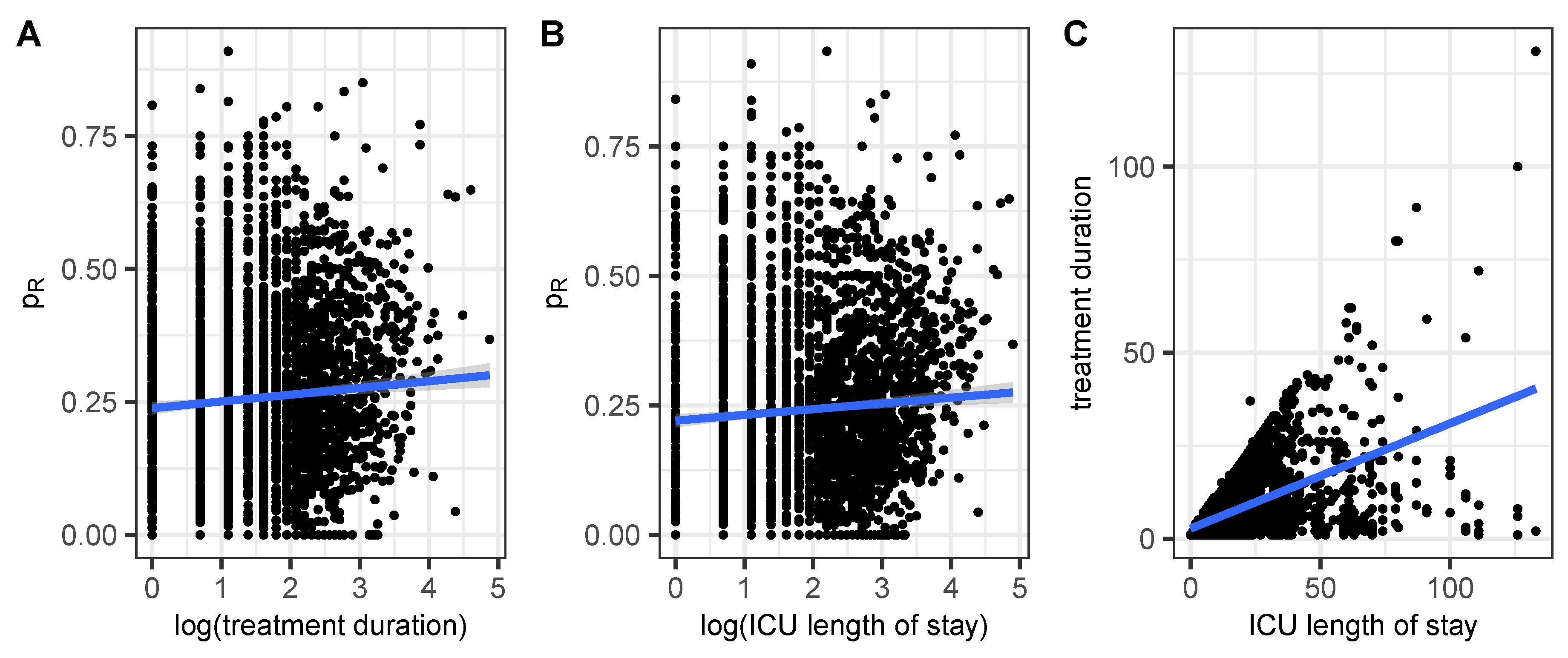
Figure 2.
Share of resistance within an antibiogram belonging to a patient/treatment sequence versus A) the length of the treatment sequence and B) the length of the ICU stay. Panel C shows the scatter plot of the two durations to check consistency.
Figure 2.
Share of resistance within an antibiogram belonging to a patient/treatment sequence versus A) the length of the treatment sequence and B) the length of the ICU stay. Panel C shows the scatter plot of the two durations to check consistency.
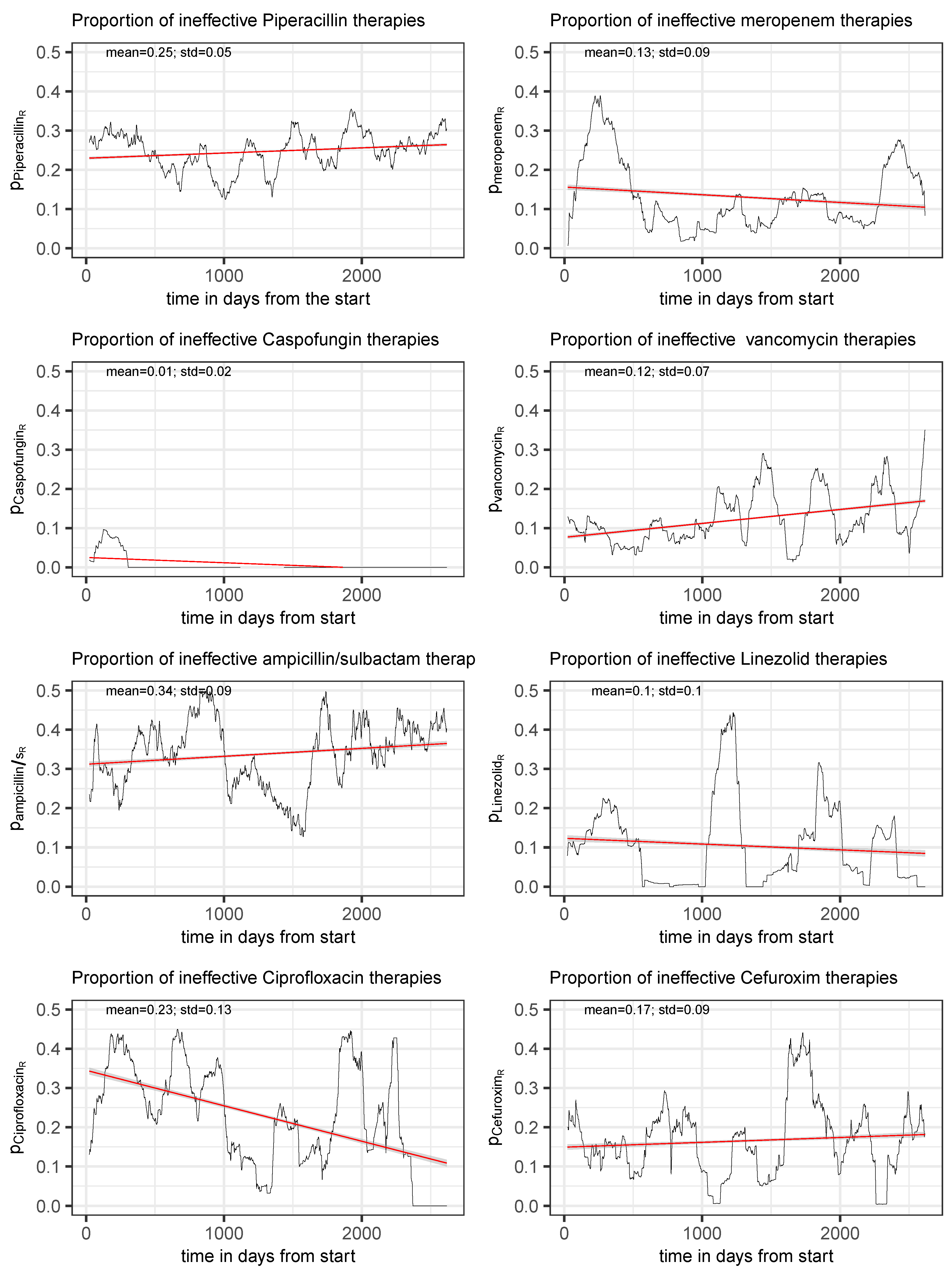
Figure 3.
Time series of the proportion of the total consumption of an antibiotic to which resistance of at least one of the treated pathogens was detected, shown for the eight most frequently administered antimicrobials. The red line represents a simple fitted linear model to visualize the trend.
Figure 3.
Time series of the proportion of the total consumption of an antibiotic to which resistance of at least one of the treated pathogens was detected, shown for the eight most frequently administered antimicrobials. The red line represents a simple fitted linear model to visualize the trend.
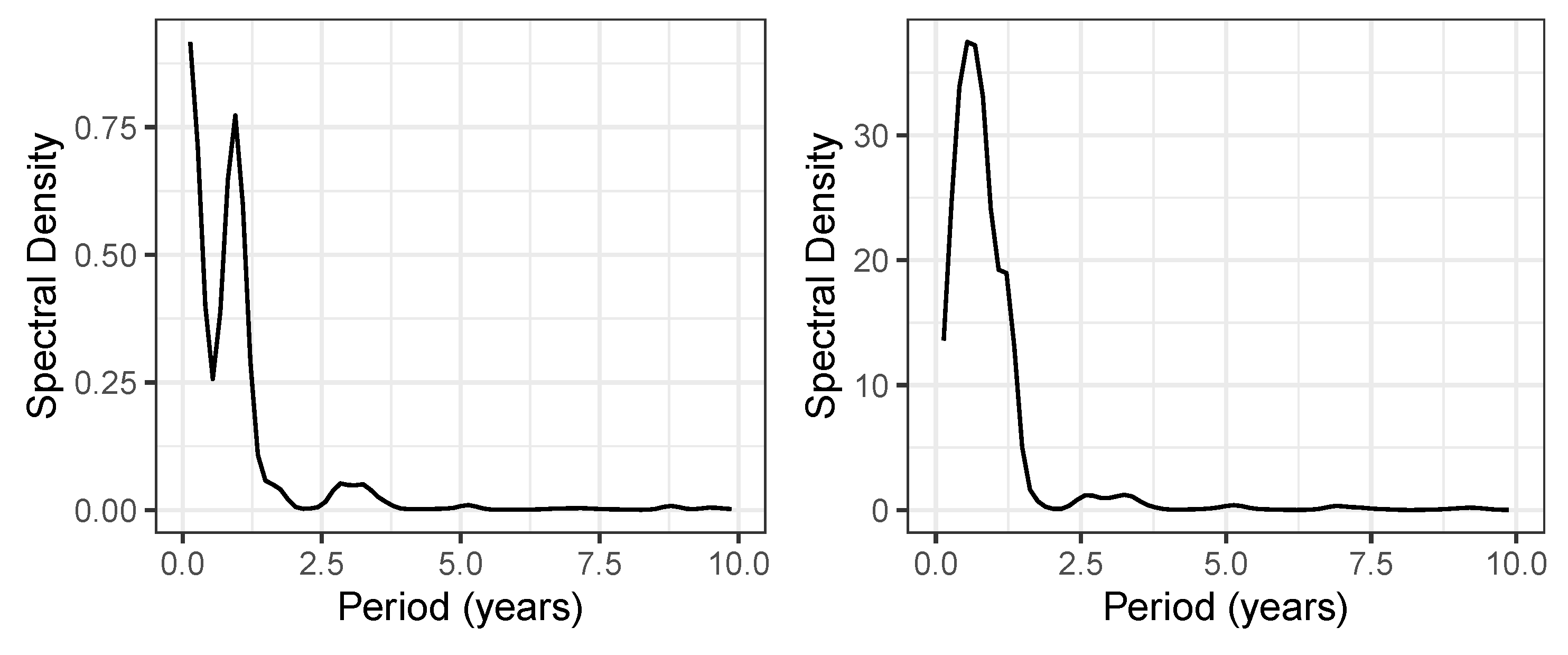
Figure 4.
Spectral density for the piperacillin consumption density time series. Left: Spectral density of , i.e. the proportion of ineffective applications. Right: Spectral density of piperacillin total consumption time series.
Figure 4.
Spectral density for the piperacillin consumption density time series. Left: Spectral density of , i.e. the proportion of ineffective applications. Right: Spectral density of piperacillin total consumption time series.
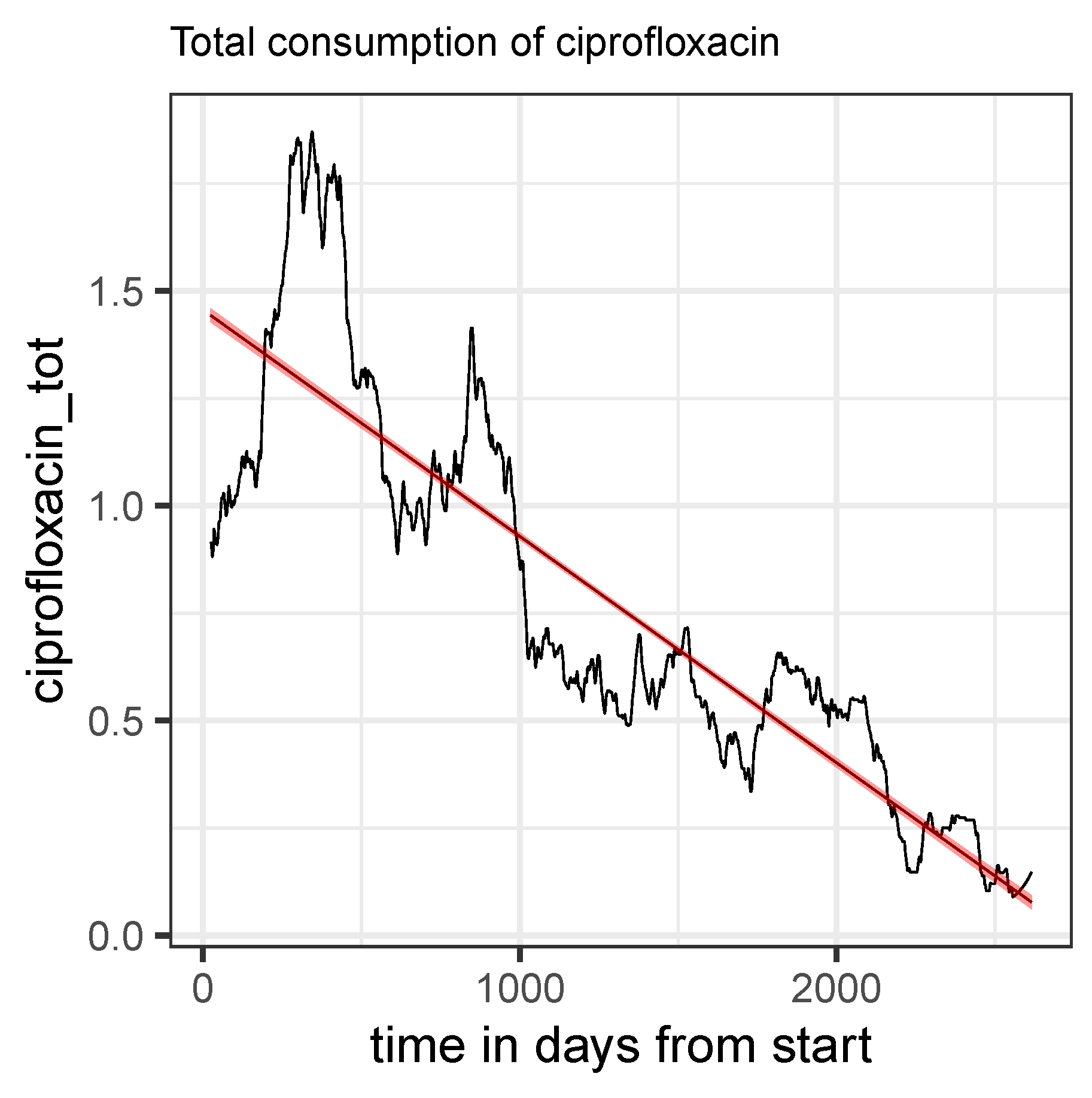
Figure 5.
Time series of total consumption of ciprofloxacin (black curve) along with a linear regression line (red).
Figure 5.
Time series of total consumption of ciprofloxacin (black curve) along with a linear regression line (red).
Figure 6.
Average dose per application in the course of time (moving average over intervalls of 180 days) along with a linear regression line plus confidence band for piperacillin/tazobactam, meropenem, ciprofloxacin, Cefuroxim, Vancocymin i.v., and Vancocymin p.o. as indicated in the header line of each panel. The time scale for ciprofloxacin is logarithmized to address the apparent exponential decay.
Figure 6.
Average dose per application in the course of time (moving average over intervalls of 180 days) along with a linear regression line plus confidence band for piperacillin/tazobactam, meropenem, ciprofloxacin, Cefuroxim, Vancocymin i.v., and Vancocymin p.o. as indicated in the header line of each panel. The time scale for ciprofloxacin is logarithmized to address the apparent exponential decay.
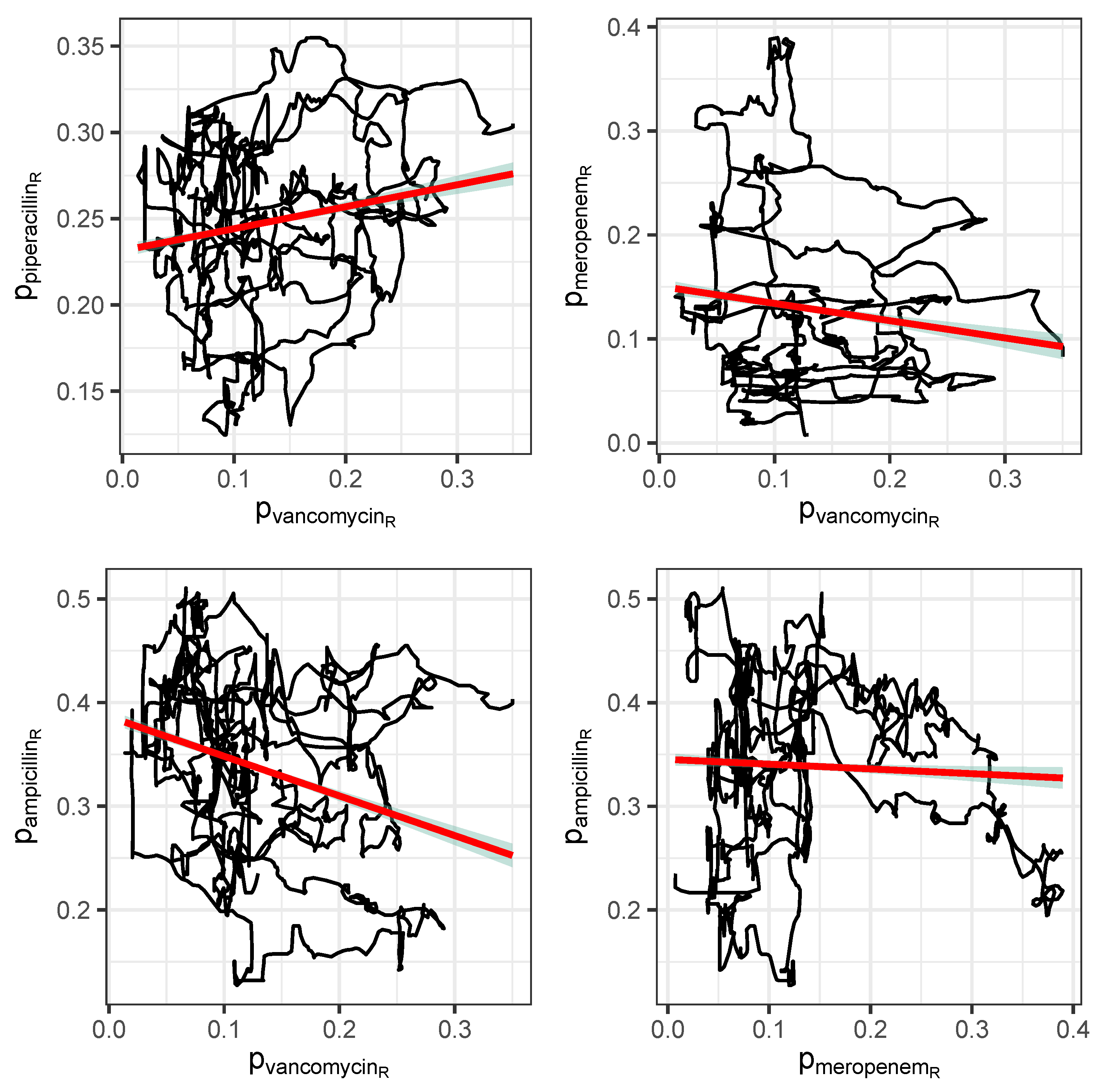
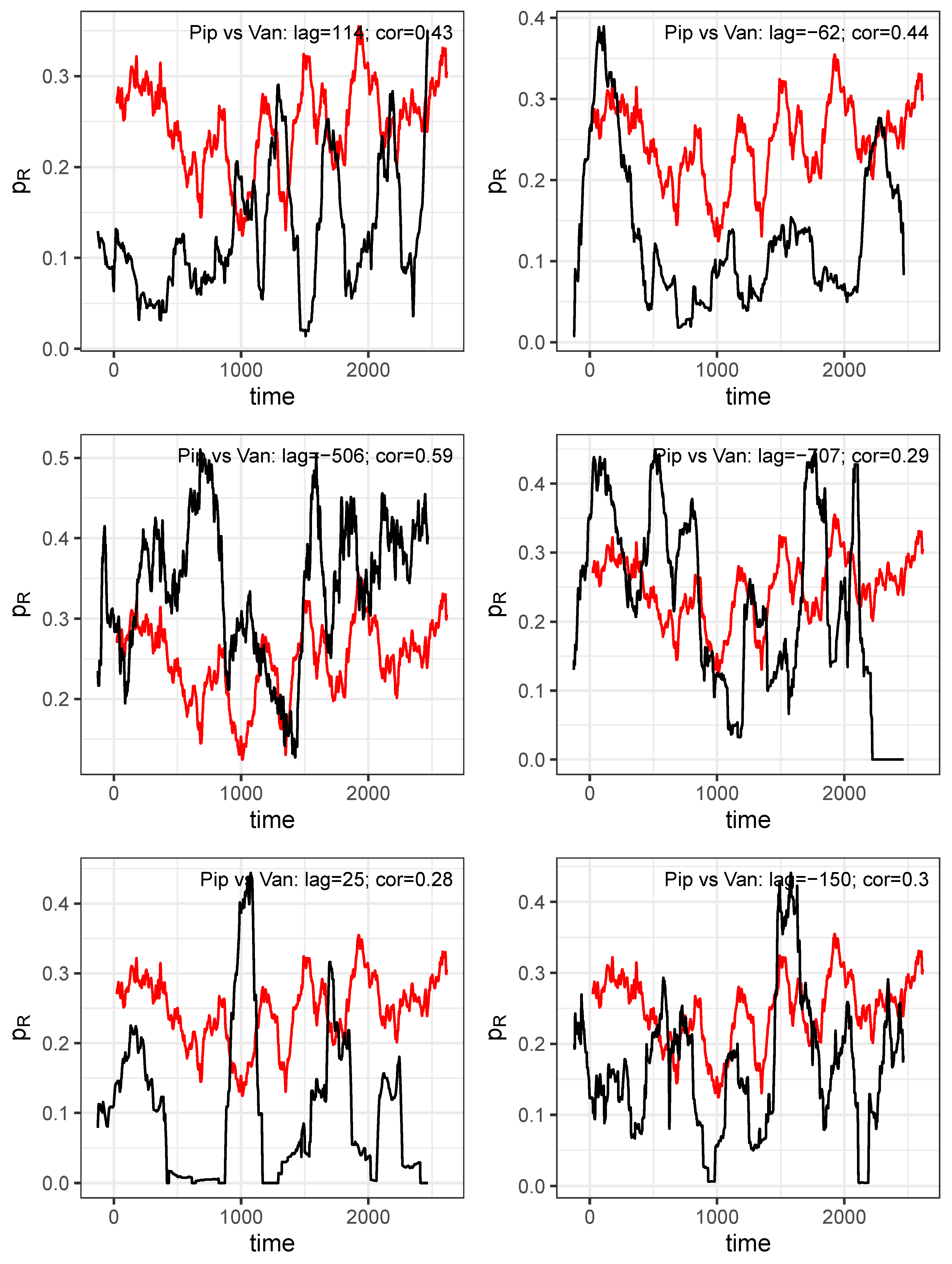
Figure 7.
Correlations between consumption time series depicted as trajectory versus with respect to antibiotics A and B, respectively.
Figure 7.
Correlations between consumption time series depicted as trajectory versus with respect to antibiotics A and B, respectively.
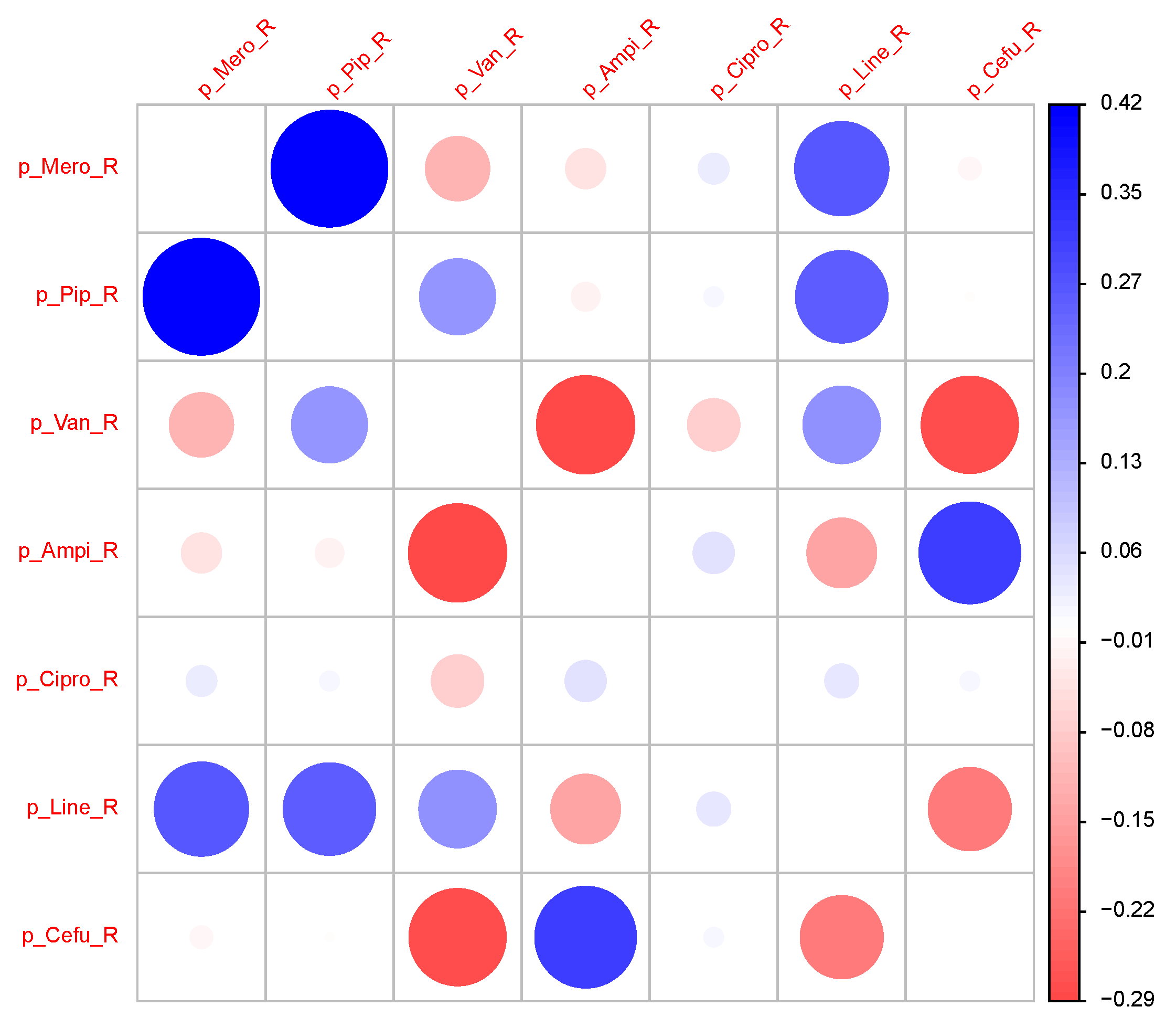
Figure 8.
Correlation Matrix of time series of the proportions of ineffective consumption.
Figure 8.
Correlation Matrix of time series of the proportions of ineffective consumption.
Figure 9.
Pairs of time series shifted against each other with delay derived from maximum cross correlations.
Figure 9.
Pairs of time series shifted against each other with delay derived from maximum cross correlations.
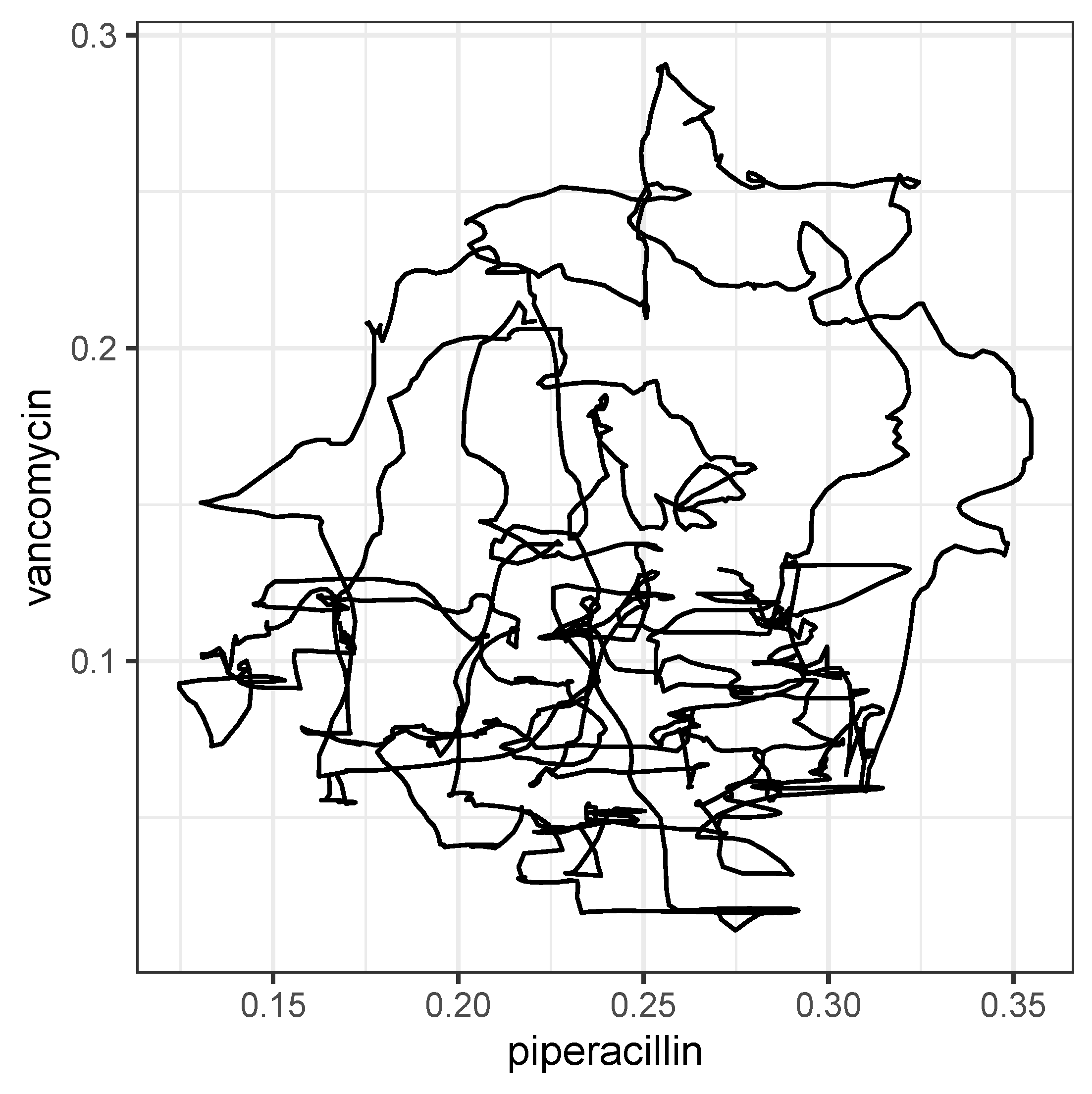
Figure 10.
Trajectory produced on the basis of mutally shifted time series and .
Figure 10.
Trajectory produced on the basis of mutally shifted time series and .
Table 1.
Summary table of demographic/epidemiological characteristics stratified by sex. Age in years and Age_group dichotomised in two groups at median. Subjects are ward stays. Three ward stays missing due to missing sex indication.
Table 1.
Summary table of demographic/epidemiological characteristics stratified by sex. Age in years and Age_group dichotomised in two groups at median. Subjects are ward stays. Three ward stays missing due to missing sex indication.
| Characteristic |
female
N = 4,141 |
male
N = 5,057 |
p-value |
| Age |
69 (56, 80) |
64 (52, 75) |
<0.001 |
| Age_group |
|
|
<0.001 |
| gt median |
2,271 (55%) |
2,279 (45%) |
|
| leq median |
1,870 (45%) |
2,778 (55%) |
|
| Hospitalization Duration (Days) |
13 (7, 25) |
15 (7, 28) |
0.002 |
| ICU Duration (Days) |
2 (1, 5) |
2 (1, 5) |
0.004 |
| Discharge Destination |
|
|
0.002 |
| death |
742 (18%) |
801 (16%) |
|
| external hospital |
1,434 (35%) |
1,686 (33%) |
|
| home |
1,965 (47%) |
2,570 (51%) |
|
| Median (Q1, Q3); n (%); Wilcoxon rank sum test; Pearson’s Chi-squared test. |
Table 2.
Summary table of demographic characteristics stratified by antibiotic treatment flag. Subjects are ward stays.
Table 2.
Summary table of demographic characteristics stratified by antibiotic treatment flag. Subjects are ward stays.
| Characteristic |
Overall
N = 9,201 |
w/o AB treatment
N = 4,281 |
with AB treatment
N = 4,920 |
p-value |
| Sex |
|
|
|
<0.001 |
| female |
4,141 (45%) |
2,120 (50%) |
2,021 (41%) |
|
| male |
5,057 (55%) |
2,161 (50%) |
2,896 (59%) |
|
| Unknown |
3 |
0 |
3 |
|
| Age |
66 (54, 78) |
66 (52, 78) |
66 (55, 77) |
0.4 |
| Destination |
|
|
|
<0.001 |
| death |
1,545 (17%) |
487 (11%) |
1,058 (22%) |
|
| external hospital |
3,121 (34%) |
1,405 (33%) |
1,716 (35%) |
|
| home |
4,535 (49%) |
2,389 (56%) |
2,146 (44%) |
|
| Hospital Duration |
14 (7, 26) |
9 (4, 16) |
21 (11, 37) |
<0.001 |
| ICU Duration |
2 (1, 5) |
1 (1, 2) |
4 (1, 9) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Wilcoxon rank sum test |
Table 3.
Frequencies of the different numbers of sequences per patient.
Table 3.
Frequencies of the different numbers of sequences per patient.
| sequences per patient |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
10 |
| frequency |
3222 |
506 |
123 |
29 |
12 |
4 |
2 |
1 |
1 |
Table 4.
Frequency table for the occurances of simultaneous antimicrobial treatments per patient per day
Table 4.
Frequency table for the occurances of simultaneous antimicrobial treatments per patient per day
| n_AB per patient per day |
occurrances |
| 1 |
14419 |
| 2 |
7998 |
| 3 |
4169 |
| 4 |
1814 |
| 5 |
701 |
| 6 |
229 |
| 7 |
61 |
| 8 |
21 |
| 10 |
1 |
Table 5.
Frequency table showing the number of occurences of each sensibility class S, I, R, and n.a., respectively.
Table 5.
Frequency table showing the number of occurences of each sensibility class S, I, R, and n.a., respectively.
| sensibility |
challenges |
distinct IDs |
| n.a. |
537 |
148 |
| I |
12309 |
2477 |
| R |
41525 |
2951 |
| S |
101223 |
3406 |
Table 6.
Frequently isolated pathogens.
Table 6.
Frequently isolated pathogens.
| Pathogen |
n |
| Escherichia coli |
3091 |
| Staphylococcus epidermidis |
2664 |
| Candida albicans |
2299 |
| Enterococcus faecium |
1745 |
| Staphylococcus aureus |
1579 |
| Klebsiella pneumoniae |
1336 |
| Candida glabrata |
1265 |
| Pseudomonas aeruginosa |
1126 |
| Enterococcus faecalis |
644 |
| Enterobacter cloacae |
614 |
Table 7.
Results from linear regression: Share of resistance versus logarithm of duration of treatment sequence.
Table 7.
Results from linear regression: Share of resistance versus logarithm of duration of treatment sequence.
| Characteristic |
Beta |
95% CI |
p-value |
| log(duration) |
0.01 |
0.01, 0.02 |
<0.001 |
| CI = Confidence Interval |
Table 8.
Results from linear regression: Share of resistance versus logarithm of ICU length of stay.
Table 8.
Results from linear regression: Share of resistance versus logarithm of ICU length of stay.
| Characteristic |
Beta |
95% CI |
p-value |
| log(ICU.Stay + 1) |
0.01 |
0.00, 0.02 |
<0.001 |
| CI = Confidence Interval |
Table 9.
Results from linear regression: Share of resistance versus hospital discharge destination.
Table 9.
Results from linear regression: Share of resistance versus hospital discharge destination.
| Characteristic |
Beta |
95% CI |
p-value |
| Destination: |
|
|
|
| external hospital |
— |
— |
|
| home |
-0.001 |
-0.015, 0.012 |
0.865 |
| death |
0.002 |
-0.014, 0.018 |
0.789 |
| CI = Confidence Interval |
Table 10.
Results from linear regression: Share of resistance versus number of distinct treatment sequences per patient (n_seq).
Table 10.
Results from linear regression: Share of resistance versus number of distinct treatment sequences per patient (n_seq).
| Characteristic |
Beta |
95% CI |
p-value |
| n_seq |
0.04 |
0.03, 0.05 |
<0.001 |
| CI = Confidence Interval |
Table 11.
The 9 most frequently administered antibiotics.
Table 11.
The 9 most frequently administered antibiotics.
| Antibiotic |
n_Days |
n_Indiv |
| Piperacillin/Tazobactam i.v. |
8227 |
1752 |
| Meropenem i.v. |
6643 |
1011 |
| Caspofungin i.v. |
3598 |
439 |
| Vancomycin i.v. |
3455 |
637 |
| Ampicillin/Sulbactam i.v. |
2927 |
903 |
| Flucloxacillin i.v. |
2448 |
406 |
| Linezolid i.v. |
2434 |
371 |
| Ciprofloxacin i.v. |
2384 |
547 |
| Cefuroxim i.v. |
2265 |
596 |
Table 12.
Linear regression of the proportion of ineffective piperacillin/tazobactam consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 12.
Linear regression of the proportion of ineffective piperacillin/tazobactam consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.182 |
0.170, 0.195 |
0.000 |
| Mibi Time |
0.002 |
0.001, 0.003 |
0.000 |
| Total Consumption |
0.023 |
0.017, 0.028 |
0.000 |
| CI = Confidence Interval |
Table 13.
Summary table of performed piperacillin tests stratified by observed sensibility class.
Table 13.
Summary table of performed piperacillin tests stratified by observed sensibility class.
| Antibiotic |
Sensibility |
n |
| Piperacillin |
I |
352 |
| Piperacillin |
R |
3242 |
| Piperacillin |
S |
1459 |
| Piperacillin/Tazobactam |
|
3 |
| Piperacillin/Tazobactam |
I |
1169 |
| Piperacillin/Tazobactam |
R |
1313 |
| Piperacillin/Tazobactam |
S |
3925 |
Table 14.
Summary table of combinations of performed piperacillin tests.
Table 14.
Summary table of combinations of performed piperacillin tests.
| Antibiotic |
n |
| Both |
5017 |
| Piperacillin |
36 |
| Piperacillin/Tazobactam |
1393 |
Table 15.
Most common pathogens tested for piperacillin (with and w/o tazobactam) resistance stratified by sensibility.
Table 15.
Most common pathogens tested for piperacillin (with and w/o tazobactam) resistance stratified by sensibility.
| Pathogen |
Sensibility |
n |
| Escherichia coli |
S |
2141 |
| Escherichia coli |
I |
650 |
| Escherichia coli |
R |
1736 |
| Klebsiella pneumoniae |
S |
641 |
| Klebsiella pneumoniae |
R |
1213 |
| Pseudomonas aeruginosa |
S |
433 |
| Pseudomonas aeruginosa |
I |
714 |
| Pseudomonas aeruginosa |
R |
813 |
| Serratia marcescens |
S |
576 |
| Proteus mirabilis |
S |
542 |
| Klebsiella oxytoca |
R |
374 |
Table 16.
Three most common pathogens tested for piperacillin/tazobactam resistance stratified by sensibility.
Table 16.
Three most common pathogens tested for piperacillin/tazobactam resistance stratified by sensibility.
| Pathogen |
Sensibility |
n |
| Escherichia coli |
S |
1583 |
| Escherichia coli |
I |
650 |
| Escherichia coli |
R |
376 |
| Klebsiella pneumoniae |
S |
641 |
| Klebsiella pneumoniae |
I |
79 |
| Klebsiella pneumoniae |
R |
382 |
| Klebsiella pneumoniae |
|
3 |
| Pseudomonas aeruginosa |
S |
217 |
| Pseudomonas aeruginosa |
I |
370 |
| Pseudomonas aeruginosa |
R |
394 |
Table 17.
Summary table of epidemiological characteristics of piperacillin-treated patients stratified by observed sensibility.
Table 17.
Summary table of epidemiological characteristics of piperacillin-treated patients stratified by observed sensibility.
| Characteristic |
I
N = 185 |
n.a.
N = 747 |
R
N = 309 |
S
N = 511 |
p-value |
| Sex |
|
|
|
|
0.7 |
| female |
69 (37%) |
299 (40%) |
130 (42%) |
210 (41%) |
|
| male |
116 (63%) |
448 (60%) |
178 (58%) |
301 (59%) |
|
| Unknown |
0 |
0 |
1 |
0 |
|
| Age |
70 (60, 80) |
68 (56, 78) |
67 (58, 76) |
69 (59, 79) |
0.031 |
| Destination |
|
|
|
|
0.2 |
| death |
54 (29%) |
216 (29%) |
98 (32%) |
139 (27%) |
|
| external hospital |
82 (44%) |
293 (39%) |
112 (36%) |
227 (44%) |
|
| home |
49 (26%) |
238 (32%) |
99 (32%) |
145 (28%) |
|
| ICU Duration |
7 (2, 15) |
5 (2, 10) |
8 (3, 21) |
7 (3, 15) |
<0.001 |
| Hospital Duration |
22 (12, 39) |
15 (8, 24) |
35 (18, 54) |
22 (13, 36) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test. |
Table 18.
Linear regression of the proportion of ineffective meropenem consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 18.
Linear regression of the proportion of ineffective meropenem consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.040 |
0.030, 0.049 |
0.000 |
| Mibi Time |
-0.024 |
-0.026, -0.022 |
0.000 |
| Total Consumption |
0.083 |
0.077, 0.088 |
0.000 |
| CI = Confidence Interval |
Table 19.
Summary table of performed meropenem tests stratified by observed sensibility class.
Table 19.
Summary table of performed meropenem tests stratified by observed sensibility class.
| Antibiotic |
Sensibility |
n |
| Meropenem |
I |
222 |
| Meropenem |
R |
291 |
| Meropenem |
S |
6685 |
Table 20.
Most common pathogens tested for meropenem resistance stratified by observed sensibility.
Table 20.
Most common pathogens tested for meropenem resistance stratified by observed sensibility.
| Pathogen |
Sensibility |
n |
| Escherichia coli |
S |
2617 |
| Escherichia coli |
R |
4 |
| Klebsiella pneumoniae |
S |
1071 |
| Klebsiella pneumoniae |
I |
15 |
| Klebsiella pneumoniae |
R |
17 |
| Pseudomonas aeruginosa |
S |
590 |
| Pseudomonas aeruginosa |
I |
192 |
| Pseudomonas aeruginosa |
R |
214 |
| Enterobacter cloacae |
S |
512 |
| Enterobacter cloacae |
I |
4 |
| Enterobacter cloacae |
R |
5 |
| Proteus mirabilis |
S |
390 |
| Proteus mirabilis |
R |
1 |
| Klebsiella oxytoca |
S |
366 |
| Klebsiella oxytoca |
I |
1 |
Table 21.
Summary table of epidemiological characteristics of meropenem-treated patients stratified by observed sensibility.
Table 21.
Summary table of epidemiological characteristics of meropenem-treated patients stratified by observed sensibility.
| Characteristic |
I
N = 32 |
n.a.
N = 307 |
R
N = 86 |
S
N = 586 |
p-value |
| Sex |
|
|
|
|
0.8 |
| female |
13 (41%) |
124 (40%) |
31 (36%) |
222 (38%) |
|
| male |
19 (59%) |
183 (60%) |
55 (64%) |
363 (62%) |
|
| Unknown |
0 |
0 |
0 |
1 |
|
| Age |
63 (50, 73) |
64 (54, 75) |
63 (53, 71) |
66 (55, 75) |
0.060 |
| Destination |
|
|
|
|
0.12 |
| death |
9 (28%) |
120 (39%) |
35 (41%) |
185 (32%) |
|
| external hospital |
16 (50%) |
101 (33%) |
32 (37%) |
227 (39%) |
|
| home |
7 (22%) |
86 (28%) |
19 (22%) |
174 (30%) |
|
| ICU Duration |
9 (3, 29) |
7 (2, 14) |
14 (5, 27) |
10 (3, 20) |
<0.001 |
| Hospital Duration |
36 (19, 49) |
20 (10, 33) |
40 (26, 77) |
27 (16, 46) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test |
Table 22.
Crosstable showing the frequencies of observed sensibility classes of all pathogens challenged with caspofungin.
Table 22.
Crosstable showing the frequencies of observed sensibility classes of all pathogens challenged with caspofungin.
| Pathogen |
n.a. |
I |
R |
S |
| Candida albicans |
63 |
0 |
0 |
83 |
| Candida dubliniensis |
4 |
0 |
0 |
0 |
| Candida glabrata |
50 |
0 |
0 |
46 |
| Candida guilliermondii |
1 |
0 |
0 |
0 |
| Candida krusei |
6 |
0 |
0 |
0 |
| Candida lusitaniae |
0 |
0 |
0 |
1 |
| Candida norvegensis |
0 |
0 |
0 |
1 |
| Candida orthopsilosis |
1 |
0 |
0 |
0 |
| Candida parapsilosis |
11 |
1 |
4 |
12 |
| Candida tropicalis |
5 |
0 |
0 |
19 |
| Clavispora lusitaniae |
1 |
0 |
0 |
0 |
Table 23.
Most common pathogens tested for vancomyvin resistance stratified by sensibility.
Table 23.
Most common pathogens tested for vancomyvin resistance stratified by sensibility.
| Pathogen |
Sensibility |
n |
| Staphylococcus epidermidis |
S |
1589 |
| Enterococcus faecium |
S |
976 |
| Enterococcus faecium |
R |
383 |
| Enterococcus faecalis |
S |
528 |
| Staphylococcus hominis |
S |
306 |
| Staphylococcus hominis |
R |
1 |
| Staphylococcus capitis |
S |
219 |
| Staphylococcus haemolyticus |
S |
161 |
| Staphylococcus aureus |
S |
115 |
| Streptococcus constellatus |
S |
59 |
Table 24.
Linear regression of the proportion of ineffective vancomycin consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 24.
Linear regression of the proportion of ineffective vancomycin consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.120 |
0.109, 0.132 |
0.000 |
| Mibi Time |
0.013 |
0.012, 0.014 |
0.000 |
| Total Consumption |
-0.031 |
-0.038, -0.023 |
0.000 |
| CI = Confidence Interval |
Table 25.
Summary table of epidemiological characteristics of vancomycin-treated patients stratified by observed sensibility.
Table 25.
Summary table of epidemiological characteristics of vancomycin-treated patients stratified by observed sensibility.
| Characteristic |
n.a.
N = 219 |
R
N = 75 |
S
N = 393 |
p-value |
| Sex |
|
|
|
0.015 |
| female |
103 (47%) |
35 (47%) |
142 (36%) |
|
| male |
116 (53%) |
39 (53%) |
251 (64%) |
|
| Unknown |
0 |
1 |
0 |
|
| Age |
66 (53, 76) |
64 (57, 72) |
64 (54, 74) |
0.6 |
| Destination |
|
|
|
0.067 |
| death |
89 (41%) |
28 (37%) |
130 (33%) |
|
| external hospital |
71 (32%) |
27 (36%) |
174 (44%) |
|
| home |
59 (27%) |
20 (27%) |
89 (23%) |
|
| ICU Duration |
6 (2, 12) |
9 (3, 22) |
13 (4, 23) |
<0.001 |
| Hospital Duration |
18 (6, 32) |
51 (33, 87) |
30 (16, 50) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test. |
Table 26.
List of the 23 antimicrobials given to the patient with the most administrations during his/her hospital stay.
Table 26.
List of the 23 antimicrobials given to the patient with the most administrations during his/her hospital stay.
| Ertapenem i.v. |
Valganciclovir p.o. |
Colistin i.v. |
| Fluconazol i.v. |
Piperacillin/Tazobactam i.v. |
Meropenem i.v. |
| Ganciclovir i.v. |
Linezolid i.v. |
Gentamicin i.v. |
| Metronidazol i.v. |
Micafungin i.v. |
Ceftolozan/Tazobactam i.v. |
| Caspofungin i.v. |
Tigecyclin i.v. |
Tobramycin i.v. |
| Imipenem/Cilastatin i.v. |
Flucloxacillin i.v. |
Voriconazol p.o. |
| Erythromycin i.v. |
Cefepim i.v. |
Ampicillin/Sulbactam i.v. |
| Vancomycin i.v. |
Ciprofloxacin i.v. |
|
Table 27.
Summary table of performed ampicillin/sulbactam tests stratified by observed sensibility class.
Table 27.
Summary table of performed ampicillin/sulbactam tests stratified by observed sensibility class.
| Antibiotic |
Sensibility |
n |
| Ampicillin |
|
1 |
| Ampicillin |
I |
510 |
| Ampicillin |
R |
6455 |
| Ampicillin |
S |
1274 |
| Ampicillin/Sulbactam |
I |
1085 |
| Ampicillin/Sulbactam |
R |
3081 |
| Ampicillin/Sulbactam |
S |
910 |
Table 28.
Most common pathogens tested for meropenem resistance stratified by observed sensibility.
Table 28.
Most common pathogens tested for meropenem resistance stratified by observed sensibility.
| Pathogen |
Sensibility |
n |
| Escherichia coli |
S |
385 |
| Escherichia coli |
I |
474 |
| Escherichia coli |
R |
1329 |
| Klebsiella pneumoniae |
S |
249 |
| Klebsiella pneumoniae |
I |
235 |
| Klebsiella pneumoniae |
R |
449 |
| Enterobacter cloacae |
R |
420 |
| Proteus mirabilis |
S |
87 |
| Proteus mirabilis |
I |
165 |
| Proteus mirabilis |
R |
49 |
| Serratia marcescens |
R |
293 |
Table 29.
Linear regression of the proportion of ineffective ampicillin/sulbactam consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 29.
Linear regression of the proportion of ineffective ampicillin/sulbactam consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.272 |
0.253, 0.291 |
0.000 |
| Mibi Time |
0.009 |
0.007, 0.011 |
0.000 |
| Total Consumption |
0.028 |
0.016, 0.040 |
0.000 |
| CI = Confidence Interval. |
Table 30.
Summary table of epidemiological characteristics of ampicillin/sulbactam-treated patients stratified by observerd sensibility.
Table 30.
Summary table of epidemiological characteristics of ampicillin/sulbactam-treated patients stratified by observerd sensibility.
| Characteristic |
I
N = 77 |
n.a.
N = 449 |
R
N = 292 |
S
N = 85 |
p-value |
| Sex |
|
|
|
|
0.5 |
| female |
35 (45%) |
185 (41%) |
108 (37%) |
32 (38%) |
|
| male |
42 (55%) |
264 (59%) |
184 (63%) |
53 (62%) |
|
| Age |
71 (56, 79) |
67 (53, 77) |
68 (58, 77) |
66 (57, 75) |
0.4 |
| Destination |
|
|
|
|
0.002 |
| death |
14 (18%) |
66 (15%) |
55 (19%) |
23 (27%) |
|
| external hospital |
34 (44%) |
143 (32%) |
115 (39%) |
31 (36%) |
|
| home |
29 (38%) |
240 (53%) |
122 (42%) |
31 (36%) |
|
| ICU Duration |
5 (3, 12) |
3 (1, 7) |
7 (3, 15) |
8 (2, 15) |
<0.001 |
| Hospital Duration |
21 (13, 38) |
14 (9, 25) |
28 (15, 49) |
24 (12, 39) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test. |
Table 31.
Summary table of epidemiological characteristics of Linezolid-treated patients stratified by observerd sensibility.
Table 31.
Summary table of epidemiological characteristics of Linezolid-treated patients stratified by observerd sensibility.
| Characteristic |
n.a.
N = 103 |
R
N = 24 |
S
N = 244 |
p-value |
| Sex |
|
|
|
>0.9 |
| female |
42 (41%) |
9 (38%) |
102 (42%) |
|
| male |
61 (59%) |
15 (63%) |
141 (58%) |
|
| Unknown |
0 |
0 |
1 |
|
| Age |
66 (54, 76) |
62 (49, 73) |
65 (55, 75) |
0.6 |
| Destination |
|
|
|
0.6 |
| death |
44 (43%) |
8 (33%) |
85 (35%) |
|
| external hospital |
34 (33%) |
9 (38%) |
83 (34%) |
|
| home |
25 (24%) |
7 (29%) |
76 (31%) |
|
| ICU Duration |
6 (2, 15) |
15 (2, 49) |
11 (4, 22) |
0.009 |
| Hospital Duration |
25 (12, 42) |
62 (30, 89) |
41 (23, 62) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test. |
Table 32.
Linear regression of the proportion of ineffective linezolid consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 32.
Linear regression of the proportion of ineffective linezolid consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.048 |
0.031, 0.065 |
0.000 |
| Mibi Time |
0.002 |
0.000, 0.005 |
0.087 |
| Total Consumption |
0.057 |
0.046, 0.069 |
0.000 |
| CI = Confidence Interval. |
Table 33.
Linear regression of the proportion of ineffective ciprofloxacin consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 33.
Linear regression of the proportion of ineffective ciprofloxacin consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.054 |
0.025, 0.083 |
0.000 |
| Mibi Time |
0.005 |
0.001, 0.010 |
0.010 |
| Total Consumption |
0.200 |
0.181, 0.219 |
0.000 |
| CI = Confidence Interval. |
Table 34.
10 most frequent pathogens isolated in patients treated with fluoroquinolones.
Table 34.
10 most frequent pathogens isolated in patients treated with fluoroquinolones.
| Pathogen |
n |
| Staphylococcus epidermidis |
969 |
| Candida albicans |
884 |
| Escherichia coli |
648 |
| Enterococcus faecium |
505 |
| Candida glabrata |
433 |
| Pseudomonas aeruginosa |
419 |
| Klebsiella pneumoniae |
383 |
| Staphylococcus aureus |
380 |
| Enterobacter cloacae |
238 |
| Serratia marcescens |
165 |
Table 35.
Frequency of observed fluoroquinolone sensibility classes.
Table 35.
Frequency of observed fluoroquinolone sensibility classes.
| Sensibility class |
n |
| n.a. |
3 |
| I |
295 |
| R |
1370 |
| S |
2065 |
Table 36.
Summary table of epidemiological characteristics of ciprofloxacin-treated patients stratified by observed sensibility.
Table 36.
Summary table of epidemiological characteristics of ciprofloxacin-treated patients stratified by observed sensibility.
| Characteristic |
I
N = 37 |
n.a.
N = 135 |
R
N = 109 |
S
N = 266 |
p-value |
| Sex |
|
|
|
|
0.080 |
| female |
18 (49%) |
64 (47%) |
42 (39%) |
94 (35%) |
|
| male |
19 (51%) |
71 (53%) |
67 (61%) |
172 (65%) |
|
| Age |
64 (57, 78) |
68 (54, 77) |
65 (54, 74) |
69 (56, 77) |
0.2 |
| Destination |
|
|
|
|
0.6 |
| death |
7 (19%) |
40 (30%) |
28 (26%) |
62 (23%) |
|
| external hospital |
20 (54%) |
56 (41%) |
53 (49%) |
135 (51%) |
|
| home |
10 (27%) |
39 (29%) |
28 (26%) |
69 (26%) |
|
| ICU Duration |
14 (6, 23) |
7 (1, 12) |
14 (4, 28) |
10 (5, 20) |
<0.001 |
| Hospital Duration |
32 (22, 49) |
18 (9, 31) |
38 (21, 62) |
28 (16, 41) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test. |
Table 37.
Linear regression of the proportion of ineffective cefuroxim consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
Table 37.
Linear regression of the proportion of ineffective cefuroxim consumption on time and total consumption. "Mibi Time" refers to the time of the microbiological examination in years from start of the study period and "Total Consumption" refers to an estimated DDD.
| Characteristic |
Beta |
95% CI |
p-value |
| (Intercept) |
0.280 |
0.254, 0.306 |
0.000 |
| Mibi Time |
-0.019 |
-0.024, -0.013 |
0.000 |
| Total Consumption |
-0.188 |
-0.223, -0.152 |
0.000 |
| Mibi Time * Total Consumption |
0.034 |
0.027, 0.041 |
0.000 |
| CI = Confidence Interval. |
Table 38.
Summary table of epidemiological characteristics stratified by observed sensibility with respect to all 8 main antimicrobial representatives.
Table 38.
Summary table of epidemiological characteristics stratified by observed sensibility with respect to all 8 main antimicrobial representatives.
| Characteristic |
I
N = 158 |
n.a.
N = 1,492 |
R
N = 391 |
S
N = 473 |
p-value |
| Sex |
|
|
|
|
0.6 |
| female |
63 (40%) |
593 (40%) |
152 (39%) |
203 (43%) |
|
| male |
95 (60%) |
898 (60%) |
238 (61%) |
270 (57%) |
|
| Unknown |
0 |
1 |
1 |
0 |
|
| Age |
73 (60, 81) |
66 (55, 77) |
68 (59, 77) |
69 (60, 78) |
<0.001 |
| Destination |
|
|
|
|
<0.001 |
| death |
38 (24%) |
290 (19%) |
87 (22%) |
134 (28%) |
|
| external hospital |
78 (49%) |
469 (31%) |
143 (37%) |
196 (41%) |
|
| home |
42 (27%) |
733 (49%) |
161 (41%) |
143 (30%) |
|
| ICU Duration |
6 (2, 15) |
3 (1, 8) |
5 (2, 14) |
5 (2, 12) |
<0.001 |
| Hospital Duration |
19 (12, 33) |
16 (9, 27) |
28 (15, 47) |
21 (11, 34) |
<0.001 |
| n (%); Median (Q1, Q3); Pearson’s Chi-squared test; Kruskal-Wallis rank sum test. |