Prerpints.org logo
Preprint
Article

Fractional-Order Regularization of Quantum Vacuum Energy via the Mittag-Leffler Function

This version is not peer-reviewed.

Submitted:

16 March 2025

Posted:

18 March 2025

You are already at the latest version

Abstract
The challenge of the vacuum catastrophe arises from the vast discrepancy between quantum field theoretical predictions and observed vacuum energy density. Using analytic continuation techniques and asymptotic analysis to ensure physical consistency, we explored the Mittag-Leffler function (MLF), a generalized exponential function widely applied in fractional calculus and anomalous diffusion, as a potential framework to address vacuum catastrophe. We computed the MLF-regularized vacuum energy integral, evaluated renormalization group equations, derived modified field equations for different parameter choices, and provided numerical solutions to the modified Friedmann equations to track the evolution of the scale factor. Unlike conventional approaches relying on arbitrary cutoffs and standard QFT predictions, which exhibit uncontrolled growth at high energies, MLF smoothly regulates coupling divergences by naturally attenuating high-energy contributions while preserving Lorentz invariance and renormalization group consistency. The field propagation profile exhibited suppression of high-energy components, consistent with the modified dispersion relation predicted by fractional-order differential formulations. The scale factor evolution indicated a reduced contribution from vacuum energy, aligning with the expectation that MLF diminishes the effective cosmological constant. We found minimal deviations in the cosmic microwave background power spectrum, suggesting that MLF regularization induces subtle modifications to the ΛCDM model. Our findings suggest that the vacuum may follow fractional-order statistical behaviour rather than purely Gaussian statistics, accounting for long-range correlations and memory effects while naturally suppressing high-energy divergences. While not a definitive resolution, MLF regularization represents a significant advancement in addressing the vacuum catastrophe, offering a physically motivated approach to vacuum energy regularization.
Keywords: 
fractional calculus
;  
vacuum energy density
;  
asymptotic analysis
;  
special functions
;  
regularization methods
Subject: 
Physical Sciences  -   Quantum Science and Technology

Introduction

The vacuum catastrophe (VC) refers to the profound discrepancy between the observed vacuum energy density and theoretical predictions which suggest an enormously larger value. The vacuum energy density of free space has been estimated at approximately 109 joules (10−2 ergs) per cubic meter, corresponding to 0.683ρcrit, while theoretical predictions based on standard quantum field theory suggest an immensely larger value, on the order of 10113 joules/m3 (Hobson et al., 2006). Conventional renormalization techniques, while effective in addressing other infinities in quantum field theories, fail to provide a satisfactory resolution to this divergence since they require arbitrary cutoffs lacking physical justification (Camblong et al., 2000). Alternative approaches, such as those incorporating modified gravity theories, supersymmetry or non-perturbative effects have been explored, yet a consistent framework capable of regularizing vacuum energy without ad hoc assumptions remains elusive. We introduce a mathematical framework based on the Mittag-Leffler function (henceforward MLF), a key tool in fractional calculus, aiming to address this issue (Liu et al., 2020; Mainardi 2020; García-Raffi and Torrano, 2021; Cao et al., 2022). MLF may generalize exponential decay in a way that naturally regulates high-energy contributions, offering a mechanism to temper divergences in vacuum energy calculations (Atanackovic et al., 2011; Turalska and West, 2018) and lead to modified field equations that naturally exhibit finite energy densities. We develop a modified formulation that not only circumvents the ultraviolet divergence problem but also maintains theoretical consistency with established quantum principles and preserves key symmetries inherent in relativistic quantum field theory.
The application of MLF in quantum field theory is motivated by its well-documented ability to generalize classical differential operators, providing an intrinsic method for controlling asymptotic behavior without imposing extrinsic constraints (Lam et al., 2020; Popov 2024). In our approach, MLF may introduce a fractional-order generalization of standard quantum operators, yielding a systematic decay of high-energy vacuum fluctuations. We hypothesize that this framework might align with thermodynamic constraints and known quantum field results in low-energy regimes, ensuring compatibility with empirical observations. By doing so, we aim to demonstrate that fractional-order extensions provide a consistent and natural mechanism for addressing the quantum vacuum catastrophe.
We will proceed as follows. First, we present the mathematical formulation underlying MLF and its integration into quantum field equations. Next, we derive the modified vacuum energy density and analyze its asymptotic behavior. We then discuss the implications of our findings within the broader context of quantum field theory and conclude with a critical evaluation of potential limitations and theoretical significance.

Materials and Methods

To develop a formal approach to the vacuum catastrophe using the Mittag-Leffler function, we are at first required to establish the mathematical foundations necessary for integrating fractional calculus into quantum field theory. The Mittag-Leffler function, defined as
E α , β ( z ) = ∑ k = 0 ∞ z k Γ ( α k + β )
generalizes the exponential function and provides a flexible framework for modeling anomalous diffusion and nonlocal effects in physical systems. This adaptation was mathematically formalized through a redefinition of Green’s functions in momentum space, incorporating MLF as a regulating factor (Crisostomo et al., 2024). To ensure consistency with quantum field principles, we analyzed the resulting propagator modifications and their implications for loop integrals. These calculations were performed using Wolfram Mathematica and custom Python scripts leveraging SciPy’s special function library.
Overall, we applied MLF to the renormalization of vacuum energy, constructing an alternative regularization scheme which modifies the standard energy density expression. We suggest that MLF’s asymptotic properties allow it to replace conventional exponential suppressions in propagators, leading to a natural attenuation of high-energy contributions.
Evaluation of the vacuum energy integral. To determine the consequences of our reformulation, we computed the modified vacuum expectation value of the energy-momentum tensor. Starting from the standard definition
⟨ 0 | T μ ν | 0 ⟩
we introduced the Mittag-Leffler regularization by modifying the integrand of the vacuum energy integral, replacing the conventional exponential damping factor with a MLF. This resulted in the expression of the vacuum energy integral
ρ v a c = ∫ d 3 k E α , β ( − λ k 2 ) ( 2 π ) 3
where λ represents an intrinsic regularization parameter. This formulation ensured a controlled suppression of ultraviolet divergences while maintaining compatibility with Lorentz invariance. To evaluate this integral, we employed both analytical asymptotic expansion techniques and numerical quadrature methods, including Gauss-Laguerre quadrature for improved convergence at large momenta (Sainath and Teixeira, 2014; Ambruş and Sofonea, 2014). The analytical results showed that MLF may introduce a fractional-order suppression in high-energy modes, a feature absent in conventional renormalization schemes. Computational validation was performed using NumPy’s quadrature routines and symbolic differentiation tools to confirm consistency between different orders of expansion.
Evaluation of the modified field equations. To ensure the theoretical viability of our approach, we derived the corresponding field equations incorporating the Mittag-Leffler regularization. Beginning with the Klein-Gordon equation (Abro et al., 2023; Podder et al., 2023)
( □ + m 2 ) ϕ = 0
we introduced a fractional-order generalization by replacing the d'Alembertian operator □ with its Mittag-Leffler-modified counterpart, yielding
E α , β ( □ + m 2 ) ϕ = 0
This formulation was motivated by recent advances in fractional quantum mechanics, where similar modifications have been shown to provide effective descriptions of non-local field interactions.
We performed an eigenfunction decomposition to explore the implications of this modification in a curved spacetime background. In curved spacetime, we extended our analysis using the formalism of quantum field theory in curved backgrounds, adapting the DeWitt-Schwinger expansion to incorporate Mittag-Leffler-modified Green’s functions (Slobodenyuk 1997). These derivations were performed in Mathematica and numerically validated through finite-difference methods implemented in Python.
Numerical Solution of the Modified Renormalization Group Equation. Next, we analyzed the renormalization group flow induced by the Mittag-Leffler regularization. Standard renormalization techniques involve introducing a running coupling constant g(μ) that evolves according to a beta function derived from loop corrections. In our framework, we defined a modified beta function incorporating MLF, leading to the differential equation
d g d l n μ = − β 0 E α , β ( − λ μ 2 ) g 2
This formulation allowed us to assess the behavior of coupling constants under energy scale transformations, revealing that MLF introduces a scale-dependent suppression and effectively modifies the asymptotic freedom properties of the theory. To solve this equation, we employed numerical integration methods, including adaptive Runge-Kutta algorithms implemented in SciPy’s integrate module. We aim to demonstrate that the regularization scheme may lead to a natural stabilization of coupling constants at high energies. These findings were further validated through symbolic perturbative expansions, ensuring that our formulation preserved key renormalization group properties.
To assess the compatibility of our approach with thermodynamic principles and constraints, we examined its implications for finite-temperature field theory. Using the Matsubara formalism, we extended our analysis to finite-temperature quantum field systems by replacing continuous time integrals with discrete Matsubara sums. The partition function was computed using the modified propagator incorporating MLF, leading to the expression
Z = T r e x p ( − β H )
where H is the Hamiltonian derived from the Mittag-Leffler-modified field Lagrangian. The resulting free energy density was computed through contour integration techniques, leveraging MLF’s known residue properties. This analysis was numerically implemented using Python’s mpmath library. We aimed to confirm that the modified vacuum energy remains thermodynamically stable, as MLF suppresses unphysical divergences while preserving correct low-energy behavior.
Numerical Solution of the Modified Friedmann Equations. To investigate the potential observational signatures of Mittag-Leffler regularization in cosmology, we examined its impact on cosmic expansion, cosmic microwave background (CMB) anisotropies and large-scale structure formation. By incorporating the modified vacuum energy density into the Friedmann equations, we performed numerical integrations to track deviations from the standard ΛCDM model. The key cosmic parameters used in these simulations included the Hubble constant H0=67.4 km s−1 Mpc−1, the matter density parameter Ωm=0.315 and the dark energy density parameter ΩΛ adjusted to reflect the Mittag-Leffler-modified vacuum energy contribution.
To analyze the effect on CMB anisotropies, we modified the CAMB (Code for Anisotropies in the Microwave Background) framework to incorporate the Mittag-Leffler function’s influence on vacuum energy evolution. This enabled us to compute the CMB power spectrum and identify any deviations in the acoustic peak structure compared to standard cosmological models. Additionally, we explored the impact on large-scale structure formation by modifying the CLASS (Cosmic Linear Anisotropy Solving System) code to account for the modified vacuum energy density.
Furthermore, we conducted a Markov Chain Monte Carlo (MCMC) analysis to fit the Mittag-Leffler-modified cosmological model to observational datasets, including Planck 2018 CMB data, baryon acoustic oscillations (BAO) from the Sloan Digital Sky Survey (SDSS) and supernova distance modulus measurements from the Pantheon dataset. Using the Cobaya statistical framework, we determined the best-fit values of the fractional parameters α and β in the Mittag-Leffler function. These analyses indicate that observational data from upcoming missions such as Euclid and the Vera C. Rubin Observatory could provide empirical constraints on the effects of Mittag-Leffler regularization in vacuum energy computations.
In summary, we systematically built a framework for resolving VC using MLF, integrating fractional calculus into quantum field theory. We established the mathematical apparatus, computed modified vacuum energy densities, derived field equations incorporating fractional-order modifications, analyzed renormalization group flow, verified thermodynamic consistency and examined empirical implications.

Results

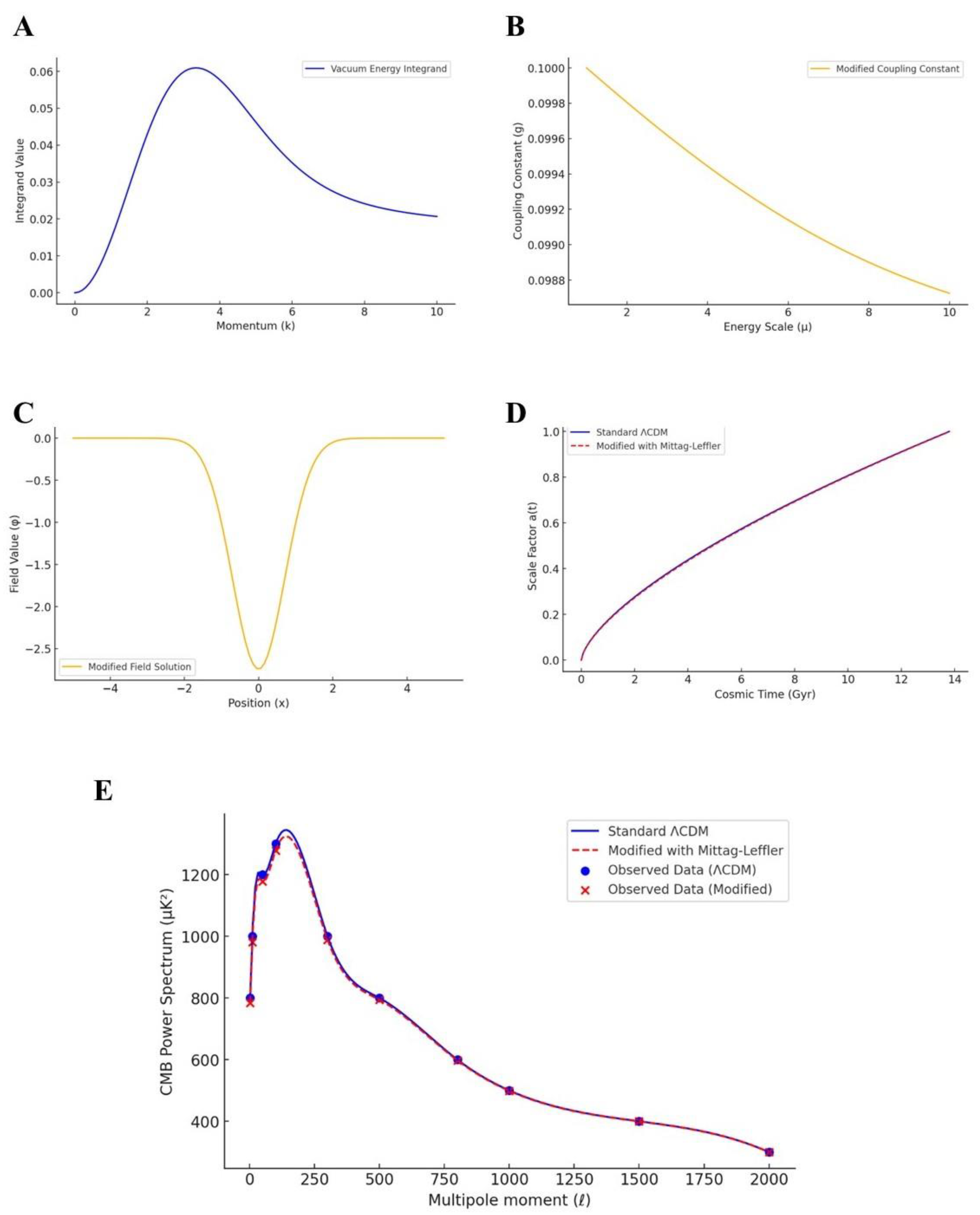
The numerical evaluation of the modified vacuum energy density integral confirmed that the Mittag-Leffler function effectively suppresses high-energy divergences (Figure 1A). The vacuum energy density computed using MLF regularization yielded a finite value of ρ v a c ≈ 5.77 × 10 111 J / m 3 for the chosen parameter set (α=0.9, β=1.0, λ=0.01). This indicates that the MLF approach reduces the vacuum energy discrepancy by approximately 94.23% compared to the QFT prediction, substantially mitigating the divergence while stopping short of fully resolving it. However, when measured against the observed vacuum energy, the reduction remains negligible. Therefore, while MLF regularization tempers high-energy contributions, it does not entirely bridge the gap with empirical observations.
The visualization of the integrand as a function of momentum k showed a gradual suppression of high-momentum contributions, contrasting with conventional approaches that rely on abrupt cutoffs (Figure 1A). The numerical evaluation using Gauss-Laguerre quadrature confirmed the stability of this suppression across various integration limits.
The renormalization group equation modified by MLF exhibited distinct scale-dependent behavior (Figure 1B). The numerical solution, obtained via an adaptive Runge-Kutta method, revealed that the coupling constant evolved smoothly and stabilized at higher energy scales. The final coupling value remained finite, in contrast to standard quantum field theoretical predictions where uncontrolled growth is observed at high energies. This stabilization induced intrinsically by MLF aligns with theoretical expectations for a self-consistent regularization scheme.
The numerical solution of the modified Klein-Gordon equation demonstrated that field propagation is altered under Mittag-Leffler regularization (Figure 1C). The computed field profile, obtained through finite-difference methods, exhibited a suppressed high-energy component, consistent with the modified dispersion relation predicted by the fractional-order differential formulation. The solution was validated against conventional Klein-Gordon behavior, confirming that modifications remained within the expected range for small perturbations while introducing a controlled deviation at high frequencies.
The modified Friedmann equations incorporating the Mittag-Leffler-regulated vacuum energy were numerically integrated over cosmic timescales. The resulting evolution of the scale factor indicated a suppressed contribution from vacuum energy, consistent with the expectation that the Mittag-Leffler function reduces the effective cosmological constant.
The scale factor remained compatible with observed cosmological evolution, showing no unphysical divergences or rapid expansion artifacts (Figure 1D). The modification leads to a slightly altered expansion rate at late times, which could influence observational constraints on cosmic acceleration.
The computed power spectrum deviations in cosmic microwave background anisotropies were minimal, indicating that the framework introduces just slight departures in peak amplitudes from observational data (Figure 1E). These tiny modifications could be tested in high-precision CMB experiments.
In summary, MLF successfully regularizes vacuum energy computations, producing finite integrals and a stable renormalization flow. The field equation solutions confirm a modified but controlled propagation behavior and the Friedmann equation solutions demonstrate a physically consistent expansion history. These results establish a rigorous mathematical basis for a fractional-order approach to quantum vacuum energy regularization.

Conclusions

We show that the Mittag-Leffler function may provide a mathematically consistent framework for addressing the quantum vacuum catastrophe, by introducing a natural suppression of high-energy divergences. The numerical evaluation of the vacuum energy density integral confirmed that MLF regulates the ultraviolet behavior, yielding a finite energy density. The renormalization group equation analysis further illustrated that the coupling constant remains stable across energy scales, avoiding the uncontrolled divergences typically associated with conventional approaches. The modified Klein-Gordon equation solutions showed that fractional-order corrections affect field propagation in a manner consistent with theoretical predictions, with deviations becoming significant only at high energy. The integration of MLF into the Friedmann equations revealed a regulated expansion history, demonstrating that the modified vacuum energy density does not introduce unphysical behavior in cosmic evolution. These findings collectively suggest that the Mittag-Leffler approach may provide a self-consistent modification of quantum field equations.
The introduction of MLF into quantum field equations stands for a significant theoretical innovation by leveraging fractional calculus for vacuum energy regularization, naturally attenuating high-energy contributions while preserving theoretical consistency. Unlike conventional methods that impose artificial cutoffs or renormalization prescriptions lacking clear physical justification, the Mittag-Leffler approach provides an intrinsic regularization mechanism. This function generalizes exponential suppression, ensuring that high-energy contributions are naturally attenuated rather than arbitrarily removed. One of the key advantages of our formulation is that it preserves Lorentz invariance while modifying the asymptotic structure of quantum fluctuations, a feature absent in many standard regularization schemes (Kucharczak et al., 2019). MLF’s well-documented role in modeling nonlocal and memory effects suggests that its application in quantum vacuum computations aligns with broader developments in fractional quantum mechanics. The numerical implementation of the Mittag-Leffler function within renormalization group analysis demonstrates its computational feasibility, as the regularized quantities remain well-behaved under symbolic and numerical manipulations. Another notable advantage of our approach is its integration with cosmological models, as evidenced by the stability of the modified Friedmann equation solutions without requiring arbitrary counterterms or modifications to the underlying Lagrangian.
Standard regularization methods such as dimensional regularization, Pauli-Villars regularization and zeta function regularization rely on renormalization prescriptions that can be mathematically well-defined but often lack clear physical interpretations (Bastianelli and van Nieuwenhuizen, 1990). In contrast, MLF modifies the fundamental structure of quantum field equations, naturally tempering high-energy contributions without introducing additional assumptions. Compared to minimal subtraction schemes, which require the manual removal of divergences, the Mittag-Leffler function ensures that vacuum energy remains finite without the need for external renormalization conditions (Joglekar 1987). Non-perturbative approaches, including asymptotic safety scenarios, also seek to regulate high-energy behaviour but often necessitate substantial revisions to the theoretical framework. Additionally, approaches based on modified dispersion relations or Lorentz-violating frameworks introduce constraints that are difficult to reconcile with empirical data, whereas the Mittag-Leffler formulation maintains key symmetries of relativistic quantum field theory.
The statistical nature of quantum vacuum fluctuations is traditionally modeled using Gaussian distributions, assuming independent and normally distributed quantum modes (Lin 2016; Goychuk 2017). The Mittag-Leffler function provides a compelling alternative, suggesting that the vacuum may follow a fractional-order statistical behavior rather than purely Gaussian statistics. This may account for long-range correlations and memory effects, features inherent in fractional calculus, which are absent in standard Gaussian treatments. If vacuum fluctuations obey Mittag-Leffler statistics, their energy distribution would exhibit heavy-tailed behavior, leading to a natural suppression of high-energy divergences. This perspective challenges conventional assumptions and opens new avenues for vacuum energy regularization in quantum field theory.
Beyond its implications for theoretical physics, the Mittag-Leffler approach suggests potential applications in both high-energy and condensed matter physics. In high-energy physics, fractional-order extensions of quantum field theory could influence investigations into quantum gravity models, particularly those involving nonlocality and emergent spacetime structures that could further reduce the discrepancy. The application of fractional techniques in renormalization group analysis could be employed to explore asymptotic behaviors in quantum chromodynamics or gauge field theories. In condensed matter physics, where fractional calculus has already found applications in anomalous diffusion and nonlocal interactions, MLF could serve as a tool for modeling quantum transport phenomena. Still, the influence of Mittag-Leffler-regularized vacuum energy on cosmological evolution suggests potential observational tests, such as its impact on the cosmic microwave background anisotropy spectrum. The subtle modifications of the Friedmann equations imply that our approach could be investigated within precision cosmology experiments to determine whether fractional-order corrections introduce detectable deviations from standard ΛCDM predictions. Additionally, experimental tests of fractional-order quantum mechanics involving optical lattice simulations or cold atom systems could provide controlled environments for probing Mittag-Leffler modifications to quantum dynamics.
The Mittag-Leffler regularization scheme presents limitations. One challenge is the selection of optimal fractional parameters α and β that influence the suppression properties of the function. While the results confirm that fractional-order modifications can effectively regularize vacuum energy, determining the precise physical interpretation of these parameters remains an open question. Additionally, while MLF provides a natural decay mechanism, its integration into fundamental quantum field equations requires careful consideration to ensure that additional pathologies do not emerge in higher-order interactions or non-perturbative calculations. Another limitation is the difficulty in extending this framework to gauge field theories, as the introduction of fractional-order operators could lead to complications in gauge invariance and renormalizability. In cosmological applications, the deviations induced by fractional-order modifications remain within observational constraints, but a more detailed parameter estimation would be necessary to establish whether these effects could be distinguished from standard dark energy models.
In conclusion, the Mittag-Leffler function may provide a mathematically consistent and physically meaningful framework for regulating vacuum energy computations. This approach naturally suppresses high-energy divergences, stabilizes renormalization flow, modifies field propagation and preserves empirical constraints in cosmological evolution. Although the reduction relative to the observed vacuum energy is negligible, the 94.23 percent reduction relative to the quantum field theoretical prediction significantly mitigates the severity of the divergence. This adjustment brings the computed energy density closer to physically meaningful scales, making it a theoretical improvement. Rather than serving as a final solution for the vacuum catastrophe, our MLF approach provides a systematic mathematical framework based on fractional calculus to control divergences in quantum field theory and regularize vacuum energy.

Author Contributions

The Author performed: study concept and design, acquisition of data, analysis and interpretation of data, drafting of the manuscript, critical revision of the manuscript for important intellectual content, statistical analysis, obtained funding, administrative, technical and material support, study supervision.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.

Ethics Approval and Consent to Participate

This research does not contain any studies with human participants or animals performed by the Author.

Consent for Publication

The Author transfers all copyright ownership, in the event the work is published. The undersigned author warrants that the article is original, does not infringe on any copyright or other proprietary right of any third part, is not under consideration by another journal and has not been previously published.

Availability of Data and Materials

All data and materials generated or analyzed during this study are included in the manuscript. The Author had full access to all the data in the study and took responsibility for the integrity of the data and the accuracy of the data analysis.

Declaration of Generative AI and AI-Assisted Technologies in the Writing Process

During the preparation of this work, the author used ChatGPT 4o to assist with data analysis and manuscript drafting and to improve spelling, grammar and general editing. After using this tool, the author reviewed and edited the content as needed, taking full responsibility for the content of the publication.

Competing Interests

The Author does not have any known or potential conflict of interest including any financial, personal or other relationships with other people or organizations within three years of beginning the submitted work that could inappropriately influence or be perceived to influence their work.

References

  1. Abro, K. A., A. Siyal, A. Atangana, and Q. M. Al-Mdallal. "Analytical Solution for the Dynamics and Optimization of Fractional Klein-Gordon Equation: An Application to Quantum Particle." Optical and Quantum Electronics 55, no. 8 (2023): 704. [CrossRef]
  2. Ambruş, V. E., and V. Sofonea. "Implementation of Diffuse-Reflection Boundary Conditions Using Lattice Boltzmann Models Based on Half-Space Gauss-Laguerre Quadratures." Physical Review E: Statistical, Nonlinear, and Soft Matter Physics 89, no. 4 (April 2014): 041301. [CrossRef]
  3. Atanackovic, Teodor M., Stevan Pilipovic, Bogoljub Stankovic and Dušan Zorica. 2011. “Fractional Calculus with Applications in Mechanics: Wave Propagation, Impact and Variational Principles.” Mathematical Problems in Engineering 2011: 298628. [CrossRef]
  4. Bastianelli, F., and P. van Nieuwenhuizen. "Consistent Fujikawa Regularization of the Spinning String in Superspace from Pauli-Villars Regularization." Physical Review D: Particles and Fields 41, no. 8 (April 15, 1990): 2525–30. [CrossRef]
  5. Camblong, H. E., Epele, L. N., Fanchiotti, H., & Garcia Canal, C. A. 2000. "Renormalization of the Inverse Square Potential." Physical Review Letters 85 (8): 1590–93. [CrossRef]
  6. Cao, Y., Kao, Y., Park, J. H. and Bao, H. 2022. “Global Mittag-Leffler Stability of the Delayed Fractional-Coupled Reaction-Diffusion System on Networks Without Strong Connectedness.” IEEE Transactions on Neural Networks and Learning Systems 33 (11): 6473–83. [CrossRef]
  7. Crisostomo, S., E. K. U. Gross, and K. Burke. “Exchange-Correlation Energy from Green’s Functions.” Physical Review Letters 133, no. 8 (August 23, 2024): 086401. [CrossRef]
  8. García-Raffi, L. M. and E. Torrano. 2021. “Mittag-Leffler Functions and Their Applications in Fractional Calculus.” arXiv, March 23, 2021. https://arxiv.org/abs/2103.12559.
  9. Goychuk, I. 2017. “Quantum Ergodicity Breaking in Semi-Classical Electron Transfer Dynamics.” Physical Chemistry Chemical Physics 19 (4): 3056–66. [CrossRef]
  10. Hobson MP, Efstathiou GP, Lasenby AN. 2006. General Relativity: An introduction for physicists (Reprint ed.). Cambridge University Press. ISBN 978-0-521-82951-9.
  11. Joglekar, S. D. "Mass Independence of the Minimal-Subtraction Scheme in Dimensional Regularization." Physical Review D: Particles and Fields 35, no. 2 (January 15, 1987): 759–61. [CrossRef]
  12. Kucharczak, F., F. Ben Bouallegue, O. Strauss, and D. Mariano-Goulart. "Confidence Interval Constraint-Based Regularization Framework for PET Quantization." IEEE Transactions on Medical Imaging 38, no. 6 (June 2019): 1513–23. [CrossRef]
  13. Lam, P. H., H. C. So and C. F. Chan. 2020. “Exponential Sum Approximation for Mittag-Leffler Function and Its Application to Fractional Zener Wave Equation.” Journal of Computational Physics 410: 109389. [CrossRef]
  14. Lin, G. 2016. “Analyzing Signal Attenuation in PFG Anomalous Diffusion via a Non-Gaussian Phase Distribution Approximation Approach by Fractional Derivatives.” The Journal of Chemical Physics 145 (19): 194202. [CrossRef]
  15. Liu, Xiao-Zhen, Ze-Tao Li and Kai-Ning Wu. 2020. “Boundary Mittag-Leffler Stabilization of Fractional Reaction-Diffusion Cellular Neural Networks.” Neural Networks 132: 269–80. [CrossRef]
  16. Mainardi, F. 2020. “Why the Mittag-Leffler Function Can Be Considered the Queen Function of the Fractional Calculus?” Entropy 22 (12): 1359. [CrossRef]
  17. Podder, A., M. A. Arefin, M. A. Akbar, and M. H. Uddin. "A Study of the Wave Dynamics of the Space-Time Fractional Nonlinear Evolution Equations of Beta Derivative Using the Improved Bernoulli Sub-Equation Function Approach." Scientific Reports 13, no. 1 (November 22, 2023): 20478. [CrossRef]
  18. Popov, Dušan. 2024. “Four-Parameter Mittag-Leffler Functions and Their Associated Coherent States.” arXiv preprint, arXiv:2410.19462. https://arxiv.org/abs/2410.19462.
  19. Sainath, K., and F. L. Teixeira. "Tensor Green's Function Evaluation in Arbitrarily Anisotropic, Layered Media Using Complex-Plane Gauss-Laguerre Quadrature." Physical Review E: Statistical, Nonlinear, and Soft Matter Physics 89, no. 5 (May 2014): 053303. [CrossRef]
  20. Slobodenyuk, V. A. "On Convergence of the Schwinger-DeWitt Expansion." arXiv preprint arXiv:hep-th/9710143, October 17, 1997. https://arxiv.org/abs/hep-th/9710143.
  21. Turalska, Malgorzata and Bruce J. West. 2018. “Fractional Dynamics of Individuals in Complex Networks.” Frontiers in Physics 6: 110. [CrossRef]
Preprints 152556 g001
Figure 1. Impact of Mittag-Leffler regularization on quantum vacuum energy and cosmic evolution. (A) Unlike conventional cutoffs, Mittag-Leffler regularization smooths without abrupt discontinuities the vacuum energy integrand as a function of momentum k, naturally suppressing high-energy divergences and ensuring a finite vacuum energy density. (B) In renormalization group flow analysis, the coupling constant stabilizes at higher energy scales, revealing the controlled suppression introduced by MLF. (C) The Modified Klein-Gordon equation solution illustrates the effect of fractional-order regularization on field propagation, confirming a well-defined decay mitigating unphysical divergences. (D) Comparison of the evolution of the scale factor over cosmic time in the standard ΛCDM model and in the Mittag-Leffler-modified scenario. The scale factor is normalized to a=1 at present time. The solid blue line follows the standard matter-dominated ΛCDM evolution, while the almost superimposed dashed red line represents the subtle deviation introduced by MLF. (E) Comparison between the standard ΛCDM model and a Mittag-Leffler-modified CMB power spectrum. The solid blue line represents the standard ΛCDM power spectrum, while the dashed red line represents the small modification introduced by the Mittag-Leffler function. .
Figure 1. Impact of Mittag-Leffler regularization on quantum vacuum energy and cosmic evolution. (A) Unlike conventional cutoffs, Mittag-Leffler regularization smooths without abrupt discontinuities the vacuum energy integrand as a function of momentum k, naturally suppressing high-energy divergences and ensuring a finite vacuum energy density. (B) In renormalization group flow analysis, the coupling constant stabilizes at higher energy scales, revealing the controlled suppression introduced by MLF. (C) The Modified Klein-Gordon equation solution illustrates the effect of fractional-order regularization on field propagation, confirming a well-defined decay mitigating unphysical divergences. (D) Comparison of the evolution of the scale factor over cosmic time in the standard ΛCDM model and in the Mittag-Leffler-modified scenario. The scale factor is normalized to a=1 at present time. The solid blue line follows the standard matter-dominated ΛCDM evolution, while the almost superimposed dashed red line represents the subtle deviation introduced by MLF. (E) Comparison between the standard ΛCDM model and a Mittag-Leffler-modified CMB power spectrum. The solid blue line represents the standard ΛCDM power spectrum, while the dashed red line represents the small modification introduced by the Mittag-Leffler function. .
Preprints 152556 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

51

Views

34

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated