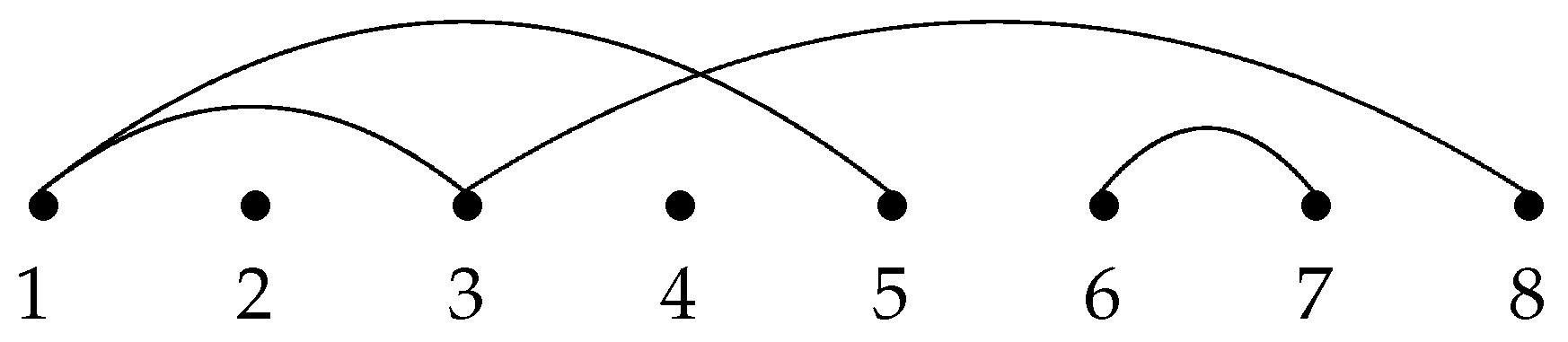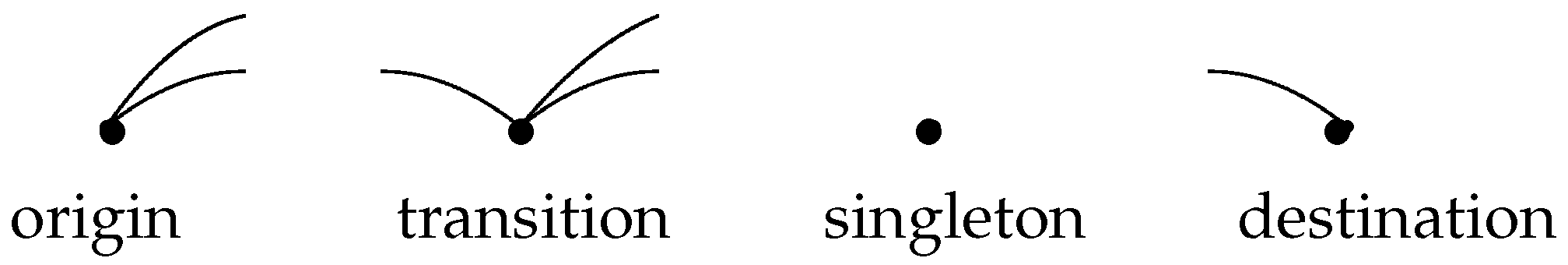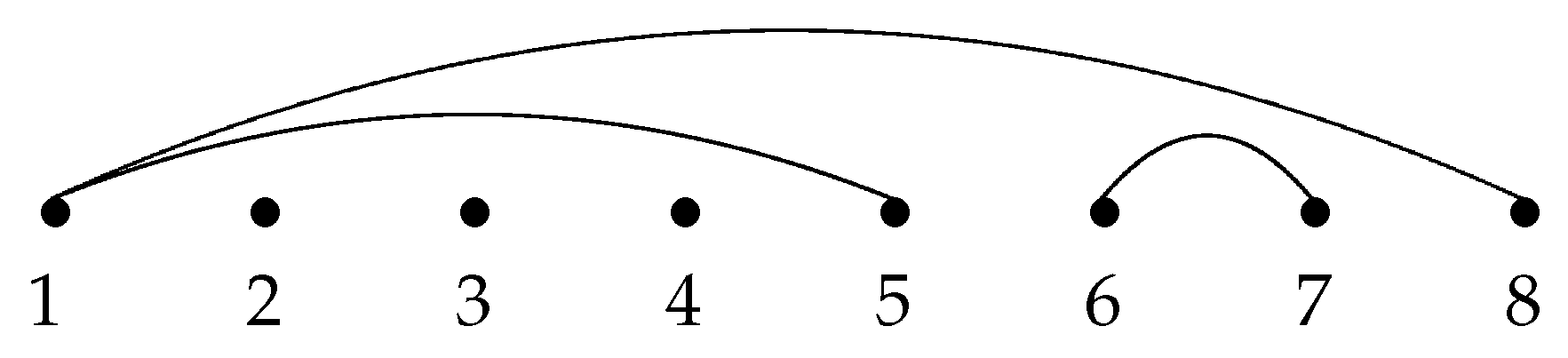Marking Algorithms in Permutation Tableaux and Transformations on Linked Partitions

1. Introduction

Steingrímsson and Williams [8] proposed a new combinatorial structure, the permutation tableaux, when enumerated completely positive Grassmannian elements. They introduced the definition and properties of permutation tableaux in detail and constructed a bijection between the set of permutation tableaux of length n containing k rows and the set of permutations of length n with k weak exceedances. Corteel and Kim [2] defined permutation tableaux of type B and gave a generalized bijection from permutation tableaux of type B to permutations of type B.

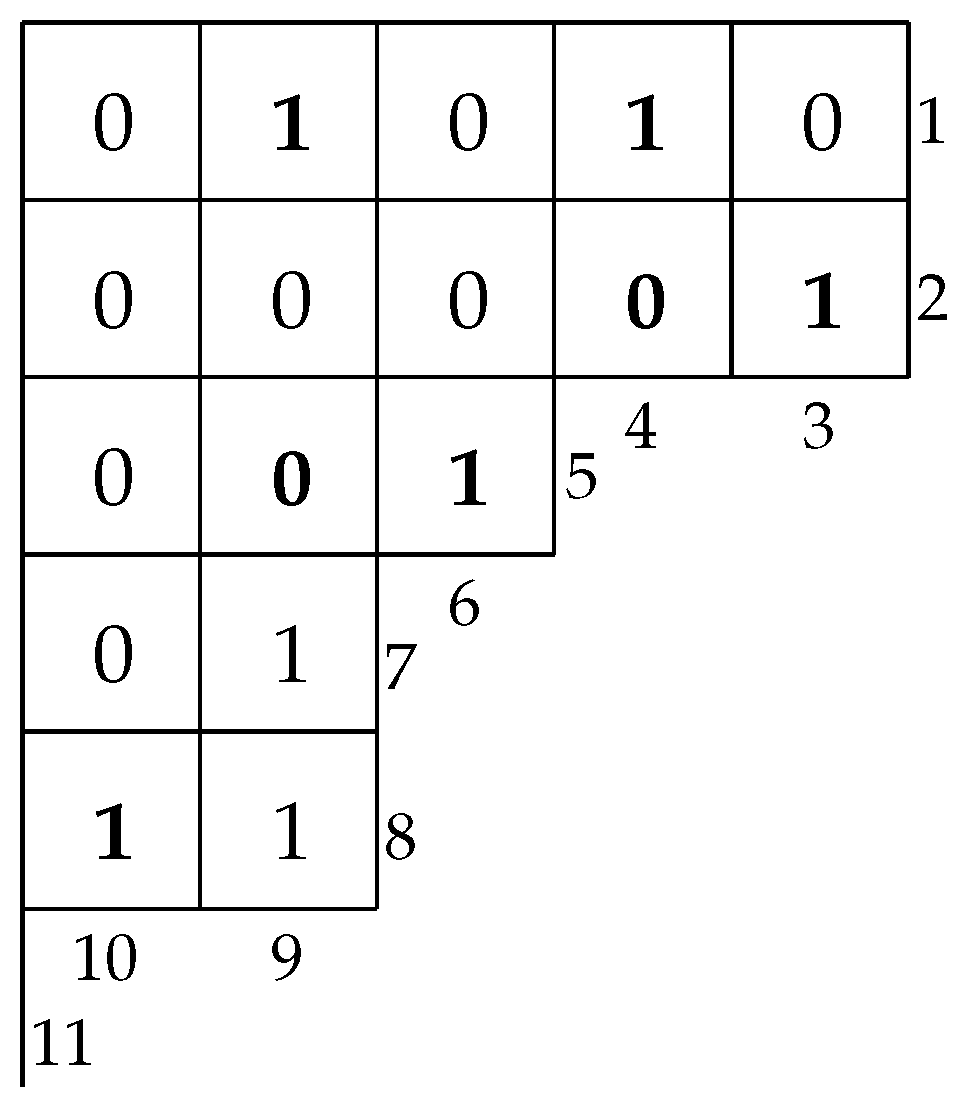
A permutation tableau is defined as a Ferrers diagram possibly with empty rows such that the cells are filled with 0’s and 1’s, and

(1)

each column contains at least one 1,

(2)

there does not exist any 0 with a 1 above in the same column and a 1 to the left of the same row.

The length of a permutation tableau is defined as the number of rows plus the number of columns. A 0 in a permutation tableau is restricted if there is a 1 above it in the same column. A row is unrestricted if it does not contain a restricted entry. A 1 is a topmost one if it contains no 1 above itself in the same column. Let $\left[n\right]$=$1,2,\cdots ,n$. A permutation tableau T of length n is labeled by the elements in $\left[n\right]$ in increasing order from the top right corner to the bottom left corner. We use row i to denote the row with label i, column j to denote the column with label j. We use $(i,j)$ to denote the cell in row i and column j. The shape of a permutation tableau T is meant to be the shape of the underlying Ferrers diagram of T with empty rows allowed. In other words, the shape of T is a partition $({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k)$, where ${\lambda }_i$ is the number of cells in the i-th row of the underlying Ferrers diagram of T, for $i=1,2,\cdots ,k$. For example, there is a permutation tableau of length 11 and shape $(5,5,3,2,2,0)$ in Figure 1, which has un-restricted row $1,7,8,11$ and two rightmost restricted 0’s in $(2,4)$ and $(5,9)$, respectively.

Linked partitions was first introduced by Dykema [7] in the study of the unsymmetrized T-transform in free probability theory. A linked partition of $\left[n\right]$ is a collection of nonempty subsets $B_1,B_2,\dots ,B_m$ of $\left[n\right]$, called blocks, such that the union of $B_1,B_2,\dots ,B_m$ is $\left[n\right]$, and any two distinct blocks are nearly disjoint. Two blocks $B_i$ and $B_j$ are said to be nearly disjoint if for any $k\in B_i\cap B_j$, one of the following conditions holds:

(1)

$k=min\left(B_i\right),\left|B_i\right|>1$ and $k\ne min\left(B_j\right)$, or

(2)

$k=min\left(B_j\right),\left|B_j\right|>1$ and $k\ne min\left(B_i\right)$.

The linear representation of a linked partition was defined by Chen, Wu and Yan [6]. Given a linked partition $\tau$ of $\left[n\right]$, list n vertices in a horizontal line with labels $1,2,\dots ,n$. For any block, $B=\{i_1,i_2,\dots ,i_k\}$, where $k\ge 2$ and $i_1<i_2<\cdots <i_k$, draw an arc from $i_1$ to $i_j$ for $j=2,\dots ,k$. For $i<j$, we use a pair $(i,j)$ to represent an arc from i to j, and we call i and j the left-hand and right-hand endpoint of arc $(i,j)$, respectively. For the sake of convenience, we also adopt the linear representation to set partitions. Two arcs $(i_1,j_1)$ and $(i_2,j_2)$ form a crossing if $i_1<i_2<j_1<j_2$, and form a nesting if $i_1<i_2<j_2<j_1$. We denote the crossing number and the nesting number of the linked partition $\tau$ by $cr\left(\tau \right)$ and $ne\left(\tau \right)$, respectively.

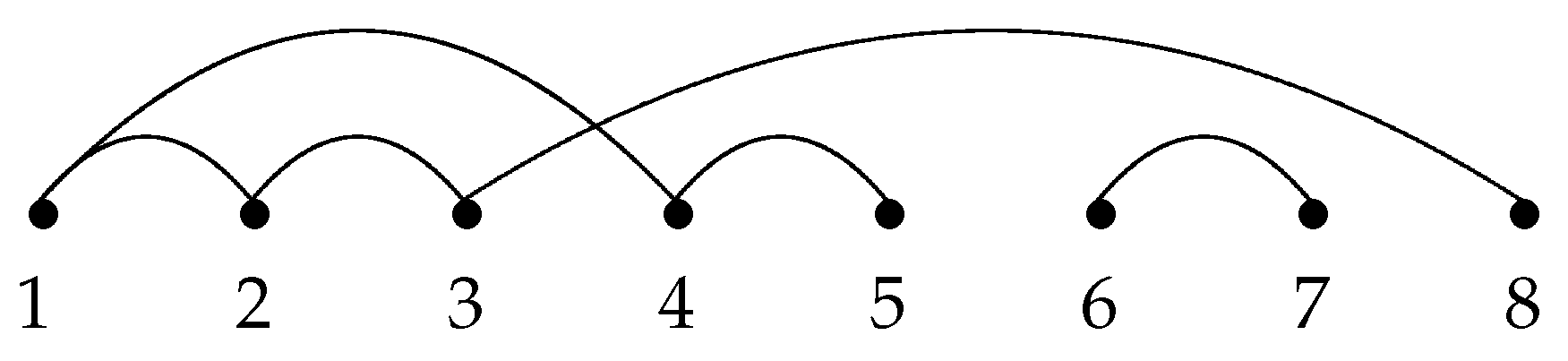
For example, the linear representation of linked partition $\tau =\{1,3,5\}\left\{2\right\}\{3,8\}\left\{4\right\}\{6,7\}$ is shown in Figure 2. There is only one crossing formed by arcs $(1,5)$ and $(3,8)$,and one nesting formed by arcs $(3,8)$ and $(6,7)$, i.e., $cr\left(\tau \right)=1$ and $ne\left(\tau \right)=1$.

Given a linked partition, a vertex in the linear representation of $\tau$ is called an origin if it is only a left-hand endpoint, or a transient if it is both a left-hand point and a right-hand endpoint, or a singleton if it is an isolated vertex, or a destination if it is only a right-hand endpoint. Figure 3 illustrates the four types of vertices. It is clear that origin, transition and singleton are the minimum elements of the blocks, the total number of which is equal to the number of blocks of linked partitions. It should be pointed out that for any right-hand endpoint j, there is at most one vertex i such that $1\le i<j$ and i is connected to j in the linear representation of a linked partition.

Chen et al.[3] established a bijection between partitions and vacillating tableaux to prove that the crossing numbers and the nesting numbers of partitions of $\left[n\right]$ have a symmetric joint distribution by fixing the sets of minimal block elements and maximal block elements, as well as all over all matchings on $\left[2n\right]$. They also obtained a corollary that the number of k-noncrossing partitions is equal to the number of k-nonnesting partitions, which is also true for matchings. Chen, Wu and Yan [6] bijectively proved that the number of noncrossing linked partitions of $\left[n\right]$ is equal to the number of large Schröder paths of length $2(n-1)$, and gave a one-to-one correspondence between linked partitions of $\left[n\right]$ and the increasing trees containing $n+1$ vertices. In addition, by defining linked cycles, they showed that crossing number and nesting number have a symmetric joint distribution over the set of linked partitions of $\left[n\right]$ by fixing the vertex labeling. Chen, Liu and Wang [5] gave a bijection between linked partitions of $\left[n\right]$ containing k blocks and permutations of $\left[n\right]$ containing $k-1$ descents, as well as a bijection between linked partitions of $\left[n\right]$ containing k blocks and permutation tableaux of length n containing k rows. Based on the positions of topmost 1’s and rightmost restricted 0’s, they also defined $I_2$-avoiding and $J_2$-avoiding permutation tableaux. Moreover, they illustrated a bijection between noncrossing linked partitions of n and $J_2$-avoiding permutation tableaux of length n, and a bijection between nonnesting linked partitions of n and $I_2$-avoiding permutation tableaux of length n. Chen, Guo and Pang [4] introduced the structure of vacillating Hecke tableaux and used Hecke insertion algorithm proposed by Buch et al. [1] to establish a one-to-one correspondence between vacillating Hecke tableaux and linked partitions, and also proved that the crossing number and the nesting number of a linked partition can be determined by the maximal number of rows and the maximal number of columns of diagrams in the corresponding vacillating Hecke tableau.

In this paper, we establish the relationship of internal sturctual charactoristics between linked partitions and permutation tableaux. Especially, we present the crossing number and nesting number of linked partitions by the positional relationship between the topmost 1’s and rightmost restricted 0’s in permutation tableaux. For this target, we first introduce some new structual statistics of permutation tableaux in Section 2, such as the diagonal pattern, front-out condition, back-out condition, ceiling index and floor index. In Section 3, we describe two marking algorithms for permutation tableaux in the view of columns and rows, respectively. In Section 4, we construct a tugging transformation and a rebound transformation to linked partitions, which show a closed relationship between original partitions and linked partitions: for any linked partition $\tau$ of n, there is a unique partition $\pi$ of n such that $\tau$ is generated by applying tugging operation to $\pi$. Finally, based on the bijection between linked partitions and permutations, obtained by Chen, Liu and Wang [5], we deduce that the crossing number and nesting number of a linked partition can be determined by the markers in the corresponding permutation tableau.

2. Structural Statistics in Permutation Tableaux

Let $PT\left(n\right)$ be the set of permutation tableaux of length n, $n\ge 4$. Let $T\in PT\left(n\right)$, the label of columns in T are $j_1,j_2,\dots ,j_m$, $j_1<j_2<\cdots <j_m,m\ge 2,n-m\ge 2$. A permutation tableau is uniquely determined by its topmost 1’s and rightmost restricted 0’s. It can be fully proven that if the positions of topmost 1’s are given, then all the cells above these positions which are in the same columns are filled with 0’s; if the positions of the rightmost restricted 0’s are given, then all the cells to the left of these positions which are in the same rows are filled with 0’s; and last to fill the remaining cells with 1’s. We denote the topmost1’s and the rightmost restricted 0’s by $t.m.1$’s and $r.r.0$’s for convenience.

Definition 1.

Two cells $(i_1,j_1)$ and $(i_2,j_2)$ in permutation tableau T are formed a diagonal pattern, if $i_1<i_2<j_1<j_2$ and $(i_2,j_1)$ is a cell of T. See Figure 4.

For any column $j_a,1<a\le m$, assume that there exists at least one $r.r.0$, denote the row label of its $t.m.1$ by $i_1$ and the row labels of all $r.r.0$’s by $i_2,i_3,\dots ,i_k$, respectively, where $i_1<i_2<i_3<\cdots <i_k$.

Definition 2.

We call $r.r.0$ in $(i_2,j_a)$ satisfing the front-out condition if there exists at least one $t.m.1$ or $r.r.0$ in cells $(i_1+1,j_b),(i_1+2,j_b),\cdots ,(i_2-1,j_b)$,$1\le b\le a-1$, and cell $(i_2,j_b)$ is in T. Figure 5 illustrates the condition for $j_b=j_{a-1}$.

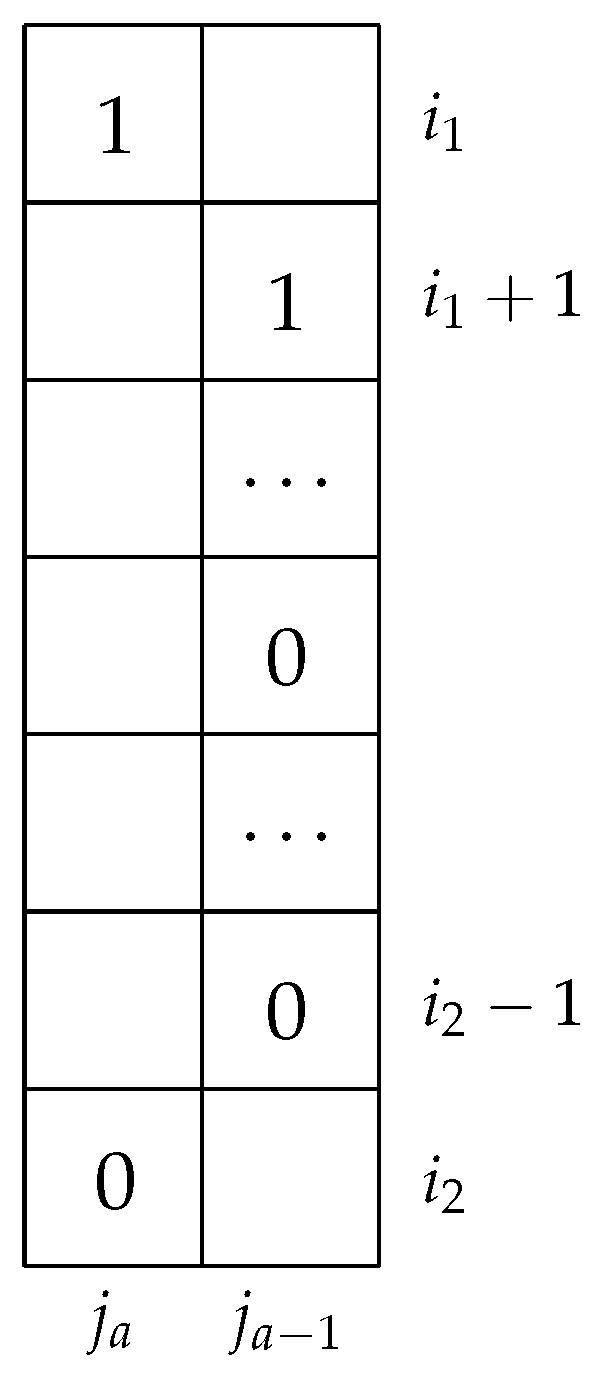
Definition 3.

We call $r.r.0$ in $(i_2,j_a)$ satisfing the back-out condition, if there exists at least a $t.m.1$ and possibly $r.r.0$ in cells $(i_1,j_b)$, $(i_1+1,j_b)$, ⋯, $(i_2-1,j_b)$, $1\le b\le a-1$, and the cells meet one of the following conditions: .

(a)

there does not exist any $r.r.0$ under cell $(i_2,j_a)$ in column $j_a$, and cell $(i_2,j_{a-1})$ is in T;

(b)

there are $r.r.0$’s under cell $(i_2,j_a)$ in column $j_a$ but cannot form a diagonal with $(t,j_{a-1})$, t is the row label of the possible cells in column $j_{a-1}$, $i_1\le t\le i_2-1$;

(c)

there exists at least one cell filled with a $r.r.0$ in row i and column $j_b$, $i_2<i<i_3$, and cell $(i_3,j_{a-1})$ is in T.

Figure 6 illustrates the condition $j_b=j_{a-1}$.

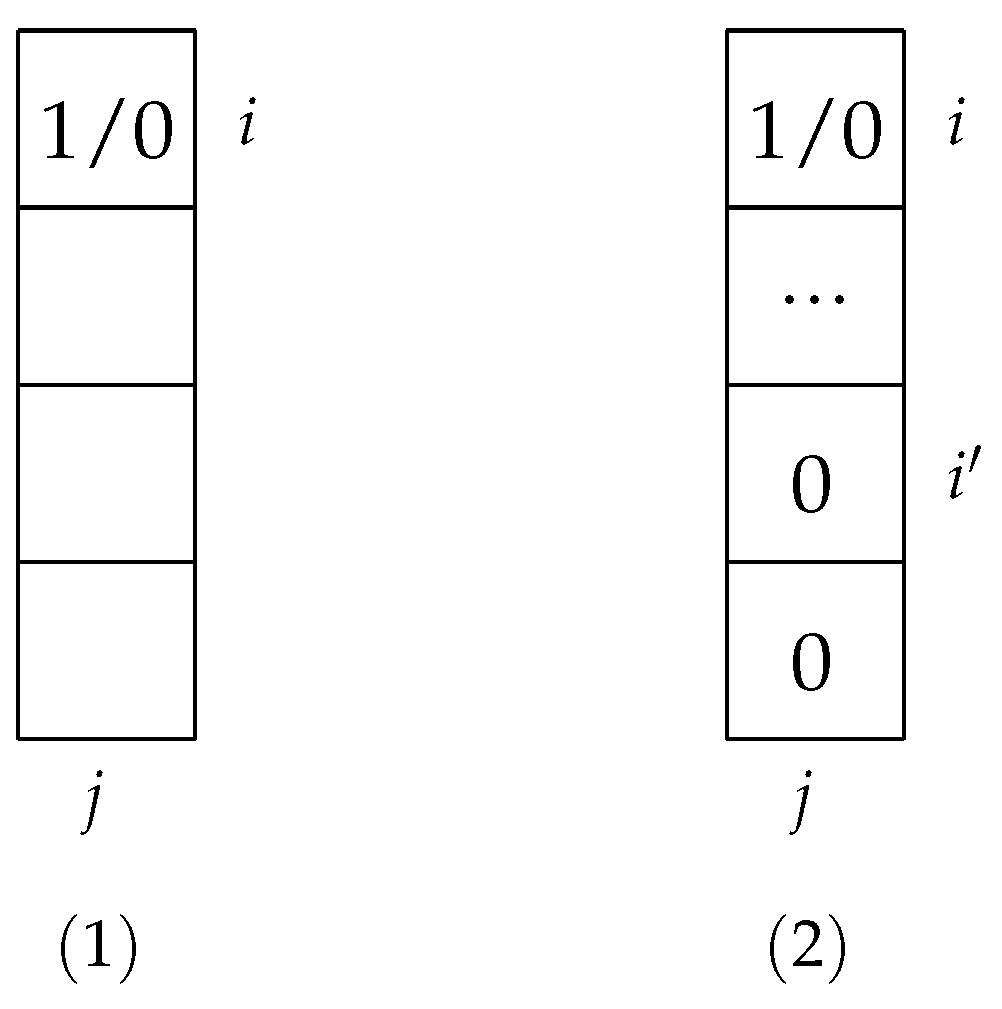
Definition 4.

The ceiling index of any cell $(i,j)$ filled with a $t.m.1$ or a $r.r.0$ in T is defined as row label i.

Definition 5.

The floor index of cell $(i,j)$ filled with a $t.m.1$ or a $r.r.0$ in T is defined as column label j, if there does not exist any $r.r.0$ below cell $(i,j)$ in column j, see Figure 7(1); otherwise, its floor index is defined as row lable $i^{\prime }$ of cell $(i^{\prime },j)$, where cell $(i^{\prime },j)$ is filled with a $r.r.0$ and $|i^{\prime }-i|$ is minimum. See Figure 7(2).

3. Marking Algorithms for Permutation Tableaux

In this section, we mainly introduce a marking algorithm and two statistics for permuatation tableaux, callded row indication and column indication.

Let T be a permutation tableau of length n with u rows and v columns, where $n\ge 4,v\ge 2$, $n=u+v$. Denote the column labels of T by $j_1$, $j_2$, …, $j_v$, $j_1<j_2<\cdots <j_v$. We introduce the column marking algorithm for permutation tableaux. We carry out the marking process to column $j_2$, $j_3$, …, $j_v$ in order.

For column $j_a,1<a\le v$, we consider the positions of $t.m.1$’s and $r.r.0$’s in columns $j_a$ and $j_{a-1}$. Denote the row label of $t.m.1$ in column $j_a$ by $i_1$. Assume that there is at least one $r.r.0$ in this column, and denote the row labels of those $r.r.0$’s by $i_2,\dots ,i_f,i_1<i_2<\cdots <i_f$.

If $t.m.1$’s in columns $j_a$ and $j_{a-1}$ form the diagonal pattern, then add a $“•”$ in the cell $(i_1,j_a)$. First, we consider the marking condition to cell $(i_2,j_a)$. If there exist $t.m.1$ or $r.r.0$’s in cells $(i_1+1,j_{a-1}),(i_1+2,j_{a-1}),\dots ,(i_2-1,j_{a-1})$, then add a $“•”$ in cell $(i_2,j_a)$. Denote the largest row label in column $j_{a-1}$ by $i_c$ such that $|i_2-i_c|$ is minimum.

If the cells in columns $j_a$ and $j_{a-1}$ satisfy one of the following conditions, then add a $“•”$ to cell $(i_2,j_a)$.

(1)

either there does not exist any $r.r.0$ under cell $(i_2,j_a)$ in the same column, or there exists a $r.r.0$ under cell $(i_2,j_a)$ in the same column but does not form a diagonal pattern with cell $(i_c,j_{a-1})$;

(2)

there exists a $r.r.0$ in column $j_{a-1}$, denoted its row label by i such that $i_2<i<i_3$.

The number of $“•”$’s in cell $(i_2,j_a)$ is called the column indication of cell$(i_2,j_a)$ about column $j_{a-1}$, denoted by $C[(i_2,j_a);j_{a-1}]$. Repeat the above process to get $C[(i_3,j_a);j_{a-1}]$, $C[(i_4,j_a);j_{a-1}]$,…, $C[(i_f,j_a);j_{a-1}]$. The column marking algorithm on column $j_a$ corresponding to column $j_{a-1}$ is completed. By the same way, we apply the column marking algorithm to column $j_a$ corresponding to any column $j_k$, $k=a-2,\dots ,1$. Finally, The column marking algorithm of column $j_a$ is completed. Repeat the above process to the columns of T from $j_2$ to $j_v$. Then the column marking algorithm for T is terminated.

Let

$$C\left[(i_2,j_a)\right]=\sum _{k=1}^{a-1}C[(i_2,j_a);j_k],C\left[j_a\right]=\sum _{t=1}^{f}C\left[(i_t,j_a)\right]$$

be the column indication of cell $(i_2,j_a)$ and column $j_a$, respectively.

Definition 6.

Let ${\mathbb{Z}}^{+}$ be the set of nonnegative integers and $\mathcal{T}$ be the set of permutation tableaux. Define a funciton F from $\mathcal{T}$ to ${\mathbb{Z}}^{+}$, such that for any $T\in \mathcal{T}$,

$$F\left(T\right)=\sum _{q=1}^{v}C\left[j_q\right],$$

where the value of $F\left(T\right)$ is called the column indication of T.

Next, we introduce row marking algorithm. Let T be a permutation tableau of length n with u rows and v columns, where $n\ge 4,v\ge 2$, $n=u+v$. Denote the row labels of T by $i_1,i_2,\dots ,i_u,i_1<i_2<\cdots <i_u$. We carry out the marking process to row $i_2$, $i_3$, …, $i_u$ in order. Assume that there exists a cell $(i_b,j)$ containing $t.m.1$ or $r.r.0$ in row $i_b$, for any $1<b\le u$. According to Definition 4, its ceiling index is $i_b$, and denote its floor index by t. If there exist k cells containing $t.m.1$ or $r.r.0$, whose ceiling index is less than $i_b$ and floor index is greater than t, then add k*’s to cell $(i_b,j)$, $k\ge 0$. Let row indication of cell $(i_b,j)$ be k, denoted by $N\left[(i_b,j)\right]=k$.

Repeat the process for the other cells in row $i_b$. Let $N\left[i_b\right]$ be the total number of *’s in row $i_b$. And we can mark cells in the other rows individually. The above process is the row marking algorithm for permutation tableaux.

Definition 7.

Let ${\mathbb{Z}}^{+}$ be the set of nonnegative integers and $\mathcal{T}$ be the set of permutation tableaux. Define a funciton G from $\mathcal{T}$ to ${\mathbb{Z}}^{+}$, such that for any $T\in \mathcal{T}$,

$$G\left(T\right)=\sum _{b=1}^{u}N\left[i_b\right],$$

where the value of $G\left(T\right)$ is called the row indication of T.

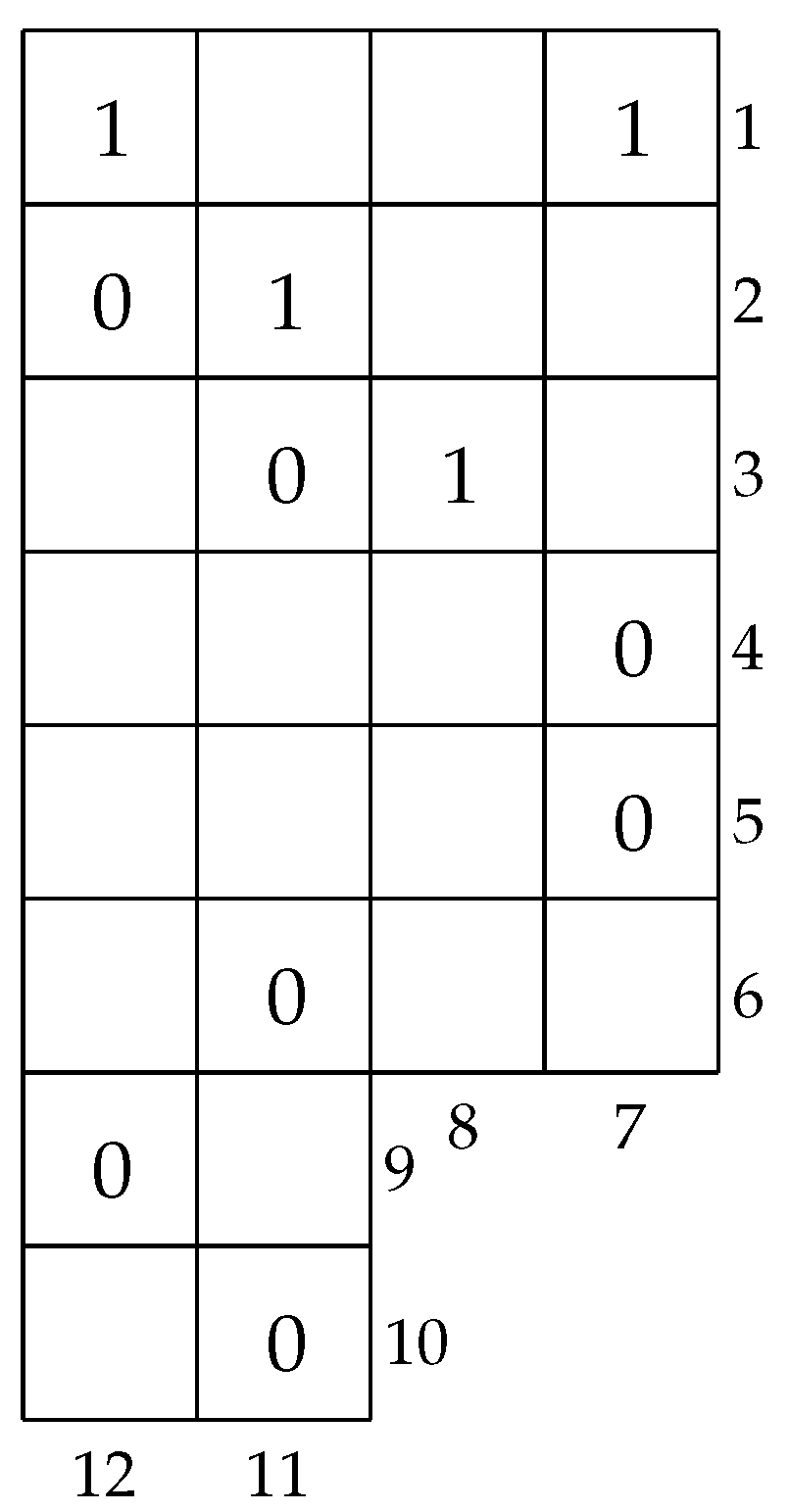
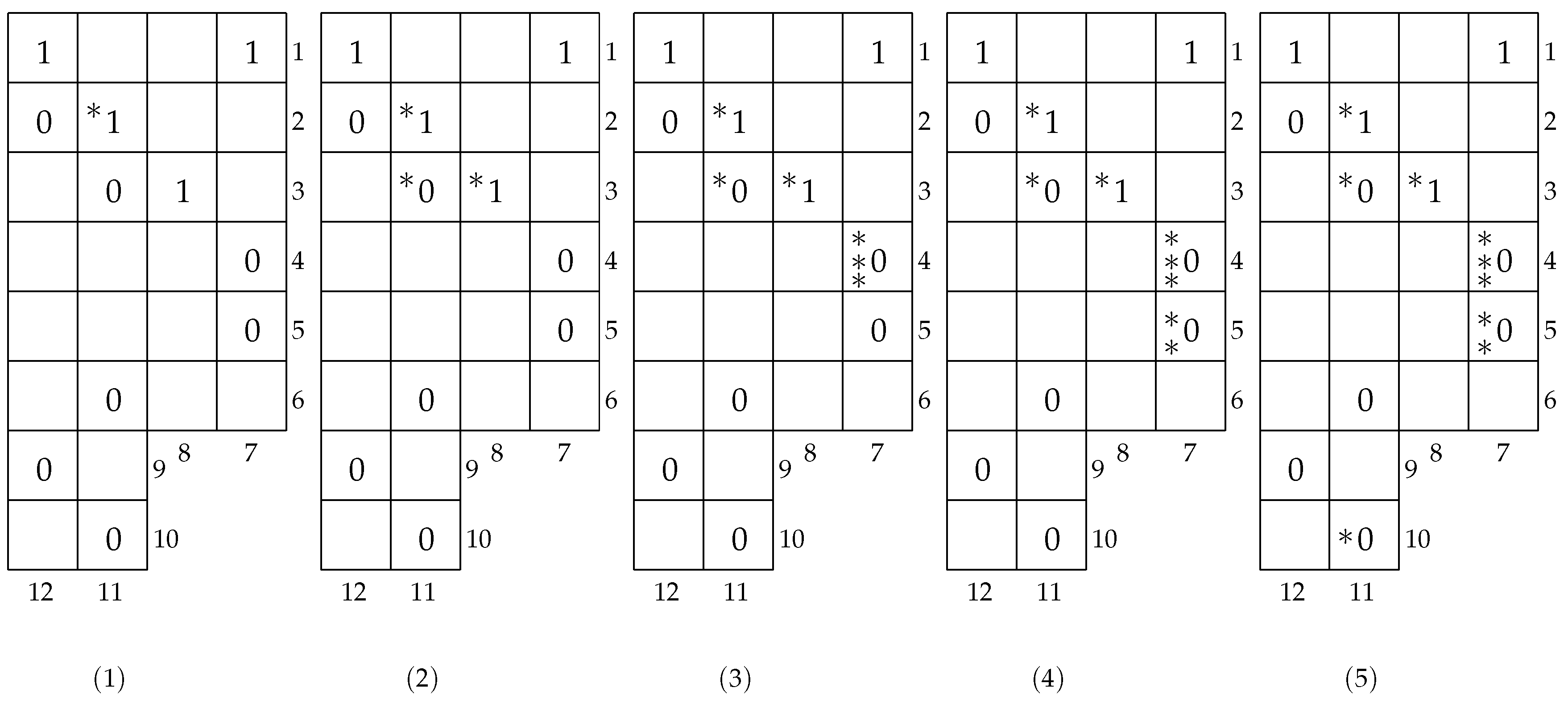
For example, let us apply the above two marking algorithms to permutation tableau $T_1$ in Figure 8 and get its row and column indication. The row labels of $T_1$ are $1,2,3,4,5,6,9$ and 10, and its cloumn labels are $7,8,11,12$.

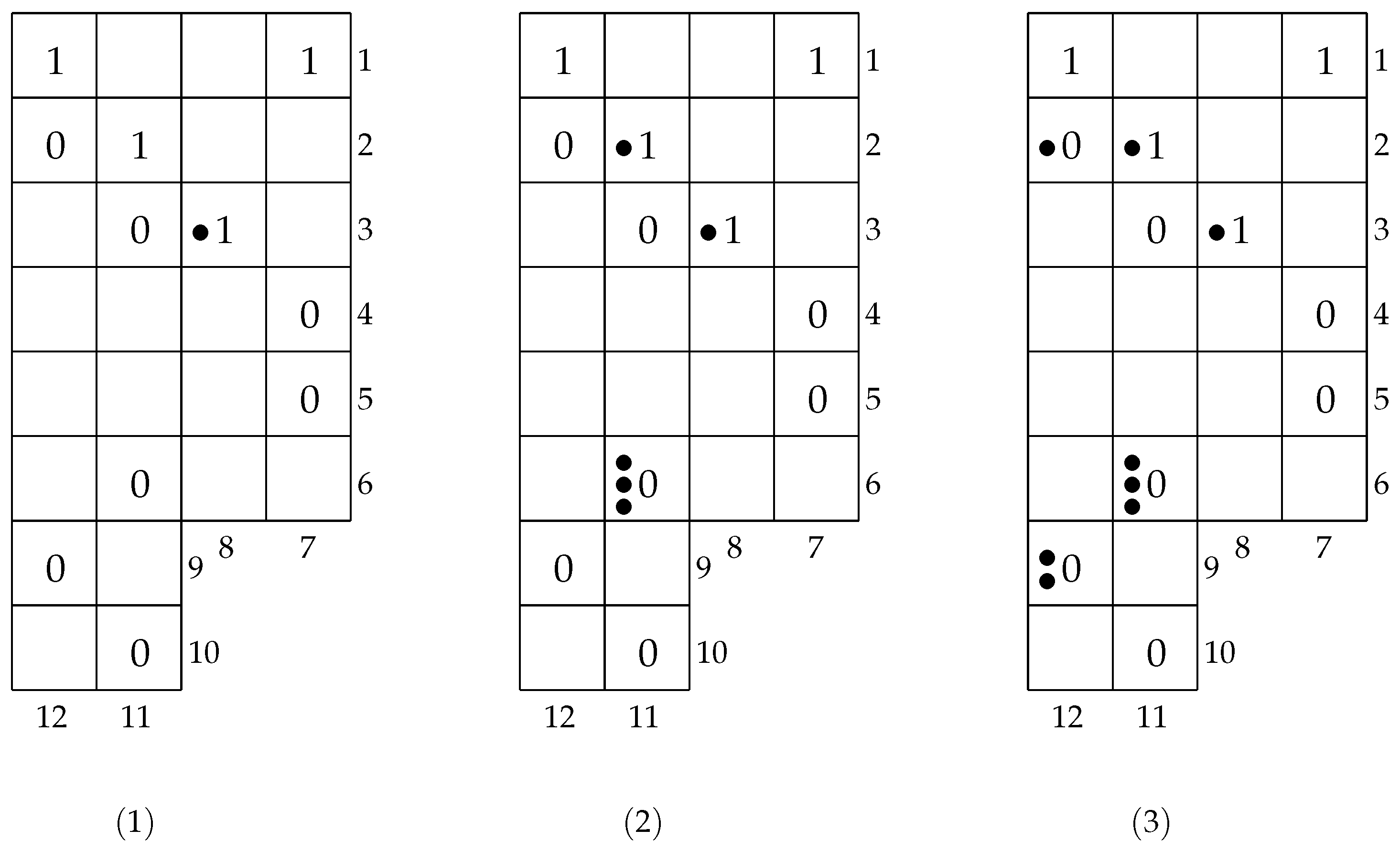
According to the column marking algorithm, we possibly mark the cells containing $t.m.1$’s and $r.r.0$’s in columns $8,11,12$ from left to right in order. For column 8, we only add a • to cell $(3,8)$, since the 1’s in cells $(3,8)$ and $(1,7)$ form a diagonal pattern. Let $C\left[\right(3,8);7]=1$, see Figure 9(1). For columns 11 and 8, firstly note that cell $(6,11)$ satisfies the back-out condition, so add a • to the cell and let $C\left[\right(6,11);8]=1$. For columns 11 and 7, cells $(2,11)$ and $(1,7)$ form a diagonal pattern, where implies $C\left[\right(2,11);7]=1$. Because cell $(6,11)$ satisfies both the front-out condition and the back out condition, add two •’s to $(6,11)$ and get $C\left[\right(6,11);7]=2$. See Figure 9(2). Similarly, for column 12, we have $C\left[\right(9,12);11]=2,C\left[\right(2,12);7]=1$. See Figure 9(3). Finally, we obtain

$$\begin{array}{cc}\hfill F\left(T_1\right)& =C\left[7\right]+C\left[8\right]+C\left[11\right]+C\left[12\right]\hfill \\ \hfill & =0+C\left[\right(3,8);7]+\left(C\right[(6,11);8]+C[(2,11);7]+C[(6,11);7\left]\right)\hfill \\ \hfill & +\left(C\right[(9,12);11]+C[(2,12);7\left]\right)\hfill \\ \hfill & =0+1+4+3\hfill \\ \hfill & =8.\hfill \end{array}$$

According to the row marking algorithm, we possibly mark the cells containing $t.m.1$’s and $r.r.0$’s in rows $2,3,4,5,6,9,10$ from top to bottom in order. For row 2, we just add a * to cell $(2,11)$, becasue its ceiling index is 2, which is greater than the ceiling index of $(1,7)$, and its floor index is 3, which is less than the floor index of $(1,7)$. Let $N\left[\right(2,11);1]=1$. See Figure 10$\left(1\right)$. Similarly, for row 3, add one *’s to $(3,11)$ and add one * to $(3,8)$. Note $N\left[\right(3,11);2]=1$, $N\left[\right(3,8);2]=1$, see Figure 10(2). For row 4, add three *’s to $(4,7)$, and let $N\left[\right(4,7);2]=1$, $N\left[\right(4,7);3]=2$, see Figure 10(3). For row 5, add two *’s to $(5,7)$, note $N\left[\right(5,7);2]=1$, $N\left[\right(5,7);3]=1$, see Figure 10(4). Row 6 and 9 do not satisfy row marking condition and are not marked. For row 10, add one * to $(10,11)$, let $N\left[\right(10,11);9]=1$, see Figure 10(5). Finally, we obtain

$$\begin{array}{cc}\hfill G\left(T_1\right)& =N\left[1\right]+N\left[2\right]+N\left[3\right]+N\left[4\right]+N\left[5\right]+N\left[6\right]+N\left[9\right]+N\left[10\right]\hfill \\ \hfill & =0+N\left[\right(2,11);1]+\left(N\right[(3,8);2]+N[(3,11);2\left]\right)+\left(N\right[(4,7);2]+N[(4,7);3\left]\right)\hfill \\ \hfill & +\left(N\right[(5,7);2]+N[(5,7);3\left]\right)+0\hfill \\ \hfill & +0+N\left[\right(10,11);9]\hfill \\ \hfill & =0+1+2+3+2+0+0+1\hfill \\ \hfill & =9.\hfill \end{array}$$

4. Transformations on Linked Partitions

In this section, we introduce two transformations, called tugging and rebound, and a recursive generating procedure. Let us describe these two transformations.

Definition 8.

In a linked parition τ, if there exist a singleton k, and an arc $(i,j)$ such that $i<k<j$, then we call k a tuggable singleton of arc $(i,j)$, as shown in Figure 11(a). If there exist an origion r, a destination t and an arc $(i,j)$ such that $i<r<t<j$, where both r and t are contained in the same block B and $t=max\left(B\right)$, then we call r a tuggable origin of arc $(i,j)$, as shown in Figure 11(b).

Both tuggable singletons and tuggable origins are called tuggable vertices. Arc $(i,j)$ is called a tuggable arc.

Definition 9.

If there exist arcs $(i,j)$ and $(i^{\prime },j^{\prime })$ satisfying $i^{\prime }\le i<j<j^{\prime }$, then we say that arc $(i^{\prime },j^{\prime })$ covers arc $(i,j)$. The number of arcs covering arc $(i,j)$ is called the level of arc $(i,j)$, denoted by ${\ell }_{(i,j)}$.

Definition 10.

For any arcs $(i,j)$ and $(i^{\prime },j^{\prime })$, if ${\ell }_{(i,j)}>{\ell }_{(i^{\prime },j^{\prime })}$, or ${\ell }_{(i,j)}={\ell }_{(i^{\prime },j^{\prime })}$ but $i<i^{\prime }$, then we call arc $(i,j)$ having higher level than arc $(i^{\prime },j^{\prime })$, denoted by $(i,j)\succ (i^{\prime },j^{\prime })$ . We call $\alpha =[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k]$ the arc sequence of τ, if ${\alpha }_t$’s are all its arcs, $1\le t\le k$, and ${\alpha }_1\succ {\alpha }_2\succ \cdots \succ {\alpha }_k$.

For example, as shown in Figure 2, linked parition $\tau$ has two tuggable singletons 2, 4, and a unique tuggable origion 6. Moreover, ${\ell }_{(1,3)}={\ell }_{(6,7)}=1$ and $(1,3)\succ (6,7)$, ${\ell }_{(1,5)}={\ell }_{(3,8)}=0$ and $(1,5)\succ (3,8)$. So the arc sequence of $\tau$ is

$$\alpha =[{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4]=[(1,3),(6,7),(1,5),(3,8)].$$

Definition 11.

Given a linked parition of τ, if there exists a tuggable vertice k of any arc $(i,j)$, then we remove arc $(i,j)$ from τ and add arcs $(i,k)$ and $(k,j)$. Denote the resulting gragh by ${\tau }^{\prime }$. The transformation from τ to ${\tau }^{\prime }$ is denominated as a tugging operation on arc $(i,j)$ at vertice k.

${\tau }^{\prime }$ is a linked partition because each vertex is a right-hand endpoint of at most one arc. The procedure of carrying out tugging operation on arcs at any one of tuggable vertices in $\tau$ or doing nothing is called a tugging transformation to $\tau$. Note that tuggable vertices of ${\tau }^{\prime }$ are those of $\tau$ except k.

As illustrated in Figure 12, ${\tau }_1$ is obtained from performing tugging transformation to $\tau$ in Figure 2: firstly, we tug arc $(1,3)$ at tuggable singleton 2, tug arc $(1,5)$ at tuggable singleton 4, and finally do nothing for arc $(3,8)$, however 6 is its tuggable origin.

Next we introduce the inverse transformation of tugging transformation for linked partitions.

Definition 12.

Given a linked parition of ${\tau }^{\prime }$. Suppose there exists a transition k connecting arcs $(i,k)$ to $(k,j)$, where both k and j are in block B, $k=min\left(B\right)$ and $j=max\left(B\right)$, we remove arcs $(i,k)$ and $(k,j)$ from ${\tau }^{\prime }$, while adding arc $(i,j)$. Denote the resulting gragh by ${\tau }^{\prime \prime }$. The transformation from ${\tau }^{\prime }$ to ${\tau }^{\prime \prime }$ is denominated as a rebound operation on arcs $(i,k)$ and $(k,j)$ at transition k.

It is not difficult to find that ${\tau }^{\prime \prime }$ is also a linked partition. The procedure of performing a single rebound operation on arcs at any one of transitions in a linked partition or doing nothing is called a rebound transformation to $\tau$. As illustrated in Figure 13, ${\tau }_2$ is obtained from performing rebound transformations to ${\tau }_1$ in Figure 12 at transitions 2, 3 and 4 in order.

The tugging procedure is the way to perform tugging transformation to set partitions of $\left[n\right]$, thus giving to linked partitions a nice recursive structure. Next we define this tugging procedure and we present a generation table for linked partitions.

A set partition $\pi$ of $\left[n\right]$ is a collection of disjoint nonempty subsets of $\left[n\right]$, that is

$$\pi =\left\{B_1,B_2,\dots ,B_m\right\},$$

where $B_i$’s are called blocks, $i=1,2,\dots ,m$ and whose union is $\left[n\right]$.

Given $\tau$ is a set partition of $\left[n\right]$, i.e., $\tau$ does not have any transition, then performing tugging transformation to $\tau$. The result linked partition ${\tau }^{\prime }$ satisfies that either ${\tau }^{\prime }=\tau$ or it has own possible tuggable vertices. Repeat the above process for ${\tau }^{\prime }$ and continue like this. Therefore, given set partitions ${\tau }_1$, ${\tau }_2$ and ${\tau }_1\ne {\tau }_2$, exerting tugging transformation on ${\tau }_1$ and ${\tau }_2$, respectively, the result of linked partitions ${\tau }_1^{\prime }$ and ${\tau }_2^{\prime }$ must be different from each other.

On the contraty, given a linked partition $\tau$, we can get set partitions by exerting rebound transformation at all of transitions. Thus, the following conclusion is provided.

Theorem 1.

All of linked partitions of $\left[n\right]$ can be generated by all of set partitions of $\left[n\right]$ performed tugging transformation.

For any $n\ge 1$, $j\ge 2$, we construct a generating table for the set of linked partitions on $\left[n\right]$: we list set partitions of $\left[n\right]$ in the first column, and draw the linked partitions in i-th column, which are obtained from performing tugging operation to those in $(i-1)$-th column at possibly tuggable vertices for only once. We claim that the generating table must conclude all of linked partitions on $\left[n\right]$. Aussme $\tau$ is a linked partitions on $\left[n\right]$. If $\tau$ does not have any transition, then $\tau$ is in the first column; otherwise we perform rebound operation to $\tau$ at all transitions, as a result of which we get a set partition in the first column. In conclusion, we can get linked partitions by the above recursive procedure.

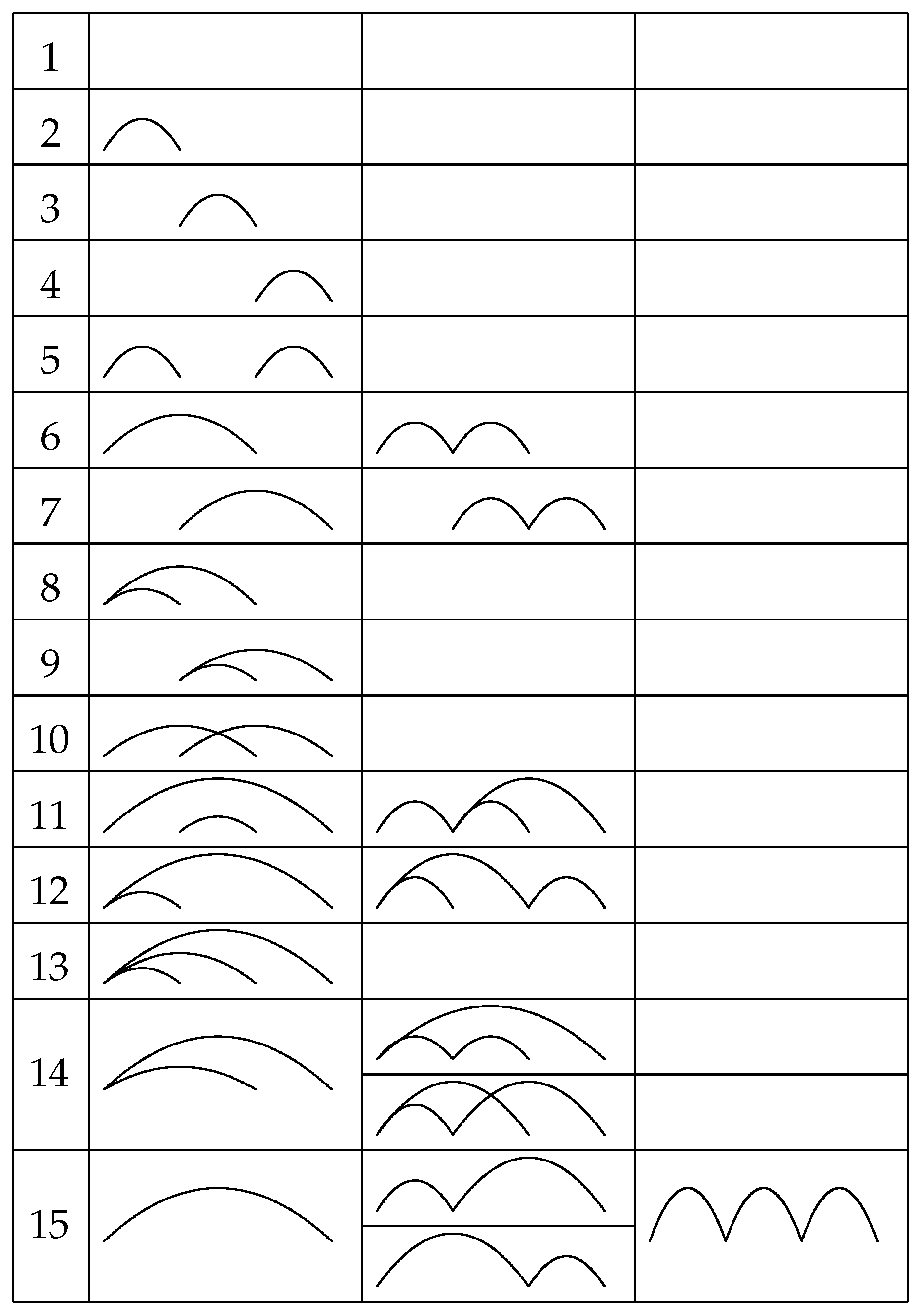
In Figure 14, we demonstrate that linked partitions of $\{1,2,3,4\}$ can be obtained from set partitions of $\{1,2,3,4\}$.

5. Main Theorem

Review that Chen, Liu and Wang [5] proved a bijection $\phi$ between linked partitions and permutation tableaux. Combining bijection $\phi$ with marking algorithms, we are led to the main result that $cr\left(\tau \right)$ and $ne\left(\tau \right)$ in any linked partition $\tau$ can be indicated by a linear function of the number of different markers in $\varphi \left(\tau \right)$.

Theorem 2

(Chen, Liu and Wang [5]). For $n\ge 1$ and $1\le k\le n$, there is a bijection φ between a linked partition of $\left[n\right]$ with k blocks and a permutation tableau T of length n with k rows.

It is not difficult to have the following result.

Proposition 1.

Let τ be a linked partition and $T=\phi \left(\tau \right)$ be the correspending permutation tableau.

(1)

If τ is a set partition, i.e. then there does not exist any $r.r.0$ in T.

(2)

If there exists a tuggable vertex k in τ, then performing the tugging transformation to k is equivalent to adding a $r.r.0$ in the k-th row of T.

Furthermore, based on Theorem 1, we have

Theorem 3.

Permutation tableaux of length n can be generated from the permutation tableaux only contained $t.m.1$’s by adding $r.r.0$’s in the cells that satisfy the definition.

Based on bijection $\phi$ between linked paritions and permutation tableaux in Theorem 2, we have the following conclusion.

Theorem 4.

Let τ be a linked partition of $\left[n\right]$ and $cr\left(\tau \right)=m$, $ne\left(\tau \right)=\ell$. If permutation tableau $T=\phi \left(\tau \right)$, then $F\left(T\right)=m$ and $G\left(T\right)=\ell$.

The interpretation of bijection $\phi$ implies that applying the tugging transformation to some arcs in a linked partition $\tau$ corresponds to the process of adding $r.r.0$’s in permutation tableau $T=\phi \left(\tau \right)$. Moreover, judging whether certain cells meet the front-out condition, the back-out condition or form a diagonal pattern in T, is to determine whether a new crossing is generated after tugging an arc in $\tau$. Comparing the size relationship between the ceiling index and the floor index of two cells in T, is to determine whether the corresponding arcs in $\tau$ form a nesting or not. Then by applying the column and row marking algorithm in T, respectively, one can thoroughly identify the crossings and nestings in $\tau$, and finally get $cr\left(\tau \right)$ and $ne\left(\tau \right)$ from the total numer of •’s and *’s. Hence we have the desired theorem.