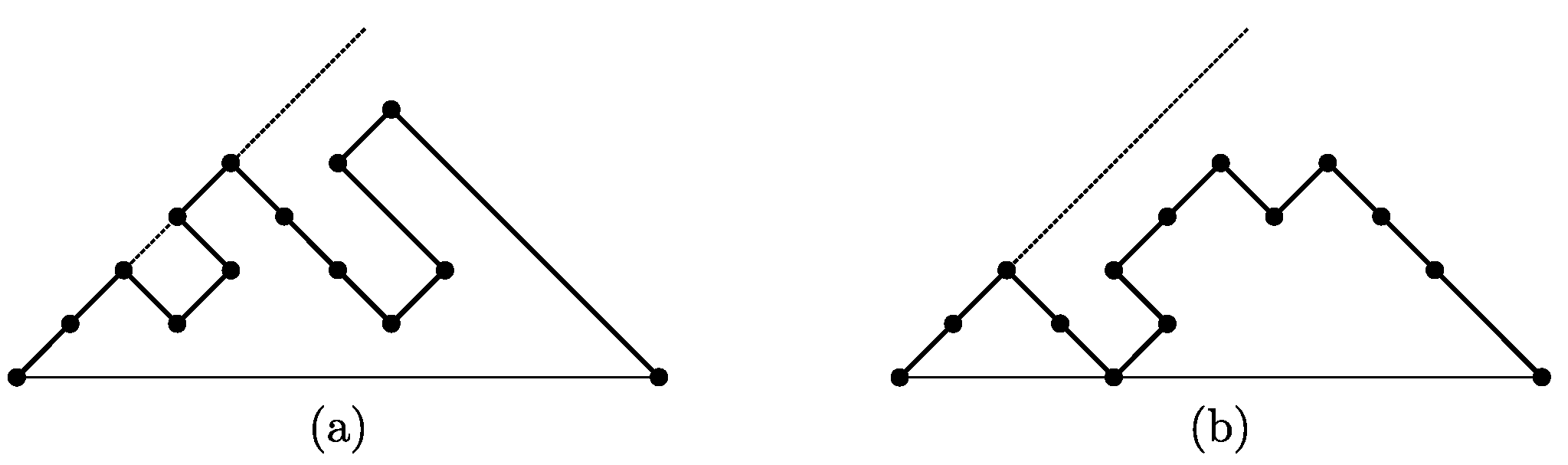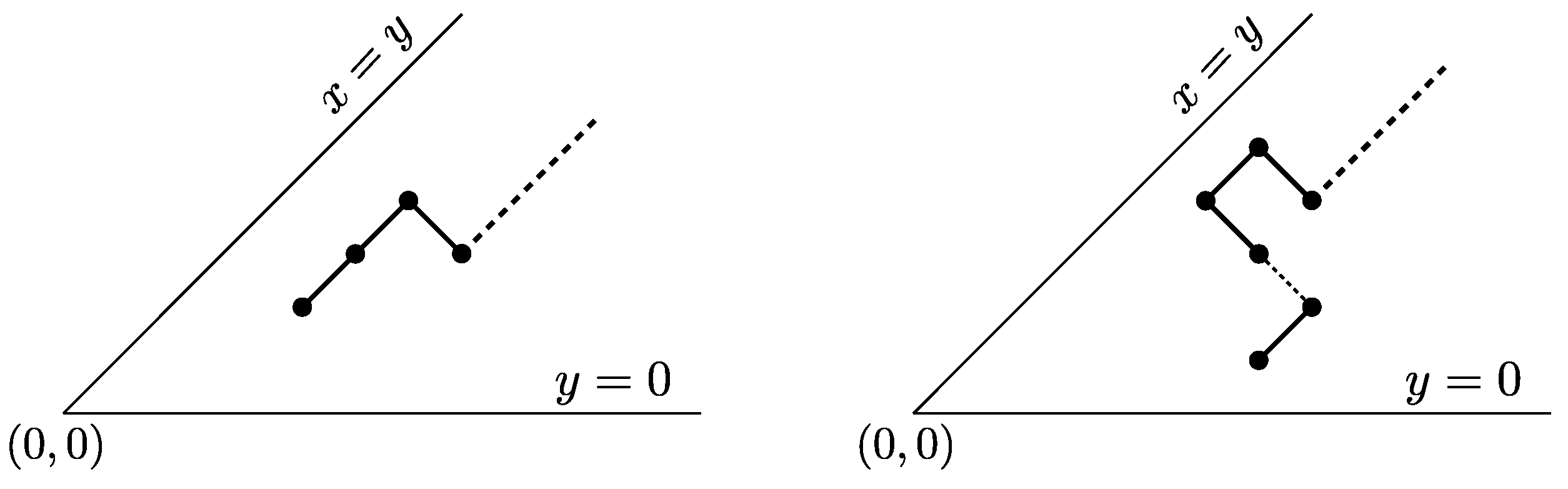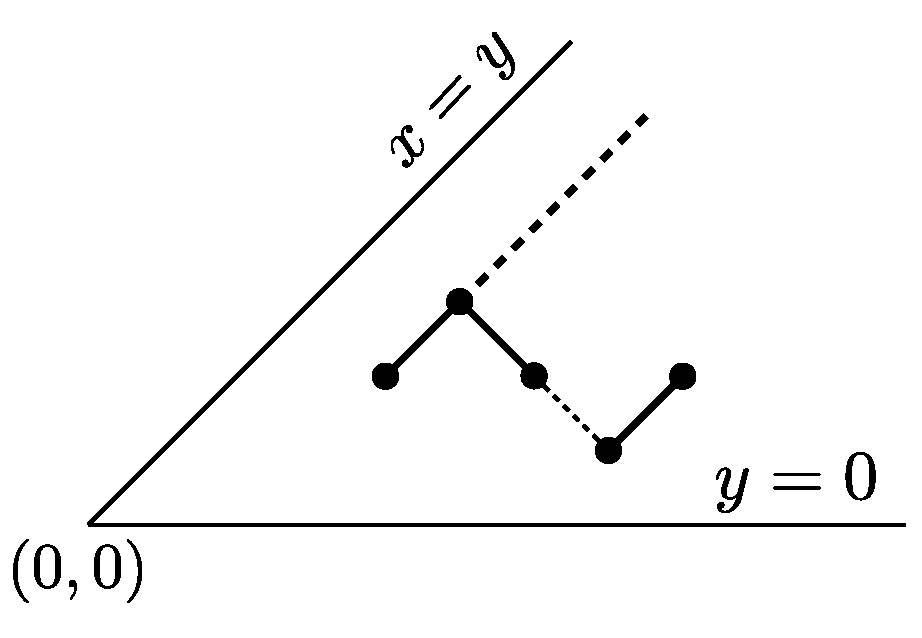Constrained Underdiagonal Paths and pattern Avoiding Permutations

1. Introduction and Basic Definitions

1.1. Permutations and Pattern Avoidance

Let $S_n$ denote the set of permutations of length (size) n. A pattern $\tau$ of length $k\le n$ is a permutation in $S_k$. A permutation $\pi \in S_n$ avoids the pattern $\tau$ if $\pi$ does not contain any subsequence order-isomorphic to $\tau$.

A (Babson-Steingrímsson-)pattern $\tau$ of length k is any permutation of $S_k$ where two adjacent entries may or may not be separated by a dash – see [1]. Such patterns are also called vincular patterns. The absence of a dash between two adjacent entries in the pattern indicates that in any pattern-occurrence the two entries are required to be adjacent: a permutation $\pi$ of length $n\ge k$contains the vincular pattern $\tau$, if it contains $\tau$ as pattern, and moreover, there is an occurrence of the pattern $\tau$ where the entries of $\tau$ not separated by a dash are consecutive entries of the permutation $\pi$; otherwise, $\pi$avoids the vincular pattern $\tau$. Let $\mathcal{T}$ be a set of patterns. We denote by $S_n\left(\mathcal{T}\right)$ the family of permutations of length n that avoid any pattern in $\mathcal{T}$, and by $S\left(\mathcal{T}\right)={\cup }_n{S}_n\left(\mathcal{T}\right)$.

To avoid ambiguity, when the pattern does not contain dashes, we speak of classical pattern avoidance. For example $S_n\left(231\right)$ (resp. $S_n(23-1)$) denotes the family of permutations of length n avoiding the classical pattern 231 (resp. the vincular pattern $23-1$). For further details on pattern avoidance in permutations and related problems, we address the interested reader to [12,17].

1.2. Inversion Sequences

For $n\ge 0$, let $\left[n\right]=\{0,\dots ,n\}$. Given a permutation $\pi \in S_n$, its left inversion table$\ell \left(\pi \right)$ is the array $({\ell }_1,\dots ,{\ell }_n)$ such that ${\ell }_i=\left|\{j:j>iand{\pi }_i>{\pi }_j\}\right|$. It is well-known that $\ell :S_n\to [n-1]\times \dots \times \left[1\right]\times \left[0\right]$ is a bijection.

An inversion sequence of length n is any integer sequence $e=(e_0,\dots ,e_{n-1})$ satisfying $0\le e_i\le i$, for all $i=1,\dots ,n-1$, i.e. and element of $I_n=\left[0\right]\times \left[1\right]\times \dots \times [n-1]$.

Let us consider the bijective mapping $\mathrm{L}:S_n\to I_n$, such that $\mathrm{L}\left(\pi \right)$ is the reverse of the left inversion table of $\pi$, precisely $\mathrm{L}\left(\pi \right)=({\ell }_n,\dots ,{\ell }_1)$. This bijection is actually at the origin of the name inversion sequences, and $\mathrm{L}\left(\pi \right)$ is called the inversion sequence corresponding to$\pi$.

The study of pattern-containment or pattern-avoidance in inversion sequences was first introduced in [20], and then further investigated in [13]. Namely, in [20], Mansour and Shattuck studied inversion sequences that avoid permutations of length 3, while in [13], Corteel et al. proposed the study of inversion sequences avoiding subwords of length 3. The definition of inversion sequences avoiding words (which may in addition be permutations) is straightforward: for instance, the inversion sequences that avoid the word 110 are those with no $i<j<k$ such that $e_i=e_j>e_k$ (resp. $e_i<e_k<e_j$).

In [21], the notion of pattern avoidance was then further extended to triples of binary relations $({\rho }_1,{\rho }_2,{\rho }_3)$. A handful of Wilf equivalences among the 343 possible sets of inversion sequences avoiding patterns of relation triples were conjectured in [21] and proved later in [11,16,18].

Equivalently to what happens for permutations, a vincular pattern in an inversion sequence is a pattern containing dashes showing the entries that don’t need to occur consecutively. An inversion sequence e of length n contains the vincular pattern p of length k if there are $i_1<i_2<\dots <i_k$ such that the entries $e_{i_1}{e}_{i_2}\dots e_{i_k}$ is order isomorphic to p and such that the entries which are not separated by dashes occur consecutively. Otherwise, e avoids p. For instance, the inversion sequence $e=(0,1,2,3,2)$ contains the pattern $p=0-21$ since for example the entries $e_2{e}_4{e}_5$ are order isomorphic to $0-21$, but the inversion sequence $e=(0,1,2,0,1)$ avoids it (however, it contains the classical pattern 021).

Although permutations and inversion sequences are in practice the same objects, the avoidance of some (vincular) patterns in permutations can only seldom be translated into the avoidance of (vincular) patterns in inversion sequences. So in this paper we will study, using the concepts of underdiagonal paths and generating trees, defined in the next section, some cases where the inversion sequences corresponding to a family of pattern avoiding permutations can be represented in terms of pattern avoidance.

1.3. Underdiagonal Paths

An underdiagonal path of size n[7] is a lattice path made of up $U=(1,1)$, down $D=(1,-1)$, west $W=(-1,1)$ steps, running from $(0,0)$ to $(2n,0)$, and such that:

• the path is weakly bounded by the lines $y=0$ and $x=y$, and
• a D (resp. W) step cannot be followed by a W (resp. D) step.

The up steps of an underdiagonal path P of size n will usually be referred to as $U_1,\dots ,U_n$, from left to right.

To an underdiagonal path P of size n, we can associate the inversion sequence $d\left(P\right)=(d_1,\dots ,d_n)$, where $d_i$ is the distance of $U_i$ from the diagonal $x=y$ (see Figure 2). It readily follows that the mapping d is a bijection, thus the number of underdiagonal paths of size n is $n!$.

By abuse of notation, we will often represent an underdiagonal path as the word in the alphabet $\{U,D,W\}$, obtained by reading its steps from left to right.

1.4. Generating Trees

Consider a combinatorial class $\mathcal{C}$, that is to say a set of discrete objects equipped with a notion of size such that the number of objects of size n is finite, for any n. We assume also that $\mathcal{C}$ contains exactly one object of size 1. A generating tree for $\mathcal{C}$ is an infinite rooted tree whose vertices are the objects of $\mathcal{C}$ each appearing exactly once in the tree, and such that objects of size n are at level n (with the convention that the root is at level 1). The children of some object $c\in \mathcal{C}$ are obtained by adding an atom (i.e. a piece of object that makes its size increase by 1) to c. Since every object appears only once in the generating tree, not all possible additions are acceptable. We enforce the unique appearance property by considering only additions that follow some prescribed rules and call growth of $\mathcal{C}$ the process of adding atoms according to these rules.

To illustrate these definitions, we describe the classical growth for the family of Dyck paths, as given by [3]. Recall that a Dyck path of semi-length n is a lattice path using up $U=(1,1)$ and down $D=(1,-1)$ unit steps, running from $(0,0)$ to $(2n,0)$ and remaining weakly above the x-axis. Observe that Dyck paths are precisely all underdiagonal paths containing no W steps.

The atoms we consider are $UD$ factors, a.k.a. peaks, which are added to a given Dyck path. To ensure that all Dyck paths appear exactly once in the generating tree, a peak is inserted only in a point of the last descent, defined as the longest suffix containing only D letters. More precisely, the children of the Dyck path $wU{D}^k$ are $wU\mathbf{UD}{D}^k$, $wUD\mathbf{UD}{D}^{k-1}$,..., $wU{D}^{k-1}\mathbf{UD}D$, $wU{D}^k\mathbf{UD}$.

The first few levels of the generating tree for Dyck paths are shown in Figure 1 (left).

When the growth of $\mathcal{C}$ is particularly regular, we encapsulate it in a succession rule. This applies more precisely when there exist statistics whose evaluations control the number of objects produced in the generating tree. A succession rule consists of one starting label (axiom) corresponding to the value of the statistics on the root object and of a set of productions encoding the way in which these evaluations spread in the generating tree – see Figure 1(right). The growth of Dyck paths presented earlier is governed by the statistics “length of the last descent”, so that it corresponds to the following succession rule, where each label $\left(k\right)$ indicates the number of D steps of the last descent in a Dyck path,

$${\mathsf{\Omega }}_C=\left\{\begin{array}{c}\left(1\right)\hfill \\ \\ \left(k\right)\hfill & ⇝\left(1\right),\left(2\right),\cdots ,\left(k\right),(k+1).\hfill \end{array}\right.$$

Obviously, as we discuss in [8], the sequence enumerating the class $\mathcal{C}$ can be recovered from the succession rule itself, without reference to the specifics of the objects in $\mathcal{C}$: indeed, the nth term of the sequence is the total number of labels (counted with repetition) that are produced from the root by $n-1$ applications of the set of productions, or equivalently, the number of nodes at level n in the generating tree. For instance, the well-know fact that Dyck paths are counted by Catalan numbers (sequence A000108 in [19]) can be recovered by counting nodes at each level n in the above generating tree.

For more details about generating trees, and the solution of the associated functional equations we address the reader to [2,3,6].

1.5. Contents of the Paper

Composing the bijections:

• $\mathrm{L}$ between permutations of length n and inversion sequences of length n, and
• $d^{-1}$ between inversion sequences of length n and underdiagonal paths of size n,

we obtain a bijection P between permutations of length n and underdiagonal paths of size n. So, given $\pi \in S_n$, and $\mathrm{L}\left(\pi \right)=(t_1,\dots ,t_n)$ the inversion sequence corresponding to $\pi$, $P\left(\pi \right)$ is the unique underdiagonal path of size n with up steps $U_1\dots U_n$, where the distance of $U_i$ from the diagonal $x=y$ is given by $t_i$. On the other side, given an underdiagonal path P of size n, we define $\pi \left(P\right)$ as the permutation of length n such that $\mathrm{L}\left(\pi \right)=d\left(P\right)$ (see Figure 2).

The aim of this paper is to study and enumerate families of underdiagonal paths which are obtained by restricting the bijection P to subclasses of $S_n$ avoiding some vincular patterns.

For a given pattern $\tau$, we will focus on the family $P\left(\tau \right)$ of underdiagonal paths corresponding to permutations in $S\left(\tau \right)$, precisely:

$$P\left(\tau \right)=\left\{P\right(\pi ):\pi \in S(\tau \left)\right\},$$

and the family $\mathrm{L}\left(\tau \right)$ of inversion sequences corresponding to permutations in $S\left(\tau \right)$, precisely:

$$\mathrm{L}\left(\tau \right)=\left\{\mathrm{L}\right(\pi ):\pi \in S(\tau \left)\right\}.$$

We will focus our investigation on patterns of length 3 and 4. Precisely:

• patterns of length 3 of type: ${\sigma }_1{\sigma }_2-{\sigma }_3$, where ${\sigma }_3\ne 3$, precisely $13-2$, $23-1$, $31-2$, $32-1$ (Section 2);
• patterns of length 3 of type: ${\sigma }_1-{\sigma }_2{\sigma }_3$, where ${\sigma }_1=1$, precisely $1-23$, $1-32$ (Section 3);
• patterns of length 4 of type: ${\sigma }_1-{\sigma }_2{\sigma }_3-{\sigma }_4$, where ${\sigma }_1=1$, ${\sigma }_4\ne 4$, precisely $1-34-2$, $1-43-2$, $1-24-3$, $1-42-3$ (Section 4).

We will reach our goal by providing, for each pattern $\tau$ above, a characterization of the underdiagonal paths of $P\left(\tau \right)$ in terms of geometrical constrains, or equivalently, in terms of the avoidance of some specific configurations, which will be formalized by the avoidance of some factors in the words coding the path. Moreover, we will give a characterization of the inversion sequences of $\mathrm{L}\left(\tau \right)$, in terms of pattern avoidance. Finally, we will determine a recursive growth of these families by means of generating trees and then, when it is possible, find their enumerative sequence.

We point out that, for all the patterns of length 3 not listed above (and not equivalent to one of them up to symmetries), it is not possible to provide a characterization of the corresponding families of inversion sequence in terms of pattern avoidance, hence of the associated underdiagonal paths.

Finally, we would like to point out that the investigation of underdiagonal paths and their connections with pattern avoiding permutations was started in [7], with the introduction and the study of steady paths, which will be recalled in Section 3.

2. Patterns of Length 3: ${\sigma }_1{\sigma }_2-{\sigma }_3$, with ${\sigma }_3\ne 3$

In this section we will take into account the study of families of underdiagonal paths corresponding to permutations avoiding one pattern ${\sigma }_1{\sigma }_2-{\sigma }_3$, where ${\sigma }_3\ne 3$ (namely $13-2$, $23-1$, $31-2$, or $32-1$).

2.1. The Family $P(13-2)$: Dyck Paths

It is known (and easy to prove) that a permutation avoids the vincular pattern $13-2$ if and only if it avoids the classical pattern 132, thus $S_n(13-2)=S_n\left(132\right)$. It is also known [15] that the cardinality of $S_n\left(132\right)$ is given by the nth Catalan number.

We will give a further proof of this fact by showing that $P(13-2)$ is the family of Dyck paths, i.e. underdiagonal paths without W steps.

Proposition 1.

Let π be a permutation of length n. Then, $\pi \in S_n(13-2)$ if and only if $P\left(\pi \right)$ is a Dyck path.

Proof. 

We proceed by contrapositive, proving that $P\left(\pi \right)$ contains a W step if and only if $\pi$ contains the pattern $13-2$. So, let $P=P\left(\pi \right)$ contain a factor $U_i{W}^h{U}_{i+1}$, with $0<i<n$, $h>0$. Then, with $d\left(P\right)=(d_1,\dots ,d_n)$, we have that $(d_n,\dots ,d_1)=({\ell }_1,\dots ,{\ell }_n)$ is the left inversion table of $\pi$, and $d_{i+1}={\ell }_{n-i}<{\ell }_{n-i+1}=d_i$. This occurs if and only if ${\pi }_{n-i}<{\pi }_{n-i+1}$, and moreover, there is some $j>n-i+1$ such that ${\pi }_{n-i}<{\pi }_j<{\pi }_{n-i+1}$ (otherwise ${\ell }_{n-i}={\ell }_{n-i+1}$). So, ${\pi }_{n-i}{\pi }_{n-i+1}{\pi }_j$ gives rise to an occurrence of $13-2$ in $\pi$.    □

The following is a neat consequence of Proposition 1.

Corollary 2.

$\mathrm{L}(13-2)=I\left(10\right)$.

2.2. The Family $P(23-1)$: ${(UU,WU)}_d$-Avoiding Paths

An underdiagonal path P is ${(UU,WU)}_d$-avoiding path if every factor $U_i{U}_{i+1}$ and $W{U}_i$ in P is such that the up step $U_i$ lies on the diagonal $x=y$ (Figure 3).

Proposition 3.

Let π be a permutation of length n. Then, $\pi \in S_n(23-1)$ if and only if $P\left(\pi \right)$ is a ${(UU,WU)}_d$-avoiding path.

Proof. 

We proceed by contrapositive, proving that $P\left(\pi \right)$ contains a factor $UU$ or $WU$, where U is not on the diagonal, if and only if $\pi$ contains the pattern $23-1$. Then, let $P\left(\pi \right)$ contain a factor $U_i{W}^h{U}_{i+1}$, with $d_i\ge d_{i+1}>0$, for some $0<i<n$, $h\ge 0$. Therefore, the left inversion table of $\pi$ is:

$$\ell \left(\pi \right)=(d_n,\dots ,d_{i+1},d_i,\dots ,d_1)=({\ell }_1,\dots ,{\ell }_{n-i},{\ell }_{n-i+1},\dots ,{\ell }_n),$$

with ${\ell }_{n-i}\le {\ell }_{n-i+1}$. This is equivalent to say that ${\pi }_{n-i}<{\pi }_{n-i+1}$. Moreover, since ${\ell }_{n-i}=d_{i+1}>0$, there is some $j>n-i+1$ such that ${\pi }_{n-i}{\pi }_{n-i+1}{\pi }_j$ forms a pattern $23-1$.    □

We recall from [12] that the family of permutations avoiding the pattern $23-1$ is enumerated by the Bell numbers (sequence A000110 in [19]). So, we have that:

Corollary 4.

For any $n\ge 0$, the number of ${(UU,WU)}_d$-avoiding paths of size n is given by the nth Bell number.

Corollary 5.

$\mathrm{L}(23-1)=I(0-11,0-21)$.

Proof. 

An inversion sequence $d=(d_1,\dots ,d_n)$ corresponds to a ${(UU,WU)}_d$-avoiding path P, i.e. $d=d\left(P\right)$ if and only if there is no index $i<n$ such that $0<d_{i+1}\le d_i$, thus it avoids one of the two patterns $0-11$, and $0-21$.    □

2.3. The Family $P(31-2)$: $DD$-Avoiding Paths

An underdiagonal path P is $DD$-avoiding if it does not contain any factor $DD$.

Proposition 6.

Let π be a permutation of length n. Then, $\pi \in S(31-2)$ if and only if $P\left(\pi \right)$ is a $DD$-avoiding path.

Proof. 

We prove that $P\left(\pi \right)$ contains a factor $DD$ if and only if $\pi$ contains a pattern $31-2$. So, there is an index i, $0<i<n$ such that $P\left(\pi \right)$ contains the factor $U_{i}DD{D}^h{U}_{i+1}$, $h\ge 0$. Therefore, $d_{i+1}\ge d_i+2$. Correspondingly, in the left inversion table $\ell \left(\pi \right)$ of $\pi$, we have ${\ell }_{n-i}\ge {\ell }_{n-i+1}+2$. This occurs if and only if ${\pi }_{n-i}>{\pi }_{n-i+1}$ and there is a $j>n-i+1$ such that ${\pi }_{n-i}>{\pi }_j>{\pi }_{n-i+1}$, so ${\pi }_{n-i}{\pi }_{n-i+1}{\pi }_j$ forms a pattern $31-2$.    □

Since the family of permutations avoiding the pattern $31-2$ is enumerated by the Catalan numbers [1], we have that:

Corollary 7.

For any $n\ge 0$, the number of $DD$-avoiding paths of size n is given by the nth Catalan number.

From the proof of Proposition 6, we immediately have that $\mathrm{L}(23-1)$ is given by the inversion sequences $(d_1,\dots ,d_n)$ such that there is no index $i=1\dots n$ satisfying $d_{i+1}\ge d_i+2$. This property cannot be expressed in terms of classical pattern avoidance, and by abuse of notation we write this family as $I\left(\widehat{02}\right)$.

2.4. The Family $P(32-1)$: ${\left(UDU\right)}_d$-Avoiding Paths

An underdiagonal path P is ${\left(UDU\right)}_d$-avoiding if, for every factor $UDU$, the first U step lies on the diagonal $x=y$ (see Figure 4).

Proposition 8.

Let π be a permutation of length n. Then, $\pi \in S(32-1)$ if and only if $P\left(\pi \right)$ is a ${\left(UDU\right)}_d$-avoiding path.

Proof. 

We proceed by contrapositive, proving that $P\left(\pi \right)$ contains a factor $UDU$ such that the first U step is not on the diagonal $x=y$ if and only if $\pi$ contains a pattern $32-1$. So, let us assume that there is an index i, $0<i<n$ such that $P\left(\pi \right)$ contains the factor $U_{i}D{U}_{i+1}$ and $U_i$ is not on $x=y$. Therefore, $d_{i+1}-1=d_i>0$. Using the same arguments as in the proofs above, this leads to an occurrence of the pattern $32-1$ in $\pi$.    □

Since the family of permutations avoiding the pattern $32-1$ is enumerated by the Bell numbers [1], we have that:

Corollary 9.

For any $n\ge 0$, the number of ${\left(UDU\right)}_d$-avoiding paths of size n is given by the nth Bell number.

From the proof of Proposition 8, we immediately have that:

Corollary 10.

$\mathrm{L}(32-1)=I(0-12)$.

3. Patterns of Length 3: $1-{\sigma }_2{\sigma }_3$

In this section we will study families of underdiagonal paths corresponding to permutations avoiding patterns $1-23$, and $1-32$.

3.1. The Family $P(1-23)$: Strong Steady Paths

An underdiagonal path P is strong steady if the two following conditions are satisfied:

(SS1)

for every factor $U_i{U}_{i+1}$ of P, the suffix of P following of $U_i{U}_{i+1}$ lies strictly below the line parallel to $x=y$, and passing from $U_i$ (see Figure 5, left).

(SS2)

for every factor $W{U}_i$ of P, the suffix of P following of $W{U}_i$ lies strictly below the line parallel to $x=y$, and passing from $U_i$ (see Figure 5, right).

The name strong steady is due to the fact that these paths are a proper subset of steady paths that we will study in Section 4, and already introduced in [7].

We call the edge line of P the line $y=x-t$, with $t\ge 0$ an even integer, which supports the up step of the rightmost occurrence of either $UU$ or $WU$ in P.

Proposition 11.

Let π be a permutation of length n. Then, $\pi \in S(1-23)$ if and only if $P\left(\pi \right)$ is a strong steady path.

Proof. 

We proceed by contrapositive, proving that $P\left(\pi \right)$ is not strong steady if and only if $\pi$ contains an occurrence of $1-23$. Then, assuming that P is not strong steady, one of the two Conditions (SS1) or (SS2) should be violated, which is equivalent to say that (see also Figure 5), for some $1<i<n$, there are two up steps $U_i$ and $U_{i+1}$ and step $U_j$, $j>i+1$, which is above the border line at $U_{i+1}$. It is equivalent to say that $d_i\ge d_{i+1}\ge d_j$. Therefore, in $\pi$, we have ${\pi }_{n-j+1}<{\pi }_{n-i}<{\pi }_{n-i+1}$, i.e. an occurrence of the pattern $1-23$.    □

Since the family of permutations avoiding the pattern $1-23$ is enumerated by the Bell numbers [1], we have that:

Corollary 12.

For any $n\ge 0$, the number of strong steady paths of size n is given by the nth Bell number.

From the proof of Proposition 11, we immediately have that:

Corollary 13.

$\mathrm{L}(1-23)=I(00-0,10-0,11-0,21-0)$.

3.2. The Family $P(1-32)$: Strong $UDU$-Constrained Paths

An underdiagonal path P is strong $UDU$-constrained if, for every factor $U_i{D}^{h+1}{U}_{i+1}$ of P, $0<i<n$,$h\ge 0$, the suffix of P on the right of $U_{i+1}$ lies strictly below the line parallel to $x=y$, and passing from $U_i$.

Again, the line parallel to $x=y$, and passing from $U_i$, will be referred to as the edge line at $U_i$.

Figure 6. The strong $UDU$-constrain. The dotted line lies immediately below the edge line, and it delimits the region forbidden to the suffix of the path.

Figure 6. The strong $UDU$-constrain. The dotted line lies immediately below the edge line, and it delimits the region forbidden to the suffix of the path.

Proposition 14.

Let π be a permutation of length n. Then, $\pi \in S(1-32)$ if and only if $P\left(\pi \right)$ is strong $UDU$-constrained.

Proof. 

As usual, we proceed by contrapositive. So, we assume that $P\left(\pi \right)$ is not strong $UDU$-constrained. Then, for some $0<i<n$, there is a factor $U_{i}D{U}_{i+1}$ of P, and an up step $U_j$, $j>i+1$, which is weakly above the edge line at $U_i$, which is equivalent to say that, in $d\left(P\right)$, we have: $d_j\le d_i<d_{i+1}$. Again, this means that the entries of $\pi$ in positions $n-i$, $n-i+1$, $n-j+1$, give rise to an occurrence of $1-32$.    □

Since the family of permutations avoiding the pattern $1-32$ is enumerated by the Bell numbers [1], we have that:

Corollary 15.

For any $n\ge 0$, the number of strong $UDU$-constrained paths of size n is given by the nth Bell number.

From the proof of Proposition 14, we immediately have that:

Corollary 16.

$\mathrm{L}(1-32)=I(01-0,12-0)$.

Remark 17.

We point out that, for all the other patterns of length 3 not listed above, we cannot provide a characterization of the corresponding families of inversion sequences in terms of pattern avoidance, hence of their associated underdiagonal paths.

Let us consider, for example, the case of the classic pattern 231. If a permutation contains the pattern 231, then its left inversion table $\ell \left(\pi \right)$ contains three entries ${\ell }_i$, ${\ell }_j$, ${\ell }_h$, with $i<j<h$, such that ${\ell }_h<{\ell }_i$ and ${\ell }_h<{\ell }_j$, i.e., one of the patterns 110, 210 and 120. But the converse does not hold, since we can show the permutation $\pi =2143\in S\left(231\right)$, with left inversion table $\ell \left(\pi \right)=\left(1010\right)$, containing the pattern 110. So it is not possible to provide a characterization of $S\left(231\right)$ in terms of pattern avoidance of the corresponding inversion sequences.

Table 1. The families of patterns considered in Section 2 and Section 3, and the corresponding constrained underdiagonal paths, inversion sequences, and number sequences.

Permutation patterns	Underdiagonal Paths	Inversion Sequences	Number Sequence
$13-2$	Dyck Paths	$I\left(10\right)$	Catalan numbers
$23-1$	${(UU,WU)}_d$-avoiding	$I(0-11,0-21)$	Bell numbers
$31-2$	$DD$-avoiding	$I\left(\widehat{02}\right)$	Catalan numbers
$32-1$	${\left(UDU\right)}_d$-avoiding	$I(0-12)$	Bell numbers
$1-23$	strong steady	$I(00-0,10-0,11-0,21-0)$	Bell numbers
$1-32$	strong $UDU$-constrained	$I(01-0,12-0)$	Bell numbers

Table 1. The families of patterns considered in Section 2 and Section 3, and the corresponding constrained underdiagonal paths, inversion sequences, and number sequences.

Permutation patterns	Underdiagonal Paths	Inversion Sequences	Number Sequence
$13-2$	Dyck Paths	$I\left(10\right)$	Catalan numbers
$23-1$	${(UU,WU)}_d$-avoiding	$I(0-11,0-21)$	Bell numbers
$31-2$	$DD$-avoiding	$I\left(\widehat{02}\right)$	Catalan numbers
$32-1$	${\left(UDU\right)}_d$-avoiding	$I(0-12)$	Bell numbers
$1-23$	strong steady	$I(00-0,10-0,11-0,21-0)$	Bell numbers
$1-32$	strong $UDU$-constrained	$I(01-0,12-0)$	Bell numbers

4. Patterns of Length 4: ${\sigma }_1-{\sigma }_2{\sigma }_3-{\sigma }_4$, with ${\sigma }_1=1$, ${\sigma }_4\ne 4$

We study separately the patterns $1-34-2$, $1-43-2$, $1-24-3$, $1-42-3$.

4.1. The Family $P(1-34-2)$: Steady Paths

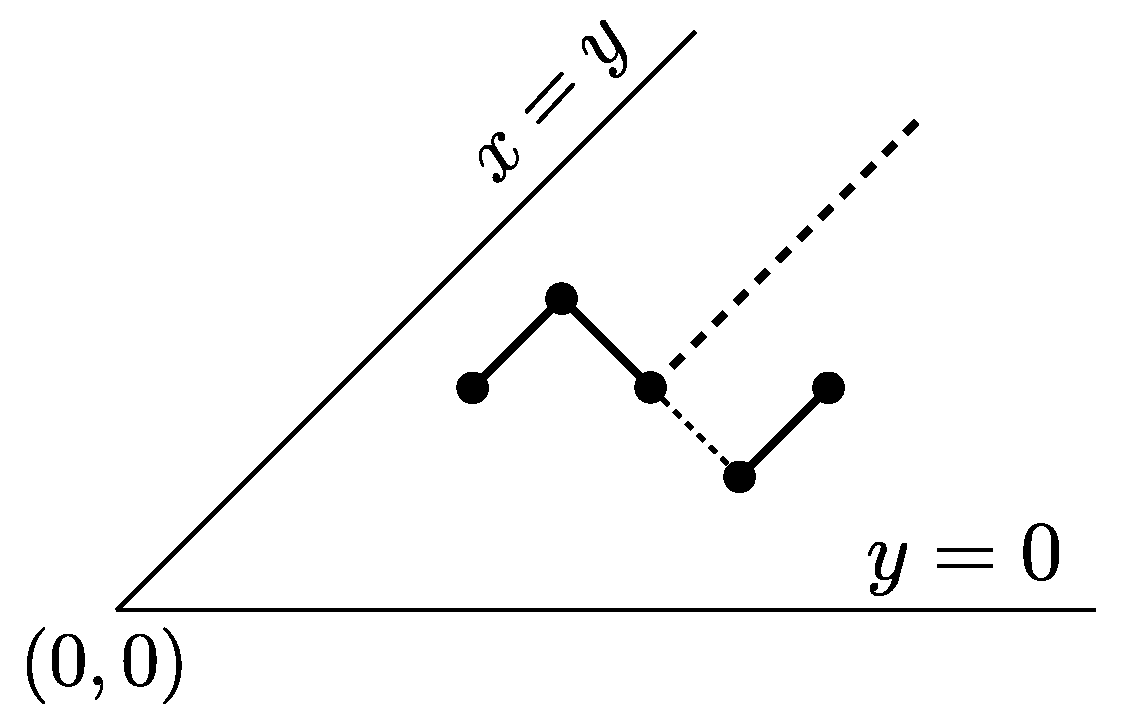
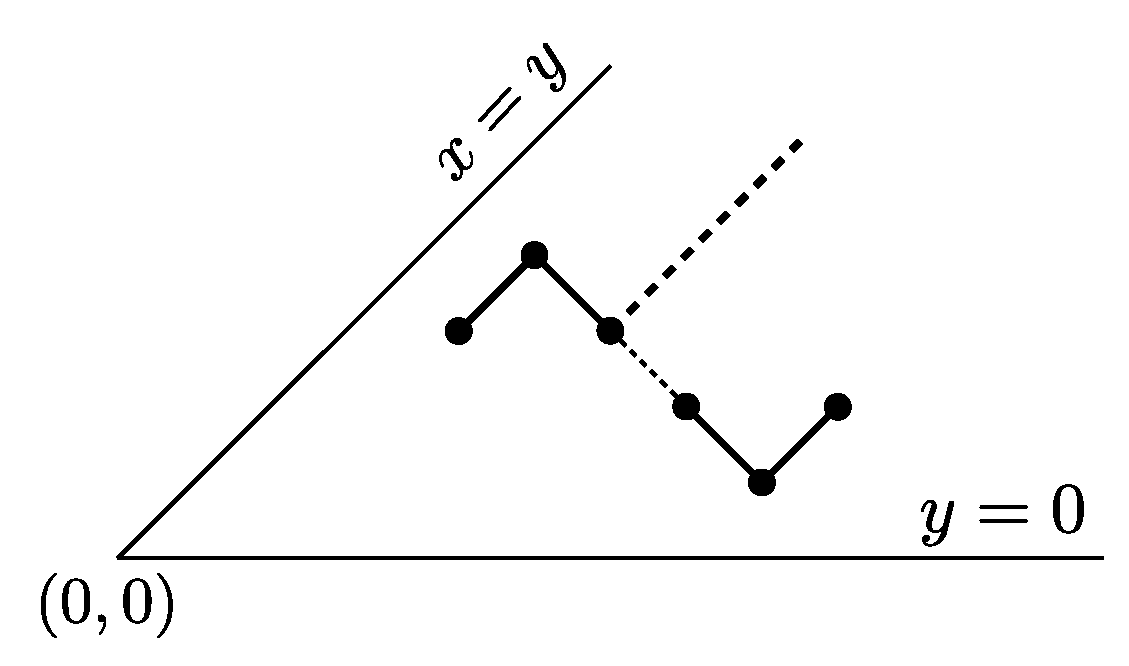
An underdiagonal path P is a steady path if the two following conditions are satisfied:

(S1)

for every factor $U_i{U}_{i+1}$ of P, the suffix of P following $U_i{U}_{i+1}$ lies weakly below the line parallel to $x=y$, and passing through $U_i$.

(S2)

for every factor $W{U}_i$ of P, the suffix of P following $W{U}_i$ lies weakly below the line parallel to $x=y$, and passing through $U_i$.

Clearly, a strong steady path is also a steady path, while the converse does not hold. We call the edge line of P the line $y=x-t$, with $t\ge 0$ an even integer, which supports the up step of the rightmost occurrence of either $UU$ or $WU$ in P.

Figure 7 (a) shows an example of a steady path whose edge line coincides with $y=x$, whereas the edge line of the steady path depicted in Figure 7 (b) is $y=x-6$. Figure 7 (c),(d) show two different examples of underdiagonal paths that are not steady paths. We also point out that steady paths are a subfamily of those “skew Dyck paths” studied in [14].

Steady paths were introduced in [7], as one of the several combinatorial families enumerated by powered Catalan numbers. The investigation of [7] starts from powered Catalan inversion sequences $I_n\left(110\right)$, and then the authors provide bijections among the families enumerated by their number sequence.

The sequence of powered Catalan numbers is registered on [19] as A113227, and its first terms are:

$$1,1,2,6,23,105,549,3207,20577,143239,1071704,8555388,72442465,647479819,\dots$$

D. Callan [10] proves that the nth term of the sequence can be obtained as $p_n={\sum }_{k=0}^n{c}_{n,k}$, where $c_{n,k}$ is recursively defined by:

$$\left\{\begin{array}{cc}{c}_{0,0}=1,\hfill & \\ c_{n,0}=0,\hfill & \mathrm{for}n\ge 1\hfill \\ c_{n,k}=c_{n-1,k-1}+k{\displaystyle {\sum }_{j=k}^{n-1}}{c}_{n-1,j},\hfill & \mathrm{for}n\ge 1,and1\le k\le n.\hfill \end{array}\right.$$

(1)

Proposition 18

([13], Theorem 13). For $n\ge 1$ and $0\le k\le n$, the number of powered Catalan inversion sequences having k zeros is given by the term $c_{n,k}$ of Equation (1). Thus, the number of powered Catalan inversion sequences of length n is $p_n$, for every $n\ge 1$.

Proposition 18 can be rephrased in terms of succession rules, as done below with the rule ${\mathsf{\Omega }}_{pC}$. More precisely, for $n\ge 1$ and $k\ge 1$, the number of nodes at level n that carry the label $\left(k\right)$ in the generating tree associated with ${\mathsf{\Omega }}_{pC}$ is precisely the quantity $c_{n,k}$ given by Equation (1).

Proposition 19.

The family of powered Catalan inversion sequences grows according to the following succession rule

$${\mathsf{\Omega }}_{pC}=\left\{\begin{array}{c}\left(1\right)\hfill \\ \\ \left(k\right)\hfill & ⇝\hfill & \left(1\right),{\left(2\right)}^2,{\left(3\right)}^3,\dots ,{\left(k\right)}^k,(k+1).\hfill \end{array}\right.$$

We notice that ${\mathsf{\Omega }}_{pC}$ is extremely similar to the Catalan succession rule ${\mathsf{\Omega }}_C$ (see page ): specifically, the productions of ${\mathsf{\Omega }}_{pC}$ are the same as in ${\mathsf{\Omega }}_C$, but with multiplicities appearing as “powers”. Hence, the name powered Catalan.

The authors of [7] prove the following statements (we report here the proof for the sake of completeness):

Proposition 20.

Let π be a permutation of length n. Then, $\pi \in S_n(1-34-2)$ if and only if $P\left(\pi \right)$ is a steady path.

Proof. 

As usual, we will proceed by contrapositive. Let P be an underdiagonal path of size n which is not steady. So, one of the two conditions (S1) or (S2) must be violated, i.e. there must be in P an up step $U_i$ not lying on the main diagonal such that it forms a factor either $U_i{U}_{i+1}$ or $W{U}_i$, and an up step $U_j$, which is on the right of $U_i$, lying above the line parallel to $y=x$ and passing through $U_i$. First, suppose $U_i$ forms a factor $U_i{U}_{i+1}$. Then, in $d\left(P\right)$, we have $d_i=d_{i+1}$ and $0\le d_j<d_i$, with $j>i+1$. Let us consider then the permutation $\pi$ with left inversion table $({\ell }_1,\dots ,{\ell }_n)=(d_n,\dots ,d_1)$, i.e. such that $P=P\left(\pi \right)$. It holds that ${\pi }_{n-j+1}<{\pi }_{n-i}<{\pi }_{n-i+1}$. Moreover, since $d_{i+1}=d_i>d_j\ge 0$, there is an index $k>n-i+1$ such that ${\pi }_k<{\pi }_{n-i}$ and ${\pi }_k>{\pi }_{n-j+1}$. Therefore, ${\pi }_{n-j+1}{\pi }_{n-i}{\pi }_{n-i+1}{\pi }_k$ is an occurrence of the pattern $1-34-2$. On the other hand, if $U_i$ forms a factor $W{U}_i$, there exists $U_{i-1}$ such that $d_i<d_{i-1}$. Then, in $d\left(P\right)$ we have $0\le d_j<d_i<d_{i-1}$, with $j>i$. Let $\pi$ be the permutation with left inversion table $(d_n,\dots ,d_1)$. It holds that ${\pi }_{n-j+1}<{\pi }_{n-i+1}<{\pi }_{n-i+2}$. Moreover, since $d_i>d_j\ge 0$, there is an index $k>n-i+2$ such that ${\pi }_k<{\pi }_{n-i+1}$ and ${\pi }_k>{\pi }_{n-j+1}$. Finally, ${\pi }_{n-j+1}{\pi }_{n-i+1}{\pi }_{n-i+2}{\pi }_k$ is an occurrence of the pattern $1-34-2$.

The above argument can be inverted proving that if $\pi$ is a permutation containing an occurrence of $1-34-2$, then $P\left(\pi \right)$ is not steady (see also [7]).    □

We provide a growth for the family of steady paths that results in the following proposition.

Proposition 21.

The family of steady paths grows according to the following succession rule:

$${\mathsf{\Omega }}_S=\left\{\begin{array}{ccc}(0,2)\hfill & & \\ \\ (h,k)\hfill & ⇝\hfill & (h+k-1,2),\dots ,(h+1,k),\hfill \\ & \hfill & (0,k+1),\dots ,(0,h+k+1).\hfill \end{array}\right.$$

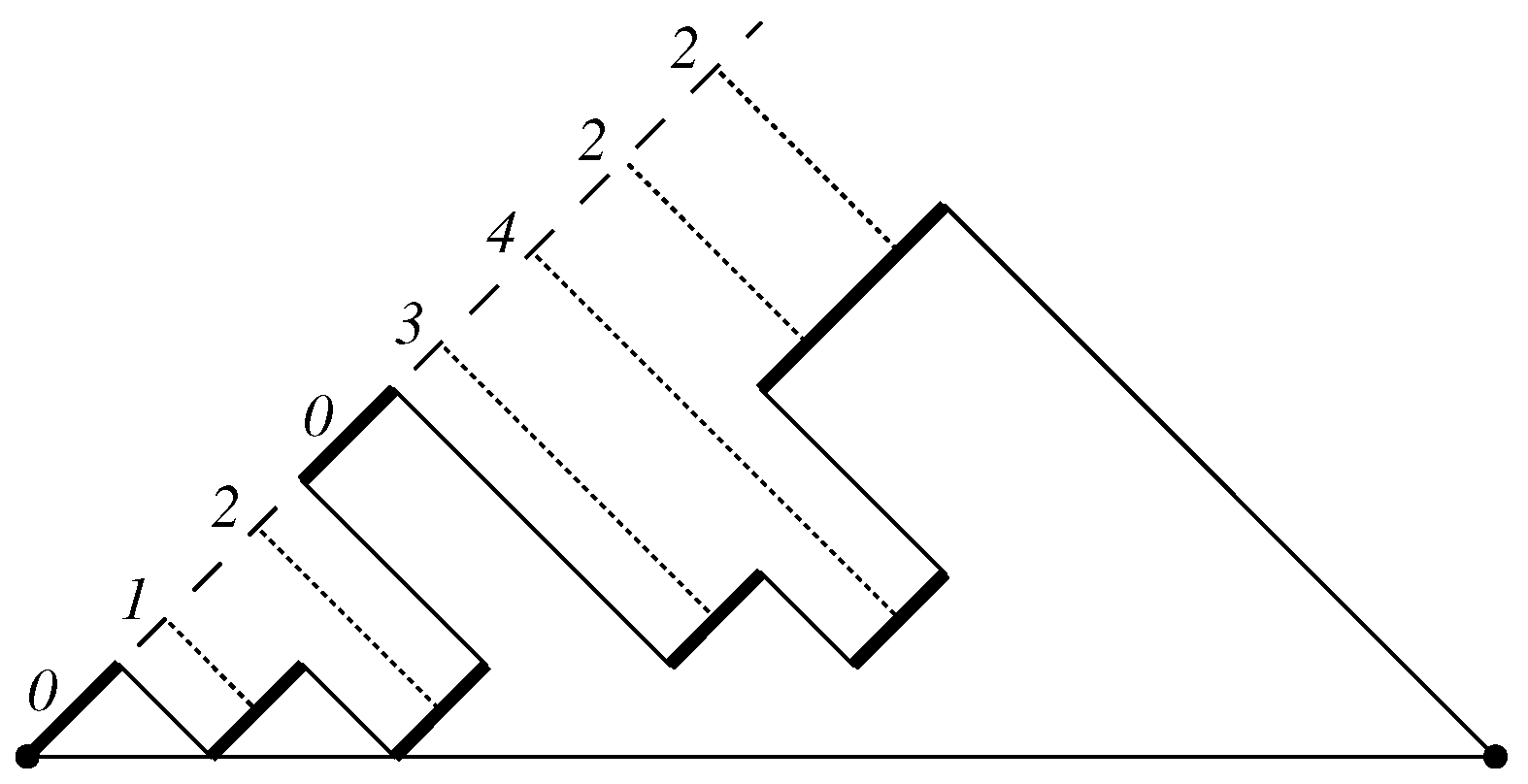
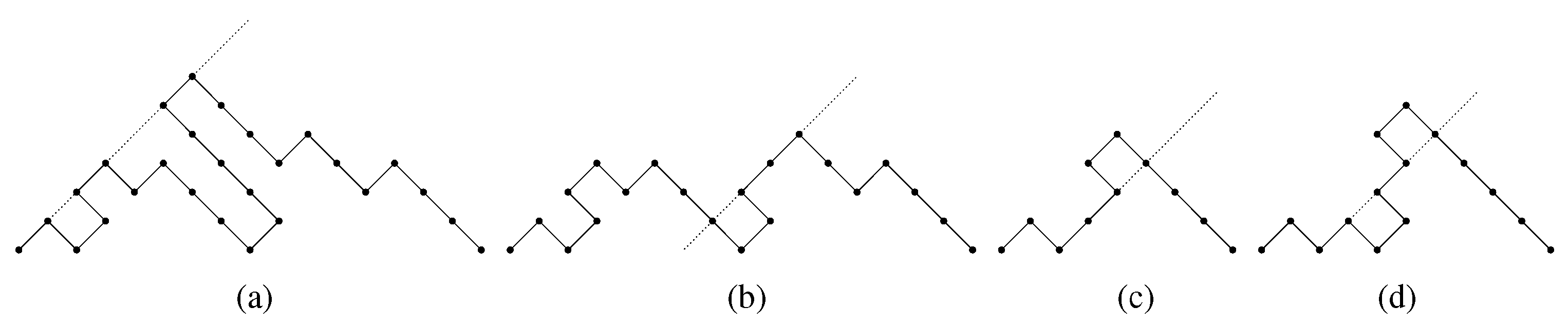
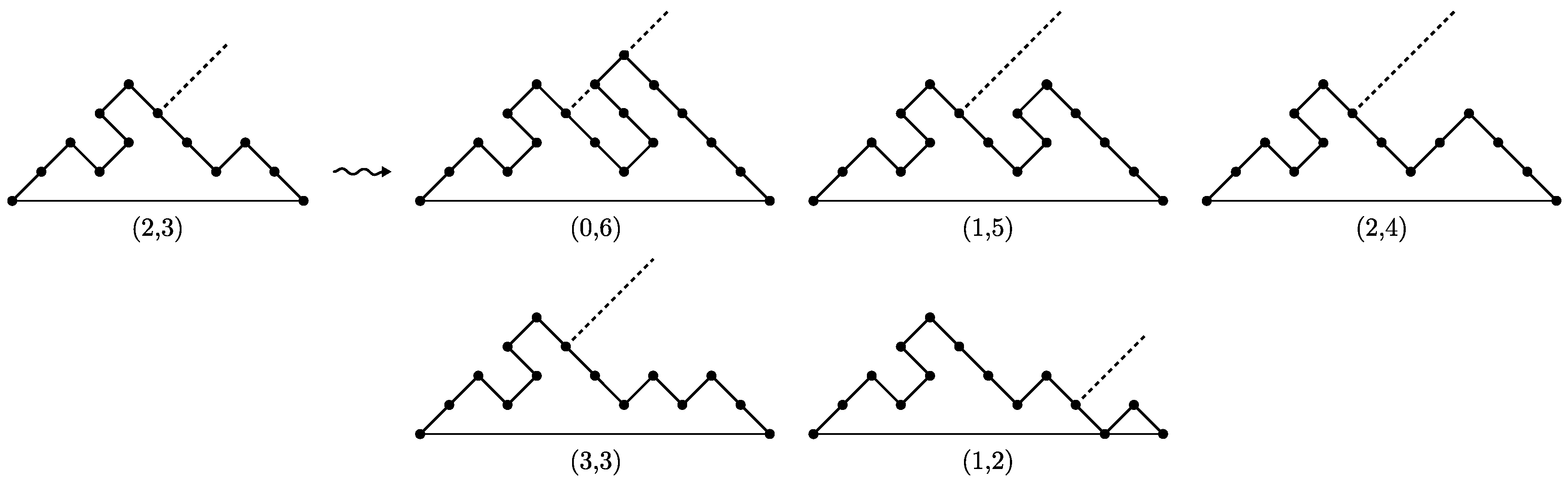
Proof. 

We start observing that every steady path P of size $n+1$ ends with a factor $W^{r}U{D}^{r+s+1}$, with $r,s\ge 0$, and that removing the factor $W^{r}U{D}^{r+s+1}$ from P we obtain a steady path of size n. So, we define a recursive growth of steady paths, such that every steady path of size $n+1$ is uniquely produced from a steady path of size n by adding the last up step, and prove that this growth can be described by the succession rule ${\mathsf{\Omega }}_S$.

Let P be a steady path of size n, ending with a factor $W^{r}U{D}^{r+s+1}$, with $r,s\ge 0$. Let us denote its last up step by $\overline{U}$. We assign to P the label $(h,k)$, where h is the distance between $\overline{U}$ and the edge line, and $k=r+s+2$, i.e. k is the length of P last descent plus one. Then, $k\ge 2$, whereas $h\ge 0$. The steady path $UD$ of minimal length has label $(0,2)$.

The steady path P of label $(h,k)$ produces $h+k$ steady paths of size $n+1$, by applying the following operations:

• We add an occurrence of $UD$ just following a sequence of t consecutive down steps in the last descent, with $1\le t\le r+s+1=k-1$. For every t, thsi operation produces a steady path with label $(h+t,k+1-t)$.
• We add an occurrence of $UD$ just following $\overline{U}$, thus producing a factor $\overline{U}UD$. Therefore, the obtained steady path has edge line passing through $\overline{U}$, hence its label is $(0,k+1)$.
• We add an occurrence of $W^{t}U{D}^{t+1}$ just following $\overline{U}$, with $1\le t\le h$. Therefore we obtain a new occurrence of $WU$, in the rightmost position, then the edge line of the obtained path passes through the added up step. The label of this path is $(0,t+k+1)$.

Hence steady paths growth can be described by means of the succession rule ${\mathsf{\Omega }}_S$.    □

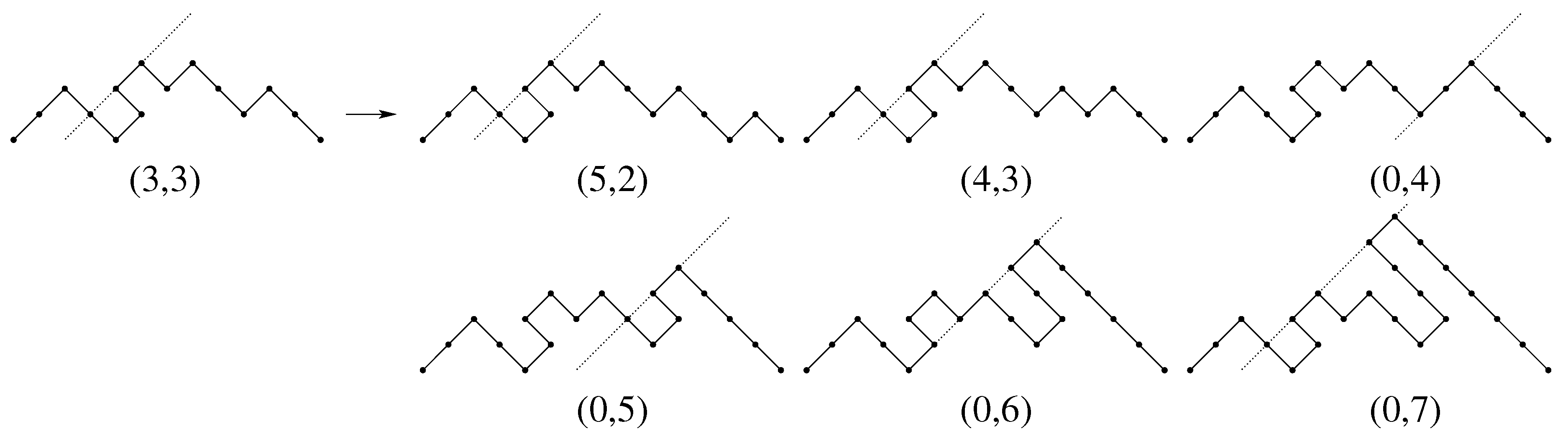
Figure 8 depicts the growth of a steady path of size n with edge line $y=x-2$; for any path, the corresponding edge line is drawn.

From the proof of Proposition 20, we immediately have the following corollary (not reported in [7]):

Corollary 22.

$\mathrm{L}(1-34-2)=I(11-0,21-0)$.

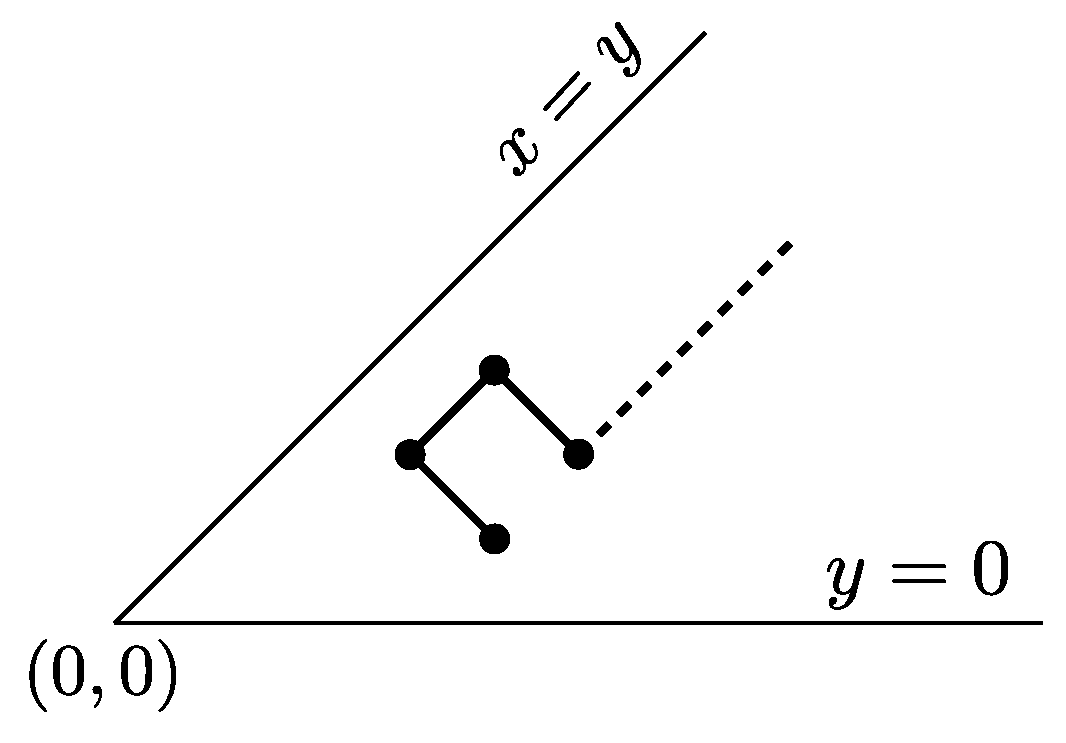
4.2. The Family $P(1-43-2)$: $UDU$-Constrained Paths

A $UDU$-constrained path P is a path such that, for every factor $U_i{D}^{h+1}{U}_{i+1}$ of P, $0<i<n$, $h\ge 0$, the suffix of P on the right of $U_{i+1}$ lies weakly below the line parallel to $x=y$, and passing from $U_i$ (see Figure 9).

Again, the line the line parallel to $x=y$, and passing from $U_i$, will be referred to as the edge line at $U_i$.

Proposition 23.

Let π be a permutation of length n. Then, $\pi \in S(1-43-2)$ if and only if $P\left(\pi \right)$ is $UDU$-constrained.

Proof. 

As usual, we will proceed by contrapositive. Let P be an underdiagonal path of size n which is not $UDU$-constrained. So, there are indices $0<i<n-2$, $i+1<j\le n$, such that $U_i{D}^{h+1}{U}_{i+1}$, $h\ge 0$, is a factor of P, and $U_j$ lies above the edge line at $U_i$. Therefore, in $d\left(P\right)$ we have $0\le d_j<d_i<d_{i+1}$. Let us consider then the permutation $\pi$ with left inversion table $(d_n,\dots ,d_1)$, i.e. such that $P=P\left(\pi \right)$. It holds that ${\pi }_{n-j+1}<{\pi }_{n-i+1}<{\pi }_{n-i}$. Moreover, since $d_i>d_j\ge 0$, there is an index $k>n-i+1$ such that ${\pi }_k<{\pi }_{n-i+1}<{\pi }_{n-i}$ and ${\pi }_k>{\pi }_{n-j+1}$. Finally, ${\pi }_{n-j+1}{\pi }_{n-i}{\pi }_{n-i+1}{\pi }_k$ is an occurrence of the pattern $1-43-2$.

The above argument can be neatly inverted proving that if $\pi$ is a permutation containing an occurrence of $1-43-2$, then $P\left(\pi \right)$ is not $UDU$-constrained.    □

Proposition 24.

The number of $UDU$-constrained paths of size n is the nth powered Catalan number.

Proof. 

We prove it by showing that $S(1-43-2)$ grows according to the rule:

$${\mathsf{\Omega }}_S=\left\{\begin{array}{ccc}(0,2)\hfill & & \\ \\ (h,k)\hfill & ⇝\hfill & (h+k-1,2),\dots ,(h+1,k),\hfill \\ & \hfill & (0,k+1),\dots ,(0,h+k+1).\hfill \end{array}\right.$$

which governs the growth of steady paths enumerated by powered Catalan numbers.

Let $\pi \in S_n(1-43-2)$. We made it grow by adding an element $x\in \left[n\right]=\{1,\dots ,n+1\}$ on the right, and we denote by $\pi ·x$ the obtained permutation. More precisely, the entry ${\pi }_i^{\prime }$ of $\pi ·x$ is:

$${\pi }_i^{\prime }=\left\{\begin{array}{cc}{\pi }_i+1& \mathrm{if}x\le {\pi }_i\\ {\pi }_i& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

We say that x is an active entry if $\pi ·x$ avoids the pattern $1-43-2$. Precisely, if there are indices $i,j$, with $i<j<n$, such that ${\pi }_i{\pi }_j{\pi }_{j+1}$ is an occurrence of $1-32$, i.e. ${\pi }_i<{\pi }_{j+1}<{\pi }_j$, then every entry $k\in \{{\pi }_i+1,\dots ,{\pi }_{j+1}\}$ is not active. Actually, given an occurrence ${\pi }_i{\pi }_j{\pi }_{j+1}$ of the pattern $1-32$, non active entries are exactly all $k\in \{2,\dots ,{\pi }_{j+1}\}$. Let h (resp. k) be the number of active entries less than (resp. greater than or equal to) ${\pi }_n$. Observe that entries 1 and $n+1$ are always active, thus $k\ge 1$, and $h+k\ge 2$. The label of the the length 1 permutation is $(0,2)$.

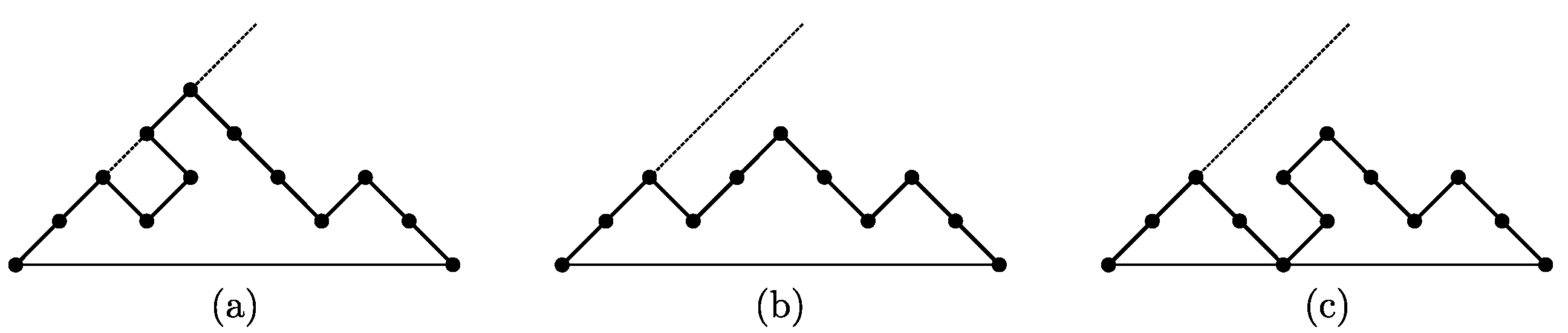
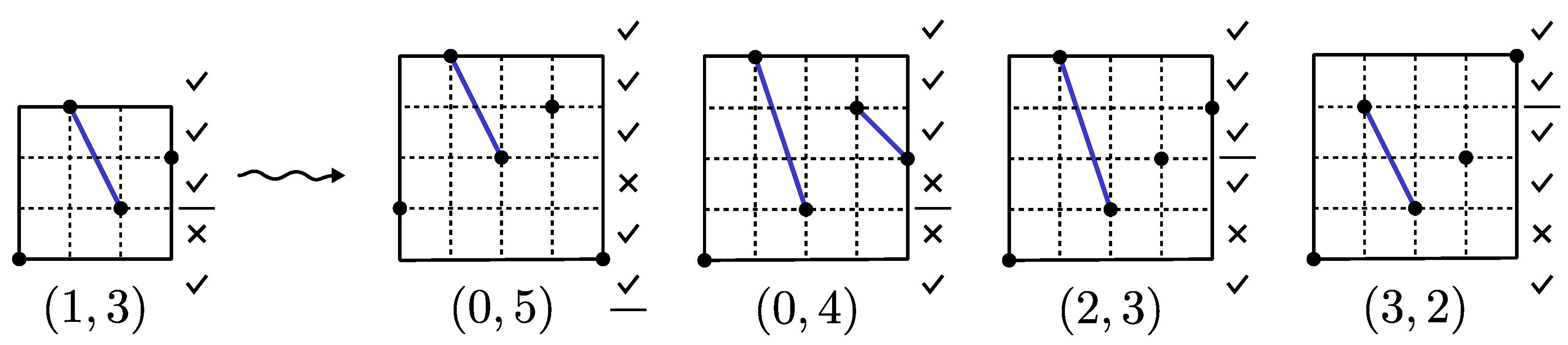
So, let $(h,k)$ be the label of $\pi$, and let x be an active entry of $\pi$. The labels of ${\pi }^{\prime }=\pi ·x$ are (see also the example in Figure 10):

• $x=1$: in this case ${\pi }_i^{\prime }={\pi }_i+1$, for all i. The last two entries of ${\pi }^{\prime }$, i.e. ${\pi }_n+1$ and 1 do not produce a new occurrence of $1-32$. So, ${\pi }^{\prime }$ has the same active entries as $\pi$, plus $n+2$, so it has label $(0,k+1+h)$.
• $1<x\le {\pi }_n$: in this case ${\pi }_n^{\prime }={\pi }_n+1$. The entries $x-1{\pi }_n^{\prime }x$ of ${\pi }^{\prime }$ produce a new occurrence of $1-32$, so the entries less than or equal to x become non active in ${\pi }^{\prime }$. So, if x is the ith active entry for $\pi$, $1<i\le h$, then ${\pi }^{\prime }=\pi ·x$ has label $(0,k+1+h-i)$.
• $x>{\pi }_n$: in this case ${\pi }_n^{\prime }={\pi }_n$. The entries ${\pi }_n^{\prime }x$ of ${\pi }^{\prime }$ produce an ascent, so ${\pi }^{\prime }$ has the same active entries as $\pi$, plus $n+2$. So, if x is the jth active entry for $\pi$, $1\le j\le k-1$, then ${\pi }^{\prime }$ has label $(h+j,k+1-j)$.

Then, we have that the growth of $S(1-43-2)$ is described by the succession rule ${\mathsf{\Omega }}_S$.

Figure 10. The growth of a permutation avoiding $1-43-2$ according to the rule ${\mathsf{\Omega }}_S$.

Figure 10. The growth of a permutation avoiding $1-43-2$ according to the rule ${\mathsf{\Omega }}_S$.

   □

Remark 25.

Although both steady paths and UDU-constrained paths are enumerated by the sequence of powered Catalan numbers, we didn’t find a direct bijection between the two families. Thus, we leave the question of establishing a correspondence as an open problem for further investigation.

From the proof of Proposition 23 it follows that:

Proposition 26.

$\mathrm{L}(1-43-2)=I(12-0)$.

4.3. The Family $P(1-42-3)$: Strong $DD$-Constrained Paths

A strong $DD$-constrained path P is a path such that, for every factor $U_i{D}^{h+2}{U}_{i+1}$ of P, $0<i<n$, $h\ge 0$, the suffix of P on the right of the factor $U_{i+1}D$ lies strictly below the line parallel to $x=y$, and passing from $U_i$ (see Figure 11).

Again, the line the line parallel to $x=y$, and passing from $U_i$, will be referred to as the edge line at $U_i$.

Proposition 27.

Let π be a permutation of length n. Then, $\pi \in S(1-42-3)$ if and only if $P\left(\pi \right)$ is strong $DD$-constrained.

Proof. 

As usual, we will proceed by contrapositive. Let $P\left(\pi \right)$ be an underdiagonal path of size n which is not strong $DD$-constrained. So, there are indices $0<i<n-2$, $i+1<j\le n$, with the factor $U_i{D}^{h+2}{U}_{i+1}$, $h\ge 0$, and $U_j$ lies weakly above the edge line at $U_i$. Then, in $d\left(P\right)$, we have $d_{i+1}\ge d_i+2$, and $d_j\le d_i$. Accordingly, in the permutation $\pi$, from $d_j\le d_i$, we have that ${\pi }_{n-j+1}<{\pi }_{n-i+1}$. Moreover since $d_{i+1}\ge d_i+2$, we have that ${\pi }_{n-i}>{\pi }_{n-i+1}$ and there is a k greater than $n-i+1$ such that ${\pi }_{n-i+1}<{\pi }_k<{\pi }_{n-i}$. Thus the entries ${\pi }_{n-j+1}{\pi }_{n-i}{\pi }_{n-i+1}{\pi }_k$ form an occurrence of $1-42-3$.

The above argument can be neatly inverted proving that if $\pi$ is a permutation containing an occurrence of $1-42-3$, then $P\left(\pi \right)$ is not strong $DD$-constrained.    □

From the proof of Proposition 27, we immediately have that $\mathrm{L}(1-42-3)$ is given by the inversion sequences $(d_1,\dots ,d_n)$ such that there are no indices $i,j$ satisfying $d_j\le d_i$ and $d_{i+1}\ge d_i+2$. This property cannot be expressed in terms of classical pattern avoidance, and by abuse of notation we write this family as $I(\widehat{02}-0,\widehat{13}-0)$.

Remark 28.

The permutations avoiding the pattern $1-42-3$ are the same as permutations avoiding the “barred pattern” $25\overline{1}34$, where a barred pattern is a pattern where some of the entries are barred. For a permutation π to avoid the barred pattern τ means that every subsequence of π which is order-isomorphic to the sequence of unbarred entries of π can be extended (exactly to the positions) to the one in π order-isomorphic to τ. So, in practice, the avoidance of $25\overline{1}34$ in π requires that every occurrence of 2534 in π is contained in an occurrence of a 25134.

Since permutations avoiding $25\overline{1}34$ are enumerated by sequence A137538 in [19], from Proposition 27 it follows:

Corollary 29.

The family of strong $DD$-constrained paths is enumerated by the sequence A137538 in [19].

The first terms of A137538 are:

$$1,1,2,6,23,104,532,3004,18426,121393,851810,6325151,49448313,405298482,\dots$$

We point out that the reference in [19] does not give any further information about the properties of the sequence. Therefore, in this section, our aim is to provide more information about the sequence, and we start determining a growth for the family of strong $DD$-constrained paths by means of a generating tree.

Proposition 30.

The family of strong $DD$-constrained paths grows according to the following succession rule

$${\mathsf{\Omega }}_D=\left\{\begin{array}{ccc}(0,2)\hfill & & \\ \\ (h,k)\hfill & ⇝\hfill & (0,k+1+h),\dots ,(h,k+1)(h+1,k),\hfill \\ & \hfill & (1,k-1),\dots ,(k-2,2).\hfill \end{array}\right.$$

Proof. 

We define a a recursive growth for strong $DD$-constrained paths such that every path of size $n+1$ is uniquely produced from a path of size n by adding the last up step, and prove that this growth can be described by the succession rule ${\mathsf{\Omega }}_D$.

Let P be a strong $DD$-constrained path of size n, and let us denote by $\overline{U}$ its last up step. To P we assign the label $(h,k)$, where h is the distance between $\overline{U}$ and the edge line, and k is the length of the last descent of P plus one. Then, $k\ge 2$, and $h\ge 0$. The path $UD$ of size 1 has label $(0,2)$.

The path P with label $(h,k)$ produces $h+k$ strong $DD$-constrained paths of size $n+1$, by applying the following operations:

• add a factor $W^{t}U{D}^{t+1}$ following $\overline{U}$, with $1\le t\le h$. For every t, this operation produces a strong $DD$-constrained path with label $(h-t,k+1+t)$.
• add a factor $UD$ following $\overline{U}$, thus obtaining a factor $\overline{U}UD$. Then the obtained path has label $(h,k+1)$.
• add a factor $UD$ following $\overline{U}D$, thus obtaining a factor $\overline{U}DU$. Then the obtained path has label $(h+1,k)$.
• add a factor $UD$ immediately following a sequence of t consecutive down steps in the last descent, with $2\le t\le k-1$, thus obtaining the factor $\overline{U}D\dots DU$, then the obtained path has the edge line immediately below $\overline{U}$, so it has label $(t-1,k+1-t)$.

Finally, strong $DD$-constrained paths grow according to the rule ${\mathsf{\Omega }}_D$.    □

Figure 12 depicts the growth of a strong $DD$-constrained path of size 5; for any path, the dotted line delimiting the region forbidden to the suffix of the path is drawn.

Using standard techniques [2,3] we can translate the rule ${\mathsf{\Omega }}_D$ into the setting of generating functions. For $h\ge 0$ and $k\ge 2$, let $D_{h,k}\left(z\right)\equiv D_{h,k}$ denote the generating function of strong $DD$-constrained paths having label $(h,k)$ and let

$$D(x,y;z)\equiv D(x,y)=\sum _{h\ge 0,k\ge 2}{D}_{h,k}{x}^h{y}^k.$$

The generating function of strong $DD$-constrained paths is thus $D(1,1)$. The rule ${\mathsf{\Omega }}_D$ translates into a functional equation for the multivariate generating function $D(x,y)$ of strong $DD$-constrained paths.

Proposition 31.

The generating function $D(x,y)$ satisfies the following functional equation:

$$\begin{array}{ccc}D(x,y)\hfill & =\hfill & y^{2}z+{\displaystyle \frac{x^{2}z}{x-y}}\left(D(x,y)-{\displaystyle \frac{y^2}{x^2}}D(y,y)\right)\hfill \\ \hfill & \hfill & +{\displaystyle \frac{y^{2}z}{x(x-y)}}\left(D(1,x)-{\displaystyle \frac{x^2}{y^2}}D(1,y)\right).\hfill \end{array}$$

(2)

Proof. 

It follows from the productions of the rule ${\mathsf{\Omega }}_D$:

$$\begin{array}{ccc}\hfill D(x,y)& =& y^{2}z+\sum _{P\in \mathcal{D}}\left(x^0{y}^{h+k+1}+\dots +x^h{y}^{k+1}+x^{h+1}{y}^k\right)z^{s+1}\hfill \\ & & +\sum _{P\in \mathcal{D}}\left(x{y}^{k-1}+\dots +x^{k-2}{y}^2\right)z^{s+1}\hfill \\ & =& y^{2}z+{\displaystyle \frac{x^{2}z}{x-y}}\left(\sum _{P\in \mathcal{D}}\left(1-{\left({\displaystyle \frac{y}{x}}\right)}^{h+2}\right)x^h{y}^k{z}^s\right)\hfill \\ & & +{\displaystyle \frac{y^{2}z}{x(x-y)}}\left(\sum _{P\in \mathcal{D}}\left(1-{\left({\displaystyle \frac{y}{x}}\right)}^{k-2}\right)x^k{z}^s\right).\hfill \end{array}$$

   □

Replacing $x=1$ in the previous equation, we obtain the following relation:

$$\begin{array}{ccc}\hfill D(1,y)& =& y^{2}z+{\displaystyle \frac{z}{1-y}}\left(D(1,1)-D(y,y)\right).\hfill \end{array}$$

4.4. The Family $P(1-24-3)$: Strong $WU$-Constrained Paths

A strong $WU$-constrained path P is a path such that, for every factor $W{U}_i$ of P (if any), $0<i\le n$, the suffix of P on the right of this factor lies strictly below the line parallel to $x=y$, and passing from $U_i$ (see Figure 13).

Again, the line the line parallel to $x=y$, and passing from $U_i$, will be referred to as the edge line at $U_i$.

Proposition 32.

Let π be a permutation of length n. Then, $\pi \in S(1-24-3)$ if and only if $P\left(\pi \right)$ is strong $WU$-constrained.

Proof. 

As usual, we will proceed by contrapositive. Let $P\left(\pi \right)$ be an underdiagonal path of size n which is not strong $WU$-constrained. So, there are indices $j>i$, such that $U_i{W}^h{U}_{i+1}$, with $h\ge 1$, is a factor of $P\left(\pi \right)$, and $U_j$ lies weakly above the edge line at $U_{i+1}$. Therefore, in $d\left(P\right)$ we have $d_j\le d_{i+i}<d_i$. Accordingly, in the permutation $\pi$, from $d_j\le d_{i+1}$, we have that ${\pi }_{n-j+1}<{\pi }_{n-i}$. Moreover since $0\le d_{i+1}<d_i$, we have that ${\pi }_{n-i}<{\pi }_{n-i+1}$ and there is a k greater than $n-i+1$ such that ${\pi }_{n-i}<{\pi }_k<{\pi }_{n-i+1}$. Thus the entries ${\pi }_{n-j+1}{\pi }_{n-i}{\pi }_{n-i+1}{\pi }_k$ form an occurrence of $1-24-3$.

The above argument can be neatly inverted proving that if $\pi$ is a permutation containing an occurrence of $1-24-3$, then $P\left(\pi \right)$ is not strong $WU$-constrained.    □

From the proof of Proposition 32, we immediately have that:

Corollary 33.

$\mathrm{L}(1-24-3)=I(10-0,21-0)$.

We will prove that strong $WU$-constrained paths, as strong $DD$-constrained paths, are enumerated by the sequence A137538 in [19]. Although we have not a direct bijection between the two families of paths, we will show a bijection between the two corresponding families of permutations, borrowed from [5].

Proposition 34.

The families $S_n(1-42-3)$ and $S_n(1-24-3)$ are Wilf-equivalent.

Proof. 

We define a recursive bijection $\varphi :S_n(1-42-3)\to S_n(1-24-3)$ which preserves the left-to-right minima. We recall that an entry ${\pi }_i$ of $\pi$ is a left-to-right minima if, for any $j<i$, then ${\pi }_i<{\pi }_j$.

So, let $\pi \in S_n(1-42-3)$. We decompose $\pi$ as:

$$\pi =m_t{\alpha }_t{m}_{t-1}{\alpha }_{t-1}\dots m_1{\alpha }_1,$$

where $t\ge 1$, and $m_t>m_{t-1}>\dots >m_1=1$ are the left-to-right minima of $\pi$. We observe that ${\alpha }_1$ avoids the pattern $31-2$, since $m_1=1$ is on the left of ${\alpha }_1$, and the presence of a pattern $31-2$ in ${\alpha }_1$ would imply a pattern $1-42-3$ in $\pi$. Assuming that $t\ge 2$, with $2\le i\le t$, let $R_i$ be the set of entries of $\pi$ on the right of $m_{i-1}$ which are greater that $m_i$. Let $s_1<s_2<\dots <s_r$ be the entries of $R_i$ (if not empty). Let us define:

• $T_{i,1}=\{s-1\}\cap {\alpha }_i$;
• $T_{i,j}=[s_{j-1},s_j]\cap {\alpha }_i$, with $2\le j\le r$;
• $T_{i,r+1}=[s_r,n]\cap {\alpha }_i$.

If $R_i$ is empty, then we set $T_{i,1}={\alpha }_i$.

All the entries of $T_{i,r+1}$ must be on the right of all the elements of $T_{i,j}$, for all $j\le r$. Indeed, if an entry of $T_{i,r+1}$ was on the left of some entry of $T_{i,j}$, $j\le r$, then $\pi$ would contain an occurrence of $1-42-3$, where $m_i$ plays the role of 1, and $s_r$ plays the role of 3.

Repeating the same argument, we can prove that every entry of $T_{i,j}$ must be on the right of all entries of $T_{i,k}$, with $j>k$. So, ${\alpha }_i$ can be decomposed as:

$${\alpha }_i=T_{i,1}{T}_{i,2}\dots T_{i,r+1}.$$

We also observe that every $T_{i,j}$ should avoid the pattern $31-2$, because of the entry $m_i$ on the left (being $m_i$ less than every entry of ${\alpha }_i$).

For a given permutation $\tau$, let ${\tau }^{\prime }$ be the set of entries obtained by replacing the entry h by entry $n+1-h$. We observe the mapping ′ is bijective and transforms every pattern $31-2$ into a pattern $13-2$.

Then, for every i such that $2\le i\le t$, let us define ${\alpha }_i^{*}$ as:

$${\alpha }_i^{*}=T_{i,r+1}^{\prime }{T}_{i,r}^{\prime }\dots T_{i,1}^{\prime },$$

where $T_{i,j}^{\prime }$ is obtained applying ′ on the reduced permutation of $T_{i,j}$. Finally, we define $\varphi$ as:

$$\varphi \left(\pi \right)=m_t{\alpha }_t^{*}{m}_{t-1}{\alpha }_{t-1}^{*}\dots m_2{\alpha }_2^{*}{m}_1{\alpha }_1^{\prime }.$$

Then, $\varphi \left(\pi \right)\in S_n(1-24-3)$, and has the same left-to-right minima as $\pi$.    □

Table 2. The families of patterns of length 4 considered in Section 4.

Permutation patterns	Underdiagonal Paths	Inversion Sequences	Number Sequence
$1-34-2$	Steady Paths	$I(11-0,21-0)$	Powered Catalan numbers
$1-43-2$	$UDU$-constrained	$I(12-0)$	Powered Catalan numbers
$1-42-3$	Strong $DD$-constrained	$I(\widehat{02}-0,\widehat{13}-0)$	A137538
$1-24-3$	Strong $WU$-constrained	$I(10-0,21-0)$	A137538

Table 2. The families of patterns of length 4 considered in Section 4.

Permutation patterns	Underdiagonal Paths	Inversion Sequences	Number Sequence
$1-34-2$	Steady Paths	$I(11-0,21-0)$	Powered Catalan numbers
$1-43-2$	$UDU$-constrained	$I(12-0)$	Powered Catalan numbers
$1-42-3$	Strong $DD$-constrained	$I(\widehat{02}-0,\widehat{13}-0)$	A137538
$1-24-3$	Strong $WU$-constrained	$I(10-0,21-0)$	A137538

5. Further Work

In this paper we started from a simple representation of permutations as lattice paths, called underdiagonal paths, and then studied families of underdiagonal paths $P\left(\tau \right)$ which are obtained by restricting ourselves to subclasses of $S_n$ avoiding some vincular patterns $\tau$. We have considered patterns of length 3 and 4, and provided a combinatorial characterization and the enumeration of the corresponding paths.

The authors believe that this study looks promising and should be extended to patterns of greater lengths, starting with length 5. Some partial results in this direction were obtained by studying families of underdiagonal paths satisfying only one of the two conditions (S1) and (S2) of steady paths. A (positive) result is that underdiagonal paths satisfying condition (S2) ($WU$-constrained paths) are those corresponding to the patterns $1-35-2-4,1-35-4-2$, precisely $P(1-35-2-4,1-35-4-2)$. On the other side, underdiagonal paths satisfying condition (S1) cannot be characterized in terms of properties of the sequence $d\left(P\right)$, hence of geometrical constraints.

Another remarkable problem which should be faced is the most general problem of characterizing the combinatorial properties of a pattern $\tau$ such that the family $P\left(\tau \right)$ can be described in terms of constrained underdiagonal paths.