SITL-Based Formal Verification of Cyber-Physical Systems Software: Reliability Model, Method and Implementation

1. Introduction

1.1. Motivation

The current world relies heavily on various types of Cyber-Physical Systems (CPS) [1], which integrate computational elements with physical processes [2]. The CPS software is one of the most complex parts, playing a crucial role in their overall functionality and performance [3]. The complexity of the software, which is due to the complexity of the mathematical models that describe the behavior of the CPS, becomes a challenge for critical systems, where the requirements for reliability and safety are extremely strict, which is due to the high cost of failure. Despite such requirements, huge number of international, national and branch standards the statistics of accidents of aviation, rocket-space, transport and other systems, the specific cause of which are hidden software errors, remain unacceptable.

Reducing the risks of dangerous failures is possible by enhancing and implementing new methods of independent verification and validation that take into account the specific features of mathematical models, control algorithms and relevant programming languages, in particular, such a common language as C++. The possibility of identification and compatible use of such features and invariants is one of the ways to reduce the risks of residual faults and their tolerance during the functioning of systems.

1.2. State of the Art

The rise of CPSs including Unmanned Aerial Vehicles (UAVs) and UAV swarms, complex systems of Internet of Things (IoT), has ushered in a new era of interconnected devices and intelligent automation. However, ensuring their reliability and security remains a critical challenge, as failures or vulnerabilities can have severe consequences. This reason accelerates developing formal methods and tools for designing, verification and validation methods and tools, first of all, for software and software-hardware platforms

The author of [4] provides a concise review of formal verification methods for CPS. However, modern CPS and UAVs often incorporate embedded software exceeding thousands of megabytes of C/C++ code. Likewise, contemporary IoT devices rely on embedded software reaching tens of megabytes in size. Krichen [5] explores modern formal verification and validation techniques specifically designed for IoT systems.

Most existing C software model checkers and automated theorem proves are effective only for small-scale C/C++ programs. The primary challenge is selecting the most suitable verification tools from the numerous available options. To address software correctness at the compilation stage, Hoare [6] proposed using compiler-based formal verification, offering a promising approach for enhancing reliability in large-scale embedded systems.

C++ is extensively used in aerospace and defense systems, including flight control systems, navigation systems, and simulation software. C++ is widely used in the development of CPS due to its performance, efficiency, and rich feature set [7]. C++ is known for producing highly optimized code, which is crucial for real-time processing tasks in CPS. Systems such as autonomous vehicles, industrial robots, and medical devices require real-time performance. C++ provides fine-grained control over system resources, such as memory and CPU usage, which is essential for the efficient operation of CPS, especially those with limited hardware capabilities. C++ is used to program microcontrollers and embedded systems, which are integral to CPS. It allows developers to write low-level code for hardware interaction while offering high-level abstractions. C++ code can be compiled for various platforms, making it a versatile choice for embedded systems that may need to run on different hardware architectures.

The object-oriented features of C++ support the development of modular and reusable code. This benefits CPS, where complex systems can be broken down into manageable components. C++ allows developers to encapsulate hardware details and create abstract interfaces, simplifying CPS's development and maintenance. C++'s STL [8,9] provides a collection of ready-to-use data structures and algorithms, which can save development time and improve code reliability. The Boost C++ Libraries [10,11] offer additional functionality and are often used in CPS for signal processing, networking, and inter-process communication tasks. C++ supports multithreading, which is essential for CPS, which needs to perform multiple tasks simultaneously [12].

This is especially important in systems that require real-time data processing and response. Libraries and frameworks such as OpenMP [13] and Intel Threading Building Blocks (TBB) [14] are available for C++, enabling the development of parallel applications that can leverage multi-core processors. Various static analysis tools are available for C++ to detect potential errors and vulnerabilities in the code, which is crucial for the safety and reliability of CPS [15]. C++ code can be subjected to formal verification techniques to ensure it meets the required specifications and performs correctly under all conditions [16]. C++ is used to develop software for autonomous vehicles, including sensor data processing, decision-making algorithms, and control systems.

In industrial automation, C++ develops control software for robotic arms, conveyor systems, and other automated machinery. Medical devices such as MRI machines, CT scanners, and infusion pumps often rely on C++ for their software, ensuring precise and reliable operation. C++ plays a crucial role in developing Cyber-Physical Systems due to its performance, efficiency, and versatility [17]. Its ability to handle real-time processing, manage resources effectively, and support modular and reusable code makes it an ideal choice for CPS development. With powerful libraries, frameworks, and tools, C++ continues to be a critical language in ensuring the reliability and efficiency of complex CPS across various industries.

However, ensuring software quality, reliability and safety (SQ) remains a significant challenge [18]. The Software Development Life Cycle (SDLC) enhances software quality by incorporating structured stages that ensure thorough planning, precise requirement analysis, robust design, meticulous implementation, comprehensive testing, seamless deployment, and continuous maintenance. Early QA involvement, iterative feedback through Agile or DevOps practices, MIL (Model-in-the-Loop), SIL (Software-in-the-Loop), PIL (Processor-in-the-Loop), HIL (Hardware-in-the-Loop), automated testing, and consistent monitoring are integrated into each phase. This approach ensures that software is reliable, meets user expectations, is free of defects, and performs well, ultimately leading to higher user satisfaction and successful project outcomes [19].

One practical approach to enhancing SQ is through formal verification, a method that rigorously checks the correctness of software against its specifications [20]. Formal verification can be particularly effective when utilizing the International System of Units (SI units) as a standard for consistency and accuracy. By using SI units to verify CPS software formally, we can ensure that the interactions between the software and physical components are precisely defined and adhered to, reducing errors and improving reliability [21]. Other formal verification approach uses Siano's propositions [22,23]. Siano's method extends the SI system by incorporating orientation as a fundamental dimension, enabling a more nuanced analysis of directed physical quantities in theoretical and practical applications.

To enhance CPS software correctness at the compilation stage, we propose a compiler-based formal verification technique, inspired by Hoare [6], that integrates C++ meta- programming and SI units. This approach offers a promising solution for improving the reliability of large-scale embedded systems.

1.3. Objectives and Approach

Goal of this study is developing model and method of software verification by use of SI based Template Libraries (TL) to improve the reliability of cyber-physical system and IoT software by addressing SI prefixes, units, and orientation errors in C/C++ programs without increasing memory usage.

Objectives are the following:

-

to investigate the reliability of using SI units for dimensional analysis;

-

to develop a reliability model for the SI system;

-

to consider the extended SI system, which defines directed units in space;

-

to compare the reliability of the standard and extended SI unit systems and examine the statistical characteristics of these unit systems;

-

to explore using dimensional and orientation aspects of physical quantities and SI prefixes for input data and report generation;

-

to create a template library based on dimensional and orientation analysis using modern metaprogramming methods;

-

to verify the created template library, and finally, assess the effectiveness of the library and validate it.

The main contribution of this research is the development of a novel SITL-based approach and method enhancing software verification in cyber-physical systems and IoT applications. This TL leverages SI units, prefixes, and orientation analysis to detect and prevent errors in C/C++ programs at compile time without increasing memory usage.

2. Materials and Methods

2.1. Reliability Model for the SI Unit

Detailed research of the internal structure of SI units is essential for developing formal software verification for SI-based units. This involves understanding the base and derived units, their interrelationships, and how they are used in various scientific and engineering contexts.

A detailed understanding of the internal structure of SI units is foundational for developing robust software verification systems. By focusing on the precise definitions and relationships of both fundamental and derived units, incorporating dimensional and orientational analysis, and using advanced software techniques, we can significantly enhance the reliability and accuracy of software in scientific and engineering applications. This comprehensive approach ensures the software adheres to international standards and effectively bridges the gap between theoretical models and practical implementations.

SI is a globally accepted system for measurement that provides a consistent framework for quantifying physical properties [24].

It consists of sets of SI units: base units (see Table 1), derived units [25] and non-derived units, and coherent and non-coherent units [26].

These base units are non-derived because they are not defined in terms of other units; instead, they serve as the foundational units from which other units are derived.

Derived units are combinations of base units that measure other physical quantities, such as Newton (N) for force, joule (J) for energy, and Pascal (Pa) for pressure. Understanding these combinations is crucial for accurate software verification. Derived units must be coherent with base units, meaning they are derived directly without conversion factors other than 1.

Coherent units in the SI system are derived strictly from the seven base units without additional factors. This ensures consistency, maintaining straightforward and accurate equations and calculations. In a coherent system, derived quantities have units chosen such that the proportionality constant is one, simplifying the equations and ensuring direct proportionality to the base units.

Every SI unit is a derived unit (derived from SI base units) and a coherent unit (fits into equations without additional factors). However, some derived SI units can be non-coherent, involving additional numerical factors or different bases:

• Liter (L): A derived unit of volume (1 L = 1 dm³ = 10⁻³ m³), not coherent due to the factor of 1000 cm³.
• Hectare (ha): A derived unit of area (1 ha = 10,000 m²), not coherent due to the factor of 10,000.
• Bar (bar): A unit of pressure (1 bar = 10⁵ Pa), not coherent as it involves the factor 10⁵ Pa.

Derived Units: Defined in terms of base units (e.g., volume, area, pressure).

Non-Coherent Units: Derived units with additional numerical factors or based on different unit systems, not aligning directly with base units without conversion factors.

Base Units: The seven fundamental SI units are considered non-derived and coherent.

The relationship between derived and coherent SI units is shown in Table 2.

Later, we will focus on the seven fundamental SI units, SI-derived units with special names, and selected SI-derived units and constants from various subject areas. The relationships between these units are shown in Figure 1.

Existing SI units have two problems:

• We cannot identify the direction of vector quantities (Acceleration, Force, etc).
• Different SI quantities have equivalent dimensions (for example, Moment of Force [Newton meter], Heat [Joule], Torque [Newton meter], Work [Joule], and Angular Momentum).

Let us demonstrate the SI units from different subject areas, such as geometry, chemistry, physics, and physical constants (see Table 3 and Table 4). The underlined SI quantities are vector quantities, while dimensionless quantities have a dimension of 1.

According to Table 1, Table 3, and Table 4, our universal set includes 192 items comprising various SI quantities and constants. Of these, 8 are dimensionless quantities and constants, while 184 are dimensioned. The set also includes 104 different dimensions, with one dimensionless quantity.

Table 1, Table 3, and Table 4 also indicate that some SI quantities are vectors (57 items), while others, including various SI quantities and constants, are scalars (135 items).

Siano’s proposition extends the SI system by incorporating orientation and categorizing the items in the universal set into non-oriented quantities (scalars) and X, Y, and Z axis-oriented quantities (vectors). With these proposed extensions, the universal set expands to 306 items, covering 197 distinct dimensions and orientations. Thus, the universal set can be divided into four subsets. See Table 5.

In Table 5, the numerator represents the number of different dimensions and orientations, while the denominator indicates the number of different quantities and constants in Tables 1,3,4.

Based on their physical dimensions, the universal and extended universal sets can be divided into subsets where each item shares the same dimension (see Table 6 and Figure 2).

According to Table 6, the standard SI universal set has 61 distinct items, each with a unique dimension, while the extended SI universal set has 131 distinct items, each with a unique dimension. There are 23 and 42 subsets with a cardinality of 2 (23/42 different pairs of quantities that share the same dimension), and so on.

Let us define the reliability of the SI and extended SI systems as the probability of correctly using quantities, as shown in equation (1):

$$\eta =1-{\displaystyle \frac{1}{{\displaystyle \sum _{i=1}^n{S}_i}}}{\displaystyle \sum _{i=1}^n\frac{C_i-1}{C_i}{S}_i},$$

(1)

where η represents the reliability, Si is the number of items in the I - subset, and Ci is the cardinality of the i - subset.

According to Equation (1), the reliability of the standard SI unit system is 0.747. In contrast, the extended SI unit system proposed by Siano has a reliability of 0.806. However, the reliability of the SI unit system is significantly influenced by the distribution of physical quantities. In our universal set, which includes 104 distinct dimensions and 192 physical quantities, the system's reliability decreases to 0.542. Similarly, applying an orientation-based extension of the SI system—expanding the total number of constants and physical quantities to 306—results in a reliability of 0.644. Siano's extension improves system reliability by factors of 1.09 (0.806 / 0.747) to 1.19 (0.644 / 0.542) compared to the standard SI system.

Siano's Extension Significantly Enhances System Reliability Compared to the Standard SI.

According to SI, all units have dimensions described as:

$$T^{pt}{L}^{pl}{M}^{pm}{I}^{pi}{\Theta }^{p\theta }{N}^{pn}{J}^{pj},$$

(2)

where T is time, L is length, M is mass, I is electric current, θ is thermodynamic temperature, N is the amount of substance, and J is luminous intensity. The exponents pt, pl, pm, pi, pθ, pn, and pj represent the integral powers of the SI base units.

Let us introduce the distributions of base unit powers for items in the universal set (see Table 7), where the subscript D refers to different dimensions, and the subscript Q refers to different quantities and constants in the universal set.

According to Siano, we can extend the SI dimension by orientation.

$$T^{pt}{L}^{pl}{M}^{pm}{I}^{pi}{\Theta }^{p\theta }{N}^{pn}{J}^{pj}{O}^{po},$$

(3)

where $O^{po}$ is an integral parameter defining the orientation of the physical SI unit (0 represents an orientationless unit, 1 represents an X-oriented unit, 2 represents a Y-oriented unit, and 3 represents a Z-oriented unit).

This extension introduces an eight-dimensional parameter to identify different directed SI units (e.g., Force, Length). Thus, we can use such a vector to identify different SI units:

$$pt,pl,pm,pi,p\theta ,pn,pj,po$$

(4)

pt, pl, pm, pi, pθ, pn, and pj are integral powers of some SI base units, and po is an orientation of a physical unit as an integral number.

Let us introduce the distributions of base unit powers for items in the extended universal set (see Table 8), where the subscript D refers to different dimensions, and the subscript Q refers to different quantities and constants in the extended universal set.

According to Table 7 and Table 8, we observe that for all items, the powers of the base units fall within the interval [−6, 5]. This data will be used for the subsequent development of the SITL.

2.2. SITL Implementation

The vector of dimension and orientation (4) can be used as template arguments for software formal verification through dimensional and orientational analysis. [27]. By representing physical quantities as vectors, where each element corresponds to the exponent of a base unit in the quantity's dimensional and orientational analysis, we achieve several advantages:

• Encoding the dimensional and orientational information directly into the template arguments ensures that any operations involving physical quantities are dimensionally consistent at compile time, allowing for early error detection in the development process.
• This method facilitates automatic and accurate unit conversions, ensuring all calculations adhere to the correct dimensional and orientational rules.
• Using vectors as template arguments introduces strong typing for physical quantities, preventing accidental mixing of incompatible units and reducing the likelihood of logical errors in the code. The explicit representation of dimensions and orientations within the type system enhances code readability. It makes it more self-explanatory, as the units of measurement are embedded directly in the type definitions.
• Representing dimensions and orientations with vectors provides a clear and intuitive way to understand the relationships between different physical quantities, making the code easier to read and maintain. [28].
• General dimensional and orientational operations and checks can be encapsulated in reusable template functions and classes, streamlining the development process and reducing code duplication.
• By leveraging compile-time template metaprogramming, we can optimize quantity-related calculations and reduce runtime overhead, resulting in more efficient and performant software.
• Using dimensional and orientational vectors as template arguments enhances the rigor of formal verification methods, providing a mathematically sound framework for verifying the correctness of software involving physical quantities. This approach aids in validating the underlying mathematical models, ensuring they accurately reflect the real-world phenomena they are intended to represent.
• As new physical quantities and units are introduced, they can be easily integrated into the existing framework by extending the vector representation. This ensures that the system remains scalable and adaptable to future requirements.
• This method is applicable across various domains, from engineering and physics to finance and healthcare, providing a versatile tool for developing high-quality, reliable software.

In conclusion, using a vector of base unit powers as template arguments for formal verification offers a powerful and effective way to ensure software systems’ dimensional consistency, accuracy, and robustness. By embedding dimensional and orientational information directly into the type system, we can leverage the full capabilities of template metaprogramming to create safer, more efficient, and easier-to-maintain code [29].

2.2.1. Implementation of Data Type Template for Physical Quantity

The proposed SITL includes a class template that allows for the creation of a C++ class based on the fundamental type of data used for physical values, quantity names, and SI base unit dimensions and orientations:

          template<typename QuantityType, typename QuantityName,
          int s, int M, int kg, int A, int K, int mol, int cd, int O>
          class SIUnit { }
		  

The proposed template includes constructors, additional helper methods, and a unary minus operator.

2.2.2. Implementation of Templates for Additive Arithmetic Operators

The addition operator template uses metaprogramming to check the dimensions and orientation arguments. Implementing the subtraction, condition, and assignment operators is similar to the addition operator’s.

          template <typename QL, typename SIL,
                int sL, int ML, int kgL, int aL, int kL, int mL, int cL, int oL,
                typename QR, typename SIR,
                int sR, int MR, int kgR, int aR, int kR, int mR, int cR, int oR,
                typename std::enable_if <
                sL == sR && ML == MR && kgL == kgR && aL == aR &&
                kL == kR && mL == mR && cL == cR && oL == oR, bool>::type = true      >
          SIUnit<decltype(QL()+QR()), SIL, sL, ML, kgL, aL, kL, mL, cL, oL>
                            operator+(
                            const SIUnit<QL, SIL, sL, ML, kgL, aL, kL, mL, cL, oL>& left,
                            const SIUnit<QR, SIR, sR, MR, kgR, aR, kR, mR, cR, oR>& right
                                       ) {
          return SIUnit<decltype(QL()*QR()),SIL,sL,ML, kgL, aL, kL, mL, cL, oL>  (left.getValue() + right.getValue());
                }
		  

The text above shows that the equivalence of dimension and orientation vectors is checked before performing additive operations. If the vectors are different, the operation is not executed. In this case, the compiler generates a message indicating that the operation is impossible for variables with different physical types or orientations. This prevents data addition, subtraction, or comparison with other types or directions in space.

2.2.3. Implementation of Templates for Multiplicative Operators

The multiplication operator template uses metaprogramming to create the results' dimensions and orientation based on the arguments' dimensions and orientation. The implementation of the division operator is similar to that of the multiplication operator.

          template <typename QL, typename SIIL,
                int sL, int ML, int kgL, int aL, int KL, int mL, int cL, int kL,
                typename QR, typename SIIR,
                int sR, int MR, int kgR, int aR, int KR, int mR, int cR, int kR>
                SIUnit<decltype(QL()* QR()),SIIL,
                            sL + sR, ML + MR, kgL + kgR, aL + aR,
                            KL + KR, mL + mR, cL + cR, KLKR(kL, kR)>
                            operator *(
                const SIUnit <QL, SIIL, sL, ML, kgL, aL, KL, mL, cL, kL>& left,
                const SIUnit <QR, SIIR, sR, MR, kgR, aR, KR, mR, cR, kR>& right)
                {
                return SIUnit <decltype(QL() * QR()), SI0,
                            sL + sR, ML + MR, kgL + kgR,
                            aL + aR, KL + KR, mL + mR, cL + cR, KLKR(kL, kR)>(left.getValue() * right.getValue());
                }
		    

The multiplication operator template creates a vector of physical type for the result as the sum of the coordinates of the multiplier vectors. The division operator template creates a vector of physical type for the result as the difference between the coordinates of the vectors of the first and second arguments of the division operator. The numerical result is determined as usual. The Siano table shows the direction of the resultant (see Table 9).

There are also similar templates for multiplicative operations with constants.

SITL also includes templates for trigonometric functions such as sin, cos, tan, arcsin, arccos, and arctan and C++ template functions for √X and X^N.

2.2.4. Implementation of physical quantities templates

The proposed SITL uses two macros for creating SI templates for scalar and directed units:

          // Base Units: s, m, kg, A, K, mol, cd, or
          SIScalarUnit(Mass, kilogram, kg, 0, 0, 1, 0, 0, 0, 0)
          SIScalarUnit(Time, second, s, 1, 0, 0, 0, 0, 0, 0)
          SIDirectedUnit(Length, meter, m, 0, 1, 0, 0, 0, 0, 0)
		  

These macros create all SI physical quantities in different subject areas.

Later, we can use templates for physical quantities as follows:

          Mass<double> d; // Mass quantity with double precision
          // X-component of velocity with double precision
          VelocityX<double> vx;
		  

As you can see, creating new software variables that correspond to specific SI physical quantities and certain fundamental SI types is very simple.

2.2.5. Implementation of SI Prefixes in SITL

SI prefixes, along with SI base and derived units, form the core of the international system of units. They allow for the expression of quantities in decimal multiples and sub-multiples, making values more manageable and on a ‘human scale’ (between 0.1 and 1000, ideally between 1 and 100). This facilitates more straightforward conceptualization, communication, and interpretation across different disciplines and locations [30].

The kilogram is the only SI unit whose name and symbol include a prefix. Historically, names and symbols for mass units are based on the gram, not the kilogram. For instance, 10⁻⁶ kg is referred to as a milligram (mg), not a microkilogram (μkg) [31].

However, using SI prefixes in software can lead to errors and failures in CPS. To address this, SITL provides templates of functions for handling SI prefixes from 10⁻³⁰ to 10³⁰ [32].

Later, we can use C++ 20 standard literals and user-defined literals for setting and printing of number values as follows:

          Mass<double> m(1000), m_nano111(111._nano), m_micro15(-15._micro), m0_01(0.01);
          Current<double> currentI1(2.), currentI2(-2.0_nano), currentI3(2.0_kilo);
          Volume<double> w0(23.0_milli);
		   

Using literals prevents errors in input data and ensures the generation of accurate reports.

2.2.6. Verification of the SI-Based Template Library

The proposed SITL optimally uses memory. The memory size of a physical quantity is equal to the size of the fundamental type used for that quantity. For example:

          Mass<double> v(1000); // uses only 8 bytes,
          Mass<float> mf[100]; // uses only 400 bytes.
		   

Verifying the SITL involved using tens of thousands of test cases. This testing process ensures the correctness and reliability of the SITL code.

3. Results and Implementation

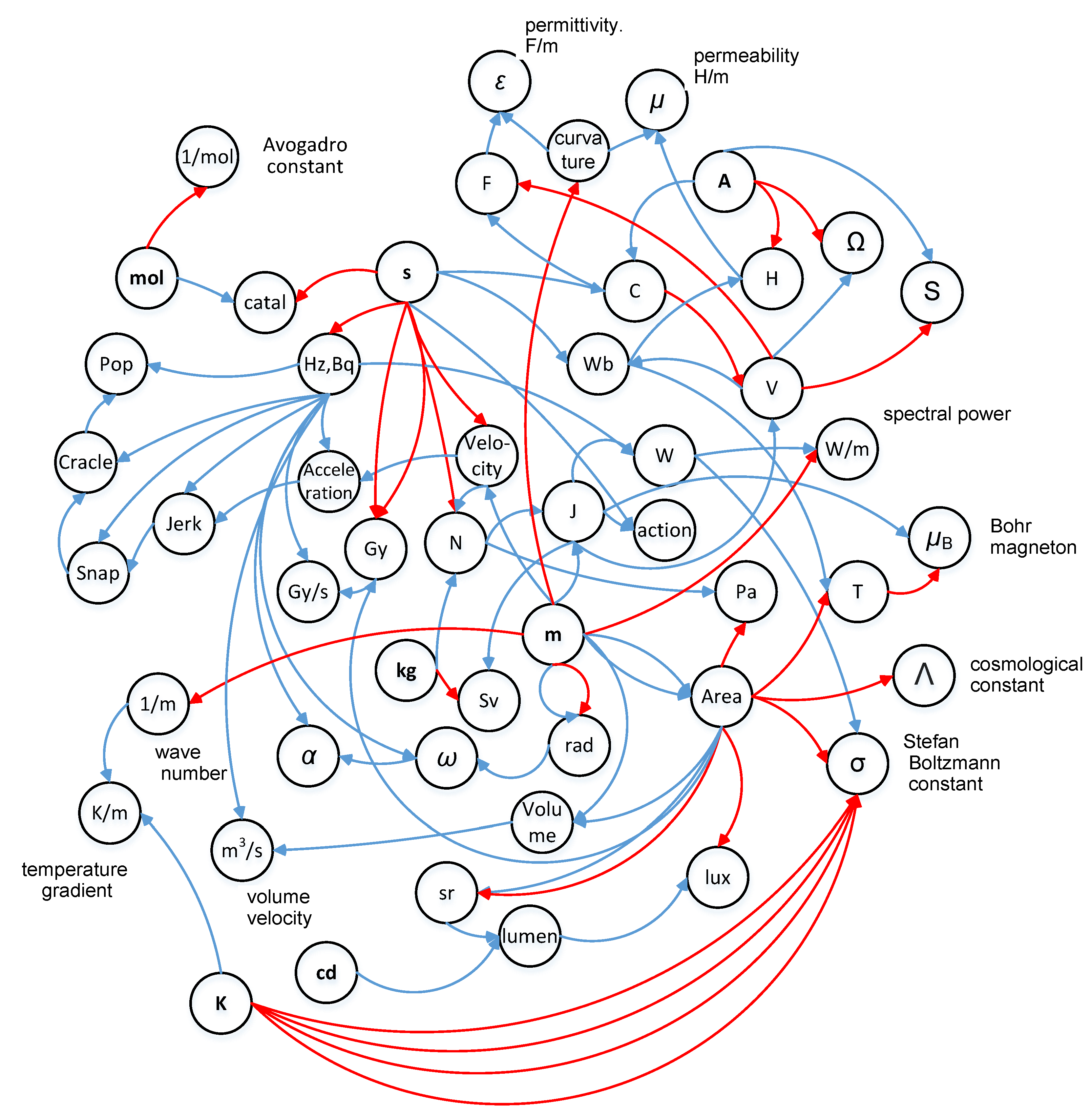
3.1. Validation of the SI-Based Template Library

The validation of the SITL involved implementing and integrating the Euler system of differential equations using standard C++20. This system is a core component of the guidance system for Unmanned Aerial Vehicles (UAVs), drones, and various spacecraft.

Implementations used the Runge-Kutta method [33]. The proposed SITL facilitated writing clearer code and provided enhanced formal verification during compile time.

        #define VX AngularVelocityX<double>
        #define VY AngularVelocityY<double>
        #define VZ AngularVelocityZ<double>
		 
        #define AX AngularAccelerationX<double>
        #define AY AngularAccelerationY<double>
        #define AZ AngularAccelerationZ<double>
			 
        using namespace SI;
        using namespace Geometry;
        using namespace Mechanics;
			 
        AngularVelocityX<double> wx0(0.);
        AngularVelocityY<double> wy0(0.);
        AngularVelocityZ<double> wz0(0.);
			 
        MomentOfInertia<double> Ixx = 10, Iyy = 20, Izz = 30;
        MomentOfForceX<double> Mx = 2;
        MomentOfForceY<double> My = 4;
        MomentOfForceZ<double> Mz = 6;
			 
        AX<double> E1(Time<double> t, VX wx, VY wy, VZ wz)
        {
        return (Mx - (Izz - Iyy) * wy * wz) /Ixx;
        }
        AY<double> E2(Time<double> t, VX wx, VY wy, VZ wz) {
        return ((My - (Ixx - Izz) * wz * wx) / Iyy);
        }
        AZ<double> E3(Time<double> t, VX wx, VY wy, VZ wz) {
        return (Mz - (Iyy - Ixx) * wx * wy) / Izz;
        }
			 
        Time<double> T0 = 0.0, T_end = 10.0, step = 0.5, tis;
        typedef AX<double>(*EFX)(Time<double>, VX wx, VY wy, VZ wz);
        typedef AY<double>(*EFY)(Time<double>, VX wx, VY wy, VZ wz);
        typedef AZ<double>(*EFZ)(Time<double>, VX wx, VY wy, VZ wz);
			 
        void rungeKutta4SI(EFX fx, EFY fy, EFZ fz )
        {
        Dimensionless<double> ndl = ((T_end - T0) / step);
        int n = int(ndl.getValue());
        std::vector<SI::Time<double>> t(n + 1);
        t[0] = T0;
        std::size_t nefv =3;
        vector <VX> wx(n+1);
        vector <VY> wy(n+1);
        vector <VZ> wz(n+1);
        wx[0] = wx0; wy[0] = wy0; wz[0] = wz0;
        AVX k1x, k2x, k3x, k4x, wx_;
        AVY k1y, k2y, k3y, k4y, wy_;
        AVZ k1z, k2z, k3z, k4z, wz_;
			 
        //++++++++++++++++++++++++++++++++++++
        for (int i = 0; i < n; ++i)
        {
        k1x = step * fx(t[i], wx[i], wy[i], wz[i]);
        k1y = step * fy(t[i], wx[i], wy[i], wz[i]);
        k1z = step * fz(t[i], wx[i], wy[i], wz[i]);
        tis= t[i]+step/2.; wx_= wx[i]+k1x/2.;
        wy_ = wy[i]+k1y/2.; wz_=wz[i]+k1z/2.
        k2x =step*fx(tis, wx1, wy1, wz1);
        k2y =step*fy(tis, wx1, wy1, wz1);
        k2z =step*fz(tis, wx1, wy1, wz1);
        wx_= wx[i]+k2x/2.; wy_= wy[i]+k2y/2.;
        wz_= wz[i]+k2z/2.;
        k3x =step*fx(tis, wx_, wy_, wz_);
        k3y =step*fy(tis, wx_, wy_, wz_);
        k3z =step*fz(tis, wx_, wy_, wz_);
        tis= t[i]+step; wx_= wx[i] + k3x;
        wy_= wy[i] + k3y; wz_= wz[i] + k3z
        k4x = step * fx(tis, wx_, wy_, wz_);
        k4y = step * fy(tis, wx_, wy_, wz_);
        k4z = step * fz(tis, wx_, wy_, wz_);
			 
        wx[i+1]=wx[i]+(k1x+2*k2x+2*k3x+k4x)/6;
        wy[i+1]=wy[i]+(k1y+2*k2y+2*k3y+k4y)/6;
        wz[i+1]=wz[i]+(k1z+2*k2z+2*k3z+k4z)/6;
        t [i+1]=t[i] + step;
        }
        }
		 

The validation of the SITL confirms its accuracy and reliability for use in various applications.

3.2. Usage SITL for CPS Formal Verification

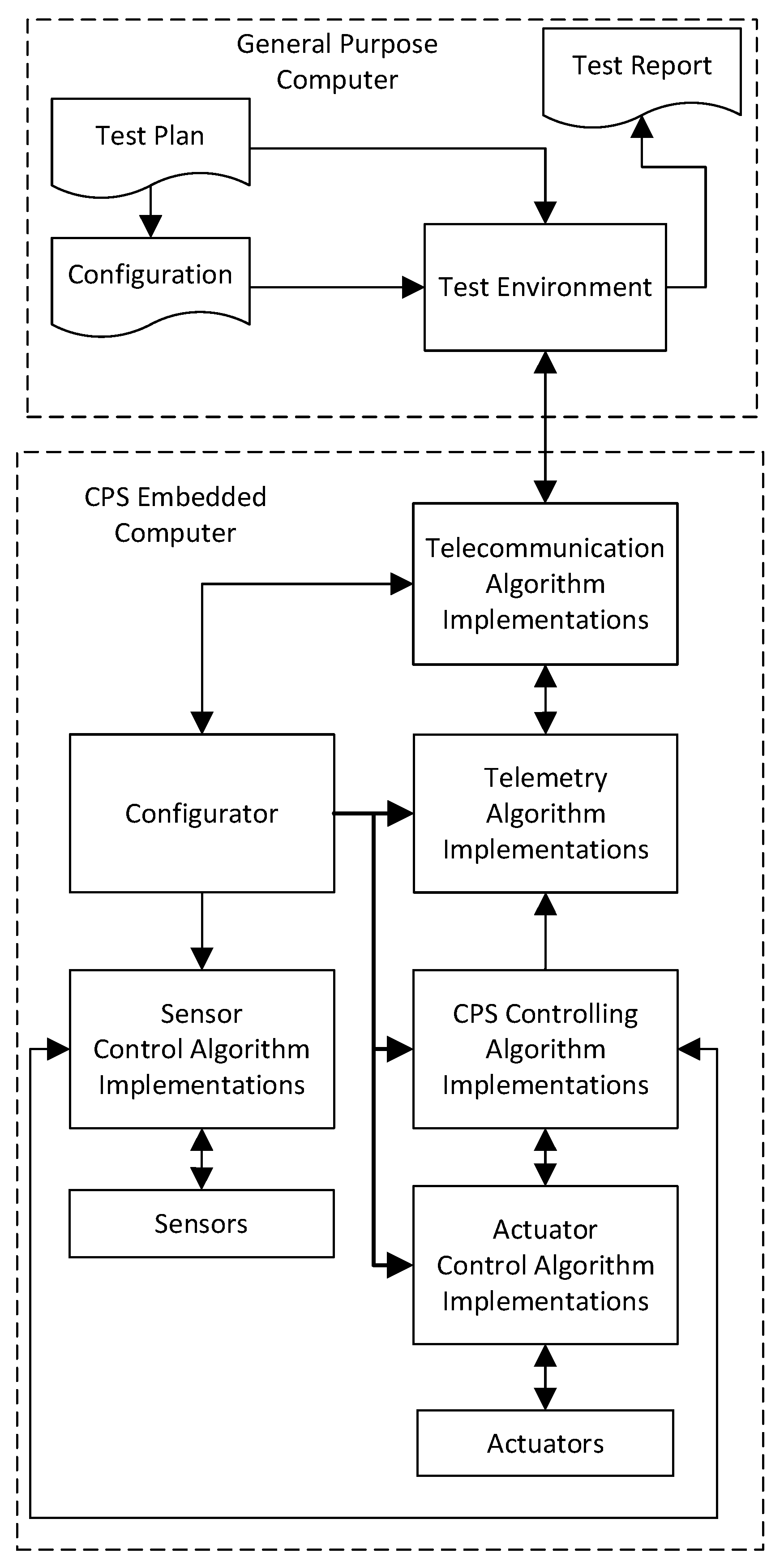
The proposed SITL was used to verify CPS software. According to Figure 3, CPS software verification involves a General Purpose Computer with a Test Environment. Following the Test Plan and CPS software configuration, this environment sends test data and configurations to the CPS. The configuration includes embedded algorithms and defines the primary tasks of the CPS, allowing for the modification of algorithms based on the available onboard sensors and actuators. The Test Environment sends configuration and test data to the CPS, while the CPS transmits telemetry back to the Test Environment and Earth.

CPS software includes six sets of algorithms.

3.2.1. Configurator Algorithms

Configurator Algorithms (CA) are pivotal in managing and adapting embedded algorithms within a CPS based on specific configurations and requirements. They provide the flexibility to modify and update the system’s functionality by selecting and replacing embedded algorithms.

CA enables the selection of appropriate embedded algorithms based on predefined configuration settings. This selection process ensures that the correct algorithms are applied for the current operational context, whether for data processing, control, or communication tasks. For example, in a satellite mission, configurator algorithms might choose between different image processing algorithms based on the type of observations being made.

One of the key strengths of CA is its ability to reconfigure the CPS dynamically. This means the system can adapt to changing conditions or requirements by loading and activating different algorithms without restarting or redeploying the entire system. For instance, in autonomous vehicles, configurator algorithms could switch between different navigation algorithms depending on the vehicle’s operating environment.

CA facilitates the replacement of existing algorithms with new or updated ones downloaded from the Test Environment (Earth). This capability allows for continuous improvement and adaptation of the system’s functionality, ensuring it remains up-to-date with the latest enhancements or fixes.

CA manages and applies configuration settings that determine which algorithms are used. This includes handling various parameters and options that affect algorithm behavior. CA ensures that the system operates according to the specified requirements and optimizes performance based on the current operational goals.

CA supports version control by ensuring that the correct versions of algorithms are used and are compatible with the existing system components. They help prevent conflicts and ensure that updates or replacements do not disrupt system stability or functionality. Version control mechanisms might ensure new algorithms are compatible with the existing hardware and software infrastructure.

CA performs testing and validation before applying new or updated algorithms to ensure they meet the required performance and reliability standards. This may involve running simulations or conducting preliminary tests to verify that the new algorithms operate correctly and integrate seamlessly with the existing system.

Integrating SITL with CA enhances their capability to manage algorithms that involve physical quantities and units. SITL ensures that any algorithms selected or replaced adhere to dimensional and orientation standards, providing a consistent and reliable framework for algorithm functionality. This integration also supports formal verification of algorithms to ensure they conform to SI units and maintain accuracy across different configurations.

CA includes mechanisms for error handling and rollback in case of issues during algorithm replacement or configuration changes. If a new algorithm fails to perform as expected, the system can revert to a previous stable version, ensuring continuity and minimizing disruptions.

CA optimizes system performance by selecting algorithms that best match the current operational conditions. This includes adjusting computational resources and tuning algorithm parameters for optimal efficiency and effectiveness.

In summary, configurator algorithms are crucial for managing and adapting embedded algorithms in a Cyber-Physical System. They enable dynamic reconfiguration, support algorithm replacement from the Test Environment, and ensure the system operates according to specified configurations. By integrating SITL, configurator algorithms can achieve greater accuracy and consistency in handling physical quantities, enhancing the overall reliability and performance of the CPS.

3.2.2. Telecommunication Algorithms

Telecommunication Algorithms (TA) are crucial in managing and facilitating communication between CPS and their Test Environment, often located on Earth. They ensure the effective exchange of information necessary for configuring, testing, and monitoring CPS operations.

TA handles the reception of configuration data sent from Earth to the CPS. This data may include parameters for system setup, operational commands, and updates. For example, configuration data might specify orbital adjustments, sensor calibrations, or operational modes in a satellite mission.

TA is responsible for transmitting test data from the CPS to Earth. This data can be used to validate the system's performance, conduct experiments, or assess the results of various tests.

TA manages the transmission of telemetry information back to Earth, providing real-time updates on the CPS’s status and performance. This information typically includes data from sensors, system health indicators, and operational logs. Effective telemetry ensures mission control on Earth clearly and accurately understands the CPS’s condition and activities.

To efficiently transmit large volumes of data, TA incorporates data coding. This helps reduce the amount of data that must be sent, optimize bandwidth usage, and minimize transmission delays. Ensuring data integrity during transmission is critical.

TA includes error detection and correction mechanisms to identify and rectify any data corruption or loss that may occur during transmission. This is especially important in environments with high levels of noise or interference, such as space communications.

TA implements communication protocols that define how data is formatted, transmitted, and received. Protocols ensure that data exchange adheres to standards and can be interpreted correctly by both the CPS and ground-based systems.

TA incorporates encryption and authentication mechanisms to protect data from unauthorized access or tampering. Secure communication protocols help safeguard the integrity and confidentiality of the transmitted data.

TA ensures that data is transmitted over the correct channels and that channel usage is optimized for the specific needs of the CPS and its test environment.

TA handles feedback and acknowledgment messages to confirm the successful receipt of data or commands. This feature helps ensure that communications are effectively established and maintained, providing a mechanism for error reporting and resolution.

In summary, telecommunication algorithms are essential for managing the communication between CPS and their test environments. They facilitate the configuration and test data exchange, transmit telemetry information, and ensure data integrity and security. By incorporating SITL, these algorithms can achieve greater accuracy and reliability in handling physical quantities, further enhancing communication effectiveness in complex CPS applications.

3.2.3. CPS Controlling Algorithms

CPS Controlling Algorithms (CPSCA) are essential for effectively managing and operating CPS. They orchestrate the functioning of CPS based on predefined tasks and configurations, and they predict the system's state using a comprehensive software model. This involves several key aspects:

CPSCA is responsible for managing tasks defined in the system’s configuration. This includes scheduling, prioritizing, and executing CPS functions according to the system’s operational requirements. For instance, in an autonomous vehicle, these tasks might involve navigation, obstacle avoidance, and real-time decision-making based on sensor inputs.

Using a software model of the CPS, CPSCA predicts the system's future state. This model is built based on physical laws, system dynamics, and historical data. Simulating different scenarios and input conditions helps the software model anticipate how the system will behave, allowing for proactive adjustments and optimizations.

CPSCA continuously monitors the CPS’s performance and makes real-time adjustments based on the predictions from the software model. This dynamic control is crucial for maintaining optimal performance, efficiency, and safety. In industrial automation, for instance, controlling algorithms might adjust machinery operations to compensate for wear and tear or to adapt to changing production requirements.

CPSCA integrates with sensor data to update the software model and refine predictions. Sensors provide real-time feedback on the system’s state, which is used to validate and adjust the projections. For example, in aerospace applications, sensors might provide data on altitude, speed, and orientation, which is then used to update flight control algorithms and ensure accurate navigation.

CPSCA are designed to handle uncertainties and variabilities in the system’s environment and operation. This includes accounting for unexpected changes or disturbances, such as hardware failures or environmental factors. Advanced algorithms incorporate probabilistic models and adaptive control techniques to manage such uncertainties effectively.

CPSCA aims to optimize the CPS performance by minimizing resource usage, improving response times, and enhancing overall efficiency. This might involve optimizing energy consumption in smart buildings or maximizing throughput in manufacturing processes.

Ensuring the safety and reliability of the CPS is a critical aspect of controlling algorithms. These algorithms incorporate safety checks, fault detection, and recovery mechanisms to prevent or mitigate failures.

CPSCA uses adaptive control strategies to adjust their behavior based on changing conditions or new information. This allows the CPS to remain robust and flexible in the face of evolving requirements or environmental changes.

By employing SITL within CPSCA, developers can ensure that all physical quantities involved in the control processes adhere to rigorous dimensional and orientation standards. This integration helps maintain consistency and correctness across various system components, leading to more reliable and accurate control actions. SITL’s ability to enforce dimensional correctness and support formal verification further enhances the robustness of control algorithms, making them more effective in managing complex CPS operations.

In summary, CPSCA is vital for managing and optimizing the CPS performance. They rely on sophisticated software models, real-time data integration, and adaptive control strategies to ensure the system operates efficiently, safely, and accurately. Using SITL in these algorithms ensures that dimensional and orientation consistency is maintained, contributing to the overall reliability and effectiveness of the CPS.

3.2.4. Telemetry Algorithms

Telemetry Algorithms employ orthogonal polynomials to efficiently process different subsets of telemetry data, enabling high data compression [[35[M1] ]. The algorithms can significantly reduce the data size while preserving critical information by selecting the appropriate polynomials for specific data types, such as sensor readings or environmental conditions.

Incorporating the SITL into these algorithms ensures that the dimensional and orientational consistency of the telemetry data is rigorously maintained throughout the compression process. Using SITL helps verify the correctness of units and their relationships during data handling, which is critical in applications where even minor inconsistencies could lead to mission failure.

This effective compression minimizes the bandwidth required for transmitting large volumes of telemetry data and reduces the energy consumption needed for communication between spacecraft and Earth [34]. As a result, combining orthogonal polynomials and SITL ensures data integrity, unit consistency, and energy efficiency, contributing to extended mission lifespans and improved performance in resource-constrained environments like spacecraft, satellites, and deep-space probes.

3.2.5. Actuator Control Algorithms

Actuator Control Algorithms play a critical role in the control and performance verification of CPS actuators, such as onboard engines for orientation and orbit correction, electric motors, gyroscopes for object orientation, pumps, and fans. Precise control over these actuators is essential for the stable and reliable functioning of systems like spacecraft, satellites, and autonomous vehicles.

Incorporating the SITL into actuator control algorithms enhances their accuracy and reliability by ensuring that all physical quantities—such as force, torque, velocity, and angular momentum—are managed with dimensional consistency and orientation correctness. SITL verifies that all interactions between actuators and the control algorithms adhere to the strict rules of SI units, preventing issues such as mismatched units, incorrect scaling, or directional errors, which could otherwise result in system failure.

For example, in the case of onboard engines used for orientation and orbit correction, SITL helps ensure that the thrust calculations are dimensionally accurate while verifying the direction of force application. Similarly, for gyroscopes controlling object orientation, SITL confirms that angular momentum and rotational forces are correctly modeled in magnitude and orientation, reducing the risk of misalignment or incorrect rotational control.

By using Siano orientation integrated with SITL, the algorithms can also account for the directional properties of these actuators, providing a more nuanced and reliable control mechanism for CPS. This extension is particularly valuable when dealing with actuators that operate in three-dimensional space, as it ensures that both scalar and directional components of physical quantities are accurately modeled and controlled.

Additionally, SITL supports compile-time verification of these algorithms, which ensures that any potential errors, such as unit mismatches or incorrect dimensional operations, are detected and resolved early in the development process. This leads to more robust and efficient control algorithms with lower runtime overhead and higher reliability.

In conclusion, by integrating SITL into actuator control algorithms, developers can ensure precise and error-free control of CPS actuators across various applications. Whether controlling spacecraft engines, motors, or gyroscopes, SITL enhances these systems' accuracy and efficiency, contributing to safer and more reliable operations in mission-critical environments.

3.2.6. Sensor Control Algorithms

Sensor Control Algorithms (SCA) are critical for managing and verifying the performance of various CPS sensors, such as gyroscopes, accelerometers, cameras, radar systems, magnetic field sensors, and cosmic ray detectors. The accuracy and reliability of these sensors are essential for collecting precise data that informs control decisions, navigation, and operational adjustments in real time, especially in mission-critical systems like spacecraft, autonomous vehicles, and industrial automation.

Incorporating the SITL into SCA enhances the reliability of sensor data processing by ensuring that all measured quantities—such as acceleration, angular velocity, magnetic field strength, and cosmic radiation intensity—are handled with strict adherence to SI units and dimensional consistency. SITL verifies that each sensor output is dimensionally correct, preventing unit mismatches that could lead to errors in subsequent computations, control decisions, or system responses.

For instance, in the case of gyroscopes and accelerometers, SITL ensures that rotational and linear measurements are dimensionally consistent with the system’s requirements for navigation and orientation. This is crucial for maintaining stability and accurate positioning in CPS, such as satellites or drones. In radar systems, SITL guarantees that distance, velocity, and time measurements are correctly aligned with SI units, reducing the risk of errors during target detection or speed measurement.

Furthermore, Siano's extension of the SI system, integrated into SITL, allows SCA to account for the directional properties of measured quantities. This is particularly valuable for sensors like magnetic fields and cosmic ray detectors, where both the magnitude and direction of the field or radiation must be considered. By leveraging Siano’s orientation, SITL provides a more nuanced representation of the sensor outputs, improving the accuracy of directional measurements and enhancing system performance in complex environments.

SITL also enables compile-time verification of SCA, detecting potential errors—such as unit inconsistencies or incorrect dimensional operations—early in development. This leads to safer, more efficient, and error-free software implementations. With SITL, developers can ensure that sensor data is not only accurate in terms of physical quantities but also aligned with the specific needs of the system’s control mechanisms.

In conclusion, by integrating SITL into SCA, developers can enhance sensor data's accuracy, dimensional consistency, and reliability across a wide range of CPS applications. Whether managing the precise measurements from gyroscopes, radars, or magnetic field sensors, SITL ensures that the data is handled correctly, providing a robust foundation for real-time decision-making and system optimization. This ultimately leads to more reliable and efficient sensor management, which is critical for mission success in aerospace, autonomous systems, and scientific exploration.

All embedded algorithms are implemented in C++20 using the SITL. This modern approach leverages C++20’s advanced features and the robustness of SITL to ensure that the algorithms are efficient but also reliable and maintainable.

3.2.7. SITL Benefits

Using SITL provides several benefits for the formal verification of embedded software:

• Dimensional and Orientational Consistency: SITL ensures that all physical quantities in the embedded algorithms adhere to correct SI units and orientations. This is crucial for embedded systems where precise measurements and calculations are required, such as in aerospace, robotics, and automotive applications.
• Formal Verification: SITL enables rigorous formal verification of embedded software by checking dimensional correctness and consistency at compile time. This helps to detect errors early in the development process, ensuring that the software behaves correctly with the given hardware configurations and that the unit operations conform to the defined physical laws.
• Hardware Configuration Changes: Embedded systems often change hardware configurations due to upgrades or repairs. SITL helps maintain software correctness despite these changes by validating that the software remains compliant with SI units and dimensions even when the hardware components are altered or replaced. This ensures that the algorithms continue to perform as expected without introducing errors due to hardware modifications.
• Software Configuration Changes: Besides hardware changes, software configurations may also be updated or modified. SITL provides a framework for ensuring that these configuration changes do not compromise the correctness of the algorithms. By continuously verifying dimensional and orientational accuracy, SITL helps maintain the integrity of the software across different configurations.
• Enhanced Code Maintainability: Implementing algorithms with SITL in C++20 facilitates formal verification and improves code maintainability. Using modern C++20 features, such as concepts, literals, and ranges, combined with SITL’s type-safe unit management, results in more accessible code to understand, extend, and modify while ensuring that any changes adhere to strict correctness standards.
• Efficiency and Performance: C++20’s features and SITL’s compile-time checks contribute to the efficiency and performance of the embedded algorithms. By catching errors early and ensuring dimensional correctness, SITL helps reduce runtime overhead and computational inefficiencies, leading to more optimized and faster-executing embedded software.
• Robust Error Detection: SITL's compile-time checks provide robust error detection capabilities, helping to identify issues related to unit mismatches, incorrect calculations, or logical errors before the software is deployed. This proactive approach to error management enhances the overall reliability and stability of the embedded systems.

Implementing embedded algorithms in C++20 using SITL offers significant advantages in formal verification, code maintainability, and performance. SITL ensures that the software remains correct and reliable, even when hardware or software configurations change, making it a powerful tool for developing high-integrity embedded systems.

4. Discussion

The SITL introduced in this work provides a robust framework for handling dimensional and orientational analysis within software systems, particularly in the context of formal verification for CPS. By integrating extended SI units directly into C++ templates and leveraging metaprogramming techniques, SITL enforces dimensional and orientational consistency at compile time, significantly reducing errors arising from incorrect unit conversions or incompatible physical quantities.

One of the most notable contributions of SITL is its support for dimensional and orientational vectors as template arguments. This feature strengthens type safety and simplifies the process of developing software systems that require rigorous mathematical models, such as those used in engineering simulations, scientific computations, and control systems. The introduction of Siano orientation extends the applicability of SI units by allowing for the representation of directional properties, which is critical for accurately modeling real-world interactions in domains like robotics, aerodynamics, and electromagnetic systems.

Using the SI system extended by Siano increases the reliability of dimensional analysis by 10–19% compared to the standard SI system. A feature of the extended SI is its ability to check the direction of physical quantities, ensuring dimensional correctness and the accurate handling of directional properties. This addition plays a significant role in applications where the vector nature of physical quantities is crucial.

Statistical analysis of SI quantities and units further allows the definition of intervals for the powers of base units, ranging from [−6…5]. This range is used to determine the components in the SI unit vector, aiding in a more structured and precise representation of physical units. This statistical rigor enhances the system's overall reliability by providing boundaries for unit magnitudes.

Including templates for trigonometric functions and different additive/multiplicative operations broadens SITL’s utility, ensuring it can handle various calculations. The use of SI prefixes, from quecto (10⁻³⁰) to quetta (10³⁰), allows the library to manage a variety of scales, making it suitable for applications from quantum physics to cosmology.

SITL’s broad applicability spans various domains:

Engineering and Simulation: Verification software at compile time ensures that simulations involving complex physical interactions are accurate and maintain dimensional consistency throughout calculations.

Scientific Research: The adherence to strict SI standards ensures the integrity of both experimental and theoretical work, reducing the likelihood of errors in unit conversions or physical modeling.

Cyber-Physical Systems: The orientation-aware unit system improves the modeling of CPS by ensuring the accurate handling of scalar and directional quantities. This is crucial in systems where the physical direction of forces or velocities must be considered.

Using the SITL in formal verification offers several advantages, enhancing the accuracy, consistency, and efficiency of software development and testing:

1. Consistency and Accuracy:

-

Standardization: Ensures that all measurements and calculations adhere to internationally recognized standards, reducing errors from unit mismatches.

-

Precision: Provides a uniform framework for representing physical quantities, leading to more precise and reliable results.

2. Error Reduction:

-

Compile-Time Checking: SITL performs compile-time checks to verify the correctness of unit conversions and arithmetic operations, catching potential errors early in development.

-

Type Safety: Using strong typing for different units and directions, SITL prevents mixing incompatible units and directions, minimizing logical errors.

-

Prefix Safety: Using strong typing for different Si prefixes, SITL prevents mixing incompatible prefixes, minimizing logical errors.

-

Clear Code: Explicit representation of units makes the code easier to understand and maintain, with units of all variables and parameters specified.

3. [Efficiency:

-

Reduced Debugging Time: By catching unit-related errors at compile time, developers spend less time debugging and focusing more on core functionalities.

-

Reusable Components: SITL provides reusable components and functions for standard unit conversions and calculations, streamlining the development process.

-

Performance: SITL enhances productivity by leveraging features of C++20, resulting in more efficient code execution.

4. Scalability:

Adaptability: New units or unit systems can be integrated into the SITL without significantly changing the codebase.

Flexibility: Supports various applications across different domains, from engineering and physics to chemistry and mechanics.

Memory Usage: Using SITL does not require additional memory beyond what is needed for the fundamental data types.

5. Compliance and Interoperability:

-

Regulatory Compliance: Ensures compliance with industry standards and regulatory requirements, which often mandate the use of SI units.

-

Interoperability: Facilitates easier integration and data exchange between systems and software that adhere to SI standards.

6. Formal Verification:

-

Mathematical Rigor: Incorporates rigorous mathematical techniques to verify software correctness, particularly in high-precision, high-reliability applications.

-

Model Validation: Assists in validating mathematical models used in simulations and computational tasks, ensuring accurate representation of real-world phenomena.

Despite SITL’s advantages, there are some limitations. The heavy reliance on compile-time checks and template metaprogramming may lead to increased compilation times in larger applications. Additionally, using C++ templates could limit its adoption in environments where other programming languages or dynamic typing are more common.

Future research could focus on expanding SITL’s functionality to cover advanced physical models, such as those involving tensors or multi-dimensional fields. Integrating SITL with real-time systems or embedded platforms would make the library more versatile in practical applications. Besides, the suggested method could be added by more traditional formal models based on predicate description [36].

Efforts could also be made to optimize the template metaprogramming techniques used in SITL to reduce compilation overhead. Exploring compatibility with other languages or libraries could help extend its reach across various interdisciplinary projects.

5. Conclusions

Key results of the study based on SITL approach are as follows: introducing a dimensional and orientation-based verification framework for CPS and IoT software; establishing a reliability model for both standard and extended SI unit systems; developing an advanced metaprogramming approach for integrating SI-based type safety into C++ programs; comparing the statistical reliability of the standard and extended SI systems; demonstrating the practical application of SI-based verification through case studies and real-world software validation.

By integrating SI principles into modern software verification, this research provides a systematic method for improving the correctness and reliability of embedded software in CPS and IoT environments. This article focuses on the SITL that leverages extended SI units and validating SI prefixes and performing dimensional and orientational analysis. Notably, the proposed SITL does not require additional memory resources.

The SITL offers a powerful and innovative framework for ensuring dimensional and orientational consistency in software that models physical systems. By integrating SI units into C++ templates and employing static assertions at compile time, SITL significantly reduces the risk of errors in unit conversions and operations, providing an essential tool for developers working in fields such as engineering, scientific research, and CPS.

Introducing Siano orientation into the SI system extends the library's capabilities, allowing it to handle directional properties in physical quantities. This makes SITL a valuable asset for traditional scalar quantities and applications requiring vector and directional analysis, ensuring comprehensive support for both types of interactions.

SITL's adaptability, support for SI prefixes, and coverage of a wide range of mathematical operations—including trigonometric functions—underscore its versatility and utility. The library’s rigorous approach to formal verification provides a mathematically sound foundation for improving the reliability and accuracy of software that relies on physical units, ultimately enhancing the quality of both simulations and real-world applications.

In conclusion, while SITL demonstrates excellent potential to improve software reliability, further research and development are necessary to unlock its full capabilities. Expanding the library with specialized tools for quantitative code quality assessment based on statistical characteristics would enhance its effectiveness.

Then work could focus on extending SITL to support more advanced physical models, such as tensors and multi-dimensional fields, and integrating it with real-time systems and embedded platforms to increase its versatility. Additionally, optimizing metaprogramming techniques to reduce compilation overhead and exploring cross-language compatibility would broaden SITL’s impact across various fields.