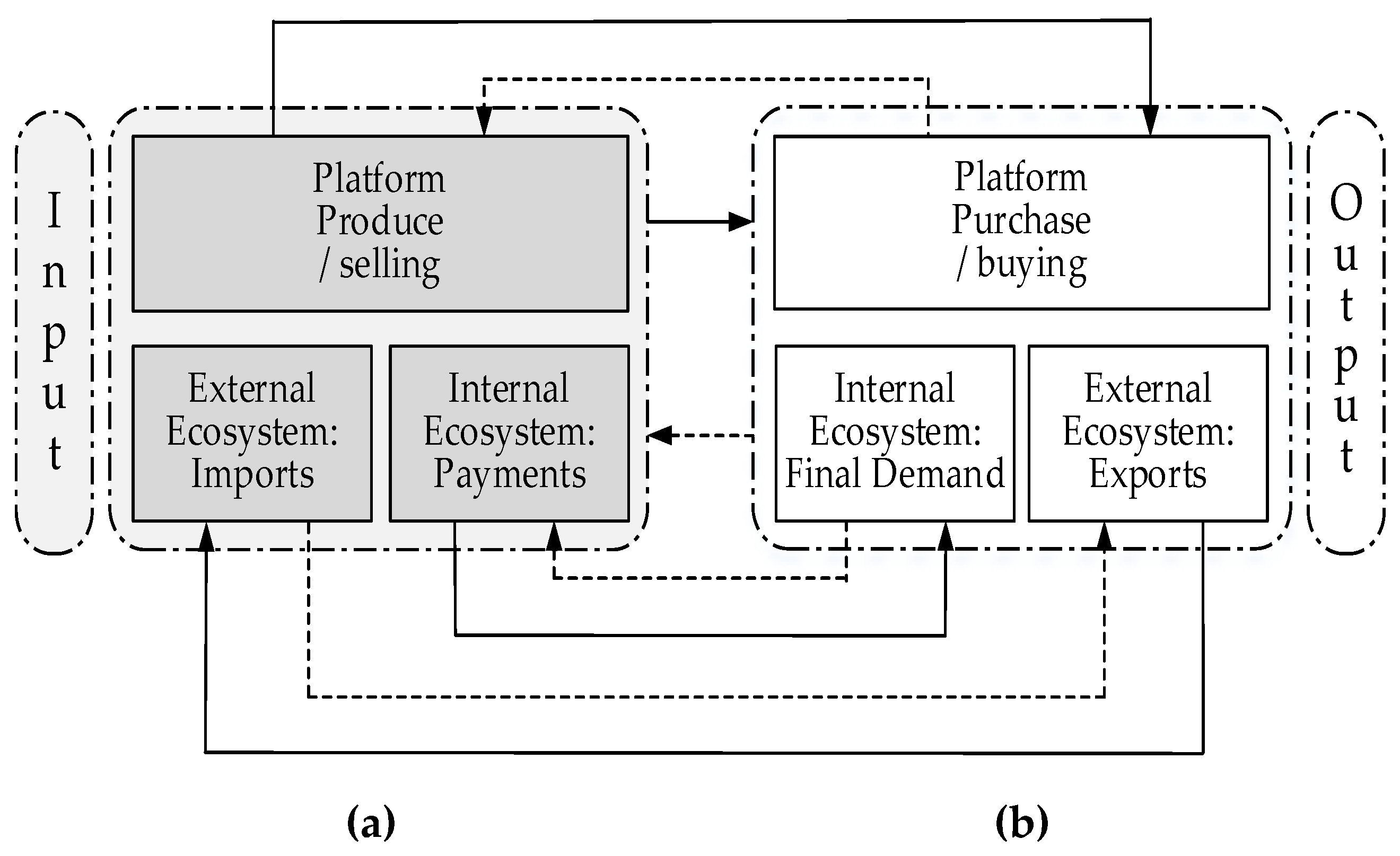
3.3.1. An Algorithm for Determine the Equilibrium on the External Ecosystem
Entry: Let – the external ecosystem export (inflow and (or) supply for foreign currency) transactions of the total output of financial and insurance activities industry, , , a billion U.S. dollars (see Table 1, column (f)); – the external ecosystem import (outflow and (or) demand for foreign currency) transactions of the total input of financial and insurance activities industry, , , a billion U.S. dollars (see Table 1, column (e)).
Outcome: Equilibrium transactions of the external ecosystem import and exports, respectively, of the total input and the total output of the financial and insurance activities industry.
Step 1: To create the supply function as a data set on the normalized external ecosystem export transactions [0;1] from the domain of the observation , .
(i) Sorting by growth of data
,
, i.e. rearrange the elements of observation data
,
into a sequence such that the following chains of inequalities hold:
, and denote by
,
(see Table 3, column (f)), where
and
(ii) Calculate the cumulative sum of sorted data
,
:
(iii) To normal the cumulative sum of sorted data
,
:
and denote by
,
(see Table 4, column (f));
(iv) To build and to visualize the supply as function to normalized of external ecosystem export transactions from domain of the observation ,
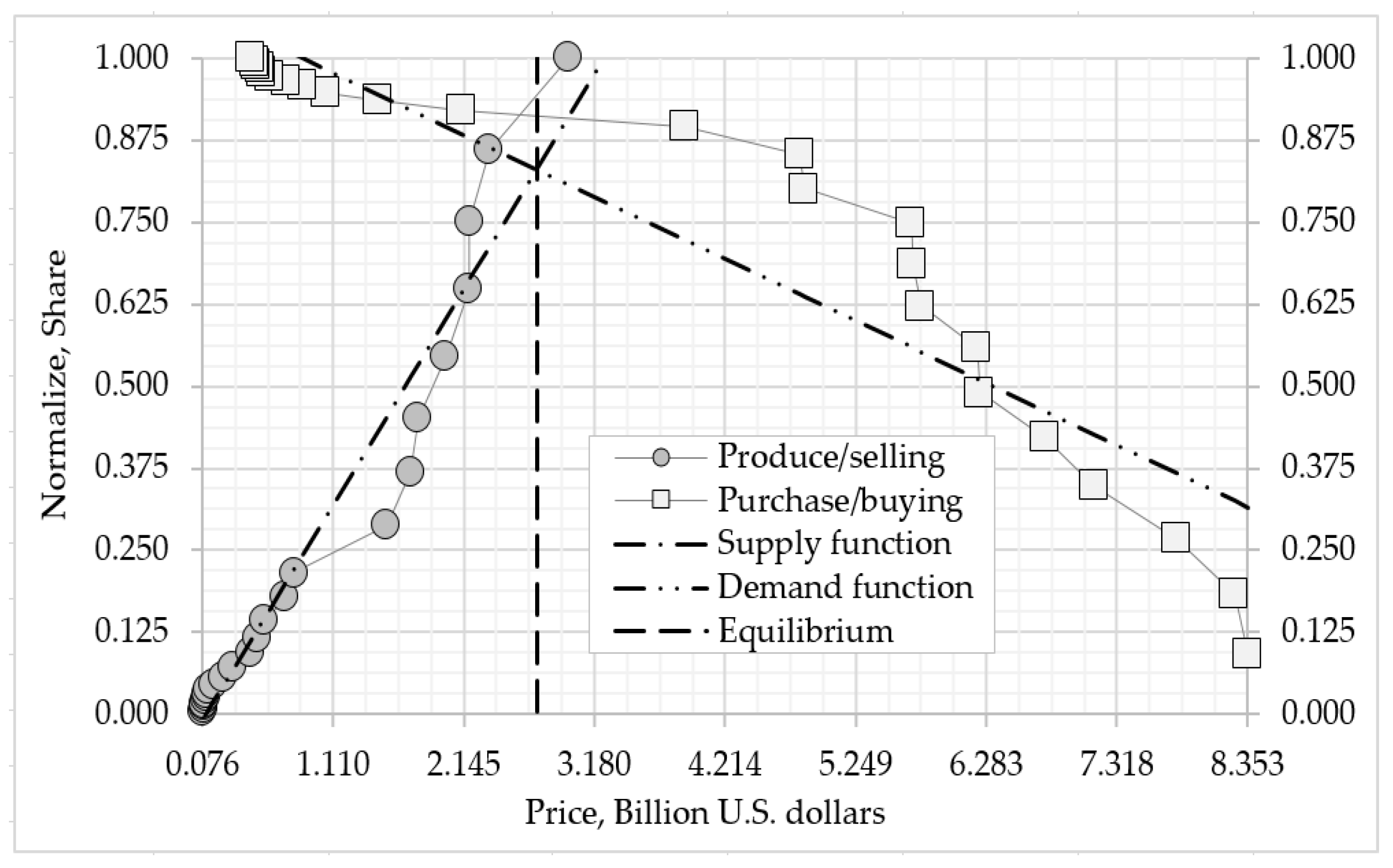
(see Figure 6, histogram with a round marker with a gray fill);
Step 2: Create the regression equations for the supply function of the external ecosystem export transactions , .
(i) Calculate the slope between the dependent and the independent variable , ;
(ii) Calculate the intercept between the dependent and the independent variable , ;
(iii) Calculate the R–square for the regression equation between the dependent and the independent variable , ;
(iv) Calculate the p–value of parameters for the regression equation between the dependent and the independent variable , ;
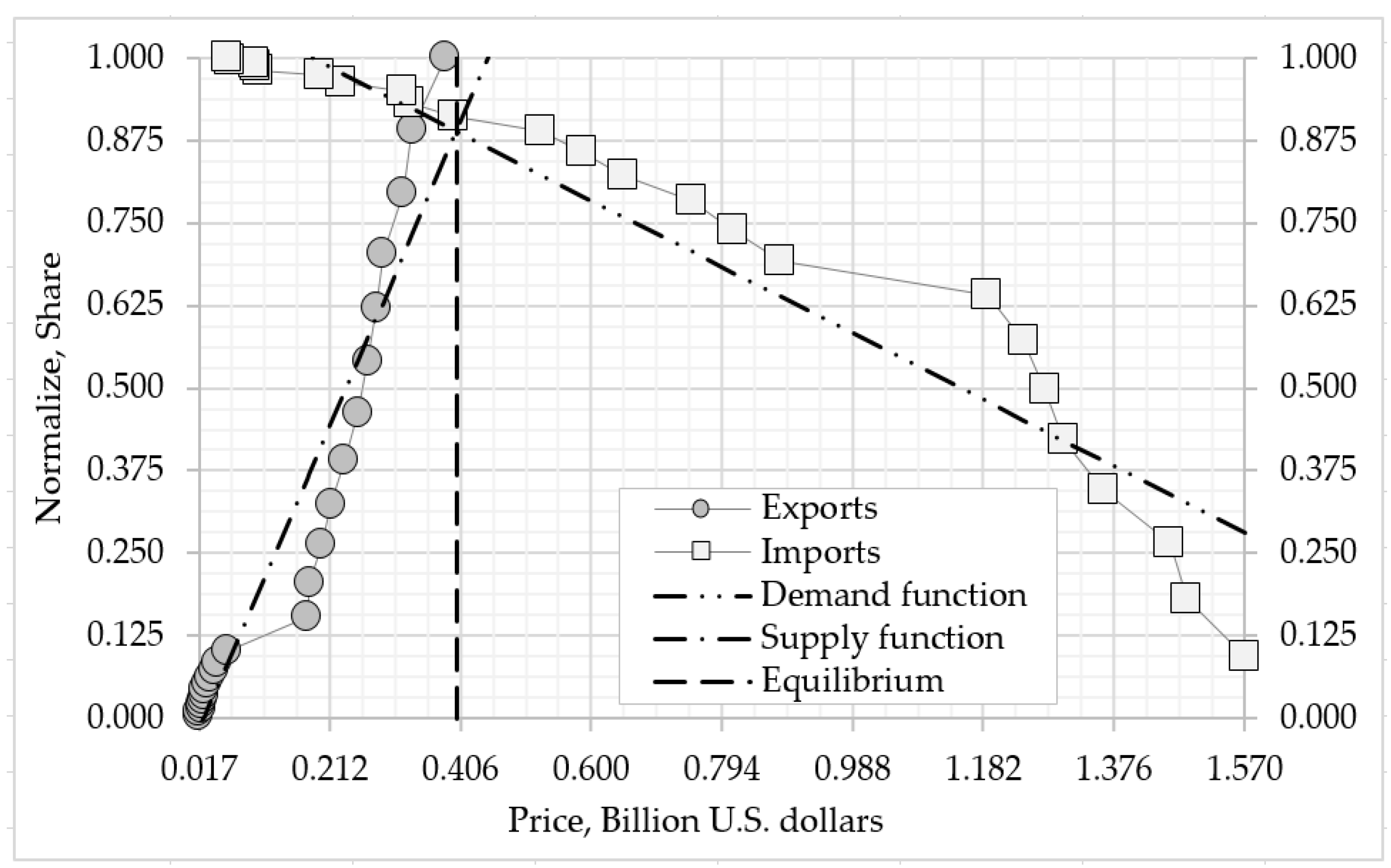
Figure 6.
Observation, regression equations, and equilibrium of the external ecosystem import and export transactions in the financial and insurance activities industry.
Figure 6.
Observation, regression equations, and equilibrium of the external ecosystem import and export transactions in the financial and insurance activities industry.
(v) Calculate the standard errors of parameters for the regression equation between the dependent and the independent variable , ;
(vi) To build the regression equations for the supply function of the normalized data of the internal ecosystem payment transactions
on domain of the observation data
,
[
30]:
where unknown parameters Slope’, Intercept’, R–square, p–value, and Standard errors will be estimated by the least squares in the above sub steps (i)–(v);
(vii) Visualize the regression equations for the supply function of the normalized data of the external ecosystem export transactions on the domain of the observation data , (see Figure 6, a dotted line with one dot, Table 8, column (a)).
Table 8.
Results of the intelligent analysis of equilibrium growth in the external ecosystem.
Table 8.
Results of the intelligent analysis of equilibrium growth in the external ecosystem.
| Year |
(a) |
(b) |
(c) |
(d) |
(e) |
(f) |
Year |
(a) |
(b) |
(c) |
(d) |
(e) |
(f) |
|
0.026 |
–0.009 |
UV |
1.933 |
–0.363 |
UV |
|
0.089 |
0.089 |
OV |
0.460 |
0.126 |
OV |
|
0.029 |
–0.011 |
UV |
1.765 |
–0.281 |
UV |
|
0.111 |
0.070 |
OV |
0.400 |
0.125 |
OV |
|
0.031 |
–0.010 |
UV |
1.599 |
–0.141 |
UV |
|
0.135 |
0.065 |
OV |
0.355 |
0.040 |
OV |
|
0.034 |
–0.012 |
UV |
1.445 |
–0.084 |
UV |
|
0.161 |
0.052 |
OV |
0.318 |
0.013 |
OV |
|
0.036 |
–0.014 |
UV |
1.297 |
0.004 |
OV |
|
0.189 |
0.044 |
OV |
0.282 |
0.038 |
OV |
|
0.040 |
–0.014 |
UV |
1.153 |
0.122 |
OV |
|
0.220 |
0.033 |
OV |
0.256 |
–0.027 |
UV |
|
0.043 |
–0.016 |
UV |
1.012 |
0.230 |
OV |
|
0.252 |
0.016 |
OV |
0.233 |
–0.036 |
UV |
|
0.046 |
–0.017 |
UV |
0.877 |
0.311 |
OV |
|
0.286 |
–0.006 |
UV |
0.221 |
–0.116 |
UV |
|
0.050 |
–0.017 |
UV |
0.777 |
0.105 |
OV |
|
0.322 |
–0.032 |
UV |
0.210 |
–0.108 |
UV |
|
0.055 |
–0.016 |
UV |
0.685 |
0.125 |
OV |
|
0.360 |
–0.040 |
UV |
0.198 |
–0.099 |
UV |
|
0.060 |
–0.017 |
UV |
0.600 |
0.149 |
OV |
|
0.401 |
–0.067 |
UV |
0.191 |
–0.127 |
UV |
|
0.068 |
–0.007 |
UV |
0.526 |
0.120 |
OV |
|
0.447 |
–0.064 |
UV |
0.184 |
–0.126 |
UV |
Step 3: To create the demand function as a data set on the normalized of the external ecosystem import transactions [0;1] from the domain of the observation , .
(i) Descending sorted of data
,
, i.e. rearrange the elements of observation data
,
into a sequence such that the following chains of inequalities hold:
, and denote by
,
(see Table 3, column (e)), where
and
(ii) Calculate the cumulative sum of sorted data
,
:
(iii) To normal the cumulative sum of sorted data
,
:
and denote by
,
;
(iv) To build and visualize the demand function to normalized external ecosystem import transactions
from the domain of the observation
,
(see
Figure 6, histogram with a square marker with a white fill);
Step 4: Create the regression equations for the demand function of the external ecosystem import transactions: , .
(i) Calculate the slope between the dependent and the independent variable , ;
(ii) Calculate the intercept between the dependent and the independent variable , ;
(iii) Calculate the R–square for the regression equation between the dependent and the independent variable , ;
(iv) Calculate the p–value of parameters for the regression equation between the dependent and the independent variable , ;
(v) Calculate the standard errors of parameters for the regression equation between the dependent and the independent variable , ;
(vi) To build the regression equations for the demand function of the external ecosystem import transactions
,
[
35]:
where unknown parameters Slope, Intercept, R–square, p–value, and Standard errors will be estimated by the least squares in the above sub-steps (i)–(v);
(vii) Visualize the regression equations for the demand function of the external ecosystem import transactions , (see Figure 6, the dotted line with two dots, Table 8, column (d)).
Step 5: Find the equilibrium transactions of the external ecosystem export for the financial and insurance activities industry, i.e. prove that .
(i) Construct equations for the equilibrium transactions of the external ecosystem the exports
and import
from the equality condition of equations (24) and (25), i.e.
. Indeed, from (24) and (25) we obtain:
(ii) Find the normalized sequences , , such that these functions satisfied conditions (26):
(iia) If for , , the following holds:
then we use linear interpolation and ensure convergence of the iteration using the gradient method [
31]:
(iib) If for
,
,
the following holds:
or
Then, respectively, we use linear extrapolation and ensure convergence of the iteration by the gradient method [
31]:
or
Step 6: Find the equilibrium transactions of the external ecosystem imports for the financial and insurance activities industry, i.e. prove that
.
(i) Construct equations for the equilibrium transactions of the external ecosystem exports
and the external ecosystem import
from the equality condition of equations (24) and (25), i.e.
. Indeed, from (24) and (25) we obtain:
(ii) Find the normalized sequences , , such that these functions satisfied conditions (30):
(iia) If for
,
,
the following holds:
then we use linear interpolation and ensure convergence of the iteration using the gradient method [
36]:
(iib) If for
,
,
the following holds:
or
Then, respectively, we use linear extrapolation and ensure convergence of the iteration by the gradient method [
36]:
or
3.3.2. Simulation and Its Application in Intelligent Analysis of Equilibrium Growth of the External Ecosystem
In
Section 3.3, the behavior of external ecosystem export (inflow and (or) supply for foreign currency) transactions is evaluated using the supply function, while the behavior of external ecosystem imports (outflow and (or) demand for foreign currency) transactions is evaluated using the demand function.
First, the regression equation (24) is created for external ecosystem export agent behavior, where the dependent variable is normalized export transactions, and the independent variable is observed export transactions.
The regression equation, using the Slope’ and Intercept’ parameters and the normalized external ecosystem exports transaction dependent variable values estimated through the least squares, provides the estimated supply function values:
Also, the values obtained by subtracting the observed export transactions from the calculated export transactions represent the estimates of the external ecosystem export behavior.
Thus, we use computational model to detect the equilibrium to identify time phases of undervalued and overvalued nominal estimate and linguistic variables in the external ecosystem export of the financial and insurance activities industry we get (see Table 8, column (b)-(c)):
- -
The first phase of undervalued the external ecosystem export of the financial and insurance activities industry is characterized by a flow of transactions with the following attributes: an entry point of 0.009, a peak deviation of 0.017, and an exit point of 0.007 billion U.S. dollars in undervalued transactions;
- -
The phase of overvalued external ecosystem export of the financial and insurance activities industry is characterized by a flow of transactions with the following attributes: an entry point of 0.089, a peak deviation of 0.070, and an exit point of 0.016 billion U.S. dollars in overvalued transactions;
- -
The second phase of undervalued the external ecosystem export of the financial and insurance activities industry is characterized by a flow of transactions with the following attributes: an entry point of 0.006, a peak deviation of 0.067, and an exit point of 0.064 billion U.S. dollars in undervalued transactions.
Next, for the external ecosystem import behavior, a regression equation (25) is created, where the dependent variable is the normalized export transactions and the independent variable is the observed import transactions. Using Slope, Intercept parameters, values of normalized import transaction dependent variable, and least squares were estimated the parameters of the regression equation and the demand function values are calculated:
Also, the values obtained by subtracting the observed import transactions from the calculated import transactions represent the estimates of the external ecosystem import behavior.
We now apply computational model to establish equilibrium, determine time phases of undervaluation and overvaluation of nominal estimate and linguistic variables within the external ecosystem import in the financial and insurance activities industry (see Table 8, column (e)-(f)):
- -
The first phase of undervalued of the external ecosystem import of the financial and insurance activities industry is characterized by a flow of transactions with the following attributes: an entry point of 0.363, a peak deviation of 0.281, and an exit point of 0.084 billion U.S. dollars in undervalued transactions;
- -
The phase of overvalued external ecosystem import of the financial and insurance activities industry is characterized by a flow of transactions with the following attributes: an entry point of 0.004, a peak deviation of 0.149, and an exit point of 0.038 billion U.S. dollars in overvalued transactions;
- -
The second phase of undervalued the external ecosystem import of the financial and insurance activities industry is characterized by a flow of transactions with the following attributes: an entry point of 0.027, a peak deviation of 0.127, and an exit point of 0.126 billion U.S. dollars in undervalued transactions.
Also, in
Section 3.3, based on studies of the behavior of import and export agents, work is carried out to detect the equilibrium points of the stochastic dynamic state of the external ecosystem. Indeed, regression equations (24) and (25) are constructed respectively by applying the least squares method to the supply function of the import transactions data and the demand function of the export transactions. This, in turn, the problem of determining the equilibrium points in the behavior of the mentioned import and export agents leads to the problem of calculating the intersection points of the linear equations (24) of supply and (25) of demand function.
First, for the external ecosystem import agent, if the equilibrium point lies in the feasible domain of the solution, then the desired point is detected using the linear interpolation and the gradient method defined by equation (27). The stopping criterion for iterative calculations is obtained from equality (26). Also for the import of the external ecosystem, if the equilibrium point does not belong to the feasible domain of solution, then the desired point is detected by equation (28) for the left side, and equation (29) for the right side and It is determining by linear extrapolation and gradient method. The stopping criterion for iterative calculations is obtained from equality (26).
Second, for an export of an external ecosystem, if the equilibrium point lies in the feasible domain of solution, then the desired point is detected by linear interpolation and gradient method, defined by equation (31). The criterion for stopping the iterative calculations is obtained from equality (30). Also, for the export of the external ecosystem, if the equilibrium point does not belong to the feasible domain of solution, then the desired point is detected by equation (32) for the left part and (33) for the right part, and It is determining by linear extrapolation and gradient method. The criterion for stopping the iterative calculations is obtained from equilibrium (30).
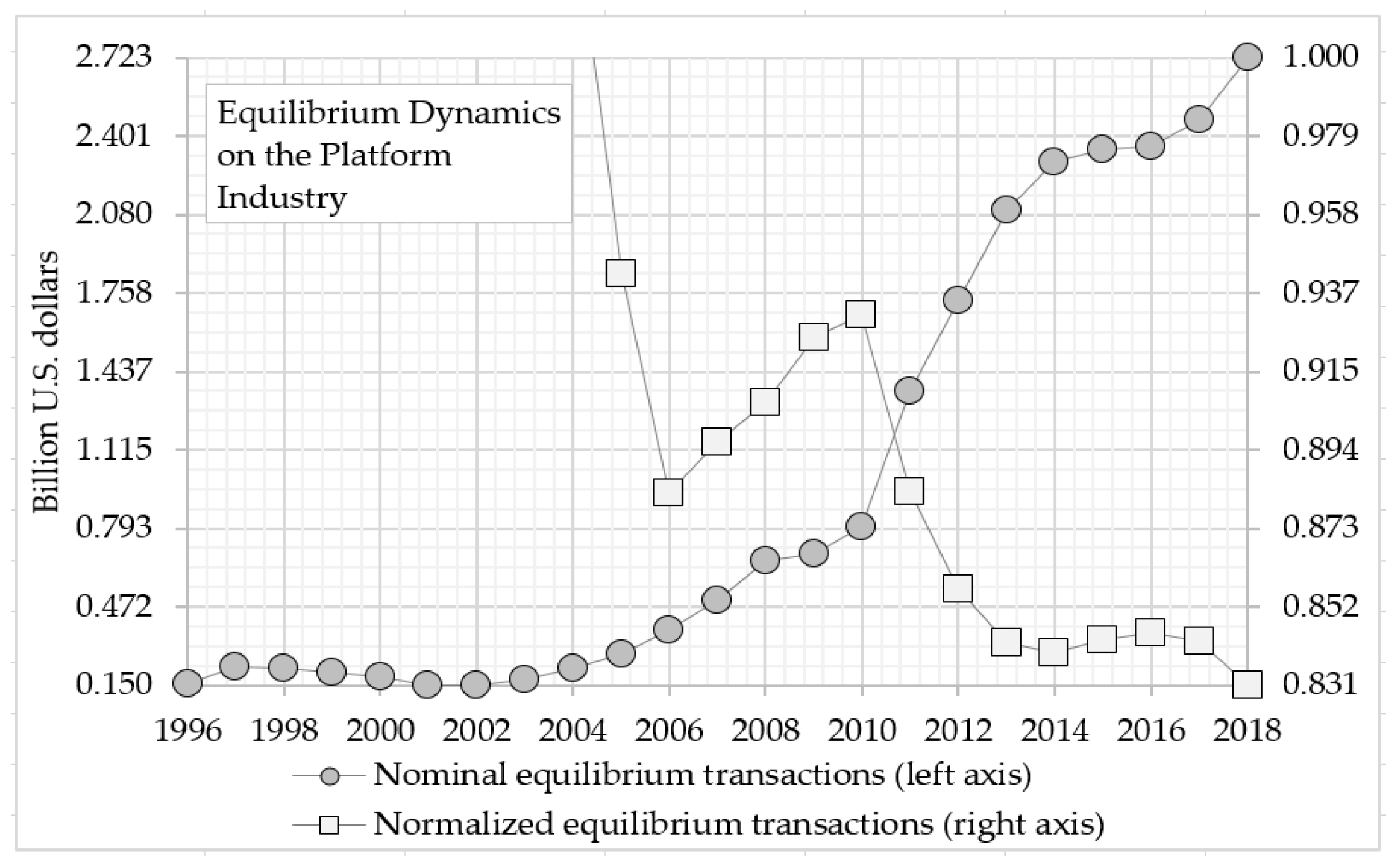
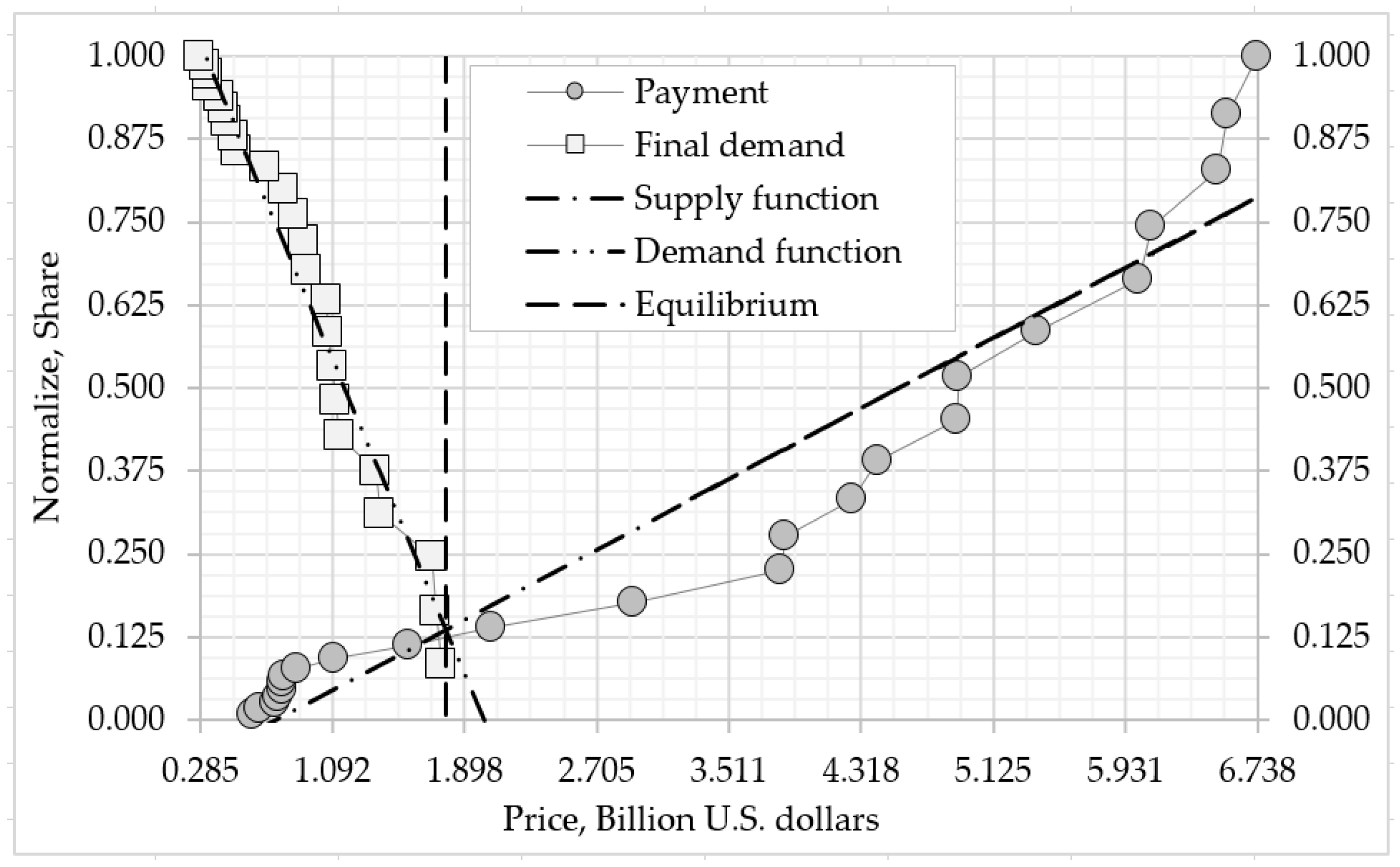
As a result, the equilibrium transaction behavior of the export and the import agents of the external ecosystem industry was completely determining by the above model and distributed into the following time phases (see Figure 7, the histogram with round marker with gray fill and the histogram with square marker with white fill, Table 6, column (e)-(f)):
- -
The first time phases cover the period from 1995 to 2004. This period is distinguished by the fact that it does not belong to the feasible domain of solution for the equilibrium transactions of external ecosystem import and export agents. That is, for first time phases the financial and insurance industry has an entry point of 0.019, a peak deviation of 0.033, and an exit point of 0.041 billion U.S. dollars;
Figure 7.
Nominal and normalized equilibrium dynamics of the external ecosystem import and export transactions in the financial and insurance activities industry.
Figure 7.
Nominal and normalized equilibrium dynamics of the external ecosystem import and export transactions in the financial and insurance activities industry.
- -
The initial median average was 0.024 and the final median average of the first-time phases was 0.033 billion U.S. dollars. That is, in the first time phase, the median average absolute value of equilibrium transactions in the financial and insurance sector increased by 0.009 billion U.S. dollars, and the median average relative value of equilibrium transactions decreased by 138.41%;
- -
The second time phases cover the period from 2005 to 2018, this period is in the feasible domain of solution of equilibrium transactions of import and export agents of the external ecosystem. That is, for the second time phase the financial and insurance industry has an entry point of 0.042, a peak deviation of 0.395, and an exit point of 0.400 billion U.S. dollars;
- -
The initial median average was 0.234 and the final median average for the second time phase was 0.386 billion U.S. dollars. That is, in the second time phase, the median average absolute value of equilibrium transactions in the financial and insurance sector increased by 0.152 billion U.S. dollars, and the median average relative value of equilibrium transactions increased by 165.07%.
Thus, analyzing the entry points, peak deviations, exit points, time phases, and increase or decrease of median average values of these transactions enables a deeper insight into the fundamental patterns of inter-industry linkages, which help address theoretical and practical issues related to external ecosystem agent’s behavior.
Based on the results of
Section 3.3, we created substantiated and implemented of the computational model on the determine equilibrium states for external ecosystem transactions by alignment import (outflow and (or) demand for foreign currency) and export (inflow and (or) supply for foreign currency) flows. The novelty of these results are determine equilibrium transactions; analysis of time phases of undervalued and overvalued transactions; classification of time phases of equilibrium growth within the area of admissible solutions of the external ecosystem imports and exports, classifying equilibrium transactions and the significance may be to use resources efficiently and ensure sustainable growth in the financial and insurance activities of Kazakhstan.