Submitted:
03 March 2025
Posted:
04 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
- (1)
- A sparse SAR image enhancement method based on complex images is introduced for automotive applications. The limitations of the conventional unweighted regularization method are revealed, particularly in scenarios with radar RCS distributed over a wide dynamic range. The inconsistent resolution enhancement and amplitude bias of the conventional unweighted regularization method are quantitatively analyzed.
- (2)
- Existing frameworks for constructing more flexible penalty terms, reweighting and penalty modifying frameworks, are reviewed. A novel approach combining these two frameworks is proposed to leverage the advantages of both.
- (3)
- A novel image enhancement method, termed MSR regularization, is proposed for automotive SAR. MSR constructs its penalty term by integrating penalty terms from both reweighting and penalty modifying frameworks. On one hand, a novel weighting scheme is introduced, which localizes the global scattering point enhancement problem to the mainlobe scale, effectively suppressing sidelobes. On the other hand, a multi-segment regularization strategy is employed to eliminate distortion of the enhanced results. Correspondingly, a new thresholding function, the TRUTH function, is introduced as a fast solver for multi-segment regularization problem.
- (4)
- An iterative algorithm for enhancing automotive SAR images using MSR is presented. Real data experiments are conducted to validate the feasibility and effectiveness of the proposed method.
2. Problem Formulation and Related Works
2.1. Problem Formulation and Regularization Method
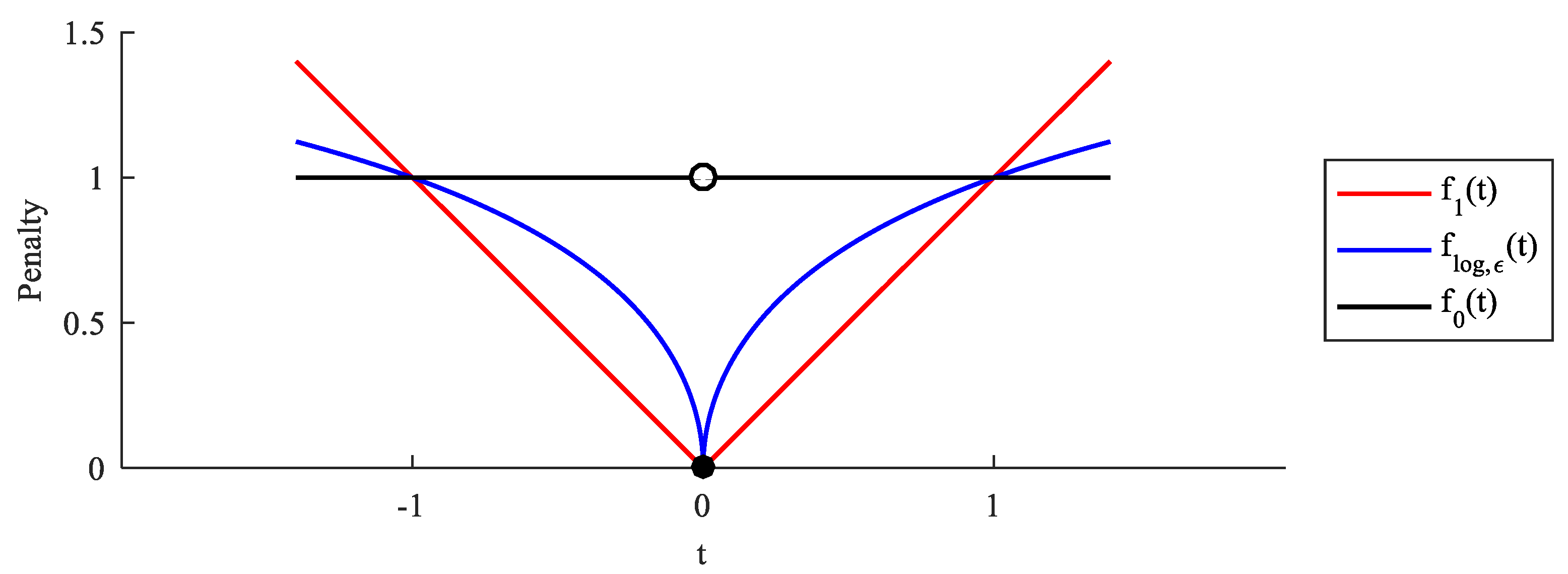
2.2. Limitations of Regularization Method for SAR Image Enhancement
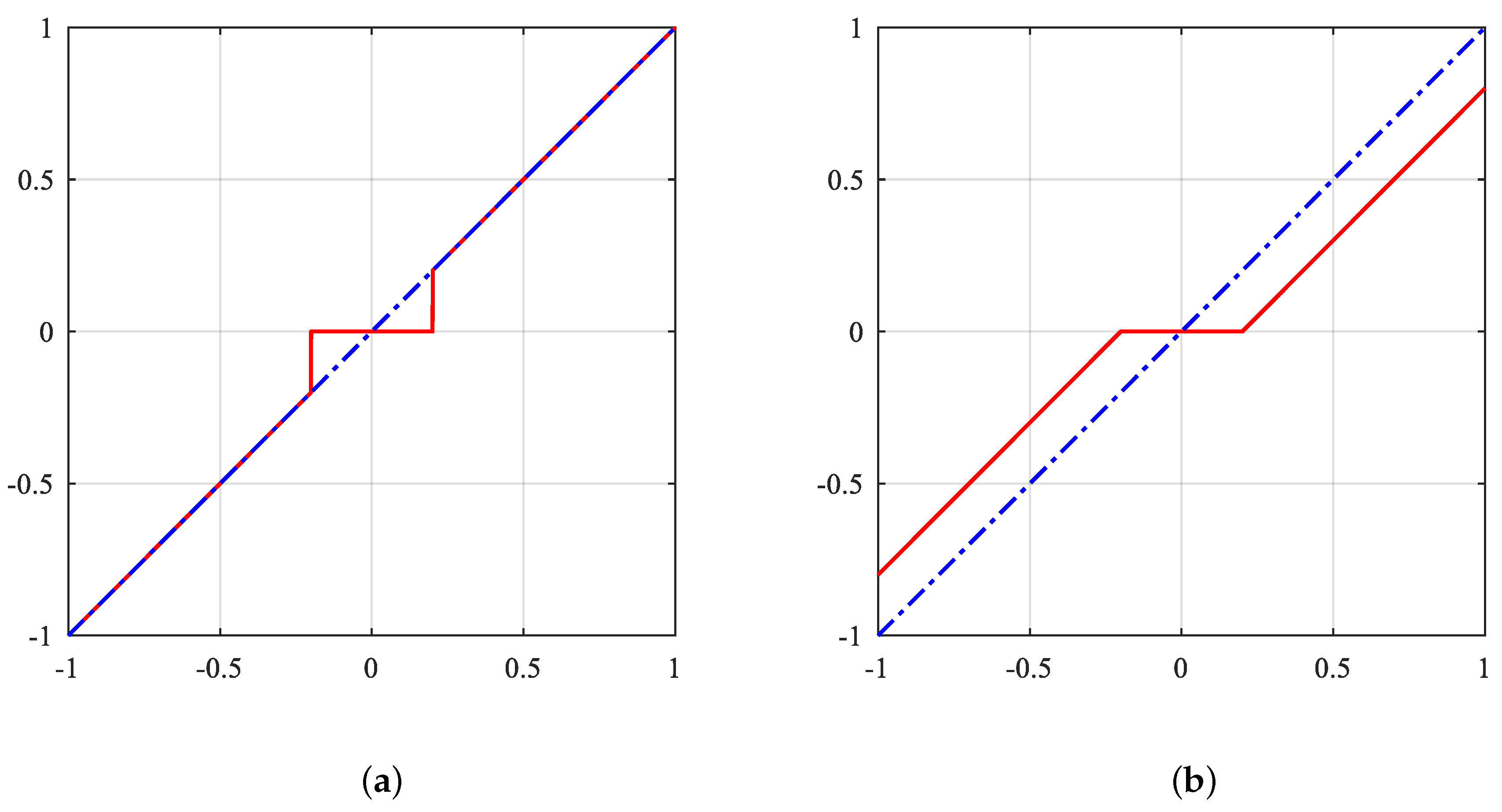
2.3. Related Works About Reweighted Regularization
2.4. Related Works About Modified Penalty Term
2.5. Summary of Related Works
3. Multi-Segment-Reweighted Regularization and Iteration Algorithm
3.1. A Combination Framework
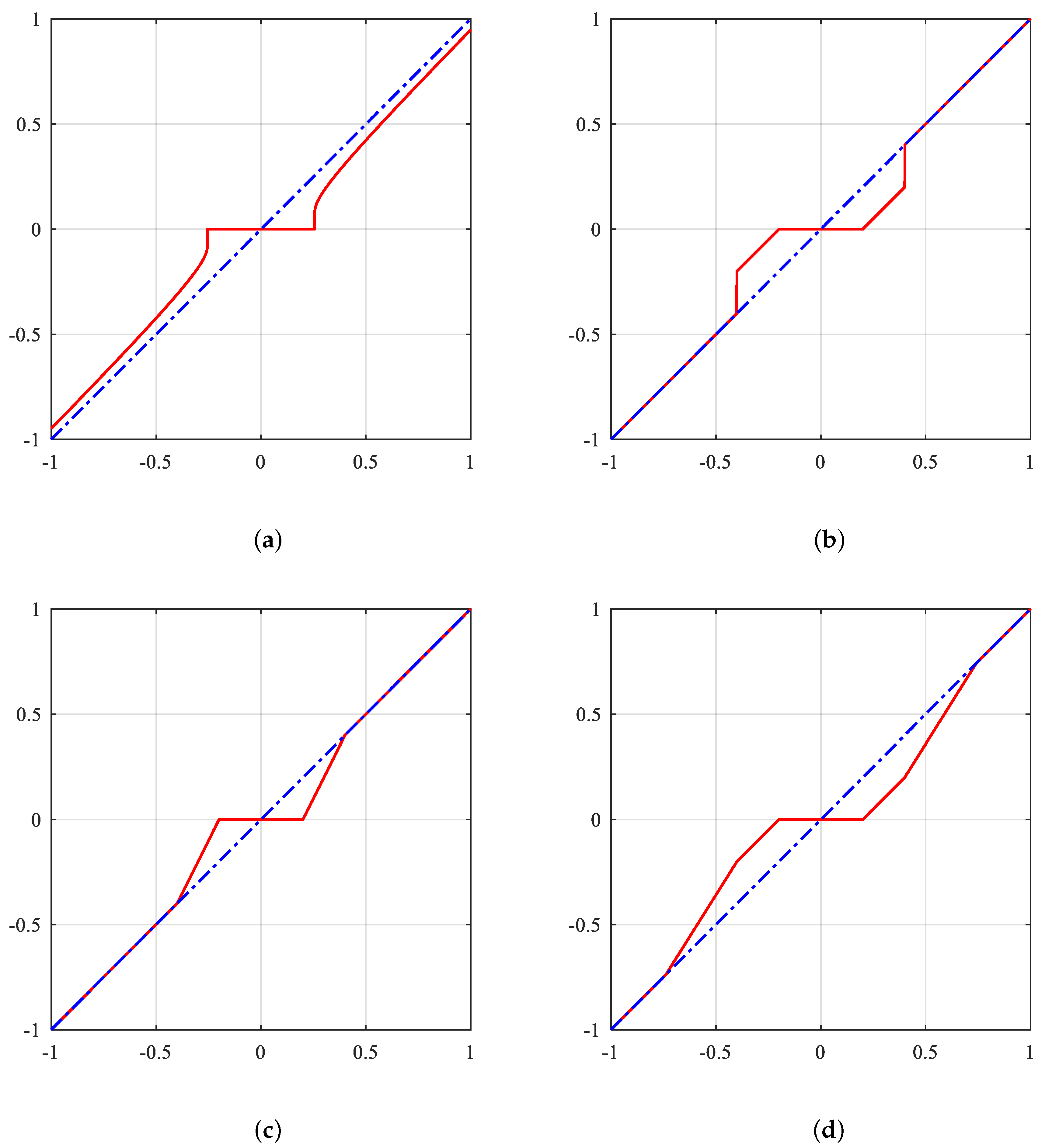
3.2. weighting Scheme for Consistent Enhancement
3.3. Multi-Segment Regularization
3.4. Iteration Algorithm
- Set the iteration count k to zero and initialize ;
- Update the weights from according to the designed weighting scheme;
- Solve the reweighted regularization minimization problem:
- Terminate algorithm when update of converges or when k attains maximum number of iterations. Otherwise, k plus one and go to step 2.
| Algorithm 1 Iteration Algorithm for Enhancement of Automotive SAR Image via MSR. |
|
Input: RMA recovered SAR image .
Initial: Model parameter , Update step size , Convergent tolerance , Iteration count , Maximum iterative steps , Thresholding function , Initial resorted image .
while and do
end while
Output: Restored SAR image .
|
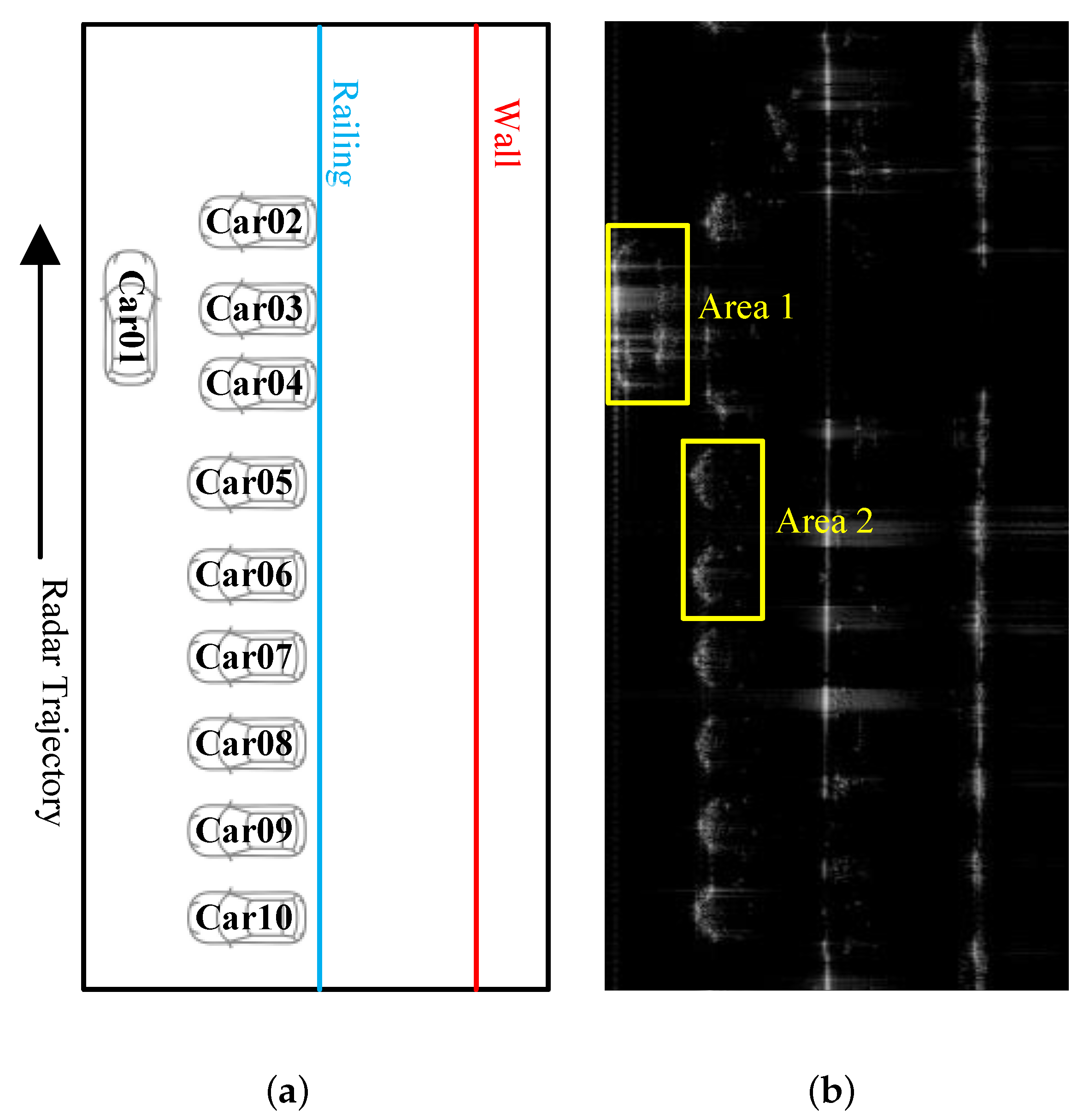
4. Real Data Experiment
4.1. Experiment Setup
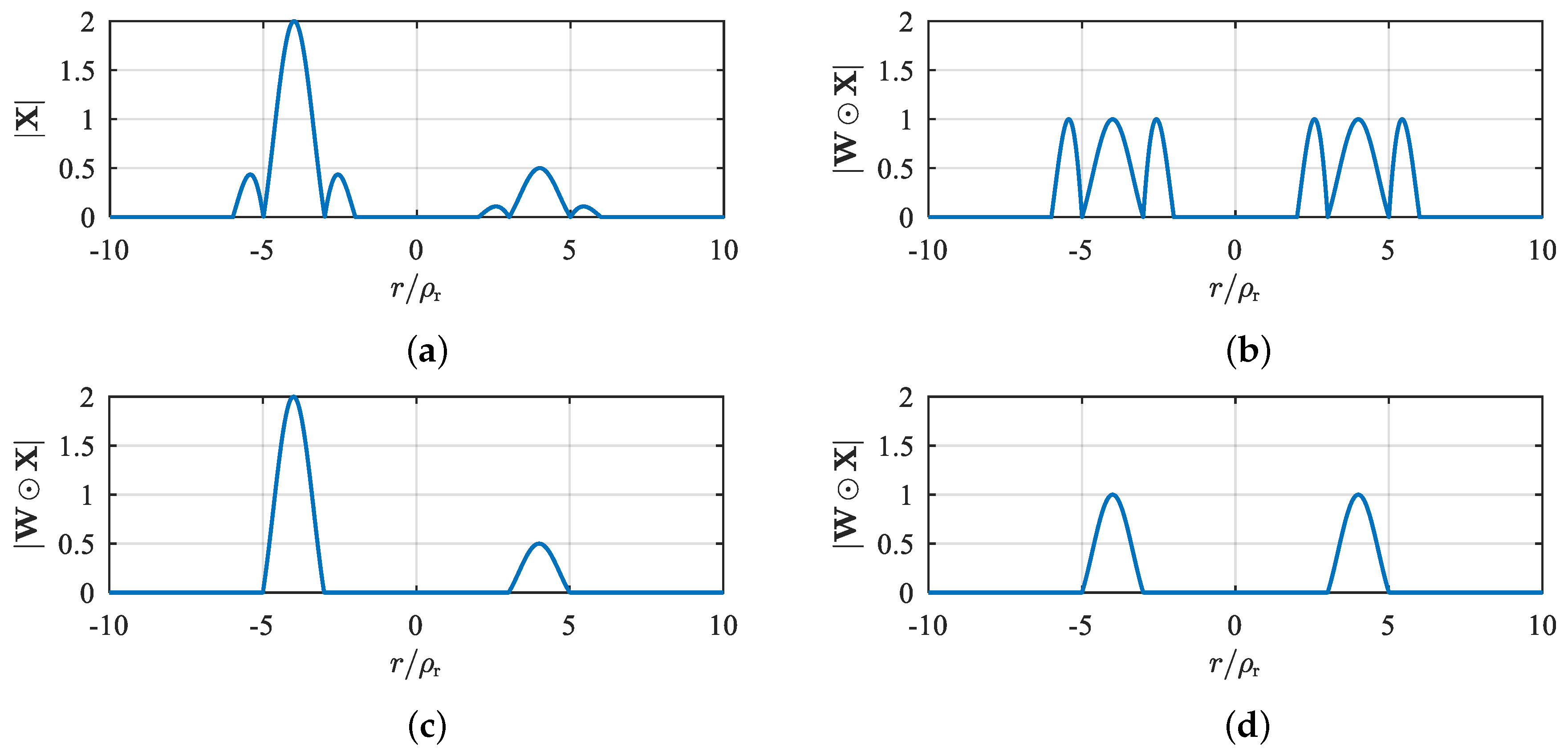
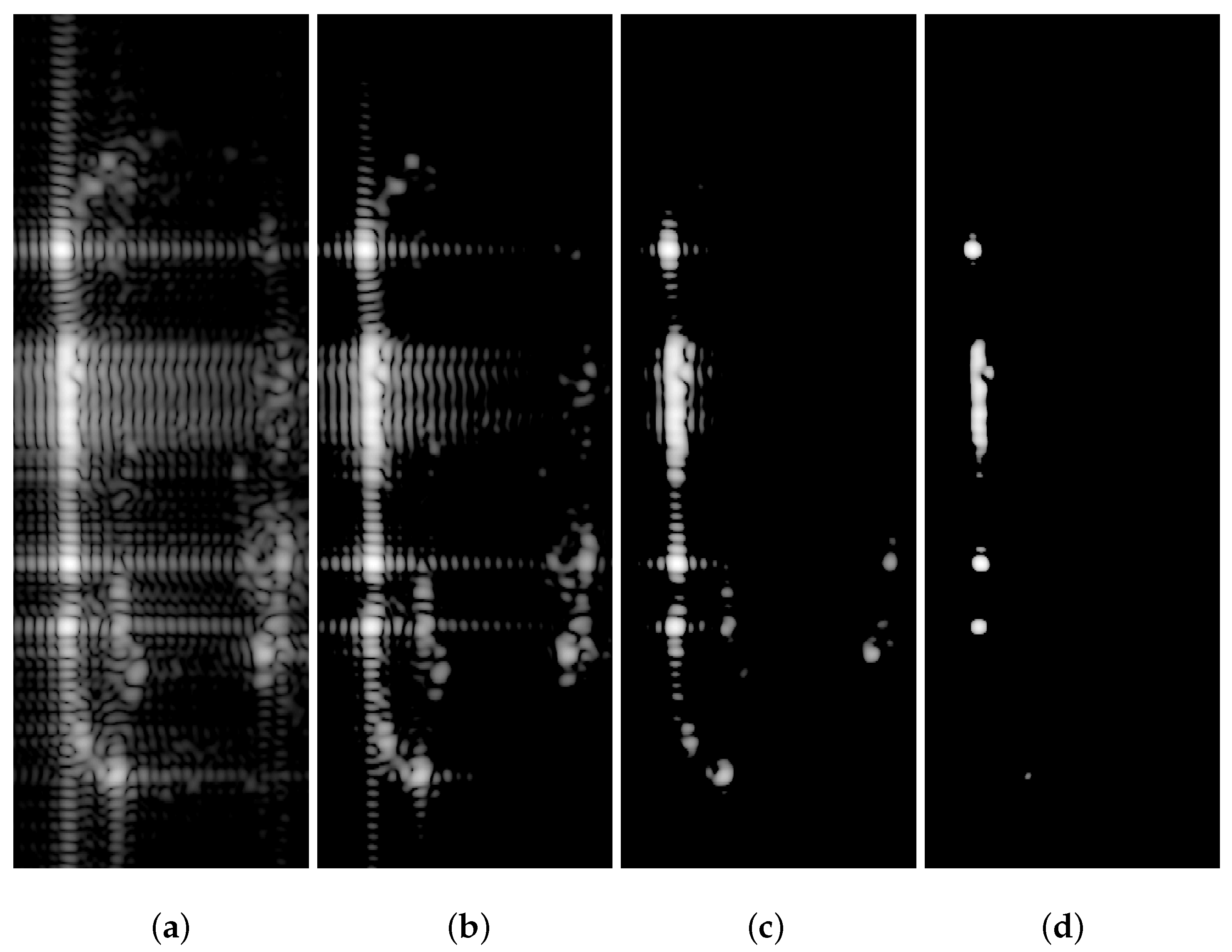
4.2. The Outperformance of Our Weighting Scheme
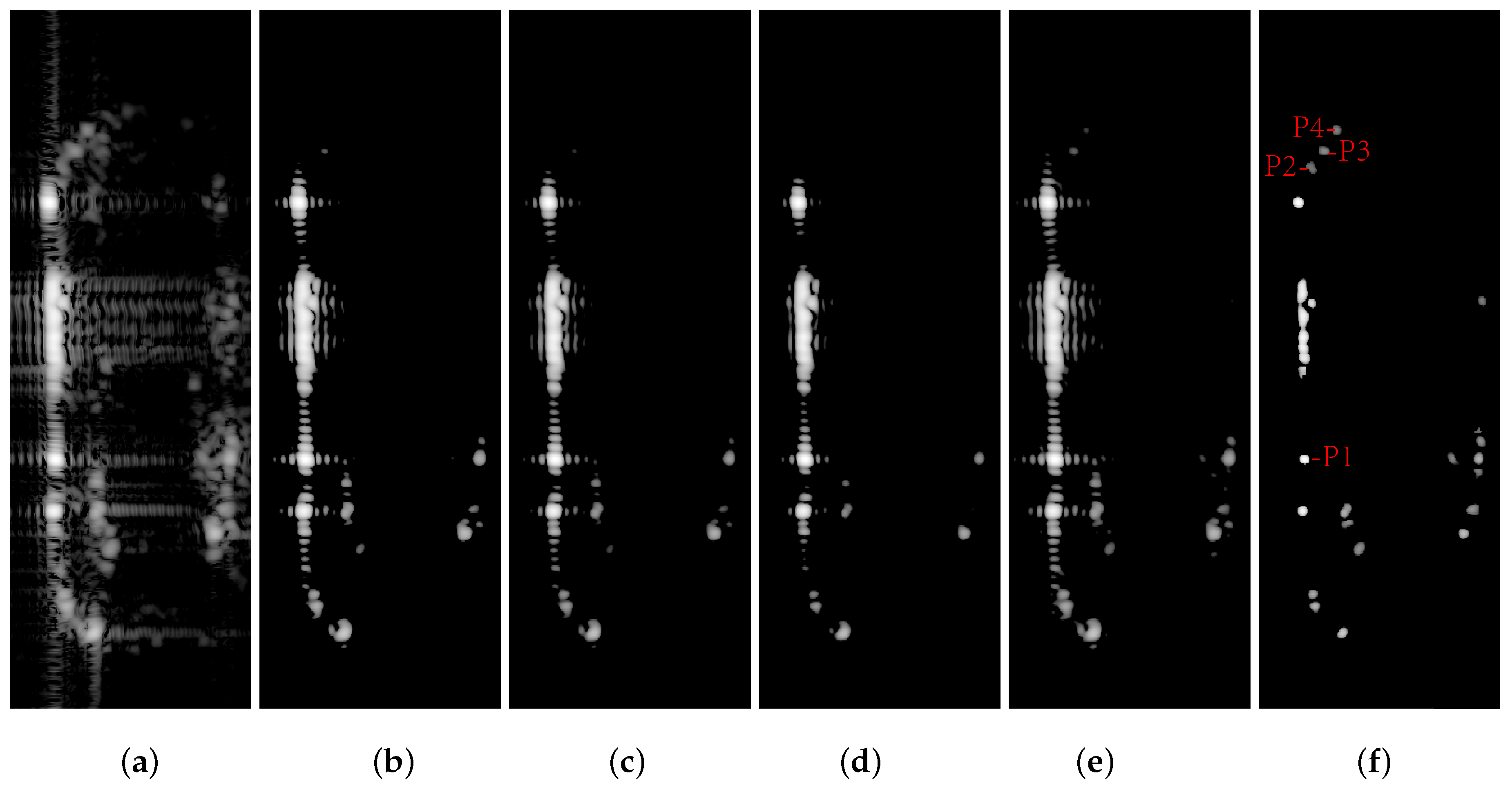
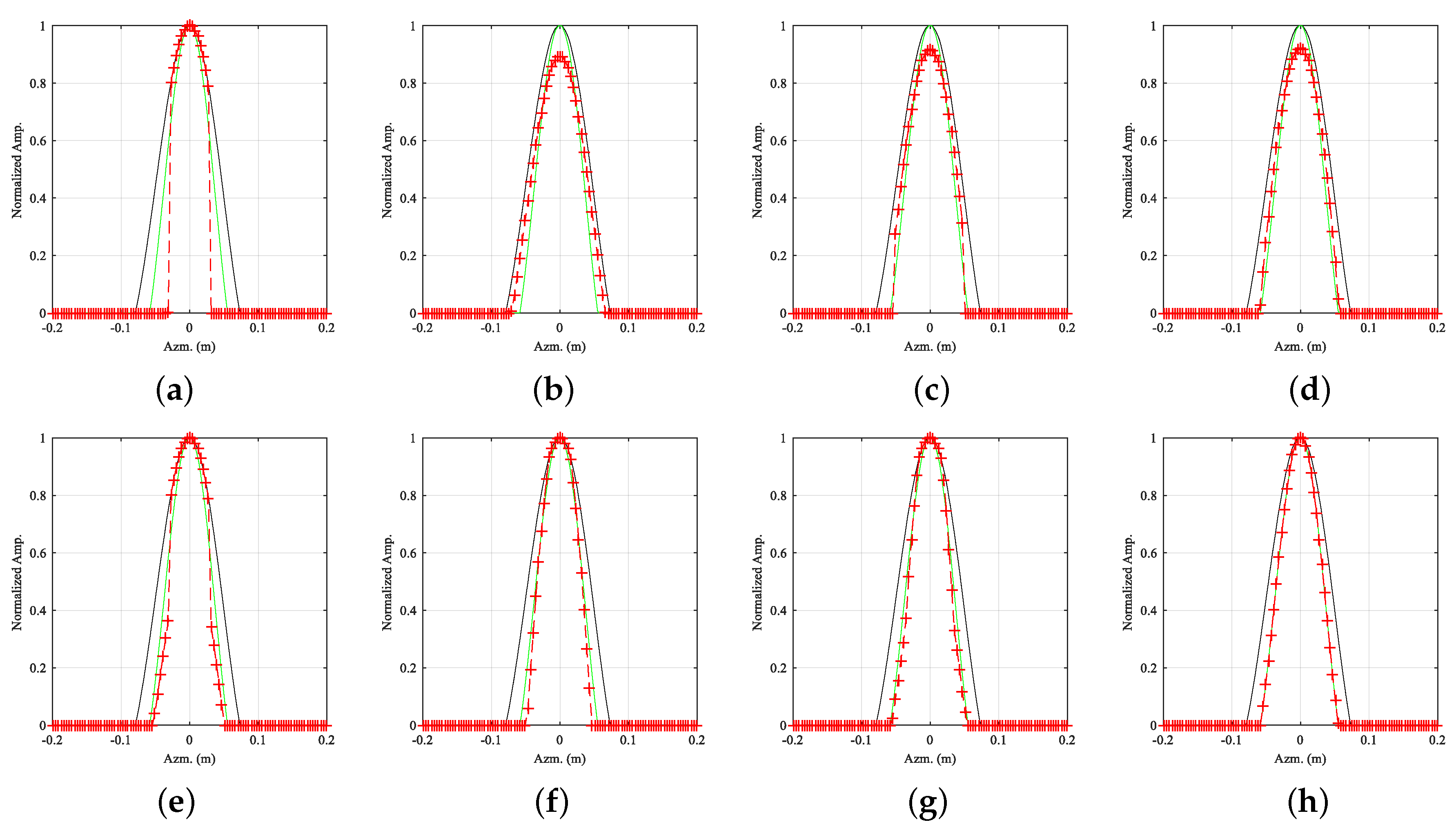
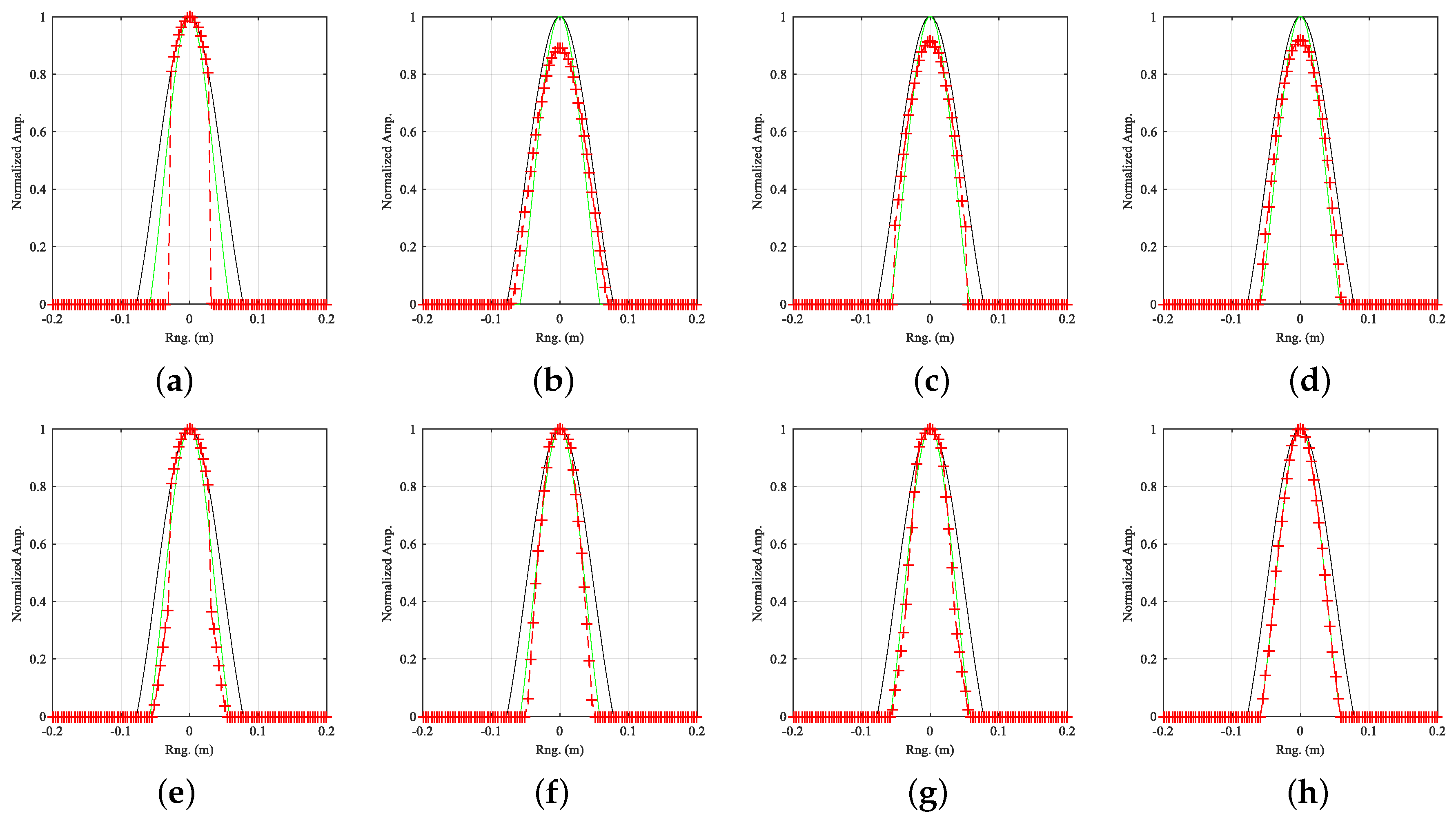
4.3. Undistorted Enhancement Ability of TRUTH Function
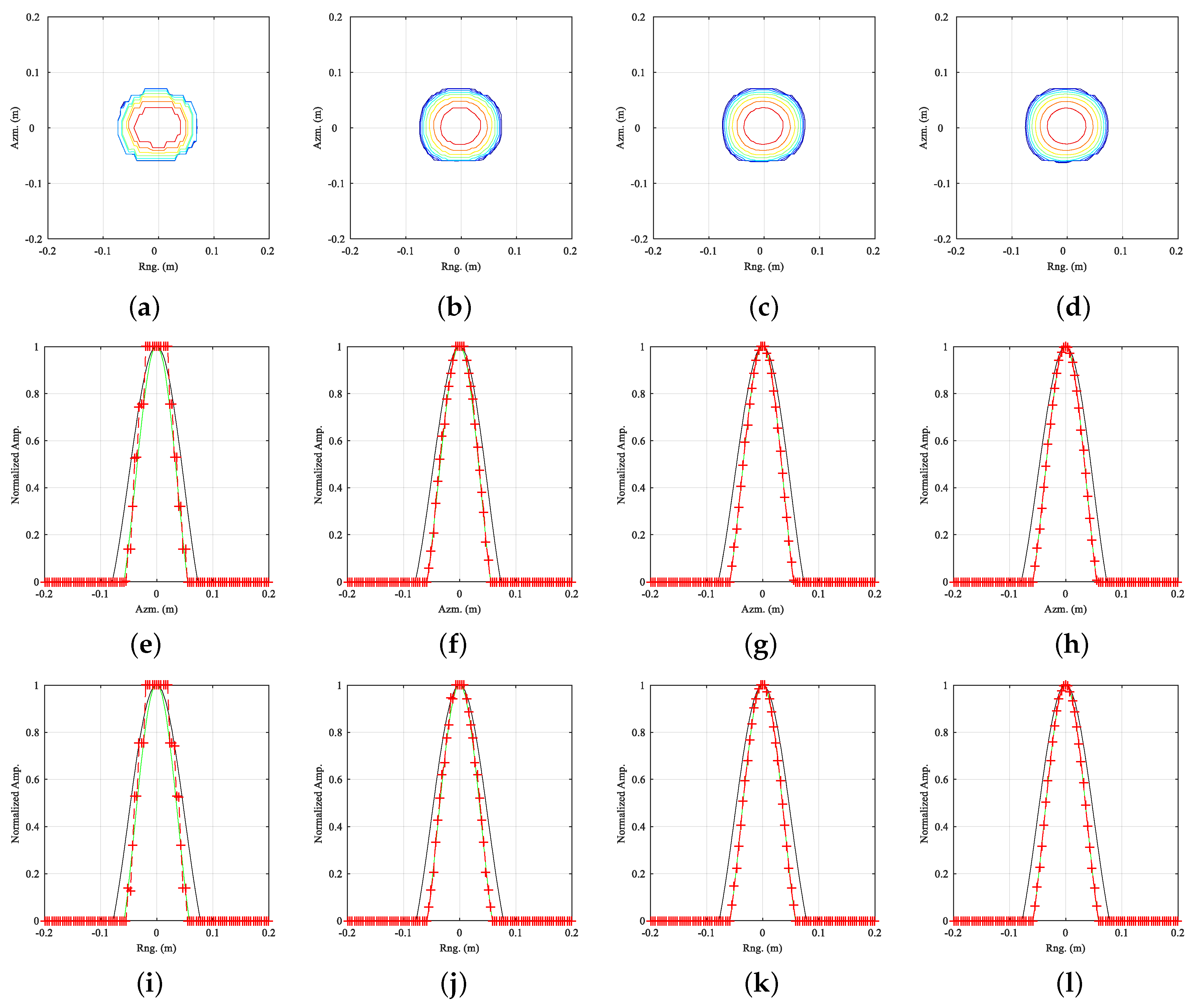
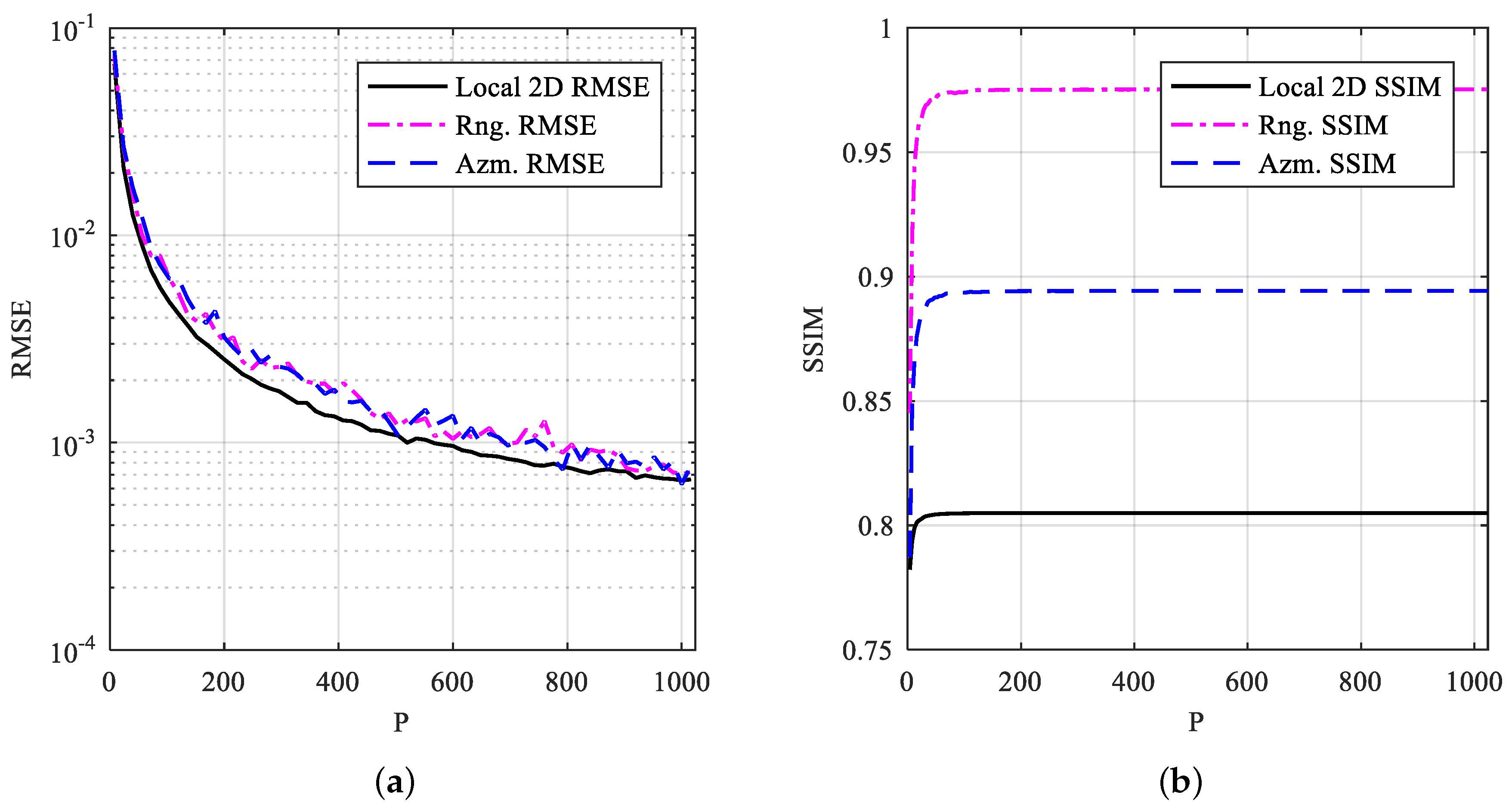
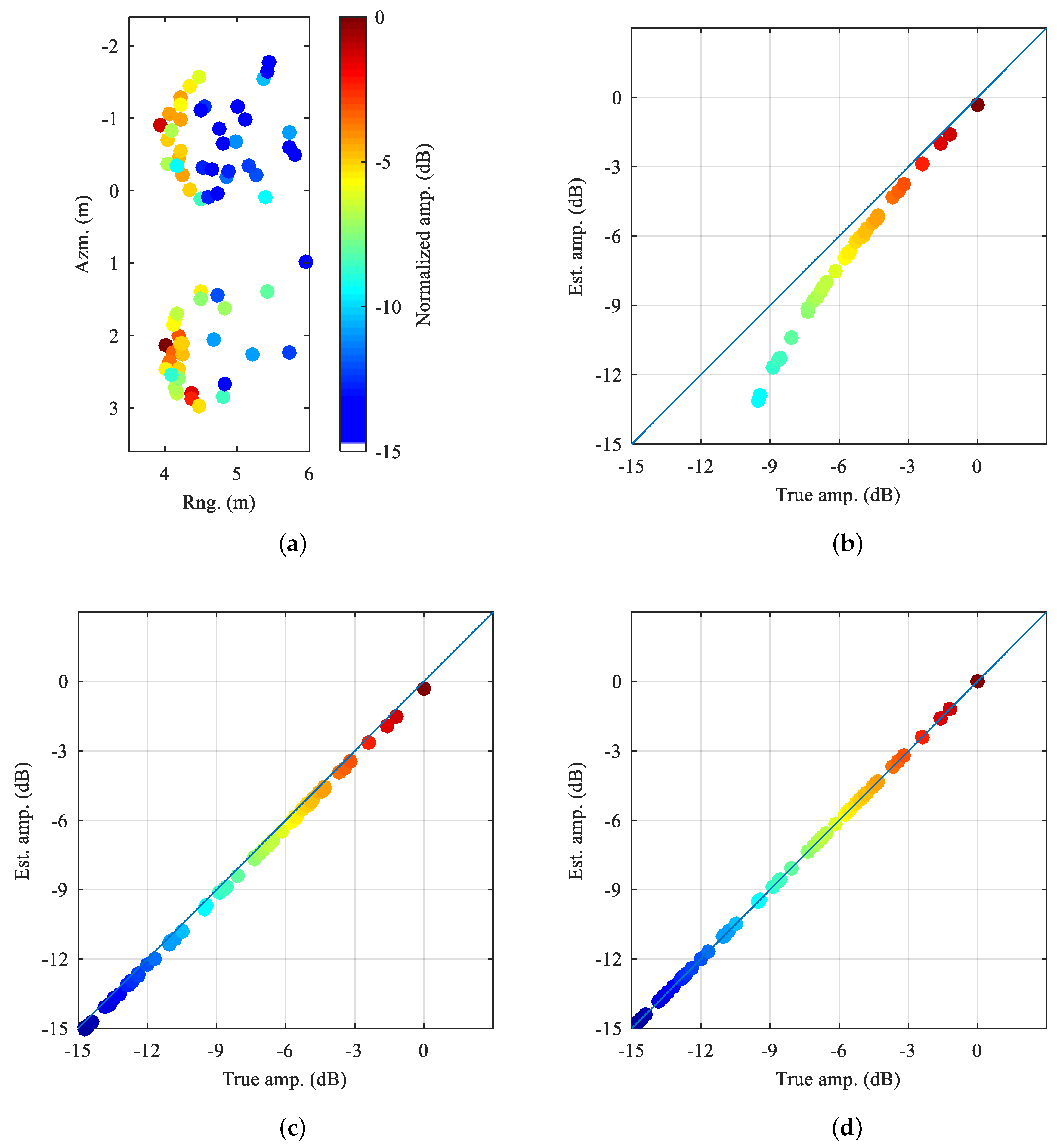
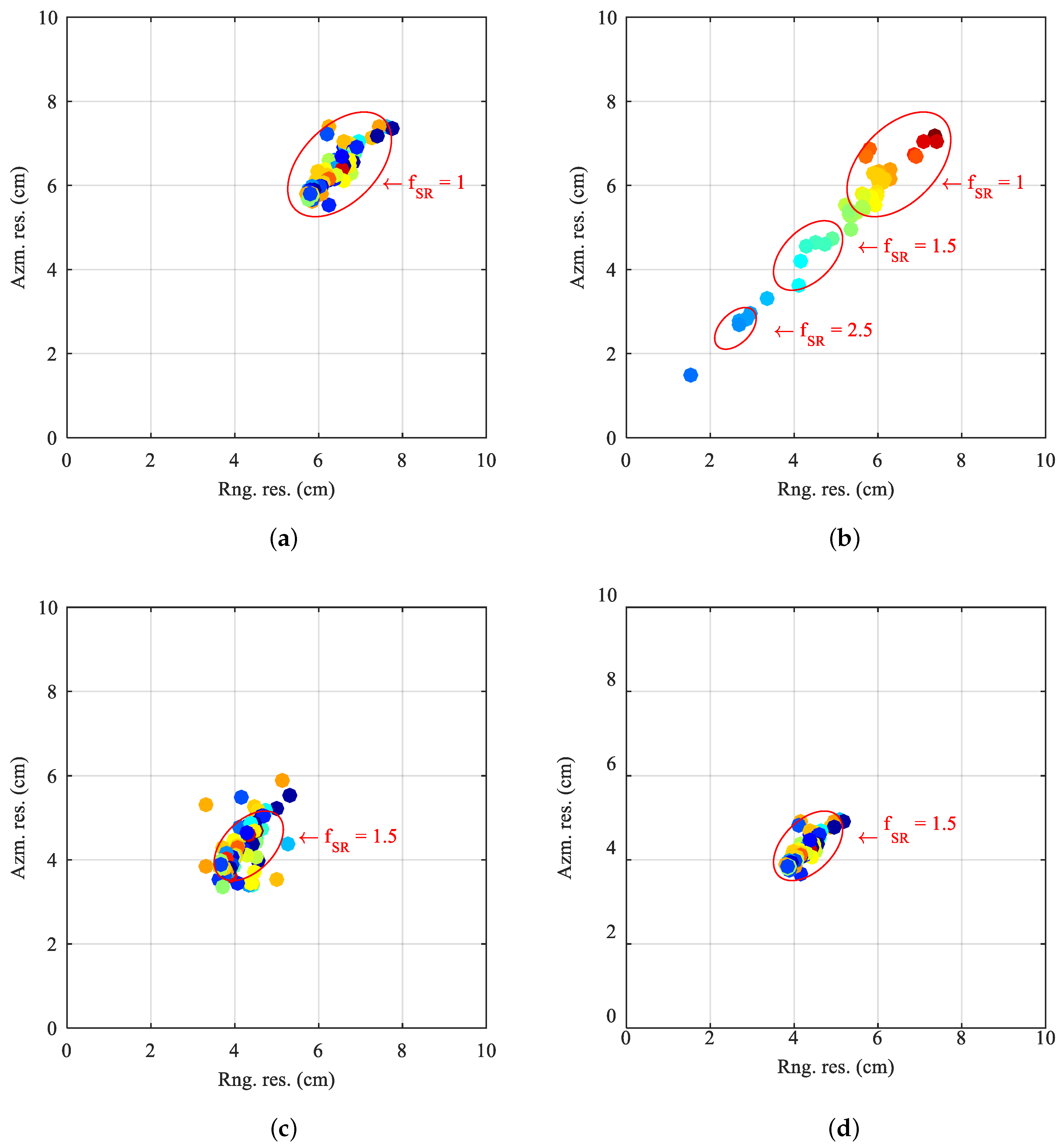
4.4. Consistent Enhancement Ability of MSR Regularization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alland, S.; Stark, W.; Ali, M.; Hegde, M. Interference in automotive radar systems: characteristics, mitigation techniques, and current and future research. IEEE Signal Process Mag. 2019, 36, 45–59. [Google Scholar] [CrossRef]
- Andres, M.; Feil, P.; Menzel, W.; Bloecher, H.L.; Dickmann, J. Analysis of automobile scattering center locations by SAR measurements. In Proceedings of the 2011 IEEE RadarCon (RADAR); 2011; pp. 109–112. [Google Scholar]
- Feger, R.; Haderer, A.; Stelzer, A. Experimental verification of a 77-GHz synthetic aperture radar system for automotive applications. In Proceedings of the 2017 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM); 2017; pp. 111–114. [Google Scholar]
- Wang, C.; Pei, J.; Li, M.; Zhang, Y.; Huang, Y.; Yang, J. Parking information perception based on automotive millimeter wave SAR. In Proceedings of the 2019 IEEE Radar Conference (RadarConf); 2019; pp. 1–6. [Google Scholar]
- Clarke, D.; Andre, D.; Zhang, F. Synthetic aperture radar for lane boundary detection in driver assistance systems. In Proceedings of the 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI); 2016; pp. 238–243. [Google Scholar]
- Wang, R.; Pei, J.; Zhang, Y.; Li, M.; Huang, Y.; Wu, J. An auxiliary parking method based on automotive millimeter wave SAR. In Proceedings of the IGARSS 2019 - 2019 IEEE International Geoscience and Remote Sensing Symposium; 2019; pp. 2503–2506. [Google Scholar]
- Bilik, I.; Longman, O.; Villeval, S.; Tabrikian, J. The rise of radar for autonomous vehicles: signal processing solutions and future research directions. IEEE Signal Processing Mag. 2019, 36, 20–31. [Google Scholar] [CrossRef]
- Laribi, A.; Hahn, M.; Dickmann, J.; Waldschmidt, C. Performance Investigation of Automotive SAR Imaging. In Proceedings of the 2018 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM); 2018; pp. 1–4. [Google Scholar]
- Cetin, M.; Karl, W. Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization. IEEE Trans. Image Process. 2001, 10, 623–631. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.C.; Hong, W.; Wu, Y.R. Sparse microwave imaging: principles and applications. Sci. China Inf. Sci. 2012, 55, 1722–1754. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, W.; Quan, X.; Ling, W.K.; Zhang, Z. Data-driven sampling pattern design for sparse spotlight SAR imaging. Electron. Lett. 2022, 58, 920–923. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, J.; Zhang, B.; Wu, Y. RMA-based azimuth-range decouple method for automotive SAR sparse imaging. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3480–3492. [Google Scholar] [CrossRef]
- Bi, H.; Bi, G.; Zhang, B.; Hong, W. Complex-image-based sparse SAR imaging and its equivalence. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5006–5014. [Google Scholar] [CrossRef]
- Wei, Z.H.; Zhang, B.; Xu, Z.; Han, B.; Hong, W.; Wu, Y. An improved SAR imaging method based on nonconvex regularization and convex optimization. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1580–1584. [Google Scholar]
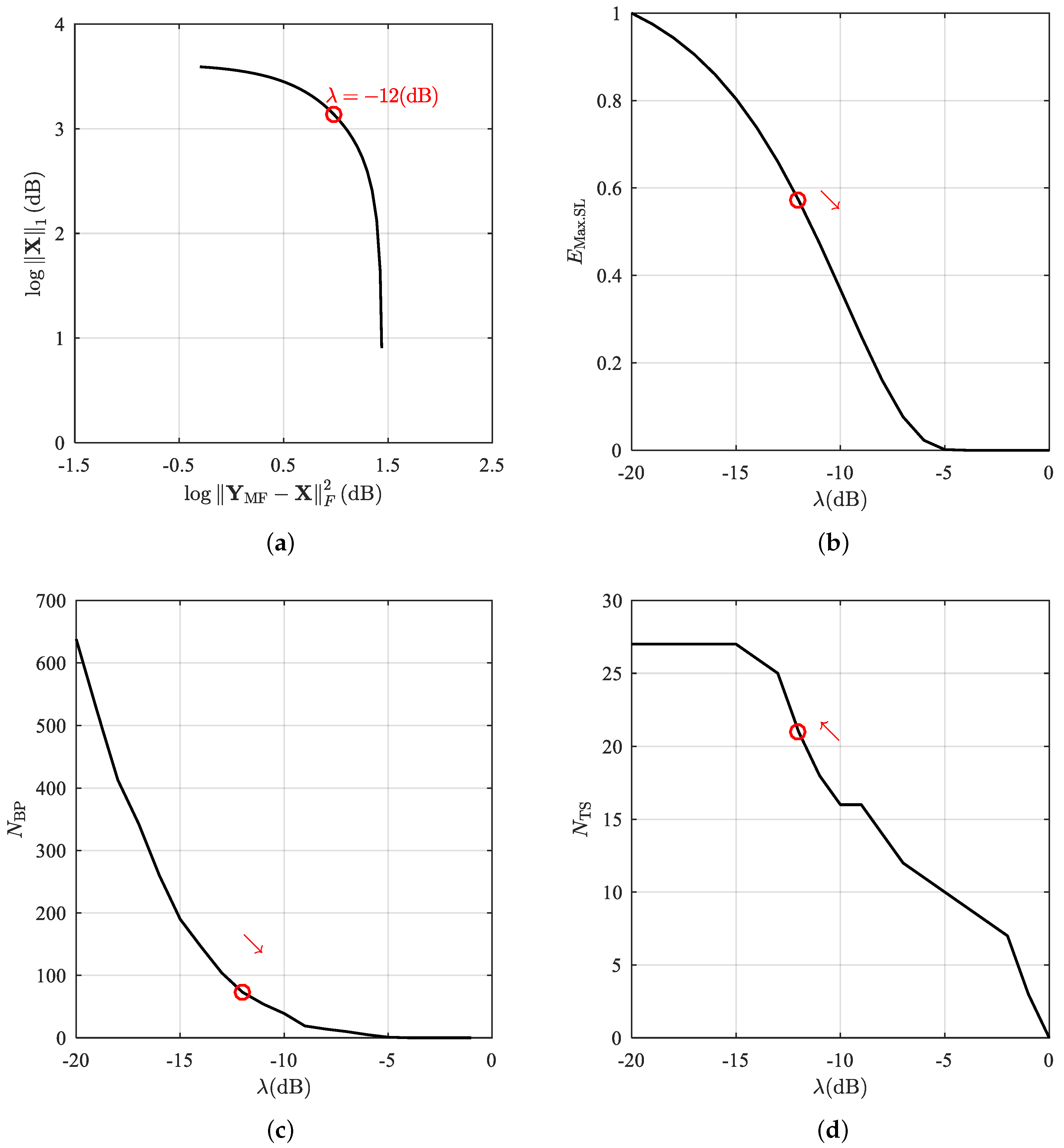
- Batu, O.; Cetin, M. Parameter selection in sparsity-driven SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 3040–3050. [Google Scholar] [CrossRef]
- Liu, M.; Xu, Z.; Xu, Z.; Wei, Z.; Zhang, B.; Wu, Y. Improved adaptive parameter estimation for sparse SAR imaging based on complex image and azimuth-range decouple. In Proceedings of the IGARSS 2019 - 2019 IEEE International Geoscience and Remote Sensing Symposium; 2019; pp. 819–822. [Google Scholar]
- Fan, Y.Z.; Wang, K.; Li, J.; Zhou, G.; Zhang, B.; Wu, Y. L-Hypersurface based parameters selection in composite regularization models with application to SAR and TomoSAR imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8297–8309. [Google Scholar]
- Candès, E.; Wakin, M.; Boyd, S. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar]
- Zhang, S.H.; Liu, Y.; Li, X.; Hu, D. Enhancing ISAR image efficiently via convolutional reweighted ℓ1 minimization. IEEE Trans. Image Process. 2021, 30, 4291–4304. [Google Scholar]
- Ni, J.C.; Luo, Y.; Wang, D.; Liang, J.; Zhang, Q. Saliency-based SAR target detection via convolutional sparse feature enhancement and Bayesian inference. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar]
- Krishnan, D.; Fergus, R. Fast image deconvolution using hyper-Laplacian priors. In Proceedings of the Advances in Neural Information Processing Systems 22. MIT Press; 2009; pp. 1033–1041. [Google Scholar]
- Selesnick, I. Sparse regularization via convex analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar]
- Fan, J. Comments on «Wavelets in statistics: a review» by A. Antoniadis. J. Ital. Statist. Soc. 1997, 6, 131. [Google Scholar]
- Castillo-Rubio, C.; Llorente-Romano, S.; Burgos-Garcia, M. Robust SVA method for every sampling rate condition. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 571–580. [Google Scholar]
- Antoniadis, A. Wavelets in statistics: a review. J. Ital. Statist. Soc. 1997, 6, 97–130. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar]
- Xu, Z.B.; Chang, X.Y.; Xu, F.M.; Zhang, H. L1/2 regularization: a thresholding representation theory and a fast solver. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1013–1027. [Google Scholar]
- Clyde, M.; Parmigiani, G.; Vidakovic, B. Multiple shrinkage and subset selection in wavelets. Biometrika 1998, 85, 391–401. [Google Scholar]
- Moulin, P.; Liu, J. Analysis of multiresolution image denoising schemes using generalized Gaussian and complexity priors. IEEE Trans. Inf. Theory. 1999, 45, 909–919. [Google Scholar]
- Zhu, X.X.; He, F.; Ye, F.; Dong, Z.; Wu, M.Q. Sidelobe suppression with resolution maintenance for SAR images via sparse representation. Sensors 2018, 5, 1589. [Google Scholar]
- Zou; Hui. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429.
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar]
- Breiman, L. Better subset regression using the nonnegative garrote. Technometrics 1995, 37, 373–384. [Google Scholar]
- Kan, T.; xin, G.; xiaowei, L.; zhongshan, L. Implementation of Real-time Automotive SAR Imaging. In Proceedings of the 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM); 2020; pp. 1–4. [Google Scholar]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar]
- Zhang, Y.; Tuo, X.; Huang, Y.; Yang, J. A TV forward-looking super-resolution imaging method based on TSVD strategy for scanning radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4517–4528. [Google Scholar]
- Horé, A.; Ziou, D. Image quality metrics: PSNR vs. In SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition; 2010; pp. 2366–2369. [Google Scholar]
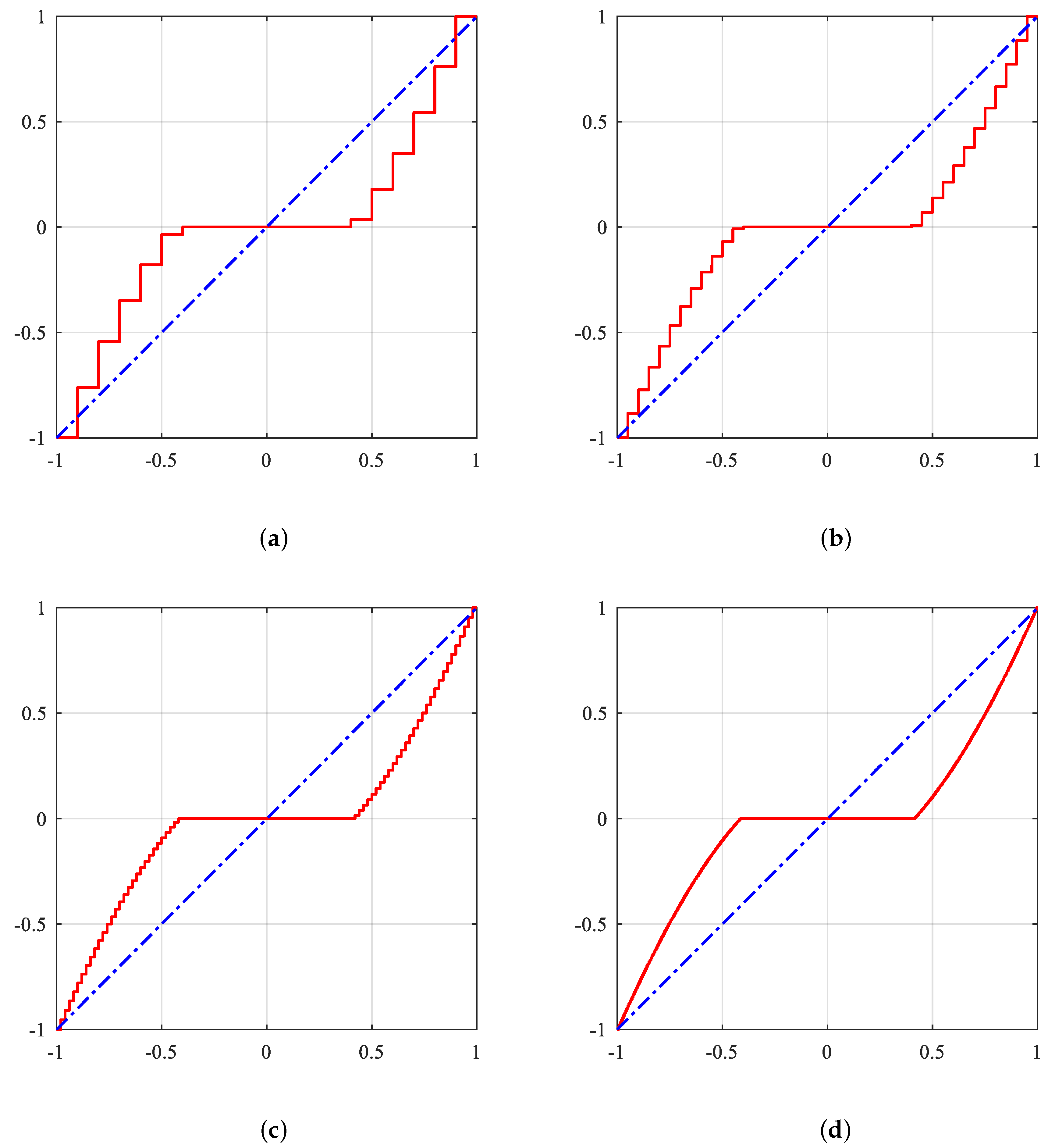
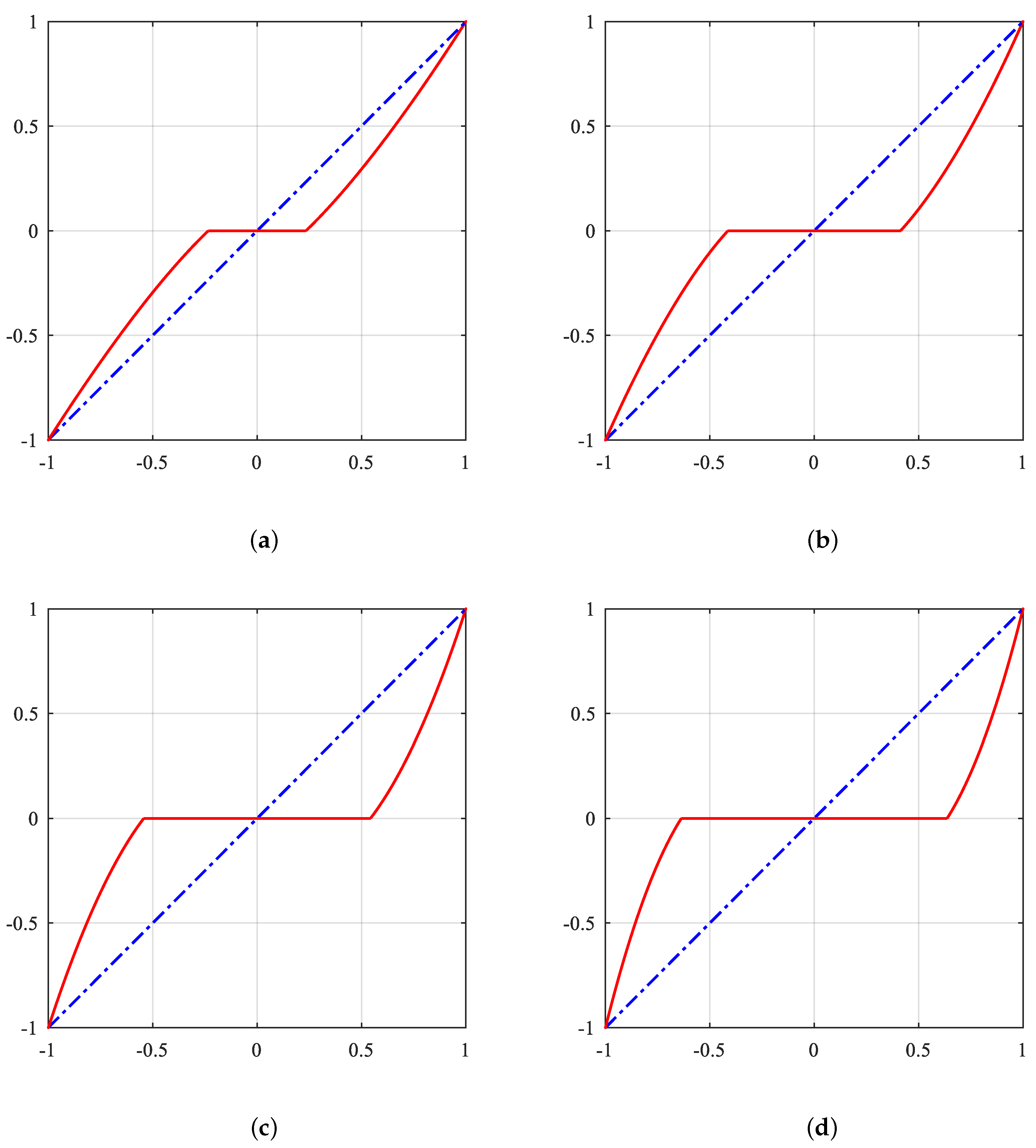


| Optimization Methods | Reweighting Norm | Equivalent Penalty | Adaptive Lasso * |
|---|---|---|---|
| Problem Formula | |||
| Weighting Scheme 1(WS1) | (When allowed to expand) | ||
| Weighting Scheme 2(WS2) | (When allowed to be neglected) | ||
| Weighting Scheme 3(WS3) | (When allowed to be neglected) | ||
| Weighting Scheme 4(WS4) | (When allowed to be neglected) | ||
| Weighting Scheme 5(WS5) | (When allowed to be neglected) | ||
| Weighting Scheme 6(WS6) | (When allowed to be neglected) |
| Method | RMA | SVA | WS1 | WS2 | WS3 | WS6 | WS7 | Ours |
|---|---|---|---|---|---|---|---|---|
| Figure label | Figure 9(a) | Figure 10(a) | Figure 9(c) | Figure 10(b) | Figure 10(c) | Figure 10(d) | Figure 10(e) | Figure 10(f) |
| IE | 5.22* | 3.85 | 0.54 | 0.61 | 0.61 | 0.42 | 0.78 | 0.20* |
| IC | 1.32 | 1.83 | 5.50 | 5.19 | 5.01 | 6.34 | 4.53 | 9.35 |
| ENL | 9.41E-2 | 5.30E-2 | 1.48E-2 | 1.59E-2 | 1.84E-2 | 1.23E-2 | 1.85E-2 | 5.60E-3 |
| RaRes(dB) | 6.29 | 7.28 | 9.64 | 9.51 | 9.23 | 10.01 | 9.21 | 11.56 |
| TBR(dB) | 7.86 | 9.24 | 13.64 | 13.20 | 11.71 | 15.23 | 12.37 | Inf |
| 638 | 237 | 73 | 86 | 93 | 54 | 104 | 0 | |
| 27 | 27 | 21 | 23 | 23 | 18 | 24 | 27 | |
| (dB) | -13.50 | -22.30 | -19.52 | -18.77 | -16.33 | -22.57 | -17.22 | -Inf |
| (dB) | -7.34 | -10.31 | -9.71 | -9.45 | -8.17 | -10.98 | -9.26 | -Inf |
| (dB) | -15.47 | -20.38 | -18.99 | -18.53 | -16.52 | -21.19 | -17.58 | -Inf |
| (dB) | -8.92 | -11.19 | -10.03 | -9.91 | -9.12 | -10.85 | -9.96 | -Inf |
| Threshold | Hard | Soft | Half | Garrote+ | Firm | Mix | SCAD | TRUTH |
|---|---|---|---|---|---|---|---|---|
| Peak Bias(dB) | 0* | 0.49* | 0.38 | 0.36 | 0 | 0 | 0 | 0 |
| Local 2D RMSE | 0.2437 | 0.1572 | 0.0898 | 0.0788 | 0.0885 | 0.1174 | 0.0639 | 0.0011 |
| Rng. RMSE | 0.0885 | 0.0671 | 0.0534 | 0.0503 | 0.0509 | 0.0620 | 0.0453 | 0.0015 |
| Azm. RMSE | 0.0881 | 0.0643 | 0.0524 | 0.0492 | 0.0493 | 0.0614 | 0.0445 | 0.0014 |
| Local 2D SSIM | 0.7775 | 0.7750 | 0.7949 | 0.7983 | 0.7904 | 0.7908 | 0.7994 | 0.8050 |
| Rng. SSIM | 0.8312 | 0.8662 | 0.9264 | 0.9427 | 0.9096 | 0.8990 | 0.9476 | 0.9753 |
| Azm. SSIM | 0.7713 | 0.8088 | 0.8636 | 0.8684 | 0.8417 | 0.8304 | 0.8719 | 0.8943 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





