Submitted:
01 March 2025
Posted:
04 March 2025
You are already at the latest version
Abstract
Currently in order to calculate the number of covalent bonds for cyclic unsaturated organic molecules there are equations that include the index of hydrogen deficiency (IHD), a σ-bonds derivation from the Euler characteristic for planar graphs and other empirical formulations. However the IHD which is also known as the degree of unsaturation (DOU) requires to assign a numerical value for the pi(π) bonds and rings without knowing their precise number in a molecule, and all the other equations that are used to determine the numerical value of sigma(σ) and single bonds are made up of variables such as the number of rings, double and triple bonds. In this manuscript we present a novel type of mathematical model that was deduced by using chemical graph theory and can be applied to calculate the value of covalent bonds and rings for cyclic organic molecules with double or triple bonds only knowing the number of atoms, their corresponding valences and a new chemical concept which we called total unsaturation (TU) that represents the degree of unsaturation expressed as a percentage. The objective of this study is to highlight a deeper mathematical relationship formed by multiple structural elements of a molecule in order to enhance the correlations between graph theory and organic chemistry from a different perspective that is primarly focused on the number of bonds.
Keywords:
1. Introduction
2. Materials and Methods
3. Results and Discussion
- 1)
-
For cyclic unsaturated molecules with double bonds in whichandand
- 2)
-
For cyclic unsaturated molecules with double bonds in whichandand
- 3)
-
For cyclic unsaturated molecules with triple bonds in whichandand
- 4)
-
For cyclic unsaturated molecules with triple bonds in whichandand
3.1. Cyclic unsaturated molecules with double bonds in which
3.1.1. First example
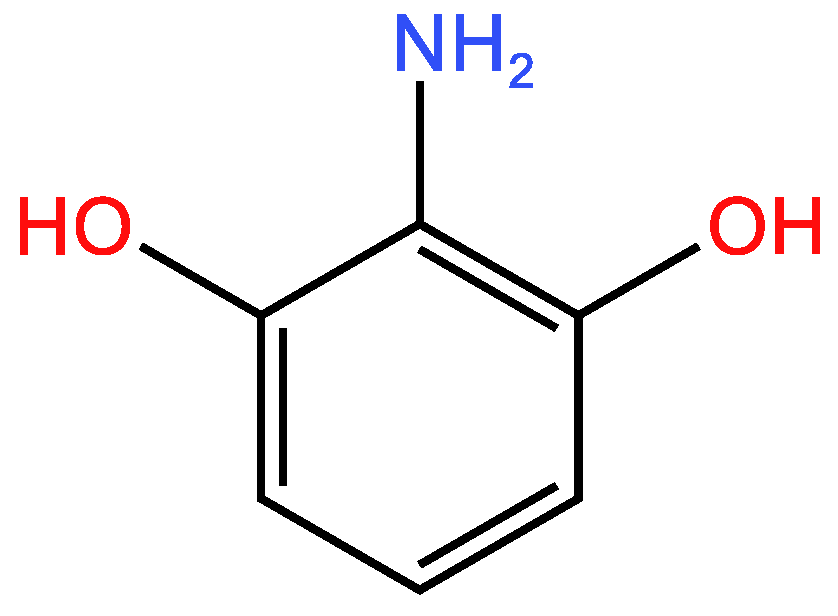
| Examples of Unsaturated Cyclic Molecules with double bonds |
σ-bonds |
Single bonds |
π-bonds and double bonds |
Ring/Rings |
| 12 | 9 | 3 ; 3 | 1 | |
| 30 | 24 | 6 ; 6 | 2 | |
| 29 | 23 | 6 ; 6 | 2 | |
| 38 | 29 | 9 ; 9 | 3 | |
| 33 | 24 | 9 ; 9 | 3 | |
| 48 | 36 | 12 ; 12 | 4 | |
| 57 | 45 | 12 ; 12 | 4 | |
| 67 | 52 | 15 ; 15 | 5 | |
| 57 | 42 | 15 ; 15 | 5 | |
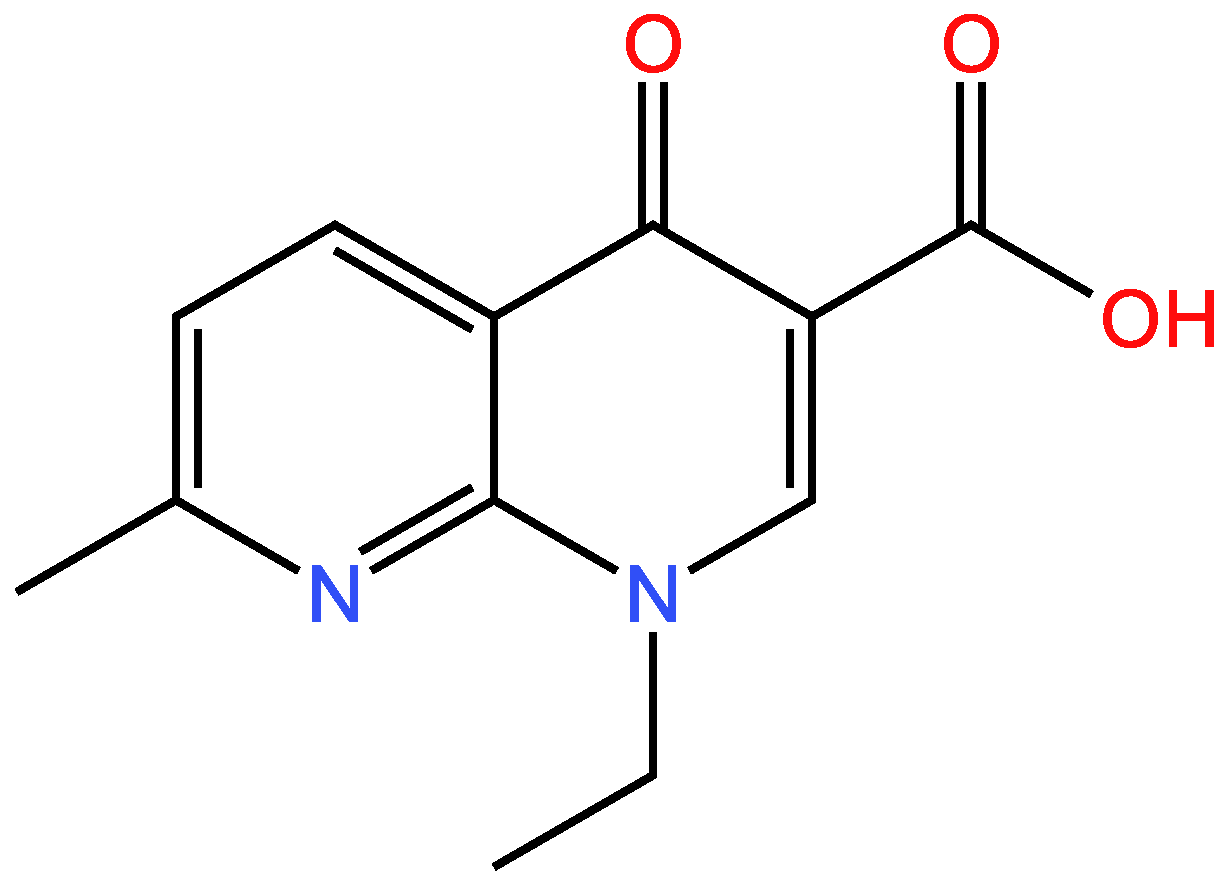
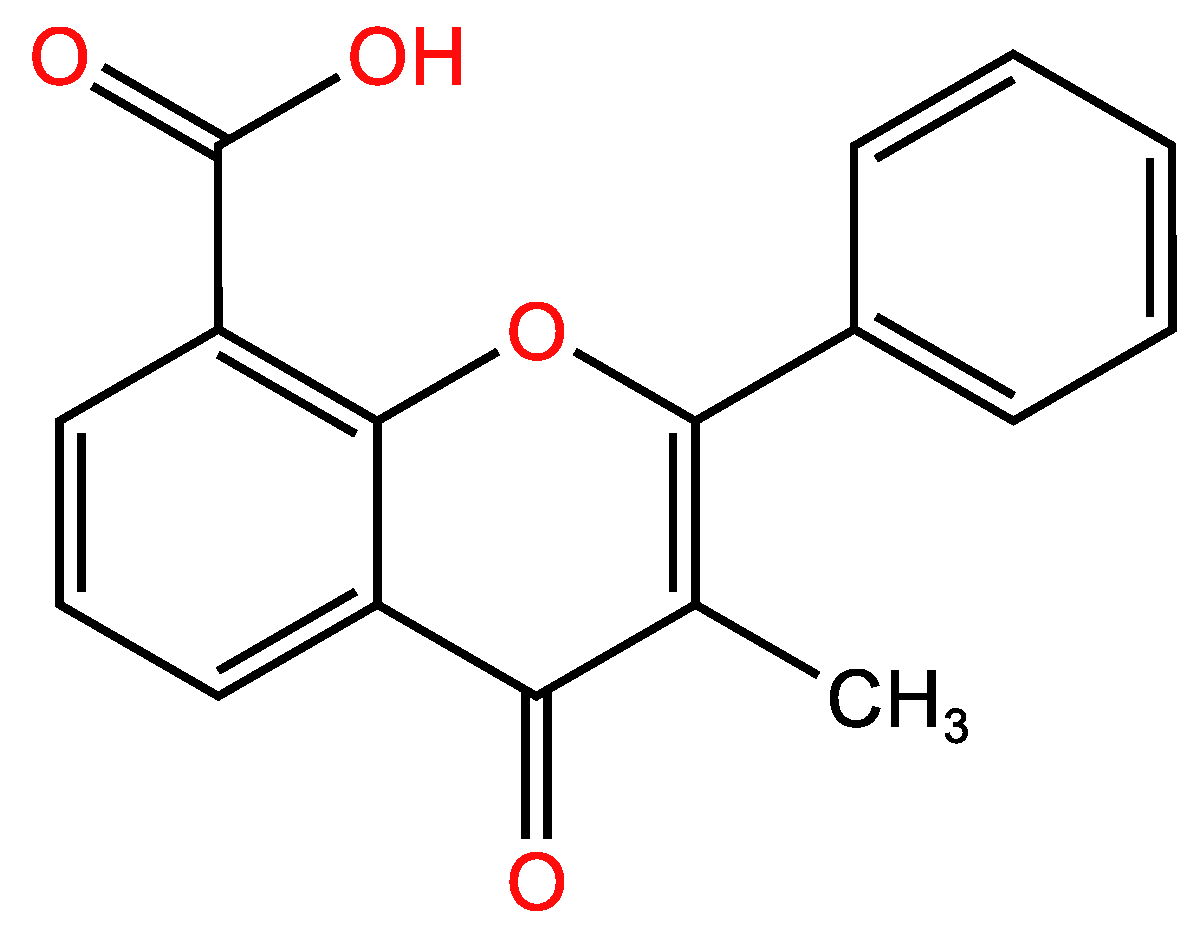
3.1.2. Second example
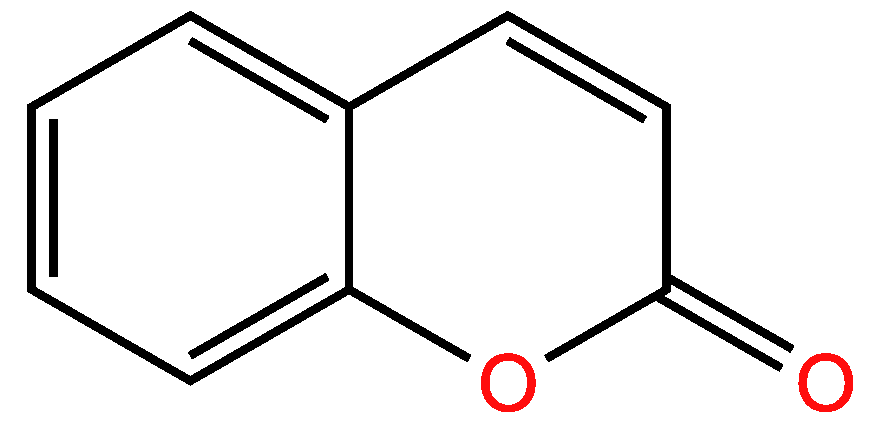
| Examples of Unsaturated Cyclic Molecules with double bonds |
σ-bonds |
Single bonds |
π-bonds and double bonds |
Ring/Rings |
| 19 | 14 | 5 ; 5 | 2 | |
| 38 | 28 | 10 ; 10 | 4 | |
| 36 | 26 | 10 ; 10 | 4 | |
| 55 | 40 | 15 ; 15 | 6 | |
| 93 | 78 | 15 ; 15 | 6 | |
| 86 | 66 | 20 ; 20 | 8 | |
| 88 | 68 | 20 ; 20 | 8 | |
| 122 | 97 | 25 ; 25 | 10 | |
| 110 | 85 | 25 ; 25 | 10 | |
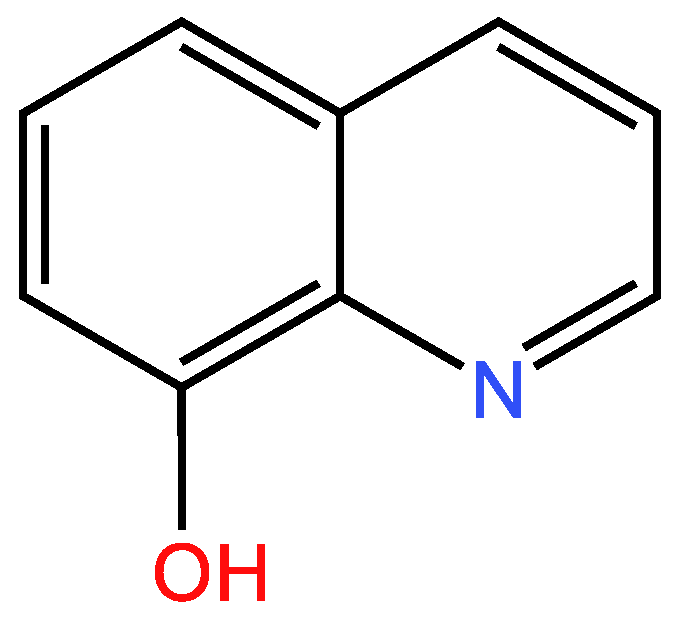
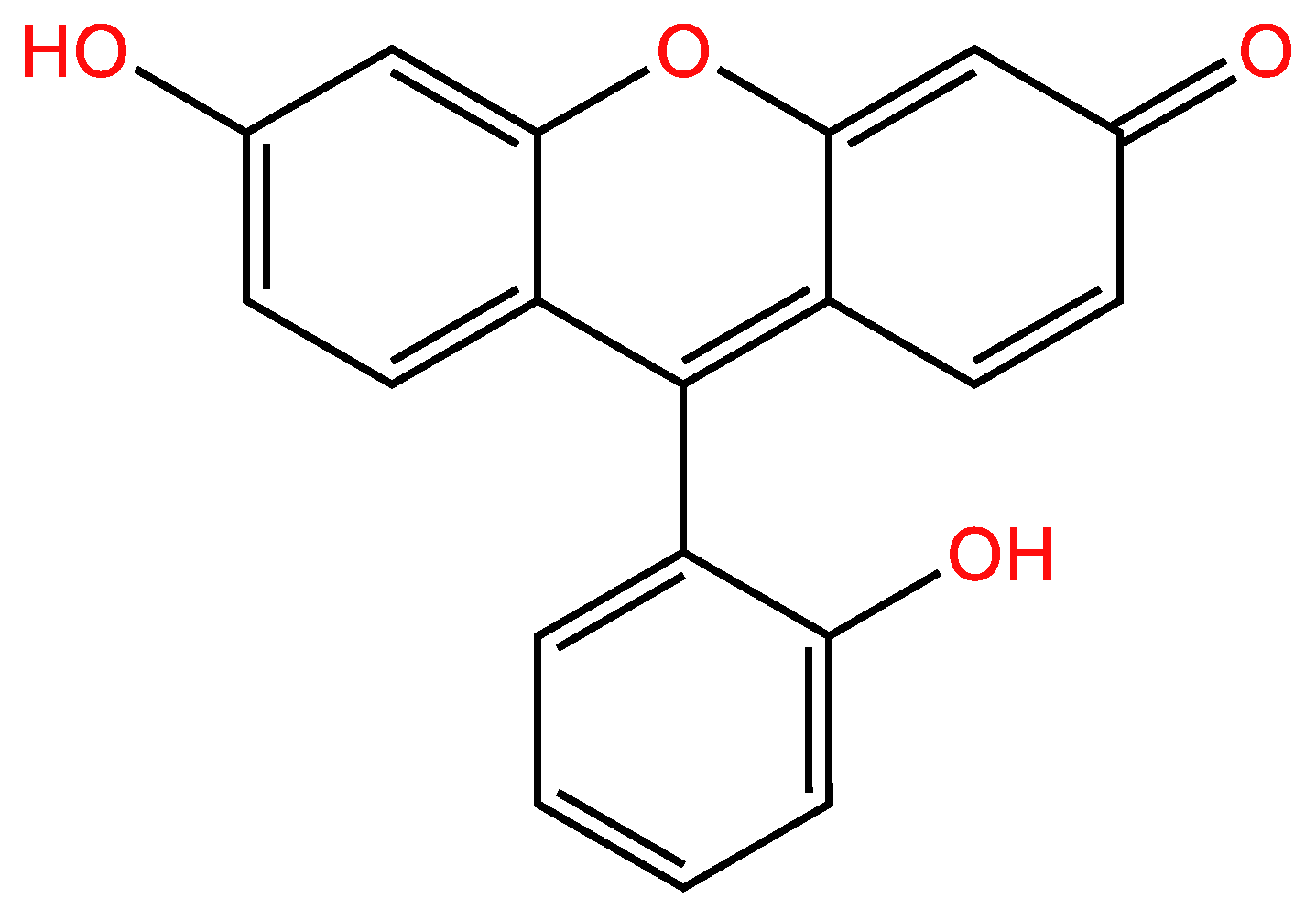
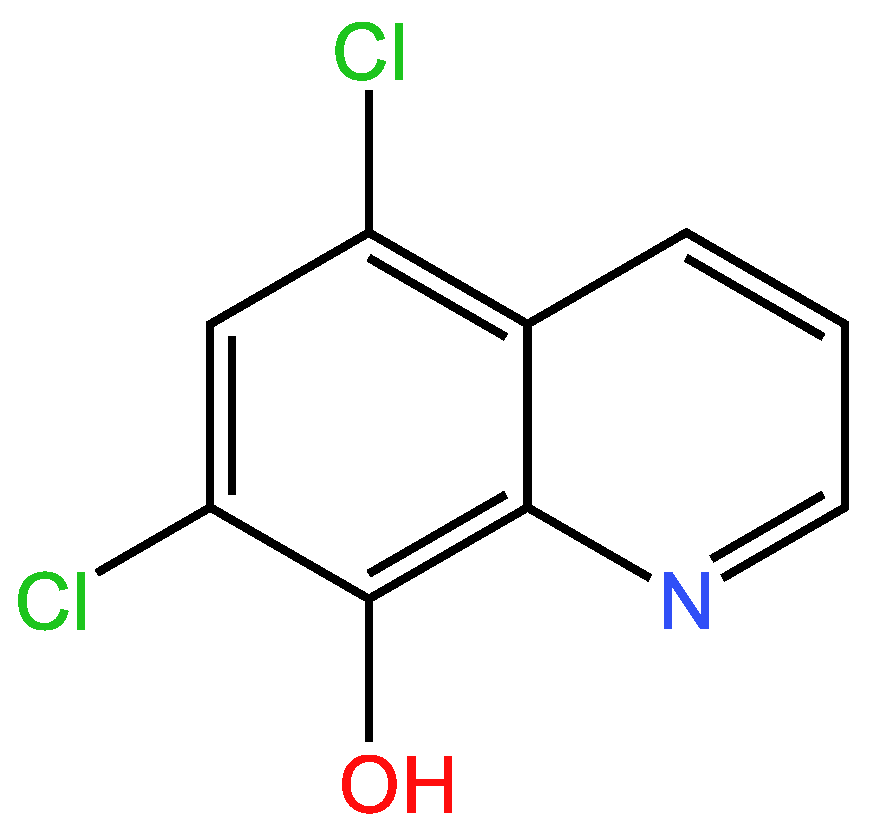
3.2. Cyclic unsaturated molecules with double bonds in which
3.2.1. First example
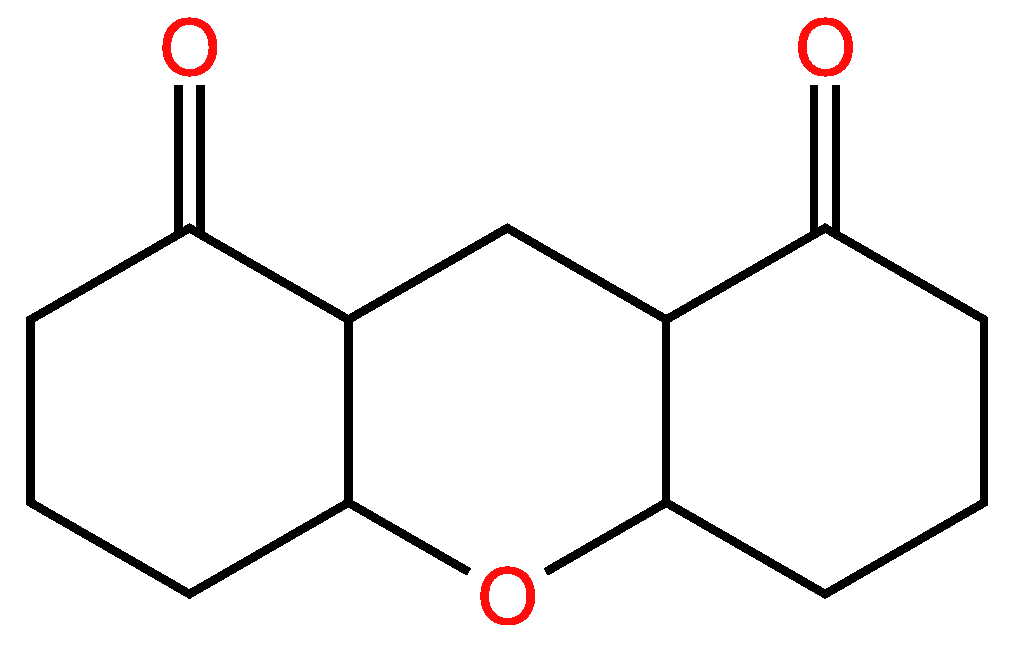
| Examples of Unsaturated Cyclic Molecules with double bonds |
σ-bonds |
Single bonds |
π-bonds and double bonds |
Ring/Rings |
| 38 | 36 | 2 ; 2 | 3 | |
| 36 | 34 | 2 ; 2 | 3 | |
| 37 | 35 | 2 ; 2 | 3 | |
| 67 | 63 | 4 ; 4 | 6 | |
| 71 | 67 | 4 ; 4 | 6 | |
| 133 | 127 | 6 ; 6 | 9 | |
| 125 | 119 | 6 ; 6 | 9 | |
| 171 | 163 | 8 ; 8 | 12 | |
| 175 | 167 | 8 ; 8 | 12 | |
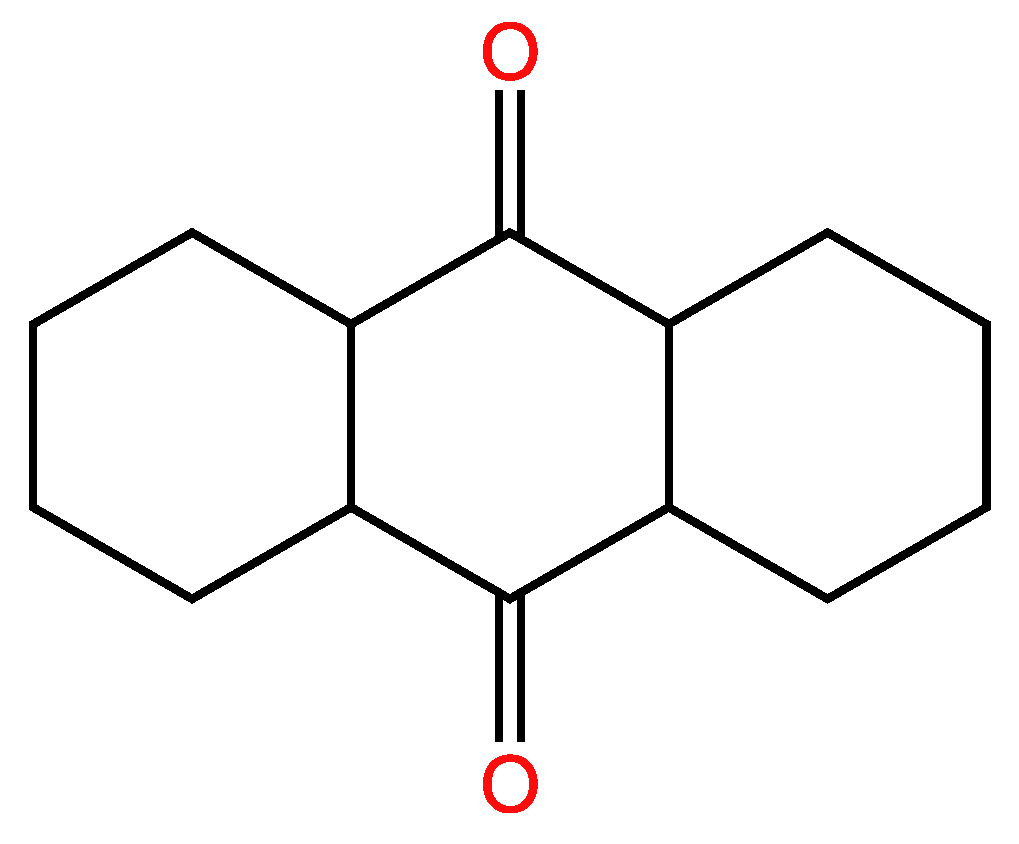
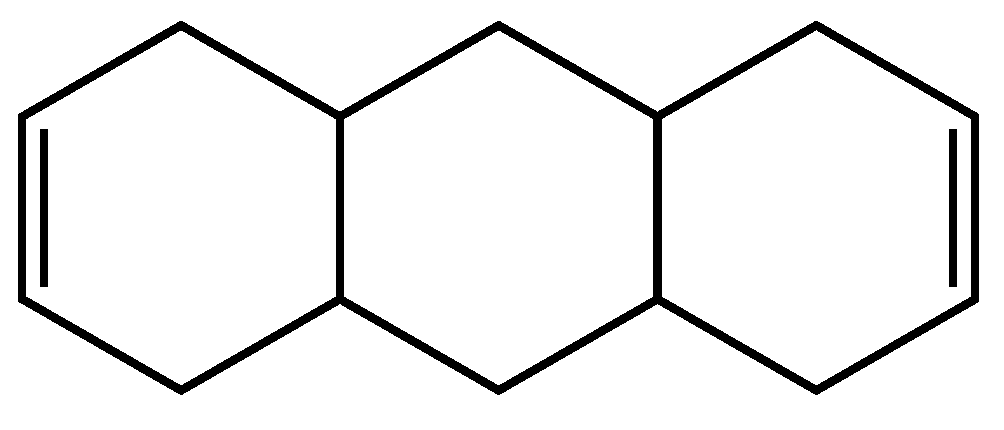
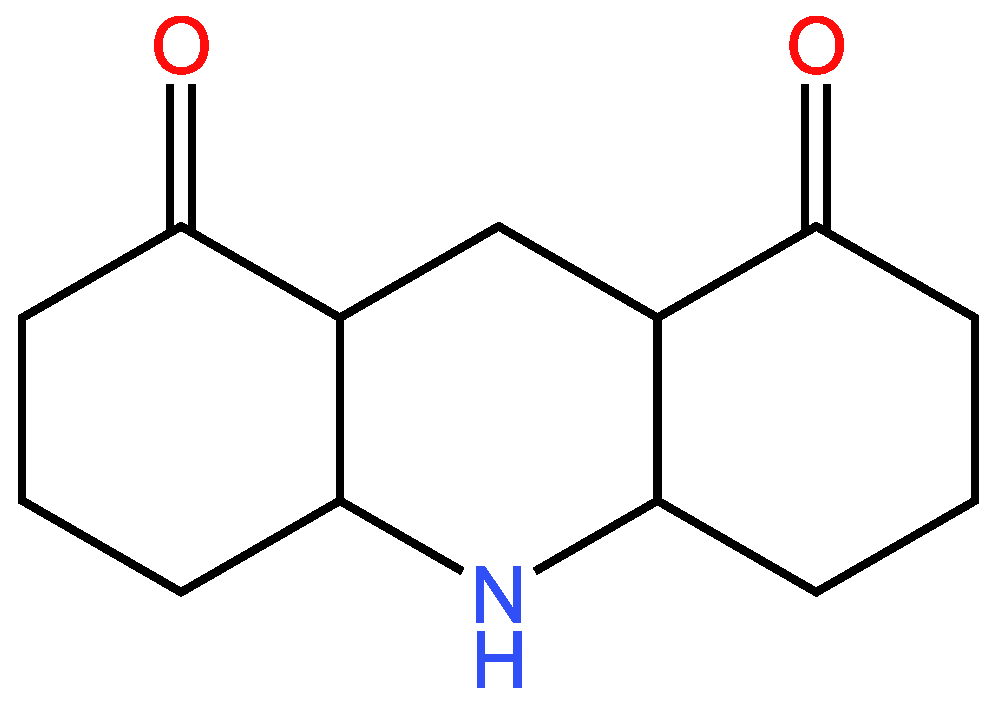
3.2.2. Second example
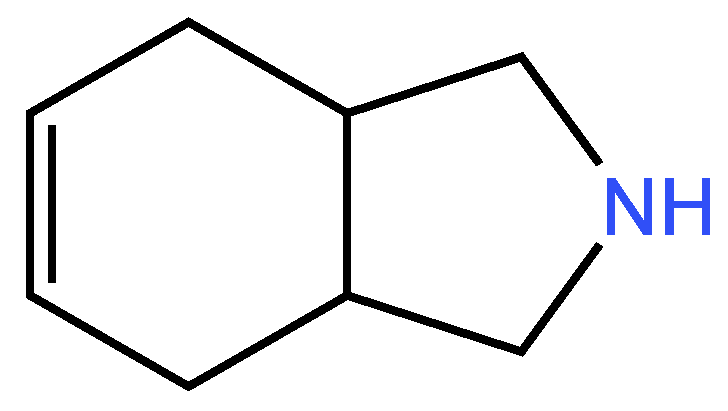
| Examples of Unsaturated Cyclic Molecules with double bonds |
σ-bonds |
Single bonds |
π-bonds and double bonds |
Ring/Rings |
| 22 | 21 | 1 ; 1 | 2 | |
| 32 | 31 | 1 ; 1 | 2 | |
| 26 | 25 | 1 ; 1 | 2 | |
| 56 | 54 | 2 ; 2 | 4 | |
| 63 | 61 | 2 ; 2 | 4 | |
| 71 | 68 | 3 ; 3 | 6 | |
| 95 | 92 | 3 ; 3 | 6 | |
| 87 | 83 | 4 ; 4 | 8 | |
| 90 | 86 | 4 ; 4 | 8 | |
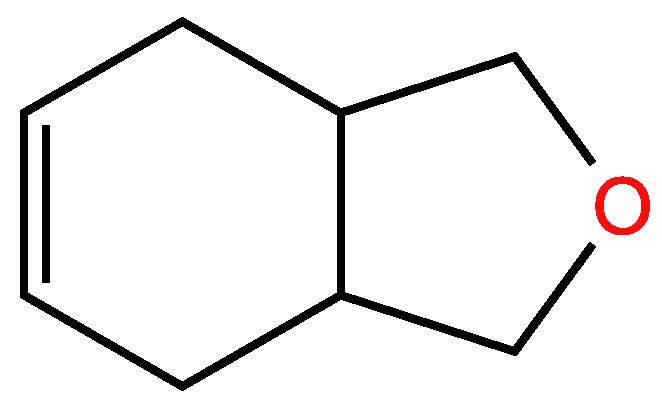

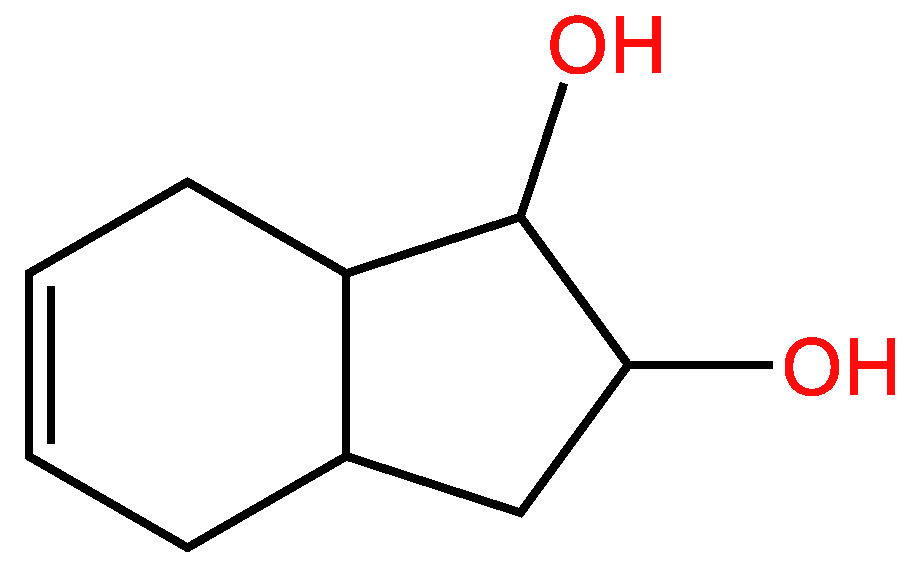
3.3. Cyclic unsaturated molecules with triple bonds in which
3.3.1. First example
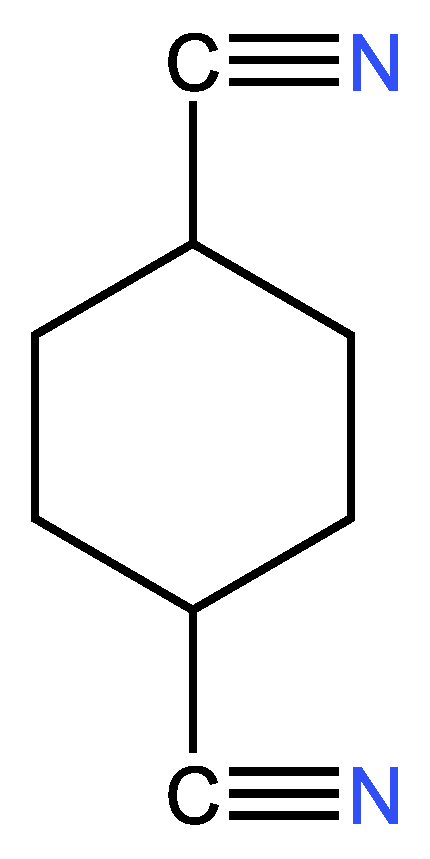
| Examples of Unsaturated Cyclic Molecules with triple bonds |
σ-bonds |
Single bonds |
π-bonds and triple bonds |
Ring/Rings |
| 23 | 21 | 4 ; 2 | 1 | |
| 10 | 8 | 4 ; 2 | 1 | |
| 15 | 13 | 4 ; 2 | 1 | |
| 25 | 21 | 8 ; 4 | 2 | |
| 27 | 23 | 8 ; 4 | 2 | |
| 56 | 50 | 12 ; 6 | 3 | |
| 47 | 41 | 12 ; 6 | 3 | |
| 55 | 47 | 16 ; 8 | 4 | |
| 84 | 76 | 16 ; 8 | 4 | |
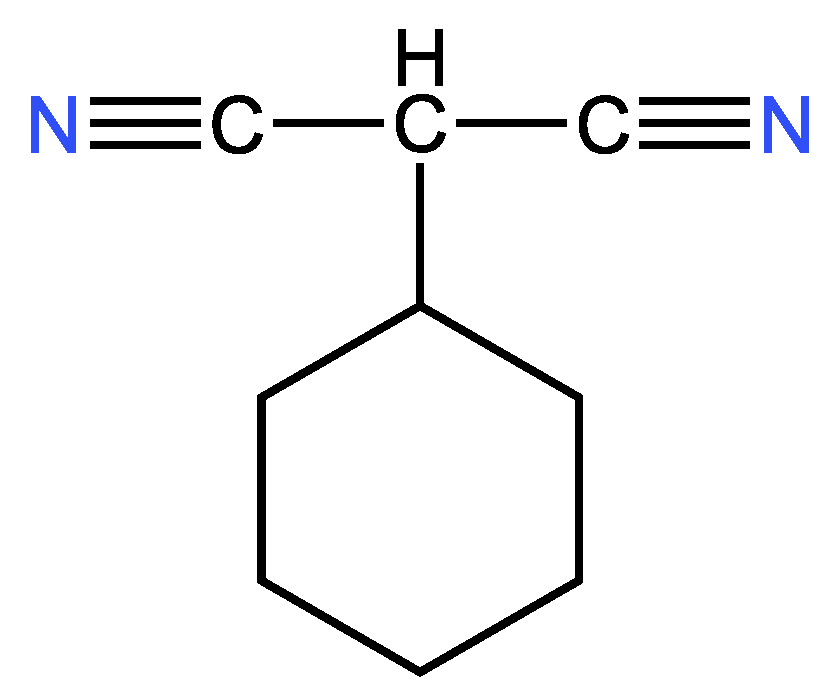
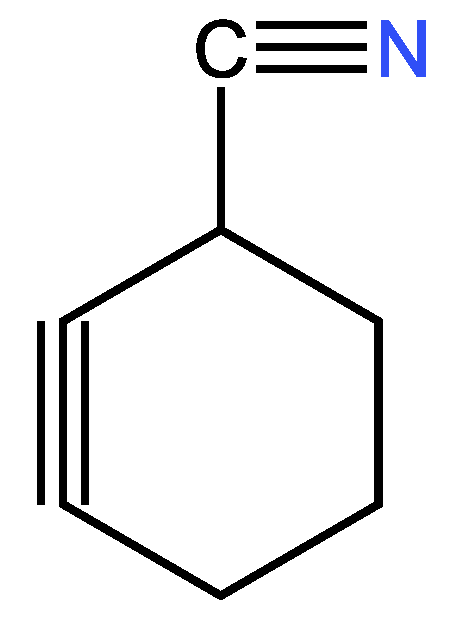
3.3.2. Second example
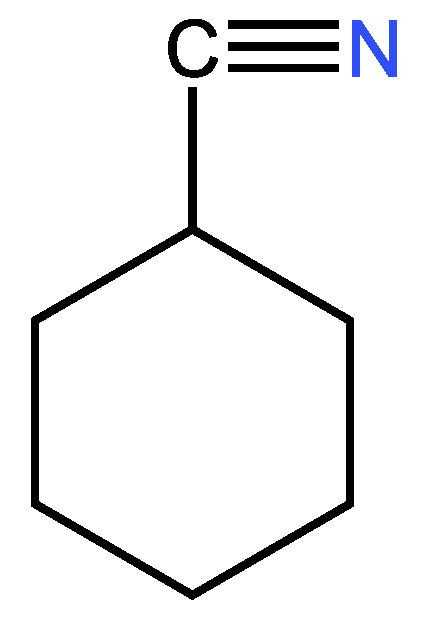
| Examples of Unsaturated Cyclic Molecules with triple bonds |
σ-bonds |
Single bonds |
π-bonds and triple bonds |
Ring/Rings |
| 16 | 15 | 2 ; 1 | 1 | |
| 19 | 18 | 2 ; 1 | 1 | |
| 18 | 17 | 2 ; 1 | 1 | |
| 32 | 30 | 4 ; 2 | 2 | |
| 33 | 31 | 4 ; 2 | 2 | |
| 44 | 41 | 6 ; 3 | 3 | |
| 55 | 52 | 6 ; 3 | 3 | |
| 50 | 46 | 8 ; 4 | 4 | |
| 58 | 54 | 8 ; 4 | 4 | |
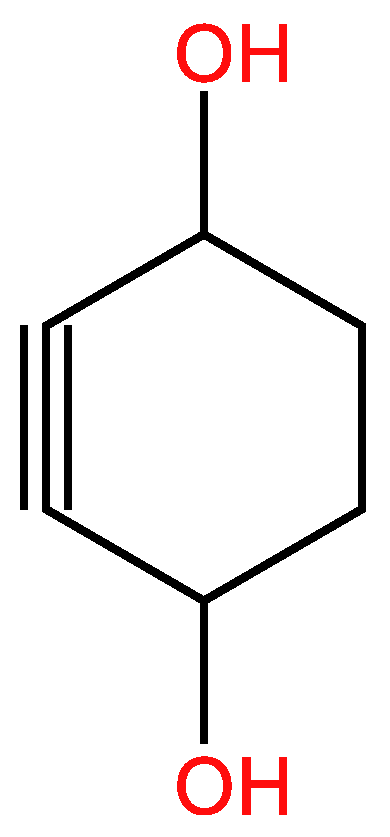
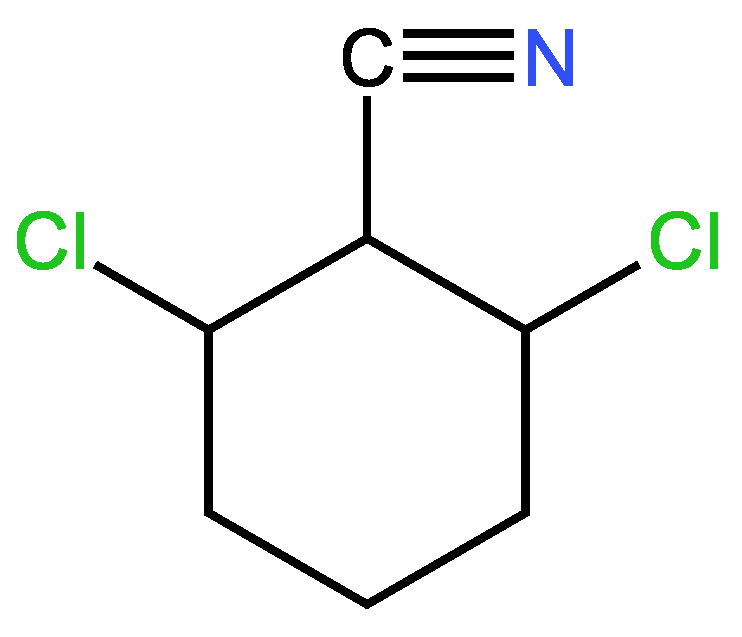
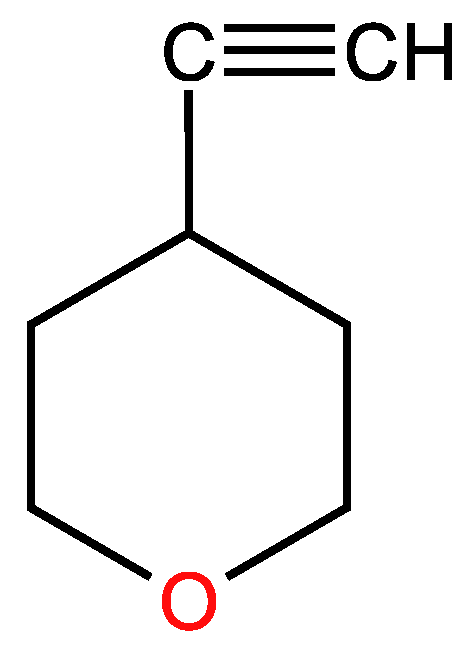
3.4. Cyclic unsaturated molecules with triple bonds in which
3.4.1. First example
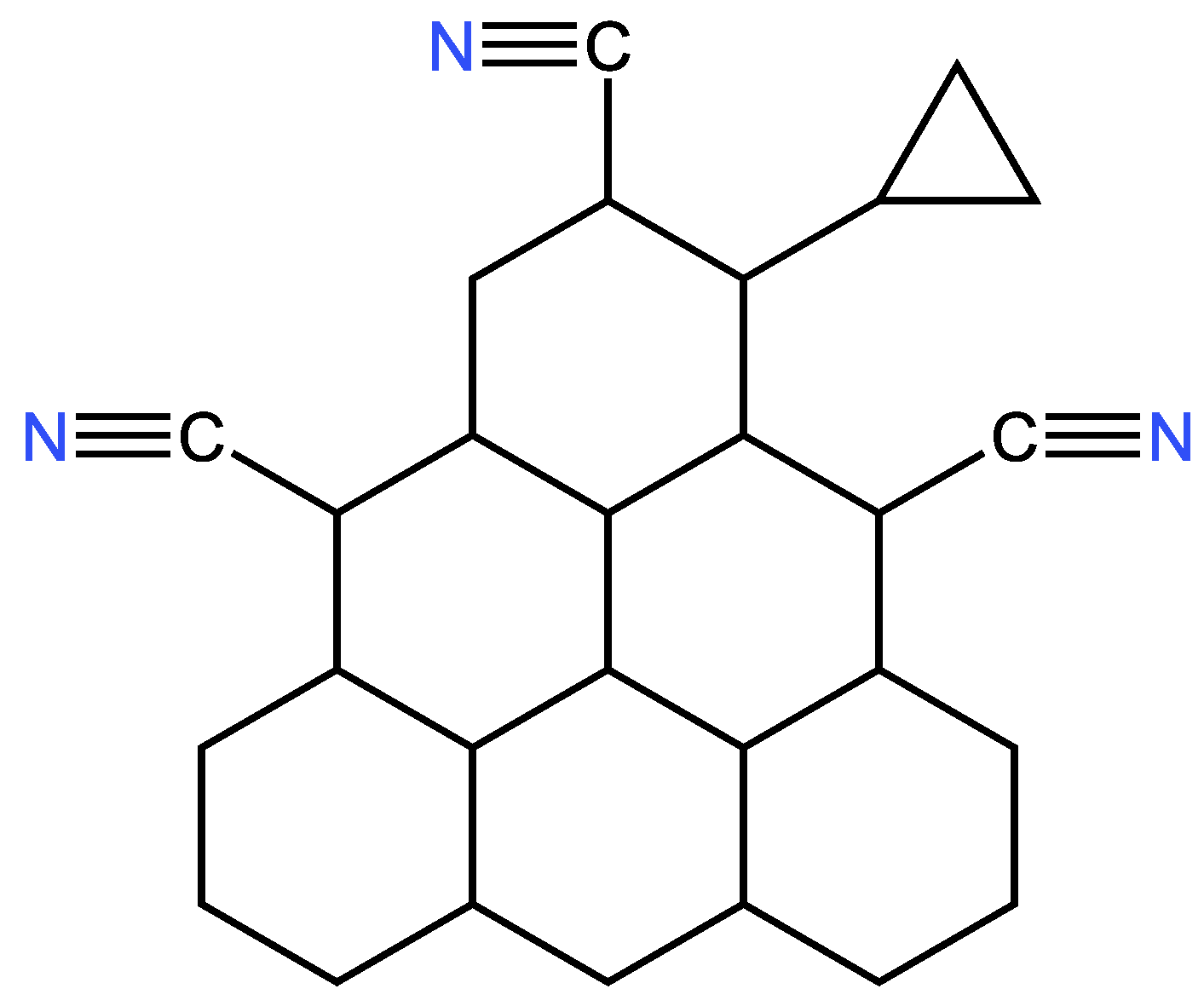
| Examples of Unsaturated Cyclic Molecules with triple bonds |
σ-bonds |
Single bonds |
π-bonds and triple bonds |
Ring/Rings |
| 68 | 65 | 6 ; 3 | 7 | |
| 169 | 163 | 12 ; 6 | 14 | |
| 161 | 155 | 12 ; 6 | 14 | |
| 143 | 134 | 18 ; 9 | 21 | |
| 123 | 114 | 18 ; 9 | 21 | |
| 267 | 255 | 24 ; 12 | 28 | |
| 267 | 255 | 24 ; 12 | 28 | |
| 339 | 324 | 30 ; 15 | 35 | |
| 377 | 362 | 30 ; 15 | 35 | |
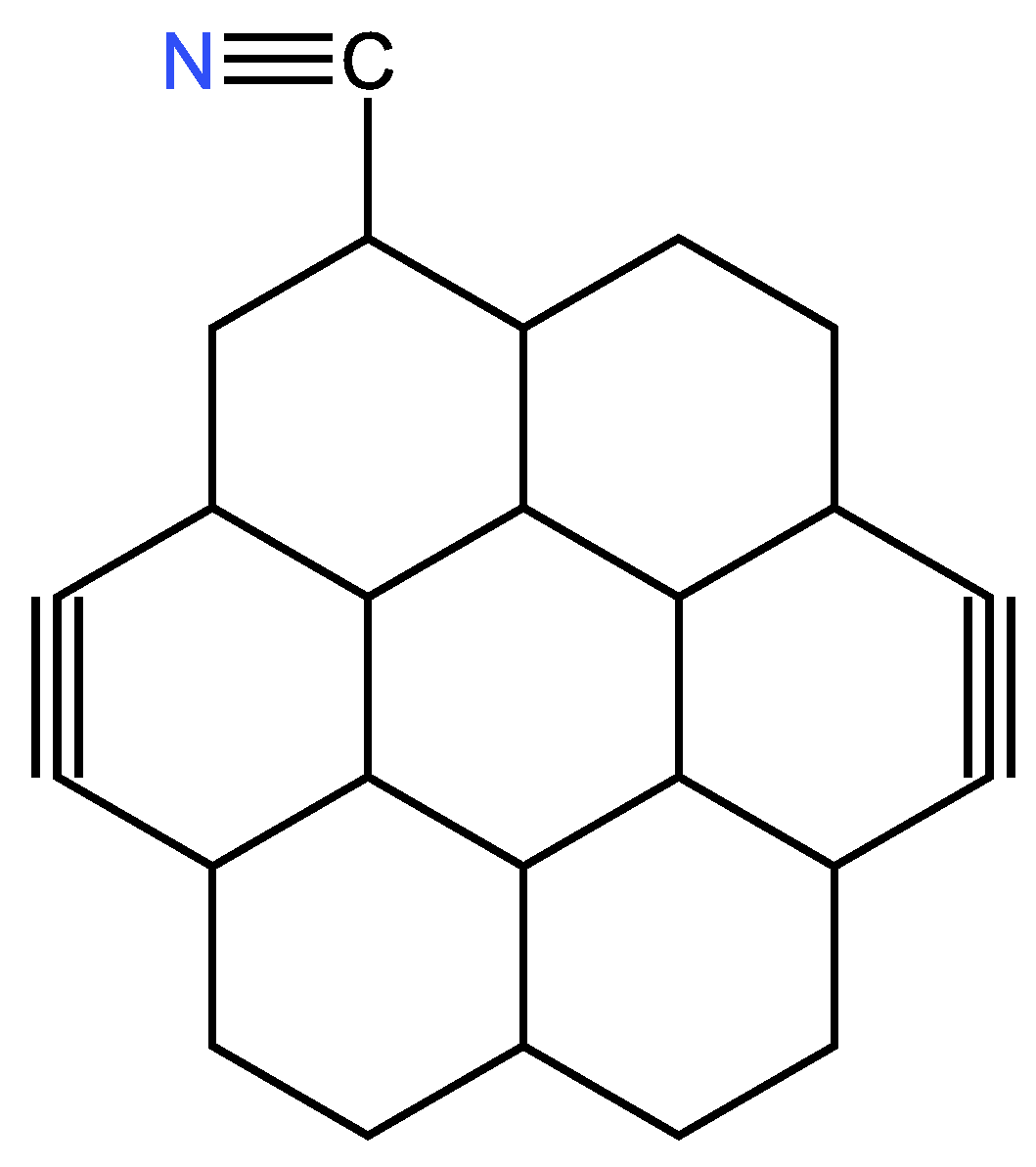
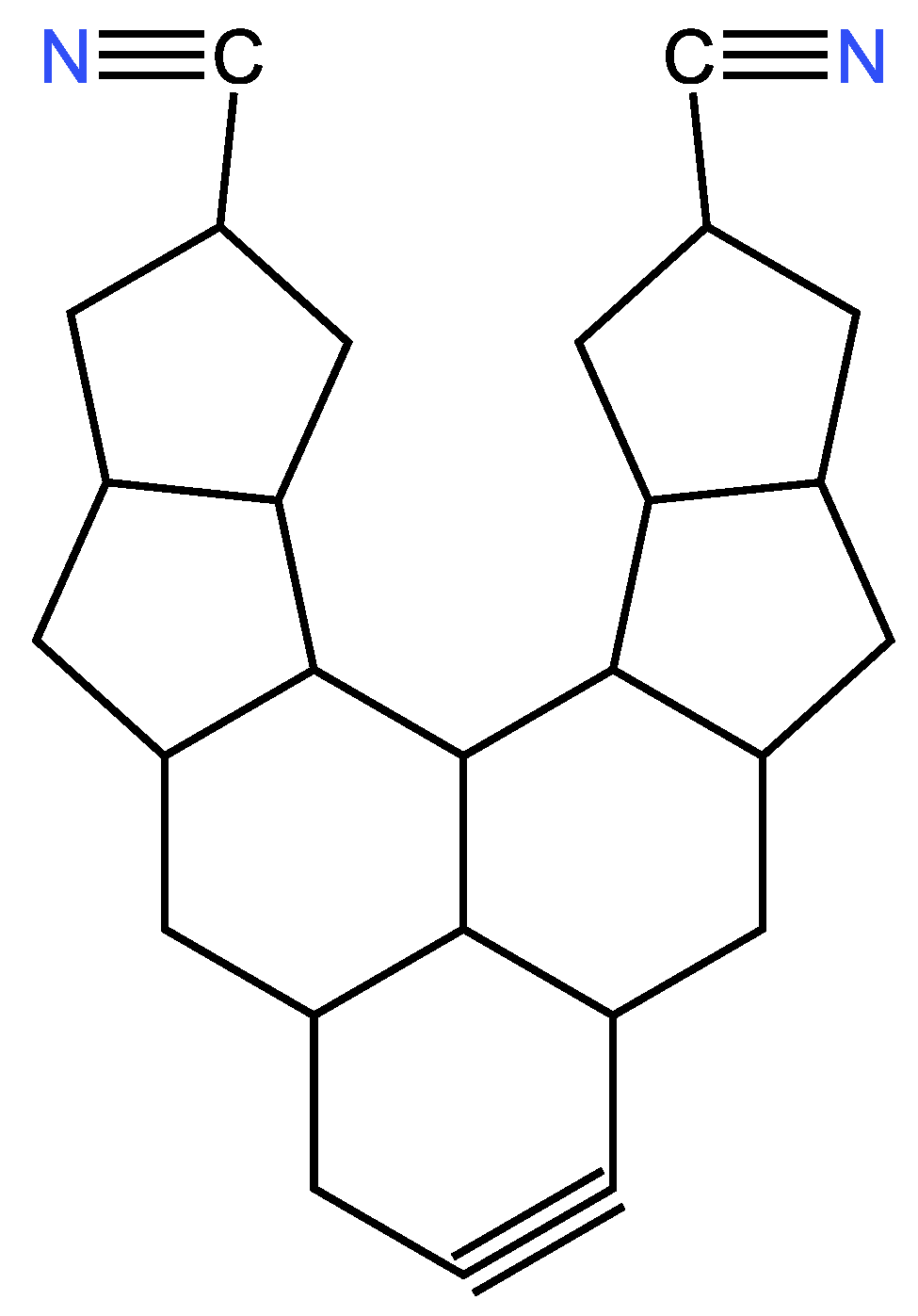
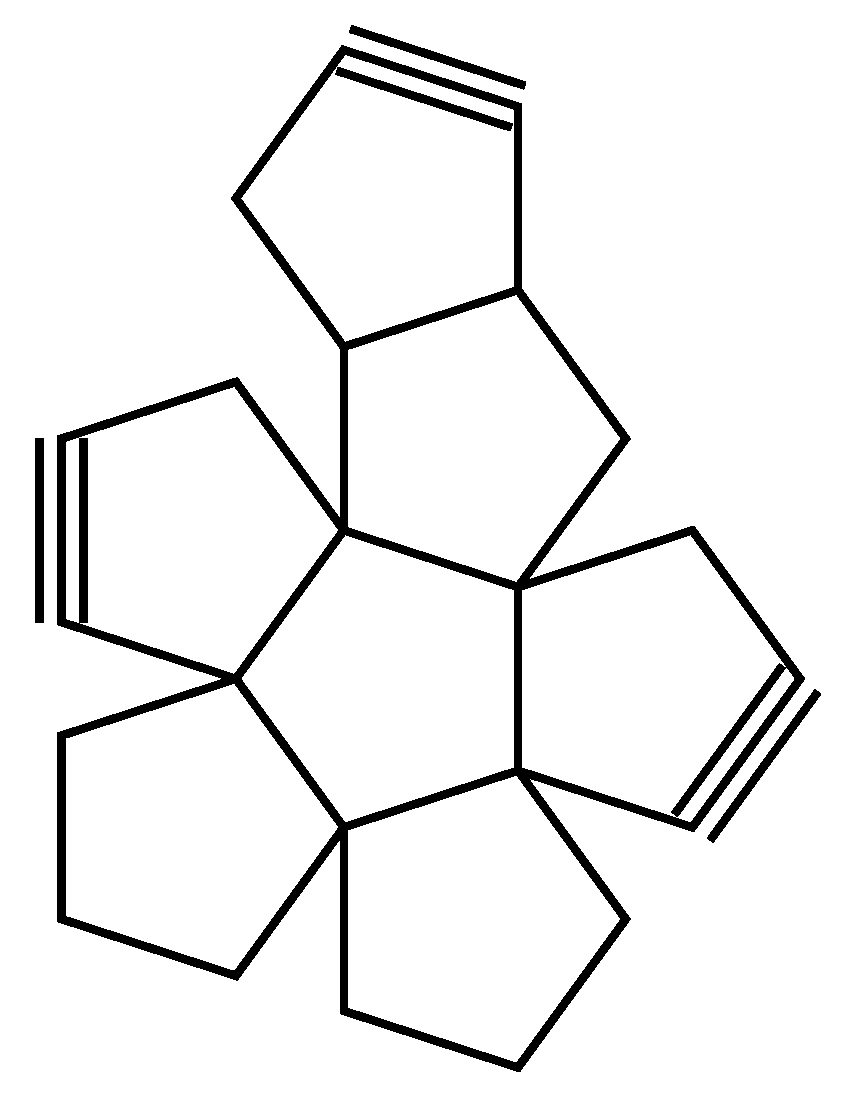
3.4.2. Second example
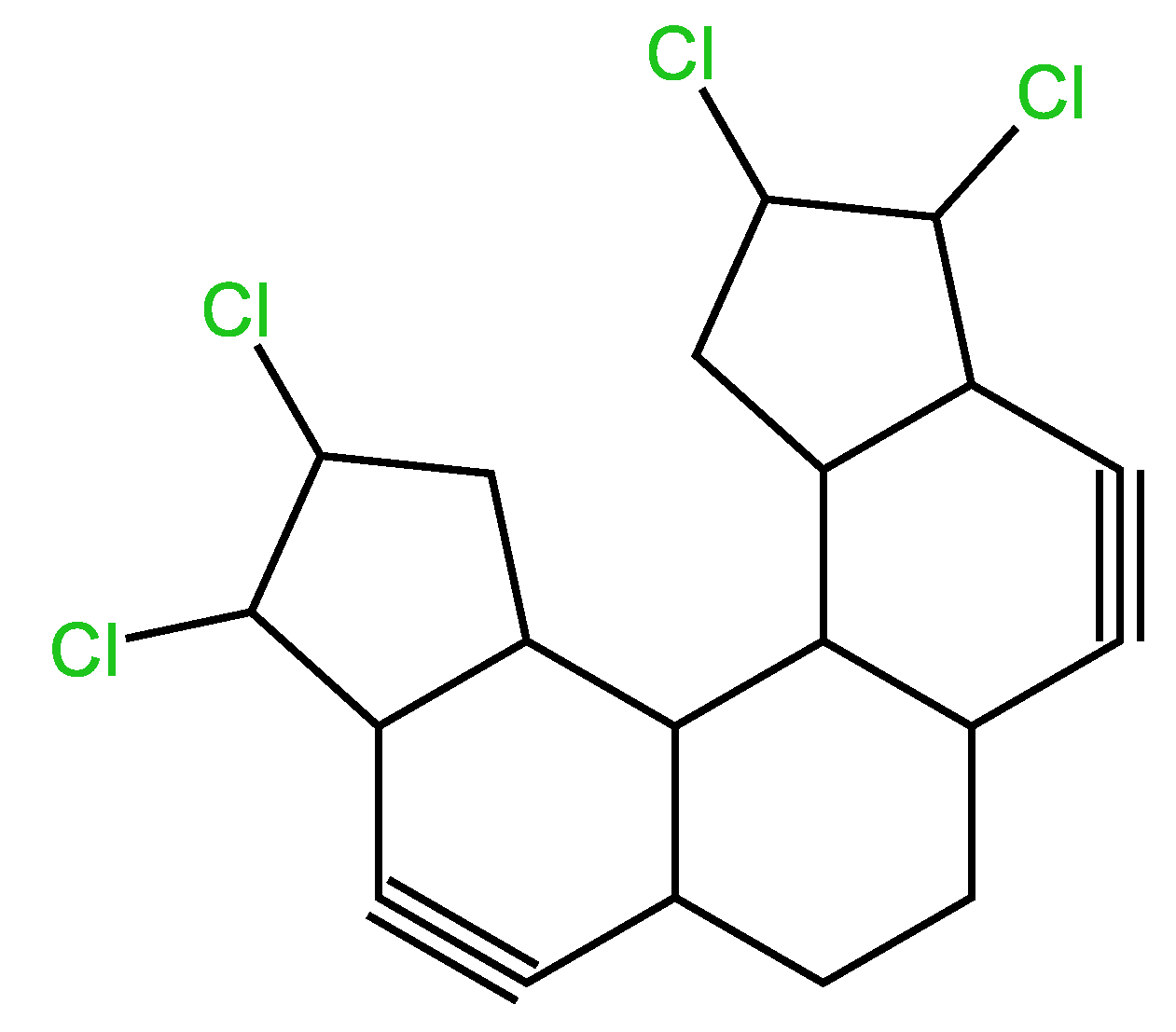
| Examples of Unsaturated Cyclic Molecules with triple bonds |
σ-bonds |
Single bonds |
π-bonds and triple bonds |
Ring/Rings |
| 57 | 55 | 4 ; 2 | 5 | |
| 96 | 92 | 8 ; 4 | 10 | |
| 100 | 96 | 8 ; 4 | 10 | |
| 120 | 114 | 12 ; 6 | 15 | |
| 124 | 118 | 12 ; 6 | 15 | |
| 170 | 162 | 16 ; 8 | 20 | |
| 168 | 160 | 16 ; 8 | 20 | |
| 173 | 163 | 20 ; 10 | 25 | |
| 163 | 153 | 20 ; 10 | 25 | |
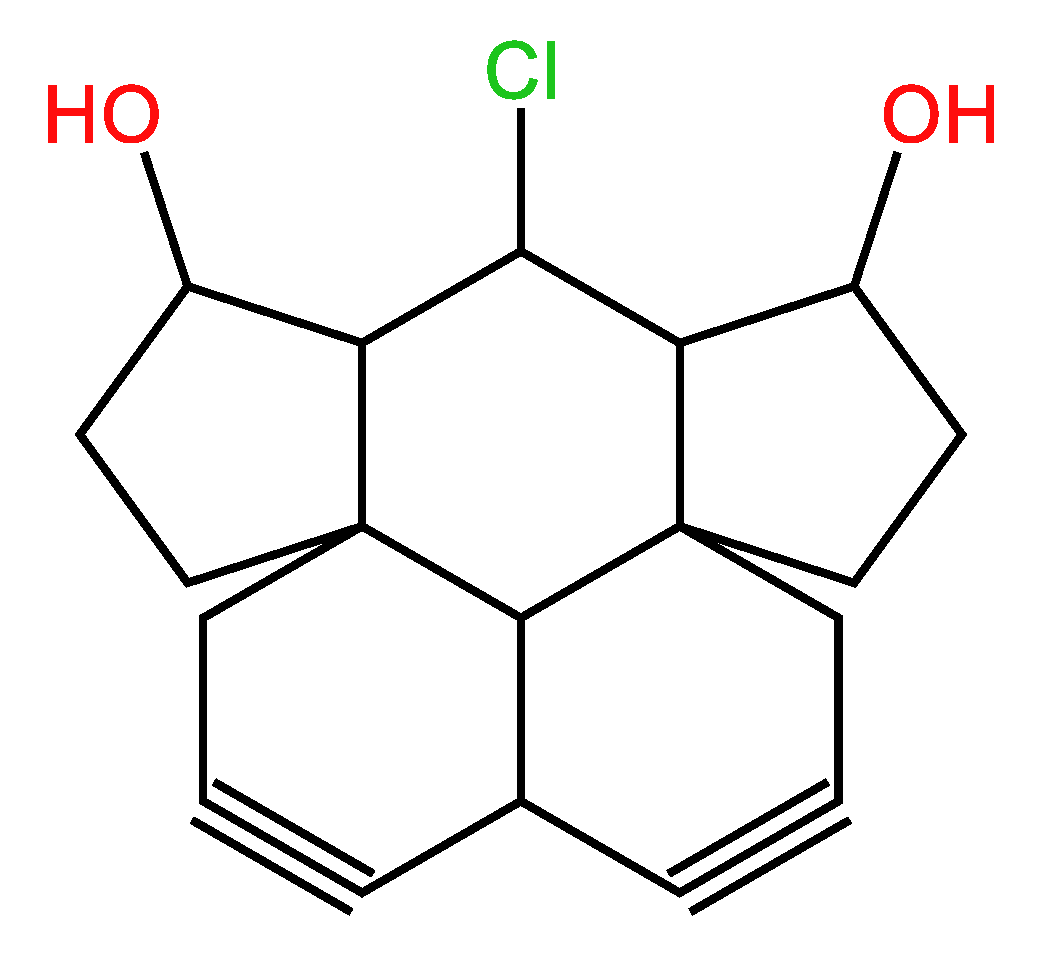
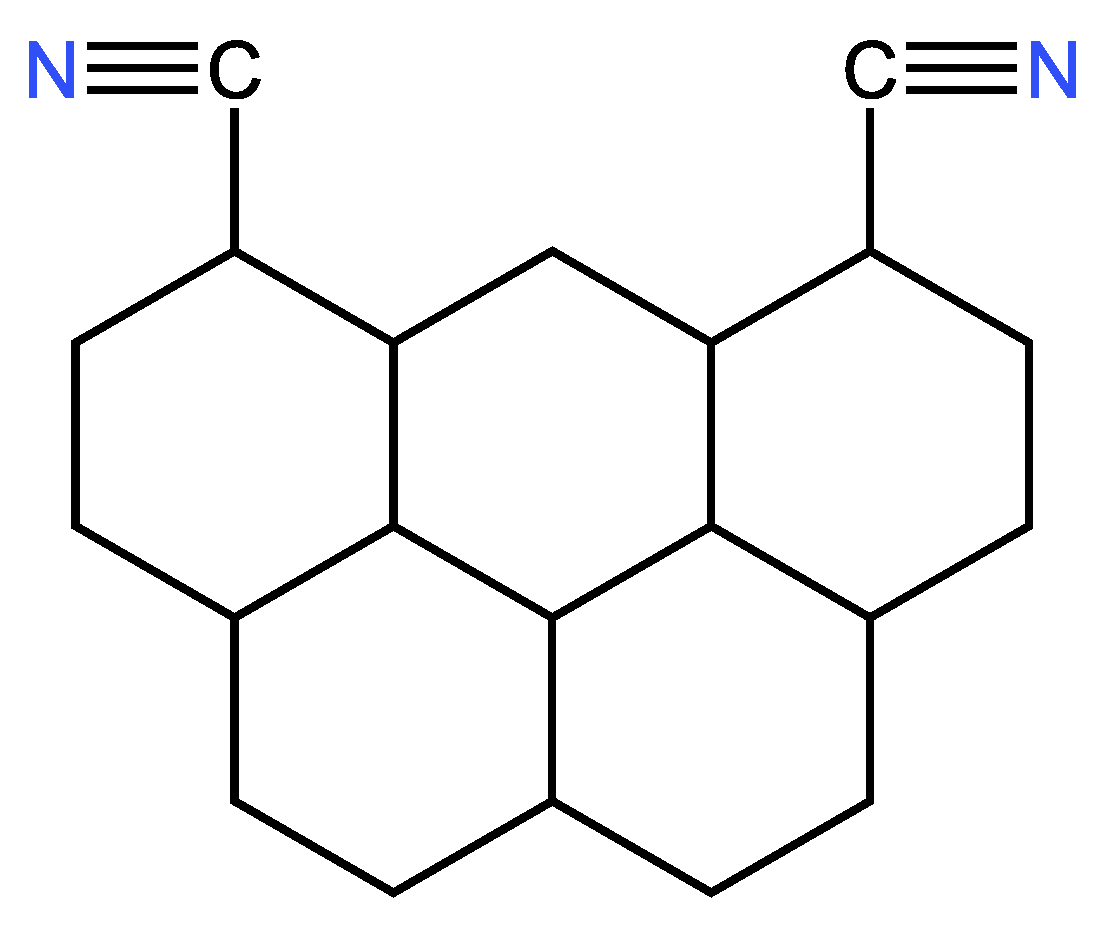
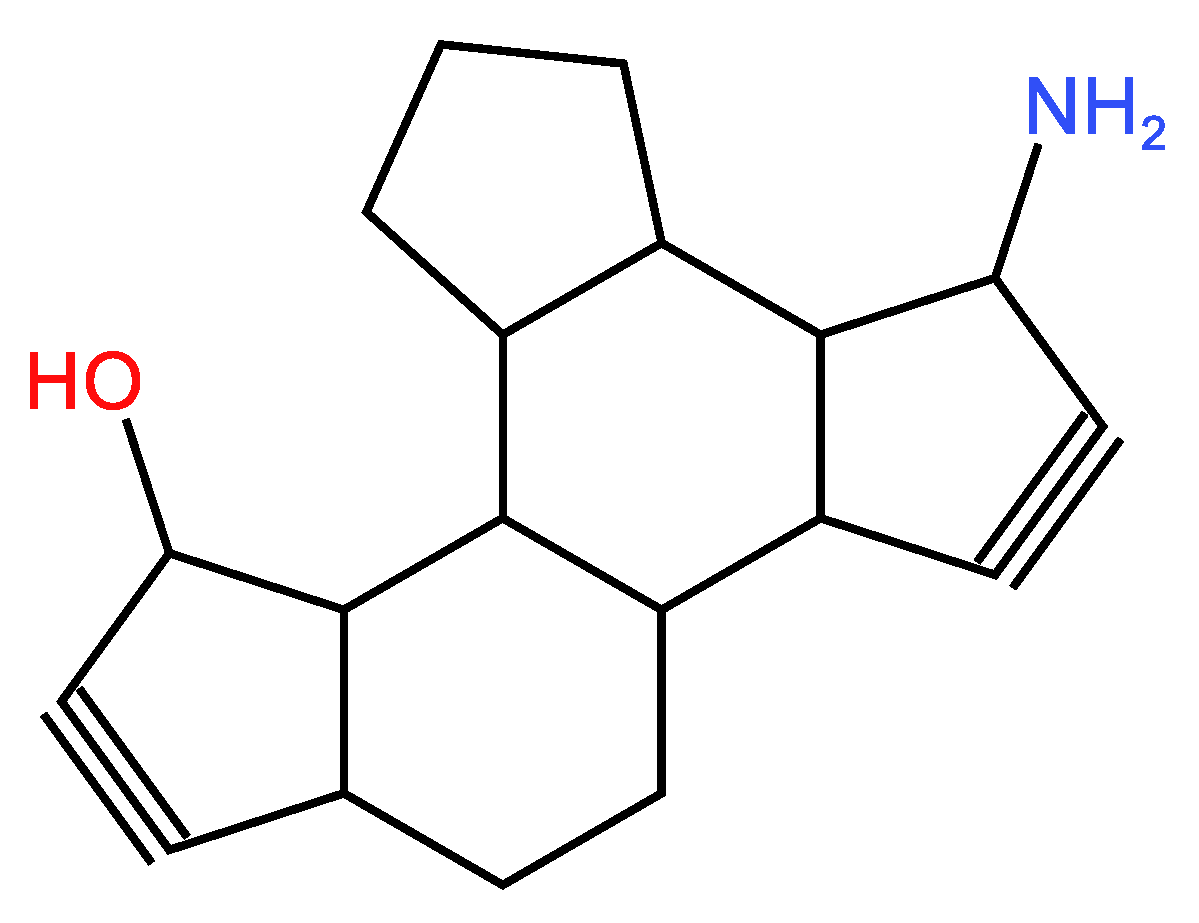
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Bonchev, D.; Rouvray, D.H. Chemical Graph Theory Introduction and Fundamentals. CRC Press LLC 2018. [Google Scholar]
- Gutman, I. Chemical Graph Theory—The Mathematical Connection. Adv. Quantum. Chem. 2006, 51, 125–138. [Google Scholar] [CrossRef]
- Leite, L.S.G.; Banerjee, S.; Wei, Y.; Elowitt, J.; Clark, A.E. Modern chemical graph theory. WIREs. Comput. Mol. Sci. 2024, 14. [Google Scholar] [CrossRef]
- Balaban, A.T. Applications of Graph Theory in Chemistry. J. Chem. Inf. Comput. Sci. 1985, 25, 334–343. [Google Scholar] [CrossRef]
- Zhao, L.; Schwarz, W.H.E.; Frenking, G. The Lewis electron-pair bonding model: the physical background, one century later. Nat. Rev. Chem. 2019, 3, 35–47. [Google Scholar] [CrossRef]
- Shaik, S.; Danovich, D.; Hiberty, P.C. Valence Bond Theory—Its Birth, Struggles with Molecular Orbital Theory, Its Present State and Future Prospects. Molecules 2021, 26, 1624. [Google Scholar] [CrossRef]
- Badertscher, M.; Bischofberger, K.; Munk, M.E.; Pretsch, E. A novel formalism to characterize the degree of unsaturation of organic molecules. J. Chem. Inf. Comput. Sci. 2001, 41, 889–893. [Google Scholar] [CrossRef]
- Raheja, L. ; Quick Calculation of Sigma and Pi bonds. AIJRA 2017, 2. [Google Scholar]
- Gavrilă, V. C.; Nicolescu, T. O. A Theoretical Framework for the Calculation of the Number of Covalent Bonds in Unsaturated Organic Compounds. Am. J. Phys. Chem. 2024, 13, 72–82. [Google Scholar] [CrossRef]
- Das, A.; Adhikari, S.; Pal, D.; Paul, B.; Sanjeev, R.; Jagannadham, V. Rapid Calculation of the Number of π-bonds, σ-bonds, Single and Triple Bonds in Aliphatic Unsaturated Open Chain and Cycloalkynes. World Journal of Chemical Education 2014, 2, 1–3. [Google Scholar]
- Gavrilă, V. C.; Nicolescu, T. O. New Equations for Rapid Calculation of π-bonds, σ-bonds, Single, Double and Triple Bonds in Open Chain Alcohols and Cycloamines. Int. J. chem. math. phys. 2024, 8, 9–15. [Google Scholar] [CrossRef]
- Xiaoyue, M. Development of Computational Chemistry and Application of Computational Methods. Journal of Physics: Conference Series 2022, 2386, 12005. [Google Scholar]
- Alberts, M.; Laino, T.; Vaucher, A.C. Leveraging infrared spectroscopy for automated structure elucidation. Commun. Chem. 2024, 7. [Google Scholar] [CrossRef]
- Reguant, A.I.; Reis, H.; Medved, M.; Luis, J.M.; Zaleśny, R. A new computational tool for interpreting the infrared spectra of molecular complexes. Phys. Chem. Chem. Phys. 2023, 25, 11658–11664. [Google Scholar] [CrossRef]
- Leniak, A.; Pietruś, W.; Kurczab, R. From NMR to AI: Designing a Novel Chemical Representation to Enhance Machine Learning Predictions of Physicochemical Properties. J. Chem. Inf. Model. 2024, 64, 3302–3321. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Chen, M. S.; Rotskoff, G. M.; Kanan, M. W.; Markland, T. E. Accurate and Efficient Structure Elucidation from Routine One-Dimensional NMR Spectra Using Multitask Machine Learning. ACS Cent. Sci. 2024, 10, 2162–2170. [Google Scholar] [CrossRef] [PubMed]
- Scheubert, K.; Hufsky, F.; Böcker, S. Computational mass spectrometry for small molecules. J. Cheminform. 2013, 5. [Google Scholar] [CrossRef]
- Beck, A.G.; Muhoberac, M.; Randolph, C.E.; Beveridge, C.H.; Wijewardhane, P.R.; Kenttämaa, H.I.; Chopra, G. Recent Developments in Machine Learning for Mass Spectrometry. ACS Meas. Sci. Au 2024, 4, 233–246. [Google Scholar] [CrossRef]
- López, C.S.; Faza, O.N. Overview of the computational methods to assess aromaticity. Aromaticity 2021, 41–71. [Google Scholar] [CrossRef]
- Ponting, D.J.; Deursen, R.V.; Ott, M.A. Machine Learning Predicts Degree of Aromaticity from Structural Fingerprints. J. Chem. Inf. Model. 2020, 60, 4560–4568. [Google Scholar]
- Kumar, M.D. A Study on Importance of Microsoft Excel Data Analysis Statistical Tools in Research Works. Journal of Management & Educational Research Innovation 2023, 1, 76–83. [Google Scholar]
- Einax, J.W.; Crouch, S.R.; Holler, F.J. Applications of Microsoft® Excel in analytical chemistry, 2nd ed. Anal. Bioanal. Chem. 2013, 405, 7559–7560. [Google Scholar]
- Ferreira, C.T.T.; Silva, C.C. The Roles of Mathematics in the History of Science: The Mathematization Thesis. Transversal: International Journal for the Historiography of Science 2020, 6, 6–25. [Google Scholar]
- Miller, D.D. Chapter 7 - The calculated uncertainty of scientific discovery: From Maths to Deep Maths. Handbook of Statistics 2023, 49, 203–226. [Google Scholar] [CrossRef]
- Liu, J.B. Novel Applications of Graph Theory in Chemistry and Drug Designing. Combinatorial Chemistry & High Throughput Screening 2022, 25, 439–440. [Google Scholar] [CrossRef]
- Lê, J. K.; Schmid, T. The Practice of Innovating Research Methods. Organ. Res. Methods 2022, 25, 308–336. [Google Scholar]
- Wang, Z.X.; Livingstone, K.; Hümpel, C.; Daniliuc, C.G.; Lichtenfeld, C.M.; Gilmour, R. Regioselective, catalytic 1,1-difluorination of enynes. Nat. Chem. 2023, 15, 1515–1522. [Google Scholar] [CrossRef]
- Kitazawa, Y.; Kochi, T.; Kakiuchi, F. Hydroarylative cyclization of enynes with aromatic ketones catalyzed by a low-valent iron-phosphine complex. Tetrahedron Letters 2025, 155. [Google Scholar] [CrossRef]
- Sharma, B.; García, L.P.; Chaudhary, G.R.; Kaur, G. Innovative approaches to cationic and anionic (catanionic) amphiphiles self-assemblies: Synthesis, properties, and industrial applications. Adv. Colloid Interface Sci. 2025, 337. [Google Scholar] [CrossRef]
- Gao, H.; Jiang, J.; Huang, Y.; Wang, H.; Sun, J.; Jin, Z.; Wang, J.; Zhang, J. Synthesis of hydrogels for adsorption of anionic and cationic dyes in water: ionic liquid as a crosslinking agent. SN Appl. Sci. 2022, 4, 118. [Google Scholar] [CrossRef]
- Bradley, D.; Branley, C.P.; Peeks, M.D. A straightforward method to quantify the electron-delocalizing ability of π-conjugated molecules. Phys. Chem. Chem. Phys. 2022, 24, 11486–11490. [Google Scholar] [CrossRef] [PubMed]
- Box, V.G.S.; Yu, H.W. Pi-Electron Delocalization in Organic Molecules with C-N Bonds. Journal of Chemical Education 1997, 74, 1293. [Google Scholar] [CrossRef]
- Walton, J.R.; Rivera, L.A.R.; Lucchese, R.R.; Bevan, J.W. Is there any fundamental difference between ionic, covalent, and others types of bond? A canonical perspective on the question. Phys. Chem. Chem. Phys. 2017, 19. [Google Scholar] [CrossRef]
- Hei, X.; Liu, W.; Zhu, K.; Teat, S.J.; Jensen, S.; Li, M.; O’Carroll, D.M.; Wei, K.; Tan, K.; Cotlet, M.; Thonhauser, T.; Li, J. Blending Ionic and Coordinate Bonds in Hybrid Semiconductor Materials: A General Approach toward Robust and Solution-Processable Covalent/Coordinate Network Structures. J. Am. Chem. Soc. 2020, 142, 4242–4253. [Google Scholar] [CrossRef]
- Yanofsky, N.S.; Zelcer, M. The Role of Symmetry in Mathematics. Found. Sci. 2017, 22, 495–515. [Google Scholar]
- Tantillo, D.J.; Applied Theoretical Organic Chemistry. WORLD SCIENTIFIC (EUROPE), 2018.
- Mitchell, J. M.; Flight, R. M.; Moseley, H. N. B. Deriving Lipid Classification Based on Molecular Formulas. Metabolites 2020, 10, 122. [Google Scholar] [CrossRef]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17. [Google Scholar]
- Hasan, M.R.; Alsaiari, A.A.; Fakhurji, B.Z.; Molla, M.H.R.; Asseri, A.H.; Sumon, M.A.A.; Park, M.N.; Ahammad, F.; Kim, B. Application of Mathematical Modeling and Computational Tools in the Modern Drug Design and Development Process. Molecules 2022, 27, 4169. [Google Scholar] [CrossRef]
- Sadybekov, A.V.; Katritch, V. Computational approaches streamlining drug discovery. Nature 2023, 616, 673–685. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





