A Unified PT-Even Torsion Framework for the Dark Sector: Cosmology, Galaxies, and Collider Signatures

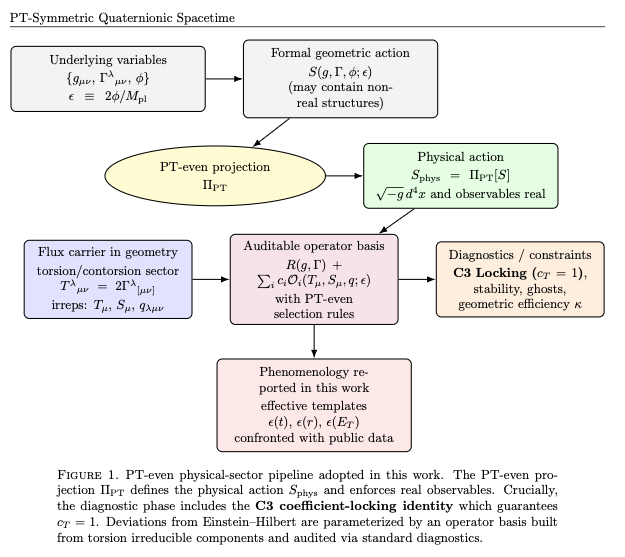
We present a four-dimensional, PT-symmetric quaternion-inspired extension of General Relativity formulated in a PT-even Palatini posture. Rather than treating a quaternionic "imaginary metric" as a physical spacetime tensor, we define the physical sector by a PT-even projection operator $\Pi_{PT}$ acting on the action and on composite observables:$$S_{phys} \equiv \Pi_{PT} [S(g, \Gamma, \phi; \epsilon)]$$ so that the measure and all reported observables are real by construction. The fundamental fields are a real (or PT-even) metric $g_{\mu\nu}$, an independent affine connection $\Gamma^{\lambda}_{\mu\nu}$ (allowing torsion), and a single real scalar spurion $\phi$ that controls a dimensionless flux amplitude $\epsilon \equiv 2\phi/M_{pl}$ in the connection/torsion sector. Nontrivial quaternionic/noncommutative effects are parameterized by a white-box operator basis $\Delta\mathcal{L} = \sum_i c_i \mathcal{O}_i(T_{\mu}, S_{\mu}, q_{\lambda\mu\nu}, g; \epsilon)$, built from the irreducible torsion components, with PT selection rules specifying which operators survive in $S_{phys}$.We then adopt a minimal-alignment phenomenology: the same spurion family $\epsilon$ is represented by scale-dependent templates $\epsilon(t)$, $\epsilon(r)$, and $\epsilon(E_T)$, which can be confronted with public data across three regimes:(i) late-time acceleration in SN Ia cosmology;(ii) approximately flat galaxy rotation curves in the SPARC sample;and (iii) missing transverse energy spectra at the LHC.In this work, we emphasize interpretational consistency: the three profiles are not claimed to arise from one universal PDE valid across all scales; instead, they are effective templates corresponding to different kinematic reductions of the same PT-even spurion sector, with scale-dependent effective couplings. The Palatini torsion posture provides an immediate diagnostic interface to stability. Crucially, consistent with the companion symmetry analysis, the PT-even projection imposes a coefficient-locking identity (C3) that enforces equality between the gravitational and kinematic couplings ($K=G$) for tensor modes. This structural locking guarantees exact tensor luminality ($c_T = 1$) at the leading order without parameter tuning, naturally satisfying the stringent GW170817 constraints. This work therefore serves as the phenomenological front-end, applying the strictly bounded PT-even framework to public data.