Secure Communications for UAV Relay Networks: A MPC-Based Trajectory Tracking Approach

1. Introduction

Unmanned aerial vehicles (UAVs) have garnered significant attention in recent years due to their potential to revolutionize various sectors, including communication, surveillance, and transportation [1,2,3,4,5]. Among the various applications, UAVs are increasingly being considered as relays in communication networks [6,7,8]. The ability of UAVs to operate at different altitudes and provide coverage over vast areas makes them ideal candidates for communication relays in situations where traditional infrastructure is impractical or unavailable [9]. In [10], an energy efficiency maximization algorithm for UAV relay with a circular trajectory is proposed, where the problem focuses on optimizing speed and load factor to balance power consumption and communication capacity. Zeng et al. [11] explore throughput maximization for UAV relays with a rectilinear trajectory, optimizing both power allocation and trajectory design to enhance performance under mobility constraints and information-causality conditions. While the concept of using UAV relays with a fixed location or on a fixed trajectory has been explored in several studies, there is a growing interest in mobile UAV relays, which provide enhanced flexibility and performance over their stationary counterparts [12]. A mobile UAV relay can follow dynamic paths and adjust its position to optimize communication performance, thereby improving coverage and reducing the likelihood of interference or signal blockage [13,14,15,16].

However, the line-of-sight (LoS) channel between UAVs and ground stations introduces significant security risks that must be addressed [13,17,18,19]. While UAV-based relay networks offer high throughput and low latency, their reliance on LoS paths can expose the system to various security vulnerabilities, including unauthorized interception of signals and cyber-attacks [20,21,22]. The security of UAV-assisted communication has been studied in [19,23,24,25], focusing on physical layer security (PLS) techniques. The authors in [23,24] optimized UAV relays by designing power allocation for secure communications. In [25], the authors improved secrecy rates by exploiting UAV mobility, while Wu et al. [19] proposed real-time UAV trajectory design in integrated sensing and communication (ISAC) systems, using an extended Kalman filtering (EKF)-based method for tracking to maximize secrecy rate.

Beyond the security challenges in UAV relay networks, the deployment of mobile UAVs also presents additional complexities, such as the need for accurate trajectory planning and control to ensure that communication links remain stable and reliable [26,27,28]. Current methods for mobile UAV relay systems often suffer from limitations in trajectory tracking accuracy and real-time adaptability, highlighting the need for more sophisticated control approaches [29,30,31,32]. Linear quadratic regulator (LQR)-based has been widely used for controlling UAVs in stationary applications, where it optimizes the control inputs based on a quadratic cost function. For example, an innovative method for adjusting the weighting matrices in linear quadratic LQR and LQR-proportional integral (PI) controllers significantly enhanced the robustness and tracking capabilities of quadrotor stabilization [33]. However, when considering dynamic scenarios, such as mobile UAV relays, the more advanced model predicted control (MPC) approach becomes critical. MPC allows for real-time optimization of the UAV’s trajectory, accounting for both the current state and future predictions, which is particularly important in environments with changing communication requirements or constraints [34,35]. While existing studies focus on either secure communication or trajectory control in UAV relay networks, their integration remains unexplored. To the best of our knowledge, this is the first work jointly optimizes security and trajectory tracking using MPC-based approach. This paper addresses this gap by proposing a framework that ensures both secure and efficient UAV relay operations. The main contributions of this work are summarized as follows:

• We propose a novel framework that jointly optimizes the transmit power and UAV trajectory, aiming to enhance the security of UAV-assisted relay networks, which ensures a balance between efficient communication and robust security against potential eavesdropping. To address the resultant non-convex secrecy rate maximization problem, we first divide the original problem into two sub-problems that optimize the UAV transmit power and trajectory separately by leveraging the successive convex approximation (SCA) techniques.
• We employ a MPC-based approach to adaptively control the UAV’s trajectory that improves secure communication. By considering future states and disturbances, the MPC method optimizes the control input termed velocity in each time slot, enabling the UAV to follow the trajectory efficiently while adapting to practical constraints and disturbances, enhancing the system’s resilience to dynamic environmental changes and security threats.
• Extensive simulation results demonstrate the effectiveness of the proposed framework. The joint optimization of power allocation and trajectory design leads to significant improvements in communication security, while the MPC-based path tracking ensures robust performance, highlighting the superiority of our approach compared to traditional methods, particularly in dynamic and uncertain environments.

The remainder of this paper is structured as follows: Section 2 presents a detailed description of the proposed UAV relay network system, including both the secure communication model and the trajectory control model. Next, Section 3 formulates and solves the UAV power allocation and trajectory design problem, followed by the MPC-based trajectory tracking discussed in Section 4. Section 5 presents the simulation results. Finally, Section 6 offers the conclusion of the paper.

Notations: Bold lowercase and uppercase letters, such as $\mathbf{a}$ and $\mathbf{A}$, represent vectors and matrices, respectively. ${\mathbb{R}}^M$ denotes the M-dimensional real-valued column vectors. ${\left(·\right)}^T$ and ${\left(·\right)}^{-1}$ denote the transposition and inverse operation, respectively. $\parallel ·\parallel$ indicates the ${\ell }_2$-norm of a matrix. $\mathcal{N}\left(a,b\right)$ is employed to represent a Gaussian distribution of mean a and variance b. Additionally, $\mathrm{diag}\left(·\right)$ represents a diagonal matrix, and ${\mathbf{I}}_M$ refers to the $M\times M$ identity matrix.

2. System Model

As depicted in Figure 1, we consider a downlink communication scenario, where a base station (BS) is employed to serve a ground user (Bob) in the presence of an eavesdropper (Eve), with both out of the coverage of BS. Consequently, we assume that the transmission between the BS and UAV is in the absence of eavesdropping. A single-antenna UAV is utilized as an amplify-and-forward (AF) relay to assist the success of downlink transmission. For ease of exposition, we focus on a total duration of length T, which is further split into N time slots with the duration of each time slot $\Delta t$. Notably, the value of $\Delta t$ should be small enough, enabling the UAV location within each time slot to approximately remain unchanged. During downlink transmission, the UAV dynamically adjusts its locations to provide stable and secure service to Bob. To this end, we denote the UAV’s horizontal location in time slot n as ${\mathbf{q}}_n={[x_n,y_n]}^T$ with a constant flight altitude H, which depends on the territorial building’s height. In practice, the UAV is possibly influenced by environmental uncertainties, such as wind and weather impacts. 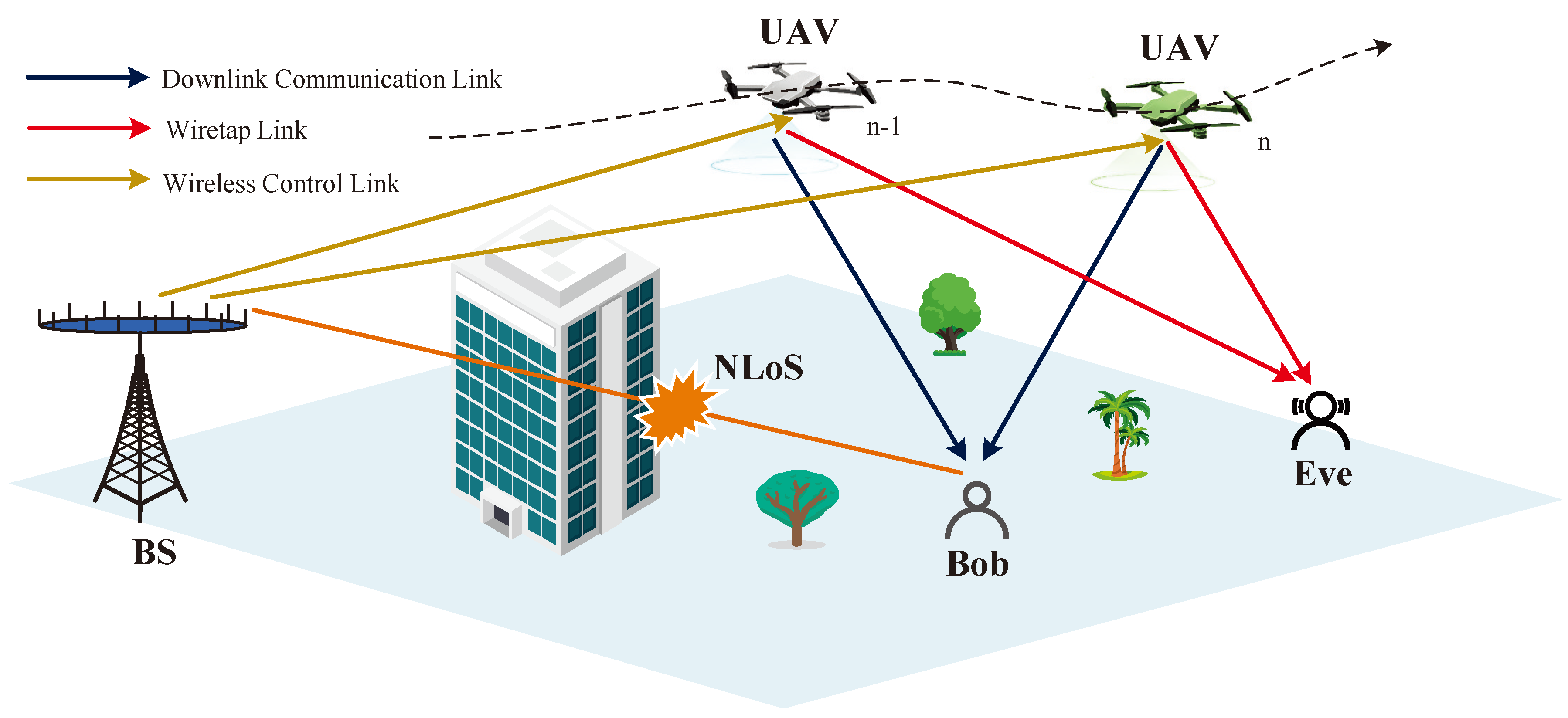To address these variations against secure communication design, in this section, we first introduce the UAV-enabled secure communication model, followed by presenting the trajectory control model.

2.1. Secure Communication Model

We consider that Bob and Eve are both on the ground with fixed locations, denoted by ${\mathbf{q}}_b={[x_b,y_b]}^T$ and ${\mathbf{q}}_e={[x_e,y_e]}^T$, respectively. For simplicity, we assume that the BS is located at ${\mathbf{b}}_0={[0,0]}^T$. According to [36,37,38], we consider that the channels from UAV to Bob and Eve are both dominated by LoS links and the Doppler effect induced by UAV mobility can be well compensated. Consequently, the channel gain from the BS to UAV, the UAV to Bob and Eve can be respectively expressed as

$$h_{au,n}={\rho }_0{d}_{au,n}^{-2}={\displaystyle \frac{{\rho }_0}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{b}}_0{\left|\right|}^2}},n=1,\cdots ,N,$$

(1)

$$h_{ub,n}={\rho }_0{d}_{ub,n}^{-2}={\displaystyle \frac{{\rho }_0}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_b{\left|\right|}^2}},n=1,\cdots ,N,$$

(2)

$$h_{ue,n}={\rho }_0{d}_{ue,n}^{-2}={\displaystyle \frac{{\rho }_0}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_e{\left|\right|}^2}},n=1,\cdots ,N,$$

(3)

where $d_{au,n}$, $d_{ub,n}$, and $d_{ue,n}$ are the corresponding distances in time slot n. The term ${\rho }_0$ represents the channel gain at a unit reference distance. Denote $p_{0,n}$ and $p_{u,n}$ as the transmit powers associated with the BS and UAV in time slot n, respectively. Then, the corresponding achieved rates from the BS to UAV, the UAV to Bob and Eve can be respectively given by

$$R_{au,n}={log}_2(1+{\displaystyle \frac{p_{0,n}{\rho }_0/{\sigma }_0^2}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{b}}_0{\left|\right|}^2}}),n=1,\cdots ,N,$$

(4)

$$R_{ub,n}={log}_2(1+{\displaystyle \frac{p_{u,n}{\rho }_0/{\sigma }_0^2}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_b{\left|\right|}^2}}),n=1,\cdots ,N,$$

(5)

$$R_{ue,n}={log}_2(1+{\displaystyle \frac{p_{u,n}{\rho }_0/{\sigma }_0^2}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_e{\left|\right|}^2}}),n=1,\cdots ,N,$$

(6)

with ${\sigma }_0^2$ being the noise variance.

2.2. Trajectory Control Model

Once the optimal trajectory of the UAV is designed, the BS derives the corresponding control strategies, taking into account both the reference trajectory and the UAV’s real-time state, and subsequently sends the commands to the UAV for path tracking. In this work, we assume that the uplink feedforward channel and the downlink feedback channel between the BS and the UAV are both ideal, as our focus is solely on the design of control strategies. This implies that the UAV can perfectly receive the control input, while the BS can accurately estimate the UAV’s state. Specifically, we model the BS and the UAV as a liner control system, with the discrete-time system equations at time instant n formulated as [39,40,41]

$${\mathbf{q}}_{n+1}=\mathbf{A}{\mathbf{q}}_n+\mathbf{B}{\mathbf{v}}_n,$$

(7)

$${\mathbf{y}}_n=\mathbf{C}{\mathbf{q}}_n,$$

(8)

where ${\mathbf{v}}_n={\left[v_{x,n},v_{y,n}\right]}^{\mathrm{T}}\in {\mathbb{R}}^2$ denotes the control input, i.e, the UAV’s velocity over the time interval $\left(n▵t,\left(n+1\right)▵t\right]$, ${\mathbf{y}}_n\in {\mathbb{R}}^2$ represents the UAV’s state estimation result at the BS, $\mathbf{A}$, $\mathbf{B}$, and $\mathbf{C}$ are fixed state evolution matrix, input matrix, and deterministic matrix, respectively, defined as

$$\mathbf{A}={\mathbf{I}}_{2\times 2},\mathbf{B}=\left[\begin{array}{cc}▵t& 0\\ 0& ▵t\end{array}\right]\in {\mathbb{R}}^{2\times 2},\mathbf{C}={\mathbf{I}}_{2\times 2}.$$

(9)

Furthermore, in light of the UAV’s mechanical constraints, a new state-space model is introduced, where the increment in the UAV’s velocity, defined as $▵{\mathbf{v}}_n={\mathbf{v}}_n-{\mathbf{v}}_{n-1}$, is chosen as the control input. Simultaneously, the state-space variable ${\mathbf{q}}_n$ and the previous control input ${\mathbf{v}}_{n-1}$ are combined to form the new state ${\widehat{\mathbf{q}}}_{n+1}$. Consequently, the discrete-time system equations are redefined as

$${\widehat{\mathbf{q}}}_{n+1}=\widehat{\mathbf{A}}{\widehat{\mathbf{q}}}_n+\widehat{\mathbf{B}}▵{\mathbf{v}}_n,$$

(10)

$${\widehat{\mathbf{y}}}_n=\widehat{\mathbf{C}}{\widehat{\mathbf{q}}}_n,$$

(11)

where

$$\left\{\begin{array}{c}{\widehat{\mathbf{q}}}_n=\left[\begin{array}{c}{\mathbf{q}}_n\\ {\mathbf{v}}_{n-1}\end{array}\right]\in {\mathbb{R}}^4\hfill \\ \widehat{\mathbf{A}}=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ {\mathbf{0}}_{2\times 2}& {\mathbf{I}}_{2\times 2}\end{array}\right]\in {\mathbb{R}}^{4\times 4},\widehat{\mathbf{B}}=\left[\begin{array}{c}\mathbf{B}\\ {\mathbf{I}}_{2\times 2}\end{array}\right]\in {\mathbb{R}}^{4\times 2},\hfill \\ \widehat{\mathbf{C}}=\left[\begin{array}{cc}\mathbf{C}& {\mathbf{0}}_{2\times 2}\end{array}\right]\in {\mathbb{R}}^{2\times 4},{\widehat{\mathbf{y}}}_n={\mathbf{y}}_n.\hfill \end{array}\right.$$

(12)

3. UAV Power Allocation and Trajectory Design

To counteract malicious eavesdropping, in this section, we focus on the joint optimization of UAV power allocation and trajectory design to ensure secure communication in UAV-assisted relay networks.

3.1. Problem Formulation

The secrecy rate ${\tilde{R}}_n$ in time slot n is defined as the difference between the achievable rate at Bob and Eve, i.e., ${\tilde{R}}_n=R_{ub,n}-R_{ue,n}$. The goal is to maximize the cumulative secrecy rate over the entire communication duration T by jointly taking into account the UAV transmit power $p_{u,n}$ and UAV trajectory ${\mathbf{q}}_n$. We further denote ${\mathcal{P}}_u=\{p_{u,n},n=1\cdots N\}$ and $\mathcal{Q}=\{{\mathbf{q}}_n,n=1\cdots N\}$ as the variable sets that collect the UAV transmit power, and trajectory variables across all time slots. Consequently, the secrecy rate maximization problem can be formulated as:

$$\begin{array}{}\mathrm{(13a)}& \hfill \underset{\{{\mathcal{P}}_u,\mathcal{Q}\}}{max}& \sum _{n=1}^N{\tilde{R}}_n\hfill \mathrm{(13b)}& \hfill \mathrm{s}.\mathrm{t}.& R_{ub,n}\le R_{au,n},\forall n,\hfill \mathrm{(13c)}& \hfill & \left|\right|{\mathbf{q}}_{n+1}-{\mathbf{q}}_n\left|\right|\le V_{\max }\Delta t,\forall n,\hfill \mathrm{(13d)}& \hfill & \sum _{n=1}^N{p}_{u,n}\le P_{\max ,u},p_{u,n}\ge 0,\forall n,\hfill \mathrm{(13e)}& \hfill & {\mathbf{q}}_1={\mathbf{q}}_I,{\mathbf{q}}_N={\mathbf{q}}_F,\hfill \end{array}$$

where $V_{\max }$ is the maximum velocity of the UAV and $P_{\max ,u}$ denotes the maximum transmit power budget corresponding to the UAV, respectively. ${\mathbf{q}}_I$ and ${\mathbf{q}}_F$ are the preset initial and final point. Constraint (13b) ensures that the achievable rate at Bob must not exceed the received rate at the UAV, while constraint (13c) denotes the UAV maximum travel distance within a single time slot. Moreover, constraint (13e) requires that the UAV return to its original at the end. Nevertheless, it is worth mentioning that problem (13) is non-convex, and consequently, it is challenging to deal with (13) by utilizing the traditional convex optimization methods. As a compromise, we propose a computationally efficient algorithm to obtain a locally optimal solution in what follows.

3.2. Efficient Solutions

In this subsection, we propose an AO-based algorithm to transform the original problem into a series of sub-problems and solve them iteratively to obtain an efficient solution. In particular, problem (13) can be decomposed into two subproblems, i.e., sub-problem 1: optimizing transmit powers with a fixed trajectory and sub-problem 2: optimizing the trajectory with other variables fixed. To begin with, we solve subproblem 1, which can be particularized as

$$\begin{array}{}\mathrm{(14a)}& \hfill \underset{\left\{{\mathcal{P}}_u\right\}}{max}& \sum _{n=1}^N{log}_2(1+p_{u,n}{\gamma }_{ub,n})-{log}_2(1+p_{u,n}{\gamma }_{ue,n})\hfill \mathrm{(14b)}& \hfill \mathrm{s}.\mathrm{t}.& {log}_2(1+p_{u,n}{\gamma }_{ub,n})\le R_{au,n},\forall n,\hfill \mathrm{(14c)}& \hfill & \sum _{n=1}^N{p}_{u,n}\le P_{\max ,u},p_{u,n}\ge 0,\forall n,\hfill \end{array}$$

where ${\gamma }_{ub,n}=h_{ub,n}/{\sigma }_0^2$ and ${\gamma }_{ue,n}=h_{ue,n}/{\sigma }_0^2$. Although problem (14) is still non-convex, it can be iteratively solved by adopting the SCA technique. Specifically, the non-convex term in the objective function is $-{log}_2(1+p_{u,n}{\gamma }_{ue,n})$. In the k-th iteration, we approximate this term by performing a first-order Taylor expansion around the current power allocation $p_{u,n}^{\left(k\right)}$, i.e.,

$${log}_2(1+p_{u,n}{\gamma }_{ue,n})\approx {log}_2\left(1+p_{u,n}^{\left(k\right)}{\gamma }_{ue,n}\right)+{\displaystyle \frac{{\gamma }_{ue,n}}{ln2\left(1+p_{u,n}^{\left(k\right)}{\gamma }_{ue,n}\right)}}\left(p_{u,n}-p_{u,n}^{\left(k\right)}\right)\triangleq {\widehat{R}}_{ue,n}.$$

(15)

Substitute (15) into the objective function, we arrive at the following convex approximation

$${\tilde{R}}_n\approx \sum _{n=1}^N\left[{log}_2(1+p_{u,n}{\gamma }_{ub,n})-{\widehat{R}}_{ue,n}.\right]$$

(16)

Hence, in the k-th iteration, the following convex optimization problem is solved:

$$\begin{array}{cc}\hfill & \underset{\left\{{\mathcal{P}}_u\right\}}{max}\sum _{n=1}^N{\tilde{R}}_n\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.p_{u,n}\le (2^{R_{au,n}}-1)/{\gamma }_{ub,n},\forall n,\hfill \\ \hfill & \sum _{n=1}^N{p}_{u,n}\le P_{max,u},p_{u,n}\ge 0,\forall n.\hfill \end{array}$$

(17)

Problem (18) now is convex and thus can be efficiently addressed via standard solvers, e.g., CVX [42]. Subsequently, we optimize the UAV trajectory given the power variable ${\mathcal{P}}_u$, which is given by

$$\begin{array}{}\mathrm{(18a)}& \hfill \underset{\mathcal{Q}}{max}& \sum _{n=1}^N{log}_2(1+{\displaystyle \frac{{\beta }_{u,n}}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_b{\left|\right|}^2}})-{log}_2(1+{\displaystyle \frac{{\beta }_{u,n}}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_e{\left|\right|}^2}})\hfill \mathrm{(18b)}& \hfill & \mathrm{s}.\mathrm{t}.{log}_2(1+{\displaystyle \frac{{\beta }_{u,n}}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_b{\left|\right|}^2}})\le {log}_2(1+{\displaystyle \frac{{\beta }_{0,n}}{H^2+\left|\right|{\mathbf{q}}_n-{\mathbf{b}}_0{\left|\right|}^2}})\forall n,\hfill \mathrm{(18c)}& \hfill & \left|\right|{\mathbf{q}}_{n+1}-{\mathbf{q}}_n\left|\right|\le V_{\max }\Delta t,\forall n,\hfill \mathrm{(18d)}& \hfill & {\mathbf{q}}_1={\mathbf{q}}_I,{\mathbf{q}}_N={\mathbf{q}}_F,\hfill \end{array}$$

with ${\beta }_{u,n}=p_{u,n}{\rho }_0/{\sigma }_0^2$ and ${\beta }_{0,n}=p_{0,n}{\rho }_0/{\sigma }_0^2$. We first note that $R_{ub,n}$ has a convex lower-bound at the given point ${\mathbf{q}}_n^r$ by invoking the SCA method, such that we arrive

$$\begin{array}{cc}\hfill R_{ub,n}^{lb}\ge & {log}_2\left(1+{\displaystyle \frac{{\beta }_{u,n}}{H^2+{∥{\mathbf{q}}_n^r-{\mathbf{q}}_b∥}^2}}\right)-{\displaystyle \frac{{\beta }_{u,n}}{ln2}}\left({\displaystyle \frac{1}{1+\frac{{\beta }_{u,n}}{\left(H^2+{∥{\mathbf{q}}_n^r-{\mathbf{q}}_b∥}^2\right)}}}\right)\times {\displaystyle \frac{\parallel {\mathbf{q}}_n-{\mathbf{q}}_b{\parallel }^2-{∥{\mathbf{q}}_n^r-{\mathbf{q}}_b∥}^2}{{\left(H^2+{∥{\mathbf{q}}_n^r-{\mathbf{q}}_b∥}^2\right)}^2}}.\hfill \end{array}$$

(19)

Moreover, introducing an auxiliary variable ${\theta }_n=\left|\right|{\mathbf{q}}_n-{\mathbf{q}}_e{\left|\right|}^2$, we can transform the objective function into a convex form with an additional constraint

$$\begin{array}{cc}\hfill {\theta }_n& \le {∥{\mathbf{q}}_n^r-{\mathbf{q}}_e∥}^2+2{\left({\mathbf{q}}_n^r-{\mathbf{q}}_e\right)}^{\mathrm{T}}\left({\mathbf{q}}_n-{\mathbf{q}}_n^r\right).\hfill \end{array}$$

(20)

Similarly, one can employ SCA technique to convert constraint (18b) into

$${\beta }_{u,n}\left(H^2+{\parallel {\mathbf{q}}_n-{\mathbf{b}}_0\parallel }^2\right)\le {\beta }_{0,n}\left(\parallel {\mathbf{q}}_n^r-{\mathbf{q}}_b{\parallel }^2+2{\left({\mathbf{q}}_n^r-{\mathbf{q}}_b\right)}^T\left({\mathbf{q}}_n-{\mathbf{q}}_n^r\right)\right).$$

(21)

As a result, problem (18) can be approximated as

$$\begin{array}{cc}\hfill \underset{\mathcal{Q},{\theta }_n}{max}& \sum _{n=1}^N{R}_{ub,n}^{lb}-{log}_2(1+{\beta }_{u,n}/(H^2+{\theta }_n))\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(18\mathrm{c}\right),\left(18\mathrm{d}\right),\left(20\right),\left(21\right),\hfill \end{array}$$

(22)

which is a convex problem and can be solved by CVX [43]. In a nutshell, the original problem can be solved by iteratively dealing with problems (18) and (22). Since there exists a finite upper bound due to the power constraint, the proposed algorithm can be guaranteed to converge.

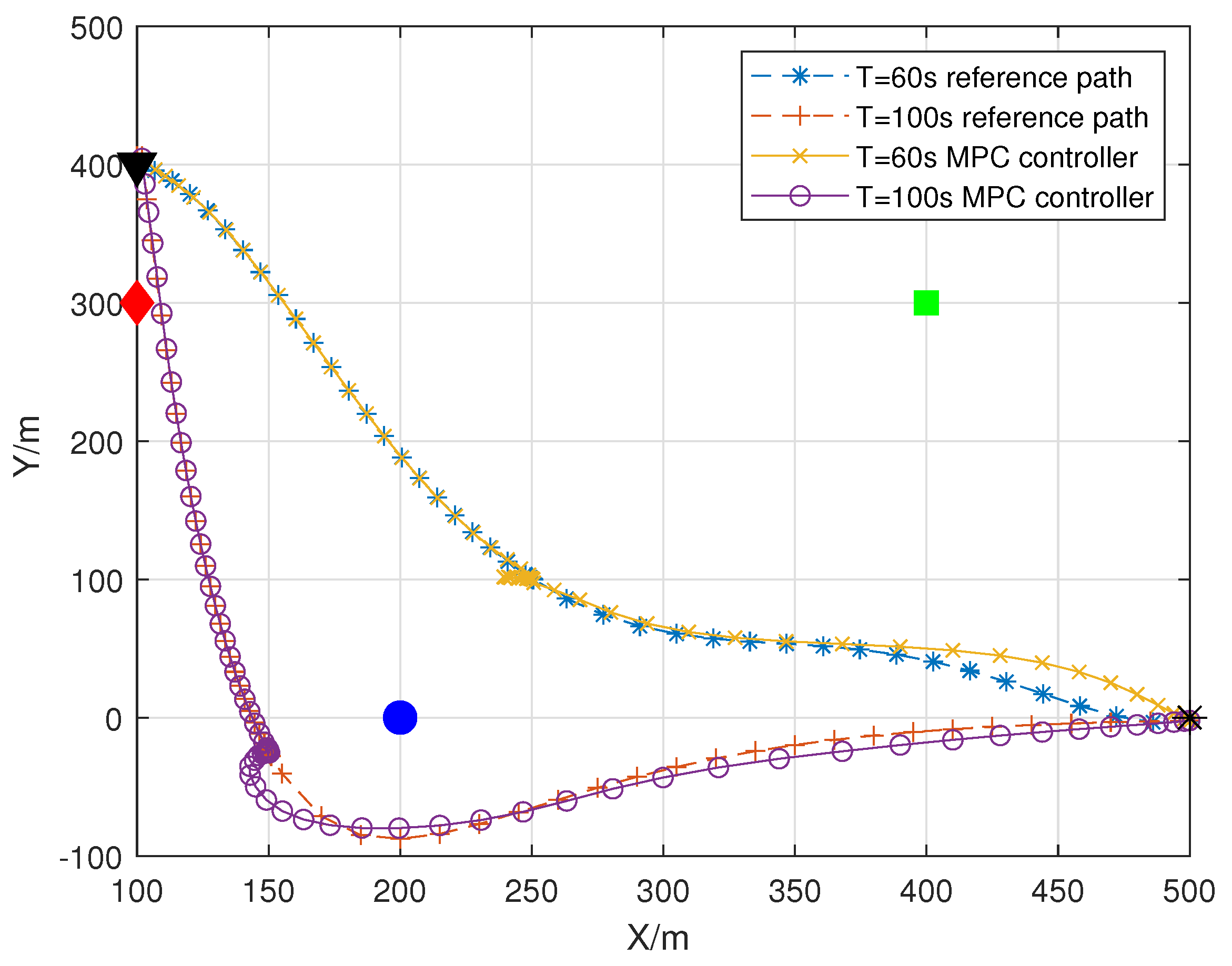
4. MPC-Based Trajectory Tracking

In this section, we employ a MPC-based approach to achieve precise trajectory tracking. The primary objective of MPC is to compute a sequence of control inputs within the prediction horizon, denoted as $N_1$, thereby minimizing the deviation between the reference path optimized in Section 3 and the trajectory predicted by the MPC framework. Accordingly, the control cost function at time instant n is formulated as [44]

$$J_n=\sum _{i=0}^{N_1-1}{\mathbf{e}}_{n+i\mid n}^{\mathrm{T}}{\mathbf{R}}_1{\mathbf{e}}_{n+i\mid n}+▵{\mathbf{v}}_{n+i\mid n}^{\mathrm{T}}{\mathbf{R}}_2▵{\mathbf{v}}_{n+i\mid n}+{\mathbf{e}}_{n+N}^{\mathrm{T}}{\mathbf{R}}_3{\mathbf{e}}_{n+N}$$

(23)

where ${\mathbf{e}}_n={\widehat{\mathbf{q}}}_n-{\widehat{\mathbf{q}}}_{n,\mathrm{ref}}$ represents the error between the true state and the reference optimal state, ${\mathbf{e}}_{n+i\mid n}$ indicates the predicted state deviation at time instant $n+i$, given ${\mathbf{e}}_{n\mid n}={\mathbf{e}}_n$, $▵{\mathbf{v}}_{n+i\mid n}$ denotes the control input at time $n+i$, predicted at time n, while ${\mathbf{R}}_1\in {\mathbb{R}}^{4\times 4}$ and ${\mathbf{R}}_2\in {\mathbb{R}}^{2\times 2}$ are positive definite weighting matrices for the states and inputs, respectively. In (23), the first term corresponds to the state cost, which penalizes deviations from the reference state ${\widehat{\mathbf{q}}}_{n,\mathrm{ref}}$. The second term represents the input cost, penalizing deviations from the steady-state input. Finally, the third term corresponds to the terminal cost, which compensates for the control cost and approximates the result for $N_1=\infty$, thereby enhancing control performance, where ${\mathbf{R}}_3\in {\mathbb{R}}^{4\times 4}$ is the solution to the discrete Riccati function [45], given by

$${\mathbf{R}}_3={\mathbf{R}}_1+{\widehat{\mathbf{A}}}^{\mathrm{T}}{\mathbf{R}}_3\widehat{\mathbf{A}}-{\widehat{\mathbf{A}}}^{\mathrm{T}}{\mathbf{R}}_3\widehat{\mathbf{B}}{\left({\mathbf{R}}_2+{\widehat{\mathbf{B}}}^{\mathrm{T}}{\mathbf{R}}_3\widehat{\mathbf{B}}\right)}^{-1}{\widehat{\mathbf{B}}}^{\mathrm{T}}{\mathbf{R}}_3\widehat{\mathbf{A}}.$$

(24)

Given that perfect knowledge of the control state ${\widehat{\mathbf{q}}}_n$ and control input $▵{\mathbf{v}}_n$ is available on the UAV and BS sides, the MPC-based trajectory tracking optimization problem is formulated as

$$\begin{array}{}\mathrm{(25a)}& \hfill \underset{{\left\{▵{\mathbf{v}}_{n+i\mid n}\right\}}_{i=0}^{N_1-1}}{min}& J_n\hfill \mathrm{(25b)}& \hfill \mathrm{s}.\mathrm{t}.& ▵{\mathbf{v}}_{n+i\mid n}\in \mathit{v},i=0,\dots ,N_1-1,\hfill \mathrm{(25c)}& \hfill & \left(10\right),\left(11\right),\hfill \end{array}$$

where (25b) denotes the control input constraint, with $\mathit{v}$ representing the velocity increment limit of the UAV. Notably, while the control inputs for the entire prediction horizon can be obtained by solving problem (25), only the control input corresponding to the current sampling interval, i.e., ${\mathbf{v}}_n={\mathbf{v}}_{n-1}+▵{\mathbf{v}}_n^{★}$, is applied and transmitted to the UAV. At each subsequent time step, this process is repeated with updated information and a rolling prediction horizon.

To address the formulated problem, we begin by expressing $J_n$ in a quadratic form. Using the control system equations (10) and (11), the predicted control states over the prediction horizon are computed as

$$\begin{array}{cc}\hfill {\widehat{\mathbf{q}}}_{n\mid n}& ={\widehat{\mathbf{q}}}_n,\hfill \\ \hfill {\widehat{\mathbf{q}}}_{n+1\mid n}& =\widehat{\mathbf{A}}{\widehat{\mathbf{q}}}_n+\widehat{\mathbf{B}}▵{\mathbf{v}}_{n\mid n},\hfill \\ \hfill {\widehat{\mathbf{q}}}_{n+2\mid n}& =\widehat{\mathbf{A}}{\widehat{\mathbf{q}}}_{n+1\mid n}+\widehat{\mathbf{B}}▵{\mathbf{v}}_{n+1\mid n}\hfill \\ \hfill & ={\widehat{\mathbf{A}}}^2{\widehat{\mathbf{q}}}_n+\widehat{\mathbf{A}}\widehat{\mathbf{B}}▵{\mathbf{v}}_{n\mid n}+\widehat{\mathbf{B}}▵{\mathbf{v}}_{n+1\mid n},\hfill \\ \hfill & ⋮\hfill \\ \hfill {\widehat{\mathbf{q}}}_{n+N_1\mid n}& ={\widehat{\mathbf{A}}}^{N_1}{\widehat{\mathbf{q}}}_n+{\widehat{\mathbf{A}}}^{N_1-1}\widehat{\mathbf{B}}▵{\mathbf{v}}_{n\mid n}+\dots +\widehat{\mathbf{B}}▵{\mathbf{v}}_{n+N_1-1\mid n},\hfill \end{array}$$

(26)

which can be expressed as the matrix form, i.e,

$${\mathbf{Q}}_n=\mathbf{M}{\widehat{\mathbf{q}}}_n+\mathbf{F}▵{\mathbf{V}}_n,$$

(27)

where ${\mathbf{Q}}_n$ and $▵{\mathbf{V}}_n$ represent the new control state and input matrices, respectively, which are defined as

$${\mathbf{Q}}_n=\left[\begin{array}{c}{\widehat{\mathbf{q}}}_{n\mid n}\\ {\widehat{\mathbf{q}}}_{n+1\mid n}\\ ⋮\\ {\widehat{\mathbf{q}}}_{n+N_1\mid n}\end{array}\right]\in {\mathbb{R}}^{4N_1+4},▵{\mathbf{V}}_n=\left[\begin{array}{c}▵{\mathbf{v}}_{n\mid n}\\ ▵{\mathbf{v}}_{n+1\mid n}\\ ⋮\\ ▵{\mathbf{v}}_{n+N_1-1\mid n}\end{array}\right]\in {\mathbb{R}}^{2N_1},$$

(28)

with

$$\mathbf{M}=\left[\begin{array}{c}{\mathbf{I}}_{4\times 4}\\ \widehat{\mathbf{A}}\\ ⋮\\ {\widehat{\mathbf{A}}}^{N_1}\end{array}\right]\in {\mathbb{R}}^{\left(4N_1+4\right)\times 4},\mathbf{F}=\left[\begin{array}{cccc}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ \widehat{\mathbf{B}}& \mathbf{0}& \cdots & \mathbf{0}\\ \widehat{\mathbf{A}}\widehat{\mathbf{B}}& \widehat{\mathbf{B}}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{\mathbf{A}}}^{N_1-1}\widehat{\mathbf{B}}& {\widehat{\mathbf{A}}}^{N_1-2}\widehat{\mathbf{B}}& \cdots & \widehat{\mathbf{B}}\end{array}\right]\in {\mathbb{R}}^{\left(4N_1+4\right)\times 2N_1}.$$

(29)

Let us denote the reference state matrix as

$${\mathbf{Q}}_{n,\mathrm{ref}}=\left[\begin{array}{c}{\widehat{\mathbf{q}}}_{k,\mathrm{ref}}\\ {\widehat{\mathbf{q}}}_{n+1,\mathrm{ref}}\\ ⋮\\ {\widehat{\mathbf{q}}}_{n+N_1,\mathrm{ref}}\end{array}\right]\in {\mathbb{R}}^{4N_1+4},$$

(30)

which includes the reference position and velocity of the UAV over the prediction horizon. Consequently, the control cost is equivalently reformulated as

$$J_n={\left({\mathbf{Q}}_n-{\mathbf{Q}}_{n,\mathrm{ref}}\right)}^{\mathrm{T}}{\overline{\mathbf{R}}}_1\left({\mathbf{Q}}_n-{\mathbf{Q}}_{n,\mathrm{ref}}\right)+▵{\mathbf{V}}_n^{\mathrm{T}}{\overline{\mathbf{R}}}_2▵{\mathbf{V}}_n,$$

(31)

where ${\overline{\mathbf{R}}}_1=\mathrm{diag}\left({\mathbf{R}}_1,\dots ,{\mathbf{R}}_1,{\mathbf{R}}_3\right)$ and ${\overline{\mathbf{R}}}_2=\mathrm{diag}\left({\mathbf{R}}_2,\dots ,{\mathbf{R}}_2\right)$. Substituting (27) into (31) yields the reformulated control cost function

$$J_n=▵{\mathbf{V}}_n^{\mathrm{T}}\mathbf{H}▵{\mathbf{V}}_n+\mathbf{E}▵{\mathbf{V}}_n+G,$$

(32)

where

$$\mathbf{H}={\mathbf{F}}^{\mathrm{T}}{\overline{\mathbf{R}}}_1\mathbf{F}+{\overline{\mathbf{R}}}_2,$$

(33)

$$\mathbf{E}=2\left({\widehat{\mathbf{q}}}_n^{\mathrm{T}}{\mathbf{M}}^{\mathrm{T}}-{\mathbf{Q}}_{n,\mathrm{ref}}^{\mathrm{T}}\right){\overline{\mathbf{R}}}_1\mathbf{F},$$

(34)

$$G={\widehat{\mathbf{q}}}_n^{\mathrm{T}}{\mathbf{M}}^{\mathrm{T}}{\overline{\mathbf{R}}}_1\mathbf{M}{\widehat{\mathbf{q}}}_n-2{\widehat{\mathbf{q}}}_n^{\mathrm{T}}{\mathbf{M}}^{\mathrm{T}}{\overline{\mathbf{R}}}_1{\mathbf{Q}}_{n,\mathrm{ref}}+{\mathbf{Q}}_{n,\mathrm{ref}}^{\mathrm{T}}{\overline{\mathbf{R}}}_1{\mathbf{Q}}_{n,\mathrm{ref}}.$$

(35)

Therefore, problem (25) is equivalently transformed into

$$\begin{array}{}\mathrm{(36a)}& \hfill \underset{▵{\mathbf{V}}_n}{min}& J_n\hfill \mathrm{(36b)}& \hfill \mathrm{s}.\mathrm{t}.& ▵{\mathbf{V}}_n\in \mathit{V},\hfill \end{array}$$

where $\mathit{V}$ constrains the control input matrix $▵{\mathbf{V}}_n$. Since the objective function $J_n$ is quadratic with positive definite weighting matrix $\mathbf{H}$, problem (36) can be efficiently solved as a convex QP problem by employing standard techniques [42,43]. At every time slot, the MPC-based optimization problem is solved and the optimal control input is calculated as $▵{\mathbf{v}}_n^{★}={\left(▵{\mathbf{V}}_n^{★}\right)}_1$, where ${\left(▵{\mathbf{V}}_n^{★}\right)}_1$ corresponds to the first two elements of $▵{\mathbf{V}}_n^{★}\in {\mathbb{R}}^{2N_1}$.

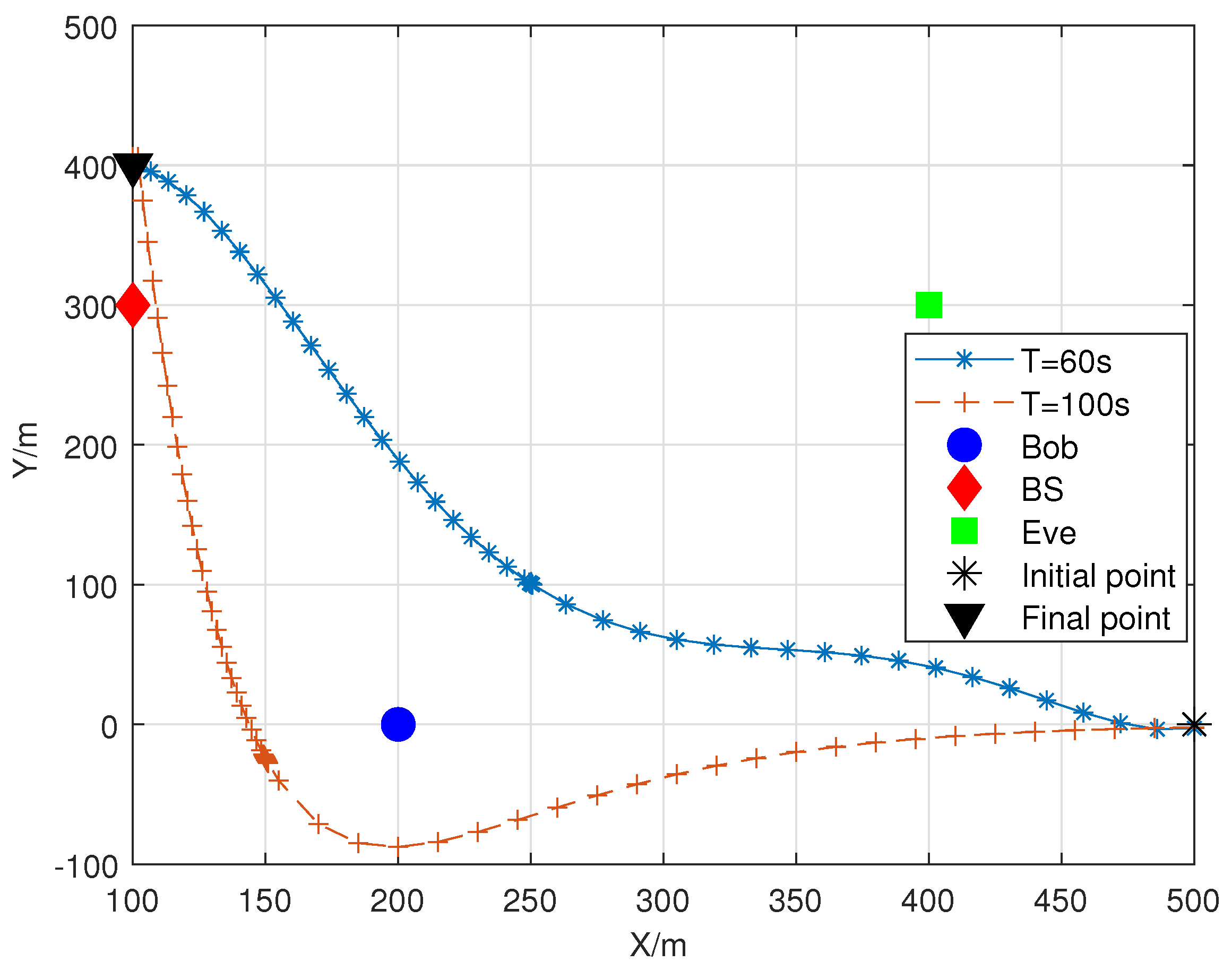
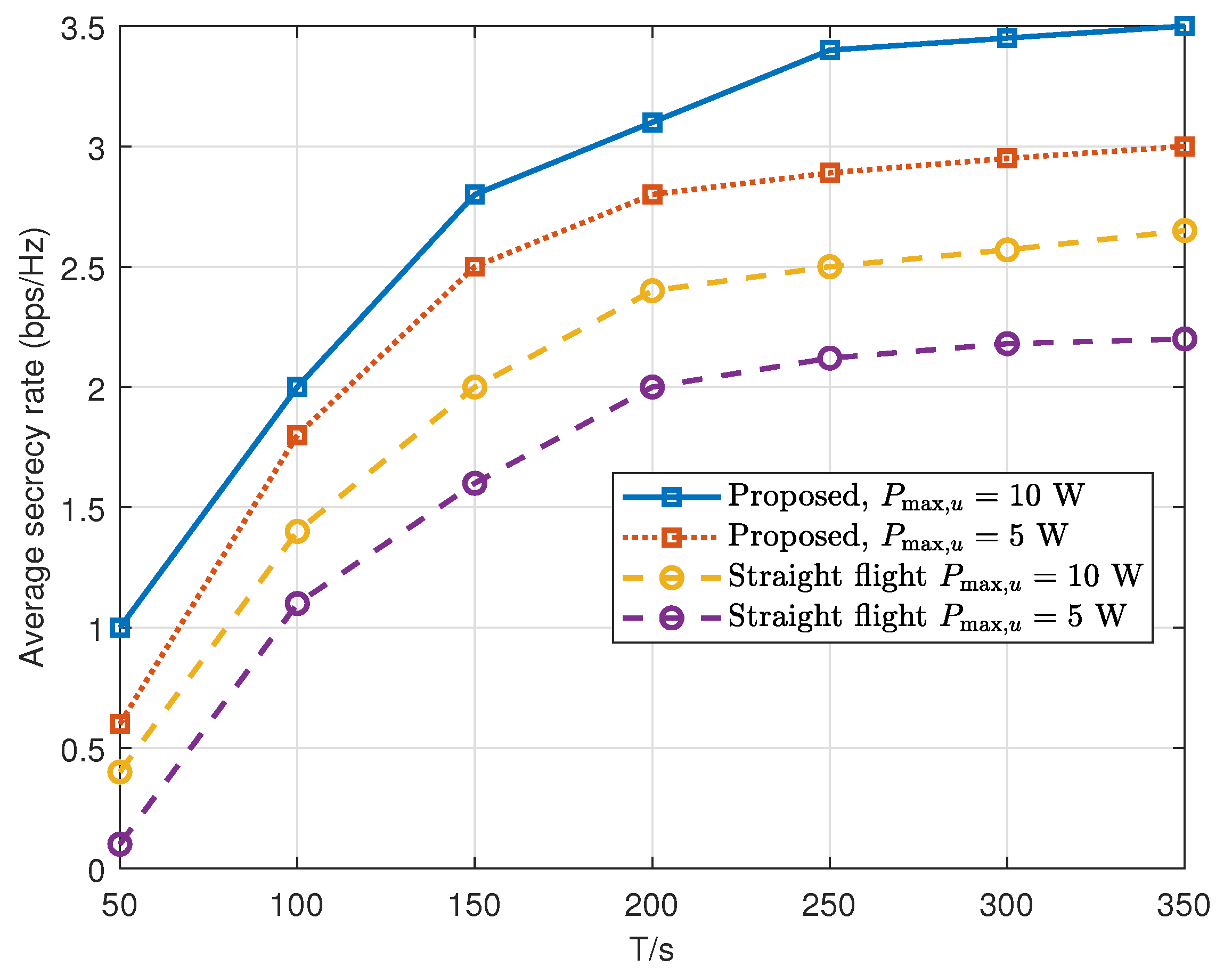
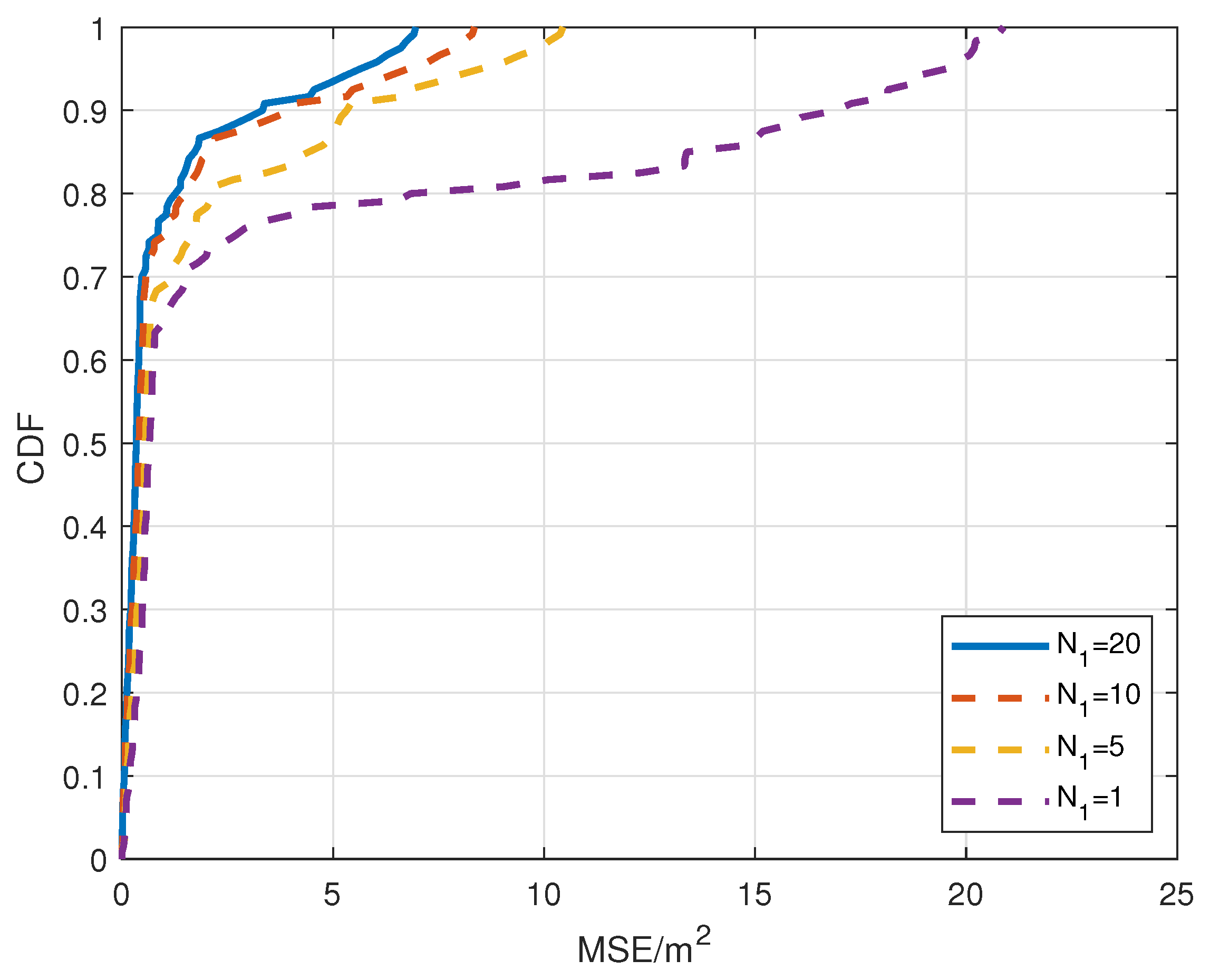
5. Simulation Results

In this section, we present the simulation results to verify the effectiveness of our proposed algorithm. Unless otherwise specified, the system parameters are set as follows: the maximum UAV speed is $V_{max}=30$ m/s, the channel gain at a unit reference distance is ${\rho }_0=-60$ dB and the received noise at the receivers is set to ${\sigma }_0^2=-110$ dBm. The locations corresponding to the BS, Bob, and Eve are set to ${\mathbf{b}}_0={[100,300]}^T$ m, ${\mathbf{q}}_b={[200,0]}^T$ m, and ${\mathbf{q}}_e={[400,300]}^T$ m, respectively. Moreover, we set the initial point and the final point to ${\mathbf{q}}_I={[500,0]}^T$ m and ${\mathbf{q}}_F={[100,400]}^T$ m, respectively. As for the control part, the weighting matrices for the states and inputs, ${\mathbf{R}}_1$ and ${\mathbf{R}}_2$, are both identity matrices.

Figure 2 illustrates the UAV’s trajectory under varying total durations, demonstrating how the UAV dynamically adjusts its path to optimize secure communication. As the total mission duration increases, the UAV’s trajectory becomes closer to Bob and the BS. This is because a longer flight time enables the UAV to better fly away from Eve. The trajectory for the $T=60$ s demonstrates a steeper descent toward the final position, reflecting a more direct path to the goal. In contrast, the trajectory for the longer duration $T=100$ s is more gradual, indicating that the UAV takes a longer path to the final position. This behavior is expected as the UAV has more time to adjust its trajectory, potentially avoiding eavesdropping. Moreover, the UAV tends to hover closer to Bob during critical communication periods for enhancing the system throughput.

Figure 3 depicts the average secrecy rate as a function of time duration for different transmit powers compared to the benchmark scheme straight flight approach, in which the UAV directly flies from the initial point to the destination. It is evident that for both proposed and straight flight trajectories, increasing the transmit power from 5 W to 10 W results in a higher average secrecy rate, highlighting the trade-off between power and security. Furthermore, the proposed design, which adapts the UAV’s trajectory based on the available time, outperforms the straight-flight approach in all cases, suggesting that adjusting the UAV’s flight path can significantly enhance communication security, especially when combined with higher transmit power. Additionally, the average secrecy rate tends to stabilize over longer durations. The reason is that the UAV, with long flight durations, is capable of flying to hover over Bob, providing considerable communication service.

Figure 4 illustrates the UAV’s trajectory tracking performance using MPC. At the start, a noticeable deviation from the reference path occurs as the UAV adjusts its velocity and position to align with the desired trajectory. Similarly, some tracking errors appear at the hovering position, likely due to the difficulty in maintaining precise stabilization. However, as the UAV progresses, the tracking accuracy improves significantly, closely following the reference path. This demonstrates the effectiveness of the MPC controller in continuously refining the UAV’s motion, enabling smooth and accurate trajectory tracking despite initial deviations. Figure 5 shows the cumulative distribution function (CDF) of the mean squared error (MSE) between the UAV’s actual trajectory and the reference trajectory under different prediction horizons. The MSE quantifies the tracking error, with lower values indicating better adherence to the reference path. As expected, the CDF curve shifts to the right as the prediction horizon decreases, with the $N_1=20$ case achieving the best tracking performance, showing a higher proportion of lower MSE values. This demonstrates that a larger prediction horizon allows the MPC controller to plan further ahead, leading to more accurate trajectory tracking. As the prediction horizon decreases, the controller has less foresight, which results in larger tracking errors. This highlights the importance of a sufficiently large prediction horizon for optimal trajectory tracking in dynamic environments.

6. Conslusions

In this paper, we have presented a novel framework for secure communications in UAV-assisted relay networks. Our approach jointly optimized the UAV’s transmit power and trajectory, addressing the security vulnerabilities posed by the reliance on LoS channels. By employing a MPC-based approach, we have demonstrated how the UAV’s trajectory can be adaptively controlled in real-time, improving the resilience of the system against dynamic environmental conditions and potential eavesdropping threats. We first formulated a non-convex secrecy rate maximization problem and proposed an efficient solution using SCA techniques. The MPC-based path tracking ensured that the UAV could follow the optimized trajectory efficiently, even under practical constraints and disturbances. Simulation results show that the proposed joint optimization framework significantly enhances communication security, providing robust performance under dynamic conditions.