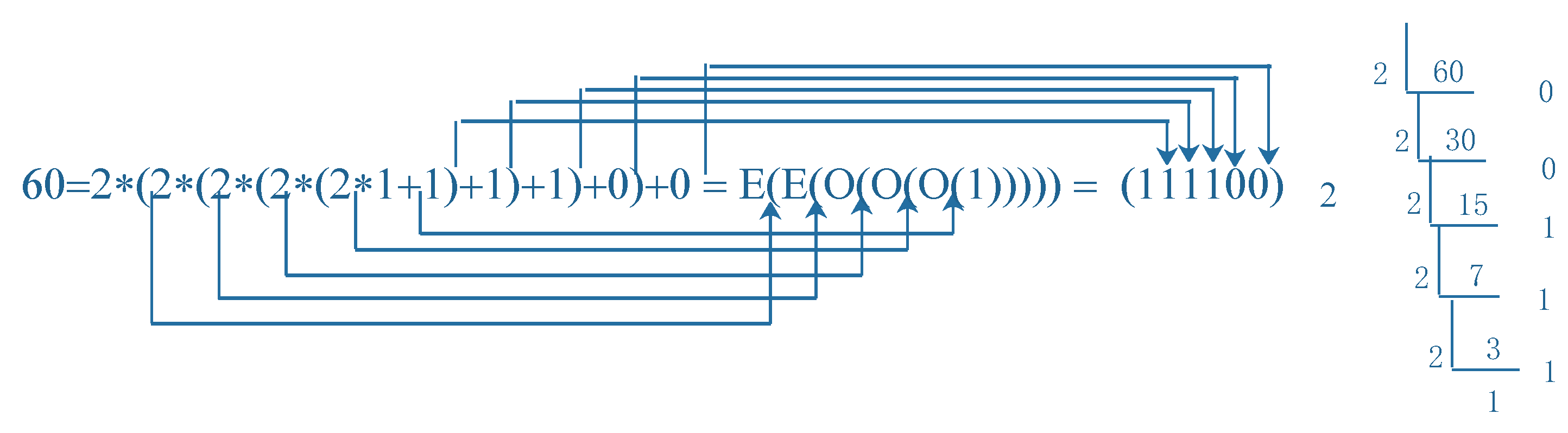Binary Representation of Natural Numbers and Collatz Conjecture

1. Introduction

In the study of number theory, odd and even numbers are a fundamental pair of ideas. The set of natural numbers can be divided into odd and even sets. There are many conjectures that attempt to generalize the fact of different kinds of natural numbers discovered in a restricted range to the entire infinite set of natural numbers. This article will discuss the famous Collatz conjecture, which states that for each natural number n, if it is even, divided by 2, if it is odd, multiplied by 3, and added 1, and so on, the eventual value must be 1. It is also referred to as the $3n+1$ conjecture and was put forth in 1937 by Lothar Collatz, also known as the $3n+1$ problem. Because it is an extremely simple to state, extremely hard to solve problem, the mathematician Paul Erdos once said of this conjecture: "Mathematics may not be ready for such problems" [1,2].

Inspired by Euler’s dot-line graph in graph theory for solving the Konigsberg Seven Bridge problem, we have confidence that a similar solution can be found. Leveraging our knowledge of piecewise and iteration functions, binary strings, and full binary trees, we utilize binary strings to illustrate the step-by-step progression of odd-function and/or even-function iterations, concealed within the Decimal Number System. While the prune strategy of the full binary tree which is equivalent to the Collatz function, we are convinced that the existing framework is adequate to substantiate the conjecture.

In the natural number set, we say a pair notions even and odd, if and only if a number n has a remainder of 0 or 1 upon division by 2. The number 1 is the smallest big natural number. The result of the finite times of the iteration of even-number and /or odd-number is n which concealed the procedure of the iteration of even-number and /or odd-number from 1. For the binary string of n represents the procedure of iteration of even-number and /or odd-number from 1.

The Collatz conjecture talks about the inverse procedure of a given natural number n to 1. In binary string the function $3n+1$ is equivalent to $n+(2n+1)$ which is the add function of two binary strings, one is shifted to left one bit and appends 1 in the last bit, another one is itself. In binary string the function ${\displaystyle \frac{n}{2}}$ is to delete all zeros in right last substring. Those facts are the key opinions to discuss the Collatz conjecture.

For the Collatz conjecture, we can describe it as a piecewise function:

$$T\left(n\right)=\left\{\begin{array}{cc}3n+1,& \mathrm{if}n\mathrm{is}\mathrm{odd},\mathrm{the}\mathrm{result}\mathrm{must}\mathrm{be}\mathrm{even},\\ {\displaystyle \frac{n}{2}}& \mathrm{if}n\mathrm{is}\mathrm{even},\mathrm{the}\mathrm{result}\mathrm{is}\mathrm{either}\mathrm{odd}\mathrm{or}\mathrm{even}.\end{array}\right.$$

(1)

The following sequence is obtained via the iteration of the Collatz function:

$\Lambda =\{n,T\left(n\right),T\left(T\left(n\right)\right),T\left(T\left(T\left(n\right)\right)\right),\cdots \}=\{n,T\left(n\right),T^2\left(n\right),T^3\left(n\right),\cdots \}$.

Consequently, the Collatz conjecture can be stated as follows:

Collatz conjecture 1: For any natural number n, there is a finite natural number m, and the sequence $\Lambda$ always leads to the integer 1, that is, $T^m\left(n\right)=1$.

The series $\Lambda$ is an infinite sequence of ultimately period [4,5]. So we give another statement of the Collatz conjecture as the following.

Collatz conjecture 2: The series $\Lambda$ is an infinite sequence of ultimately period, the preperiod $\eta \left(n\right)$ varies with the initial value n, but the ultimately period is always $\{1,4,2\}$.

2. A Graph and Algebra Representation of the Natural Numbers

Natural numbers are gradually formed in the long-term practice of human beings, which is mainly used to represent the number of things and the order of things. Natural numbers should be expressed in an appropriate way, and their forms of representation are not small differences in different periods of human civilization, and the Arabic numbers 1,2,3,... And decimal values to express natural numbers. Strictly speaking, the infinite set of all natural numbers N = (1,2,3,...) Together with the addition (+) and multiplication (•) operations defined therein, they form the natural number system.

Natural numbers are mainly used to represent the number of things and the order of things, resulting in a pair of logical thinking methods and mathematical induction, as well as iterative technical methods.

Although the decimal system is very convenient in daily life, and the process of natural numbers is encapsulated by ten Arabic numbers. Although Gottfried Wilhelm Leibniz [11] in 1703 gave a paper talking about the binary string role, the invention of electronic computers is in 1946, which prompts us to re-understand and think about the meaning and function of natural numbers in binary.

2.1. The Iteration of Odd-Number and /or Even-Number Function

A natural number is considered even if it can be divided by 2; if not, it is considered odd. According to the Peano axiom, the smallest natural number is 1. The set $N=\{1,2,3,\cdots \}$ of natural numbers can be divided into odd and even sets; in this paper, we will use the usual definition of natural numbers.

$\left\{\mathbf{natural}\mathbf{number}\right\}=\left\{\mathbf{odd}\mathbf{number}\right\}\bigcup \left\{\mathbf{even}\mathbf{number}\right\}$.

In the set of natural numbers where 1 is the smallest odd number and 2 is the smallest even number, we can use the function $n=2k-1$ to indicate that n it is an odd, and the function $n=2k$ to indicate that it is an even, where k is any natural number.

We introduce two functions $O\left(x\right)=2x+1$ to express odd numbers greater than 1, and $E\left(x\right)=2x$ to express even numbers, where x is any natural number in N.

We define a strictly increase monotonically piecewise function $f\left(n\right)$, from a natural number n it generates two cases: odd or even numbers:

$$f\left(n\right)=\left\{\begin{array}{cc}2n+1=O\left(n\right),& \mathrm{the}\mathrm{result}\mathrm{is}\mathrm{odd}\mathrm{number},\\ 2n=E\left(n\right),& \mathrm{the}\mathrm{result}\mathrm{is}\mathrm{even}\mathrm{number}.\end{array}\right.$$

(2)

Definition 1 A natural number n is obtained by finite iterations of the odd-number function$O\left(x\right)=2x+1$ or (and) the even-number function$E\left(x\right)=2x$ several times, namely

$$n=f\left(f(\cdots f\left(1\right))\right)=f^k\left(1\right),$$

the function per function f is either an odd number function $O\left(x\right)$ or an even number function $E\left(x\right)$.

For example, $f\left(1\right)=O\left(1\right)=3,f\left(1\right)=E\left(1\right)=2$,

$7=f^2\left(1\right)=2·3+1=2·(2·1+1)+1)=O\left(O\left(1\right)\right)$,

$\begin{array}{l}189=2·94+1=2·(2·\left(47\right)+1=2·(2·(2·23+1))+1=2·(2·(2·(2·11+1)+1))+1\\ =2·(2·(2·(2·(2·5+1)+1)+1))+1=2·(2·(2·(2·(2·(2·2+1)+1)+1)+1))+1\\ =2·(2·(2·(2·(2·(2·(2·1)+1)+1)+1)+1))+1=f^7\left(1\right)=O\left(E\right(O(O\left(O\left(O\left(E\left(1\right)\right)\right)\right)\end{array}$.

Any natural integer n is the value of the finite-time iteration function of the odd-number and even-number functions starting at 1.

Definition 2 The inverse functions $f^{-1}\left(x\right)$,

$$f^{-1}\left(n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n-1}{2}},& \mathrm{If}n\mathrm{is}\mathrm{odd}\mathrm{number}\mathrm{and}n>1,\\ {\displaystyle \frac{n}{2}},& \mathrm{If}n\mathrm{is}\mathrm{even}\mathrm{number}.\end{array}\right.$$

(3)

Therefore, If $n=f\left(f(\cdots f\left(1\right))\right)=f^r\left(1\right)$, then $f^{-r}\left(n\right)=1$.

2.2. Use the Binary String to Represent the Process of Iteration from 1

By employing binary string representations for natural numbers, we establish a more transparent framework for characterizing the iterative processes of both odd-number and even-number functions originating from 1. Within this framework, the binary string serves as an explicit encoding of the functional iteration sequence, where each bit position systematically indicates the application order of the fundamental operations $O\left(x\right)$ (odd-number function) and $E\left(x\right)$ (even-number function).

The binary string representation of a natural number encodes its corresponding sequence of odd-even functional iterations. Specifically, in this encoding scheme, each bit position from left to right corresponds to a distinct iteration step, where the appearance of a 1 in the $i^{th}$ bit position signifies the application of the odd number function $O\left(x\right)$ at the $i^{th}$ iteration, while a 0 in the $i^{th}$ bit position indicates the application of the even number function $E\left(x\right)$ at that step.

To convert a given natural number n to its binary string, we can use the following recursion steps:

1. Iterate over the number n, repeatedly dividing it by 2 and keeping track of the remaining.

2. Append the remainder to the binary string from right to left.

3. Continue dividing n by 2 until it reaches 0.

For instance, the procedure of the iteration function from 1 to 60 is shown in Figure 1.

2.3. Use an Algebra Expression to Represent the Process of the Iteration from 1

For a given natural number n, we obtain its binary string $n={(1\times \cdots \times )}_2$ and algebra expression as $n=2^r+2^m+\cdots$, Thus for the multiplication

$2n=2^{r+1}+2^{m+1}+\cdots$

and

$3n+1=(2n+1)+n=2^{r+1}+2^{m+1}+\cdots +2^0+2^r+2^m+\cdots$.

For example, for $7={\left(111\right)}_2=2^2+2^1+2^0$, there are $2·7={\left(1110\right)}_2=2^3+2^2+2^1,$$3·7+1={\left(10110\right)}_2=2·7+(7+1)=2^3+2^2+2^1+2^0+2^2+2^1+2^0=2^4+2^2+2^1$.

2.4. Use a Graph to Represent the Process of the Iteration from 1 and a Natural Number Tree

In order to give an intuitive impression, we provide a full binary tree to represent the procedure of iteration function of the odd-functions $O\left(x\right)$ and /or even-functions $E\left(x\right)$ of a given natural number n, the root is the smallest number 1. For per vertex, its left-child is an even number which double itself, its binary string is appended by 0, right-child is an odd number which double itself and add 1, its binary string is appended by 1. The full binary tree, as in Figure 2, is a very good representation of some natural numbers, we can call it as a natural number tree [7,8].

Proposition 1 A binary string’s length indicates its level in the full binary tree, and a binary string’s length minus one represents the number of times the odd- and /or even-number iterative functions occur.

For a natural number n, its binary string, composed of 0s and 1s from left to right, represents the path starting from the root node 1, and tracing down to the current node n in the full binary tree. In this tree, each node only has one path leading from the root to itself. As an illustration, the procedures for the composite odd number 21 and the even number 28 are depicted in Figure 3.

For the above example, for $7={\left(111\right)}_2$, there are $2·7=14={\left(1110\right)}_2,$ $3·7+1=(2·7+1)+7=22={\left(1111\right)}_2+{\left(111\right)}_2={\left(10110\right)}_2$.

2.5. Another Partition of the Natural Number Set

To analyze the iterative functions of the odd-function and /or even-function, we introduce a new partition of the natural number set within the full binary tree. We designate distinct names to the numbers located on the left path, right path, and between the two paths in the tree.

We give the definitions of three kinds of natural number:

Definition 3(i) A natural number, $O^m\left(1\right)=2^m-1=2^{m-1}+2^{m-2}+\cdots +2+1={(11\cdots 1)}_2$, is obtained by applying the odd-number function $O\left(x\right)$m iterations. We call it as pure odd number. For instance, those are pure odd numbers: $3={\left(11\right)}_2,7={\left(111\right)}_2,15={\left(1111\right)}_2,31={\left(11111\right)}_2,63={\left(111111\right)}_2,\cdots$. These are located in the full binary tree of Figure 2, which is in the right path.

(ii) A natural number, $E^m\left(1\right)=2^m={(10\cdots 0)}_2$ , is obtained by applying the even-number function $E\left(x\right)$m iterations. We call it as pure even number. For instance, those are pure even numbers: $2={\left(10\right)}_2$, $4={\left(100\right)}_2$, $8={\left(1000\right)}_2$, $16={\left(10000\right)}_2$, $32={\left(100000\right)}_2$, $64={\left(1000000\right)}_2$. Those are located in the left path of the full binary tree of the Figure 2.

(iii) The natural number obtained by the iteration of odd function $O\left(x\right)$ and /or even function $E\left(x\right)$, we call it as mixed number. Such as, $18={\left(10010\right)}_2,28={\left(11100\right)}_2,67={\left(1000011\right)}_2,309={\left(100110101\right)}_2$. Those are in the inside of the left and right paths of the full binary tree, the Figure 2.

In particular, the natural numbers obtained by the finite alternately iterations of the odd function $O\left(x\right)$ and the even function $E\left(x\right)$, namely, ${\left[E\left(O\left(1\right)\right)\right]}^m={(101\cdots 101)}_2$. Such as $5={\left(101\right)}_2,21={\left(10101\right)}_2,85={\left(1010101\right)}_2,341={\left(101010101\right)}_2,1365={\left(10101010101\right)}_2,5461={\left(1010101010101\right)}_2,\cdots .$ We call it as hard numbers.

Proposition 2 The set of natural numbers can be divided into three sets:

{natural number}=

{pure even number}∪{pure odd number}∪{mixed number},

where {mixed number}={mixed even number}∪{mixed odd number}.

Example (1) 60, 97 are mixed numbers.

(2)$64,1180591620717411303424$ are pure even numbers.

(3)$63,1180591620717411303423$ are pure odd numbers.

When we convert those natural numbers from decimal to binary, the facts are obvious.

(1) $60={\left(111100\right)}_2$ is a mixed-even number, $97={\left(1100001\right)}_2$ is a mixed-odd number.

(2) $64=2^6=\left(1000000\right)$, $1180591620717411303424=2^{70}=(10000\cdots 0)$ are pure even numbers:

(3) $63={\left(111111\right)}_2$, $1180591620717411303423=2^{70}-1=(11\cdots 1)$ are pure odd numbers.

Thus for a given natural number $n=f^r\left(1\right)$, we first convert it to binary string which length is r, secondly in the level r of the natural number tree and from the top 1 along the path to the binary string. The traversal path in the full binary tree from the root down along the arcs, for each natural integer n, is its binary string $1\times \times$, where the left-child appended 0 for each node is an even number and the right-child appended 1 for each node is an odd number. For instance, in Figure 3, $21={\left(10101\right)}_2$ originates at the root 1 and proceeds down 2,5,10, ultimately reaching 21. To the nodes, $1\to 10\to 101\to 1010\to 10101$, 0,1,0,1 are appended. In addition, for $28={\left(11100\right)}_2$, the appendix 1,1,0,0 is added to the nodes, $1\to 11\to 111\to 1110\to 11100$, accordingly in dicimal it traces from the root 1 down 3,7,14, and ultimately reaches 28.

3. Find the Traversal Path to Its Root in the Natural Number Tree

3.1. The Iteration of Piecewise Function

A piecewise function is a mathematical function that is defined by different rules or formulas over different intervals or regions of its domain. Piecewise functions are commonly used to model situations where different rules apply in different circumstances or to account for discontinuities in a function’s behavior. The Collatz function, denoted by $T\left(n\right)$, can be expressed as a piecewise function, with separate cases for odd and even numbers.

An iterative function is a function that is repeatedly applied to its own output. In other words, the output of the function is used as the input for the next iteration of the function. Iterative methods involve using iterate functions to repeatedly update an initial estimate or solution until a desired level of accuracy is achieved. Iteration means repetition, and with more repetition, things will change in nature.

In order to proof the Collatz conjecture 1 in Section 1, finding the beingness and finiteness of the number m in the expression $T^m\left(n\right)=1$ for a natural number n is the main challenge. Iteration is the key to Collatz conjecture, and although there are only two cases where piecewise functions are combined with iterative functions, the result is difficult to control.

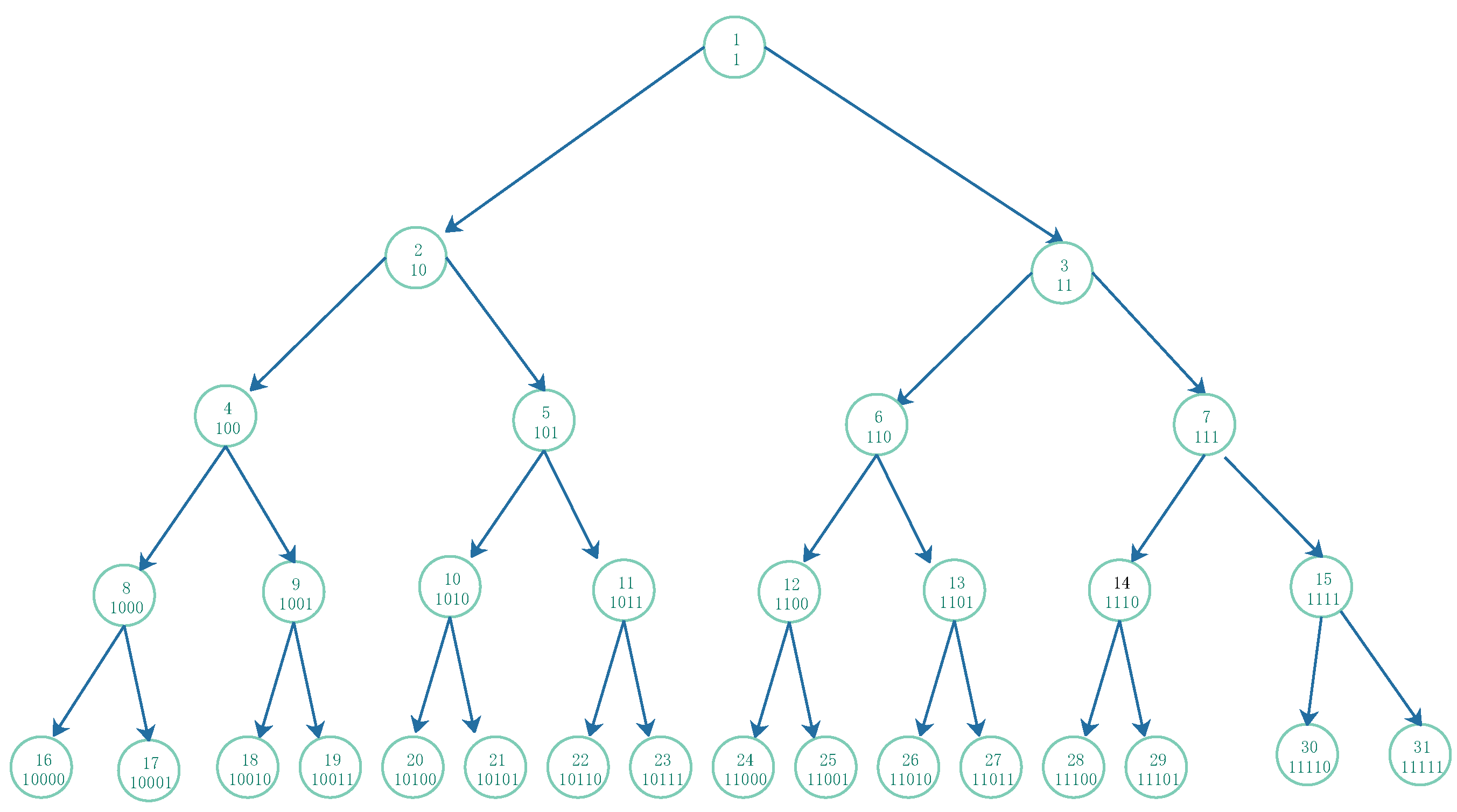
For given natural k, the iterative formula $f^k\left(1\right)=n$ for a given natural number n, we know that k is the length of the binary string of n minus 1, it is also the level of the full binary tree. In decimal notation, we represent n, which obscures the iteration process of odd- and /or even-number functions. When n is represented as a binary string, it can be used to understand how odd- and /or even-number functions iterative work.

3.2. The Collatz Function and the Reduced Collatz Function

As the Collatz function $T\left(n\right)$ (1), we can get the result about the $f\left(x\right)$ and $f^{-1}\left(x\right)$

$$T\left(n\right)=\left\{\begin{array}{cc}3n+1=(2n+1)+n=f\left(n\right)+n,& \mathrm{if}n\mathrm{is}\mathrm{odd}\mathrm{number},\\ {\displaystyle \frac{n}{2}}=f^{-1}\left(n\right)& \mathrm{if}n\mathrm{is}\mathrm{even}\mathrm{number}.\end{array}\right.$$

(4)

The iteration of the Collatz function is the key topic in discuss the proof procedure, we have the reduced Collatz function [2,3,6] $RT\left(x\right)$

$$RT\left(n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{3n+1}{2^m}}=T^{m+1}\left(n\right)=f^{1-m}\left(n\right)+f^{-m}\left(n\right)& \mathrm{if}n\mathrm{is}\mathrm{odd},\mathrm{the}\mathrm{result}\mathrm{must}\mathrm{be}\mathrm{odd}.\\ {\displaystyle \frac{n}{2^r}}=T^r\left(n\right)=f^{-r}\left(n\right)& \mathrm{if}n\mathrm{is}\mathrm{even},\mathrm{the}\mathrm{result}\mathrm{must}\mathrm{be}\mathrm{odd}.\end{array}\right.$$

(5)

where m is the number of the zeros of the end substring of the number $3n+1$, and r is the number of the zeroe of the end-substring of the number n.

There are many different points for piecewise functions when comparing the Collatz function $T\left(x\right)$ with the inverse function $f^{-1}\left(x\right)$, and the reduced Collatz function $RT\left(x\right)$ with the inverse function iteration $f^{-k}\left(x\right)=O(E(\cdots \left(E\left(x\right)\right))$.

1) For any natural number x function $f^{-1}\left(x\right)$ and $f^{-r}\left(x\right)={\left(f^{-1}\left(n\right)\right)}^r$ are strictly monotonically decreasing.

2) The function $T\left(x\right)$ is increasing in the case x is an odd, in the other case, is decreasing.

3) The function $RT\left(x\right)$ that describes the procedure of the iterative function of $T\left(x\right)$, is wavy when x is a pure or mixed odd number and decreases when x is pure even or mixed even.

$RT\left(n\right)$	${\displaystyle \frac{n}{2}}$	${\displaystyle \frac{n}{2^2}}$	${\displaystyle \frac{n}{2^3}}$	${\displaystyle \frac{n}{2^4}}$	⋯
$T\left(n\right)$	$T^1\left(n\right)$	$T^2\left(n\right)$	$T^3\left(n\right)$	$T^4\left(n\right)$	⋯
$monotonicity$	↓	$\downarrow \downarrow$	$\downarrow \downarrow \downarrow$	$\downarrow \downarrow \downarrow \downarrow$	⋯
$compare$	$RT\left(n\right)<n$	$RT\left(n\right)<n$	$RT\left(n\right)<n$	$RT\left(n\right)<n$	⋯
$RT\left(n\right)$	${\displaystyle \frac{3n+1}{2}}$	${\displaystyle \frac{3n+1}{2^2}}$	${\displaystyle \frac{3n+1}{2^3}}$	${\displaystyle \frac{3n+1}{2^4}}$	⋯
$T\left(n\right)$	$T^2\left(n\right)$	$T^3\left(n\right)$	$T^4\left(n\right)$	$T^5\left(n\right)$	⋯
$monotonicity$	$\uparrow \downarrow$	$\uparrow \downarrow \downarrow$	$\uparrow \downarrow \downarrow \downarrow$	$\uparrow \downarrow \downarrow \downarrow \downarrow$	⋯
$compare$	$RT\left(n\right)>n$	$RT\left(n\right)<n$	$RT\left(n\right)<n$	$RT\left(n\right)<n$	⋯

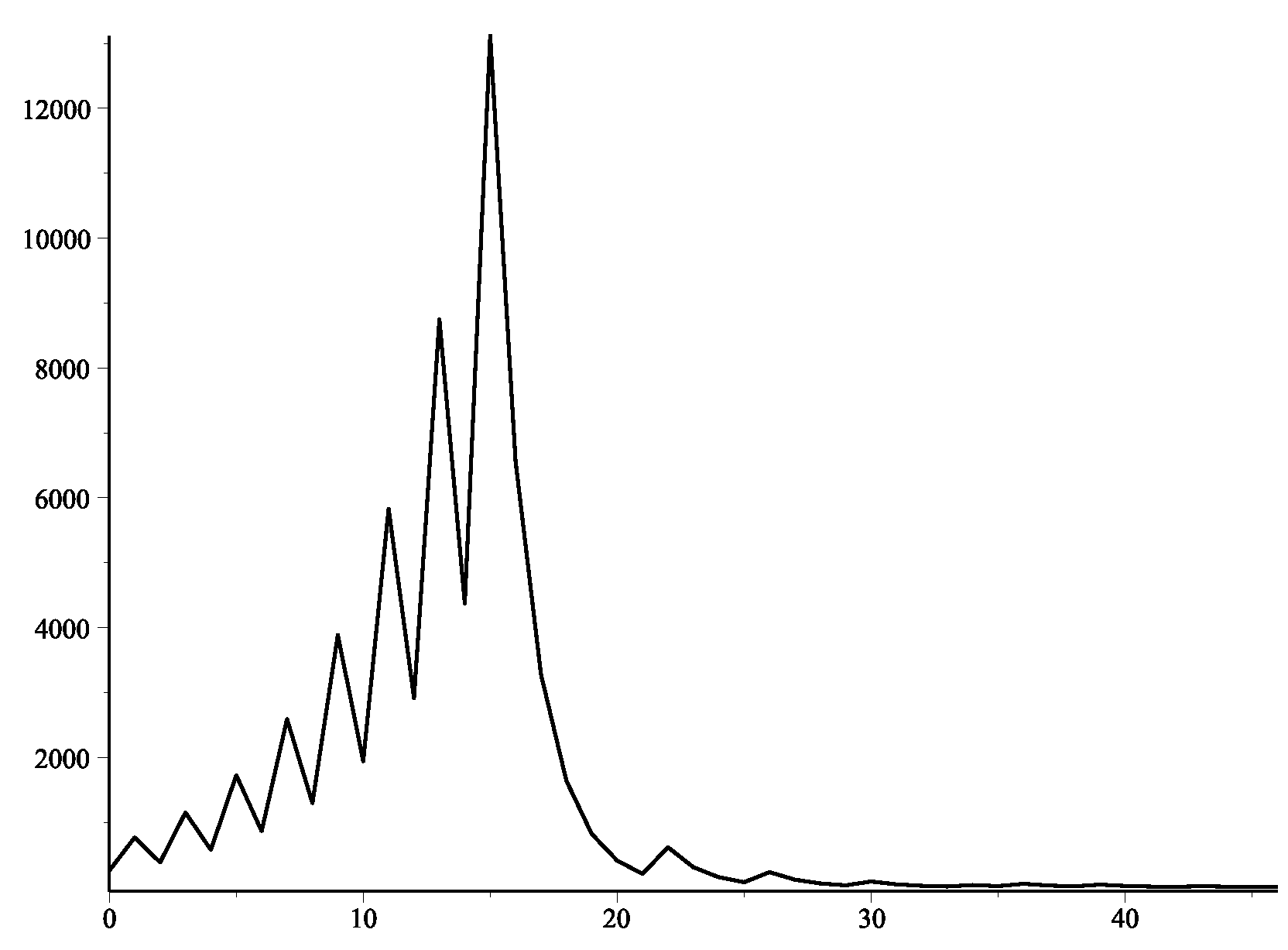
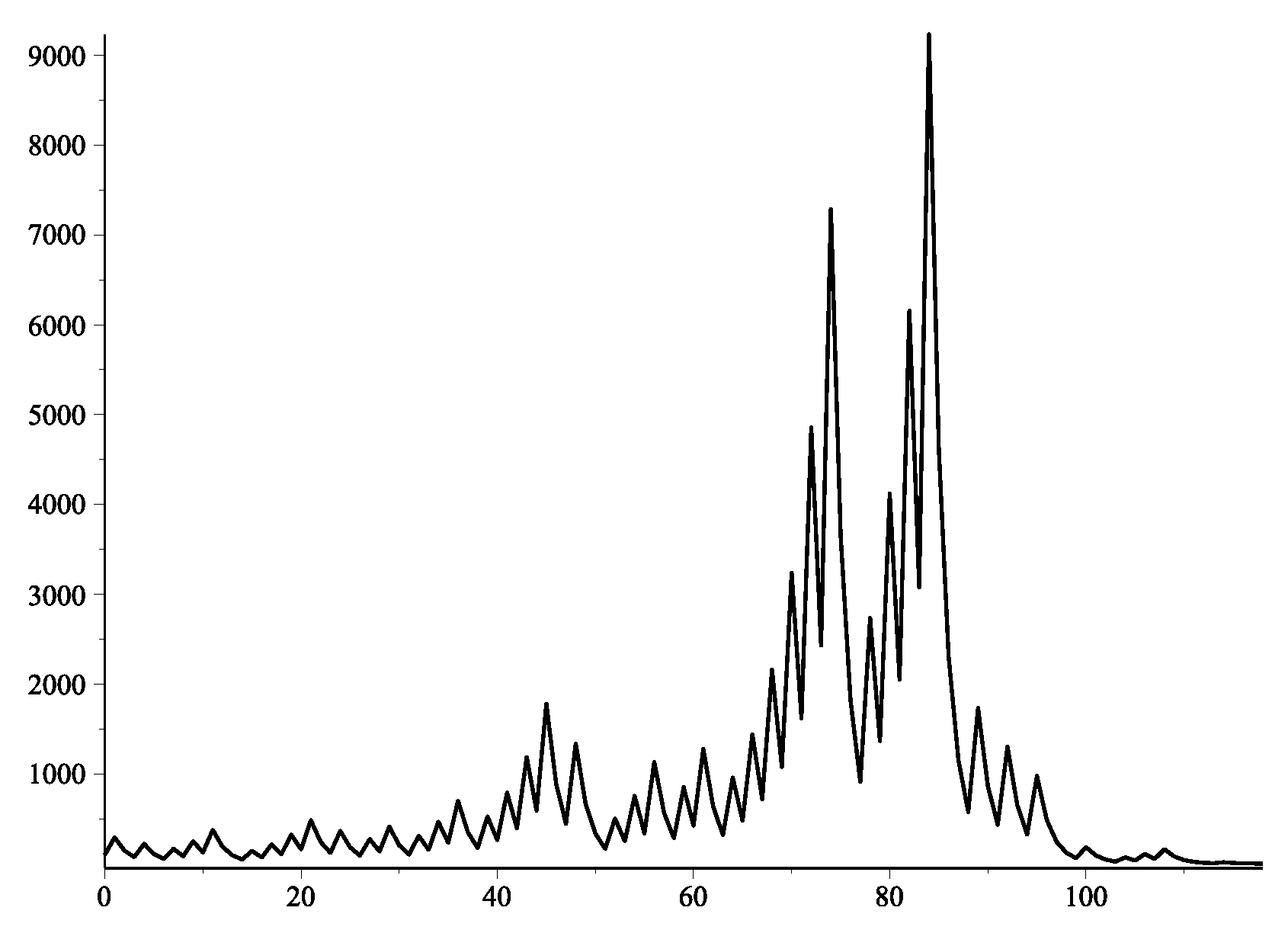
The function $RT\left(x\right)$ describes the iterative procedure of $T\left(x\right)$. The wavy function is increasing at first, then goes through one or more decreasing processes, either as "increase – decrease – increase" or "increase – decrease ⋯ decrease – increase." For example, the iterated sequence of Collatz functions is plotted in Figure 4 and 5, where the starting values are pure odd $255=2^8-1={\left(11111111\right)}_2$ and mixed odd numbers $97={\left(1100001\right)}_2$, respectively.

For a given natural number n, the Collatz iterative function converges to 1 in a finite number of steps and cycles indefinitely between numbers 1, 4, and 2 for an infinite number of iterations.

3.3. Using Binary String to Explore the Collatz Conjecture

If the Collatz function (1) is expressed in binary form as

$$T\left(n\right)=\left\{\begin{array}{cc}{(1\times \times \times 10\cdots 0)}_2,& \mathrm{if}n\mathrm{is}\mathrm{odd},\mathrm{the}\mathrm{result}\mathrm{must}\mathrm{be}\mathrm{even},\\ {(1\times \cdots \times \times )}_2,& \mathrm{if}n\mathrm{is}\mathrm{even},\mathrm{the}\mathrm{result}\mathrm{is}\mathrm{either}\mathrm{odd}\mathrm{or}\mathrm{even}.\end{array}\right.$$

(6)

The characteristics of the left side and right side and the penultimate bit of the binary string are illustrated by the Figure 6.

Then we use binary string to illustrate the reduced Collatz function (4) as the follows,

$$RT\left(n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{{(1\times \times \times 10\cdots 0)}_2}{{(10\cdots 0)}_2}}={(1\times \times \times 1)}_2,& \mathrm{if}n\mathrm{is}\mathrm{an}\mathrm{odd},\mathrm{the}\mathrm{result}\mathrm{is}\mathrm{an}\mathrm{odd},\\ {\displaystyle \frac{{(1\times \times \times 10\cdots 0)}_2}{{(10\cdots 0)}_2}}={(1\times \times \times 1)}_2& \mathrm{if}n\mathrm{is}\mathrm{an}\mathrm{even},\mathrm{the}\mathrm{result}\mathrm{is}\mathrm{an}\mathrm{odd}.\end{array}\right.$$

(7)

where × is 0 or 1.

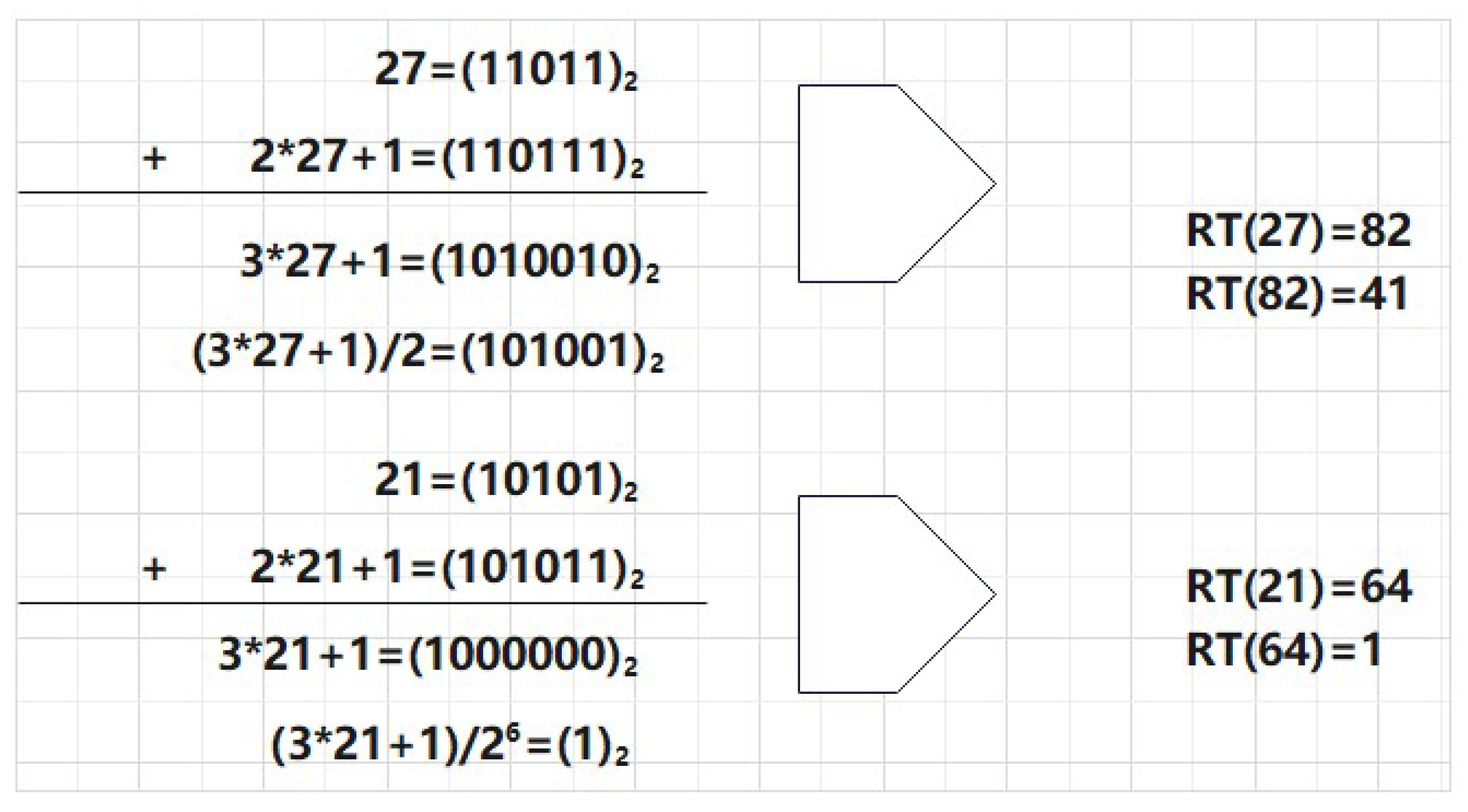
We adopt the binary representation method for specific natural numbers and use mathematical experimental methods to obtain their Collatz sequences. The following are three kinds forms to describe the Collatz sequences respectively: (i)algebra expression, (ii)tabular, and (iii)scratch paper. We use the binary representation method for specific natural numbers and employ mathematical experimental techniques to generate their Collatz sequences. The Collatz sequences for the numbers $n=10027,9$ are presented in three different formats:

(A) For the formula $T^{91}\left(10027\right)=1$, we apply the mathematical software Maple get the sequence $T^i\left(10027\right),i=0..210$ are algebra expression, and in decimal and binary as the follows.

		${\displaystyle \frac{3^{30}}{2^{61}}}·$10027
10027=(10011100101011)${}_2\to$	(111010110000010)${}_2\to$	(11101011000001)2	${\displaystyle \frac{3^{29}}{2^{61}}}$
15041=(11101011000001)${}_2\to$	(1011000001000100)${}_2\to$	(10110000010001)2	${\displaystyle \frac{3^{28}}{2^{60}}}$
11281=(10110000010001)${}_2\to$	(1000010000110100)${}_2\to$	(10000100001101)2	${\displaystyle \frac{3^{27}}{2^{58}}}$
8461=(10000100001101)${}_2\to$	(110001100101000)${}_2\to$	(110001100101)2	${\displaystyle \frac{3^{26}}{2^{56}}}$
3173=(110001100101)${}_2\to$	(10010100110000)${}_2\to$	(1001010011)2	${\displaystyle \frac{3^{25}}{2^{53}}}$
595=(1001010011)${}_2\to$	(11011111010)${}_2\to$	(1101111101)2	${\displaystyle \frac{3^{24}}{2^{49}}}$
893=(1101111101)${}_2\to$	(101001111000)${}_2\to$	(101001111)2	${\displaystyle \frac{3^{23}}{2^{48}}}$
335=(101001111)${}_2\to$	(1111101110)${}_2\to$	(111110111)2	${\displaystyle \frac{3^{22}}{2^{45}}}$
503=(111110111)${}_2\to$	(10111100110)${}_2\to$	(1011110011)2	${\displaystyle \frac{3^{21}}{2^{44}}}$
755=(1011110011)${}_2\to$	(100011011010)${}_2\to$	(10001101101)2	${\displaystyle \frac{3^{20}}{2^{43}}}$
1133=(10001101101)${}_2\to$	(110101001000)${}_2\to$	(110101001)2	${\displaystyle \frac{3^{19}}{2^{42}}}$
425=(110101001)${}_2\to$	(10011111100)${}_2\to$	(100111111)2	${\displaystyle \frac{3^{18}}{2^{39}}}$
319=(100111111)${}_2\to$	(1110111110)${}_2\to$	(111011111)2	${\displaystyle \frac{3^{17}}{2^{37}}}$
479=(111011111)${}_2\to$	(10110011110)${}_2\to$	(1011001111)2	${\displaystyle \frac{3^{16}}{2^{36}}}$
719=(1011001111)${}_2\to$	(100001101110)${}_2\to$	(10000110111)2	${\displaystyle \frac{3^{15}}{2^{35}}}$
1079=(10000110111)${}_2\to$	(110010100110)${}_2\to$	(11001010011)2	${\displaystyle \frac{3^{14}}{2^{34}}}$
1619=(11001010011)${}_2\to$	(1001011111010)${}_2\to$	(100101111101)2	${\displaystyle \frac{3^{13}}{2^{33}}}$
2429=(100101111101)${}_2\to$	(1110001111000)${}_2\to$	(1110001111)2	${\displaystyle \frac{3^{12}}{2^{32}}}$
911=(1110001111)${}_2\to$	(101010101110)${}_2\to$	(10101010111)2	${\displaystyle \frac{3^{11}}{2^{29}}}$
1367=(10101010111)${}_2\to$	(1000000000110)${}_2\to$	(100000000011)2	${\displaystyle \frac{3^{10}}{2^{28}}}$
2051=(100000000011)${}_2\to$	(1100000001010)${}_2\to$	(110000000101)2	${\displaystyle \frac{3^9}{2^{27}}}$
3077=(110000000101)${}_2\to$	(10010000010000)${}_2\to$	(1001000001)2	${\displaystyle \frac{3^8}{2^{26}}}$
577=(1001000001)${}_2\to$	(11011000100)${}_2\to$	(110110001)2	${\displaystyle \frac{3^7}{2^{22}}}$
433=(110110001)${}_2\to$	(10100010100)${}_2\to$	(101000101)2	${\displaystyle \frac{3^6}{2^{20}}}$
325=(101000101)${}_2\to$	(1111010000)${}_2\to$	(111101)2	${\displaystyle \frac{3^5}{2^{18}}}$
61=(111101)${}_2\to$	(10111000)${}_2\to$	(10111)2	${\displaystyle \frac{3^4}{2^{14}}}$
23=(10111)${}_2\to$	(1000110)${}_2\to$	(100011)2	${\displaystyle \frac{3^3}{2^{11}}}$
35=(100011)${}_2\to$	(1101010)${}_2\to$	(110101)2	${\displaystyle \frac{3^2}{2^{10}}}$
53=(110101)${}_2\to$	(10100000)${}_2\to$	(101)2	${\displaystyle \frac{3}{2^9}}$
5=(101)${}_2\to$	(10000)${}_2\to$	(1)2	${\displaystyle \frac{1}{2^4}}$

$$\begin{array}{ccc}\hfill T^{91}\left(10027\right)& =& {\displaystyle \frac{1}{2^4}}+{\displaystyle \frac{3}{2^9}}+{\displaystyle \frac{3^2}{2^{10}}}+{\displaystyle \frac{3^3}{2^{11}}}+{\displaystyle \frac{3^4}{2^{14}}}+{\displaystyle \frac{3^5}{2^{18}}}+{\displaystyle \frac{3^6}{2^{20}}}+{\displaystyle \frac{3^7}{2^{22}}}+{\displaystyle \frac{3^8}{2^{26}}}+{\displaystyle \frac{3^9}{2^{27}}}\hfill \\ & & +{\displaystyle \frac{3^{10}}{2^{28}}}+{\displaystyle \frac{3^{11}}{2^{29}}}+{\displaystyle \frac{3^{12}}{2^{32}}}+{\displaystyle \frac{3^{13}}{2^{33}}}+{\displaystyle \frac{3^{14}}{2^{34}}}+{\displaystyle \frac{3^{15}}{2^{35}}}+{\displaystyle \frac{3^{16}}{2^{36}}}+{\displaystyle \frac{3^{17}}{2^{37}}}+{\displaystyle \frac{3^{18}}{2^{39}}}\hfill \\ & & +{\displaystyle \frac{3^{19}}{2^{42}}}+{\displaystyle \frac{3^{20}}{2^{43}}}+{\displaystyle \frac{3^{21}}{2^{44}}}+{\displaystyle \frac{3^{22}}{2^{45}}}+{\displaystyle \frac{3^{23}}{2^{48}}}+{\displaystyle \frac{3^{24}}{2^{49}}}+{\displaystyle \frac{3^{25}}{2^{53}}}+{\displaystyle \frac{3^{26}}{2^{56}}}+{\displaystyle \frac{3^{27}}{2^{58}}}\hfill \\ & & +{\displaystyle \frac{3^{28}}{2^{60}}}+{\displaystyle \frac{3^{29}}{2^{61}}}+{\displaystyle \frac{3^{30}}{2^{61}}}·10027\hfill \\ & =& 1\hfill \end{array}$$

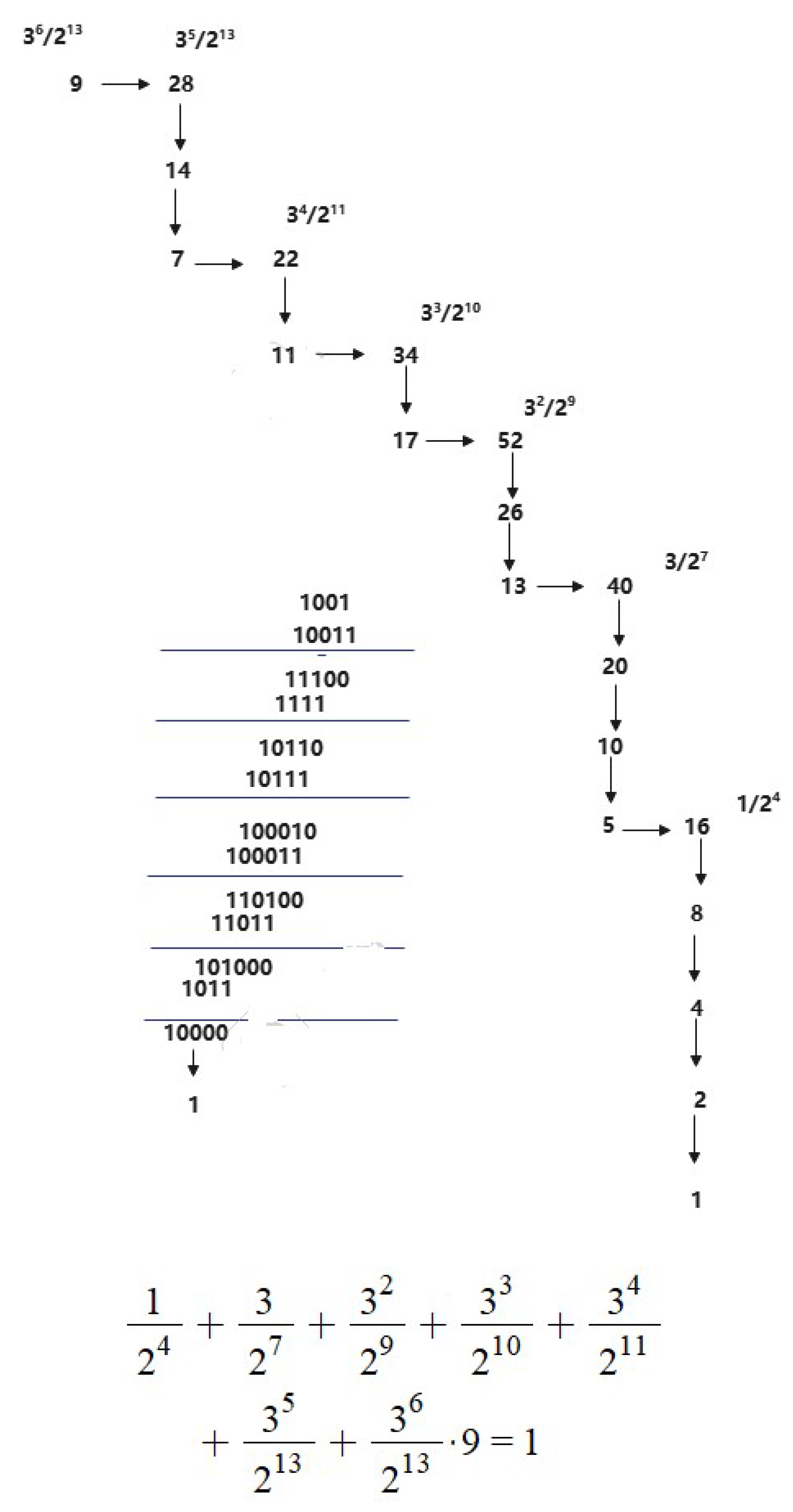
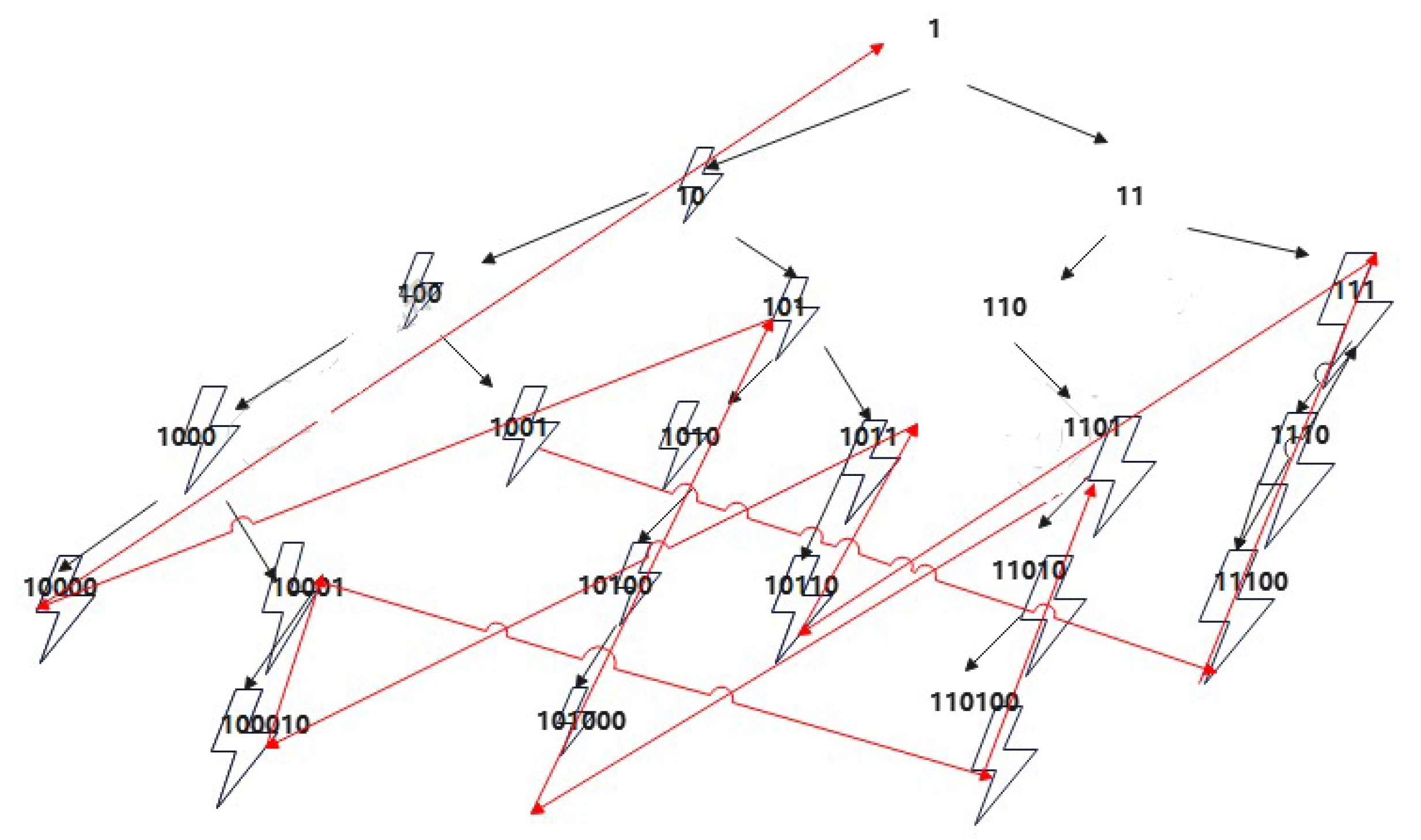
(B) For the formula $T^{19}\left(9\right)=1$, we get the sequence $T^i\left(9\right),i=0..18$ are in decimal and binary as the following scratch paper as in Figure 7. The horizontal arrow line means the 3n+1 operation, and Vertical arrow line meams the n/2 operation. There 6 $3n+1$ denoted by $3^i$ where $i=0..6$, and 13 $n/2$ by $2^j$ where $j=4..13$ in algebra expression.

We observe the procedure of iterative Collatz function, namely the reduced Collatz function (7), i.e., the Collatz sequences, which we pay close attention to the zeros in the right-hand side of binary strings of an even number and the end-substring between the first 0 encountered from right to left which is made of 1. For instance, for 1011001 the end-substring is 1, for 1011001111 the end-substring is 1111, for 11111 the end-substring is itself 11111. There are many properties of the end substrings.

In the Collatz sequence represented by a binary string looking backward from n:

(1) If there are several zeros at the end, remove one at a time until all zeros are deleted, and the number becomes an odd.

(2) When the number of bits at the end-substring is r (r>1), the adjacent binary string must have only a single zero at the end. Remove this zero to make it the next odd number which , and the number of bits at the end-substring is $r-1$, continues these steps until only a 1 is left at the end.

(3) If the number of digits at the end-substring is only one, the adjacent binary string must end with several zeros. Deleting these zeros in sequence will result in the following two scenarios at the end of the binary string: (i) one bit 1, (ii) more than one bit 1.

Since the iterative process of the piecewise function (7) is the key to solving the problem, and either result is odd, so we only discuss the odd numbers to discuss the Collatz squences.

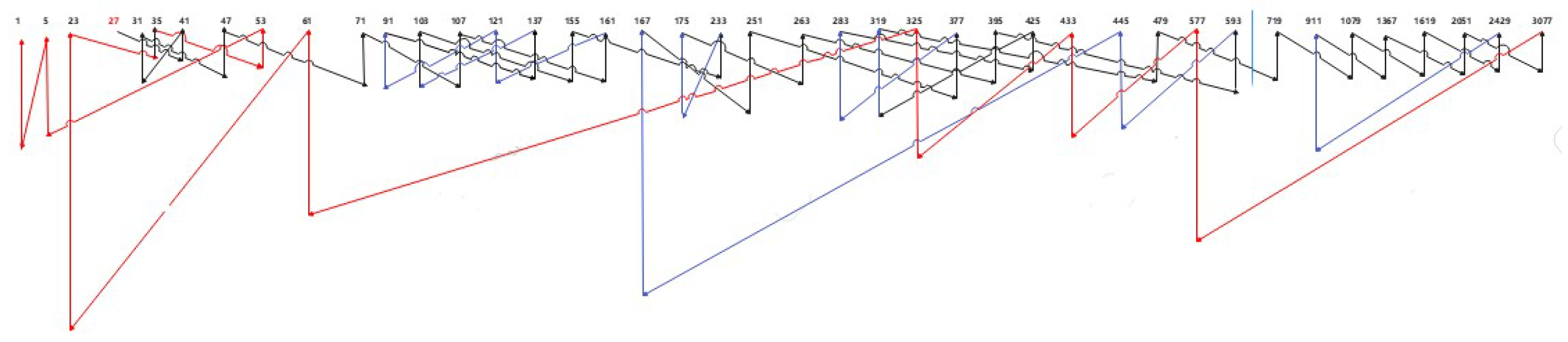
In papers [9,10], the Sarkovskii order is defined for the set of natural numbers. By relocating the last row number to the first column, we obtain a modified version of the Sarkovskii order as follows:

$\begin{array}{ccccccccccc}1,& 3,& 5,& 7,& 9,& 11,& 13,& 15,& 17,& 19,& \cdots \\ 2,& 2·3,& 2·5,& 2·7,& 2·9,& 2·11,& 2·13,& 2·15,& 2·17,& 2·19,& \cdots \\ 2^2,& 2^2·3,& 2^2·5,& 2^2·7,& 2^2·9,& 2^2·11,& 2^2·13,& 2^2·15,& 2^2·17,& 2^2·19,& \cdots \\ 2^3,& 2^3·3,& 2^3·5,& 2^3·7,& 2^3·9,& 2^3·11,& 2^3·13,& 2^3·15,& 2^3·17,& 2^3·19,& \cdots \\ 2^4,& 2^4·3,& 2^4·5,& 2^4·7,& 2^4·9,& 2^4·11,& 2^4·13,& 2^4·15,& 2^4·17,& 2^4·19,& \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}$

In the first row, its are odd numbers from left to right, that is $1,3,5,7,9,11,13,\cdots$, from the second row, each number is multiplying each number in its previous row by 2, etc.

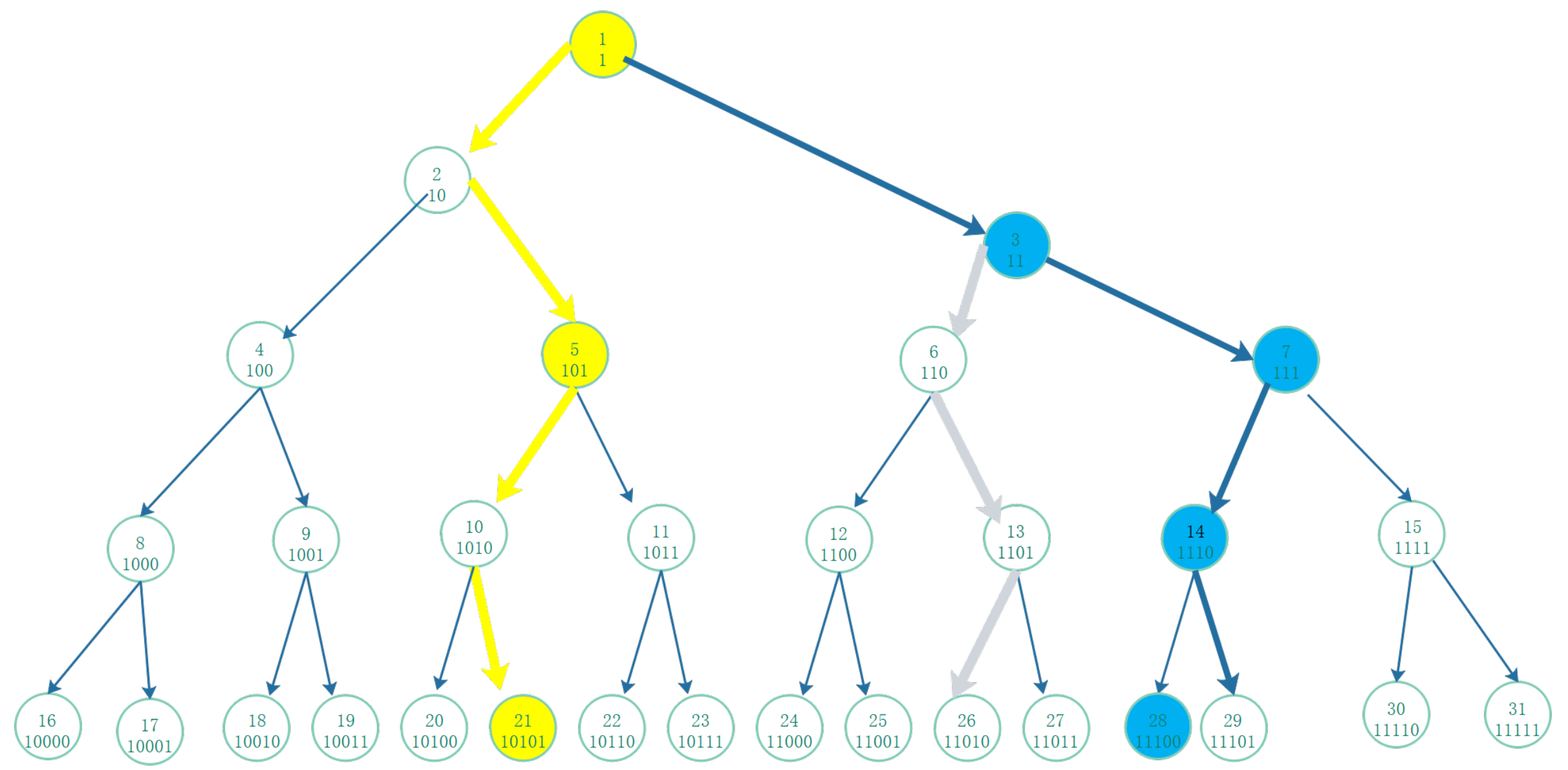
We show the Collatz squence of 27 in the modified Sarkovskii order of the natural set, shown in Figure 8.

In the scratch paper, we find that: (i) For any odd number n, the graph is made from two types of components, when the length of the end-substring is bigger than one, its is left hook and the length of the end-substring is one, its right hook. (ii) There is not point of intersection.

3.4. The Prune Strategy of the Natural Number Tree

The prune strategy For any given natural number n, if it is even, we can prune its vertex and return to its parent vertex. If it is odd, we prune its vertex and proceed to the vertex corresponding to $3n+1$.

The function ${\displaystyle \frac{n}{2}}$ in a binary string simply removes the last zero, preserving the overall structure of n. In contrast, the function $3n+1=(2n+1)+n$ completely changes the binary string structure of n by adding bits by bits. Therefore, we apply the Collatz function to implement the pruning strategy in the natural number tree. This process continues until we eventually reach the root vertex 1.

For additional samples, please refer to references [7,8].

4. Discuss the Collatz Conjecture

For any natural number n, in its natural number tree, we utilize the prune strategy of the Collatz function to achieve our goal of proof the Collatz conjecture.

We have known that mathematics formula about geometric progression with initial term 1 and common ratio x, the sum of the first k terms is

$$x^k+x^{k-1}+\cdots +x+1={\displaystyle \frac{x^{k+1}-1}{x-1}}$$

(8)

when $x=2$, there are two formulas

$$2^{k-1}+2^{k-2}+\cdots 2+1=2^k-1$$

(9)

$$2^k+2^k=2^{k+1}$$

(10)

The substantive characteristics is that the powers of 2 must be continuous natural numbers, this is the key to our proof method to solve the Collatz conjecture.

Proof. 

For a given natural number n, it can always be represented by a binary string, that is, it must be found on the full binary tree we mentioned earlier, which means that its structure can be determined by the difference between the corresponding powers in the binary string representation. Every time the Collatz function operation is performed, its structure is adjusted accordingly, and $3n+1$ can add a term $2^r$ between the corresponding two terms $2^{r+1},2^{m+1}$. Similarly, ${\displaystyle \frac{3n+1}{2^h}}$ can change the power of each bit term by term. This ensures that the bits in its binary string will definitely change.

(i) For a given natural number $n=2^k$ is a pure even, then the smallest natural number 1 can be reached by simply repeating the k times Collatz function divided by 2.

If $n={(1\times \cdots \times 10\cdots 0)}_2=2^m+\cdots +2^k$ is a mixed even number, one can delete all zeros in end, it becomes as a mixed odd ${\displaystyle \frac{n}{2^k}}={(1\times 1)}_2=2^{m-k}+\cdots +2^0$.

(ii) when a given natural number n is either pure odd or mixed odd, its binary string as $n={(1\times \cdots \times 1)}_2=2^r+2^m+\cdots +1$, then

$$\begin{array}{cc}& 3n+1=(2n+1)+n\hfill \\ & =2^{r+1}+2^{m+1}+\cdots +2+1+2^r+2^m+\cdots +1\hfill \\ & =2^{r+1}+2^{m+1}+\cdots +2^0+2^0+2^r+2^m+\cdots +2^0\hfill \\ & =2^{r+1}+2^r+2^{m+1}+2^m+\cdots +\cdots +2^h\hfill \end{array}$$

If the length of the end-substring of n is 1, the length of end-substring of the binary string $3x+1$ is either 1 or bigger than 1.

Two formulas (8) and (9) can be used to modify the structure of the binary string n to the binary string $3n+1$. That is, there is an appended term $2^{r-h}$ in two equivalent terms, $2^{r+1-h}$ and $2^{m+1-h}$. When the zeros in the middle of a binary string are compared to a bubble, it means that these zeros are gradually being driven out of the rightmost end by $3n+1$. It is the same as progressively removing the bubbles hidden in the sponge using a means $3n+1$. Once 3n+1, 0 shifts one bit to the right, i.e., the length of the associated binary substring is reduced by one bit, when the length of the end-substring is greater than 1. The end-substring length of the binary string $3x+1$ is either greater than or equal to 1 if the length of the end-substring of n is 1.

We shall then divide $3n+1$ by the last term $2^h$,

$$\begin{array}{cc}& {\displaystyle \frac{3n+1}{2^h}}=2^{r+1-h}+2^{r-h}+2^{m+1-h}+2^{m-h}+\cdots +\cdots +2^0\hfill \end{array}$$

get another odd number, this is the value of reduced Collatz function (4) or (6). And so on, finitely steps after finally we get a pure even number $2^t$, this is the case in above (i), thus the Collatz conjecture hold on.

We illustrate the procedure by a mixed odd number $n=67$ and hard number set in the following,

$$\begin{array}{cc}\hfill & 67={\left(1000011\right)}_2=2^6+2^1+2^0\hfill \\ \hfill & 3·67+1=2·67+67+1=2^7+2^2+2^1+2^6+2^1+2^0+2^0=2^7+2^6+2^3+2^1\hfill \\ \hfill & 3·101+1=2·101+101+1=2^7+2^6+2^3+2^1+2^6+2^5+2^2+2^0+2^0=2^8+2^5+2^4\hfill \\ \hfill & 3·19+1=2·19+19+1=2^5+2^2+2^1+2^4+2^1+2^0+2^0=2^5+2^4+2^3+2^1\hfill \\ \hfill & 3·29+1=2·29+29+1=2^5+2^4+2^3+2^1+2^4+2^3+2^2+2^0=2^6+2^4+2^3\hfill \\ \hfill & 3·11+1=2·11+11+1=2^4+2^2+2^1+2^3+2^1+2^0+2^0=2^5+2^1\hfill \\ \hfill & 3·17+1=2·17+17+1=2^5+2^1+2^4+2^0+2^0=2^5+2^4+2^2\hfill \\ \hfill & 3·13+1=2·13+13+1=2^4+2^3+2^1+2^3+2^2+2^0+2^0=2^5+2^3\hfill \\ \hfill & 3·5+1=2·5+5+1=2^3+2^1+2^2+2^0+2^0=2^4\hfill \\ \hfill & 1\hfill \end{array}$$

For a special class of mixed numbers, the hard number ${\displaystyle \frac{4^k-1}{3}}={(101\cdots 101)}_2$, then its Collatz sequent result is

$$\begin{array}{cc}\hfill & a_k={\displaystyle \frac{4^k-1}{3}}={\displaystyle \frac{4^k-1}{4-1}}=4^{k-1}+4^{k-2}+\cdots +4+1={(101\cdots 101\cdots 101)}_2,\hfill \\ \hfill & T\left(a_k\right)=3a_k+1=4^k=2^{2k}={(10\cdots 0)}_2,T^{2k+1}\left(a_k\right)=1.\hfill \end{array}$$

This means that the Collatz conjecture is valid for this case. Therefore we have proved the Collatz conjecture 1 at section 1 of this paper. □