Distinguishing Black Holes from String-Inspired Euler-Heisenberg Theory Through Shadow Images

1. Introduction

In recent years, the study of shadow images has gained prominence due to astronomical observations of black holes. Notably, the optical appearances of the M87* and SgrA* systems obtained by the Event Horizon Collaboration in 2019 [74] and 2022[2] have been significant. There are still some conjectures about their true nature—whether they are black holes, wormholes, or other compact objects. While waiting for further observations, theoretical studies on related topics have proliferated to identify these systems. For instance, there are many works on calculating shadows and weak/strong gravitational lensing effects for wormholes[2,9,10,11,12,13,14,15,16,17,13,14,15,16,17], boson stars [18,19,20], and naked singularities [21,22,23,24,25]. A widely recognized view is that these objects are black holes, although there are many black hole candidates from various theories. Thus, studies of black hole shadow images are very important.

Former investigations on black hole shadows can be traced back to Bardeen in 1972, who demonstrated that the shadow shape of a Kerr black hole is not a circle [26]. Luminet was the first to establish the optical appearance of Schwarzschild black holes surrounded by a shining and rotating accretion disk using numerical methods[27]. Gralla et al. examined the shadow images of Schwarzschild black holes illuminated by a geometrically and optically thin accretion disk using ray-tracing methods in Ref.[28]. A comprehensive review on calculating shadow images is provided in Ref.[29]. Furthermore, recent works on the shadow images and optical appearances of various black holes can be found in Ref.[30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. All these works indicate that as a major topic in gravity, it has garnered widespread attention in the scientific community.

On the other hand, an abundance of astronomical data suggests that General Relativity (GR) has its boundaries, particularly in explaining phenomena such as Dark Energy and the inflationary period of the cosmos. As a result, the reliability of GR is likely to face questions in exceptional circumstances. It is widely recognized that GR is predominantly a low-energy theory. These observations prompt us to investigate alternative gravitational theories [53,54]. A focal point of interest lies in the derivation of an effective four-dimensional theory, offering insights into quantum corrections that modify Einstein’s theory of gravity. These corrections encompasses the Gauss-Bonnet term [55,56,57] and nonlinear electromagnetic corrections [58,59]. In fact, the nonlinear electrodynamics plays an important role in these strong field regimes, where the intensity of electromagnetic fields can become comparable to the strength of gravitational fields [60,61,62]. During the primordial stages of the universe, for instance, when energy densities were exceptionally high, the gravitational-electromagnetic interplay was pronounced. Nonlinear electrodynamics could be also instrumental in simulating the behavior of these fields throughout cosmic evolution [63].

In this work, we focus on a string-inspired theory that involves classical Euler-Heisenberg electrodynamics coupled to a non-trivial dilaton field. Very recently, Bakopoulos et al. present an exact spherically symmetric string-inspired Euler-Heisenberg black hole solution [64]. Later, A. Vachher et al. examine and compare the gravitational lensing, in the strong field limit, for this magnetically charged black holes [65]. In addition, testing gravitational theories by the shadow images is one of the most interesting directions. Black hole system, as a strong gravity regime, is a useful tool to test the General Relativity and other theories. A well-studied theory is the GR coupled to the Euler-Heisenberg theory.

Throughout this paper, we adopt the Planck units $8\pi G=c=1$ and the $(-,+,+,+)$ convention.

2. The Theory and the Solution

We’d like to introduce the String-inspired Euler-Heisenberg theory briefly. The action of this theory reads as [64]

$$\begin{array}{c}\hfill S={\displaystyle \frac{1}{16\pi }}\int d^{4}x\sqrt{-g}\left[R-2{\partial }^{\mu }\varphi {\partial }_{\mu }\varphi -e^{-2\varphi }{F}^2-f\left(\varphi \right)(2\alpha F_{\sigma }^{\rho }{F}_{\lambda }^{\sigma }{F}_{\gamma }^{\lambda }{F}_{\rho }^{\gamma }-\beta F^4)\right],\end{array}$$

(1)

where R is Ricci scalar, $F^2=F_{\mu \nu }{F}^{\mu \nu }\sim E^2-B^2$ is the usual Faraday scalar, and $F^4=F_{\mu \nu }{F}^{\mu \nu }{F}_{\rho \sigma }{F}^{\rho \sigma }$ with usual field strength $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$. Moreover, parameters $\alpha$ and $\beta$ denote the coupling constants between the scalar field $\varphi$ and non-linear Euler-Heisenberg electrodynamic terms with dimensions (length)². Then, the field equations from Eq.(1) are given by

$$\begin{array}{ccc}& & G_{\mu \nu }-2{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi +g_{\mu \nu }{\partial }^{\lambda }\varphi {\partial }_{\lambda }\varphi -2^{-2\varphi }(F_{\mu }^{\lambda }{F}_{\nu \lambda }-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }{F}^2)\hfill \end{array}$$

$$\begin{array}{ccc}& & -f\left(\varphi \right)\left(8\alpha F_{\mu }^{\rho }{F}_{\nu }^{\lambda }{F}_{\rho }^{\eta }{F}_{\lambda \eta }-\alpha F_{\sigma }^{\rho }{F}_{\lambda }^{\sigma }{F}_{\gamma }^{\lambda }{F}_{\delta }^{\gamma }-4\beta F_{\mu }^{\eta }{F}_{\nu \eta }{F}^2+{\displaystyle \frac{1}{2}}{g}_{\mu \nu }\beta F^4\right)=0,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & 4\square \varphi +2e^{-2\varphi }{F}^2-{\displaystyle \frac{df\left(\varphi \right)}{d\varphi }}\left(2\alpha F_{\sigma }^{\rho }{F}_{\lambda }^{\sigma }{F}_{\gamma }^{\lambda }{F}_{\delta }^{\gamma }-\beta F^4\right)=0,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & {\partial }_{\mu }\left[\sqrt{-g}\left(4F^{\mu \nu }(2\beta f\left(\varphi \right)F^2-e^{-2\varphi })-16\alpha F_{\kappa }^{\mu }{F}_{\lambda }^{\kappa }{F}^{\nu \lambda }\right)\right]=0.\hfill \end{array}$$

(4)

In this paper, we assume that the scalar function $f\left(\varphi \right)$ takes the following form [64]

$$\begin{array}{c}\hfill f\left(\varphi \right)=-[3cosh\left(2\varphi \right)+2]=-{\displaystyle \frac{1}{2}}\left(3e^{-2\varphi }+3e^{2\varphi }+4\right).\end{array}$$

(5)

Considering static and spherical symmetry metric ansatz

$$\begin{array}{c}\hfill d{s}^2=-h\left(r\right)d{t}^2+f^{-1}\left(r\right)d{r}^2+r^{2}d{\Omega }_2^2,\end{array}$$

(6)

in which $h\left(r\right)$ and $f\left(r\right)$ are functions of r and $d{\Omega }_2^2=d{\theta }^2+{sin}^2\theta d{\phi }^2$ the unit 2 sphere and substituting the ansatz into the field equations (2)()(), we can obtain the black hole solution

$$\begin{array}{ccc}& & h\left(r\right)=1-{\displaystyle \frac{4M^2}{Q_m^2+\sqrt{Q_m^4+4M^2{r}^2}}}-{\displaystyle \frac{2(\alpha -\beta )Q_m^4}{r^6}},\hfill \\ & & f\left(r\right)=1-{\displaystyle \frac{{(Q_m^4+4M^2{r}^2)}^{3/2}}{4M^2{r}^4}}+{\displaystyle \frac{Q_m^4}{4M^2{r}^2}}+{\displaystyle \frac{Q_m^6}{4M^2{r}^4}}+{\displaystyle \frac{Q_m^2}{r^2}}-{\displaystyle \frac{(\alpha -\beta )Q_m^4(Q_m^4+4M^2{r}^2)}{2M^2{r}^8}},\hfill \\ & & \varphi \left(r\right)=-{\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{\sqrt{Q_m^4+4M^2{r}^2}-Q_m^2}{\sqrt{Q_m^4+4M^2{r}^2}+Q_m^2}}\right),\hfill \end{array}$$

(7)

where the Maxwell four-vector takes the form

$$\begin{array}{c}\hfill A_{\mu }=(0,0,0,Q_{m}cos\theta )\end{array}$$

(8)

and $Q_m$ stands for the magnetic charge carried by the black hole.

Considering scalar free scenario $\varphi =0$, and $f(\varphi =0)=1$, the black hole solution reads as

$$\begin{array}{c}\hfill h\left(r\right)=f\left(r\right)=1-{\displaystyle \frac{2M}{r}}+{\displaystyle \frac{Q_m}{r^2}}+{\displaystyle \frac{2(\alpha -\beta )Q_m^4}{5r^6}},\end{array}$$

(9)

which is the Einstein-Euler-Heisenberg black hole obtained in Ref.[66].

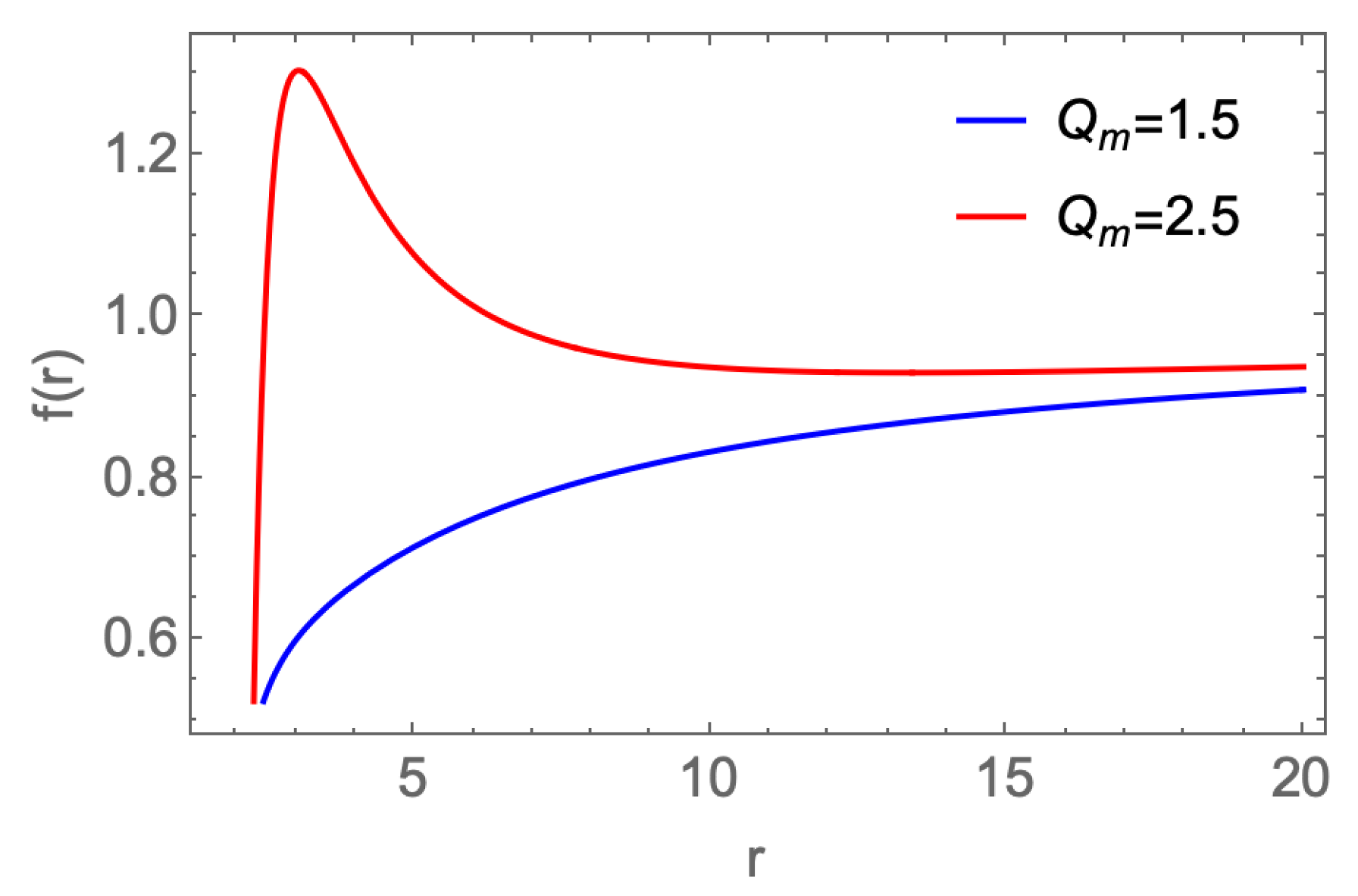
We set $\gamma =\alpha -\beta$, there are two kinds of black holes, namely the single horizon with $\gamma >0$ and the double horizons with $\gamma <1$. In this work, we focus on the single horizon black holes, in which the so-called doppelgänge Black Holes arise. Throughout this paper, we fix $\gamma =1$ without loss of generality. The metric functions $g_{rr}^{-1}=f\left(r\right)$ are shown in Figure 1, we found that there are two kinds of behaviors of the $f\left(r\right)$ while the $g_{tt}=h\left(r\right)$ are alway monotonically increase. For the black holes in the normal Maxwell theory, namely the RN black holes, the metric functions $f\left(r\right)$ is monotonically increasing to be 1 in the asymptotic flat region. Interestingly, for the large $Q_m$ black holes in the string-inspired Euler-Heisenberg theory, the $g_{rr}$ is no longer monotonic. We’ll see it affects the shadow images.

3. Geodesics

The free particles moving in a spacetime described by (6), there are two conserved quantities, namely the energy $E=-h\left(r\right)\dot{t}$ and the angular momentum $L=r^{2}sin{\theta }^2\dot{\varphi }$. The dot depicts the derivative with respect to the affine parameter. Take the advantage of the spherical symmetry, we focus on the equatorial plane, then $sin\left(\theta \right)=1$.

It’s straightforward to derive the first-order equation by the geodesic equation [15],

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{dr}{d\phi }}\right)}^2={\displaystyle \frac{r^{2}f\left(r\right)}{h\left(r\right)}}({\displaystyle \frac{1}{b^2}}-V_i),\end{array}$$

(10)

where $i=p,n$ and $b={\displaystyle \frac{L^2}{E^2}}$ the impact parameter, and the effective potential for massive particles (time-like geodesics)

$$\begin{array}{c}\hfill V_n={\displaystyle \frac{h\left(r\right)}{r^2}}+{\displaystyle \frac{h\left(r\right)}{L}},\end{array}$$

(11)

while for photons (null geodesics)

$$\begin{array}{c}\hfill V_p={\displaystyle \frac{h\left(r\right)}{r^2}}.\end{array}$$

(12)

Analysis the effective potentials yield the important orbits, such as the innermost stable circular orbit (ISCO) and photon sphere, around the black holes. Let’s discuss it case by case as follows.

3.1. Time-like Geodesics and ISCO

As a black hole spacetime, it usually admits an special orbit to massive particles, where the particles with the specific angular momentum $L_c$ can do circular motion in the innermost orbit stably. Such orbit goes by the name of the innermost stable circular orbit (ISCO). In mathematics, the ISCO is an orbit satisfied

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial V_n}{\partial r}}{{|}_{r=r_{isco}}=0,{\displaystyle \frac{{\partial }^2{V}_n}{\partial r^2}}|}_{r=r_{isco}}=0.\end{array}$$

(13)

One can solve an alternative equation [40]

$$\begin{array}{c}\hfill r_{isco}-{\displaystyle \frac{3h\left(r_{isco}\right)h^{\prime }\left(r_{isco}\right)}{2h^{\prime }{\left(r_{isco}\right)}^2-h\left(r_{isco}\right)h^{\prime \prime }\left(r_{isco}\right)}}=0\end{array}$$

(14)

to obtain the ISCO.

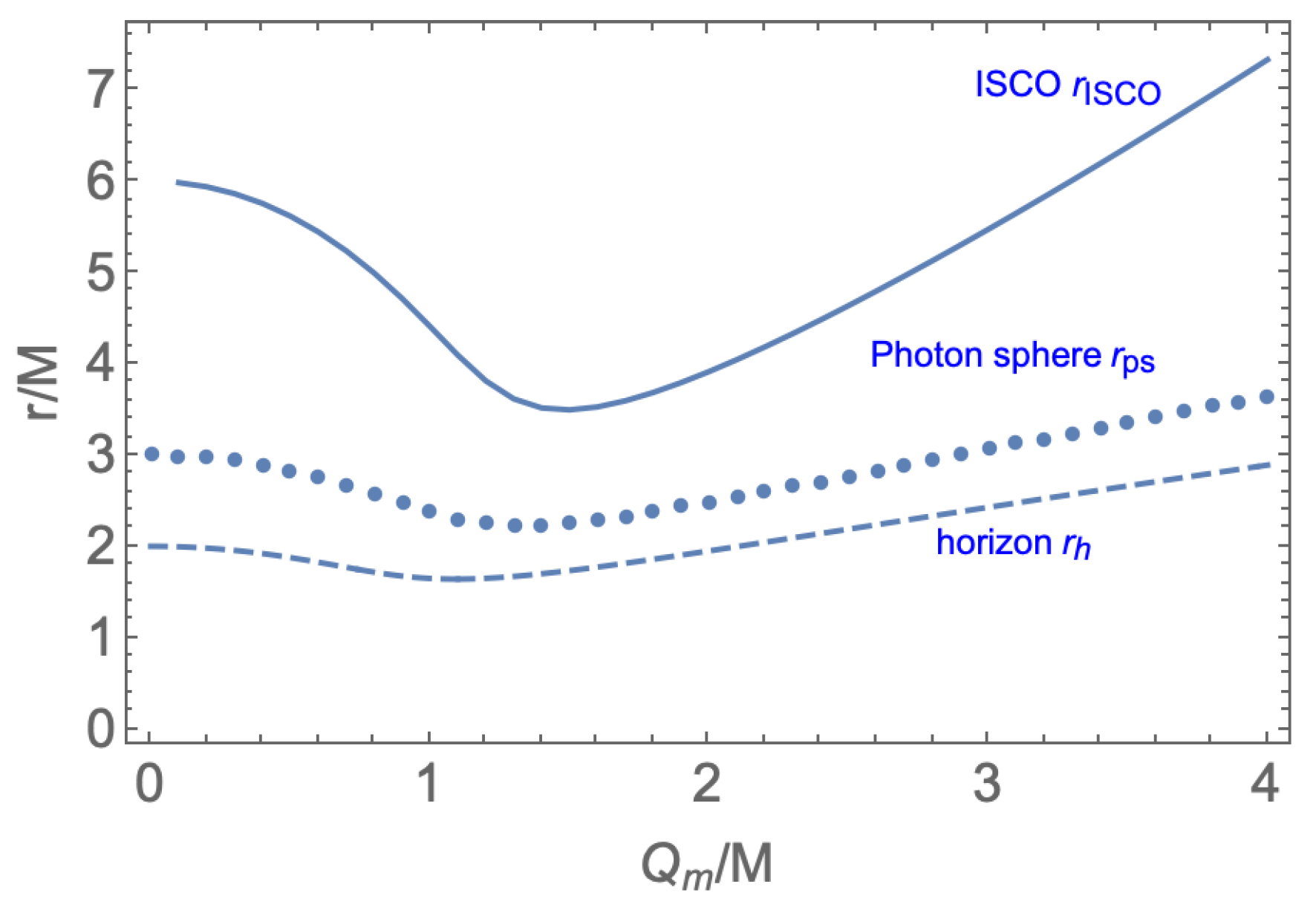
The analytical form of the ISCO is complicated and we present it as functions of $Q_m$ in Figure 2. It shows that the radii of ISCO are not monotonically increasing or decreasing with $Q_m$ increased. For the small $Q_m$ black holes, the radius of ISCO increase when the magnetic charge $Q_m$ decreased and reduce to a maximum $r_{ISCO}=6M$ when $Q_m$ vanished. Note that it coincide with ISCO of Schwarzschild black hole. For the large $Q_m$ black holes, the behavior is exactly the opposite to the small $Q_m$ case: the radius of ISCO increase along with $Q_m$ increased. Furthermore, black holes with the same mass and horizon radii but possess different $Q_m$ share not the same radii of ISCO. Hence one can distinguish them by the size of ISCOs. Moreover, the different size of ISCOs also affects the black hole shadows.

3.2. Null Geodesics and Photon Sphere

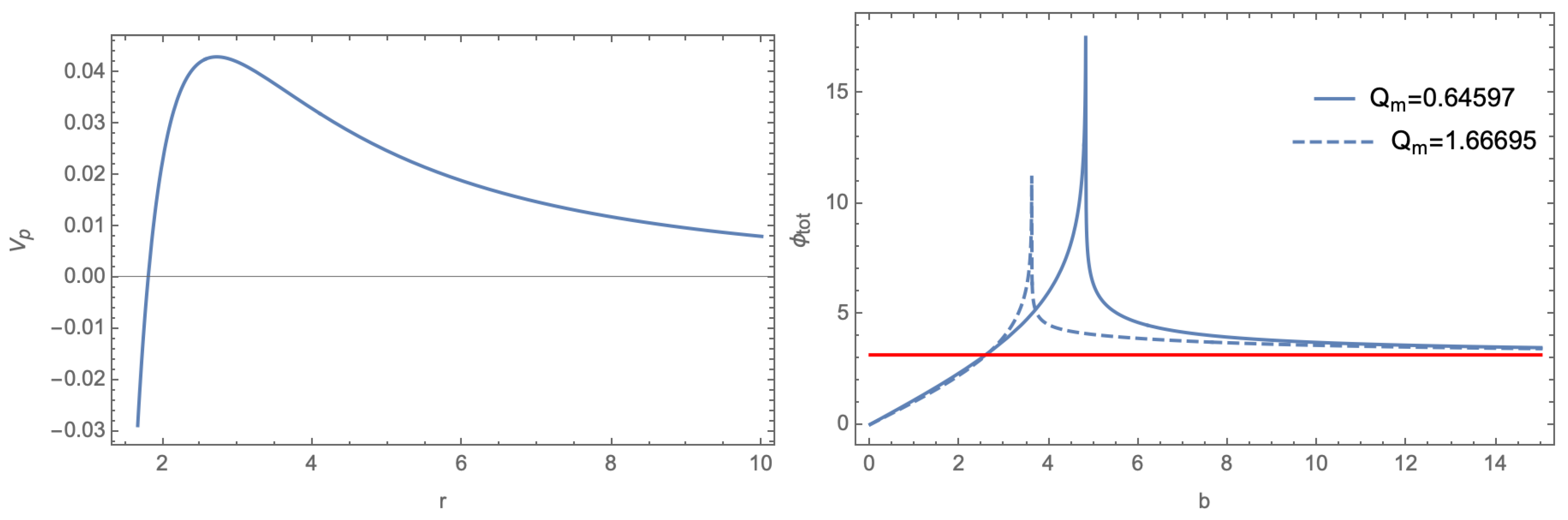
The effective potential (12) has a maximum $V_p^{max}$ located at $r_{ps}$. This is what we called the “photon sphere" of a black hole. The critical impact parameter $b_c={\displaystyle \frac{1}{V_p^{max}}}$. According to (10), it implies that the photons with $b<b_c$ have no turning point and will fall into the black hole horizon. An typical example of the effective potential for photons is presented in the left figure of Figure 12.

The photon sphere is very important in the optical appearances of black holes. We present the location of photon sphere with increasing $Q_m$ in Figure 2. Similar to the case of ISCO above, the behaviors of the photon sphere to the small and large $Q_m$ are different, and the two doppelgänge black holes share two different photon spheres.

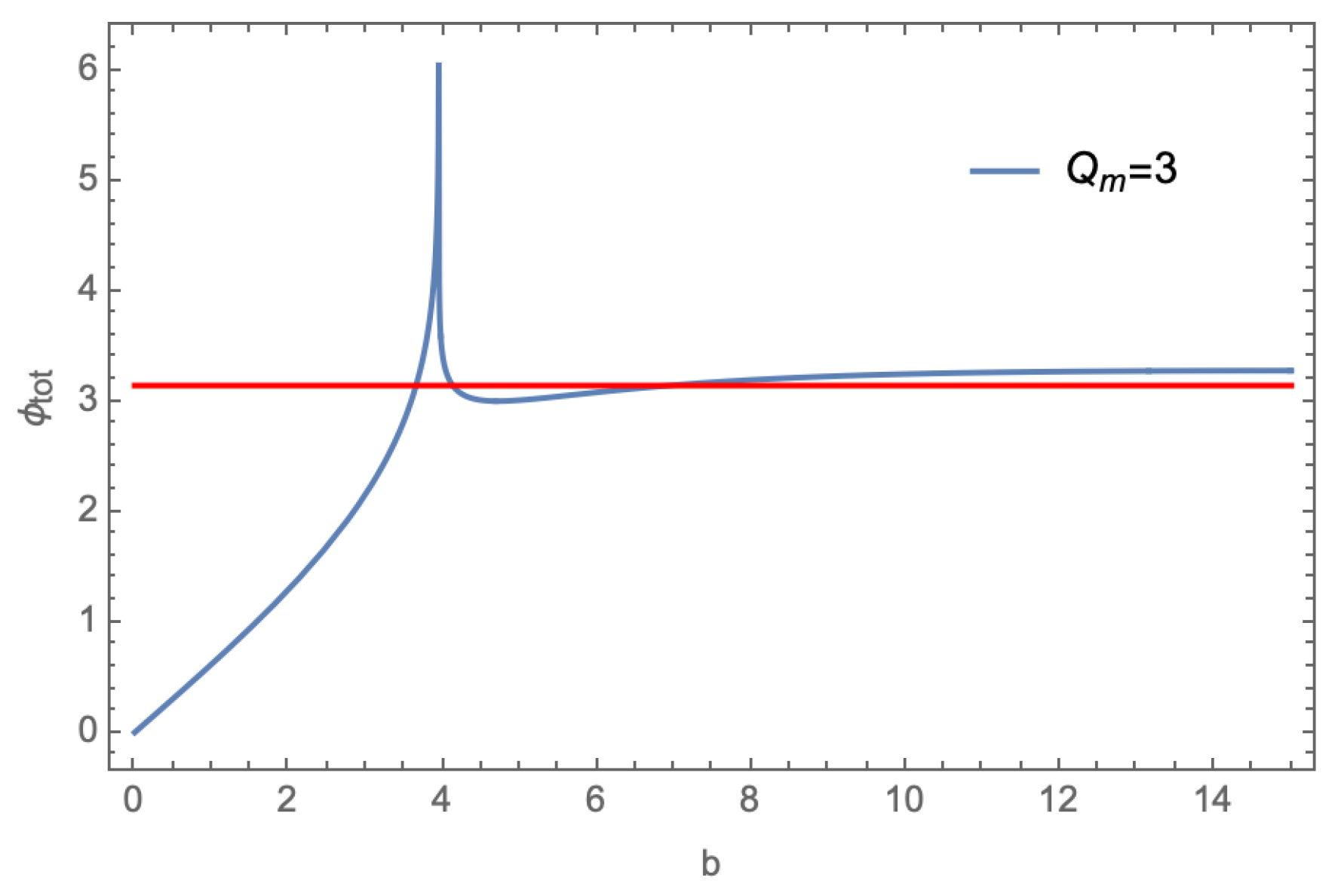
The total deflection angle is obtaining by integrating (10) directly, we show the results in the right figure of Figure 12 and Figure 4. In the thin disk model1, setting $n={\displaystyle \frac{{\varphi }_{tot}}{2\pi }}$, one can see the three special bright regions[28]:

• Direct emission: created by the photons with $n<3/4$. The photons intersect with the thin disk once;
• Lensing ring: created by the photons with $3/4<n<5/4$. The photons intersect with the thin disk twice;
• Photon ring: created by the photons with $n>5/4$. The photons intersect with the thin disk more than twice;

In the right figure of Figure 3, it shows that the doppelgänge black holes have different direct emissions, photon rings and lensing rings. In Figure 4, we found a novel phenomenon on the deflection angle curve: the deflection angle is not monotonic decreasing when $b>b_c$. This only arise in the large $Q_m$ case due to the non-monotonic behavior of the metric function $f\left(r\right)$ (see Figure 1).

Figure 3. Left figure: An typical shape of $V_p$ with $Q_m=0.64597$. Right figure: The total deflection angle of a pair of the doppelgänge black holes. They possess the same horizon radii and black hole masses. 

Figure 3. Left figure: An typical shape of $V_p$ with $Q_m=0.64597$. Right figure: The total deflection angle of a pair of the doppelgänge black holes. They possess the same horizon radii and black hole masses. 

Figure 4. The total deflection angle with $Q_m=3$. 

Figure 4. The total deflection angle with $Q_m=3$. 

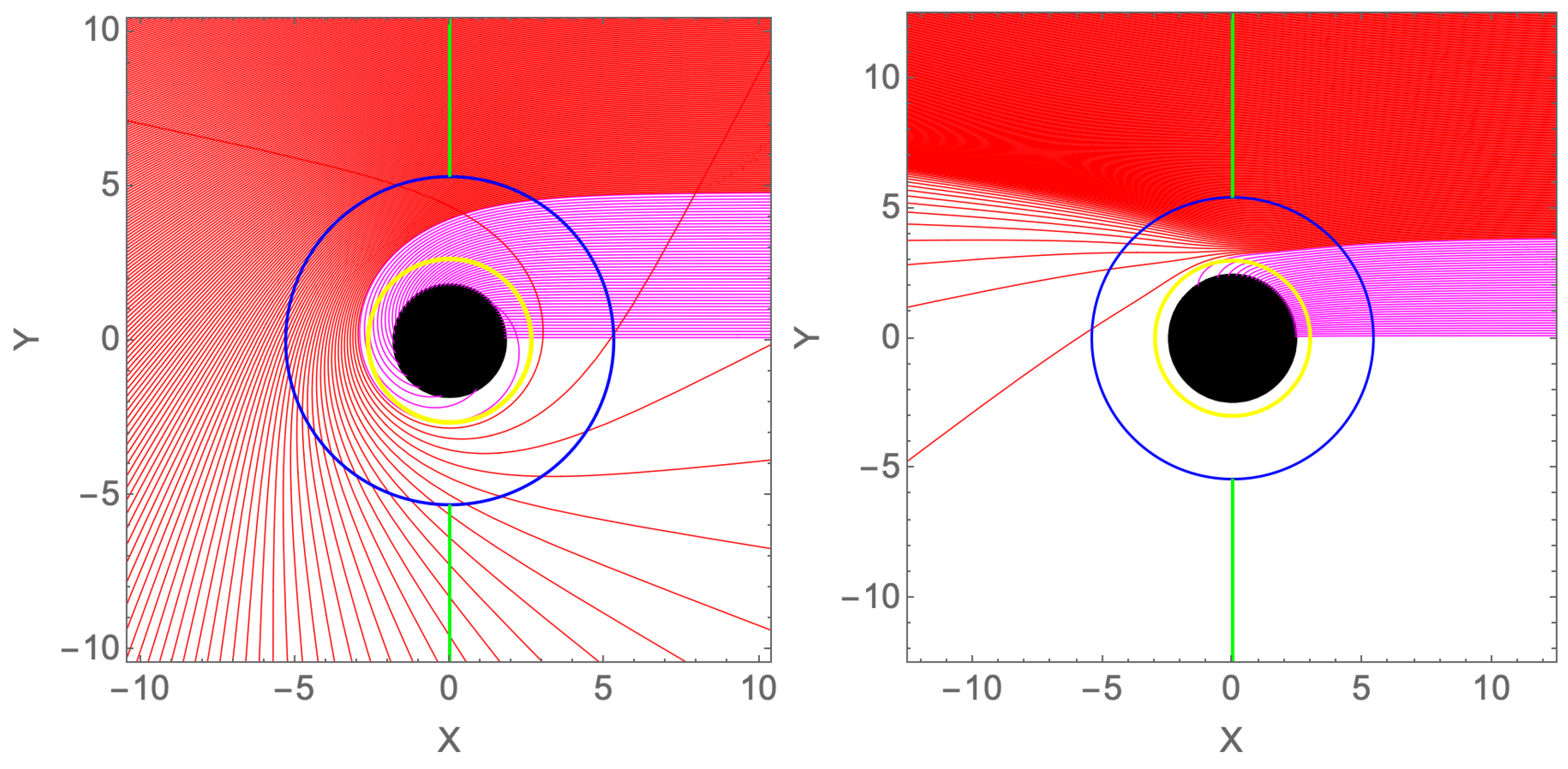
The first-order equation (10) can be solved numerically. We plot two typical figures of the geodesics in Figure 5. The up one in Figure 5 is the black holes corresponding to the right figure of Figure 12, where the deflection angle is monotonic decreasing when $b>b_c$. The down one in Figure 5 corresponding the black holes in Figure 4, where the repulsive effect happens in $b>b_c$ is showed.

4. Shadow Images

Depends on the forms of accretion, it usually has two kinds of optical appearances to black holes. The fist one is the thin disk model, where the accretion disk extends from the ISCO and its intensity is monotonically decreasing. The second model is considering a spherical accretion enclosed the black hole, and it can be static or free falling to the black hole.

4.1. Thin Disk Model

We consider an optically and geometrically thin disk extends from the ISCO as the light source. The shadow images are affected by intensity function on the disk. Based on the astrophysics scenarios[19], we adopt the following models for the emitted intensity,

$$\begin{array}{c}\hfill I_{em}\left(r\right)=I_0{\left({\displaystyle \frac{r_{ISCO}}{r}}\right)}^4{\displaystyle \frac{1+tanh\left(50(r-r_{ISCO})\right)}{2}},\end{array}$$

(15)

where $I_0$ is a normalization factor. The ray-tracing method [39,41] is used in constructing the shadow images, where the observed intensity can be derived as

$$\begin{array}{c}\hfill I_{obs}\left(b\right)=\sum _n{g}_{tt}^2{I}_{em}{\left(r\right)|}_{r=r_n\left(b\right)},\end{array}$$

(16)

where $r_n\left(b\right)$ is the transfer function that indicates the radii of the nth intersection with the accretion disk.

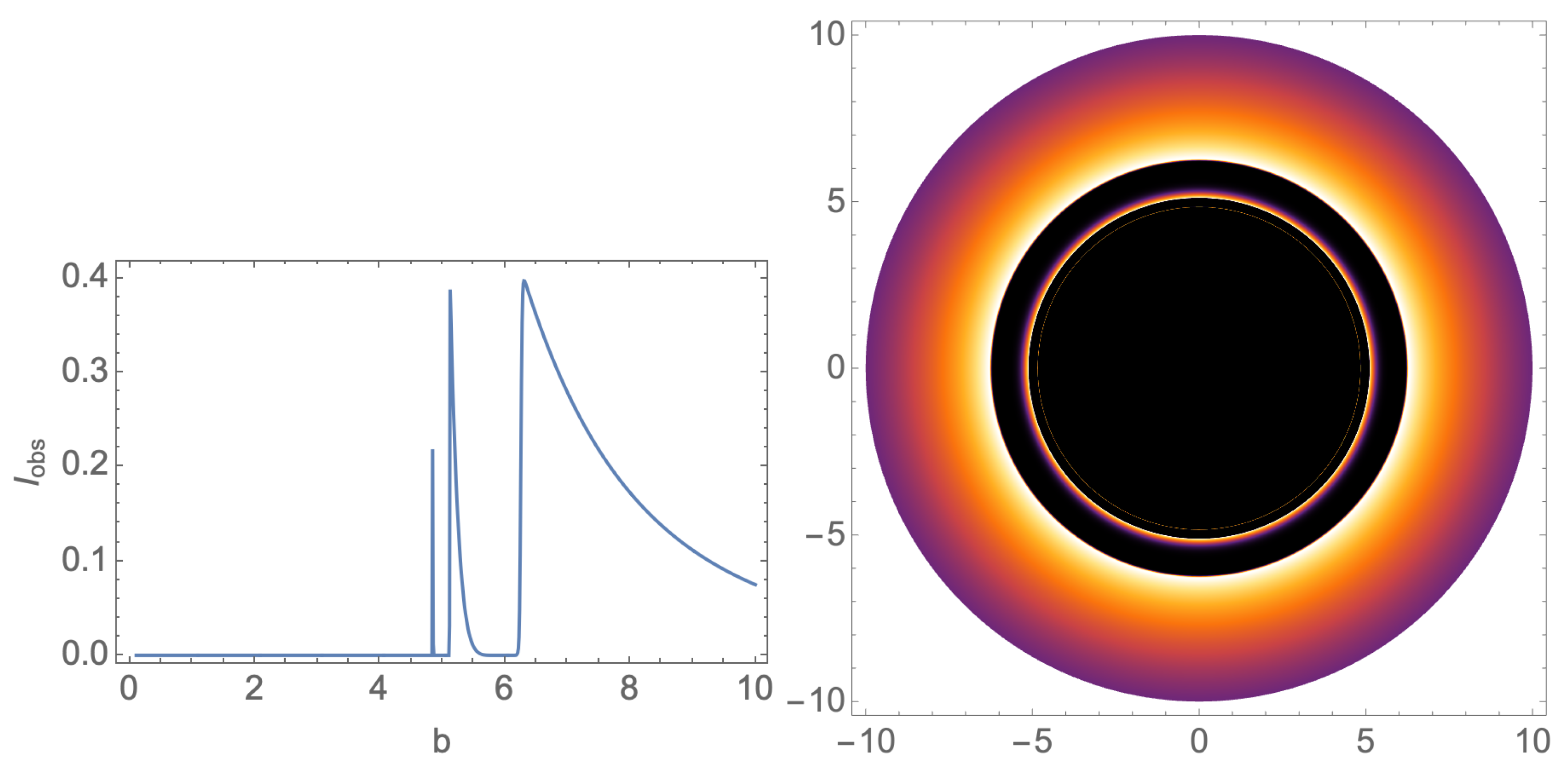
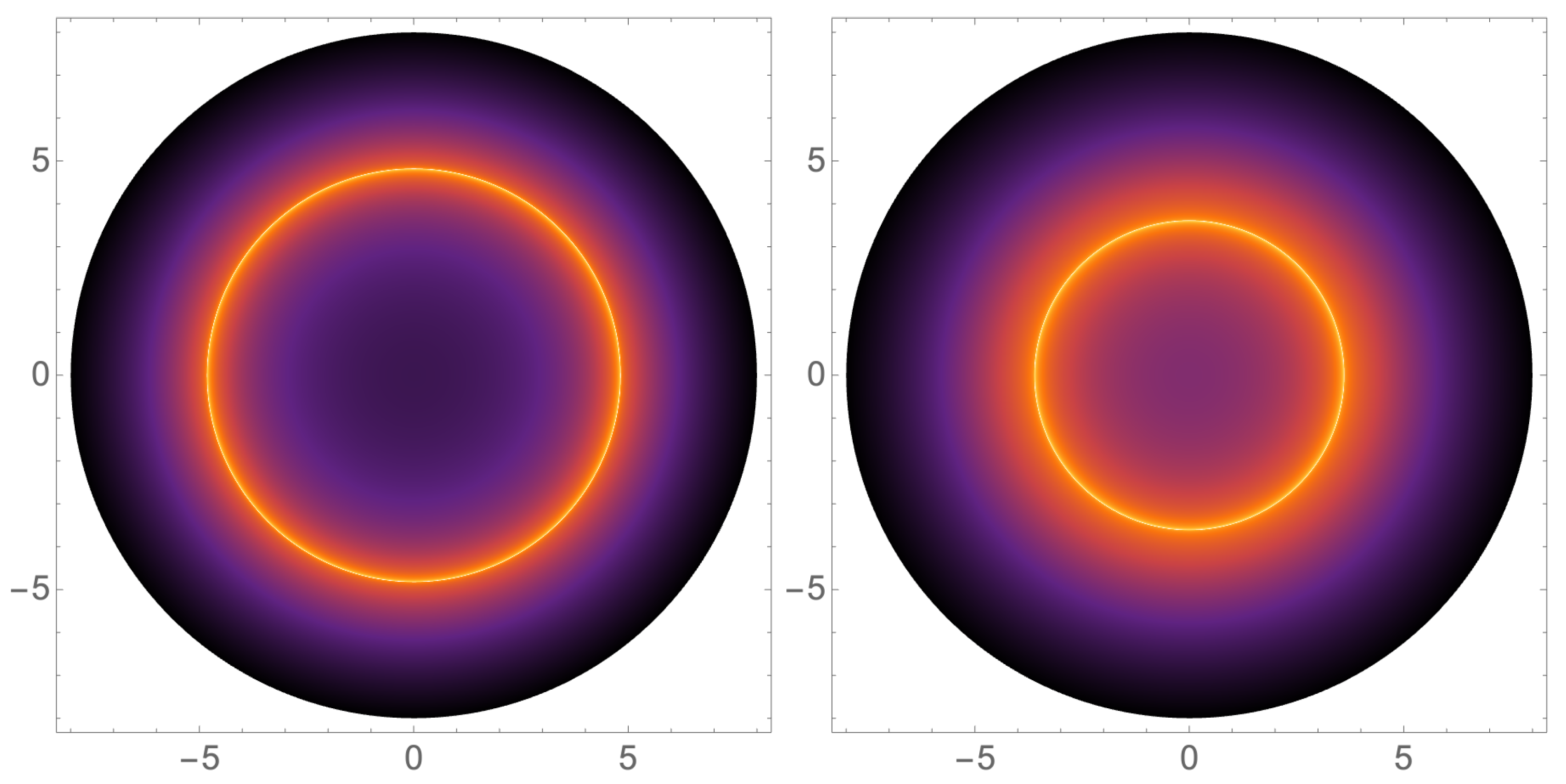
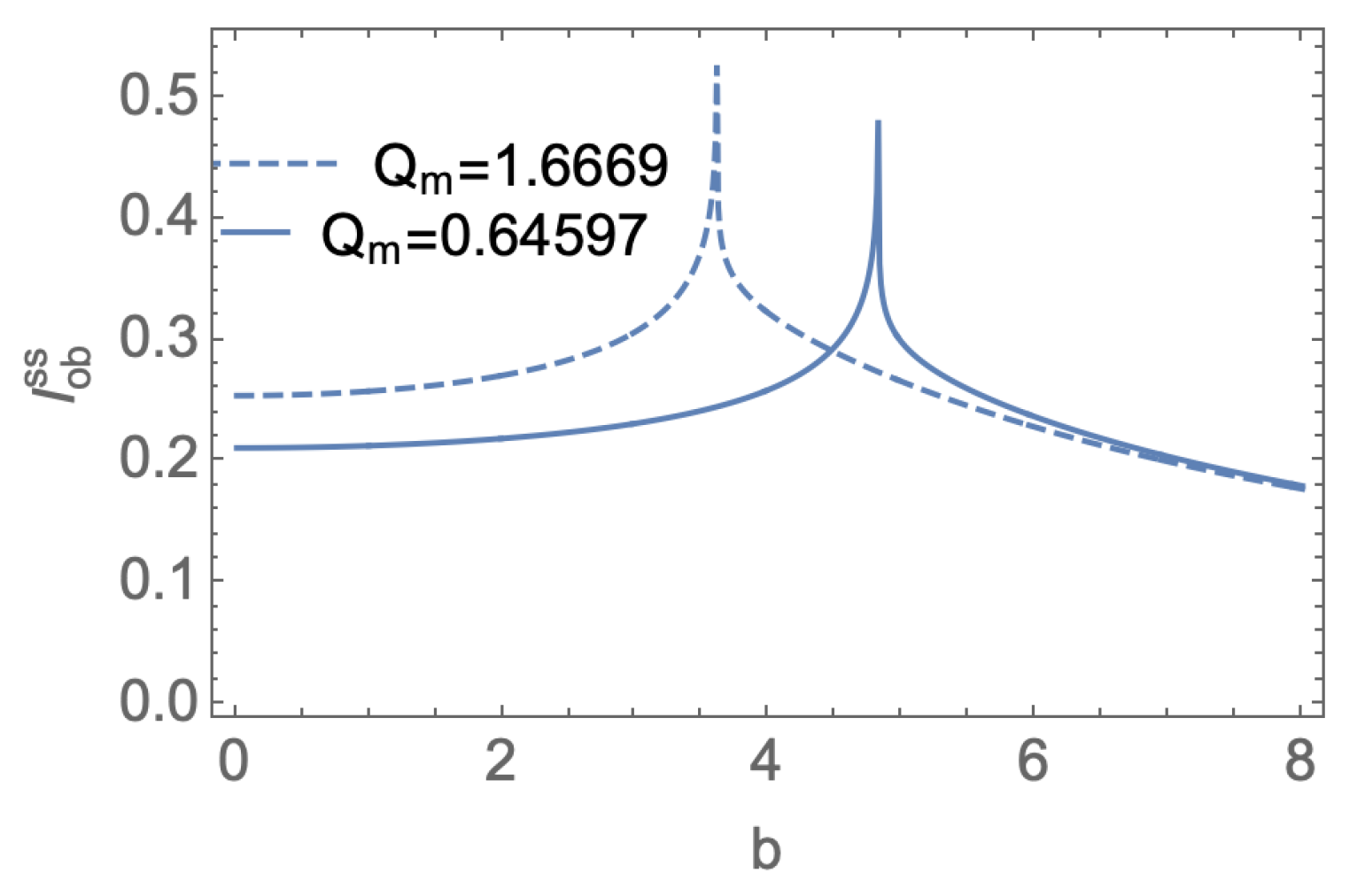
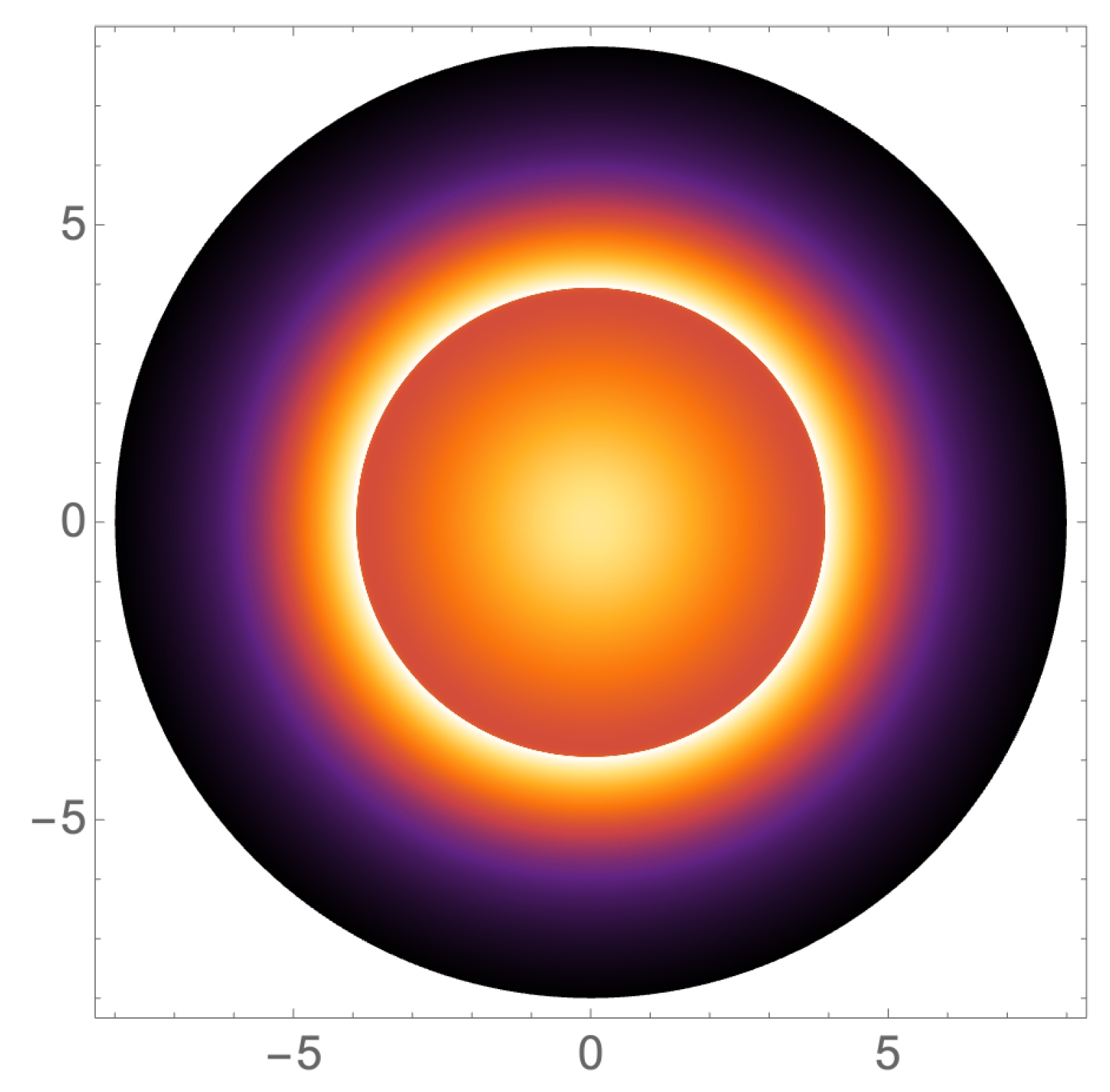
The numeric results of the observed intensity and the corresponding shadow images to the doppelgänge black holes are shown in Figure 6 and Figure 7. It shows that the doppelgänge black holes can be distinguished from the shadow images illuminated by the thin accretion disk model. This is mainly due to the different radii of their photon spheres and ISCOs, even for such black holes share the same horizon radii and mass.

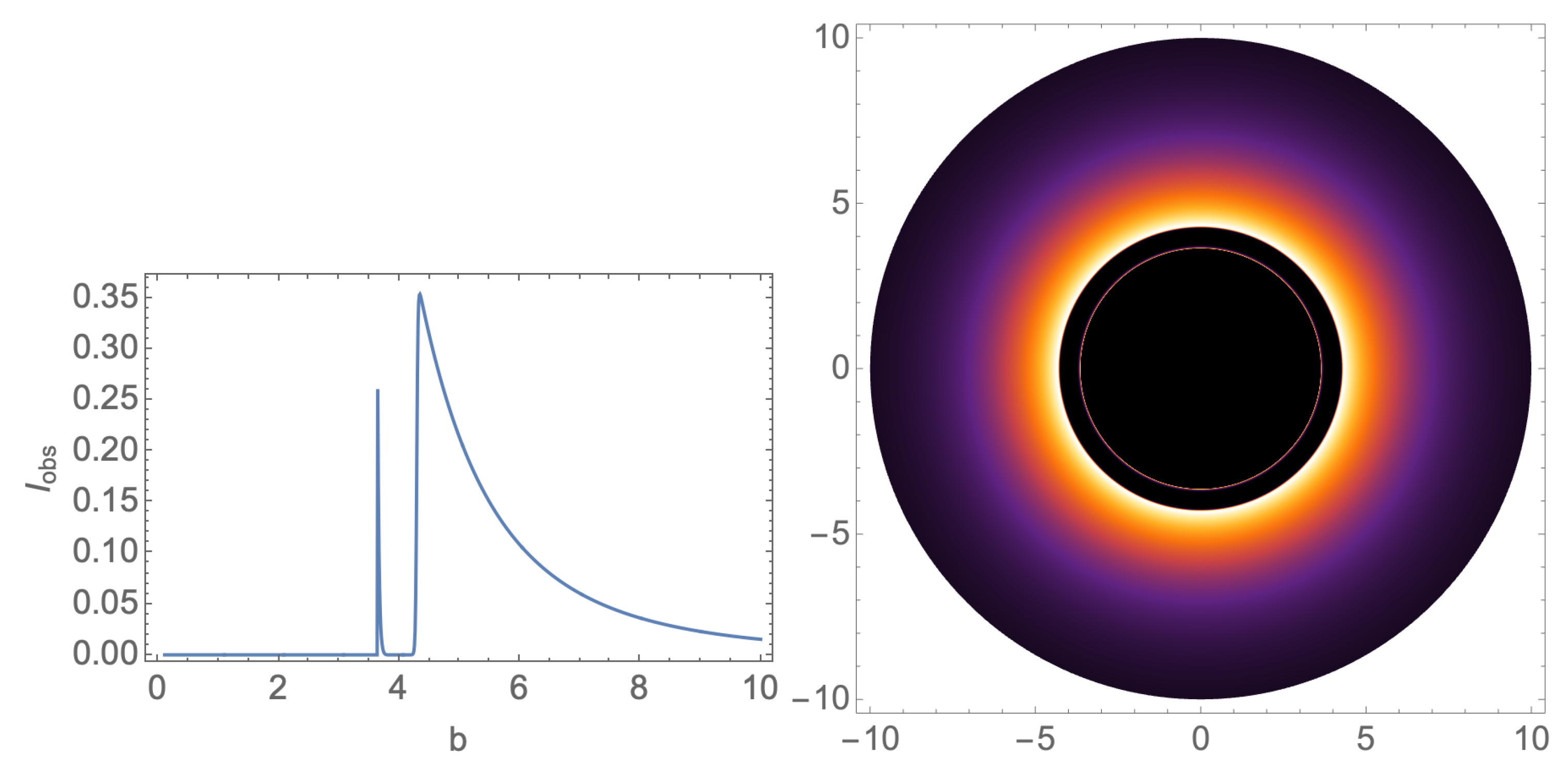
As we discuss above, the metric function $g_{rr}=f\left(r\right)$ are no longer monotonic increased in the large $Q_m$ case. In Figure 8, we present the results related to a large $Q_m$ case. We see, because of the unusual behavior of the metric function, there is no clear bright ring inside the shadow.

4.2. Static Spherical Accretion Model

Another possible accretion model in astrophysics is the spherical accretion flow model. As a ideal model, it usually consider the accretion distributed outside the black hole horizon with spherically.

To begin with, we consider the static accretion model. The observed specific intensity of photon with a frequency ${\nu }_o$ to an distant observer is given by [42,67]

$$\begin{array}{c}\hfill I\left({\nu }_o\right)=\int g^{3}j\left({\nu }_e\right)d{l}_{prop},\end{array}$$

(17)

where ${\nu }_e$ is the intrinsic photon frequency, $g={\displaystyle \frac{{\nu }_o}{{\nu }_e}}=\sqrt{h\left(r\right)}$ the red-shift factor, the infinitesimal proper length is denoted by $d{l}_{prop}$ and $j\left({\nu }_e\right)$ is the emissivity per unit volume in the rest frame of the emitter. Then total observed intensity is a sum up of all the possible specific intensity,

$$\begin{array}{c}\hfill I_{obs}^{ss}=\int I\left({\nu }_o\right)d{\nu }_o.\end{array}$$

(18)

Furthermore, we consider the radiation is monochromatic with fixed a frequency ${\nu }_f$, which means

$$\begin{array}{c}\hfill j_{{\nu }_e}\propto {\displaystyle \frac{\delta ({\nu }_e-{\nu }_f)}{r^2}}.\end{array}$$

(19)

Finally, the observed intensity (18) reduces to

$$\begin{array}{c}\hfill I_{obs}^{ss}=\int {\displaystyle \frac{h{\left(r\right)}^2}{r^2}}\sqrt{{\displaystyle \frac{1}{f\left(r\right)}}+{\displaystyle \frac{h\left(r\right)b^2}{f\left(r\right)(r^2-b^{2}h{\left(r\right)}^2)}}}dr.\end{array}$$

(20)

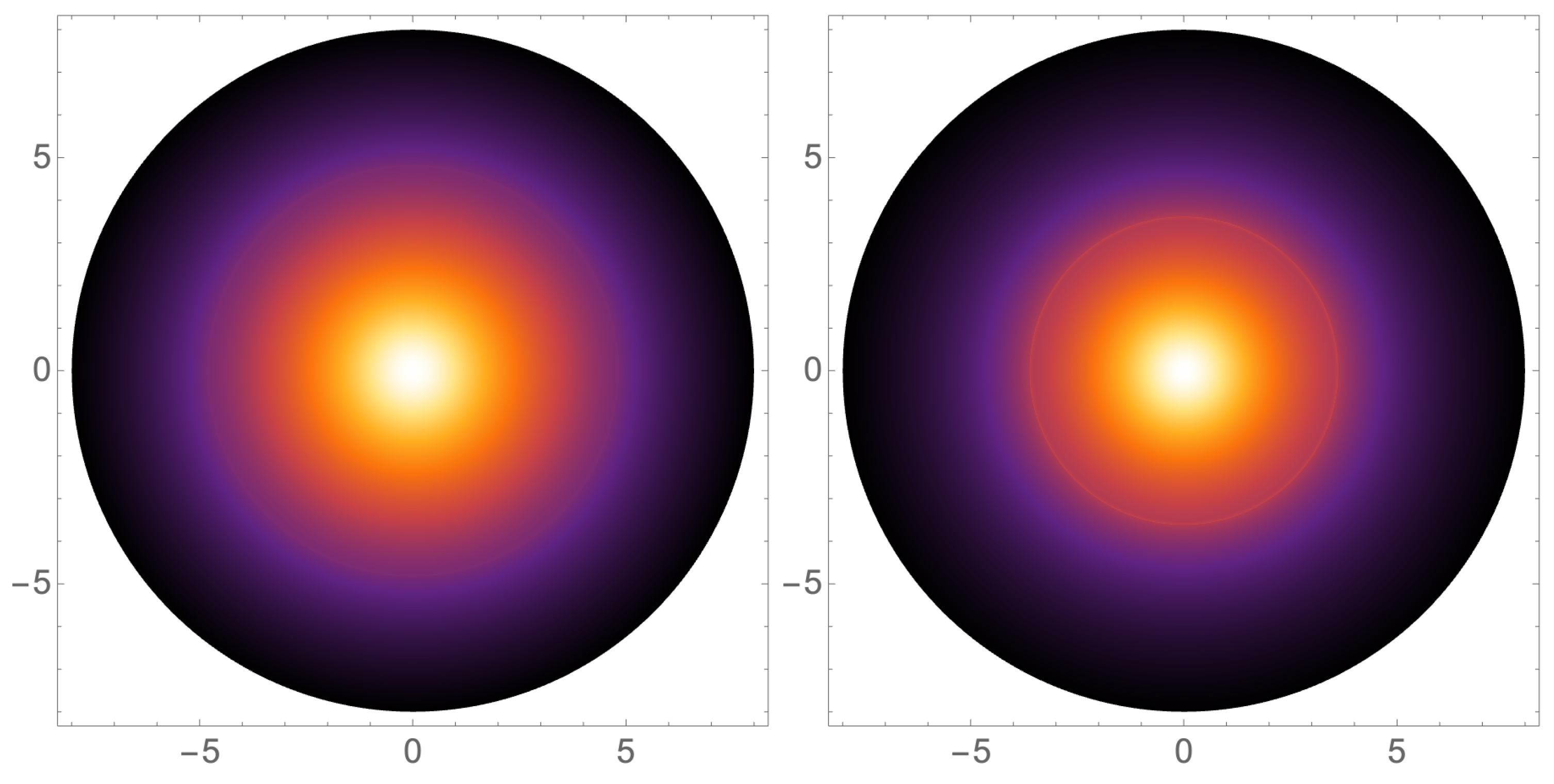
To the doppelgänge black holes, they give rise to different $I_{obs}^{ss}$. We show an example in Figure 9, and the related images are shown in Figure 10

The large $Q_m$ black holes do not reveal novel features in the static model, hence we don’t show them here. However, the more realistic case is that the matter falls into the horizon, namely the the infalling spherical accretion flow model. Then the large $Q_m$ black holes are quite different from the small $Q_m$ one.

4.3. Infalling Spherical Accretion Flow Model

The (18) is hold for infalling accretion case. But the red-shift factor depends the velocity of the accretion flow, namely,

$$\begin{array}{c}\hfill g={\displaystyle \frac{k_{\mu }{u}_o^{\mu }}{k_{\nu }{u}_e^{\nu }}},\end{array}$$

(21)

where $(k^{\mu },u_o^{\mu },u_e^{\nu })$ are the four-velocities of the photons, the stationary distant observers and the infaling accretion flow, respectively. It is straightforward to obtain all the non-vanished components of all the four-velocities are

$$\begin{array}{c}\hfill k_t={\displaystyle \frac{1}{b}},k_r=\sqrt{{\displaystyle \frac{1}{b^{2}h\left(r\right)f\left(r\right)}}-{\displaystyle \frac{1}{f\left(r\right)r^2}}},u_e^t={\displaystyle \frac{1}{h\left(r\right)}},u_e^r=-\sqrt{{\displaystyle \frac{f\left(r\right)}{h\left(r\right)}}-f\left(r\right)},\end{array}$$

(22)

and $u_o^{\mu }=(1,0,0,0)$. Finally, the observed intensity of the infalling accretion flow model is given by

$$\begin{array}{c}\hfill I_{obs}^{si}=\int {\displaystyle \frac{g^3}{r^2}}{\left(\sqrt{{\displaystyle \frac{1}{h\left(r\right)}}({\displaystyle \frac{1}{f\left(r\right)}}-{\displaystyle \frac{b^{2}h\left(r\right)}{f\left(r\right)r^2}})}\right)}^{-1}dr.\end{array}$$

(23)

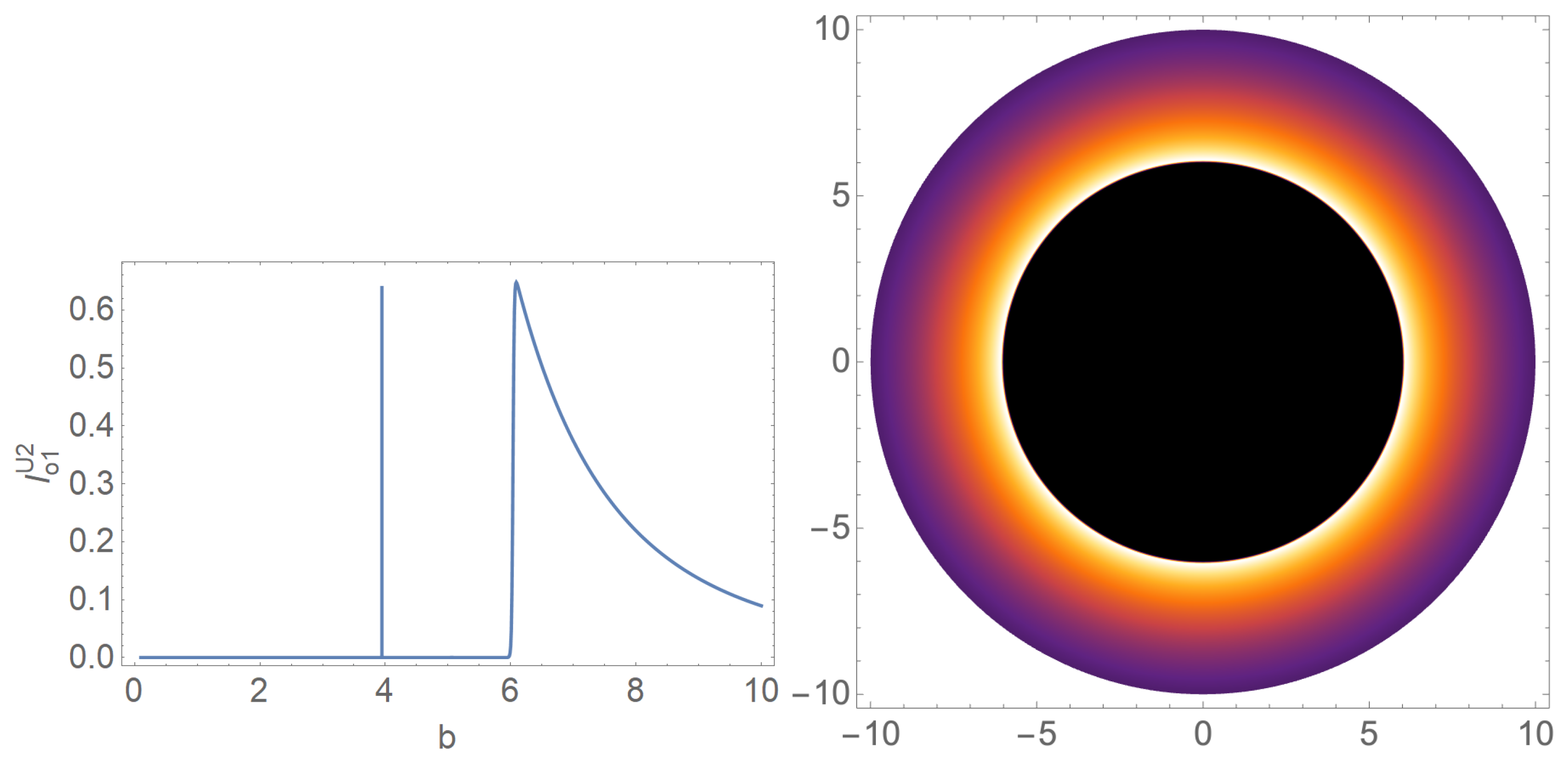
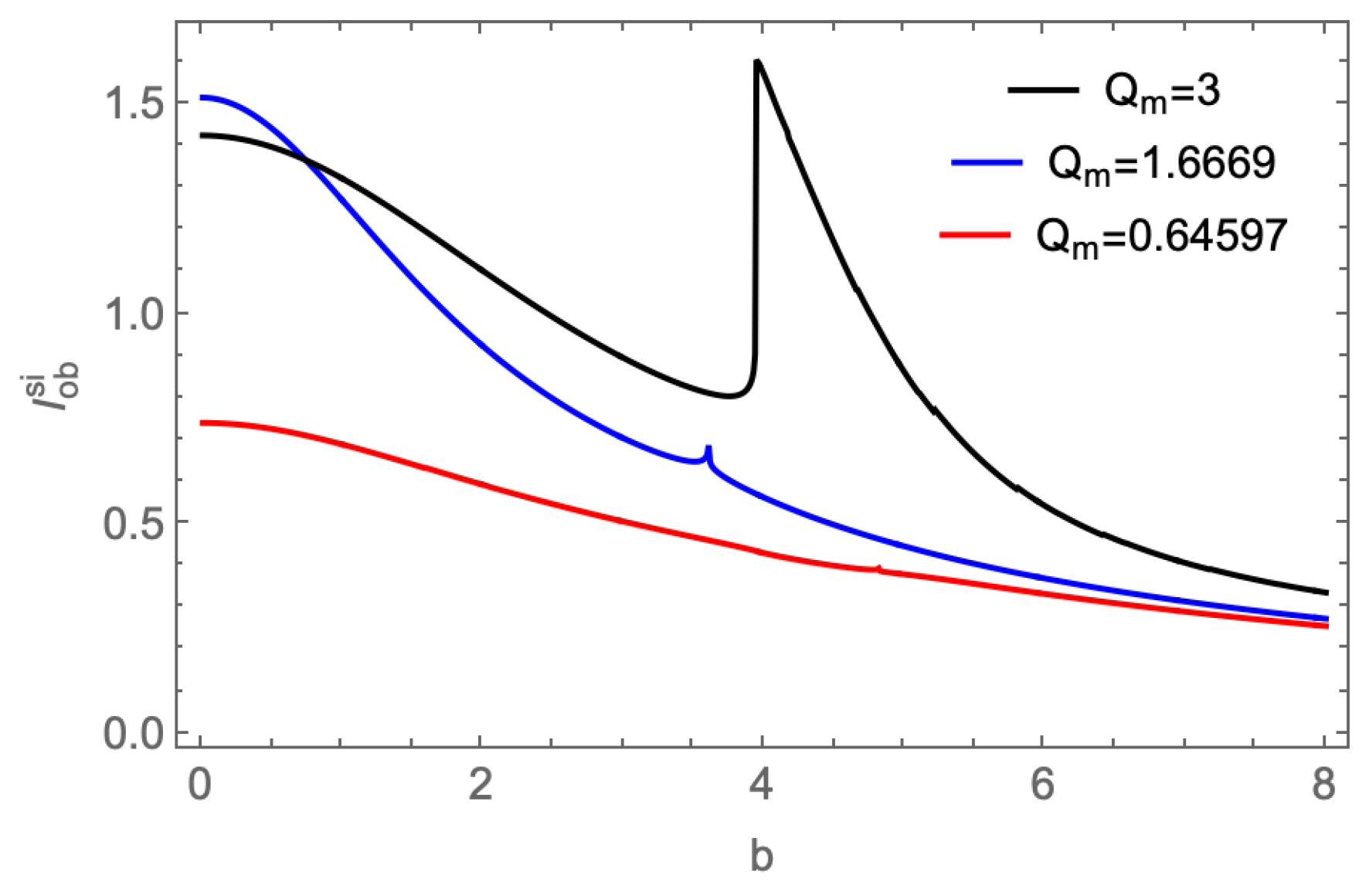
Three examples of the $I_{obs}^{si}$ corresponding to the doppelgänge black holes and large $Q_m$ black hole are shown in Figure 11. It it clear that the we could also distinguish the doppelgänge black holes in this model. Furthermore, the $I_{obs}^{si}$ of the large $Q_m$ black hole shows a distinct peak. We present the shadow images related to these cases in Figure 12.

5. Conclusion and Outlook

The phenomenon of having doppelgänge black holes in the string-inspired Euler-Heisenberg theory is quite attractive. In Ref.[64], the authors pointed out that a pair of the doppelgänge black holes could share different thermodynamics. In our work, we have investigated the optical appearances of such black holes in detail. The analysis of time-like and null geodesics is examined. We found even for the black holes have the same mass and horizon radii, the ISCOs and photon spheres are intrinsically different. It follows that the shadow images cast by the doppelgänge black holes could be also different. We have studied three types of accretion models, including the thin disk, static and infalling spherical flow accretions, to establish the shadow images. Our results reveal that one can easily identify the doppelgänge black holes by their optical appearances. It would be really helpful for future observations.

On the other hand, we found the black holes with large magnetic charge $Q_m$ in this theory play an intriguing property. Unlike the RN solution, the metric function $g_{rr}$ is non-monotonic with r. This fact leads the total deflection angle to be unusual. The repulsive effect arises in the vicinity of the photon sphere, which gives rise to an unclear bright ring inside the shadow. This would be a novel feature and can be detected in future observations.

For future works, one of the interesting directions is to explore the rotating doppelgänge black holes. It is a question that will the rotation affect the difference between the rotating doppelgänge black holes? Furthermore, astronomical black holes usually contain rotation, thus the results on the rotating doppelgänge black holes would be more realistic.

One would ask, are there doppelgänge black hole solutions apart from the string-inspired Euler-Heisenberg theory? Ignoring the no-hair conjecture, the answer could be “No". Then it is valuable to check the shadow properties of doppelgänge black holes in other theories. The results could be useful to clarify the gravitational theories.